Теорема Кронекера-Капелли — онлайн справочник для студентов
Рассмотрим систему из m линейных алгебраических уравнений (СЛАУ) с n неизвестными:
\(\ \left\{\begin{array}{l}{a_{11} x_{1}+a_{12} x_{2}+\ldots+a_{1 n} x_{n}=b_{1}} \\ {a_{21} x_{1}+a_{22} x_{2}+\ldots+a_{2 n} x_{n}=b_{2}} \\ {\dots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots} \\ {a_{m 1} x_{1}+a_{m 2} x_{2}+\ldots+a_{m n} x_{n}=b_{m}}\end{array}\right. \)
Выпишем основную матрицу этой системы \(\ \mathrm{A} \) и расширенную матрицу \(\ \overline{A} \):
\(\ A=\left( \begin{array}{cccc}{a_{11}} & {a_{12}} & {\cdots} & {a_{1 n}} \\ {a_{21}} & {a_{22}} & {\cdots} & {a_{2 n}} \\ {\ldots} & {\ldots} & {\ldots} & {\ldots} \\ {a_{m 1}} & {a_{m 2}} & {\cdots} & {a_{m n}}\end{array}\right) \), \(\ \overline{A}=\left( \begin{array}{ccccc}{a_{11}} & {a_{12}} & {\cdots} & {a_{1 n}} & {b_{1}} \\ {a_{21}} & {a_{22}} & {\cdots} & {a_{2 n}} & {b_{2}} \\ {\ldots} & {\cdots} & {\cdots} & {\cdots} & {\cdots} \\ {a_{m 1}} & {a_{m 2}} & {\cdots} & {a_{m n}} & {b_{m}}\end{array}\right) \)
Теорема
СЛАУ- согласуется тогда и только тогда, когда ранг его основной матрицы \(\ \mathrm{A} \) равен ранга его расширенной матрицы \(\ \overline{A} \):
\(\ r(A)=r(\overline{A}) \)
Более того, система имеет уникальное решение, если ранг равен числу неизвестных \(\ r(A)=r(A)=r(\overline{A})=n \) и бесконечному множеству решений, если ранг меньше числа неизвестных
ОПРЕДЕЛЕНИЕ
Рангом матрицы является максимальное число линейно независимых строк этой системы.
Ранг матрицы является наивысшим из порядков ненулевых миноров этой матрицы.
Правило вычисления ранга матрицы с использованием несовершеннолетних
При нахождении ранга матрицы необходимо перейти от миноров меньших порядков к несовершеннолетним высших порядков. Более того, если найден минор \(\ \mathrm{k}-\mathrm{го} \) порядка, определитель которого отличен от нуля, тогда требуется рассчитать только миноры \(\ (k+1)-r o \) порядка, граничащие с этим минором \(\ \mathrm{k}-\mathrm{го} \) порядка. Если все они равны нулю, то ранг матрицы равен \(\ k \).
Примеры решения проблем
ПРИМЕР 1
Чтобы исследовать систему совместимости:
\(\ \left\{\begin{array}{l}{2 x_{1}-x_{2}-3 x_{3}+x_{4}=1} \\ {x_{1}+2 x_{2}+4 x_{3}-x_{4}=2} \\ {4 x_{1}+3 x_{2}+5 x_{3}-x_{4}=5}\end{array}\right. \)
Выпишем основные и расширенные матрицы данной системы.
\(\ A=\left( \begin{array}{cccc}{2} & {-1} & {-3} & {1} \\ {1} & {2} & {4} & {-1} \\ {4} & {3} & {5} & {-1}\end{array}\right) \), \(\ \overline{A}=\left( \begin{array}{ccccc}{2} & {-1} & {-3} & {1} & {1} \\ {1} & {2} & {4} & {-1} & {2} \\ {4} & {3} & {5} & {-1} & {5}\end{array}\right) \)
Мы вычисляем ранги этих матриц с помощью несовершеннолетних.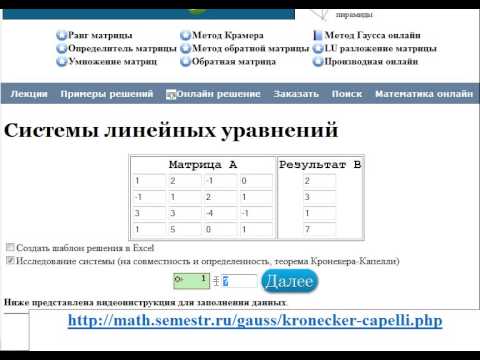
{123}=\left| \begin{array}{ccc}{2} & {-1} & {1} \\ {1} & {2} & {2} \\ {4} & {3} & {1}\end{array}\right|=-20 \neq 0
\)
Его определитель не равен нулю, поэтому ранг расширенной матрицы \(\ r(\overline{A})=3 \) .По теореме Кронекера-Капелли, поскольку \(\ r(A) \neq r(\overline{A}) \) , данная система линейных алгебраических уравнений несовместима и не имеет решений.
У этой системы линейных алгебраических уравнений нет решений.
ПРИМЕР 2
Проверьте, совместима ли система, если да, найдите ее решение:
\(\ \left\{\begin{array}{l}{x+y+z=2} \\ {2 x-2 y+z=6} \\ {x-y-z=0}\end{array}\right. \)
Выпишем основные и расширенные матрицы данной системы.
\(\ A=\left( \begin{array}{ccc}{1} & {1} & {1} \\ {2} & {-2} & {1} \\ {1} & {-1} & {-1}\end{array}\right) \), \(\ \overline{A}=\left( \begin{array}{cccc}{1} & {1} & {1} & {2} \\ {2} & {-2} & {1} & {6} \\ {1} & {-1} & {-1} & {0}\end{array}\right) \)
Мы вычисляем ранги этих матриц с использованием элементарных строковых преобразований.
Рассмотрим расширенную матрицу \(\
\overline{A}
\). Оставьте первую строку без изменений, добавьте первую строку, умноженную на \(\
(-2)
\) на вторую строку, добавьте первую строку, умноженную на \(\
(-1)
\), на третью строку, получим:
\(\ \left( \begin{array}{cccc}{1} & {1} & {1} & {2} \\ {2} & {-2} & {1} & {6} \\ {1} & {-1} & {-1} & {0}\end{array}\right) \sim \left( \begin{array}{cccc}{1} & {1} & {1} & {2} \\ {0} & {-4} & {-1} & {2} \\ {0} & {-2} & {-2} & {-2}\end{array}\right) \)
Затем мы оставляем первую строку неизменной, уменьшаем третью строку на \(\ (-2) \) и переставляем вторую и третью строки, получаем:
\(\ \left( \begin{array}{cccc}{1} & {1} & {1} & {2} \\ {2} & {-2} & {1} & {6} \\ {1} & {-1} & {-1} & {0}\end{array}\right) \sim \left( \begin{array}{cccc}{1} & {1} & {1} & {2} \\ {0} & {-4} & {-1} & {2} \\ {0} & {-2} & {-2} & {-2}\end{array}\right) \)
Оставьте первые две строки без изменений, добавьте второй, умноженный на 4, на третье:
\(\ \left( \begin{array}{cccc}{1} & {1} & {1} & {2} \\ {0} & {1} & {1} & {1} \\ {0} & {-4} & {-1} & {2}\end{array}\right) \sim \left( \begin{array}{cccc}{1} & {1} & {1} & {2} \\ {0} & {1} & {1} & {1} \\ {0} & {0} & {3} & {6}\end{array}\right) \)
Таким образом, матрицы \(\
A
\) и \(\
\overline{A}
\) имеют три линейно независимых ряда, поэтому их ранги равны \(\
r(A)=r(\overline{A})=3
\) .
\(\ \left\{\begin{array}{l}{x+y+z=2} \\ {y+z=1} \\ {3 z=6}\end{array}\right. \)
Вычислите значения неизвестных в последовательности. Из последнего уравнения получаем \(\ z=2 \). Подставляя это значение неизвестного во второе уравнение, получим:
\(\ y+2=1 \Rightarrow y=-1 \)
Теперь подставим значения неизвестных, найденные в первом уравнении:
\(\ x+(-1)+2=2 \Rightarrow x=1 \)
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Теорема Лагранжа Теорема синусов Теорема косинусов Теорема Виета
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое Принимаю Политику конфиденциальностиПодпишись на рассылку, чтобы не пропустить информацию об акциях
Элементы матрицы C4×5 заданы по вариантам.
Бесплатный доступ к решению задачЭлементы матрицы C4×5 заданы по вариантам: C=1431 -1013 242-2 495-3 1431 1. Считая матрицу C4×5 матрицей однородной системы C∙X=0, найти для этой системы: а) фундаментальную систему решений; б) общее решение; в) какое-нибудь частное решение. 2. Считая матрицу C4×5 расширенной матрицей неоднородной системы C*∙X=C**, где C=C*C**, решить эту систему, предварительно исследовав её совместность по теореме Кронекера-Капелли.
Решение
Потяни, чтобы посмотреть
Применяя к расширенной матрице, последовательность элементарных операций стремимся, чтобы каждая строка, кроме, быть может, первой, начиналась с нулей, и число нулей до первого ненулевого элемента в каждой следующей строке было больше, чем в предыдущей.
Запишем систему в виде расширенной матрицы:
1431 -1013 242-2 495-3 1431 0000→1000 -1444 2-4-4-4 4-7-7-7 1000 0000→1000 -1400 2-400 4-700 1000 0000
Теперь исходную систему можно записать как:
x1-x2+2×3+4×4+x5=04×2-4×3-7×4=0
Необходимо переменные x3, x4, x5 принять в качестве свободных переменных и через них выразить остальные переменные.
x1=-x3-2,25×4-x5x2=x3+1,75x4x3=x3x4=x4x5=x5
Заданная система уравнений имеет множество решений.
Подставим в качестве свободных переменных число 1.
Тогда при x3=1, x4=1, x5=1, получаем x1=-1-2,25∙1-1=-4,25×2=1+1,75∙1=2,75×3=1×4=1×5=1
Фундаментальное решение системы уравнений имеет вид: X=-4,252,75111
Частное решение системы уравнений при x3=x4=x5=0 имеет вид: X=00000
2 . Считая матрицу C4×5 расширенной матрицей неоднородной системы C*∙X=C**, где C=C*C**, решить эту систему, предварительно исследовав её совместность по теореме Кронекера-Капелли.
1431 -1013 242-2 495-3 1431
Исследуем совместность СУ по теореме Кронекера-Капелли.
Определим ранг основной матрицы:
rang 1431 -1013 242-2 495-3 1431=2
rang 1431 -1013 242-2 495-3=2
Следовательно, ранг основной и расширенной матрицы совпадает, и система уравнений является совместной.
Решим неоднородную систему уравнений: 1431 -1013 242-2 495-3 1431.
Применяя к расширенной матрице, последовательность элементарных операций стремимся, чтобы каждая строка, кроме, быть может, первой, начиналась с нулей, и число нулей до первого ненулевого элемента в каждой следующей строке было больше, чем в предыдущей.
Решение СЛАУ методом Гаусса.
Запишем систему в виде расширенной матрицы:
1431 -1013 242-2 495-3 1431→1000 -1444 2-4-4-4 4-7-7-7 1000→1000 -1400 2-400 4-700 1000
Теперь исходную систему можно записать как:
x1-x2+2×3+4×4=14×2-4×3-7×4=0
Из уравнения 2 системы найдем переменную x2:
x2=x3+1,75×4
Из уравнения 1 системы найдем переменную x1:
x1=1-x3-2,25×4
Для нахождения частного решения системы необходимо переменную x3, x4 принять в качестве свободной переменной и через нее выразить остальные переменные.
x1=1×2=0x3=0x4=0
Контрольная работа № 3.
Аналитическая геометрия.
теорема Руше-Капелли
теорема Руше-КапеллиНеобходимое и достаточное условие для того, чтобы система m уравнений и n неизвестных имела решение, состоит в том, что ранг ее матрицы коэффициентов равен рангу ее расширенной матрицы.
- $$r = r’$$ Совместимая система.
- $$r = r’= n$$ Определить совместимую систему.
- $$r = r’\neq n$$ Неопределенная совместимая система.
- $$r = r’= n$$ Определить совместимую систему.
- $$r \neq r’$$ Несовместимая система.
где, как мы сказали, $$r$$ — ранг матрицы системы, а $$r’$$ — ранг расширенной матрицы системы.
Очевидно, что для правильного использования вышеупомянутой теоремы необходимо усвоить, что такое ранг матрицы и как он вычисляется.
Когда техническая часть не вызывает затруднений, эта теорема позволяет нам обсуждать системы уравнений.
См. следующий пример:
Пусть система уравнений будет: $$$\left\{ \begin{array}{c} 2x-y-2z=-2 \\ -x+y+z=0 \\ x-2y+z=8 \\ 2x-2y=6 \ конец{массив} \right.$$$
1) Матрица коэффициентов и ранг равны
$$$\begin{pmatrix} 2 & -1 & -2 \\ -1 & 1 & 1 \\ 1 & -2 & 1 \\ 2 & -2 & 0 \end{pmatrix}$$$
(и ранг считается)
$$$|2|=2\neq0; \\\слева| \begin{matrix} 2 & -1 \\ -1 & 1 \end{matrix} \right|=1\neq0; \\\слева| \begin{matrix} 2 & -1 & -2 \\ -1 & 1 & 1 \\ 1 & -2 & 1 \end{matrix} \right|=2\neq0$$$
т.