Решение задач линейного программирования онлайн
Назначение сервиса. Онлайн-калькулятор предназначен для решения задач линейного программирования симплексным методом путем перехода к КЗЛП и СЗЛП. При этом задача на минимум целевой функции сводятся к задаче на поиск максимума через преобразование целевой функцииF*(X) = -F(X). Также имеется возможность составить двойственную задачу.
Решение происходит в три этапа:
- Переход к КЗЛП. Любая ЗЛП вида ax ≤ b, ax ≥ b, ax = b (F(X) → extr) сводится к виду ax = b, F(X) → max;
- Переход к СЗЛП. КЗЛП вида ax = b сводится к виду ax ≤ b, F(X) → max;
- Решение симплексным методом;
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Инструкция. Выберите количество переменных и количество строк (количество ограничений). Полученное решение сохраняется в файле Word.
Количество переменных
2345678910
Выберите количество переменных и количество строк (количество ограничений). Полученное решение сохраняется в файле Word.
Количество переменных
2345678910
Количество строк (количество ограничений)
12345678910
Как привести задачу линейного программирования к канонической форме
Как привести каноническую задачу линейного программирования к стандартной форме
F*(X) = -F(X). Обе задачи имеют одно и то же решение X*, и при этом min(F(X)) = -max(F*(X)).
Проиллюстрируем этот факт графически:
| F(x) → min |
F(x) → max |
Опорный план – план с определёнными через свободные базисными переменными.

Базисный план – опорный план с нулевыми базисными переменными.
Оптимальный план – базисный план, удовлетворяющий оптимальной функции цели (ФЦ).
Ведущий (разрешающий) элемент – коэффициент свободной неизвестной, которая становится базисной, а сам коэффициент преобразуется в единицу.
Направляющая строка – строка ведущего элемента, в которой расположена с единичным коэффициентом базисная неизвестная, исключаемая при преобразовании (строка с минимальным предельным коэффициентом, см. далее).
Направляющий столбец – столбец ведущего элемента, свободная неизвестная которого переводится в базисную (столбец с максимальной выгодой, см. далее).
Переменные x1, …, xm, входящие с единичными коэффициентами только в одно уравнение системы, с нулевыми – в остальные, называются базисными или зависимыми. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Переход осуществляется с помощью метода Гаусса–Жордана. Основная идея этого метода состоит в сведении системы m уравнений с n неизвестными к каноническому виду при помощи элементарных операций над строками.
Переход осуществляется с помощью метода Гаусса–Жордана. Основная идея этого метода состоит в сведении системы m уравнений с n неизвестными к каноническому виду при помощи элементарных операций над строками.
Остальные n-m переменных (xm+1,…, xn) называются небазисными или независимыми переменными.
Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных x j≥0, что эквивалентно условию неотрицательности bj≥0.
Допустимое базисное решение является угловой точкой допустимого множества S задачи линейного программирования и называется иногда опорным планом.
Если среди неотрицательных чисел bj есть равные нулю, то допустимое базисное решение называется вырожденным (вырожденной угловой точкой) и соответствующая задача линейного программирования называется вырожденной.
Пример №1. Свести задачу линейного программирования к стандартной ЗЛП.
F(X) = x1 + 2x2 — 2x3 → min при ограничениях:
4x1 + 3x2 — x3≤10
— 2x2 + 5x3≥3
x1 + 2x3=9
Для приведения ЗЛП к канонической форме необходимо:
4x1 + 3x2-1x3 + 1x4 + 0x5 = 10
0x1-2x2 + 5x3 + 0x4-1x5 = 3
1x1 + 0x2 + 2x3 + 0x4 + 0x5 = 9
F(X) = — x1 — 2x2 + 2x3
Переход к СЗЛП.

Расширенная матрица системы ограничений-равенств данной задачи:
| 4 | 3 | -1 | 1 | 0 | 10 |
| 0 | -2 | 5 | 0 | -1 | 3 |
| 1 | 0 | 2 | 0 | 0 | 9 |
Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x4.
2. В качестве базовой переменной выбираем x2.
Разрешающий элемент РЭ=-2. Строка, соответствующая переменной x2, получена в результате деления всех элементов строки x2 на разрешающий элемент РЭ=-2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули. Все остальные элементы определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
| 4-(0 • 3):-2 | 3-(-2 • 3):-2 | -1-(5 • 3):-2 | 1-(0 • 3):-2 | 0-(-1 • 3):-2 | 10-(3 • 3):-2 |
| -2 : -2 | 5 : -2 | 0 : -2 | -1 : -2 | 3 : -2 | |
| 1-(0 • 0):-2 | 0-(-2 • 0):-2 | 2-(5 • 0):-2 | 0-(0 • 0):-2 | 0-(-1 • 0):-2 | 9-(3 • 0):-2 |
Получаем новую матрицу:
| 4 | 0 | 61/2 | 1 | -11/2 | 141/2 |
| 0 | 1 | -21/2 | 0 | 1/2 | -11/2 |
| 1 | 0 | 2 | 0 | 0 | 9 |
3.
 В качестве базовой переменной выбираем x3.
В качестве базовой переменной выбираем x3.Разрешающий элемент РЭ=2. Строка, соответствующая переменной x3, получена в результате деления всех элементов строки x3 на разрешающий элемент РЭ=2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x3 записываем нули. Все остальные элементы определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
| 4-(1 • 61/2):2 | 0-(0 • 61/2):2 | 61/2-(2 • 61/2):2 | 1-(0 • 61/2):2 | 141/2-(9 • 61/2):2 | |
| 0-(1 • -21/2):2 | 1-(0 • -21/2):2 | -21/2-(2 • -21/2):2 | 0-(0 • -21/2):2 | 1/2-(0 • -21/2):2 | -11/2-(9 • -21/2):2 |
| 1 : 2 | 0 : 2 | 2 : 2 | 0 : 2 | 0 : 2 | 9 : 2 |
Получаем новую матрицу:
| 3/4 | 0 | 0 | 1 | -11/2 | -143/4 |
| 11/4 | 1 | 0 | 0 | 1/2 | 93/4 |
| 1/2 | 0 | 1 | 0 | 0 | 41/2 |
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (4,2,3).

Соответствующие уравнения имеют вид:
3/4x1 + x4 — 11/2x5 = -143/4
11/4x
1/2x1 + x3 = 41/2
Выразим базисные переменные через остальные:
x4 = — 3/4x1 + 11/2x5-143/4
x2 = — 11/4x1 — 1/2x5+93/4
x3 = — 1/2x1+41/2
Подставим их в целевую функцию:
F(X) = — x1 — 2(- 11/4x1 — 1/2x5+93/4) + 2(- 1/2x1+41/2)
или
F(X) = 1/2x1 + x5-101/2 → max
Система неравенств:
— 3/4x1 + 11/2x5-143/4 ≥ 0
— 11/4x1 — 1/2x5+93/4 ≥ 0
— 1/2x1+41/2 ≥ 0
Приводим систему неравенств к следующему виду:
3/4x1 — 11/2x5 ≤ -143/4
11/4x1 + 1/2x5 ≤ 93/4
1/2x1 ≤ 41/2
F(X) = 1/2x1 + x5-101/2 → max
Упростим систему.

3/4x1 — 11/2x2 ≤ -143/4
11/4x1 + 1/2x2 ≤ 93/4
1/2x1 ≤ 41/2
F(X) = 1/2x1 + x2-101/2 → max
Пример №2. Найдите сначала графическим методом, а затем симплекс-методом решение задачи
F(X) = x1 + x2 — x3 + x5+15 → max (min) при ограничениях:
-3x1 + x2 + x3=3
4x1 + 2x2 — x4=12
2x1 — x2 + x5=2
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0, x5 ≥ 0
Онлайн Калькулятор: Симплекс Метод
F(x) = 3x1 + 4x2 → max
| 000 | 2x1 + x2 ≤ 600 |
| 0x1 + 0x2 ≤ 225 | |
| 5x1 +4x2 ≤ 1000 | |
| 2x2 ≥ 150 | |
| 0x1 + 0x2 ≥ 0 |
F(x) = 3x1 + 4x2 + 0x3 + 0x4 + 0x5 + 0x6 + 0x7 — Mx8 — Mx9 → max
| 000 | 2x1 + x2 + x3 = 600 |
| + x4 = 225 | |
| 5x1 + 4x2 + x5 = 1000 | |
| 2x2 — x6 + x8 = 150 | |
| — x7 + x9 = 0 |
Предварительный этап:
Предварительный этап начинается с того что необходимо избавиться от отрицательных значений(если таковые имеются) в правой части ограничений. Для чего соответствующие ограничения умножаем на -1. После данной манипуляции знак неравенства меняем на противоположный.
Для чего соответствующие ограничения умножаем на -1. После данной манипуляции знак неравенства меняем на противоположный.
Далее необходимо избавиться от неравенств, для чего в левую часть неравенств вводим компенсирующие переменные. Если неравенство вида ≤, то компенсирующая переменная имеет знак +, если неравенство вида ≥, то компенсирующая переменная имеет знак -. Компенсирующие переменные входят в целевую функцию задачи с нулевым коэффициентом.
Теперь в системе ограничений необходимо найти достаточное количество базисных переменных. В каждом ограничении должна быть одна базисная переменная. Базисной является переменная, которая имеет при себе коэффициент 1 и встречается только в одном ограничении. Если в каком-то ограничении нет базисных переменных, то добавляем их искусственно, причем искусственные переменные входят в целевую функцию с коэффициентом -M, если целевая функция стремится к мах и с М, если целевая функция стремится к min.
Итерация: 1
| B | Cb | P | x1 | x2↓ | x3 | x4 | x5 | x6 | x7 | x8 | x9 | Q |
| 3 | 4 | 0 | 0 | 0 | 0 | 0 | -M | -M | ||||
| x3 | 0 | 600 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 600 |
| x4 | 0 | 225 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ∞ |
| x5 | 0 | 1000 | 5 | 4 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 250 |
| x8 ← | -M | 150 | 0 | 2 | 0 | 0 | 0 | -1 | 0 | 1 | 0 | 75 |
| x9 | -M | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 1 | ∞ |
| max | -150M | -3 | -2M-4 | 0 | 0 | 0 | M | M | 0 | 0 | ||
Вычисление элементов таблицы:
Элементы колонки базис(B)
Переносим в таблицу базовые элементы, которые мы определили на предварительном этапе:
B1 = x3;
B2 = x4;
B3 = x5;
B4 = x8;
B5 = x9;
Элементы колонки Cb
Каждая ячейка этого столбца равна коэффициенту, который соответствует базовой переменной в соответствующей строке.
Cb1 = 0;
Cb2 = 0;
Cb3 = 0;
Cb4 = -M;
Cb5 = -M;
Значения упрявляемых переменных и колонки P
На данном этапе никаких вычислений не нужно, просто переносим значения из предварительного этапа в соответствующие ячейки таблицы:
P1 = 600;
P2 = 225;
P3 = 1000;
P4 = 150;
P5 = 0;
x1,1 = 2;
x1,2 = 1;
x1,3 = 1;
x1,4 = 0;
x1,5 = 0;
x1,6 = 0;
x1,7 = 0;
x1,8 = 0;
x1,9 = 0;
x2,1 = 0;
x2,2 = 0;
x2,3 = 0;
x2,4 = 1;
x2,5 = 0;
x2,6 = 0;
x2,7 = 0;
x2,8 = 0;
x2,9 = 0;
x3,1 = 5;
x3,2 = 4;
x3,3 = 0;
x3,4 = 0;
x3,5 = 1;
x3,6 = 0;
x3,7 = 0;
x3,8 = 0;
x3,9 = 0;
x4,1 = 0;
x4,2 = 2;
x4,3 = 0;
x4,4 = 0;
x4,5 = 0;
x4,6 = -1;
x4,7 = 0;
x4,8 = 1;
x4,9 = 0;
x5,1 = 0;
x5,2 = 0;
x5,3 = 0;
x5,4 = 0;
x5,5 = 0;
x5,6 = 0;
x5,7 = -1;
x5,8 = 0;
x5,9 = 1;
Значение целевой функции
Рассчитываем значение целевой функции, поэлементно умножая столбик Cb на столбик P, сложив результаты произведений.
MaxP = (Cb1 * P1) + (Cb11 * P2 + (Cb21 * P3 + (Cb31 * P4 + (Cb41 * P5 = (0 * 600) + (0 * 225) + (0 * 1000) + (-M * 150) + (-M * 0) = -150M;
Оценки управляемых переменных
Рассчитываем оценки для каждой управляемой переменной, поэлементно умножив значение с колонки переменной, на значение с колонки Cb, суммируем результаты произведений, и с их суммы вычитаем коэффициент целевой функции, при этой переменной.
Maxx1 = ((Cb1 * x1,1) + (Cb2 * x2,1) + (Cb3 * x3,1) + (Cb4 * x4,1) + (Cb5 * x5,1) ) — kx1 = ((0 * 2) + (0 * 0) + (0 * 5) + (-M * 0) + (-M * 0) ) — 3 = -3;
Maxx2 = ((Cb1 * x1,2) + (Cb2 * x2,2) + (Cb3 * x3,2) + (Cb4 * x4,2) + (Cb5 * x5,2) ) — kx2 = ((0 * 1) + (0 * 0) + (0 * 4) + (-M * 2) + (-M * 0) ) — 4 = -2M-4;
Maxx3 = ((Cb1 * x1,3) + (Cb2 * x2,3) + (Cb3 * x3,3) + (Cb4 * x4,3) + (Cb5 * x5,3) ) — kx3 = ((0 * 1) + (0 * 0) + (0 * 0) + (-M * 0) + (-M * 0) ) — 0 = 0;
Maxx4 = ((Cb1 * x1,4) + (Cb2 * x2,4) + (Cb3 * x3,4) + (Cb4 * x4,4) + (Cb5 * x5,4) ) — kx4 = ((0 * 0) + (0 * 1) + (0 * 0) + (-M * 0) + (-M * 0) ) — 0 = 0;
Maxx5 = ((Cb1 * x1,5) + (Cb2 * x2,5) + (Cb3 * x3,5) + (Cb4 * x4,5) + (Cb5 * x5,5) ) — kx5 = ((0 * 0) + (0 * 0) + (0 * 1) + (-M * 0) + (-M * 0) ) — 0 = 0;
Maxx6 = ((Cb1 * x1,6) + (Cb2 * x2,6) + (Cb3 * x3,6) + (Cb4 * x4,6) + (Cb5 * x5,6) ) — kx6 = ((0 * 0) + (0 * 0) + (0 * 0) + (-M * -1) + (-M * 0) ) — 0 = M;
Maxx7 = ((Cb1 * x1,7) + (Cb2 * x2,7) + (Cb3 * x3,7) + (Cb4 * x4,7) + (Cb5 * x5,7) ) — kx7 = ((0 * 0) + (0 * 0) + (0 * 0) + (-M * 0) + (-M * -1) ) — 0 = M;
Maxx8 = ((Cb1 * x1,8) + (Cb2 * x2,8) + (Cb3 * x3,8) + (Cb4 * x4,8) + (Cb5 * x5,8) ) — kx8 = ((0 * 0) + (0 * 0) + (0 * 0) + (-M * 1) + (-M * 0) ) — -M = 0;
Maxx9 = ((Cb1 * x1,9) + (Cb2 * x2,9) + (Cb3 * x3,9) + (Cb4 * x4,9) + (Cb5 * x5,9) ) — kx9 = ((0 * 0) + (0 * 0) + (0 * 0) + (-M * 0) + (-M * 1) ) — -M = 0;
Элементы колонки Q
Поскольку среди оценок управляемых переменных есть отрицательные значения, текущая таблица еще не имеет оптимального решения. Поэтому в базис введем переменную с наименьшей отрицательной оценкой.
Поэтому в базис введем переменную с наименьшей отрицательной оценкой.
Количество переменных в базисе всегда постоянно, поэтому необходимо выбрать, какую переменную вывести из базиса, для чего мы рассчитываем Q.
Элементы столбика Q рассчитываем поделив значения из колонки P на значение с колонки, соответствующие переменной которая вводится в базис:
Q1 = P1 / x1,2 = 600 / 1 = 600;
Q2 = P2 / x2,2 = 225 / 0 = ∞;
Q3 = P3 / x3,2 = 1000 / 4 = 250;
Q4 = P4 / x4,2 = 150 / 2 = 75;
Q5 = P5 / x5,2 = 0 / 0 = ∞;
Выводим из базиса переменную с наименьшим положительным значением Q.
На пересечении строки, которая соответствует переменной что выводится из базиса, и столбца который соответствует переменной что вводится в базис, расположен разрешающий элемент.
Данный элемент позволит нам рассчитать элементы таблицы следующей итерации.
Итерация: 2
| B | Cb | P | x1↓ | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | Q |
| 3 | 4 | 0 | 0 | 0 | 0 | 0 | -M | -M | ||||
| x3 | 0 | 525 | 2 | 0 | 1 | 0 | 0 | 0.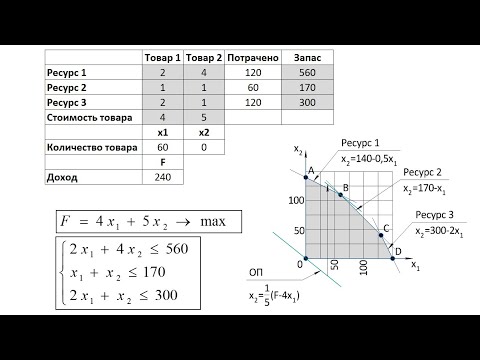 5 5 | 0 | -0.5 | 0 | 262.5 |
| x4 | 0 | 225 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ∞ |
| x5 ← | 0 | 700 | 5 | 0 | 0 | 0 | 1 | 2 | 0 | -2 | 0 | 140 |
| x2 | 4 | 75 | 0 | 1 | 0 | 0 | 0 | -0. 5 5 | 0 | 0.5 | 0 | ∞ |
| x9 | -M | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 1 | ∞ |
| max | 300 | -3 | 0 | 0 | 0 | 0 | -2 | M | M+2 | 0 | ||
Вычисление элементов таблицы:
Элементы колонки базис(B)
За результатами вычислений предыдущей итерации убираем с базиса переменную x8 и ставим на ее место x2. Все остальные ячейки остаются без изменений.
Все остальные ячейки остаются без изменений.
Элементы колонки Cb
Каждая ячейка этого столбца равна коэффициенту, который соответствует базовой переменной в соответствующей строке.
Cb1 = 0;
Cb2 = 0;
Cb3 = 0;
Cb4 = 4;
Cb5 = -M;
Значения упрявляемых переменных и колонки P(В качестве исходных данных берутся данные из предыдущей итерации)
Заполняем нулями все ячейки, соответствующие переменной, которая только что была введена в базис:(Разрешающий элемент остается без изменений)
x1,2 = 0;
x2,2 = 0;
x3,2 = 0;
x5,2 = 0;
Переносим в текущую таблицу строку с разрешающим элементом с предыдущей таблицы, поэлементно поделив ее значения на разрешающий элемент:
P4 = P4 / x4,2 = 150 / 2 = 75;
x4,1 = x4,1 / x4,2 = 0 / 2 = 0;
x4,2 = x4,2 / x4,2 = 2 / 2 = 1;
x4,3 = x4,3 / x4,2 = 0 / 2 = 0;
x4,4 = x4,4 / x4,2 = 0 / 2 = 0;
x4,5 = x4,5 / x4,2 = 0 / 2 = 0;
x4,6 = x4,6 / x4,2 = -1 / 2 = -0. 5;
5;
x4,7 = x4,7 / x4,2 = 0 / 2 = 0;
x4,8 = x4,8 / x4,2 = 1 / 2 = 0.5;
x4,9 = x4,9 / x4,2 = 0 / 2 = 0;
Остальные пустые ячейки, за исключением строки оценок и колонки Q, рассчитываем методом прямоугольника, относительно разрешающего элемента:
P1 = (P1 * x4,2) — (x1,2 * P4) / x4,2 = ((600 * 2) — (1 * 150)) / 2 = 525;
P2 = (P2 * x4,2) — (x2,2 * P4) / x4,2 = ((225 * 2) — (0 * 150)) / 2 = 225;
P3 = (P3 * x4,2) — (x3,2 * P4) / x4,2 = ((1000 * 2) — (4 * 150)) / 2 = 700;
P5 = (P5 * x4,2) — (x5,2 * P4) / x4,2 = ((0 * 2) — (0 * 150)) / 2 = 0;
x1,1 = ((x1,1 * x4,2) — (x1,2 * x4,1)) / x4,2 = ((2 * 2) — (1 * 0)) / 2 = 2;
x1,2 = ((x1,2 * x4,2) — (x1,2 * x4,2)) / x4,2 = ((1 * 2) — (1 * 2)) / 2 = 0;
x1,4 = ((x1,4 * x4,2) — (x1,2 * x4,4)) / x4,2 = ((0 * 2) — (1 * 0)) / 2 = 0;
x1,5 = ((x1,5 * x4,2) — (x1,2 * x4,5)) / x4,2 = ((0 * 2) — (1 * 0)) / 2 = 0;
x1,6 = ((x1,6 * x4,2) — (x1,2 * x4,6)) / x4,2 = ((0 * 2) — (1 * -1)) / 2 = 0. 5;
5;
x1,7 = ((x1,7 * x4,2) — (x1,2 * x4,7)) / x4,2 = ((0 * 2) — (1 * 0)) / 2 = 0;
x1,8 = ((x1,8 * x4,2) — (x1,2 * x4,8)) / x4,2 = ((0 * 2) — (1 * 1)) / 2 = -0.5;
x1,9 = ((x1,9 * x4,2) — (x1,2 * x4,9)) / x4,2 = ((0 * 2) — (1 * 0)) / 2 = 0;
x2,1 = ((x2,1 * x4,2) — (x2,2 * x4,1)) / x4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
x2,2 = ((x2,2 * x4,2) — (x2,2 * x4,2)) / x4,2 = ((0 * 2) — (0 * 2)) / 2 = 0;
x2,4 = ((x2,4 * x4,2) — (x2,2 * x4,4)) / x4,2 = ((1 * 2) — (0 * 0)) / 2 = 1;
x2,5 = ((x2,5 * x4,2) — (x2,2 * x4,5)) / x4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
x2,6 = ((x2,6 * x4,2) — (x2,2 * x4,6)) / x4,2 = ((0 * 2) — (0 * -1)) / 2 = 0;
x2,7 = ((x2,7 * x4,2) — (x2,2 * x4,7)) / x4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
x2,8 = ((x2,8 * x4,2) — (x2,2 * x4,8)) / x4,2 = ((0 * 2) — (0 * 1)) / 2 = 0;
x2,9 = ((x2,9 * x4,2) — (x2,2 * x4,9)) / x4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
x3,1 = ((x3,1 * x4,2) — (x3,2 * x4,1)) / x4,2 = ((5 * 2) — (4 * 0)) / 2 = 5;
x3,2 = ((x3,2 * x4,2) — (x3,2 * x4,2)) / x4,2 = ((4 * 2) — (4 * 2)) / 2 = 0;
x3,4 = ((x3,4 * x4,2) — (x3,2 * x4,4)) / x4,2 = ((0 * 2) — (4 * 0)) / 2 = 0;
x3,5 = ((x3,5 * x4,2) — (x3,2 * x4,5)) / x4,2 = ((1 * 2) — (4 * 0)) / 2 = 1;
x3,6 = ((x3,6 * x4,2) — (x3,2 * x4,6)) / x4,2 = ((0 * 2) — (4 * -1)) / 2 = 2;
x3,7 = ((x3,7 * x4,2) — (x3,2 * x4,7)) / x4,2 = ((0 * 2) — (4 * 0)) / 2 = 0;
x3,8 = ((x3,8 * x4,2) — (x3,2 * x4,8)) / x4,2 = ((0 * 2) — (4 * 1)) / 2 = -2;
x3,9 = ((x3,9 * x4,2) — (x3,2 * x4,9)) / x4,2 = ((0 * 2) — (4 * 0)) / 2 = 0;
x5,1 = ((x5,1 * x4,2) — (x5,2 * x4,1)) / x4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
x5,2 = ((x5,2 * x4,2) — (x5,2 * x4,2)) / x4,2 = ((0 * 2) — (0 * 2)) / 2 = 0;
x5,4 = ((x5,4 * x4,2) — (x5,2 * x4,4)) / x4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
x5,5 = ((x5,5 * x4,2) — (x5,2 * x4,5)) / x4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
x5,6 = ((x5,6 * x4,2) — (x5,2 * x4,6)) / x4,2 = ((0 * 2) — (0 * -1)) / 2 = 0;
x5,7 = ((x5,7 * x4,2) — (x5,2 * x4,7)) / x4,2 = ((-1 * 2) — (0 * 0)) / 2 = -1;
x5,8 = ((x5,8 * x4,2) — (x5,2 * x4,8)) / x4,2 = ((0 * 2) — (0 * 1)) / 2 = 0;
x5,9 = ((x5,9 * x4,2) — (x5,2 * x4,9)) / x4,2 = ((1 * 2) — (0 * 0)) / 2 = 1;
Значение целевой функции
Рассчитываем значение целевой функции, поэлементно умножая столбик Cb на столбик P, сложив результаты произведений.
MaxP = (Cb1 * P1) + (Cb11 * P2 + (Cb21 * P3 + (Cb31 * P4 + (Cb41 * P5 = (0 * 525) + (0 * 225) + (0 * 700) + (4 * 75) + (-M * 0) = 300;
Оценки управляемых переменных
Рассчитываем оценки для каждой управляемой переменной, поэлементно умножив значение с колонки переменной, на значение с колонки Cb, суммируем результаты произведений, и с их суммы вычитаем коэффициент целевой функции, при этой переменной.
Maxx1 = ((Cb1 * x1,1) + (Cb2 * x2,1) + (Cb3 * x3,1) + (Cb4 * x4,1) + (Cb5 * x5,1) ) — kx1 = ((0 * 2) + (0 * 0) + (0 * 5) + (4 * 0) + (-M * 0) ) — 3 = -3;
Maxx2 = ((Cb1 * x1,2) + (Cb2 * x2,2) + (Cb3 * x3,2) + (Cb4 * x4,2) + (Cb5 * x5,2) ) — kx2 = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 1) + (-M * 0) ) — 4 = 0;
Maxx3 = ((Cb1 * x1,3) + (Cb2 * x2,3) + (Cb3 * x3,3) + (Cb4 * x4,3) + (Cb5 * x5,3) ) — kx3 = ((0 * 1) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * 0) ) — 0 = 0;
Maxx4 = ((Cb1 * x1,4) + (Cb2 * x2,4) + (Cb3 * x3,4) + (Cb4 * x4,4) + (Cb5 * x5,4) ) — kx4 = ((0 * 0) + (0 * 1) + (0 * 0) + (4 * 0) + (-M * 0) ) — 0 = 0;
Maxx5 = ((Cb1 * x1,5) + (Cb2 * x2,5) + (Cb3 * x3,5) + (Cb4 * x4,5) + (Cb5 * x5,5) ) — kx5 = ((0 * 0) + (0 * 0) + (0 * 1) + (4 * 0) + (-M * 0) ) — 0 = 0;
Maxx6 = ((Cb1 * x1,6) + (Cb2 * x2,6) + (Cb3 * x3,6) + (Cb4 * x4,6) + (Cb5 * x5,6) ) — kx6 = ((0 * 0. 5) + (0 * 0) + (0 * 2) + (4 * -0.5) + (-M * 0) ) — 0 = -2;
5) + (0 * 0) + (0 * 2) + (4 * -0.5) + (-M * 0) ) — 0 = -2;
Maxx7 = ((Cb1 * x1,7) + (Cb2 * x2,7) + (Cb3 * x3,7) + (Cb4 * x4,7) + (Cb5 * x5,7) ) — kx7 = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * -1) ) — 0 = M;
Maxx8 = ((Cb1 * x1,8) + (Cb2 * x2,8) + (Cb3 * x3,8) + (Cb4 * x4,8) + (Cb5 * x5,8) ) — kx8 = ((0 * -0.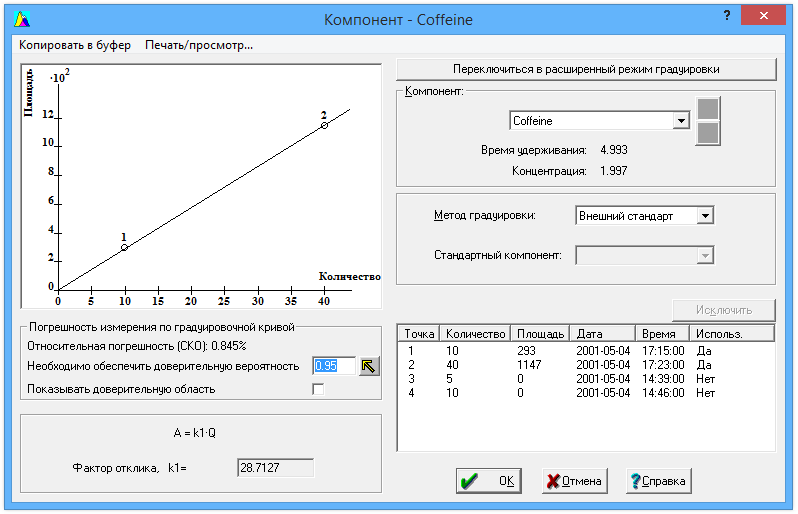 5) + (0 * 0) + (0 * -2) + (4 * 0.5) + (-M * 0) ) — -M = M+2;
5) + (0 * 0) + (0 * -2) + (4 * 0.5) + (-M * 0) ) — -M = M+2;
Maxx9 = ((Cb1 * x1,9) + (Cb2 * x2,9) + (Cb3 * x3,9) + (Cb4 * x4,9) + (Cb5 * x5,9) ) — kx9 = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * 1) ) — -M = 0;
Элементы колонки Q
Поскольку среди оценок управляемых переменных есть отрицательные значения, текущая таблица еще не имеет оптимального решения. Поэтому в базис введем переменную с наименьшей отрицательной оценкой.
Количество переменных в базисе всегда постоянно, поэтому необходимо выбрать, какую переменную вывести из базиса, для чего мы рассчитываем Q.
Элементы столбика Q рассчитываем поделив значения из колонки P на значение с колонки, соответствующие переменной которая вводится в базис:
Q1 = P1 / x1,1 = 525 / 2 = 262.5;
Q2 = P2 / x2,1 = 225 / 0 = ∞;
Q3 = P3 / x3,1 = 700 / 5 = 140;
Q4 = P4 / x4,1 = 75 / 0 = ∞;
Q5 = P5 / x5,1 = 0 / 0 = ∞;
Выводим из базиса переменную с наименьшим положительным значением Q.
На пересечении строки, которая соответствует переменной что выводится из базиса, и столбца который соответствует переменной что вводится в базис, расположен разрешающий элемент.
Данный элемент позволит нам рассчитать элементы таблицы следующей итерации.
Итерация: 3
| B | Cb | P | x1 | x2 | x3 | x4 | x5 | x6↓ | x7 | x8 | x9 | Q |
| 3 | 4 | 0 | 0 | 0 | 0 | 0 | -M | -M | ||||
| x3 | 0 | 245 | 0 | 0 | 1 | 0 | -0. 4 4 | -0.3 | 0 | 0.3 | 0 | -816.67 |
| x4 | 0 | 225 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ∞ |
| x1 ← | 3 | 140 | 1 | 0 | 0 | 0 | 0.2 | 0.4 | 0 | -0. 4 4 | 0 | 350 |
| x2 | 4 | 75 | 0 | 1 | 0 | 0 | 0 | -0.5 | 0 | 0.5 | 0 | -150 |
| x9 | -M | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 1 | ∞ |
| max | 720 | 0 | 0 | 0 | 0 | 0. 6 6 | -0.8 | M | M+0.8 | 0 | ||
Вычисление элементов таблицы:
Элементы колонки базис(B)
За результатами вычислений предыдущей итерации убираем с базиса переменную x5 и ставим на ее место x1. Все остальные ячейки остаются без изменений.
Элементы колонки Cb
Каждая ячейка этого столбца равна коэффициенту, который соответствует базовой переменной в соответствующей строке.
Cb1 = 0;
Cb2 = 0;
Cb3 = 3;
Cb4 = 4;
Cb5 = -M;
Значения упрявляемых переменных и колонки P(В качестве исходных данных берутся данные из предыдущей итерации)
Заполняем нулями все ячейки, соответствующие переменной, которая только что была введена в базис:(Разрешающий элемент остается без изменений)
x1,1 = 0;
x2,1 = 0;
x4,1 = 0;
x5,1 = 0;
Переносим в текущую таблицу строку с разрешающим элементом с предыдущей таблицы, поэлементно поделив ее значения на разрешающий элемент:
P3 = P3 / x3,1 = 700 / 5 = 140;
x3,1 = x3,1 / x3,1 = 5 / 5 = 1;
x3,2 = x3,2 / x3,1 = 0 / 5 = 0;
x3,3 = x3,3 / x3,1 = 0 / 5 = 0;
x3,4 = x3,4 / x3,1 = 0 / 5 = 0;
x3,5 = x3,5 / x3,1 = 1 / 5 = 0. 2;
2;
x3,6 = x3,6 / x3,1 = 2 / 5 = 0.4;
x3,7 = x3,7 / x3,1 = 0 / 5 = 0;
x3,8 = x3,8 / x3,1 = -2 / 5 = -0.4;
x3,9 = x3,9 / x3,1 = 0 / 5 = 0;
Остальные пустые ячейки, за исключением строки оценок и колонки Q, рассчитываем методом прямоугольника, относительно разрешающего элемента:
P1 = (P1 * x3,1) — (x1,1 * P3) / x3,1 = ((525 * 5) — (2 * 700)) / 5 = 245;
P2 = (P2 * x3,1) — (x2,1 * P3) / x3,1 = ((225 * 5) — (0 * 700)) / 5 = 225;
P4 = (P4 * x3,1) — (x4,1 * P3) / x3,1 = ((75 * 5) — (0 * 700)) / 5 = 75;
P5 = (P5 * x3,1) — (x5,1 * P3) / x3,1 = ((0 * 5) — (0 * 700)) / 5 = 0;
x1,1 = ((x1,1 * x3,1) — (x1,1 * x3,1)) / x3,1 = ((2 * 5) — (2 * 5)) / 5 = 0;
x1,3 = ((x1,3 * x3,1) — (x1,1 * x3,3)) / x3,1 = ((1 * 5) — (2 * 0)) / 5 = 1;
x1,4 = ((x1,4 * x3,1) — (x1,1 * x3,4)) / x3,1 = ((0 * 5) — (2 * 0)) / 5 = 0;
x1,5 = ((x1,5 * x3,1) — (x1,1 * x3,5)) / x3,1 = ((0 * 5) — (2 * 1)) / 5 = -0. 4;
4;
x1,6 = ((x1,6 * x3,1) — (x1,1 * x3,6)) / x3,1 = ((0.5 * 5) — (2 * 2)) / 5 = -0.3;
x1,7 = ((x1,7 * x3,1) — (x1,1 * x3,7)) / x3,1 = ((0 * 5) — (2 * 0)) / 5 = 0;
x1,8 = ((x1,8 * x3,1) — (x1,1 * x3,8)) / x3,1 = ((-0.5 * 5) — (2 * -2)) / 5 = 0.3;
x1,9 = ((x1,9 * x3,1) — (x1,1 * x3,9)) / x3,1 = ((0 * 5) — (2 * 0)) / 5 = 0;
x2,1 = ((x2,1 * x3,1) — (x2,1 * x3,1)) / x3,1 = ((0 * 5) — (0 * 5)) / 5 = 0;
x2,3 = ((x2,3 * x3,1) — (x2,1 * x3,3)) / x3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
x2,4 = ((x2,4 * x3,1) — (x2,1 * x3,4)) / x3,1 = ((1 * 5) — (0 * 0)) / 5 = 1;
x2,5 = ((x2,5 * x3,1) — (x2,1 * x3,5)) / x3,1 = ((0 * 5) — (0 * 1)) / 5 = 0;
x2,6 = ((x2,6 * x3,1) — (x2,1 * x3,6)) / x3,1 = ((0 * 5) — (0 * 2)) / 5 = 0;
x2,7 = ((x2,7 * x3,1) — (x2,1 * x3,7)) / x3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
x2,8 = ((x2,8 * x3,1) — (x2,1 * x3,8)) / x3,1 = ((0 * 5) — (0 * -2)) / 5 = 0;
x2,9 = ((x2,9 * x3,1) — (x2,1 * x3,9)) / x3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
x4,1 = ((x4,1 * x3,1) — (x4,1 * x3,1)) / x3,1 = ((0 * 5) — (0 * 5)) / 5 = 0;
x4,3 = ((x4,3 * x3,1) — (x4,1 * x3,3)) / x3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
x4,4 = ((x4,4 * x3,1) — (x4,1 * x3,4)) / x3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
x4,5 = ((x4,5 * x3,1) — (x4,1 * x3,5)) / x3,1 = ((0 * 5) — (0 * 1)) / 5 = 0;
x4,6 = ((x4,6 * x3,1) — (x4,1 * x3,6)) / x3,1 = ((-0. 5 * 5) — (0 * 2)) / 5 = -0.5;
5 * 5) — (0 * 2)) / 5 = -0.5;
x4,7 = ((x4,7 * x3,1) — (x4,1 * x3,7)) / x3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
x4,8 = ((x4,8 * x3,1) — (x4,1 * x3,8)) / x3,1 = ((0.5 * 5) — (0 * -2)) / 5 = 0.5;
x4,9 = ((x4,9 * x3,1) — (x4,1 * x3,9)) / x3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
x5,1 = ((x5,1 * x3,1) — (x5,1 * x3,1)) / x3,1 = ((0 * 5) — (0 * 5)) / 5 = 0;
x5,3 = ((x5,3 * x3,1) — (x5,1 * x3,3)) / x3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
x5,4 = ((x5,4 * x3,1) — (x5,1 * x3,4)) / x3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
x5,5 = ((x5,5 * x3,1) — (x5,1 * x3,5)) / x3,1 = ((0 * 5) — (0 * 1)) / 5 = 0;
x5,6 = ((x5,6 * x3,1) — (x5,1 * x3,6)) / x3,1 = ((0 * 5) — (0 * 2)) / 5 = 0;
x5,7 = ((x5,7 * x3,1) — (x5,1 * x3,7)) / x3,1 = ((-1 * 5) — (0 * 0)) / 5 = -1;
x5,8 = ((x5,8 * x3,1) — (x5,1 * x3,8)) / x3,1 = ((0 * 5) — (0 * -2)) / 5 = 0;
x5,9 = ((x5,9 * x3,1) — (x5,1 * x3,9)) / x3,1 = ((1 * 5) — (0 * 0)) / 5 = 1;
Значение целевой функции
Рассчитываем значение целевой функции, поэлементно умножая столбик Cb на столбик P, сложив результаты произведений.
MaxP = (Cb1 * P1) + (Cb11 * P2 + (Cb21 * P3 + (Cb31 * P4 + (Cb41 * P5) = (0 * 245) + (0 * 225) + (3 * 140) + (4 * 75) + (-M * 0) = 720;
Оценки управляемых переменных
Рассчитываем оценки для каждой управляемой переменной, поэлементно умножив значение с колонки переменной, на значение с колонки Cb, суммируем результаты произведений, и с их суммы вычитаем коэффициент целевой функции, при этой переменной.
Maxx1 = ((Cb1 * x1,1) + (Cb2 * x2,1) + (Cb3 * x3,1) + (Cb4 * x4,1) + (Cb5 * x5,1) ) — kx1 = ((0 * 0) + (0 * 0) + (3 * 1) + (4 * 0) + (-M * 0) ) — 3 = 0;
Maxx2 = ((Cb1 * x1,2) + (Cb2 * x2,2) + (Cb3 * x3,2) + (Cb4 * x4,2) + (Cb5 * x5,2) ) — kx2 = ((0 * 0) + (0 * 0) + (3 * 0) + (4 * 1) + (-M * 0) ) — 4 = 0;
Maxx3 = ((Cb1 * x1,3) + (Cb2 * x2,3) + (Cb3 * x3,3) + (Cb4 * x4,3) + (Cb5 * x5,3) ) — kx3 = ((0 * 1) + (0 * 0) + (3 * 0) + (4 * 0) + (-M * 0) ) — 0 = 0;
Maxx4 = ((Cb1 * x1,4) + (Cb2 * x2,4) + (Cb3 * x3,4) + (Cb4 * x4,4) + (Cb5 * x5,4) ) — kx4 = ((0 * 0) + (0 * 1) + (3 * 0) + (4 * 0) + (-M * 0) ) — 0 = 0;
Maxx5 = ((Cb1 * x1,5) + (Cb2 * x2,5) + (Cb3 * x3,5) + (Cb4 * x4,5) + (Cb5 * x5,5) ) — kx5 = ((0 * -0. 4) + (0 * 0) + (3 * 0.2) + (4 * 0) + (-M * 0) ) — 0 = 0.6;
4) + (0 * 0) + (3 * 0.2) + (4 * 0) + (-M * 0) ) — 0 = 0.6;
Maxx6 = ((Cb1 * x1,6) + (Cb2 * x2,6) + (Cb3 * x3,6) + (Cb4 * x4,6) + (Cb5 * x5,6) ) — kx6 = ((0 * -0.3) + (0 * 0) + (3 * 0.4) + (4 * -0.5) + (-M * 0) ) — 0 = -0.8;
Maxx7 = ((Cb1 * x1,7) + (Cb2 * x2,7) + (Cb3 * x3,7) + (Cb4 * x4,7) + (Cb5 * x5,7) ) — kx7 = ((0 * 0) + (0 * 0) + (3 * 0) + (4 * 0) + (-M * -1) ) — 0 = M;
Maxx8 = ((Cb1 * x1,8) + (Cb2 * x2,8) + (Cb3 * x3,8) + (Cb4 * x4,8) + (Cb5 * x5,8) ) — kx8 = ((0 * 0. 3) + (0 * 0) + (3 * -0.4) + (4 * 0.5) + (-M * 0) ) — -M = M+0.8;
3) + (0 * 0) + (3 * -0.4) + (4 * 0.5) + (-M * 0) ) — -M = M+0.8;
Maxx9 = ((Cb1 * x1,9) + (Cb2 * x2,9) + (Cb3 * x3,9) + (Cb4 * x4,9) + (Cb5 * x5,9) ) — kx9 = ((0 * 0) + (0 * 0) + (3 * 0) + (4 * 0) + (-M * 1) ) — -M = 0;
Элементы колонки Q
Поскольку среди оценок управляемых переменных есть отрицательные значения, текущая таблица еще не имеет оптимального решения. Поэтому в базис введем переменную с наименьшей отрицательной оценкой.
Количество переменных в базисе всегда постоянно, поэтому необходимо выбрать, какую переменную вывести из базиса, для чего мы рассчитываем Q.
Элементы столбика Q рассчитываем поделив значения из колонки P на значение с колонки, соответствующие переменной которая вводится в базис:
Q1 = P1 / x1,6 = 245 / -0.3 = -816.67;
Q2 = P2 / x2,6 = 225 / 0 = ∞;
Q3 = P3 / x3,6 = 140 / 0.4 = 350;
Q4 = P4 / x4,6 = 75 / -0.5 = -150;
Q5 = P5 / x5,6 = 0 / 0 = ∞;
Выводим из базиса переменную с наименьшим положительным значением Q.
На пересечении строки, которая соответствует переменной что выводится из базиса, и столбца который соответствует переменной что вводится в базис, расположен разрешающий элемент.
Данный элемент позволит нам рассчитать элементы таблицы следующей итерации.
Итерация: 4
| B | Cb | P | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | Q |
| 3 | 4 | 0 | 0 | 0 | 0 | 0 | -M | -M | ||||
| x3 | 0 | 350 | 0. 75 75 | 0 | 1 | 0 | -0.25 | 0 | 0 | 0 | 0 | |
| x4 | 0 | 225 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| x6 | 0 | 350 | 2.5 | 0 | 0 | 0 | 0.5 | 1 | 0 | -1 | 0 | |
| x2 | 4 | 250 | 1. 25 25 | 1 | 0 | 0 | 0.25 | 0 | 0 | 0 | 0 | |
| x9 | -M | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 1 | |
| max | 1000 | 2 | 0 | 0 | 0 | 1 | 0 | M | M | 0 | ||
Вычисление элементов таблицы:
Элементы колонки базис(B)
За результатами вычислений предыдущей итерации убираем с базиса переменную x1 и ставим на ее место x6. Все остальные ячейки остаются без изменений.
Все остальные ячейки остаются без изменений.
Элементы колонки Cb
Каждая ячейка этого столбца равна коэффициенту, который соответствует базовой переменной в соответствующей строке.
Cb1 = 0;
Cb2 = 0;
Cb3 = 0;
Cb4 = 4;
Cb5 = -M;
Значения упрявляемых переменных и колонки P(В качестве исходных данных берутся данные из предыдущей итерации)
Заполняем нулями все ячейки, соответствующие переменной, которая только что была введена в базис:(Разрешающий элемент остается без изменений)
x1,6 = 0;
x2,6 = 0;
x4,6 = 0;
x5,6 = 0;
Переносим в текущую таблицу строку с разрешающим элементом с предыдущей таблицы, поэлементно поделив ее значения на разрешающий элемент:
P3 = P3 / x3,6 = 140 / 0. 4 = 350;
4 = 350;
x3,1 = x3,1 / x3,6 = 1 / 0.4 = 2.5;
x3,2 = x3,2 / x3,6 = 0 / 0.4 = 0;
x3,3 = x3,3 / x3,6 = 0 / 0.4 = 0;
x3,4 = x3,4 / x3,6 = 0 / 0.4 = 0;
x3,5 = x3,5 / x3,6 = 0.2 / 0.4 = 0.5;
x3,6 = x3,6 / x3,6 = 0.4 / 0.4 = 1;
x3,7 = x3,7 / x3,6 = 0 / 0. 4 = 0;
4 = 0;
x3,8 = x3,8 / x3,6 = -0.4 / 0.4 = -1;
x3,9 = x3,9 / x3,6 = 0 / 0.4 = 0;
Остальные пустые ячейки, за исключением строки оценок и колонки Q, рассчитываем методом прямоугольника, относительно разрешающего элемента:
P1 = (P1 * x3,6) — (x1,6 * P3) / x3,6 = ((245 * 0.4) — (-0.3 * 140)) / 0.4 = 350;
P2 = (P2 * x3,6) — (x2,6 * P3) / x3,6 = ((225 * 0. 4) — (0 * 140)) / 0.4 = 225;
4) — (0 * 140)) / 0.4 = 225;
P4 = (P4 * x3,6) — (x4,6 * P3) / x3,6 = ((75 * 0.4) — (-0.5 * 140)) / 0.4 = 250;
P5 = (P5 * x3,6) — (x5,6 * P3) / x3,6 = ((0 * 0.4) — (0 * 140)) / 0.4 = 0;
x1,1 = ((x1,1 * x3,6) — (x1,6 * x3,1)) / x3,6 = ((0 * 0.4) — (-0.3 * 1)) / 0.4 = 0.75;
x1,2 = ((x1,2 * x3,6) — (x1,6 * x3,2)) / x3,6 = ((0 * 0. 4) — (-0.3 * 0)) / 0.4 = 0;
4) — (-0.3 * 0)) / 0.4 = 0;
x1,3 = ((x1,3 * x3,6) — (x1,6 * x3,3)) / x3,6 = ((1 * 0.4) — (-0.3 * 0)) / 0.4 = 1;
x1,4 = ((x1,4 * x3,6) — (x1,6 * x3,4)) / x3,6 = ((0 * 0.4) — (-0.3 * 0)) / 0.4 = 0;
x1,5 = ((x1,5 * x3,6) — (x1,6 * x3,5)) / x3,6 = ((-0.4 * 0.4) — (-0.3 * 0.2)) / 0.4 = -0.25;
x1,6 = ((x1,6 * x3,6) — (x1,6 * x3,6)) / x3,6 = ((-0. 3 * 0.4) — (-0.3 * 0.4)) / 0.4 = 0;
3 * 0.4) — (-0.3 * 0.4)) / 0.4 = 0;
x1,8 = ((x1,8 * x3,6) — (x1,6 * x3,8)) / x3,6 = ((0.3 * 0.4) — (-0.3 * -0.4)) / 0.4 = 0;
x1,9 = ((x1,9 * x3,6) — (x1,6 * x3,9)) / x3,6 = ((0 * 0.4) — (-0.3 * 0)) / 0.4 = 0;
x2,1 = ((x2,1 * x3,6) — (x2,6 * x3,1)) / x3,6 = ((0 * 0.4) — (0 * 1)) / 0.4 = 0;
x2,2 = ((x2,2 * x3,6) — (x2,6 * x3,2)) / x3,6 = ((0 * 0. 4) — (0 * 0)) / 0.4 = 0;
4) — (0 * 0)) / 0.4 = 0;
x2,3 = ((x2,3 * x3,6) — (x2,6 * x3,3)) / x3,6 = ((0 * 0.4) — (0 * 0)) / 0.4 = 0;
x2,4 = ((x2,4 * x3,6) — (x2,6 * x3,4)) / x3,6 = ((1 * 0.4) — (0 * 0)) / 0.4 = 1;
x2,5 = ((x2,5 * x3,6) — (x2,6 * x3,5)) / x3,6 = ((0 * 0.4) — (0 * 0.2)) / 0.4 = 0;
x2,6 = ((x2,6 * x3,6) — (x2,6 * x3,6)) / x3,6 = ((0 * 0. 4) — (0 * 0.4)) / 0.4 = 0;
4) — (0 * 0.4)) / 0.4 = 0;
x2,8 = ((x2,8 * x3,6) — (x2,6 * x3,8)) / x3,6 = ((0 * 0.4) — (0 * -0.4)) / 0.4 = 0;
x2,9 = ((x2,9 * x3,6) — (x2,6 * x3,9)) / x3,6 = ((0 * 0.4) — (0 * 0)) / 0.4 = 0;
x4,1 = ((x4,1 * x3,6) — (x4,6 * x3,1)) / x3,6 = ((0 * 0.4) — (-0.5 * 1)) / 0.4 = 1.25;
x4,2 = ((x4,2 * x3,6) — (x4,6 * x3,2)) / x3,6 = ((1 * 0. 4) — (-0.5 * 0)) / 0.4 = 1;
4) — (-0.5 * 0)) / 0.4 = 1;
x4,3 = ((x4,3 * x3,6) — (x4,6 * x3,3)) / x3,6 = ((0 * 0.4) — (-0.5 * 0)) / 0.4 = 0;
x4,4 = ((x4,4 * x3,6) — (x4,6 * x3,4)) / x3,6 = ((0 * 0.4) — (-0.5 * 0)) / 0.4 = 0;
x4,5 = ((x4,5 * x3,6) — (x4,6 * x3,5)) / x3,6 = ((0 * 0.4) — (-0.5 * 0.2)) / 0.4 = 0.25;
x4,6 = ((x4,6 * x3,6) — (x4,6 * x3,6)) / x3,6 = ((-0. 5 * 0.4) — (-0.5 * 0.4)) / 0.4 = 0;
5 * 0.4) — (-0.5 * 0.4)) / 0.4 = 0;
x4,8 = ((x4,8 * x3,6) — (x4,6 * x3,8)) / x3,6 = ((0.5 * 0.4) — (-0.5 * -0.4)) / 0.4 = 0;
x4,9 = ((x4,9 * x3,6) — (x4,6 * x3,9)) / x3,6 = ((0 * 0.4) — (-0.5 * 0)) / 0.4 = 0;
x5,1 = ((x5,1 * x3,6) — (x5,6 * x3,1)) / x3,6 = ((0 * 0.4) — (0 * 1)) / 0.4 = 0;
x5,2 = ((x5,2 * x3,6) — (x5,6 * x3,2)) / x3,6 = ((0 * 0.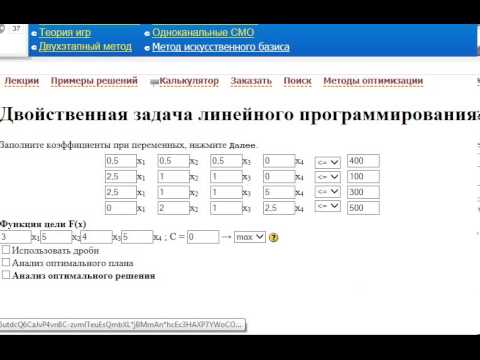 4) — (0 * 0)) / 0.4 = 0;
4) — (0 * 0)) / 0.4 = 0;
x5,3 = ((x5,3 * x3,6) — (x5,6 * x3,3)) / x3,6 = ((0 * 0.4) — (0 * 0)) / 0.4 = 0;
x5,4 = ((x5,4 * x3,6) — (x5,6 * x3,4)) / x3,6 = ((0 * 0.4) — (0 * 0)) / 0.4 = 0;
x5,5 = ((x5,5 * x3,6) — (x5,6 * x3,5)) / x3,6 = ((0 * 0.4) — (0 * 0.2)) / 0.4 = 0;
x5,6 = ((x5,6 * x3,6) — (x5,6 * x3,6)) / x3,6 = ((0 * 0.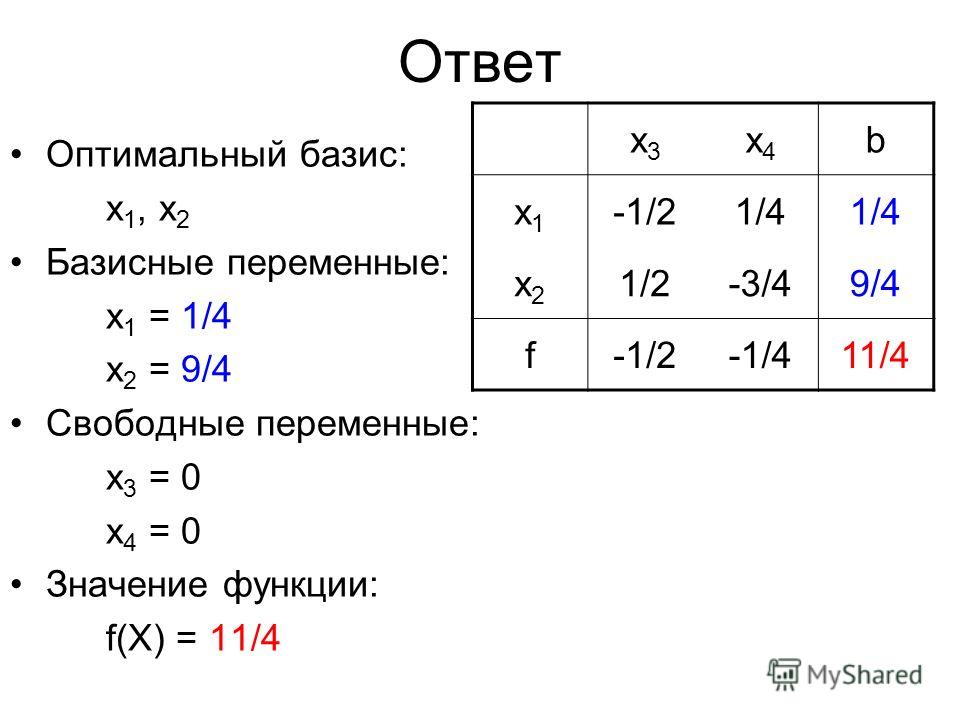 4) — (0 * 0.4)) / 0.4 = 0;
4) — (0 * 0.4)) / 0.4 = 0;
x5,8 = ((x5,8 * x3,6) — (x5,6 * x3,8)) / x3,6 = ((0 * 0.4) — (0 * -0.4)) / 0.4 = 0;
x5,9 = ((x5,9 * x3,6) — (x5,6 * x3,9)) / x3,6 = ((1 * 0.4) — (0 * 0)) / 0.4 = 1;
Значение целевой функции
Рассчитываем значение целевой функции, поэлементно умножая столбик Cb на столбик P, сложив результаты произведений.
MaxP = (Cb1 * P1) + (Cb11 * P2 + (Cb21 * P3 + (Cb31 * P4 + (Cb41 * P5 = (0 * 350) + (0 * 225) + (0 * 350) + (4 * 250) + (-M * 0) = 1000;
Оценки управляемых переменных
Рассчитываем оценки для каждой управляемой переменной, поэлементно умножив значение с колонки переменной, на значение с колонки Cb, суммируем результаты произведений, и с их суммы вычитаем коэффициент целевой функции, при этой переменной.
Maxx1 = ((Cb1 * x1,1) + (Cb2 * x2,1) + (Cb3 * x3,1) + (Cb4 * x4,1) + (Cb5 * x5,1) ) — kx1 = ((0 * 0.75) + (0 * 0) + (0 * 2.5) + (4 * 1.25) + (-M * 0) ) — 3 = 2;
Maxx2 = ((Cb1 * x1,2) + (Cb2 * x2,2) + (Cb3 * x3,2) + (Cb4 * x4,2) + (Cb5 * x5,2) ) — kx2 = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 1) + (-M * 0) ) — 4 = 0;
Maxx3 = ((Cb1 * x1,3) + (Cb2 * x2,3) + (Cb3 * x3,3) + (Cb4 * x4,3) + (Cb5 * x5,3) ) — kx3 = ((0 * 1) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * 0) ) — 0 = 0;
Maxx4 = ((Cb1 * x1,4) + (Cb2 * x2,4) + (Cb3 * x3,4) + (Cb4 * x4,4) + (Cb5 * x5,4) ) — kx4 = ((0 * 0) + (0 * 1) + (0 * 0) + (4 * 0) + (-M * 0) ) — 0 = 0;
Maxx5 = ((Cb1 * x1,5) + (Cb2 * x2,5) + (Cb3 * x3,5) + (Cb4 * x4,5) + (Cb5 * x5,5) ) — kx5 = ((0 * -0. 25) + (0 * 0) + (0 * 0.5) + (4 * 0.25) + (-M * 0) ) — 0 = 1;
25) + (0 * 0) + (0 * 0.5) + (4 * 0.25) + (-M * 0) ) — 0 = 1;
Maxx6 = ((Cb1 * x1,6) + (Cb2 * x2,6) + (Cb3 * x3,6) + (Cb4 * x4,6) + (Cb5 * x5,6) ) — kx6 = ((0 * 0) + (0 * 0) + (0 * 1) + (4 * 0) + (-M * 0) ) — 0 = 0;
Maxx7 = ((Cb1 * x1,7) + (Cb2 * x2,7) + (Cb3 * x3,7) + (Cb4 * x4,7) + (Cb5 * x5,7) ) — kx7 = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * -1) ) — 0 = M;
Maxx8 = ((Cb1 * x1,8) + (Cb2 * x2,8) + (Cb3 * x3,8) + (Cb4 * x4,8) + (Cb5 * x5,8) ) — kx8 = ((0 * 0) + (0 * 0) + (0 * -1) + (4 * 0) + (-M * 0) ) — -M = M;
Maxx9 = ((Cb1 * x1,9) + (Cb2 * x2,9) + (Cb3 * x3,9) + (Cb4 * x4,9) + (Cb5 * x5,9) ) — kx9 = ((0 * 0) + (0 * 0) + (0 * 0) + (4 * 0) + (-M * 1) ) — -M = 0;
Ответ:
Поскольку среди оценок управляемых переменных нет отрицательных значений, текущая таблица имеет оптимальное решение.
Значение целевой функции:
F* = 1000
Переменные которые присутствуют в базисе, равны соответствующим ячейкам колонки P, все остальные переменные равны нулю:
x1 = 0;
x2 = 250;
Ответ:
F* = 1000
X* = (0; 250)
Условные обозначения:
| xi↓ | — вводим переменную в базис; |
| xi ← | — выводим переменную с базиса; |
| xi | — разрешительный елемент; |
| xi | — базисной елемент; |
| B | — базис; |
| Cb | — коэффициент при базисной переменной; |
| P | — план; |
Метод решения задачи.
 Программа — калькулятор
Программа — калькуляторПрограмма — калькулятор
курсовая работа
Проанализировав поставленную задачу, я пришел к выводу, что необходимо разработать синтаксический анализатор выражений, для реализации которого я использовал алгоритм множественного выбора. При разборе выражение разбивается на составные части — термы, который в свою очередь состоит из факторов. Факторами могут являться числа или подвыражения, состоящего из других факторов. Терм является произведением или отношением факторов. Поочередно, анализируя каждый введенный символ, программа объединяет их в факторы, а готовые факторы в термы, после подсчета которых выдается окончательный ответ. Это правило очень важно, так как должен соблюдаться строгий приоритет выполнения операций, то есть вложенные элементы должны иметь операторы с более высоким приоритетом. Сначала, если есть функции, вычисляется их значение. У арифметических операций приоритет следующий: сначала выполняется возведение в степень, затем умножение, деление, сложение и вычитание. Если выражение содержит скобки, то в первую очередь вычисляется подвыражение во вложенных скобках самого нижнего уровня, а затем по возрастанию уровня.
Если выражение содержит скобки, то в первую очередь вычисляется подвыражение во вложенных скобках самого нижнего уровня, а затем по возрастанию уровня.
Делись добром 😉
Графическое решение задач линейного программирования
2.2 Метод решения задачи
Алгоритм графического способа решения задач линейного программирования заключается: 1) Построить прямые уравнения, которые получаются в результате замены в ограничения знаков неравенств на знаки равенств; 2) Найти полуплоскости…
Информационно-аналитическая система «MTTS»
1. МЕТОД РЕШЕНИЯ ПОСТАВЛЕННОЙ ЗАДАЧИ
Информационно-аналитическая система «МТТS» представляет собой приложение…
Линейное программирование
2. ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛП
Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется для решения задач двумерного пространства. Задачи трёхмерного пространства решаются очень редко, т.к…
Метод аддитивной оптимизации
2.
 2 Метод решения задачи
2 Метод решения задачиАддитивный критерий оптимальности определяется по формуле (6). , i = 1,2, …m (6) где — частные критерии, — весовые коэффициенты (7) Обобщенная функция цели (6) может быть использована для свертывания частных критериев оптимальности…
Моделирование производственной системы
Постановка задачи и метод ее решения
система моделирование технический контроль Целью данного курсового проекта является создание модели, которая бы демонстрировала работу токаря в течение одной рабочей смены. В процессе работы, рабочий берет со склада заготовки…
Поиск вершины в графе между двумя заданными вершинами
3.1 Метод решения задачи
Для решения поставленной задачи наиболее подходит метод обхода графа в глубину, который заключается в следующем: при обходе в глубину мы посещаем первый узел, а затем идем вдоль ребер графа, пока не упремся в тупик…
Программа — калькулятор
Метод решения задачи
Проанализировав поставленную задачу, я пришел к выводу, что необходимо разработать синтаксический анализатор выражений, для реализации которого я использовал алгоритм множественного выбора. ..
..
Программирование на языке высокого уровня
2.1 Метод решения задачи
Задачу можно разбить на три отдельные подзадачи: 1. Поиск в файле записей, в которых возраст сотрудника больше заданного возраста, и вывод списка таких сотрудников. 2. Поиск во входном файле записей…
Разработка игровой системы «Тетрис»
1.3 Выбранный метод решения задачи
Для работы с данными размещения фигур на игровом поле постоянно нужен индексированный доступ к элементам, поэтому был выбран двумерный массив, который предоставляет прямой и быстрый доступ к нужному элементу…
Разработка конвертора на языке С++ для перевода программ на языке Паскаль в текст программы на языке С++
3. Метод решения задачи
Разработка компиляторов полна красивых примеров решения сложных задач, возникающих при реальной работе над компиляторами, путем математического абстрагирования. Они служат прекрасной иллюстрацией того…
Решение транспортной задачи методом потенциалов
2.
 3 Метод решения задачи
3 Метод решения задачиМетод потенциалов является модификацией симплекс-метода решения задачи линейного программирования применительно к транспортной задаче. Он позволяет, отправляясь от некоторого допустимого решения…
Создание базы данных владельцев автомобилей
3.1 Метод решения задачи
Задачу можно разбить на семь отдельные подзадачи: 1. Поиск в файле записей, в которых номер автомобиля совпадает с заданным, и вывод владельцев таких номеров. 2. Поиск в файле записей, в которых марка автомобиля совпадает с заданной маркой…
Создание игровой программы «Морской бой»
2. Метод решения задачи
Для решения поставленной задачи программного средства необходимо осуществить алгоритм искусственного интеллекта, который будет выполнять задачу второго игрока. Для этого необходимо разбить исходный код на несколько частей…
Создание проигрывателя MP3 Player
3.1 Модель (метод) решения задачи
Концептуальная модель представлена следующей схемой:
Рисунок 2. Концептуальная модель проекта
В этой схеме входные данные представляют файлы MP3, находящиеся как в памяти компьютера, так и на других носителях…
Концептуальная модель проекта
В этой схеме входные данные представляют файлы MP3, находящиеся как в памяти компьютера, так и на других носителях…
Электронный помощник преподавателя дисциплины «Математические методы». Задача управления запасами
2. МЕТОД РЕШЕНИЯ ЗАДАЧИ
Данный программный продукт реализован в среде Delphi, которая обладает удобным и практичным интерфейсом, позволяющим быстро и удобно совершать те или иные действия, находить ошибки и оперативно исправлять их…
Калькулятор графический Texas Instruments TI-84 Plus CE-T Python Edition
Прораммируемый графический калькулятор нового поколения Texas Instruments TI-84 Plus CE-T Python для школьников и студентов — идеальный инструмент для решения математических задач и научной работы, в том числе для статистических и финансовых вычислений.Цветной дисплей высокого разрешения с подсветкой. Обновленный современный дизайн. Перезаряжаемая батарея TI. Простой в использовании. Благодаря передовым технологиям пользователь имеет возможность добавлять на свой калькулятор приложения и дополнительные функции в области математики и науки. 12 мощных приложений загружены на калькулятор Texas Instruments TI-84 Plus CE-T и готовы к использованию. Режим Экзамена — контроль учащихся во время экзамена. Построение графиков. Возможность загружать и использовать изображения, построение графика по фотографии. Поддерживает программирование Python, TI Basic, Lua и ASM.
Благодаря передовым технологиям пользователь имеет возможность добавлять на свой калькулятор приложения и дополнительные функции в области математики и науки. 12 мощных приложений загружены на калькулятор Texas Instruments TI-84 Plus CE-T и готовы к использованию. Режим Экзамена — контроль учащихся во время экзамена. Построение графиков. Возможность загружать и использовать изображения, построение графика по фотографии. Поддерживает программирование Python, TI Basic, Lua и ASM.
Область применения
Математика, тригонометрия, геометрия, алгебра и начала анализа, высшая математика, линейная алгебра, статистика, физика, химия, биология, финансовые вычисления, программирование, STEM, IB Diploma, вступительные экзамены в колледж и университет PSAT, SAT и ACT и на AP тестах.
Возьмите с собой калькулятор Texas Instruments TI-84 plus CE-T на экзамен
- SAT, PSAT и ACT вступительные экзамены в университет.
- AP экзамены, во время которых требуется графический калькулятор.

- Одобрен для пользования во время экзамена IB.
Яркие цвета. Оптимальный дисплей.
С помощью данного дисплея обзор концептов станет намного удобнее. Между уравнениями, данными и цветными графиками связь стала быстрее и лучше:
- Благодаря дисплею с высоким разрешением и подсветкой данные на экране читаются лучше.
- Разграничение множественных цветных графиков, уравнений, и других объектов.
- Графики будут просматриваться проще с использованием линий сетки.
Больше пользы, отсутствие необходимости менять батарею
Перезаряжаемую батарею TI Rechargeable Battery можно легко зарядить, используя USB кабель, сетевое зарядное устройство или специальное устройство для заряда батареи TI-84 Plus CE-T Charging Station.
Уже знакомый набор функций серии TI-84 Plus
Меню и навигация по нему структурированы таким же образом, как в уже знакомом TI-84 Plus, что делает калькулятор простым в использовании. Встроенная функция MathPrint позволяет вводить и просматривать математические символы, формулы и дроби такими, какие они в учебнике.
Встроенная функция MathPrint позволяет вводить и просматривать математические символы, формулы и дроби такими, какие они в учебнике.
Как в жизни
Математические понятия и концепты лучше понимаются через изображения. Загружайте фотографии с компьютера на калькулятор и чертите поверх них, чтобы процесс изучения давался вам легче.
Платформа для программирования на Python
Теперь владельцы устройств смогут программировать на языке Python (в дополнение к Lua и Basic, которые были доступны ранее). Python — высокоуровневый язык программирования, который используется в различных сферах IT — разработка приложений, парсинг, машинное обучение, web-сайты и др. Это один из самых популярных языков программирования наряду с Java, С и С++.
TI не просто внедрила новый язык программирования, но проработала платформу для его интуитивного изучения и решения математических, научных, инжиниринговых задач. Компания предложила простой интерфейс для кодинга с минимальными усилиями: у владельцев калькуляторов будет возможность выбрать функцию из списка вместо запоминания ее синтаксиса, визуализировать код на графиках, воспользоваться встроенными подсказками. Уникальные опции откроет интеграция с микроконтроллерами TI-Innovator Hub и роботом-вездеходом TI-Innovator Rover. Компания даже проработала решения для учителей, чтобы им не приходилось придумывать интересные задачи для программирования на Python с нуля.
Уникальные опции откроет интеграция с микроконтроллерами TI-Innovator Hub и роботом-вездеходом TI-Innovator Rover. Компания даже проработала решения для учителей, чтобы им не приходилось придумывать интересные задачи для программирования на Python с нуля.
Встроенные приложения графического калькулятора TI-84 Plus CE-T
Приложение TI-Innovator Hub
Приложение TI-Innovator Hub запускается на калькуляторе с ОС версии 5.2 и выше автоматически, когда оно загружено на калькулятор. Программный редактор Python, TI-Basic оснащен подпунктом HUB, чтобы вы могли использовать подсказки в выполнении команд и ввода данных при программировании в приложении TI-Innovator Hub. Экономьте свое время, используя этот пункт меню, чтобы вставлять полные команды приложения TI- Innovator Hub вместо того, чтобы печатать их вручную с клавиатуры при написании программ.
Приложение Cabri Jr.
Приложение позволяет строить, анализировать и трансформировать математические модели и геометрические диаграммы на вашем графическом калькуляторе. Вы можете: Выполнять аналитические, трансформационные функции и функцию Эвклидовой геометрии. Интерактивно строить геометрические фигуры по точкам или группе точек для линий, многоугольников, кругов и других основных геометрических фигур. Переделывать геометрические объекты по ходу выполнения работы, чтобы видеть образцы, выдвигать гипотезы и делать выводы.
Вы можете: Выполнять аналитические, трансформационные функции и функцию Эвклидовой геометрии. Интерактивно строить геометрические фигуры по точкам или группе точек для линий, многоугольников, кругов и других основных геометрических фигур. Переделывать геометрические объекты по ходу выполнения работы, чтобы видеть образцы, выдвигать гипотезы и делать выводы.
Приложение CellSheet
Позволяет работать с электронными таблицами прямо в графическом калькуляторе. Создание формул для ячеек и использование встроенных функций. В ячейки можно поместить: целые числа, действительные числа, формулы, переменные текстовые и числовые последовательности, функции. Каждая электронная таблица содержит 999 строк и 26 колонн. Лимит вводимых данных сводится только к вместимости оперативной памяти. Сохраняйте координатные пары (х, y) в списки, чтобы просматривать и оптимизировать функции для линейного программирования
Приложение Conic Graphing
Представляет уравнения в виде функции, параметрическом и полярном формате, и предоставляет простой способ рисования четырех конических фигур: эллипс, круг, парабола, гипербола. Введите необходимые параметры, чтобы рисовать, отслеживать или решать задачи с необходимыми данными.
Введите необходимые параметры, чтобы рисовать, отслеживать или решать задачи с необходимыми данными.
Приложение Inequality Graphing
Предоставляет новые функции для графических уравнений и неравенств, а также нахождение отношений между ними. Вы можете: Вводить неравенства, используя символы отношения. Строить графики неравенств и выделять области пересечения и наложения. Вводить неравенства (только вертикальные линии) в редакторе X=. Отслеживать интересующие вас точки (например, пересечения) между объектами. Сохранять пары координат (х, y) в списки, чтобы просматривать и оптимизировать функции для линейного программирования.
Приложение Periodic Table
Дает графическое представление элементов периодической системы. Приложение позволяет вам: Просматривать и изучать элементы периодической системы. Находить данные о свойствах и полезную информацию об известных элементах. Сортировать элементы по порядковому номеру, в алфавитном порядке или в алфавитном порядке по первым символам. Идентифицировать группы элементов по области (инертные газы, галогены и т.д.) и блокам (p-, d-, s-, f-). Экспортировать данные о свойствах в списки для их дальнейшего анализа. Изображать основные свойства (атомные радиусы, электроотрицательность и т.д.) в сравнении с порядковым номером, чтобы проиллюстрировать периодическую природу элементов.
Идентифицировать группы элементов по области (инертные газы, галогены и т.д.) и блокам (p-, d-, s-, f-). Экспортировать данные о свойствах в списки для их дальнейшего анализа. Изображать основные свойства (атомные радиусы, электроотрицательность и т.д.) в сравнении с порядковым номером, чтобы проиллюстрировать периодическую природу элементов.
Приложение Polynomial Root Finder and Simultaneous Equation Editor
Данное приложение: Вычисляет корни (ноли) многочленов со степенью от 1 до 10 с удобным и простым интерфейсом. Позволяет вам сохранять решения в списки, загружать список в приложение для коэффициента многочлена, и сохранять многочлен в переменную Y на графике после выхода из приложения. Находит решения к системам линейных уравнений. Позволяет вам загружать матрицы, содержащие коэффициенты линейных систем, и проверять, имеет ли эта система уникальное решение, бесконечное количество решений или ни одного.
Приложение Probability Simulation
Изучайте теорию вероятности с интерактивными анимациями, имитирующими бросок костей и подбрасывание монеты, а также генерируйте случайные числа на своем калькуляторе. Опции включают: гистограммы, таблицу данных о попытках, настройки для определения количества попыток, способы сбора данных, оценивание. Кроме того, студенты могут экспортировать данные для их дальнейшего использования.
Опции включают: гистограммы, таблицу данных о попытках, настройки для определения количества попыток, способы сбора данных, оценивание. Кроме того, студенты могут экспортировать данные для их дальнейшего использования.
Приложение Science Tools
Данное приложение позволяет вам выполнять конвертации единиц на своем калькуляторе. Элементы приложения включают в себя: калькулятор значимых цифр, константы и конвертации, подсказки по данным и графикам, калькулятор векторов
Приложение SmartPad CE-T
Подсоединение калькулятора как удаленной клавиатуры. Приложение SmartPad позволяет вам использовать свой калькулятор в качестве удаленной клавиатуры.
Приложение Transformation graphing
Приложение Transformation graphing позволяет вам увидеть эффект изменения значений коэффициентов без выхода из экрана графика. Приложение Transformation graphing влияет только на режим черчения функций. Х является независимой переменной, а Y — зависимой. Приложение недоступно в параметрическом, полярном и последовательном графических режимах. Приложение Transformation graphing позволяет вам манипулировать с 4 коэффициентами на графике: А, В, С и D. Все другие переменные будут значиться как константы, используя значения из памяти. Вы можете проследить трансформацию функции или анимировать трансформацию, используя функции проигрывания, паузы, скорости воспроизведения.
Приложение Transformation graphing позволяет вам манипулировать с 4 коэффициентами на графике: А, В, С и D. Все другие переменные будут значиться как константы, используя значения из памяти. Вы можете проследить трансформацию функции или анимировать трансформацию, используя функции проигрывания, паузы, скорости воспроизведения.
Приложение Vernier EasyData
Используйте приложение EasyData от Vernier Software Technology, чтобы совершать исследования. Приложение EasyData автоматически запускает сбор данных, если используется датчик Vernier EasyTemp и загружает встроенные эксперименты для каждого из поддерживаемых датчиков Vernier.
Встроенные функции графического калькулятора TI-84 Plus CE-T
- Загрузка изображений в калькулятор.
- 15 цветов для работы с графиками.
- Изменение стиля и цвета оси и сетки на графике.
- Каталог помощи по синтаксической структуре.
- Алфавитный КАТАЛОГ всех операций калькуляторов TI в одном меню.

- Доступ к более сложным функциям через диалоговое окно меню.
- Вычисление действительных и сложных чисел с точностью до 14 символов, отображение 10 цифр плюс 2-числовой степени.
- Графики — 10 прямоугольных функций, 6 параметрических выражений, 6 полярных выражений, и 3 рекурсивно определенных последовательностей.
- Определение, сохранение, построение и анализ до 10 графических функций одновременно.
- Режим построения последовательностей показывает диаграммы распределения по времени/ паутинную/ ступенчатую и фазовую диаграммы.
- Заданные пользователем имена списка. Показывает до 999 элементов.
- 17 интерактивных возможностей масштабирования.
- Численный расчет в виде таблицы для всех режимов построения графиков
- Интерактивный анализ значения функции, корней, максимальных и минимальных значений, интегралов и производных.
- 8 разных стилей построения графика для просмотра построенного графика в разном виде.

- Опция горизонтального и вертикального разделения экрана.
- Одновременный просмотр графика и таблицы.
- Сохраняет до 10 матриц 50×50.
- Операции с матрицами, включая преобразования, транспозицию, определитель, прибавление, строчную ступенчатую форму и линейные системы. Конвертация матриц в списки и обратно.
- Списочный статистический анализ с одной и двумя переменными, включая следующие модели регрессии: логистическую, синусоидальную, медиан-медианную, линейную, логарифмическую, экспоненциальную, степенную, квадратную многочленную, кубическую многочленную и многочленную в четвертой степени.
- 3 формулировки статистических графиков для графиков рассеяния, линейных xy графиков, гистограмм, обычных диаграмм и диаграмм вида «ящик с усами» графика нормального распределения.
- Более сложные статистические функции, включая 10 функций проверки гипотезы, 7 функций доверительной области и однофакторный дисперсионный анализ отклонений.

- 15 функций распределения вероятностей, включая режимы Нормальный, Студент-t, Хи-квадрат, Двучленный и Пуассоновский.
- Функции для бизнеса, включая временную стоимость денег (Time-Value-of-Money (TVM), денежные потоки (cashflows) и амортизацию. Полноэкранный интерактивный редактор для решения задач с TVM.
- Интерактивный редактор вычисления уравнений позволяет решать в числовом значении различные переменные в уравнении.
- 11 вычислений регрессии.
Мобильная лаборатория Texas Instruments
Поддержка сбора данных. Калькулятор совместим с системой CBL 2, датчиком движения CBR 2, системами Vernier EasyLink и Vernier EasyTemp, позволяющими собирать и анализировать практические данные и 50 датчиками Vernier.
Возможности подключения
Обновляемый графический калькулятор Texas Instruments TI-84 plus ce-t позволит вам насладиться передовыми технологиями и функциональностью, а также даст возможность использовать программное обеспечение и приложения (Apps). Для подключения к ПК нужен TI соединительный кабель (в комплекте) и программное обеспечение TI Connect CE для передачи информации на компьютер и обратно.
Для подключения к ПК нужен TI соединительный кабель (в комплекте) и программное обеспечение TI Connect CE для передачи информации на компьютер и обратно.
Инструкция к графическому калькулятору Texas Instruments TI-84 Plus CE-T на русском языке
Разрешен для использования во время экзаменов: SAT, AP (углубленное изучение), PSAT/NMQT, ACT, International Baccalaureate IB, Praxis
Подходит для вычислений в следующих сферах: Начальная алгебра, Тригонометрия, Геометрия, Алгебра и начала анализа, Анализ/АР анализ, Статистика/АР статистика, Финансы и бизнес, Математика уровня колледжа, Линейная алгебра
Технические характеристики графического калькулятораПитание: перезаряжаемая батарея TI Rechargeable Battery (в комплекте)
Обновляемая операционная система: есть
Встроенные приложения: есть
Возможность использования изображений: есть
Система компьютерной алгебры (CAS): нет
Программное обеспечение для ПК: нет
Каталог функций
Помощник по каталогу
Встроенные часы с отображением даты и времени.
Твердая защитная крышка
Память
Доступная память для хранения результатов расчетов и приложений Flash ROM: 3.0Мб
Доступная оперативная память RAM: 154Кб
Вызов уравнения
Дисплей
Цветной дисплей
Разрешение экрана: 140 DPI; 16-битная цветовая схема.
Дисплей (строки х знаки): 10х26
Размер дисплея: 320 x 240 пикселей (2.8″ диагональ).
Инженерная запись
Научная запись
Pretty-Print для ввода и вывода (как в учебнике)
Разделение экрана (вертикальный/горизонтальный): 2
Возможности подключения
USB кабель соединения ПК: в комплекте
Программа подключения к ПК
Кабель соединения калькулятор-калькулятор: мини-USB кабель
Встроенный USB-порт
Размер (В х Ш х Т): 192 х 89 х 27
Вес: 268г
Функции графического калькулятораМатематика
Решение систем уравнений: Флеш
Нахождение корня полинома: Флеш
Гиперболические
Тригонометрические функции
Логические операции
Комплексные числа
Численный решатель
Операции с дробями
Высшая математика (Calculus)
Максимум, Минимум
Шаблоны интегралов и производных
Численное интегрирование
Численное дифференцирование
Графический анализ (Graphing)
Конические графики: Флеш
Графики неравенств: Флеш
Графическое преобразование: Флеш
Таблица значений функции
Масштабирование, трассировка
Графические стили множественной функции
Последовательность
Полярные
Параметрические
Функция
Функции компьютерной алгебры (CAS): нет
Статистические функции
Сочетания и перестановки
Случайные числа
Количество моделей регрессии: 10
Линейная регрессия
Среднее значение, Стандартное отклонение
Статистика (1-2 переменные)
Таблицы: Флеш
Круговая диаграмма / Столбиковая диаграмма: Флеш
Manual Fit Line
Вероятностное моделирование: Флеш
Дедуктивная статистика, Вероятностное распределение
Сочетания, Перестановки, Случайные числа
Точечные диаграммы
Отслеживаемые гистограммы
Сохраненные формулы столбцов
Максимальный размер списка данных: 999
Количество списков: нет ограничений
Именованные списки
Минимальные и максимальные значения
Медиана, квартили
Матрицы
Максимальное количество: до 10
Размер: 50 х 50
Вычисления с матрицами
Наука
Физические константы: Флеш
Метрические преобразования: Флеш
Значащие цифры: Флеш
DataMate: Флеш
Совместимость с CBR 2
Совместимость с CBL 2
Перевод единиц измерения: Флеш
Финансовые функции
Модифицированная внутренняя норма доходности MIRR, Чистая будущая стоимость NFV
Временная стоимость денег TVM
Денежные потоки Cash Flows, Амортизация
Интерактивный решатель временной стоимости денег TVM
Языки программирования
Python, TI BASIC, Lua, Ассемблер
Пользовательские программы
Флэш приложения
Приложение App4Math
Приложение Cabri Jr
Приложение CellSheet
Теории конических систем (Conics)
Построение графиков неравенств (Inequality Graphing)
Вычисление корня многочлена/ Одновременное решение уравнений
Вероятностное имитационное моделирование
Приложение TI Test Guard
Трансформационное построение графиков
TI Test Guard
Transformation Graphing
Приложение Vernier EasyData
Графический калькулятор TI-84 Plus CE-T PE
Описание
Графический калькулятор TI-84 Plus CE-T Python Edition от Texas Instruments (Техас Инструментс) — последняя новейшая модель калькулятора для учащихся, студентов, научных работников в сферах точных наук, математики, финансов, статистики, а также программирования.
- Графический калькулятор TI-84 Plus CE-T разрешен к использованию на экзаменах: Scholastic Aptitude Test (SAT), IB ® Diploma Programme, ACT, PreACT, PSAT, Advanced Placement (AP) test Biology, AP Physics, AP Math, AP Chemistry, AP Statistics, STEM, и других связанных с ними тестах.
Основные отличия от предыдущих моделей:
- Цветной четкий экран высокого разрешения с подсветкой
- Перезаряжаемая батарея от TI (Texas Instruments)
- Размер дисплея: 320 x 240 пикселей (2.8″ диагональ).
Разрешение дисплея: 140 DPI; 16-битная цветовая схема.
Работает от перезаряжаемой батареи TI Rechargeable Battery (в комплекте).
Память 3 MB FLASH ROM для хранения и использования данных приложений.
Доступно 154KB памяти RAM.
USB порт для подключения калькулятора к компьютеру, другому калькулятору TI-84 Plus, TI-84 Plus Silver Edition, TI-84 Plus C Silver Edition и другим графическим калькуляторам TI-84 Plus CE-T.
Твердая защитная крышка.
Встроенные часы с отображением даты и времени.
ПРЕДУСТАНОВЛЕННЫЕ ПРИЛОЖЕНИЯ
Приложение Cabri Jr.
Приложение позволяет строить, анализировать и трансформировать математические модели и геометрические диаграммы на вашем графическом калькуляторе. Вы можете: Выполнять аналитические, трансформационные функции и функцию Эвклидовой геометрии. Интерактивно строить геометрические фигуры по точкам или группе точек для линий, многоугольников, кругов и других основных геометрических фигур. Переделывать геометрические объекты по ходу выполнения работы, чтобы видеть образцы, выдвигать гипотезы и делать выводы.
Приложение CellSheet
Позволяет работать с электронными таблицами прямо в графическом калькуляторе. Создание формул для ячеек и использование встроенных функций. В ячейки можно поместить: целые числа, действительные числа, формулы, переменные текстовые и числовые последовательности, функции. Каждая электронная таблица содержит 999 строк и 26 колонн. Лимит вводимых данных сводится только к вместимости оперативной памяти. Сохраняйте координатные пары (х, y) в списки, чтобы просматривать и оптимизировать функции для линейного программирования
Лимит вводимых данных сводится только к вместимости оперативной памяти. Сохраняйте координатные пары (х, y) в списки, чтобы просматривать и оптимизировать функции для линейного программирования
Приложение Conic Graphing
Представляет уравнения в виде функции, параметрическом и полярном формате, и предоставляет простой способ рисования четырех конических фигур: эллипс, круг, парабола, гипербола. Введите необходимые параметры, чтобы рисовать, отслеживать или решать задачи с необходимыми данными.
Приложение Inequality Graphing
Предоставляет новые функции для графических уравнений и неравенств, а также нахождение отношений между ними. Вы можете: Вводить неравенства, используя символы отношения. Строить графики неравенств и выделять области пересечения и наложения. Вводить неравенства (только вертикальные линии) в редакторе X=. Отслеживать интересующие вас точки (например, пересечения) между объектами. Сохранять пары координат (х, y) в списки, чтобы просматривать и оптимизировать функции для линейного программирования.
Приложение Periodic Table
Дает графическое представление элементов периодической системы. Приложение позволяет вам: Просматривать и изучать элементы периодической системы. Находить данные о свойствах и полезную информацию об известных элементах. Сортировать элементы по порядковому номеру, в алфавитном порядке или в алфавитном порядке по первым символам. Идентифицировать группы элементов по области (инертные газы, галогены и т.д.) и блокам (p-, d-, s-, f-). Экспортировать данные о свойствах в списки для их дальнейшего анализа. Изображать основные свойства (атомные радиусы, электроотрицательность и т.д.) в сравнении с порядковым номером, чтобы проиллюстрировать периодическую природу элементов.
Приложение Polynomial Root Finder and Simultaneous Equation Editor
Данное приложение: Вычисляет корни (ноли) многочленов со степенью от 1 до 10 с удобным и простым интерфейсом. Позволяет вам сохранять решения в списки, загружать список в приложение для коэффициента многочлена, и сохранять многочлен в переменную Y на графике после выхода из приложения. Находит решения к системам линейных уравнений. Позволяет вам загружать матрицы, содержащие коэффициенты линейных систем, и проверять, имеет ли эта система уникальное решение, бесконечное количество решений или ни одного.
Находит решения к системам линейных уравнений. Позволяет вам загружать матрицы, содержащие коэффициенты линейных систем, и проверять, имеет ли эта система уникальное решение, бесконечное количество решений или ни одного.
Приложение Probability Simulation
Изучайте теорию вероятности с интерактивными анимациями, имитирующими бросок костей и подбрасывание монеты, а также генерируйте случайные числа на своем калькуляторе. Опции включают: гистограммы, таблицу данных о попытках, настройки для определения количества попыток, способы сбора данных, оценивание. Кроме того, студенты могут экспортировать данные для их дальнейшего использования.
Приложение Science Tools
Данное приложение позволяет вам выполнять конвертации единиц на своем калькуляторе. Элементы приложения включают в себя: калькулятор значимых цифр, константы и конвертации, подсказки по данным и графикам, калькулятор векторов
Приложение SmartPad CE-T
Подсоединение калькулятора как удаленной клавиатуры. SmartPad позволяет вам использовать свой калькулятор в качестве удаленной клавиатуры.
SmartPad позволяет вам использовать свой калькулятор в качестве удаленной клавиатуры.
Приложение TI-Innovator Hub
TI-Innovator Hub запускается на калькуляторе с ОС версии 5.2 и выше автоматически, когда оно загружено на калькулятор. Программный редактор TI-Basic оснащен подпунктом HUB, чтобы вы могли использовать подсказки в выполнении команд и ввода данных при программировании в приложении TI-Innovator Hub. Экономьте свое время, используя этот пункт меню, чтобы вставлять полные команды приложения TI- Innovator Hub вместо того, чтобы печатать их вручную с клавиатуры при написании программ.
Приложение Transformation graphing
Приложение Transformation graphing позволяет вам увидеть эффект изменения значений коэффициентов без выхода из экрана графика. Transformation graphing влияет только на режим черчения функций. Х является независимой переменной, а Y — зависимой. Приложение недоступно в параметрическом, полярном и последовательном графических режимах. Приложение Transformation graphing позволяет вам манипулировать с 4 коэффициентами на графике: А, В, С и D. Все другие переменные будут значиться как константы, используя значения из памяти. Вы можете проследить трансформацию функции или анимировать трансформацию, используя функции проигрывания, паузы, скорости воспроизведения.
Все другие переменные будут значиться как константы, используя значения из памяти. Вы можете проследить трансформацию функции или анимировать трансформацию, используя функции проигрывания, паузы, скорости воспроизведения.
Приложение Vernier EasyData
Используйте приложение EasyData от Vernier Software Technology, чтобы совершать исследования. Приложение EasyData автоматически запускает сбор данных, если используется датчик Vernier EasyTemp и загружает встроенные эксперименты для каждого из поддерживаемых датчиков Vernier.
Встроенные функцииTI-84 Plus CE-T
- Загрузка изображений в калькулятор.
- 15 цветов для работы с графиками.
- Изменение стиля и цвета оси и сетки на графике.
- Каталог помощи по синтаксической структуре.
- Алфавитный КАТАЛОГ всех операций калькуляторов TI в одном меню.
- Доступ к более сложным функциям через диалоговое окно меню.
- Вычисление действительных и сложных чисел с точностью до 14 символов, отображение 10 цифр плюс 2-числовой степени.

- Графики — 10 прямоугольных функций, 6 параметрических выражений, 6 полярных выражений, и 3 рекурсивно определенных последовательностей.
- Определение, сохранение, построение и анализ до 10 графических функций одновременно.
- Режим построения последовательностей показывает диаграммы распределения по времени/ паутинную/ ступенчатую и фазовую диаграммы.
- Заданные пользователем имена списка. Показывает до 999 элементов.
- 17 интерактивных возможностей масштабирования.
- Численный расчет в виде таблицы для всех режимов построения графиков
- Интерактивный анализ значения функции, корней, максимальных и минимальных значений, интегралов и производных.
- 8 разных стилей построения графика для просмотра построенного графика в разном виде.
- Опция горизонтального и вертикального разделения экрана.
- Одновременный просмотр графика и таблицы.
- Сохраняет до 10 матриц 50×50.
- Операции с матрицами, включая преобразования, транспозицию, определитель, прибавление, строчную ступенчатую форму и линейные системы.
 Конвертация матриц в списки и обратно.
Конвертация матриц в списки и обратно. - Списочный статистический анализ с одной и двумя переменными, включая следующие модели регрессии: логистическую, синусоидальную, медиан-медианную, линейную, логарифмическую, экспоненциальную, степенную, квадратную многочленную, кубическую многочленную и многочленную в четвертой степени.
- 3 формулировки статистических графиков для графиков рассеяния, линейных xy графиков, гистограмм, обычных диаграмм и диаграмм вида «ящик с усами» графика нормального распределения.
- Более сложные статистические функции, включая 10 функций проверки гипотезы, 7 функций доверительной области и однофакторный дисперсионный анализ отклонений.
- 15 функций распределения вероятностей, включая режимы Нормальный, Студент-t, Хи-квадрат, Двучленный и Пуассоновский.
- Функции для бизнеса, включая временную стоимость денег (Time-Value-of-Money (TVM), денежные потоки (cashflows) и амортизацию. Полноэкранный интерактивный редактор для решения задач с TVM.

- Интерактивный редактор вычисления уравнений позволяет решать в числовом значении различные переменные в уравнении.
- 11 вычислений регрессии.
Программирование:
- Поддерживает программирование TI Basic и ASM
- Программные возможности и количество программ ограничено лишь доступной памятью.
- Также предлагаем вариант TI 84 PLUS CE-T Python Edition с возможностью программировать на Python.
Заключительные характеристики:
Графический калькулятор TI-84 Plus CE-T приходит на смену TI-84 или TI-84 Plus, которые уже давно присутствуют на рынке калькуляторов Texas Instruments, и является последним поколением этого семейства. Представлен в мае 2015 года.
Калькулятор имеет следующие преимущества:
-высокое разрешение экрана 140 dpi, высокая яркость и подсветка;
-возможность выбирать цвет линий для разных графиков;
-калькулятор на 30% тоньше и легче, чем предыдущие модели TI-84, вес всего 164 г. ;
;
-зарядка от сети или через USB-порт компьютера, внешнего блока питания; при этом, более ранние члены семейства калькуляторов TI-84 Plus для питания используют 4 щелочные батареи типа ААА. В новой модели TI-84 Plus CE-T внутренняя литий-ионная батарея (типа 3.7L1200SPA) емкостью 1200 мАч и напряжением 3,7 В обеспечивает 50 часов работы от одной зарядки;
TI-84 Plus CE-T был разработан для большинства стран Европы и поддерживает режим «Press-to-Test», при котором отключаются архивы и некоторые разделы памяти. И также в этом режиме у калькулятора мигает внешний светодиод, по которому экзаменатор визуально контролирует, что калькулятор работает в разрешенном для экзамена режиме.
На сегодняшний день графический калькулятор TI-84 Plus CE-T для экзаменов SAT и международного бакалавриата является абсолютным лидером продаж.
Урок «Калькулятор — информатика, уроки
Урок «Калькулятор» для 7 класс
Цель: Ознакомить учащихся с принципами работы стандартного приложения Windows® «Калькулятор», применяя малоиспользуемые возможности.
Задачи: Научить выполнению арифметического счёта; практическому использованию текстового редактора; закреплению навыков копипейста; ввести понятие линейного алгоритма и подготовить к пониманию ситуации использования алгоритмов на практике.
Знания: Учащиеся получают знания практического использования приложения «Калькулятор», пополнение словаря термином «Алгоритм»; понимание процедур, состоящих из последовательности действий.
Ожидаемый результат: Подготовить учащихся к пониманию и использованию алгоритмических структур.
Умение: В ходе занятия учащиеся обретают навык самостоятельного использования приложений Windows®, вырабатывают алгоритмическое мышление.
Вводная часть (3 мин.)
Здравствуйте. Каждому из вас приходилось решать математические задачи, прибегая к помощи настольного калькулятора или функции калькулятора в сотовом телефоне.
Сегодня мы начнём изучение программы Калькулятор, а так же повторим использование текстового редактора и команды использования буфера обмена. В конце урока, после объяснения, мы выполним практическую работу, за которую можно будет оценить вас с хорошей стороны.
В конце урока, после объяснения, мы выполним практическую работу, за которую можно будет оценить вас с хорошей стороны.
Вопросы к повторению:
Как называются программы, способные создавать и редактировать текстовые документы, назовите их (текстовые редакторы, Блокнот, Word Pad).
Что такое буфер обмена (участок памяти для хранения и переноса цифровых данных в виде текста, графики, звука, видео между приложениями).
Какие команды используют при работе с буфером обмена (копировать, вставить, вырезать).
Назовите сочетания клавиш для вызова команд работы с буфером обмена (Ctrl+C,Ctrl+Insert, Ctrl+V, Shift+Insert, Ctrl+X, Shift+Delete).
Какие операции над числами можно выполнить в калькуляторе сотового телефона (сложение, вычитание, умножение, деление).
Основная часть (20 мин.)
Калькулятор это приложение Windows®, моделирующая работу с обычным электронным калькулятором. Оно позволяет выполнять арифметические действия в режиме Обычный. В старших классах нам пригодится режим Инженерный, в котором можно произвести более сложные вычисления, узнать, как переводят числа в систему, которой владеет компьютер, подсчитать среднее значения вводимых данных и многое другое.
В старших классах нам пригодится режим Инженерный, в котором можно произвести более сложные вычисления, узнать, как переводят числа в систему, которой владеет компьютер, подсчитать среднее значения вводимых данных и многое другое.
Запуск Калькулятора осуществляется по команде Пуск-Программы-Стандартные-Калькулятор (демонстрация запуска). Интерфейс состоит из стандартного заголовка, строки меню, индикатора результата, индикатора использования дополнительной памяти, числовых и специальных кнопок. Числовые кнопки выводят на индикатор цифры, кнопки с изображением арифметических действий позволяют задать команду действия; «=» для получения результата. Кнопки «С» (Clear) подготавливают калькулятор к новому примеру, стирая все данные в памяти; «СЕ» (Clear Edit) очищает строку индикатора; «Backspace» удаляет последнюю цифру. Функция «sqrt» предназначена для извлечения корня квадратного; «%» для вычисления процента от чисел, «1/x» вычисляет обратное значение числа.
Рассмотрим работу калькулятора на примере вычисления выражения: «2+3=». Для получения результата вводим последовательно друг за другом данные, нажимая кнопки:
2 |
| + |
| 3 |
| = |
Сначала первое слагаемое «2» высвечивается на индикаторе, после ввода «+» и второго слагаемого заменяется цифрой «3». Первое слагаемое попадает в ячейку памяти, называемой x. Индикатор связан с ячейкой памяти y (это похоже на названия неизвестных в математике). После «=» на индикатор выводится результат вычисления. Обратите внимание на «1/x», где указано имя ячейки.
Для хранения промежуточных вычислений используется ещё одна ячейка памяти «М» (Memory). «MC» (Memory Clear) очистка дополнительной ячейки, «MR» (MemoryRead) читать из памяти, «MS» (Memory Set) установить данное в память, «M+» дополнить данное ячейки m данным индикатора y. На дополнительном индикаторе высвечивается М, это событие означает, что в ячейке есть информация.
Методическое примечание: работа учеников в тетради заключается в конспектировании обозначений кнопок калькулятора в режиме Обычный, представленных преподавателем и находящихся в учебнике.
Дополнительную память используют при хранении промежуточного результата, или результирующих данных. Пример выражения просуммирует результат произведений: «2×3+4×5 =».
Приведём последовательность нажатия кнопок, отрисованных в окне приложения Калькулятор, заметим, что если числа и знаки арифметических действий можно ввести с клавиатуры, то действия работы с дополнительной памятью доступны только из окна программы:
2 |
| × |
| 3 |
| = |
| MS |
|
|
|
|
|
|
|
|
|
4 |
| × |
| 5 |
| = |
| M+ |
|
|
|
|
|
|
|
|
|
MR |
|
|
|
|
|
|
|
|
Калькулятор связано со сторонними приложениями с помощью буфера обмена, и поэтому результат вычислений можно перенести в текстовый редактор командой Правка-Копировать (на стороне калькулятора), Правка-Вставить (на стороне стороннего приложения).
Методическое примечание: на уроке по теме «Текстовый редактор WordPad: буфер обмена» можно обзорно объяснить работу калькулятора в режиме Обычный для вычисления простейших выражений и переноса результатов вычислений в текстовый редактор с помощью буфера обмена. В практическом задании (например, создание прайс-листа с использованием изображения и ценника) в текстовый документ помещается рисунок, созданный в графическом редакторе и числовые значения, вычисленные в калькуляторе.
Для наглядности введём данный пример «2*3+4*5=» в приложение Блокнот, описав знак умножения символом «*». Выполним вычисления и результат перенесём из калькулятора. При решении похожих выражений возникает необходимость вновь и вновь вводить выражения, используя клавиши дополнительной клавиатуры или отрисованные кнопки интерфейса окна приложения. Поэтому предлагаю ускорить вычисления и воспользоваться «шпаргалками», записанными в блокноте. Воспользуемся тем, что приложение калькулятор с помощью буфера обмена может перенести не только результаты вычислений из индикатора и обратно, но и математическое выражение, записанное в Блокноте в Калькулятор.
Рисунок 1. Комплект используемых приложений.
Выделим выражение «2*3+4*5=», скопируем его в буфер обмена, в режиме калькулятора Инженерный вставим из буфера и получим результат «26».
Методическое примечание: в режиме Обычный калькулятор не учитывает приоритет арифметических действий, выполняя действия по-порядку, как записано. Поэтому для выполнения данной работы используем режим Инженерный. Для первичной демонстрации можно использовать режим обычный, но только используя пример вычисления выражений с одним действием «2+2=», содинаковым приоритетом действий «2+2+2=», специально подготовленный пример «2*2+2=», или используя скобки «2+(2*2)=». Для продолжения вычислений перейти в режим Инженерный (для математически подготовленных учащихся можно назвать причину перехода в другой режим).
Для решения примеров с использованием дробей необходимо помнить правило: все дроби записываются в строку, поэтому «двухэтажных» дробей не бывает. Например,⅔ в Блокноте запишем строкой 2/3. Для более сложных примеров используют скобки, способные изменить порядок вычислений, например «2*(3+4)=». «(2+3)/(6-1)=» вычисляется выражение в числителе, затем знаменателе, последнее действие – деление.
Например,⅔ в Блокноте запишем строкой 2/3. Для более сложных примеров используют скобки, способные изменить порядок вычислений, например «2*(3+4)=». «(2+3)/(6-1)=» вычисляется выражение в числителе, затем знаменателе, последнее действие – деление.
Методическое примечание: данное выражение можно было бы посчитать непосредственно в режиме Обычный, используя дополнительную память и вычисления начать со знаменателя, что не всегда очевидно для школьника:
6 |
| — |
| 1 |
| = |
| MS |
|
|
|
|
|
|
|
|
|
2 |
| + |
| 3 |
| = |
| / |
|
|
|
|
|
|
|
|
|
MR |
| = |
|
|
|
|
|
|
Инженерный режим позволяет использовать скобки, при этом запись выражения становится прозрачной и придерживается математической записи выражения, хотя количество действий не изменяется:
( |
| 2 |
| + |
| 3 |
| ) |
|
|
|
|
|
|
|
|
|
/ |
| ( |
| 6 |
| — |
| 1 |
|
|
|
|
|
|
|
|
|
) |
| = |
|
|
|
|
|
|
Способ с использованием дополнительного текстового редактора позволяет показать связь между приложениями и повторить навыки использования текстового редактора и буфера обмена.
Имеет все преимущества использования текстового файла:
сохранение для последующей работы;
редактирование при решении подобных примеров;
наглядное представление выражения.
Создаётся понимание того, что алгоритм может быть записан пользователем в текстовом редакторе и выполняется исполнителем.
Вся запись в Блокноте записывается в одну строку, в одну линию и состоит из отдельных символов. В калькулятор из буфера обмена информация тоже вводится посимвольно, последовательно, друг за другом, команда за командой (если считать каждый символ командой ввода этого символа). Такую последовательность команд для решения исполнителем примеров называют Алгоритмом, исполнителем является калькулятор. В старших классах мы будем использовать более сложные алгоритмы для решения задач на компьютере, а сегодня решим простые математические примеры данным приёмом.
Практическая часть (20 мин. )
)
Практическая работа состоит из двух примеров в варианте. Запустите Блокнот, Калькулятор, переведите калькулятор в режим Инженерный (Вид-Инженерный). Выберите задание. В Блокноте введите первый пример в одну строку, используя скобки, помня правило написания дробей. Выделите написанный пример со знаком равенства и скопируйте его в буфер обмена. Вставьте в Калькулятор из буфера обмена последовательность символов и получите результат. Запишите ваше выражение из Блокнота в тетрадь. Очистите калькулятор и приступите к следующему примеру. Если целая часть числа равна нулю, то для его записи в выражениях ноль можно опустить и начать запись с десятичной запятой («0,4» = « ,4»).
Методическое примечание: данное замечание полнее раскрывает понятие «Математическое выражение», записанное по правилам алгоритмичесих языков программирования.
Вариант 1.
1.
Рисунок 2. Пример 1.
(ответ: 10; (3-0,5)*(1+6*0,5)/(2*0,5)=)
2.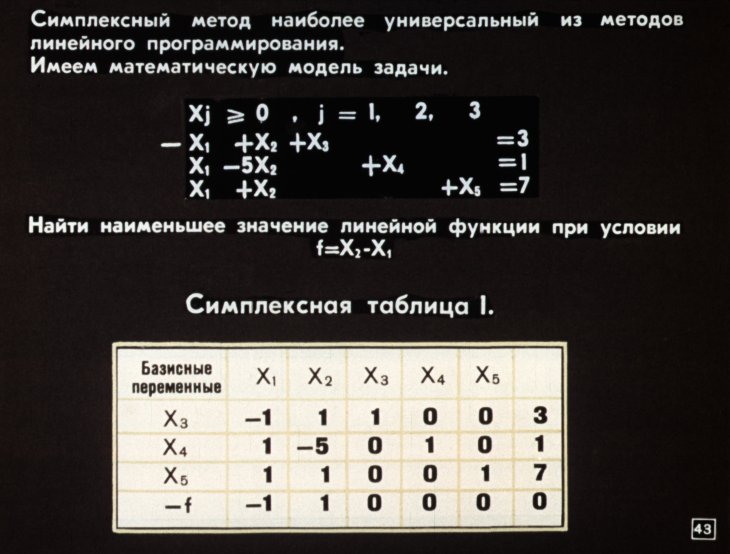
Рисунок 3. Пример 2.
(ответ: 2; (28-34+63*2)/(55+20/4)=)
Вариант 2.
1.
Рисунок 4. Пример 1.
(ответ: 27; (5-,5)*(2+4*2,5)/(4*,5)=)
2.
Рисунок 5. Пример 2.
(ответ: 2; (20-46+73*2)/( 30/5+54)=)
Заключение (2 мин.)
Сегодня на уроке мы повторили возможности работы с Блокнотом, буфером обмена и узнали о применении текстового редактора при работе с приложением Калькулятор. Все последовательности действий называются алгоритмом, мы смогли их реализовать и получить результат, при этом исполнял наши алгоритмы калькулятор. Мы использовали линейный алгоритм. В старших классах вы узнаете о существовании других типов алгоритмов. Вы сможете писать алгоритмы на особых языках программирования и вас можно будет назвать программистами. Урок окончен, благодарю.
Методическое примечание: в конце урока даётся оценка работы и выставляется отметка.
Калькулятор линейного программирования + онлайн-решатель с бесплатными шагами
Калькулятор линейного программирования — это бесплатный онлайн-калькулятор, который обеспечивает наилучшее оптимальное решение для заданной математической модели.
Этот онлайн-калькулятор решает проблему поиска правильного решения или оптимизированного вывода желаемых математических моделей, предоставляя быстрое, надежное и точное решение.
Пользователь просто должен ввести целевую функцию вместе с системой линейных ограничений и решение появится на их экранах всего за несколько секунд. Калькулятор линейного программирования является наиболее эффективным инструментом линейной оптимизации и может использоваться для эффективного и логичного решения сложных и трудоемких задач и моделей.
Что такое калькулятор линейного программирования?
Калькулятор линейного программирования — это онлайн-калькулятор, который можно использовать для линейной оптимизации различных математических моделей.
Это удобный и удобный инструмент с простым в использовании интерфейсом, который помогает пользователю найти точное и оптимизированное решение для заданных ограничений быстрее, чем любой другой математический метод, применяемый вручную.
Калькулятор линейного программирования помогает пользователю избежать долгих математических вычислений и получить желаемый ответ, просто нажав одну кнопку.
Калькулятор может решать задачи, содержащие максимум девять различных переменных не более того. Требуется «, » в качестве разделителя для нескольких ограничений в одном поле.
Давайте узнаем больше о калькуляторе и о том, как он работает.
Как пользоваться калькулятором линейного программирования?
Вы можете использовать калькулятор линейного программирования , введя целевую функцию и указав ограничения. После того, как вы закончите вводить все входные данные, вам просто нужно нажать кнопку отправки, и подробное решение будет отображаться на экране всего за несколько секунд.
Ниже приведены подробные пошаговые инструкции по поиску наилучшего возможного решения для заданной целевой функции с указанными ограничениями. Выполните эти простые шаги и узнайте максимумы и минимумы функций.
Шаг 1
Рассмотрите желаемую целевую функцию и укажите ее ограничения.
Шаг 2
Теперь введите целевую функцию на вкладке, указанной как Целевая функция .
Шаг 3
После добавления целевой функции введите условия всех ограничений на вкладке с именем Тема . Калькулятор может принять максимум девяти ограничений и имеет больше вкладок для него под названием More Constraints . Чтобы добавить несколько ограничений в один блок, вы должны использовать «, » в качестве разделителя.
Шаг 4
После заполнения всех полей ввода выберите категорию оптимизации из Оптимизировать выпадающее меню. Есть три варианта, которые вы можете выбрать, чтобы найти максимума целевой функции, минимума целевой функции или вы можете выбрать оба.
Есть три варианта, которые вы можете выбрать, чтобы найти максимума целевой функции, минимума целевой функции или вы можете выбрать оба.
Параметры в раскрывающемся меню представлены следующим образом:
- Макс.
- Мин.
- Макс./мин.
Шаг 5
отображаться в окне результатов.
Не добавляйте в калькулятор более девяти ограничений, иначе он не даст желаемых результатов.
Шаг 6
Вы можете просмотреть окно результатов под макетом калькулятора. Окно Результат содержит следующие блоки:
Интерпретация ввода
Этот блок показывает ввод , введенный пользователем, и то, как он был интерпретирован калькулятором. Этот блок помогает пользователю разобраться, не было ли ошибок во входных данных.
Глобальный максимум
В этом блоке показаны рассчитанные глобальных максимума заданной целевой функции.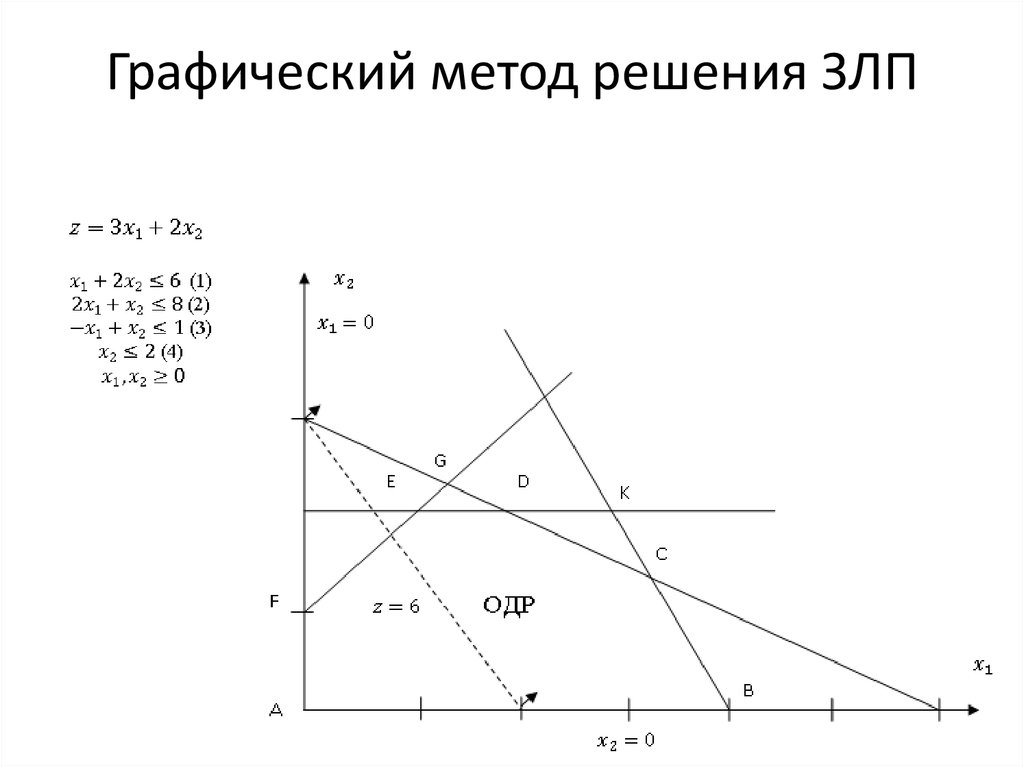 Глобальные максимумы — это общее наибольшее значение целевой функции.
Глобальные максимумы — это общее наибольшее значение целевой функции.
Глобальный минимум
Этот блок отображает глобальных минимума заданной целевой функции. Глобальные минимумы — это общее наименьшее значение данной функции с указанными ограничениями.
3D-график
В этом блоке отображается интерпретация 3D целевой функции. Он также указывает точки максимума и минимума на трехмерном графике.
Контурный график
Контурный график представляет собой двухмерное представление глобальных максимумов и глобальных минимумов целевой функции на графике.
Как работает калькулятор линейного программирования?
Калькулятор линейного программирования работает путем вычисления наилучшего оптимального решения целевой функции с использованием техники линейного программирования, которая также называется Линейная оптимизация.
Математическая оптимизация — это метод, используемый для поиска наилучшего возможного решения математической модели, такой как определение максимальной прибыли или анализ размера стоимости проекта и т. д. Это тип линейного программирования, который помогает оптимизировать линейную функцию при условии, что заданные ограничения выполняются.
д. Это тип линейного программирования, который помогает оптимизировать линейную функцию при условии, что заданные ограничения выполняются.
Чтобы лучше понять работу Калькулятора линейного программирования , давайте обсудим некоторые важные концепции.
Что такое линейное программирование (ЛП)?
Линейное программирование — это метод математического программирования, который стремится следовать наилучшему оптимальному решению математической модели при заданных условиях, называемых ограничениями. Он берет различные неравенства, применяемые к определенной математической модели, и находит оптимальное решение.
Линейное программирование подвергается только ограничениям линейного равенства и неравенства. Это применимо только к линейным функциям, которые являются функциями первого порядка. линейная функция обычно изображается прямой линией, а стандартная форма имеет вид y = ax + b.
В линейном программировании есть три компонента: переменные решения, целевая функция и ограничения. Обычная форма линейной программы задается следующим образом:
Первым шагом является определение переменной решения, которая является неизвестным элементом в задаче.
переменная решения = x
Затем решите, является ли требуемая оптимизация максимальным или минимальным значением. 9T \times X \]
Где C — вектор.
Наконец, вам нужно описать ограничения, которые могут быть в форме равенств или неравенств, и они должны быть указаны для заданных переменных решения.
Ограничения для целевой функции могут быть определены как:
\[ AX \leq B \]
\[ X \geq 0 \]
Где A и B — векторы. Поэтому линейное программирование является эффективным методом оптимизации различных математических моделей.
Таким образом, калькулятор линейного программирования использует процесс линейного программирования для решения задач за секунды.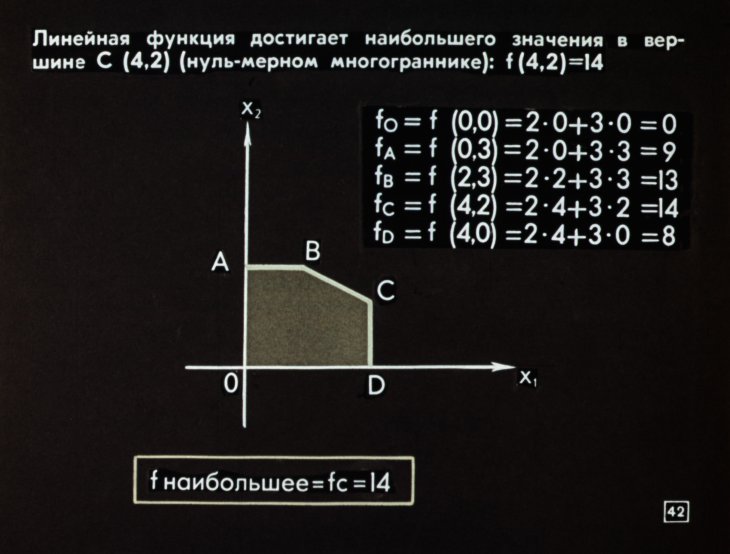
Благодаря своей эффективности может использоваться в различных областях обучения. Математики и бизнесмены широко используют его, и это очень полезный инструмент для инженеров, помогающий им решать сложные математические модели, формируемые для различных целей проектирования, планирования и программирования.
Представление линейных программ
A линейная программа может быть представлен в различных формах. Во-первых, это требует определения максимизации или минимизации целевой функции, а затем ограничений. Ограничения могут быть как в виде неравенств $( \leq , \geq )$, так и в виде равенства ( = ).
Линейная программа может иметь переменные решения, представленные как $ x_1, x_2, x_3, …….., x_n $.
Таким образом, общая форма линейной программы задается как:
Минимизация или максимизация:
\[ y = c_o + c_1x_1 + c_2x_2 + …. + c_nx_n \]
Тема:
\[ a_1i x_1+ a_2ix_2 + a_3ix_3 +……. + a_nix_n = b_i \]
\[ a_1ix_1 + a_2ix_2 + a_3ix_3 +……. + a_nix_n \leq b_i \]
+ a_nix_n \leq b_i \]
\[ a_1ix_1+ a_2ix_1 + a_3ix_2 +……. + a_nix_n \geq b_i \]
Где i = 1,2,3,……..,m.
\[ x_k \geq 0 \]
\[ x_k < 0 \]
\[ x_k > 0 \]
Где k = 1,2,3,……..,m.
Здесь $x_k$ — переменная решения, а $a_in$, $b_i$ и $c_i$ — коэффициенты целевой функции.
Решенные примеры
Давайте обсудим некоторые примеры линейной оптимизации математических задач с использованием Калькулятора линейного программирования .
Пример 1
Максимизируйте и минимизируйте целевую функцию, заданную как:
\[ 50x_1 + 40x_2 \]
Ограничения для вышеупомянутой целевой функции задаются как:
\[3x_1 + 1x_2 <= 27005 \]
\[ 6x_1 + 4x_2 >= 600 \]
\[ 5x_1 + 5x_2 = 600 \]
\[ x_1 \geq 0 \]
\[ x_2 \geq 0 \]
Используйте калькулятор для оптимизации данной функции.
Решение
Выполните шаги, описанные ниже:
Шаг 1
Выберите параметр макс. /мин. в раскрывающемся меню «Оптимизировать».
/мин. в раскрывающемся меню «Оптимизировать».
Шаг 2
Введите целевую функцию и функциональные ограничения в указанные блоки.
Шаг 3
Теперь нажмите кнопку отправки, чтобы просмотреть результаты.
Общий максимум функции задается как:
\[ max( 50x_1 + 40x_2 )_{at ( x_1, x_2 )} = (120, 0 ) \]
Глобальный минимум функции задается как:
\[ min ( 50x_1 + 40x_2 )_ {at ( x_1, x_2 )} = (60, 60 ) \]
Трехмерный график показан на рисунке 1:
Рисунок 1
Контурный график приведен на рисунке 2 ниже:
Рисунок 2
Пример 2
План диеты, составленный диетологом, содержит три типа питательных веществ из двух типов пищевых категорий. Исследуемые питательные вещества включают белки, витамины и крахмал. Пусть две категории продуктов будут $x_1$ и $x_2$.
Ежедневно необходимо потреблять определенное количество каждого питательного вещества. Питательная ценность белков, витаминов и крахмала в пище $x_1$ составляет 2, 5 и 7 соответственно. Для пищевой категории $x_2$ питательная ценность белков, витаминов и крахмала составляет 3,6 и 8 соответственно.
Для пищевой категории $x_2$ питательная ценность белков, витаминов и крахмала составляет 3,6 и 8 соответственно.
Суточная потребность каждого питательного вещества составляет 8, 15 и 7 соответственно.
Стоимость каждой категории $2$ за $кг$. Определите целевую функцию и ограничения, чтобы узнать, сколько пищи необходимо потреблять в день, чтобы минимизировать затраты.
Решение
Переменными решения являются $x_1$ и $x_2$.
Целевая функция задается как:
\[ y = 2x_1 + 2x_2 \]
Различные ограничения для данной целевой функции, проанализированные на основе данных, приведенных выше:
\[ x_1 \geq 0 \]
\[ x_2 \geq 0 \]
\[ 2x_1 + 3x_2 > 8 \]
\[ 5x_1 + 6x_2 > 15 \]
\[ 7x_1 + 8x_2 > 7 \]
Все ограничения неотрицательны так как количество еды не может быть отрицательным.
Введите все данные в калькулятор и нажмите кнопку отправки.
Получены следующие результаты:
Локальный минимум
\[ min( 2x_1 + 2x_2 ) = (0, 2,67)
3D-график
Трехмерное представление показано на рисунке 3 ниже:
5 Контур 3Рисунок 3 Участок
Контурный график показан на рисунке 4:
Рисунок 4
Все математические изображения/графики созданы с помощью GeoGebra.
Математические калькуляторы Список
Здесь появятся таблицы (шаги). О калькуляторе линейного программирования:Линейное программирование считается лучшей оптимизацией метод решения целевой функции с заданной линейной переменные и линейные ограничения. Он также обеспечивает оптимальную решение заданной линейной задачи. Основная цель определенных метод заключается в том, чтобы узнать значение переменных, которые необходимы максимизировать или минимизировать целевую функцию. Однако целевая функция используется для определения суммы или
значение, которое должно быть оптимизировано, а ограничения используются для
определить диапазон переменной. В основном состоит из четырех основных
компоненты, которые представляют собой целевую функцию, ограничения, данные и
переменная решения. Все эти компоненты являются обязательными для нахождения
Решение проблемы. Итак, после получения базовой информации о том, что это такое, давайте посмотрим, как
использовать калькулятор задач линейного программирования.
Это основные шаги, которые необходимо выполнить при использовании линейной задачи.
калькулятор. Когда вы используете калькулятор линейного программирования, вы
следует выбрать ввод для максимизации или минимизации для данного
линейная задача. Некоторые калькуляторы обеспечивают только максимизацию
функциональность для решения линейной задачи, которая известна как
Калькулятор максимизации. Как решить задачи линейного программирования?Кроме того, проблемы также могут быть решены с помощью линейного программирования Калькулятор ТИ 84 плюс. Можно сказать, что это техника решения и найти максимальное и минимальное значение многомерной и целевая функция, которая ограничена неравенствами внутри система. Однако эти неравенства можно решить с помощью линейного программирования калькулятор ти 84 плюс. Он основан на теореме о том, что если система неравенств присутствует в задаче, то следует оценить целевая функция в точке пересечения, где наименьшее значение — это минимальное значение функции, а наибольшее value — максимальное значение функции. Таким образом, неравенства могут быть решены. Чтобы узнать максимальное и минимальное значение для данной линейной задачи с помощью TI-84 plus, выполните следующие действия:
Таким образом, с помощью описанных выше шагов линейные задачи могут быть решены с
калькулятор линейного программирования, который обеспечивает функцию TI-84
плюс. Другой инструмент доступен для решения линейных задач с
другой подход, который представляет собой калькулятор линейного программирования с 3
переменные. Вы можете использовать этот калькулятор, когда у вас есть более одного
линейное уравнение или три линейных уравнения для решения задачи с
три заданные переменные. Когда вы используете калькулятор LP для решения своей задачи, он предоставляет прямое решение максимизации или минимизации. Хотя, если вы хотите найти минимальный элемент набора данных для шага линейной задачи пошагово, то доступен калькулятор минимизации. В то же самое Кстати, вы можете использовать калькулятор максимизации, чтобы узнать максимальный элемент набора данных для данной линейной задачи шаг за шагом. Это будет помочь вам понять линейные задачи более подробно. Несколько других инструментов: Еще один аналогичный инструмент — калькулятор целевой функции.
который помогает решать задачи двумерного программирования с
заданная система линейных неравенств и заданная линейная цель
функция. Вы можете получить несколько возможных решений для вашей проблемы
через этот калькулятор. Кроме того, он также известен как
Калькулятор оптимального решения. Когда можно получить минимальное или максимальное значение для линейного уравнения с системой неравенств можно получить оптимальную решение. Подведение итогов!Кроме того, это инструмент для предоставления решения для математический метод, который используется для получения наилучшего результата в заданная линейная задача и математическая модель, которая представлена линейные отношения. И последнее, но не менее важное: я думаю, что из приведенной выше информации теперь вы можете легко решить все свои проблемы без какой-либо путаницы. Так, просто начните использовать этот бесплатный онлайн-инструмент и сэкономьте свое время. Также, поделитесь этой информацией со своими друзьями, которые также хотят узнать эти простые методы решения проблем. |
Калькулятор угловых точек| Линейное программирование
Этот калькулятор угловых точек поможет вам решить задачу линейного программирования и найти угловых точек допустимой области . Он также найдет угловую точку, в которой происходит максимальное или минимальное значение целевой функции .
Он также найдет угловую точку, в которой происходит максимальное или минимальное значение целевой функции .
Если какой-либо из этих терминов вызывает недоумение, не волнуйтесь. Мы здесь, чтобы сделать вашу жизнь проще😉. В этой статье мы обсудим линейное программирование , вычисление и поиск допустимых областей, как найти угловые точки алгебраически и графически , а также максимизировать или минимизировать целевую функцию . Так что, пожалуйста, возьмите чашку кофе ☕️ и давайте вместе разберемся с математикой угловых точек!
Задача линейного программирования (LPP)
Модель условной оптимизации — это математическая модель, которая находит наилучшее решение (или оптимальное решение ), который удовлетворяет заданному набору ограничений.
Модель оптимизации с ограничениями состоит из трех основных частей:
Переменные решения — это переменные в проблеме или системе, которые мы должны оптимизировать.
 Их представляют алгебраические символы, например, xxx,yyy или x1x_1x1, x2x_2x2 и т. д.
Их представляют алгебраические символы, например, xxx,yyy или x1x_1x1, x2x_2x2 и т. д.Целевая функция — это оценивающий критерий , который мы должны максимизировать или минимизировать. Это функция из переменные решения и, возможно, показатель прибыли, время обработки и т. д., которые мы должны максимизировать или минимизировать.
Ограничения — это система равенств или неравенств, представляющая любые ограничения, обусловленные технологией, физикой, экономикой и т. д. Например, ограничение может ограничивать количество денег, затрачиваемых в каждом процессе, количество веса, разрешенного в каждом мешке, и т. д. Оптимальное решение задачи должно удовлетворять всем ограничениям.
Линейная программа представляет собой модель оптимизации с ограничениями, которая отвечает следующим требованиям:
- Переменные решения должны быть непрерывными в заданном диапазоне.

- Целевая функция и левая часть ограничений (неравенства) должны быть линейными функциями .
Математически мы можем записать задачу линейного программирования (LPP) как:
Максимизация/минимизация P=pxx+pyy\scriptsize \text{Максимизация/минимизация } P = p_x x + p_y y Развернуть/свернуть P=pxx+pyy
≤при условии a1x+b1y=c1≥≤a2x+b2y=c2≥⋮≤anx+bny=cn≥\scriptsize\begin{align*} &\leq\\ \text{при условии}\kern{4em} a_1 x + b_1 y &= c_1\\ & \geq\\\\ &\leq\\ a_2 x + b_2 y &= c_2\\ & \geq\\ \vdots\kern{1.5em}&\\ &\leq\\ a_n x + b_n y &= c_n\\ & \geq\\ \end{align*}при условии a1x+b1ya2x+b2y⋮anx+bny≤=c1≥≤=c2≥≤=cn≥
, где:
- ППС – Целевая функция ;
- px,pyp_x, p_ypx,py – Коэффициенты из переменных решения в целевой функции ;
- x,yx,yx,y – Переменные решения ;
- a1,a2,an,b1,b2,bna_1,a_2, a_n, b_1,b_2,b_na1,a2,an,b1,b2,bn – Коэффициенты из переменных решения в ограничения ; и
- c1,c2,cnc_1, c_2, c_nc1,c2,cn – Константы в равенстве или неравенстве, используемые для выражения ограничений .

Обычно переменные решения должны быть неотрицательными , т. е. x≥0x\geq0x≥0, y≥0y\geq0y≥0. Это тоже ограничения на модель, и мы можем выразить их, выбрав соответствующие значения для коэффициентов ana_nan и bnb_nbn в ограничениях.
Допустимая область и угловые точки
Набор точек, удовлетворяющих ограничениям LPP, называется допустимым набором . Если мы нанесем все ограничения на график, область, пересекающая все эти неравенства, будет содержать допустимое множество. Мы называем этот регион возможная область .
Возможная область (заштрихована) и ее угловые точки на графике. Обратите внимание, что каждая точка допустимой области удовлетворяет всем ограничениям. угловых точек (или крайних точек) допустимой области являются точками пересечения двух (или более) ограничений. Возможная область может быть ограниченной или неограниченной, но должна иметь по крайней мере одну угловую точку.
Хотя каждая точка допустимого множества технически является решением для LPP, оптимальное решение — это решение, которое должно максимизировать или минимизировать целевую функцию . В линейном программировании хотя бы одна угловая точка является оптимальным решением .
Как найти угловые точки алгебраически
Попробуем понять, как найти угловые точки алгебраически на примере. Рассмотрим следующий LPP:
Максимизируйте P=30x+40y\scriptsize \text{Максимизируйте}\kern{4.4em} P = 30 x + 40 yМаксимизируйте P=30x+40y
при условии 2x+3y≤18x+y≤9x+2y≤16x≥0y≥0\scriptsize\begin{align*} \text{при условии}\kern{5em} 2 x + 3 y &\leq 18\\ х + у &\leq 9\\ х+2у &\leq 16\\ х& \geq 0\\ у& \geq 0 \end{align*}subject to 2x+3yx+yx+2yxy≤18≤9≤16≥0≥0
Мы можем найти угловые точки алгебраически, выполнив следующие шаги:
- Преобразование в неравенств в ограничениях на равенств .
 Получим следующую систему линейных уравнений:
Получим следующую систему линейных уравнений:
2x+3y=18x+y=9x+2y=16x=0y=0\kern{4.8em}\scriptsize\begin{align*} 2 х + 3 у &= 18\\ х + у &=9\\ х+2у &=16\\ х& = 0\\ у& = 0 \end{align*}2x+3yx+yx+2yxy=18=9=16=0=0
- Решите этих линейных уравнений, взяв набор любых двух уравнений одновременно, чтобы найти пересекающихся точка , удовлетворяющая обоим уравнениям. Давайте проиллюстрируем это для первых двух уравнений:
2x+3y=18x+y=9\kern{4.8em}\scriptsize\begin{align*} 2 х + 3 у &= 18\\ х + у &=9{nd}\text{ уравнение}\\ Подставив y=0 во второе уравнение
x=9\kern{6em}\scriptsize x = 9x=9
Следовательно, точка (9,0)(9,0)(9,0) является решением для уравнения 2x+3y=182x+3y=182x+3y=18 и x+y=9x+y=9x+y=9. Точно так же найдите решения для любого другого набора уравнений, чтобы получить их точки пересечения. Кроме того, вы можете использовать наш калькулятор системы уравнений или калькулятор метода подстановки, чтобы найти решения быстрее и проще!
Уравнения | Точка пересечения |
|---|---|
2x+3y=182x+3y=182x+3y=18,x+y=9x+y=9x+y=9 | (9,0)(9,0)(9,0) |
2x+3y=182x+3y=182x+3y=18,x+2y=16x+2y=16x+2y=16 | (-12,14)(-12,14)(-12,14) |
2x+3y=182x+3y=182x+3y=18,x=0x=0x=0 | (0,6)(0,6)(0,6) |
2x+3y=182x+3y=182x+3y=18,y=0y=0y=0 | (9,0)(9,0)(9,0) |
х+у=9х+у=9х+у=9, х+2у=16х+2у=16х+2у=16 | (2,7)(2,7)(2,7) |
х+у=9х+у=9х+у=9, х=0х=0х=0 | (0,9)(0,9)(0,9) |
х+у=9х+у=9х+у=9, у=0у=0у=0 | (9,0)(9,0)(9,0) |
х+2у=16х+2у=16х+2у=16, х=0х=0х=0 | (0,8)(0,8)(0,8) |
х+2у=16х+2у=16х+2у=16, у=0у=0у=0 | (16,0)(16,0)(16,0) |
х=0х=0х=0, у=0у=0у=0 | (0,0)(0,0)(0,0) |
- Применить неравенство ограничения к этому набору из пересекающихся точек и извлечь точки, которые удовлетворяют все данных неравенств.
 Эти точки являются нашими угловыми точками ! Любая точка, которая не удовлетворяет всем неравенствам ограничений, лежит на вне допустимой области .
Эти точки являются нашими угловыми точками ! Любая точка, которая не удовлетворяет всем неравенствам ограничений, лежит на вне допустимой области .
Например, точка (9,0)(9,0)(9,0) удовлетворяет всем ограничениям:
2(9)+3(0)=18≤18(9)+(0) =9≤9(9)+2(0)=9≤16(9)=9≥0(0)=0≥0\scriptsize\begin{align*} 2 (9) + 3 (0) &= 18 \leq 18\\ (9) + (0) &=9 \leq 9\\ (9)+2(0) &=9 \leq16\\ (9)& = 9 \geq 0\\ (0)& = 0 \geq 0 \end{выравнивание*}2(9)+3(0)(9)+(0)(9)+2(0)(9)(0)=18≤18=9≤9=9≤16=9≥0=0≥0
Следовательно, (9,0)(9,0)(9,0) является угловой точкой . С другой стороны, точка (−12,14)(-12,14)(−12,14) не удовлетворяет ограничению x≥0x\geq0x≥0 и, следовательно, лежит вне возможных регион .
Проверьте свое понимание, применяя ограничения для оставшихся точек, чтобы получить оставшиеся угловые точки. Вы можете проверить свой ответ по таблице угловых точек в конце следующего раздела.
Как графически найти угловые точки неравенств
Давайте продолжим использовать ту же задачу LPP, которую мы представили в предыдущем разделе. Чтобы графически найти угловые точки допустимой области, выполните следующие действия:
- Преобразуйте неравенства в ограничениях в равенства . Мы получим следующие линейных уравнения :
2x+3y=18x+y=9x+2y=16x=0y=0\kern{4.8em}\scriptsize\begin{align*} 2 х + 3 у &= 18\\ х + у &=9\\ х+2у &=16\\ х& = 0\\ у& = 0 \end{align*}2x+3yx+yx+2yxy=18=9=16=0=0
- Постройте эти линии на графике . Одним из простых способов является нахождение x- и y-отрезков . Чтобы получить точку пересечения x для линии 2x+3y=182x+3y=182x+3y=18, подставьте y=0y=0y=0; мы получаем х=9х=9х=9. Следовательно, (9,0)(9,0)(9,0) является точкой пересечения по оси x.
 Точно так же подставьте x=0x=0x=0, чтобы получить точку пересечения y (0,6)(0,6)(0,6). Вы можете использовать наш калькулятор формы пересечения наклона, чтобы найти пересечения из уравнения прямой.
Точно так же подставьте x=0x=0x=0, чтобы получить точку пересечения y (0,6)(0,6)(0,6). Вы можете использовать наш калькулятор формы пересечения наклона, чтобы найти пересечения из уравнения прямой.
- Затенение область графа, которая удовлетворяет всем ограничениям . Это возможная область LPP. Это пересечение всех неравенств ограничений.
- Извлечь угловых точек из вершин из граница допустимой области . Полученные таким образом угловые точки:
Угловые точки |
|---|
(9,0)(9,0)(9,0) |
(0,6)(0,6)(0,6) |
(0,0)(0,0)(0,0) |
Как найти оптимальное решение с помощью угловых точек?
Оптимальное решение задачи линейного программирования будет иметь хотя бы одну из угловых точек. Чтобы найти оптимальное решение по угловым точкам, выполните следующие действия:
Чтобы найти оптимальное решение по угловым точкам, выполните следующие действия:
- Оцените целевую функцию в каждой угловой точке .
- Если цель состоит в том, чтобы максимизировать целевую функцию , найти угол точки, которая дает наибольшее значение целевой функции .
- Если цель состоит в том, чтобы минимизировать целевую функцию , найти угловую точку , которая дает наименьшее значение целевой функции .
Помните, что можно найти несколько угловых точек, обеспечивающих оптимальное решение.
Оценим целевую функцию в нашем примере, чтобы найти оптимальное решение:
Угловая точка | P=30x+40yP = 30x+40yP=30x+40y | |
|---|---|---|
(9,0)(9,0)(9,0) | 270270270 | Максимум |
(0,6)(0,6)(0,6) | 240240240 | |
(0,0)(0,0)(0,0) | 000 |
Поскольку наша цель состояла в том, чтобы максимизировать P=30x+40yP = 30x+40yP=30x+40y, оптимальное решение равно 270270270 и находится в угловой точке (9,0)(9,0)(9,0).
Как использовать этот калькулятор угловых точек (онлайн-решатель LP)
Этот калькулятор угловых точек представляет собой простой инструмент для решения данного LPP путем нахождения угловых точек неравенств (или ограничений) и вычисления целевой функции . Он может обрабатывать две переменные решения и до пять ограничений :
- Введите коэффициенты pxp_xpx и pyp_ypy из целевая функция .
- Выберите , должен ли этот калькулятор линейного программирования минимизировать или максимизировать целевую функцию.
- Выберите количество ограничений в линейной программе.
- Введите коэффициенты aaa, bbb и ccc каждого ограничения .
- Этот калькулятор угловых точек сгенерирует таблицу всех угловых точек , за которой следуют оптимальное решение путем вычисления целевой функции и ограничений.

💡 Совет: изо всех сил пытаетесь добавить неотрицательных (или неположительных ) ограничений на переменные решения? Вы можете сделать это, введя 000 и 111 в качестве переменной коэффициентов ! Например, чтобы применить ограничение x≥0x \geq 0x≥0, введите a1a_1a1 как 111, b1b_1b1 как 000 и c1c_1c1 как 000. Убедитесь, что вы выбрали правильный знак неравенства!
Если результаты не отображаются, значит, калькулятор не нашел угловых точек на основе введенных вами данных, и это неразрешимая задача . Попробуйте ослабить ограничения, чтобы создать достижимую область.
Часто задаваемые вопросы
Какая точка допустимой области максимизирует целевую функцию?
максимальное (или минимальное) значение целевой функции должно встречаться в любой из угловых точек допустимой области . Чтобы определить эту точку, выполните следующие действия:
Чтобы определить эту точку, выполните следующие действия:
- Оцените целевую функцию в каждой угловой точке допустимой области.
- Определите максимальное среди этих расчетных значений. Точка угла , в которой находится это значение, является точкой, в которой максимизирует целевую функцию .
В некоторых случаях можно найти более одной угловой точки, которая максимизирует целевую функцию.
Может ли область осуществимости состоять из двух отдельных частей?
№ . область допустимости в задаче линейного программирования представляет собой пересечение различных областей, каждая из которых удовлетворяет конкретному ограничению (неравенству). Следовательно, его область допустимости всегда одна область пространства, которая удовлетворяет всем ограничениям , ограниченным или неограниченным.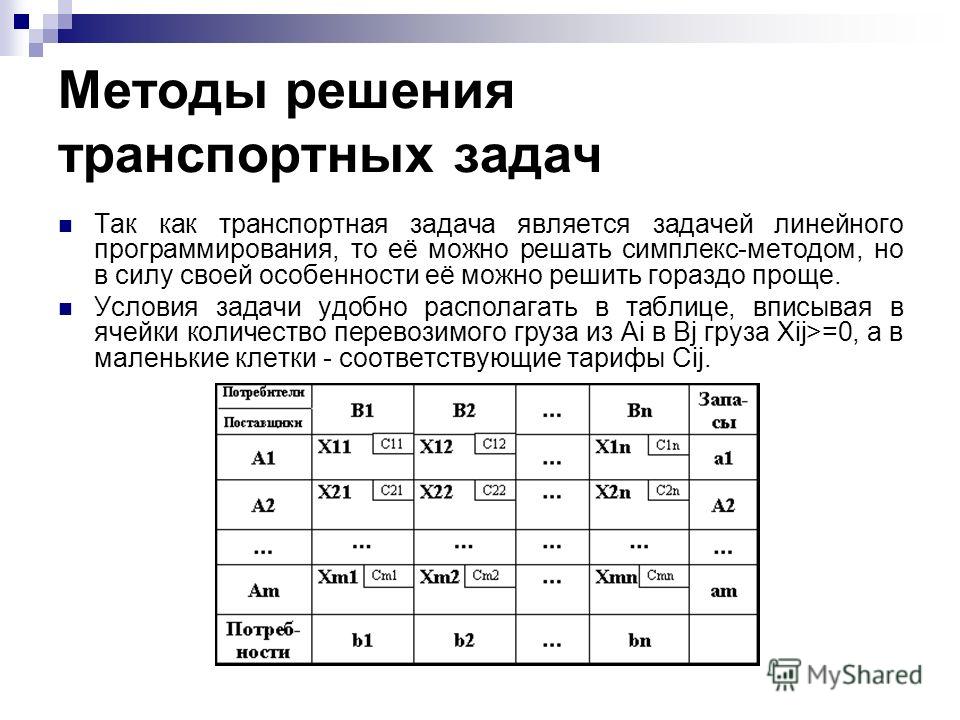
Любая ли система неравенств имеет допустимую область?
№ . Некоторые задачи могут не иметь области пересечения, удовлетворяющей всем ограничениям (неравенствам). Мы называем такую проблему невыполнимой проблемой . Возможно, вам придется ослабить некоторые ограничения, чтобы обеспечить возможную область и оптимальное решение.
Калькулятор задач линейного программирования: шаги, графики
Калькулятор LP — это бесплатный онлайн-инструмент. Таким образом, он обеспечивает наилучшее оптимальное решение с учетом ограничений. Затем любой онлайн-калькулятор LP ускоряет вычисления. Кроме того, он представляет наилучшее оптимальное решение для поставленных целевых функций с системой линейных ограничений за доли секунды. Затем LP также популярен как линейная оптимизация. Кроме того, это подмножество математического программирования. Он также популярен как математическая оптимизация.
Итак, это метод предоставления оптимального решения или вывода в математической модели. Затем в процедуре мы можем увидеть переменные значения той или иной целевой функции, например максимизировать или минимизировать. Кроме того, ограничения устанавливают диапазон в LP. С другой стороны, целевая функция определяет оптимизируемую величину. Затем LP чаще всего используется в математике. Но мы можем применить его в различных областях исследования.
Затем в процедуре мы можем увидеть переменные значения той или иной целевой функции, например максимизировать или минимизировать. Кроме того, ограничения устанавливают диапазон в LP. С другой стороны, целевая функция определяет оптимизируемую величину. Затем LP чаще всего используется в математике. Но мы можем применить его в различных областях исследования.
В этой статье речь пойдет об этом калькуляторе. Итак, продолжайте читать, чтобы узнать больше об этом.
Содержание
Калькулятор задач линейного программированияТаким образом, LP является наиболее эффективным подходом оптимизации для решения целевых функций. Кроме того, он предоставляет линейные переменные и линейные ограничения. Затем он также дает лучшее решение данной линейной проблемы. Кроме того, основной целью подхода является определение значений переменных, необходимых для максимизации или уменьшения целевой функции.
С другой стороны, мы можем использовать его для описания количества или значения, которое необходимо оптимизировать. Таким образом, мы можем использовать ограничения для определения диапазона переменной. Кроме того, он состоит из четырех основных компонентов. Итак, это целевая функция, ограничения, данные и переменная решения. Затем все эти элементы должны присутствовать, чтобы решить задачу.
Таким образом, мы можем использовать ограничения для определения диапазона переменной. Кроме того, он состоит из четырех основных компонентов. Итак, это целевая функция, ограничения, данные и переменная решения. Затем все эти элементы должны присутствовать, чтобы решить задачу.
Итак, теперь, когда вы знаете, что это такое, давайте посмотрим, как использовать калькулятор задач LP.
По сути, это бесплатный онлайн-калькулятор. Он дает наиболее эффективное и оптимальное решение для заданных ограничений за считанные секунды. Чтобы использовать его, выполните следующие действия:
- Сначала введите ограничения и целевую функцию в соответствующие поля ввода.
- Затем в предложенном инструменте нажмите кнопку отправки, чтобы найти лучшее решение линейной проблемы.
- Затем откроется новое окно. Так, он отображает наилучшее решение заданной задачи в виде графика.
Кроме того, это основные шаги по использованию этого калькулятора. При использовании калькулятора LP вы должны выбрать, максимизировать или минимизировать ввод для указанной линейной проблемы. Калькулятор максимизации — это калькулятор, который предоставляет возможности максимизации исключительно для решения линейной задачи. Однако, если вы используете исключительно функции минимизации для вычисления проблемы, это может считаться калькулятором минимизации.
При использовании калькулятора LP вы должны выбрать, максимизировать или минимизировать ввод для указанной линейной проблемы. Калькулятор максимизации — это калькулятор, который предоставляет возможности максимизации исключительно для решения линейной задачи. Однако, если вы используете исключительно функции минимизации для вычисления проблемы, это может считаться калькулятором минимизации.
Кроме того, проблемы можно решить с помощью калькулятора LP TI 84 Plus. Это стратегия решения и определения максимального и минимального значений многомерной и целевой функции, которая связана неравенствами в системе.
Однако эти неравенства можно решить с помощью калькулятора LP TI 84 Plus. Он основан на том принципе, что если задача содержит систему неравенств, то целевая функция должна оцениваться в точке пересечения, где наименьшее значение является минимальным значением функции, а наибольшее значение — максимальным значением функции. Неравенство может быть разрешено таким образом.
Неравенство может быть разрешено таким образом.
Выполните следующие процедуры, чтобы получить максимальное и минимальное значения для данной линейной задачи с помощью TI-84 Plus:
- Постройте график для системы ограничений, заданной в линейной задаче.
- Определите область пересечения, а затем нарисуйте область пересечения.
- После этого найдите точки соединения в регионе и сохраните их на графике.
- Отображение сохраненных точек пересечения в калькуляторе TI-84 Plus.
- Составьте список неравенств, используя показанные точки пересечения.
Определите формулу для своей функции, а затем используйте ее для определения элементов неравенства.
Затем нажмите E, чтобы оценить функцию, и вы получите максимальное и минимальное значения из системы неравенства.
Калькулятор задач линейного программирования Использует С помощью вышеуказанных методов можно решить линейные задачи с помощью калькулятора LP, такого как TI-84 plus. Калькулятор LP с тремя переменными — еще один инструмент, доступный для решения линейных задач с использованием другого метода. Если у вас есть более одного линейного уравнения или три линейных уравнения для решения задачи с тремя предоставленными переменными, вы можете использовать этот калькулятор. Чтобы решить три линейных уравнения для конкретной линейной задачи, просто введите все три уравнения в этот инструмент, и вы получите ответ.
Калькулятор LP с тремя переменными — еще один инструмент, доступный для решения линейных задач с использованием другого метода. Если у вас есть более одного линейного уравнения или три линейных уравнения для решения задачи с тремя предоставленными переменными, вы можете использовать этот калькулятор. Чтобы решить три линейных уравнения для конкретной линейной задачи, просто введите все три уравнения в этот инструмент, и вы получите ответ.
Когда вы используете калькулятор LP для решения задачи, он даст вам прямое решение максимизации или минимизации. Однако калькулятор минимизации доступен, если вы хотите шаг за шагом определить минимальный элемент набора данных для линейной задачи. Точно так же вы можете использовать калькулятор максимизации для итеративного определения максимального элемента набора данных для заданной линейной задачи. Это поможет вам лучше понять линейные вопросы.
Калькулятор задач линейного программирования с графиком Графический метод: Поскольку модели LP очень важны во многих секторах, для их решения на протяжении многих лет было создано несколько различных типов алгоритмов. Известными примерами являются метод Simplex, венгерский подход и другие. Графический метод является одним из наиболее фундаментальных способов решения проблемы LP.
Известными примерами являются метод Simplex, венгерский подход и другие. Графический метод является одним из наиболее фундаментальных способов решения проблемы LP.
Читайте также: Молярная масса молекулы кислорода – определение, формула и пример
В принципе, эта стратегия работает практически для всех видов проблем, но ее становится все труднее решать по мере увеличения числа факторов выбора и ограничений. В результате мы продемонстрируем это на базовом примере только с двумя переменными. Итак, начнем с графического способа.
Калькулятор задач линейного программирования Графический методСначала мы рассмотрим шаги алгоритма:
Шаг 1: Создайте задачу LP (LP).В предыдущей части мы обсуждали математическую формулировку выпуска LP. Это самый важный этап, поскольку все последующие шаги зависят от нашего анализа.
Шаг второй: Постройте график и нарисуйте на нем линии ограничений. График должен иметь «n» измерений, где «n» — количество переменных выбора. Это должно дать вам представление о том, насколько сложным будет этот этап по мере увеличения числа факторов выбора. Нужно понимать, что нельзя представить себе более трех измерений. Ограниченные линии формируются путем соединения горизонтальных и вертикальных точек пересечения, заданных в каждом уравнении зависимости.
Это должно дать вам представление о том, насколько сложным будет этот этап по мере увеличения числа факторов выбора. Нужно понимать, что нельзя представить себе более трех измерений. Ограниченные линии формируются путем соединения горизонтальных и вертикальных точек пересечения, заданных в каждом уравнении зависимости.
Используется для определения области доступного пространства, что может привести к жизнеспособному решению. Как вы проверяете? Простой способ — вставить координаты начала координат (0,0) в задачу и посмотреть, имеет ли целевая функция физическое решение или нет. Если true, допустимая сторона — это сторона линий зависимости, на которой расположено начало координат. В противном случае он находится на противоположной стороне.
Этап 4. Определение жизнеспособной области решения Жизнеспособная область решения на графике соответствует всем ограничениям. Его также можно рассматривать как пересечение допустимых областей каждой ограничительной линии. Любая точка в этой области даст правильное решение нашей целевой функции.
Его также можно рассматривать как пересечение допустимых областей каждой ограничительной линии. Любая точка в этой области даст правильное решение нашей целевой функции.
Поскольку мы работаем с линейными уравнениями, это, несомненно, будет прямая линия. Во избежание недоразумений ее необходимо рисовать отдельно от ограничительных линий. Выберите постоянное значение в уравнении целевой функции случайным образом, чтобы сделать его легко различимым.
Шаг 6: Определение наилучшего места Максимальное количество точек Оптимальная точка всегда находится в одном из возможных углов области. Где я могу найти его? Поместите линейку параллельно целевой функции на лист графика. Постарайтесь сохранить ориентацию этой линейки в пространстве. Нам просто нужно направление прямой линии целевой функции. Начните с дальнего левого угла графика и двигайтесь к исходной точке.
Найдите точку касания линейки с допустимой областью, ближайшую к началу координат, если целью является минимизация целевой функции. Это лучший момент для минимизации функции.
Найдите точку касания линейки с допустимой областью, наиболее удаленной от начала координат, если цель состоит в том, чтобы максимизировать целевую функцию. Это лучшее место для максимального использования функции.
Калькулятор задач линейного программирования транспортПредприятие хочет сократить расходы на транспортировку продукта с двух заводов до пяти отдельных клиентов. Каждое производство имеет ограниченный запас, и каждый потребитель имеет определенную потребность. Как продукт должен распространяться компанией?
Решение
1) Переменными являются количество товаров, отгруженных с каждого объекта клиентам. В рабочем листе Transport1 они помечены как отгруженные продукты.
2) При использовании параметра «Предполагать неотрицательное» логическое ограничение: «Отгруженные продукты» >= 0,
Два других ограничения: Всего получено >= Спрос и Всего отгружено >= Объем.
3) Цель состоит в том, чтобы максимально снизить затраты. Полная стоимость поставлена к этому.
Примечания
В своей самой простой форме это транспортная задача. Тем не менее, эта стратегия обычно используется для экономии десятков тысяч долларов в год. На рабочем листе Transport2 мы рассмотрим двухуровневую транспортную задачу, а на рабочем листе Transport3 мы рассмотрим многопродуктовую двухуровневую транспортную задачу.
Уравнение расчета задачи линейного программирования Уравнение расчета задачи линейного программирования 1 максимум и минимум для целевой функции 50x+40y.Ответ:
В свете этого f(x,y)=50x+40y является целевой функцией.
Ограничения следующие:
2x+3y = 1500, x=0, y=0
2x+y=1000
y=1000-2x
2x+3y=1500
Тогда 3y=1500-2x
Тогда y=(1500-2x)/3
Atlast, y=500-2x/5
Сейчас , график будет выглядеть так: заштрихованная область представляет жизнеспособную область.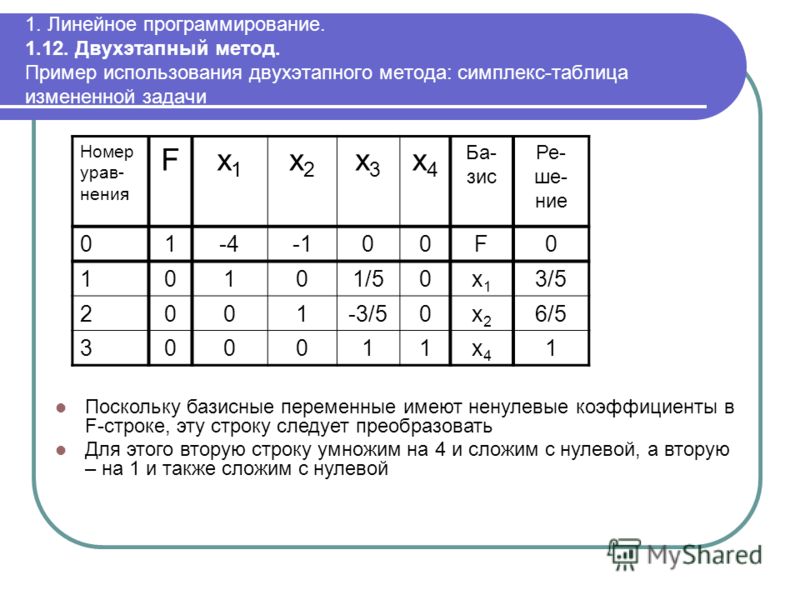
(0,500), (375,250) и (0,500) — вершины (500,0).
f(x,y)=50x+40y
Заменить вершины в целевой функции.
f(0,500)=50*0+40*500=20000
Тогда f(375250)=50*375+40*250=28750
f(500,0)=50*500+40*0 =25 000
Минимум равен (0,500)
Максимально возможные значения (275,250)
Калькулятор задач линейного программирования Уравнение 2Определите максимальное и минимальное значения z = 5x + 3y при заданных условиях.
x + 2y ≤ 14
3x – y ≥ 0
x – y ≤ 2
Решение:
Три неравенства показывают ограничения. Жизнеспособная зона — это область плоскости, которая будет отмечена.
(z) = 5x + 3y — уравнение оптимизации. Вы должны найти угловые положения (x,y), которые приводят к наибольшему и наименьшему значению z.
Для начала решите каждое неравенство отдельно.
Итак, x + 2y ≤ 14 ⇒ y ≤ -(1/2)x + 7
Тогда 3x – y ≥ 0 ⇒ y ≤ 3x
Тогда x – y ≤ 2 ⇒ y ≥ x – 2
Теперь соедините линии, чтобы создать систему линейных уравнений для определения местоположения углов.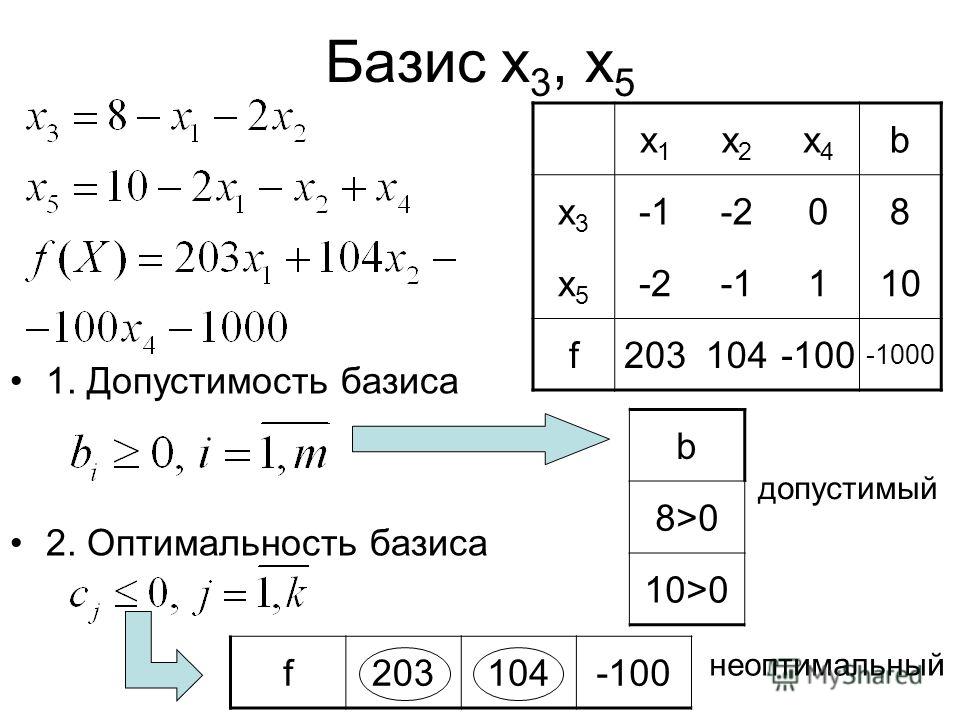
y = -(½) x + 7
y = 3x
Угловые положения получаем путем решения вышеупомянутых уравнений (2, 6)
y = -2/x + 7
y = – 2 x
Мы получаем положения углов, решая вышеупомянутые уравнения (6, 4)
3x = y
y = – 2 x
Мы получаем положения углов, решая вышеупомянутые уравнения (-1, -3). Максимальное и наименьшее значения уравнения оптимизации для линейных систем расположены в углах допустимой зоны. Чтобы получить лучший ответ, просто введите эти три точки в уравнение z = 3x + 4y.
(2, 6): z = 5(2) + 3(6) = 10 + 18 = 28
(6, 4): z = 5(6) + 3(4) = 30 + 12 = 42
(-1, -3): z = 5(-1) + 3(-3) = -5 -9= -14
В результате максимум z = 42 находится в (6, 4), а наименьший из z = -14 находится в (-1, -3).
Калькулятор задач линейного программирования Симплекс-метод Симплекс-метод является одним из наиболее известных способов решения задач ЛП. Это итеративная процедура поиска наилучшего практического ответа. Значение фундаментальной переменной преобразуется таким образом, чтобы получить наибольшее значение целевой функции. Алгоритм симплексной техники LP представлен ниже:
Значение фундаментальной переменной преобразуется таким образом, чтобы получить наибольшее значение целевой функции. Алгоритм симплексной техники LP представлен ниже:
Шаг 1: Определите конкретную проблему. Например, напишите ограничения неравенства и целевую функцию.
Шаг 2: Преобразуйте предоставленные неравенства в уравнения, включив резервную переменную в каждое выражение неравенства.
Шаг 3: Создайте первую симплексную таблицу. В нижней строке напишите целевую функцию. В этом случае каждое ограничение неравенства отображается в отдельной строке. Теперь проблему можно представить в виде расширенной матрицы, известной как первая симплексная таблица.
Шаг 4: Найдите самый отрицательный элемент в нижней строке, что поможет вам найти сводную колонку. Самый сильный отрицательный элемент в нижней строке указывает наибольший коэффициент в целевой функции, что поможет нам как можно быстрее увеличить значение целевой функции.
Шаг 5: Определите частные. Чтобы найти частное, разделите элементы в крайнем правом столбце на элементы в первом столбце (исключая нижнюю строку). Наименьшее частное идентифицировало строку.
Поворотным элементом будет строка, идентифицированная на этом шаге, и элемент, идентифицированный на этом шаге.
Шаг 6: Используйте поворот, чтобы убедиться, что все остальные элементы в столбце равны нулю.
Шаг 7: Остановите процедуру, если в нижней строке нет отрицательных значений. В противном случае перейдите к шагу 4.
Шаг 8: Наконец, найдите решение, соответствующее итоговой симплексной таблице.
Приложение Калькулятор задач линейного программированияРазличные секторы широко используют оптимизацию и LP. Итак, люди использовали LP в производственной сфере и сфере услуг. В этой части мы рассмотрим многочисленные применения LP.
Производственные отрасли используют LP для изучения своих сетей снабжения. Производственные отрасли стараются быть максимально эффективными в своей деятельности. Модель LP может консультировать фирму по изменениям в ее организации хранения, персонале и узких местах производства. Посмотрите это видео, чтобы более подробно ознакомиться с примером использования склада компанией Cequent, расположенной в США. Люди использовали LP, чтобы максимизировать полочное пространство в организованной розничной торговле.
Производственные отрасли стараются быть максимально эффективными в своей деятельности. Модель LP может консультировать фирму по изменениям в ее организации хранения, персонале и узких местах производства. Посмотрите это видео, чтобы более подробно ознакомиться с примером использования склада компанией Cequent, расположенной в США. Люди использовали LP, чтобы максимизировать полочное пространство в организованной розничной торговле.
Сегодня на рынке так много товаров, что очень важно понимать, чего хотят покупатели. Big Bazaar, Walmart, Hypercity, Reliance и другие ритейлеры активно используют оптимизацию. Товары в магазине тщательно позиционируются в зависимости от того, как люди делают покупки. Покупатели должны иметь возможность просто идентифицировать и выбирать соответствующие товары. Это недостижимо из-за таких ограничений, как ограниченное пространство на полках и разнообразие продуктовой линейки.
Мы можем использовать оптимизацию для сокращения затрат в дополнение к оптимизации маршрутов доставки.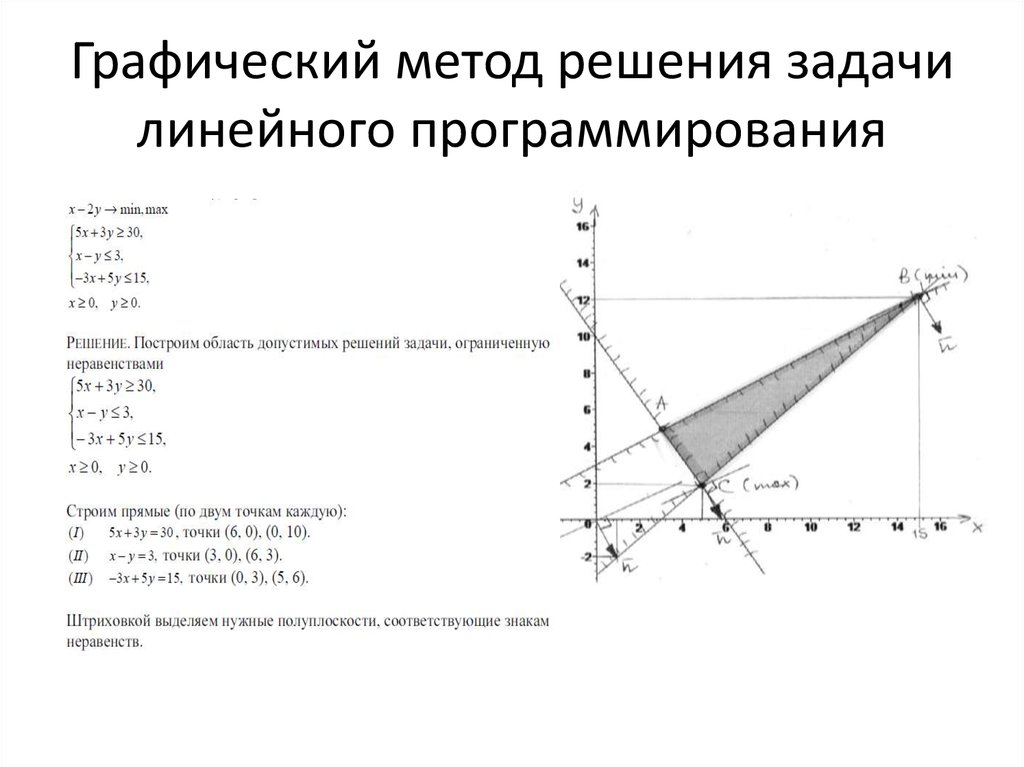
Это вариант известной дилеммы коммивояжера. Мы можем использовать оптимизацию, чтобы найти наиболее эффективный путь развития отрасли. Это требует нескольких продавцов, посещающих несколько городов. FedEx, Amazon и другие компании используют кластерный и жадный алгоритм для расчета маршрутов доставки.
Калькулятор задач линейного программирования ЦельНаша цель — сократить эксплуатационные расходы и время. Оптимизации также используются в машинном обучении. Ядром контролируемого обучения является LP. Подбирая математическую модель на основе размеченных входных данных, систему обучают определять значения из неизвестных входных данных.
LP, с другой стороны, предлагает широкий спектр применения. Акционеры, спортивные, фондовые рынки и другие организации используют LP в реальном мире.
Формулировка калькулятора задачи линейного программирования Шаг 1Таким образом, вся площадь выращивания пшеницы = X (в гектарах)
Тогда Y — это общая площадь для выращивания ячменя (в гектарах)
Факторы моего выбора 90 X и Y.
Потому что всю продукцию земли можно продать на рынке. Целью фермера будет максимизировать весь свой заработок. Чистая прибыль показана как для пшеницы, так и для ячменя. Фермер получает чистую прибыль в размере 50 долларов США на гектар пшеницы и 120 долларов США на гектар ячменя.
Max Z = 50X + 120Y — наша целевая функция.
Шаг 3: Задокументируйте ограничения1. Предположим, что общий бюджет фермера составляет 10 000 долларов США.
Нам также предоставляется стоимость выращивания пшеницы и ячменя за акр. У нас есть ограничение на общие расходы, понесенные фермером. В результате наше уравнение: 10 000 = 100X + 200Y.
2. Следующим ограничением является верхний предел общего количества человеко-дней, доступных для горизонта планирования. Общее количество доступных человеко-дней составляет 1200. В таблице показано количество человеко-дней на гектар для пшеницы и ячменя.
1200 = 10X + 30Y
3. Общая площадь, доступная для посадки, является третьим ограничением. Все доступное пространство составляет 110 га. В результате уравнение принимает вид
110 X + Y
Шаг 4: Ограничение неотрицательностиЗначения X и Y будут больше или равны 0.
Это само собой разумеется.
X = 0 и Y = 0
Некоторые часто задаваемые вопросы Как найти оптимальное решение в калькуляторе LP?- Сначала заполните целевую функцию и ограничения в соответствующих полях ввода.
- Затем, чтобы получить лучший ответ, нажмите кнопку «Отправить».
- Наконец, в новом окне вы увидите наилучшее оптимальное решение и график.
В одной из вершин области появится идеальное значение, указывающее набор возможных решений, если задачу ЛП можно оптимизировать. Наибольшее или наименьшее значение f(x,y)=ax+by+c в наборе жизнеспособных решений, изображенных на графике, например, происходит в точке A, B, C, D, E или F.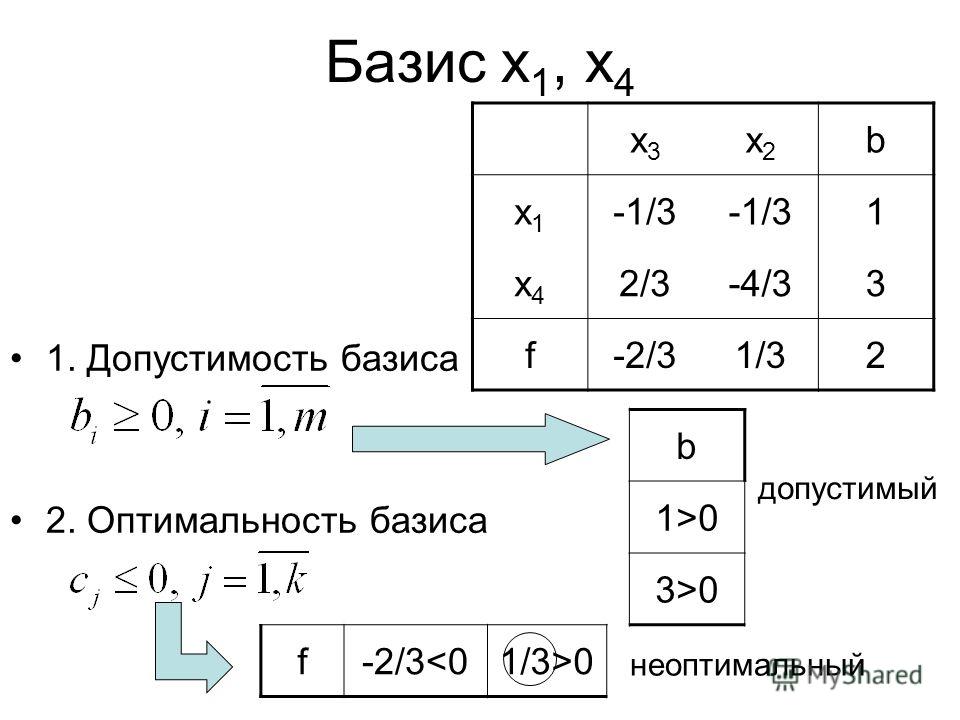
Допустимая область — это область графа, содержащая все точки, удовлетворяющие всем неравенствам в системе. Сначала изобразите каждое неравенство в системе, а затем жизнеспособную область. Затем найдите точку, где все графики перекрываются. Это мыслимый диапазон.
Сложный ли LP?LP может быть решена за полиномиальное время, однако целочисленная LP может быть упрощена до SAT, что сделает ее NP-сложной (на самом деле можно показать, что она NP-полная, но это менее тривиально). В результате, если PNP, LP проще (вычислительно), чем ILP.
Что такое LPP с примером?(LPP) — проблемы. Мы использовали его для определения наилучшего значения для данной линейной функции. Идеальным значением может быть как наибольшее, так и наименьшее значение. Линейная функция является целевой функцией в этом контексте.
Как рассчитать увеличение? % Увеличение = Увеличение / Исходное число 100. Это вычисляет общее процентное изменение или увеличение. Чтобы вычислить процентное снижение, сначала определите разницу (уменьшение) между двумя рассматриваемыми цифрами. Затем разделите сокращение на исходное число и умножьте результат на 100.
Это вычисляет общее процентное изменение или увеличение. Чтобы вычислить процентное снижение, сначала определите разницу (уменьшение) между двумя рассматриваемыми цифрами. Затем разделите сокращение на исходное число и умножьте результат на 100.
Используя графический метод, решите следующую задачу LP.
минимизации: z = 5x + 4y
4x + y ≥ 40,
2x + 3y ≥ 90,
x, y ≥ 0
Раствор:
Использование. , получаем уравнения прямых как 4x + y = 40 и 2x + 3y = 90.
4x + y = 40 ходов (0, 40) и (10, 0). Любая точка на этой линии или выше выполняет 4x + y 40.
2x + 3y = 90 ходов (0, 30) и (45, 0). Любая точка на этой линии или выше соответствует 2x + 3y ≥ 90.
| Corner Points | Z = 5x + 4y |
| A = (45, 0) | 225 |
| B = (3, 28) | 127 |
| C = (0, 40) | 160 |
Поскольку минимальное значение Z равно 127, B (3, 28) обеспечивает наилучший вариант.
Ответ: Наименьшее число Z равно 127, а лучший вариант — (3, 28)
Калькулятор линейного программирования
Содержание
Калькулятор линейного программирования— это бесплатный онлайн-инструмент, который отображает наилучшее оптимальное решение для заданного ограничения. Калькулятор линейного программирования STUDYQUERIES работает более эффективно и отображает лучшее оптимальное решение всего за доли секунды для заданной целевой функции и системы линейных ограничений.
Как пользоваться калькулятором линейного программирования?Чтобы использовать калькулятор линейного программирования, выполните следующие действия:
- Шаг 1: Введите целевую функцию и ограничения в соответствующие поля ввода
- Шаг 2: Теперь нажмите «Отправить», чтобы получить наилучший результат
- Шаг 3: Лучшее оптимальное решение и график отобразятся в новом окне
Калькулятор линейного программированияЧто такое линейное программирование?
Линейное программирование (ЛП, также известное как линейная оптимизация) — это математический метод для достижения наилучшего результата (например, максимальной прибыли или наименьших затрат) в рамках математической модели, требования которой представлены линейными отношениями. Математическое программирование (также называемое математической оптимизацией) — это тип линейного программирования.
Математическое программирование (также называемое математической оптимизацией) — это тип линейного программирования.
По сути, линейное программирование — это метод оптимизации линейной целевой функции с учетом ограничений линейного равенства и линейного неравенства. Это множество состоит из выпуклого многогранника, где выпуклый многогранник определяется как пересечение конечного числа полупространств, где каждое полупространство определяется линейным неравенством. Действительнозначная аффинная (линейная) функция, заданная на этом многограннике, определяет его целевую функцию.
Если точка многогранника имеет наименьшее (или наибольшее) значение этой функции, то линейное программирование находит ее. 9T\times X$$ в этом случае) называется целевой функцией.
Калькулятор линейного программирования Неравенства $$Ax ≤ B$$ и $$x ≥ 0$$ — это ограничения, определяющие выпуклый многогранник, по которому должна быть оптимизирована целевая функция. Когда два вектора имеют одинаковые размеры, они сравнимы.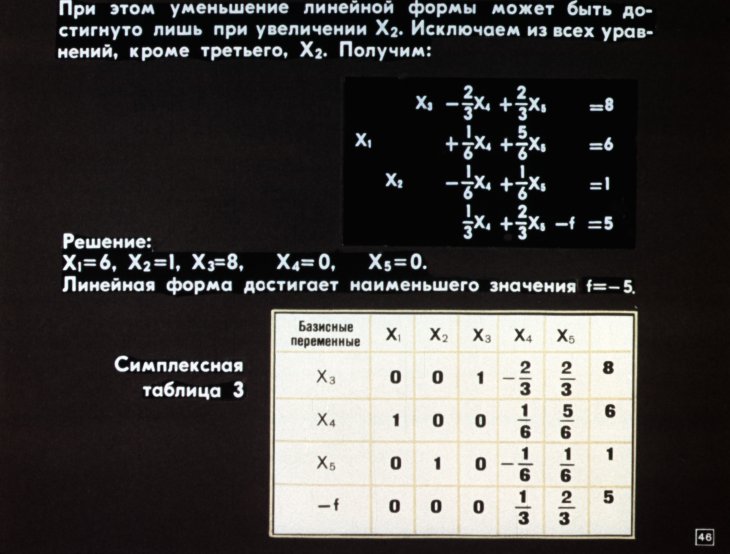 Каждая запись в первом векторе меньше или равна соответствующей записи во втором векторе, поэтому первый вектор меньше или равен второму вектору.
Каждая запись в первом векторе меньше или равна соответствующей записи во втором векторе, поэтому первый вектор меньше или равен второму вектору.
Линейное программирование может принести пользу различным областям обучения. Математики и деловые люди широко используют его, в то время как некоторые инженеры также используют его для решения некоторых задач. Производство, транспорт, энергетика и телекоммуникации входят в число отраслей, в которых используются модели линейного программирования. Его можно использовать для моделирования различных типов проблем при планировании, маршрутизации, составлении расписаний, назначении и проектировании.
Пример: Рассмотрим компанию по производству шоколада, которая производит только два типа шоколада — А и В. Для обоих видов шоколада требуется только молоко и шоколад. Для производства каждой единицы A и B требуется следующее количество:
Для каждой единицы А требуется 1 единица молока и 3 единицы шоколада
Для каждой единицы B требуется 1 единица молока и 2 единицы шоколада
На кухне компании всего 5 единиц молока и 12 единиц шоколада. С каждой продажи компания получает прибыль в размере
С каждой продажи компания получает прибыль в размере
6 рупий за единицу А продано
рупий 5 за единицу B продано.
Теперь компания хочет максимизировать свою прибыль. Сколько единиц продукции А и В она должна произвести соответственно?
Общие термины, используемые в линейном программированииМы можем изучить некоторые термины, используемые в линейном программировании, как
.- Переменные решения: Мои результаты будут определяться переменными решения. Эти переменные представляют конечный результат. Определение переменных решения — это первый шаг к решению любой проблемы. Мои переменные решения — это общее количество единиц для A и B, обозначенное X и Y соответственно.
- Объективная функция: Определяется как цель принятия решения. Как показано в приведенном выше примере, компания хочет увеличить общую прибыль, представленную Z. Целью оптимизации является увеличение прибыли.

- Ограничения: Ограниченные переменные — это те, которые ограничивают или ограничивают переменные принятия решений. Обычно они ограничивают значение переменных решения. Моими ограничениями в приведенном выше примере являются ограниченная доступность ресурсов «Молоко» и «Шоколад».
- Ограничение неотрицательности: Для всех линейных программ переменные решения всегда должны иметь положительные значения. Это означает, что значения переменных решения должны быть больше или равны 0.
Определение задачи линейного программирования включает следующие шаги:
- Определите, какие переменные необходимо учитывать
- Вам нужно написать целевую функцию
- Опишите ограничения
- Ограничение отрицательности должно быть указано явно
Линейное программирование — это задача, в которой переменные решения, целевые функции и ограничения являются линейными функциями.
Это называется задачей линейного программирования, когда выполняются все три условия.
Методы решения задач линейного программированияЛинейное программирование может быть решено различными способами с использованием таких инструментов, как R, открытый решатель и другие инструменты, включая графический метод и симплексный метод. Мы подробно обсудим симплекс-метод и графический метод, которые являются двумя наиболее важными методами.
Симплексный метод линейного программированияОдним из самых популярных методов решения задач линейного программирования является симплекс-метод. Решение повторяется несколько раз, пока оно не будет соответствовать всем требованиям. С помощью этого метода значение базовой переменной преобразуется для получения максимального значения целевой функции. Симплексный алгоритм линейного программирования представлен ниже.
- Шаг 1: Установите заданную проблему.
 (Например, напишите неравенства и целевые функции.)
(Например, напишите неравенства и целевые функции.) - Шаг 2: Чтобы решить данные неравенства, добавьте переменную резерва к каждому выражению неравенства.
- Шаг 3: Создайте начальную симплексную таблицу. Запишите целевую функцию внизу. Каждое ограничение неравенства отображается в отдельной строке. Теперь мы можем представить задачу в виде расширенной матрицы, также известной как исходная симплексная таблица.
- Шаг 4: Определите самую большую отрицательную запись в нижней строке, которая будет использоваться для определения сводного столбца. Самая большая отрицательная запись в нижней строке представляет собой наибольший коэффициент в целевой функции, что позволяет нам максимально быстро увеличивать ее значение.
- Шаг 5: Вычислите частные. Нам нужно разделить записи в крайнем правом столбце на записи в первом столбце, исключая нижнюю строку, чтобы вычислить частное.
 Строка определяется наименьшим частным. Точка поворота будет взята из строки, определенной на этом шаге, а также из элемента, определенного на этом шаге.
Строка определяется наименьшим частным. Точка поворота будет взята из строки, определенной на этом шаге, а также из элемента, определенного на этом шаге. - Шаг 6: Выполните поворот, чтобы все остальные записи в столбце были нулевыми.
- Шаг 7: Если в нижней строке нет отрицательных записей, остановите процесс. В противном случае продолжите с шага 4.
- Шаг 8: Определите решение, связанное с окончательной симплексной таблицей.
Оптимизация линейного программирования с двумя переменными выполнена графическим методом. Графический метод — лучший способ найти оптимальное решение задачи с двумя переменными решения. В этом методе на множество неравенств накладываются ограничения. После этого неравенства строятся в плоскости XY.
Таким образом, область пересечения будет рассматриваться, чтобы помочь определить достижимую область после того, как все неравенства будут нанесены на график YX. Помимо описания того, какие значения может содержать наша модель, допустимая область обеспечивает оптимальное решение. Вот пример, который поможет вам лучше понять концепцию линейного программирования.
Помимо описания того, какие значения может содержать наша модель, допустимая область обеспечивает оптимальное решение. Вот пример, который поможет вам лучше понять концепцию линейного программирования.
Давайте лучше разберемся с этим на примере.
Пример: Фермер недавно приобрел участок земли площадью 110 га. Он планирует выращивать на этой земле пшеницу и ячмень. Благодаря качеству солнца и прекрасному климату региона можно продать всю продукцию пшеницы и ячменя. Согласно приведенным ниже данным, он хочет знать, как посадить каждый сорт на 110 гектарах с учетом затрат, чистой прибыли и потребности в рабочей силе:
Пример линейного программирования графического методаВ течение горизонта планирования у фермера есть бюджет в размере 10 000 долларов США, и он доступен для 1 200 человеко-дней. Убедитесь, что фермер получает максимальную отдачу от своих денег.
Решение: Чтобы решить эту задачу, мы сначала сформулируем нашу линейную программу.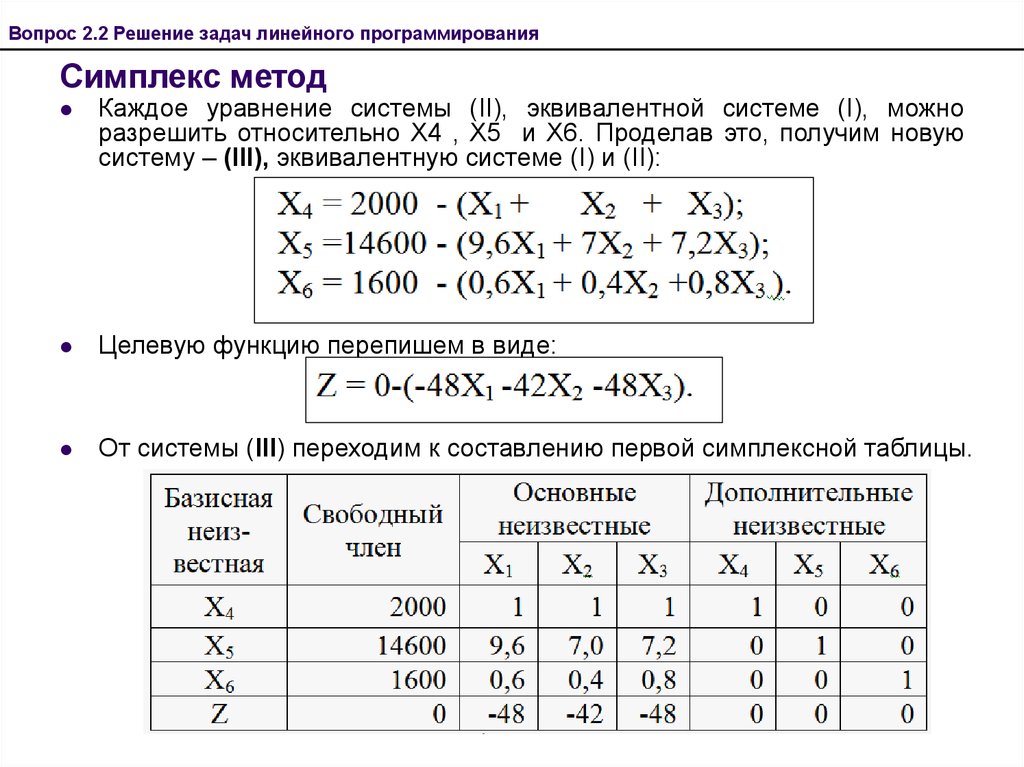
Формулировка линейной задачи
Шаг 1: Определение переменных решения
Общая площадь выращивания $$Пшеницы = X (га)$$
Общая площадь выращивания $$Ячменя = Y (га)$$
Мои переменные решения — X и Y.
Шаг 2: Формулировка целевой функции
Вся продукция земли может быть продана на рынке. Фермер хотел бы получить максимальную прибыль от своего урожая. Ячмень и пшеница имеют соответствующую чистую прибыль. Пшеница приносит фермеру 50 долларов США за гектар, а ячмень приносит 120 долларов США за гектар.
Наша целевая функция (заданная Z): $$Max Z = 50X + 120Y$$
Шаг 3: Запись ограничений
- Согласно бюджету фермера, у него есть 10 000 долларов США. Так же как и стоимость производства пшеницы и ячменя на гектар, мы также получаем эту информацию. Фермеры ограничены в общей сумме, которую они могут потратить. Итак, наше уравнение принимает вид: $100X + 200Y ≤ 10 000$$ .
- Следующее ограничение — это верхний предел количества человеко-дней, доступных для горизонта планирования. Доступно 1200 человеко-дней. В таблице указано количество человеко-дней на гектар пшеницы и ячменя. $10X + 30Y ≤ 1200$$
- Третье ограничение касается площади, доступной для плантаций. Для плантаций доступно 110 га. Таким образом, уравнение принимает следующий вид: $$X + Y ≤ 110$$

Шаг 4: Ограничение неотрицательности
X и Y будут больше или равны 0. Это очевидно.
$$X ≥ 0, Y ≥ 0$$
Мы разработали нашу линейную программу. Давайте решим это сейчас.
Поскольку мы знаем, что $$X, Y ≥ 0.$$, мы будем рассматривать только первый квадрант.
Я упрощу все уравнения, прежде чем строить график для приведенных выше уравнений.
$$100X + 200Y ≤ 10 000$$ можно упростить до $$X + 2Y ≤ 100$$, разделив на 100.
$$10X + 30Y ≤ 1200$$ можно упростить до $$X + 3Y ≤ 120$$, разделив на 10.
Третье уравнение в упрощенной форме: $$X + Y ≤ 110.$$
Поместите первые две линии на график в первый квадрант (как показано ниже)
Когда действуют ограничения бюджета и человеко-дней, получается оптимальное возможное решение. Это означает, что точка, в которой пересекаются уравнения $$X + 2Y ≤ 100$$ и $$X + 3Y ≤ 120$$, дает нам оптимальное решение.
Оптимальные значения X и Y равны (60,20).
Чтобы максимизировать прибыль, фермер должен сажать пшеницу и ячмень на 60 га земли и 20 га земли соответственно.
Ожидается, что компания получит максимальную прибыль в размере
$$Max Z = 50 x 60 + 120 x 20 $$
= 5400 долларов США
Графический метод линейного программированияВсему, чему здесь учат, также обучали в бесплатном онлайн-курсе «Линейное программирование для специалистов по науке о данных».
Приложения линейного программирования Оптимизация и линейное программирование широко используются в различных отраслях промышленности. Производство и сфера услуг регулярно используют линейное программирование. В этом разделе мы собираемся изучить различные приложения линейного программирования.
Производство и сфера услуг регулярно используют линейное программирование. В этом разделе мы собираемся изучить различные приложения линейного программирования.
- Линейное программирование используется в обрабатывающей промышленности для анализа своих цепочек поставок. Производственные отрасли стремятся сделать операции максимально эффективными. Модель линейного программирования может порекомендовать производителям изменения в планировке склада, рабочей силе и устранении узких мест в производстве. Посмотрите это видео, чтобы более подробно ознакомиться с кейсом Warehouse от американской компании Cequent.
- В организованной розничной торговле линейное программирование также используется для оптимизации места на полках. Сегодня на рынке так много продуктов, что крайне важно понимать, чего хотят клиенты. Big Bazaar, Walmart, Hypercity, Reliance и другие агрессивно используют оптимизацию. Товары в магазине стратегически размещены в соответствии с тем, как покупатели делают покупки.
 Клиенты должны иметь возможность легко находить и выбирать подходящие продукты. Из-за ограничений, таких как ограниченное пространство на полках и широкий ассортимент товаров, это невозможно.
Клиенты должны иметь возможность легко находить и выбирать подходящие продукты. Из-за ограничений, таких как ограниченное пространство на полках и широкий ассортимент товаров, это невозможно. - Помимо оптимизации маршрутов доставки, оптимизация также используется для оптимизации затрат. Это расширение популярной задачи коммивояжера. Для отрасли, в которой несколько продавцов посещают несколько городов, оптимизация используется для поиска наиболее эффективного маршрута. FedEx, Amazon и т. д. определяют маршруты доставки с помощью кластерного и жадного алгоритма. Наша цель – сократить эксплуатационные расходы и время.
- В машинном обучении также используются оптимизации. Линейное программирование является основой обучения с учителем. Система обучена определять значения из неизвестных входных данных путем подбора математической модели на основе размеченных входных данных.
- Что ж, у линейного программирования есть много других приложений.
 В реальном мире линейное программирование применяется Акционерами, Спортом, Фондовыми рынками и т. д. Узнайте больше.
В реальном мире линейное программирование применяется Акционерами, Спортом, Фондовыми рынками и т. д. Узнайте больше.
В области оптимизации линейное программирование широко применяется по целому ряду причин. Концепция линейного программирования применяется во многих аспектах анализа операций. Задачи линейного программирования, такие как запросы к сетевым потокам и запросы к потокам с несколькими товарами, считаются достаточно важными, чтобы вызвать обширные исследования функциональных алгоритмов для их решения.
Часто задаваемые вопросыДля чего используется линейное программирование?
С помощью линейного программирования вы можете найти оптимальное решение проблемы при заданном наборе ограничений. Сформулировав нашу реальную проблему в виде математической модели, мы сможем ее решить. Задействованы линейные неравенства и целевые функции ограничения-ограничения.
Что такое примеры линейного программирования?
Самый классический пример задачи линейного программирования — когда компания должна выделить свои ресурсы для создания двух разных продуктов.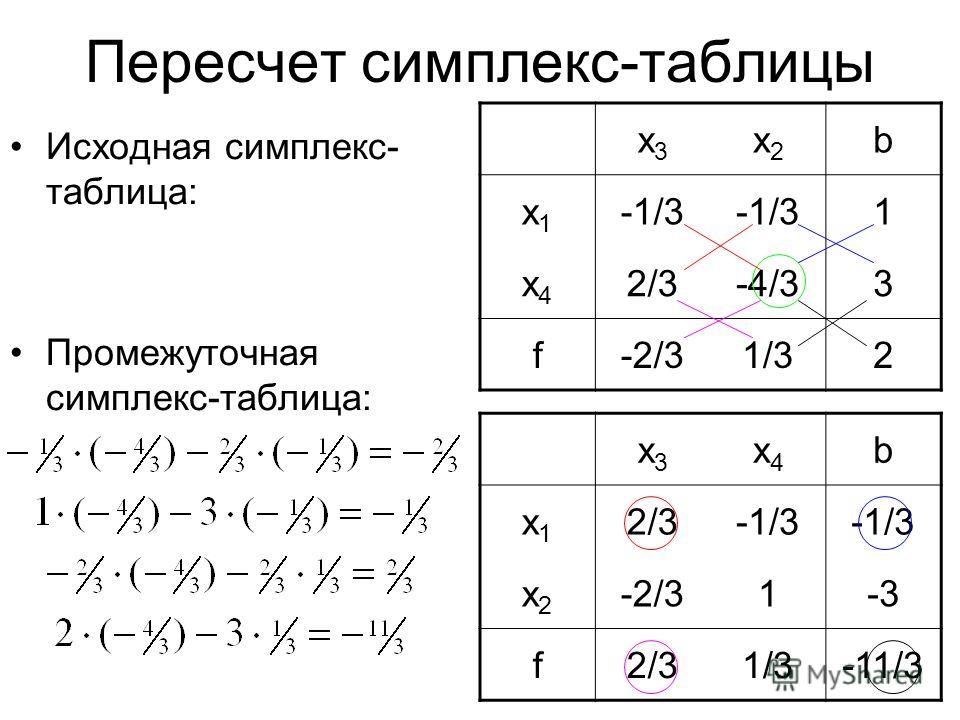 Различные продукты требуют разного количества времени и денег, которые обычно являются ограниченными ресурсами, и они продаются по разным ценам.
Различные продукты требуют разного количества времени и денег, которые обычно являются ограниченными ресурсами, и они продаются по разным ценам.
Что такое формула линейного программирования?
Его можно определить как задачу, в которой линейная функция максимизируется или минимизируется при линейных ограничениях. В математике f(x,y) называется целевой функцией, где ax + by + c представляет эту функцию.
Как решить задачу линейного программирования?
шага для решения задачи линейного программирования
- Шаг 1: Определите переменные решения.
- Шаг 2: Запишите целевую функцию.
- Шаг 3: Определение набора ограничений.
- Шаг 4: Выберите метод решения задачи линейного программирования.
- Шаг 5: Построить график.
- Шаг 6: Определите допустимую область.

Какие существуют типы линейного программирования?
Различные типы линейного программирования:
- Решение линейного программирования симплекс-методом.
- Решение линейного программирования с использованием R.
- Решение задач линейного программирования графическим методом.
- Решение линейного программирования с использованием открытого решателя.
Какова основная концепция линейного программирования?
Линейное программирование — это математический метод поиска оптимальных решений задач, которые можно выразить с помощью линейных уравнений и неравенств. Если реальную проблему можно точно представить математическими уравнениями линейной программы, метод найдет наилучшее решение проблемы.
Почему это называется линейным программированием?
Одна из областей математики, которая широко используется в комбинаторной оптимизации, называется линейным программированием (ЛП).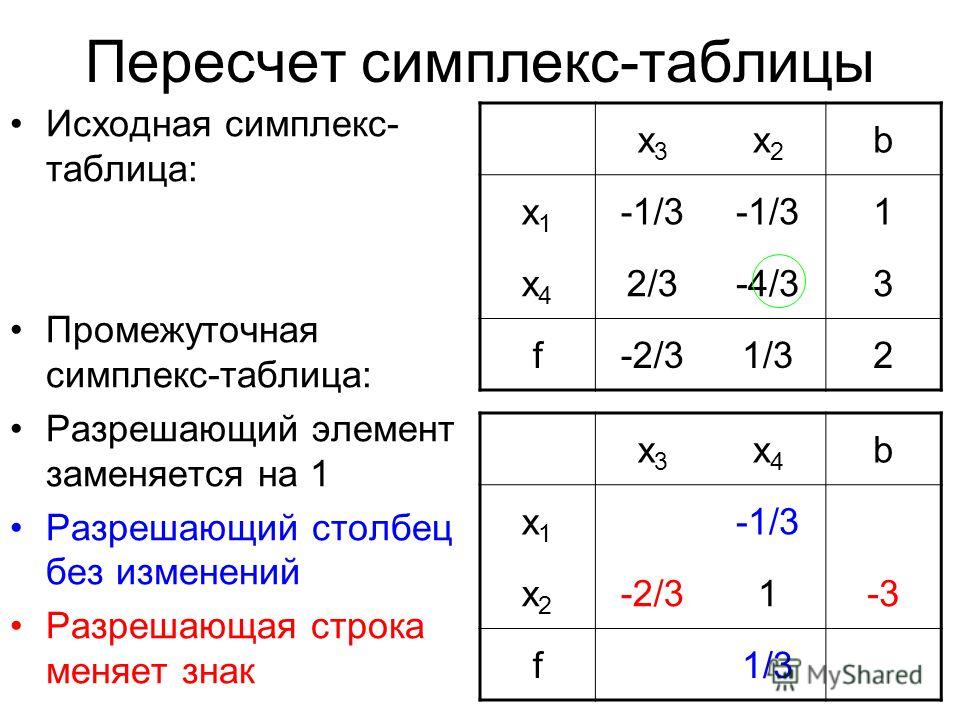 Она получила свое название от того факта, что задача ЛП — это задача оптимизации, в которой целевая функция и все ограничения являются линейными.
Она получила свое название от того факта, что задача ЛП — это задача оптимизации, в которой целевая функция и все ограничения являются линейными.
Онлайн-калькулятор: симплекс-метод
F(x) = 3x 1 + 4x 2 → max
| 000 | 2x 1 + x 2 ≤ 600 |
| 0x 1 + 0x 2 ≤ 225 | |
| 5x 1 +4x 2 ≤ 1000 | |
| 2x 2 ≥ 150 | |
| 0x 1 + 0x 2 ≥ 0 |
F(x) = 3x 1 + 4x 2 + 0x 3 + 0x 4 + 0x 5 + 0x 6 + 0x 7 — Мх 8 — Мх 9 → max
| 000 | 2x 1 + x 2 + x 3 = 600 |
| + x 4 = 225 | |
| 5x 1 + 4x 2 + x 5 = 1000 | |
| 2x 2 — x 6 + x 8 = 150 | |
| — x 7 + x 9 = 0 |
Preliminary stage:
Предварительный этап начинается с необходимости избавиться от отрицательных значений (если они есть) в правой части ограничений. Для чего соответствующие ограничения умножаются на -1. После этой манипуляции знак неравенства меняется на противоположный.
Для чего соответствующие ограничения умножаются на -1. После этой манипуляции знак неравенства меняется на противоположный.
Далее необходимо избавиться от неравенств, для чего в левой части неравенств введем компенсирующие переменные. Если неравенство вида ≤, то компенсирующая переменная имеет знак +, если неравенство вида ≥, то компенсирующая переменная имеет знак -. Компенсирующие переменные входят в целевую функцию задачи с нулевым коэффициентом.
Теперь в системе ограничений необходимо найти достаточное количество базовых переменных. Каждое ограничение должно иметь одну базовую переменную. Базовая — это переменная, имеющая при себе коэффициент 1 и встречающаяся только в одном ограничении. Если в каком-то ограничении нет базисных переменных, то мы добавляем их искусственно, и искусственные переменные входят в целевую функцию с коэффициентом -М, если целевая функция стремится к max и М, если целевая функция стремится к min.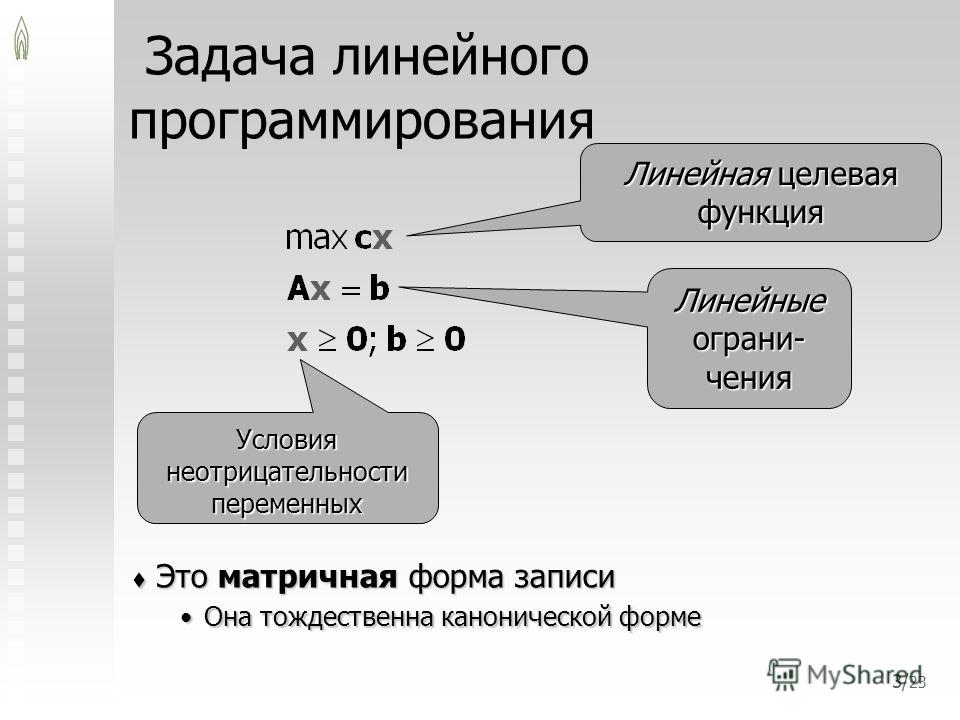
Iteration: 1
| B | Cb | P | x 1 | x 2 ↓ | x 3 | x 4 | x 5 | x 6 | x 7 | x 8 | x 9 | Q |
| 3 | 4 | 0 | 0 | 0 | 0 | 0 | -M | -M | ||||
| x 3 | 0 | 600 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 600 |
| x 4 | 0 | 225 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ∞ |
| x 5 | 0 | 1000 | 5 | 4 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 250 |
| x 8 ← | -M | 150 | 0 | 2 | 0 | 0 | 0 | -1 | 0 | 1 | 0 | 75 |
| x 9 | -M | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 1 | ∞ |
| max | -150M | — 3 | -2M-4 | 0 | 0 | 0 | M | M | 0 | 0 | ||
Calculation of table elements:
Elements of the column basis (B)
Переносим в таблицу основные элементы, которые мы определили на предварительном этапе:
B 1 = x 3 ;
В 2 = х 4 ;
В 3 = х 5 ;
В 4 = х 8 ;
В 5 = х 9 ;
Элементы столбца Cb
Каждая ячейка этого столбца равна коэффициенту, который соответствует базовой переменной в соответствующей строке.
Кб 1 = 0;
Кб 2 = 0;
Кб 3 = 0;
Кб 4 = -М;
Кб 5 = -М;
Значения переменных переменных и столбца P
На данном этапе расчеты не нужны, достаточно перенести значения из предварительного этапа в соответствующие ячейки таблицы:
P 1 = 600;
Р 2 = 225;
P 3 = 1000;
Р 4 = 150;
P 5 = 0;
х 1,1 = 2;
x 1,2 = 1;
x 1,3 = 1;
x 1,4 = 0;
х 1,5 = 0;
х 1,6 = 0;
х 1,7 = 0;
х 1,8 = 0;
x 1,9 = 0;
х 2,1 = 0;
х 2,2 = 0;
х 2,3 = 0;
х 2,4 = 1;
х 2,5 = 0;
х 2,6 = 0;
х 2,7 = 0;
х 2,8 = 0;
х 2,9 = 0;
х 3,1 = 5;
х 3,2 = 4;
x 3,3 = 0;
х 3,4 = 0;
х 3,5 = 1;
х 3,6 = 0;
х 3,7 = 0;
х 3,8 = 0;
x 3,9 = 0;
x 4,1 = 0;
х 4,2 = 2;
x 4,3 = 0;
х 4,4 = 0;
х 4,5 = 0;
х 4,6 = -1;
х 4,7 = 0;
х 4,8 = 1;
x 4,9 = 0;
x 5,1 = 0;
х 5,2 = 0;
х 5,3 = 0;
x 5,4 = 0;
х 5,5 = 0;
х 5,6 = 0;
х 5,7 = -1;
х 5,8 = 0;
х 5,9 = 1;
Значение целевой функции
Значение целевой функции вычисляем путем поэлементного умножения столбца Cb на столбец P, сложения результатов произведений.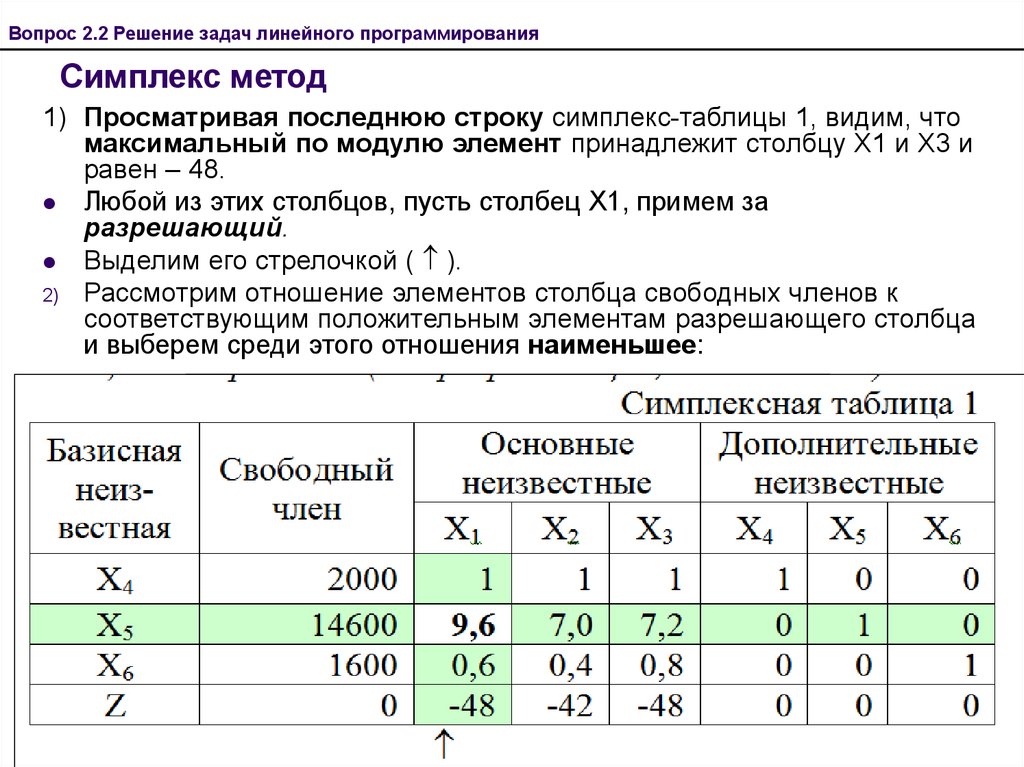
Макс. P = (Cb 1 * P 1 ) + (Cb 11 * Р 2 + (Сб 21 * Р 3 + (Сб 31 * Р 4 + (Сб 41 * Р ) (6 * Р 50919 3 (6 * Р 50919)0 * 225) + (0 * 1000) + (-M * 150) + (-M * 0) = -150M; значение из столбца переменной, на значение из столбца Cb, суммируя результаты произведений, и вычитая из их суммы коэффициент целевой функции, с этой переменной.
Макс. x 1 = ((Cb 1 * x 1,1 ) + (Cb 2 * x 2,1 ) + (Cb 9,19363 2,1 ) + (Cb 9,9363 ) + (Cb 4 * x 4,1 ) + (Cb 5 * x 5,1 ) ) — k x 1 = ((0 * 2) + (0 * 0) + (0 * 5) + (-М * 0) + (-М * 0)) — 3 = -3;
Max x 2 = ((Cb 1 * x 1,2 ) + (Cb 2 * x 2,2 ) + (Cb 3 * х 3,2 ) + (Сб 4 * х 4,2 ) + (Сб 5 * х 5,2 ) ) — к х ) — к х (0 * 1) + (0 * 0) + (0 * 4) + (-М * 2) + (-М * 0)) — 4 = -2М-4;
Макс. x 3 = ((Cb 1 * x 1,3 ) + (Cb 2 * x 2,3 ) + (19 4 x ) + (Сб 4 * х 4,3 ) + (Сб 5 * х 5,3 )) — к х 3 = ((0 * 1) + (0 * 0) + (0 * 0) + (-М * 0) + (-М * 0)) — 0 = 0;
x 3 = ((Cb 1 * x 1,3 ) + (Cb 2 * x 2,3 ) + (19 4 x ) + (Сб 4 * х 4,3 ) + (Сб 5 * х 5,3 )) — к х 3 = ((0 * 1) + (0 * 0) + (0 * 0) + (-М * 0) + (-М * 0)) — 0 = 0;
Макс. x 4 = ((Cb 1 * x 1,4 ) + (Cb 2 * x 2,4 ) + (194 x ) + (Cb 4 * x 4,4 ) + (Cb 5 * x 5,4 ) ) — k x 4 = ((0 * 0) + (0 * 1) + (0 * 0) + (-М * 0) + (-М * 0)) — 0 = 0;
Макс. x 5 = ((Cb 1 * х 1,5 ) + (Сб 2 * х 2,5 ) + (Сб 3 * х 3,5 ) + (Сб 3 х 4 5 ) + (Cb 5 * x 5,5 ) ) — k x 5 = ((0 * 0) + (0 * 0) + (0 * 1) + (-M * 0) + (-М * 0)) — 0 = 0;
x 5 = ((Cb 1 * х 1,5 ) + (Сб 2 * х 2,5 ) + (Сб 3 * х 3,5 ) + (Сб 3 х 4 5 ) + (Cb 5 * x 5,5 ) ) — k x 5 = ((0 * 0) + (0 * 0) + (0 * 1) + (-M * 0) + (-М * 0)) — 0 = 0;
Макс. х 6 = ((Кб 1 * х 1,6 ) + (Кб 2 * х 2,6 ) + (Кб 3 *
Max x 7 = ((Cb 1 * x 1,7 ) + (Cb 2 * x 2,7 ) + (Cb 3 x
Макс. x 8 = ((Cb 1 * x 1,8 ) + (Cb 2 * x 2,8 ) + (Cb 9,938 3 х ) + (Cb 4 * x 4,8 ) + (Cb 5 * x 5,8 ) ) — k x 8 = ((0 * 0) + (0 * 0) + (0 * 0) + (-М * 1) + (-М * 0)) — -М = 0;
x 8 = ((Cb 1 * x 1,8 ) + (Cb 2 * x 2,8 ) + (Cb 9,938 3 х ) + (Cb 4 * x 4,8 ) + (Cb 5 * x 5,8 ) ) — k x 8 = ((0 * 0) + (0 * 0) + (0 * 0) + (-М * 1) + (-М * 0)) — -М = 0;
Max x 9 = ((Cb 1 * x 1,9 ) + (Cb 2 * x 2,9 ) + (Cb 3 * х 3,9 ) + (Сб 4 * х 4,9 ) + (Сб 5 * х 5,9 ) ) — к 9 х (0 * 0) + (0 * 0) + (0 * 0) + (-М * 0) + (-М * 1)) — -М = 0;
Элементы столбца Q
Поскольку среди оценок контролируемых переменных есть отрицательные значения, текущая таблица еще не имеет оптимального решения. Поэтому в базис вводим переменную с наименьшей отрицательной оценкой.
Поэтому в базис вводим переменную с наименьшей отрицательной оценкой.
Количество переменных в базе всегда постоянно, поэтому необходимо выбрать, какую переменную вывести из базы, для чего вычисляем Q.
Элементы столбца Q вычисляются путем деления значений из столбец Р на значение из столбца, соответствующего той переменной, которая введена в основу:
Q 1 = P 1 / x 1,2 = 600 / 1 = 600;
Q 2 = P 2 / x 2,2 = 225/0 = ∞;
Q 3 = P 3 / x 3,2 = 1000 / 4 = 250;
Q 4 = P 4 / x 4,2 = 150 / 2 = 75;
Q 5 = P 5 / x 5,2 = 0 / 0 = ∞;
Выводим из базы переменную с наименьшим положительным значением Q.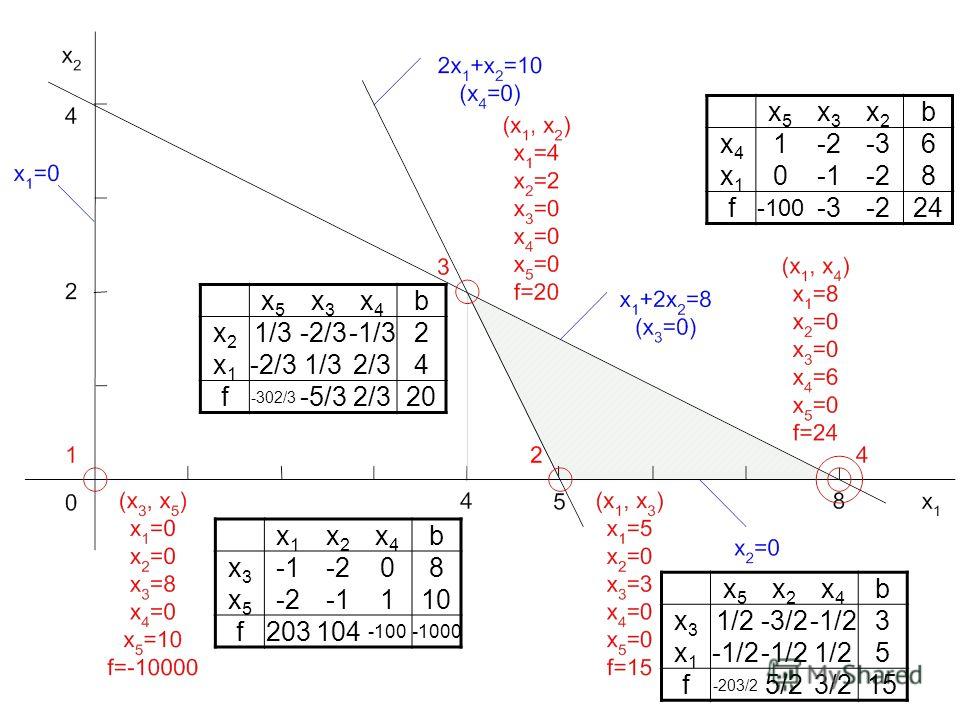
На пересечении строки, соответствующей переменной, выводимой из базы, и столбца, соответствующего переменной, вводимой в базу основа, является разрешающим элементом.
Этот элемент позволит нам вычислить элементы таблицы следующей итерации.
Iteration: 2
| B | Cb | P | x 1 ↓ | x 2 | x 3 | x 4 | x 5 | x 6 | x 7 | x 8 | x 9 | Q | 0642
| 3 | 4 | 0 | 0 | 0 | 0 | 0 | -M | -M | ||||
| x 3 | 0 | 525 | 2 | 0 | 1 | 0 | 0 | 0.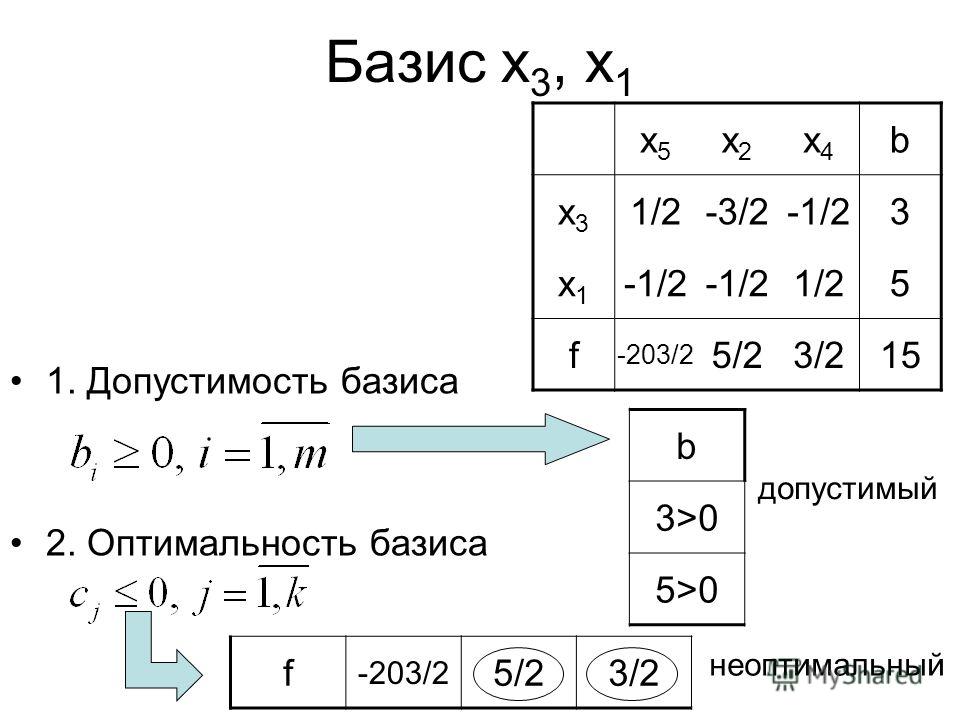 5 5 | 0 | -0.5 | 0 | 262.5 |
| x 4 | 0 | 225 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ∞ |
| x 5 ← | 0 | 700 | 5 | 0 | 0 | 0 | 1 | 2 | 0 | -2 | 0 | 140 |
| x 2 | 4 | 75 | 0 | 1 | 0 | 0 | 0 | -0. 5 5 | 0 | 0.5 | 0 | ∞ |
| x 9 | -M | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 1 | ∞ |
| max | 300 | -3 | 0 | 0 | 0 | 0 | -2 | M | M+2 | 0 | ||
Расчет элементов таблицы:
Элементы основания столбца (В)
По результатам расчетов предыдущей итерации удаляем из основания переменную x 8 и ставим на ее место x 2 . Все остальные ячейки остаются без изменений.
Все остальные ячейки остаются без изменений.
Элементы столбца Cb
Каждая ячейка этого столбца равна коэффициенту, который соответствует базовой переменной в соответствующей строке.
Кб 1 = 0;
Кб 2 = 0;
Кб 3 = 0;
Кб 4 = 4;
Кб 5 = -М;
Значения переменных переменных и столбца P (За исходные данные взяты данные предыдущей итерации)
Заполнить все ячейки нулями, соответствующими только что введенной в основу переменной:(Разрешение элемент остается без изменений)
x 1,2 = 0;
х 2,2 = 0;
x 3,2 = 0;
х 5,2 = 0;
Переносим строку с разрешающим элементом из предыдущей таблицы в текущую, поэлементно разделив ее значения на разрешающий элемент:
P 4 = P 4 / x 4,2 = 150 / 2 = 75;
х 4,1 = х 4,1 / х 4,2 = 0 / 2 = 0;
х 4,2 = х 4,2 / х 4,2 = 2/2 = 1;
х 4,3 = х 4,3 / х 4,2 = 0 / 2 = 0;
х 4,4 = х 4,4 / х 4,2 = 0 / 2 = 0;
х 4,5 = х 4,5 / х 4,2 = 0 / 2 = 0;
х 4,6 = х 4,6 / х 4,2 = -1 / 2 = -0,5;
х 4,7 = х 4,7 / х 4,2 = 0 / 2 = 0;
х 4,8 = х 4,8 / х 4,2 = 1/2 = 0,5;
х 4,9 = х 4,9 / х 4,2 = 0 / 2 = 0;
Остальные пустые ячейки, кроме строки оценок и столбца Q, рассчитываются методом прямоугольников, относительно разрешающего элемента:
P 1 = (P 1 * x 4,2 ) — (х 1,2 * Р 4 ) / х 4,2 = ((600 * 2) — (1 * 150)) / 2 = 525;
П 2 = (П 2 * x 4,2 ) — (x 2,2 * P 4 ) / x 4,2 = ((225 * 2) — (0 * 150)) / 2 = 225 ;
Р 3 = (Р 3 * х 4,2 ) — (х 3,2 * Р 4 ) / х 4,2 = ((2) — (1000 4*150))/2=700;
P 5 = (P 5 * x 4,2 ) — (x 5,2 * P 4 ) / x 4,2 = — (0 * 2) 0 * 150)) / 2 = 0;
х 1,1 = ((х 1,1 * х 4,2 ) — (х 1,2 * х 4,1 )) / х 4,2 = ((2 * 2) — (1 * 0)) / 2 = 2;
х 1,2 = ((х 1,2 * х 4,2 ) — (х 1,2 * х 4,2 )) / х 4,2 = ((1 * 2) — (1 * 2)) / 2 = 0;
х 1,4 = ((х 1,4 * х 4,2 ) — (х 1,2 * х 4,4 )) / х 4,2 = ((0 * 2) — (1 * 0)) / 2 = 0;
х 1,5 = ((х 1,5 * х 4,2 ) — (х 1,2 * х 4,5 )) / х 4,2 = ( (0 * 2) — (1 * 0)) / 2 = 0;
х 1,6 = ((х 1,6 * х 4,2 ) — (х 1,2 * х 4,6 )) / х 4,2 = ((0 * 2) — (1 * -1)) / 2 = 0,5;
х 1,7 = ((х 1,7 * х 4,2 ) — (х 1,2 * х 4,7 )) / х 4,2 = ((0 * 2) — (1 * 0)) / 2 = 0;
х 1,8 = ((х 1,8 * х 4,2 ) — (х 1,2 * х 4,8 )) / х 4,2 = ((0 * 2) — (1 * 1)) / 2 = -0,5;
х 1,9 = ((х 1,9 * х 4,2 ) — (х 1,2 * х 4,9 )) / х 4,2 = ((0 * 2) — (1 * 0)) / 2 = 0;
х 2,1 = ((х 2,1 * х 4,2 ) — (х 2,2 * х 4,1 )) / х 4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
х 2,2 = ((х 2,2 * х 4,2 ) — (х 2,2 * х 4,2 )) / х 4,2 = ((0 * 2) — (0 * 2)) / 2 = 0;
х 2,4 = ((х 2,4 * х 4,2 ) — (х 2,2 * х 4,4 )) / х 4,2 = ((1 * 2) — (0 * 0)) / 2 = 1;
х 2,5 = ((х 2,5 * х 4,2 ) — (х 2,2 * х 4,5 )) / х 4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
х 2,6 = ((х 2,6 * х 4,2 ) — (х 2,2 * х 4,6 )) / х 4,2 = ((0 * 2) — (0 * -1)) / 2 = 0;
х 2,7 = ((х 2,7 * х 4,2 ) — (х 2,2 * х 4,7 )) / х 4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
х 2,8 = ((х 2,8 * х 4,2 ) — (х 2,2 * х 4,8 )) / х 4,2 = ((0 * 2) — (0 * 1)) / 2 = 0;
х 2,9 = ((х 2,9 * х 4,2 ) — (х 2,2 * х 4,9 )) / х 4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
х 3,1 = ((х 3,1 * х 4,2 ) — (х 3,2 * х 4,1 )) / х 4,2 = ((5 * 2) — (4 * 0)) / 2 = 5;
х 3,2 = ((х 3,2 * х 4,2 ) — (х 3,2 * х 4,2 )) / х 4,2 = ((4*2) — (4*2))/2=0;
х 3,4 = ((х 3,4 * х 4,2 ) — (х 3,2 * х 4,4 )) / х 4,2 = ((0 * 2) — (4 * 0)) / 2 = 0;
х 3,5 = ((х 3,5 * х 4,2 ) — (х 3,2 * х 4,5 )) / х 4,2 = ((1 * 2) — (4 * 0)) / 2 = 1;
х 3,6 = ((х 3,6 * х 4,2 ) — (х 3,2 * х 4,6 )) / х 4,2 = ((0*2)-(4*-1))/2=2;
х 3,7 = ((х 3,7 * х 4,2 ) — (х 3,2 * х 4,7 )) / х 4,2 = ((0 * 2) — (4 * 0)) / 2 = 0;
х 3,8 = ((х 3,8 * х 4,2 ) — (х 3,2 * х 4,8 )) / х 4,2 = ((0 * 2) — (4 * 1)) / 2 = -2;
х 3,9 = ((х 3,9 * х 4,2 ) — (х 3,2 * х 4,9 )) / х 4,2 = ((0 * 2) — (4 * 0)) / 2 = 0;
х 5,1 = ((х 5,1 * х 4,2 ) — (х 5,2 * х 4,1 )) / х 4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
х 5,2 = ((х 5,2 * х 4,2 ) — (х 5,2 * х 4,2 )) / х 4,2 = ((0 * 2) — (0 * 2)) / 2 = 0;
х 5,4 = ((х 5,4 * х 4,2 ) — (х 5,2 * х 4,4 )) / х 4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
х 5,5 = ((х 5,5 * х 4,2 ) — (х 5,2 * х 4,5 )) / х 4,2 = ((0 * 2) — (0 * 0)) / 2 = 0;
х 5,6 = ((х 5,6 * х 4,2 ) — (х 5,2 * х 4,6 )) / х 4,2 = ((0 * 2) — (0 * -1)) / 2 = 0;
х 5,7 = ((х 5,7 * х 4,2 ) — (х 5,2 * х 4,7 )) / х 4,2 = ((-1 * 2) — (0 * 0)) / 2 = -1;
х 5,8 = ((х 5,8 * х 4,2 ) — (х 5,2 * х 4,8 )) / х 4,2 = ((0 * 2) — (0 * 1)) / 2 = 0;
х 5,9 = ((х 5,9 * х 4,2 ) — (х 5,2 * х 4,9 )) / х 4,2 = ((1 * 2) — (0 * 0)) / 2 = 1;
Значение целевой функции
Значение целевой функции вычисляем путем поэлементного умножения столбца Cb на столбец P, сложения результатов произведений.
Max P = (Cb 1 * P 1 ) + (Cb 11 * P 2 + (Cb 21 * P 3 + (Cb 31 * P 4 + (Cb 41 * P 5 = (0 * 525) + (0 * 225) + (0 * 700) + (4 * 75) + (-M * 0) = 300;
Оценено Контрольные переменные
Мы вычисляем оценки для каждой контролируемой переменной путем поэлементного умножения значения из столбца переменных на значение из столбца Cb, суммирования результатов произведений и вычитания коэффициента целевой функции из их суммы с этой переменной.
Макс. x 1 = ((Cb 1 * x 1,1 ) + (Cb 2 * x 2,1 ) + (Cb 9,19363 2,1 ) + (Cb 9,9363 ) + (Cb 4 * x 4,1 ) + (Cb 5 * x 5,1 ) ) — k x 1 = ((0 * 2) + (0 * 0) + (0 * 5) + (4 * 0) + (-М * 0)) — 3 = -3;
Max x 2 = ((Cb 1 * x 1,2 ) + (Cb 2 * x 2,2 ) + (Cb 3 * х 3,2 ) + (Сб 4 * х 4,2 ) + (Сб 5 * х 5,2 ) ) — к х ) — к х (0 * 0) + (0 * 0) + (0 * 0) + (4 * 1) + (-М * 0)) — 4 = 0;
Макс. x 3 = ((Cb 1 * x 1,3 ) + (Cb 2 * x 2,3 ) + (19 4 x ) + (Сб 4 * х 4,3 ) + (Сб 5 * х 5,3 )) — к х 3 = ((0 * 1) + (0 * 0) + (0 * 0) + (4 * 0) + (-М * 0)) — 0 = 0;
x 3 = ((Cb 1 * x 1,3 ) + (Cb 2 * x 2,3 ) + (19 4 x ) + (Сб 4 * х 4,3 ) + (Сб 5 * х 5,3 )) — к х 3 = ((0 * 1) + (0 * 0) + (0 * 0) + (4 * 0) + (-М * 0)) — 0 = 0;
Макс. x 4 = ((Cb 1 * x 1,4 ) + (Cb 2 * x 2,4 ) + (194 x ) + (Cb 4 * x 4,4 ) + (Cb 5 * x 5,4 ) ) — k x 4 = ((0 * 0) + (0 * 1) + (0 * 0) + (4 * 0) + (-М * 0)) — 0 = 0;
Макс. x 5 = ((Cb 1 * х 1,5 ) + (Сб 2 * х 2,5 ) + (Сб 3 * х 3,5 ) + (Сб 4 х 9, * 4 5 ) + (Cb 5 * x 5,5 ) ) — k x 5 = ((0 * 0) + (0 * 0) + (0 * 1) + (4 * 0 ) + (-М * 0)) — 0 = 0;
x 5 = ((Cb 1 * х 1,5 ) + (Сб 2 * х 2,5 ) + (Сб 3 * х 3,5 ) + (Сб 4 х 9, * 4 5 ) + (Cb 5 * x 5,5 ) ) — k x 5 = ((0 * 0) + (0 * 0) + (0 * 1) + (4 * 0 ) + (-М * 0)) — 0 = 0;
Макс. х 6 = ((Кб 1 * х 1,6 ) + (Кб 2 * х 2,6 ) + (Кб 3 *
Max x 7 = ((Cb 1 * x 1,7 ) + (Cb 2 * x 2,7 ) + (Cb 3 x
Макс. x 8 = ((Cb 1 * x 1,8 ) + (Cb 2 * x 2,8 ) + (Cb 9,938 3 х ) + (Cb 4 * x 4,8 ) + (Cb 5 * x 5,8 ) ) — k x 8 = ((0 * -0,5) + (0 * -0,5) + ( * 0) + (0 * -2) + (4 * 0,5) + (-М * 0)) — -М = М+2;
x 8 = ((Cb 1 * x 1,8 ) + (Cb 2 * x 2,8 ) + (Cb 9,938 3 х ) + (Cb 4 * x 4,8 ) + (Cb 5 * x 5,8 ) ) — k x 8 = ((0 * -0,5) + (0 * -0,5) + ( * 0) + (0 * -2) + (4 * 0,5) + (-М * 0)) — -М = М+2;
Max x 9 = ((Cb 1 * x 1,9 ) + (Cb 2 * x 2,9 ) + (Cb 3 * х 3,9 ) + (Сб 4 * х 4,9 ) + (Сб 5 * х 5,9 ) ) — к 9 х (0 * 0) + (0 * 0) + (0 * 0) + (4 * 0) + (-М * 1)) — -М = 0;
Элементы столбца Q
Поскольку среди оценок контролируемых переменных есть отрицательные значения, текущая таблица еще не имеет оптимального решения. Поэтому в базис вводим переменную с наименьшей отрицательной оценкой.
Поэтому в базис вводим переменную с наименьшей отрицательной оценкой.
Количество переменных в базе всегда постоянно, поэтому необходимо выбрать, какую переменную вывести из базы, для чего вычисляем Q.
Элементы столбца Q вычисляются путем деления значений из столбец Р на значение из столбца, соответствующего той переменной, которая введена в основу:
Q 1 = P 1 / x 1,1 = 525 / 2 = 262,5;
Q 2 = P 2 / x 2,1 = 225/0 = ∞;
Q 3 = P 3 / x 3,1 = 700 / 5 = 140;
Q 4 = P 4 / x 4,1 = 75 / 0 = ∞;
Q 5 = P 5 / x 5,1 = 0 / 0 = ∞;
Выводим из базы переменную с наименьшим положительным значением Q.
На пересечении строки, соответствующей переменной, выводимой из базы, и столбца, соответствующего переменной, вводимой в базу основа, является разрешающим элементом.
Этот элемент позволит нам вычислить элементы таблицы следующей итерации.
Iteration: 3
| B | Cb | P | x 1 | x 2 | x 3 | x 4 | x 5 | x 6 ↓ | x 7 | x 8 | x 9 | Q |
| 3 | 4 | 0 | 0 | 0 | 0 | 0 | -M | -M | ||||
| x 3 | 0 | 245 | 0 | 0 | 1 | 0 | -0. 4 4 | -0.3 | 0 | 0.3 | 0 | -816.67 |
| x 4 | 0 | 225 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ∞ |
| x 1 ← | 3 | 140 | 1 | 0 | 0 | 0 | 0. 2 2 | 0.4 | 0 | -0.4 | 0 | 350 |
| x 2 | 4 | 75 | 0 | 1 | 0 | 0 | 0 | -0.5 | 0 | 0.5 | 0 | -150 |
| x 9 | -M | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 1 | ∞ |
| max | 720 | 0 | 0 | 0 | 0 | 0. 6 6 | -0.8 | M | M+0.8 | 0 | ||
Расчет элементов таблицы:
Элементы основания столбца (Б)
По результатам расчетов предыдущей итерации удалим из основания переменную x 5 и подставим в нее место х 1 . Все остальные ячейки остаются без изменений.
Элементы столбца Cb
Каждая ячейка этого столбца равна коэффициенту, который соответствует базовой переменной в соответствующей строке.
Кб 1 = 0;
Кб 2 = 0;
Кб 3 = 3;
Кб 4 = 4;
Кб 5 = -М;
Значения переменных переменных и столбца P (За исходные данные взяты данные предыдущей итерации)
Заполнить все ячейки нулями, соответствующими только что введенной в основу переменной:(Разрешение элемент остается без изменений)
x 1,1 = 0;
x 2,1 = 0;
x 4,1 = 0;
x 5,1 = 0;
Переносим строку с разрешающим элементом из предыдущей таблицы в текущую, поэлементно разделив ее значения на разрешающий элемент:
P 3 = P 3 / x 3,1 = 700 / 5 = 140;
х 3,1 = х 3,1 / х 3,1 = 5 / 5 = 1;
х 3,2 = х 3,2 / х 3,1 = 0 / 5 = 0;
х 3,3 = х 3,3 / х 3,1 = 0 / 5 = 0;
х 3,4 = х 3,4 / х 3,1 = 0 / 5 = 0;
х 3,5 = х 3,5 / х 3,1 = 1 / 5 = 0,2;
х 3,6 = х 3,6 / х 3,1 = 2 / 5 = 0,4;
х 3,7 = х 3,7 / х 3,1 = 0 / 5 = 0;
х 3,8 = х 3,8 / х 3,1 = -2 / 5 = -0,4;
х 3,9 = х 3,9 / х 3,1 = 0 / 5 = 0;
Остальные пустые ячейки, кроме строки оценок и столбца Q, рассчитываются методом прямоугольников, относительно разрешающего элемента:
P 1 = (P 1 * x 3,1 ) — (х 1,1 * Р 3 ) / х 3,1 = ((525 * 5) — (2 * 700)) / 5 = 245;
С 2 = (P 2 * x 3,1 ) — (x 2,1 * P 3 ) / x 3,1 = ((225 * 5) — (0 * 700 )) / 5 = 225;
Р 4 = (Р 4 * х 3,1 ) — (х 4,1 * Р 3 ) / х 3,1 = ((75 * 5) 0 * 700)) / 5 = 75;
P 5 = (P 5 * x 3,1 ) — (x 5,1 * P 3 ) / x 3,1 = — (0 * 5) 0 * 700)) / 5 = 0;
х 1,1 = ((х 1,1 * х 3,1 ) — (х 1,1 * х 3,1 )) / х 3,1 = ( (2*5) — (2*5))/5=0;
х 1,3 = ((х 1,3 * х 3,1 ) — (х 1,1 * х 3,3 )) / х 3,1 = ((1 * 5) — (2 * 0)) / 5 = 1;
х 1,4 = ((х 1,4 * х 3,1 ) — (х 1,1 * х 3,4 )) / х 3,1 = ((0 * 5) — (2 * 0)) / 5 = 0;
х 1,5 = ((х 1,5 * х 3,1 ) — (х 1,1 * х 3,5 )) / х 3,1 = ((0 * 5) — (2 * 1)) / 5 = -0,4;
х 1,6 = ((х 1,6 * х 3,1 ) — (х 1,1 * х 3,6 )) / х 3,1 = ((0,5 * 5) — (2 * 2)) / 5 = -0,3;
х 1,7 = ((х 1,7 * х 3,1 ) — (х 1,1 * х 3,7 )) / х 3,1 = ((0 * 5) — (2 * 0)) / 5 = 0;
х 1,8 = ((х 1,8 * х 3,1 ) — (х 1,1 * х 3,8 )) / х 3,1 = ((-0,5*5)-(2*-2))/5=0,3;
х 1,9 = ((х 1,9 * х 3,1 ) — (х 1,1 * х 3,9 )) / х 3,1 = ((0 * 5) — (2 * 0)) / 5 = 0;
х 2,1 = ((х 2,1 * х 3,1 ) — (х 2,1 * х 3,1 )) / х 3,1 = ((0 * 5) — (0 * 5)) / 5 = 0;
х 2,3 = ((х 2,3 * х 3,1 ) — (х 2,1 * х 3,3 )) / х 3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
х 2,4 = ((х 2,4 * х 3,1 ) — (х 2,1 * х 3,4 )) / х 3,1 = ((1 * 5) — (0 * 0)) / 5 = 1;
х 2,5 = ((х 2,5 * х 3,1 ) — (х 2,1 * х 3,5 )) / х 3,1 = ((0 * 5) — (0 * 1)) / 5 = 0;
х 2,6 = ((х 2,6 * х 3,1 ) — (х 2,1 * х 3,6 )) / х 3,1 = ((0 * 5) — (0 * 2)) / 5 = 0;
х 2,7 = ((х 2,7 * х 3,1 ) — (х 2,1 * х 3,7 )) / х 3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
х 2,8 = ((х 2,8 * х 3,1 ) — (х 2,1 * х 3,8 )) / х 3,1 = ((0 * 5) — (0 * -2)) / 5 = 0;
х 2,9 = ((х 2,9 * х 3,1 ) — (х 2,1 * х 3,9 )) / х 3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
х 4,1 = ((х 4,1 * х 3,1 ) — (х 4,1 * х 3,1 )) / х 3,1 = ((0 * 5) — (0 * 5)) / 5 = 0;
х 4,3 = ((х 4,3 * х 3,1 ) — (х 4,1 * х 3,3 )) / х 3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
х 4,4 = ((х 4,4 * х 3,1 ) — (х 4,1 * х 3,4 )) / х 3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
х 4,5 = ((х 4,5 * х 3,1 ) — (х 4,1 * х 3,5 )) / х 3,1 = ((0 * 5) — (0 * 1)) / 5 = 0;
х 4,6 = ((х 4,6 * х 3,1 ) — (х 4,1 * х 3,6 )) / х 3,1 = ((-0,5*5)-(0*2))/5=-0,5;
х 4,7 = ((х 4,7 * х 3,1 ) — (х 4,1 * х 3,7 )) / х 3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
х 4,8 = ((х 4,8 * х 3,1 ) — (х 4,1 * х 3,8 )) / х 3,1 = ((0,5*5)-(0*-2))/5=0,5;
х 4,9 = ((х 4,9 * х 3,1 ) — (х 4,1 * х 3,9 )) / х 3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
х 5,1 = ((х 5,1 * х 3,1 ) — (х 5,1 * х 3,1 )) / х 3,1 = ((0 * 5) — (0 * 5)) / 5 = 0;
х 5,3 = ((х 5,3 * х 3,1 ) — (х 5,1 * х 3,3 )) / х 3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
х 5,4 = ((х 5,4 * х 3,1 ) — (х 5,1 * х 3,4 )) / х 3,1 = ((0 * 5) — (0 * 0)) / 5 = 0;
х 5,5 = ((х 5,5 * х 3,1 ) — (х 5,1 * х 3,5 )) / х 3,1 = ((0 * 5) — (0 * 1)) / 5 = 0;
х 5,6 = ((х 5,6 * х 3,1 ) — (х 5,1 * х 3,6 )) / х 3,1 = ((0 * 5) — (0 * 2)) / 5 = 0;
х 5,7 = ((х 5,7 * х 3,1 ) — (х 5,1 * х 3,7 )) / х 3,1 = ((-1*5)-(0*0))/5=-1;
х 5,8 = ((х 5,8 * х 3,1 ) — (х 5,1 * х 3,8 )) / х 3,1 = ((0 * 5) — (0 * -2)) / 5 = 0;
х 5,9 = ((х 5,9 * х 3,1 ) — (х 5,1 * х 3,9 )) / х 3,1 = ((1 * 5) — (0 * 0)) / 5 = 1;
Значение целевой функции
Значение целевой функции вычисляем путем поэлементного умножения столбца Cb на столбец P, сложения результатов произведений.
Max P = (Cb 1 * P 1 ) + (Cb 11 * P 2 + (Cb 21 * P 3 + (Cb 31 * P 4 + (Cb 41 * P5) = (0 * 245) + (0 * 225) + (3 * 140) + (4 * 75) + (-M * 0) = 720;
Оцененные контрольные переменные
Рассчитываем оценки для каждой контролируемой переменной, поэлементно умножая значение из столбца переменных на значение из столбца Cb, суммируя результаты произведений и вычитая коэффициент целевой функции из их сумма с этой переменной
Макс. x 1 = ((Cb 1 * x 1,1 ) + (Cb 2 * x 2,1 ) + (Cb 9,19363 2,1 ) + (Cb 9,9363 ) + (Cb 4 * x 4,1 ) + (Cb 5 * x 5,1 ) ) — k x 1 = ((0 * 0) + (0 * 0) + (3 * 1) + (4 * 0) + (-М * 0)) — 3 = 0;
Max x 2 = ((Cb 1 * x 1,2 ) + (Cb 2 * x 2,2 ) + (Cb 3 * х 3,2 ) + (Сб 4 * х 4,2 ) + (Сб 5 * х 5,2 ) ) — к х ) — к х (0 * 0) + (0 * 0) + (3 * 0) + (4 * 1) + (-М * 0)) — 4 = 0;
Макс. x 3 = ((Cb 1 * x 1,3 ) + (Cb 2 * x 2,3 ) + (19 4 x ) + (Сб 4 * х 4,3 ) + (Сб 5 * х 5,3 )) — к х 3 = ((0 * 1) + (0 * 0) + (3 * 0) + (4 * 0) + (-М * 0)) — 0 = 0;
x 3 = ((Cb 1 * x 1,3 ) + (Cb 2 * x 2,3 ) + (19 4 x ) + (Сб 4 * х 4,3 ) + (Сб 5 * х 5,3 )) — к х 3 = ((0 * 1) + (0 * 0) + (3 * 0) + (4 * 0) + (-М * 0)) — 0 = 0;
Макс. x 4 = ((Cb 1 * x 1,4 ) + (Cb 2 * x 2,4 ) + (194 x ) + (Cb 4 * x 4,4 ) + (Cb 5 * x 5,4 ) ) — k x 4 = ((0 * 0) + (0 * 1) + (3 * 0) + (4 * 0) + (-М * 0)) — 0 = 0;
Макс. x 5 = ((Cb 1 * х 1,5 ) + (Сб 2 * х 2,5 ) + (Сб 3 * х 3,5 ) + (Сб 4 х 9, * 4 5 ) + (Cb 5 * x 5,5 ) ) — k x 5 = ((0 * -0,4) + (0 * 0) + (3 * 0,2) + (4 * 0) + (-М * 0)) — 0 = 0,6;
x 5 = ((Cb 1 * х 1,5 ) + (Сб 2 * х 2,5 ) + (Сб 3 * х 3,5 ) + (Сб 4 х 9, * 4 5 ) + (Cb 5 * x 5,5 ) ) — k x 5 = ((0 * -0,4) + (0 * 0) + (3 * 0,2) + (4 * 0) + (-М * 0)) — 0 = 0,6;
Макс. х 6 = ((Кб 1 * х 1,6 ) + (Кб 2 * х 2,6 ) + (Кб 3 *
Max x 7 = ((Cb 1 * x 1,7 ) + (Cb 2 * x 2,7 ) + (Cb 3 x
Макс. x 8 = ((Cb 1 * x 1,8 ) + (Cb 2 * x 2,8 ) + (Cb 9,938 3 х ) + (Cb 4 * x 4,8 ) + (Cb 5 * x 5,8 ) ) — k x 8 = ((0 * 0 * 0,3) + (0 * 0 * 0,3) + (0 * 0 * 0,3) 0) + (3 * -0,4) + (4 * 0,5) + (-М * 0)) — -М = М+0,8;
x 8 = ((Cb 1 * x 1,8 ) + (Cb 2 * x 2,8 ) + (Cb 9,938 3 х ) + (Cb 4 * x 4,8 ) + (Cb 5 * x 5,8 ) ) — k x 8 = ((0 * 0 * 0,3) + (0 * 0 * 0,3) + (0 * 0 * 0,3) 0) + (3 * -0,4) + (4 * 0,5) + (-М * 0)) — -М = М+0,8;
Макс. x 9 = ((Cb 1 * x 1,9 ) + (Cb 2 * x 2,9 ) + (Сб 3 * х 3,9 ) + (Сб 4 * х 4,9 ) + (Сб 5 * х 5,9 ) ) — к 9196 9 = ((0 * 0) + (0 * 0) + (3 * 0) + (4 * 0) + (-М * 1)) — -М = 0;
Элементы столбца Q
Поскольку среди оценок контролируемых переменных есть отрицательные значения, текущая таблица еще не имеет оптимального решения. Поэтому в базис вводим переменную с наименьшей отрицательной оценкой.
Поэтому в базис вводим переменную с наименьшей отрицательной оценкой.
Количество переменных в базе всегда постоянно, поэтому необходимо выбрать, какую переменную вывести из базы, для чего вычисляем Q.
Элементы столбца Q вычисляются путем деления значений из столбец P значением из столбца, соответствующего переменной, которая введена в основу:
Q 1 = P 1 / x 1,6 = 245 / -0,3 = -816,67;
Q 2 = P 2 / x 2,6 = 225/0 = ∞;
Q 3 = P 3 / x 3,6 = 140 / 0,4 = 350;
Q 4 = P 4 / x 4,6 = 75 / -0,5 = -150;
Q 5 = P 5 / x 5,6 = 0 / 0 = ∞;
Выводим из базы переменную с наименьшим положительным значением Q.
На пересечении строки, соответствующей переменной, выводимой из базы, и столбца, соответствующего переменной, вводимой в базу основа, является разрешающим элементом.
Этот элемент позволит нам вычислить элементы таблицы следующей итерации.
Iteration: 4
| B | Cb | P | x 1 | x 2 | x 3 | x 4 | x 5 | x 6 | x 7 | x 8 | x 9 | Q |
| 3 | 4 | 0 | 0 | 0 | 0 | 0 | -M | -M | ||||
| x 3 | 0 | 350 | 0. 75 75 | 0 | 1 | 0 | -0.25 | 0 | 0 | 0 | 0 | |
| x 4 | 0 | 225 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| x 6 | 0 | 350 | 2.5 | 0 | 0 | 0 | 0. 5 5 | 1 | 0 | -1 | 0 | |
| x 2 | 4 | 250 | 1.25 | 1 | 0 | 0 | 0.25 | 0 | 0 | 0 | 0 | |
| x 9 | -M | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 1 | |
| max | 1000 | 2 | 0 | 0 | 0 | 1 | 0 | M | M | 0 | ||
Calculation of table elements:
Элементы базиса столбца (В)
По результатам расчетов предыдущей итерации убираем из базиса переменную x 1 и ставим вместо нее x 6 . Все остальные ячейки остаются без изменений.
Все остальные ячейки остаются без изменений.
Элементы столбца Cb
Каждая ячейка этого столбца равна коэффициенту, который соответствует базовой переменной в соответствующей строке.
Кб 1 = 0;
Кб 2 = 0;
Кб 3 = 0;
Кб 4 = 4;
Кб 5 = -М;
Значения переменных переменных и столбца P (За исходные данные взяты данные предыдущей итерации)
Заполнить все ячейки нулями, соответствующими только что введенной в основу переменной:(Разрешение элемент остается без изменений)
x 1,6 = 0;
х 2,6 = 0;
х 4,6 = 0;
х 5,6 = 0;
Переносим строку с разрешающим элементом из предыдущей таблицы в текущую, поэлементно разделив ее значения на разрешающий элемент:
P 3 = P 3 / x 3,6 = 140 / 0,4 = 350;
х 3,1 = х 3,1 / х 3,6 = 1 / 0,4 = 2,5;
х 3,2 = х 3,2 / х 3,6 = 0 / 0,4 = 0;
х 3,3 = х 3,3 / х 3,6 = 0 / 0,4 = 0;
х 3,4 = х 3,4 / х 3,6 = 0 / 0,4 = 0;
х 3,5 = х 3,5 / х 3,6 = 0,2 / 0,4 = 0,5;
х 3,6 = х 3,6 / х 3,6 = 0,4 / 0,4 = 1;
х 3,7 = х 3,7 / х 3,6 = 0 / 0,4 = 0;
х 3,8 = х 3,8 / х 3,6 = -0,4/0,4 = -1;
х 3,9 = х 3,9 / х 3,6 = 0 / 0,4 = 0;
Остальные пустые ячейки, кроме строки оценок и столбца Q, рассчитываются методом прямоугольников, относительно разрешающего элемента:
P 1 = (P 1 * x 3,6 ) — (х 1,6 * Р 3 ) / х 3,6 = ((245 * 0,4) — (-0,3 * 140)) / 0,4 = 350;
П 2 = (П 2 * х 3,6 ) — (х 2,6 * Р 3 ) / х 3,6 = ((225 * 0,4) — (0 * 140)) / 0,4 = 225 ;
P 4 = (P 4 * x 3,6 ) — (x 4,6 * P 3 ) / x 3,6 = ((4) — ( 0) -0,5*140))/0,4=250;
P 5 = (P 5 * x 3,6 ) — (x 5,6 * P 3 ) / x 3,6 = ((0) — ( 0. 0 * 140)) / 0,4 = 0;
0 * 140)) / 0,4 = 0;
х 1,1 = ((х 1,1 * х 3,6 ) — (х 1,6 * х 3,1 )) / х 3,6 = ((0 * 0,4) — (-0,3 * 1)) / 0,4 = 0,75;
х 1,2 = ((х 1,2 * х 3,6 ) — (х 1,6 * х 3,2 )) / х 3,6 = ((0 * 0,4) — (-0,3 * 0)) / 0,4 = 0;
х 1,3 = ((х 1,3 * х 3,6 ) — (х 1,6 * х 3,3 )) / х 3,6 = ((1 * 0,4) — (-0,3 * 0)) / 0,4 = 1;
х 1,4 = ((х 1,4 * х 3,6 ) — (х 1,6 * х 3,4 )) / х 3,6 = ((0 * 0,4) — (-0,3 * 0)) / 0,4 = 0;
х 1,5 = ((х 1,5 * х 3,6 ) — (х 1,6 * х 3,5 )) / х 3,6 = ((-0,4 * 0,4) — (-0,3 * 0,2)) / 0,4 = -0,25;
х 1,6 = ((х 1,6 * х 3,6 ) — (х 1,6 * х 3,6 )) / х 3,6 = ((-0,3 * 0,4) — (-0,3 * 0,4)) / 0,4 = 0;
х 1,8 = ((х 1,8 * х 3,6 ) — (х 1,6 * х 3,8 )) / х 3,6 = ((0,3 * 0,4) — (-0,3 * -0,4)) / 0,4 = 0;
х 1,9 = ((х 1,9 * х 3,6 ) — (х 1,6 * х 3,9 )) / х 3,6 = ((0 * 0,4) — (-0,3 * 0)) / 0,4 = 0;
х 2,1 = ((х 2,1 * х 3,6 ) — (х 2,6 * х 3,1 )) / х 3,6 = ((0 * 0,4) — (0 * 1)) / 0,4 = 0;
х 2,2 = ((х 2,2 * х 3,6 ) — (х 2,6 * х 3,2 )) / х 3,6 = ((0 * 0,4) — (0 * 0)) / 0,4 = 0;
х 2,3 = ((х 2,3 * х 3,6 ) — (х 2,6 * х 3,3 )) / х 3,6 = ((0 * 0,4) — (0 * 0)) / 0,4 = 0;
х 2,4 = ((х 2,4 * х 3,6 ) — (х 2,6 * х 3,4 )) / х 3,6 = ((1 * 0,4) — (0 * 0)) / 0,4 = 1;
х 2,5 = ((х 2,5 * х 3,6 ) — (х 2,6 * х 3,5 )) / х 3,6 = ((0 * 0,4) — (0 * 0,2)) / 0,4 = 0;
х 2,6 = ((х 2,6 * х 3,6 ) — (х 2,6 * х 3,6 )) / х 3,6 = ((0 * 0,4) — (0 * 0,4)) / 0,4 = 0;
х 2,8 = ((х 2,8 * х 3,6 ) — (х 2,6 * х 3,8 )) / х 3,6 = ((0 * 0,4) — (0 * -0,4)) / 0,4 = 0;
х 2,9 = ((х 2,9 * х 3,6 ) — (х 2,6 * х 3,9 )) / х 3,6 = ((0 * 0,4) — (0 * 0)) / 0,4 = 0;
х 4,1 = ((х 4,1 * х 3,6 ) — (х 4,6 * х 3,1 )) / х 3,6 = ((0 * 0,4) — (-0,5 * 1)) / 0,4 = 1,25;
х 4,2 = ((х 4,2 * х 3,6 ) — (х 4,6 * х 3,2 )) / х 3,6 = ((1 * 0,4) — (-0,5 * 0)) / 0,4 = 1;
х 4,3 = ((х 4,3 * х 3,6 ) — (х 4,6 * х 3,3 )) / х 3,6 = ((0 * 0,4) — (-0,5 * 0)) / 0,4 = 0;
х 4,4 = ((х 4,4 * х 3,6 ) — (х 4,6 * х 3,4 )) / х 3,6 = ((0 * 0,4) — (-0,5 * 0)) / 0,4 = 0;
х 4,5 = ((х 4,5 * х 3,6 ) — (х 4,6 * х 3,5 )) / х 3,6 = ((0 * 0,4) — (-0,5 * 0,2)) / 0,4 = 0,25;
х 4,6 = ((х 4,6 * х 3,6 ) — (х 4,6 * х 3,6 )) / х 3,6 = ((-0,5 * 0,4) — (-0,5 * 0,4)) / 0,4 = 0;
х 4,8 = ((х 4,8 * х 3,6 ) — (х 4,6 * х 3,8 )) / х 3,6 = ((0,5 * 0,4) — (-0,5 * -0,4)) / 0,4 = 0;
х 4,9 = ((х 4,9 * х 3,6 ) — (х 4,6 * х 3,9 )) / х 3,6 = ((0 * 0,4) — (-0,5 * 0)) / 0,4 = 0;
х 5,1 = ((х 5,1 * х 3,6 ) — (х 5,6 * х 3,1 )) / х 3,6 = ((0 * 0,4) — (0 * 1)) / 0,4 = 0;
х 5,2 = ((х 5,2 * х 3,6 ) — (х 5,6 * х 3,2 )) / х 3,6 = ((0 * 0,4) — (0 * 0)) / 0,4 = 0;
х 5,3 = ((х 5,3 * х 3,6 ) — (х 5,6 * х 3,3 )) / х 3,6 = ((0 * 0,4) — (0 * 0)) / 0,4 = 0;
х 5,4 = ((х 5,4 * х 3,6 ) — (х 5,6 * х 3,4 )) / х 3,6 = ((0 * 0,4) — (0 * 0)) / 0,4 = 0;
х 5,5 = ((х 5,5 * х 3,6 ) — (х 5,6 * х 3,5 )) / х 3,6 = ((0 * 0,4) — (0 * 0,2)) / 0,4 = 0;
х 5,6 = ((х 5,6 * х 3,6 ) — (х 5,6 * х 3,6 )) / х 3,6 = ((0 * 0,4) — (0 * 0,4)) / 0,4 = 0;
х 5,8 = ((х 5,8 * х 3,6 ) — (х 5,6 * х 3,8 )) / х 3,6 = ((0 * 0,4) — (0 * -0,4)) / 0,4 = 0;
х 5,9 = ((х 5,9 * х 3,6 ) — (х 5,6 * х 3,9 )) / х 3,6 = ((1 * 0,4) — (0 * 0)) / 0,4 = 1;
Значение целевой функции
Значение целевой функции вычисляем путем поэлементного умножения столбца Cb на столбец P, сложения результатов произведений.
Макс. P = (Cb 1 * P 1 ) + (Cb 11 * P 2 + (Cb 21 * P 9)1963 3 + (Кб 31 * Р 4 + (Кб 41 * Р 5 = (0 * 350) + (0 * 225) + (0 * 350) + (4 * 250) + (-M * 0) = 1000;
Оцененные контрольные переменные
Рассчитываем оценки для каждой контролируемой переменной, поэлементно умножая значение из столбца переменных на значение из столбца Cb, суммируя результаты произведений и вычитание коэффициента целевой функции из их суммы с этой переменной.0005
Макс. x 1 = ((Cb 1 * x 1,1 ) + (Cb 2 * x 2,1 ) + (Cb 9,19363 2,1 ) + (Cb 9,9363 ) + (Cb 4 * x 4,1 ) + (Cb 5 * x 5,1 ) ) — k x 1 = ((0 * 0,75) + (0 * 0,75) + (0 * 0,75) 0) + (0 * 2,5) + (4 * 1,25) + (-М * 0)) — 3 = 2;
Max x 2 = ((Cb 1 * x 1,2 ) + (Cb 2 * x 2,2 ) + (Cb 3 * х 3,2 ) + (Сб 4 * х 4,2 ) + (Сб 5 * х 5,2 ) ) — к х ) — к х (0 * 0) + (0 * 0) + (0 * 0) + (4 * 1) + (-М * 0)) — 4 = 0;
Макс. x 3 = ((Cb 1 * x 1,3 ) + (Cb 2 * x 2,3 ) + (19 4 x ) + (Сб 4 * х 4,3 ) + (Сб 5 * х 5,3 )) — к х 3 = ((0 * 1) + (0 * 0) + (0 * 0) + (4 * 0) + (-М * 0)) — 0 = 0;
x 3 = ((Cb 1 * x 1,3 ) + (Cb 2 * x 2,3 ) + (19 4 x ) + (Сб 4 * х 4,3 ) + (Сб 5 * х 5,3 )) — к х 3 = ((0 * 1) + (0 * 0) + (0 * 0) + (4 * 0) + (-М * 0)) — 0 = 0;
Макс. x 4 = ((Cb 1 * x 1,4 ) + (Cb 2 * x 2,4 ) + (194 x ) + (Cb 4 * x 4,4 ) + (Cb 5 * x 5,4 ) ) — k x 4 = ((0 * 0) + (0 * 1) + (0 * 0) + (4 * 0) + (-М * 0)) — 0 = 0;
Макс. x 5 = ((Cb 1 * х 1,5 ) + (Сб 2 * х 2,5 ) + (Сб 3 * х 3,5 ) + (Сб 4 х 9, * 4 5 ) + (Cb 5 * x 5,5 ) ) — k x 5 = ((0 * -0,25) + (0 * 0) + (0 * 0,5) + (4 * 0,25) + (-М * 0) ) — 0 = 1;
x 5 = ((Cb 1 * х 1,5 ) + (Сб 2 * х 2,5 ) + (Сб 3 * х 3,5 ) + (Сб 4 х 9, * 4 5 ) + (Cb 5 * x 5,5 ) ) — k x 5 = ((0 * -0,25) + (0 * 0) + (0 * 0,5) + (4 * 0,25) + (-М * 0) ) — 0 = 1;
Макс. х 6 = ((Кб 1 * х 1,6 ) + (Кб 2 * х 2,6 ) + (Кб 3 *
Max x 7 = ((Cb 1 * x 1,7 ) + (Cb 2 * x 2,7 ) + (Cb 3 x
Макс. x 8 = ((Cb 1 * x 1,8 ) + (Cb 2 * x 2,8 ) + (Cb 9,938 3 х ) + (Cb 4 * x 4,8 ) + (Cb 5 * x 5,8 ) ) — k x 8 = ((0 * 0) + (0 * 0) + (0 * -1) + (4 * 0) + (-М * 0)) — -М = М;
x 8 = ((Cb 1 * x 1,8 ) + (Cb 2 * x 2,8 ) + (Cb 9,938 3 х ) + (Cb 4 * x 4,8 ) + (Cb 5 * x 5,8 ) ) — k x 8 = ((0 * 0) + (0 * 0) + (0 * -1) + (4 * 0) + (-М * 0)) — -М = М;
Max x 9 = ((Cb 1 * x 1,9 ) + (Cb 2 * x 2,9 ) + (Cb 3 * х 3,9 ) + (Сб 4 * х 4,9 ) + (Сб 5 * х 5,9 ) ) — к 9 х (0 * 0) + (0 * 0) + (0 * 0) + (4 * 0) + (-М * 1)) — -М = 0;
Результат:
Поскольку среди оценок контролируемых переменных нет отрицательных значений, текущая таблица имеет оптимальное решение.







 Конвертация матриц в списки и обратно.
Конвертация матриц в списки и обратно.

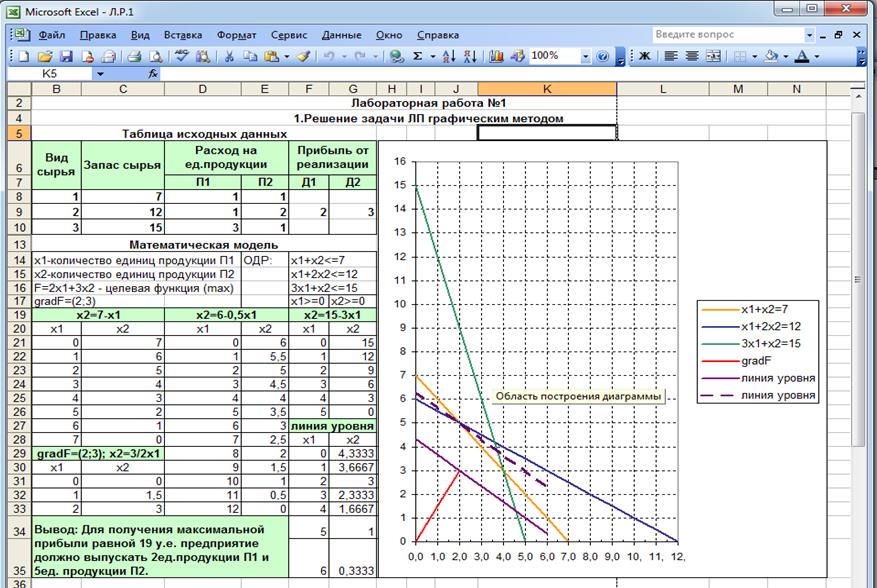 С другой стороны, если вы используете только
функциональность минимизации для расчета проблемы может быть
считается калькулятором минимизации.
С другой стороны, если вы используете только
функциональность минимизации для расчета проблемы может быть
считается калькулятором минимизации.
 Чтобы решить три линейных уравнения для заданного
линейная задача, вам просто нужно ввести все эти уравнения в этом
инструмент, и вы получите свое решение.
Чтобы решить три линейных уравнения для заданного
линейная задача, вам просто нужно ввести все эти уравнения в этом
инструмент, и вы получите свое решение. Причина в том, что вы можете получить оптимальную
решения, когда значения целевой функции достигают своего
точка пересечения или максимальное или минимальное значение.
Причина в том, что вы можете получить оптимальную
решения, когда значения целевой функции достигают своего
точка пересечения или максимальное или минимальное значение.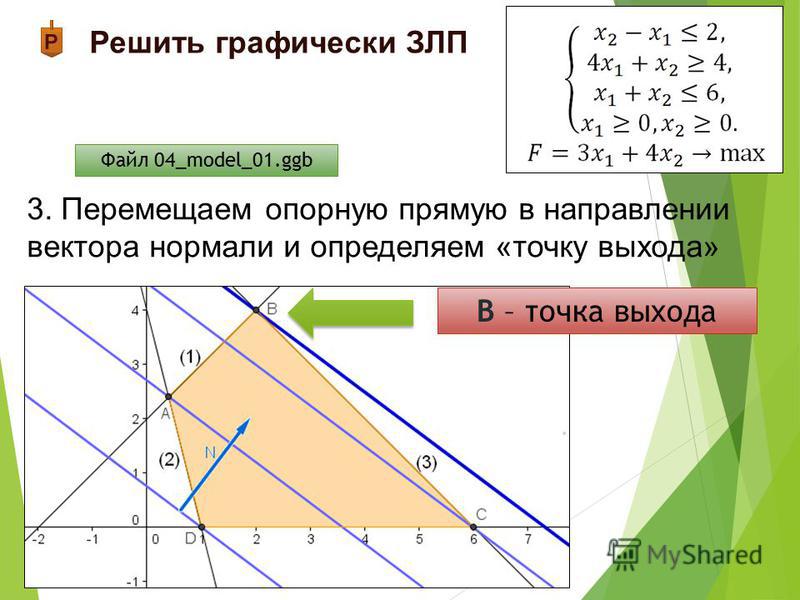 Их представляют алгебраические символы, например, xxx,yyy или x1x_1x1, x2x_2x2 и т. д.
Их представляют алгебраические символы, например, xxx,yyy или x1x_1x1, x2x_2x2 и т. д.

 Получим следующую систему линейных уравнений:
Получим следующую систему линейных уравнений:
 Эти точки являются нашими угловыми точками ! Любая точка, которая не удовлетворяет всем неравенствам ограничений, лежит на вне допустимой области .
Эти точки являются нашими угловыми точками ! Любая точка, которая не удовлетворяет всем неравенствам ограничений, лежит на вне допустимой области .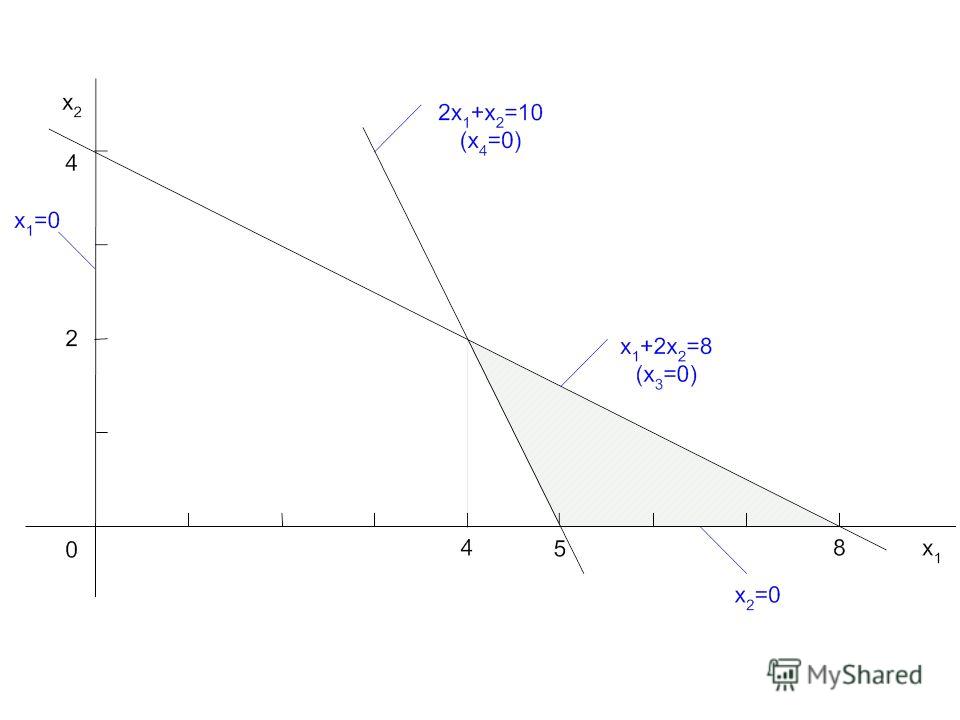 Точно так же подставьте x=0x=0x=0, чтобы получить точку пересечения y (0,6)(0,6)(0,6). Вы можете использовать наш калькулятор формы пересечения наклона, чтобы найти пересечения из уравнения прямой.
Точно так же подставьте x=0x=0x=0, чтобы получить точку пересечения y (0,6)(0,6)(0,6). Вы можете использовать наш калькулятор формы пересечения наклона, чтобы найти пересечения из уравнения прямой.

 (Например, напишите неравенства и целевые функции.)
(Например, напишите неравенства и целевые функции.) Строка определяется наименьшим частным. Точка поворота будет взята из строки, определенной на этом шаге, а также из элемента, определенного на этом шаге.
Строка определяется наименьшим частным. Точка поворота будет взята из строки, определенной на этом шаге, а также из элемента, определенного на этом шаге. Клиенты должны иметь возможность легко находить и выбирать подходящие продукты. Из-за ограничений, таких как ограниченное пространство на полках и широкий ассортимент товаров, это невозможно.
Клиенты должны иметь возможность легко находить и выбирать подходящие продукты. Из-за ограничений, таких как ограниченное пространство на полках и широкий ассортимент товаров, это невозможно. В реальном мире линейное программирование применяется Акционерами, Спортом, Фондовыми рынками и т. д. Узнайте больше.
В реальном мире линейное программирование применяется Акционерами, Спортом, Фондовыми рынками и т. д. Узнайте больше.