2. Метод Гаусса
Пусть дана система линейных уравнений снеизвестными:
(1)
Запишем систему (1) в матричном виде:
(2)
где — — матрица;
— вектор – столбец неизвестных;
— вектор – столбец правых частей.
Метод Гаусса состоит в последовательном исключении неизвестных системы путем ее равносильного преобразования. При этом в численных методах с целью хорошей алгоритмизации задачи преобразованию подвергаются не сами уравнения, а исходные данные – матрица A и вектор правых частей b, соединенных в одну расширенную матрицу. Метод имеет прямой и обратный ход.
Прямой
ход состоит
в исключении элементов, расположенных
ниже элементов главной диагонали матрицы A, т.е приведение матрицы А к верхнетреугольному виду с единицами
на главной диагонали.
каждый элемент строки, в которой находится ведущий элемент (a11 – в первой строке на первом шаге, a22 – во второй строке на втором шаге…) делится на ведущий элемент. При этом предполагается, что ведущие элементы отличны от нуля.
исключаются элементы столбцов, лежащие ниже ведущих строк. Для исключения элементов первого столбца используется первая ведущая строка, для элементов второго столбца – вторая…
Формулы пересчета прямого хода:
(3)
где k=1,2,…,n-1, k – номер шага,
i=k+1,…,n;
j=k+1,…,n.
По определению полагаем ,
.
Обратный ход позволяет последовательно одно за другим вычислять значения неизвестных, начиная с последнего. Для этого переходим к системе, включающей х1, х2,…,хn.
(4)
Реальные
математические расчеты производятся
с приближенными числами, т.е. неизбежны
ошибки округлений. Знаменатель дроби
в формуле (3) может оказаться равным нулю
или очень маленьким числом. В результате
выполнение алгоритма может прекратиться
или будет получен результат, далекий
от реального. Чтобы избежать этой
ситуации, на каждом шаге прямого хода
строки рассматриваемой матрицы
переставляют так, чтобы деление
производилось на наибольший по модулю
в обрабатываемом подстолбце элемент.
Числа, на которые производится деление,
называются ведущими или главными
элементами. Соответственно, метод
Гаусса, исключающий деление на ноль и
уменьшающий влияние ошибок округлений,
— это метод Гаусса с постолбцовым выбором
главного элемента.
УТОЧНЕНИЕ КОРНЕЙ, ПОЛУЧЕННЫХ МЕТОДОМ ГАУССА
Пусть для системы найдено приближенное решениех0.
Полагая
для уточнения корня будем иметь уравнение:
(5)
где — (6)
невязка для приближенного решения х0.
Таким образом, чтобы найти , нужно решить СЛАУ с прежней матрицейА и новым свободным членом . Для этого к основной схеме вычислений нужно присоединить столбецсвободных членов, преобразовать его по прежним правилам, получая поправкинеизвестных. Далее находят уточненные значения неизвестных, прибавляя к приближенному значению х0 соответствующие поправки :.
Пример
1. Найти
решение СЛАУ методом Гаусса с постолбцовым
выбором главного элемента. Произвести
уточнение решения.
Произвести
уточнение решения.
; .
Решение произведем в табличном виде:
ai1 | ai2 | ai3 | bi | |
2,6 3,0 | -4,5 3,0 3,5 | -2,0 4,3 3,0 | 19,07 3,21 -18,25 | -0,007 -0,011 0,016 |
3,0 2,6 | 3,5 3,0 -4,5 | 3,0 4,3 -2,0 | -18,25 3,21 19,07 | 0,016 -0,011 -0,007 |
1 0 0 | -0,583 -2,983 | -0,5 5,8 -0,7 | 3,042 -5,915 11,162 | -0,0027 -0,003 -0,0001 |
1 0 0 | -0,583 1 0 | -0,5 1,221 | 3,042 1,245 7,447 | -0,0027 0,0006 -0,002 |
0 0 | -0,583 1 0 | -0,5 1,221 1 | 3,042 -1,245 2,531 | -0,0027 -0,0006 -0,0007 |
Для
обратного хода перейдем к системе,
включающей неизвестные хi , и
последовательно одно за другим вычисляем
их значения, начиная с х3.
Итак, вектор решения:
Уточним решение. Для этого полученный вектор решения х будем считать начальным приближение х0.Подставим его в исходную схему и найдем невязку по формуле (6).
Полученный вектор невязок используем как новый свободный член системы Аδ= ε, приписывая его как столбец к основной схеме вычислений. Решая СЛАУ с прежней матрицей А и новым свободным членом, получаем вектор поправокнеизвестных:
Уточняем решение по формуле
:
Уточненный вектор решения:
ПРИМЕНЕНИЕ МЕТОДА ГАУССА К ВЫЧИСЛЕНИЮ ОПРЕДЕЛИТЕЛЕЙ
Метод
Гаусса может быть использован при
вычислении определителей.
.
Таким образом, detA равен произведению всех ведущих элементов.
При использовании модификации метода Гаусса с постолбцовым выбором главного элемента производится перестановка строк матрицы, что может изменить знак detА. Поэтому в результате нужно учесть четность количества перестановок:
где — количество перестановок строк.
Найдем определитель для матрицы А из Примера 1 главы 4:
det A = (-1)1*(-6,0)*4,75*2,942= 83,847
ПРИМЕНЕНИЕ МЕТОДА ГАУССА К ВЫЧИСЛЕНИЮ ОБРАТНОЙ МАТРИЦЫ
Пусть
дана матрица
Для нахождения обратной матрицыбудем использовать основное соотношение,
где Е –
единичная матрица n-го
порядка. Т.е. будем исходить из того, что
обратная матрица
является решением матричного уравнения:
Т.е. будем исходить из того, что
обратная матрица
является решением матричного уравнения:
(7)
Представляя искомую матрицу , как набор векторов-столбцов:
а единичную матрицу Е как набор единичных векторов:
…,
матричное уравнение (7) в соответствии с правилами умножения матриц заменяем эквивалентной системой векторно-матричных уравнений:
…, . (8)
Каждое из последних уравнений имеет вид (1) и может быть решено методом Гаусса. Все СЛАУ (8) имеют одну и ту же матрицу коэффициентов, но разные правые части, составляющие единичную матрицу. В результате завершения работы алгоритма будут получаться столбец за столбцом элементы обратной матрицы . Заметим, что элементы строк обратной матрицы получаются в обратном порядке.
Пример
2. Решить
систему линейных уравнений методом
Гаусса. Уточнить решение. Найти
определитель и обратную матрицу
,
включив процесс в общий алгоритм метода
Гаусса.
Уточнить решение. Найти
определитель и обратную матрицу
,
включив процесс в общий алгоритм метода
Гаусса.
НАХОЖДЕНИЕ ОБРАТНОЙ МАТРИЦЫ МЕТОДОМ ГАУССА.
ai1 | ai2 | ai3 | bi | Ei | e1 | e2 | e3 |
1,15 1,00 | 0,42 0,55 0,35 | 100,71 0,32 3,00 | -198,70 2,29 -0,65 | 0,00035 0,00014 -0,00000 | 1 0 0 | 0 1 0 | 0 0 1 |
1 0 0 | 0,46218 -0,11151 | 0,26891 100,40076 2,73109 | 1,92437 -200,91303 -2,57437 | 0,00012 0,00021 -0,00012 | 0 1 0 | 0,84034 -0,96639 -0,84034 | 0 0 1 |
1 0 0 | 0,46218 1 0 | 0,26891 -24,34141 | 1,92437 22,94486 -198,35474 | 0,00012 0,00107 0,00033 | 0 0 1 | 0,84034 7,49100 -0,13107 | 0 -8,91424 -0,99403 |
1 0 0 | 0,46218 1 0 | 0,26891 -24,34561 1 | 1,92437 22,94856 -2,03053 | 0,00012 0,00107 0,00000 | 0 0 0,01024 | 0,84034 7,49100 -0,00134 | 0 -8,91424 -0,01018 |
*Используя постолбцовый выбор главного элемента:
Решение:
Определитель:
Вектор поправок:
Уточненное решение:
Находим обратную матрицу :
Обратная матрица :
ЛЕКЦИЯ 6 ВЫЧИСЛЕНИЕ ОБРАТНОЙ МАТРИЦЫ МЕТОДОМ ГАУССА
ЛЕКЦИЯ 6 ВЫЧИСЛЕНИЕ ОБРАТНОЙ МАТРИЦЫ МЕТОДОМ ГАУССА • Рассмотренный нами метод Гаусса используют для вычисления обратной матрицы. • Прежде, чем научиться его применять на практике, дадим несколько определений.
• Прежде, чем научиться его применять на практике, дадим несколько определений.
• ОПРЕДЕЛЕНИЕ 1. Квадратная матрица размерности n, на главной диагонали которой стоят 1, • а остальные элементы 0, называется • единичной матрицей размерности n. • Назовем ее Е. • 1 0 0. . . 0 • 0 1 0. . . 0 • 0 0 1. . . 0 • . . • 0 0 0. . . 1
• ОПРЕДЕЛЕНИЕ 2. Для любого действительного числа, а 0, существует число, называемое обратным для «а» , такое, что • • а-1 а = а а -1 = 1. •
• Аналогичным свойством обладают и матрицы. • Пусть А — произвольная квадратная матрица размерности n. • Тогда справедлива следующая запись • Е А = А Е = А. •
• Матрица В называется обратной для матрицы А, • если А В = В А = Е, • где Е — единичная матрица.
• Матрица А имеет обратную матрицу тогда и только тогда, • когда ее определитель не равен нулю. • Вычислим обратную матрицу для заданной матрицы А • (
Контрольный пример • этот пример следует взять в качестве контрольного при нахождении обратной матрицы методом Гаусса в соответствующей лабораторной работе:
Контрольный пример • Дано: матрица А = • 1 2 -1 • 1 3 1 • 2 4 -1 • Обозначим искомую обратную матрицу Х. • Х= • х1 y 1 z 1 • x 2 y 2 z 2 • x 3 y 3 z 3
• Х= • х1 y 1 z 1 • x 2 y 2 z 2 • x 3 y 3 z 3
• Так как Х — обратная матрица для матрицы А, • то по определению обратной матрицы можно записать А Х = Е , • где Е — единичная матрица • Е= • 1 0 0 • 0 1 0 • 0 0 1
• Перемножим матрицы А и Х по правилу умножения матриц и • приравняем элементы матрицыпроизведения А Х • соответствующим элементам матрицы Е.
• • • Перемножить 1 2 -1 х1 y 1 z 1 1 0 0 1 3 1 • x 2 y 2 z 2 = 0 1 0 2 4 -1 x 3 y 3 z 3 0 0 1 А Х Е
Получение 1 столбца матрицыпроизведения • 1). 1 -ю строку умножаем на 1 -й столбец, • все складываем и получаем 1 -ый элемент 1 -го столбца произведения. • 2). 2 — строку умножаем на 1 — й столбец , • все складываем и • получаем 2 -ой элемент 1 -го столбца произведения. • 3). 3 строку умножаем на 1 столбец, • все складываем и • получаем 3 -ий элемент 1 -го столбца произведения.
Получим 1 -ю систему: • х 1+ 2 х 2 — х 3= 1 • х 1+ 3 х 2+ х 3= 0 • 2 х 1+ 4 х 2 — х 3= 0
2 -ой столбец матрицыпроизведения • • • 1). 1 -ю строку умножаем на 2 -ой столбец, все складываем, получаем 1 -ый элемент 2 -го столбца произведения. 2). 2 -ю строку умножаем на 2 -ой столбец, все складываем, получаем 2 -ой элемент 2—го столбца произведения. 3). 3 -ю строку умножаем на 2 -ой столбец, Все складываем, получаем 3 -ий элемент 2—го столбца произведения.
1 -ю строку умножаем на 2 -ой столбец, все складываем, получаем 1 -ый элемент 2 -го столбца произведения. 2). 2 -ю строку умножаем на 2 -ой столбец, все складываем, получаем 2 -ой элемент 2—го столбца произведения. 3). 3 -ю строку умножаем на 2 -ой столбец, Все складываем, получаем 3 -ий элемент 2—го столбца произведения.
Получили 2 — ю систему линейных уравнений. • у 1+ 2 у 2 — у 3= 0 • у 1 + 3 у 2+ у 3 = 1 • 2 у 1 + 4 у 2 — у 3 = 0
3 -ий столбец матрицыпроизведения • • • 1). 1 -ю строку умножаем на 3 -ий столбец, все складываем, получаем 1 -ый элемент 3 -го столбца произведения. 2). 2 -ю строку умножаем на 3 -й столбец, все складываем, получаем 2 -ой элемент 3—го столбца произведения, все складываем, • 3). 3 -ю строку умножаем на 3 -й столбец, • все складываем, • получаем 3 -й элемент 3—го столбца произведения.
Получили 3 — ю систему линейных уравнений. • z 1+ 2 z 2 — z 3= 0 • z 1+3 z 2+z 3=0 • 2 z 1+4 z 2 -z 3=1
• Найти матрицу Х означает решить эти 3 системы линейных уравнений. • Каждую из них можно решить методом Гаусса. •
• Каждую из них можно решить методом Гаусса. •
• Однако эти системы отличаются друг от друга только столбцом свободных членов. • Поэтому рационально решать их вместе. • Объединим все исходные данные в общую таблицу (как в методе Гаусса, при этом столбцов свободных членов будет 3).
• • Х 1 1 1 2 Х 2 2 3 4 Х 3 Св. член Св. Член -1 1 0 0 1 0 -1 0 0 1
• Применим метод Гаусса для решения систем линейных уравнений к этой таблице трижды • с разными столбцами свободных членов. Получим • х1 • х2 • х3 ( Это 1 -ый столбец обратной матрицы). • у1 • у2 • у3 ( Это 2 -ой столбец обратной матрицы). • z 1 • z 2 • z 3 ( Это 3 -й столбец обратной матрицы).
• В результате вычислений получим следующую обратную матрицу • Х= • — 7 -2 5 • 3 1 -2 • -2 0 1
• Этот результат должен быть получен в контрольном примере к лабораторной работе. • После нахождения обратной матрицы в программе следует сделать проверку, • а именно, перемножить исходную и обратную матрицы, • чтобы получилась единичная матрица.
Проверка • • 1 1 2 2 -1 -7 -2 5 3 1 -2 4 -1 -2 0 1 А Х 1 0 0 = 0 1 0 0 0 1 Е
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ • 1. Какая матрица называется единичной? • 2. Какая матрица называется обратной к данной матрице? • 2. Почему метод Гаусса для решения систем линейных уравнений можно использовать для нахождения обратной матрицы к данной?
• ВНИМАНИЕ! Для закрепления изученного теоретического материала следует выполнить лабораторную работу № 7.
Метод обратной матрицы
Если , то существует матрица , обратная к данной. Умножим исходную систему уравнений (2.1) на обратную матрицу слева. Получим
.
Известно, что произведение обратной матрицы на исходную дает единичную матрицу , и, следовательно, получаем , или
(2.3)
Решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы. Проблемы использования этого метода те же, что и при использовании метода Крамера: нахождение обратной матрицы – трудоемкая операция. Однако для небольших m решение может быть получено с помощью функций Excel.
Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы. Проблемы использования этого метода те же, что и при использовании метода Крамера: нахождение обратной матрицы – трудоемкая операция. Однако для небольших m решение может быть получено с помощью функций Excel.
ПРИМЕР 2.3. С помощью метода обратной матрицы решить систему
Занесем на рабочий лист Excel матрицу коэффициентов
и вектор правых частей .
Выделим на рабочем листе область размером ячейки для обратной матрицы и вызовем функцию МОБР. В поле Массив занесем адреса ячеек исходной матрицы A, и, нажав комбинацию клавиш Ctrl+Shift+Enter, получим A-1:
| 0.195489 | -0.16541 | -0.02256 |
| -0.1015 | 0. 278195 278195
| -0.00752 |
| -0.07895 | 0.105263 | 0.105263 |
Полученную обратную матрицу умножим на вектор правых частей . Для этого выделим столбец из трех ячеек и вызовем функцию МУМНОЖ. В поля Массив 1 и Массив 2 занесем адреса ячеек, в которых находятся найденная обратная матрица и вектор правых частей, после чего, нажав комбинацию клавиш Ctrl+Shift+Enter,получим решение СЛАУ
| 1.037594 |
| 0.345865 |
| 0.157895 |
Замечание. Если одна из клавиш Ctrlили Shiftне нажата, вычисления будут выполнены не во всем выделенном диапазоне, а только в одной ячейке. В этом случае весь процесс вызова функции необходимо повторить.
Метод Гаусса
Наиболее известным и популярным прямым методом решения СЛАУ является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных. Метод состоит из двух этапов. На первом (прямом) этапе исходная система сводится к системе с треугольной матрицей, которая решается на втором (обратном) этапе. На прямом этапе используются следующие эквивалентные преобразования строк расширенной матрицы системы: перестановка строк, умножение строки на ненулевую константу, сложение строк.
Этот метод заключается в последовательном исключении неизвестных. Метод состоит из двух этапов. На первом (прямом) этапе исходная система сводится к системе с треугольной матрицей, которая решается на втором (обратном) этапе. На прямом этапе используются следующие эквивалентные преобразования строк расширенной матрицы системы: перестановка строк, умножение строки на ненулевую константу, сложение строк.
Прямой этап.Пусть в системе уравнений
первый элемент. Назовем его ведущимэлементом первой строки. Разделим все элементы этой строки на , и исключим из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при в соответствующей строке. Получим
.
Если , то на него можно разделить второе уравнение, а затем исключить из всех остальных уравнений. С помощью аналогичных преобразований приходим к системе уравнений с верхней треугольной матрицей
С помощью аналогичных преобразований приходим к системе уравнений с верхней треугольной матрицей
(2.4)
Обратный этап.Решаем систему (2.4) с верхней треугольной матрицей в обратном порядке:
. (2.5)
В случае если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Кроме того, если какие-либо ведущие элементы малы, то это приводит к усилению ошибок округления и ухудшению точности счета. Поэтому обычно используется другой вариант метода Гаусса – схема Гаусса с выбором главного элемента. Путем перестановки строк и других эквивалентных преобразований добиваются выполнения условия: , т.е. осуществляется выбор первого главного элемента. Переставляют уравнения так, чтобы в первом уравнении коэффициент был максимальный по модулю. Разделив первую строку на главный элемент, как и прежде, исключают из остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй главный элемент и т. д.
д.
ПРИМЕР 2.4.Рассмотрим применение метода Гаусса с выбором главного элемента на примере следующей системы уравнений:
.
В первом уравнении коэффициент при равен 0, во втором 1 и в третьем -2, т.е. максимальный по модулю коэффициент находится в третьем уравнении. Поэтому переставим третье уравнение на место первого:
.
В третьем уравнении коэффициент при равен 0. Исключим из второго уравнения:
Рассмотрим второе и третье уравнения. Исключим из третьего уравнения. Для этого умножим второе на -0.5 и сложим с третьим:
.
Далее находим значения обратным ходом: из третьего уравнения получаем , из второго , и из первого . Выполним проверку:
.
Такая перестановка уравнений необходима для того, чтобы уменьшить влияние ошибок округления на конечный результат.
Часто возникает необходимость в решении СЛАУ, матрицы которых являютсяслабо заполненными, т. е. содержат много нулевых элементов. В то же время эти матрицы имеют определенную структуру. Среди таких систем выделим системы с матрицами ленточной структуры, в которых ненулевые элементы располагаются на главной диагонали и на нескольких побочных диагоналях. Для решения систем с ленточными матрицами коэффициентов вместо метода Гаусса можно использовать более эффективные методы. Для случая трехдиагональных матриц разработан экономичный метод прогонки.
е. содержат много нулевых элементов. В то же время эти матрицы имеют определенную структуру. Среди таких систем выделим системы с матрицами ленточной структуры, в которых ненулевые элементы располагаются на главной диагонали и на нескольких побочных диагоналях. Для решения систем с ленточными матрицами коэффициентов вместо метода Гаусса можно использовать более эффективные методы. Для случая трехдиагональных матриц разработан экономичный метод прогонки.
Метод прогонки
Рассмотрим метод прогонки для СЛАУ вида:
(2.6)
Решение данной системы ищем в виде:
(2.7)
Здесь ai, bi – неизвестные прогоночные коэффициенты. Как и метод Гаусса, метод прогонки состоит из двух этапов. На первом (прямом) этапе определяются прогоночные коэффициенты, на втором (обратном) вычисляется вектор решения.
Прямой этап.Сравнивая соотношение (2.7) при i=2: и следствие первого уравнения системы (2. 6): , получим формулы для первых прогоночных коэффициентов: .
6): , получим формулы для первых прогоночных коэффициентов: .
Подставляя (2.7) во второе уравнение (2.6), получим:
.
Или, после преобразования,
,
откуда
Сравнивая с (2.7), получим
.
Таким образом, можно найти все .
Обратный этап.Подставляя последнее прогоночное соотношение (2.7) в последнее уравнение (2.6), получим:
.
Затем, последовательно применяя (2.7), находим:
.
Таким образом, алгоритм метода прогонки можно представить в виде:
1. Находим ;
2. Для вычисляем
.
3. Находим .
4. Для находим: .
Теорема. Пусть коэффициенты , системы уравнений при отличны от нуля и пусть при . Тогда прогонка корректна и устойчива.
При выполнении этих условий знаменатели в алгоритме метода прогонки не обращаются в нуль и, кроме того, погрешность вычислений, внесенная на каком либо шаге расчетов, не будет возрастать при переходе к следующим шагам. Данное условие есть не что иное, как условие диагонального преобладания.
Данное условие есть не что иное, как условие диагонального преобладания.
Дата добавления: 2021-09-07; просмотров: 129; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре… Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит… Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации — обмен информацией между организацией и её внешней средой… Интересное: Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является. Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны… Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 6 из 8Следующая ⇒
Методы решения систем линейных алгебраических уравнений разделяются на точные и итерационные. Итерационные методы позволяют получать корни системы с заданной точностью путем сходящихся бесконечных процессов. К их числу относятся: метод простой итерации, метод Зейделя, метод релаксации и др. Эффективность применения итерационных методов существенно зависят от удачного выбора начального приближения и быстроты сходимости процесса. Все вышеперечисленные методы (точные и приближенные) имеют свои преимущества и недостатки и поэтому для выбора оптимального (лучшего) метода для решения конкретной системы линейных уравнений требуются знания пользователя. А. Пусть дана система n линейных уравнений с n неизвестными Запишем эту систему в матричном виде х = или в общем матричном виде А∙Х=В, где: А — матрица коэффициентов; Х – вектор искомых параметров; В – вектор свободных членов. Рассмотрим решение линейной системы уравнений различными методами. Метод обратной матрицы Дана система линейных уравнений А∙Х=В. Умножим правую и левую части системы на обратную матрицу А-1 А-1∙А∙Х= А-1∙В Так как А-1∙А=Е, то Е∙Х= А-1∙В ЕХ=Х Так как ЕХ=Х то, Х= А-1∙В. Таким образом данный метод заключается в нахождении обратной матрицы коэффициентов А-1 и ее умножении на вектор свободных членов В. Нахождение обратной матрицы А-1 при порядке n>4 требует много времени, поэтому метод обратной матрицы редко употребляется.
Метод Крамера Известно, что . Отсюда , где , , …, где Итак, метод Крамера заключается в вычислении (n+1)-го определителя (∆1, ∆2, ∆3, …, ∆n) для матриц n-го порядка. Наиболее распространенным способом решения системы линейных уравнений является метод последовательного исключения неизвестных или метод Гаусса.
Метод Гаусса Рассмотрим на простейшем примере известный со школы способ исключения неизвестных при решении систем уравнений. Пусть дана система: Умножим первое уравнение на такой коэффициент , чтобы в обоих уравнениях коэффициент при х1 стал бы одинаковым Теперь вычтем его из второго уравнения, т.е. -2х1+х2=7
Мы выполнили операцию исключения неизвестной х1 из второго уравнения. Запишем систему уравнения после этого исключения в следующем виде. Первое уравнение записываем в исходном виде.
Второе уравнение содержит лишь одно неизвестное, которое легко вычисляется х2=3. Проведенные действия и составляют сущность метода Гаусса. Рассмотрим преобразования по методу Гаусса для системы уравнений n-го порядка.
Вычтем из второго уравнения первое, умноженное на . При этом во втором уравнении будет уничтожен коэффициент при х1. Затем из третьего уравнения также вычтем первое, умноженное на . Проделав аналогичные преобразования с остальными уравнениями системы, превратим в нуль все коэффициенты первого столбца, кроме элемента а11. Получим следующую систему:
Затем при помощи второго уравнения преображенной системы исключим из третьего, четвертого и т. а11х1+ а12х2+ а13х3+… +а1nхn=b1 … … … Последовательно продолжая этот процесс, исключим из системы все коэффициенты, лежащие ниже главной диагонали. В результате получим треугольную систему уравнений. а11х1+ а12х2+ а13х3+… +а1nхn=b1 … … … Процесс получения треугольной системы называется “прямым ходом” по методу Гаусса. Треугольная система легко решается “обратным ходом”. Из последнего уравнения определяется последнее неизвестное . Затем из предпоследнего уравнения постановкой найденного значения хn определяется хn-1. При решении системы линейных уравнений методом Гаусса все вычисления можно поместить в следующую таблицу. Рассмотрим таблицу на примере решения системы уравнений третьего порядка.
Уравнения 1), 2) и 3) составляют искомую треугольную матрицу после “прямого хода”. Коэффициенты а11, , — называются “ведущими” элементами. При “обратном ходе” можно использовать строки таблицы, содержащие единицы, т.е. вспомогательные уравнения. Имеем далее ПРИМЕР:
Треугольная система 4 х1+х2+2х3=12 7,5 х2+3х3=24 2,8 х3=8,4 или х1+0,25х2+0,5х3=3 х2+0,4х3=3,2 х3=3 Обратный ход х2=3,2-0,4∙3=2 х1=3-0,25∙2-0,5∙3=1 Вычисление определителя методом Гаусса (третий способ, без вывода) Определитель матицы А равен произведению всех “ведущих” элементов при преобразовании ее по методу Гаусса. Для вычисления определителя матрицы А выполняется только “прямой” ход методом Гаусса, причем столбец свободных членов В становится излишним. ПРИМЕР: дана матрица detА=4∙7,5∙2,8=84 Вычисление обратной матрицы методом Гаусса А∙А-1 = Е Матрицы А и Е известны, требуется определить А-1. Обозначим столбцы матрицы А-1 через х1, х2, …, хn т.е. Столбцы для матрицы Е обозначим через Е1, Е2, …, Еn Тогда можем записать n систем уравнений Ах1=Е1 Ах2=Е2 Ахn=Еn Развернем первое матричное уравнение Ах1=Е1 х = Другие матричные уравнения аналогичны. Следовательно, для получения обратной матрицы А-1 достаточно выполнить n решений методом Гаусса систем линейных уравнений с разными правыми частями — y столбцами матрицы Е. Полученные решения х1, х2, …, хn будут столбцами искомой обратной матрицы А-1. Трангуляции матрицы Квадратную матрицу А можно представить как произведение двух треугольных матриц А=LW, где L – нижняя треугольная матрица, W – верхняя треугольная матрица. Матрица W вычисляется при прямом ходе Гаусса а11а12а13 … а1n 0 … 0 0 … … … … … … 0 0 0 … У матрицы L наоборот все элементы выше главной диагонали нулевые. Остальные элементы матрицы L вычисляются в результате деления элементов по столбцам, полученных при том же прямом ходе Гаусса, на ведущие элементы. Требуется решить системы уравнений Ах=В Так как А=LW то LWх=В Обозначим Wх=Z Тогда вместо системы Ах=В можем записать ей эквивалентную LZ=В Wx=Z (5) Решение эквивалентной системы с треугольными матрицами L и W занимает гораздо меньше времени, чем решение исходной системы Ах=В. Это обстоятельство очень важно при необходимости решать систему уравнений многократно при одной и той же матрице А и разных векторах свободных членов В, что обычно имеет место при расчетах режимов работы электрических систем. Триангуляция же матрицы А проводится только один раз. То есть элементы матрицы А – это, как правило, параметры схемы замещения эл. системы, В – вектор узловых токов или мощностей. Часто ставится задача определения параметров большего числа режимов при изменении токов или мощностей потребителей в узлах при неизменной схеме замещения. Если триангуляция матрицы А осуществлена, то можно быстро пользуясь системой (5) посчитать необходимые режимы, меняя в этой системе вектор В. Для каждого режима сначала решается треугольная подсистема LZ=В относительно Z последовательной подстановкой в уравнения подсистемы найденных значений неизвестных из предыдущих уравнений, начиная с Z1 Z1 =b1 =b2 =b3 … … … … … =bn Значение Z1 уже известно из первого уравнения, Z2 определяется из второго уравнения подстановкой в него значения Z1 и т. Метод Жордана-Гаусса Метод Жордана-Гаусса называют еще методом Гаусса без обратного хода. Сущность его состоит в том, что на втором шаге переменная исключается из всех уравнений, кроме второго, на третьем шаге исключается также из всех уравнений, кроме третьего и т.д. После шагов в каждом уравнении остается одна неизвестная, т.е. получим решение системы таким образом, исключение переменных по методу Жордана-Гаусса эквивалентно преобразованию матрицы коэффициентов в единичную. Рассмотрим таблицу вычислений по методу Жордана-Гауса.
Нахождение обратной матрицы методом Жордана-Гаусса Рассмотрим вычислительную процедуру определителя А-1 на конкретном примере. А∙А-1=Е Пусть А х1х2 х3Е1Е2Е3 х =
Проверка: х = По такой же вычислительной схеме можно вычислять значения переменных х1, х2, х3, …, х при одной матрице коэффициента А и разных столбцах свободных членов В1, В2, В3, …, Вn. Недостатки метода Гаусса (его недостатки и способы их устранения) 1. Если определитель матрицы А мал, то из-за ошибок округлений сильно снижается точность получения искомых корней. 2. Метод Гаусса требует, чтобы диагональные элементы в процессе исключения переменных не были равны нулю (т.к. строки делятся на них). Поэтому часть применяют метод Гаусса с выбором главного элемента, который заключается в следующем. При обращении в нуль элементов первого столбца из всей матрицы выбирается наибольший элемент и затем в нуль элементы второго столбца, рассматривается сокращенная матрица (путем вычеркивания в уже полученной системе первого уравнения) и в ней наибольший элемент переставляется на ее первое место и т.д. 3. Метод Гаусса требует большего объема памяти ЭВМ по сравнению с итерационными методами. Существуют различные приемы по сокращению занимаемой памяти ЭВМ при решении методом Гаусса электроэнергетических задач. Например, необходимо решить систему Yy∙Uy=Iy при использовании метода узловых напряжений.
Перенумерация
(30 х 70) Я=10 х 10=100 Я=52 (26) В ряде случаев для нахождения корней системы линейных уравнений удобнее пользоваться приближенными итерационными методами (или методами последовательных приближений). Метод простой итерации Дана система линейных уравнений Предположим, что диагональные элементы аii, i = 1- n не равны 0. В любом случае строки и столбцы можно поменять местами так, чтобы диагональные элементы не были равны 0. Разделим каждую строку на ее диагональный элемент: первую строку на , вторую строку на и т.д. Получим следующую систему где ; . В матричном виде эту систему можно записать + х = или . Отсюда . (1) Выполненная выше операция называется приведением системы линейных уравнений к виду, удобному для итераций.
Зададим произвольное начальное значение всех неизвестных корней системы (в матричном виде Х = Х(0))и подставим это значение в правую часть системы уравнений (1). Вычислим , где Х(0) – начальное (исходное) приближение к корням системы уравнений, Х(1) — первое приближение к корням системы уравнений. Затем процесс повторим, подставив найденные на первой итерации значения Х=Х(1) в правую часть системы уравнений и вычислим вторые приближения корней . И так далее. Итерационный процесс повторяем до тех пор, пока на какой-нибудь к-й итерации не выполнится условие <ε, где ε – заданная точность определения корней системы. Поскольку в вектор Х входит n неизвестных, то условие окончания итерационного процесса, должно быть выполнено для всех n корней. Пример: дана система линейных уравнений Приведем систему уравнений к виду, удобному для итерации Зададим начальные приближения к корням равными нулю и точность расчета ε = 0,001. Начнем итерационный процесс вычисления корней. 1 итерация 2 итерация и т.д. до выполнения условий Вычисления сведем в таблицу
Примечание: число цифр после запятой в вычисляемых приближениях к корням надо брать на один порядок больше чем в заданной точности ε. ⇐ Предыдущая12345678Следующая ⇒ Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… |
404 Cтраница не найдена
Размер:
AAA
Изображения Вкл. Выкл.
Обычная версия сайта
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
Pers.
 narod.ru. Обучение. Лекции по численным методам. Методы решения систем линейных алгебраических уравнений
Pers.narod.ru. Обучение. Лекции по численным методам. Методы решения систем линейных алгебраических уравнений
narod.ru. Обучение. Лекции по численным методам. Методы решения систем линейных алгебраических уравнений
Pers.narod.ru. Обучение. Лекции по численным методам. Методы решения систем линейных алгебраических уравнений
Этот сайт больше не обновляется. Подключите Javascript, чтобы увидеть новый адрес страницы или перейдите к статье
|
Pers.narod.ru. Обучение. Лекции по численным методам. Методы решения систем линейных алгебраических уравнений |
2. Методы решения систем линейных алгебраических уравнений
Прямые методы решения СЛАУ:
Метод Крамера
Метод обратной матрицы
Метод Гаусса
Итерационные методы решения линейных алгебраических систем:
Метод простой итерации или метод Якоби
Метод Гаусса – Зейделя
К решению систем линейных
алгебраических уравнений сводятся многочисленные практические задачи ( по
некоторым оценкам более 75% всех задач). Можно с полным основанием утверждать,
что решение линейных систем является одной из самых распространенных и важных
задач вычислительной математики.
Можно с полным основанием утверждать,
что решение линейных систем является одной из самых распространенных и важных
задач вычислительной математики.
Конечно, существует много методов и современных пакетов прикладных программ для решения СЛАУ, но для того, чтобы их успешно использовать, необходимо разбираться в основах построения методов и алгоритмов, иметь представления о недостатках и преимуществах используемых методов.
Постановка задачи
Требуется найти решение системы m линейных уравнений, которая записывается в общем виде как
,
Эту систему уравнений можно записать также в матричном виде:
,
где , , .
A – матрица системы, – вектор правых частей, – вектор неизвестных.
При известных A и требуется найти такие , при подстановке которых в систему уравнений
она превращается в тождество.
Необходимым и достаточным условием существования единственного решения СЛАУ является условие det A≠0, т.е. определитель матрицы A не равен нулю. В случае равенства нулю определителя матрица A называется вырожденной и при этом СЛАУ либо не имеет решения, либо имеет их бесчисленное множество.
В дальнейшем будем предполагать наличие единственного решения.
Все методы решения линейных алгебраических задач можно разбить на два класса: прямые (точные) и итерационные (приближенные).
Прямые методы решения СЛАУ
Метод Крамера
При небольшой размерности системы m (m = 2,…,5) на практике часто используют формулы Крамера для решения СЛАУ:
(i = 1, 2, …, m). Эти
формулы позволяют находить неизвестные в виде дробей, знаменателем которых
является определитель матрицы системы, а числителем – определители матриц Ai,
полученных из A заменой столбца коэффициентов при вычисляемом неизвестном
столбцом свободных членов.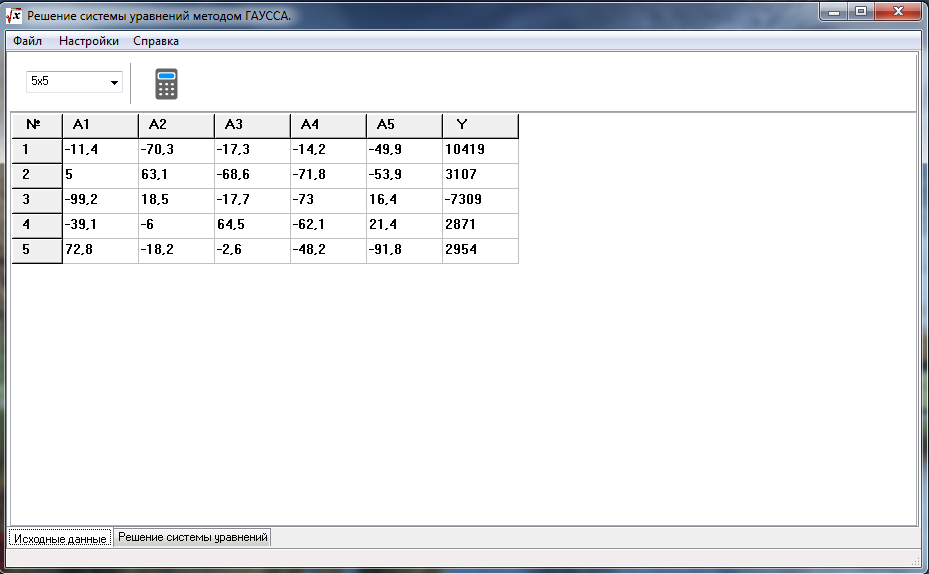 Так А1 получается из матрицы А
заменой первого столбца на столбец правых частей f.
Так А1 получается из матрицы А
заменой первого столбца на столбец правых частей f.
Например, для системы двух линейных уравнений
Размерность системы (т.е., число m) является главным фактором, из–за которого формулы Крамера не могут быть использованы для численного решения СЛАУ большого порядка. При непосредственном раскрытии определителей решение системы с m неизвестными требует порядка m!*m арифметических операций. Таким образом, для решения системы, например, из m = 100 уравнений потребуется совершить 10158 вычислительных операций (процесс займёт примерно 1019 лет), что не под силу даже самым мощным современным ЭВМ
Метод обратной матрицы
Если det A ≠ 0, то
существует обратная матрица . Тогда решение СЛАУ записывается в виде: . Следовательно, решение
СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны
между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы.
Проблемы использования этого метода те же, что и при использовании метода Крамера:
нахождение обратной матрицы – трудоемкая операция.
Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны
между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы.
Проблемы использования этого метода те же, что и при использовании метода Крамера:
нахождение обратной матрицы – трудоемкая операция.
Метод Гаусса
Наиболее известным и популярным прямым методом решения СЛАУ является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений
первый элемент . Назовем его ведущим элементом первой строки. Поделим все элементы этой строки на и исключим x1 из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при в соответствующей строке. Получим
.
Если , то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей
.
Из нее в обратном порядке находим все значения xi:
.
Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных – обратным. В случае если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Кроме того, если какие–либо ведущие элементы малы, то это приводит к усилению ошибок округления и ухудшению точности счета. Поэтому обычно используется другой вариант метода Гаусса – схема Гаусса с выбором главного элемента. Путем перестановки строк, а также столбцов с соответствующей перенумерацией коэффициентов и неизвестных добиваются выполнения условия:
, j = i+1,i+ 2, …, m;
т.е. осуществляется выбор первого главного
элемента. Переставляя уравнения так, чтобы в первом уравнении коэффициент a11 был максимальным по модулю. Разделив
первую строку на главный элемент, как и прежде, исключают x1 из
остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй
главный элемент и т.д.
Разделив
первую строку на главный элемент, как и прежде, исключают x1 из
остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй
главный элемент и т.д.
Рассмотрим применение метода Гаусса с выбором главного элемента на примере следующей системы уравнений:
В первом уравнении коэффициент при =0, во втором = 1 и в третьем = -2, т.е. максимальный по модулю коэффициент в третьем уравнении. Поэтому переставим третье и первое уравнение:
Исключим из второго и третьего уравнений с помощью первого. Во втором уравнении исключать не надо. Для исключения из третьего уравнения умножим первое на 0.5 и сложим с третьим:
Рассмотрим второе и третье уравнения. Максимальный по модулю элемент при в третьем. Поэтому поместим его на место второго:
Исключим из третьего уравнения. Для
этого умножим второе на -0.5 и сложим с третьим:
Для
этого умножим второе на -0.5 и сложим с третьим:
Обратный ход: .
Проверка: 0.5*8+0=4, -3+8-0=5, -2*(-3)+0=6.
Такая перестановка уравнений необходима для того, чтобы уменьшить влияние ошибок округления на конечный результат.
Часто возникает
необходимость в решении СЛАУ, матрицы которые являются слабо заполненными,
т.е. содержат много нулевых элементов. В то же время эти матрицы имеют определенную
структуру. Среди таких систем выделим системы с матрицами ленточной структуры,
в которых ненулевые элементы располагаются на главной диагонали и на нескольких
побочных диагоналях. Для решения систем с ленточными матрицами коэффициентов
вместо метода Гаусса можно использовать более эффективные методы. Например, метод
прогонки, который мы рассмотрим позже при решении краевой задачи для
обыкновенного дифференциального уравнения второго порядка.
Итерационные методы решения линейных алгебраических систем
Метод простой итерации или метод Якоби
Напомним, что нам требуется решить систему линейных уравнений, которая в матричном виде записывается как:
,
где , , .
Предположим, что диагональные элементы матриц A исходной системы не равны 0 (aii ≠ 0, i = 1, 2, …, n). Разрешим первое уравнение системы относительно x1, второе относительно x2 и т.д. Получим следующую эквивалентную систему, записанную в скалярном виде:
(1),
Теперь, задав нулевое приближение , по рекуррентным соотношениям (1) можем выполнять итерационный процесс, а именно:
(2)Аналогично
находятся следующие приближения , где в (2) вместо необходимо подставить .
Или в общем случае:
. (3)
или
Условие окончания итерационного процесса .
Достаточное условие сходимости: Если выполнено условие диагонального преобладания, т.е. , то итерационный процесс (3) сходится при любом выборе начального приближения. Если исходная система уравнений не удовлетворяет условию сходимости, то ее приводят к виду с диагональным преобладанием.
Выбор начального приближения влияет на количество итераций, необходимых для получения приближенного решения. Наиболее часто в качестве начального приближения берут или .
Замечание. Указанное выше условие сходимости
является достаточным, т.е. если оно выполняется, то процесс сходится. Однако
процесс может сходиться и при отсутствии диагонального преобладания, а может и
не сойтись.
Однако
процесс может сходиться и при отсутствии диагонального преобладания, а может и
не сойтись.
Пример.
Решить систему линейных уравнений с точностью :
|
|
8 |
4 |
2 |
|
10 |
|
x1 |
|
|
= |
3 |
5 |
1 |
= |
5 |
= |
x2 |
|
|
|
3 |
–2 |
10 |
|
4 |
|
x3 |
|
Решение прямыми методами, например, обратной матрицей, даёт решение:
.
Найдем решение методом простой итерации. Проверяем условие диагонального преобладания: , , .
Приводим систему уравнений к виду (1):
.
Начальное приближение . Дальнейшие вычисления оформим в виде таблицы:
|
k |
x1 |
x2 |
x3 |
точность |
|
0 |
0 |
0 |
0 |
|
|
1 |
1. |
1.000 |
0.400 |
1.2500 |
|
2 |
0.650 |
0.170 |
0.225 |
0.8300 |
|
3 |
1.109 |
0. |
0.239 |
0.4588 |
|
……… |
||||
|
4 |
0.908 |
0.287 |
0.180 |
0. |
|
5 |
1.061 |
0.419 |
0.185 |
0.1537 |
|
6 |
0.994 |
0.326 |
0.165 |
0.0931 |
|
7 |
1. |
0.370 |
0.167 |
0.0515 |
|
8 |
1.023 |
0.594 |
0.160 |
0.2235 |
|
9 |
0.913 |
0. |
0.212 |
0.1101 |
|
10 |
0.906 |
0.505 |
0.242 |
0.0764 |
|
11 |
0.937 |
0.495 |
0. |
0.0305 |
|
12 |
0.945 |
0.516 |
0.218 |
0.0210 |
|
…… |
||||
|
13 |
0. |
0.523 |
0.220 |
0.0077 |
Здесь
,
И т.д., пока не получим, в последнем столбце величину меньшую 0.01, что произойдет на 13 – ой итерации.
Следовательно, приближенное решение имеет вид:
Метод Гаусса – Зейделя
Расчетные формулы имеют вид:
т.е. для подсчета i–й компоненты (k+1)–го приближения к искомому вектору используется уже
вычисленное на этом, т. е. (k+1)–м шаге, новые
значения первых i–1 компонент.
е. (k+1)–м шаге, новые
значения первых i–1 компонент.
Подробные формулы имеют вид:
Достаточное условие сходимости этого метода такое же, как и для метода простой итерации, т.е. диагональное преобладание:
Начальное приближение:
Найдем решение предыдущей системы уравнений методом Гаусса – Зейделя.
Расчетные формулы:
|
k |
x1 |
x2 |
x3 |
точность |
|
0 |
0 |
0 |
0 |
|
|
1 |
1. |
0.250 |
0.075 |
1.2500 |
|
2 |
1.106 |
0.321 |
0.132 |
0.1438 |
|
3 |
1.056 |
0. |
0.151 |
0.0500 |
|
4 |
1.042 |
0.344 |
0.156 |
0.0139 |
|
5 |
1.039 |
0.346 |
0. |
0.0036 |
Из таблицы видно, что нужная точность достигнута уже на 5–ой итерации вместо 13–ой по методу простой итерации и значения корней более близки к значениям, полученным методом обратной матрицы.
Исключение по Гауссу и форма эшелона строк
Обратная матрица — не совсем простая задача, если вы еще не знакомы с методом исключения по Гауссу. Обратная матрица используется в большом количестве алгоритмов, одним из самых простых из которых является линейная регрессия.
Обращение матрицы состоит из двух шагов:
- Проверка на обратимость матрицы путем нахождения определителя
- Обращение матрицы по гауссову варианту исключения Гаусса-Жордана
- Проверка обратимости матрицы
- Объяснение ранга матрицы
- Ранг: Линейные комбинации
- Вычисление определителя матрицы
- Инвертирование матрицы
- Инициализация исключения Гаусса-Жордана
- Объяснение сокращенной формы эшелона рядов
- Обозначения и операции
- Полный пример инвертирования матрицы
- Ссылки
Проверка обратимости матрицы
Понятие ранга в линейной алгебре связано с размерностью. Все матрицы имеют размер $m \times n$, где $m$ — количество строк, а $n$ — количество столбцов.
Все матрицы имеют размер $m \times n$, где $m$ — количество строк, а $n$ — количество столбцов.
Ранг матрицы
- Ранг $1$: Когда матрица является линией, она имеет ранг $1$.
- Ранг $2$: когда матрица является плоской, она имеет ранг $2$.
- Говорят, что матрица имеет полный ранг тогда и только тогда, когда матрица не содержит столбца в виде линейной комбинации двух столбцов, потому что это означает
Любая данная матрица может иметь только такой высокий ранг, как число столбцов $n$ для этой матрицы. Но матрица с $n=3$ может иметь только ранг $2$, потому что какое-то преобразование может сжать векторы-столбцы на плоскость — и ранг может быть даже уменьшен до ранга $1$, если преобразование сжимает векторы на прямую. линия.
Давайте посмотрим, что это значит.
Линейные комбинации
Мы определяем три вектора $\vec{v}$, $\vec{u}$ и $\vec{w}$ и комбинируем их как векторы-столбцы в матрице $A$.
$$ \vec{v} = \begin{bmatrix} 2\\ 0\\ 1 \end{bmatrix} ,\четверка \vec{и} = \begin{bматрица} 1\\ 2\\ 1 \end{bmatrix} ,\четверка \vec{ш} = \begin{bmatrix} 1\\ -2\\ 0 \end{bmatrix} ,\четверка А = \begin{bматрица} 2 &1 &1 \\ 0 &2 &-2 \\ 1 &1 &0 \end{bmatrix} $$
Если мы выполним сложение векторов над $\vec{u}$ и $\vec{w}$, то результатом будет вектор $\vec{v}$.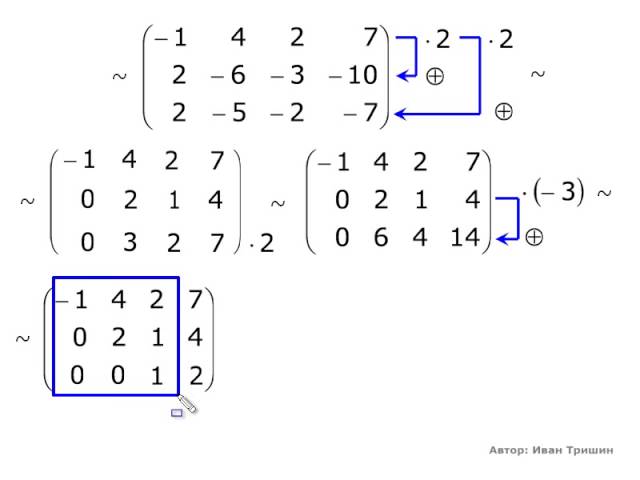 Это означает, что $\vec{v}$ является линейной комбинацией $\vec{u}$ и $\vec{w}$, т.е. матрица $A$ не имеет полного ранга.
Это означает, что $\vec{v}$ является линейной комбинацией $\vec{u}$ и $\vec{w}$, т.е. матрица $A$ не имеет полного ранга.
$$ \vec{u} + \vec{w} = \begin{bматрица} 1+1\\ 2+(-2)\\ 1+0 \end{bmatrix} знак равно \begin{bматрица} 2\\ 0\\ 1 \end{bmatrix} $$
Точно так же, если вычесть $\vec{v}$ и $\vec{u}$, вы обнаружите, что они являются линейной комбинацией $\vec{w}$.
Геометрическая интерпретация линейных комбинаций состоит в том, что мы теряем информацию , если используем конкретное преобразование, связанное с матрицей $A$, потому что результирующая матрица преобразования больше не охватывает все три измерения пространства.
Вышеупомянутая матрица $A$ имеет ранг $2$, и, как мы увидим позже, мы можем вычислить ранг матрицы, пытаясь уменьшить матрицу до сокращенной ступенчатой формы строк . Но пока мы можем определить, можно ли инвертировать матрицу, вычислив определитель.
Вычисление определителя
Когда определитель матрицы равен нулю, ранг матрицы не является полным, а это означает, что мы не можем инвертировать матрицу. Точно так же есть 23 других свойства, которые вы можете использовать, чтобы проверить, является ли матрица обратимой.
Точно так же есть 23 других свойства, которые вы можете использовать, чтобы проверить, является ли матрица обратимой.
Для матрицы 3×3 следующая формула:
$$ \начать{выравнивать} Дет (А) знак равно det\left(\begin{bmatrix} а&б&в\\ д&е&е\\ g&h&i \end{bmatrix}\справа)\\ &=aei + bfg + cdh — ceg — bdi — afh \end{выравнивание} $$
Давайте подставим число и найдем решение.
$$ \начать{выравнивать} Дет (А) знак равно det\left(\begin{bmatrix} 2 &1 &1 \\ 0 &2 &-2 \\ 1 &1 &0 \end{bmatrix}\справа)\\ &=2*2*0 + 1*(-2)*1 + 1*0*1 — 1*2*1 — 1*0*0 — 2*(-2)*1\\ &=0 \end{выравнивание} $$
Итак, матрица $A$ необратима, так как определитель равен нулю, хотя если бы у нас была обратимая матрица, то определитель был бы отличен от нуля . Другими словами, мы не можем найти обратную матрицу $A$, но если бы у нас была другая матрица $B$, где $det(B) \ne 0$, мы смогли бы найти обратную.
Обратите внимание, что вычисление определителя возможно только для квадратных матриц, т.е. матриц, в которых количество строк $m$ равно количеству столбцов $n$.
Инвертирование матрицы
После того, как мы проверили, является ли матрица обратимой, и оказалось, что она обратима, мы можем продолжить и использовать исключение Гаусса для инвертирования матрицы. В частности, метод называется исключением Гаусса-Жордана, который является вариантом алгоритма исключения Гаусса.
Инициализация алгоритма
Следующая матрица $B$ обратима, так как определитель матрицы не равен нулю. Мы будем использовать матрицу в качестве примера.
$$ Б = \begin{bматрица} 1 &5 &-1 \\ 2 &2 &-2 \\ -1 &4 &3 \end{bmatrix} $$
Алгоритм инициализируется путем сбора матрицы $B$ с левой стороны, разделенной вертикальной линией, а затем единичной матрицы для $B$, обозначенной как $I$. Единичная матрица представляет собой матрицу с единицами по диагонали от верхнего левого угла к нижнему правому (главная диагональ) и нулями в остальных элементах.
$$ [B|I] =\влево[ \begin{массив}{ccc|ccc} 1 &5 &-1 &1 &0 &0\\ 2 &2 &-2 &0 &1 &0\\ -1 &4 &3 &0 &0 &1 \конец{массив} \Правильно] $$
При выполнении операций мы выполняем их как над матрицей $B$, так и над матрицей $I$. После многих операций матрица B будет преобразована в ступенчатую форму строк, а единичная матрица $I$ будет обратной матрице $B$.
Цель исключения Гаусса-Жордана состоит в том, чтобы преобразовать матрицу в уменьшенную ступенчатую форму строк .
Давайте на минутку посмотрим, что это значит.
Сокращенная форма эшелона строк
Чтобы матрица была представлена в виде сокращенного эшелона строк, она должна удовлетворять следующим условиям:
- Все записи в строке должны быть равны $0$ до первого вхождения числа $1$.
- Первый $1$ в строке всегда находится справа от первого $1$ в строке выше.
- Все строки, состоящие только из $0$, размещаются под строками, в которых их нет.

- Первый $1$ в строке содержит только $0$ в одной и той же записи во всех строках выше $1$. Другими словами, первый $1$ в строке содержит только $0$ в том же столбце для всех строк выше $1$.
Эти условия подразумевают, что строка ниже первого $1$ в любой заданной строке содержит $0$ ниже и левее первого $1$.
Вот примеры матриц, которые ЯВЛЯЮТСЯ в сокращенной эшелонированной форме строк:
$$ А = \begin{bматрица} 1 и 0 и 0 \\ 0 и 1 и 0 \\ 0 и 0 и 1 \end{bmatrix} ,\четверка Б = \begin{bматрица} 1 & -2 & 0 & 0\\ 0 и 0 и 1 и 0\\ 0 и 0 и 0 и 1 \end{bmatrix} ,\четверка С = \begin{bматрица} 1 и 0 и -2 и 0 и 3 \\ 0 и 1 и 3 и 0 и 5\\ 0 и 0 и 0 и 1 и 6 \end{bmatrix} $$
Вот примеры матриц, НЕ представленных в сокращенной эшелонированной форме строк:
$$ А = \begin{bматрица} 2 и 1 и 0 \\ 0 и 0 и 1 \\ 0 и 0 и 0 \end{bmatrix} ,\четверка Б = \begin{bматрица} 1 и 0 и 0 \\ 0 и 1 и 0 \\ 0 и 1 и 0 \end{bmatrix} ,\четверка С = \begin{bматрица} 1 и 0 и 0 \\ 0 & 0 & 0 \\ 0 и 1 и 0 \end{bmatrix} ,\четверка Д = \begin{bматрица} 1 и 7 и 0 \\ 0 и 1 и -2 \\ 0 и 0 и 1 \end{bmatrix} $$
Обратите внимание, что матрица в форме сокращенного эшелона строк также имеет форму эшелона строк.
Обозначения и операции
Ниже приведены операции, которые мы можем выполнить в процессе исключения, чтобы преобразовать матрицу в форму сокращенного эшелона строк.
Обычно принятые обозначения для выполнения операций со строками выглядят следующим образом: означает, что $R_x$ становится равным строке $R_y$. Но это не так просто, потому что мы можем использовать три основные операции со строками, которые могут быстро запутаться.
- Добавление строки: мы можем добавить одну строку к другой строке, например,
. $R_3 \rightarrow R_2 + R_3$.
Обратите внимание, что это также означает, что мы можем выполнять вычитание,
например. $R_3 \rightarrow -R_2 + R_3$. - Умножение строк: мы можем складывать или вычитать одну и ту же строку на некоторую величину,
например. $R_3 \rightarrow 2R_2 — 1/4R_1 + R_3$.
Обратите внимание, что мы также можем выполнять деление при умножении. - Перестановка строк: мы можем поменять местами строки в матрице, чтобы они занимали место друг друга, например.
 $R_3 \rightarrow R_2$ и $R_2 \rightarrow R_3$.
$R_3 \rightarrow R_2$ и $R_2 \rightarrow R_3$.
Можно даже подумать об очень простом умножении или делении строк, когда вы делите строку на $2$ или умножаете строку на $3$.
При выполнении этих матричных операций вручную важно поддерживать чистоту и организованность, иначе вы быстро потеряете из виду то, что делали. За всей арифметикой трудно уследить.
Полный пример
Наконец-то мы собрали все вместе, мы понимаем, что такое сокращенная ступенчатая форма строк, и мы знакомы с операциями, которые мы можем выполнять для преобразования матрицы в сокращенную ступенчатую форму строк.
Теперь пришло время рассмотреть пример и применить то, что мы только что узнали. То есть применить алгоритм Гаусса-Жордана, чтобы инвертировать матрицу. Помните, что цель состоит в том, чтобы преобразовать матрицу в форму сокращенного эшелона строк, что означает, что матрица должна удовлетворять определенным условиям, перечисленным в разделе «Форма сокращенного эшелона строк».
$$ [B|I] =\влево[ \begin{массив}{ccc|ccc} 1 &5 &-1 &1 &0 &0\\ 2 &2 &-2 &0 &1 &0\\ -1 &4 &3 &0 &0 &1 \конец{массив} \Правильно] $$
Цель первых нескольких операций — преобразовать первый столбец так, чтобы ниже первого $1$ было только $0$.
- Сначала прибавляем $-2R_1$ к $R_2$
- Во-вторых прибавляем $R_1$ к $R_3$
$$ \оставил[ \begin{массив}{ccc|ccc} 1 &5 &-1 &1 &0 &0\\ 2 &2 &-2 &0 &1 &0\\ -1 &4 &3 &0 &0 &1 \конец{массив} \Правильно] R_2 \rightarrow -2R_1 + R_2 \оставил[ \begin{массив}{ccc|ccc} 1 &5 &-1 &1 &0 &0\\ 0 &-8 &0 &-2 &1 &0\\ -1 &4 &3 &0 &0 &1 \конец{массив} \Правильно] $$
$$ \оставил[ \begin{массив}{ccc|ccc} 1 &5 &-1 &1 &0 &0\\ 0 &-8 &0 &-2 &1 &0\\ -1 &4 &3 &0 &0 &1 \конец{массив} \Правильно] R_3 \стрелка вправо R_1 + R_3 \оставил[ \begin{массив}{ccc|ccc} 1 &5 &-1 &1 &0 &0\\ 0 &-8 &0 &-2 &1 &0\\ 0 &9 &2 &1 &0 &1 \конец{массив} \Правильно] $$
Во второй строке мы видим, что в строке нет $1$, поэтому мы должны это изменить. А во-вторых, нам также нужно, чтобы ниже и левее первого $1$ во второй строке были только $0$.
А во-вторых, нам также нужно, чтобы ниже и левее первого $1$ во второй строке были только $0$.
- Во-первых, делим $R2$ на $-8$
- Во-вторых, прибавляем $-9R_2$ к $R_3$
$$ \оставил[ \begin{массив}{ccc|ccc} 1 &5 &-1 &1 &0 &0\\ 0 &-8 &0 &-2 &1 &0\\ 0 &9 &2 &1 &0 &1 \конец{массив} \Правильно] R_2 \rightarrow \ frac{1}{-8}R_2 \оставил[ \begin{массив}{ccc|ccc} 1 &5 &-1 &1 &0 &0\\ 0 &1 &0 &0,25 &-0,125 &0\\ 0 и 9&2 &1 &0 &1 \конец{массив} \Правильно] $$
$$ \оставил[ \begin{массив}{ccc|ccc} 1 &5 &-1 &1 &0 &0\\ 0 &1 &0 &0,25 &-0,125 &0\\ 0 &9 &2 &1 &0 &1 \конец{массив} \Правильно] R_3 \rightarrow -9R_2 + R_3 \оставил[ \begin{массив}{ccc|ccc} 1 &5 &-1 &1 &0 &0\\ 0 &1 &0 &0,25 &-0,125 &0\\ 0 &0 &2 &-1,25 &1,125 &1 \конец{массив} \Правильно] $$
Далее мы позаботимся о последнем столбце, в котором также нет $1$. Мы делаем это, разделив $R_3$ на $2$.
$$ \оставил[ \begin{массив}{ccc|ccc} 1 &5 &-1 &1 &0 &0\\ 0 &1 &0 &0,25 &-0,125 &0\\ 0 &0 &2 &-1,25 &1,125 &1 \конец{массив} \Правильно] R_3 \rightarrow \ frac{1}{2}R_3 \оставил[ \begin{массив}{ccc|ccc} 1 &5 &-1 &1 &0 &0\\ 0 &1 &0 &0,25 &-0,125 &0\\ 0 &0 &1 &-0,625 и 0,5625 &0,5 \конец{массив} \Правильно] $$
Напомню правило 4 из раздела «Форма эшелона с уменьшенным рядом».
Первый $1$ в строке содержит только $0$ в одной и той же записи во всех строках выше $1$. Другими словами, первый $1$ в строке содержит только $0$ в том же столбце для всех строк выше $1$.
Это означает, что нам нужно избавиться от $5$ и $-1$ в первой строке. На следующих шагах мы также преобразуем некоторые записи в дроби вместо десятичных, чтобы они лучше отображались на экране.
- Во-первых, мы добавляем $R_3$ к $R_1$
- Во-вторых, мы добавляем $-5R_2$ к $R_1$
$$ \оставил[ \begin{массив}{ccc|ccc} 1 &5 &-1 &1 &0 &0\\ 0 &1 &0 &0,25 &-0,125 &0\\ 0 &0 &1 &-0,625 и 0,5625 &0,5 \конец{массив} \Правильно] R_1 \стрелка вправо R_3 + R_1 \оставил[ \begin{массив}{ccc|ccc} 1 &5 &0 &\frac{3}{8} &\frac{9}{16} &\frac{1}{2}\\ 0 &1 &0 &\frac{1}{4} &-\frac{1}{8} &0\\ 0 &0 &1 &-\frac{5}{8} & \frac{9{16} &\фракция{1}{2} \конец{массив} \Правильно] $$
$$ \оставил[ \begin{массив}{ccc|ccc} 1 &5 &0 &\frac{3}{8} &\frac{9}{16} &\frac{1}{2}\\ 0 &1 &0 &\frac{1}{4} &-\frac{1}{8} &0\\ 0 &0 &1 &-\frac{5}{8} & \frac{9}{16} &\frac{1}{2} \конец{массив} \Правильно] R_1 \стрелка вправо -5R_2 + R_1 \оставил[ \begin{массив}{ccc|ccc} 1 &0 &0 &-\frac{7}{8} &1\frac{3}{16} &\frac{1}{2}\\ 0 &1 &0 &\frac{1}{4} &-\frac{1}{8} &0\\ 0 &0 &1 &-\frac{5}{8} & \frac{9{16} &\фракция{1}{2} \конец{массив} \Правильно] $$
Вот и все, мы преобразовали матрицу $B$ в уменьшенную ступенчатую форму строк, что означает, что единичная матрица $I$ была преобразована в обратную $B$.
$$ обратный (В) = \begin{bматрица} -\frac{7}{8} &1\frac{3}{16} &\frac{1}{2}\\ \frac{1}{4} &-\frac{1}{8} &0\\ -\frac{5}{8} & \frac{9}{16} &\frac{1}{2} \end{bmatrix} знак равно \begin{bматрица} -0,875 и 1,1875 &0,5\\ 0,25 &-0,125 &0\\ -0,625 и 0,5625 и 0,5 \end{bmatrix} $$
Обладая очень базовыми навыками программирования, вы можете использовать Python с пакетом NumPy для довольно простого выполнения обратной операции.
импортировать numpy как np B = np.массив([[1,5,-1],[2,2,-2],[-1,4,3]]) inv = np.linalg.inv(B) печать (инв.)
Это дает тот же результат, который мы получили от наших операций со строками, и может быть хорошим инструментом для проверки ваших результатов при исключении вручную.
массив([[-0,875, 1,1875, 0,5],
[0.25, -0.125, 0.],
[-0,625, 0,5625, 0,5]])
Ссылки
Хорошее видео для понимания общей концепции рангов, определителей и обратных матриц:
youtube.com/embed/uQhTuRlWMxw?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Другой пример того, как найти обратную матрицу от Khan Academy:
Нахождение обратной матрицы методом исключения Гаусса-Жордана и методом сопряженных матриц | by Pollux Rey
Пропустите эту часть, если считаете, что уже уверены в своих знаниях о матрицах до обратной матрицы.
Предположим, что у нас есть система из N Линейные уравнения с N Неизвестные из формы
, где A ‘S являются коэффициентами, x ‘ S — Университет и ‘с. являются константами, мы можем представить эту систему в виде матрицы. Матричная форма системы будет
Матричная форма системы будет
Назовем первую матрицу слева A , затем следующие X и Б . Число называется матрицей коэффициентов . Матрица коэффициентов A равна квадрату , так как она имеет n на n элементов. Матрица n -×1 X называется вектором решения , и если мы умножим X на X A 90, 90, получится 90, 90.0071 n -by-1 B , который является постоянным вектором .
Система линейных уравнений может иметь единственное решение , бесконечно много решений или не иметь решения , вообще. Графически мы получим единственное решение, если все прямые в пересекаются ровно в одной точке ; бесконечно много, если все они представляют одну строку ; и нет решения, если прямые параллельны друг другу . Рисунок ниже иллюстрирует это:
Рисунок ниже иллюстрирует это:
С другой стороны, давайте посмотрим на количество решений линейной системы с использованием матриц. Давайте объясним это один за другим, используя примеры.
Уникальное решение
Если у нас есть эта расширенная матрица (это означает, что матрица коэффициентов и постоянный вектор соединены линией в качестве их разделителя),
и результирующая сокращенная по строкам матрица, полученная с помощью исключения Гаусса-Жордана, равна
, то решение уникально, потому что количество опорных точек (единицы в левой части расширенной матрицы) равно количеству столбцов в матрице (см. Ранг матрицы). Если мы подставим решение в систему, левая часть сверится с константами справа.
Бесконечное множество решений
Дана матрица
, ее сокращенная форма строки равна
Как видите, полученная матрица имеет нулевую строку, что указывает на то, что система имеет бесконечно много решений. Кроме того, количество сводных точек меньше количества столбцов. Решения, которые мы получили,
Кроме того, количество сводных точек меньше количества столбцов. Решения, которые мы получили,
немного подкорректируем и получим
где x_{3} — свободная переменная и может быть любым вещественным числом.
Если мы допустим x_{3} = 1 , x_{1} = -2 и x_{2} = -1 . Если мы допустим x_{3} = 3 , x_{1} = 0 и x_{2} = 1 . Подставляйте значения по одному, вы получите одинаковые значения констант в данной матрице.
Нет решения
Пусть у нас есть матрица в RREF, скажем,
Обратите внимание, что последняя строка имеет ненулевое значение вектора констант, но имеет нули в матрице коэффициентов.
Да, это неправильно, потому что
Определитель матрицы
Как мы упоминали ранее, если ранг матрицы равен количеству ее столбцов, то система имеет единственное решение. Но кроме этого есть еще один способ узнать количество решений линейной системы по ее определитель (см. формальное определение определителя матрицы). По сути, вы выбираете строку или столбец в матрице. Затем получите определитель подматрицы каждой сущности — представьте, что строки и столбца, которым принадлежит сущность, не существует. После того, как вы получите значения во всех объектах выбранной вами строки/столбца, умножьте каждый определитель на соответствующий объект, сложите их (обратите внимание на знаки!), и вы получите определитель матрицы.
Но кроме этого есть еще один способ узнать количество решений линейной системы по ее определитель (см. формальное определение определителя матрицы). По сути, вы выбираете строку или столбец в матрице. Затем получите определитель подматрицы каждой сущности — представьте, что строки и столбца, которым принадлежит сущность, не существует. После того, как вы получите значения во всех объектах выбранной вами строки/столбца, умножьте каждый определитель на соответствующий объект, сложите их (обратите внимание на знаки!), и вы получите определитель матрицы.
Если определитель матрицы не равен нулю, это означает, что матрица обратима.
Мы знаем, что
Если определитель матрицы коэффициентов A , det(A) , отличен от нуля, то A имеет обратный Если A имеет обратную и если мы умножим ее на приведенное выше уравнение, то получится, что
Это означает, что мы можем найти решение системы, используя обратную матрицу при условии, что B задано . В этой статье мы представим два способа его получения: Исключение Гаусса-Жордана и Метод сопряженных матриц .
В этой статье мы представим два способа его получения: Исключение Гаусса-Жордана и Метод сопряженных матриц .
Исключение Гаусса-Жордана
Выше мы видели, что если A умножить на обратную, получится единичная матрица I (связка единиц на главной диагонали матрицы и с 0). Математически,
Если мы поменяем местами A и обратно,
Если мы будем думать усерднее, это будет похоже на решение для 9{-1} . Что мы сделали ранее, так это увеличили A и B и использовали исключение Гаусса-Джордана, чтобы получить X . Это то, что мы также собираемся сделать здесь, мы сложим A и I вместе и уменьшим число строк, чтобы получить обратную A .
Давайте сначала изложим некоторые термины.
Ранее мы упоминали, как получить определитель матрицы, но теперь мы углубимся в то, из чего состоит определитель.
Минор матрицыМинор матрицы , M_{i,j} , это определитель, полученный при игнорировании значений в 7 0 7 0 0 1 й i j -й столбец вашей матрицы.
Кофактор матрицы
Кофактор матрицы , C_{i,j} , является минором со знаком . Отсюда следует формула
Определитель матрицы
Предположим, что у нас есть квадратная матрица
Определитель A равен
, если мы хотим разложить по i -й строке, или
по 90 до 1, если мы хотим разложить по 90 до 1 -й столбец. Расширение C_{i,j} приведет кили
. Чтобы лучше понять эти три концепции, давайте ответим на следующие
(Элементарная линейная алгебра Рона Ларсона, 8-е издание, стр.
116)
Найти миноры и кофакторы матрицы
Сопряжение матрицы
Транспонирование матрицы кофакторов называется сопряжением матрицы — , то есть когда вы создаете новую матрицу и значения для этой матрицы равны кофакторы для каждого значения в старой матрице, затем вы помещаете значения первой строки результирующей матрицы в первый столбец и так далее. Математически говоря,
Как получить обратную матрицу для этого метода?
Рассмотрим произведение A и adj(A) ,
Если мы умножим выделенные строку и столбец, как показано на фотографии ниже,
вы получите
Теперь давайте выделим середину ряд в A и средняя колонка в B
Единственный способ получить DET (A) снова — это когда I = J . В противном случае он равен 0 (см. Разложение определителей Лапласа). Итак, если это так, то главная диагональ произведения A и adj(A) равно
Разложение определителей Лапласа). Итак, если это так, то главная диагональ произведения A и adj(A) равно
Используя приведенное выше уравнение, мы получим
Таким образом, для этого метода, чтобы получить обратную матрицу, мы должны получить ее сопряженную и разделить ее на его определитель.
Найдите обратную матрицу двумя методами и используйте ее для решения следующей системы линейных уравнений , Метод сопряженной матрицы требует больших вычислительных ресурсов, чем метод исключения Гаусса-Жордана, поскольку создание новой матрицы для кофакторов неэффективно. Помимо этого, есть лучшие способы решения неизвестных, такие как разложение LU или просто использование исключения Гаусса.
Источники
Элементарная линейная алгебра от Рона Ларсона
Предварительная инженерная математика от Алана Джеффри
Гаусс Джордан Элиминация-Аль-Аноэрация.
линейная система уравнений. Мы также можем использовать его, чтобы найти обратную обратимую матрицу. Давайте сначала посмотрим на определение:
Исключение Гаусса-Жордана или исключение Гаусса — это алгоритм решения системы линейных уравнений путем представления ее в виде расширенной матрицы, сокращения ее с помощью операций над строками и представления системы в сокращенной строке. -ступенчатая форма для нахождения значений переменных.
В этом уроке мы подробно рассмотрим метод исключения Гаусса и способы решения системы линейных уравнений с использованием метода исключения Гаусса-Жордана. Примеры и практические вопросы будут следовать.
Что такое исключение Гаусса?
Исключение Гаусса — это структурированный метод решения системы линейных уравнений. Таким образом, это алгоритм, который можно легко запрограммировать для решения системы линейных уравнений. Основная цель Gauss-Jordan Elimination:
- для представления системы линейных уравнений в расширенной матричной форме
- затем выполнение операций со строками $ 3 $ до тех пор, пока не будет получена сокращенная эшелонированная форма строк (RREF)
- Наконец, мы можем легко распознать решения из RREF
Давайте посмотрим, что такое расширенная матричная форма, $3$ операции над строками, которые мы можем выполнять над матрицей, и уменьшенная эшелонированная форма строки матрицы.
Расширенная матрица
Система линейных уравнений показана ниже:
$ \begin{align*} 2x + 3y &= \,7 \\ x – y &= 4 \end{align*} $
Мы запишем расширенную матрицу этой системы, используя коэффициенты уравнений и записать его в стиле , показанном ниже:
$ \left[ \begin{array}{ r r | r } 2 & 3 & 7 \\ 1 & -1 & 4 \end{array} \right] $
Пример использования одновременных уравнений $ 3 $ показан ниже:
$ \begin{align*} 2x + y + z &= \,10 \\ x + 2y + 3z &= 1 \\ – x – y – z &= 2 \end{align*} $
Представление этой системы в виде расширенной матрицы:
$ \left[ \begin{array}{ r r r | r } 2 & 1 & 1 & 10 \\ 1 & 2 & 3 & 1 \\ – 1 & – 1 & – 1 & 2 \end{array} \right] $
Операции со строками над матрицей
Есть $ 3 $ элементарные операции со строками , которые мы можем выполнять с матрицами. Это не изменит решения системы. Это:
- Перестановка $ 2 $ строк
- Умножение строки на ненулевой ($\neq 0 $) скаляр
- Добавить или вычесть скалярное число, кратное одной строке, другой строке.
Сокращенная форма строки-эшелона
Основная цель метода исключения Гаусса Жордана состоит в том, чтобы использовать элементарные операции со строками на расширенной матрице, чтобы преобразовать ее в форму сокращенного ряда строк (RREF). Говорят, что матрица находится в сокращенной ступенчатой форме строк , также известной как строк канонической формы , если выполняются следующие $ 4 $ условия:
- строк с нулевыми элементами (все элементы этой строки равны $ 0 $ s) находятся внизу матрицы.
- ведущая запись (первая ненулевая запись в строке) каждой ненулевой строки расположена справа ведущей записи строки непосредственно над ней.
- Первая запись в любой ненулевой строке равна $ 1 $.
- Все записи в столбце, содержащем ведущую запись ($ 1 $), являются нулями.
Как выполнить исключение Гаусса Жордана
В методе исключения Гаусса Жордана нет определенных шагов, но приведенный ниже алгоритм описывает шаги, которые мы выполняем, чтобы получить сокращенную эшелонированную форму расширенной матрицы.

- Поменять местами строки так, чтобы все строки с нулевыми элементами оказались внизу матрицы.
- Поменять местами строки так, чтобы строка с самой большой крайней левой цифрой находилась в верхней части матрицы.
- Умножьте верхнюю строку на скаляр, который преобразует первую запись верхней строки в $ 1 $ (если первая запись верхней строки равна $ a $, умножьте ее на $ \frac{ 1 }{ a } $, чтобы получить $1$).
- Прибавьте или вычтите кратные числа из верхней строки к другим строкам, чтобы все записи в столбце ведущей записи верхней строки были равны нулю.
- Выполните шаги $ 2–4 $ для следующего крайнего левого ненулевого элемента , пока все ведущие элементы каждой строки не будут равны $ 1 $.
- Поменяйте местами строки так, чтобы первая запись каждой ненулевой строки находилась справа от первой записи строки непосредственно над ней
На первый взгляд, запомнить шаги не так просто. Это вопрос решения нескольких проблем, пока вы не освоите процесс.
Существует также фактор интуиции , который играет БОЛЬШУЮ роль в выполнении метода исключения Гаусса-Жордана.
Давайте рассмотрим несколько примеров, чтобы пояснить процесс решения системы линейных уравнений с помощью метода исключения Гаусса-Жордана . Пример 1 3x } – 4y &= { 14 } \end{align*} $
Решение
Первым шагом является запись расширенной матрицы системы. Мы покажем это ниже:
$ \left[ \begin{array}{ r r | r } – 1 & 2 & – 6 \\ 3 & -4 & 14 \end{array} \right] $
Теперь наша задача состоит в том, чтобы привести матрицу к приведенной эшелонированной форме строк (RREF), выполнив $ 3 $ элементарные операции со строками.
Расширенная матрица, которая у нас есть:
$ \left[ \begin{array}{ r r | r } – 1 & 2 & – 6 \\ 3 & – 4 & 14 \end{array} \right] $
Шаг 1:
Мы можем умножить первую строку на $ – 1 $, чтобы получить начальную запись $ 1 $. Ниже показано:
$ \left[ \begin{array}{ r r | r } 1 & – 2 & 6 \\ 3 & – 4 & 14 \end{array} \right] $
Шаг 2:
Теперь мы можем умножить первую строку на $ 3 $ и вычесть ее из второй ряд.
Ниже показано:
$ \left[ \begin{array}{ r r | r } 1 & -2 & 6 \\ {3 – ( 1 \times 3 ) } & { -4 – ( -2 \times 3 ) } & { 14 – ( 6 \times 3 ) } \end{array} \ справа] $
$ = \left[ \begin{array}{ r r | r } 1 & – 2 & 6 \\ 0 & 2 & – 4 \end{array} \right] $
У нас есть $ 0 $ в качестве первой записи второй строки.
Шаг 3:
Чтобы сделать вторую запись второй строки $ 1 $, мы можем умножить вторую строку на $ \ frac { 1 }{ 2 } $. Ниже показано:
$ \left[ \begin{array}{ r r | r } 1 & – 2 & 6 \\ { \frac{ 1 }{ 2 } \times 0} & { \frac{ 1 }{ 2 } \times 2 } & { \frac{ 1 }{ 2 } \times – 4} \end{массив} \right] $
$ = \left[ \begin{array}{ r r | r } 1 & – 2 & 6 \\ 0 & 1 & – 2 \end{array} \right] $
Шаг 4:
Мы почти у цели!
Вторая запись первой строки должна быть $0 $. Для этого умножаем вторую строку на $2$ и прибавляем к первой строке. Ниже показано:
$ \left[ \begin{array}{ r r | r } { 1 + (0 \times 2 ) } & { – 2 + (1 \times 2 ) } & {6 + ( – 2 \times 2 ) } \\ 0 & 1 & – 2 \end{array} \ справа] $
$ = \left[ \begin{array}{ r r | r } 1 & 0 & 2 \\ 0 & 1 & – 2 \end{array} \right] $
Это сокращенный эшелон строк формы .
Из расширенной матрицы мы можем написать два уравнения (решения):
$ \begin{align*} x + 0y &= \, 2 \\ 0x + y &= -2 \end{align*} $
$ \begin{align*} x &= \, 2 \\ y &= – 2 \end{align*} $
Таким образом, решением системы уравнений является $ x = 2 $ и $ y = – 2$.
Пример 2Решите систему, показанную ниже, с помощью метода исключения Гаусса Жордана: align*} $
РешениеЗапишем расширенную матрицу системы уравнений:
$ \left[ \begin{array}{ r r | r } 1 & 2 & 4 \\ 1 & – 2 & 6 \end{array} \right] $
Теперь мы выполняем элементарные операции со строками над этой матрицей, пока не придем к сокращенной ступенчатой форме строк.
Шаг 1:
Умножаем первую строку на $1$ и затем вычитаем ее из второй строки. По сути, это вычитание первой строки из второй строки:
$ \left[ \begin{array}{ r r | r } 1 & 2 & 4 \\ 1 – 1 & – 2 – 2 & 6 – 4 \end{массив} \right] $
$ =\left[ \begin{array}{ r r | r } 1 & 2 & 4 \\ 0 & – 4 & 2 \end{array} \right] $
Шаг 2:
Умножаем вторую строку на $ -\frac{ 1 }{ 4 }$, чтобы получить вторая запись ряда, $1$:
$\left[ \begin{array}{ r r | r } 1 & 2 & 4 \\ 0 \times -\frac{ 1 }{ 4 } & – 4 \times -\frac{ 1 }{ 4 } & 2 \times -\frac{ 1 }{ 4 } \end {массив} \right] $
$ =\left[ \begin{array}{ r r | r } 1 & 2 & 4 \\ 0 & 1 & -\frac{ 1 }{ 2 } \end{array} \right] $
Шаг 3:
Наконец, мы умножаем вторую строку на $ – 2 $ и добавьте его к первой строке, чтобы получить уменьшенную форму эшелона строк этой матрицы:
$\left[ \begin{array}{ r r | r } 1+(- 2\times 0) & 2+( — 2 \times 1) & 4 + ( — 2 \times -\frac{ 1 }{ 2 } ) \\ 0 & 1 & -\frac{ 1 }{ 2 } \end{массив} \right] $
$=\left[ \begin{array}{ r r | r } 1 & 0 & 5 \\ 0 & 1 & -\frac{ 1 }{ 2 } \end{array} \right] $
Это сокращенный ряд строк формы .
Из расширенной матрицы мы можем написать два уравнения (решения):
$ \begin{align*} x + 0y &= \, 5 \\ 0x+ y &= -\frac{ 1 }{ 2 } \end {align*} $
$ \begin{align*} x &= \, 5 \\ y &= -\frac{ 1 }{ 2 } \end{align*} $
Таким образом, решение системы уравнений есть $ x = 5 $ и $ y = -\frac{ 1 }{ 2 } $.
Практические вопросы
Решите систему, показанную ниже, используя метод исключения Гаусса Жордана:
$ \begin{align*} 2x + y &= \, – 3 \\ – x – y &= 2 \end{align*} $
Решите систему, показанную ниже, используя метод исключения Гаусса-Жордана:
$ \begin{align*} x + 5y &= \, 15 \\ – x + 5y &= 25 \end{align*} $
Ответы
Предыдущий урок | Главная страница | Следующий урок
Начнем с записи расширенной матрицы системы уравнений:
$ \left[ \begin{array}{r r | r} 2 & 1 & – 3 \\ – 1 & – 1 & 2 \end{array} \right] $
Теперь мы выполняем элементарные операции со строками, чтобы получить наше решение.
Первый,
Меняем местами знаки второй строки и меняем местами строки. Итак, имеем:
$ \left[ \begin{array}{r r | r} 1 & 1 & – 2 \\ 2 & 1 & – 3 \end{array} \right] $
Второй,
Вычитаем дважды первую строку из второй строки:
$ \left[ \begin{array}{ р р | r} 1 & 1 & – 2 \\ 2 – ( 2 \times 1 ) & 1 – ( 2 \times 1 ) & – 3 – ( 2 \times – 2 ) \end{array} \right] $
$ = \left[ \begin{array}{r r | r} 1 & 1 & – 2 \\ 0 & – 1 & 1 \end{array} \right] $
Третий,
Инвертируем вторую строку, чтобы получить:
$ = \left[\begin{array}{r r | r} 1 & 1 & – 2 \\ 0 & 1 & – 1 \end{array} \right] $
Наконец,
Вычитаем вторую строку из первой и получаем:
$ = \left[\begin{ массив}{r r | r} 1 & 0 & – 1 \\ 0 & 1 & – 1 \end{array} \right] $Из этой расширенной матрицы мы можем написать два уравнения (решения):
$ \begin{align*} x + 0y &= \, – 1 \\ 0x+ y &= – 1 \end{align*} $
$ \begin{align*} x &= \, – 1 \ \ y &= – 1 \end{align*} $
Таким образом, решением системы уравнений является $ x = – 1 $ и $ y = – 1 $.
- Расширенная матрица системы:
$ \left[\begin{array}{r r|r} 1 & 5 & 15 \\ – 1 & 5 & 25 \end{array} \right] $
Давайте привести эту матрицу к сокращенному ступенчатому виду строк и найти решение системы.Во-первых,
Отмените первую строку, затем вычтите ее из второй строки, чтобы получить:
$ \left[ \begin{array}{r r|r} 1 & 5 & 15 \\ – 1 – ( – 1 ) & 5 – ( – 5 ) & 25 – ( – 15) \end{массив} \right] $
$ =\left[ \begin{array}{r r|r} 1 & 5 & 15 \\ 0 & 10 & 40 \end {array} \right] $
Second,
Разделите вторую строку на $10$, чтобы получить:
$ \left[\begin{array}{r r | r} 1 & 5 & 15 \\ 0 & 1 & 4 \end{array} \right] $
Затем
Умножьте вторую строку на $ 5 $ и вычтите ее из первой строки, чтобы окончательно получить решение:
$ \left[\begin{array}{r r | r} 1 – ( 5 \times 0 ) & 5 – ( 5 \times 1 ) & 15 – ( 5 \times 4 ) \\ 0 & 1 & 4 \end{array} \right] $
$ =\left[ \begin{массив}{r r | r} 1 & 0 & – 5 \\ 0 & 1 & 4 \end{array} \right] $
Это сокращенная форма эшелона строк (RREF).Из этой дополненной матрицы мы можем написать два уравнения (решения):
$ \begin{align*} x &= \, – 5 \\ y &= 4 \end{align*} $
Таким образом, решение системы уравнений $ x = – 5 $ и $ y = 4 $.
2.2: Системы линейных уравнений и метод Гаусса-Жордана
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 37847
- Рупиндер Секон и Роберта Блум
- Колледж Де Анза
Цели обучения
В этом разделе вы научитесь
- представлять систему линейных уравнений в виде расширенной матрицы
- Решите систему с помощью элементарных операций со строками.
В этом разделе мы научимся решать системы линейных уравнений, используя процесс, называемый методом Гаусса-Жордана. Процесс начинается с того, что сначала система выражается в виде матрицы, а затем сводится к эквивалентной системе с помощью простых операций со строками. Процесс продолжается до тех пор, пока решение не станет очевидным из матрицы. Матрица, которая представляет систему, называется расширенная матрица , а арифметическая операция, используемая для перехода от системы к сокращенной эквивалентной системе, называется строковой операцией .
Пример \(\PageIndex{1}\)
Запишите следующую систему в виде расширенной матрицы.
\[\begin{array}{l}
2 x+3 y-4 z=5 \\
3 x+4 y-5 z=-6 \\
4 x+5 y-6 z=7
\end{array}\nonumber \]Решение
Представим полученную информацию в матричной форме. Поскольку система полностью определяется своей матрицей коэффициентов и матрицей постоянных членов, расширенная матрица будет включать только матрицу коэффициентов и постоянную матрицу.
Итак, расширенная матрица, которую мы получаем, выглядит следующим образом:
\[\left[\begin{array}{ccc|c}
2 & 3 & -4 & 5 \\
3 & 4 & -5 & -6 \\
4 & 5 & -6 & 7
\конец{массив}\номер\право]\неномер \]В последнем разделе мы представили систему уравнений как \(AX = B\), где \(A\) представляет собой матрицу коэффициентов, а \(B\) — матрицу постоянных членов. В качестве расширенной матрицы мы записываем матрицу как \(\left[\begin{array}{l|l}A & B \end{array}\right]\). Понятно, что вся информация сохраняется в этой матричной форме, и только буквы \(x\), \(y\) и \(z\) отсутствуют. Учащийся может написать \(x\), \(y\) и \(z\) поверх первых трех столбцов, чтобы упростить переход.
Пример \(\PageIndex{2}\)
Для следующей расширенной матрицы запишите систему уравнений, которую она представляет.
\[\left[\begin{array}{ccccc}
1 & 3 & -5 & | & 2 \
2 & 0 & -3 & | & -5 \
3 & 2 & -3 & | & -1
\end{array}\right]\nonumber \]Решение
Систему легко получить, как показано ниже.
\[\begin{array}{l}
x+3 y-5 z=2 \\
2 x-3 z=-5 \\
3 x+2 y-3 z=-1
\end{массив}\номер \]Как только система выражается в виде расширенной матрицы, метод Гаусса-Джордана сводит систему к ряду эквивалентных систем, используя операции со строками. Это сокращение строк продолжается до тех пор, пока система не будет выражена в так называемой сокращенной эшелонированной форме строк . Сокращенная эшелонированная форма строки матрицы коэффициентов имеет единицы вдоль главной диагонали и нули в других местах. Решение легко получить из этой формы.
Этот метод не сильно отличается от алгебраических операций, которые мы использовали в методе исключения в первой главе. Основное отличие состоит в том, что он носит алгоритмический характер и, следовательно, легко может быть запрограммирован на компьютере.
Далее мы решим систему двух уравнений с двумя неизвестными, используя метод исключения, а затем покажем, что этот метод аналогичен методу Гаусса-Жордана.
Пример \(\PageIndex{3}\)
Решите следующую систему методом исключения.
\[\begin{array}{l}
x+3 y=7 \\
3 x+4 y=11
\end{array} \nonumber \]Решение
Умножаем первое уравнение на – 3, и добавить его ко второму уравнению.
\begin{align}
-3 x-9 y &=-21 \\
3 x+4 y &=11 \\ \hline
-5y &=-10
\end{align}Делая это мы преобразовали нашу исходную систему в эквивалентную систему:
\begin{aligned}
x+3 y &=7 \\
-5 y &=-10
\end{aligned}Делим второе уравнение на – 5 и получаем следующую эквивалентную систему.
\begin{aligned}
x+3 y &=7 \\
y &=2
\end{aligned}Теперь умножаем второе уравнение на – 3 и прибавляем к первому, получаем
\ [\begin{массив}{l}
x=1 \\
y=2
\end{массив}\номер\]Пример \(\PageIndex{4}\)
Решите следующую систему из примера 3 методом Гаусса-Жордана и покажите сходство обоих методов, написав уравнения рядом с матрицами.
\begin{array}{l}
x+3 y=7 \\
3 x+4 y=11
\end{array}Решение
Расширенная матрица для системы выглядит следующим образом.
\[\left[\begin{array}{cccc}
1 & 3 & | & 7 \
3 & 4 & | & 11
\end{массив}\right] \quad\left[\begin{array}{c}
x+3 y=7 \\
3 x+4 y=11
\end{массив}\right] \nonumber \]Умножаем первую строку на – 3 и прибавляем ко второй строке.
\[\left[\begin{массив}{cccc}
1 и 3 и | & 7 \
0 & -5 & | & -10
\end{массив}\right] \quad\left[\begin{array}{c}
x+3 y&=7 \\
-5 y&=-10
\end{массив}\right] \nonumber \]Делим вторую строку на – 5, получаем,
\[\left[\begin{array}{llll}
1 & 3 & | & 7 \
0 & 1 & | & 2
\end{массив}\right] \quad\left[\begin{array}{rl}
x+3 y & =7 \\
y & =2
\end{массив}\right] \nonumber \]Наконец, мы умножаем вторую строку на – 3 и добавляем к первой строке, и мы получаем,
\[\left[\begin{array}{llll}
1 & 0 & | & 1 \
0 & 1 & | & 2
\end{массив}\right] \quad\left[\begin{array}{l}
x=1 \\
y=2
\end{массив}\right] \nonumber \]Теперь мы перечислим три операции со строками, которые использует метод Гаусса-Жордана.
Операции со строками
- Любые две строки в расширенной матрице можно поменять местами.
- Любая строка может быть умножена на ненулевую константу.
- Константа, кратная строке, может быть добавлена к другой строке.
Легко видеть, что эти операции с тремя строками могут изменить внешний вид системы, но они не меняют решение системы.
Операция с первой строкой гласит, что если поменять местами любые две строки системы, полученная новая система будет иметь то же решение, что и старая. Рассмотрим пример в двух уравнениях с двумя неизвестными. Рассмотрим систему
\begin{выровнено}
x+3 y&=7 \\
3 x+4 y&=11
\end{выровнено}Меняем местами ряды и получаем,
\begin{выровнено}
3 x+4 y&=11 \\
x+3 y&=7
\end{выровнено}Ясно, что эта система имеет то же решение, что и предыдущая.
Вторая операция утверждает, что если строку умножить на любую ненулевую константу, новая полученная система будет иметь то же решение, что и старая.
Рассмотрим вышеприведенную систему еще раз,
\begin{выровнено}
x+3 y&=7 \\
3 x+4 y&=11
\end{выровнено}Умножаем первую строку на –3, получаем,
\begin{align}
-3 x-9 y &=-21 \\
3 x+4 y &=11
\end{align}Опять же, очевидно, что эта новая система имеет то же решение, что и исходная.
Третья операция со строками утверждает, что любая константа, кратная одной строке, добавленная к другой, сохраняет решение. Рассмотрим нашу систему,
\begin{выровнено}
x+3 y&=7 \\
3 x+4 y&=11
\end{выровнено}Если мы умножим первую строку на -3 и прибавим ко второй строке, мы получим
\begin{выровнено}
x+3 y&=7 \\
-5 y&=-10
\end{выровнено}И снова сохраняется то же решение.
Теперь, когда мы поняли, как работают операции с тремя строками, пришло время представить метод Гаусса-Жордана для решения систем линейных уравнений. Как упоминалось ранее, метод Гаусса-Жордана начинается с расширенной матрицы, и с помощью ряда операций со строками заканчивается матрицей, которая находится в уменьшенный рядный эшелон формы .
Матрица находится в сокращенном эшелоне строк формы , если первый ненулевой элемент в каждой строке равен 1, а столбцы, содержащие эти 1, имеют все остальные элементы как нули. Форма сокращенного эшелона строк также требует, чтобы начальный элемент в каждой строке был справа от ведущего элемента в строке над ним, а строки, содержащие все нули, были перемещены вниз вниз. Сформулируем метод Гаусса-Жордана следующим образом.
Метод Гаусса-Джордана
- Напишите расширенную матрицу.
- При необходимости поменяйте местами строки, чтобы получить ненулевое число в первой строке, первом столбце.
- Используйте операцию строки, чтобы получить 1 в качестве записи в первой строке и первом столбце.
- Используйте операции со строками, чтобы сделать все остальные записи нулями в первом столбце.
- При необходимости поменяйте местами строки, чтобы получить ненулевое число во второй строке, втором столбце.
Используйте операцию со строками, чтобы сделать эту запись 1. Используйте операции со строками, чтобы сделать все остальные записи нулями во втором столбце.
- Повторите шаг 5 для строки 3, столбца 3. Продолжайте движение по главной диагонали, пока не дойдете до последней строки или пока число не станет равным нулю.
Окончательная матрица называется редуцированной формой строки-эшелона.
Пример \(\PageIndex{5}\)
Решите следующую систему методом Гаусса-Жордана.
\begin{align}
2 x+y+2 z &=10 \\
x+2 y+z &=8 \\
3 x+y-z &=2
\end{align}Решение
Пишем расширенную матрицу.
\[\left[\begin{array}{ccccc}
2 & 1 & 2 & | & 10 \
1 & 2 & 1 & | & 8 \
3 & 1 & -1 & | & 2
\end{array}\right] \nonumber \]Нам нужна 1 в первой строке, в первом столбце. Это можно получить, разделив первую строку на 2 или поменяв местами вторую строку с первой. Перестановка строк — лучший выбор, потому что таким образом мы избегаем дробей.
\[\left[\begin{массив}{ccccc}
1 и 2 и 1 и | & 8 \
2 & 1 & 2 & | & 10 \
3 & 1 & -1 & | & 2
\end{array}\right] \quad \text { мы поменяли местами строку 1 (R1) и строку 2 (R2) }\nonumber \]Нам нужно сделать все остальные записи нулями в столбце 1. Чтобы сделать запись (2) ноль в строке 2, столбце 1, умножаем строку 1 на — 2 и прибавляем ко второй строке. Получаем
\[\left[\begin{array}{ccccc}
1 & 2 & 1 & | & 8 \
0 & -3 & 0 & | &-6\
3 и 1 и -1 и | & 2
\end{array}\right] \quad-2 R 1+R 2 \nonumber \]Чтобы сделать запись (3) нулем в строке 3 столбца 1, мы умножаем строку 1 на — 3 и добавить его в третью строку. Получаем
\[\left[\begin{array}{ccccc}
1 & 2 & 1 & | & 8 \
0 & -3 & 0 & | &-6\
0&-5&-4&| & -22
\end{array}\right] \quad-3 R 1+R 3 \nonumber \]До сих пор мы сделали 1 в левом углу, а все остальные записи в этом столбце — нулями. Теперь мы переходим к следующей диагональной записи, строке 2, столбцу 2.
Нам нужно сделать эту запись (–3) равной 1, а все остальные записи в этом столбце сделать нулями. Чтобы сделать строку 2, столбец 2 равным 1, мы делим всю вторую строку на -3.
\[\left[\begin{array}{ccccc}
1 & 2 & 1 & | & 8 \
0 & 1 & 0 & | & 2 \
0 & -5 & -4 & | & -22
\end{array}\right] \quad \mathrm{R} 2 \div(-3) \nonumber \]Затем мы делаем все остальные записи нулями во втором столбце.
\[\left[\begin{array}{ccccc}
1 & 0 & 1 & | & 4 \
0 & 1 & 0 & | & 2 \
0 & 0 & -4 & | & -12
\end{array}\right] \quad-2 R 2+R 1 \text { и } 5 R 2+R 3 \nonumber \]Мы делаем последнюю диагональную запись равной 1, разделив строку 3 на – 4.
\[\left[\begin{array}{ccccc}
1 & 0 & 1 & | & 4 \
0 & 1 & 0 & | & 2 \\
0 & 0 & 1 & | & 3
\end{array}\right] \quad \quad R 3 \div(-4) \nonumber \]Наконец, мы обнуляем все остальные записи в столбце 3.
\[\left[\begin {массив}{ccccc}
1 & 0 & 0 & | & 1 \
0 & 1 & 0 & | & 2 \
0 и 0 и 1 и | & 3
\end{array}\right] \quad-\mathrm{R} 3+\mathrm{R} 1 \nonumber \]Ясно, что решение имеет вид \(x =1\), \(y = 2\) и \(z = 3\).
Прежде чем покинуть этот раздел, мы упомянем некоторые термины, которые могут нам понадобиться в четвертой главе.
Процесс получения 1 в местоположении и последующего обнуления всех остальных записей в этом столбце называется поворотом .
Число, состоящее из 1, называется поворотным элементом , , а строка, содержащая опорный элемент, называется сводной строкой .
Мы часто умножаем основную строку на число и прибавляем ее к другой строке, чтобы получить ноль в последней. Строка, к которой добавляется кратная сводной строке, называется целевой строкой .
Эта страница под названием 2.2: Системы линейных уравнений и метод Гаусса-Джордана распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Рупиндером Секоном и Робертой Блум с использованием исходного контента, который был отредактирован в соответствии со стилем. и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Рупиндер Сехон и Роберта Блум
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу Оглавление
- нет
- Метки
- расширенная матрица
- Метод Гаусса-Жордана
- поворотный элемент
- поворотный ряд
- поворотный
- уменьшенный ряд эшелона форма
- рядная операция
- источник@https://www.
deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
- целевая строка
Исключение Жордана Гаусса посредством поворота
Исключение Жордана Гаусса посредством поворотаСистема линейных уравнений может привести к матричной форме. Каждый уравнение становится строкой, и каждый переменная становится столбцом. Ан добавлен дополнительный столбец для справа. Система показаны линейные уравнения и результирующая матрица.
Система линейных уравнений…
3x + 2y - 4z = 3 2x + 3y + 3z = 15 5x - 3y + z = 14становится расширенной матрицей…
х и г справа 3 2 -4 3 2 3 3 15 5 -3 1 14 Цель при решении системы уравнений состоит в том, чтобы по возможности привести расширенную матрицу к сокращенной ступенчато-строковой форме.
Существуют три элементарные операции со строками, которые можно использовать для размещения матрицы в редуцированная рядно-кулисная форма.
Каждое из требований редуцированной ступенчато-строковой матрицы может быть удовлетворено с помощью элементарной строки операции.
- Если есть строка, состоящая только из нулей, то она находится внизу матрицы.
Поменяйте местами две строки матрицы, чтобы переместить строку со всеми нулями вниз.- Первый ненулевой элемент любой строки равен единице. Этот элемент называется ведущим.
Умножить (разделить) строку на ненулевую константу, чтобы сделать первый ненулевой элемент в один.- Ведущий в любом ряду находится справа от ведущего в предыдущем ряду.
Умножить строку на ненулевую константу и добавить ее к другой строке, заменив эту строку. Суть этой элементарной операции со строками состоит в том, чтобы превратить числа в нули. Делая числа под ведущими в ноль, он заставляет первый ненулевой элемент любой строки быть справа от ведущего предыдущего ряда.- Все элементы выше и ниже ведущей единицы равны нулю.
Умножить строку на ненулевую константу и добавить ее к другой строке, заменив эту строку. смысл этой элементарной операции со строками состоит в том, чтобы сделать числа равными нулю. Разница здесь что вы очищаете (обнуляете) элементы над ведущим, а не чуть ниже ведущий.Что такое поворот?
Цель поворота — сделать элемент выше или ниже ведущего в ноль.
«Опорный элемент» или «опорный элемент» — это элемент в левой части матрицы. что вы хотите элементы выше и ниже равны нулю.
Обычно этот элемент равен единице. Если вы можете найти книгу, в которой упоминается поворот, они, как правило, сказать вам, что вы должны развернуться на один. Если ограничиться тремя элементарными рядами операций, то это верное утверждение.
Однако, если вы хотите объединить вторую и третью элементарные операции над строками, вы придумать еще одну операцию над строками (не элементарную, но все же допустимую).
- Вы можете умножить строку на ненулевую константу и добавить ее к ненулевому кратному другой строку, заменяя эту строку.
И что? Если вам необходимо развернуться на одном, то вы должны иногда использовать второй элементарную операцию со строкой и разделить строку на ведущий элемент, чтобы сделать ее единицей. Деление приводит к дробям. Хотя дроби — ваши друзья, вы с меньшей вероятностью сделаете ошибку если вы их не используете.
В чем подвох? Если вы не будете ориентироваться на единицу, вы, вероятно, столкнетесь с большими числами. Самый люди готовы работать с большими числами, чтобы избежать дробей.
Сводной процесс
Поворот работает, потому что общее кратное (не обязательно наименьшее) общее кратное) двух чисел всегда можно найти путем умножения два числа вместе. Возьмем пример, который у нас был раньше, и очистить первую колонку.
х и г справа 3 2 -4 3 2 3 3 15 5 -3 1 14 Полезные советы
- Хоть и не обязательно вертеться на один, но очень желательно.
Поворот на единицу означает, что вы умножаете на 1 (что легко сделать).
- Поворачиваться по главной диагонали приятно, но не обязательно. Некоторым людям нравится начинать с верхнего левого угла и двигаться вниз к Нижний правый.
- Пока вы выполняете поворот только один раз для строки и столбца, столбцы, которые были очищены, останутся очищенными.
- Так как целью поворота является очистка столбца свода, выбор столбец, в котором уже есть нули, экономит время, потому что у вас нет чтобы изменить строку, содержащую ноль.
Выбор оси
- Выберите столбец с наибольшим количеством нулей.
- Использовать строку или столбец только один раз
- Повернуть на одну, если возможно
- Поворот по главной диагонали
- Никогда не поворачивайте на ноль
- Никогда не поворачивайте на правую сторону
Поскольку в первом ряду никого нет, у нас есть два варианта: Либо мы делим первую строку на три и работаем с дробями, или делаем поворот на три и получить большие числа.
Это тот вариант, который я собираюсь использовать. я повернусь на тройке в R 1 C 1 . Идите вперед и обведите это как опорный элемент. В зависимости от вашего браузера вы могут видеть элементы поворота, обведенные красным или просто с * перед ним.
х г г справа *3 2 -4 3 2 3 3 15 5 -3 1 14 Идея состоит в том, чтобы превратить числа в рамку (желтые) в ноль. Использование комбинированного операция строки (это не элементарная операция), это может сделать 3R 2 — 2R 1 → R 2 и 3R 3 — 5R 1 → R 3 .
Единственная неизменяемая строка — это строка, содержащая опорный элемент (элемент 3). Весь смысл процесса поворота состоит в том, чтобы сделать значения в прямоугольниках равными нулю. Перепишите сводную строку и очистите (обнулите) опорную колонку.
х и г справа *3 2 -4 3 0 0 Чтобы заменить значения в строке 2, каждый новый элемент получается путем умножения элемент заменяется во второй строке на 3 и вычитается в 2 раза элемент в первом строку из того же столбца, что и заменяемый элемент.
Чтобы выполнить поворот, поместите один палец на шарнир (обведено кружком). номер), и один палец на заменяемом элементе. Перемножьте эти два числа вместе. Теперь поместите один палец на цифре в рамке в той же строке, что и элемент, который вы замена и другого пальца в поворотном ряду и то же самое столбец как номер, который вы заменяете. Умножьте эти два числа вместе. Возьмите изделие с осью и вычесть произведение без опоры.
х и г справа *3 2 -4 3 2 3 3 15 5 -3 1 14 Чтобы заменить 3 в R 2 C 2 , вы должны взять 3(3) — 2(2) = 9 — 4 = 5.
Чтобы заменить 3 в R 2 C 3 , вы должны взять 3(3) — 2(-4) = 9 + 8 = 17.
Чтобы заменить 15 в R 2 C 4 , вы должны взять 3(15) — 2(3) = 45 — 6 = 39.
Чтобы заменить -3 в R 3 C 2 , вы должны взять 3(-3) — 5(2) = -9 — 10 = -19.
Для замены 1 в R 3 C 3 , вы должны взять 3(1) — 5(-4) = 3 + 20 = 23
Чтобы заменить 14 в R 3 C 4 , вы должны взять 3(14) — 5(3) = 42 — 15 = 27.
Вот как выглядит процесс.
х и г справа поворотный ряд, копия
3поворотный ряд, копия
2сводная строка, копия
-4поворотный ряд, копия
3поворотная стойка, прозрачная
03(3) — 2(2)
53(3) — 2(-4)
173(15) — 2(3)
39поворотная стойка, прозрачная
03(-3) — 5(2)
-193(1) — 5(-4)
233(14) — 5(3)
27Или, если убрать комментарии, то матрица после первого пивота выглядит так.
х и г справа 3 2 -4 3 0 5 17 39 0 -19 23 27 Пришло время повторить весь процесс. Проходим и выбираем другое место для разворота. Мы хотел бы, чтобы это было на главной диагонали, единице или имело нули в столбце. К сожалению, у нас не может быть ни того, ни другого. Но так как мы должны умножить все другие числа по оси, мы хотим, чтобы она была маленькой, поэтому мы будем поворачиваться на 5 в Р 2 C 2 и уберите 2 и -19.
х и г справа 3 2 -4 3 0 *5 17 39 0 -19 23 27 Начните с копирования сводной строки (2-я строка) и очистки сводного столбца (2-я строка). столбец). Ранее очищенные столбцы останутся очищенными.
х и г справа 0 0 *5 17 39 0 0 Вот расчеты для нахождения следующего взаимодействия.
Будьте внимательны в 3-ю строку, где мы вычитаем -19 раз значение. Поскольку мы вычитаем минус, я пошел дальше и написал плюс 19.
х и г справа 5(3) — 2(0)
15поворотная стойка, прозрачная
05(-4) — 2(17)
-545(3) — 2(39)
-63поворотный ряд, копия
0поворотный ряд, копия
5сводная строка, копия
17поворотный ряд, копия
39предварительно очищенный
0поворотная стойка, прозрачная
05(23) + 19(17)
4385(27) + 19(39)
876И полученная матрица.
х и г справа 15 0 -54 -63 0 5 17 39 0 0 438 876 Обратите внимание, что все элементы в первой строке кратны 3 и все элементы в последней строке кратны 438. Мы разделим, чтобы уменьшить количество строк.
х и г справа 5 0 -18 -21 0 5 17 39 0 0 1 2 Это дало нам дополнительное преимущество: 1 именно там, где мы хотим, чтобы оно было вращаться.
Итак, мы начнем с 1 в R 3 C 3 и очистим -18 и 17. Обведите ваш центр и обведите остальные числа этот столбец, чтобы очистить.
х и г справа 5 0 -18 -21 0 5 17 39 0 0 *1 2 Скопируйте вниз сводную строку и очистите сводную колонку. Ранее очищенные столбцы останется очищенным до тех пор, пока вы не выполните поворот в строке или столбце дважды.
х и г справа 0 0 0 0 0 0 *1 2 Обратите внимание, что с каждым разом требуется выполнить меньше вычислений.
Вот расчеты для этой опоры. Опять же, поскольку значение в сводном столбце в первая строка -18 и мы вычитаем, я написал это как + 18.
х и г справа 1(5) +18(0)
5ранее очищено
0поворотная стойка, прозрачная
01(-21) + 18(2)
15предварительно очищенный
01(5) — 17(0)
5поворотная стойка, прозрачная
01(39) — 17(2)
5поворотный ряд, копия
0поворотный ряд, копия
0поворотный ряд, копия
1поворотный ряд, копия
2И полученная матрица.
х и г справа 5 0 0 15 0 5 0 5 0 0 1 2 Обратите внимание, что первая и вторая строки кратны 5, поэтому мы можем уменьшить их. ряды.
х и г справа 1 0 0 3 0 1 0 1 0 0 1 2 И окончательный ответ: x = 3, y = 1 и z = 2.
Вы также можете записать это как упорядоченная тройка {(3,1,2)}.
Надеюсь, вы заметили, что когда я работал над этим примером, я не следовал подсказкам Я дал. Это потому, что я хотел, чтобы вы увидели, что произойдет, если вы не развернетесь. на одном. Был один, на главной диагонали, в исходной матрице, и было бы лучше начать там.
Резюме
- Тщательно выбирайте поворотный элемент.
- Выбор столбца с нулями означает меньший поворот.
- Выбор единицы в качестве опорной уменьшает числа, упрощает умножение и оставляет ненулевые элементы в очищенном столбце одинаковые (менее поворотные)
- Поворот по главной диагонали означает, что вам не придется менять ряды, чтобы поместить матрицу в редуцированная рядно-кулисная форма.
- Не поворачиваться на ноль.
- Не поворачиваться на правую сторону.
- Использовать строку или столбец только один раз
- Возьмем продукт с стержнем минус продукт без стержня
Особые случаи
Если вы получили строку со всеми нулями, кроме правой части, то система не имеет решения.
Если вы получаете строку из всех нулей, а количество ненулевых строк меньше, чем количество переменных, то система зависима, ответов у вас будет много, и вам нужно написать свой ответ в параметрической форме.
Исключение Гаусса-Джордана | Brilliant Math & Science Wiki
Систему уравнений можно представить в нескольких матричных формах. Один из способов состоит в том, чтобы реализовать систему как матричное произведение коэффициентов системы и вектор-столбца ее переменных. Квадратная матрица называется матрицей коэффициентов , потому что она состоит из коэффициентов переменных в системе уравнений:
Произведение матриц: 2x+4y+7z=43x+3y+2z=85x+6y+3z=0 ⟶[247332563][xyz]=[480]. \text{Произведение матриц: }\quad \begin{массив}{c c c c c c c} 2x & + & 4y & + & 7z & = & 4\\ 3x & + & 3y & + & 2z & = & 8\\ 5x & + & 6y & + & 3z & = & 0 \конец{массив} \longrightarrow \оставил[ \begin{массив}{с с с} 2 и 4 и 7\\ 3 и 3 и 2\\ 5 и 6 и 3 \конец{массив} \Правильно] \оставил[ \начать{массив}{с} Икс \\ у \\ г \конец{массив} \Правильно] = \ влево[ \начать{массив}{с} 4\\ 8\ 0 \end{массив} \right].
Произведение матриц: 2x3x5x+++4y3y6y+++7z2z3z===480⟶⎣⎡235436723⎦⎤⎣⎡xyz⎦⎤=⎣⎡480 ⎦⎤.
Альтернативное представление, называемое расширенной матрицей , создается путем сшивания столбцов матриц вместе и разделения вертикальной чертой. Матрица коэффициентов помещается слева от этой вертикальной полосы, а константы в правой части каждого уравнения помещаются справа от вертикальной полосы:
Расширенная матрица: 2x+4y+7z=43x+3y+ 2z=85x+6y+3z=0⟶[247433285630]. \text{Дополненная матрица: } \quad \quad \begin{массив}{c c c c c c c} 2x&+&4y&+&7z&=&4\ 3x&+&3y&+&2z&=&8\ 5x&+&6y&+&3z&=&0\ \конец{массив} \longrightarrow \оставил[ \begin{массив}{c c c | в} 2 и 4 и 7 и 4 \\ 3 и 3 и 2 и 8 \\ 5 и 6 и 3 и 0 \end{массив}\right]. Расширенная матрица: 2x3x5x+++4y3y6y+++7z2z3z===480⟶⎣⎡235436723480⎦⎤.
Матрицами, которые представляют эти системы, можно манипулировать таким образом, чтобы обеспечить легко читаемые решения. Эта манипуляция называется сокращением строки.
Методы сокращения строк преобразуют матрицу в сокращенную эшелонированную форму строк без изменения решений системы.
сокращенная ступенчатая форма строки матрицы AAA (\big((обозначается rref(A)) \text{rref}(A)\big)rref(A)) является матрицей одинаковой размерности, которая удовлетворяет следующему:
- Крайний левый ненулевой элемент в каждой строке равен 1 1 1. Этот элемент называется опорным.
- Любой столбец может иметь не более 1 1 1 точки поворота. Если у столбца есть стержень, то остальные элементы в столбце будут равны 0 0 0.
- Для любых двух столбцов C1C_{1} C1 и C2C_{2}C2, которые имеют сводные значения в строках R1 R_{1} R1 и R2, R_{2}, R2 соответственно, если сводные значения находятся в C1 C_{1 } C1 находится слева от точки поворота в C2 C_{2}C2, тогда R1 R_{1} R1 выше R2 R_{2} R2. Другими словами, для любых двух опорных точек P1 P_{1}P1 и P2P_{2}P2, если P2 P_{2}P2 находится справа от P1 P_{1}P1, то P2 P_{2} P2 ниже P1 P_{1}P1.
- Строки, состоящие только из нулей, находятся внизу матрицы.
Чтобы преобразовать любую матрицу в ее уменьшенную ступенчатую форму строк, выполняется исключение Гаусса-Жордана. Существуют три элементарные операции со строками, используемые для получения формы уменьшенного эшелона строк:
- Переключить две строки.
- Умножить строку на любую ненулевую константу.
- Добавить скалярное число, кратное одной строке, к любой другой строке.
Найдите rref(A) \text{rref}(A)rref(A) методом исключения Гаусса-Жордана, где А=[26−216−4−149]. A = \left[ \begin{массив}{c c c} 2 и 6 и -2\\ 1 и 6 и -4 \\ -1 и 4 и 9 \\ \end{массив}\right].A=⎣⎡21−1664−2−49⎦⎤.
Крайний левый элемент в первой строке должен быть равен 1, поэтому первая строка делится на 2:
[26−216−4−149]→Разделить первую строку на 2.[13−116−4−149]. \left[ \begin{массив}{c c c} 2 и 6 и -2\\ 1 и 6 и -4 \\ -1 и 4 и 9 \\ \конец{массив}\справа] \ce{->[\large \text{Разделить первую строку на 2.
}]} \left[ \begin{массив}{c c c} 1 и 3 и -1\\ 1 и 6 и -4 \\ -1 и 4 и 9\\ \end{массив}\right]. ⎣⎡21−1664−2−49⎦⎤Разделите первую строку на 2.⎣⎡11−1 364−1−49⎦⎤.
Верхний левый элемент является опорным, поэтому остальные элементы в первом столбце должны быть равны 0. Это можно сделать, вычитая первую строку из второй строки. Кроме того, первую строку можно добавить к третьей строке, чтобы получить необходимые нули в первом столбце:
.[13−116−4−149]→RX2−RX1 и RX3+RX1[13−103−3078]. \left[ \begin{массив}{c c c} 1 и 3 и -1\\ 1 и 6 и -4 \\ -1 и 4 и 9\\ \конец{массив}\справа] \ce{->[\large R_2 — R_1 \text{ и } R_3 + R_1]} \left[ \begin{массив}{c c c} 1 и 3 и -1\\ 0 и 3 и -3 \\ 0 и 7 и 8 \\ \end{массив}\right]. ⎣⎡11−1364−1−49⎦⎤RX2−RX1 и RX3+RX1⎣⎡100 337−1−38⎦⎤.
Теперь, когда крайний левый столбец равен [100], \left[ \begin{array}{c} 1\\ 0 \\ 0 \\ \end{array}\right], ⎣⎡100⎦⎤, средний элемент можно сделать равным 1, разделив вторую строку на 3:
[13−103−3078]→ Разделить вторую строку на 3 [13−101−1078].
\left[ \begin{массив}{c c c} 1 и 3 и -1\\ 0 и 3 и -3 \\ 0 и 7 и 8 \\ \конец{массив}\справа] \ce{->[\large \text{Поделить вторую строку на 3.}]} \left[ \begin{массив}{c c c} 1 и 3 и -1\\ 0 и 1 и -1 \\ 0 и 7 и 8 \\ \end{массив}\right]. ⎣⎡100337−1−38⎦⎤Поделите вторую строку на 3.⎣⎡100 317−1−18⎦⎤.
Верхний и нижний элементы во втором столбце можно сделать равными 0 с помощью соответствующих операций над строками:
[13−101−1078]→RX1−3 RX2 и RX3−7 RX2[10201−10015]. \left[ \begin{массив}{c c c} 1 и 3 и -1\\ 0 и 1 и -1 \\ 0 и 7 и 8 \\ \конец{массив}\справа] \ce{->[\large R_1 — 3R_2 \text{ и } R_3 — 7R_2]} \left[ \begin{массив}{c c c} 1 и 0 и 2\\ 0 и 1 и -1 \\ 0 и 0 и 15 \\ \end{массив}\right]. ⎣⎡100317−1−18⎦⎤RX1−3RX2 и RX3−7RX2⎣⎡100 0102−115⎦⎤.
Теперь средний столбец [010], \left[ \begin{array}{c} 0 \\ 1\\ 0 \\ \end{array}\right], ⎣⎡010⎦⎤, метод переходит к третьему столбцу путем деления третьей строки на 15:
[10201−10015]→ Разделить третью строку на 15.
[10201−1001]. \left[ \begin{массив}{c c c} 1 и 0 и 2\\ 0 и 1 и -1 \\ 0 и 0 и 15 \\ \конец{массив}\справа] \ce{->[\large \text{Разделим третью строку на 15.} ]} \left[ \begin{массив}{c c c} 1 и 0 и 2\\ 0 и 1 и -1 \\ 0 и 0 и 1 \\ \end{массив}\right]. ⎣⎡1000102−115⎦⎤Разделите третью строку на 15.⎣⎡100 0102−11⎦⎤.
На последнем этапе процесса к первой и второй строкам добавляются числа, кратные третьей строке, так что последний столбец становится [001]: \left[ \begin{array}{c} 0 \\ 0 \\ 1\\ \end{массив}\right]: ⎣⎡001⎦⎤:
[10201−1001]→RX1−2 RX3 и RX2+RX3 ⋅ [100010001]. □ \left[ \begin{массив}{c c c} 1 и 0 и 2\\ 0 и 1 и -1 \\ 0 и 0 и 1 \\ \конец{массив}\справа] \ce{->[\large R_1 — 2R_3 \text{ и } R_2 + R_3. ]} \left[ \begin{массив}{c c c} 1 и 0 и 0\\ 0 и 1 и 0 \\ 0 и 0 и 1 \\ \end{массив}\right]. \ _\площадь ⎣⎡1000102−11⎦⎤RX1−2RX3 и RX2+RX3⋅⎣⎡100010001⎦⎤. □
A = [14−564022−1] A = \left[ \begin{array}{ccc} 1 и 4 и -5 \\ 6 и 4 и 0 \\ 2&2&-1\ \end{array} \right] A=⎣⎡162442−50−1⎦⎤
Какова сумма всех элементов в rref(A)? \text{rref}(A)?rref(A)?
Примечание : rref(A)\text{rref}(A) rref(A) обозначает «эшелонированную форму сокращенной строки» матрицы A.

 ..
..
 Точные методы представляют собой конечные алгоритмы для вычисления корней системы. Это — метод обратной матрицы, метод Крамера, метод Гаусса, метод Жордана-Гаусса, метод главных элементов, метод квадратных корней и др. Несмотря на то, что методы называются точными, результаты вычислений имеют погрешности вследствие неизбежных округлений при выполнении действий.
Точные методы представляют собой конечные алгоритмы для вычисления корней системы. Это — метод обратной матрицы, метод Крамера, метод Гаусса, метод Жордана-Гаусса, метод главных элементов, метод квадратных корней и др. Несмотря на то, что методы называются точными, результаты вычислений имеют погрешности вследствие неизбежных округлений при выполнении действий.
 Если число велико, то вычисление определителей является трудоемкой задачей.
Если число велико, то вычисление определителей является трудоемкой задачей. Подставив полученное значение х2 в первое уравнение, можем вычислить и первое неизвестное х1.
Подставив полученное значение х2 в первое уравнение, можем вычислить и первое неизвестное х1.
 д. уравнений коэффициенты второго столбца лежащие ниже
д. уравнений коэффициенты второго столбца лежащие ниже После решения системы уравнений методом Гаусса необходимо делать проверку, подставляя в исходные уравнения найденные значения переменных хi (i= 1, …, n).
После решения системы уравнений методом Гаусса необходимо делать проверку, подставляя в исходные уравнения найденные значения переменных хi (i= 1, …, n). Число шагов преобразований в “прямом ходе” методом Гаусса равно n-1.
Число шагов преобразований в “прямом ходе” методом Гаусса равно n-1.

 Сначала вычисляются элементы первого столбца матрицы L делением на ведущий элемент а11, затем после первого шага “прямым ходом” метода Гаусса вычисляются элементы второго столбца, начиная с диагонального, делением на ведущий элемент а11 и т.д.
Сначала вычисляются элементы первого столбца матрицы L делением на ведущий элемент а11, затем после первого шага “прямым ходом” метода Гаусса вычисляются элементы второго столбца, начиная с диагонального, делением на ведущий элемент а11 и т.д.
 д. Определяются все Z. Затем аналогично решается вторая треугольная подсистема Wx=Z путем обратной подстановки, начиная с хn (аналогично обратному ходу методом Гаусса).
д. Определяются все Z. Затем аналогично решается вторая треугольная подсистема Wx=Z путем обратной подстановки, начиная с хn (аналогично обратному ходу методом Гаусса).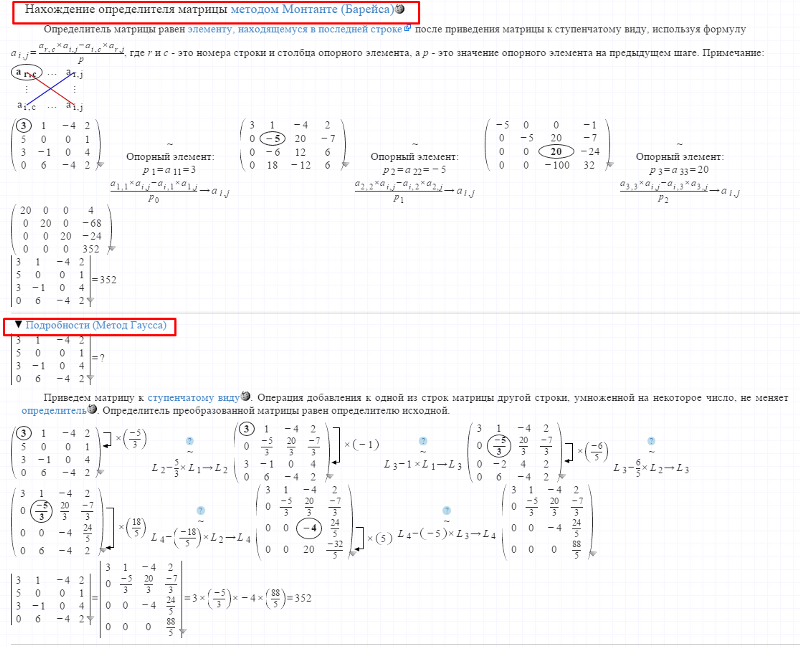 .
.


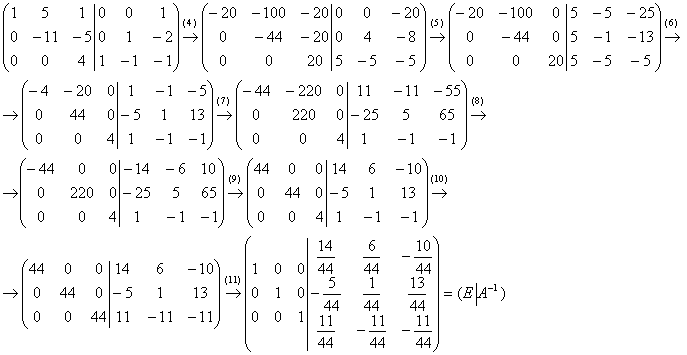



 250
250 565
565 2781
2781 046
046 582
582 229
229 937
937 250
250 340
340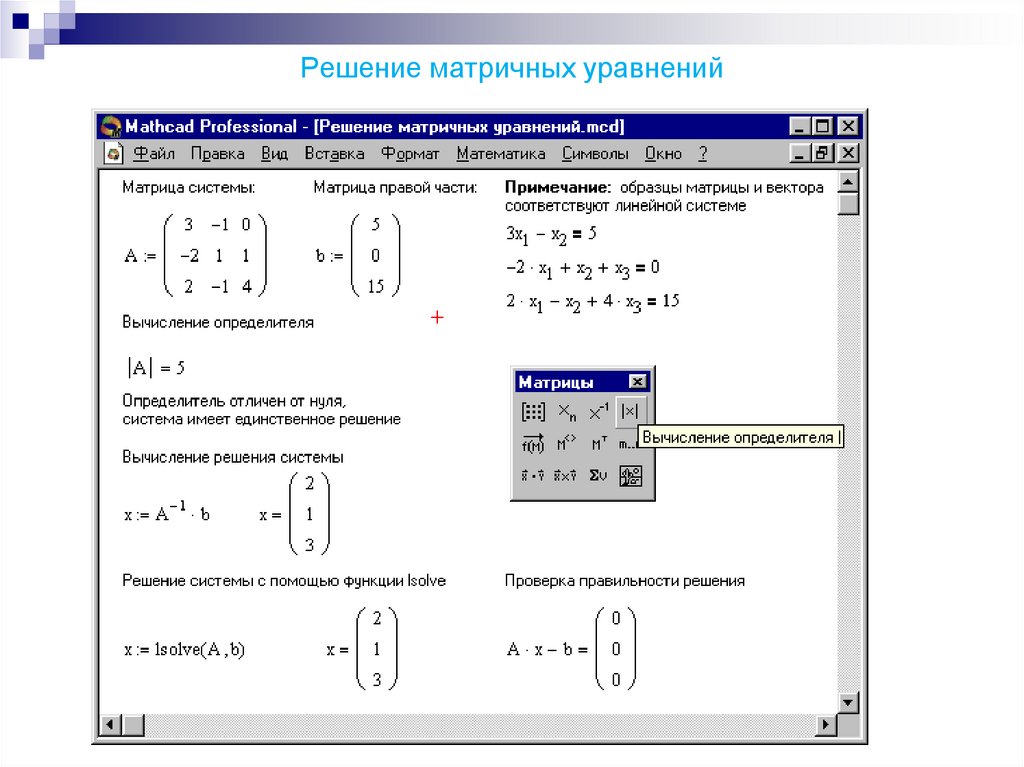 157
157
 $R_3 \rightarrow R_2$ и $R_2 \rightarrow R_3$.
$R_3 \rightarrow R_2$ и $R_2 \rightarrow R_3$. 116)
116)  линейная система уравнений. Мы также можем использовать его, чтобы найти обратную обратимую матрицу. Давайте сначала посмотрим на определение:
линейная система уравнений. Мы также можем использовать его, чтобы найти обратную обратимую матрицу. Давайте сначала посмотрим на определение:


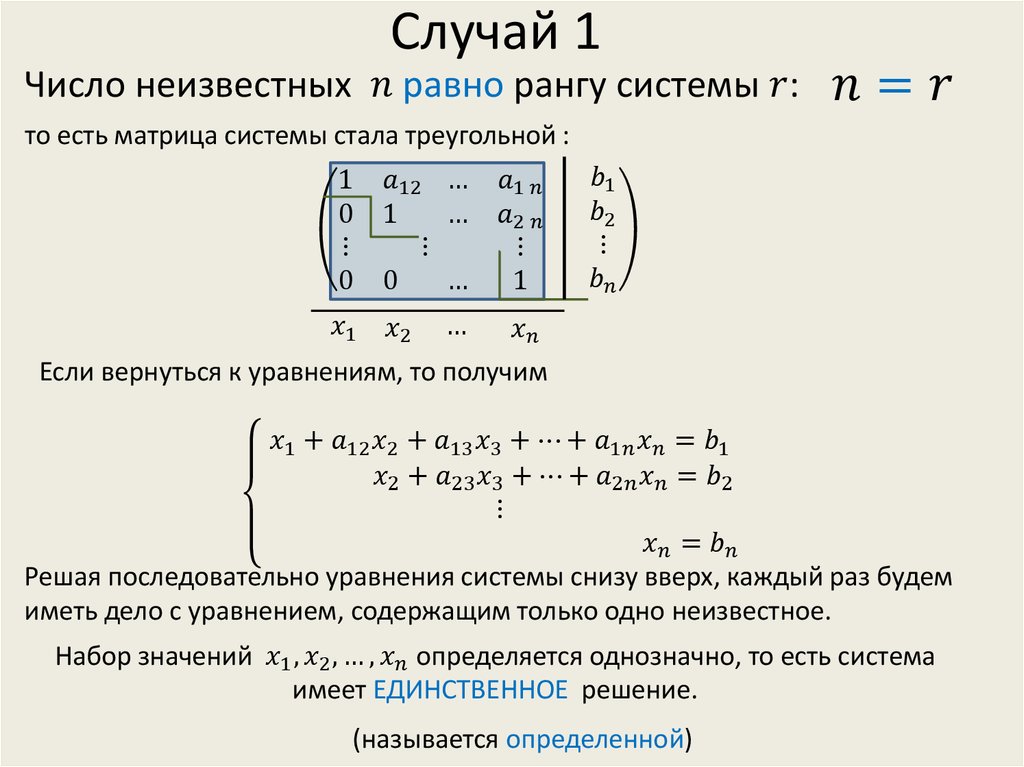 Существует также фактор интуиции , который играет БОЛЬШУЮ роль в выполнении метода исключения Гаусса-Жордана.
Существует также фактор интуиции , который играет БОЛЬШУЮ роль в выполнении метода исключения Гаусса-Жордана. Ниже показано:
Ниже показано: Из расширенной матрицы мы можем написать два уравнения (решения):
Из расширенной матрицы мы можем написать два уравнения (решения): Из расширенной матрицы мы можем написать два уравнения (решения):
Из расширенной матрицы мы можем написать два уравнения (решения):

 Из этой дополненной матрицы мы можем написать два уравнения (решения):
Из этой дополненной матрицы мы можем написать два уравнения (решения):
 Итак, расширенная матрица, которую мы получаем, выглядит следующим образом:
Итак, расширенная матрица, которую мы получаем, выглядит следующим образом:

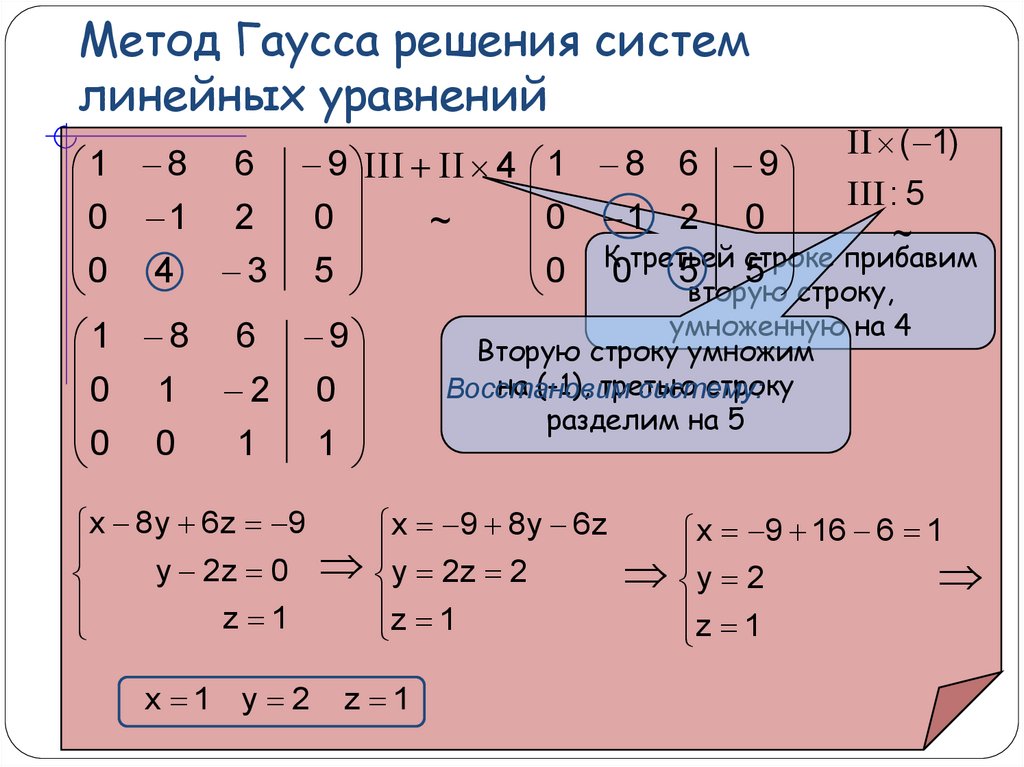

 Рассмотрим вышеприведенную систему еще раз,
Рассмотрим вышеприведенную систему еще раз,
 Используйте операцию со строками, чтобы сделать эту запись 1. Используйте операции со строками, чтобы сделать все остальные записи нулями во втором столбце.
Используйте операцию со строками, чтобы сделать эту запись 1. Используйте операции со строками, чтобы сделать все остальные записи нулями во втором столбце.
 Нам нужно сделать эту запись (–3) равной 1, а все остальные записи в этом столбце сделать нулями. Чтобы сделать строку 2, столбец 2 равным 1, мы делим всю вторую строку на -3.
Нам нужно сделать эту запись (–3) равной 1, а все остальные записи в этом столбце сделать нулями. Чтобы сделать строку 2, столбец 2 равным 1, мы делим всю вторую строку на -3.

 deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
deanza.edu/faculty/bloomroberta/math21/afm3files.html.html


 Поворот на единицу означает, что вы умножаете на 1 (что легко сделать).
Поворот на единицу означает, что вы умножаете на 1 (что легко сделать). Это тот вариант, который я собираюсь использовать. я повернусь
на тройке в R 1 C 1 . Идите вперед и обведите это как опорный элемент. В зависимости от вашего браузера вы
могут видеть элементы поворота, обведенные красным или просто с * перед ним.
Это тот вариант, который я собираюсь использовать. я повернусь
на тройке в R 1 C 1 . Идите вперед и обведите это как опорный элемент. В зависимости от вашего браузера вы
могут видеть элементы поворота, обведенные красным или просто с * перед ним.




 Будьте внимательны
в 3-ю строку, где мы вычитаем -19 раз значение. Поскольку мы вычитаем
минус, я пошел дальше и написал плюс 19.
Будьте внимательны
в 3-ю строку, где мы вычитаем -19 раз значение. Поскольку мы вычитаем
минус, я пошел дальше и написал плюс 19.
 Итак, мы начнем с 1 в R 3 C 3 и очистим -18 и 17. Обведите ваш центр и обведите остальные числа
этот столбец, чтобы очистить.
Итак, мы начнем с 1 в R 3 C 3 и очистим -18 и 17. Обведите ваш центр и обведите остальные числа
этот столбец, чтобы очистить. Вот
расчеты для этой опоры. Опять же, поскольку значение в сводном столбце в
первая строка -18 и мы вычитаем, я написал это как + 18.
Вот
расчеты для этой опоры. Опять же, поскольку значение в сводном столбце в
первая строка -18 и мы вычитаем, я написал это как + 18.
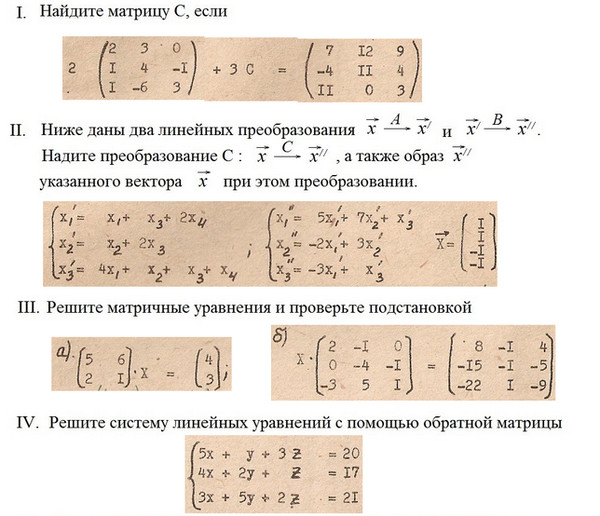 Вы также можете записать это как
упорядоченная тройка {(3,1,2)}.
Вы также можете записать это как
упорядоченная тройка {(3,1,2)}.
 Произведение матриц: 2x3x5x+++4y3y6y+++7z2z3z===480⟶⎣⎡235436723⎦⎤⎣⎡xyz⎦⎤=⎣⎡480 ⎦⎤.
Произведение матриц: 2x3x5x+++4y3y6y+++7z2z3z===480⟶⎣⎡235436723⎦⎤⎣⎡xyz⎦⎤=⎣⎡480 ⎦⎤. Методы сокращения строк преобразуют матрицу в сокращенную эшелонированную форму строк без изменения решений системы.
Методы сокращения строк преобразуют матрицу в сокращенную эшелонированную форму строк без изменения решений системы.
 }]}
\left[ \begin{массив}{c c c}
1 и 3 и -1\\
1 и 6 и -4 \\
-1 и 4 и 9\\
\end{массив}\right].
⎣⎡21−1664−2−49⎦⎤Разделите первую строку на 2.⎣⎡11−1 364−1−49⎦⎤.
}]}
\left[ \begin{массив}{c c c}
1 и 3 и -1\\
1 и 6 и -4 \\
-1 и 4 и 9\\
\end{массив}\right].
⎣⎡21−1664−2−49⎦⎤Разделите первую строку на 2.⎣⎡11−1 364−1−49⎦⎤. \left[ \begin{массив}{c c c}
1 и 3 и -1\\
0 и 3 и -3 \\
0 и 7 и 8 \\
\конец{массив}\справа]
\ce{->[\large \text{Поделить вторую строку на 3.}]}
\left[ \begin{массив}{c c c}
1 и 3 и -1\\
0 и 1 и -1 \\
0 и 7 и 8 \\
\end{массив}\right].
⎣⎡100337−1−38⎦⎤Поделите вторую строку на 3.⎣⎡100 317−1−18⎦⎤.
\left[ \begin{массив}{c c c}
1 и 3 и -1\\
0 и 3 и -3 \\
0 и 7 и 8 \\
\конец{массив}\справа]
\ce{->[\large \text{Поделить вторую строку на 3.}]}
\left[ \begin{массив}{c c c}
1 и 3 и -1\\
0 и 1 и -1 \\
0 и 7 и 8 \\
\end{массив}\right].
⎣⎡100337−1−38⎦⎤Поделите вторую строку на 3.⎣⎡100 317−1−18⎦⎤. [10201−1001]. \left[ \begin{массив}{c c c}
1 и 0 и 2\\
0 и 1 и -1 \\
0 и 0 и 15 \\
\конец{массив}\справа]
\ce{->[\large \text{Разделим третью строку на 15.} ]}
\left[ \begin{массив}{c c c}
1 и 0 и 2\\
0 и 1 и -1 \\
0 и 0 и 1 \\
\end{массив}\right].
⎣⎡1000102−115⎦⎤Разделите третью строку на 15.⎣⎡100 0102−11⎦⎤.
[10201−1001]. \left[ \begin{массив}{c c c}
1 и 0 и 2\\
0 и 1 и -1 \\
0 и 0 и 15 \\
\конец{массив}\справа]
\ce{->[\large \text{Разделим третью строку на 15.} ]}
\left[ \begin{массив}{c c c}
1 и 0 и 2\\
0 и 1 и -1 \\
0 и 0 и 1 \\
\end{массив}\right].
⎣⎡1000102−115⎦⎤Разделите третью строку на 15.⎣⎡100 0102−11⎦⎤.