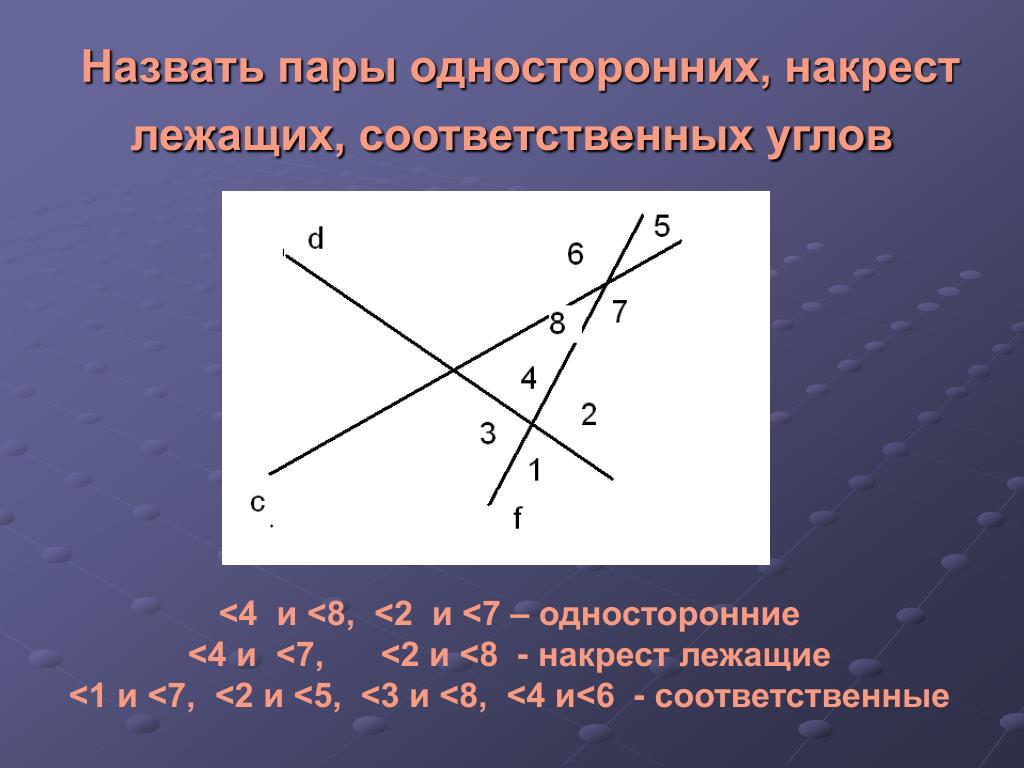
Соответственные углы равны. Соответственные углы при параллельных прямых.
- Альфашкола
- Статьи
- Соответственные углы
В геометрии пары углов могут относиться друг к другу различными способами. В этом статье мы научимся определять соответственные углы.
Соответствующие пары углов на приведенном выше рисунке: \( b <—> f; c <—> g ; a <—> e.\)
Секущая — это прямая линия, пересекающая две или более прямых линий. Соответственные углы — это углы, которые находятся в одном и том же относительном положении на пересечении поперечной и по крайней мере двух линий.
Если две линии параллельны, то соответственные углы равны.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Ирина Евгеньевна Русакова
Репетитор по математике
Стаж (лет)
Образование:
Пермский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 5-11 классов и информатике для 1-11 классов. Готовлю к ОГЭ, ЕГЭ. Окончила Пермский государственный университет в 2009 году. Педагогический стаж 10 лет. Квалификационная категория Первая. Педагогическое кредо: Скажи мне, и я забуду, покажи мне, и я, может быть запомню, вовлеки меня, и я пойму. Алгоритмика для начальных классов: могу научить детей начальной школы правильно составлять алгоритмы. Составлять алгоритмы для простых исполнителей, рисовать картинки определенные с помощью алгоритма исполнителю и др.
Готовлю к ОГЭ, ЕГЭ. Окончила Пермский государственный университет в 2009 году. Педагогический стаж 10 лет. Квалификационная категория Первая. Педагогическое кредо: Скажи мне, и я забуду, покажи мне, и я, может быть запомню, вовлеки меня, и я пойму. Алгоритмика для начальных классов: могу научить детей начальной школы правильно составлять алгоритмы. Составлять алгоритмы для простых исполнителей, рисовать картинки определенные с помощью алгоритма исполнителю и др.
Виктория Анатольевна Луковская
Репетитор по математике
Стаж (лет)
Образование:
Таганрогский педагогический институт им. А.П. Чехова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 4-11 классов. Математика дисциплинирует и воспитывает ум, это основа для всех наук. Очень люблю работать с детьми! Уроки проходят в комфортной обстановке, к каждому ученику подхожу индивидуально, объясняю доступно и понятно. На занятиях применяю игровые приемы, схемы, графики и презентации, для того, чтобы учащимся было интересно.
Математика дисциплинирует и воспитывает ум, это основа для всех наук. Очень люблю работать с детьми! Уроки проходят в комфортной обстановке, к каждому ученику подхожу индивидуально, объясняю доступно и понятно. На занятиях применяю игровые приемы, схемы, графики и презентации, для того, чтобы учащимся было интересно.
Жанна Александровна Бояркина
Репетитор по математике
Стаж (лет)
Образование:
Благовещенский государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов. Всегда готова поделиться знаниями! Считаю, что учить наизусть скучные правила необязательно. Главное — понимать что и как, тогда ученик и без скучных заучиваний сможет свободно сформулировать любое правило, а полученные знания будут прочными и навсегда.
Готовлю к ОГЭ и ЕГЭ, мои ученики показывают хорошие и отличные результаты на экзаменах.
На уроках придерживаюсь трех единств: наглядно, понятно, просто.
Всегда готова поделиться знаниями! Считаю, что учить наизусть скучные правила необязательно. Главное — понимать что и как, тогда ученик и без скучных заучиваний сможет свободно сформулировать любое правило, а полученные знания будут прочными и навсегда.
Готовлю к ОГЭ и ЕГЭ, мои ученики показывают хорошие и отличные результаты на экзаменах.
На уроках придерживаюсь трех единств: наглядно, понятно, просто.
Похожие статьи
- Жизни математиков (часть 1)
- Формула площади эллипса
- РУДН: Физика (факультет)
- 3 причины изучать математику, даже если вы убежденный «гуманитарий»
- Уравнения смешанного типа
- ЕГЭ по математике, базовый уровень. Задачи на исследование функций (вариант 4)
- Зелень в рационе ребенка: когда и какую можно давать
- Как использовать материнский капитал на образование: полная инструкция для родителей
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Основы планиметрии.
 Точка, прямая, луч, отрезок и уголНа этой странице вы узнаете
Точка, прямая, луч, отрезок и уголНа этой странице вы узнаете- Что общего у солнечного луча и геометрического?
- Можно ли кого-то наказать углом?
- Одинаковы ли прямые?
В жизни мы часто встречаемся с такими выражениями как “точка на карте”, “идти по прямой” или “угол комнаты”. Но знали ли вы, что в этих фразах упоминаются термины из геометрии?
Для начала давайте разберемся именно с геометрическими терминами.
Что такое точка, прямая, луч, отрезок и угол?
Точка – это математический объект, точного определения для которого не существует.
Прямая – это бесконечная линия.
Луч – это прямая, ограниченная точкой с одной стороны. У луча есть начало, но нет конца.
| Что общего у солнечного луча и геометрического? Солнечный луч и геометрический луч отличаются друг от друга почти во всем. |
Отрезок – это прямая, ограниченная точками с обеих сторон. Отрезок состоит из бесконечного множества точек, лежащих на линии между концами отрезка.
Чем отличается луч от отрезка?
Луч ограничен только с одной стороны, а отрезок ограничен с двух.
Угол – это фигура, образованная двумя лучами, исходящими из одной точки.
| Можно ли кого-то наказать углом? Провинившегося ребенка могут поставить в угол. Возможно ли поставить кого-то в геометрический угол? Да. Для такого наказания можно использовать не только прямой угол, но и тупой, и даже некоторые острые углы. Только, пожалуй, не очень узкие острые углы, иначе человек туда просто не поместится. |
Давайте детально рассмотрим углы
Элементы угла
Виды углов и их градусная мера
Существует четыре вида углов.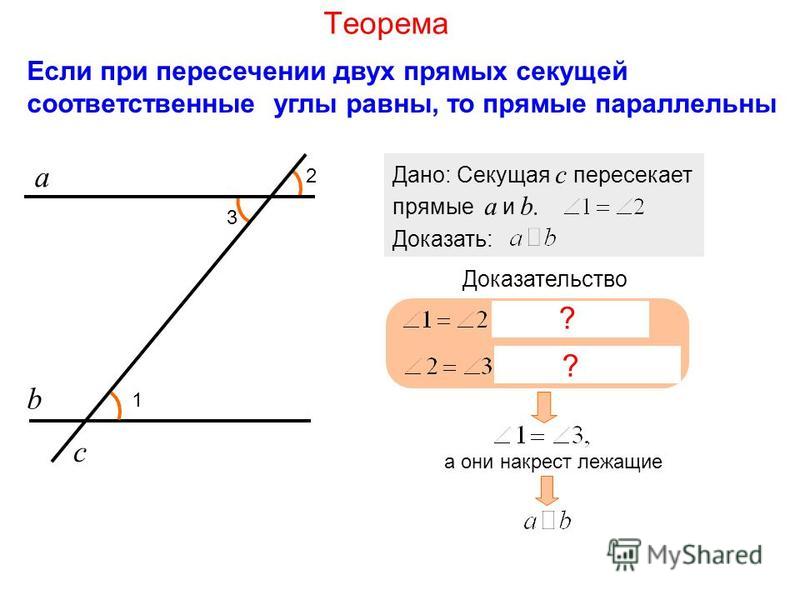
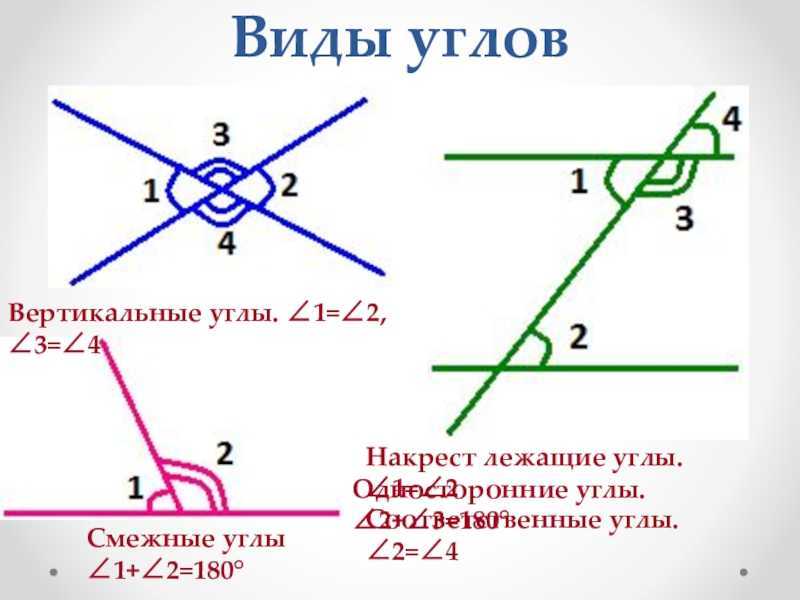
Смежные и вертикальные углы
Смежные углы – это два угла, у которых одна общая сторона, а две другие лежат на одной прямой. Такие углы в сумме дают 1800.
Вертикальные углы – это углы, вершиной которых является одна и та же точка, стороны одного такого угла являются продолжениями сторон другого такого угла. Вертикальные углы всегда равны.
Теперь давайте перейдём к прямым и их расположению на плоскости.
Пересекающиеся и параллельные прямые
Пересекающиеся прямые – это прямые, у которых есть одна общая точка.
Перпендикулярные прямые – это прямые, пересекающиеся под прямым углом. Такие прямые образуют четыре прямых угла при пересечении.
А что такое параллельные прямые?
Параллельные прямые – это прямые, не имеющие ни одной общей точки.
Параллельные и перпендикулярные прямые можно встретить не только в планиметрии, но и в повседневной жизни, например, рельсы и шпалы.
| Одинаковы ли прямые? Какие могут быть прямые на плоскости? |
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Следствия из аксиомы параллельных прямых:
- Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую параллельную прямую.
- Если одна из двух параллельных прямых параллельна третьей прямой, то все эти прямые параллельны друг другу.
Чтобы доказать, что прямые являются параллельными, используются признаки параллельности прямых.
Прежде чем перейти к признакам параллельности прямых, рассмотрим углы при пересечении двух прямых секущей.
Секущая – это прямая, пересекающая несколько других прямых.
При таком расположении прямых можно выделить три вида углов:
- накрест лежащие углы,
- односторонние углы,
- соответственные углы.

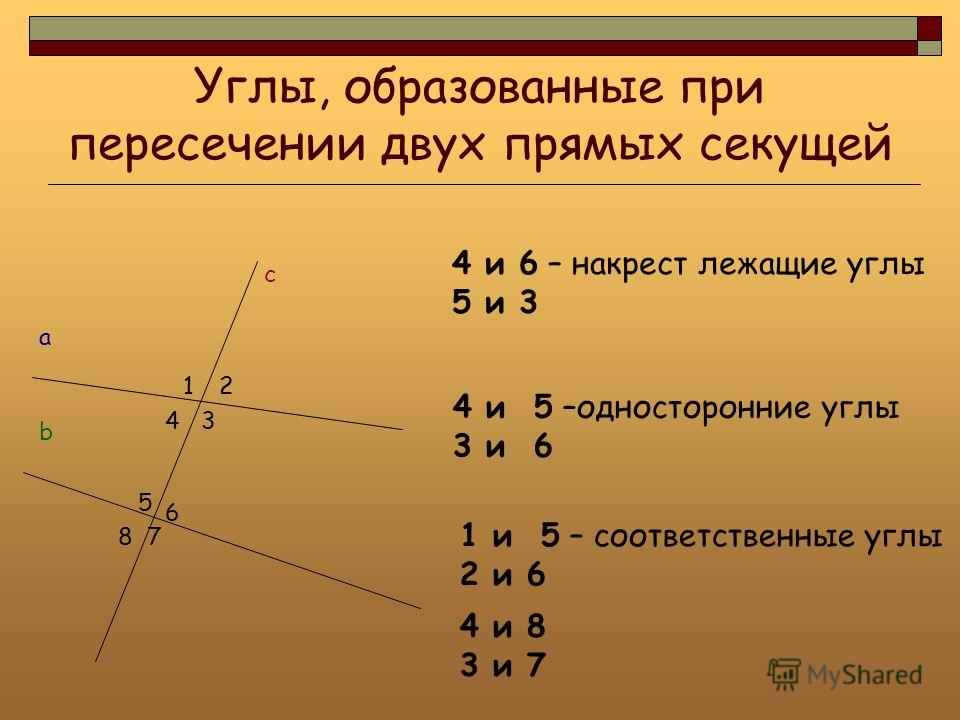
Рассмотрим данные углы на примере
Накрест лежащие: 4 и 6, 3 и 5.
Односторонние: 4 и 5, 3 и 6.
Соответственные: 1 и 5, 4 и 8, 2 и 6, 3 и 7.
А теперь вернёмся к признакам
Признаки параллельности прямых:
Теорема 1:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Теорема 2:
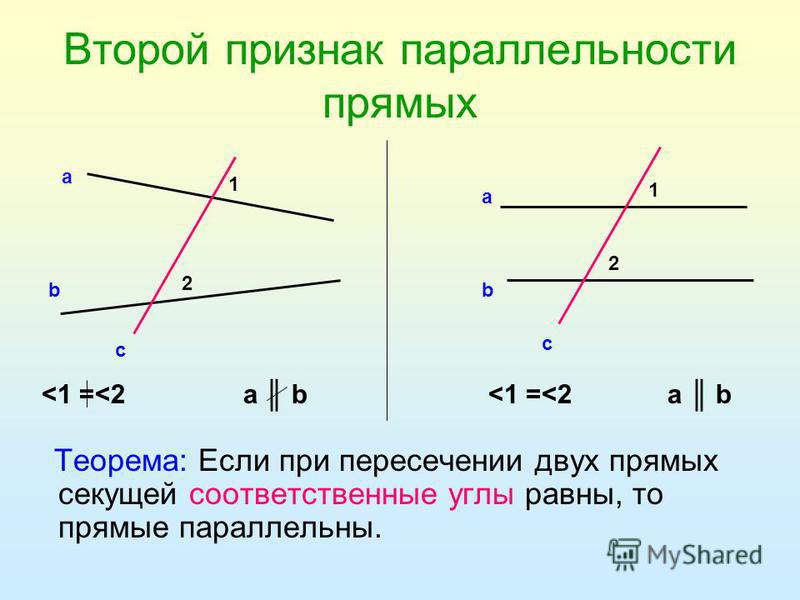
Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.
Теорема 3:
Если при пересечении двух прямых секущей сумма односторонних углов равна 1800,то прямые параллельны.
Также существуют свойства параллельности прямых. Что мы назовем свойствами параллельности прямых?
Удивительно, но это те же самые признаки, только ставшие перевертышами. Свойства действуют в обратную сторону. Посмотрим, какие свойства параллельных прямых бывают:
- Если прямые параллельны, то при пересечении этих прямых секущей накрест лежащие углы равны.

- Если прямые параллельны, то при пересечении этих прямых секущей соответственные углы равны.
- Если прямые параллельны, то при пересечении этих прямых секущей сумма односторонних углов равна 1800.
- Основными геометрическими элементами являются точка, прямая, луч, отрезок, угол.
- Углы бывают смежные и вертикальные.
- Прямые бывают пересекающиеся и параллельные. К пересекающимся прямым относятся и перпендикулярные прямые.
- Углы при пересечении двух прямых секущей: накрест лежащие, односторонние и соответственные.
- Для определения параллельных прямых существует три признака. Также существуют и свойства параллельных прямых, которыми являются обратные признакам утверждения.
Аксиома – это утверждение, не требующее доказательства.
Проверь себяЗадание 1.
Какими углами являются углы 1 и 2?
- Вертикальными
- Накрест лежащими
- Смежными
- Односторонними
Задание 2.
Какими углами являются углы 4 и 8?
- Вертикальными
- Соответственными
- Смежными
- Односторонними
Задание 3.
Угол 4 равен 600. Чему равен угол 5?
- 1200
- 600
- 300
- 200
Задание 4.
Угол 4 равен 600. Чему равен угол 7?
- 1200
- 600
- 300
- 200
Задание 5.
Угол 5 равен 500. Чему равен угол 8?
- 1500
- 650
- 1300
- 500
Ответы: 1. – 3; 2. – 2; 3. – 2; 4. – 1; 5. – 4
урок геометрии по теме «Соответственные углы»
org/Person»>Герман Евгения Николаевна, учитель математикиКиренского района Иркутской области
Цели урока: Триединая дидактическая цель: Цель обучения:формирование понятия «соответственные углы»; организация работы обучающихся по отработке действий по формированию понятия: распознавания, выведение следствий из факта принадлежности объекта объему данного понятия. Цель развития: формирование у обучающихся мыслительных операций: сравнения и аналогии, развитие устной и письменной речи обучающихся, развитие алгоритмического мышления, формирование и развитие умственных действий распознавания и выведения следствия. Цель воспитания: воспитание потребностей в приобретении и углублении знаний, обеспечение учебного сотрудничества с учителем. Методы обучения:репродуктивный, объяснительно-иллюстративный. Приемы обучения: использование заданий наводящих вопросов, побуждающих к актуализации знаний, объяснение, демонстрация, показ.
Посмотреть публикацию
Скачать свидетельство о публикации(справка о публикации находится на 2 листе в файле со свидетельством)
Скачать справку о публикации
Ваши документы готовы. Если у вас не получается скачать их, открыть или вы допустили ошибку, просьба написать нам на электронную почту [email protected] (обязательно укажите номер публикации в письме)
Если у вас не получается скачать их, открыть или вы допустили ошибку, просьба написать нам на электронную почту [email protected] (обязательно укажите номер публикации в письме)
ПЛАН ПО ФОРМИРОВАНИЮ ПОНЯТИЯ
Тема урока: Соответственные углы.
Класс: 7
Тип урока: урок формирования понятий – соответственные углы.
Цели урока:
Триединая дидактическая цель:
Цель обучения:формирование понятия «соответственные углы»; организация работы обучающихся по отработке действий по формированию понятия: распознавания, выведение следствий из факта принадлежности объекта объему данного понятия.
Цель развития: формирование у обучающихся мыслительных операций: сравнения и аналогии, развитие устной и письменной речи обучающихся, развитие алгоритмического мышления, формирование и развитие умственных действий распознавания и выведения следствия.
Цель воспитания: воспитание потребностей в приобретении и углублении знаний, обеспечение учебного сотрудничества с учителем.
Методы обучения: репродуктивный, объяснительно-иллюстративный.
1. ПОДГОТОВИТЕЛЬНЫЙ ЭТАП
Цель: актуализация понятий: плоскость, полуплоскость, угол, виды углов, параллельные прямые.
Актуализация умений: определять расположение точек относительно прямой
Метод обучения: репродуктивный.
Прием обучения: фронтальный опрос с использованием тренировочных карточек.
У: Рисуем в тетрадях область, ограниченную плавной линией. Какую фигуру мы договорились обозначать подобным образом?
О: плоскость
У: Какие еще предметы напоминают нам плоскость? Чем характеризуется плоскость?
О: Поверхность парты, тетрадный лист. Плоскость распространяется во все стороны неограниченно.
У: Обозначим нашу плоскость греческой буквой α. При помощи линейки проводим прямую, разделяющую нашу плоскость на две части и дадим этой прямой имя а.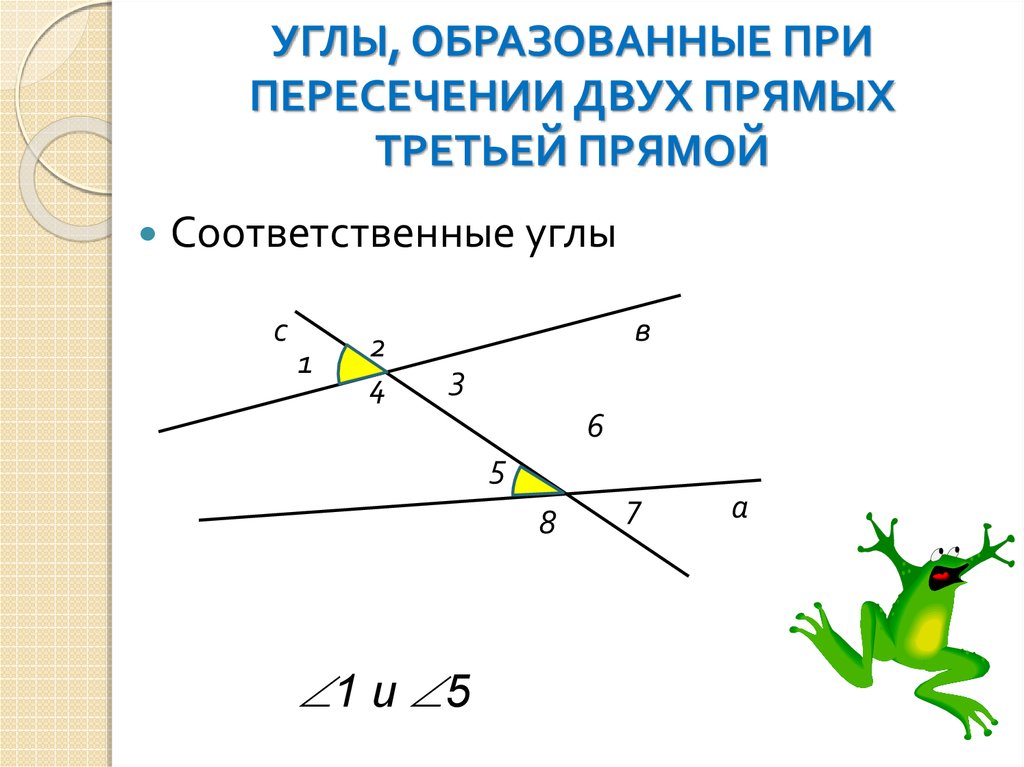
О: А принадлежит а, В принадлежит а;
Е принадлежит γ, F принадлежит γ;
С принадлежит β, D принадлежит β.
У: А теперь самостоятельно определим соотношение полуплоскостей, прямой и точек по отношению друг к другу, выполнив задание на карточке.
Задание: определите расположение точек относительной прямой и полуплоскостей? Ответ: точки___________принадлежат полуплоскости_____________ точки___________принадлежат полуплоскости_____________ точки___________принадлежат прямой____________________ |
У: Проверяем выполнение карточки, озвучивая ответ с места. Какая геометрическая фигура называется углом?
О: Углом называется фигура на плоскости, состоящая из точки – вершины и двух лучей – сторон, выходящих из этой вершины.
У: Какие виды углов вам известны?
О: Углы, отличающиеся по градусной мере (тупой, острый, прямой и развернутый – углы «одиночки») и вертикальные и смежные- «парные углы»
У: Определите виды углов, представленные на рисунке:
Задание: определите виды углов( по одному примеру)? Тупой угол___ВСА_______ Острый угол__CBD_______ Развернутый угол__ABD______ Прямой угол___-_______ Смежные углы__ABC, CBD__________ Вертикальные углы_BDC, EDF__________ |
Во время выполнения задания, учитель проверяет правильность выполнения карточки.
У: Какие прямые называются параллельными?
О: две прямые называются параллельными, если они не пересекаются.
2. МОТИВАЦИОННЫЙ ЭТАП
Цель: побуждение интереса к изучению понятия соответственные углы.
Прием мотивации: показ практической значимости правильного определения параллельности.
Прием обучения: создание ситуации, свидетельствующей о недостатке знаний.
Оборудование: презентация.
НА слайде представлены фотографии разрушенного дома, автомобильной аварии.
У: Вот к таким последствиям может привести несоблюдение принципа параллельности при возведении и сооружении объектов жизнеобеспечения. Так при постройке дома, если элементы (каркас) здания располагаются не параллельно, это влияет на прочность здания.
Дорожная размета в виде полос, разграничивающих встречные потоки и область проезжей части, проведенных не параллельно друг к другу приводит к аварии. Кроме того, электропровода, натянутые не параллельно друг к другу, могут сомкнуться, что приведет к замыканию, а, следовательно, и к прекращению подачи электроэнергии и в худшем случае, к пожару.
Возникает вопрос, как определить, что некоторые прямые, являются параллельными? Геометрия дает ответ на данный вопрос при помощи работы с углами, градусную меру которых вычислить на практике значительно проще.
.
ОРИЕНТИРОВОЧНЫЙ ЭТАП
Цель: ввести определение и организовать работу обучающихся по усвоению понятия «соответственные углы».
Метод обучение: объяснительно-иллюстративный.
Приемы обучения: демонстрация, показ, объяснение.
А) Введение определения
Цель: ввести определение понятия «соответственные углы»
Способ: конкретно-индуктивный.
У: Изобразим плоскость. Разделим нашу плоскость прямой, а на две полуплоскости и дадим им имена β и γ. Отметим на этой прямой две точки А и В. В плоскости β также отметим две точки, назовем их C и D. Через точку А на прямой и точку C на полуплоскости проведем одну прямую, и через две оставшиеся точки проведем вторую прямую. Прямая а называется секущей прямых в и с.
Чем отличается секущая, от двух других прямых.
О: имеет две общих точки с этими двумя прямыми.
Отметим дугами углы 1 и 2 . Что мы можем сказать об этих углах относительно того, как они расположены по отношению к секущей а ?
О: расположены с одной стороны от секущей а в одной полуплоскости ,,.
У: что мы можем сказать о расположении этих углов относительно двух прямых, отличных от секущей?
О: они расположены по одну сторону от этих прямых.
У: Что является сторонами этих углов?
О: стороной угла 1 является секущая и прямая AD стороной угла 2 является эта же секущая и прямая ВС.
У: Итак, давайте подведем итог, о том, что
два угла,
образованные при пересечении двух прямых секущей, то есть расположенные между секущей и каждой из этих прямых;
расположенные в одной полуплоскости от общей секущей;
расположенные с одной стороны от двух прямых – называются соответственными.
А теперь дадим определение соответственным углам.
О: Соответственные углы – это два угла, образованные при пересечении двух прямых секущей, расположенные по одну сторону от прямых и в одной полуплоскости от общей секущей.
Б) Формирование ведущего действия – распознавание понятия соответственные углы
Цель: формировать действие распознавания соответственных углов.
Способ управления деятельностью: прямой.
Метод обучения: объяснительно-иллюстративный.
Представление в материализованном виде
У: Проверим, какие из углов являются соответственными.
пример | Проверка существенных признаков |
1 и 2 – это углы + Стороной угла 1 является секущая а и прямая в.+ Стороной угла 2 является секущая а и прямая с.+ Углы расположены по одну сторону от прямых в и с + Углы расположены в одной полуплоскости от секущей а+ Так как все признаки выполняются, следовательно, углы 1 и 2 являются соответственными. | |
1 и 2 – это углы+ Стороной угла 1 является секущая с и прямая а.+ Стороной угла 2 является эта же секущая с и прямая в.+ Углы расположены по одну сторону от прямых а и в + Углы расположены в одной полуплоскости от секущей с+ Так как все признаки выполняются, следовательно, углы 1 и 2 являются соответственными. | |
1 и 2 – это углы+ Прямая с не является секущей по отношению к прямым а и в, следовательно стороной углов 1 и 2 не может быть прямая, именуемая секущей Так как связь между существенными признаками конъюнктивная, и если один из признаков не выполняется, то нет смысла проверять выполнение остальных признаков и можно сделать вывод, что представленные углы не являются соответственными. | |
1 и 2 – это углы+ Стороной угла 1 является секущая с и прямая а.+ Стороной угла 2 является секущая с и прямая в.+ Углы расположены по одну сторону от прямых а и в- Так как связь между существенными признаками конъюнктивная, и если один из признаков не выполняется, то нет смысла проверять выполнение остальных признаков и можно сделать вывод, что представленные углы не являются соответственными. | |
1 и 2 – это углы+ Сторонами углов являются секущая с и две прямых а и в + Углы расположены по одну сторону от прямых а и в + Углы расположены в одной полуплоскости от секущей с- Так как связь между существенными признаками конъюнктивная, и если один из признаков не выполняется, следовательно данная пара углов не является соответственными |
Этап громкой и внутренней речи:
У: выполните задание на карточке
Определите, являются выделенные углы 1 и 2 соответственными?
Пример | Секущая | Признаки: | Вывод |
в | Стороной угла 1 является секущая и прямая . Стороной угла 2 является эта же секущая и вторая прямая .+ Углы расположены по одну сторону от прямых + Углы расположены в одной полуплоскости от общей секущей+ | Соответственные углы | |
а | Стороной угла 1 является секущая и прямая .+ Стороной угла 2 является эта же секущая и прямая . + Углы расположены по одну сторону от прямых.- Углы расположены в одной полуплоскости от секущей | Не соответственные углы | |
в | Стороной угла 1 является секущая и прямая в.- Стороной угла 2 является эта же секущая и прямая с. Углы расположены по одну сторону от прямых Углы расположены в одной полуплоскости от секущей | Не соответственные углы |
У: проверяем задание зачитывая по очереди ответ.
В) Формирование действия выведения следствий из факта принадлежности объекта объему данного понятия
Цель: показ применения изученного понятия на практике.
Способ управления деятельностью: прямой.
Метод обучения: объяснительно-иллюстративный.
Ориентировочная основа
У: Давайте представим, какие выводы мы можем сделать, если нам будет известно, что углы соответственные?
О: одна пара сторон принадлежит секущей, а вторая пара сторон лежат в одной полуплоскости от некоторой прямой, являющейся секущей.
У: Посмотрим, ответы на какие вопросы мы можем получить, если выполним следующее упражнение. (текст упражнения на слайде)
Задание: Известно, что углы АВС и АКМ – соответственные., при чем точки А, В, К лежат на одной прямой а. Определите, в одной или в разных плоскостях лежат точки С и М? 1 шаг. Выполняем рисунок, согласно условий задачи. Дано: Углы АВС и АКМ — соответственные А, В, К а Найти: расположение точек С и М Относительно прямой а. Решение: Вершины углов лежат на одной прямой – следовательно прямая а – секущая. Стороной углов является секущая, а второй стороной являются лучи ВС и КМ. Так ка углы соответственные, то эти лучи лежат в одной полуплоскости, и следовательно точки С и М также лежат в одной полуплоскости. |
Этап громкой и внутренней речи
У: самостоятельно выполните следующее упражнение (задание на карточках)
Задание: В треугольнике АВС, точка К принадлежит стороне АВ. Известно, что углы ВКМ и ВАС соответственные и равны между собой. Пересекает ли луч КМ сторону треугольника ВС? Решение: Ответ: да, пересекает |
4. ЭТАП ПЕРВОНАЧАЛЬНОГО ПРИМЕНЕНИЯ ПОНЯТИЯ
Цель: показ применения изученного понятия на практике.
У: Решите упражнения.
Задание 1.Выявите все пары соответственных углов. Сколько их? Обоснуйте свой ответ по алгоритму. |
Задание2. Определите секущую и связанные с ней соответственные углы, обозначив их цифрами (без дополнтиельных построений) 1.Секущая__________ 2.Пара соответственных углов_______ 1.Секущая__________ 2.Пара соответственных углов_______ 1.Секущая__________ 2.Пара соответственных углов_______ |
5. ПОДВЕДЕНИЕ ИТОГОВ УРОКА
У: Ответьте на следующие вопросы:
Мы все углы, которые на сегодняшний день изучили условно разделили на две большие группы, это углы «одиночки » и «парные» углы. К каким углам можно отнести соответственные углы?
О: к «парным» углам
У: А чем они отличаются от вертикальных и смежных углов.
О: образуются при пересечении двух прямых секущей.
У: Сколько всего пар соответственных углов можно выделить при одной секущей, пересекающей две прямые?
О: 4 пары.
ДОМАШНЕЕ ЗАДАНИЕ
У: Выучить определения понятия соответственные углы, выполнить задание на карточке (перечислить соответственные углы).
Задание: Перечислите пары соответственных углов при секущих e, d, c, b, дав им «имена», состоящие из трех букв. Дайте «имя» точкам ?
Секущая _____________ Пара соответственных__________ Пара соответственных__________ Пара соответственных__________ Пара соответственных__________ | Секущая _____________ Пара соответственных__________ Пара соответственных__________ Пара соответственных__________ Пара соответственных__________ |
Секущая _____________ Пара соответственных__________ Пара соответственных__________ Пара соответственных__________ Пара соответственных__________ | Секущая _____________ Пара соответственных__________ Пара соответственных__________ Пара соответственных__________ Пара соответственных__________ |
Внутренние односторонние углы — теория, правило и свойства » Kupuk.net
Чтобы дать верное определение внутренним односторонним углам, нужно отличать их от вертикальных, смежных, соответственных и накрест лежащих.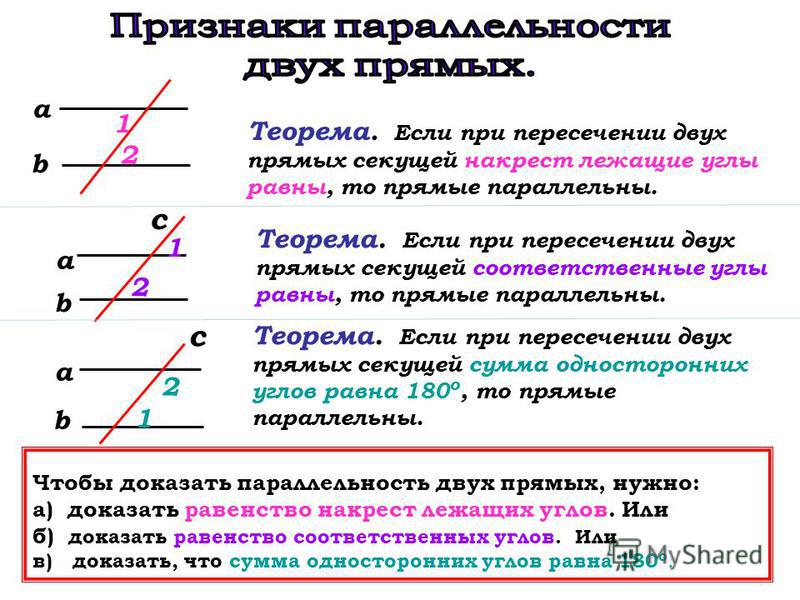 Их объединяет то, что они могут быть образованы двумя параллельными прямыми и пересекающей их линией. Утверждение о том, что сумма внутренних односторонних углов составляет 180 градусов, позволяет доказать теорему о параллельности прямых.
Их объединяет то, что они могут быть образованы двумя параллельными прямыми и пересекающей их линией. Утверждение о том, что сумма внутренних односторонних углов составляет 180 градусов, позволяет доказать теорему о параллельности прямых.
Углы по определению
Прямая, которая пересекает другие линии, идущие параллельно друг другу, образует не только внутренние, но и внешние углы. Один из них дополняет другой до 180 градусов. Это свойство можно доказать как для смежных, так и односторонних внутренних, каждый из которых имеет соответственный внешний.
Углы, расположенные на одной стороне от секущей, пересекающей 2 линии, идущие параллельно, называются накрест лежащими. Они отличаются от односторонних, образуя с ними смежные. В сумме они составляют 180 градусов.
Отрезок между линиями, проведенными параллельно между собой, можно обозначить AB. Если представить, что AB=0, то параллельные будут совпадать, а соответственные углы и односторонние станут смежными.
Их сумма должна быть 180 градусов.
Доказательство теоремы
Прямые являются параллельными, если сумма односторонних внутренних углов равна 180. Нужно доказать теорему по исходным данным. Секущая АВ является линией пересечения параллельных а и b.
Для доказательства теоремы можно допустить, что линии не являются параллельными, значит они пересекают друг друга в определенной точке С. Секущая АВ образует с а и b треугольник АВС, поскольку точка С лежит в одной из двух плоскостей относительно АВ. На линии а расположена сторона треугольника АС, а на b — ВС.
Если в противоположной полуплоскости отложить точку С1, то она образует с АВ другой треугольник АВС1. При этом по построению углы ВАС и АВС1 равны. Сумма САВ и СВА составляет 180, что указано в условии задачи. Следовательно, сторона АС1 принадлежит а, аналогично, ВС1 — линии b.
Точка пересечения С линий а и b принадлежит этим прямым. Вместе с тем точка С1 не может лежать на каждой из них, поскольку она находится в полуплоскости, где линии по построению не пересекаются.
Если в сумме односторонние углы составляют 180, то треугольника АВС1 не существует, значит а || b.
Следствие из свойства прямых
На прямую а может быть опущен единственный перпендикуляр из любой точки А, которая не принадлежит данной линии. Доказательство утверждения состоит из следующих шагов:
Итак, отрезок АВ является единственным перпендикуляром, проходящим через точку А.
Построение параллелограмма
Если односторонние углы не прямые, то один из них является острым, а другой — тупым, то есть меньшим или большим по величине. Если через каждый из них провести биссектрисы, то они должны пересечь противоположные стороны в определенных точках. Для этого достаточно отложить отрезки на параллельных линиях, равные AB, используя циркуль.
Секущая и отрезки, принадлежащие проведенным биссектрисам, образуют 2 треугольника вместе с параллельными. Напротив большего угла будет находиться биссектриса, отсекающая наибольший отрезок. Это подтверждает теорема о соотношении между углами и сторонами разностороннего треугольника.
Соединив точки пересечения биссектрис с параллельными прямыми, можно построить четырехугольник ABCD. Чтобы доказать, что полученная фигура является параллелограммом, достаточно учесть следующее:

Отложив от A и B равноудаленные точки C и D, можно получить линию CD, которая параллельна AB. Тогда CD — отрезок, перпендикулярный параллельным прямым BC и AD. Поскольку все отрезки полученной фигуры ABCD пересекаются перпендикулярно, то она является прямоугольником по построению.
Доказательство теоремы позволяет определять, какой является величина второго из двух внутренних односторонних углов при параллельных прямых и секущей. Решение задач по геометрии позволяет найти их градусную меру и в зависимости от разности между ними.
Признаки параллельности прямых. Секущая | Геометрия
Содержание
Как мы выяснили на прошлом уроке, прямая, пересекающая данную прямую, пересечет также прямую, параллельную данной.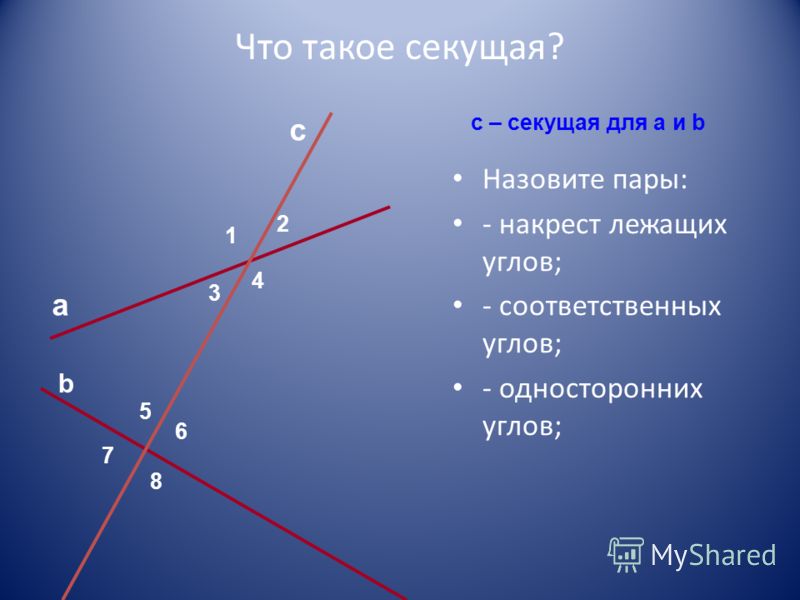 Это следствие из аксиомы параллельности открывает нам возможность сформулировать конкретные признаки параллельности прямых, по которым можно доказательно заключать о параллельности тех или иных прямых. Вы все правильно поняли: от аксиом мы наконец переходим к теоремам.
Это следствие из аксиомы параллельности открывает нам возможность сформулировать конкретные признаки параллельности прямых, по которым можно доказательно заключать о параллельности тех или иных прямых. Вы все правильно поняли: от аксиом мы наконец переходим к теоремам.
Даны прямые $a$ и $b$, параллельные друг другу, и прямая $c$, которая пересекает данные прямые в двух точках.
Подобная прямая, пересекающая две прочие прямые, в геометрии называется секущей. Секущая может проводиться как по отношению к параллельным прямым, так и к непараллельным.
Секущая — прямая пересекающая две прямые, лежащие в одной плоскости, в двух разных точках.
Обращаем внимание на углы при секущей: секущая при пересечении с параллельными прямыми образует восемь углов, которые на чертеже обозначены заглавными латинскими буквами: A, B, C и так далее. Некоторые пары углов при секущей настолько важны, что за ними даже закреплены отдельные названия:
Некоторые пары углов при секущей настолько важны, что за ними даже закреплены отдельные названия:
- односторонние углы — $\angle{A}$ и $\angle{H}$, $\angle{B}$ и $\angle{G}$;
- накрест лежащие углы — $\angle{A}$ и $\angle{G}$, $\angle{B}$ и $\angle{H}$;
- соответственные углы — $\angle{A}$ и $\angle{E}$, $\angle{B}$ и $\angle{F}$, $\angle{D}$ и $\angle{H}$,
$\angle{C}$ и $\angle{G}$;
Внутренние и внешние углы при секущей
Внутренние углы при секущей — это углы, которые находятся в общих для прямых полуплоскостях. Однако секущая также образует и внешние углы — те, что располагаются в не пересекающихся полуплоскостях прямых. Посмотрите на чертежи: для наглядности «зоны» внутренних и внешних углов выделены цветом.
К внутренней «зоне» относятся углы $\angle{A}$, $\angle{B}$, $\angle{H}$ и $\angle{G}$.
К внешней «зоне» относятся углы $\angle{D}$, $\angle{C}$, $\angle{E}$ и $\angle{F}$.
Примечательно, что соответственные углы — это пары, состоящие из одного внутреннего и одного внешнего угла. А при должном внимании вы могли догадаться, что накрест лежащие и односторонние углы были выше нами указаны только для внутренней «зоны». Аналогичные пары вообще-то имеются и во внешней «зоне».
{"questions":[{"content":"Закрепим. Расположите пары углов согласно их названию. Теперь мы будем учитывать как внутреннюю область, так и внешнюю. [[image-2]] [[grouper-1]]","widgets":{"grouper-1":{"type":"grouper","labels":["Внутренние накрест лежащие углы","Внешние накрест лежащие углы","Внутренние односторонние углы","Внешние односторонние углы","Соответственные углы"],"items":[["$\\angle{A}$ и $\\angle{G}$","$\\angle{B}$ и $\\angle{H}$"],["$\\angle{D}$ и $\\angle{F}$","$\\angle{C}$ и $\\angle{E}$"],["$\\angle{A}$ и $\\angle{H}$","$\\angle{B}$ и $\\angle{G}$"],["$\\angle{D}$ и $\\angle{E}$","$\\angle{C}$ и $\\angle{F}$"],["$\\angle{A}$ и $\\angle{E}$","$\\angle{B}$ и $\\angle{F}$","$\\angle{D}$ и $\\angle{H}$","$\\angle{C}$ и $\\angle{G}$"]]},"image-2":{"type":"image","url":"https://obrazavr. ru/wp-content/uploads/2022/03/angles-ABCD.svg"}}}]}
ru/wp-content/uploads/2022/03/angles-ABCD.svg"}}}]}Признаки параллельности прямых: накрест лежащие углыОчевидно, что проведение секущей — это специальный геометрический метод для определения параллельности прямых. По тому, являются ли те или иные пары углов, образованные секущими, равными, можно заключать о параллельности или непараллельности прямых. Одна из таких пар — накрест лежащие углы.
Признак параллельности прямых по накрест лежащим углам. Если при пересечении двух прямых секущей накрест лежащие углы равны, то такие прямые параллельны.
Доказательство. Проведем прямые $a,$ $b$ и секущую $c$, пересекающую прямые в точках $A$ и $B$ соответственно. По условию прямые образуют с секущей пару равных накрест лежащих углов$\angle{1}$ и $\angle{2}$. Воспользуемся методом от противного и предположим, что прямые не параллельны. Тогда они будут пересекаться в некоторой точке $C$. \circ$. Мы пришли к противоречию.
\circ$. Мы пришли к противоречию.
Следовательно прямые параллельны. Теорема доказана.
Внешние
накрест лежащие углы!Заметьте, что при доказательстве мы опирались на равенство внутренних накрест лежащих углов, хотя, если взять признак параллельности прямых, тексте теоремы указана общая формулировка — «накрест лежащие углы», без обозначения их расположения относительно полуплоскостей прямых.
Ответ прост: если доказать признаки параллельности прямых, опираясь на равенство внутренних накрест лежащих углов, внешнее расположение — не более чем условность.
Возьмем для примера $\angle{B}$ и $\angle{H}$. Для $\angle{B}$: внешний $\angle{D}$ — с ним вертикальный; внешний $\angle{C}$ — смежный. Аналогично для $\angle{H}$: $\angle{F}$ и $\angle{E}$ соответственно.
Вертикальные углы равны, поэтому получаем равенство $\angle{D}$ и $\angle{F}.$ У равных углов смежные с ними углы также будут равны, отсюда $\angle{C}=\angle{E}$.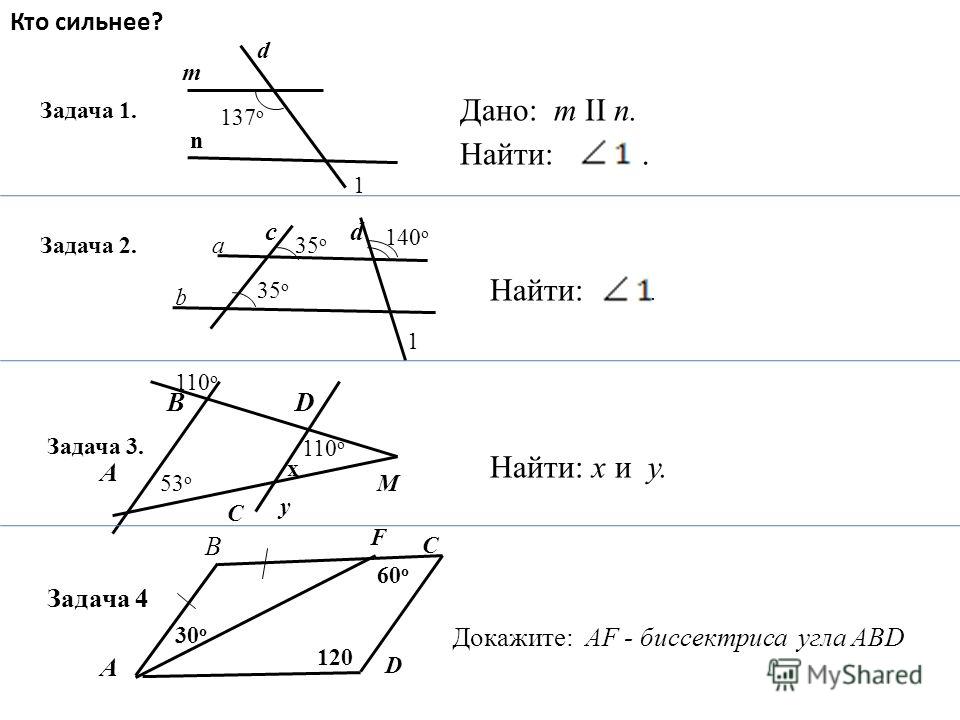 Поэтому теорема обычно доказывается по внутренним накрест углам, ведь равенство таких же внешних — прямое следствие.
Поэтому теорема обычно доказывается по внутренним накрест углам, ведь равенство таких же внешних — прямое следствие.
Признаки параллельности прямых: задача
Отрезки $AB$ и $CD$ пересекаются в общей середине $O$. Докажите, что прямые $AC$ и $BD$ при этом параллельны.
Дано:
$AB, CD$
$AO=OB$
$CO=OD$
Найти:
$AC\parallel{BD}$
Решение
Рассмотрим треугольники $\bigtriangleup{AOC}$ и $\bigtriangleup{BDO}$. Они равны по первому признаку: по условию $AO=OB$ и $CO=OD$, углы $\angle{COA}$ и $\angle{BOD}$ равны как вертикальные. Следовательно $\angle{ACD}=\angle{BDC}$. Данные углы являются внутренними накрест лежащими. Тогда $AC\parallel{BD}$ согласно признаку параллельности по накрест лежащим углам.
Признак параллельности прямых по соответственным углам.
Если при пересечении двух прямых секущей соответственные углы равны, то такие прямые параллельны.
Доказательство. Пусть прямые $a$ и $b$ при пересечении секущей $c$ образуют пару равных соответственных углов — $\angle{A}=\angle{B}$. Угол $\angle{D}$ является вертикальным по отношению к $\angle{A}$. Следовательно $\angle{A}=\angle{D}=\angle{B}$. Поскольку $\angle{D}$ и $\angle{B}$ — накрест лежащие углы, прямые $a$ и $b$ являются параллельными. Теорема доказана.
{"questions":[{"content":"[[image-1]] Можно ли говорить о том, что прямые $a$ и $b$ параллельны, если известно, что углы $\\angle{A}$ и $\\angle{B}$ равны? [[choice-5]]","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/03/test-angles.svg"},"choice-5":{"type":"choice","options":["Да","Нет"],"explanations":["Естественно! 😊Углы $\\angle{A}$ и $\\angle{B}$ являются соответственными. Их равенство определяет параллельность $a$ и $b$, так как если соответственные углы равны, то прямые параллельны. \circ$. Они являются односторонними при секущей $AB$ для отрезков $AC$ и $BD$. Следовательно $AC\parallel{BD}$.
\circ$. Они являются односторонними при секущей $AB$ для отрезков $AC$ и $BD$. Следовательно $AC\parallel{BD}$.
«Признак» или «теорема»?
Все доказанные признаки параллельности прямых так или иначе в научном понимании является теоремами. При этом, тем не менее, в формулировках слово «теорема» не фигурировало: мы все время пользовались обозначением «признак».
Причина здесь — амбивалентность, создаваемая словосочетанием «теорема параллельности». Есть аксиома параллельности, а есть, значит, еще и теорема? Тогда аксиома совсем не аксиома, если ей можно противопоставить теорему параллельности. Замена «теорема» на «признак» разрешает данную двойственность.
Есть, конечно, еще одна причина… Но это разговор для целого отдельного урока. Этот урок, к слову, следующий. Загляните.
{"questions":[{"content":"Время подвести итог. Выберите из предложенных вариантов три доказанных нами признака параллельности прямых. \\circ$, то такие прямые параллельны.","Если при пересечении двух прямых секущей накрест односторонние углы равны, то такие прямые параллельны."],"answer":[0,1,2]}}}]}
\\circ$, то такие прямые параллельны.","Если при пересечении двух прямых секущей накрест односторонние углы равны, то такие прямые параллельны."],"answer":[0,1,2]}}}]}Углы с соответственными сторонами
☰
Обычно рассматривают углы либо с соответственными параллельными сторонами, либо с соответственно перпендикулярными сторонами. Рассмотрим сначала первый случай.
Пусть даны два угла ABC и DEF. Их стороны соответственно параллельны: AB || DE и BC || EF. Такие два угла будут либо равны, либо их сумма будет равняться 180°. На рисунке ниже в первом случае ∠ABC = ∠DEF, а во втором ∠ABC + ∠DEF = 180°.
Доказательство, что это действительно так, сводится к следующему.
Рассмотрим, углы с соответственно параллельными сторонами, расположенные как на первом рисунке. При этом продлим прямые AB и EF до пересечения. Обозначим точку пересечения буквой G. Кроме того для наглядности последующего доказательства на рисунке продлена сторона BC.
Так как прямые BC и EF параллельны, то если прямая AB пересекает одну из них, то она обязательно пересечет и другую. То есть прямая AB является секущей для двух параллельных прямых. Как известно, в таком случае накрест лежащие углы при секущей равны, односторонние составляют в сумме 180°, соответственные равны.
То есть, какую бы пару углов мы не взяли при вершинах B и G (один угол от одной, другой от второй), мы всегда получим либо равные углы, либо дающие в сумме 180°.
Однако прямые AB и DE тоже параллельны. Для них уже прямая EF — это секущая. Значит, любые пары углов из вершин G и E будут в сумме составлять либо 180°, либо равняться друг другу. Отсюда следует, что и пары углов из вершин B и E будут подчиняться данному правилу.
Например, рассмотрим углы ∠ABC и ∠DEF. Угол ABC равен углу BGE, так как эти углы соответственные при параллельных прямых BC и EF. В свою очередь угол BGE равен углу DEF, так как эти углы соответственны при параллельных AB и DE. Таким образом доказано, ∠ABC и ∠DEF.
Таким образом доказано, ∠ABC и ∠DEF.
Теперь рассмотрим углы ∠ABC и ∠DEG. Угол ABC равен углу BGE. Но ∠BGE и ∠DEG — это односторонние углы при параллельных прямых (AB || DE), пересеченных секущей (EF). Как известно, такие углы в сумме составляют 180°. Если мы посмотрим на второй случай на первом рисунке, то поймем, что он соответствует паре углов ABC и DEG на втором рисунке.
Таким образом, два разных угла, у которых стороны соответственно параллельны, либо равны друг другу, либо составляют в сумме 180°. Теорема доказана.
Следует отметить особый случай — когда углы развернутые. В таком случае они будут очевидно равны друг другу.
Теперь рассмотрим углы с соответственно перпендикулярными сторонами. Этот случай выглядит сложнее, так как взаимное расположение углов разнообразнее. На рисунке ниже три примера того, как могут располагаться углы с соответственно перпендикулярными сторонами. Однако в любом случае одна сторона первого угла (или ее продолжение) перпендикулярна одной стороне второго угла, а вторая сторона первого угла перпендикулярна второй стороне второго угла.
Рассмотрим один из случаев. При этом проведем в одном угле биссектрису и через произвольную ее точку проведем перпендикуляры к сторонам ее угла.
Здесь даны углы ABC и DEF с соответственно перпендикулярными сторонами: AB ⊥ DE и BC ⊥ EF. На биссектрисе угла ABC взята точка G, через которую проведены перпендикуляры к этому же углу: GH ⊥ AB и GI ⊥ BC.
Рассмотрим треугольники BGH и BGI. Они прямоугольные, так как в них углы H и I прямые. В них углы при вершине B равны, так как BG — биссектриса угла ABC. Также у рассматриваемых треугольников сторона BG общая и является гипотенузой для каждого из них. Как известно, прямоугольные треугольники равны друг другу, если равны их гипотенузы и один из острых углов. Таким образом, ∆BGH = ∆BGI.
Так как ∆BGH = ∆BGI, то ∠BGH = ∠BGI. Поэтому угол HGI можно представить не как сумму этих двух углов, а как один из них умноженный на 2: ∠HGI = ∠BGH * 2.
Угол ABC можно представить как сумму двух углов: ∠ABC = ∠GBH + ∠GBI. Поскольку слагаемые углы равны друг другу (т. к. образуются биссектрисой), то угол ABC можно представить как произведение одного из них и числа 2: ∠ABC = ∠GBH * 2.
Поскольку слагаемые углы равны друг другу (т. к. образуются биссектрисой), то угол ABC можно представить как произведение одного из них и числа 2: ∠ABC = ∠GBH * 2.
Углы BGH и GBH — это острые углы прямоугольного треугольника, а значит в сумме составляют 90°. Посмотрим на равенства, которые получаются:
∠BGH + ∠GBH = 90°
∠HGI = ∠BGH * 2
∠ABC = ∠GBH * 2
Сложим два последних:
∠HGI + ∠ABC = ∠BGH * 2 + ∠GBH * 2
Вынесем общий множитель за скобку:
∠HGI + ∠ABC = 2(∠BGH + ∠GBH)
Так как сумма углов в скобках равна 90°, то получается, что углы HGI и ABC в сумме составляют 180°:
∠ABC + ∠HGI = 2 * 90° = 180°
Итак, мы доказали, что сумма углов HGI и ABC составляет 180°. А теперь снова посмотрим на рисунок и вернем свой взор на угол, с которым у угла ABC соответственно перпендикулярные стороны. Это угол DEF.
Прямые GI и EF параллельны друг другу, так как обе они перпендикулярны одной и той же прямой BC. А как известно, прямые, которые перпендикулярны одной и той же прямой, параллельны друг другу. По этой же самой причине DE || GH.
А как известно, прямые, которые перпендикулярны одной и той же прямой, параллельны друг другу. По этой же самой причине DE || GH.
Как ранее уже было доказано, углы с соответственно параллельными сторонами либо в сумме составляют 180°, либо равны друг другу. Значит, либо ∠DEF = ∠HGI, либо ∠DEF + ∠HGI = 180°.
Однако ∠ABC + ∠HGI = 180°. Отсюда делается вывод, что и в случае с соответственно перпендикулярными сторонами углы или равны, или составляют в сумме 180°.
Хотя в данном случае мы ограничились доказательством только суммы. Но если мысленно продлить сторону EF в обратном направлении, то увидим угол, который равен углу ABC, и при этом его стороны также перпендикулярны углу ABC. Доказать равенство таких углов можно, рассматривая углы с соответственно параллельными сторонами: ∠DEF и ∠HGI.
Соответствующие углы – определение, теорема, примеры
Соответствующие углы – это углы, которые образуются при пересечении двух параллельных прямых секущей. Открытие и закрытие коробки для завтрака, сборка кубика Рубика и бесконечные параллельные железнодорожные пути — вот несколько повседневных примеров соответствующих углов. Они формируются в соответствующих углах или соответствующих углах с поперечной.
Открытие и закрытие коробки для завтрака, сборка кубика Рубика и бесконечные параллельные железнодорожные пути — вот несколько повседневных примеров соответствующих углов. Они формируются в соответствующих углах или соответствующих углах с поперечной.
| 1. | Что такое соответствующие углы? |
| 2. | Как найти соответствующие углы? |
| 3. | Теорема о соответствующих углах |
| 4. | Часто задаваемые вопросы о соответствующих углах |
Что такое соответствующие углы?
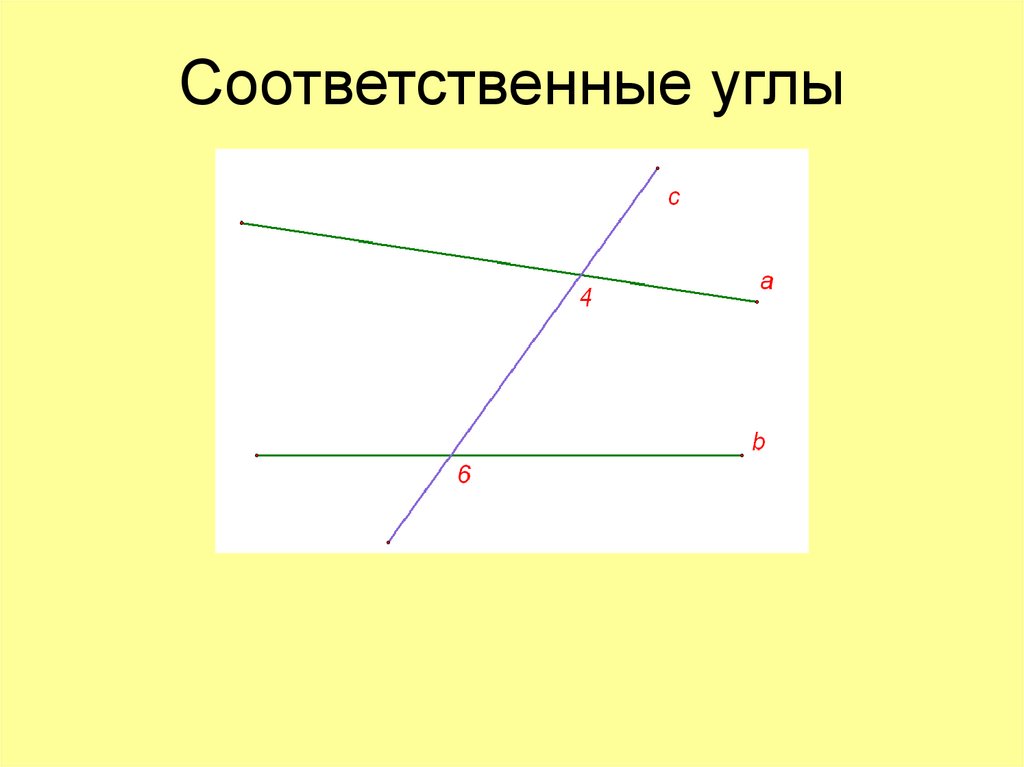
Соответствующее определение углов говорит нам, что когда две параллельные прямые пересекаются третьей, известно, что углы, которые занимают одно и то же относительное положение при каждом пересечении, являются соответствующими углами друг к другу.
Согласно геометрии и определению соответствующих углов мы можем сказать, что:
- Прямые 1 и 2 параллельны.
 Таким образом имеем две параллельные линии
Таким образом имеем две параллельные линии - Линия 3 пересекает прямые 1 и 2. Таким образом, мы пересекли параллельные прямые
- Из диаграммы видно, что углы 1 и 2 занимают одинаковое взаимное положение - верхние правые боковые углы в области пересечения.
Следовательно, наше соответствующее определение углов кажется оправданным . Следовательно, мы можем сказать, что углы 1 и 2 являются соответствующими углами.
Теперь, когда мы поняли определение соответствующих углов, мы можем выяснить, являются ли любые два заданных угла соответствующими или нет на любой данной диаграмме. Само слово «соответствие» предполагает, что углы могут быть как неравными, так и эквивалентными (конгруэнтными). Удивительно, но соответствующие углы, образованные секущей, пересекающей две параллельные прямые, являются углами, которые конгруэнтны. При пересечении секущей двух непараллельных прямых соответствующие углы не равны.
Как найти соответствующие углы?
Мы знаем, что каждая точка пересечения имеет 4 угла. Теперь каждый из четырех углов в первой области пересечения будет иметь еще один с таким же относительным положением во второй области пересечения.
Теперь каждый из четырех углов в первой области пересечения будет иметь еще один с таким же относительным положением во второй области пересечения.
Теперь мы разделим каждый из этих четырех углов на разные категории. Посмотрите в таблице ниже, чтобы лучше понять различные типы соответствующих углов.
| Наименование углов | Местоположение |
|---|---|
| Углы 1 и 5 | Верхний правый угол |
| Углы 2 и 6 | Верхний левый угол |
| Углы 3 и 7 | Нижний правый угол |
| Уголки 4 и 8 | Нижний левый угол |
Теорема о соответствующих углах
Согласно теореме о соответствующих углах утверждение « Если прямая пересекает две параллельные прямые, то соответствующие углы в двух областях пересечения равны» верно в любом случае.
Теорема, обратная для соответствующих углов
Теорема, обратная для соответствующих углов, будет выглядеть так: «Если соответствующие углы в двух областях пересечения конгруэнтны, то две прямые называются параллельными .
Что если секущая пересекает две параллельные прямые и пара соответственных углов тоже равны? Тогда две прямые, пересекаемые секущей, называются параллельными. Это обратная теорема о соответствующем угле.
Важные замечания о соответствующих углах
- Когда две параллельные прямые пересекаются третьей, углы, которые занимают одно и то же относительное положение при каждом пересечении, называются соответствующими углами друг к другу.
- Соответствующие углы равны друг другу.
- Если соответствующие углы в двух областях пересечения равны, то говорят, что две прямые параллельны.
Задающий вопрос о соответствующих углах
Следующая информация была дана относительно углов A, B, C и D:
- A и B являются соответствующими углами
- В и С дополнительные уголки
- C и D - внутренние углы
Найдите угол (кроме B), который будет равен углу A.
Примеры соответствующих углов
Пример 1: Вы когда-нибудь замечали высокое здание? В большинстве высотных зданий каждый из его этажей спроектирован точно так же, особенно стены дома на каждом этаже. Сравните соответствующие углы в таком случае.
Решение:
Давайте рассмотрим нижние плитки пола 1 как линию 1, а плитку пола 2 как линию 2. Теперь мы знаем, что линия 3 пересекает линии 1 и 2. На этом рисунке вы можете заметить геометрию соответствующих углов. .
Видите ли вы сходство между углами 1 и 2? Вы можете видеть, что углы 1 и 2 являются соответствующими углами. Мало того, что все этажи всегда строятся параллельно друг другу, можно сказать, что линии 1 и 2 параллельны.
Следовательно, ∠1 соответствует ∠2
Пример 2: Вы когда-нибудь замечали параллельные линии на железнодорожных путях? Есть несколько пересечений различных меньших линий с двумя основными параллельными линиями пути.
 Сравните углы, образованные пересечением.
Сравните углы, образованные пересечением.Решение:
Видите ли вы какое-либо сходство между понятиями равных углов и углов 1 и 2 на приведенной ниже диаграмме? Вспомните определение, которое мы использовали для соответствующих углов, чтобы соответствовать нашим углам, показанным здесь.
Как видите, если мы считаем, что линии пути параллельны, то углы 1 и 2 можно считать соответствующими углами. Это соответствует соответствующим углам в математическом определении. Таким образом, если угол 1 равен 90 градусов, то угол 2 также будет равен 90 градусам.
Следовательно, ∠1 с соответствует ∠2 и угол 1 = угол 2 = 90 градусов.
Пример 3: Вам когда-нибудь попадались две параллельные улицы? Обычно между двумя улицами есть соединительная дорога, которая также пересекает ее. Теперь попробуйте связать углы, образуемые улицей в каждой точке пересечения, с двумя параллельными дорогами.
Решение:
Примените наше определение соответствующих углов к углам, показанным здесь.
 Вы увидите, что по нашему определению эти углы совпадают!
Вы увидите, что по нашему определению эти углы совпадают!Мало того, что все улицы всегда построены параллельно друг другу, мы также можем сказать, что углы, находящиеся на одних и тех же относительных позициях на улицах, всегда будут соответствующими углами.
Следовательно, углы, образованные параллельными улицами, являются соответствующими углами.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по соответствующим углам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о соответствующих углах
Что такое соответствующие углы в геометрии?
Соответствующие углы в геометрии определяются как углы, которые образуются при соответствующих углах с секущей. При пересечении двух параллельных прямых секущая образует пару соответствующих углов.
При пересечении двух параллельных прямых секущая образует пару соответствующих углов.
☛ Чтобы узнать больше о соответствующих углах, проверьте сейчас:
- Типы углов
- Пары углов
Какие бывают два типа соответствующих углов?
В соответствии с определением соответствующих углов мы можем разделить соответствующие углы на два типа, перечисленных ниже:
- Соответственные углы - поперечными и параллельными прямыми: Соответственные углы равны.
- Соответствующие углы - поперечными непараллельными прямыми: Образуемые соответствующие углы не равны.
☛ Ознакомьтесь с таблицами соответствующих углов, чтобы попрактиковаться.
Сумма соответствующих углов равна 180?
Да, сумма соответствующих углов может составлять 180. В некоторых случаях, когда оба угла равны 90 градусов, сумма будет равна 180 градусам. Эти углы называются дополнительными соответственными углами.
☛ Проверьте дополнительные углы сейчас для получения дополнительной информации.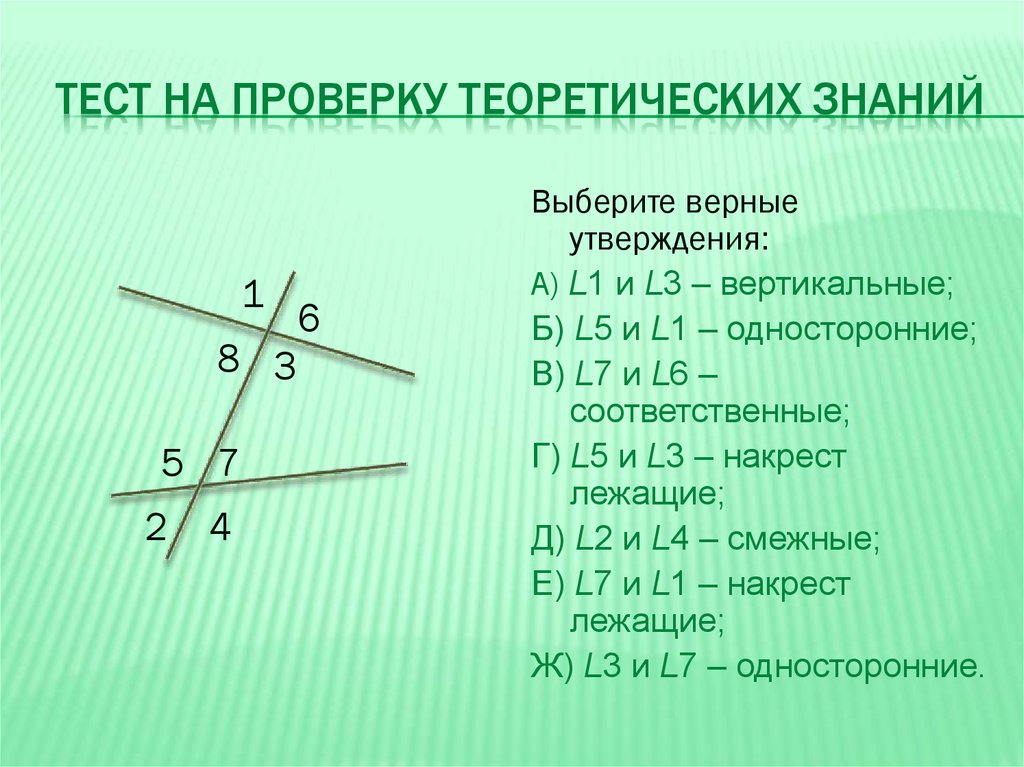
Что такое альтернативные и соответствующие углы?
Альтернативные углы — это углы, которые находятся в относительно противоположных положениях друг к другу; в то время как соответствующие углы - это углы, которые находятся в относительно одинаковых положениях друг к другу.
Могут ли соответствующие углы быть смежными внутренними углами?
Никакие соответствующие углы не могут рассматриваться как последовательные внутренние углы, потому что последовательные внутренние углы — это углы, лежащие по одну сторону от поперечной, но находящиеся внутри двух параллельных прямых.
Могут ли соответствующие углы быть прямыми?
Если секущей перпендикулярна к данным параллельным прямым, то соответствующие углы секущей, пересекающей параллельные прямые, прямые, все углы прямые.
☛ Проверьте Дополнительные углы сейчас для лучшего понимания.
Как выглядят соответствующие углы?
При пересечении двух параллельных прямых секущей образующиеся таким образом углы, занимающие одно и то же относительное положение при каждом пересечении, являются соответствующими углами. Когда две параллельные прямые пересекаются секущей, то углы в одних и тех же углах каждой прямой называются соответствующими углами, и секущая будет выглядеть как прямая.
Когда две параллельные прямые пересекаются секущей, то углы в одних и тех же углах каждой прямой называются соответствующими углами, и секущая будет выглядеть как прямая.
Что вы понимаете под постулатом о соответствующих углах?
Согласно постулату о соответствующих углах, соответствующие углы равны, если секущая пересекает две параллельные прямые.
Что такое постулат обращения соответствующих углов?
Мы только что прочитали, что постулат о соответствующих углах утверждает, что соответствующие углы конгруэнтны, если секущая пересекает две параллельные прямые. В то время как постулаты обращения соответствующих углов говорят, что если соответствующие углы в двух областях пересечения конгруэнтны, то две линии называются параллельными.
Сумма соответствующих углов равна 90 градусам?
Если соответствующие углы равны, то в некоторых случаях, когда оба угла по 45 градусов, сумма будет 90 градусов. Эти углы известны как дополнительные соответствующие углы.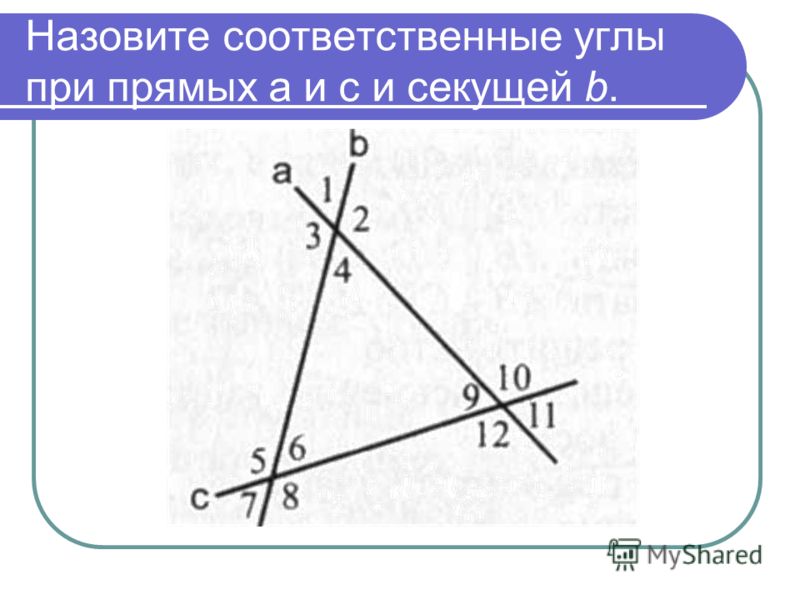
☛ Проверьте дополнительные углы, чтобы узнать больше.
Соответствие углов – объяснение и примеры
Прежде чем перейти к теме соответствующих углов, давайте сначала напомним себе об углах, параллельных и непараллельных прямых и поперечных прямых.
В геометрии угол состоит из трех частей: вершины и двух сторон или сторон. Вершина угла находится там, где встречаются две стороны или линии угла, а стороны угла — это просто стороны угла.
Параллельные линии — это две или более линий на двумерной плоскости, которые никогда не встречаются и не пересекаются. С другой стороны, непараллельные прямые — это две или более пересекающихся прямых. Поперечная линия – это линия, пересекающая или проходящая через две другие прямые. Поперечная линия может проходить через две параллельные или непараллельные прямые.
Что такое соответствующий угол?
Углы, образованные при пересечении поперечной линией двух прямых, называются соответственными углами .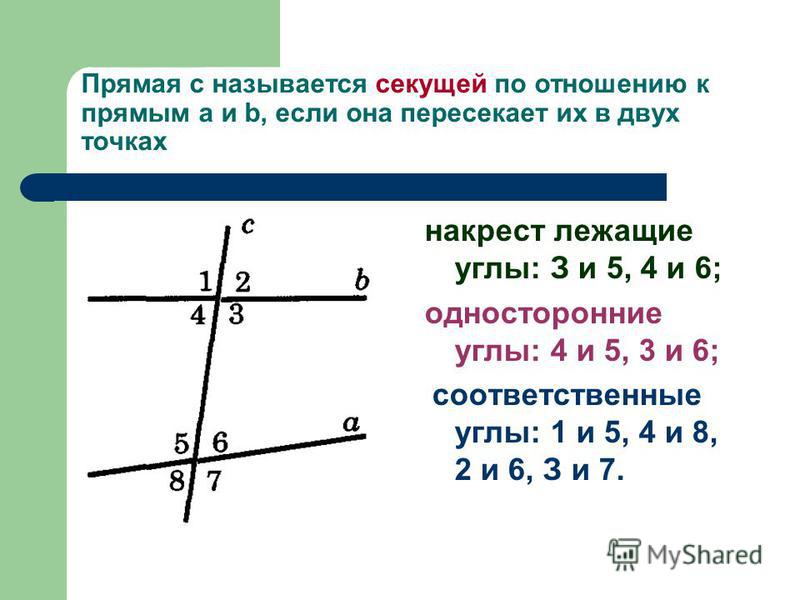 Соответствующие углы расположены в одном и том же взаимном положении, на пересечении поперечной и двух или более прямых.
Соответствующие углы расположены в одном и том же взаимном положении, на пересечении поперечной и двух или более прямых.
Правило соответствующих углов или соответствующих углов постулирует, что соответствующие углы равны, если секущей пересекаются две параллельные прямые.
Соответственные углы равны, если поперечная прямая пересекает не менее двух параллельных прямых.
На приведенной ниже диаграмме показаны соответствующие углы, образованные при пересечении поперечной линией двух параллельных прямых:
На приведенной выше диаграмме пара соответствующих углов:
- < a и < e
- < b и < g
- < d и < f
- < c и < h
5 0003 На рисунке выше две параллельные линии. Нам нужно это доказать. Углы прямые образуется при пересечении поперечной линией хотя бы двух непараллельных прямых, которые не равны между собой и фактически не имеют между собой никакого отношения. Иллюстрация: Пара соответствующих углов состоит из одного внутреннего и другого внешнего угла. Внутренние углы — это углы, расположенные в углах пересечений. Углы, образованные вне пересекающихся параллельных прямых. Внешний угол и внутренний угол составляют пару соответствующих углов. Иллюстрация: Внутренние уголки включают; b, c, e и f, а внешние углы включают; а, г, г и з. Следовательно, пары соответствующих углов включают: О соответствующих углах можно сделать следующие выводы: Один из способов решения соответствующих углов - нарисовать букву F на данной диаграмме. Расположите букву лицом в любом направлении и соотнесите углы соответственно. Пример 1 Учитывая ∠d = 30°, найдите недостающие углы на диаграмме ниже. Решение Указано, что тий D = 30 ° тий D = ♂ B (вертикально противоположные углы) Следовательно, ♂ B = 300003 . Следовательно, тий F = 30 ° ∠ a + 30° = 180° тий a = 150 ° тий A = тий E = (Соответствующие углы) Следовательно, тий = 150 ° ↑ D = 222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 годы. (соответствующие углы) Пример 2 Два соответствующих угла фигуры равны 9x + 10 и 55. Найдите значение x. Решение Два соответствующих угла всегда равны. Следовательно, 9x + 10 = 55 9x = 55 - 10 9x = 45 x = 5 Пример 3 Два соответствующих углы показателя рисунка 7Y - 12 и 5Y + 6. Решение Сначала нам нужно определить значение y. Два соответствующих угла всегда равны. Следовательно, 7у – 12 = 5у + 6 7у – 5у = 12 + 6 2y = 18 y = 9 Величина соответствующего угла, 5y + 6 = 5 (9) + 6 = 51
Соответствующий внутренний угол
Соответствующий внешний угол
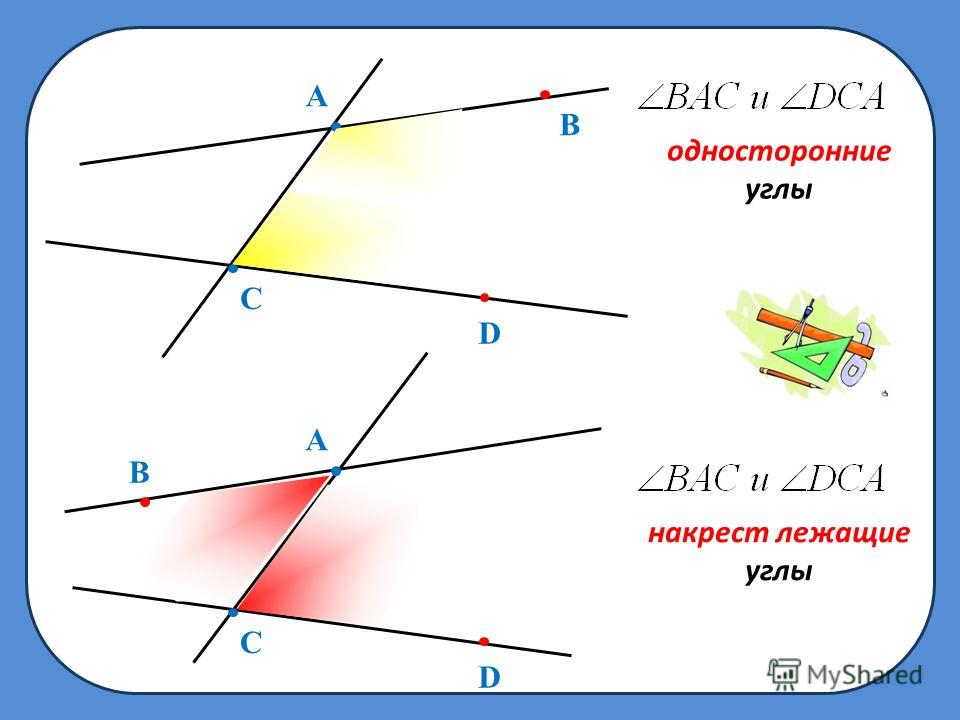 Соответственные углы равны, если секущая пересекает две параллельные прямые. Если секущая пересекает непараллельные прямые, то образующиеся соответствующие углы не равны и никак не связаны.
Соответственные углы равны, если секущая пересекает две параллельные прямые. Если секущая пересекает непараллельные прямые, то образующиеся соответствующие углы не равны и никак не связаны. Как найти соответствующие углы?
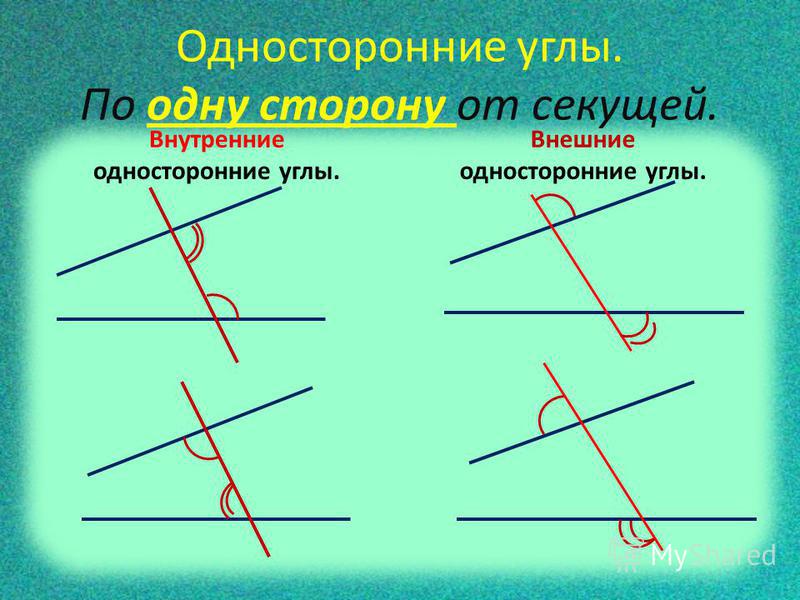 Тий G = 30 ° (соответствующие углы)
Тий G = 30 ° (соответствующие углы)
Теперь, тий D = ♂ F (Соответствующие углы)
R B + ° ATER + ° ATER + ° ATER + ° ATER + ° B9032 + ° ATER + ° B9032 + ° ATER + ° B9032 + ° C9032 + ° C9032 + ° C9032 + ° C9032 + ° C9032 + ° C + ° C + ° ATER + ° ATERSTIONS ATRIC дополнительные углы) Найдите модуль соответствующего угла.
Найдите модуль соответствующего угла. Применение соответствующих углов игнорировать. Соблюдайте их, если у вас когда-нибудь будет шанс.
- Обычно окна имеют горизонтальные и вертикальные решетки, образующие несколько квадратов. Каждая вершина квадрата образует соответствующие углы.
- Мост стоит на столбах. Все столбы соединены таким образом, что соответствующие углы равны.
- Железнодорожные пути спроектированы так, что все соответствующие углы на пути равны.
Поперечные
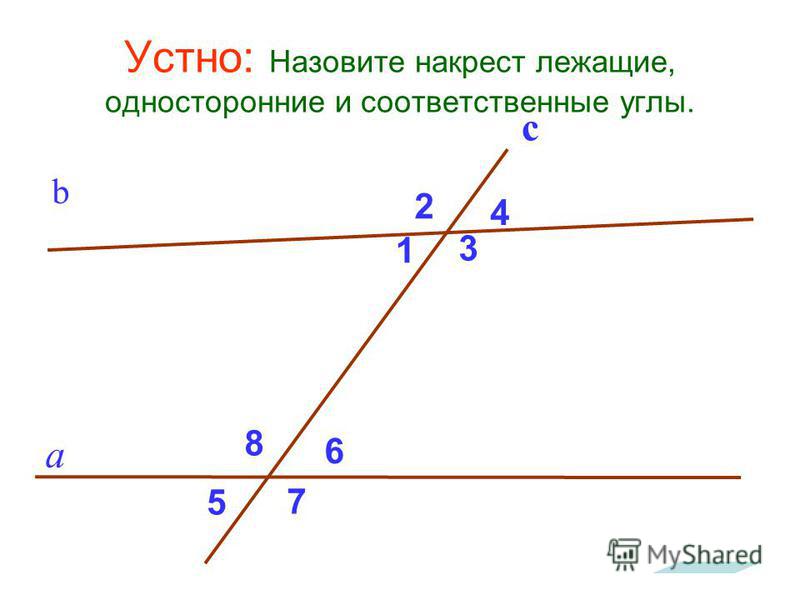
Горячая математика В геометрии а поперечный это линия, пересекающая две или более других (часто
параллельно
) линии.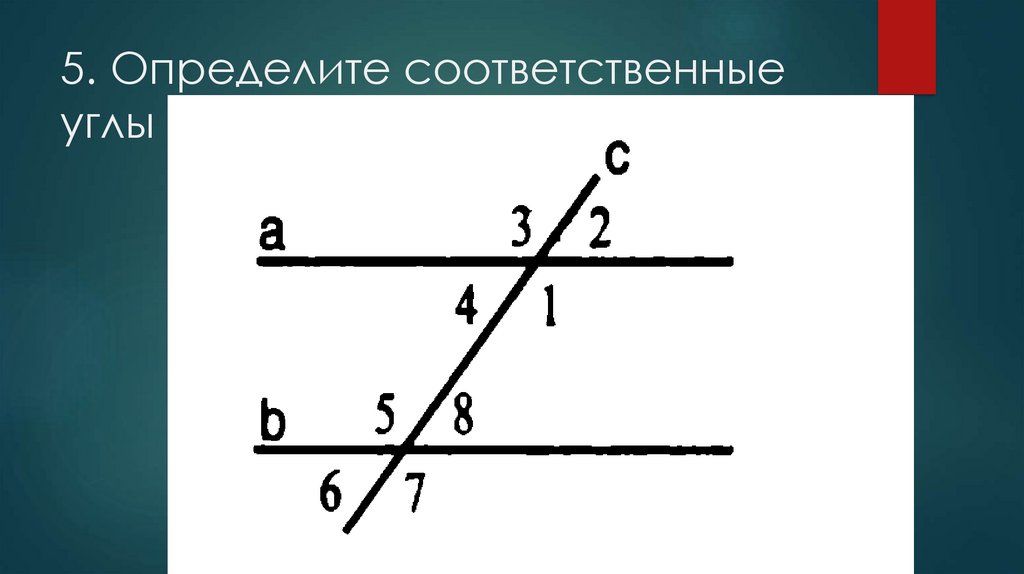
На рисунке ниже линия н представляет собой поперечные линии разреза л а также м .
При пересечении двух или более прямых секущей углы, занимающие одно и то же относительное положение, называются соответствующие углы .
На рисунке пары соответствующих углов:
∠ 1 а также ∠ 5 ∠ 2 а также ∠ 6 ∠ 3 а также ∠ 7 ∠ 4 а также ∠ 8
Если прямые параллельны, то соответствующие углы равны конгруэнтный .
Когда две прямые пересекаются секущей, пары углов по одну сторону от этой и внутри двух прямых называются углами. последовательные внутренние углы .
На приведенном выше рисунке последовательные внутренние углы равны:
∠ 3 а также ∠ 6 ∠ 4 а также ∠ 5
Если две параллельные прямые пересечь секущей, то образуются пары последовательных внутренних углов. дополнительный
.
дополнительный
.
Когда две прямые пересекаются секущей, пары углов по обе стороны от этой и внутри двух прямых называются углами. альтернативные внутренние углы .
На приведенном выше рисунке альтернативные внутренние углы:
∠ 3 а также ∠ 5 ∠ 4 а также ∠ 6
Если две параллельные прямые пересечь секущей, то образованные параллельные внутренние углы равны конгруэнтный .
Когда две прямые пересекаются секущей, пары углов по обе стороны от этой секущей и вне двух прямых называются углами. альтернативные внешние углы .
На приведенном выше рисунке альтернативные внешние углы:
∠ 2 а также ∠ 8 ∠ 1 а также ∠ 7
Если две параллельные прямые пересечь секущей, то образующиеся накрест внешние углы равны
конгруэнтный
.
Пример 1:
На приведенной выше схеме линии Дж а также к разрезаются поперек л . Углы ∠ с а также ∠ е находятся…
А. Соответствующие углы
B. Последовательные внутренние углы
C. Альтернативные внутренние углы
D. Альтернативные внешние углы
Углы ∠ с а также ∠ е лежат по обе стороны от поперечной л и внутри двух строк Дж а также к .
Следовательно, они являются альтернативными внутренними углами.
Правильный выбор С .
Пример 2:
На приведенном выше рисунке, если линии А Б ↔ а также С Д ↔ параллельны и м ∠ А Икс Ф знак равно 140 ° тогда в чем мера ∠ С Д Е ?
Углы
∠
А
Икс
Ф
а также
∠
С
Д
Е
лежат по одну сторону от поперечной
Е
Ф
↔
и внутри двух строк
А
Б
↔
а также
С
Д
↔
.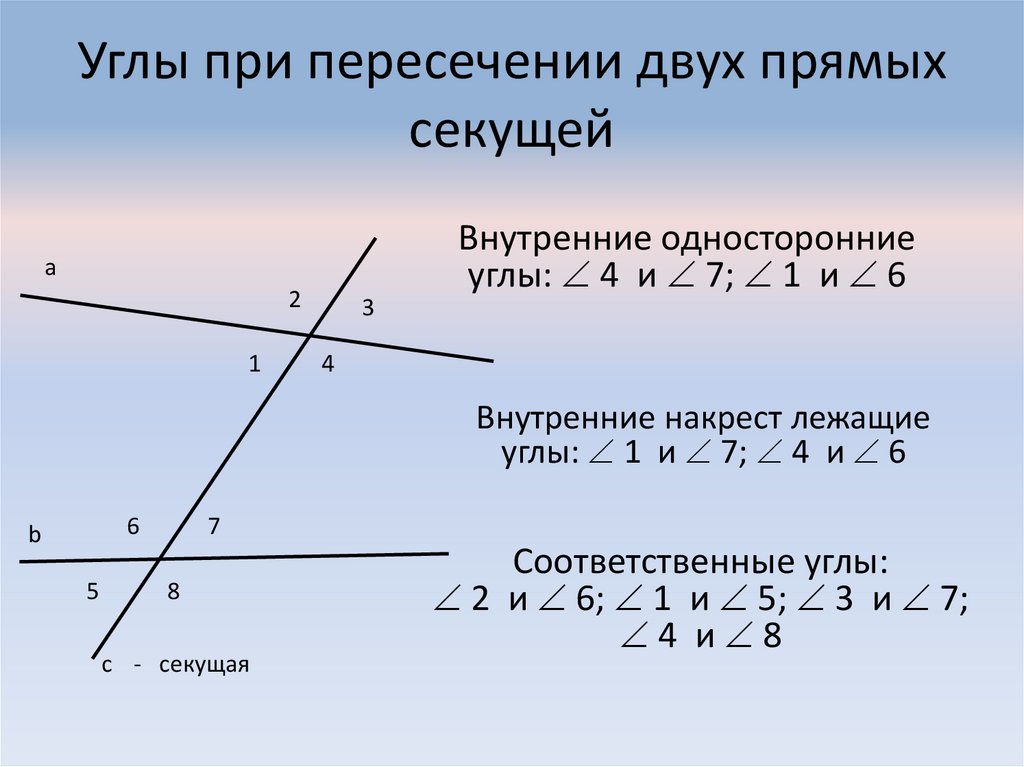 Значит, это последовательные внутренние углы.
Значит, это последовательные внутренние углы.
Поскольку линии А Б ↔ а также С Д ↔ параллельны, т. теорема о последовательных внутренних углах , ∠ А Икс Ф а также ∠ С Д Е являются дополнительными.
То есть, м ∠ А Икс Ф + м ∠ С Д Е знак равно 180 ° .
Но, м ∠ А Икс Ф знак равно 140 ° .
Подставить и решить.
140 ° + м ∠ С Д Е знак равно 180 ° 140 ° + м ∠ С Д Е − 140 ° знак равно 180 ° − 140 ° м ∠ С Д Е знак равно 40 °
Соответствующие углы – определение и теорема с примерами
Определение
Соответствующие углы – это пары углов, которые занимают одно и то же относительное положение на каждом пересечении, когда секущая пересекает две параллельные прямые.
На приведенном выше рисунке показаны две параллельные прямые AB и CD, пересекаемые поперечной GH. Пары соответствующих углов на данном рисунке:
∠1 и ∠5
∠3 и ∠6
∠4 и ∠7
∠2 и ∠8
Соответствующие углы равны, если секущая пересекает хотя бы две параллельные прямые.
На данном рисунке AB∥CD,
Таким образом,
∠1 = ∠5, ∠3 = ∠6, ∠4 = ∠7, ∠2 = ∠8
Соответствующие углы, образованные при пересечении секущей хотя бы две непараллельные прямые не равны и также не имеют отношения друг к другу.
Свойства
- Расположены на одной стороне поперечной
- Состоит из одного внутреннего и одного внешнего угла
- Они равны, если секущая пересекает две параллельные прямые
- Они не связаны, если секущая пересекает две непараллельные прямые
- Они являются дополнительными, если секущая перпендикулярно пересекает две параллельные прямые.
- Внешние углы по одну сторону от секущей являются дополнительными, если две прямые параллельны.
 То же самое и с внутренними углами.
То же самое и с внутренними углами.
Типы соответствующих углов
Два типа соответственных углов:
1) Соответствующий внутренний угол : Находится на внутренней стороне пересечения параллельных прямых и поперечных.
2) Соответствующий внешний угол : Находится на внешней стороне пересечения между параллельными линиями и поперечными.
Теорема о соответствующих углах
Теорема о соответствующих углахДокажите теорему о соответствующих углах
Чтобы доказать:
∠1 = ∠5, ∠3 = ∠6, ∠4 = ∠7, ∠2 = ∠8
Доказательство:
Дано, PQ и RS — две параллельные прямые, пересекаемые поперечной IJ.
Теперь, если PQ∥ RS
Тогда по теореме о соответствующих углах мы можем написать : Таким образом, единственный способ доказать конгруэнтность соответствующих углов - это параллельность данных прямых. Таким образом, теорема о соответствующих углах верна без доказательства.
Теорема обращения соответствующих углов
Теорема обращения соответствующих угловДокажите теорему обращения соответствующих углов
Чтобы доказать:
PQ∥ RS
Доказательство два: прямые, пересекаемые секущей IJ, и ∠1 = ∠5, ∠3 = ∠6, ∠4 = ∠7, ∠2 = ∠8 — пары соответствующих углов
.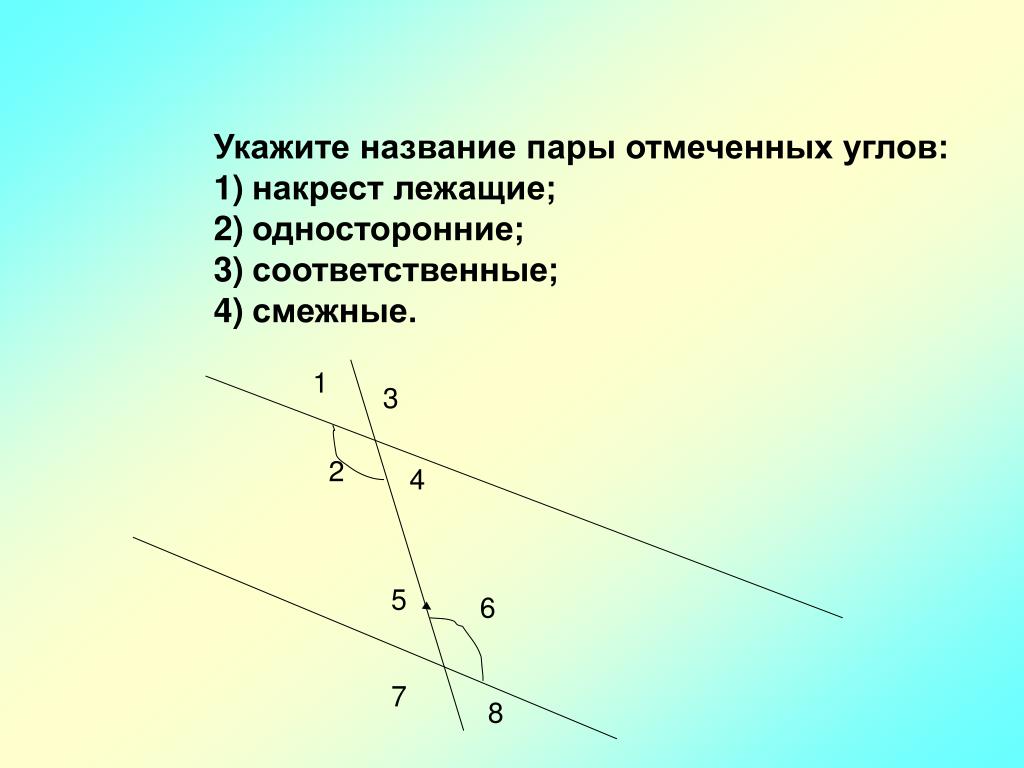 Тогда по теореме, обращенной к внутренним углам,
Тогда по теореме, обращенной к внутренним углам,
PQ∥ RS
Следовательно доказано
Вспомните : Таким образом, единственный способ доказать параллельность данных прямых — это просто конгруэнтность соответствующих углов. Таким образом, теорема, обратная о соответствующих углах, принимается как истинная без доказательства.
Как найти соответствующие углы
Давайте рассмотрим несколько примеров, чтобы лучше понять концепцию.
Найдите недостающие углы на данном рисунке. Учитывая, что ∠3 = 45°
Решение:
Дано, ∠3 = 45°
∠3 = ∠4 (вертикально противоположные углы)
Следовательно, ∠4 = 45°
Теперь
∠4 =∠7 = 45° (соответствующие углы)
∠3 =∠6 (соответствующие углы)
Следовательно, ∠6 = 45°
Теперь,
∠1 + ∠4 = 180° (дополнительные углы)
∠1 + 45° = 180°
∠1 = 180° – 45°
∠1 = 135°
Аналогично,
∠1 = ∠2 (вертикально противоположные углы)
Следовательно, ∠2 = 135°
Опять же,
∠1 = ∠5 (соответствующие углы)
Следовательно, ∠5 = 135°
Аналогично,
∠2 = ∠8 (соответствующие углы)
Следовательно, ∠8 = 135°
Два соответствующих угла измеряют (2x +10)° и 70°. Найдите значение х.
Найдите значение х.
Решение:
Согласно теореме о соответствующих углах, два соответствующих угла равны.
Таким образом,
(2x +10)° = 70°
2x = 70° – 10°
x = 60°/2
x = 30°
Два соответствующих угла данной фигуры равны 6y- 14 и 4y + 6. Найдите модуль соответствующего угла.
Решение:
Согласно теореме о соответствующих углах, два соответствующих угла равны.
Таким образом,
6y-14 = 4y + 6
6y – 4y = 6 + 14
2y = 20
y = 10
Таким образом, величина равна
6y-14 = 6 x 10 – 14 = 46°
Примеры в реальной жизни
- Окна имеют горизонтальные и вертикальные решетки, образующие несколько квадратов. Каждая вершина образует соответствующие углы
- Мост, стоящий на опоре, в которой опоры соединены друг с другом так, что соответствующие углы равны
- Конструкция железнодорожного пути, в которой соответствующие углы сохранены равными
- Углы, образованные кубиком Рубика
Часто задаваемые вопросы
Q1. Соответствующие углы дополнительные
Соответствующие углы дополнительные
Ans . Соответственные углы являются дополнительными только в том случае, если секущая перпендикулярно пересекает две параллельные прямые.
Соответствующие углы - Математика GCSE
Здесь мы узнаем о соответствующих углах , в том числе, как распознать совпадение углов и применить это для решения проблем.
Существуют также рабочие листы с углами в параллельных линиях, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные указания о том, что делать дальше, если вы все еще застряли.
Что такое соответствующие углы?
Соответствующие углы — это углы, лежащие по одну сторону от поперечной линии и равные по величине . Они либо оба тупые, либо оба острые.
Соответствующие углы равны
Что такое соответствующие углы?
Как считать с соответствующими углами
Для расчета с соответствующими углами:
- Выделите углы, которые вы уже знаете.

- Используйте соответствующие углы, чтобы найти недостающий угол.
- Используйте базовый факт угла для расчета недостающего угла .
Как считать с соответствующими углами
Таблица соответствующих углов
Получите бесплатную таблицу соответствующих углов, содержащую более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксТаблица соответствующих углов
Получите бесплатную таблицу соответствующих углов, содержащую более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Примеры соответственных углов
Пример 1: соответствующие углы
Рассчитайте величину недостающего угла θ. Обосновать ответ.
- Выделите углы, которые вы уже знаете.
2 Используйте соответствующие углы, чтобы найти недостающий угол.
Здесь мы можем обозначить соответствующий угол на диаграмме как 75°.
3 Используйте базовый факт угла для расчета недостающего угла. 9{\ круг} \end{aligned}\]
Пример 2: соответствующие углы
Вычислить размер недостающего угла θ. Обосновать ответ.
Выделите углы, которые вы уже знаете.
Используйте соответствующие углы, чтобы найти недостающий угол.
Мы можем идентифицировать два новых угла 63 ° и 56 ° , используя соответствующие углы.
Используйте базовый факт угла для расчета недостающего угла. 9{\ круг} \end{aligned}\]
Пример 3: соответствующие углы с алгеброй
Вычислите размер недостающего угла θ. Обосновать ответ.
Выделите углы, которые вы уже знаете.
Здесь нам нужно найти значение x, чтобы найти значение θ.
Используйте соответствующие углы, чтобы найти недостающий угол.
Взаимное расположение двух углов 4x -14 и 3x+7 делает их соответствующими углами. Это позволяет нам найти значение x, поскольку два угла равны: 9{\ круг} \end{aligned}\]
Поскольку x = 21 ° , у нас есть два угла 4x – 14 = 3x + 7 = 70 ° .
Используйте базовый факт угла для расчета недостающего угла.
Здесь мы можем объединить тот факт, что у нас есть равнобедренный треугольник и сумма углов на прямой 180 ° .
Поскольку треугольник равнобедренный с основанием на одной параллельной линии, углы по обе стороны от верхней вершины треугольника симметричны (это также можно рассчитать с помощью правила альтернативного угла). 9{\ круг} \end{aligned}\]
Распространенные заблуждения
- Перепутывание фактов об углах
Существует множество фактов об углах, и альтернативные углы легко перепутать с соответствующими углами. Чтобы этого не произошло, представьте, что соответствующие углы находятся под буквой F.
Чтобы этого не произошло, представьте, что соответствующие углы находятся под буквой F.
- Использование транспортира для измерения угла
Большинство диаграмм не в масштабе, поэтому использование транспортира не даст правильного ответа.
Соответствие углов — это часть нашей серии уроков, посвященных пересмотру углов на параллельных линиях. Возможно, вам будет полезно начать с урока по основным углам в параллельных линиях, чтобы получить общее представление о том, чего ожидать, или использовать пошаговые руководства ниже для получения дополнительной информации по отдельным темам. Другие уроки в этой серии включают:
- Углы в параллельных прямых
- Переменные углы
- Внутренние углы
Практика соответствующих углов 9{\ круг}
(1)
3. Вычислите значение x .
(3 балла)
Показать ответ
противоположные углы равны
(1)
2x+4x-3.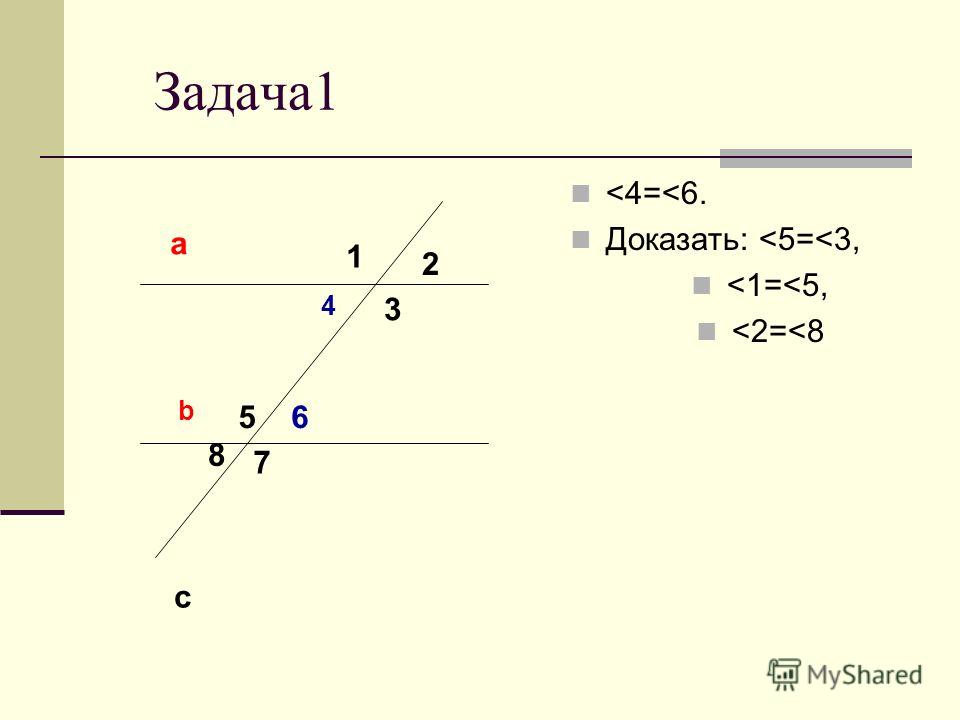
(1)
\begin{выровнено} 2x+9&=4x-3\\ 9&=2х-3\\ 12&=2x\\ 6&=х \end{выровнено}
(1)
Учебный контрольный список
Теперь вы научились:
- Применять свойства углов в точке, углов в точке на прямой, вертикально противоположных углов
- Понимать и использовать соотношение между параллельными линиями и альтернативными и соответствующими углами
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе повторения GCSE по математике.
3.4: Соответствующие углы - K12 LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2190
Определите соответствующие углы как соответствующие углы.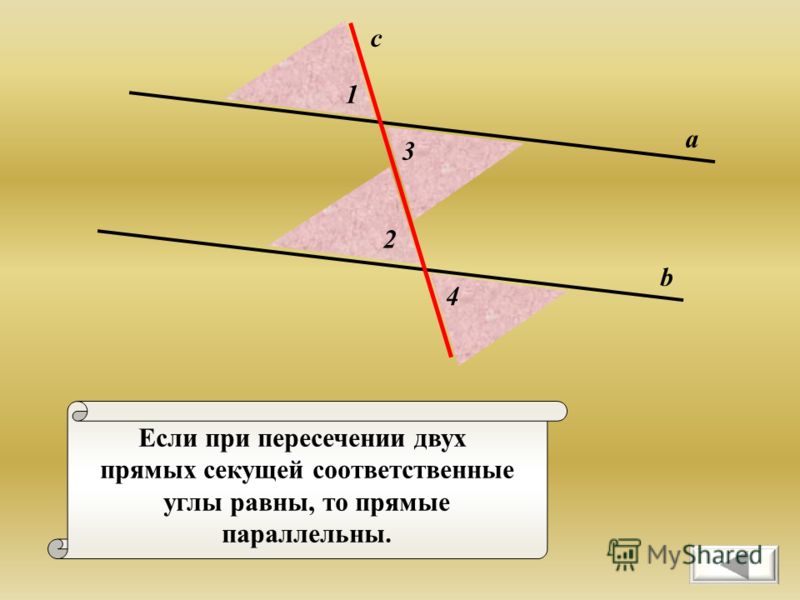
Соответствующие углы — это два угла, которые находятся в «одном месте» относительно секущей, но на разных линиях. Представьте, что четыре угла, образованные линией \(l\), сдвигаются вниз к линии \(m\). Совпадающие углы соответствуют друг другу.
Рисунок \(\PageIndex{1}\)Соответствие углов Постулат: Если две параллельные прямые пересечены секущей, то соответствующие углы равны.
Рисунок \(\PageIndex{2}\)Если \(l \параллельно m\), то \(\угол 1\конг \угол 2\).
Обратное обращение соответствующих углов Постулат: Если соответствующие углы равны при пересечении двух прямых секущей, то прямые параллельны.
Если
Рисунок \(\PageIndex{3}\), затем \(l \parallel m\).
Что, если бы вам представили два угла, находящихся в одном и том же месте относительно секущей, но на разных прямых? Как бы вы описали эти углы и что вы могли бы сказать об их величине?
Пример \(\PageIndex{1}\) 9{\circ}\).
Пример \(\PageIndex{3}\)
Найдите значение y:
Рисунок \(\PageIndex{5}\)Решение
Горизонтальные линии отмечены параллельными, а угол отмечен \(2y\ ) соответствует углу, отмеченному 80, поэтому эти два угла равны. Это означает, что \(2y=80\) и, следовательно, \(y=40\).
Пример \(\PageIndex{4}\)
Если a||b, какие пары углов конгруэнтны в соответствии с постулатом о соответствующих углах?
Рисунок \(\PageIndex{6}\) 9{\circ}\), то что мы знаем о прямых \(l\) и \(m\)? Рисунок \(\PageIndex{7}\)Решение
\(\угол 8\) и \(\угол 4\) - соответствующие углы. Поскольку \(m\угол 8=m\угол 4\), мы можем заключить, что l||m.
Обзор
- Определите, является ли пара углов \(\угол 4\) и \(\угол 2\) конгруэнтной, дополнительной или ни одной: Рисунок \(\PageIndex{8}\)
- Приведите два примера соответствующих углов на схеме:
Рисунок \(\PageIndex{9{\circ}\).

Обзор (ответы)
Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 3.3.
Ресурсы
Словарь
| Срок | Определение |
|---|---|
| Соответствующие углы | Соответствующие углы - это два угла, которые находятся в одном и том же положении относительно секущей, но на разных прямых. |
Дополнительный ресурс
Интерактивный элемент
Видео: Соответствующие принципы углов - базовые
Действия: соответствующие углы. Вопросы для обсуждения
Исследование. Углы
Эта страница под названием 3.

 Но и тот, и другой имеет начало и не имеет конца.
Но и тот, и другой имеет начало и не имеет конца. 

 +
+

 Их сумма должна быть 180 градусов.
Их сумма должна быть 180 градусов. ru/wp-content/uploads/2022/03/angles-ABCD.svg"}}}]}
ru/wp-content/uploads/2022/03/angles-ABCD.svg"}}}]} Если при пересечении двух прямых секущей соответственные углы равны, то такие прямые параллельны.
Если при пересечении двух прямых секущей соответственные углы равны, то такие прямые параллельны. \circ$. Они являются односторонними при секущей $AB$ для отрезков $AC$ и $BD$. Следовательно $AC\parallel{BD}$.
\circ$. Они являются односторонними при секущей $AB$ для отрезков $AC$ и $BD$. Следовательно $AC\parallel{BD}$.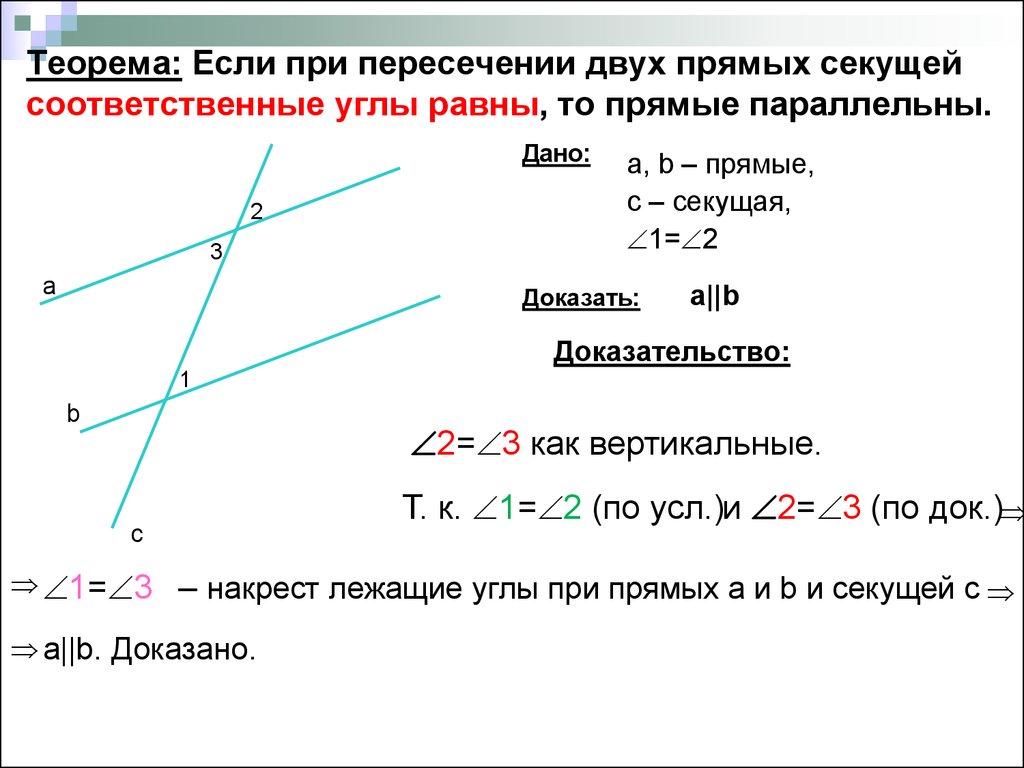 \\circ$, то такие прямые параллельны.","Если при пересечении двух прямых секущей накрест односторонние углы равны, то такие прямые параллельны."],"answer":[0,1,2]}}}]}
\\circ$, то такие прямые параллельны.","Если при пересечении двух прямых секущей накрест односторонние углы равны, то такие прямые параллельны."],"answer":[0,1,2]}}}]}
 Таким образом доказано, ∠ABC и ∠DEF.
Таким образом доказано, ∠ABC и ∠DEF.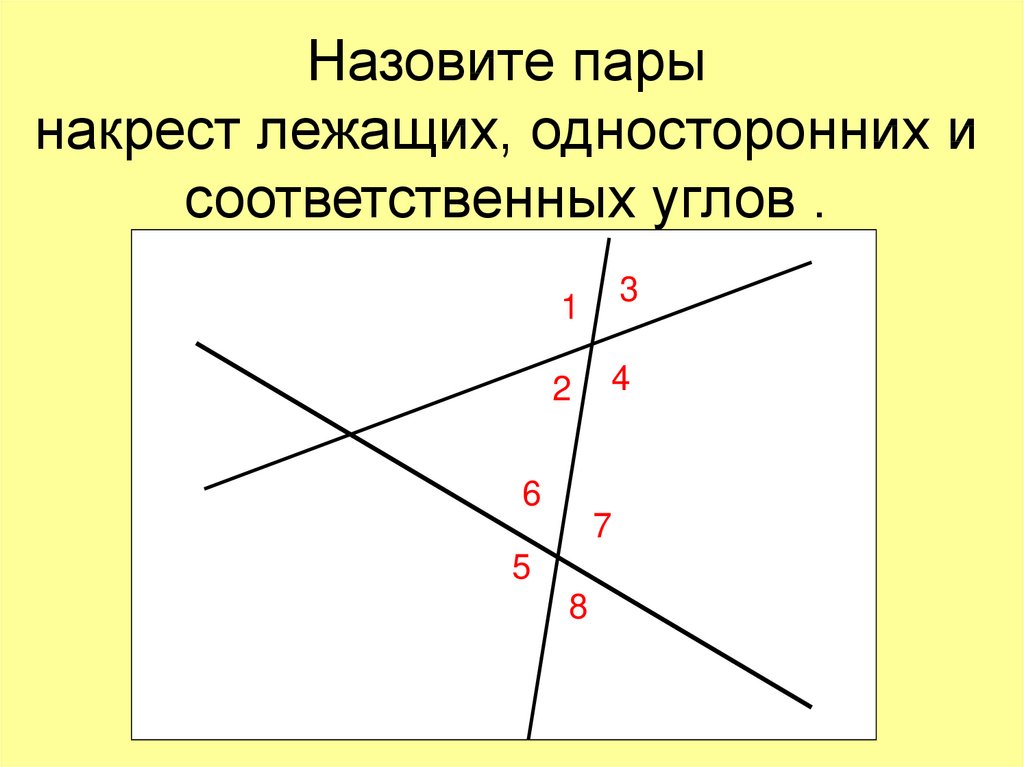
 Поскольку слагаемые углы равны друг другу (т. к. образуются биссектрисой), то угол ABC можно представить как произведение одного из них и числа 2: ∠ABC = ∠GBH * 2.
Поскольку слагаемые углы равны друг другу (т. к. образуются биссектрисой), то угол ABC можно представить как произведение одного из них и числа 2: ∠ABC = ∠GBH * 2.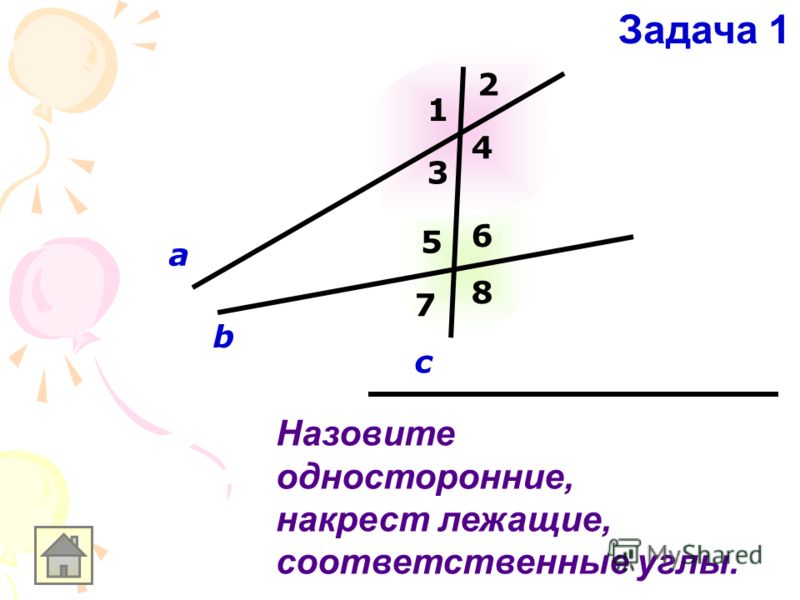 А как известно, прямые, которые перпендикулярны одной и той же прямой, параллельны друг другу. По этой же самой причине DE || GH.
А как известно, прямые, которые перпендикулярны одной и той же прямой, параллельны друг другу. По этой же самой причине DE || GH. Открытие и закрытие коробки для завтрака, сборка кубика Рубика и бесконечные параллельные железнодорожные пути — вот несколько повседневных примеров соответствующих углов. Они формируются в соответствующих углах или соответствующих углах с поперечной.
Открытие и закрытие коробки для завтрака, сборка кубика Рубика и бесконечные параллельные железнодорожные пути — вот несколько повседневных примеров соответствующих углов. Они формируются в соответствующих углах или соответствующих углах с поперечной. Таким образом имеем две параллельные линии
Таким образом имеем две параллельные линии Сравните углы, образованные пересечением.
Сравните углы, образованные пересечением. Вы увидите, что по нашему определению эти углы совпадают!
Вы увидите, что по нашему определению эти углы совпадают! То же самое и с внутренними углами.
То же самое и с внутренними углами.