калькулятор онлайн решить систему уравнений с помощью обратной матрицы
калькулятор онлайн решить систему уравнений с помощью обратной матрицыВы искали калькулятор онлайн решить систему уравнений с помощью обратной матрицы? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и калькулятор решений систем уравнений матричным методом, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «калькулятор онлайн решить систему уравнений с помощью обратной матрицы».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте.
Где можно решить любую задачу по математике, а так же калькулятор онлайн решить систему уравнений с помощью обратной матрицы Онлайн?
Решить задачу калькулятор онлайн решить систему уравнений с помощью обратной матрицы вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Как решить уравнение 5х. Решение показательных уравнений по математике
Назначение сервиса . Матричный калькулятор предназначен для решения систем линейных уравнений матричным способом (см. пример решения подобных задач).
Инструкция . Для онлайн решения необходимо выбрать вид уравнения и задать размерность соответствующих матриц.
где А, В, С — задаваемые матрицы, Х — искомая матрица. Матричные уравнения вида (1), (2) и (3) решаются через обратную матрицу A -1 . Если задано выражение A·X — B = C , то необходимо, сначала сложить матрицы C + B , и находить решение для выражения A·X = D , где D = C + B (). Если задано выражение A*X = B 2 , то предварительно матрицу B надо возвести в квадрат . Рекомендуется также ознакомиться с основными действиями над матрицами .
Пример №1
. Задание . Найти решение матричного уравнения
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X·B = C.
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1:Умножаем обе части этого равенства слева на A -1 и справа на B -1: A -1 ·A·X·B·B -1 = A -1 ·C·B -1 . Так как A·A -1 = B·B -1 = E и E·X = X·E = X, то X = A -1 ·C·B -1
Обратная матрица A -1:
Найдем обратную матрицу B -1 .
Транспонированная матрица B T:
Обратная матрица B -1:
Матрицу X ищем по формуле: X = A -1 ·C·B -1
Ответ:
Пример №2
. Задание. Решить матричное уравнение
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.
Определитель матрицы А равен detA=0
Так как A вырожденная матрица (определитель равен 0), следовательно уравнение решения не имеет.
Пример №3
. Задание. Найти решение матричного уравнения
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: X·A = B.
Определитель матрицы А равен detA=-60
Так как A невырожденная матрица, то существует обратная матрица A -1 .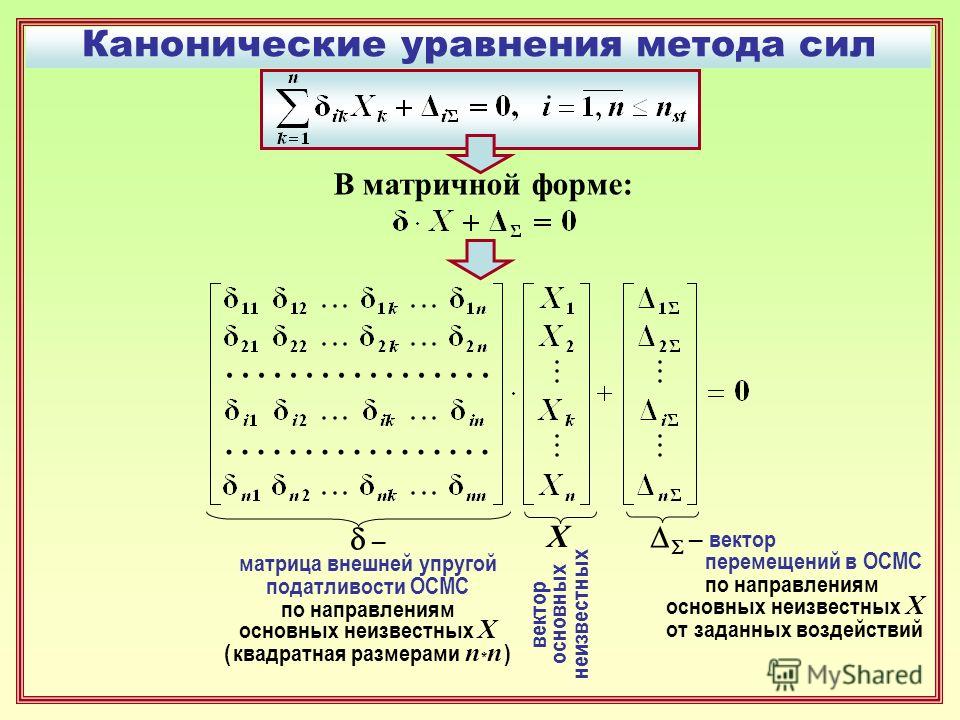
Умножим справа обе части уравнения на A -1: X·A·A -1 = B·A -1 , откуда находим, что X = B·A -1
Найдем обратную матрицу A -1 .
Транспонированная матрица A T:
Обратная матрица A -1:
Матрицу X ищем по формуле: X = B·A -1
Ответ: >
Предлагаемый вашему вниманию бесплатный калькулятор располагает богатым арсеналом возможностей для математических вычислений. Он позволяет использовать онлайн калькулятор в различных сферах деятельности: образовательной , профессиональной и коммерческой . Конечно, применение калькулятора онлайн особенно популярно у студентов и школьников , он значительно облегчает им выполнение самых разных расчётов.
Вместе с тем калькулятор может стать полезным инструментом в некоторых направлениях бизнеса и для людей разных профессий. Безусловно, необходимость применения калькулятора в бизнесе или трудовой деятельности определяется прежде всего видом самой деятельности. Если бизнес и профессия связаны с постоянными расчётами и вычислениями, то стоит опробовать электронный калькулятор и оценить степень его полезности для конкретного дела.
Данный онлайн калькулятор может
- Корректно выполнять стандартные математические функции, записанные одной строкой типа — 12*3-(7/2) и может обрабатывать числа больше, чемсчитаем огромные числа в онлайн калькулятореМы даже не знаем, как такое число назвать правильно (тут 34 знака и это совсем не предел ).
- Кроме тангенса , косинуса , синуса и других стандартных функций — калькулятор поддерживает операции по расчёту арктангенса , арккотангенса и прочих.
- Доступны в арсенале логарифмы , факториалы и другие интересные функции
- Данный онлайн калькулятор умеет строить графики !!!
Для построения графиков, сервис использует специальную кнопку (график серый нарисован) или буквенное представление этой функции (Plot). Чтобы построить график в онлайн калькуляторе, достаточно записать функцию: plot(tan(x)),x=-360..360 .
Мы взяли самый простой график для тангенса, и после запятой указали диапазон переменной X от -360 до 360.
Построить можно абсолютно любую функцию, с любым количеством переменных, например такую: plot(cos(x)/3z, x=-180..360,z=4) или ещё более сложную, какую сможете придумать. Обращаем внимание на поведение переменной X — указан промежуток от и до с помощью двух точек.
Единственный минус (хотя трудно назвать это минусом) этого онлайн калькулятора это то, что он не умеет строить сферы и другие объёмные фигуры — только плоскость.
Как работать с Математическим калькулятором
1. Дисплей (экран калькулятора) отображает введенное выражение и результат его расчёта обычными символами, как мы пишем на бумаге. Это поле предназначено просто для просмотра текущей операции. Запись отображается на дисплее по мере набора математического выражения в строке ввода.
2. Поле ввода выражения предназначено для записи выражения, которое нужно вычислить. Здесь следует отметить, что математические символы, используемые в компьютерных программах, не всегда совпадают с теми, которые обычно мы применяем на бумаге.
В обзоре каждой функции калькулятора вы найдёте правильное обозначение конкретной операции и примеры расчётов в калькуляторе. На этой странице ниже приводится перечень всех возможных операций в калькуляторе, также с указанием их правильного написания.
3. Панель инструментов — это кнопки калькулятора, которые заменяют ручной ввод математических символов, обозначающих соответствующую операцию. Некоторые кнопки калькулятора (дополнительные функции, конвертер величин, решение матриц и уравнений, графики) дополняют панель задач новыми полями, где вводятся данные для конкретного расчёта. Поле «History» содержит примеры написания математических выражений, а также ваши шесть последних записей.
Обратите внимание, при нажатии кнопок вызова дополнительных функций, конвертера величин, решения матриц и уравнений, построения графиков вся панель калькулятора смещается вверх, закрывая часть дисплея. Заполните необходимые поля и нажмите клавишу «I» (на рисунке выделена красным цветом), чтобы увидеть дисплей в полный размер.
4. Цифровая клавиатура содержит цифры и знаки арифметических действий. Кнопка «С» удаляет всю запись в поле ввода выражения. Чтобы удалять символы по одному, нужно использовать стрелочку справа от строки ввода.
Старайтесь всегда закрывать скобки в конце выражения. Для большинства операций это некритично, калькулятор online рассчитает всё верно. Однако, в некоторых случаях возможны ошибки. Например, при возведении в дробную степень незакрытые скобки приведут к тому, что знаменатель дроби в показателе степени уйдет в знаменатель основания. На дисплее закрывающая скобка обозначена бледно-серым цветом, её нужно закрыть, когда запись закончена.
| Клавиша | Символ | Операция |
|---|---|---|
| pi | pi | Постоянная pi |
| е | е | Число Эйлера |
| % | % | Процент |
| () | () | Открыть/Закрыть скобки |
| , | , | Запятая |
| sin | sin(?) | Синус угла |
| cos | cos(?) | Косинус |
| tan | tan(y) | Тангенс |
| sinh | sinh() | Гиперболический синус |
| cosh | cosh() | Гиперболический косинус |
| tanh | tanh() | Гиперболический тангенс |
| sin -1 | asin() | Обратный синус |
| cos -1 | acos() | Обратный косинус |
| tan -1 | atan() | Обратный тангенс |
| sinh -1 | asinh() | Обратный гиперболический синус |
| cosh -1 | acosh() | Обратный гиперболический косинус |
| tanh -1 | atanh() | Обратный гиперболический тангенс |
| x 2 | ^2 | Возведение в квадрат |
| х 3 | ^3 | Возведение в куб |
| x y | ^ | Возведение в степень |
| 10 x | 10^() | Возведение в степень по основанию 10 |
| e x | exp() | Возведение в степень числа Эйлера |
| vx | sqrt(x) | Квадратный корень |
| 3 vx | sqrt3(x) | Корень 3-ей степени |
| y vx | sqrt(x,y) | Извлечение корня |
| log 2 x | log2(x) | Двоичный логарифм |
| log | log(x) | Десятичный логарифм |
| ln | ln(x) | Натуральный логарифм |
| log y x | log(x,y) | Логарифм |
| I / II | Сворачивание/Вызов дополнительных функций | |
| Unit | Конвертер величин | |
| Matrix | Матрицы | |
| Solve | Уравнения и системы уравнений | |
| Построение графиков | ||
| Дополнительные функции (вызов клавишей II) | ||
| mod | mod | Деление с остатком |
| ! | ! | Факториал |
| i / j | i / j | Мнимая единица |
| Re | Re() | Выделение целой действительной части |
| Im | Im() | Исключение действительной части |
| |x| | abs() | Модуль числа |
| Arg | arg() | Аргумент функции |
| nCr | ncr() | Биноминальный коэффициент |
| gcd | gcd() | НОД |
| lcm | lcm() | НОК |
| sum | sum() | Суммарное значение всех решений |
| fac | factorize() | Разложение на простые множители |
| diff | diff() | Дифференцирование |
| Deg | Градусы | |
| Rad | Радианы | |
Применение уравнений широко распространено в нашей жизни.
{nm}:\]
Прибавляем к исходному уравнению:
Вынесем за скобки \
Выразим \
Поскольку степени одинаковые, отбрасываем их:
Ответ: \
Где можно решить показательное уравнение онлайн решателем?
Решить уравнение вы можете на нашем сайте https://сайт. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Сервис для решения уравнений онлайн поможет вам решить любое уравнение. Используя наш сайт, вы получите не просто ответ уравнения, но и увидите подробное решение, то есть пошаговое отображение процесса получения результата. Наш сервис будет полезен старшеклассникам общеобразовательных школ и их родителям.
Ученики смогут подготовиться к контрольным, экзаменам, проверить свои знания, а родители – проконтролировать решение математических уравнений своими детьми. Умение решать уравнения – обязательное требование к школьникам. Сервис поможет вам самообучаться и повышать уровень знаний в области математических уравнений. С его помощью вы сможете решить любое уравнение: квадратное, кубическое, иррациональное, тригонометрическое и др. Польза онлайн сервиса бесценна, ведь кроме верного ответа вы получаете подробное решение каждого уравнения. Преимущества решения уравнений онлайн. Решить любое уравнение онлайн на нашем сайте вы можете абсолютно бесплатно. Сервис полностью автоматический, вам ничего не придется устанавливать на свой компьютер, достаточно будет только ввести данные и программа выдаст решение. Любые ошибки в расчетах или опечатки исключены. С нами решить любое уравнение онлайн очень просто, поэтому обязательно используйте наш сайт для решения любых видов уравнений. Вам необходимо только ввести данные и расчет будет выполнен за считанные секунды.
2-4ac. Если дискриминант меньше нуля, то уравнение не имеет действительных корней (корни находятся из поля комплексных чисел), если равен нулю, то у уравнения один действительный корень, и если дискриминант больше нуля, то уравнение имеет два действительных корня, которые находятся по формуле: D= -b+-sqrt/2а. Для решения квадратного уравнения онлайн вам достаточно ввести коэффициенты такого уравнения (целые числа, дроби или десятичные значения). При наличии знаков вычитания в уравнении необходимо поставить минус перед соответствующими членами уравнения. Решить квадратное уравнение онлайн можно и в зависимости от параметра, то есть переменных в коэффициентах уравнения. С этой задачей отлично справляется наш онлайн сервис по нахождению общих решений. Линейные уравнения. Для решения линейных уравнений (или системы уравнений) на практике используются четыре основных метода. Опишем каждый метод подробно. Метод подстановки. Решение уравнений методом подстановки требует выразить одну переменную через остальные.
После этого выражение подставляется в другие уравнения системы. Отсюда и название метода решения, то есть вместо переменной подставляется ее выражение через остальные переменные. На практике метод требует сложных вычислений, хотя и простой в понимании, поэтому решение такого уравнения онлайн поможет сэкономить время и облегчить вычисления. Вам достаточно указать количество неизвестных в уравнении и заполнить данные от линейных уравнений, далее сервис сделает расчет. Метод Гаусса. В основе метода простейшие преобразования системы с целью прийти к равносильной системе треугольного вида. Из нее поочередно определяются неизвестные. На практике требуется решить такое уравнение онлайн с подробным описанием, благодаря чему вы хорошо усвоите метод Гаусса для решения систем линейных уравнений. Запишите в правильном формате систему линейных уравнений и учтите количество неизвестных, чтобы безошибочно выполнить решение системы. Метод Крамера. Этим методом решаются системы уравнений в случаях, когда у системы единственное решение.
Главное математическое действие здесь – это вычисление матричных определителей. Решение уравнений методом Крамера проводится в режиме онлайн, результат вы получаете мгновенно с полным и подробным описанием. Достаточно лишь заполнить систему коэффициентами и выбрать количество неизвестных переменных. Матричный метод. Этот метод заключается в собрании коэффициентов при неизвестных в матрицу А, неизвестных – в столбец Х, а свободных членов в столбец В. Таким образом система линейных уравнений сводится к матричному уравнению вида АхХ=В. У этого уравнения единственное решение только если определитель матрицы А отличен от нуля, иначе у системы нет решений, либо бесконечное количество решений. Решение уравнений матричным методом заключается в нахождении обратной матрицы А.
для решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн .
При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.
сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения.
Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
Матричный метод решения систем линейных уравнений
Матричный метод может применяться в решении систем линейных уравнений, в которых число неизвестных равно числу уравнений, то есть систем линейных уравнений с квадратной матрицей коэффициентов при неизвестных.
Другое условие применимости матричного метода — невырожденность матрицы коэффициентов при неизвестных, то есть неравенство нулю определителя этой матрицы.
Систему линейных уравнений, при выполнении вышеназванных условий, можно представить в
матричном виде, а затем решить её путём отыскания обратной матрицы
к матрице системы.
Решение систем линейных уравнений матричным методом основано на следующем свойстве обратной матрицы: произведение обратной матрицы и исходной матрицы равно единичной матрице. Обратная матрица обозначается символом .
Пусть нужно решить систему линейных уравнений:
Запишем эту систему уравнений в матричном виде:
Обозначим отдельно как A матрицу коэффициентов при неизвестных и как B матрицу неизвестных и матрицу свободных членов
.
Тогда
То есть, для нахождения решений системы нужно обе части уравнения умножить на матрицу, обратную матрице коэффициентов при неизвестных и приравнять соответствующие элементы полученных матриц.
Алгоритм решения системы линейных уравнений матричным методом разберём на следующем
примере системы линейных уравнений второго порядка.
Пример 1. Решить матричным методом систему линейных уравнений:
Решение состоит из следующих шагов.
Шаг 1. Составляем следующие матрицы.
Матрица коэффициентов при неизвестных:
Матрица неизвестных:
Матрица свободных членов:
Это сделано для того, чтобы применить в решении уже записанные закономерности, основанные на свойстве обратной матрицы:
По выведенному выше последнему равенству и будем вычислять решения данной системы.
Но сначала проверим, не является ли матрица коэффициентов при неизвестных вырожденной, то есть можем ли вообще применять матричный метод:
.
Определитель этой матрицы не равен нулю, следовательно, можем применять матричный метод.
Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:
.
Шаг 3. Находим матрицу неизвестных:
Итак, получили решение:
.
Сделаем проверку:
Следовательно, ответ правильный.
Для второго примера выберем систему линейных уравнений третьего порядка.
Пример 2. Решить матричным методом систему линейных уравнений:
Шаг 1. Составляем следующие матрицы.
Матрица коэффициентов при неизвестных:
Матрица неизвестных:
Матрица свободных членов:
Проверим, не является ли матрица коэффициентов при неизвестных вырожденной:
.
Определитель этой матрицы не равен нулю, следовательно, можем применять матричный метод.
Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:
.
Шаг 3. Находим матрицу неизвестных:
Итак, получили решение:
.
Сделаем проверку:
Следовательно, ответ правильный.
Решить систему уравнений матричным методом самостоятельно, а затем посмотреть решение
Пример 3. Решить матричным методом систему линейных уравнений:
Посмотреть правильное решение и ответ.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Системы линейных уравнений
Всё по теме «Системы уравнений и неравенств»
Решение систем линейных уравнений методом подстановки и методом сложения
Решение систем линейных уравнений методом Крамера
Решение систем линейных уравнений методом Гаусса
Условие совместности системы линейных уравнений.
Теорема Кронекера-Капелли
Решение систем линейных уравнений матричным методом (обратной матрицы)
Системы линейных неравенств и выпуклые множества точек
Начало темы «Линейная алгебра»
Определители
Матрицы
Поделиться с друзьями
СЛАУ примеры решения задач, формулы и онлайн калькуляторы
Содержание:
- СЛАУ: основные понятия, виды
- Критерий совместности системы
- Квадратные СЛАУ. Матричный метод решения
- Метод / Теорема Крамера
- Метод Гаусса. Метод последовательного исключения неизвестных
- Однородные СЛАУ. Фундаментальная система решений
Методы решения систем линейных уравнений широко используются в задачах математики, экономики, физики, химии и других науках.
На практике, они позволяют не делать лишних действий, а записать систему уравнений в более компактной форме и сократить время
выполнения задач. Поэтому, будущим специалистам очень важно понять основные методы решения и научиться выбирать оптимальный.
Перед изучением примеров решения задач советуем изучить теоретический материал по СЛАУ, прочитать все теоремы и методы решения. Список тем находится в правом меню.
Примеры по темам:
- СЛАУ: основные понятия, виды
- Критерий совместности системы. Теорема Кронекера-Капелли
- Квадратные СЛАУ. Матричный метод решения
- Решение методом Крамера
- Решение методом Гаусса
- Однородные СЛАУ. Фундаментальная система решений
СЛАУ: основные понятия, виды
Теоретический материал по теме — СЛАУ: основные понятия, виды.
Пример
Задание. Проверить, является ли набор ${0,3}$ решением системы $\left\{\begin{array}{l} 3 x-2 y=-6 \\ 5 x+y=3 \end{array}\right.$
Решение. Подставляем в каждое из уравнений системы $x=0$ и $y=3$ :
$$3 x-2 y=-6 \Rightarrow 3 \cdot 0-2 \cdot 3=-6 \Rightarrow-6=-6$$ $$5 x+y=3 \Rightarrow 5 \cdot 0+3=3 \Rightarrow 3=3$$
Так как в результате подстановки получили верные равенства, то делаем вывод, что заданный набор является
решением указанной СЛАУ.
Ответ. Набор ${0,3}$ является решением системы $\left\{\begin{array}{l} 3 x-2 y=-6 \\ 5 x+y=3 \end{array}\right.$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Систему $\left\{\begin{array}{l} x-y+z-4 t=0 \\ 5 x+y+t=-11 \end{array}\right.$ записать в матричной форме и выписать все матрицы, которые ей соответствуют.
Решение. Заданную СЛАУ записываем в матричной форме $A \cdot X=B$ , где матрица системы:
$$A=\left(\begin{array}{rrrr} 1 & -1 & 1 & -4 \\ 5 & 1 & 0 & 1 \end{array}\right)$$
вектор-столбец неизвестных:
$$A=\left(\begin{array}{rrrr} 1 & -1 & 1 & -4 \\ 5 & 1 & 0 & 1 \end{array}\right)$$
вектор-столбец свободных коэффициентов:
$$B=\left(\begin{array}{c} 0 \\ -11 \end{array}\right)$$
то есть, запись СЛАУ в матричной форме:
$$\left(\begin{array}{rrrr} 1 & -1 & 1 & -4 \\ 5 & 1 & 0 & 1 \end{array}\right)\left(\begin{array}{l} x \\ y \\ z \\ t \end{array}\right)=\left(\begin{array}{r} 0 \\ -11 \end{array}\right)$$
Пример
Задание.
Записать матрицу и расширенную матрицу системы
$\left\{\begin{array}{l}
2 x_{1}+x_{2}-x_{3}=4 \\
x_{1}-x_{2}=5
\end{array}\right.$
Решение. Матрица системы $A=\left(\begin{array}{rrr} 2 & 1 & -1 \\ 1 & -1 & 0 \end{array}\right)$ , тогда расширенная матрица $\tilde{A}=(A \mid B)=\left(\begin{array}{rrr|r} 2 & 1 & -1 & 4 \\ 1 & -1 & 0 & 5 \end{array}\right)$
Критерий совместности системы
Теоретический материал по теме — критерий совместности системы, теорема Кронекера-Капелли.
Пример
Задание. При каких значениях $\lambda$ система $\left\{\begin{array}{l} 2 x_{1}-x_{2}+x_{3}+x_{4}=1 \\ x_{1}+2 x_{2}-x_{3}+x_{4}=2 \\ x_{1}+7 x_{2}-4 x_{3}+2 x_{4}=\lambda \end{array}\right.$ будет совместной?
Решение. Ранг матрицы равен количеству ненулевых строк после приведения этой матрицы к ступенчатому виду. Поэтому записываем расширенную матрицу системы $\tilde{A}$ (слева от вертикальной черты находится матрица системы $A$ ):
$$\tilde{A}=\left(\begin{array}{rrrr|r} 2 & -1 & 1 & 1 & 1 \\ 1 & 2 & -1 & 1 & 2 \\ 1 & 7 & -4 & 2 & \lambda \end{array}\right)$$
и с помощью элементарных преобразований приводим ее к ступенчатому виду.
Для этого вначале от второй строки
отнимаем две вторых строки, а от третьей вторую, в результате получаем:
$$\tilde{A} \sim\left(\begin{array}{rrrr|r} 0 & -5 & 3 & -1 & -3 \\ 1 & 2 & -1 & 1 & 2 \\ 0 & 5 & -3 & 1 & \lambda-2 \end{array}\right)_{+I} \sim$$
Третью строку складываем с первой:
$$\tilde{A} \sim\left(\begin{array}{rrrr|r} 0 & -5 & 3 & -1 & -3 \\ 1 & 2 & -1 & 1 & 2 \\ 0 & 0 & 0 & 0 & \lambda-5 \end{array}\right)$$
и меняем первую и вторую строки матрицы местами
$$\tilde{A} \sim\left(\begin{array}{rrrr|r} 1 & 2 & -1 & 1 & 2 \\ 0 & -5 & 3 & -1 & -3 \\ 0 & 0 & 0 & 0 & \lambda-5 \end{array}\right)$$
Матрица приведена к ступенчатому виду. Получаем, что $rangA=2$
, $\operatorname{rang} \tilde{A}=\left\{\begin{array}{l}
2, \lambda=5 \\
3, \lambda \neq 5
\end{array}\right.
$ . Таким образом,
при $\lambda=5$ система совместна, а при
$\lambda \neq 5$ — несовместна.
Квадратные СЛАУ. Матричный метод решения
Теоретический материал по теме — матричный метод решения.
Пример
Задание. Найти решение СЛАУ $\left\{\begin{array}{l}5 x_{1}+2 x_{2}=7 \\ 2 x_{1}+x_{2}=9\end{array}\right.$ матричным методом.
Решение. Выпишем матрицу системы $\left\{\begin{array}{l}
5 x_{1}+2 x_{2}=7 \\
2 x_{1}+x_{2}=9
\end{array}\right.$ и
матрицу правых частей $B=\left(\begin{array}{l}
7 \\
9
\end{array}\right)$ . Найдем обратную
матрицу для матрицы системы. Для матрицы второго порядка обратную можно находить по следующему алгоритму: 1)
матрица должна быть невырождена, то есть ее определитель не должен равняться нулю: $|A|=1$ ; 2) элементы, стоящие на главной диагонали меняем местами,
а у элементов побочной диагонали меняем знак на противоположный и делим полученные элементы на определитель
матрицы. {-1} B=\left(\begin{array}{rr}
1 & -2 \\
-2 & 5
\end{array}\right) \cdot\left(\begin{array}{l}
7 \\
9
\end{array}\right)=$$
$$=\left(\begin{array}{r}
-11 \\
31
\end{array}\right) \Rightarrow\left(\begin{array}{l}
x_{1} \\
x_{2}
\end{array}\right)=\left(\begin{array}{r}
-11 \\
31
\end{array}\right)$$
Две матрицы одного размера равны, если равны их соответствующие элементы, то есть в итоге имеем, что $x_{1}=-11$, $x_{2}=31$
Ответ. $x_{1}=-11$, $x_{2}=31$
Пример
Задание. Решить с помощью обратной матрицы систему $\left\{\begin{array}{l} 2 x_{1}+x_{2}+x_{3}=2 \\ x_{1}-x_{2}=-2 \\ 3 x_{1}-x_{2}+2 x_{3}=2 \end{array}\right.$
Решение. Запишем данную систему в матричной форме:
$AX=B$,
где $A=\left(\begin{array}{rrr}
2 & 1 & 1 \\
1 & -1 & 0 \\
3 & -1 & 2
\end{array}\right)$ — матрица системы,
$X=\left(\begin{array}{l}
x_{1} \\
x_{2} \\
x_{3}
\end{array}\right)$ — столбец неизвестных,
$B=\left(\begin{array}{r}
2 \\
-2 \\
2
\end{array}\right)$ — столбец правых частей. {3+3}\left|\begin{array}{rr}
2 & 1 \\
1 & -1
\end{array}\right|=-3$
Таким образом,
$\tilde{A}=\left(\begin{array}{rrr} -2 & -2 & 2 \\ -3 & 1 & 5 \\ 1 & 1 & -3 \end{array}\right)$
Определитель матрицы $A$
$$\Delta=\left|\begin{array}{rrr} 2 & 1 & 1 \\ 1 & -1 & 0 \\ 3 & -1 & 2 \end{array}\right|=2 \cdot(-1) \cdot 2+1 \cdot(-1) \cdot 1+1 \cdot 0 \cdot 3-$$ $$-3 \cdot(-1) \cdot 1-(-1) \cdot 0 \cdot 2-1 \cdot 1 \cdot 2=-4 \neq 0$$
А тогда
$$\tilde{A}=-\frac{1}{4}\left(\begin{array}{rrr} -2 & -3 & 1 \\ -2 & 1 & 1 \\ 2 & 5 & -3 \end{array}\right)$$
Отсюда искомая матрица
$$X=\left(\begin{array}{c}
x_{1} \\
x_{2} \\
x_{3}
\end{array}\right)=-\frac{1}{4}\left(\begin{array}{rrr}
-2 & -3 & 1 \\
-2 & 1 & 1 \\
2 & 5 & -3
\end{array}\right)\left(\begin{array}{r}
2 \\
-2 \\
2
\end{array}\right)=$$
$$=\left(\begin{array}{r}
-1 \\
1 \\
3
\end{array}\right) \Rightarrow\left\{\begin{array}{l}
x_{1}=-1 \\
x_{2}=1 \\
x_{3}=3
\end{array}\right. $$
$$\left\{\begin{array}{l}
x_{1}=-1 \\
x_{2}=1 \\
x_{3}=3
\end{array}\right.$$
Метод / Теорема Крамера
Теоретический материал по теме — метод Крамера.
Пример
Задание. Найти решение СЛАУ $\left\{\begin{array}{l} 5 x_{1}+2 x_{2}=7 \\ 2 x_{1}+x_{2}=9 \end{array}\right.$ при помощи метода Крамера.
Решение. Вычисляем определитель матрицы системы:
$$\Delta=\left|\begin{array}{ll} 5 & 2 \\ 2 & 1 \end{array}\right|=5 \cdot 1-2 \cdot 2=1 \neq 0$$
Так как $\Delta \neq 0$ , то по теореме Крамера система совместна и имеет единственное решение. вычислим вспомогательные определители. Определитель $\Delta_{1}$ получим из определителя $\Delta$ заменой его первого столбца столбцом свободных коэффициентов. Будем иметь:
$$\Delta_{1}=\left|\begin{array}{ll} 7 & 2 \\ 9 & 1 \end{array}\right|=7-18=-11$$
Аналогично, определитель $\Delta_{2}$ получается из определителя матрицы системы $\Delta$ заменой второго столбца столбцом свободных коэффициентов:
$$\Delta_{2}=\left|\begin{array}{ll} 5 & 7 \\ 2 & 9 \end{array}\right|=45-14=31$$
Тогда получаем, что
$$x_{1}=\frac{\Delta_{1}}{\Delta}=\frac{-11}{1}=-11, x_{2}=\frac{\Delta_{2}}{\Delta}=\frac{31}{1}=31$$
Ответ. $x_{-1}=-11$, $x_{2} = 31$
Пример
Задание. При помощи формул Крамера найти решение системы $\left\{\begin{array}{l} 2 x_{1}+x_{2}+x_{3}=2 \\ x_{1}-x_{2}=-2 \\ 3 x_{1}-x_{2}+2 x_{3}=2 \end{array}\right.$
Решение. Вычисляем определитель матрицы системы:
$$\Delta=\left|\begin{array}{rrr} 2 & 1 & 1 \\ 1 & -1 & 0 \\ 3 & -1 & 2 \end{array}\right|=2 \cdot(-1) \cdot 2+1 \cdot(-1) \cdot 1+1 \cdot 0 \cdot 3-$$ $$-3 \cdot(-1) \cdot 1-(-1) \cdot 0 \cdot 2-1 \cdot 1 \cdot 2=-4 \neq 0$$
Так как определитель матрицы системы неравен нулю, то по теореме Крамера система совместна и имеет единственное решение. Для его нахождения вычислим следующие определители:
$$\Delta_{1}=\left|\begin{array}{rrr} 2 & 1 & 1 \\ -2 & -1 & 0 \\ 2 & -1 & 2 \end{array}\right|=2 \cdot(-1) \cdot 2+(-2) \cdot(-1) \cdot 1+$$ $$+1 \cdot 0 \cdot 2-2 \cdot(-1) \cdot 1-(-1) \cdot 0 \cdot 2-(-2) \cdot 1 \cdot 2=4$$ $$\Delta_{2}=\left|\begin{array}{rrr} 2 & 2 & 1 \\ 1 & -2 & 0 \\ 3 & 2 & 2 \end{array}\right|=2 \cdot(-2) \cdot 2+1 \cdot 2 \cdot 1+2 \cdot 0 \cdot 3-$$ $$-3 \cdot(-2) \cdot 1-2 \cdot 0 \cdot 2-1 \cdot 2 \cdot 2=-4$$ $$\Delta_{3}=\left|\begin{array}{rrr} 2 & 1 & 2 \\ 1 & -1 & -2 \\ 3 & -1 & 2 \end{array}\right|=2 \cdot(-1) \cdot 2+1 \cdot(-1) \cdot 2+$$ $$+1 \cdot(-2) \cdot 3-3 \cdot(-1) \cdot 2-(-1) \cdot(-2) \cdot 2-1 \cdot 1 \cdot 2=-12$$
Таким образом,
$x_{1}=\frac{\Delta_{1}}{\Delta}=\frac{4}{-4}=-1$ $x_{2}=\frac{\Delta_{2}}{\Delta}=\frac{-4}{-4}=1$ $x_{3}=\frac{\Delta_{3}}{\Delta}=\frac{-12}{-4}=3$
Ответ. $\left\{\begin{array}{l}x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3\end{array}\right.$
Метод Гаусса. Метод последовательного исключения неизвестных
Теоретический материал по теме — метод Гаусса.
Пример
Задание. Решить СЛАУ $\left\{\begin{array}{l} 2 x_{1}+x_{2}+x_{3}=2 \\ x_{1}-x_{2}=-2 \\ 3 x_{1}-x_{2}+2 x_{3}=2 \end{array}\right.$ методом Гаусса.
Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент $a_{1}$ равнялся 1 (это мы делаем для упрощения вычислений):
$$\tilde{A}=A \mid B=\left(\begin{array}{rrr|r} 2 & 1 & 1 & 2 \\ 1 & -1 & 0 & -2 \\ 3 & -1 & 2 & 2 \end{array}\right) \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 2 & 1 & 1 & 2 \\ 3 & -1 & 2 & 2 \end{array}\right)$$
Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых,
от третьей — три первых:
$$\tilde{A} \sim\left(\begin{array}{ccc|c} 1 & -1 & 0 & -2 \\ 0 & 3 & 1 & 6 \\ 0 & 2 & 2 & 8 \end{array}\right)$$
Все элементы третьей строки делим на два (или, что тоже самое, умножаем на $\frac{1}{2}$:
$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 3 & 1 & 6 \\ 0 & 1 & 1 & 4 \end{array}\right)$$
Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:
$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 3 & 1 & 6 \end{array}\right)$$
От третьей строки отнимаем вторую, умноженную на 3:
$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 0 & -2 & -6 \end{array}\right)$$
Умножив третью строку на $\left(-\frac{1}{2}\right)$ , получаем:
$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 0 & 1 & 3 \end{array}\right)$$
Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент
$$\tilde{A} \sim\left(\begin{array}{rrr|r}
1 & -1 & 0 & -2 \\
0 & 1 & 0 & 1 \\
0 & 0 & 1 & 3
\end{array}\right)$$
Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:
$$\tilde{A} \sim\left(\begin{array}{ccc|c} 1 & 0 & 0 & -1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 3 \end{array}\right)$$
Полученной матрице соответствует система
$\left\{\begin{array}{l} x_{1}+0 \cdot x_{2}+0 \cdot x_{3}=-1 \\ 0 \cdot x_{1}+x_{2}+0 \cdot x_{3}=1 \\ 0 \cdot x_{1}+0 \cdot x_{2}+x_{3}=3 \end{array}\right.$ или $\left\{\begin{array}{l} x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3 \end{array}\right.$
Ответ. $\left\{\begin{array}{l} x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3 \end{array}\right.$
Однородные СЛАУ.
Фундаментальная система решенийТеоретический материал по теме — однородные СЛАУ.
Пример
Задание. Выяснить, имеет ли однородная СЛАУ $\left\{\begin{array}{l} 3 x-2 y=-1 \\ x+3 y=7 \end{array}\right.$ ненулевые решения.
Решение. Вычислим определитель матрицы системы:
$$\Delta=\left|\begin{array}{rr} 3 & -2 \\ 1 & 3 \end{array}\right|=9-(-2)=9+2=11 \neq 0$$
Так как определитель не равен нулю, то система имеет только нулевое решение $x=y=0$
Ответ. Система имеет только нулевое решение.
Пример
Задание. Найти общее решение и ФСР однородной системы $\Delta=\left|\begin{array}{rr} 3 & -2 \\ 1 & 3 \end{array}\right|=9-(-2)=9+2=11 \neq 0$
Решение. Приведем систему к ступенчатому виду с помощью метода Гаусса. Для этого записываем матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут получаться нули):
$$A=\left(\begin{array}{rrrrr} 1 & 1 & 0 & -3 & -1 \\ 1 & -2 & 2 & -1 & 0 \\ 4 & -2 & 6 & 3 & -4 \\ 2 & 4 & -2 & 4 & -7 \end{array}\right)$$
с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем
первую, от третьей — четыре первых, от четвертой — две первых:
$$A \sim\left(\begin{array}{rrrrr} 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & -6 & 6 & 15 & 0 \\ 0 & 2 & -2 & 10 & -5 \end{array}\right)$$
Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три вторых, к четвертой прибавляем вторую:
$$A \sim\left(\begin{array}{rrrrr} 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 9 & -3 \\ 0 & 0 & 0 & 12 & -4 \end{array}\right)$$
От четвертой строки отнимем $$\frac{4}{3}$$ третьей и третью строку умножим на $$\frac{1}{3}$$ :
$$A \sim\left(\begin{array}{rrrrr} 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 3 & -1 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right)$$
Нулевые строки можно далее не рассматривать, тогда получаем, что
$$A \sim\left(\begin{array}{rrrrr} 1 & 1 & 0 & -3 & -1 \\ 0 & -2 & 2 & 2 & 1 \\ 0 & 0 & 0 & 3 & -1 \end{array}\right)$$
Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а ко второй строке прибавляем третью:
$$A \sim\left(\begin{array}{rrrrr} 1 & 1 & 0 & -6 & 0 \\ 0 & -2 & 2 & 5 & 0 \\ 0 & 0 & 0 & 3 & -1 \end{array}\right)$$
то есть получаем систему, соответствующую данной матрице:
$$\left\{\begin{array}{l}
x_{1}+x_{2}-6 x_{4}=0 \\
-2 x_{2}+2 x_{3}+5 x_{4}=0 \\
3 x_{4}-x_{5}=0
\end{array}\right. $$
Или, выразив одни переменные через другие, будем иметь:
$$\left\{\begin{array}{l} x_{1}=-x_{2}+6 x_{4} \\ x_{2}=x_{2} \\ x_{3}=x_{2}-\frac{5}{2} x_{4} \\ x_{4}=x_{4} \\ x_{5}=3 x_{4} \end{array}\right.$$
Здесь $x_{2}, x_{4}$ — независимые (или свободные) переменные (это те переменные, через которые мы выражаем остальные переменные), $x_{1},x_{3},x_{5}$ — зависимые (связанные) переменные (то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных $n$ (в рассматриваемом примере $n=5$ , так как система зависит от пяти переменных) и ранга матрицы $r$ (в этом случае получили, что $r=3$ — количество ненулевых строк после приведения матрицы к ступенчатому виду): $n-r=5-3=2$
Так как ранг матрицы $r=3$ , а количество неизвестных
системы $n=5$ , то тогда количество решений в ФСР $n-r=5-3-2$ (для проверки, это число должно равняться количеству свободных переменных).
Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки). В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:
$$\left\{\begin{array}{l} x_{1}=-x_{2}+6 x_{4} \\ x_{3}=x_{2}-\frac{5}{2} x_{4} \\ x_{5}=3 x_{4} \end{array}\right.$$
Тогда придавая в первом случае, например, независимым переменным значения
$x_{2}=1$ , $x_{4}=0$ получаем, что
$\left\{\begin{array}{l}
x_{1}=-1+6 \cdot 0=-1 \\
x_{3}=1-\frac{5}{2} \cdot 0=1 \\
x_{5}=3 \cdot 0=0
\end{array}\right.$ . Полученные значения записываем в первую
строку таблицы. Аналогично, беря $x_{2}=0$ , $x_{4}=2$, будем иметь, что
$x_{1}=12,x_{3}=-5,x_{5}=6$ , что и определяет второе решение ФСР.
В итоге получаем следующую таблицу:
Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:
$$\left\{\begin{array}{l} x_{1}=-1+6 \cdot 0=-1 \\ x_{3}=1-\frac{5}{2} \cdot 0=1 \\ x_{5}=3 \cdot 0=0 \end{array}\right.$$
Общее решение является линейной комбинацией частных решений:
$$X=C_{1} X_{1}+C_{2} X_{2}=C_{1}\left(\begin{array}{r} -1 \\ 1 \\ 1 \\ 0 \\ 0 \end{array}\right)+C_{2}\left(\begin{array}{r} 12 \\ 0 \\ -5 \\ 2 \\ 6 \end{array}\right)$$
где коэффициенты $C_{1}, C_{2}$ не равны нулю одновременно. Или запишем общее решение в таком виде:
$\left\{\begin{array}{l}
x_{1}=-C_{1}+12 C_{2} \\
x_{2}=C_{1} \\
x_{3}=C_{1}-5 C_{2} \\
x_{4}=2 C_{2} \\
x_{5}=6 C_{2}
\end{array}\right. $
$C_{1}, C_{2} \neq 0$
Придавая константам $C_{1}, C_{2}$ определенные значения и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.
Читать первую тему — СЛАУ: основные понятия, виды, раздела системы линейных алгебраических уравнений.
Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).
Пусть система линейных алгебраических уравнений задана в матричной форме , где матрицаAимеет размерностьnнаnи ее определитель отличен от нуля.
Так как , то матрицаА– обратима, то есть, существует обратная матрица. Если умножить обе части равенстванаслева, то получим формулу для нахождения матрицы-столбца неизвестных переменных. Так мы получили решение системы линейных алгебраических уравнений матричным методом.
Пример.
Решите систему линейных уравнений матричным методом.
Решение.
Перепишем систему уравнений в матричной форме:
Так
как
то
СЛАУ можно решать матричным методом. С
помощью обратной матрицы решение этой
системы может быть найдено как.
Построим обратную матрицу с помощью матрицы из алгебраических дополнений элементов матрицыА(при необходимости смотрите статьюметоды нахождения обратной матрицы):
Осталось вычислить — матрицу неизвестных переменных, умножив обратную матрицуна матрицу-столбец свободных членов(при необходимости смотрите статьюоперации над матрицами):
Ответ:
или в другой записи x1 = 4, x2 = 0, x3 = -1.
Основная проблема при нахождении решения систем линейных алгебраических уравнений матричным методом заключается в трудоемкости нахождения обратной матрицы, особенно для квадратных матриц порядка выше третьего.
Более подробное описание теории и дополнительные примеры смотрите в статье матричный метод решения систем линейных уравнений.
К началу страницы
Пусть
нам требуется найти решение системы из nлинейных уравнений сnнеизвестными
переменнымиопределитель
основной матрицы которой отличен от
нуля.
Суть метода Гауссасостоит в последовательном исключении неизвестных переменных: сначала исключаетсяx1из всех уравнений системы, начиная со второго, далее исключаетсяx2из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменнаяxn. Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называетсяпрямым ходом метода Гаусса. После завершения прямого хода метода Гаусса из последнего уравнения находитсяxn, с помощью этого значения из предпоследнего уравнения вычисляетсяxn-1, и так далее, из первого уравнения находитсяx1. Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называетсяобратным ходом метода Гаусса.
Кратко
опишем алгоритм исключения неизвестных
переменных.
Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменнуюx1из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на, к третьему уравнению прибавим первое, умноженное на, и так далее, кn-омууравнению прибавим первое, умноженное на. Система уравнений после таких преобразований примет видгде, а.
К такому же результату мы бы пришли, если бы выразили x1через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменнаяx1исключена из всех уравнений, начиная со второго.
Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке
Будем
считать, что
(в
противном случае мы переставим местами
вторую строку сk-ой, где).
Приступаем к исключению неизвестной
переменнойx2из всех
уравнений, начиная с третьего.
Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на, и так далее, кn-омууравнению прибавим второе, умноженное на. Система уравнений после таких преобразований примет видгде, а. Таким образом, переменнаяx2исключена из всех уравнений, начиная с третьего.
Далее приступаем к исключению неизвестной x3, при этом действуем аналогично с отмеченной на рисунке частью системы
Так продолжаем прямой ход метода Гаусса пока система не примет вид
С этого момента начинаем обратный ход метода Гаусса: вычисляем xnиз последнего уравнения как, с помощью полученного значенияxnнаходимxn-1из предпоследнего уравнения, и так далее, находимx1из первого уравнения.
Пример.
Решите систему линейных уравнений методом Гаусса.
Решение.
Исключим
неизвестную переменную x1из второго и третьего уравнения системы. Для этого к обеим частям второго и
третьего уравнений прибавим соответствующие
части первого уравнения, умноженные наи
насоответственно:
Теперь из третьего уравнения исключим x2, прибавив к его левой и правой частям левую и правую части второго уравнения, умноженные на:
На этом прямой ход метода Гаусса закончен, начинаем обратный ход.
Из последнего уравнения полученной системы уравнений находим x3:
Из второго уравнения получаем .
Из первого уравнения находим оставшуюся неизвестную переменную и этим завершаем обратный ход метода Гаусса .
Ответ:
x1 = 4, x2 = 0, x3 = -1.
Более детальную информацию и дополнительные примеры смотрите в разделе решение элементарных систем линейных алгебраических уравнений методом Гаусса.
К началу страницы
Решить систему тремя способами
Компьютеры admin 0 комментариев
Содержание
- 1 Любые системы уравнений
- 2 Решение системы линейных уравнений методом Крамера
- 3 Методом Гаусса
- 4 Пример решения системы линейных уравнений с помощью метода обратной матрицы
Любые системы уравнений
Этот онлайн калькулятор в два шага:
- Добавить нужное кол-во уравнений
- Ввести уравнения
Решение системы линейных уравнений методом Крамера
Это он-лайн сервис в два шага:
- Ввести количество уравнений в системе
- Ввести коэффициенты при неизвестных слагаемых
Методом Гаусса
Этот онлайн калькулятор в три шага:
- Ввести количество уравнений в системе
- Ввести количество незвестных
- Ввести коэффициенты при неизвестных слагаемых
© Контрольная работа РУ — калькуляторы онлайн
В данной статье мы расскажем о матричном методе решения системы линейных алгебраических уравнений, найдем его определение и приведем примеры решения.
Метод обратной матрицы — это метод, использующийся при решении СЛАУ в том случае, если число неизвестных равняется числу уравнений.
Найти решение системы n линейных уравнений с n неизвестными:
a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n
Матричный вид записи: А × X = B
где А = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а n 1 а n 2 ⋯ а n n — матрица системы.
X = x 1 x 2 ⋮ x n — столбец неизвестных,
B = b 1 b 2 ⋮ b n — столбец свободных коэффициентов.
Из уравнения, которое мы получили, необходимо выразить X . Для этого нужно умножить обе части матричного уравнения слева на A — 1 :
A — 1 × A × X = A — 1 × B .
Так как А — 1 × А = Е , то Е × X = А — 1 × В или X = А — 1 × В .
Обратная матрица к матрице А имеет право на существование только, если выполняется условие d e t A н е р а в е н н у л ю . Поэтому при решении СЛАУ методом обратной матрицы, в первую очередь находится d e t А .
В том случае, если d e t A н е р а в е н н у л ю , у системы имеется только один вариант решения: при помощи метода обратной матрицы. Если d e t А = 0 , то систему нельзя решить данным методом.
Пример решения системы линейных уравнений с помощью метода обратной матрицы
Решаем СЛАУ методом обратной матрицы:
2 x 1 — 4 x 2 + 3 x 3 = 1 x 1 — 2 x 2 + 4 x 3 = 3 3 x 1 — x 2 + 5 x 3 = 2
- Записываем систему в виде матричного уравнения А X = B , где
А = 2 — 4 3 1 — 2 4 3 — 1 5 , X = x 1 x 2 x 3 , B = 1 3 2 .
- Выражаем из этого уравнения X :
- Находим определитель матрицы А :
d e t A = 2 — 4 3 1 — 2 4 3 — 1 5 = 2 × ( — 2 ) × 5 + 3 × ( — 4 ) × 4 + 3 × ( — 1 ) × 1 — 3 × ( — 2 ) × 3 — — 1 × ( — 4 ) × 5 — 2 × 4 — ( — 1 ) = — 20 — 48 — 3 + 18 + 20 + 8 = — 25
d e t А не равняется 0, следовательно для этой системы подходит метод решения обратной матрицей.
- Находим обратную матрицу А — 1 при помощи союзной матрицы.
Вычисляем алгебраические дополнения А i j к соответствующим элементам матрицы А :
А 11 = ( — 1 ) ( 1 + 1 ) — 2 4 — 1 5 = — 10 + 4 = — 6 ,
А 12 = ( — 1 ) 1 + 2 1 4 3 5 = — ( 5 — 12 ) = 7 ,
А 13 = ( — 1 ) 1 + 3 1 — 2 3 — 1 = — 1 + 6 = 5 ,
А 21 = ( — 1 ) 2 + 1 — 4 3 — 1 5 = — ( — 20 + 3 ) = 17 ,
А 22 = ( — 1 ) 2 + 2 2 3 3 5 — 10 — 9 = 1 ,
А 23 = ( — 1 ) 2 + 3 2 — 4 3 — 1 = — ( — 2 + 12 ) = — 10 ,
А 31 = ( — 1 ) 3 + 1 — 4 3 — 2 4 = — 16 + 6 = — 10 ,
А 32 = ( — 1 ) 3 + 2 2 3 1 4 = — ( 8 — 3 ) = — 5 ,
А 33 = ( — 1 ) 3 + 3 2 — 4 1 — 2 = — 4 + 4 = 0 .
- Записываем союзную матрицу А * , которая составлена из алгебраических дополнений матрицы А :
А * = — 6 7 5 17 1 — 10 — 10 — 5 0
- Записываем обратную матрицу согласно формуле:
A — 1 = 1 d e t A ( A * ) T : А — 1 = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 ,
- Умножаем обратную матрицу А — 1 на столбец свободных членов В и получаем решение системы:
X = A — 1 × B = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 1 3 2 = — 1 25 — 6 + 51 — 20 7 + 3 — 10 5 — 30 + 0 = — 1 0 1
Ответ: x 1 = — 1 ; x 2 = 0 ; x 3 = 1
Эта страничка поможет решить Системы Линейных Алгебраических Уравнений (СЛАУ) методом Гаусса, матричным методом или методом Крамера, исследовать их на совместность (теорема Кронекера-Капелли), определить количество решений, найти общее, частное и базисные решения.
Введите коэффициенты при неизвестных в поля. Если Ваше уравнение имеет меньшее количество неизвестных, то оставьте пустыми поля при переменных, не входящих в ваше уравнение. Можно использовать дроби ( 13/31 ).
[ Калькулятор матриц ] в App Store
Описание
Вас когда-нибудь просили объявить размер матрицы, прежде чем начать печатать? Нет больше этого! Калькулятор матриц был разработан, чтобы исправить все недостатки наших конкурентов.
Чтобы создать матрицу, вам нужно всего лишь начать печатать. Вы можете добавить новую ячейку, проведя пальцем по клавиатуре или нажав кнопку со стрелкой. Когда вы закончите, просто нажмите кнопку операции, чтобы выполнить расчет!
Мы также заметили, что неудобно копировать матрицу из книги на свое устройство из-за необходимости переключения вида между экраном и бумагой. Это сильно утомляет наши глаза. Вот почему мы представляем совершенно новый подход, никогда ранее не использовавшийся ни в одном другом приложении! Мы позволяем пользователю сделать экран прозрачным с помощью задней камеры. Благодаря этому вам нужно только сосредоточиться на экране! Вместо того, чтобы представлять, как это работает, просто попробуйте, вам понравится так же, как и нам!
Через секунду вы забудете, что имеете дело с матрицами из-за простоты использования, похожей на базовый калькулятор.
Версия 3.2.6
Обновление значка, исправление ошибки
Рейтинги и обзоры
5 оценок
Больше операций! Больше функций!
Это красивое и очень отточенное приложение, но ТОЛЬКО умножение? Остальные операции (сложение, вычитание, деление) мне бы точно понравились. На самом деле, это очень нужно.
Закрывается
Я даже не смог увидеть эффективность этого приложения, кроме того факта, что оно продолжает закрываться без всякой причины. Пожалуйста, исправьте эту проблему
Улучшенные инструкции
Почитав отзывы, считаю, что более полная инструкция устранила бы большую часть негатива. Например, нужно перейти в настройки этого приложения, чтобы видеть через камеру и десятичные дроби вместо дробей. Пришлось включить яркость на iPhone на полную для лучшей видимости. Пришлось научиться удерживать клавишу стирания, чтобы удалить предыдущие расчеты матриц. Намного лучше, чем вручную. Пролистывание влево и вправо — хорошая функция, просто нужно объяснить, что свайп должен быть в области клавиатуры.
Спасибо за ваш отзыв, я очень рад видеть, что есть такие умные пользователи, как вы, которые используют Калькулятор матриц. Пожалуйста, свяжитесь с нами по электронной почте.
Разработчик Доминик Варшевски указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика.
Данные, используемые для отслеживания вас
Следующие данные могут использоваться для отслеживания вас в приложениях и на веб-сайтах, принадлежащих другим компаниям:
- Идентификаторы
- Данные об использовании
Данные, не связанные с вами
Могут быть собраны следующие данные, но они не связаны с вашей личностью:
- Идентификаторы
- Данные об использовании
Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста. Узнать больше
Информация
- Продавец
- Доминик Варшевски
- Размер
- 7,8 МБ
- Категория
- Утилиты
- Возрастной рейтинг
- 4+
- Авторское право
- © appassion.net
- Цена
- Бесплатно
- Сайт разработчика
- Тех. поддержка
- Политика конфиденциальности
Еще от этого разработчика
Вам также может понравиться
Калькулятор матричных операций — с пояснениями
- Калькуляторы
- ::
- Матрицы
- ::
- Калькулятор матричных операций
Этот решатель выполняет операции с матрицами, т. е. умножение , сложение и вычитание .
Калькулятор создаст пошаговое объяснение каждой из этих операций.
работающий…
Полиномиальные калькуляторы
Факторные полиномы
- Полиномиальные корни
- Синтетический отдел
- Полиномиальные операции
- Графические полиномы
- Расширить и упростить
- Генерировать из корней
Рациональные выражения
Упрощение
- Умножение/деление
- Сложение/вычитание
Подкоренные выражения
Рационализировать знаменатель
- Упрощение
Решение уравнений
Квадратные уравнения (с шагами)
- Полиномиальные уравнения
- Решение уравнений — с шагами
Квадратное уравнение
Решение (с шагами)
- Квадратичный плоттер
- Факторинг трехчленов
Геометрия
Равносторонний треугольник
- Прямоугольный треугольник
- Косой треугольник
- Калькулятор площади
- Калькулятор прямоугольника
- Калькулятор круга
Калькулятор шестиугольника
- Калькулятор ромба
Комплексные номера
Модуль, обратный, полярная форма
- Подразделение
- Упростить выражение
Системы уравнений
Система 2×2
- Система 3х3
- Система 4×4
Матрицы
Векторы (2D и 3D)
- Сложить, вычесть, умножить
- Калькулятор определителя
- Матрица обратная
- Характеристический полином
- собственные значения
- Собственные векторы
- Разложение матрицы
Расчетные калькуляторы
Калькулятор лимита
- Калькулятор производных
- Интегральный калькулятор
Последовательности и серии
Арифметические последовательности
- Геометрические последовательности
- Найти n й Срок
Аналитическая геометрия
Расстояние и середина
- Калькулятор треугольника
- Графические линии
- Пересечение линий
- Двухточечная форма
- Расстояние от линии до точки
- Параллельно/Перпендикулярно
- Уравнение окружности
- Круг из 3 точек
- Пересечение круговой линии
Тригонометрия
Градусов в Радиан
- Триггер Уравнения
Номера
Длинная дивизия
- Вычислить выражения
- Калькулятор дробей
- Наибольший общий делитель НОД
- Наименее распространенная кратная LCM
- Простые множители
- Научная нотация
- Калькулятор процентов
- Dec / Bin / Hex
- Калькулятор вероятности
- Распределения вероятностей
Описательная статистика
- Стандартное отклонение
- Z — Калькулятор очков
- Нормальное распределение
- Калькулятор Т-теста
- Корреляция и регрессия
Финансовые калькуляторы
Простые проценты
- Сложные проценты
- Калькулятор амортизации
- Калькулятор ренты
Прочие калькуляторы
Наборы
Проблемы с работой
примеров
пример 1:ex 1:
Умножить : $ \left[ \begin{массив}{cc} -3 и 2\ -5 и 4 \end{массив} \right] \cdot \left[ \begin{массив}{cc} -\frac{1}{2} & -3 \\ -6 & \фракция{4}{3} \end{массив} \right]$
пример 2:ex 2:
Умножить : $ \left[ \begin{массив}{cc} 4 и 2 и -2 \\ 3 и 8 и 6 \end{массив} \right] \cdot \left[ \begin{массив}{cc} 2 и 6 \\ 3 & -1 \\ -5 и 11 \end{массив} \right]$
пример 3:ex 3:
$$ \left[ \begin{array}{cc} 4 & \ гидроразрыв {2} {3} & -2 & \ гидроразрыв {1} {2} \\ -3 & 4 & -3 & \frac{3}{2} \\ 5 и 1 и -3 и 7 \\ \frac{1}{4} & 5 & 1 & 6 \end{массив} \right] \cdot \left[ \begin{массив}{cc} 5 и 2 & -\frac{5}{2} & 4 \\ 5 и 1 и 1 и 0 \\ 2 и 0 и 1 и -1 \\ 0 и -3 и 4 и 1 \end{array} \right]$$
Как ввести матрицу?
1: Матрица ввода, начиная с верхнего левого угла.
| Пример: Для ввода матрицы: | $ \left[ \begin{массив}{cc} -7 и 1/4\ -1,3 и -2/5 \end{массив} \right] $ | тип |
2: Нули вводить не нужно.
| Пример: Для ввода матрицы: | $ \left[ \begin{массив}{ccc} 0 и 1 и 0 \\ -1 & 0 & 0 \\ 0 и 0 и 2/3 \end{массив} \right] $ | тип |
3: Вы можете скопировать и вставить матрицу из Excel в 3 шага.
| Шаг 1: Скопируйте матрицу из Excel | Шаг 2: Выберите верхнюю правую ячейку | Шаг 3: Нажмите Ctrl+V |
4: Вам не нужно использовать полосы прокрутки, так как калькулятор автоматически удалит пустые строки и столбцы.
5: Для удаления матрицы
| Выделить всю матрицу | и нажмите удалить |
Поиск в нашей базе данных более 200 калькуляторов
227 700 716 Решенные проблемы
калькулятор кофакторов
Созданы Anna Szczepanek, Phd
Просматривали Wojciech SAS, Phd Candiddate и Jackater
: Phd 150007:
70008: , 2022
Содержание:- Как определить матрицу кофакторов?
- Как найти матрицу кофакторов?
- Матрица кофакторов 2×2
- Как использовать этот калькулятор матрицы кофакторов?
- Нахождение обратной матрицы методом кофакторов
- Часто задаваемые вопросы
Добро пожаловать в калькулятор матрицы кофакторов Omni! Не стесняйтесь использовать его всякий раз, когда вам нужно найти матрицу кофакторов данной квадратной матрицы. Если вы хотите узнать, как мы определяем матрицу кофакторов , или ищите пошаговую инструкцию на как найти матрицу кофакторов , не смотрите дальше! Прокрутите вниз, чтобы найти статью, в которой можно найти еще больше: мы расскажем, как быстро и легко вычислить матрицу кофактора 2×2 и раскроем секрет нахождения обратной матрицы методом кофактора!
Вы ищете кофактор метод расчета определителей? Посетите наш специальный калькулятор расширения кофактора!
Как определить матрицу кофакторов?
Матрица сомножителей данной квадратной матрицы состоит из первых миноров умножить на знаковые множители :
- Первый минор является определителем матрицы, вырезанной из исходной матрицы путем удаления одной строки и одного столбца.
- Коэффициент знака равен
-1, если индекс удаленной строки плюс индекс удаленного столбца равен нечетному числу; в противном случае коэффициент знака равен1.
Более формально, пусть A — квадратная матрица размера n × n . Рассмотрим i,j=1,...,n .
-
(i, j)-минор является определителем(n-1) × (n-1)подматрицыA, образованной удалениемi-й строки иj-й столбец. - Коэффициент знака равен
(-1) i+j. - Умножая минор на знаковый множитель, получаем
(i, j)-кофактор .
Помещение всех отдельных кофакторов в матрицу приводит к матрице кофакторов . Не волнуйтесь, если вы чувствуете себя немного ошеломленными всеми этими теоретическими знаниями — в следующем разделе мы превратим их в пошаговую инструкцию по нахождению матрицы кофакторов. Однако сначала давайте подробнее обсудим модель знакового фактора.
Шаблон знакового коэффициента
Формально знаковый коэффициент определяется как (-1) i+j , где i и j — индекс строки и столбца (соответственно) элемента, который мы сейчас рассматриваем. На самом деле, знаки, которые мы получаем таким образом, образуют красивый чередующийся узор , что облегчает запоминание знакового фактора:
матрицы, а затем чередует «-/+» в первой строке. Вторая строка начинается с «-», затем чередуются «+/−» и т. д.
Как найти матрицу кофакторов?
Предположим, A — это n × n матрица с действительными или комплексными элементами. Чтобы найти матрицу кофакторов A , выполните следующие действия:
Вычеркнуть
i-ю строку иj-й столбецA. Вы получаете(n - 1) × (n - 1)подматрицуA.Вычислите определитель этой подматрицы. Вы нашли
(i, j)-минор изА.Определить коэффициент знака
(-1) i+j.Умножьте
(i, j)— минор числаAна знаковый коэффициент. В результате получается именно (i, j)-кофакторA!Повторить шаги 1-4 для всех
i,j = 1,...,n.
👉 Если вам когда-нибудь понадобится вычислить матрицу сопряжения , помните , что это просто транспонирование матрицы кофакторов A .
Cofactor matrix 2×2
As an example, let’s discuss how to find the cofactor of the 2 x 2 matrix:
| ⌈ | a | b | ⌉ |
| ⌊ | в | г | ⌋ |
Коэффициентов четыре, поэтому мы повторим шаги 1, 2 и 3 из предыдущего раздела четыре раза.
Пусть
i=1иj=1.Когда мы вычеркнем первую строку и первый столбец, мы получим матрицу
1 × 1, единственный коэффициент которой равенd. Определитель такой матрицы также равен d. Знаковый множитель равен(-1) 1+1 = 1, поэтому(1, 1)-кофактор исходной матрицы2 × 2равенd.Пусть
i=1иj=2.Аналогично, удаление первой строки и второго столбца дает матрицу
1 × 1, содержащуюc. Его определитель равенc. Знаковый множитель равен(-1) 1+2 = -1, а(1, 2)-кофактор исходной матрицы равен-c.Пусть
i=2иj=1.Удалив вторую строку и первый столбец, получим
1 × 1 9Матрица 0569, содержащаяb. Его определитель равенb. Знаковый множитель равен(-1) 2+1 = -1, поэтому(2, 1)-кофактор нашей матрицы равен-b.Пусть
i=2иj=2.Наконец, мы удаляем вторую строку и второй столбец, что приводит к матрице
1 × 1, содержащейa. Его определитель равен(-1) 2+2 = 1, поэтому(2, 2)-кофактор исходной матрицы2 × 2равенa.
Далее запишем матрицу кофакторов , поставив (i, j) -кофактор в i -ю строку и j -й столбец:
-
(1, 1 )-кофактор идет в первую строку и первый столбец:
| ⌈ | д | ⌉ | |
| ⌊ | ⌋ |
86868 ( 686868 ( Как видите, определить матрицу кофакторов В отличие от случая Выберите размер матрицы ; Введите коэффициенты вашей матрицы; Совет: калькулятор матрицы кофакторов обновляет предварительный просмотр матрицы по мере ввода коэффициентов в поля калькулятора. Используйте эту функцию, чтобы проверить правильность матрицы. Вы можете найти матрицу кофакторов исходной матрицы в нижней части калькулятора. Матрица кофакторов играет важную роль, когда мы хотим инвертировать матрицу . Чтобы найти матрицу кофакторов матрицы 2x2, следуйте этим инструкциям: Чтобы найти Обратная матрица Чтобы найти миноры и кофакторы, вам нужно: Анна Щепанек, доктор философии Размер матрицы Введите коэффициенты в поля ниже. Пробелы интерпретируются как нули. Точность: 6 знаков после запятой. Первая строка Вторая ряд Матрица кофактора Проверьте 31 Аналогичные линейные кальцеристы алгебры 🔢 Содручающий матричный матричный матричный матричный декомпозит ... 28 еще 8 8 Затем нажмите на первую ячейку и введите значение, и перемещайтесь по матрице, нажимая «TAB» или щелкая соответствующие ячейки, чтобы
определить ВСЕ значения матрицы. Понятие обратной матрицы будет появляться во многих контекстах алгебры. Во-первых, для матриц идея состоит в том, чтобы иметь возможность оперировать ими
так же, как мы поступили бы с числами. А ведь есть разумные операции суммы, вычитания
и умножение матриц.
9{-1}\) или чаще записывается как \(\displaystyle \frac{1}{3}\). Одним из важнейших свойств этой инверсии является то, что при умножении на исходное число получается 1, это \(3 \cdot \displaystyle \frac{1}{3} = 1\).6868 (68 (868 (868 (6868 (868 (6868 (68 ( есть определитель числа ⌈ d -c ⌉ ⌊ ⌋ (2, 1) -cofactor goes to the second строка и первый столбец: ⌈ d -c ⌉ ⌊ -b ⌋ (2, 2) -cofactor goes to вторая строка и второй столбец: ⌈ d -c ⌉ ⌊ -b a ⌋ 2 × 2 совсем несложно. Как использовать этот калькулятор матрицы кофакторов?
2 × 2 , вычисление матрицы кофакторов для большей матрицы может быть утомительным — представьте себе вычисление нескольких десятков кофакторов... Не волнуйтесь! Калькулятор матрицы кофакторов Omni здесь, чтобы сэкономить ваше время и усилия! Выполните следующие действия, чтобы использовать наш калькулятор как профессионал: Нахождение обратной матрицы методом кофакторов
Если вы хотите найти обратную матрицу A с помощью матрицы кофакторов, выполните следующие действия: A . A . A . 1/детерминант(А) . Часто задаваемые вопросы
Как найти кофактор матрицы 2×2?
Как найти миноры матрицы 2×2?
(i, j) -й минор матрицы 2×2, вычеркните i -ю строку и j -й столбец вашей матрицы. Оставшийся элемент — это минор, который вы ищете. В частности: Как найти обратную матрицу с помощью кофактора?
A -1 определяется по формуле:
A -1 = 1/det(A) × cofactor(A) T ,5 9 det
A ; и кофактор(A) T является транспонированием матрицы кофактора матрицы A . Как найти миноры и кофакторы матрицы?
(i, j) -й минор, вычеркните i -ю строку и j -й столбец вашей матрицы и вычислите определитель оставшейся матрицы. (i, j) -й кофактор, умножьте (i, j) -й минор на знаковый коэффициент (-1) i+j . Invertible Matrix Calculator - Mathccracker.com
Invertible Matrix Calculator - Mathccracker.com
.
Инструкции: Используйте этот калькулятор, чтобы найти обратную матрицу, которую вы предоставили, показывая шаг за шагом. Сначала нажмите на одну из кнопок ниже, чтобы указать размерность матрицы. Подробнее об этом Калькулятор обратимой матрицы с шагами
Как определить и обратимую матрицу
Другими словами, обратная заданная матрица \(A\) — это матрица, обладающая тем свойством, что умножение этой матрицы на оригинал приводит к тождественная матрица I.
Как вычислить обратную матрицу?
Существует множество различных способов вычисления обратной матрицы \(A\). Одним из наиболее часто используемых методов является
формула сопряжения, в основе которой лежит вычислитель целой кучи определителей
подматриц, полученных удалением одной строки и одного столбца \(A\).
Обратите внимание, что этот калькулятор обратного вычисления также дает возможность вычислить обратное значение с помощью метода приведения по Гауссу к вычислить сокращенную форму эшелона строк расширенной матрицы.
Существует также метод поворота для преобразования исходной матрицы \(A\) в идентичность с использованием элементарных матриц, при этом отслеживая умножение из тех элементарных матриц, которая оказывается обратной. 9{-1}\]
Существуют также методы обратимости, основанные на некоторых разложениях, и, в конечном счете, матрицы с определенной полезной структурой могут быть
быстрее обрабатываются с точки зрения нахождения их обратных с помощью специализированных методов, применимых только к определенным структурам.
Какова формула обратной матрицы? 9{-1} = \displaystyle \frac{1}{\det(A)} adj(A)\]
На первый взгляд все просто! Но это не так много, когда размер матрицы большой. Действительно, приведенная выше формула говорит вам что для того, чтобы найти обратную, вам нужно вычислить определитель матрицы, а также вам нужно вычислить сопряженную матрицу.
Вопреки тому, что может показаться на первый взгляд, это может быть очень трудоемким из-за большого размера матрицы (например, \(n > 4\)). Итак, хорошо, что у нас есть компактная формула, но это не обязательно означает, что она не будет трудоемкой.
Как инвертировать матрицу 2x2?
Во-первых, вы должны убедиться, что \(\det(A) \ne 0\). {2+2} а
\end{bmatrix} = \begin{bmatrix}
д&-с \\\\-б&а
\конец{bmatrix}\]
9T = \displaystyle \frac{1}{ad - bc} \begin{bmatrix}
д&-б\-с&а
\конец{bmatrix}\]
Достаточно просто, да? Вы хотите попробовать для 3x3?
Как найти обратную матрицу 3x3?
Первым требованием, как и для всех матриц, является вычисление определителя и проверка того, что \(\det(A) \ne 0\). Затем нам нужно вспомнить общий присоединенная формула 9Т\]
где \(C\) — матрица кофакторов. Если бы вы написали это явно, вы бы получили что-то вроде этого: для \(A\) общая матрица 3x3:
\[ A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}\] 9Т\]
Для общей матрицы 3x3 \(A\) ее определитель равен
\[ \det(A) = a(e i - hf) - b(d i - g f) + c(d h - g e)\]
Также матрица кофакторов
\[ C = \begin{bmatrix} (-1)^{1+1} \begin{vmatrix} e & f\\\\ h& i \end{vmatrix} & (-1)^{1+2} \ begin{vmatrix} d & f\\\\ g & i \end{vmatrix} & (-1)^{1+3} \begin{vmatrix} d & e\\\\ g & h \end{vmatrix} \\\\ (-1)^{2+1} \begin{vmatrix} b & c \\\\ h & i \end{vmatrix} & (-1)^{2+2} \begin{vmatrix} a & c\\\\ g & i \end{vmatrix} & (-1)^{2+3} \begin{vmatrix} a & b\ \\\ g & h \end{vmatrix} \\\\ (-1)^{3+1} \begin{vmatrix} b & c\\\\ e & f \end{vmatrix} & (-1)^{3+2} \begin{vmatrix} a & c\ \\\ d& f \end{vmatrix} & (-1)^{3+3} \begin{vmatrix} a & b\\\\ d & e \end{vmatrix} \end{bmatrix}\] \[ = \begin{bmatrix} ei-fh & - (di - gf) & dh - ge \\ - (bi - hc) & ai - gc & - (ah - gb) \\ bf - ec & - (af-dc) & ae - db \end{bmatrix}\] \[ = \begin{bmatrix} ei-fh & gf - di & dh - ge \\ hc - bi & ai - gc & gb - ah \\ bf - ec & dc - af & ae - db \end{bmatrix}\] 9Т = \begin{bматрица} ei - fh & hc - bi & bf - ec \\ gf - di & ai - gc & dc - af \\ dh - ge & gb - ah & ae - db \конец{bmatrix}\]
Итак, наконец, у нас есть формула обратного выражения:
9T = \displaystyle \frac{1}{a(e i - hf) - b(d i - g f) + c(d h - g e))} \begin{bmatrix} ei - fh & hc - bi & bf - ec \\ gf - di & ai - gc & dc - af \\ dh - ge & gb - ah & ae - db \end{bmatrix} \] Готовы запомнить это? Конечно нет. {i+j}\). Опять же здесь, при вычислении субдетерминантов
убедитесь, что вы выбрали строку/столбец с наибольшим количеством нулей.
Шаг 3: Получив определитель исходной матрицы и матрицы кофакторов, разделите каждый компонент матрицы кофакторов на определитель, и результатом этого, наконец, является обратная матрица.
Как пользоваться этим обратным калькулятором
- Укажите размер матрицы
- Введите числа, определяющие матрицу
- Выберите метод, который вы предпочитаете использовать для вычисления обратного: «Сопряженная формула» или «Эшелонная форма с уменьшенной строкой».
- Нажмите «Рассчитать инверсию»
Пример: вычисление обратной матрицы
Вопрос: Рассмотрим следующую матрицу:
\[A = \begin{bmatrix}
\displaystyle 1&\displaystyle 2&\displaystyle 1\\[0. 6em]\displaystyle 2&\displaystyle 1&\displaystyle 4\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 1
\end{bmatrix}
\]
Найдите обратное значение по формуле сопряжения.
Решение: Нам нужно вычислить обратную заданную матрицу \(3 x 3\).
Шаг 1: Вычисление определителя матрицы
Используя формулу субдетерминанта, получаем:
\[ \begin{vmatrix}
\displaystyle 1&\displaystyle 2&\displaystyle 1\\[0.6em]\displaystyle 2&\displaystyle 1&\displaystyle 4\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 1
\end{vmatrix}
= 1 \cdot \left( 1 \cdot \left( 1 \right) - 1 \cdot \left(4 \right) \right) - 2 \cdot \left( 2 \cdot \left( 1 \right) - 1 \cdot \left(4 \right) \right) + 1 \cdot \left( 2 \cdot \left( 1 \right) - 1 \cdot \left(1 \right) \right)\] \[ = 1 \ cdot \left( -3 \right) - 2 \cdot \left( -2 \right) + 1 \cdot \left( 1 \right) = 2\]
9{ 3 3} = \begin{vmatrix}
\displaystyle 1&\displaystyle 2\\[0. 6em]\displaystyle 2&\displaystyle 1
\end{vmatrix}
= 1 \cdot \left( 1 \right) - 2 \cdot \left(2 \right) = -3\]
Подводя итоги, матрица миноров:
\[M = \begin{bmatrix} \displaystyle -3&\displaystyle -2&\displaystyle 1\\[0.6em]\displaystyle 1&\displaystyle 0&\displaystyle -1\\[0.6em]\displaystyle 7&\displaystyle 2&\displaystyle -3 \end{bmatrix} \] 9{ 6} \влево(-3\вправо) = 3\]
Подводя итог, матрица кофакторов:
\[C = \begin{bmatrix} \displaystyle -3&\displaystyle 2&\displaystyle 1\\[0.6em]\displaystyle -1&\displaystyle 0&\displaystyle 1\\[0.6em]\displaystyle -7&\displaystyle -2&\displaystyle 3 \end{bmatrix} \]
Шаг 3: Вычисление сопряженной матрицы из матрицы кофакторов
Теперь нам нужно транспонировать найденную матрицу кофакторов для вычисления сопряженной матрицы. Получаем: 9{-1} = \frac{1}{\det(A)} adj(A) = \frac{1}{2} \begin{bmatrix}
\displaystyle -3&\displaystyle -1&\displaystyle -7\\[0. 6em]\displaystyle 2&\displaystyle 0&\displaystyle -2\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 3
\end{bmatrix}
= \begin{bmatrix}
\displaystyle \frac{1}{2}\times\left(-3\right)&\displaystyle \frac{1}{2}\times\left(-1\right)&\displaystyle \frac{1}{ 2}\times\left(-7\right)\\[0.6em]\displaystyle \frac{1}{2}\times2&\displaystyle \frac{1}{2}\times0&\displaystyle \frac{1}{ 2}\times\left(-2\right)\\[0.6em]\displaystyle \frac{1}{2}\times1&\displaystyle \frac{1}{2}\times1&\displaystyle \frac{1}{ 2}\раз3
\end{bmatrix}
= \begin{bmatrix}
\displaystyle -\frac{3}{2}&\displaystyle -\frac{1}{2}&\displaystyle -\frac{7}{2}\\[0.6em]\displaystyle 1&\displaystyle 0&\displaystyle - 1\\[0.6em]\displaystyle \frac{1}{2}&\displaystyle \frac{1}{2}&\displaystyle \frac{3}{2}
\end{bmatrix}
\]
, что завершает вычисление обратной матрицы \(A\).
Numericware i: идентично с помощью калькулятора матрицы состояний
Обзор
. 2017 10 марта; 13:1176934316688663.
дои: 10.1177/1176934316688663. Электронная коллекция 2017.
Бонгсон Ким 1 , Уильям Д Бивис 1
принадлежность
- 1 Агрономический факультет Университета штата Айова, Эймс, Айова, США.
- PMID: 28469375
- PMCID: PMC5395260
- DOI: 10.1177/1176934316688663
Бесплатная статья ЧВК
Обзор
Bongsong Kim et al. Эвол Биоинформ Онлайн. .
Бесплатная статья ЧВК
. 2017 10 марта; 13:1176934316688663.
дои: 10.1177/1176934316688663. Электронная коллекция 2017.
Авторы
Бонгсон Ким 1 , Уильям Д Бивис 1
принадлежность
- 1 Агрономический факультет Университета штата Айова, Эймс, Айова, США.
- PMID: 28469375
- PMCID: PMC5395260
- DOI:
10. 1177/1176934316688663
Абстрактный
Мы представляем программное обеспечение Numericware i для вычисления матриц идентичности по штатам (IBS) на основе генотипических данных. Вычисление матрицы IBS с большим набором данных требует большой памяти компьютера и требует длительного времени обработки. Numericware i решает эти проблемы с помощью двух алгоритмических методов: многопоточности и прямого прерывания. Многопоточность позволяет вычислительным процедурам одновременно выполняться на нескольких процессорах центрального процессора (ЦП). Прямое прерывание устраняет ограничение памяти, разделяя набор данных на подмножества соответствующего размера. Numericware i позволяет рассчитать матрицу IBS для большого набора генотипических данных с помощью портативного или настольного компьютера. Для сравнения с другим программным обеспечением мы рассчитали матрицы генетических отношений с использованием Numericware i, SPAGeDi и TASSEL с тем же набором генотипических данных. Numericware i вычисляет коэффициенты IBS от 0 до 2, в то время как SPAGeDi и TASSEL производят различные диапазоны значений, включая отрицательные значения. Коэффициент корреляции Пирсона между матрицами от Numericware i и TASSEL был высоким и составлял 0,9.972, тогда как SPAGeDi показал низкую корреляцию с Numericware i (0,0505) и TASSEL (0,0587). Работая с многомерным набором данных из 500 сущностей по 10 000 000 SNP, Numericware i потратила 382 минуты, используя 19 потоков ЦП и 64 ГБ памяти, разделив набор данных на 3 части, в то время как SPAGeDi и TASSEL потерпели неудачу с одним и тем же набором данных. Numericware i находится в свободном доступе для Windows и Linux по лицензии CC-BY 4.0 по адресу https://figshare.com/s/f100f33a8857131eb2db.
Ключевые слова: Рубка вперед; Матрица генетического родства; Идентичен по матрице состояний; Многопоточность; Программное обеспечение i.
Заявление о конфликте интересов
Похожие статьи
Numericware N: Калькулятор матрицы взаимосвязей числителей.
Ким Б., Бивис В.Д., Леон Дж. Ким Б. и др. Дж. Херед. 2016;107(7):686-690. doi: 10.1093/jhered/esw057. Epub 2016 11 октября. Дж. Херед. 2016. PMID: 27729447
ICGRM: интегративное построение матрицы геномных отношений, объединяющей несколько геномных регионов для большого набора данных.
Цзян Д., Синь С., Е Дж., Юань И., Фан М. Цзян Д. и др. Биоинформатика BMC.
2019 26 декабря; 20 (1): 731. дои: 10.1186/s12859-019-3319-у.
Биоинформатика BMC. 2019.
PMID: 31878869
Бесплатная статья ЧВК.TASSEL-GBS: высокопроизводительный конвейер для генотипирования путем секвенирования.
Glaubitz JC, Casstevens TM, Lu F, Harriman J, Elshire RJ, Sun Q, Buckler ES. Glaubitz JC и соавт. ПЛОС Один. 28 февраля 2014 г.; 9(2):e
. doi: 10.1371/journal.pone.00. Электронная коллекция 2014.
ПЛОС Один. 2014.
PMID: 24587335
Бесплатная статья ЧВК.Высокопроизводительные вычисления для регистрации деформируемых изображений: на пути к новой парадигме адаптивной лучевой терапии.
Самант С.С., Ся Дж., Муян-Озчелик П., Оуэнс Д.Д. Самант С.С. и др. мед. физ. 2008 авг; 35 (8): 3546-53.
дои: 10.1118/1.2948318.
мед. физ. 2008.
PMID: 18777915Полностью трехмерная реконструкция ПЭТ-изображений в режиме списка во время полета на графических процессорах с использованием CUDA.
Cui JY, Pratx G, Prevrhal S, Levin CS. Cui JY и др. мед. физ. 2011 Декабрь; 38 (12): 6775-86. дои: 10.1118/1.3661998. мед. физ. 2011. PMID: 22149859
Посмотреть все похожие статьи
Цитируется
Неравновесие по сцеплению и структура популяции в базовой коллекции Brassica napus (L.).
Рахман М., Хок А., Рой Дж. Рахман М. и др. ПЛОС Один. 2022 1 марта; 17 (3): e0250310. doi: 10.1371/journal.pone.0250310. Электронная коллекция 2022. ПЛОС Один. 2022. PMID: 35231054 Бесплатная статья ЧВК.
Анализ генетического разнообразия мировой коллекции льна (Linum usitatissimum L.).
Хок А., Фидлер Д.Д., Рахман М. Хок А. и др. Геномика BMC. 2020 14 августа; 21 (1): 557. doi: 10.1186/s12864-020-06922-2. Геномика BMC. 2020. PMID: 32795254 Бесплатная статья ЧВК.
Классификация Oryza sativa образцов в Indica и Japonica с использованием модели логистической регрессии с фенотипическими данными.
Ким Б. Ким Б. Пир Дж. 2019 7 ноября; 7: e7259. doi: 10.7717/peerj.7259. Электронная коллекция 2019. Пир Дж. 2019. PMID: 31720092 Бесплатная статья ЧВК.
использованная литература
- Кокерхэм CC, Вейр BS. Дисперсия фактического инбридинга. Теория народной биологии. 1983;23:85–109.
-
пабмед
- Кокерхэм CC, Вейр BS.
- Райт С. Коэффициенты инбридинга и родства. Я Нат. 1922; 56: 330–338.
- Эмик Л.О., Террилл К.Э. Систематические процедуры расчета коэффициентов инбридинга. Дж. Херед. 1949;40:51–55. - пабмед
- Эдинг Х., Мейвиссен Т.Е. Маркерные оценки межпопуляционного и внутрипопуляционного родства для сохранения генетического разнообразия. Джей Аним Порода Генет. 2001; 118: 141–159.
- Эдинг Х., Мейвиссен Т.Е. Маркерные оценки межпопуляционного и внутрипопуляционного родства для сохранения генетического разнообразия.
- Бернардо Р. Селекция по количественным признакам растений. Вудбери, Миннесота: Stemma Press; 2002.
Типы публикаций
матричный калькулятор | Лучший калькулятор умножения матриц
Введение в матричный калькулятор
Сегодня мы обсудим работу матричного калькулятора . Матричная математика на самом деле представляет собой набор элементов, расположенных в строках и столбцах, и комбинацию линейного уравнения. В матричной математике
числа 1, 2, 3, 4,…..n
называются элементами или элементами матрицы. Матрица представлена следующими символами () , [] , || || , например.
$$\left[\begin{matrix} 2 & 1 & 3 \\ 4 & 2 & 1 \\ 3 & 3 & 2 \\ \end{matrix}\right] 3*3 $$
Есть например, многие типы матрицы; матрица-строка, матрица-столбец, квадратная матрица, нулевая матрица, единичная матрица, диагональная матрица, скалярная матрица, треугольная матрица, транспонированная матрица, симметричная матрица, косая матрица, равная матрица, алгебраическая матрица. Теперь мы узнаем, как матричный калькулятор выполняет свою функцию.
Несомненно, матрицы имеют различные приложения не только в различных разделах математики, но и в физике, экономике, технике, статистике и экономике. Итак, калькулятор равенства матриц в настоящее время имеет свои реальные преимущества.
Также найдите другие математические инструменты, такие как калькулятор правил логирования и калькулятор обратного логарифма.
Как матричный калькулятор умножает матричные уравнения
Давайте начнем с работы калькулятора симметричных матриц . Сначала я дам вам знать о размерах каждой матрицы, потому что не каждую матрицу можно умножить на другую матрицу. Итак, давайте посмотрим на размер этой первой матрицы, которая имеет 2 строки и 3 столбца, а вторая матрица имеет 3 строки и 3 столбца.
Таким образом, первая матрица представляет собой матрицу два на три. Если мы посмотрим на вторую матрицу, это матрица три на три. Таким образом, чтобы перемножить две матрицы вместе, столбцы в первой матрице должны быть равны строкам во второй матрице.
$$\left[\begin{matrix} 2 & 3 & 1 \\ 2 & -7 & 4 \\ \end{matrix}\right].\left[\begin{matrix} 3 & 4 & 5 \ \ 1 & 1 & 4 \\ 2 & 1 & 4 \\ \end{matrix}\right]$$
Эти два внутренних числа должны совпадать. Если эти два числа не совпадают, симметричный калькулятор не может перемножить две матрицы. Итак, убедитесь, что эти числа одинаковы, прежде чем умножать матрицы. Внешние числа дают вам размер новой матрицы после того, как вы сделали умножение. Здесь внешние числа 2 и 3, поэтому новый размер матрицы будет матрицей 2 на 3.
Теперь давайте начнем, что мы делаем, когда перемножаем две матрицы. Умножим строки первой матрицы на столбцы второй.
$$\left[\begin{matrix} 2 & 3 & 1 \\ 2 & -7 & 4 \\ \end{matrix}\right].\left[\begin{matrix} 3 & 4 & 5 \\ 1 & 1 & 4 \\ 2 & 1 & 4 \\ \end{matrix}\right]$$
калькулятор кососимметричных матриц умножит 2 первой матрицы на 3 второй матрицы, и так на. Мы выделили их одним цветом, чтобы было легче понять.
Матричный симметричный калькулятор будет умножать следующие столбцы с той же строкой.
После этого он применяет умножение ко 2-й строке первой матрицы со всеми столбцами 2-й матрицы.
Наконец,
$$=\left[\begin{matrix}11& 12& 26\\7&5&-2 \end{matrix}0\right 7$0\right Калькулятор кососимметричных матриц работает эффективно для вычисления результатов.
Калькулятор умножения матриц
В A есть матрица n*n, I также матрица n*n, в данном случае матрица n*n B. Она будет обозначаться как B = A -1 и будет сказано как обратную матрицу (AA -1 = A -1 A = I). Обратная матрица обозначается A -1 .
Чтобы получить обратную матрицу A, для которой существует A -1 , вычислитель равенства матриц выполняет следующие шаги. Прежде всего, сформируйте расширенную матрицу [A/I], в которой I является единичной матрицей размера n*n. Затем, чтобы получить матрицу [I/B], выполните преобразования строк на [A/I]. На самом деле здесь матрица B равна A -1 . На последнем шаге проверьте это, показав, что эти матрицы равны друг другу, например. B.A = A.B = I.
Связанный: используйте другие бесплатные математические инструменты, такие как калькулятор таблицы z-score, для практики и обучения.
Следует отметить, что каждая матрица не имеет обратной, а имеет только квадратную матрицу. Не обязательно, чтобы у каждой матрицы была обратная. И особое свойство обратной матрицы состоит в том, что она уникальна, но если она существует. Любая матрица имеет не более одной матрицы.
Как найти лучший матричный калькулятор?
Существует множество калькуляторов матричного произведения для нахождения матричного произведения . Вы найдете все эти калькуляторы матричных решений в Интернете, но ключ в том, чтобы найти лучший, который вычисляет матрицу без ошибок.
Calculatored имеет массу конвертеров и калькуляторов, и калькулятор матричных произведений является одним из них.