| Алгоритм Луна Вычисляет контрольную сумму последовательности цифр при помощи алгоритма Луна, вычисляет проверочную цифру (цифру, которую можно добавить к исходной последовательности, чтобы получить последовательность с контрольной суммой оканчивающейся на 0). |
| Антилогарифм Калькулятор для вычисления антилогарифма. |
| Аппроксимация функции одной переменной Калькулятор использует методы регрессии для аппроксимации функции одной переменной. |
| Арифметика римских чисел Калькулятор поддерживающий основные математические действия (сложение, вычитание, умножение и деление) над целыми числами, представленными римскими цифрами. |
| Быстрое возведение в степень по модулю Калькулятор возводит большие числа в степень по модулю |
| Вероятность возникновения некоторого числа событий при проведении нескольких испытаний. Испытания Бернулли. Используя формулу Бернулли, вычисляет вероятность возникновения нескольких событий. |
| Взаимно простые числа и попарно взаимно простые числа Этот калькулятор проверяет, являются ли введенные числа взаимно простыми и попарно взаимно простыми. Правило проверки описано под калькулятором. |
| Выражение длины разными единицами Калькулятор выражает заданную длину через разные единицы. |
| Вычисление выражений с несколькими переменными Калькулятор вычисляет значение математического выражения с несколькими переменными. |
| Вычисление производной по ее определению Этот онлайн калькулятор выполняет численное дифференцирование — приближенное вычисление производной функции в заданной точке. Используется метод перехода к пределу последовательными приближениями до достижения заданной точности. |
| Вычисление частной производной по ее определению Этот онлайн калькулятор выполняет численное дифференцирование функции нескольких переменных — приближенное вычисление всех частных производных функции в заданной точке — по всем переменным. |
| Генератор нормально распределенных случайных чисел Калькулятор генерирует заданное количество нормально распределенных случайных чисел, используя преобразование Бокса-Мюллера над равномерно распределенными случайными числами, полученными из встроенного в Javascript генератора случайных чисел. |
| Генератор последовательности выпадания чисел Калькулятор генерирует последовательность выпадания чисел из заданного диапазона. Например, порядок вытаскивания бочонков в лото — числа от 1 до 90 будут перечислены в случайном порядке, или лотерея «5 из 36». |
| Генератор случайной матрицы Этот онлайн калькулятор генерирует случайную матрицу с заданными параметрами. |
| Двоично-десятичное кодирование Калькулятор преобразует число из десятичное в двоичное, но записанное упакованным двоично-десятичным кодом, и наоборот. |
| Дополнение числа Этот онлайн калькулятор вычисляет дополнение числа и дополнение числа с уменьшенным основанием для заданной системы счисления |
| Дроби с факториалом Этот онлайн калькулятор вычисляет результат деления, когда и в числителе и в знаменателе находится факториал числа |
| Египетские дроби Калькулятор преобразует дробь в Египетскую дробь. |
| Египетские числа Калькулятор отображает числа в виде набора древнеегипетских иероглифов. |
| Задача про бочку и ведра Как набрать из бочки определенный объем воды, используя ведра разного размера? |
| Запись математических выражений Содержит калькулятор с примерами записи математических выражений. |
| Золотое сечение Расчет длин отрезков в золотом сечении. |
| Из египетской дроби в рациональное число Калькулятор преобразует египетскую дробь в простую дробь |
| Интерполяционный многочлен Лагранжа (полином Лагранжа) Этот онлайн калькулятор строит интерполяционный многочлен Лагранжа для заданного набора точек. Калькулятор также строит график, на который выводит как полином Лагранжа, так и базисные полиномы, интерполирует заданные точки и показывает пошаговое решение. |
| Интерполяционный многочлен Ньютона (полином Ньютона) Этот онлайн калькулятор строит интерполяционный многочлен Ньютона для заданного набора точек. |
| Ковариация Этот онлайн калькулятор рассчитывает значение ковариации, или корреляционного момента для двух дискретных случайных величин |
| Корень и степень Возведение в произвольную степень, извлечение корня произвольной степени. |
| Линейная рекуррентная последовательность Этот онлайн калькулятор выполняет расчет заданного числа членов линейной рекуррентной последовательности (возвратной последовательности), а также выводит их сумму нарастающим итогом. |
| Линейные диофантовы уравнения с двумя переменными Калькулятор решает линейные диофантовы уравнения с двумя переменными. |
| Мальтузианская модель роста Этот онлайн калькулятор по заданным начальным параметрам строит график мальтузианской модели роста также известной как экспоненциальный закон. |
| Метод Крамера с подробным решением Калькулятор для решения систем линейных уравнений методом Крамера. |
| Метод Рунге — Кутты Этот онлайн калькулятор реализует классический метод Рунге — Кутты (встречается также название метод Рунге — Кутта) четвертого порядка точности. Метод используется для решения дифференциальных уравнений первой степени с заданным начальным значением |
| Метод Эйлера Этот онлайн калькулятор реализует метод Эйлера, числовой метод решения дифференциальных уравнений первой степени первого порядка точности. |
| Метод итераций (метод последовательных приближений) Отыскание корней функциональных уравнений методом итераций (последовательных приближений). |
| Модель Ферхюльста Этот онлайн калькулятор по заданным начальным параметрам строит график уравнения Ферхюльста — Пирла, или логистическую кривую. |
| Наибольший общий делитель (НОД) двух целых чисел Этот калькулятор находит наибольший общий делитель (НОД) двух целых чисел алгоритмом Евклида. |
| Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК) нескольких чисел Этот калькулятор находит наибольший общий делитель (НОД) и наименьшее общее кратное (НОК) двух и более целых чисел, выполняя разложение чисел на простые множители. Описание алгоритма можно найти под калькулятором. |
| Наименьшее общее кратное и наибольший общий делитель двух целых чисел Нахождение наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК) двух целых чисел. |
| Наименьший общий знаменатель для двух или нескольких дробей Нахождение наименьшего общего знаменателя для двух или нескольких дробей. |
| Непрерывная дробь Калькулятор представляет обычную дробь в виде непрерывной (цепной) дроби. |
| Нормальное распределение Строит график плотности вероятности и функции плотности распределения для нормального распределения. |
| Обратная матрица Нахождение обратной матрицы с помощью союзной матрицы. |
| Обратная матрица по модулю Нахождение обратной матрицы по модулю с помощью союзной матрицы и обратного элемента в кольце по модулю. |
| Олимпиадные задания Калькуляторы, решающие несколько олимпиадных задач по математике. |
| Определение ранга матрицы Калькулятор, определяющий ранг матрицы |
| Определитель (детерминант) матрицы Расчет определителя (детерминанта) матрицы по определению. |
| Определитель матрицы методом Гаусса Нахождение определителя матрицы путем преобразования матрицы к треугольному виду. Работает в рациональных и комплексных числах |
| Остаток от деления Калькулятор выдает остаток от деления двух целых (или дробных) чисел. |
| Перевод меры угла из часовой системы в градусную и из градусной системы в часовую Статья содержит два калькулятора, первый предназначен для перевода угла из часовой меры в градусную, второй — из градусной меры в часовую |
| Подсчет суммы и произведения чисел, соответствующих буквам в слове Нумерологический калькулятор по запросу пользователя. |
| Поиск пропущенных номеров При помощи этого калькулятора можно искать пропуски в последовательности номеров. |
| Поиск простых чисел. Решето Эратосфена. Калькулятор находит простые числа используя алгоритм, известный как «Решето Эратосфена» |
| Приведение матрицы к треугольному виду Приведение матрицы к треугольному виду методом Гаусса и методом Барейса. |
| Производная показательно-степенной функции Функция возводится в степень самой себя заданное количество раз и затем берется производная. |
| Пропорция Расчет неизвестного члена пропорции. Создано по запросу пользователя. |
| Разложение квадратной матрицы на симметричную и кососимметричную матрицы Этот онлайн калькулятор представляет квадратную матрицу как сумму симметричной и кососимметричной матрицы |
| Распределение Стьюдента Вычисляет значение функции распределения и плотности вероятности для распределения Стьюдента. |
| Расстояние Левенштейна Калькулятор для расчета расстояния Левенштейна между двумя словами. |
| Расчет спирали Расчет неизвестных размеров спирали по известным размерам. Параметры спирали: внешний диаметр, внутренний диаметр, толщина (шаг спирали), длина спирали, число витков. |
| Расширенный алгоритм Евклида Калькулятор, реализующий расширенный алгоритм Евклида. |
| Результант Калькулятор вычисляет результант для двух многочленов. Также отображается матрица Сильвестра. |
| Решение задач Калькулятор выводит и вычисляет значения недостающих переменных из заданных формул и входных параметров. |
| Решение задач на арифметическую прогрессию Этот онлайн калькулятор помогает решить некоторые типы задач на арифметическую прогрессию |
| Решение задач на геометрическую прогрессию Этотонлайн калькулятор помогает решить некоторые типы задач на геометрическую прогрессию |
| Решение канонической задачи линейного программирования симплекс-методом Решение канонической задачи линейного программирования однофазным симплекс-методом. |
| Решение квадратных уравнений Квадратные уравнения — это уравнения вида axx+bx+c=0. Например, 4xx+2x+1=0. Такие уравнения решаются через дискриминант. Данный калькулятор поможет вам быстрее высчитать значение квадратного уравнения. Только прежде его приведите к вышеуказанному виду. Например, из 5xx-2x-0=0 в 5xx+(-2x)+0=0, из 3xx=0 в 3xx+0x+0=0. |
| Решение неоднородной системы линейных алгебраических уравнений матричным методом Решение неоднородной системы линейных алгебраических уравнений (СЛАУ) матричным методом (методом решения через обратную матрицу). |
| Решение системы линейных алгебраических уравнений методом Гаусса Калькулятор решает систему линейных алгебраических уравнений, заданных в виде матрицы методом Гаусса. Выдается пошаговое решение. |
| Решение системы линейных алгебраических уравнений методом Гаусса с сохранением дробей Калькулятор решает систему линейных алгебраических уравнений, заданных в виде матрицы, методом Гаусса, сохраняя дроби на всем протяжении процесса. |
| Решение системы линейных уравнений методом Гаусса с нахождением общего решения Решает систему линейных алгебраических уравнений методом Гаусса. Умеет выводить решение для совместных неопределенных систем линейных уравнений. Кроме того, выводит результат в формате с плавающей точкой и в формате дроби. |
| Решение системы нелинейных уравнений Этот онлайн калькулятор пытается найти решение системы нелинейных уравнений методом покоординатного поиска. |
| Решение сравнений по модулю Этот калькулятор находит решения линейных сравнений, или сравнений первой степени по модулю m |
| Сложение / вычитание многочленов Калькулятор вычисляет сумму или разность двух многочленов |
| Соотношения между двумя числами Всевозможные соотношения между двумя числами. Создано по запросу пользователя. |
| Стандартный вид числа Преобразует число в стандартный вид — произведение мантиссы от 1 до 10 и порядка числа 10. |
| Сумма сумм арифметической прогрессии Калькулятор вычисляет ряд сумм арифметической прогрессии до указанного номера, а также ряд, представляющий суммы сумм прогрессии. |
| Сумма чисел Этот онлайн калькулятор поможет вычислить сумму чисел записанных друг за другом. |
| Таблица независимых испытаний по формуле Бернулли Этот онлайн калькулятор рассчитывает вероятность k успехов при выполнении n повторных независимых испытаний с заданной вероятностью успеха p (схема Бернулли), для k меняющегося от нуля до n. |
| Теорема Байеса Этот онлайн калькулятор рассчитывает апостериорные вероятности событий в соответствии с теоремой Байеса |
| Тест простоты Миллера-Рабина Калькулятор проверяет является ли число составным, используя тест Миллера-Рабина. |
| Тест простоты Ферма Выполняет тест простоты числа, основанный на малой теореме Ферма по заданным основаниям. |
| Транспонирование матрицы Транспонирование матрицы, что тут еще сказать. |
| Умножение матриц Калькулятор умножает две матрицы. |
| Уравнение Мальтуса Этот онлайн калькулятор рассчитывает неизвестный параметр мальтузианского уравнения по известным параметрам. |
| Уравнение прямой по двум точкам Данный онлайн калькулятор находит формулы параметрического уравнения прямой и уравнения прямой с угловым коэффициентом по координатам двух точек, принадлежащих прямой. |
| Факториал Этот онлайн калькулятор рассчитывает факториал положительного целого числа. Практически любого положительного целого числа — он ограничен только временем, которое вы готовы потратить, чтобы дождаться окончания расчета. Я, например, дождался результата расчета факториала 100000! |
| Факторизация целых чисел. Перебор делителей Факторизация целых чисел методом перебора делителей. |
| Функция распределения дискретной случайной величины Функция распределения случайной величины используется для описания систем, представления опытных данных в аналитической форме для статистического анализа. |
| Центрированное скользящее среднее Этот калькулятор рассчитывает центрированное скользящее среднее для заданного периода усреднения |
| Числа Ацтеков Калькулятор преобразует целые положительные числа в форму записи числа Ацтеков. |
| Числительные Майя Калькулятор переводит число в систему счисления Майя |
| Числовые ребусы — замена цифр буквами Решатель числовых ребусов. Числовые или математические ребусы — математические выражения, в котором все или часть цифр заменены на некоторые символы, например, буквы. Требуется вместо каждого символа подставить нужную цифру, чтобы выражение было верным. |
Таблица и график функции биноминального распределения показывает вероятность всех возможных случаев.
Калькулятор показывает пошаговое решение, интерполирует заданные точки, а также строит график.
Приведено подробное решение — калькулятор выводит все промежуточные матрицы и значения определителей.
Вычисляет квантили Стьюдента для заданного количества степеней свободы и заданной вероятности.
В конце результат выдается как в виде действительного числа, так и в виде дроби с числителем и знаменателем.
Площадь круга (окружности): онлайн калькулятор, формулы, примеры решений
Фигура {$ main.figures[data.figure] $}
Рассчитываем {$ main.types[data.type] $}
Радиусили диаметр
Стороныили диагонали
Введите 2 величины
Сторона A
Сторона B
Диагонали
Угол α{$ main.
angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Введите 3 величины
Сторона A
Сторона B
Сторона C
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Угол γ{$ main.angles[data.angle] $}
Введите 2 величины
Сторона A
Сторона B
Сторона C
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Введите 2 величины
Сторона
Высота
Диагональ 1
Диагональ 2
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Введите 3 величины
Сторона A
Сторона B
Высота ha
Высота hb
Диагональ 1
Диагональ 2
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.
angles[data.angle] $}
Введите 3 величины
Основание A
Основание C
Высота H
Дополните боковые стороны для поиска периметра
Сторона B
Сторона D
Введите 1 величину
Сторона AРадиус описанной окружности (R)
Радиус вписанной окружности (r)
Количество сторон многоугольника
Введите 1 величину
Сторона A
Радиус описанной окружности (R)
Радиус вписанной окружности (r)
Введите 1 величину
Сторона A = радиусу описанной окружности (R)
Радиус вписанной окружности (r)
Результат расчёта
- Периметр: {$ result.p|number:4 $}
- Площать: {$ result.s|number:4 $}
Круг — это часть плоскости, ограниченная окружностью. В свою очередь окружность — замкнутая кривая, которая состоит из бесконечного количества равноудаленных от некоторого центра точек.
Круг занимает важное место в жизни человека, и во многих ситуациях вам может понадобиться узнать площадь круга.
Геометрия круга
Круг — заданное множество точек плоскости, которые удалены от центра круга на расстояние, не превышающее его радиус. Окружность — внешняя граница круга, но в случае, если радиус окружности равен нулю, то фигура превращается в точку. Круг и прямая, как и циркуль с линейкой — самые важные инструменты для геометра, ведь при помощи них легко построить любое, даже самое сложное геометрическое тело. Круг всегда очаровывал людей, и с самой древности фигура считалась символом бесконечного космоса, пространства и времени. Математики шутят, что круг — это многоугольник с бесконечным количеством углов.
Круги чрезвычайно эффективны: такие фигуры охватывают максимальную площадь для заданного периметра, соответственно, имеют минимальный периметр при охвате определенной области. Благодаря этому свойству в природе существует множество круглых объектов, которые в трехмерном пространстве преобразуются в шары или сферы.
К примеру, благодаря минимизации периметра образуются такие природные объекты, как капли воды, снежные комья или целые планеты.
Большое значение в геометрии круга имеет число Пи, которое отображает отношение длины окружности к диаметру круга. Это соотношение известно геометрам с древних времен: изначально люди полагали, что неизменное для любого круга значение равно примерно 3,1. Древние вавилоняне считали, что данное соотношение равняется 25/8, а Архимед пришел к выводу, что Пи можно выразить в виде дроби 22/7. Впрочем, в Древней Греции число Пи не имело названия. До работы Леонарда Эйлера число Пи называли лудольфовым числом.
Площадь круга
Площадь круга выражается одной из самых простых математических формул:
S = pi R2
Для подсчета площади вам необходимо узнать только радиус окружности или ее диаметр. В последнем случае формула несколько изменится:
S = (pi/4) D2
Круг довольно часто встречается в реальной жизни. В инженерии машин и механизмов используются детали, сечения которых — круг.
К примеру, в технике распространены такие цилиндрические детали, как валы, цилиндры, конденсаторы, поршни, оси и тому подобное. Круги также можно встретить в строительстве, производстве мебели, микропроцессорной технике или архитектуре, поэтому инженеры используют в своих расчетах простые формулы для определения площади круга. Рассмотрим пару абстрактных примеров.
Примеры из реальной жизни
DVD-диск
Сегодня DVD-диски утратили звание самого популярного носителя информации, но это не мешает нам измерить площадь болванки. Стандартный диск имеет отверстие диаметром 15 мм, а сама болванка имеет диаметр 120 мм. Таким образом, площадь диска Sd составит:
Sd = Sb – So,
где So – площадь пустого отверстия.
Введем данные в форму онлайн-калькулятора и получим такие результаты:
Sb = 376,9 и So = 47,12
Выполняем несложный расчет и получаем:
Sd = 376,9 — 47,12 = 328,79
Таким образом, площадь стандартного DVD-диска составляет 328,79 квадратных миллиметров.
Основание конуса
Все мы знаем, что в основании объемного конуса лежит круг. Коническую форму имеют многие реальные объекты, к примеру, обычный дорожный конус. Если вы хотите узнать площадь основания такой фигуры, то вам достаточно замерить радиус конуса и ввести эти данные в форму калькулятора. Допустим, радиус выбранной фигуры составляет 15 см. Тогда площадь круга, лежащего в основании, будет равна:
S =94,24
Это означает, что площадь основания дорожного конуса составляет 94,24 квадратных сантиметров.
Заключение
Круг — фигура на плоскости, поэтому в реальной жизни круги встречаются как составные части объемных объектов, к примеру, основания цилиндрических или конических деталей, а также «плоские» объекты, как медали, диски или блинчики. Если вам необходимо подсчитать площадь круга, зная его радиус или диаметр, воспользуйтесь нашим онлайн-калькулятором, который быстро и точно предоставит вам результат.
Формула Эйлера и калькулятор тождеств Эйлера
Ниже приведен калькулятор и интерактивный график, который позволяет вам исследовать концепции, лежащие в основе знаменитой и необычной формулы Эйлера:
e iθ = cos( θ ) + i sin( θ )
Когда мы устанавливаем θ = π, мы получаем классическое Тождество Эйлера:
e iπ + 1 = 0
Формула Эйлера используется во многих областях науки и техники.
Это очень удобное тождество в математике, так как оно может значительно упростить выполнение многих вычислений, особенно связанных с тригонометрией. Мы видели часть этой концепции в произведениях и частных комплексных чисел ранее.
Леонард Эйлер был блестящим и плодовитым швейцарским математиком, чей вклад в физику, астрономию, логику и инженерию был неоценим. Он, безусловно, был одним из величайших математиков в истории. 9п
И формулу, и тождество можно использовать для выполнения вычислений, а также для графических функций. Калькулятор можно использовать для ввода комплексного числа и вычисления различных степеней этого числа, а также для построения графика функции. График можно увеличить или уменьшить, а комплексное число можно изменить, чтобы увидеть, как оно влияет на график.
Формула Эйлера и тождество очень полезны в математике и технике, поскольку они могут значительно упростить выполнение многих вычислений. Попробуйте поиграть с калькулятором и графиком, чтобы увидеть, что вы можете обнаружить!
Формула Эйлера, калькулятор тождества и график
На следующем графике реальная ось (обозначенная «Re») горизонтальна, а воображаемая ось (`j=sqrt(-1)`, обозначенная «Im») вертикальна, как обычно.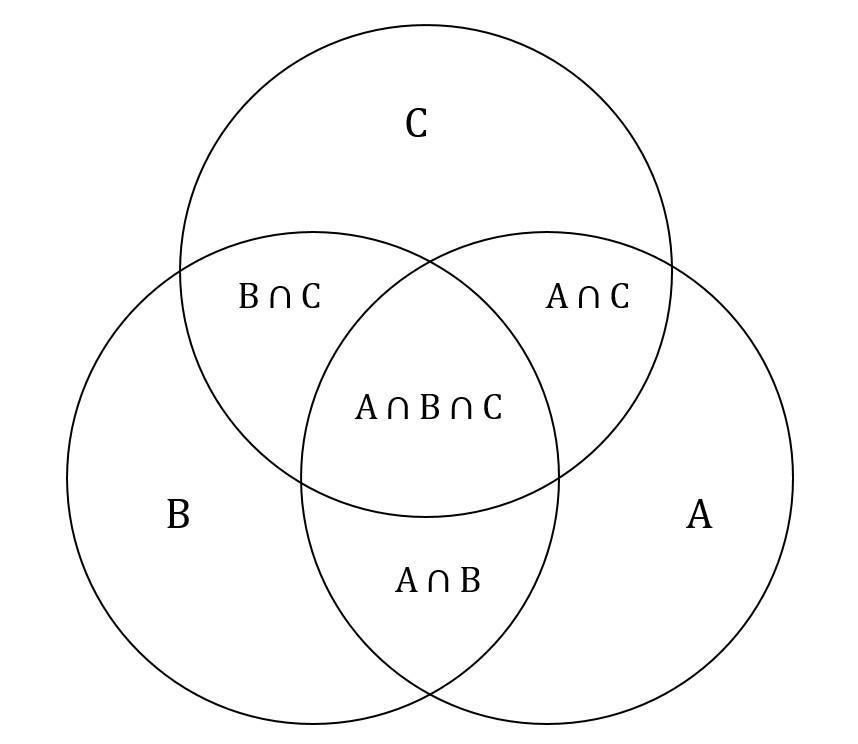
Точка P представляет комплексное число. Угол θ , разумеется, в радианах.
Чем заняться
- Выберите, будут ли ваши углы выражаться десятичными знаками или числами, кратными π.
- Выберите i или j в качестве символа мнимого числа. (Во многих учебниках используется и для символа мнимого числа, но в IntMath, как и во многих инженерных учебниках, используется j , чтобы попытаться уменьшить путаницу с символом тока в электронике.)
- Вы можете перетащить точку P , чтобы изменить угол θ.
- Когда вы установите θ = π, вы увидите (эквивалент) Тождество Эйлера: e iπ = − 1
Углы: кратные π
Мнимый символ: i j
Формула Эйлера
Прямоугольный и полярный эквиваленты
Некоторая справочная информация о том, что происходит, и дополнительные пояснения см.
на предыдущих страницах,
Комплексные числа и полярная форма комплексного числа
См. также калькулятор полярного преобразования в прямоугольное и прямоугольного в полярное, на котором основано приведенное выше:
Онлайн-калькулятор полярных координат в прямоугольные
Комплексная экспоненциальная форма
В математике комплексная экспоненциальная функция — это функция вида f(z) = ea(z), где z — комплексное число, а a — произвольная комплексная константа. Функция целая, что означает, что она определена и дифференцируема для всех комплексных чисел z. В отличие от вещественно-показательных функций сложные показательные функции не являются взаимно однозначными; то есть два разных комплексных числа могут иметь одинаковый образ под функцией. 9{-би}.
Сложные функции
Комплексная функция — это функция вида f(z) = u(x, y) + iv(x, y), где z = x + iy — комплексная переменная, u и v — вещественнозначные функции две действительные переменные x и y, а i — мнимая единица измерения.
В этой статье будут рассмотрены некоторые свойства сложных функций с упором на формулу Эйлера и тождество Эйлера.
Сложные функции имеют множество приложений в физике и технике, а также в чистой математике. В физике они используются для моделирования волновых явлений, а в технике — для проектирования электрических цепей. В чистой математике они изучаются сами по себе как красивые и интригующие объекты. 9(i*pi) + 1 = 0. Это уравнение важно, поскольку оно связывает вместе пять наиболее важных чисел в математике: e, pi, i, 1 и 0.
Дифференциальные уравнения чрезвычайно полезны в математическом моделировании и находят применение в самых разных областях, от физики до экономики. Следовательно, они являются важным инструментом для понимания и прогнозирования изменений.
Если у вас есть твердое понимание формулы Эйлера и тождества Эйлера, вы можете относительно легко выполнять широкий спектр вычислений. Это делает формулу бесценным инструментом для математиков, инженеров и других ученых.
Имея это в виду, мы рекомендуем вам использовать приведенный выше калькулятор, чтобы изучить, как это тождество можно использовать для упрощения различных уравнений.
Далее мы переходим к тому, как вычислять произведения и частные числа комплексных чисел
.Онлайн-калькулятор: Метод Эйлера
Исследование Математика
Этот онлайн-калькулятор реализует метод Эйлера, который является численным методом первого порядка для решения дифференциальных уравнений первой степени с заданным начальным значением.
Вы можете использовать этот калькулятор для решения дифференциальных уравнений первой степени с заданным начальным значением, используя метод Эйлера.
Чтобы использовать этот метод, у вас должно быть дифференциальное уравнение вида
Введите правую часть уравнения f(x,y) в поле y’ ниже.
Вам также потребуется начальное значение
и точка, для которой вы хотите аппроксимировать значение.
Последний параметр метода – размер шага – это буквально шаг по касательной для вычисления следующего приближения кривой функции.
Если вы знаете точное решение дифференциального уравнения в форме y=f(x) , вы также можете ввести его. В этом случае калькулятор также наносит решение вместе с аппроксимацией на график и вычисляет абсолютную ошибку для каждого шага аппроксимации.
Описание метода находится под калькулятором.
Метод Эйлера
Начальное значение x
Начальное значение y
Точка аппроксимации
Размер шага
Точное решение (не обязательно)0003
Дифференциальное уравнение
Приблизительное значение y
Приблизительное значение
Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.
Метод Эйлера
Итак, предположим, что мы имеем следующее
Если мы вычислим
, то найдем производную y’ в начальной точке.
Для достаточно малых , мы можем аппроксимировать следующее значение
Или, короче,
И в общем случае
Мы продолжаем вычислять следующие значения y , используя это соотношение, пока не достигнем целевой точки x .
В этом суть метода Эйлера. это размер шага. Ошибка на каждом шаге (локальная ошибка усечения) примерно пропорциональна квадрату размера шага, поэтому метод Эйлера более точен, если размер шага меньше. Однако глобальная ошибка усечения является кумулятивным эффектом локальных ошибок усечения и пропорциональна размеру шага, поэтому метод Эйлера считается методом первого порядка.
Более сложные методы позволяют достичь более высокого порядка (и большей точности). Одна из возможностей состоит в том, чтобы использовать больше вычислений функций.