Калькулятор онлайн по тригонометрии: Тригонометрический калькулятор | Microsoft Math Solver

Триг-Калькулятор — Mathcracker.Com

Инструкции: Используйте тригонометрический калькулятор для вычисления и оценки любого тригонометрического выражения, которое вы предоставите. Пожалуйста, введите тригонометрическое выражение, которое вы хотите вычислить, или тригонометрическую функцию, которую вы хотите проанализировать, в поле формы ниже.

Подробнее об этом триг-калькуляторе

Этот триггерный калькулятор позволит вам оценить любое тригонометрическое выражение, которое вы предоставите.

Убедитесь, что вы предоставили любое допустимое тригонометрическое выражение, это может быть что-то прямое, например cos(pi/2), или что-то не полностью упрощенное, например sin(1/3*pi+3/4*pi).

Вы также можете задать триггерную функцию типа sin(1/3*pi x +3/4*pi + x), и калькулятор проанализирует и, если возможно, выдаст соответствующий период, частоту и т.д., вместе с его график .

После ввода правильного тригонометрического выражения достаточно нажать кнопку «Вычислить», и все этапы вычисления будут показаны.

тригонометрические выражения весьма необходимы, особенно когда вы решение треугольников .

Обычно любой тригонометрический расчет просто свести к вычислению нескольких заметных углов для косинус и синус .

Как выполнять тригонометрические расчеты?

Вычисление тригонометрии может быть очень общей и широкой задачей, которая может иметь конкретные стратегии, которые работают лучше всего в зависимости от конкретного тригонометрического вычисления, которое вам нужно сделать, и от того, какие тригонометрические функции задействованы, но есть некоторые общие стратегии, которые могут послужить вам хорошую службу.

Каковы этапы вычисления тригонометрии

• Шаг 1: Четко определите тригонометрическое выражение, которое вы хотите вычислить, и упростите числа и дроби настолько, насколько это возможно. Например, если у вас есть cos(1+1/2), вы сначала заметите, что 1+1/2 = 3/2, поэтому вам нужно фактически cos(3/2)
• Шаг 2: После того как возможные дроби и простые числа сгруппированы и, по возможности, оперируют ими, определите, существуют ли триггерные функции, отличные от синуса и косинуса. Если они есть, выразите все в терминах синуса и косинуса
• Шаг 3: Теперь пройдитесь по всем частям, которые теперь включают только синус и косинус , и оценить, есть ли заметные углы, кратные или дольные π
• Шаг 4: Непосредственно оцените эти выражения с помощью заметных углы которые можно упростить. Те, которые не могут быть упрощены напрямую (если таковые имеются), оставляют как есть, или дают приближенное ( округлённое значение ) из них

Принято оставлять их такими, какие они есть выражения которые не имеют известных простых упрощений. Например, cos(1/4) не имеет простого сокращения, поэтому его обычно оставляют как есть. Но, например, cos(π/3) = 1/2, поэтому такие простые редукции, очевидно, выполняются

Тригонометрический калькулятор с шагами

Преимущество этот калькулятор заключается в том, что он покажет вам все соответствующие этапы процесса.

Процесс прост: он заключается в следующем упрощение выражений в которых используются только числа, дроби и общие числовые выражения с прямой оценкой.

Затем, и только затем вы должны приступить к вычислению тригонометрии, чтобы максимально прояснить ситуацию, прежде чем приступать к вычислению тригонометрии.

Преимущества использования приложения тригонометрического калькулятора

Вы можете подумать: о, хорошо, я довольно хорошо знаю свои триггерные функции для основных заметных углов, поэтому мне не нужно приложение триггерного калькулятора. Это вполне может быть так, хотя вы можете немного колебаться, когда вам предложат что-то вроде \(\sin\left(\displaystyle\frac{345}{11}\pi\right)\).

… Можете ли вы упростить это? Является ли это заметным углом?

Это действительно хорошо — пытаться решать задачи вручную, тренируя свою тригонометрическую память, но приложение триггерного калькулятора может помочь вам, по крайней мере, проверить свои ответы.

Пример: вычисление тригонометрии

Вычислите триггерное выражение: \(\sin\left(\frac{5}{4}\pi\right)\)

Отвечать: Необходимо вычислить следующее тригонометрическое выражение:

\[ \sin\left(\frac{5\pi}{4}\right)\]

Рассматривая данное тригонометрическое выражение, мы можем найти один примечательный угол, который равен \(\sin\left(\frac{5\pi{}}{4}\right)\).

▹ Для угла \(\frac{5\pi{}}{4}\) графически получаем:

Приведенное тригонометрическое выражение может быть упрощено как:

\( \displaystyle \sin\left(\frac{5\pi{}}{4}\right)\)

Evaluating the trigonometric expression at the notable angle \(\displaystyle\frac{5\pi{}}{4}\) we get that: \(\displaystyle \sin\left(\frac{5\pi{}}{4}\right) = -\frac{ \sqrt{2}}{ 2}\)

\( = \,\,\)

\(\displaystyle -\frac{ \sqrt{2}}{ 2}\)

Заключение:

Мы заключаем, что \(\displaystyle \sin\left(\frac{5\pi}{4}\right) = -\frac{1}{2}\sqrt{2} \approx -0. 7071\).

Пример: использование триггерного калькулятора

Уменьшить : \(\displaystyle \cos\left(\frac{1}{3} + \frac{5}{4}\right)\)

Отвечать: Теперь нам нужно работать дальше:

\[ \cos\left(\frac{1}{3}+\frac{5}{4}\right)\]

Этот тригонометрический член может быть упрощен следующим образом:

\( \displaystyle \cos\left(\frac{1}{3}+\frac{5}{4}\right)\)

Grouping and operating all the integer terms and fractions: \(\displaystyle \frac{ 1}{ 3}+\frac{ 5}{ 4}=\frac{ 1}{ 3} \times \frac{ 4}{ 4}+\frac{ 5}{ 4} \times \frac{ 3}{ 3}=\frac{ 4+5 \times 3}{ 12}=\frac{ 4+15}{ 12}=\frac{ 19}{ 12}\)

\( = \,\,\)

\(\displaystyle \cos\left(\frac{19}{12}\right)\)

Заключение: Сделан вывод, что \(\displaystyle \cos\left(\frac{1}{3}+\frac{5}{4}\right) = \cos\left(\frac{19}{12}\right) \approx -0. 0125\).

Пример: упрощение тригонометрии

Рассчитайте \( \sin\left(\frac{2}{3} \times \frac{6}{5} \pi\right)+ \frac{2}{5}\cdot \cos(\frac{\pi}{4}) \).

Отвечать: Рассматривая данное тригонометрическое выражение, мы можем найти один примечательный угол, который равен \(\cos\left(\frac{\pi{}}{4}\right)\).

▹ Для угла \(\frac{\pi{}}{4}\) графически получаем:

Приведенное тригонометрическое выражение может быть упрощено как:

\( \displaystyle \sin\left(\frac{2}{3}\cdot\frac{6}{5}\pi{}\right)+\frac{2}{5}\cos\left(\frac{\pi{}}{4}\right)\)

Evaluating the trigonometric expression at the notable angle \(\displaystyle\frac{\pi{}}{4}\) we get that: \(\displaystyle \cos\left(\frac{\pi{}}{4}\right) = \frac{1}{2}\sqrt{2}\)

\( = \,\,\)

\(\displaystyle \sin\left(\frac{2}{3}\cdot\frac{6}{5}\pi{}\right)+\frac{2}{5}\cdot\frac{1}{2}\sqrt{2}\)

Grouping and operating all the integer terms and fractions: \(\displaystyle \frac{ 2}{ 3} \times \frac{ 6}{ 5}=\frac{ 2 \times 6}{ 3 \times 5}=\frac{ 2 \times (\cancel{3} \times 2)}{ \cancel{3} \times 5}=\frac{ 2 \times 2}{ 5}=\frac{ 4}{ 5}\)

\( = \,\,\)

\(\displaystyle \sin\left(\frac{4}{5}\pi{}\right)+\frac{2}{5}\cdot\frac{1}{2}\sqrt{2}\)

Evaluating the trigonometric expression at the notable angle \(\displaystyle\frac{4}{5}\pi{}\) we get that: \(\displaystyle \sin\left(\frac{4}{5}\pi{}\right) = \frac{1}{4}\sqrt{-2\sqrt{5}+10}\)

\( = \,\,\)

\(\displaystyle \frac{1}{4}\sqrt{-2\sqrt{5}+10}+\frac{\frac{2}{5}\cdot1}{2}\sqrt{2}\)

Grouping and operating all the integer terms and fractions: \(\displaystyle \frac{ 2}{ 5} \times \frac{ 1}{ 2}=\frac{ 2}{ 5 \times 2}=\frac{ \cancel{2}}{ 5 \times \cancel{2}}=\frac{ 1}{ 5}\)

\( = \,\,\)

\(\displaystyle \frac{1}{4}\sqrt{-2\sqrt{5}+10}+\frac{1}{5}\sqrt{2}\)

Заключение: Мы заключаем, что \(\displaystyle \sin\left(\frac{2}{3}\cdot\frac{6}{5}\pi\right)+\frac{2}{5}\cos\left(\frac{\pi}{4}\right) = \frac{1}{5}\sqrt{2}+\frac{1}{4}\sqrt{-2\sqrt{5}+10} \approx 0. 8706\).

Больше калькуляторов по геометрии

Работа с триггерными функциями тесно связана с работой с треугольниками, поэтому при работе с калькулятор треугольника вы найдете множество триггерных расчетов.

Решение тригонометрических функций ⋆ Компьютерные технологии

Онлайн калькулятор на нашем сайте легко и быстро решает тригонометрические функции, вам не понадобится таблица тригонометрических функций. С нашим калькулятором можно навсегда забыть, что такое таблица Брадиса! Наш бесплатный калькулятор позволяет решать и самые простые задачи (например, найти косинус или синус угла), и сложные выражения с использованием обратных и гиперболических функций тригонометрии.

Кнопки калькулятора для решения тригонометрических функций:

Наш тригонометрический калькулятор может осуществлять вычисления как в градусах, так и в радианах. Таким образом, найти косинус угла можно вне зависимости от единицы измерения, в которой он задан. Это очень удобно и экономит массу времени при емких расчетах. Прежде чем приступить к вычислениям, нужно на панели управления указать, какая единица измерения углов будет использоваться: градусы (Deg) или радианы (Rad).

Выбор единицы измерения угла:

Обратите внимание, что в одной операции нельзя использовать разные единицы измерения углов, другими словами выражение «сумма синус 30 градусов и косинус пи =» — будет посчитано неверно!

Ниже перечислены способы решений различных тригонометрических функций в нашем онлайн калькуляторе.

Простые тригонометрические функции

Простые тригонометрические функции: синус — sin(α), косинус — cos(β) и тангенс — tan(y). Рядом указаны их обозначения так, как они используются в калькуляторе (в зарубежной литературе тангенс сокращенно обозначается tan, в русской — tg).

Кнопки калькулятора, отвечающие за простые тригонометрические функции:

Функция косинуса является четной, поэтому ее значение для отрицательного угла будет положительным. Синус, тангенс и котангенс — нечетные тригонометрические функции, соответственно, значения тригонометрических функции для отрицательных углов также будут отрицательными. Онлайн калькулятор сам учитывает четность тригонометрических функций при умножении и делении. Вам не потребуется постоянно обращать внимание на соблюдение правила знаков.

Пример вычислений с простыми тригонометрическими функциями:

Обратные тригонометрические функции

Обратные тригонометрические функции: арксинус — asin(), арккосинус — acos() и арктангенс — atan().

Кнопки калькулятора, отвечающие за обратные тригонометрические функции:

Если не вдаваться в формулы и подробности относительно единичной окружности, то обратные тригонометрические функции можно объяснить на простом примере: арккосинус x — это угол, косинус которого равен x. Обратные тригонометрические функции являются многозначными, и одному значению аргумента принадлежит множество значений самой функции.

Пример выражения с обратными тригонометрическими функциями:

Гиперболические функции

Гиперболические функции: гиперболический синус — sinh(), гиперболический косинус — cosh() и гиперболический тангенс tanh(). Гиперболические (круговые) функции — семейство элементарных тригонометрических функций, выраженных через экспоненту.

Кнопки калькулятора, отвечающие за гиперболические функции:

Пример решения гиперболической функции:

Обратные гиперболические функции: гиперболический арксинус — asinh(), гиперболический арккосинус — acosh() и гиперболический арктангенс — atanh().

Кнопки калькулятора, отвечающие за обратные гиперболические функции:

Пример решения обратной гиперболической функции:

Все функции нашего бесплатного калькулятора собраны в одном разделе. Функции онлайн калькулятора >>

Онлайн-калькуляторы и решатели тригонометрии

Представлены простые в использовании онлайн-калькуляторы тригонометрии и решатели для различных тем по тригонометрии. Их можно использовать для практики и численного исследования свойств тригонометрических функций, чтобы получить глубокое понимание этих функций.

Тригонометрия

• Преобразование градусов в радианы.
• Преобразовать радианы в градусы.
• Калькулятор степени. Сложение и вычитание углов в градусах, минутах и ​​секундах (DMS).
• Решение синусоидальных уравнений. Онлайн-калькулятор решения простых тригонометрических уравнений с синусоидой вида sin x = a.
• Решатель косинусных уравнений. Онлайн-калькулятор и решатель тригонометрических уравнений с функцией косинуса вида cos x = a.
• Решатель касательных уравнений. Онлайн-калькулятор и решатель простых тригонометрических уравнений с функцией тангенса вида tan x = a.
• Найдите котерминальный угол. Калькулятор для нахождения точного значения котерминального угла к заданному тригонометрическому углу.
• Калькулятор шести тригонометрических функций. Онлайн-калькулятор, вычисляющий шесть тригонометрических функций: sin(x), cos(x), tan(x), cot(x), sec(x) и csc(x) заданного угла.
• Найдите опорный угол к тригонометрическому углу в стандартном положении.
• Найдите квадрант угла. Найдите квадрант угла в стандартном положении.
• Преобразование углов из десятичной дроби в градусы, минуты и секунды.
• Преобразование углов из градусов, минут и секунд в десятичные градусы.

Обратные тригонометрические функции

• Калькулятор Arcsin(x). Вычислить обратную тригонометрическую функцию arcsin(x) в радианах и градусах.
• Калькулятор Arccos(x). Вычислить обратную тригонометрическую функцию arccos(x) в радианах и градусах.
• Калькулятор арктан(х). Вычислить обратную тригонометрическую функцию arctan(x) в радианах и градусах.
• Калькулятор Arccot(x). Вычислить обратную тригонометрическую функцию arccot(x) в радианах и градусах.
• Arcsec(x) Калькулятор. Вычислить обратную тригонометрическую функцию arcsec(x) в радианах и градусах.
• Калькулятор Arccsc(x). Вычислить обратную тригонометрическую функцию arccsc(x) в радианах и градусах.

Тригонометрические пайки

• Тригонометрические соотношения в калькуляторе прямоугольного треугольника с учетом сторон треугольника.

Гиперболические функции

• Калькулятор гиперболических функций
• Калькулятор обратных гиперболических функций.

Другие математические калькуляторы и решатели .

Калькулятор Sohcahtoa

Калькулятор SOHCAHTOA использует эту конкретную мнемонику для решения тригонометрических функций прямоугольного треугольника.

В этом техническом чтении ниже мы поможем вам понять фактическое значение SOHCATOA и то, как это может быть удобно при разрешении различных углов и сторон триггера.

Что такое SOHCATOA?

В тригонометрии SOHCAHTOA определяется следующим образом:

SOH (Sin(θ))= Перпендикуляр/Гипотенуза

CAH (Cos(θ)) = Основание/Гипотенуза

TOA (Tan(θ))= Перпендикуляр/Гипотенуза 9000 4

Наш решатель SOHCATOA также рассматривает те же коррелированные формулы, чтобы отобразить измерения сторон и углов треугольника.

Как SOHCATOA помогает запомнить соотношение триггеров?

Большинству из нас до сих пор трудно запомнить коэффициенты срабатывания. Без сомнения, нужно иметь дело только с тремя сторонами и углами. Но вероятность точного припоминания каждый раз для нас все равно меркнет. Учитывая эту проблему, мы разработали калькулятор SOH CAH TOA, чтобы помочь вам определить правильное тригонометрическое соотношение.

Проще говоря, давайте посмотрим на следующий треугольник ниже:

В этом треугольнике три стороны обозначены как:

Противоположная (Перпендикулярная)

Сторона, противоположная острому углу )

Сторона, соединенная с острым углом и противолежащая

Гипотенуза

Самая длинная сторона прямоугольного треугольника, один конец которой соединен с основанием, а другой — с противоположным

Калькулятор SOHCATOA поможет вам определить все эти отношения в считанные секунды, тем самым сокращая время ваших длительных вычислений.

Давайте закодируем здесь, что мы также разработали еще один калькулятор теоремы Пифагора, который значительно упрощает работу, пока вы собираетесь определять только стороны треугольника.

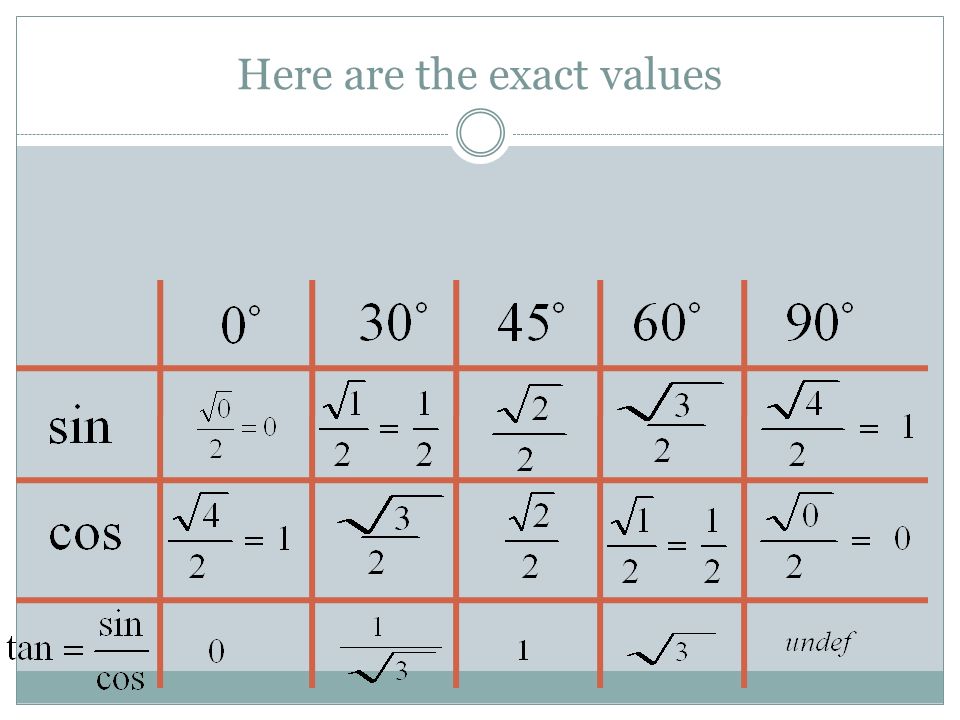
SOHCATOA Измерения популярных углов:

Тригонометрия работает с некоторыми основными измерениями углов, которые формируют основу для вычислений углов и сторон по данному предмету. Они даны следующим образом:

	$ $ {\ Displaystyle \ грех \ тета} $ $	$ $ {\ Displaystyle \ соз \ тета} $ $	$ $ {\ Displaystyle \ загар \ тета = \ грех \ тета {\ большой /} \ соз \ тета} $ $
0° = 0 радиан	$ $ {\ displaystyle {\ frac {\ sqrt {\ mathbf {\ color {blue} {0}}}} {2}} = \; \; 0} $ $	$ $ {\ displaystyle {\ frac {\ sqrt {\ mathbf {\ color {red} {4}}}} {2}} = \; \; 1} $ $	$ $ {\ displaystyle \; \; 0 \; \; {\ Big /} \; \; 1 \; \; = \; \; 0} $ $
30° = π/6 радиан	$ $ {\ displaystyle {\ frac {\ sqrt {\ mathbf {\ color {teal} {1}}}} {2}} = \; \, {\ frac {1} {2}}} $ $	$ $ {\ displaystyle {\ frac {\ sqrt {\ mathbf {\ color {оранжевый} {3}}}} {2}}} $ $	$ $ {\ displaystyle \; \, {\ frac {1} {2}} \; {\ Big /} {\ frac {\ sqrt {3}} {2}} = {\ frac {1} {\ кврт {3}}}} $$
45° = π/4 радиана	$ $ {\ displaystyle {\ frac {\ sqrt {\ mathbf {\ color {green} {2}}}} {2}} = {\ frac {1} {\ sqrt {2}}}} $ $	$ $ {\ displaystyle {\ frac {\ sqrt {\ mathbf {\ color {green} {2}}}} {2}} = {\ frac {1} {\ sqrt {2}}}} $ $	$ $ {\ displaystyle {\ frac {1} {\ sqrt {2}}} {\ Big /} {\ frac {1} {\ sqrt {2}}} = \; \; 1} $ $
60° = π/3 радиана	$ $ {\ displaystyle {\ frac {\ sqrt {\ mathbf {\ color {оранжевый} {3}}}} {2}}} $ $	$ $ {\ displaystyle {\ frac {\ sqrt {\ mathbf {\ color {teal} {1}}}} {2}} = \; {\ frac {1} {2}}} $ $	$ $ {\ displaystyle {\ frac {\ sqrt {3}} {2}} {\ Big /} \; {\ frac {1} {2}} \; \, = {\ sqrt {3}}} $$
90° = π/2 радиан	$ $ {\ displaystyle {\ frac {\ sqrt {\ mathbf {\ color {red} {4}}}} {2}} = \; \, 1} $ $	$ $ {\ displaystyle {\ frac {\ sqrt {\ mathbf {\ color {blue} {0}}}} {2}} = \; \, 0} $ $	$ $ {\ displaystyle \; \; 1 \; \; {\ Big /} \; \; 0 \; \; =} Не определено $$

Основные соотношения SOHCAHTOA:

Ниже приведены наиболее широко применяемые соотношения SOHCAHTOA в исчислении и аналитической геометрии:

Синус:

Синус = перпендикуляр/гипотенуза 9 0005

Косинус:

Косинус = основание/гипотенуза

Тангенс:

Тангенс = перпендикуляр/основание

Секанс: 9{-1}x

Какие еще мнемоники можно использовать для запоминания коэффициентов срабатывания треугольника?

Еще одно наиболее часто используемое предложение, которое поможет вам вспомнить триггерные функции, выглядит следующим образом:

«У Оскара была куча яблок»

Из чего следует, что:

• Sin(θ) = / Had
• Cos(θ) = A / куча
• Tan(θ) = Из / Яблоки

Иллюстрации:

Разберем пример, который поможет вам применить SOHCATOA для нахождения стороны и угла прямоугольного треугольника!

Утверждение:

Для треугольника, указанного ниже, примените SOH CAH TOA, чтобы найти угол и сторону r:

Решение:

Здесь мы имеем:

sin(20°) = 10/r 900 04

r{sin(20°)} = 10

r = 10/sin(20°)

r = 10/0,3420

r = 29,239

Теперь вы, должно быть, думаете, как найти углы, используя SOHCATOA. Позвольте нам вести вас!

Угол 1 = 90°

Угол 2 = 20°

Угол 3 = ?

Итак:

Угол 3 = 90° – 20°

Угол 3 = 70°

Работа калькулятора SOHCAHTOA:

Ниже приведено руководство по вводу, которое поможет вам узнать, как используйте этот калькулятор треугольника SOHCATOA:

Ввод:

• Среди 6 полей ввода введите только два в соответствующие поля
• После этого просто нажмите кнопку расчета

Вывод:

Бесплатный калькулятор SOH CAH TOA использует SOHCAHTA для нахождения углов и сторон введенных отношений треугольника

Часто задаваемые вопросы:

Является ли SOHCAHTOA только для прямоугольных треугольников?

Да, обязательно! SOHCATOA применимо только к прямоугольным треугольникам. Если у вас остроугольные, тупоугольные или косоугольные треугольники, вы ничего не получите от этой техники.