Повторение — мастер Иванова
В разделе ПОВТОРЕНИЕ представлены материалы, содержащие ключевые вопросы школьной программы за 1-9, а также за 10-11 классы.
.Рассмотрим каждую группу и подгруппу чисел.
1)Целые числа. В их состав входят:
а) натуральные числа.
Натуральными называют числа, которые используют при перечислении и подсчете объектов, как неодушевленных, так и одушевленных.
Например, нам нужно посчитать количество столов в аудитории. Мы начинаем считать: 1-й стол, 2-й стол, 3-й стол и т.д.
«0» не является натуральным числом, так его не используют при счете объектов.
Примеры натуральных чисел: 1; 2; 3;…;25; 68;…; 183; 574;… и так до бесконечности.
.
Рассмотрим понятие цифра.
Всего цифр десять: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9.
Цифры используют для записи любого числа.
Например, для записи натурального числа 35 используют две цифры, такие как «3» и «5».
Еще пример: для записи числа 42098 используют пять цифр: «4», «2», «0», «9», «8».
«2» одновременно называют и числом и цифрой. А вот «61» называют только числом (и для его записи использовали две цифры – «6» и «1»).
.
б) противоположные натуральным – отрицательные числа.
Пример: -2; -56; -193;………
в) число 0 (ноль).
.
Итак, если для обозначения натуральных чисел используют латинскую букву n, то общая запись целых чисел будет выглядеть так:
–n; 0; n.
Произвольные примеры целых чисел: 75; -12; 167; -653; 0; 12; 3; 1; -1; и т.д.
.
2)Дробные числа. В их состав входят:
а) обыкновенные дроби.
Любая обыкновенная дробь имеет следующую форму записи:
pq.. (q≠0).
Одна или несколько равных частей единицы называются обыкновенной дробью. Дробь 3/4 означает, что единицу разделили на 4 части и взяли 3 таких части.
Дробь можно рассматривать и как результат деления натуральных чисел. Частное от деления натуральных чисел а и b можно записать в виде дроби a/b — где делимое а — числитель, а делитель b — знаменатель.
Правильная и неправильная дробь.
Дробь, в которой числитель меньше знаменателя, называется правильной, а дробь, где числитель больше или равен знаменателю, — неправильной.
Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и к произведению прибавить числитель данной дроби. Полученная сумма будет числителем дроби, а знаменателем остается знаменатель дробной части.
Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления — это целая часть, остаток — это числитель, делитель — это знаменатель.
.
.б) десятичная дробь.
Для записи десятичной дроби используют знак «,», отделяющий целую часть от дробной.
Дробные числа, знаменатель которых равен 10, 100, 1000 и т. д., можно записать не только в виде обыкновенных, но и в виде десятичных дробей.
.
.Конечные десятичные дроби
Пример: разделим при помощи калькулятора число 5 на 2. Получим на экране калькулятора число 2,5, состоящее из двух цифр, разделенных десятичным знаком «,». После запятой всего одна цифра «5». То есть после вычисления получена конечная запись.
Примеры конечных десятичных дробей: 45,08; 0,2176; -3,1; и т.д.
Бесконечные периодические десятичные дроби
Пример: разделим при помощи калькулятора число 1 на 3.
Получим на экране калькулятора запись 0,3333333333…….
То есть, если бы ширину экрана на калькуляторе можно было бы продолжать до бесконечности, то и количество «3»-ек продолжалось бы так же до бесконечности. Такую дробь называют бесконечной периодической десятичной дробью с периодом, равным «3» и записывают: 0,(3). В скобках указывается период, с которым «3»-ка после запятой повторяется.
Еще пример: 309,501501501….. Здесь периодически повторяются три цифры «5», «0» и «1». Можно так записать нашу дробь 309,(501).
.
3)Иррациональные числа.
.
Иррациональные числа еще называют бесконечными непериодическими десятичными дробями.
Этот вид чисел может иметь «непредсказуемую» форму, например: √2, e, π, log23 и т.д.
То есть, подобные числа внешне не очень напоминают нам десятичную дробь, но если каждое из них преобразовать или выполнить вычислительную операцию при помощи специального калькулятора, то мы получим знакомую нам запись числа в виде бесконечной (непериодической) десятичной дроби:
√2=1,4142135623095…..
π=3,1415926535…….
Если вы успели заметить, в каждом числе после «,» цифры не повторяются. Это и есть запись бесконечных непериодических десятичных дробей.
…………………………………………………………………………..
…………………………………………………………………………….
Закрепление изученного материала
Рассмотрим такой пример:
Дано число 2.
К какой группе чисел можно его отнести?
Число 2 можно отнести к натуральным числам.
Помимо этого число 2 можно назвать цифрой.
Число 2 так же относится к целым числам.
И даже к дробным. Если представить его в таком виде, т.е. в виде обыкновенной дроби: 21… Ведь дробная черта в обыкновенной дроби означает действие «деление», а при делении любого числа на «1», число не меняется по своей сути, а меняет лишь внешний вид записи. 21.. является неправильной обыкновенной дробью.
Число 2 можно представить даже в виде десятичной дроби (например, в Excel можно задать формат числа в ячейке с двумя знаками после запятой): 2,00.
.
Рассмотрим еще один пример:
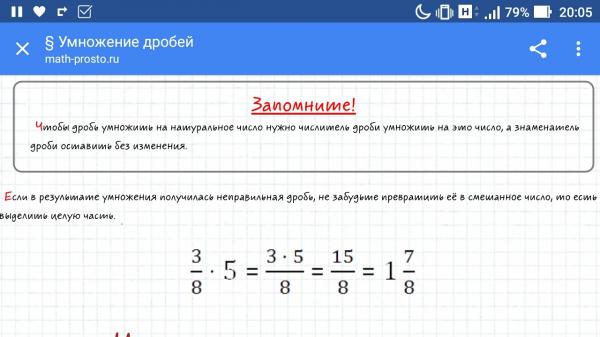
Число 512.. является обыкновенной дробью и входит в группу под названием дробные числа. Но при записи этой дроби использовались числа, которые можно по отдельности назвать как натуральными, так и целыми («5» и «12»). То есть что получается? Получается, что натуральные числа входят в состав целых, а целые включены в группу рациональных.
Наглядно такую конструкцию можно увидеть при помощи кругов Эйлера:
.
………………………………………………………………
………………………………………………………………
ДОМАШНЕЕ ЗАДАНИЕ
Выберите правильные числовые ответы из предложенных:
1)натуральные числа: 5; -1; 63; -63; 0; 317..; 0,25; √8; –3√2.
2)целые числа: 5; -5; 0; 28; 0,28; -0,28; 254..; 425..; 3876; -3876.
3)бесконечные периодические десятичные дроби:
-45,743743743…..; -45,7437433743…..; 45,45454545…..;
-45,45454545…..; 0,555555555…..; 0,555555556…..; -0,55555556.
4) бесконечные непериодические десятичные дроби (иррациональные числа):
11,03030303…..; -11,03030303…..; 11,030303030…..;
√4; –√4; √2; –√2; 0; 5,5; 3321,89898899…..
Как использовать научный калькулятор для решения дробей
Базовый калькулятор поможет вам решить простые операции.
Однако научный калькулятор лучше служит для упрощения сложных задач математики, физики и техники. Он может выполнять многофункциональные задачи одновременно. например, помогает быстро и точно решать дроби.
многие пользователи не знают о его быстрых командах. Вот полное руководство, которое поможет вам оптимально использовать ваше устройство при работе с дробями.
Содержание
- 1 Как использовать научный калькулятор для решения дробей
- 1.1 Шаг 1. Переключитесь в математический режим
- 1.2 Шаг 2. Найдите вкладку дробей на устройстве
- 1.3 Шаг 3. Навигация от no8 к числителю
- 1.5 Как изменить ответ в десятичной форме
- 1.6 Преобразование ответа смешанного числа в неправильную дробь
- 1.7 Как преобразовать десятичную дробь в неправильную дробь
- 1.8 Как решать смешанные числа на калькуляторе
- 1.9 Что делать, если в калькуляторе нет отдельной функции дроби
- 2 Часто задаваемые вопросы
- 2.
1 В Как распознать символ дроби? - 2.2 Q как двигать курсор для написания смешанных чисел?
- 2.
1 В Как распознать символ дроби?Как использовать научный калькулятор для решения дробей
Вот основные шаги, которые необходимо выполнить:
Шаг 1: Переключитесь в математический режим
Нажмите кнопку режима в правом верхнем углу калькулятора.
Перемещаясь по меню, выберите MATH.
Когда вы введете этот шаблон, ваш калькулятор отобразит «MATH» в правом верхнем углу экрана.
Примечание. Возможно, вашему калькулятору не нужно выполнять описанную выше процедуру. Модифицированные версии калькуляторов не имеют этой функции. непосредственно используйте кнопку дроби, чтобы делать дроби в таких калькуляторах.
Шаг 2: Найдите вкладку дробей на вашем устройстве
Обычно научные калькуляторы используют десятичные дроби для отображения дробей, что означает, что когда вы пишете ½, будет читаться 0,5. В таком случае вам нужно переключить ваше устройство в режим дробей.
СИМВОЛ Дроби
Черный прямоугольник над белым прямоугольником или кнопки ab/c или x/y, отштампованные на вашем калькуляторе, позволяют вам записывать дроби, будь то правильные или неправильные, целые числа или смешанные числа и т. д.
Шаг 3: переход от числителя к знаменателю
В шаблоне дроби некоторые устройства отображают два поля друг над другом, а в других отображается перевернутая буква L. Эти поля позволяют вводить числа и отличать числитель от знаменателя.
Нажатие клавиши Shift перед нажатием кнопки дроби позволяет добавить поле для записи серии смешанных чисел, например 1 ½.
Кнопка управления курсором со стрелками на калькуляторе используется для перехода от числителя к знаменателю.
В калькуляторах с линейным дисплеем нет необходимости перемещать курсор, все, что вам нужно сделать, это записать целую часть, числитель и знаменатель в последовательности.
Как написать неправильную дробь
- Впишите нужное число в числитель. 9кнопка б/к.
Нажатие кнопки дроби более одного раза поможет вам написать целую и дробную части.
Вставить команду +,-,* ,/.
Нажмите равно.
Что делать, если в калькуляторе нет отдельной функции дроби
Невозможно записывать дроби на калькуляторах, не имеющих функции дроби. Тем не менее, вы все равно можете рассчитать его, используя шаги, описанные ниже.
- Напишите числитель и нажмите клавишу деления.
- Затем напишите знаменатель.
- Нажмите равно.
- Ответ будет отображаться в десятичной форме.
Запишите ответ карандашом, затем умножьте его на число по вашему выбору, которое будет считаться его знаменателем, а результат, который он вернет, будет числителем.
Например, если вы хотите выразить 0,6234 в виде дроби, вы можете написать это как 6243/10 000. А вот сократить еще больше или с однозначным знаменателем. Все, что вам нужно сделать, это умножить исходное десятичное число 0,6234 на желаемое число в качестве знаменателя.
Предположим, вы умножаете 0,6234 на 5, отображаемый ответ будет числителем той дроби, которая равна 3,1. Следовательно, вы можете рассматривать 3/5 как форму неправильной дроби.
Часто задаваемые вопросы
В Как распознать символ дроби?
A в научном калькуляторе обозначается буквами ab/c, d/c или x/y. Нажатие этой клавиши позволит вам работать с дробями.
Q как двигать курсор для написания смешанных чисел?
Используйте кнопки управления курсором со стрелками в углу, чтобы перемещать курсор от одной дроби к другой.
Калькулятор TI-15 Explorer™ Elementary
Поощряйте учащихся 3–6 классов развивать свои навыки решения задач и начинать связывать математические понятия с реальными ситуациями.
Где купить
- Обзор
- Технические характеристики
Обзор Технические характеристики
Основные функции
- Автоматическое или пошаговое упрощение дробей до меньших членов
- Преобразование неправильных дробей, дробей, смешанных чисел, десятичных дробей и процентов
- Выполнение операций в порядке M-D-A-S
- Одновременный просмотр до двух записей и результатов
Начните закладывать основу для будущих успехов в математике
Калькулятор может отображать две формы дробных результатов одновременно, позволяя учащимся начать устанавливать важные математические связи. Предложите им вручную упростить дроби и смешанные числа в традиционном формате числителя/знаменателя или включите калькулятор, чтобы автоматически упростить их или преобразовать в десятичные эквиваленты.
Вовлеките учащихся в самостоятельное решение задач
Поощряйте учащихся самостоятельно изучать математику с помощью встроенных карточек, которые проверяют их навыки сложения, вычитания, умножения и деления. Установите карточки для соответствующего возраста и типа операции. Функциональность флэш-карты дает учащимся подсказки, когда вводится неправильный ответ, и включает в себя внутреннюю таблицу результатов, позволяющую учителям проверять прогресс каждого учащегося.
Характеристики калькулятора TI-15 Explorer™
Встроенная функциональность
- Электронные карточки: три уровня сложности с помощью клавиши «уровень сложности»
- Выберите из + — x ÷ или найдите операцию
- Калькулятор позволяет ввести задачу
- Просмотр подсказок с функцией «угадай и проверь»
- Фракции отображаются в виде стопки
- Выберите результаты смешанных чисел или неправильной дроби
- Выберите автоматическое или пошаговое упрощение дробей до меньших членов
- Дисплей показывает, когда дробь необходимо упростить
- Преобразование неправильных дробей в смешанные числа
- Преобразование дробей, десятичных знаков и процентов
- Калькулятор выбирает или разрешает ввод общего множителя
- Коэффициент просмотра, используемый для упрощения
- Одновременный просмотр до двух записей и результатов
- Просмотр и редактирование предыдущих записей
- Просмотр результатов деления в виде частных с остатками, дробями или десятичными знаками
- Две постоянные операции: показать счетчики и результаты
- Клавиша отрицания
- Степени и квадратный корень
- Символическое число π
- Преобразование числа π в десятичное число
- Удалить последнюю запись или все записи и настройки
- Backspace и возможности редактирования
- Сравнивать числа и уравнения, включая неравенства
- Разрядное значение: от тысячных до тысяч
- Округлить или исправить до целого числа или десятичных разрядов
- Операционная система EOS Equation выполняет операции в порядке M-D-A-S
- До 23 уровней скобок
- Возможности восстановления после ошибок
- Позволяет сохранять в памяти настройки и предыдущие записи
Фурнитура
- Твердый пластик, клавиши с цветовой маркировкой
- Двухстрочный, 11 цифр в строке
- Аккумулятор и солнечная энергия
- Ударопрочный чехол с картой быстрого доступа
- Доступен набор для учителя (включает 10 калькуляторов, коробку для хранения, компакт-диск с руководством для учителя и плакат с калькулятором)
Поддержка
- Ограниченная гарантия сроком на один год
- Бесплатная горячая линия: 1.
9кнопка б/к.
