Калькулятор онлайн скоротити дріб: Онлайн калькулятор для сокращения дробей

Скорочення чисельник 12 розділили. Онлайн калькулятор скорочення алгебраїчних дробів з докладним рішенням дозволяє скоротити дріб і перевести неправильний дріб у правильний дріб

У цій статті ми розглянемо основні дії з алгебраїчними дробами:

• скорочення дробів
• множення дробів
• розподіл дробів

Почнемо з скорочення алгебраїчних дробів .

Здавалося б, алгоритмочевидний.

Щоб скоротити алгебраїчні дроби, потрібно

1. Розкласти чисельник та знаменник дробу на множники.

2. Скоротити однакові множники.

Проте, школярі часто роблять помилку, «зменшуючи» не множники, а доданки. Наприклад, є любителі, які в дробі «зменшують» і отримують в результаті, що, зрозуміло, неправильно.

Розглянемо приклади:

1. Скоротити дріб:

1. Розкладемо на множники чисельник за формулою квадрата суми, а знаменник за формулою різниці квадратів

2. Розділимо чисельник та знаменник на

2. Скоротити дріб:

1. Розкладемо на множники чисельник. Так як чисельник містить чотири доданки, застосуємо угруповання.

2. Розкладемо на множники знаменник. Також застосуємо угруповання.

3. Запишемо дріб, який у нас вийшов і скоротимо однакові множники:

Розмноження алгебраїчних дробів.

При множенні дробів алгебри ми чисельник множимо на чисельник, а знаменник множимо на знаменник.

Важливо!Не потрібно поспішати виконувати множення у чисельнику та знаменнику дробу. Після того, як ми записали в чисельнику добуток чисельників дробів, а в знаменнику — добуток знаменників, потрібно розкласти на множники кожен множник і скоротити дріб.

Розглянемо приклади:

3. Спростіть вираз:

1. Запишемо добуток дробів: у чисельнику добуток чисельників, а у знаменнику добуток знаменників:

2. Розкладемо кожну дужку на множники:

Тепер нам потрібно скоротити однакові множники. Зауважимо, що вирази і відрізняються лише знаком: і в результаті розподілу першого виразу на друге отримаємо -1.

Отже,

Розподіл алгебраїчних дробів ми виконуємо за таким правилом:

Тобто щоб розділити на дріб, потрібно помножити на «перевернутий».

Ми бачимо, що розподіл дробів зводиться до множення, а множення, зрештою, зводиться до скорочення дробів.

Розглянемо приклад:

4. Спростіть вираз:

Щоб зрозуміти, як скорочувати дроби, спочатку розглянемо приклад.

Скоротити дріб — значить, розділити чисельник і знаменник на те саме. І 360, і 420 закінчуються на цифру, тому можемо скоротити цей дріб на 2. У новому дробі і 180, і 210 теж діляться на 2, скорочуємо і цей дріб на 2. У числах 90 і 105 сума цифр ділиться на 3, тому обидва ці числа діляться на 3, скорочуємо дріб на 3. У новому дробі 30 і 35 закінчуються на 0 і 5, значить, обидва числа діляться на 5, тому скорочуємо дріб на 5. Дріб, що вийшов, шість сьомих — нескорочуваний. Це остаточна відповідь.

До цієї ж відповіді можемо дійти іншим шляхом.

І 360, і 420 закінчуються нулем, отже, вони діляться на 10. Скорочуємо дріб на 10. У новому дробі і чисельник 36, і знаменник 42 діляться на 2. Скорочуємо дріб на 2. У наступному дробі і чисельник 18, і знаменник на 3, отже, скорочуємо дріб на 3. Прийшли до результату – шість сьомих.

І ще один варіант вирішення.

Наступного разу розглянемо приклади скорочення дробів.

Ця стаття продовжує тему перетворення алгебраїчних дробів: розглянемо таку дію як скорочення дробів алгебри. Дамо визначення самому терміну, сформулюємо правило скорочення та розберемо практичні приклади.

Yandex.RTB R-A-339285-1

Сенс скорочення алгебраїчного дробу

У матеріалах про звичайний дроб ми розглядали її скорочення. Ми визначили скорочення звичайного дробу як розподіл її чисельника та знаменника на загальний множник.

Скорочення дробу алгебри являє собою аналогічну дію.

Визначення 1

Скорочення алгебраїчного дробу– це розподіл її чисельника та знаменника на загальний множник. При цьому, на відміну від скорочення звичайного дробу (загальним знаменником може бути тільки число), загальним множником чисельника і знаменника дробу алгебри може служити многочлен, зокрема, одночлен або число.

Наприклад, алгебраїчна дріб 3 · x 2 + 6 · x · y 6 · x 3 · y + 12 · x 2 · y 2 може бути скорочена на число 3, в результаті отримаємо: x 2 + 2 · x · y 6 · x 3 · y + 12 · x 2 · y 2 . Цей же дріб ми можемо скоротити на змінну х, і це дасть нам вираз 3 · x + 6 · y 6 · x 2 · y + 12 · x · y 2 . Також заданий дріб можна скоротити на одночлен 3 · xабо будь-який з багаточленів x + 2 · y, 3 · x + 6 · y , x 2 + 2 · x · y або 3 · x 2 + 6 · x · y.

Кінцевою метою скорочення алгебраїчного дробу є дріб простішого виду, у кращому випадку – нескоротний дріб.

Чи всі дроби алгебри підлягають скороченню?

Знову ж таки з матеріалів про звичайні дроби ми знаємо, що існують скорочені і нескоротні дроби. Нескоротні – це дроби, які мають загальних множників чисельника і знаменника, відмінних від 1 .

З алгебраїчними дробами так само: вони можуть мати спільні множники чисельника і знаменника, можуть і не мати. Наявність загальних множників дозволяє спростити вихідний дріб за допомогою скорочення. Коли спільних множників немає, оптимізувати заданий дріб способом скорочення неможливо.

У загальних випадках за заданим видом дробу досить складно зрозуміти, чи підлягає вона скороченню. Звичайно, в деяких випадках наявність загального множника чисельника та знаменника очевидна. Наприклад, в алгебраїчному дробі 3 · x 2 3 · y зрозуміло, що загальним множником є ​​число 3 .

У дробі — x · y 5 · x · y · z 3 також ми відразу розуміємо, що скоротити її можливо на х, або y, або на х · y. І все ж таки набагато частіше зустрічаються приклади алгебраїчних дробів, коли загальний множник чисельника і знаменника не так просто побачити, а ще частіше — він просто відсутній.

Наприклад, дріб x 3 — 1 x 2 — 1 ми можемо скоротити на х — 1 при цьому зазначений загальний множник у записі відсутній. А ось дріб x 3 — x 2 + x — 1 x 3 + x 2 + 4 · x + 4 піддати дії скорочення неможливо, оскільки чисельник і знаменник не мають спільного множника.

Таким чином, питання з’ясування скоротливості алгебраїчного дробу не таке просте, і найчастіше простіше працювати з дробом заданого виду, ніж намагатися з’ясувати, чи вона скоротлива. При цьому мають місце такі перетворення, які в окремих випадках дозволяють визначити загальний множник чисельника і знаменника або зробити висновок про нескоротність дробу. Розглянемо детально це питання у наступному пункті статті.

Правило скорочення алгебраїчних дробів

Правило скорочення алгебраїчних дробів

складається з двох послідовних дій:

• знаходження загальних множників чисельника та знаменника;
• у разі знаходження таких здійснення безпосередньо впливу скорочення дробу.

Найзручнішим методом відшукання загальних знаменників є розкладання на множники многочленів, що у чисельнику і знаменнику заданої алгебраїчної дробу. Це дозволяє відразу побачити наявність чи відсутність загальних множників.

Саме вплив скорочення алгебраїчної дробу виходить з основному властивості алгебраїчної дробу, що виражається рівністю undefined , де a , b , c – деякі многочлены, причому b і c – ненульові. Першим кроком дріб наводиться до вигляду a · c b · c, в якому ми відразу помічаємо загальний множник c. Другим кроком – виконуємо скорочення, тобто. перехід до дробу виду a b.

Характерні приклади

Незважаючи на певну очевидність, уточнимо про окремий випадок, коли чисельник і знаменник алгебраїчної дробу рівні. Подібні дроби тотожно рівні 1 на всій ОДЗ змінних цього дробу:

5 5 = 1; — 2 3 — 2 3 = 1; x x = 1; — 3, 2 · x 3 — 3, 2 · x 3 = 1; 1 2 · x — x 2 · y 1 2 · x — x 2 · y;

Оскільки звичайні дробиє окремим випадком алгебраїчних дробів, нагадаємо, як здійснюється їх скорочення. Натуральні числа, записані в чисельнику та знаменнику, розкладаються на прості множники, потім загальні множники скорочуються (якщо є).

Наприклад, 24 1260 = 2 · 2 · 2 · 3 2 · 2 · 3 · 3 · 5 · 7 = 2 3 · 5 · 7 = 2 105

Добуток простих однакових множників можна записати як ступеня, і в процесі скорочення дробу використовувати властивість поділу ступенів з однаковими основами. Тоді вищезгадане рішення було б таким:

24 1260 = 2 3 · 3 2 2 · 3 2 · 5 · 7 = 2 3 — 2 3 2 — 1 · 5 · 7 = 2 105

(числитель та знаменник розділені на загальний множник 2 2 · 3). Або для наочності, спираючись на властивості множення та поділу, вирішенню дамо такий вигляд:

24 1260 = 2 3 · 3 2 2 · 3 2 · 5 · 7 = 2 3 2 2 · 3 3 2 · 1 5 · 7 = 2 1 · 1 3 · 1 35 = 2 105

За аналогією здійснюється скорочення алгебраїчних дробів, у яких у чисельнику та знаменнику є одночлени з цілими коефіцієнтами.

Приклад 1

Задано алгебраїчну дріб — 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z . Необхідно зробити її скорочення.

Рішення

Можливо записати чисельник та знаменник заданого дробу як добуток простих множниківта змінних, після чого здійснити скорочення:

27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 3 · 3 · 3 · a · a · a · a · a · b · b · c · z 2 · 3 · a · a · b · b · c · c · c · c · c · c · z = = — 3 · 3 · a · a · a 2 · c · c · c · c · c · c = — 9 · a 3 2 · c 6

Однак, раціональнішим способом буде запис рішення у вигляді виразу зі ступенями:

27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 3 3 · a 5 · b 2 · c · z 2 · 3 · a 2 · b 2 · c 7 · z = — 3 3 2 · 3 · a 5 a 2 · b 2 b 2 · c c 7 · z z = — 3 3 — 1 2 · a 5 — 2 1 · 1 · 1 c 7 — 1 · 1 = · — 3 2 · a 3 2 · c 6 = · — 9 · a 3 2 · c 6 .

Відповідь:— 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 9 · a 3 2 · c 6

Коли в чисельнику та знаменнику алгебраїчного дробу є дробові числові коефіцієнти, можливо два шляхи подальших дій: або окремо здійснити поділ цих дробових коефіцієнтів, або попередньо позбутися дробових коефіцієнтів, помноживши чисельник і знаменник на якесь натуральне число. Останнє перетворення проводиться в силу основної якості алгебраїчної дробу (про нього можна почитати в статті «Приведення дробу алгебри до нового знаменника»).

Приклад 2

Задано дроб 2 5 · x 0, 3 · x 3 . Необхідно здійснити її скорочення.

Рішення

Можливо скоротити дріб таким чином:

2 5 · x 0 , 3 · x 3 = 2 5 3 10 · x x 3 = 4 3 · 1 x 2 = 4 3 · x 2

Спробуємо вирішити завдання інакше, попередньо позбавившись дробових коефіцієнтів – помножимо чисельник і знаменник на найменше загальне кратне знаменників цих коефіцієнтів, тобто. на НОК (5, 10) = 10 . Тоді отримаємо:

2 5 · x 0, 3 · x 3 = 10 · 2 5 · x 10 · 0, 3 · x 3 = 4 · x 3 · x 3 = 4 3 · x 2 .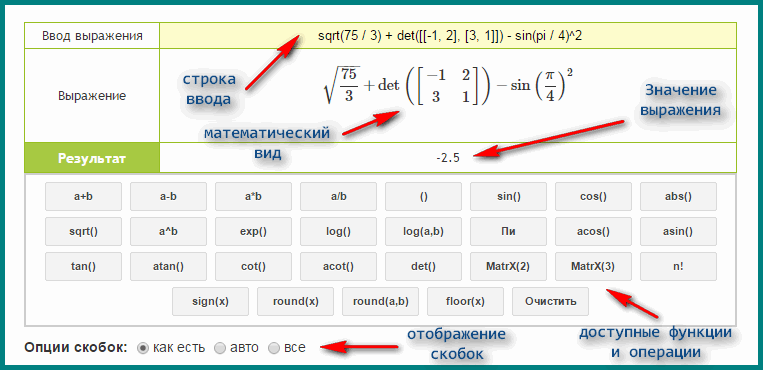

Відповідь: 2 5 · x 0 , 3 · x 3 = 4 3 · x 2

Коли ми скорочуємо алгебраїчні дроби загального вигляду, у яких чисельники і знаменники можуть бути як одночленами, і многочленами, можлива проблема, коли загальний множник який завжди відразу видно. Або більше, він просто не існує. Тоді для визначення загального множника або фіксації факту про його відсутність чисельник і знаменник дробу алгебри розкладають на множники.

Приклад 3

Задано раціональний дріб 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 . Потрібно її скоротити.

Рішення

Розкладемо на множники багаточлени в чисельнику та знаменнику. Здійснимо винесення за дужки:

2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · b 2 · (a 2 + 14 · a + 49) b 3 · (a 2 — 49)

Ми бачимо, що вираз у дужках можна перетворити з використанням формул скороченого множення:

2 · b 2 · (a 2 + 14 · a + 49) b 3 · (a 2 — 49) = 2 · b 2 · (a + 7) 2 b 3 · (a — 7) · (a + 7)

Добре помітно, що можна скоротити дріб на загальний множник b 2 · (a + 7). Зробимо скорочення:

2 · b 2 · (a + 7) 2 b 3 · (a — 7) · (a + 7) = 2 · (a + 7) b · (a — 7) = 2 · a + 14 a · b — 7 · b

Коротке рішення без пояснень запишемо як ланцюжок рівностей:

2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · b 2 · (a 2 + 14 a + 49) b 3 · (a 2 — 49) = = 2 · b 2 · (a + 7) 2 b 3 · (a — 7) · (a + 7) = 2 · (a + 7) b · (a — 7) = 2 · a + 14 a · b — 7 · b

Відповідь: 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · a + 14 a · b — 7 · b .

Трапляється, що загальні множники приховані числовими коефіцієнтами. Тоді при скороченні дробів оптимально числові множники при старших ступенях чисельника та знаменника винести за дужки.

Приклад 4

Дано алгебраїчну дріб 1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 . Необхідно здійснити її скорочення, якщо це можливо.

Рішення

На погляд у чисельника і знаменника немає спільного знаменника. Однак спробуємо перетворити заданий дріб. Винесемо за дужки множник х у чисельнику:

1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 = x · 1 5 — 2 7 · x 2 · y 5 · x 2 · y — 3 1 2

Тепер видно певну схожість виразу в дужках і виразу в знаменнику за рахунок x 2 · y

. Винесемо за дужку числові коефіцієнти при старших ступенях цих багаточленів:

x · 1 5 — 2 7 · x 2 · y 5 · x 2 · y — 3 1 2 = x · — 2 7 · — 7 2 · 1 5 + x 2 · y 5 · x 2 · y — 1 5 · 3 1 2 = = — 2 7 · x · — 7 10 + x 2 · y 5 · x 2 · y — 7 10

Тепер стає видно загальний множник, здійснюємо скорочення:

2 7 · x · — 7 10 + x 2 · y 5 · x 2 · y — 7 10 = — 2 7 · x 5 = — 2 35 · x

Відповідь: 1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 = — 2 35 · x.

Зробимо акцент на тому, що навичка скорочення раціональних дробів залежить від уміння розкладати багаточлени на множники.

Якщо ви помітили помилку в тексті, будь ласка, виділіть її та натисніть Ctrl+Enter

Минулого разу ми склали план, за яким можна навчитися швидко скорочувати дроби. Наразі розглянемо конкретні приклади скорочення дробів.

Приклади.

Перевіряємо, а чи не ділиться більше на менше (числитель на знаменник або знаменник на чисельник)? Так, у всіх трьох цих прикладах більше ділиться на менше. Таким чином, кожний дріб скорочуємо на менший з чисел (на чисельник або на знаменник). Маємо:

Перевіряємо, чи не ділиться більше на менше? Ні, не ділиться.

Тоді переходимо до перевірки наступного пункту: а чи не закінчується запис і чисельника, і знаменника одним, двома чи кількома нулями? У першому прикладі запис чисельника та знаменника закінчується нулем, у другому – двома нулями, у третьому – трьома нулями. Отже, перший дроб скорочуємо на 10, другий — на 100, третій — на 1000:

Отримали нескоротні дроби.

Більше на менше не ділиться, запис чисел нулями не закінчується.

Тепер перевіряємо, а чи не стоять чисельник та знаменник в одному стовпці у таблиці множення? 36 і 81 обидва діляться на 9, 28 і 63 — на 7, а 32 і 40 — на 8 (вони діляться ще й на 4, але якщо є можливість вибору, завжди скорочуватимемо на більше). Таким чином, приходимо до відповідей:

Усі отримані числа є нескоротними дробами.

Більше на менше не ділиться. А ось запис і чисельника, і знаменника закінчується банкрутом. Значить, скорочуємо дріб на 10:

Цей дріб ще можна скоротити. Перевіряємо за таблицею множення: і 48, і 72 поділяються на 8. Скорочуємо дріб на 8:

Отриманий дріб ще можемо скоротити на 3:

Цей дріб — нескоротний.

Більше чисел на менше не ділиться. Запис чисельника та знаменника закінчується на нуль.Отже, скорочуємо дріб на 10.

Отримані в чисельнику та знаменнику числа перевіряємо на і . Так як сума цифр і 27, і 531 діляться на 3 і на 9, то цей дріб можна скоротити як на 3, так і на 9. Вибираємо більше і скорочуємо на 9. Отриманий результат — нескоротний дріб.

На погляд алгебраїчні дроби здаються дуже складними, і непідготовлений учень може подумати, що з ними неможливо нічого зробити. Нагромадження змінних, чисел і навіть ступенів навіює страх. Тим не менш, для скорочення звичайних (наприклад, 15/25) та алгебраїчних дробів використовуються одні й ті самі правила.

Кроки

Скорочення дробів

Ознайомтеся з діями з простими дробами. Операції із звичайними та алгебраїчними дробами аналогічні. Наприклад, візьмемо дріб 15/35. Щоб спростити цей дріб, слід знайти спільний дільник . Обидва числа діляться на п’ять, тому ми можемо виділити 5 у чисельнику та знаменнику:

15

→

5 * 3

35 → 5 * 7

Тепер можна скоротити загальні множники, тобто викреслити 5 у чисельнику та знаменнику. В результаті отримуємо спрощений дріб 3/7 . У алгебраїчних виразах загальні множники виділяються так само, як і в звичайних. У попередньому прикладі ми змогли легко виділити 5 з 15 — той же принцип застосуємо і до більш складних виразів, таких як 15x — 5. Знайдемо спільний множник. У даному випадкуце буде 5, тому що обидва члени (15x і -5) діляться на 5. Як і раніше, виділимо загальний множник і перенесемо його вліво.

15x — 5 = 5 * (3x — 1)

Щоб перевірити, чи все правильно, достатньо помножити на 5 вираз, що стоїть у дужках — в результаті вийдуть ті ж числа, що були спочатку.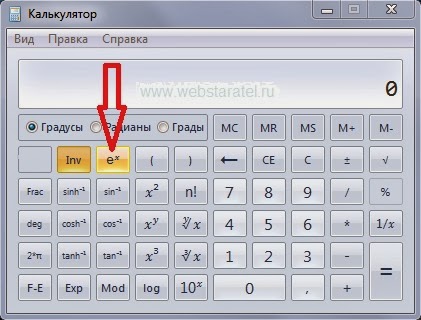 Складні члениможна виділяти так само, як і прості. Для алгебраїчних дробів застосовні самі принципи, як і звичайних. Це найпростіший спосіб скоротити дріб. Розглянемо наступний дріб:

(x+2)(x-3)

(x+2)(x+10)

Зазначимо, що і в чисельнику (згори), і в знаменнику (знизу) присутній член (x+2), тому його можна скоротити так само, як загальний множник 5 у дробі 15/35:

(x+2) (x-3)

→

(x-3)

(x+2) (x+10) → (x+10)

В результаті отримуємо спрощений вираз: (x-3)/(x+10)

Скорочення алгебраїчних дробів

Знайдіть загальний множник у чисельнику, тобто у верхній частині дробу. При скороченні алгебраїчного дробу насамперед слід спростити обидві його частини. Почніть з чисельника і постарайтеся розкласти його якомога більша кількістьмножників. Розглянемо в цьому розділі наступний дріб:

9x-3

15x+6

Почнемо з чисельника: 9x – 3.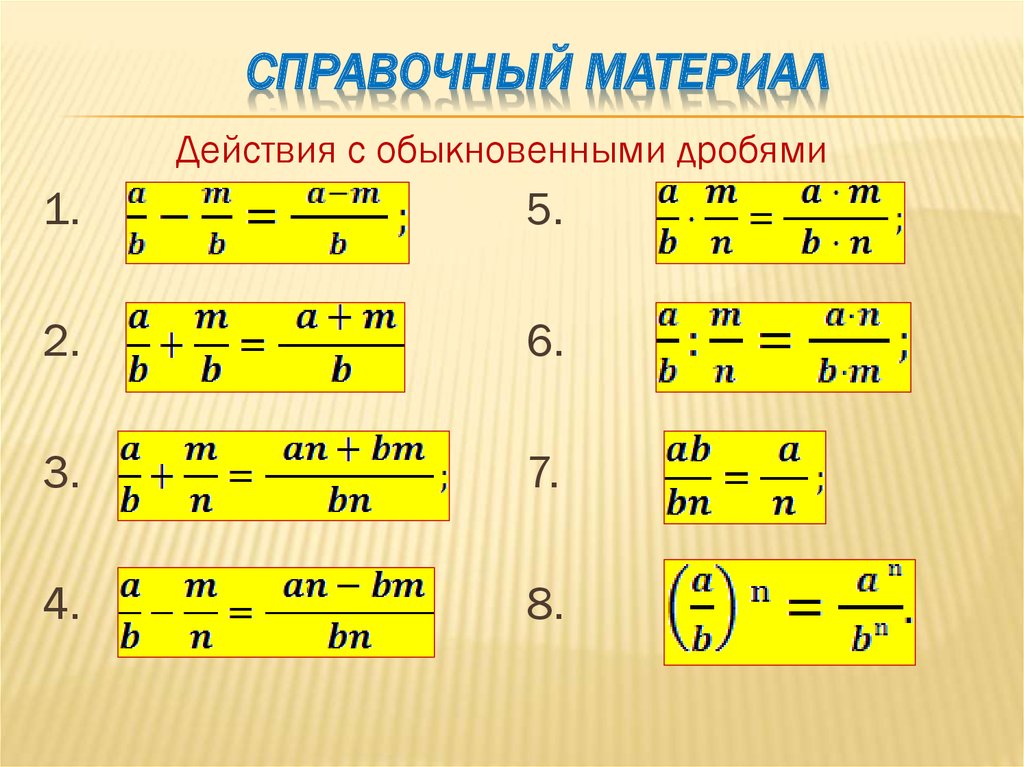 Для 9x та -3 загальним множником є ​​число 3. Винесемо 3 за дужки, як це робиться із звичайними числами: 3*(3x-1). В результаті цього перетворення вийде наступний дріб:

3(3x-1)

15x+6

Знайдіть загальний множник у чисельнику. Продовжимо виконання наведеного вище прикладу та випишемо знаменник: 15x+6. Як і раніше, знайдемо, на скільки діляться обидві частини. І в цьому випадку загальним множником є ​​3, так що можна записати: 3*(5x+2). Перепишемо дріб у такому вигляді:

3(3x-1)

3(5x+2)

Скоротіть однакові члени. На цьому етапі можна спростити дріб. Скоротіть однакові члени у чисельнику та знаменнику. У прикладі це число 3.

3 (3x-1)

→

(3x-1)

3 (5x+2) → (5x+2)

Визначте, що дріб має найпростіший вигляд. Дроб повністю спрощена в тому випадку, коли в чисельнику і знаменнику не залишилося спільних множників. Врахуйте, що не можна скорочувати ті члени, які стоять усередині дужок — у наведеному прикладі немає можливості виділити x з 3x та 5x, оскільки повними членами є (3x -1) та (5x + 2). Таким чином, дріб не піддається подальшому спрощенню, і остаточна відповідь виглядає так:

(3x-1)(5x+2)

Потренуйтесь скорочувати дроби самостійно. Кращий спосібЗасвоїти метод полягає у самостійному вирішенні завдань. Під прикладами наведено правильні відповіді.

4(x+2)(x-13)

(4x+8)

Відповідь:(x=13)

2x 2-x

5x

Відповідь:(2x-1)/5

Спеціальні прийоми

Винесіть негативний знак межі дробу. Припустимо, дано такий дріб:

3(x-4)

5(4-x)

Зауважте, що (x-4) і (4-x) «майже» ідентичні, але їх не можна скоротити відразу, оскільки вони «перевернуті». Тим не менш, (x — 4) можна записати як -1 * (4 — x), подібно до того як (4 + 2x) можна переписати у вигляді 2 * (2 + x). Це називається «зміною знака».

-1 * 3 (4-x)

5(4-x)

Тепер можна скоротити однакові члени (4-x):

-1 * 3 (4-x)

5 (4-х)

Отже, отримуємо остаточну відповідь: -3/5 . Навчіться розпізнавати різницю квадратів. Різниця квадратів — це коли квадрат одного числа віднімається з квадрата іншого числа, як у виразі (a 2 — b 2). Різницю повних квадратівзавжди можна розкласти на дві частини — суму та різницю відповідних квадратного коріння. Тоді вираз набуде наступного вигляду:

A 2 — b 2 = (a+b)(a-b)

Цей прийом дуже корисний при пошуку спільних членів в дробах алгебри.

• Перевірте, чи правильно ви розклали той чи інший вираз на множники. Для цього перемножте множники — в результаті має вийти те саме вираз.
• Щоб повністю спростити дріб, завжди виділяйте найбільші множники.

Як скорочувати великі числа в дробах. Калькулятор онлайн.Сокращеніе дробів (неправильних, змішаних)

Скорочення дробів потрібно для того, щоб привести дріб до більш простому виду, Наприклад, у відповіді отриманому в результаті рішення вираження.

Скорочення дробів, визначення і формула.

Що таке скорочення дробів? Що значить скоротити дріб?

визначення:
скорочення дробів— це поділ у дробу чисельник і знаменник на одне й те саме додатне число не рівне нулю і одиниці. В результаті скорочення виходить дріб з меншим чисельником і знаменником, що дорівнює попередній дробу згідно.

Формула скорочення дробівосновного властивості раціональних чисел.

\ (\ Frac (p \ times n) (q \ times n) = \ frac (p) (q) \)

Розглянемо приклад:
Скоротіть дріб \ (\ frac (9) (15) \)

Рішення:
Ми можемо розкласти дріб на прості множники і скоротити загальні множники.

\ (\ Frac (9) (15) = \ frac (3 \ times 3) (5 \ times 3) = \ frac (3) (5) \ times \ color (red) (\ frac (3) (3) ) = \ frac (3) (5) \ times 1 = \ frac (3) (5) \)

Відповідь: після скорочення отримали дріб \ (\ frac (3) (5) \). За основним властивості раціональних чисел первісна і вийшло дріб рівні.

\ (\ Frac (9) (15) = \ frac (3) (5) \)

Як скорочувати дроби? Скорочення дробу до нескоротних виду.

Щоб нам отримати в результаті нескоротний дріб, потрібно знайти найбільший загальний дільник(НОД)для чисельника і знаменника дробу.

Є кілька способів знайти НСД ми скористаємося в прикладі розкладанням чисел на прості множники.

Отримайте нескоротний дріб \ (\ frac (48) (136) \).

Рішення:
Знайдемо НСД (48, 136). Розпишемо числа 48 і 136 на прості множники.
48=2⋅2⋅2⋅2⋅3
136=2⋅2⋅2⋅17
НСД (48, 136) = 2⋅2⋅2 = 6

\ (\ Frac (48) (136) = \ frac (\ color (red) (2 \ times 2 \ times 2) \ times 2 \ times 3) (\ color (red) (2 \ times 2 \ times 2) \ times 17) = \ frac (\ color (red) (6) \ times 2 \ times 3) (\ color (red) (6) \ times 17) = \ frac (2 \ times 3) (17) = \ frac (6) (17) \)

Правило скорочення дробу до нескоротних виду.

1. Потрібно знайти найбільший спільний дільник для числители і знаменника.
2. Потрібно поділити чисельник і знаменник на найбільший спільний дільник в результаті поділу отримати нескоротний дріб.

приклад:
Скоротіть дріб \ (\ frac (152) (168) \).

Рішення:
Знайдемо НСД (152, 168). Розпишемо числа 152 і 168 на прості множники.
152=2⋅2⋅2⋅19
168=2⋅2⋅2⋅3⋅7
НСД (152, 168) = 2⋅2⋅2 = 6

\ (\ Frac (152) (168) = \ frac (\ color (red) (6) \ times 19) (\ color (red) (6) \ times 21) = \ frac (19) (21) \)

Відповідь: \ (\ frac (19) (21) \) нескоротний дріб.

Скорочення неправильного дробу.

Як скоротити неправильну дріб?
Правила скорочення дробів для правильних і неправильних дробів однакові.

Розглянемо приклад:
Скоротіть неправильну дріб \ (\ frac (44) (32) \).

Рішення:
Розпишемо на прості множники чисельник і знаменник. А потім загальні множники скоротимо.

\ (\ Frac (44) (32) = \ frac (\ color (red) (2 \ times 2) \ times 11) (\ color (red) (2 \ times 2) \ times 2 \ times 2 \ times 2 ) = \ frac (11) (2 \ times 2 \ times 2) = \ frac (11) (8) \)

Скорочення змішаних дробів.

Змішані дробу за тими ж правилами що і звичайні дроби. Різниця лише в тому, що ми можемо цілу частину не чіпати, а дробову частину скоротитиабо змішану дрібперевести в неправильну дріб, скоротити і перевести назад в правильну дріб.

Розглянемо приклад:
Скоротіть змішану дріб \ (2 \ frac (30) (45) \).

Рішення:
Вирішимо двома способами:
Перший спосіб:
Розпишемо дробову частину на прості множники, а цілу частина не будемо чіпати.

\ (2 \ frac (30) (45) = 2 \ frac (2 \ times \ color (red) (5 \ times 3)) (3 \ times \ color (red) (5 \ times 3)) = 2 \ frac (2) (3) \)

Другий спосіб:
Переведемо спочатку в неправильну дріб, а потім розпишемо на прості множники і скоротимо. Отриману неправильну дріб переведемо в правильну.

\ (2 \ frac (30) (45) = \ frac (45 \ times 2 + 30) (45) = \ frac (120) (45) = \ frac (2 \ times \ color (red) (5 \ times 3) \ times 2 \ times 2) (3 \ times \ color (red) (3 \ times 5)) = \ frac (2 \ times 2 \ times 2) (3) = \ frac (8) (3) = 2 \ frac (2) (3) \)

Питання по темі:
Чи можна скорочувати дроби при додаванні або відніманні?
Відповідь: ні, потрібно спочатку скласти або відняти дроби з правилами, а тільки потім скорочувати. Розглянемо приклад:

Обчисліть вираз \ (\ frac (50 + 20-10) (20) \).

Рішення:
Часто припускаються помилки скорочуючи однакові числа в чисельнику і знаменнику в нашому випадком число 20, але їх скорочувати не можна поки не виконаєте додавання і віднімання.

\ (\ Frac (50+ \ color (red) (20) -10) (\ color (red) (20)) = \ frac (60) (20) = \ frac (3 \ times 20) (20) = \ frac (3) (1) = 3 \)

На які числа можна скорочувати дріб?
Відповідь: можна скорочувати дріб на найбільший спільний дільник або звичайний дільник чисельника і знаменника. Наприклад, дріб \ (\ frac (100) (150) \).

Розпишемо на прості множники числа 100 і 150.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
Найбільшим спільним дільником буде число НСД (100, 150) = 2⋅5⋅5 = 50

\ (\ Frac (100) (150) = \ frac (2 \ times 50) (3 \ times 50) = \ frac (2) (3) \)

Отримали нескоротний дріб \ (\ frac (2) (3) \).

Але необов’язково завжди ділити на НОД не завжди потрібна нескоротний дріб, можна скоротити дріб на простий дільник чисельника і знаменника. Наприклад, у числа 100 і 150 загальний дільник 2. Скоротимо дріб \ (\ frac (100) (150) \) на 2.

\ (\ Frac (100) (150) = \ frac (2 \ times 50) (2 \ times 75) = \ frac (50) (75) \)

Отримали сократимостью дріб \ (\ frac (50) (75) \).

Які дроби можна скорочувати?
Відповідь: скорочувати можна дроби у яких чисельник і знаменник мають спільний дільник. Наприклад, дріб \ (\ frac (4) (8) \). У числа 4 і 8 є число, на яке вони обидва діляться це число 2. Тому таку дріб можна скоротити на число 2.

приклад:
Порівняйте дві дробу \ (\ frac (2) (3) \) і \ (\ frac (8) (12) \).

Ці дві дробу рівні. Розглянемо докладно дріб \ (\ frac (8) (12) \):

\ (\ Frac (8) (12) = \ frac (2 \ times 4) (3 \ times 4) = \ frac (2) (3) \ times \ frac (4) (4) = \ frac (2) (3) \ times 1 = \ frac (2) (3) \)

Звідси отримуємо, \ (\ frac (8) (12) = \ frac (2) (3) \)

Дві дробу рівні тоді і тільки тоді, коли одна з них отримана шляхом скорочення інший дробу на спільний множник чисельника і знаменника.

приклад:
Скоротіть якщо можливо такі дроби: а) \ (\ frac (90) (65) \) б) \ (\ frac (27) (63) \) в) \ (\ frac (17) (100) \) г) \ (\ frac (100) (250) \)

Рішення:
а) \ (\ frac (90) (65) = \ frac (2 \ times \ color (red) (5) \ times 3 \ times 3) (\ color (red) (5) \ times 13) = \ frac (2 \ times 3 \ times 3) (13) = \ frac (18) (13) \)
б) \ (\ frac (27) (63) = \ frac (\ color (red) (3 \ times 3) \ times 3) (\ color (red) (3 \ times 3) \ times 7) = \ frac (3) (7) \)
в) \ (\ frac (17) (100) \) нескоротний дріб
г) \ (\ frac (100) (250) = \ frac (\ color (red) (2 \ times 5 \ times 5) \ times 2) (\ color (red) (2 \ times 5 \ times 5) \ times 5) = \ frac (2) (5) \)

Увага!
До цієї теми є додаткові
матеріали в Особливому розділі 555.
Для тих, хто сильно «не дуже …»
І для тих, хто «дуже навіть …»)

Дробу в старших класах не сильно докучають. До пори до часу. Ще не зіткнетеся зі ступенями з раціональними показникамида логарифмами. А ось там …. Тиснеш, тиснеш калькулятор, а він все повне табло якихось циферок показує. Доводиться головою думати, як в третьому класі.

Давайте вже розберемося з дробом, нарешті! Ну скільки можна в них плутатися !? Тим більше, це все просто і логічно. Отже, які бувають дробу?

Види дробів. Перетворення.

дробу бувають трьох видів.

1. звичайні дроби , Наприклад:

Іноді замість горизонтальної рисочки ставлять похилу риску: 1/2, 3/4, 19/5, ну, і так далі. Тут ми часто будемо таким написанням користуватися. Верхнє число називається числителем, Нижнє — знаменником.Якщо ви постійно плутаєте ці назви (буває …), скажіть собі з виразом фразу: » Зззззапомні! Зззззнаменатель — вни зззззу! «Дивишся, все і ззззапомнітся.)

Риска, що горизонтальна, що похила, означає поділверхнього числа (чисельника) на нижню (знаменник). І все! Замість рисочки цілком можна поставити знак ділення — дві точки.

Коли поділ можливо без остачі, це треба робити. Так, замість дробу «32/8» набагато приємніше написати число «4». Тобто 32 просто поділити на 8.

32/8 = 32: 8 = 4

Я вже й не кажу про дріб «4/1». Яка теж просто «4». А якщо вже не ділиться без остачі, так і залишаємо, у вигляді дробу. Іноді доводиться зворотну операцію проробляти. Робити з цілого числа дріб. Але про це далі.

2. десяткові дроби , Наприклад:

Саме в такому вигляді потрібно буде записувати відповіді на завдання «В».

3. змішані числа , Наприклад:

Змішані числа практично не використовуються в старших класах. Для того, щоб з ними працювати, їх всяко треба переводити в звичайні дроби. Але це точно треба вміти робити! А то трапиться таке число в завданню і ЗАВІСНА … На порожньому місці. Але ми-то згадаємо цю процедуру! Трохи нижче.

найбільш універсальні звичайні дроби. З них і почнемо. До речі, якщо в дробу стоять всякі логарифми, синуси і інші літери, це нічого не змінює.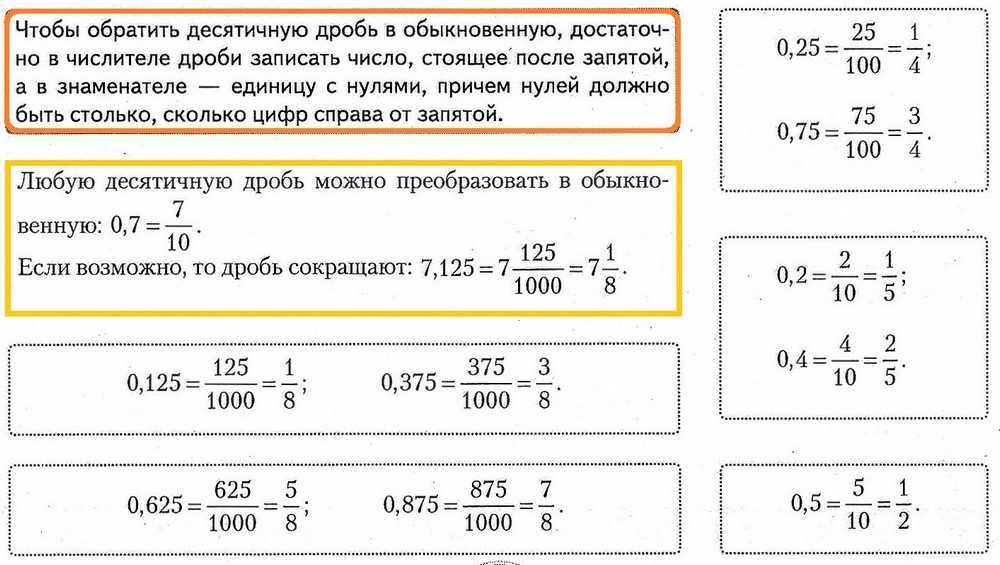 В тому сенсі що все дії з дробовими виразами нічим не відрізняються від дій зі звичайними дробами!

Основна властивість дробу.

Отже, поїхали! Для початку я вас здивую. Все різноманіття перетворень дробів забезпечується одним-єдиним властивістю! Воно так і називається, основну властивість дробу. запам’ятовуйте: якщо чисельник і знаменник дробу помножити (поділити) на одне і те ж число, дріб не зміниться.тобто:

Зрозуміло, що писати можна далі, до посиніння. Синуси і логарифми нехай вас не бентежать, з ними далі розберемося. Головне зрозуміти, що всі ці різноманітні висловлювання є одна і та ж дріб . 2/3.

А воно нам треба, всі ці перетворення? Ще й як! Зараз самі побачите. Для початку вживемо основну властивість дробу для скорочення дробів. Здавалося б, річ елементарна. Ділимо чисельник і знаменник на одне і те ж число і всі справи! Помилитися неможливо! Але … людина — істота творча. Помилитися всюди може! Особливо, якщо доводиться скорочувати НЕ дріб типу 5/10, а дробове вираження зі всякими літерами.

Як правильно і швидко скорочувати дроби, не роблячи зайвої роботи, можна прочитати в особливому розділі 555.

Нормальний учень не заморочується розподілом чисельника і знаменника на одне і те ж число (або вираз)! Він просто закреслює все однакове зверху і знизу! Тут-то і криється типова помилка, Ляп, якщо хочете.

Наприклад, треба спростити вираз:

Тут і думати нема чого, зачеркиваем букву «а» зверху і двійку знизу! отримуємо:

Все правильно. Але реально ви поділили весь чисельник і весь знаменник на «а». Якщо ви звикли просто закреслювати, то, похапцем, можете закреслити «а» в вираженні

і отримати знову

Що буде категорично невірно. Тому що тут весьчисельник на «а» вже не ділиться! Цю дріб скоротити не можна. До речі, таке скорочення — це, гм … серйозний виклик викладачеві. Такого не прощають! Запам’ятали? При скороченні ділити треба весь чисельник і весь знаменник!

Скорочення дробів сильно полегшує життя. Вийде десь у вас дріб, наприклад 375/1000. І як тепер з нею далі працювати? Без калькулятора? Множити, скажімо, складати, в квадрат зводити !? А якщо не полінуватися, так акуратненько скоротити на п’ять, та ще на п’ять, та ще … поки скорочується, коротше. Отримаємо 3/8! Куди приємніше, правда?

Основна властивість дробу дозволяє переводити звичайні дроби в десяткові і навпаки без калькулятора! Це важливо на ЄДІ, вірно?

Як переводити дроби з одного виду в інший.

З десятковими дробами все просто. Як чується, так і пишеться! Скажімо, 0,25. Це нуль цілих, двадцять п’ять сотих. Так і пишемо: 25/100. Скорочуємо (ділимо чисельник і знаменник на 25), отримуємо звичайну дріб: 1/4. Всі. Буває, і не скорочується нічого. Типу 0,3. Це три десятих, тобто 3/10.

А якщо цілих — НЕ нуль? Нічого страшного. Записуємо всю дріб без всяких комв чисельник, а в знаменник — то, що чується. Наприклад: 3,17. Це три цілих, сімнадцять сотих. Пишемо в чисельник 317, а в знаменник 100. Отримуємо 317/100. Нічого не скорочується, значить все. Це відповідь. Елементарно, Ватсон! З усього сказаного корисний висновок: будь-яку десяткову дріб можна перетворити в звичайну .

А ось зворотне перетворення, звичайної в десяткову, деякі без калькулятора не можуть зробити. А треба! Як ви відповідь записувати будете на ЄДІ !? Уважно читаємо і освоюємо цей процес.

Десяткова дріб ніж характерна? У неї в знаменнику завждикоштує 10, або 100, або 1000, або 10000 і так далі. Якщо ваша звичайна дріб має такий знаменник, проблем немає. Наприклад, 4/10 = 0,4. Або 7/100 = 0,07. Або 12/10 = 1,2. А якщо у відповіді на завдання розділу «В» вийшло 1/2? Що у відповідь писати будемо? Там десяткові потрібні …

згадуємо основну властивість дробу ! Математика прихильно дозволяє множити чисельник і знаменник на одне і те ж число. На будь-який, між іншим! Крім нуля, зрозуміло. Ось і застосуємо це властивість собі на користь! На що можна помножити знаменник, тобто 2 щоб він став 10, або 100, або 1000 (трохи менше краще, звичайно . ..)? На 5, очевидно. Сміливо множимо знаменник (це намтреба) на 5. Але, тоді і чисельник треба помножити теж на 5. Це вже математикавимагає! Отримаємо 1/2 = 1х5 / 2х5 = 5/10 = 0,5. От і все.

Однак, знаменники всякі попадаються. Попадеться, наприклад дріб 3/16. Спробуй, зміркуй тут, на що 16 помножити, щоб 100 вийшло, або 1000 … Не виходить? Тоді можна просто розділити 3 на 16. За відсутністю калькулятора ділити доведеться куточком, на папірці, як в молодших класах вчили. Отримаємо 0,1875.

А бувають і зовсім кепські знаменники. Наприклад, дріб 1/3 ну ніяк не перетвориш в хорошу десяткову. І на калькуляторі, і на папірці, ми отримаємо 0,3333333 … Це означає, що 1/3 в точну десяткову дріб НЕ перекладається. Так само, як і 1/7, 5/6 і так далі. Багато їх, неперекладних. Звідси ще один корисний висновок. Не кожна звичайна дріб перекладається в десяткову !

До речі, це корисна інформаціядля самоперевірки. У розділі «В» у відповідь треба десяткову дріб записувати. А у вас вийшло, наприклад, 4/3. Ця дріб не переводиться в десяткову. Це означає, що десь ви помилилися дорогою! Поверніться, перевірте рішення.

Отже, зі звичайними і десятковими дробами розібралися. Залишилося розібратися зі змішаними числами. Для роботи з ними їх всяко потрібно перевести в звичайні дроби. Як це зробити? Можна зловити шестикласника і запитати у нього. Але не завжди шестикласник опиниться під руками … Доведеться самим. Це не складно. Треба знаменник дробової частини помножити на цілу частину і додати чисельник дробової частини. Це буде чисельник звичайного дробу. А знаменник? Знаменник залишиться тим же самим. Звучить складно, але на ділі все елементарно. Дивимося приклад.

Нехай в завданню ви з жахом побачили число:

Спокійно, без паніки міркуємо. Ціла частина — це 1. Одиниця. Дрібна частина — 3/7. Стало бути, знаменник дробової частини — 7. Цей знаменник і буде знаменником звичайного дробу. Вважаємо чисельник. 7 множимо на 1 (ціла частина) і додаємо 3 (чисельник дробової частини). Отримаємо 10. Це буде чисельник звичайного дробу. От і все. Ще простіше це виглядає в математичної записи:

Ясненько? Тоді закріпіть успіх! Переведіть в звичайні дроби. У вас повинно вийти 10/7, 7/2, 23/10 і 21/4.

Зворотна операція — переклад неправильного дробу в змішане число — в старших класах рідко потрібно. Ну якщо вже … І якщо Ви — не в старших класах — можете заглянути в особливий Розділ 555. Там же, до речі, і про неправильні дроби дізнаєтеся.

Ну ось, практично і все. Ви згадали види дробів і зрозуміли, як переводити їх з одного виду в інший. Залишається питання: навіщо це робити? Де і коли застосовувати ці глибокі пізнання?

Відповідаю. Будь приклад сам підказує необхідні дії. Якщо в прикладі змішалися в купу звичайні дроби, десяткові, та ще й змішані числа, переводимо все в звичайні дроби. Це завжди можна зробити. Ну а якщо написано, що-небудь типу 0,8 + 0,3, то так і вважаємо, без жодного перекладу. Навіщо нам зайва робота? Ми вибираємо той шлях вирішення, який зручний нам !

Якщо в завданні суцільно десяткові дроби, Але гм … злі якісь, перейдіть до звичайних, спробуйте! Дивишся, все і налагодиться. Наприклад, доведеться в квадрат зводити число 0,125. Не так-то просто, якщо від калькулятор не відвикли! Мало того, що числа перемножувати стовпчиком треба, так ще думай, куди кому вставити! У розумі точно не вийде! А якщо перейти до звичайного дробу?

0,125 = 125/1000. Скорочуємо на 5 (це для початку). Отримуємо 25/200. Ще раз на 5. Отримуємо 5/40. О, ще скорочується! Знову на 5! Отримуємо 1/8. Легко зводимо в квадрат (в розумі!) І отримуємо 1/64. Всі!

Підіб’ємо підсумки цього уроку.

1. Дроби бувають трьох видів. Звичайні, десяткові і змішані числа.

2. Десяткові дроби і змішані числа завждиможна перевести в звичайні дроби. зворотній переклад не завждиможливий.

3. Вибір виду дробів для роботи із завданням залежить від цього самого завдання. При наявності різних видівдробів в одному завданні, найнадійніше — перейти до звичайних дробів.

Тепер можна потренуватися. Для початку переведіть ці десяткові дроби в звичайні:

3,8; 0,75; 0,15; 1,4; 0,725; 0,012

Повинні вийти ось такі відповіді (в безладді!):

На цьому і завершимо. У цьому уроці ми освіжили в пам’яті ключові моментипо дробям. Буває, правда, що освіжати особливо нічого …) Якщо вже хто зовсім міцно забув, або ще не освоїв … Тим можна пройти в особливий Розділ 555. Там все основи подробненько розписані. багато раптом все розумітипочинають. І вирішують дроби з льоту).

Якщо Вам подобається цей сайт …

До речі, у мене є ще парочка цікавих сайтів для Вас.)

Можна потренуватися у вирішенні прикладів і дізнатися свій рівень. Тестування з миттєвою перевіркою. Вчимося — з інтересом!)

можна познайомитися з функціями і похідними.

Дробу і їх скорочення — ще одна тема, яка починається в 5 класі. Тут формується база цієї дії, а потім ці вміння тягнуться ниточкою в вищу математику. Якщо учень не засвоїв, то у нього можуть виникнути проблеми в алгебрі. Тому краще усвідомити кілька правил раз і назавжди. А ще запам’ятати один заборона і ніколи його не порушувати.

Дріб і її скорочення

Що це таке, знає кожен учень. Будь-які дві цифри розташовані між горизонтальною лінією відразу сприймаються, як дріб. Однак не всі розуміють, що нею може стати будь-яке число. Якщо воно ціле, то його завжди можна розділити на одиницю, тоді вийде неправильна дріб. Але про це пізніше.

Початок завжди просте. Спочатку потрібно з’ясувати, як скоротити правильну дріб. Тобто таку, у якій чисельник менше, ніж знаменник. Для цього буде потрібно згадати основну властивість дробу. Воно стверджує, що при множенні (так само, як і розподілі) одночасно її чисельника і знаменника на однакове число виходить, рівноцінна вихідної дріб.

Дії ділення, які виконуються в цій властивості і призводять до скорочення. Тобто максимальному її спрощення. Дріб можна скорочувати до тих пір, поки над рисою і під нею є загальні множники. Коли їх вже не буде, то скорочення неможливо. І кажуть, що ця дріб нескоротний.

два способи

1.Покрокове скорочення.У ньому використовується метод прикидки, коли обидва числа діляться на мінімальний загальний множник, який зауважив учень. Якщо після першого скорочення видно, що це не кінець, то розподіл триває. Поки дріб не стане нескоротного.

2. Знаходження найбільшого загального дільника у чисельника і знаменника.Це найраціональніший спосіб того, як скорочувати дроби. Він має на увазі розкладання чисельника і знаменника на прості множники. Серед них потім потрібно вибрати всі однакові. Їх твір дасть найбільший спільний множник, на який скорочується дріб.

Обидва ці способу рівноцінні. Учневі пропонується освоїти їх і користуватися тим, який більше сподобався.

Що робити, якщо є букви і дії додавання і віднімання?

З першою частиною питання все більш-менш зрозуміло. Букви можна скорочувати так само як і числа. Головне, щоб вони виступали в ролі множників. А ось з другої у багатьох виникають проблеми.

Важливо запам’ятати! Скорочувати можна тільки числа, які є множниками. Якщо вони складові — не можна.

Для того щоб зрозуміти, як скорочувати дроби, що мають вид алгебраїчного виразу, потрібно засвоїти правило. Спочатку уявити чисельник і знаменник у вигляді твору. Потім можна скорочувати, якщо з’явилися загальні множники. Для подання у вигляді множників знадобляться такі прийоми:

• угруповання;
• винесення за дужки;
• застосування тотожностей скороченого множення.

Причому останній спосіб дає можливість відразу отримати складові у вигляді множників. Тому його необхідно використовувати завжди, якщо видно відома закономірність.

Але це ще не страшно, потім з’являються завдання зі ступенями і корінням. Ось тоді потрібно набратися сміливості і засвоїти пару нових правил.

Вираз зі ступенем

Дріб. У чисельнику і знаменнику твір. Є букви і числа. А вони ще й зведені в ступінь, яка теж складається з доданків або множників. Є чого злякатися.

Для того щоб розібратися в тому, як скорочувати дроби зі ступенями, потрібно вивчити два моменти:

• якщо в показнику ступеня стоїть сума, то її можна розкласти на множники, ступенями яких будуть вихідні складові;
• якщо різниця, то на ділене і дільник, у першого в мірою зменшуване, у другого — від’ємник.

Після виконання цих дій стають видні загальні множники. У таких прикладах немає необхідності обчислювати все ступеня. Досить просто скоротити ступеня з однаковими показниками і підставами.

Для того щоб остаточно засвоїти те, як скорочувати дроби зі ступенями, потрібно багато практикуватися. Після декількох однотипних прикладів дії будуть виконуватися вже автоматично.

А якщо у виразі варто корінь?

Його теж можна скоротити. Тільки знову ж, дотримуючись правил. Причому вірні всі ті, які були описані вище. Загалом, якщо стоїть питання про те, як скоротити дріб з корінням, то потрібно ділити.

На ірраціональні вирази теж можна розділити. Тобто якщо в чисельнику і знаменнику стоять однакові множники, укладені під знак кореня, то їх можна сміливо скорочувати. Це призведе до спрощення виразу і виконання завдання.

Якщо після скорочення під рискою дробу залишилася ірраціональність, то від неї потрібно позбутися. Іншими словами, помножити на неї чисельник і знаменник. Якщо після цієї операції з’явилися загальні множники, то їх знову потрібно буде скоротити.

Ось, мабуть, і все про те, як скорочувати дроби. Правил небагато, а заборона один. Ніколи не скорочувати складові!

Засноване на їх основному властивості: якщо чисельник і знаменник дробу розділити на один і той же ненульовий многочлен, то вийде рівна їй дріб.

Скорочувати можна тільки множники!

Члени многочленів скорочувати не можна!

Щоб скоротити алгебраїчну дріб, многочлени, які стоять в чисельнику і знаменнику, потрібно попередньо розкласти на множники.

Розглянемо приклади скорочення дробів.

У чисельнику і знаменнику дробу стоять одночлени. Вони являють собою твір, добуток(Чисел, змінних і їх ступенів), множникискорочувати можемо.

Числа скорочуємо на їх найбільший спільний дільник, тобто на найбільше число, На яке ділиться кожне з даних чисел. Для 24 і 36 це — 12. Після скорочення від 24 залишається 2, від 36 — 3.

Ступені скорочуємо на ступінь з найменшим показником. Скоротити дріб — значить, розділити чисельник і знаменник на один і той же дільник, а показники віднімаємо.

a² і a⁷ скорочуємо на a². При цьому в чисельнику від a² залишається одиниця (1 пишемо тільки в тому випадку, коли крім неї після скорочення інших множників не залишилося. Від 24 залишилася 2, тому 1, що залишилася від a², не пишемо). Від a⁷ після скорочення залишається a⁵.

b і b скорочуємо на b, отримані в результаті одиниці не пишемо.

c³º і с⁵ скорочуємо на с⁵. Від c³º залишається c²⁵, від с⁵ — одиниця (її не пишемо). Таким чином,

Чисельник і знаменник даної алгебраїчної дробу — многочлени. Скорочувати члени многочленів можна! (Не можна скоротити, наприклад, 8x² і 2x!). Щоб скоротити цю дріб, треба. У чисельнику є загальний множник 4x. Виносимо його за дужки:

І в чисельнику, і в знаменнику є однаковий множник (2x-3). Скорочуємо дріб на цей множник. У чисельнику отримали 4x, в знаменнику — 1. За 1 властивості алгебраїчних дробів, Дріб дорівнює 4x.

Скорочувати можна тільки множники (скоротити дану дріб на 25x² не можна!). Тому многочлени, які стоять в чисельнику і знаменнику дробу, потрібно розкласти на множники.

У чисельнику — повний квадрат суми, в знаменнику — різниця квадратів. Після розкладання за формулами скороченого множення отримуємо:

Скорочуємо дріб на (5x + 1) (для цього в чисельнику закреслимо двійку в показник ступеня, від (5x + 1) ² при цьому залишиться (5x + 1)):

У чисельнику є загальний множник 2, винесемо його за дужки. У знаменнику — формула різниці кубів:

В результаті розкладання в чисельнику і знаменнику отримали однаковий множник (9 + 3a + a²). Скорочуємо дріб на нього:

Многочлен в чисельнику складається з 4 складових. перший доданок з другим, третє — з четвертим і виносимо з перших дужок загальний множник x². Знаменник розкладаємо по формулі суми кубів:

У чисельнику винесемо за дужки загальний множник (x + 2):

Скорочуємо дріб на (x + 2):

Минулого разу ми склали план, завдяки якому, можна навчитися швидко скорочувати дроби. Тепер розглянемо конкретні приклади скорочення дробів.

Приклади.

Перевіряємо, а не ділиться більше число на менше (чисельник на знаменник або знаменник на чисельник)? Так, у всіх трьох цих прикладах більше число ділиться на меншу. Таким чином, кожну дріб скорочуємо на менше з чисел (на чисельник або на знаменник). маємо:

Перевіряємо, а не ділиться більше число на менше? Ні, не ділиться.

Тоді переходимо до перевірки наступного пункту: а чи не закінчується чи запис і чисельника, і знаменника одним, двома або кількома нулями? У першому прикладі запис чисельника і знаменника закінчується нулем, в другому — двома нулями, в третьому — трьома нулями. Значить, перший дріб скорочуємо на 10, другу — на 100, третю — на 1000:

Отримали нескоротні дроби.

Більше число на менше не ділиться, запис чисел нулями не закінчував.

Тепер перевіряємо, а чи не стоять чисельник і знаменник в одному стовпці в таблиці множення? 36 і 81 обидва діляться на 9, 28 і 63 — на 7, а 32 і 40 — на 8 (вони діляться ще і на 4, але якщо є можливість вибору, завжди скорочувати будемо на більшу). Таким чином, приходимо до відповідей:

Всі отримані числа є нескоротного дробу.

Більше число на менше не ділиться. А ось запис і чисельника, і знаменника закінчується нулем. Значить, скорочуємо дріб на 10:

Цю дріб ще можна скоротити. Перевіряємо по таблиці множення: і 48, і 72 діляться на 8. Скорочуємо дріб на 8:

Отриману дріб ще можемо скоротити на 3:

Ця дріб — нескоротний.

Більше з чисел на менше не ділиться. Запис чисельника і знаменника закінчується на нуль.Значіт, скорочуємо дріб на 10.

Отримані в чисельнику і знаменнику числа перевіряємо на і. Так як сума цифр і 27, і 531 діляться на 3 і на 9, то цей дріб можна скоротити як на 3, так і на 9. Вибираємо більше і скорочуємо на 9. Отриманий результат — нескоротний дріб.

Калькулятор скорости

Создано Филипом Дермой, Матеушем Мухой и Джоанной Анджеевской быстро я иду? — виды скорости

Формула средней скорости

Калькулятор скорости — как узнать свою среднюю скорость?

Средняя скорость против средней скорости

Скорость звука – любопытные факты, связанные со скоростью

Часто задаваемые вопросы

Калькулятор скорости — это инструмент, который помогает определить среднюю скорость движущегося объекта на основе пройденного расстояния за определенное время. Независимо от того, тестируете ли вы свой новый автомобиль или просто совершаете короткую пробежку или ездите на велосипеде, если вы хотите узнать, как найти среднюю скорость, этот калькулятор вам пригодится.

В приведенной ниже статье вы можете найти много ценной информации, например, что такое формула средней скорости. Мы также дадим вам несколько любопытных фактов о скорости (например, формулу скорости звука). Проверьте этот калькулятор скорости и расстояния и, наконец, найдите ответ на вопрос 9.0029 как быстро я еду?

Скорость, расстояние, время

Все мы слышали о скорость , но насколько вы уверены в своем понимании этой концепции? Скорость по определению связана исключительно с физикой. Однако, когда вы находите время подумать об этом, вы видите не векторы и формулы из вашего учебника, а велосипедиста, летящий реактивный самолет или стрелку спидометра. Мы больше связываем скорость с движущимися объектами, чем с научными уравнениями. Более того, у нас есть чувство, которое говорит нам, как быстро мы движемся, то есть мы можем ощущать, быстро ли мы движемся или нет. Например, когда вы едете на машине со скоростью 50 км/ч, это не слишком быстро по отношению к максимальной скорости автомобиля, но когда вы едете на велосипеде с той же скоростью, то это очень сильно падает. Итак, можно сказать, что человеческое восприятие скорости относительно.

Скорость автомобилей и поездов измеряется в километрах в час (км/ч) или в милях в час (миль/ч), а на самолетах и ​​кораблях мы обычно используем узлы (кн). С другой стороны, физики чаще всего используют основные единицы СИ, которые представляют собой метры в секунду (м/с). За этими единицами скрывается определение скорости, и мы можем ознакомиться с ним, изучив их. Все, что касается скорости, связано с расстоянием и временем. Единицы скорости определяются единицами пройденного расстояния, деленными на единицы времени, и это общая идея скорости. По-простому — скорость — это расстояние, пройденное за единицу времени .

Обязательно ознакомьтесь с нашим калькулятором стоимости топлива, пока вы здесь.

Как быстро я еду? — типы скорости

Скорость не является точным термином — есть несколько более точных значений, и их не следует путать друг с другом. Рассмотрим различия между мгновенной скоростью , средней скоростью и скоростью вращения . Во-первых, мы попытаемся визуализировать это на примере вождения автомобиля.

Вы едете по длинному открытому шоссе. Вы смотрите на спидометр своей машины; он показывает 100 километров в час. Отсюда вы знаете, как далеко вы проедете, если будете поддерживать постоянную скорость. Мы знаем, что на практике почти невозможно поддерживать точно постоянную скорость (хотя на шоссе с круиз-контролем это почти возможно), и наша скорость все время колеблется в большей или меньшей степени. Фактическое расстояние, которое вы проходите за час, является средним значением всех этих скоростей. Вывод — средняя скорость — это общее расстояние, пройденное за единицу времени (например, за час).

Итак, что на самом деле означает число, которое показывает ваш спидометр? Это ваша мгновенная скорость; ваша скорость в данный момент. Согласно определению из учебника, мгновенная скорость — это изменение положения объекта x между двумя моментами времени t₁ и t₂ (где этот интервал времени приближается к нулю, т. е. t₂ — t₁ -> 0).

Скорость вращения — это несколько иной термин, относящийся скорее к вращающимся объектам, чем к объектам, меняющим свое положение в пространстве. Соответственно, скорость вращения число полных оборотов, которые объект делает в единицу времени . Она выражается в радианах в секунду (рад/с) или в оборотах в минуту (об/мин). Мы не будем больше заострять внимание на этой теме, потому что это не является целью этого калькулятора скорости. Если вы хотите узнать больше об угловой скорости, перейдите к нашему калькулятору углового ускорения или калькулятору рациональной кинетической энергии.

Формула средней скорости

Так как основная цель этого калькулятора — вычисление средней скорости, давайте более подробно рассмотрим эту тему. Средняя скорость измеряется в единицах расстояния за время, и формула средней скорости выглядит следующим образом:

средняя скорость = общее расстояние / общее время

Типичные единицы измерения: километры в час (км/ч), мили в час (миль/ч). , метры в секунду (м/с) и футы в секунду (фт/с). В нашем калькуляторе миль в час единицей измерения по умолчанию является миль в час (км/ч для стран с метрическими единицами измерения), но вы можете переключаться между любыми общепринятыми единицами измерения.

🙋 Чтобы узнать больше об определении средней скорости, воспользуйтесь нашим калькулятором средней скорости изменения.

Калькулятор скорости — как узнать свою среднюю скорость?

Пользоваться этим калькулятором скоростного расстояния очень просто, и вы сразу же получите результат. Проверьте пункты ниже, чтобы узнать, как правильно использовать этот калькулятор:

1. Во-первых, вам нужно определить расстояние . Это может быть, например, расстояние, которое вы проехали от дома до другого города. Введите это в соответствующее поле.
2. Теперь необходимо определить время прохождения определенного расстояния. Введите это в калькулятор.
3. И вот, вы получите среднюю скорость .

Вы также можете нажать кнопку расширенного режима , вы получите доступ к дополнительным функциям этого калькулятора средней скорости. Здесь вы можете сравнить, какая разница во времени будет, если объект двигался с другой средней скоростью ( положительное значение , если объект движется в течение более длительного времени и ).0029 отрицательное значение , если объект перемещается в течение более короткого времени).

Средняя скорость против средней скорости

Скорость и скорость могут показаться одним и тем же, но это не так. Скорость — это скалярная величина, она определяется только величиной. Проще говоря, он говорит вам, как быстро движется объект. С другой стороны, скорость — это вектор — она определяется не только величиной, но и направлением. Он сообщает вам скорость, с которой объект меняет свое положение.

Представьте, что вы проехали на машине 100 метров вперед и 100 метров назад. Вы бы ехали с определенной средней скоростью в каждом направлении, но у вас была бы нулевая средняя скорость, поскольку скорость измеряется как скорость, с которой изменяется положение автомобиля, и в целом автомобиль не изменил своего положения. Следовательно, достаточно сказать, что средняя скорость автомобиля была 50 миль в час, но при вычислении скорости нам пришлось бы добавлять направление, скажем, 50 миль в час на восток.

И если вы хотите знать, как быстро изменялась ваша скорость или скорость, вам нужно рассчитать ускорение.

Вам нужна… потребность в скорости? Взгляните на некоторые интересные факты и поразительные цифры о скорости различных объектов и животных!

Ничто не может двигаться быстрее скорости света, даже если принять во внимание, что скорость является относительной величиной. Свет движется со скоростью 299 792 458 метров в секунду, что примерно дает 300 000 километров в час или 186 000 миль в секунду. Время, необходимое для того, чтобы свет от Солнца достиг Земли, составляет около 8 минут.

Звук распространяется по воздуху со скоростью около 343 метров в секунду, что составляет 1234,8 км/ч или 767 миль в час (при 20 °C / 68 °F). Это означает, что звуковой волне в воздухе требуется около 2,9 секунды, чтобы пройти один километр, или 4,7 секунды, чтобы пройти милю — эти данные могут быть полезны охотникам за штормами для определения расстояния освещения. В 2012 году австриец Феликс Баумгартнер преодолел звуковой барьер (своим телом!) во время свободного падения с высоты 228 000 футов. Он достиг скорости 833,9 миль в час. Для сравнения, типичный пассажир реактивного самолета летит на высоте 33 000–35 000 футов со скоростью около 500 миль в час (в зависимости от типа самолета и скорости ветра).

Вы, наверное, слышали, что самое быстрое животное на земле — гепард, и это правда. Его максимальная скорость действительно невероятна, и, согласно последним исследованиям, он может развивать скорость до 58 миль в час! Еще один удивительный пример — сапсаны. Они могут развивать скорость, превышающую… 200 миль в час в воздухе! В воде самое быстрое животное — атлантический парусник — скорость в воде 68 миль в час.

А люди? Спринтер Усэйн Болт — самый быстрый человек в истории человечества, его зарегистрированная скорость составляет 27,44 мили в час. Что интересно, ученые установили, что человек, живший 20 000 лет назад в Австралии (по имени Т8), бегал со скоростью 23 мили в час. Обратите внимание, что он сделал это босиком по грязи, в то время как Болт использует современные кроссовки и специальную дорожку.

Часто задаваемые вопросы

Является ли скорость такой же, как скорость?

Скорость и скорость очень похожи на — на самом деле единственная разница между ними состоит в том, что скорость — это скорость с направлением . Скорость — это то, что известно как скалярная величина, означающая, что ее можно описать одним числом (насколько быстро вы движетесь). Это также величина скорости. Скорость, векторное качество, должна иметь указанную как величину, так и направление, например. двигаясь со скоростью 90 миль в час на юго-восток.

Какая самая экономичная скорость движения?

В то время как наиболее экономичная скорость движения меняется с каждым транспортным средством , по общему мнению, она составляет около 50 миль в час (80 км/ч) . Однако есть несколько других вещей, которые вы можете сделать, чтобы максимизировать эффективность. Во-первых, постарайтесь поддерживать постоянную скорость , это заставит ваш двигатель работать максимально эффективно — используйте круиз-контроль на квартирах, если он у вас есть. Во-вторых, ехать на максимально возможной передаче в пределах ограничения скорости 9.0026 , это снова поможет вашему двигателю работать максимально экономично. Другие советы включают в себя выключение переменного тока и как можно меньше веса в машине .

Могут ли Карты Google определить мою скорость?

Карты Google могут сообщить вам вашу скорость, они имеют встроенный спидометр , который в настоящее время предназначен только для пользователей Android. Он включен по умолчанию, но чтобы убедиться, что он включен, перейдите в настройки → настройки навигации , и в меню параметров вождения для него будет ползунок. Это полезно как он изменит цвет, если вы превысите лимит — так что вам не придется отрывать взгляд от дороги. Вы также можете сообщать о камерах контроля скорости и ловушках , но только если вы находитесь в режиме навигации.

Как перевести мили в час в секунды?

1. Укажите текущую скорость в км/ч или милях в час.
2. Разделите его на 60, чтобы получить километры в минуту или мили в минуту.
3. Разделите еще раз на 60, чтобы получить километры в секунду или мили в секунду.
4. В качестве альтернативы разделите его на 3600 для прямого преобразования.

Какие существуют типы скорости?

Скорость имеет много различных типов и терминов для ее описания:

• Скорость — насколько быстро движется объект.
• Скорость — насколько быстро объект движется в определенном направлении.
• Ускорение — как быстро объект достигает определенной скорости.
• Постоянная скорость — Объект движется с одинаковой скоростью.
• Переменная скорость — объект, движущийся с изменяющейся скоростью.
• Средняя скорость — пройденное расстояние, деленное на время прохождения.
• Мгновенная скорость — скорость на конкретном экземпляре.

Что такое единица измерения скорости?

Единицей скорости является расстояние за время , поскольку оно определяется как количество времени, которое требуется объекту для преодоления определенного расстояния. Базовая единица , или СИ, это метры в секунду , но это не очень практично в быту. Вы, вероятно, более знакомы с такими единицами, как километров в час, миль в час и узлов. Любое расстояние во времени является единицей скорости, поэтому другими единицами скорости являются нанометры за две недели, Боинг-787 за солнечный год или бананы на Фридмана.

Как перевести мили в час в километры в час?

В перевести мили в час в километры в час :

1. Измерьте скорость.
2. Умножьте значение на 1,6.

В перевести километры в час в мили в час :

1. Измерьте скорость.
2. Умножьте значение на 0,62.

Удобный прием, если у вас нет под рукой калькулятора (например, вы за рулем), заключается в использовании последовательности Фибоначчи (1, 1, 2, 3, 5, 8…). Возьмите число, следующее в последовательности — это километры, если предыдущее было милями (например, 50 миль в час — это примерно 80 км в час).

Как найти конечную скорость?

Если у вас средняя и начальная скорость :

1. Умножьте среднюю скорость на 2.
2. Вычесть начальную скорость.
3. Осталась конечная скорость .

Если у вас есть начальная скорость, ускорение и время :

1. Умножьте время и ускорение.
2. Добавьте к этому числу начальную скорость.
3. Наслаждайтесь своими расчетами .

По какой формуле рассчитывается средняя скорость?

Самая распространенная формула для расчета средней скорости — это пройденное расстояние, деленное на затраченное время . Другая формула, если вы имеете начальную и конечную скорость , сложите их вместе и разделите на 2.

Какие существуют типы ускорения?

Есть два типа ускорения, среднее и мгновенное . Среднее ускорение — это изменение скорости, деленное на изменение времени , и то, как в среднем изменяется движение объекта со временем. Мгновенное ускорение — это производная скорости по времени или предел среднего ускорения за бесконечно малый период времени. Он используется для определения точного ускорения объекта в определенное время.

Филип Дерма, Матеуш Муха и Иоанна Анджеевска

Расстояние

Посмотреть 11 похожих велосипедных калькуляторов

Размер велосипедаPaceBiking life gain… 8 еще

Посмотреть 32 похожих калькулятора для журналистов

AveragePercentageПроцентное изменение… Еще 29

Калькулятор средней скорости — [100% бесплатно]

Этот калькулятор скорости представляет собой удобный онлайн-инструмент, который можно использовать для определения средней скорости движущегося объекта на основе пройденного расстояния и времени. Если вы хотите узнать свою скорость во время последней поездки на велосипеде, пробежки или чего-то еще, этот калькулятор средней скорости окажется чрезвычайно полезным.

Загрузка калькулятора…

Содержание

Как пользоваться калькулятором скорости?

Используйте этот калькулятор скорости, чтобы узнать значение скорости без выполнения ручных расчетов по формуле скорости. Он также известен как калькулятор средней скорости, калькулятор миль в час и калькулятор расстояния во времени. Это очень простой онлайн-инструмент, который дает мгновенные результаты. Вот шаги, которые нужно выполнить для этого калькулятора:

• Сначала введите значение расстояния и выберите единицу измерения из раскрывающегося меню.
• Затем введите значение времени, убедитесь, что оно максимально точное. Кроме того, выберите единицу измерения из выпадающего меню.
• После ввода всех необходимых значений калькулятор скорости выполнит расчет, чтобы дать вам значение скорости.

Как рассчитать скорость в час?

Все мы слышали слово «скорость» раньше и часто используем его в повседневной жизни. Но понимаете ли вы значение этого термина? По определению, скорость чисто связана и связана с физикой. Но когда вы думаете о скорости, вы не видите векторов и формул.

Вместо этого вы можете представить себе бегущего человека, быстро движущуюся машину и так далее. Большую часть времени мы связываем скорость с движущимися объектами, а не с ее научным обоснованием или объяснением. Более того, мы по-разному ощущаем скорость в зависимости от ситуации. Мы знаем, когда мы движемся быстро или медленно.

Например, когда вы едете на машине со скоростью 50 км/ч, вам не будет казаться, что это слишком быстро. Но если вы едете на велосипеде с той же скоростью, вы чувствуете себя намного быстрее. Следовательно, это означает, что мы, люди, имеем относительное восприятие скорости.

Для поездов и автомобилей скорость часто измеряется в «км/ч» или километрах в час или в «миль/ч» или милях в час. Вот где калькулятор миль в час пригодится. Конечно, вы также можете использовать его для измерения скорости кораблей и самолетов, все, что вам нужно сделать, это изменить единицу измерения на узлы.

Физики, с другой стороны, обычно используют м/с или метры в секунду для измерения скорости. За всеми этими единицами часто скрывается определение скорости. Но как только вы изучите их, вы сможете лучше с ними познакомиться. Дело в том, что скорость зависит от времени и расстояния.

Вы можете указать единицы, используемые для измерения скорости, путем деления пройденного расстояния на единицы времени. Это общее понятие скорости. Проще говоря, вы можете вычислить значение скорости, используя расстояние, пройденное за единицу времени. Имейте в виду, однако, что скорость не является точным термином.

Есть и другие, более точные значения, и их не следует путать друг с другом. Например, существуют различия между скоростью вращения, мгновенной скоростью и средней скоростью.

Несмотря на то, что вы используете этот калькулятор временных расстояний, вы все равно можете выполнять расчеты вручную. Для этого можно использовать формулу скорости:

скорость = расстояние/время

Что такое средняя скорость в физике?

Из термина «средняя скорость» можно понять, что он означает. В физике средняя скорость относится к средней скорости движущегося объекта на всем пройденном им расстоянии. Средняя скорость связана с расстоянием, пройденным любым данным объектом.

Считается скалярной величиной. Это означает, что важна только величина, а не расстояние перемещения. Вы можете рассчитать формулу средней скорости, решив отношение общего расстояния, пройденного данным объектом, ко времени, затраченному на преодоление всего расстояния. Это не средняя скорость.

Средняя скорость и средняя скорость связаны так же, как скорость и скорость. Средняя скорость относится к общему коэффициенту смещения любого данного объекта за данный период времени. Средняя скорость относится к смещению объекта, а средняя скорость относится к общему расстоянию, пройденному объектом.

Вы можете измерить среднюю скорость в единицах расстояния за время. Опять же, вы можете использовать этот калькулятор скорости, чтобы найти среднюю скорость, или вы можете выполнить расчет вручную. Для последнего вы можете найти среднюю скорость, используя следующую формулу:

средняя скорость = общее расстояние / общее время

Наиболее распространенными единицами измерения средней скорости являются «км/ч» или километры в час. , «mph» или мили в час, «m/s» или метры в секунду и «ft/s» или футы в секунду. В калькуляторе миль в час единицей измерения по умолчанию является миль в час. Однако вы можете изменить это, выбрав другую единицу измерения в раскрывающемся меню.

В чем разница между MPH и KPH?

Километры в час имеют аббревиатуру «км/ч» и относятся к количеству километров, пройденных данным объектом за один час. И наоборот, мили в час имеют аббревиатуру «миль в час» и относятся к количеству миль, пройденных данным объектом за один час. Оба являются единицами измерения, используемыми для скорости.

Если вы хотите преобразовать значение миль в час в значение километров в час, возьмите значение миль в час и умножьте его на 1,61.