формул, как рассчитать, упражнения и многое другое!
Воспользуйтесь нашим калькулятором, и мы дадим вам уравнение прямой, проходящей через две точки , а также значение ее ожидания.
Вам нужно только ввести координаты (x 1 , y 1 ) (x 2 , y 2 ) каждой из известных точек и нажать кнопку расчета, чтобы получить результат. Если вы хотите узнать , как найти уравнение прямой , и посмотреть решенные упражнения для каждого случая, продолжайте читать ниже.
Разделы статьи
- Уравнение точки-наклона прямой
- Уравнение прямой через две точки
- Непрерывное уравнение прямой
- Общее уравнение прямой
- Параметрическое уравнение прямой
- 2 90 если точка принадлежит прямой
- Формула для расчета расстояния между двумя точками на прямой
Уравнение точка-наклон прямой
Уравнение точка-наклон является одним из наиболее часто используемых уравнений.
в математических задачах и имеет вид:
y — y 1 = m (x — x 1 )
С его помощью мы можем вычислить уравнение прямой, зная наклон (м) и точка P координат (x 1 , y 1 ).
Например, вычислим уравнение прямой, если мы знаем, что она имеет наклон m=3 и проходит через точку P = (4,3). Просто подставляем в общее уравнение прямой и получаем:
у — 3 = 3 (х — 4)
Теперь упрощаем:
у = 3х -12 + 3
y = 3x — 9
Мы уже вычислили уравнение прямой, удовлетворяющее условиям задачи.
Уравнение прямой через две точки
Да Нам даны две точки и предлагается вычислить прямую проходящую через эти координаты, мы должны использовать эту формулу:
В этом случае решение задачи довольно просто, так как нам нужно только подставить в уравнение и максимально упростить его.
Чтобы увидеть, как это делается, сделаем упражнение, в котором нас попросят вычислить уравнение прямой, проходящей через точки (4, 5) и (2, 1):
Теперь мы просто уравниваем и упрощаем, и у нас остается уравнение в следующем виде:
2 (x — 4) = y — 5
Упрощаем:
2x — 8 = y — 5
2x — y + 3 = 0
У нас уже есть общее уравнение прямой, проходящей через две точки упражнения. Отсюда мы также можем рассчитать уклон, как мы видели в предыдущем разделе:
м = — A / B = — (2 / -1) = 2
Непрерывное уравнение прямой
Мы будем использовать непрерывное уравнение прямой линии, когда дает нам точку P с координатами (x 1 , y 1 ) и ее направляющий вектор координат ( v 1 , v 2 ).
Например, в случае графика над этими линиями, в котором у нас есть точка (3, 3) с направляющим вектором (2, 1) , уравнение линии будет:
Упрощая, получаем:
x — 3 = 2 (y — 3)
х — 3 = 2у — 6
x — 2y +3 = 0
Общее уравнение прямой
Общее уравнение прямой имеет вид :
Ax + By + C = 0
Действительные числа и B ≠ 0.
Из этого уравнения также мы можем нарисовать :
- La pendiente de la recta (m = — A/B).
- Ордината в начале координат (- C/B).
С этими данными у нас уже достаточно информации для представления линии на плоскости XY.
Параметрические уравнения прямой
Эти уравнения получаются из векторного уравнения и имеют следующий тип:
x = x 0 + v 1 t
y = y 0 + v 2 t
Бытие:
- (x 0 , y 0 ) координаты точки 902 на прямой
- (v 1 , v 2 ) — координаты вектора в направлении линии
Чтобы узнать, принадлежит ли точка заданной прямой, нам просто нужно coger la ecuación de esa recta y sustituir en ‘x’ e ‘y’ los valores del punto они дают нам. Если равенство выполняется, то точка будет принадлежать прямой, а если не выполняются, то нет.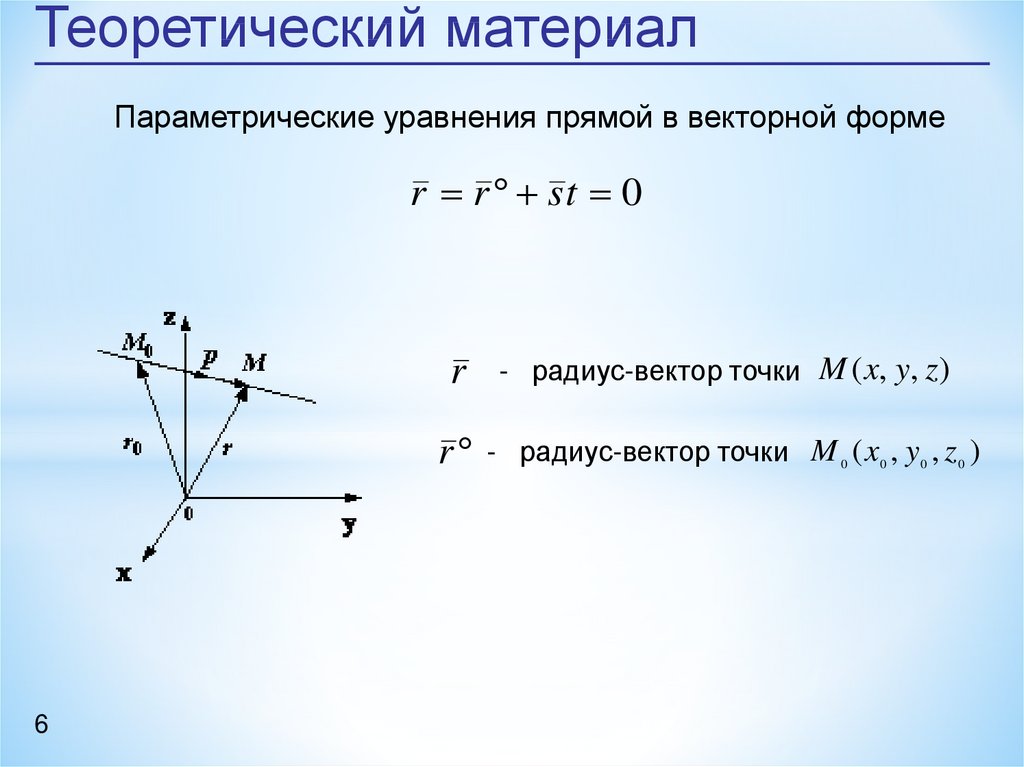
Например, лежит ли точка (1, 3) с уравнением y = 2 +3x на прямой? Посмотрим:
3 ≠ 2 + 3 → равенство не выполняется, поэтому точка (1,3) не лежит на прямой.
Что насчет точки (1, 5)?
5 = 2 + 3 → равенство выполняется, следовательно, точка (1, 5) находится на прямой.
Формула для расчета расстояния между двумя точками на прямой
Расстояние между двумя точками на прямой в декартовой плоскости можно рассчитать очень простым способом. Чтобы лучше понять это, давайте рассмотрим это на примере.
Представьте, что у вас есть две точки на плоскости с координатами:
- P1 (X1, Y1)
- Р2 (Х2, У2)
Расстояние, разделяющее две точки, получается путем применения следующей формулы математики:
Например, мы вычислим расстояние между двумя точками на примере , где:
- P1 (7 , 5)
- П2 (4, 1)
Применяя приведенную выше формулу, мы получаем, что расстояние между этими двумя точками на декартовой плоскости es:
Как видите, узнать расстояние между двумя точками очень просто.
Nacho
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En Esta веб-те Ayudo hacer cálculos у преобразования sencillas дие кон-эль-Пасо-де-лос-Años се-нос-ха olvidado Cómo себе Hace. Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.
- градусов с радианами
- Apothem
- Калькулятор Antilogarithm
- Калькулятор дивизии
- Exponent Calculator
- NEEPINELENTIA
- Калькулятор кубического корня
- Калькулятор n-го корня числа
- Калькулятор квадратных уравнений
- Онлайн-калькулятор факториала
- Калькулятор гипотенузы
- Калькулятор наибольшего общего делителя
- Калькулятор наименьшего общего кратного
- Калькулятор умножения
- Онлайн-калькулятор
Недвижимость Калькулятор прямой линии | Бесплатный инструмент для решения свойств уравнения линии
Property Калькулятор прямой линии — это бесплатный онлайн-инструмент, который вычисляет уравнение линии, находя наклон, точку пересечения по оси x и точку пересечения по оси y для заданного уравнения.
Итак, просто введите входное уравнение в поле ввода и нажмите кнопку расчета, чтобы получить результат в кратчайшие сроки.
Пример: 15x-20y=30 или 23x+19y=43 или 17x+29y=10
Калькулятор прямой линии свойств: Этот калькулятор помогает учащимся и пользователям вычислять наклон и свойства прямой линии из 2 точки в течение доли секунды и показать это с работой. Узнайте больше важных вещей, связанных со свойством прямых линий, например, что это такое, как решить его вручную самым простым способом и т. д. Кроме того, вы узнаете, как работает наш бесплатный калькулятор свойств прямых линий и отображает результат за меньшее время. .
Два свойства прямых линий в евклидовой геометрии заключаются в том, что они имеют только одно измерение, длину и всегда увеличиваются двумя способами.
Линия определяется как одномерная фигура, не имеющая толщины. Он простирается бесконечно в обоих направлениях. В системе координат прямая линия определяется с помощью стандартного уравнения.
Стандартная форма известна как уравнение линии. Если заданы значения наклона и точки пересечения, уравнение линии можно получить без особых усилий. Таким образом, его также называют формой наклона и пересечения.
Стандартная форма
Стандартная форма для выражения уравнения линии:
Уравнение линии, y = mx + b,
‘b’ — y-перехват.
Здесь приведены рекомендации по решению уравнения прямой, чтобы вы могли легко понять концепцию и сделать ваши расчеты проще и быстрее.
- Сначала возьмите данное уравнение, а затем перестройте уравнение, вычитая то, что находится справа от знака равенства из обеих частей уравнения.
- Теперь вытащите похожие термины.
- Решите уравнение, которое никогда не равно нулю, а затем решите уравнение прямой линии.
- Рассмотрим стандартную форму уравнения прямой, т.е. y=mx+b . Там, где он говорит, «y» — это то, как далеко идет линия, «x» — как далеко вдоль, «m» — это наклон или градиент, то есть насколько крута линия, а «b» — точка пересечения Y, т.
е. где линия пересекает ось Y. - Здесь точки пересечения Наклон, X и Y называются Свойствами прямой линии.
- Теперь вам нужно вычислить ее свойства, и вы закончили решение свойств прямой линии.
е. где линия пересекает ось Y.1. Как рассчитать наклон линии?
Наклон линии определяется как изменение y, деленное на изменение x. Таким образом, формула для определения наклона линии имеет следующий вид:
Наклон, м = [y 2 – y 1 ]/[x 2 – x 1 ] = подъем/набег.
2. Какова формула прямой линии?
Общее уравнение прямой линии имеет вид y = mx + c , где m — градиент, а c называется точкой пересечения на оси y.
3. Как решить свойства уравнения прямой?
Чтобы решить свойства уравнения прямой линии, вы должны вычислить форму пересечения наклона, пересечения по оси X и пересечения по оси Y. Таким образом, решение свойств прямой линии выполняется вручную легко и без усилий.