Процентное отношение двух чисел: онлайн калькулятор
Вычислить {$ main.types[data.type].toLowerCase() $}
Числитель
Знаменатель
Процент
Первое число
Второе число
Результат расчёта
{$ main.types[data.type] $}: {$ result|number:0 $}
Отношение двух любых чисел x и y – это их частное, то есть дробь вида x/y. Процентным соотношением таких чисел является частное, умноженное на 100.
История понятия
Процент происходит от латинского выражения «pro cento», которое в переводе означает «на сотню». В математике процент — это сотая часть числа. Выражение частей от целого было актуально еще в античные времена, когда люди впервые начали использовать дроби. В Древнем Египте широкой популярностью пользовались так называемые египетские дроби, которые представляли собой сумму нескольких различных дробей, обязательно содержащих в числителе единицу. Например, выражение 13/84 египетские математики выразили бы в виде суммы 1/12 + 1/14. Однако 1/100 — наиболее удобный способ выражать части числа.
Однако 1/100 — наиболее удобный способ выражать части числа.
Проценты зародились в Древнем Риме, задолго до возникновения арабской системы чисел. Многие бытовые вопросы, как то мера товаров или размер налога, определялись как сотая часть от целого. В России такие вычисления были введены гораздо позже Петром Первым, ведь русская система мер использовала числа, не кратные сотне. Проценты до сих пор активно используются в реальной жизни и занимают важное место во многих сферах деятельности.
Что такое процент
Итак, процент — это одна сотая часть чего либо. Если у нас есть 100 яблок, то 5 фруктов из них — это пять частей от сотни или 5%. Если у нас есть 200 персиков, то 23% от них означает 23 части по 2 фрукта каждая или 46 персиков. Очевидно, что эти показатели можно выразить в виде обыкновенных дробей. В случае с яблоками мы получим дробь 5 / 100 = 5%, а в ситуации с персиками — 46 / 200 = 23%. Используя данное уравнение, мы можем найти процентное соотношение двух чисел. И не только.
И не только.
Процентное соотношение двух чисел
Процент — это соотношение двух чисел, переведенное в десятичную дробь и умноженное на 100. В математической записи это выглядит следующим образом:
m / n × 100 = p,
где m – размер части, n – размер целого, p – процент.
Зная два из трех параметров, мы можем легко определить третий. Наш калькулятор использует данное выражение для поиска процента, целого или части числа. Соответственно, в программе часть обозначена как числитель, целое — как знаменатель, а процент остается процентом. На практике это выглядит следующим образом.
Примеры расчета процентов
Допустим, у нас есть 200 кг сахара. Мы хотим узнать:
- сколько сахара необходимо отгрузить, если требуется поставить 37% от исходной массы;
- 3 кг сахара просыпалось, и требуется указать процент потерянного товара.
Итак, в первой задаче нам уже известен процент p = 37, а также размер целой части n = 200. У нас есть знаменатель и процент, а требуется найти числитель. Для этого выбираем в меню калькулятора опцию «вычислить числитель» и вводим параметры процента и знаменателя. В ответе получаем 74 кг.
Для этого выбираем в меню калькулятора опцию «вычислить числитель» и вводим параметры процента и знаменателя. В ответе получаем 74 кг.
Во второй задаче у нас опять же есть значение целого (знаменатель, равный 200), а так же размер части (числитель, равный 3). Для решения задачи требуется определить процент. Для этого в меню программы выбираем «вычислить процент», вводим соответствующие значения и видим мгновенный результат в виде 2%.
Есть и третья задача. Допустим, мы не знаем, сколько сахара было изначально, но хотим это выяснить. Нам известно, что 56 кг — это 18% от первоначального объема. Теперь нам требуется найти целое или знаменатель. Выберем соответствующий пункт калькулятора и введем известные параметры, то есть процент и числитель. Таким образом, изначально на складе было 311 кг сахара.
Процентная разница между числами
Наш калькулятор также позволяет определить процентную разницу между числами. Для вычисления данного параметра используется простая формула:
(a − b) / (0,5 × (a + b)) × 100%.
Если вам для решения практических задач требуется вычислить процентную разницу между двумя значениями, то достаточно выбрать необходимый пункт в меню калькулятора и рассчитать требуемый показатель.
Пример
Допустим, за первый месяц работы вы получили чистую прибыль в размере 500 долларов, а во втором — 650 долларов. Давайте узнаем, на сколько процентов изменился ваш доход за месяц. Для этого выберите в меню программы тип калькулятора «разница в процентах» и введите заданные показатели прибыли. При этом неважно, в какую из ячеек вы вобьете числа, так как разница в любом случае будет одинакова. В результате мы получим ответ — прибыль изменилась на 26%. В нашем случае она увеличилась.
Заключение
Проценты занимают важное место в нашей жизни — расчет этих параметров необходим в практически любой деятельности человека: от продвижения сайтов до расчета технологических процессов. Используйте наши калькуляторы в своей деятельности — программы пригодятся вам как в учебе, так и на работе.
Калькулятор процентов. Рассчитать процент от числа, вычислить отношение двух чисел.
Калькулятор процентов
Калькулятор процентов поможет вам рассчитать процент от числа и вычислить отношение двух чисел.
% от числа
отношение 2 чисел
Нахождение процента от числа
Процентом называют одну сотую часть.
Рассмотрим алгоритм нахождение 15%
- 1 Число 220 это 100%, найдем 1% от числа, для
этого разделим 220 на 100:
1% от числа равен 220 ÷ 100 = 2.2 - 2 Чтобы найти 15%, умножим
значение 1% от числа на 15.
 15% от числа равно 2.2 × 15 = 33.
15% от числа равно 2.2 × 15 = 33. - 3 В итоге получаем что 15% от числа 220 равно 33%.Полностью нахождения 15% от числа можно записать: 220 ÷ 100 × 15 = 2.2 × 15 = 33
Пример Вычислить
10%, 30%, 50% от числа 760.10% от числа равно: 760 ÷ 100 × 10 = 7.6 × 10 = 76
30% от числа равно: 760 ÷ 100 × 30 = 7.6 × 30 = 228
50% от числа равно: 760 ÷ 100 × 50 = 7. 6 × 50 =
380
6 × 50 =
380
Рассмотрим пример когда нужно вычислить общее количество предметов, если известна часть.
Пример В корзине осталось
6 яблок, 15% от общего числа, вычислите общее количество яблок.Найдем чему равен 1% и умножим на 100:
100% от числа равно: 6 ÷ 15 × 100 = 0.4 × 100 = 40
Отношение чисел
Частное двух чисел называют отношением этих чисел.
Рассмотрим на примерах как находить отношение двух чисел.
Пример Найдем отношение чисел
4 и 20Число 4 составляет 20% от числа 20.
Число 20 составляет 500% от числа 4. Для вычисления разделим 20 на 4 и умножим на 100, получим 20 ÷ 4 × 100 = 500%
Из числа 4 получим 20 увеличив на 400%. Для вычисления разделим 20 на 4, умножим на 100 и отнимем 100%, получим 20 ÷ 4 × 100 — 100 = 400%
Из числа 20 получим 4
 Для вычисления разделим 4 на 20, умножим на 100 и отнимем 100%, получим 4 ÷ 20 × 100 — 100 =
-80%. Если в результате получается отрицательное значение, то число надо
уменьшать, если положительно то увеличивать.
Для вычисления разделим 4 на 20, умножим на 100 и отнимем 100%, получим 4 ÷ 20 × 100 — 100 =
-80%. Если в результате получается отрицательное значение, то число надо
уменьшать, если положительно то увеличивать.Найдем отношение двух вещественных чисел.
Пример Найдем отношение чисел
0.3 и 0.6Число 0.3 составляет 50% от числа 0.6. Для вычисления разделим 0.3 на 0.6 и умножим на 100, получим 0.3 ÷ 0.6 × 100 = 50%
Число 0. 6 составляет 200% от числа 0.3.
Для вычисления разделим 0.6 на 0.3 и умножим на 100, получим 0.6 ÷ 0.3 × 100 = 200%
6 составляет 200% от числа 0.3.
Для вычисления разделим 0.6 на 0.3 и умножим на 100, получим 0.6 ÷ 0.3 × 100 = 200%
Из числа 0.3 получим 0.6 увеличив на 100%. Для вычисления разделим 0.6 на 0.3, умножим на 100 и отнимем 100, получим 0.6 ÷ 0.3 × 100 — 100 = 100%
Из числа 0.6 получим 0.3 уменьшив число на 50%.
Для вычисления разделим 0.3 на 0.6, умножим на 100 и отнимем 100, получим 0. 3 ÷ 0.6
× 100 — 100 = -50%.
3 ÷ 0.6
× 100 — 100 = -50%.
Смотрите также
Другие страницы- Проценты
- Дроби
- Перевести проценты в десятичную дробь
- Дроби и проценты
Процент, Процентное соотношение
Процент (что означает «на сотню») это сравнение с 100.
Символ процента %. Так, например, 5 процентов записывается как 5%.
Предположим, что в комнате 4 человека.
50% это половина — 2 человека.
25% это четверть — 1 человек.
0% это ничего — 0 человек.
100% это целое — все 4 человека в комнате.
Если в комнату заходят ещё 4 человека, то их колличество становится 200%.
1% это $\frac{1}{100}$
Если всего есть 100 человек, то 1% из них это один человек.
Чтобы выразить математически число X как процент от Y вы делаете следующее:
$X : Y \times 100 = \frac{X}{Y} \times 100$
Пример: Сколько процентов от 160 составляет 80?
Решение:
$\frac{80}{160} \times 100 = 50\%$
Увеличение/Уменьшение процентного соотношения
Когда число увеличивается относительно другого числа, то величина увеличения представляется как:
Увеличение = Новое число — Старое число
Однако, когда число уменьшается относительно другого числа, то эту величину можно представить как:
Уменьшение = Старое число — Новое число
Увеличение или уменьшение числа всегда выражается на основании старого числа.
Поэтому:
%Увеличение = 100 ⋅ (Новое число — Старое число) ÷ Старое число
%Уменьшение = 100 ⋅ (Старое число — Новое число) ÷ Старое число
Например, у Вас было 80 почтовых марок и Вы начали в этом месяце собирать ещё пока общее количество почтовых марок достигло 120. Процентное увеличение числа марок, которые у Вас есть равно
Процентное увеличение числа марок, которые у Вас есть равно
$\frac{120 — 80}{80} \times 100 = 50\%$
Когда у Вас стало 120 марок, Вы и Ваш друг договорились обменять игру «Lego» на несколько из этих марок. Ваш друг взял несколько марок, которые ему понравились, и когда Вы подсчитали оставшиеся марки, то обнаружили, что у Вас осталось 100 марок. Процентное уменьшение числа марок может быть подсчитано как:
$\frac{120 — 100}{120} \times 100 = 16,67\%$
Калькулятор Процентов
| Что если % из ? | Результат: | |
| это какой процент от ? | Ответ: % | |
| это % от чего? | Ответ: | |
Как процентные соотношения помогают в реальной жизни
Есть два способа, как процентные соотношения помогают в решении наших каждодневных проблем:
1. Мы сравниваем две разных величины, когда все величины соотносятся с одной и той же основной величиной равной 100. Чтобы объяснить это, давайте рассмотрим следующий пример:
Мы сравниваем две разных величины, когда все величины соотносятся с одной и той же основной величиной равной 100. Чтобы объяснить это, давайте рассмотрим следующий пример:
Пример: Том открыл новую бакалейную лавку. За первый месяц он купил бакалеи за \$650 и продал за \$800, а во втором купил за \$800 и продал за \$1200. Надо рассчитать делает ли Том больше прибыли или нет.
Решение:
Напрямую из этих чисел мы не можем сказать растёт доход Тома или нет, потому что расходы и выручка каждый месяц разные. Для того, чтобы решить эту задачу, нам нужно соотнести все значения к фиксированной основной величине равной 100. Давайте выразим процентное соотношение его доходов к расходам в первый месяц:
(800 — 650) ÷ 650 ⋅ 100 = 23,08%
Это значит, что если Том тратил \$100, то он делал прибыль в размере 23.08 в первый месяц.
Теперь давайте применим тоже самое ко второму месяцу:
(1200 — 800) ÷ 800 ⋅ 100 = 50%
Так, во втором месяце, если Том тратил \$100, то его доход был \$50(потому что \$100⋅50% = \$100⋅50÷100=\$50). Теперь понятно,что доходы Тома растут.
Теперь понятно,что доходы Тома растут.
2. Мы можем определять количество части большей величины, если известно процентное соотношение этой части. Чтобы объяснить это, давайте рассмотрим следующий пример:
Пример: Синди хочет купить 8 метров шланга для своего сада. Она пошла в магазин и обнаружила, что там есть катушка со шлангом длиной 30 метров. Однако, она заметила, что на катушке написано, что 60% уже продано. Она должна узнать хватит ли ей оставшегося шланга.
Решение:
В табличке сказано, что
$\frac{Продано\ длина}{Всего\ длина} \times 100 = 60\%$
$Продано\ длина = \frac{60 \times 30}{100} = 18м$
Поэтому остаток 30 — 18 = 12м, которого вполне достаточно Синди.
Примеры:
1. Райн любит собирать спортивные карточки с его любимыми игроками. У него есть 32 карточки с игроками бейсбола, 25 карточки с футболистами и 47 с баскетболистами. Каково процентное соотношение карточек каждого спорта в его коллекции?
Решение:
Общее количество карточек = 32 + 25 + 47 = 104
Процентное соотношение бейсбольных карточек = 32/104 x 100 = 30,8%
Процентное соотношение футбольных карточек = 25/104 x 100 = 24%
Процентное соотношение баскетбольных карточек = 47/104 x 100 = 45,2%
Обратите внимание, что если сложить все проценты, то получится 100%, что представляет общее количество карточек.
2. На уроке был математический тест. Тест состоял из 5 вопросов; за три из них давали по три 3 балла за каждый, а за осташиеся два — по четыре балла. Вам удалось правильно ответить на два вопроса по 3 балла и на один вопрос по 4 балла. Какое процентное соотношение баллов Вы получили за этот тест?
Решение:
Общее количество = 3×3 + 2×4 = 17 баллов
Полученные балы = 2×3 + 4 = 10 баллов
Процентное соотношение полученных баллов = 10/17 x 100 = 58,8%
3. Вы купили видео игру за \$40. Потом цены на эти игры подняли на 20%. Какова новая цена видео игры?
Решение:
Увеличение цены равно 40 x 20/100 = \$8
Новая цена равна 40 + 8 = \$48
Калькулятор Процентов и Как Рассчитать Проценты
Внимание! Пожалуйста, ждите, пока страница полностью не загружена, иначе калькулятор процентов не будет работать.
Сколько будет | |
Ответ: | |
Сколько процентов число | |
Ответ: | |
Рассчитать процент разницы между двумя числами. | |
Ответ: This calculator requires JavaScript to work properly.
| |
Примеры вычисления процента
Пример 1. Процент вычисления стоимости:
Что такое составляют 30% 70$?
30% разделены на 100 и умножены на 70$:
(30/100) x 70$ или 0.3 x 70$ = 21$
Пример 2. Формула для процента:
21$ что процент 70$?
21$ разделены на 70$ и умножены на 100:
($21/70) x 100 = 30%
Пример 3. Вычисление процентного изменения:
Процентное изменение между 50$ и 70$?
70 минус 50 разделили 50 умноженных на 100:
($ $70-50) / 50 x 100 или 0. 4 x 100 = 40%
4 x 100 = 40%
Пример 4. 15 процентов (%) 200:
Что составляет 15 процентов (%) 200
15% разделены на 100 и умножены на 200:
(15/100) x 200 или 0.15 x 200 = 30
Как вычислить процент с калькулятором процента онлайн.
Калькулятор процента – процент – любое отношение или число, разделенное на 100. Это обычно представляется знаком процента (%), или сокращением (процент). Буквальное значение процента за сотню, которая, очевидно, относится к числу, разделенному на 100.
Вычисления процента, вовлеченные в нахождение процентов, не очень трудные, и любой человек без большого ведома о математике может выполнить метод, чтобы получить результаты. Люди часто должны находить проценты, в некоторый момент в жизни.
Например, если Вы идете для покупок, и Вы хотите получить пару обуви, которая является в продаже, и Вы только должны заплатить 75% первоначальной цены, и первоначальная цена упомянута как 250$. Теперь, простое вычисление процента должно было бы разделиться 75 на 100 и затем умножить его к 250$. Теперь, Вы закончите тем, что получили 25% от цены.
Теперь, простое вычисление процента должно было бы разделиться 75 на 100 и затем умножить его к 250$. Теперь, Вы закончите тем, что получили 25% от цены.
В повседневной жизни Вы так или иначе, где-нибудь добрались бы, чтобы найти калькулятор использования или процент.
Студенты, учителя, бухгалтеры и много других профессий должны представлять числа как проценты. Выполнение процедуры вручную требует большого количества времени, и выполнение его приблизительно для приблизительно 100 количеств является действительно жесткой работой и вероятно заняло бы целый день, чтобы закончить.
В конце, после расходов такого количества драгоценных часов Ваших жизненных процентов нахождения, если бы ошибка найдена, который разрушил бы все следующие вычисления также, будет очень печалить. Это могло быть утомительно и очень, очень время, пропав впустую. Даже калькулятор не может сэкономить Ваше время.
Вы закончите тем, что скучали, расстроенные и усталые; кроме того, Вы не заставите время делать что-либо еще. Используйте Калькулятор Процента Онлайн!
Используйте Калькулятор Процента Онлайн!
В современном мире, когда все компьютеризировано и информационные технологии достигли своей высоты, где Вы можете получить почти что-нибудь перед Вами просто щелчком или два, почему бы не выбрать что-то более эффективное, экономящее время и безошибочное?
Вы знаете то, что я достигаю.
Да, почему бы не использовать калькулятор процента онлайн. Они более эффективны, меньше отнимающее много времени и гарантировали безошибочные калькуляторы. Все, в чем Вы нуждаетесь, является подключением к Интернету, и калькулятор процента находится в Вашей досягаемости.
Это действительно, большая помощь для учителей, которые должны вычислить проценты результата большого количества студентов для бухгалтеров, которые должны весь день иметь дело с процентами и некоторыми студентами, которые сталкиваются с трудностью в нахождении процентов.
Процесс, чтобы использовать алькулятор процента онлайн прост тогда, Вы вообразили бы.
Все, что Вы должны будете сделать, должно вставить стоимость, соответствующее пространство, и пресса входят, чтобы получить результаты. Эти калькуляторы предоставляют Вам наиболее удобный способ вычислить процент, уменьшая процент, увеличивая процент и другие ценности.
Калькулятор процента онлайн рекомендовал для использования в офисах, школе и почти любом месте, где Вы имеете Интернет в наличии.
Калькулятор процента может сэкономить Ваше время и позволить Вам получать самые точные результаты.
Как Посчитать Разницу В Процентах Между Двумя Числами
Как рассчитать проценты в MS Excel (video)
Напечатайте числа, и калькулятор процентов покажет Вам результат вычисления процента автоматически. Даже Вы будете видетьи как рассчитать проценты (формулу для того вычисления)!
Найдите процентное отношение двух чисел: Нахождение процентного отношения двух чисел — ЭкоДом: Дом своими руками
Содержание
Нахождение процентного отношения двух чисел
Правило. Чтобы найти процентное отношение двух чисел, нужно одно число разделить на другое, а результат умножить на 100.
Чтобы найти процентное отношение двух чисел, нужно одно число разделить на другое, а результат умножить на 100.
Например, вычислить, сколько процентов составляет число 52 от числа 400.
По правилу: 52 : 400 * 100 — 13 (%).
Обычно такие отношения встречаются в задачах, когда величины заданы, а нужно определить, на сколько процентов вторая величина больше или меньше первой (в вопросе задачи: на сколько процентов перевыполнили задание; на сколько процентов выполнили работу; на сколько процентов снизилась или повысилась цена и т. д.).
Решения задач на процентное отношение двух чисел редко предполагают только одно действие. Чаше решение таких задач состоит из 2-3 действий.
Примеры.
1. Завод должен был за месяц изготовить 1 200 изделий, а изготовил 2 300 изделий. На сколько процентов завод перевыполнил план?
1-й вариант
Решение:
1 200 изделий — это план завода, или 100% плана.
1) Сколько изделий изготовил завод сверх плана?
2 300 — 1 200 = 1 100 (изд. )
)
2) Сколько процентов от плана составят сверхплановые изделия?
1 100 от 1 200 => 1 100 : 1 200 * 100 = 91,7 (%).
2-й вариант
Решение:
1) Сколько процентов составляет фактический выпуск изделий по сравнению с плановым?
2 300 от 1 200 => 2 300 : 1 200 * 100 = 191,7 (%).
2) На сколько процентов перевыполнен план?
191,7 — 100 = 91,7 (%)
Ответ: на 91,7%.
2. Урожайность пшеницы в хозяйстве за предыдущий год составила 42 ц/га и была занесена в план следующего года. В следующем году урожайность снизилась до 39 ц/га. На сколько процентов был выполнен план следующего года?
1-й вариант
Решение:
42 ц/га — это план хозяйства на этот год, или 100% плана.
1) На сколько снизилась урожайность по сравнению
с планом?
42 — 39 = 3 (ц/га)
2) На сколько, процентов план не довыполнен?
3 от 42 => 3 : 42 * 100 = 7. 1 (%).
3) Насколько процентов выполнен план этого года?
100 — 7,1 = 92,9 (%)
2-й вариант
Решение:
1) Сколько процентов составляет урожайность этого гола по сравнению с планом?
39 от 42 39 : 42 • 100 — 92,9 (%).
Ответ: 92,9%.
Отношение. Процентное отношение двух чисел
Частное двух чисел называют отношением этих чисел. Отношение можно записать как арифметическое действие «деление», а можно как обыкновенную дробь.
\(a:b=\frac{a}{b}\) – так записывают отношение чисел a и b, причем, а – предыдущий член, b – последующий член.
Например: отношение 75 к 25 можно записать в виде: \(75:25=\frac{75}{25}=3\).
Отношение двух чисел показывает:
- во сколько раз одно число больше другого;
- какую часть одно число составляет от другого.
Процентное отношение
Правило. Чтобы найти процентное отношение двух чисел, нужно одно число разделить на другое, а результат умножить на 100.
Например: вычислить, сколько процентов составляет число 52 от числа 400.
По правилу: \(52:400\cdot100\%=13 \%\).
Обычно такие отношения встречаются в задачах, когда величины заданы, а нужно определить, на сколько процентов вторая величина больше или меньше первой (в вопросе задачи: на сколько процентов перевыполнили задание; на сколько процентов выполнили работу; на сколько процентов снизилась или повысилась цена и т. д.).
д.).
Примеры.
Задача 1. Завод должен был за месяц изготовить 1 200 изделий, а изготовил 2 300 изделий. На сколько процентов завод перевыполнил план?
1-й вариант
Решение:
1 200 изделий – это план завода, или 100% плана.
1) Сколько изделий изготовил завод сверх плана?
2 300 – 1 200 = 1 100 (изд.)
2) Сколько процентов от плана составят сверхплановые изделия?
1 100 от 1 200 \(\Rightarrow\ 1100:1200\cdot100\%=91,7\%\).
2-й вариант
Решение:
1) Сколько процентов составляет фактический выпуск изделий по сравнению с плановым?
2 300 от 1 200 \(\Rightarrow\ 2300:1200\cdot100\%=191,7\%\).
2) На сколько процентов перевыполнен план?
\(191,7\%-100\%=91,7\%\).
Ответ: на 91,7%.
Задача 2. Надо вспахать участок поля в 500 га. В первый день вспахали 150 га. Сколько процентов составляет вспаханный участок от всего участка?
Решение:
Чтобы ответить на вопрос задачи, надо найти отношение (частное) вспаханной части участка ко всей площади участка и выразить его отношение в процентах:
\(150:500\cdot 100\%=\frac{150}{500}\cdot 100\%\ \)\(=\frac3{10}\cdot 100\%=0,3\cdot 100\%=30\%\).
Таким образом, мы нашли процентное отношение, то есть сколько процентов одно число (150) составляет от другого числа (500).
Задача 3. Рабочий изготовил за смену 45 деталей вместо 36 по плану. Сколько процентов фактическая выработка составляет от плановой?
Решение:
Для ответа на вопрос задачи надо найти отношение (частное) числа 45 к 36 и выразить его в процентах: \(45:36\cdot 100\%=1,25\cdot 100\%=125\%\).
Математика 5-6 классы. 31. Процентное отношение двух чисел
Математика 5-6 классы. 31. Процентное отношение двух чисел
- Подробности
- Категория: Математика 5-6 классы
Понятие о проценте
В метрической системе мер, и вообще в десятичной системе счисления, широко используются сотые части.
Сотая часть называется процентом (от латинского pro cento—на сотню, из сотни, с сотни) и обозначается %. Поэтому пишут 1 % = 0,01.
Например; 1) 1 % рубля = 0,01 рубля = 1 копейке;
2) 1 % метра = 0,01 метра = 1 сантиметру.
Запись «2 %» читается «два процента» или «две сотые». Вместо того чтобы говорить «тридцать девять сотых», говорят «тридцать девять процентов» и пишут «39 %».
Задача 1. Найти 25% от 36.
Решение.
I способ.
1) Найдем 1 % от 36:
2) Найдем 25 % от 36. Это в 25 раз больше:
II способ.
Так как 25%= 0,25, то задача сводится к нахождению 0,25 числа от 36:
Ответ. 9.
Задача 2. Найти число, 30 % которого равны 7.
Решение.
I способ.
1) Если 30% числа равны 7, то 1 % числа равен 7:30 =
2) Если 1 %,числа равен , то само число в 100 раз больше:
II способ.
Обозначим неизвестное число через тогда 0,30 • x= 7,
Ответ:
Решение задач на проценты
С процентами связаны задачи трех основных типов:
— нахождение процентов данного числа;
— нахождение числа по его процентам;
— нахождение процентного отношения чисел.
Задачи первых двух типов уже рассмотрены выше. Для их решения достаточно знать, что процент—сотая часть. Задачи третьего типа связаны с выражением в процентах отношения двух чисел.
Пример. Из 300 учеников IV и V классов школы в различных кружках занимается 138. Сколько процентов учащихся IV и V классов занимается в кружках?
Решение.
I способ. Вопрос задачи сводится к определению числа процентов, которое составляет 138 от 300. Примем 300 человек за 100%. Тогда 3 человека составляют 1 %, так как 300:100 = 3.
Определим, сколько-процентов составляют 138 учеников:
138:3=46 (%).
II способ. Отношение 138 к 300 равно
Решение обычно записывают короче:
Ответ. 46 %.
46 %.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100.
Все три типа задач на проценты можно решать с помощью одного приема как задачи на прямую пропорциональную зависимость.
Примеры.
1) Найдем 7 % от 35.
Решение. Пусть х—искомое число; тогда
Ответ.
2) Найдем число, 12 % которого равны 3.
Решение. Пусть х—искомое число; тогда
Ответ. 25.
3) Найдем процентное отношение чисел 8 и 35.
Решение. Пусть х—искомое число процентов; тогда
Ответ.
Процентное отношение двух чисел: онлайн калькулятор
Отношение двух любых чисел x и y – это их частное, то есть дробь вида x/y. Процентным соотношением таких чисел является частное, умноженное на 100.
История понятия
Процент происходит от латинского выражения «pro cento», которое в переводе означает «на сотню». В математике процент — это сотая часть числа. Выражение частей от целого было актуально еще в античные времена, когда люди впервые начали использовать дроби. В Древнем Египте широкой популярностью пользовались так называемые египетские дроби, которые представляли собой сумму нескольких различных дробей, обязательно содержащих в числителе единицу. Например, выражение 13/84 египетские математики выразили бы в виде суммы 1/12 + 1/14. Однако 1/100 — наиболее удобный способ выражать части числа.
В Древнем Египте широкой популярностью пользовались так называемые египетские дроби, которые представляли собой сумму нескольких различных дробей, обязательно содержащих в числителе единицу. Например, выражение 13/84 египетские математики выразили бы в виде суммы 1/12 + 1/14. Однако 1/100 — наиболее удобный способ выражать части числа.
Проценты зародились в Древнем Риме, задолго до возникновения арабской системы чисел. Многие бытовые вопросы, как то мера товаров или размер налога, определялись как сотая часть от целого. В России такие вычисления были введены гораздо позже Петром Первым, ведь русская система мер использовала числа, не кратные сотне. Проценты до сих пор активно используются в реальной жизни и занимают важное место во многих сферах деятельности.
Что такое процент
Итак, процент — это одна сотая часть чего либо. Если у нас есть 100 яблок, то 5 фруктов из них — это пять частей от сотни или 5%. Если у нас есть 200 персиков, то 23% от них означает 23 части по 2 фрукта каждая или 46 персиков. Очевидно, что эти показатели можно выразить в виде обыкновенных дробей. В случае с яблоками мы получим дробь 5 / 100 = 5%, а в ситуации с персиками — 46 / 200 = 23%. Используя данное уравнение, мы можем найти процентное соотношение двух чисел. И не только.
Очевидно, что эти показатели можно выразить в виде обыкновенных дробей. В случае с яблоками мы получим дробь 5 / 100 = 5%, а в ситуации с персиками — 46 / 200 = 23%. Используя данное уравнение, мы можем найти процентное соотношение двух чисел. И не только.
Процентное соотношение двух чисел
Процент — это соотношение двух чисел, переведенное в десятичную дробь и умноженное на 100. В математической записи это выглядит следующим образом:
m / n × 100 = p,
где m – размер части, n – размер целого, p – процент.
Зная два из трех параметров, мы можем легко определить третий. Наш калькулятор использует данное выражение для поиска процента, целого или части числа. Соответственно, в программе часть обозначена как числитель, целое — как знаменатель, а процент остается процентом. На практике это выглядит следующим образом.
Примеры расчета процентов
Допустим, у нас есть 200 кг сахара. Мы хотим узнать:
- сколько сахара необходимо отгрузить, если требуется поставить 37% от исходной массы;
- 3 кг сахара просыпалось, и требуется указать процент потерянного товара.

Итак, в первой задаче нам уже известен процент p = 37, а также размер целой части n = 200. У нас есть знаменатель и процент, а требуется найти числитель. Для этого выбираем в меню калькулятора опцию «вычислить числитель» и вводим параметры процента и знаменателя. В ответе получаем 74 кг.
Во второй задаче у нас опять же есть значение целого (знаменатель, равный 200), а так же размер части (числитель, равный 3). Для решения задачи требуется определить процент. Для этого в меню программы выбираем «вычислить процент», вводим соответствующие значения и видим мгновенный результат в виде 2%.
Есть и третья задача. Допустим, мы не знаем, сколько сахара было изначально, но хотим это выяснить. Нам известно, что 56 кг — это 18% от первоначального объема. Теперь нам требуется найти целое или знаменатель. Выберем соответствующий пункт калькулятора и введем известные параметры, то есть процент и числитель. Таким образом, изначально на складе было 311 кг сахара.
Процентная разница между числами
Наш калькулятор также позволяет определить процентную разницу между числами. Для вычисления данного параметра используется простая формула:
Для вычисления данного параметра используется простая формула:
(a − b) / (0,5 × (a + b)) × 100%.
Если вам для решения практических задач требуется вычислить процентную разницу между двумя значениями, то достаточно выбрать необходимый пункт в меню калькулятора и рассчитать требуемый показатель.
Пример
Допустим, за первый месяц работы вы получили чистую прибыль в размере 500 долларов, а во втором — 650 долларов. Давайте узнаем, на сколько процентов изменился ваш доход за месяц. Для этого выберите в меню программы тип калькулятора «разница в процентах» и введите заданные показатели прибыли. При этом неважно, в какую из ячеек вы вобьете числа, так как разница в любом случае будет одинакова. В результате мы получим ответ — прибыль изменилась на 26%. В нашем случае она увеличилась.
Заключение
Проценты занимают важное место в нашей жизни — расчет этих параметров необходим в практически любой деятельности человека: от продвижения сайтов до расчета технологических процессов. Используйте наши калькуляторы в своей деятельности — программы пригодятся вам как в учебе, так и на работе.
Используйте наши калькуляторы в своей деятельности — программы пригодятся вам как в учебе, так и на работе.
Калькулятор процентов. Рассчитать процент от числа, вычислить отношение двух чисел.
Отношение чисел
Частное двух чисел называют отношением этих чисел.
Рассмотрим на примерах как находить отношение двух чисел.
Пример Найдем отношение чисел
4 и 20
Число 4 составляет 20% от числа 20.
Для вычисления разделим 4 на 20 и умножим на 100,
получим 4 ÷ 20 × 100 = 20%
Число 20 составляет 500% от числа 4.
Для вычисления разделим 20 на 4 и умножим на 100,
получим 20 ÷ 4 × 100 = 500%
Из числа 4 получим 20 увеличив на 400%.
Для вычисления разделим 20 на 4, умножим на 100
и отнимем 100%, получим 20 ÷ 4 × 100 — 100 =
400%
Из числа 20 получим 4 уменьшив число на
80%.
Для вычисления разделим 4 на 20, умножим на 100
и отнимем 100%, получим 4 ÷ 20 × 100 — 100 =
-80%. Если в результате получается отрицательное значение, то число надо
уменьшать, если положительно то увеличивать.
Найдем отношение двух вещественных чисел.
Пример Найдем отношение чисел
0. 3 и 0.6
Число 0.3 составляет 50% от числа 0.6.
Для вычисления разделим 0.3 на 0.6 и умножим на
100, получим 0. 3 ÷ 0.6 × 100 = 50%
3 ÷ 0.6 × 100 = 50%
Число 0.6 составляет 200% от числа 0.3.
Для вычисления разделим 0.6 на 0.3 и умножим на
100, получим 0.6 ÷ 0.3 × 100 = 200%
Из числа 0.3 получим 0.6 увеличив на
100%.
Для вычисления разделим 0.6 на 0. 3, умножим на
100 и отнимем 100, получим 0.6 ÷ 0.3
× 100 — 100 = 100%
Из числа 0.6 получим 0.3 уменьшив число на
50%.
Для вычисления разделим 0.3 на 0.6, умножим на
100 и отнимем 100, получим 0.3 ÷ 0.6
× 100 — 100 = -50%.
Тест по математике: Процентное отношение двух чисел (Мерзляк, 6 класс) — пройти тест онлайн — игра — вопросы с ответами
Мой результат
Тест онлайн
Нашли ошибку? Выделите ошибку и нажмите Ctrl+Enter
Выбрав правильный на ваш взгляд вариант ответа, жмите на кнопку «Проверить». Если хотите сразу увидеть правильные ответы, ищите под вопросами ссылку «Посмотреть правильные ответы»
Если хотите сразу увидеть правильные ответы, ищите под вопросами ссылку «Посмотреть правильные ответы»
1.
Автобус должен проехать от одного города до другого 40 км. Проехав 30 км., он сделал остановку. Сколько процентов пути пройдено?
2.
Сколько процентов от числа 16 составляет число 4?
3.
Чтобы найти процентное отношение двух чисел, надо …
4.
Сколько процентов от числа 160 составляет число 20?
5.
В классе учатся 10 девочек и 15 мальчиков. Что показывает отношение · 100% = 60%?
6.
Процентное отношение 10 к 40 равно …
7.
Чему равно процентное отношение 12 к 15?
8.
Какой процент от 4 составляет число 3?
9.
Процентное отношение чисел 3,2 к 2 равно …
10.
Каково процентное отношение 0,9 к 7,2?
Новое и Интересное на портале
Процентное отношение двух чисел. Изменение величины в процентах — Отношения и пропорции — Математика 6 класс — А.
 С. Истер — Генеза 2014
С. Истер — Генеза 2014Глава 3 Отношения и пропорции
§27. Процентное отношение двух чисел. Изменение величины в процентах
Мы знаем два вида задач на проценты: нахождение процентов от числа и нахождение числа по его процентам. Рассмотрим еще задачи, в которых надо найти, сколько процентов составляет одно число от другого, то есть процентное отношение двух чисел.
Мы умеем находить отношение двух чисел или величин. Например, отношение числа 8 до числа 16 равен
а отношение 9 кг до 5 кг равна Поскольку отношение чисел или величин является дробью, его можно выразить в процентах, а именно:
Говорят, что число 8 составляет 50 % числа 16, а 9 кг составляет 180 % от 5 кг.
— Чтобы найти процентное отношение двух чисел, достаточно найти отношение этих чисел и умножить его на 100 %.
Чтобы узнать, сколько процентов одно число составляет от другого, достаточно первое число разделить на второе и найденную долю умножить на 100 %.
Задача 1. В классе 30 учеников, из них 27 посетили театр. Сколько процентов учащихся класса посетили театр?
Решения.
Изменение величины часто характеризуют с помощью процентов. Рассмотрим две задачи экономического содержания.
Задача 2. К снижению цен* МР3-плеер стоил 400 грн, а после снижения стал стоить 360 грн. На сколько процентов снизилась цена МР3-плеера?
Решения. Найдем сначала, сколько гривен уменьшилась цена МР3-плеера: 400 — 360 = 40 (грн). Определим, сколько процентов эта разница составляет от начальной цены МР3-плеера:
Так, цена MP3-плеера снизилась на 10 %.
Задача 3. Вкладчик положил в банк 800 грн, а через год забрал 944 грн. Сколько процентов годовых начисляет банк?
* Понятие цена и стоимость, которые случаются в некоторых задачах, воспринимай как условные величины, удобные для выполнения математических вычислений.
Решения. Прибыль равна 944 — 800 = 144 (грн). Найдем, сколько процентов это составляет от вклада:
Следовательно, банк начисляет 18 % годовых.
Чтобы узнать, на сколько процентов увеличилась или уменьшилась определенная величина, достаточно найти:
1) на сколько единиц увеличилась или уменьшилась эта величина;
2) сколько процентов составляет найдена разница от начального значения величины.
Как найти процентное отношение двух чисел? Как узнать, сколько процентов одно число составляет от другого? Как узнать, на сколько процентов увеличилась или уменьшилась определенная величина?
691. (Усно) Объясни вычисления:
1) 8 : 10 = 0,8 = 80 %; 2) 125 : 100 = 1,25 = 125 %. Что показывает ответ?
692. (Уснв) Сколько процентов от числа составляет 100 число: 1) 13; 2) 37; 3) 100; 4) 173?
693. Сколько процентов числа составляет 1000 число:
1) 150; 2) 100; 3) 250; 4) 1800?
694. Сколько процентов числа составляет его:
1) половина; 2) четверть;
3) пятая часть; 4) двадцатая часть?
695. Сколько процентов числа составляет его:
1) десятая часть; 2) двадцать пятая часть?
696. Сколько процентов составляет число 60 от числа:
Сколько процентов составляет число 60 от числа:
1) 100; 2) 120; 3) 300; 4) 20; 5) 48; 6) 5?
697. Сколько процентов число 40 составляет от числа:
1) 80; 2) 100; 3) 120; 4) 25; 5) 8?
698. Сколько процентов составляет:
1) 3 5; 2) 12 от 8; 3) от 4,5 22,5;
699. Сколько процентов составляет:
1) 12 от 16; 2) 10 от 8; 3) 1,6 от 2,5;
700. Сколько процентов составляет:
1) 1 м от 5 м; 2) 250 г от 1 кг; 3) 72° от развернутого угла?
701. Сколько процентов составляет:
1) 4 кг от 5 кг; 2) 3 км от 2000 м; 3) 18° от прямого угла?
702. В кинотеатре 480 мест. Во время демонстрации фильма было заполнено 456 мест. Какой процент мест был заполнен?
703. Контрольную работу писали 25 учеников. Три работы учитель оценил на «12». Сколько процентов составляют 12-бальные работы от общего количества работ?
704. Робинзон Крузо прочитал 90 страниц книги, в которой всего 250 страниц. Сколько процентов книги прочитал Робинзон Крузо? Какой процент книги ему осталось прочитать?
705. В классе 32 ученика, из которых 4 отсутствовали в школе по болезни. Сколько процентов учеников отсутствовали в школе и сколько процентов присутствовали?
В классе 32 ученика, из которых 4 отсутствовали в школе по болезни. Сколько процентов учеников отсутствовали в школе и сколько процентов присутствовали?
706. Определи процент содержания соли в растворе, если в 700 г раствора содержится 56 г соли.
707. Найди процент содержания железа в руде, если 40 т этой руды содержит 2,8 т железа.
708. Магазин за день продал 280 кг яблок и 120 кг груш. Сколько процентов составляет масса проданных яблок от общей массы проданных яблок и груш?
709. На тренировке во время исполнения штрафных бросков баскетболист 32 раза попал в корзину и 4 раза не попал. Сколько процентов составляет число попаданий от всего количества штрафных бросков (ответ округли до десятых процента)?
710. В связи с строительством нового микрорайона маршрут автобуса стал длиннее на 16 %. Найди длину нового маршрута, если длина предыдущего была 15 км.
711. Количество населения городка за год выросла на 5 %. Сколько населения стало в городке, если год назад в нем проживало 32 500 человек?
712. (Устно) Найди изменение величины в процентах:
(Устно) Найди изменение величины в процентах:
1) от 4 до 6 ц; 2) от 10 кг до 12 кг;
3) от 10 мин до 7 мин; 4) от 100 г до 30 г;
5) от 200 м до 180 м; 6) от 30 с до 36 с.
713. Найди в процентах изменение величины:
1) от 45 г до 54 г; 2) от 4,8 км до 3,6 км;
3) от 1 грн 70 коп.; 4) от 4000 кг до 5 т;
5) от 1 ч до 30 мин; 6) от 15 до 3 т.
714. Найди в процентах изменение величины:
1) от 24 г до 18 г; 2) от 3,2 до 4,8 ц ц;
3) от 1 кг до 1400 г; 4) от 15 мин до 1 ч;
5) от 1 т до 1 ц; 6) от 1 м 20 см до 90 см.
715. Заполни в тетради такую таблицу относительно вывоза овощей с поля в течение четырех дней:
Дни | Пн | Вт | Ср | Чт | Всего |
Масса овощей, т | 60 |
| 42 |
| 240 |
Процент от общей массы, % |
| 20 |
|
| 100 |
716. При обработке заготовки ее масса уменьшилась от 1,2 кг до 1,14 кг. На сколько процентов уменьшилась масса заготовки?
При обработке заготовки ее масса уменьшилась от 1,2 кг до 1,14 кг. На сколько процентов уменьшилась масса заготовки?
717. 1) Цена некоторого товара возросла от 64 грн до 80 грн. На сколько процентов повысилась цена?
2) Цена некоторого товара снизилась от 80 грн. до 64 грн. На сколько процентов снизилась цена?
718. 1) Первый день рабочий изготовил 120 деталей, а на другой день — 150 деталей. На сколько процентов увеличилась производительность труда рабочего?
2) Первый день рабочий изготовил 150 деталей, а второго дня — 120 деталей. На сколько процентов уменьшилась производительность труда рабочего?
719. К 160 г 15-процентного раствора соли добавили 40 г воды. Каким стало процентное содержание соли в новом растворе?
720. К сплаву массой 350 г, содержит 60 % олова, добавили 150 г олова. Каким стало процентное содержание олова в новом сплаве?
721. До снижения цен товар стоил 240 грн. Обчисли цену товара после двух последовательных снижений, если первое было на 10 %, а второе — на 5 %. На сколько процентов уменьшилась первоначальная цена товара?
На сколько процентов уменьшилась первоначальная цена товара?
722. Цена товара была 400 грн. Сначала она была повышена на 15 %, а затем снижена на 15 %. Изменилась ли при этом цена товара? Если изменилась, то как и на сколько процентов?
723. Цену на товар стоил 200 грн, снизили на 20 %. На сколько процентов нужно повысить новую цену, чтобы получить начальную?
724. Мальчик купил две книги, первая из которых на 10% дешевле второй. На сколько процентов вторая книга дороже первой?
725. Во время сушки грибы теряют 89 % своей массы. Сколько сухих грибов получим с 70 кг свежих?
726. До оператора справочного центра банка поступило некоторое количество обращений. После того как он проработал 14 % от всего количества, ему осталось проработать еще 129. Сколько всего обращений надійшло к оператору?
727. Какова вероятность того, что сумма очков на двух игральных кубиках, подброшенных одновременно, будет равняться 8?
728. Реши уравнения
729. Сравни значения таких выражений: 1 ∙ 2 ∙ 3 ∙ … ∙ 20 и 1 + 2 + 3 + … + 1 000 000.
Процентный калькулятор
Укажите любые два значения ниже и нажмите кнопку «Рассчитать», чтобы получить третье значение.
Калькулятор процентов общими фразами
Калькулятор разницы в процентах
Калькулятор процентного изменения
Укажите любые два значения ниже и нажмите кнопку «Рассчитать», чтобы получить третье значение.
В математике процент — это число или отношение, представляющее долю от 100.Часто обозначается символом «%» или просто «процентом» или «процентом». Например, 35% эквивалентно десятичной дроби 0,35 или
.
Формула процента
Хотя процентную формулу можно записать в разных формах, по сути, это алгебраическое уравнение, включающее три значения.
P × V 1 = V 2
P — это процентное соотношение, V 1 — первое значение, которое будет изменено процентным соотношением, а V 2 — результат процентного соотношения, действующего на V 1 . Предоставленный калькулятор автоматически преобразует введенный процент в десятичное число для вычисления решения. Однако, если вычислить процентное значение, возвращаемое значение будет фактическим процентом, а не его десятичным представлением.
Предоставленный калькулятор автоматически преобразует введенный процент в десятичное число для вычисления решения. Однако, если вычислить процентное значение, возвращаемое значение будет фактическим процентом, а не его десятичным представлением.
EX: P × 30 = 1,5
При решении вручную формула требует процентного значения в десятичной форме, поэтому решение для P необходимо умножить на 100, чтобы преобразовать его в процент. По сути, это то, что делает калькулятор выше, за исключением того, что он принимает значения в процентах, а не в десятичной форме.
Формула разницы в процентах
Процентная разница между двумя значениями рассчитывается путем деления абсолютного значения разницы между двумя числами на среднее значение этих двух чисел. Умножение результата на 100 даст решение в процентах, а не в десятичной форме. Обратитесь к уравнению ниже для пояснения.
| Разница в процентах = | × 100 |
Формула процентного изменения
Увеличение и уменьшение в процентах рассчитывается путем вычисления разницы между двумя значениями и сравнения этой разницы с начальным значением. Математически это включает использование абсолютного значения разницы между двумя значениями и деление результата на начальное значение, по сути, вычисление того, насколько изменилось начальное значение.
Математически это включает использование абсолютного значения разницы между двумя значениями и деление результата на начальное значение, по сути, вычисление того, насколько изменилось начальное значение.
Калькулятор процентного увеличения выше вычисляет увеличение или уменьшение определенного процента входного числа. Он в основном включает в себя преобразование процента в его десятичный эквивалент и либо вычитание (уменьшение), либо добавление (увеличение) десятичного эквивалента от и до 1, соответственно.Умножение исходного числа на это значение приведет либо к увеличению, либо к уменьшению числа на заданный процент. Обратитесь к примеру ниже для пояснения.
EX: 500 увеличено на 10% (0,1)
500 × (1 + 0,1) = 550
500 уменьшено на 10%
500 × (1 — 0,1) = 450
Вычислить процент чисел
Вычислить процент одного числа из второго числа |
Пример расчета процентов по ипотечному кредиту
: у вас есть выплата по ипотеке в размере 800 долларов. У вас есть только 600 долларов, чтобы заплатить банку. Какой процент от общей суммы денег у вас есть? Решение: 600 разделить на 800 равно 0,75. Затем умножьте на 100. Результат равен 75%. Это означает, что вы можете заплатить банку только 75% от общей суммы платежа по ипотеке, и вам потребуется небольшой заем в размере 200 долларов.
У вас есть только 600 долларов, чтобы заплатить банку. Какой процент от общей суммы денег у вас есть? Решение: 600 разделить на 800 равно 0,75. Затем умножьте на 100. Результат равен 75%. Это означает, что вы можете заплатить банку только 75% от общей суммы платежа по ипотеке, и вам потребуется небольшой заем в размере 200 долларов.
Процентное решение формулы, объясненное с использованием простого соотношения и примера определения того, какой процент равен 2 из 10.
A: B = C: D, поэтому 2 равно 10, как x равно 100.
2/10 = x / 100, тогда
Крест умножить
10 x = 200
x = 20 или 20%.
Другие калькуляторы
Калькулятор увеличения или уменьшения процентов поможет найти ответы на ваши вопросы по вычислению процентов. Чтобы вычислить процент от числа, используйте наш калькулятор процента от числа. Например, найдите 5% процентов от 70. Калькулятор процентов даст вам ответ, это 3,5.
процент увеличения между двумя числами? Проблема решена с помощью функции «Рассчитать процент увеличения». Найдите процент% увеличения с 2 до 10. Ответ — 400%.
Найдите процент% увеличения с 2 до 10. Ответ — 400%.
Найдите, что процента представляет собой число из второго числа ? Пример: узнать, какой процент равен 7 из 300. Калькулятор «Рассчитать процент от двух чисел», ответ — 2,33%.
Новинка: рассчитайте увеличение или уменьшение заработной платы с помощью нашего калькулятора дохода. Калькулятор процента увеличения заработной платы.
процентов от общего числа . Например, total = 1100, и вам нужно найти процент, равный 100.Используя наш процент от общей суммы, ответ калькулятора составляет 9,09%.
GFC и LCM — математический коэффициент и множитель . Калькулятор наибольшего общего множителя GCF может использоваться для вычисления GFC, а калькулятор наименьшего общего множителя — LCM.
Калькулятор квадратного корня . Вместо того, чтобы запоминать квадратные корни, используйте калькулятор квадратного корня из числа и делайте это на лету. Например, каков квадратный корень из 9? Все мы знаем, что это 3. А как насчет квадратного корня из 500? Узнай себя.
А как насчет квадратного корня из 500? Узнай себя.
Калькулятор процентов ошибок . Быстро рассчитайте процентную ошибку с помощью калькулятора процентов ошибок.
Калькулятор часов и минут . Найдите минуты или часы с помощью наших калькуляторов. First Calculate Hours in Minutes, очень полезно, чтобы узнать, сколько часов в 300 минутах. Калькулятор «Расчет минут в часах» полезен, чтобы узнать, сколько минут в 5 часах? Ответ: это 300 из первой математической задачи.
простая математика Математический калькулятор сложения, математический калькулятор вычитания, математический калькулятор умножения и математический калькулятор деления.
Изменение в процентах — увеличение и уменьшение в процентах
Для объяснения и повседневных примеров использования процентов, как правило, см. Нашу страницу Проценты: Введение . Для более общих расчетов процентов см. Нашу страницу Калькуляторы процентов .
Для расчета увеличения в процентах:
Первый: вычислите разницу (увеличение) между двумя числами, которые вы сравниваете.
Увеличение = новый номер — исходный номер
Затем: разделите увеличение на исходное число и умножьте ответ на 100.
% увеличение = Увеличение ÷ Исходное число × 100 .
Если ваш ответ отрицательный, то это процентное уменьшение.
Для расчета уменьшения в процентах:
Первый: определите разницу (уменьшение) между двумя числами, которые вы сравниваете.
Уменьшение = исходный номер — новый номер
Затем: разделите уменьшение на исходное число и умножьте ответ на 100.
% Уменьшение = Уменьшение ÷ Исходное число × 100
Если ваш ответ отрицательный, то это процентное увеличение.
Если вы хотите рассчитать процентное увеличение или уменьшение нескольких чисел, мы рекомендуем использовать первую формулу.Положительные значения указывают на процентное увеличение, тогда как отрицательные значения указывают на процентное уменьшение.
Калькулятор процентного изменения
Используйте этот калькулятор для вычисления процентного изменения двух чисел.
Подробнее: Калькуляторы процентов
Дополнительная литература по навыкам, которые вам нужны
Навыки, которые вам нужны. Руководство по счету
Это руководство из четырех частей познакомит вас с основами математики от арифметики до алгебры с остановками на дробях, десятичных дробях, геометрии и статистике.
Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.
Примеры — увеличение и уменьшение в процентах
В январе Дилан проработал в общей сложности 35 часов, в феврале он проработал 45,5 часов — на какой процент увеличилось рабочее время Дилана в феврале?
Чтобы решить эту проблему, сначала мы вычисляем разницу в часах между новым и старым числами. 45,5 — 35 часов = 10.5 часов. Мы видим, что Дилан в феврале проработал на 10,5 часов больше, чем в январе — это его увеличение на на . Чтобы рассчитать увеличение в процентах, теперь необходимо разделить увеличение на исходное (январское) число:
Чтобы рассчитать увеличение в процентах, теперь необходимо разделить увеличение на исходное (январское) число:
10,5 ÷ 35 = 0,3 (Инструкции и примеры деления см. На странице деления .)
Наконец, чтобы получить процентное значение, мы умножаем ответ на 100. Это просто означает перемещение десятичной точки на два столбца вправо.
0,3 × 100 = 30
Таким образом, Дилан отработал в феврале на 30% больше часов, чем в январе.
В марте Дилан снова проработал 35 часов — столько же, сколько он работал в январе (или 100% его январских часов). Какова процентная разница между февральскими часами Дилана (45,5) и его мартовскими часами (35)?
Сначала рассчитайте уменьшение количества часов, то есть: 45,5 — 35 = 10,5
Затем разделите уменьшение на исходное число (февральские часы) так:
10.5 ÷ 45,5 = 0,23 (с точностью до двух знаков после запятой).
Наконец, умножьте 0,23 на 100, чтобы получить 23%. Часы Дилана в марте были на 23% меньше, чем в феврале.
Вы, возможно, думали, что, поскольку между часами января (35) и февралем (45,5) Дилана было увеличение на 30%, то между часами февраля и марта также должно быть сокращение на 30%. Как видите, это предположение неверно.
Причина в том, что наш исходный номер в каждом случае разный (35 в первом примере и 45.5 во втором). Это подчеркивает, насколько важно рассчитывать процентное соотношение от правильной начальной точки.
Иногда проще показать процентное уменьшение как отрицательное число — для этого следуйте приведенной выше формуле для расчета процентного увеличения — ваш ответ будет отрицательным числом, если было уменьшение. В случае Дилана увеличение на на часов в период с февраля по март составляет -10,5 (отрицательно, потому что это уменьшение). Следовательно -10.5 ÷ 45,5 = -0,23. -0,23 × 100 = -23%.
Часы Дилана могут отображаться в таблице данных как:
| Месяц | часов отработали | Процент Изменение |
| Январь | 35 | |
| Февраль | 45,5 | 30% |
| Март | 35 | -23% |
Расчет значений на основе процентного изменения
Иногда бывает полезно вычислить фактические значения на основе процентного увеличения или уменьшения. В средствах массовой информации часто можно увидеть примеры того, когда это может быть полезно.
В средствах массовой информации часто можно увидеть примеры того, когда это может быть полезно.
Вы можете увидеть заголовки вроде:
Осадки в Великобритании этим летом были на 23% выше среднего.
Данные по безработице показывают снижение на 2%.
Банкиров ‘бонусы сократились на 45%.
Эти заголовки дают представление о тенденции — когда что-то увеличивается или уменьшается, но часто нет реальных данных.
Без данных цифры процентного изменения могут вводить в заблуждение.
Кередигион, графство в Западном Уэльсе, имеет очень низкий уровень насильственных преступлений.
Отчеты полиции Кередигиона за 2011 год показали 100% рост насильственных преступлений. Это поразительное число, особенно для тех, кто живет или думает о переезде в Кередигион.
Однако, когда исследуются основные данные, выясняется, что в 2010 году в Кередигионе было зарегистрировано одно насильственное преступление. Таким образом, увеличение на 100% в 2011 году означало, что было зарегистрировано два насильственных преступления.
Таким образом, увеличение на 100% в 2011 году означало, что было зарегистрировано два насильственных преступления.
Когда мы встречаемся с реальными цифрами, восприятие количества насильственных преступлений в Ceredigion значительно меняется.
Чтобы определить, насколько что-то увеличилось или уменьшилось в реальном выражении, нам нужны реальные данные.
Возьмем пример: « осадков в Великобритании этим летом было на 23% выше среднего » — мы сразу можем сказать, что в Великобритании за лето выпало почти на четверть (25%) осадков больше, чем в среднем. Однако, не зная, каков средний уровень осадков или сколько осадков выпало за рассматриваемый период, мы не можем определить, сколько осадков выпало на самом деле.
Расчет фактического количества осадков за период, если известно среднее количество осадков.
Если мы знаем, что среднее количество осадков составляет 250 мм, мы можем рассчитать количество осадков за период, вычислив 250 + 23%.
Первая тренировка 1% от 250, 250 ÷ 100 = 2,5. Затем умножьте ответ на 23, потому что количество осадков увеличилось на 23%.
Затем умножьте ответ на 23, потому что количество осадков увеличилось на 23%.
2,5 × 23 = 57,5.
Таким образом, общее количество осадков за рассматриваемый период составило 250 + 57,5 = 307,5 мм.
Расчет среднего количества осадков, если известно фактическое количество.
Если в новостном сообщении говорится о новом измерении и процентном увеличении, « осадков в Великобритании было на 23% выше среднего… Выпало 320мм дождя… ».
В этом примере мы знаем, что общее количество осадков составило 320 мм. Мы также знаем, что это на 23% выше среднего. Другими словами, 320 мм соответствует 123% (или 1,23 раза) от среднего количества осадков. Чтобы вычислить среднее значение, мы разделим общую сумму (320) на 1,23.
320 ÷ 1,23 = 260,1626. Округленное до одного десятичного знака, среднее количество осадков составляет 260,2 мм .
Теперь можно рассчитать разницу между средним и фактическим количеством осадков:
320 — 260. 2 = 59,8 мм .
2 = 59,8 мм .
Можно сделать вывод, что 59,8 мм составляет 23% от среднего количества осадков (260,2 мм), и что в реальном выражении выпало на 59,8 мм больше осадков, чем в среднем.
Мы надеемся, что вы нашли эту страницу полезной — почему бы не посетить наши другие страницы, посвященные навыкам счета? Или дайте нам знать о предмете, который вы хотели бы обсудить, на SkillsYouNeed — Свяжитесь с нами .
Калькулятор разницы в процентах
Использование калькулятора
Калькулятор процентной разницы (калькулятор процентной разницы) найдет процентную разницу между двумя положительными числами больше 0.Разница в процентах обычно рассчитывается, когда вы хотите узнать разницу в процентах между двумя числами. Для этого калькулятора порядок чисел не имеет значения, поскольку мы просто делим разницу между двумя числами на среднее значение двух чисел. Чтобы вычислить относительную разницу, от старого числа к новому, вы должны
рассчитать процентное изменение.
Связанные расчеты могут быть выполнены с помощью
Калькулятор процентов,
Калькулятор процентного изменения и преобразования могут быть решены с помощью
Десятичная дробь в процент,
Процент в десятичный,
От дробей к процентам, или
Процент к доле.
Формула разницы в процентах:
Разница в процентах равна абсолютному значению изменения значения, деленному на среднее значение двух чисел, умноженных на 100. Затем мы добавляем знак процента,%, чтобы обозначить разницу в%.
\ (\ text {Разница в процентах} = \ dfrac {| \ Delta V |} {\ left [\ dfrac {\ Sigma V} {2} \ right]} \ times 100 \)
\ (= \ dfrac {| V_1-V_2 |} {\ left [\ dfrac {(V_1 + V_2)} {2} \ right]} \ times100 \)
Например, как рассчитать разницу в процентах:
Какая разница между 5 и 7 в процентах?
Пусть V 1 = 5 и V 2 = 7 и подставим числа в нашу формулу
\ (\ dfrac {| V_1-V_2 |} {\ left [\ dfrac {(V_1 + V_2)} {2} \ right]} \ times100 \)
\ (= \ dfrac {| 5-7 |} {\ left [\ dfrac {(5 + 7)} {2} \ right]} \ times100 \)
\ (= \ dfrac {| -2 |} {\ left [\ dfrac {12} {2} \ right]} \ times100 \)
\ (= \ dfrac {2} {6} \ times100 \)
\ (= 0. 333 \ раз 100 = 33,33 \% \; \ text {difference} \)
333 \ раз 100 = 33,33 \% \; \ text {difference} \)
Обратите внимание, что если мы допустим V 1 = 7 и V 2 = 5, у нас все равно будет разница в 33,33%, потому что мы вычисляем разницу между двумя числами, а не переход от одного числа к другому,
процентное изменение.
Список литературы
Калькулятор формул процентных разностей уравнений от AJ Design Software, последнее посещение 22 февраля.2011 г.
авторов Википедии. «Процентная разница» Википедия, Бесплатная энциклопедия. Википедия, Бесплатная энциклопедия, последнее посещение 18 февраля 2011 г.
Процентное изменение, увеличение, отличие от доктора математики, последнее посещение 22 февраля 2011 г.
Калькулятор процентного увеличения
Использование калькулятора
Калькулятор процентного увеличения находит увеличение от одного значения к другому в процентах.
Введите начальное и конечное значения, чтобы найти увеличение в процентах.
Как рассчитать увеличение в процентах
- Вычесть конечное значение минус начальное значение
- Разделите эту сумму на абсолютное значение начального значения
- Умножьте на 100, чтобы получить процентное увеличение
- Если процент отрицательный, это означает, что произошло уменьшение, а не увеличение.
Формула процентного увеличения
Вы можете использовать формулу процентного увеличения для расчета любого процентного увеличения:
\ (\ text {Увеличение в процентах} = \\ \ dfrac {\ text {Окончательное значение} — \ text {Начальное значение}} {\ left | \ text {Начальное значение} \ right |} \ times 100 \)
Пример проблемы: увеличение в процентах
В прошлом году ваши любимые джинсы стоили 36 долларов за пару. В этом году они стоят 45 долларов за пару.Каков процент роста цен на эти джинсы с прошлого года по сравнению с этим годом?
Увеличение в процентах = [(Конечное значение — Начальное значение) / | Начальное значение | ] × 100
45–36 = 9
9/36 = 0,25
0,25 × 100 = 25%
Итак, цена на ваши любимые джинсы выросла на 25% по сравнению с прошлым годом по сравнению с этим годом.
Связанные калькуляторы
Используйте
Калькулятор процентного уменьшения, чтобы найти процентное уменьшение от одного значения к другому.
Используйте
Калькулятор процентной разницы, когда вы сравниваете два значения и хотите найти процентную разницу между ними.
Калькулятор процентного изменения находит изменение между двумя числами в процентах. Это похоже на поиск увеличения или уменьшения в процентах, но это изменение не помечается как увеличение или уменьшение.
Расчет процентов — служба поддержки Office
Найдите процент от общего числа
Допустим, вы правильно ответили на 42 вопроса из 50 в тесте.Каков процент правильных ответов?
Щелкните любую пустую ячейку.
Введите = 42/50 , а затем нажмите RETURN.

Результат 0,84.
Выберите ячейку, содержащую результат шага 2.
На вкладке Home щелкните
.
Результат 84,00%, что составляет процент правильных ответов на тесте.
Примечание: Чтобы изменить количество десятичных знаков, отображаемых в результате, щелкните Увеличить десятичное число
или Уменьшить десятичный
.
Найдите процент изменения между двумя числами
Допустим, ваш заработок составляет 2342 доллара в ноябре и 2500 долларов в декабре.Каков процент изменения вашего дохода за эти два месяца? Тогда, если ваш доход в январе составил 2425 долларов, каков процент изменений в вашем доходе с декабря по январь? Вы можете рассчитать разницу, вычтя новый заработок из первоначального, а затем разделив результат на исходный.
Рассчитать процент увеличения
Щелкните любую пустую ячейку.
Введите = (2500-2342) / 2342 , а затем нажмите RETURN.
Результат 0,06746.
Выберите ячейку, содержащую результат шага 2.
На вкладке Home щелкните
.
Результат 6,75%, что составляет процент увеличения заработка.
Примечание: Чтобы изменить количество десятичных знаков, отображаемых в результате, щелкните Увеличить десятичное число
или Уменьшить десятичный
.

Рассчитать процент уменьшения
Щелкните любую пустую ячейку.
Введите = (2425-2500) / 2500 , а затем нажмите RETURN.
Результат -0,03000.
Выберите ячейку, содержащую результат шага 2.
На вкладке Home щелкните
.
Результат -3,00%, что соответствует проценту уменьшения прибыли.
Примечание: Чтобы изменить количество десятичных знаков, отображаемых в результате, щелкните Увеличить десятичное число
или Уменьшить десятичный
.

Найдите сумму, зная сумму и процент
Допустим, распродажа рубашки составляет 15 долларов, что на 25% ниже первоначальной цены.Какая первоначальная цена? В этом примере вы хотите найти 75%, из которых число равно 15.
Щелкните любую пустую ячейку.
Введите = 15 / 0,75 , а затем нажмите RETURN.
Результат 20.
Выберите ячейку, содержащую результат шага 2.
В более новых версиях:
На вкладке Home щелкните
.

Результат — 20 долларов США, что является первоначальной ценой рубашки.
В Excel для Mac 2011:
На вкладке Домашняя страница в разделе Номер щелкните Валюта
Результат — 20 долларов.00, что является первоначальной ценой рубашки.
Примечание: Чтобы изменить количество десятичных знаков, отображаемых в результате, щелкните Увеличить десятичное число
или Уменьшить десятичный
.
Найдите сумму, зная сумму и процент
Допустим, вы хотите купить компьютер за 800 долларов и должны заплатить еще 8.9% налога с продаж. Сколько вам нужно платить за налог с продаж? В этом примере вы хотите найти 8,9% от 800.
Щелкните любую пустую ячейку.
org/ListItem»>Выберите ячейку, содержащую результат шага 2.
В более новых версиях:
На вкладке Home щелкните
.
В Excel для Mac 2011:
На вкладке Домашняя страница в разделе Номер щелкните Валюта
Результат 71 $.20 — сумма налога с продаж для компьютера.
Примечание: Чтобы изменить количество десятичных знаков, отображаемых в результате, щелкните Увеличить десятичное число
или Уменьшить десятичный
.
Введите = 800 * 0,089 , а затем нажмите RETURN.
Результат 71,2.
Увеличение или уменьшение числа на процент
Допустим, вы тратите в среднем 113 долларов в неделю на еду и хотите увеличить свои еженедельные расходы на питание на 25%. Сколько можно потратить? Или, если вы хотите уменьшить свое еженедельное пособие на питание со 113 долларов на 25%, каково ваше новое еженедельное пособие?
Сколько можно потратить? Или, если вы хотите уменьшить свое еженедельное пособие на питание со 113 долларов на 25%, каково ваше новое еженедельное пособие?
Увеличить число на процент
Щелкните любую пустую ячейку.
Введите = 113 * (1 + 0,25) , а затем нажмите RETURN.
Результат 141.25.
Выберите ячейку, содержащую результат шага 2.
В более новых версиях:
На вкладке Home щелкните
.
В Excel для Mac 2011:
На вкладке Домашняя страница в разделе Номер щелкните Валюта
Результат — 141 доллар.
 25, что на 25% больше еженедельных расходов на питание.
25, что на 25% больше еженедельных расходов на питание.Примечание: Чтобы изменить количество десятичных знаков, отображаемых в результате, щелкните Увеличить десятичное число
или Уменьшить десятичный
.
Уменьшить число на процент
Щелкните любую пустую ячейку.
Введите = 113 * (1-0,25) , а затем нажмите RETURN.
Результат 84,75.
Выберите ячейку, содержащую результат шага 2.
В более новых версиях:
На вкладке Home щелкните
.

В Excel для Mac 2011:
На вкладке Домашняя страница в разделе Номер щелкните Валюта
Результат — 84,75 доллара, что на 25% меньше еженедельных расходов на питание.
Примечание: Чтобы изменить количество десятичных знаков, отображаемых в результате, щелкните Увеличить десятичное число
или Уменьшить десятичный
.
См. Также
ПРОЦЕНТРАНГ (функция ПРОЦЕНТРАНГ)
Рассчитать промежуточную сумму
Рассчитать среднее
Калькулятор процентов — Расчет процентов
Что такое проценты?
Один процент равен сотой.Мы используем% для обозначения этого. Таким образом, 5 процентов равны 5%, 0,05, 5/100 или пяти сотым. Это так просто!
Это хорошо, но обычно мы используем не только проценты. Иногда мы хотим показать соотношение между двумя числами. Например: что 40% от 20? Это 40 сотых от 20, поэтому, если мы разделим 20 печенек на 100 равных частей (удачи с этим!), 40 из этих кусочков будут нашими 40% от 20 печений. Давайте посчитаем: 40/100 * 20 = 8. Здесь применим небольшой трюк: если вы хотите разделить на сотню, просто переместите запятую на два места влево.В нашем расчете 40/100 * 20 мы также можем сделать так: (40 * 20) / 100 (это то же самое). 40 * 20 равно 800. Переместите запятую на 800 на 2 позиции влево, и вы получите 8.00. Введите эти значения вверху страницы: 40 и 20. Тогда вы получите «40% от 20 равно 8».
Давайте посчитаем: 40/100 * 20 = 8. Здесь применим небольшой трюк: если вы хотите разделить на сотню, просто переместите запятую на два места влево.В нашем расчете 40/100 * 20 мы также можем сделать так: (40 * 20) / 100 (это то же самое). 40 * 20 равно 800. Переместите запятую на 800 на 2 позиции влево, и вы получите 8.00. Введите эти значения вверху страницы: 40 и 20. Тогда вы получите «40% от 20 равно 8».
В другом случае вы хотите указать, например, на сколько процентов уменьшилось или увеличилось число. Например, если у вас есть 10 яблок и вы съели 2 из них … Тогда вы потеряли 20% яблок. Почему? Поскольку 8 — это 80% от 10. Все яблоки были 100%, теперь у нас все еще есть 80%, поэтому количество яблок уменьшилось на 20% (потому что 100 — 80 = 20).Используйте для этого наш инструмент увеличения процента.
Происхождение
Термин «процент» происходит от латинского «за центр» (на сотню) и обозначается знаком%.
Проценты на решения
Процент не всегда означает несколько сотых от целого. Таким образом, решения также отображаются в процентах. К физиологическому солевому раствору, например, относится 0,9% раствор кухонной соли. Это 0,9% означает, что раствор содержит 0.9 граммов соли на 100 мл (= 100 граммов). Таким образом, процент здесь относится к весу.
Таким образом, решения также отображаются в процентах. К физиологическому солевому раствору, например, относится 0,9% раствор кухонной соли. Это 0,9% означает, что раствор содержит 0.9 граммов соли на 100 мл (= 100 граммов). Таким образом, процент здесь относится к весу.
В процентном соотношении объема часто указывается добавление: «объем», тогда мы получаем, например, 14% об. Или 14 об.%.
Процентные точки
Процентная точка, также записываемая как%, используется для обозначения абсолютной разницы между значениями, выраженной в процентах.
Таким образом, процент — это сотая часть, а процентный пункт — это расчетная единица, которая выражает изменение в процентах.
Пример
Если процентная ставка на вашем сберегательном счете повышается с 2% до 3%, вы можете выразить это как «увеличение на 50% старой процентной ставки» или как «увеличение на 1 процентный пункт» (что составляет 1% всего). «Увеличение на 1%» неясно, потому что оно может указывать на увеличение на 1% от 2 (0,02), в результате чего общая сумма составляет 2,02% вместо 3%.
Бесплатные финансовые калькуляторы | Calculators.vip
Торговля и учет
- Прибыль или убыток
- Расчет собственного капитала
- Коэффициент оборачиваемости запасов
- Калькулятор доходности аренды
- Амортизация активов
- Калькулятор амортизации
- Калькулятор накопленной амортизации
- Чистая стоимость реализации
- Калькулятор чистых активов
- Расчет наценки на товар
- Калькулятор средних запасов (Avg)
- Период оборачиваемости товара
- Расчет себестоимости
- Калькулятор предельной выручки
- Сколько вернуть сдачи
Оценка компаний, активов
- Ставка капитализации недвижимости
- Приведенная стоимость
- Доходность инвестиций (ROI)
- Временная стоимость денег (TVM)
- На сколько хватит накоплений
- Почасовая оплата труда
- Пенсионные сбережения
- Расчет дней дебиторской задолженности (DSO)
- Калькулятор простых и сложных процентов
- Средневзвешенная стоимость капитала (WACC)
- Эффективная годовая процентная ставка (EAR)
- Калькулятор горизонтального анализа
- Коэффициент оборачиваемости кредиторской задолженности
- Калькулятор запаса прочности
- Калькулятор рентабельности инвестированного капитала
- Калькулятор коэффициента покрытия долга
Маркетинг
- Эффективности email-рассылки
- Расчет эффективности рекламы
- Калькулятор конверсии сайта
- Затраты на привлечение клиентов
Налоги
- Налогооблагаемый доход
- Калькулятор НДС
- Эффективная налоговая ставка
- Налоговый щит
- Калькулятор процентного налогового щита
- Калькулятор амортизационного налогового щита
Оценка финансовых потоков
- Калькулятор непогашенной задолженности (DPO)
- Калькулятор нераспределенной прибыли (R.
 E)
E) - Предельные издержки (MC)
- Правило 72, правило 70 и правило 69.3
- Расчет дисконтированного денежного потока (DCF)
Акции и облигации
- Калькулятор цен на облигации
- Доходность облигаций (YTM)
- Доходность облигаций к досрочному погашению (YTC)
- Совокупный годовой темп роста (CAGR)
- Рассчитать дисконтирование дивидендов
- Доходности облигаций к худшему (YTW)
- Калькулятора оценки акций
- Эффективный срок до погашения облигации
- Прибыль на одну акцию
- Соотношения задолженности к собственному капиталу
- Форвардная процентная ставка
- Оценка капитальных активов
- Коэффициент Сортино
- Калькулятор коэффициента привязки
- Калькулятор Бенджамина Грэма
- Расчет маржи на Форексе
- Стоимости облигаций с нулевым купоном
- Калькулятор реинвестирования дивидендов
- Балансовая стоимость акций
- Калькулятор премии за риск
Как экономить
- Детский калькулятор сбережений
- Калькулятор скидок
- Распределение семейного бюджета
Ипотека, кредиты, вклады
- Первоначальный взнос по ипотеке
- Сравнение трех кредитов
- Калькулятор рефинансирования кредита
- Калькулятор расчета вклада
- Расчет дохода от вклада
- Калькулятор начисленных процентов
- Расчет ипотечного кредита онлайн
- Кредит до зарплаты
- Калькулятор еженедельных процентов
- Калькулятор ежемесячных процентов
- Калькулятор краткосрочного кредита
- Калькулятор срочного кредита
- Калькулятор кредитной карты
- Расчет количества периодов погашений (NPER)
- Ежедневный процент по кредиту
- Отношение кредита к стоимости (LTV)
- Ежемесячный взнос по кредиту
- Дадут ли ипотеку
- Досрочное погашение ипотеки
- Расчет эффективной процентной ставки
- Калькулятор накопления сбережений
- Расчет смешанного кредита
- Калькулятор бизнес кредитов
Экономика
- Калькулятор ВВП
- Калькулятор расчета спроса и предложения
- Калькулятор платежного баланса
- Калькулятор сравнительных преимуществ
- Паритет покупательной способности
- Предельная склонность к потреблению (MPC)
- Калькулятор обратного процента
- Калькулятор инфляции в России
- Калькулятор эффекта мультипликатора
- Калькулятор предельной полезности
Калькулятор процентов
Калькулятор процентов см.
 примеры
примеры| % от | = | |||
| Ответ |
(Введите значения в синие поля.
При необходимости выберите другое поле в качестве поля для ответа.)
Ответы округляются до 7 знаков после запятой.
Калькулятор процентов в общих фразах: см. примеры
| процентов от | это |
| сколько процентов от | ? | % |
| Сколько процентов от | это | ? | % |
| это | процентов чего? |
(Введите значения в синие поля. Ответы появятся в черных полях.)
Ответы появятся в черных полях.)
Ответы округляются до 7 знаков после запятой.
Калькулятор процентов см. примеры
Ответы округляются до 7 знаков после запятой.
Добавить или вычесть процент см. примеры
Рассчитать: чаевые, продажную цену, скидку в процентах, цену со скидкой, цену с налогом с продаж и т. д.
| Начальное значение | % от начального значения | Конечное значение | ||
| знак равно | ||||
(Введите значения в синие поля. Ответ появится в черном поле.)
Ответ появится в черном поле.)
Ответы округлены до 7 знаков после запятой.
Изменение в процентах см. примеры
Увеличение в процентах
Уменьшение в процентах
Используется при сравнении старого значения с новым или при сравнении начального значения с конечным значением.
| Начальное значение | Конечное значение | Процентное изменение | |||
| % |
Положительный ответ на процентное изменение представляет собой процентное увеличение.
Отрицательный ответ для процентного изменения означает процентное уменьшение.
Процентное изменение =
Конечное значение — Начальное значениеabs(Начальное значение)
x 100%
(где abs = абсолютное значение)
(Введите значения в синие поля. Ответ появится в черном поле.)
Ответ появится в черном поле.)
. Ответы округляются до 7 знаков после запятой.
Ошибка в процентах см. примеры
Используется при сравнении теоретического (известного) значения с экспериментальным (измеренным) значением.
| Теоретическое значение | Экспериментальное значение | Процентная ошибка | |||
| % |
Погрешность в процентах =
abs(Экспериментальное значение — Теоретическое значение)abs(Теоретическое значение)
x 100%
(где abs = абсолютное значение)
(Введите значения в синие поля. Ответ появится в черных полях. box.)
Ответы округляются до 7 знаков после запятой.
Разница в процентах см. примеры
Используйте при сравнении двух значений, когда ни одно из них не считается начальным или эталонным значением.
| Одно значение | Другое значение | Разница в процентах | |||
| % |
Примечание. Стандартного уравнения для процентной разницы для всех обстоятельств не существует. Используемое здесь уравнение делит разницу между двумя значениями на среднее значение двух значений (см. уравнение ниже). В некоторых случаях может потребоваться разделить на минимальное из двух значений или на максимальное из двух значений и т. д. Убедитесь, что используемое здесь уравнение соответствует вашим обстоятельствам.
Используемое уравнение:
Разница в процентах =
abs(одно значение — другое значение)abs((одно значение + другое значение)/2)
x 100%
(где abs = абсолютное значение)
( в синие поля, ответ появится в черном поле. )
)
Ответы округляются до 7 знаков после запятой.
Определения:
Проценты:
Процент означает на 100 или частей на 100. Его можно использовать для описания части целого или части целого. Это происходит от процентов , что является сокращением от процентов , что означает на сотню.
Знак процента: %
1 процент (1%) = 1 часть на 100 = 1/100 = 0,01 (часть меньше целого)
100 процентов (100%) = 100 частей на 100 = 100/100 = 1 (часть равна целому)
110 процентов (110%) = 110 частей на 100 = 110/100 = 1,1 (часть больше целого)
Процент:
Количество на 100, которое относится к части целого (в общем смысле), как правило, без использования определенного числа.
Процент против процента
Слово процент обычно используется с числом (пример: 10 процентов), тогда как процент обычно не используется с числом (пример: какой процент шариков красный?). Исключение составляют процентные пункты (пример: 2 процентных пункта).
Калькулятор процентов:
Калькулятор или инструмент, который использует процентную формулу для вычисления желаемого значения в этой формуле. Процентная формула содержит три переменные. Если известны любые две переменные, можно вычислить третью переменную.
Формула процентов:
Формула, используемая для решения процентных задач, которая связывает два отношения, где одно из отношений представляет собой часть или часть на 100, а другое отношение представляет собой часть или часть на целое.
Где:
A% от B например: 10% от 90 равно 9 , где A=10, B=90, C=9
Формула процентов:
A/100 x B = C как в: 10/100 x 90 = 9
Перестановка:
А100 =
ЦБ
как в:
10100 =
990
Процентная формула иногда выражается как:
процент100 =
является (частью) (целого)
как в: 10100 = 990
Решение для каждой из переменных дает:
A = (C / B) x 100 как в: A = (9 / 90) x 100 = 10
B = C / (A / 100) как в: B = 9 / (10 / 100) = 90
C = (A / 100) x B как в: C = (10 / 100) x 90 = 9
Примечание: A% = A/100, поскольку % означает на 100
Как используются проценты?
- Скидки в магазинах: скидка 25 %
- налог с продаж обычно составляет процент от покупной цены: 8% налог с продаж
- процентные ставки по сберегательным счетам обычно указываются в виде годовой процентной ставки (в апреле): 1,5% в апреле
- процентные ставки, взимаемые компаниями, выпускающими кредитные карты, и ипотечными компаниями, указаны в виде годовой процентной ставки.

- изменения процентных ставок: процентные ставки выросли на один процентный пункт с 4,5% до 5,5% Статистика
- : погрешность плюс-минус четыре процентных пункта
- Награды по кредитным картам: 2% кэшбэка за определенные покупки
- новости: рейтинги одобрения, уровень занятости и опросы могут быть выражены в процентах
- ноутбуки, планшеты и сотовые телефоны обычно имеют индикатор заряда батареи в процентах
- прогноз погоды: 20-процентная вероятность дождя
- вероятность: шанс выиграть приз составляет 1 из 10 или 10 процентов
- влажность: уровень влажности 65%
Проценты можно использовать для облегчения понимания отношения между частью и целым.
В любое время, когда вам нужно решить задачу с процентами, вам поможет калькулятор процентов.
Калькулятор процентов — Как найти процентное изменение
Онлайн-калькулятор процентов — это инструмент, который позволяет вам вычислять проценты, а также вычислять процентные значения. Проще говоря, этот калькулятор процентов использует основные формулы процентов для вычисления процентов и неизвестных значений процентов в уравнениях. Кроме того, этот калькулятор для процентов поможет вам добавить или вычесть процент из заданного числа или решить заданные уравнения.
Проще говоря, этот калькулятор процентов использует основные формулы процентов для вычисления процентов и неизвестных значений процентов в уравнениях. Кроме того, этот калькулятор для процентов поможет вам добавить или вычесть процент из заданного числа или решить заданные уравнения.
Что ж, в этом посте мы собираемся ответить, как рассчитать проценты с помощью калькулятора или вручную для любого уравнения, формулы для процентов и многое другое, что поможет вам найти проценты от всего, что вы хотите! Но прежде чем узнать обо всех этих терминах, давайте начнем с основного определения математического процента.
Сколько процентов в математике? В области математики процент может быть разработан как число или отношение, представляющее долю от 100. Обычно он обозначается знаком «%» или иногда просто «процент», а также «процент». Например, при вычислении процентов 35% будет эквивалентно десятичной дроби 0,35, а в виде дроби будет представлено как 35/100. дроби и смешанные числа в процентах.
дроби и смешанные числа в процентах.
Всякий раз, когда есть слово проценты, это обычно представление, которое используется с числом. Например, 50 процентов. Однако слово процент обычно не может использоваться с числом. Например, какой процент поля цветов красный?
Формула процентов:Хотя мы можем записать процентную формулу в разных формах, но в основном это алгебраическое уравнение, которое включает следующие три значения.
- P (в процентах) × V1= V2
- P представляет процент,
- V1 представляет собой первое значение, которое будет изменено в процентах.
- V2 — это результат процента, который работает на V1.
Калькулятор процентного увеличения преобразует введенный процент в десятичное число, чтобы найти наилучшее возможное решение. Хотя, если кто-то решает вопросы на процент, полученное значение будет фактическим процентом. Он не будет обеспечивать его десятичное представление.
Пример:
- P× 20 = 2,5
- P = 2,5 / 20 = 0,125 * 100 = 12,5%
Если вы решаете какую-либо задачу вручную, то в формуле нужно процентное значение в десятичной форме. В таком случае вам нужно умножить на 100, чтобы преобразовать в проценты, как в приведенном выше примере.
Формула процентного изменения:Наш калькулятор процентного изменения используется для расчета процентного изменения, следуя основному правилу, описанному ниже.
Любое изменение в процентах рассчитывается путем вычисления общей дисперсии между двумя значениями и последующего сравнения этой дисперсии с первым значением. Арифметически он включает в себя использование точного значения отклонения среди любых двух значений, а затем деление результата на первое значение, в основном вычисляя, в какой степени было изменено исходное значение.
Наш калькулятор вычисляет повышение или понижение определенного процента заданных входных чисел.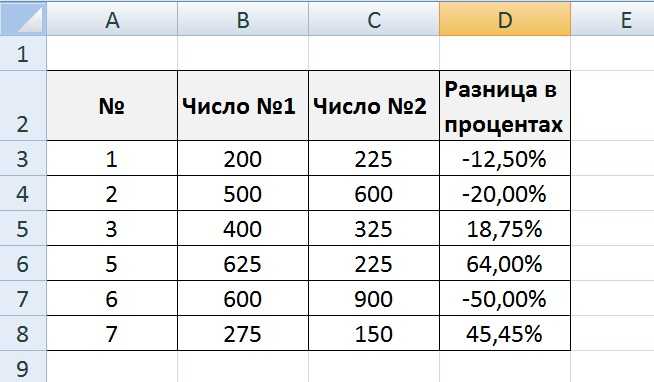 В основном это включает в себя преобразование процента в его десятичную форму, кроме того, вычитание или добавление эквивалентного десятичного числа к 1, соответственно. Это известно как процентное изменение.
В основном это включает в себя преобразование процента в его десятичную форму, кроме того, вычитание или добавление эквивалентного десятичного числа к 1, соответственно. Это известно как процентное изменение.
Пример:
Для расчета приращения в процентах имеем:
- 200 увеличено на 10%
- 10/100 = 0,1
- 200 * (1 + 0,1) = 220
Для расчета процентного уменьшения:
- 200 уменьшить на 10%
- 10/100 = 0,1
- 200 * (1 – 0,1) = 180
Как рассчитать проценты?
Просто попробуйте приведенный выше процентный калькулятор для мгновенных и точных вычислений, соответствующих задачам с процентами. Также нахождение процентов можно производить вручную с помощью формулы процентов. Тем не менее, использование калькулятора процентов — это еще один способ легко рассчитать процент.
Пример:
Сколько будет 10% от 60?
Применяя формулу: P умножить на V1 = V2
- 10% будет умножено на 60.

- 10/100 * 60 = 6.
Если кто-то хочет знать, сколько процентов C составляет D, вы просто разделите C на D на первом шаге. Теперь вы возьмете полученное число и переместите запятую на два пробела вправо. Это будет ваш процент. В этом мире технологий калькулятор процентов широко доступен онлайн для расчета процентов и процентного изменения.
Пример:
Что такое 5% от 250?
- Мы просто преобразуем его в уравнение
- П% * Х = Y
- В этом примере 5% будет «p», а 250 будет «X»> поэтому уравнение будет таким: 5% * 250 = Y
- Теперь мы преобразуем 5% в десятичную дробь. 5/100 = 0,05
- Мы заменим 0,05 на 5% в приведенном выше уравнении: 5% * 250 = Y
- 0,05 * 250 = 12.
- Д = 12.
- Следовательно, 5% от 250 будет 12
- Вы также можете проверить свой ответ с помощью процентного калькулятора.
Самая простая стратегия, чтобы узнать процент чего-либо, заключается в том, что вы должны следовать: X разделить на Y = P умножить на 100.
Пример:
каков процент 5 от 25?
Ответ будет 20%, потому что мы просто разделим число 5 на 25, а затем умножим на 100.
Как рассчитать процентное изменение?
Чтобы рассчитать процентное изменение, вы должны следовать следующей формуле:
Процентное изменение = ΔV разделить на V1×100 = (V2−V1), разделить на V1, умножить на 100
Пример:
Как найти процентное изменение выражается в росте или снижении от 3,50 до 2,625?
- В этом примере начальное значение = 3,50
- Второе значение = 2,625
- Примените формулу: = (2,625−3,50) разделить на 3,50 умножить на 100=−0,25×100=−25%изменить
- Этот расчет также можно выполнить с помощью приведенного выше калькулятора процентного изменения.
Проценты или задачи на проценты:
Давайте рассмотрим различные уравнения, соответствующие процентам или процентам.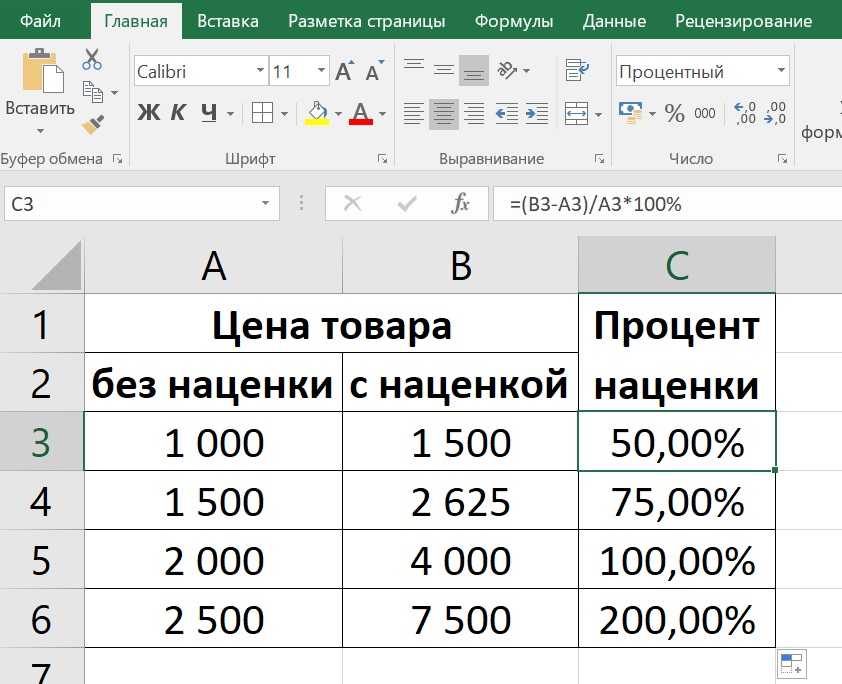 Есть несколько решенных примеров задач, которые могут подойти вам лучше всего! Кроме того, примеры форматов задач соответствуют полям ввода приведенного выше процентного калькулятора. Формулы/уравнения и примеры:
Есть несколько решенных примеров задач, которые могут подойти вам лучше всего! Кроме того, примеры форматов задач соответствуют полям ввода приведенного выше процентного калькулятора. Формулы/уравнения и примеры:
- Записывается уравнением: Y = P% * X
- «Что» называется Y, которое вы хотите решить для
- Во-первых: вы должны преобразовать проценты в десятичные числа, разделив на 100
- Решение: найдите Y, просто используя процентную формулу
- Д = П% * Х
Пример задачи: Сколько будет 20% от 50?
Решение:
- Уравнение: Y = P% * X
- Y = 20% * 50
- Преобразование процентов в десятичные числа:
- Д = (20/100) * 50
- Y = 0,2 * 50
- Д = 10
- Записывается в виде уравнения: Y = P% ? Х
- «Что» сказано P%, что вы хотите решить для
- Просто разделите обе части на X, чтобы получить P% в одной части уравнения
- Y ÷ X = (P% ? X) ÷ X, вы получаете Y ÷ X = P%, что также записывается как: P% = Y ÷ X
- Решение: просто найдите P%, используя процентное уравнение
- P% = Y ÷ X
Пример задачи: 15 сколько процентов от 60?
Решение:
- Уравнение: P% = Y / X
- П% = 15/60
- Р% = 0,25
- Преобразование десятичной дроби в проценты:
- Р% = 0,25*100
- П% = 25%
- Это можно записать в виде уравнения: Y = P% * X
- «Что» называется X, которое вы хотите решить для
- Просто разделите обе части уравнения на P%, чтобы получить X на одной стороне
- Y ÷ P% = (P% × X) ÷ P%, получается Y ÷ P% = X, также записывается как X = Y ÷ P%
- Решение: используйте формулу для вычисления процентов, чтобы найти X .
- Х = Y ÷ P%

Пример задачи: 7 составляет 66% от чего?
Решение:
- Уравнение: X = Y / P%
- Х = 7 / 66%
- Преобразование процентов в десятичные числа:
- Х = 7/(66/100)
- Х = 7/0,66
- Х = 10,61
- Это можно выразить уравнением: P% * X = Y
- «Что» — это P%, которое вам нужно решить для .
- Теперь просто разделите обе части уравнения на X, чтобы получить P% только с одной стороны
- (P% * X) ÷ X = Y ÷ X, вы получаете P% = Y ÷ X
- Решение: Решите для P%, используя формулу %
- P% = Y ÷ X
Пример задачи: Сколько процентов от 25 составляет 7?
Решение:
- Уравнение: P% = Y / X
- П% = 7/25
- Р% = 0,28
- Преобразование десятичной дроби в проценты:
- Р% = 0,28*100
- П% = 28%
- Выражается уравнением: P% × X = Y
- «Что» обозначается как X, что вам нужно решить для
- Теперь все, что вам нужно разделить обе части уравнения на P%, чтобы получить X с одной стороны
- (P% × X) ÷ P% = Y ÷ P%, получится: X = Y ÷ P%
- Используйте формулу % для решения
- Х = Y ÷ P%
Пример задачи: 30% от 9?
Решение:
- Уравнение: X = Y / P%
- Х = 9/30%
- Преобразование процентов в десятичные числа:
- Х = 9/(30/100)
- Х = 9/0,3
- Х = 30
- В терминах уравнения это записывается как: P% * X = Y
- «Что» называется Y, которое вам нужно решить для
- Просто используйте формулу для процентов, чтобы найти Y
- Д = П% * Х
Пример Задача: 7% от 27 это что?
Решение:
- Уравнение: Y = P% * X
- Y = 7% * 27
- Преобразование процентов в десятичные числа:
- Д = (7/100) * 27
- Y = 0,07 * 27
- Y = 1,89
- Записывается в виде уравнения: Y / X = P%
- «Что» выражается как X, что вам нужно решить для
- Просто умножьте обе части уравнения на X, чтобы получить X из знаменателя
- (Y / X) * X = P% * X , вы получаете: Y = P% * X
- Теперь просто разделите обе части уравнения на P%, чтобы получить X на одной стороне
- Y ÷ P% = (P% * X) ÷ P%, получается: Y ÷ P% = X
- Используйте формулу для % для решения X
- Х = Y ÷ P%
Пример: 5 от чего составляет 13%?
Решение:
- Уравнение: X = Y / P%
- Х = 5/13%
- Преобразование процентов в десятичные числа:
- Х = 5/(13/100)
- Х = 5/0,13
- Х = 38,46
- В виде уравнения это выражается как: Y / X = P%
- «Что» называется буквой Y, которую вам нужно решить для .
- Теперь просто умножьте обе части уравнения на X, чтобы получить Y на одной стороне
- (Y ÷ X) * X = P% * X, получается: Y = P% * X
- Используйте процентное уравнение для решения Y
- Д = П% * Х

Пример задачи: Сколько из 26 составляет 12%?
Решение:
- Уравнение: Y = P% * X
- Y = 12% * 26
- Преобразование процентов в десятичные числа:
- Д = (12/100) * 26
- Y = 0,12 * 26
- Y = 3,12
- Выражается уравнением: Y / X = P%
- «Что» — это P%, который вам нужно решить для .
- Просто найдите P%, используя формулу для %
- P% = Y / X
Пример: 8 из 12 это сколько процентов?
Решение:
- Уравнение: P% = Y / X
- П% = 8/12
- P% = 0,66666666666667
- Преобразование десятичной дроби в проценты:
- P% = (0,66666666666667) * 100
- Р% = 66,67%
О калькуляторе процентов:
Онлайн-калькулятор процентов с помощью онлайн-калькулятора поможет вам рассчитать проценты и неизвестные значения процентов в уравнениях. Инструмент использует простую формулу процента для расчета процентов данного уравнения. Кроме того, этот калькулятор процентов позволяет добавлять или вычитать проценты из числа или решать уравнения.
Инструмент использует простую формулу процента для расчета процентов данного уравнения. Кроме того, этот калькулятор процентов позволяет добавлять или вычитать проценты из числа или решать уравнения.
Калькулятор на 100% бесплатен и позволяет выполнять расчет процентов или сколько процентов (любого числа) за долю секунды. Вы можете легко и точно определить % возраста или больше с помощью этого калькулятора. Просто придерживайтесь этих шагов, чтобы получить точные измерения, соответствующие процентам.
Входные данные:
- Прежде всего, вы должны выбрать уравнение, для которого вы хотите вычислить процент
- Затем вы должны ввести значения в назначенные поля, соответствующие выбранному уравнению
- После этого просто нажмите кнопку расчета, чтобы получить фактическое процентное значение
Выходы:
Калькулятор процентов показывает:
- Процентное значение согласно выбранному процентному уравнению
- Показать пошаговый расчет уравнения
- Если вам нужно узнать, сколько процентов X составляет Y, то вы просто делите X на Y
- Затем вы должны взять это число и переместить запятую на две позиции вправо
- Это ваш процент (%)
Все, что вам нужно, это ввести формулу =C2/B2 в ячейку D2 и одновременно скопировать ее на столько строк, сколько вам нужно. Затем просто нажмите кнопку «Процентный стиль» (вкладка «Главная» > группа «Число»), чтобы отобразить полученные десятичные дроби в процентах.
Затем просто нажмите кнопку «Процентный стиль» (вкладка «Главная» > группа «Число»), чтобы отобразить полученные десятичные дроби в процентах.
Вы можете легко найти 70% числа: просто возьмите число и умножьте его на 70. Затем просто умножьте это на 0,01.
Как быстро считать проценты в уме?Это довольно просто, давайте рассмотрим некоторые приемы расчета процентов:
- Чтобы найти 5%, просто найдите 10% и разделите его на два
- Чтобы найти 15 %, просто найдите 10 % и прибавьте 5 %
- Чтобы найти 20 %, просто найдите 10 % и удвойте его
- Чтобы найти 25%, просто найдите 50% и разделите его пополам
- Чтобы найти 60 %, просто найдите 50 % и прибавьте 10 %
- Чтобы найти 75%, просто найдите 50% и прибавьте 25%
- .. и так далее!
Кроме того, вы можете воспользоваться онлайн-калькулятором процентного роста, чтобы вычислить проценты.
Подведение итогов:
Этот процентный калькулятор предназначен для нахождения процентной разницы между любыми двумя заданными положительными числами, которые больше 0. Он помогает вам, когда вы хотите узнать точное процентное отклонение между двумя числами. . Этот процентный калькулятор дает вам полную информацию о любом отклонении в процентах. Для этого инструмента порядок заданных чисел не учитывается, поскольку он просто выполняет расчеты для вычисления процента от числа. Таким образом, это один из лучших вариантов учебных целей.
Ссылки:Из Википедии: Знак процента и расчеты и Примеры:
Из источника Lifehacker: Рассчитайте почти любой процент в уме с помощью простых трюков и примеры
Другие языки: حاسبة النسبة المئوية, Calculadora de porcentajes, מחשבון אחture, yetrysker, ylregramas, ylredelernesh0053
Визуальный калькулятор процентов
Предыдущий
Еще онлайн-калькуляторы!
Далее
Калькулятор процентов
Этот онлайн-калькулятор процентов показывает, как процент представлен в виде доли числа. Чтобы найти процент числа от общего числа, просто введите значения в левой части калькулятора с частичным числом в качестве числителя (значение вверху) и итогом в качестве значения внизу (знаменатель). Калькулятор рассчитает процентное значение в числовом виде и покажет вам то же значение, которое представлено визуально.
Чтобы найти процент числа от общего числа, просто введите значения в левой части калькулятора с частичным числом в качестве числителя (значение вверху) и итогом в качестве значения внизу (знаменатель). Калькулятор рассчитает процентное значение в числовом виде и покажет вам то же значение, которое представлено визуально.
Этот процентный калькулятор также работает как калькулятор процентного отношения к дробям. Просто оставьте значения числителя и знаменателя пустыми (или нажмите кнопку «Очистить»), а затем введите процентное значение. Соответствующие значения будут показаны на главной панели калькулятора дробей.
Поскольку проценты по определению являются дробями от ста, если вы оставите знаменатель пустым, калькулятор выдаст 100. Если вы хотите использовать другой знаменатель, просто введите сначала знаменатель, а затем процент. Например, чтобы узнать, что такое 40% от 200, введите 200 в знаменателе, а затем 40% в процентах, чтобы получить результат.
На панели «Что такое процент» вы можете увидеть различные способы представления значений. Когда вы обновляете значения в калькуляторе, вы можете видеть, как ответ выражается в терминах, таких как…
Когда вы обновляете значения в калькуляторе, вы можете видеть, как ответ выражается в терминах, таких как…
Калькулятор будет аппроксимировать проценты до двух знаков после запятой, но вы увидите проценты с большей точностью, если калькулятор округлил их где представлены основные результаты.
Какая величина из целого равна определенному проценту?
Сколько процентов составляет некоторая сумма от целого?
Какая дробь равна определенному проценту?
Играя с этим процентным калькулятором и наблюдая, как различные дроби и проценты изменяют эти словесные описания, вы сможете лучше понять концепции процентов.
Если вы хотите сохранить настройки, которые вы вводите в процентном калькуляторе, ссылку «Поделиться этим процентом» можно скопировать и вставить в электронное письмо, в закладки браузера или на веб-страницу. Он вернется к этому процентному калькулятору и покажет проблему именно так, как вы ее видите.
Что такое проценты?
Проценты — это полезный способ представить дробную часть некоторой суммы в десятичной форме. Мы регулярно имеем дело с дробными числами, но часто дроби имеют разные знаменатели, что затрудняет их сравнение. Процент по определению — это дробь со 100 в знаменателе, поэтому сравнивать два процента проще, чем сравнивать две произвольные дроби.
Мы регулярно имеем дело с дробными числами, но часто дроби имеют разные знаменатели, что затрудняет их сравнение. Процент по определению — это дробь со 100 в знаменателе, поэтому сравнивать два процента проще, чем сравнивать две произвольные дроби.
Слово «процент» имеет латинский корень «процент», что означает «сто». Это то же корневое слово в английских словах «столетие», «сантиметр» или «столетие», и оно, конечно же, относится к денежному центу, который составляет одну сотую доллара. Латинское корневое слово в процентах должно помочь вам вспомнить, что проценты всегда являются долями от 100, и вы можете найти множество других интересных слов, связанных с сотнями и процентами, если вы обратите внимание. См. эту ссылку для более подробной информации… Откуда взялось слово «Процент»?
… но здесь, на этой странице калькулятора, мы имеем дело с математикой! Эти сотые знаменатели очень важны, и они напрямую связаны с использованием процентов и нашей десятичной системы счисления. Проценты приводятся непосредственно к числовым значениям и обратно путем перемещения десятичных разрядов.
Проценты приводятся непосредственно к числовым значениям и обратно путем перемещения десятичных разрядов.
Преобразование процентов в десятичные числа
Сотые доли представляют собой значения, отображаемые в виде двух цифр справа от десятичного знака в вещественном числе. Поскольку проценты на самом деле являются еще одним способом выражения сотых, преобразование процентов в десятичные дроби — очень простой процесс…
12% | = | = | 0.12 |
В других словах, то же самое, что и FRACTION 12, что 100, что 100, что 100, что 100, то же, что и FRACTION 12. десятичное значение 0,12. Механически преобразовать проценты в десятичные числа можно, взяв процент и переместив десятичную дробь на два разряда влево. Вот еще несколько примеров…
34% | = | = | 0.34 |
56. | = | 56.7 100 | = | 0.567 |
100% | = | 100 100 | = | 1,0 |
ПРИМЕЧАНИЕ, что 100%, то же самое, так же, как 100%, то же самое, как 100%, так же, как 100%, то же самое, как 100%, так же, как 100%, то же самое, как 100%, так же, как 100%, то же самое, как 100%, так же, как 100%, то же самое, как 100%, так же, как 100%, то же самое, как 100%, так же, как 100%, то же самое, как 100%, так же, как 100%, 100, то же самое, что 100%, то же самое, что 100% — 100, то же самое, что 100% — 100, то же самое, что 100% — 100, то же самое, что 100% — 100. конечно один. Это имеет смысл. Если у вас есть что-то на 100%, значит, у вас есть все, а не дробная часть.
Вот отличное видео, в котором вы узнаете больше о десятичных вычислениях процентов. Преобразование процентов в десятичные числа
Преобразование десятичных чисел в проценты
Обратный расчет десятичных чисел в проценты аналогичен. Здесь вы начинаете со значения в сотых долях, но мы конвертируем его в простой процент, перемещая десятичную дробь на два знака влево, а не вправо…0053
Здесь вы начинаете со значения в сотых долях, но мы конвертируем его в простой процент, перемещая десятичную дробь на два знака влево, а не вправо…0053
14%
0.232 | = | 23.2 100 | = | 23.2% |
1.0 | = | 100 100 | = | 100% |
1,25 |
1,25 |
1,25 |
1.2593 9008 |
=
125
100
=
125%
Обратите внимание на последнем примере, как мы начали с реального числа, более одного, и после перемещения Два. мы рассчитали процент больше 100. Проценты — это дроби от 100, но эти дроби могут быть неправильными. Таким образом, 125% — это идеальный процент, он просто представляет собой значение, превышающее целое. Вы часто будете видеть такие значения, когда будете думать о процентной разнице, например, если один товар стоит 125% другого.
Таким образом, 125% — это идеальный процент, он просто представляет собой значение, превышающее целое. Вы часто будете видеть такие значения, когда будете думать о процентной разнице, например, если один товар стоит 125% другого.
Как вычислять проценты
Вычислять проценты легко, если мы знаем, каким должно быть общее число чего-либо, и сравниваем его с имеющимся у нас числом. Вычисление процентов очень похоже на вычисление дроби, а затем, независимо от суммы, просто вычисление знаменателя, равного 100.
Предположим, у нас есть пакет, в котором должно быть 10 пончиков, но двух из них не хватает. Мы знаем, что общее количество пончиков должно быть 10. Если нас спросят: «Какой процент пончиков был съеден?» мы знаем, что количество пропущенных пончиков равно 2, поэтому преобразуйте дробь в проценты вот так…
Вычисление процентов может быть более трудным, если общая сумма (значение, с которого мы начинаем в качестве знаменателя) не является коэффициентом 100. Вот что действительно хорошо для вас делает калькулятор дроби в процентах на этой странице! Просто введите любые значения, которые вам нужны, и вы получите результат, возможно, в процентах с десятичным знаком. Вы будете преобразовывать дроби в проценты без напряжения.
Вот что действительно хорошо для вас делает калькулятор дроби в процентах на этой странице! Просто введите любые значения, которые вам нужны, и вы получите результат, возможно, в процентах с десятичным знаком. Вы будете преобразовывать дроби в проценты без напряжения.
Как найти прирост в процентах
Когда вы учитесь находить процентные различия между числами, например, определяя процентное изменение от одного значения к другому, вы смотрите на разницу между двумя значениями. Важная сумма — это чистое изменение между первым значением и вторым, поэтому первым шагом является вычитание. Например, если мы начали день с 10 долларами в кармане, а закончили с 15 долларами, то разница (сдача) составит 5 долларов. Если мы знаем сумму разницы, как мы рассчитываем процентное увеличение?
Процентное увеличение или процентное уменьшение определяется путем рассмотрения дроби с начальной суммой в качестве знаменателя и изменением в качестве числителя, поэтому для этого примера начальная сумма была 10 долларов США, а изменение составило 5 долларов США, поэтому наш процент рассчитывается как это…
Наш процент увеличения в этом примере составляет 50%. Вы можете получить более подробные примеры того, как рассчитать процентное изменение, здесь… Вычисление процентного увеличения и уменьшения
Вы можете получить более подробные примеры того, как рассчитать процентное изменение, здесь… Вычисление процентного увеличения и уменьшения
Рабочие таблицы процентных значений
Хотите попрактиковаться в вычислении процентов? На этом сайте есть несколько отличных процентных таблиц по ссылкам ниже!
Рабочие таблицы процентов Дроби как проценты и десятичные дроби Рабочие листы процентов к дробям Рабочие листы для преобразования дробей в проценты
Калькулятор процентов ٞ в App Store
Описание
Попробуйте лучший процентный калькулятор! Мы собрали 12 наиболее часто используемых процентных расчетов, и все они доступны под рукой.
Расчет быстрых операций, таких как:
1. % числа
2. % изменения
3. a равно b% от
4. % значения детали
5. Увеличение на %
6. Уменьшение на %
7. После % вычтено
8. После добавления %
9. Дробь к %
10. % к дроби
11. Сложный процент
Сложный процент
12. Долг/Ипотека
Условия подписки:
— Подписка автоматически продлевается в конце каждого срока.
— оплата будет снята с учетной записи iTunes при подтверждении покупки.
— Подписка продлевается автоматически, если автоматическое продление не будет отключено по крайней мере за 24 часа до окончания текущего периода.
— С аккаунта будет взиматься плата за продление в течение 24 часов до окончания текущего периода.
— Вы можете управлять своей подпиской и отключить автоматическое продление, перейдя в настройки своей учетной записи после покупки.
Политика конфиденциальности и Условия использования: https://oval.fi/privacy-policy-percentage-calculator
Версия 2.1
Добавлен новый калькулятор, помогающий вычислять проценты от нескольких значений
Рейтинги и обзоры
8,2 тыс. оценок
оценок
Процент приложения
Отлично! Мне часто нужно знать процент чисел, и это приложение покрывает все, с чем я сталкиваюсь. Спасает меня много раз и от просчетов. Я планирую использовать его ежедневно. Отличная цена! Спасибо всем за хорошо проделанную работу.
Мое личное мнение
Причина, по которой я загрузил это приложение, заключается в том, чтобы рассчитать налог и процент, но я сразу заметил, что ипотечный калькулятор не имеет возможности добавить дополнительный платеж, большинство существующих ипотечных калькуляторов не имеют этой опции, всегда заставляет меня задаться вопросом, почему нет, если вы можете собрать приложение, что такого сложного, чтобы добавить дополнительную строку, где говорится о дополнительной оплате к балансу, таким образом, люди, которые пытаются расплатиться за свой дом раньше, смогут это вычислить, давай Силиконовая долина
Здравствуйте!
Спасибо за отзыв! Я полностью согласен с тобой.
Я хотел бы получить известие от вас по адресу [email protected], чтобы мы могли обсудить любые дополнительные поля, которые, по вашему мнению, могут понадобиться.
Удобный
Я не использовал все различные функции расчета, но те, которые я использовал, просты для понимания и, следовательно, удобны для пользователя.
Разработчик, Oval Software Oy, указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика.
Данные, используемые для отслеживания вас
Следующие данные могут использоваться для отслеживания вас в приложениях и на веб-сайтах, принадлежащих другим компаниям:
- Расположение
- Идентификаторы
- Данные об использовании
Данные, связанные с вами
Следующие данные могут быть собраны и связаны с вашей личностью:
- Расположение
- Идентификаторы
- Данные об использовании
Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста. Узнать больше
Узнать больше
Информация
- Продавец
- Овал Софтвер Ою
- Размер
- 9,6 МБ
- Категория
- Утилиты
- Возрастной рейтинг
- 4+
- Авторское право
- © Oval Software Oy
- Цена
- Бесплатно
- Сайт разработчика
- Тех. поддержка
- Политика конфиденциальности
Еще от этого разработчика
Вам также может понравиться
Лучшие в мире калькуляторы процентов: увеличение процентов и многое другое
Самые простые в мире калькуляторы процентов
Здравствуйте! Мы рады, что вы здесь! Наши простые процентные калькуляторы позволят вам решить любую процентную задачу за следующие 12 секунд. Вы можете либо использовать наши процентные калькуляторы напрямую, либо просто просмотреть предоставленные нами процентные формулы, методы расчета и примеры ниже.
Вы можете либо использовать наши процентные калькуляторы напрямую, либо просто просмотреть предоставленные нами процентные формулы, методы расчета и примеры ниже.
Рассчитайте проценты самостоятельно: Что вы хотите знать?
- Сколько будет 25% от 200? Определение процентных значений »
- Сколько процентов от 200 составляет 50? Как найти процент »
- 50 составляет 25% от скольких? Найти целое число из процентов »
- 200 на сколько процентов больше/меньше 50? От одного значения к другому »
- Сколько будет 50 плюс/минус 25%? Сложение/вычитание процентов »
- 200 на 25% больше/меньше какого значения? Поиск начальных значений »
Или воспользуйтесь нашим калькулятором процентной скидки здесь.
Зачем вообще нужны проценты?
«Мне все равно больше никогда не понадобится знать, как делать эту математику!» — К сожалению, это утверждение не совсем верно. После школы проценты часто встречаются в расчетах цен, связанных с суммами в долларах и накоплением процентов. Например, процентные расчеты появляются в отношении повышения цен, скидок, НДС с чистыми и валовыми значениями или с расчетами прибыли.
После школы проценты часто встречаются в расчетах цен, связанных с суммами в долларах и накоплением процентов. Например, процентные расчеты появляются в отношении повышения цен, скидок, НДС с чистыми и валовыми значениями или с расчетами прибыли.
Формула процентов
Понимание того, как вычислять корни корня в процентах в самом слове. Происхождение этого термина можно проследить до латинской фразы, означающей «на сто», поэтому сегодня его представляют как отношение, знаменатель которого равен 100. Если мы хотим вычислить значения, выходящие за этот диапазон, мы можем возьмите наше соотношение и превратите его в пропорцию, где значение W будет нашим неизвестным или тем, что мы хотим выяснить.
Например, 25% представлено как 25/100 в форме дроби. Если мы хотим узнать, чему равно 25% от 200, мы можем составить следующую пропорцию:
\frac{25}{100}=\frac{W}{200}Затем мы можем использовать перекрестное умножение, чтобы установить правильную формулу процентов:
\text{100}\times\text{W}=\text {G}\times\text{P}
Таким образом, что W = процентное значение , G = базовое значение и P = процентное значение .
Определение процентных значений: что такое 25% от 200?
Хорошо, давайте рассмотрим эту проблему шаг за шагом. 50 % от 100 эквивалентны половине 100, поэтому 50. Но как вычислить 25 % от 200? Чтобы рассчитать это, вы можете использовать наш процентный калькулятор или прочитать раздел ниже, содержащий формулы и пояснения, чтобы лучше понять эти концепции и избежать технической помощи в будущем.
Объяснение, как рассчитать процентные значения\text{Процентное значение (W)}=\text{Базовое значение (G)}\times\frac{\text{Процентное значение (P)}}{\text{100}\% }
Открытый для понимания формулы:
Давайте войдем в мысленный пузырь и попытаемся мысленно обработать его с идеями и концепциями, с которыми мы, возможно, уже знакомы. Если мы подумаем о значении слова «проценты», которого мы касались ранее, мы можем использовать тот факт, что они являются частями целого, чтобы помочь нам понять, что могут делать калькуляторы. Например, 25% — это 25 («часть») из 100 («целое» в данном случае). Мы также можем воспользоваться тем фактом, что мы знаем, что 200 в 2 раза больше 100. Итак, если 25% от 100 равно 25, то 25% от 200 теоретически должно быть в 2 раза больше этого значения или 2 x 25, что равно 50.
Например, 25% — это 25 («часть») из 100 («целое» в данном случае). Мы также можем воспользоваться тем фактом, что мы знаем, что 200 в 2 раза больше 100. Итак, если 25% от 100 равно 25, то 25% от 200 теоретически должно быть в 2 раза больше этого значения или 2 x 25, что равно 50.
Теперь, когда у нас есть базовое представление о том, что может происходить при вычислении процентов, мы можем заняться формулой. Эта формула говорит нам, что произведение умножения процента на базовое значение, деленное на 100, является процентным значением. Если это сложно объяснить словами, вспомните следующий пример перекрестного умножения:
\frac{25}{100}=\frac{W}{200}
equals\text{100}\times\text {W}=\text{200}\times\text{25}
Формула делает еще один шаг, чтобы сообщить нам, что W или процентное значение, которое является значением, которое мы ищем в результате деления обеих частей уравнения выше на 100 или упрощенно:
\text{Процентное значение (W)}=\text{Базовое значение (G)}\times\frac{\text{Процентное значение (P)}}{\text{100}\%}
Мы хотим знать сколько будет 25% от 200. Следовательно, в этом случае наше базовое значение равно 200 (G), а процентное значение равно 25% (P).
Следовательно, в этом случае наше базовое значение равно 200 (G), а процентное значение равно 25% (P).
Давайте вспомним исходную формулу, которую мы ранее предоставили: 100 x W = G x P, и переместим члены. Деление на 100 с обеих сторон изолирует W, так что оно стоит отдельно на одной стороне уравнения, что дает нам:
W = G x P/100 или значение в процентах (W) = базовое значение (G) × процент (P)/100. %
Вставка значений, которые у нас есть, дает нам следующее: Процентное значение (W) = 200 × 25 %/100 %
Мы можем преобразовать дробь в самой правой части этого уравнения, разделив значения (разделив 25 % на 100%), чтобы получить: Процентное значение (W) = 200 × 0,25.
Наконец, мы можем напрямую выполнить эту математику в ее простейшей форме, чтобы получить 200, умноженное на 0,25, что равно 50. Значение: значение в процентах (W) = 50.
Следовательно, 25% (обозначается процентом или P) от 200 значение, G) равно 50 (или процентное значение, W)!
Как найти процент: какой процент от 200 составляет 50?
Мы знаем, что 50 составляет половину от 100, поэтому 50%. Но как посчитать, какой процент 50 составляет 200? Вы можете легко сделать это с помощью калькулятора процентного поиска или посмотреть формулы и пояснения под калькулятором для более подробного понимания. Как найти применимую процентную ставку?
Но как посчитать, какой процент 50 составляет 200? Вы можете легко сделать это с помощью калькулятора процентного поиска или посмотреть формулы и пояснения под калькулятором для более подробного понимания. Как найти применимую процентную ставку?
\text{Процент (P)}=\frac{\text{Процентное значение (W)}}{\text{Базовое значение (G)}}\times\text{100 }
Откройте для понимания формулу:
Формула утверждает, что процентное значение получается путем деления процентного значения (дивиденда) на базовое значение (делитель) и последующего умножения на 100%. С точки зрения непрофессионала, мы ищем процент (P), и наш вопрос: какой процент составляет 50 из 200?
Давайте делать это шаг за шагом. Процентное значение (W) равно 50, базовое значение (G) равно 200, и наша исходная формула выглядит следующим образом: 100 x W = G x P. Разделив обе части этого исходного уравнения на G, мы оставим только P на одной стороне уравнение, которое нам нужно, поскольку это значение, которое мы ищем.
\frac{P}{100}=\frac{50}{200}
\text{100}\times\text{50}=\text{200}\times\text{P}
\frac {\text{100}\times\text{50}}{200}=\text{P}
Наша новая, перестроенная формула: Процент (P) = Процентное значение (W) / Базовое значение (G) × 100. Вставка наших известных значений в новое уравнение дает нам: Процент = 50/200 × 100 %. Вычисление этого непосредственно превращает нашу дробь в десятичную и приводит к формуле, похожей на: Процент = 0,25 × 100 %.
Теперь все, что нам нужно сделать, это умножить 0,25 на 100 и не забыть написать % в конце. Оставив нам процентное значение 25. Таким образом, 50 (процентное значение) составляет 25% (процентное значение) от 200 (базовое значение).
Найти целое число из процентов: 50 составляет 25% от скольких?
50 — это ровно 25% «чего-то», и это что-то называется базовым значением. Вы можете рассчитать базовую стоимость либо с помощью нашего калькулятора базовой стоимости, либо научившись самостоятельно рассчитывать базовую стоимость с помощью наших формул и пояснений к калькулятору. Это очень легко, когда вы это понимаете!
Это очень легко, когда вы это понимаете!
\text{Базовое значение (G)}=\frac{\text{Процентное значение (W)}}{\text{Процентное значение (P)}}\times\text{100 }
Откройте для понимания формулу:
Базовое значение (G) обозначает целое, к которому относится процент. Другими словами, базовое значение составляет 100 процентов. Выраженное более сложным образом, основное значение (G) получается путем деления процентного значения (W) на процентное значение (P) и последующего умножения на 100. Визуализируя это, мы получаем следующее:
\frac{25} {100}=\frac{50}{G}
\text{100}\times\text{50}=\text{G}\times\text{25}
\frac{\text{100}\ раз\текст{50}}{25}=\текст{G}
Однако вы также можете упростить себе задачу, разбив ее на части. На вопрос «50 — это 25% от какого значения?» мы знаем, что основное значение (G) — это значение, которое мы ищем. Процентное значение (W) равно 50, процентное значение (P) равно 25%, и мы можем вспомнить, что наша исходная формула 100 x W = G x P. Поскольку мы ищем G, мы можем разделить на P, поэтому G изолирован на одной стороне уравнения, что приводит к следующей измененной формуле: Базовое значение (G) = Процентное значение (W)/ Процент (P) × 100 %.
Процентное значение (W) равно 50, процентное значение (P) равно 25%, и мы можем вспомнить, что наша исходная формула 100 x W = G x P. Поскольку мы ищем G, мы можем разделить на P, поэтому G изолирован на одной стороне уравнения, что приводит к следующей измененной формуле: Базовое значение (G) = Процентное значение (W)/ Процент (P) × 100 %.
Ввод наших известных значений в это дает нам: Базовое значение (G) = 50/25 x 100. Преобразование дроби в ее целочисленный эквивалент приводит к нашей формуле, выглядящей следующим образом: Базовое значение (G) = 2 x 100. Теперь, что это в его простейшей форме, непосредственное выполнение математики оставляет нам базовое значение 200. Итак, теперь мы можем с уверенностью сказать, что 50 (значение в процентах) составляет 25% (в процентах) от 200 (базовое значение)!
От одного значения к другому: 200 на сколько процентов больше/меньше 50?
При сравнении двух значений друг с другом часто интересует процентная разница между числами. Так, например, если вы хотите определить, мужчин в компании на 30% больше, чем женщин, или в этом году на федеральные выборы пришло на 28% меньше людей, чем в прошлом году. Еще одним реальным примером может быть сравнение размеров обуви. Например, переходя от размера женской обуви от 7 к 8, понимая, что разница между указанными размерами обуви составляет 0,25 дюйма, и желая узнать, какому проценту соответствует эта разница.
Так, например, если вы хотите определить, мужчин в компании на 30% больше, чем женщин, или в этом году на федеральные выборы пришло на 28% меньше людей, чем в прошлом году. Еще одним реальным примером может быть сравнение размеров обуви. Например, переходя от размера женской обуви от 7 к 8, понимая, что разница между указанными размерами обуви составляет 0,25 дюйма, и желая узнать, какому проценту соответствует эта разница.
В вопросе косвенно проводится различие, когда хотят узнать, насколько одно значение больше другого и на какой процент. А также вопрос, на сколько процентов уменьшается переход от одного значения к другому.
С помощью нашего калькулятора соотношения стоимости к стоимости вы можете легко рассчитать эти процентные различия. Кроме того, просмотр формул под этим калькулятором поможет вам научиться выполнять математические расчеты самостоятельно.
Формула для конкретного случая: Насколько больше 200 по сравнению с 50 процентами?
\text{Увеличение в процентах (P)}=\frac{\text{Высокое значение (X)}}{\text{Низкое значение (Y)}}-\text{1}
Формула для конкретного случая: Сколько меньше 50 по сравнению с 200 процентами мудрым?
\text{Процентное сокращение (P)}=\frac{\text{Нижнее значение (X)}}{\text{Высокое значение (Y)}}-\text{1}
Откройте для понимания формулы:
Насущный вопрос: каков процент снижения при переходе с [ 200 ] на [ 50 ]?
Другими словами, мы ищем разницу в процентах. Формула для процентов была упомянута выше и может быть представлена следующим образом:
Формула для процентов была упомянута выше и может быть представлена следующим образом:
Процент (P) = значение в процентах (W) / базовое значение (G) x 100
Для случая: «Насколько больше 200 по сравнению с 50 процентами?» Мы знаем, что базовое значение равно 50, а процентное значение равно 200. Если мы подставим эти значения в формулу, мы получим:
Процент (P) = 200/50 x 100
200 разделить на 50 равно 4, что дает нам…
Процент (P) = 4 x 100
Таким образом, получается:
Процент (P)=400%
Будьте осторожны! Это тот ответ, который мы ищем? Нет, мы еще не закончили. Расчетный процент (т. е. пропорция 200 к 50) равен 400%. Однако мы хотим рассчитать увеличение или уменьшение стоимости. Для этого нам все еще нужно вычесть базовое значение (100%) из 400%, которые мы получили в результате наших расчетов. Другими словами, происходит увеличение на 400% – 100% = 300% при переходе от 50 к 200.
Снова показано в виде формулы:
Процент (P) = 400% – 100%
Процент (P) = 300%
Формула ведет себя аналогично для редукций. Для случая: «Насколько меньше 50 по сравнению с 200 процентами?» Базовое значение равно 200, а процентное значение равно 50. Просто подставив эти значения в формулу, показанную выше, вы получите решение -75%. Здесь стоит знак «минус», потому что мы наблюдаем уменьшение/уменьшение стоимости. Метод расчета будет выглядеть так:
Для случая: «Насколько меньше 50 по сравнению с 200 процентами?» Базовое значение равно 200, а процентное значение равно 50. Просто подставив эти значения в формулу, показанную выше, вы получите решение -75%. Здесь стоит знак «минус», потому что мы наблюдаем уменьшение/уменьшение стоимости. Метод расчета будет выглядеть так:
Проценты (P) = 50/200 x 100
Проценты (P) = 25 %
После этого
Проценты (P) = 25–100 %
Или Проценты (P) = -75 %
Сложение/вычитание процентов : Сколько будет 50 плюс/минус 25% от 50?
Если свитер стоит 50 долларов и я получу скидку 25%, сколько он будет стоить (включая скидку)?
Давайте начнем с того, что мы знаем, 50% от 100 равно 50, и прибавить или вычесть это из 100 легко:
Сложение: Прибавление 50% от 100 к 100 дает нам 150
Вычитание: Вычитание 50 % из 100 до 100 дает нам 50
Другой простой пример… Добавление или вычитание 100 % из 100 до 100:
Сложение: Добавление 100 % из 100 дает нам 200 , и
Вычитание: Вычитание 100% из 100 до 100 дает нам 0.
навыки и умения. Если вы один из них, не волнуйтесь, мы поможем вам с расчетом. Вы можете либо использовать наши процентные надбавки и калькуляторы скидок для расчета уменьшения или увеличения стоимости, либо вы можете узнать, как работает расчет, прочитав наши связные формулы и подробные объяснения под калькулятором.
Формула для конкретного случая: Сколько будет 50 плюс 25% от 50?
\text{Процентное значение (W)}=\text{Базовое значение}\times(\text{100\%}+\text{Процент})
Формула для конкретного случая: Сколько будет 50 минус 25% от 50 ?
\text{Процентное значение (W)}=\text{Базовое значение}\times(\text{100\%}-\text{Процент})
Откройте для понимания формулы:
Наш вопрос под рукой : Если свитер стоит 50 долларов, и я получу скидку 25%, сколько он будет стоить (включая скидку)?
Упрощая текст задачи, мы действительно смотрим, сколько будет 50 плюс/минус 25% от 50?
Плюс/надбавка: Сколько будет 100% + 25% (от 50) = 125% (в процентах) от 50 (базовое значение)?
Вычесть/уменьшить: сколько будет 100% – 25% (от 50) = 75% (в процентах) от 50 (базовое значение)?
Значит ищем процент! Опять же, мы можем использовать стандартную формулу, чтобы найти значение в процентах (W) = базовое значение (G) × процент (P) / 100%.
Для случая: «Сколько будет 50 плюс 25% от 50?»
Базовое значение равно 50, а процентное значение равно 125% (как рассчитано в предыдущих строках текста выше). Если мы подставим эти значения в формулу, мы получим:
Процентное значение (W) = 50 × 125 %/ 100%
Примечание: 125 разделить на 100 равно 1,25.
Теперь мы можем использовать это и сказать,
Процентное значение (W) = 50 × 1,25, что дает нам
Процентное значение (W) = 62,5
50 (базовое значение) плюс 25% (проценты), следовательно, 62,5 ( процентное значение).
Формула та же для сокращений:
Для случая «Сколько будет 50 минус 25% (от 50)?»
Базовое значение равно 50, а процентное значение равно 75%.
Опять же, эти значения должны быть вставлены в ранее показанную формулу. Процентное значение (W) = 50 x 75 %/100 % или Процентное значение (W) = 50 x 0,75.
Результат, таким образом, Процентное значение (W) = 37,5.
Чтобы связать все это с нашим примером постановки задачи: свитер, который изначально стоил 50 долларов, теперь стоит 37,50 долларов с 25-процентной скидкой. Настоящая сделка!
Настоящая сделка!
Нахождение начальных значений: 200 на 25% больше/меньше какого значения?
Прежде чем заняться нашей основной проблемой, давайте рассмотрим более простой случай. 200 на 100% больше, чем какое значение? 200 в два раза больше, чем 100, то есть на 100% больше. Итак, ответ 100. Если это все еще немного запутанно, не стесняйтесь использовать наш процентный калькулятор «найти базовое значение» или прочитать наши формулы и пояснения, чтобы понять, как работают указанные расчеты.
Это будет формула для вопроса 200 на 25% больше, чем какое значение:
\text{Базовое значение (G)}=\frac{\text{Процентное значение (W)}}{\text{100 }\%+\text{Процентное значение (P)}}
А это формула для вопроса: 200 на 25% меньше, чем значение:
\text{Базовое значение (G)}=\frac{\text{Процентное значение (W)}}{\text{100}\%-\text{ Процент (P)}}
Откройте для понимания формулу:
Вопрос: 200 на 25% больше/меньше какого значения?
Глядя на эту постановку задачи в процентах, возникает вопрос, сколько будет 100% + 25% = 125% (в процентах) или 100% – 25% = 75% (в процентах) от 200 (значение в процентах).
Проще говоря, мы ищем основное значение. Мы уже знаем формулу для расчета базового значения: Базовое значение (G) = Процентное значение (W)/ Процентное значение (P) x 100
Для случая, когда нас спрашивают: «200 на 25% больше, чем какое значение ?» Процентное значение (W) равно 200, а процентное значение (P) равно 125%. Если мы подставим эти значения в формулу, мы получим: Базовое значение (G) = 200/125 x 100, а 200, деленное на 125, равно 1,6. Это означает, что наше базовое значение (G) = 1,6 x 100, и, таким образом, мы получаем, что базовое значение (G) = 160,
Следовательно, 200 (значение в процентах) на 25% (в процентах) больше, чем 160 (искомое базовое значение).
На вопрос «200 на 25% меньше, чем какое значение?»
Формула ведет себя аналогично:
Процентное значение снова равно 200, но на этот раз процент составляет 75%. Если вы введете эти значения в формулу, показанную выше, результат будет 266,67.
Также стоит прочитать
- Калькулятор скидок при покупках
- Сравнение размеров упаковок
Калькулятор процентов с подробным объяснением
- Калькуляторы
- ::
- Номера
- ::
- Калькулятор процентов
Этот онлайн-калькулятор решает четыре основных типа задач на проценты и задачу на увеличение/уменьшение процентов. Калькулятор создаст пошаговое объяснение для каждого типа процентной задачи.
Калькулятор создаст пошаговое объяснение для каждого типа процентной задачи.
Что такое % из ?
Номер это какой процент ?
Номер является % от какого числа?
На какое процентное увеличение/уменьшение по сравнению с к ?
работающий…
Полиномиальные калькуляторы
Факторные полиномы
- Полиномиальные корни
- Синтетический отдел
- Полиномиальные операции
- Графические полиномы
- Расширить и упростить
- Генерировать из корней
Рациональные выражения
Упрощение
- Умножение/деление
- Сложение/вычитание
Подкоренные выражения
Рационализировать знаменатель
- Упрощение
Решение уравнений
Квадратные уравнения (с шагами)
- Полиномиальные уравнения
- Решение уравнений — с шагами
Квадратное уравнение
Решение (с шагами)
- Квадратичный плоттер
- Факторинг трехчленов
Геометрия
Равносторонний треугольник
- Прямоугольный треугольник
- Косой треугольник
- Калькулятор площади
- Калькулятор прямоугольника
- Калькулятор круга
Калькулятор шестиугольника
- Калькулятор ромба
Комплексные номера
Модуль, обратный, полярная форма
- Подразделение
- Упростить выражение
Системы уравнений
Система 2×2
- Система 3х3
- Система 4×4
Матрицы
Векторы (2D и 3D)
- Сложить, вычесть, умножить
- Калькулятор определителя
- Матрица обратная
- Характеристический полином
- собственные значения
- Собственные векторы
- Разложение матрицы
Расчетные калькуляторы
Калькулятор лимита
- Калькулятор производных
- Интегральный калькулятор
Последовательности и серии
Арифметические последовательности
- Геометрические последовательности
- Найти n й Срок
Аналитическая геометрия
Расстояние и середина
- Калькулятор треугольника
- Графические линии
- Пересечение линий
- Двухточечная форма
- Расстояние от линии до точки
- Параллельно/Перпендикулярно
- Уравнение окружности
- Круг из 3 точек
- Пересечение круговой линии
Тригонометрия
Градусов в Радиан
- Триггер Уравнения
Номера
Длинная дивизия
- Вычислить выражения
- Калькулятор дробей
- Наибольший общий делитель НОД
- Наименее распространенное кратное LCM
- Простые множители
- Научная нотация
- Калькулятор процентов
- Dec / Bin / Hex
- Калькулятор вероятности
- Распределения вероятностей
Описательная статистика
- Стандартное отклонение
- Z — Калькулятор очков
- Нормальное распределение
- Калькулятор Т-теста
- Корреляция и регрессия
Финансовые калькуляторы
Простые проценты
- Сложные проценты
- Калькулятор амортизации
- Калькулятор ренты
Прочие калькуляторы
Наборы
Проблемы с работой
примеры
пример 1:ex 1:
Вычислите 45% от 120.

 15% от числа равно 2.2 × 15 = 33.
15% от числа равно 2.2 × 15 = 33.





 25, что на 25% больше еженедельных расходов на питание.
25, что на 25% больше еженедельных расходов на питание.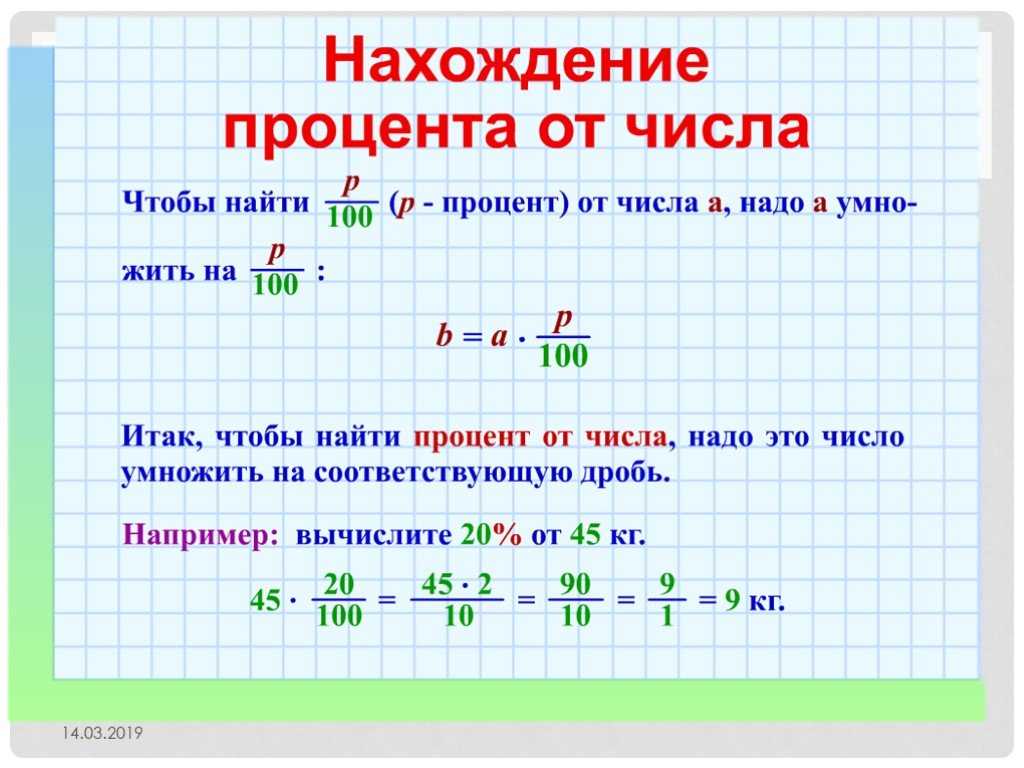
 E)
E)

 7%
7% Я хотел бы получить известие от вас по адресу
Я хотел бы получить известие от вас по адресу