Калькулятор ранг матрицы методом окаймляющих миноров онлайн калькулятор: Ранг матрицы | Онлайн калькулятор

метод окаймляющих миноров, приведение к ступенчатому виду

В данной публикации мы рассмотрим определение ранга матрицы, а также методы, с помощью которых его можно найти. Также разберем примеры для демонстрации применения теории на практике.

• Определение ранга матрицы
• Нахождение ранга матрицы
  • Метод окаймляющих миноров
  • Приведение матрицы к ступенчатому виду

Определение ранга матрицы

Ранг матрицы – ранг ее системы строк или столбцов. В любой матрице есть ее строчный и столбцовый ранги, которые равны между собой.

Ранг системы строк – это максимальное количество линейно-независимых строк. Аналогичным образом определяется ранг системы столбцов.

Примечания:

• Ранг нулевой матрицы (обозначается символом “θ“) любого размера равняется нулю.
• Ранг любого ненулевого вектора-строки или вектора-столбца равняется единице.
• Если в матрице любых размеров присутствует хотя бы один элемент, не равный нулю, значит ее ранг не меньше единицы.
• Ранг матрицы не больше её минимальной размерности.
• Элементарные преобразования, выполненные над матрицей, не меняют её ранга.

Нахождение ранга матрицы

Метод окаймляющих миноров

Ранг матрицы равняется максимальному порядку ненулевого минора.

Алгоритм следующий: находим миноры от низших порядков к высоким. Если минор n-го порядка не равняется нулю, а все последующие (n+1) равны 0, значит ранг матрицы равен n.

Пример
Чтобы было понятнее, давайте разберем практический пример и найдем ранг матрицы A ниже, пользуясь методом окаймляющих миноров.

Решение
Мы имеем дело с матрицей 4×4, следовательно, ее ранг не может быть выше 4. Также в матрице присутствуют ненулевые элементы, значит, ее ранг не меньше единицы. Итак, приступим:

1. Начинаем проверять миноры второго порядка. Для начала берем две строки первого и второго столбцов.

Минор равняется нулю.

Следовательно переходим к следующему минору (первый столбец остается, а вместо второго берем третий).

Минор равен 54≠0, следовательно ранг матрицы не меньше двух.

Примечание: Если бы и этот минор оказался равным нулю, мы бы дальше проверили следующие комбинации:

Если требуется, перебор можно аналогичным образом продолжить со строками:

• 1 и 3;
• 1 и 4;
• 2 и 3;
• 2 и 4;
• 3 и 4.

Если бы все миноры второго порядка оказались равными нулю, то ранг матрицы равнялся бы одному.

2. Нам удалось почти сразу найти минор, который нам подходит. Поэтому переходим к минорам третьего порядка.

К найденному минору второго порядка, который дал отличный от нуля результат, добавляем одну строку и один из столбцов, выделенных зеленым цветом (начнем со второго).

Минор оказался равным нулю.

Следовательно меняем второй столбец на четвертый. И со второй попытки нам удается найти минор, не равный нулю, значит ранг матрицы не может быть меньше 3.

Примечание: если бы результат снова оказался равным нулю, вместо второй строки мы бы дальше взяли четвертую и продолжили бы поиски “хорошего” минора.

3. Теперь остается определить миноры четвертого порядка с учетом найденного ранее. В данном случае он один, который совпадает с определителем матрицы.

Минор равняется 144≠0. А это значит, что ранг матрицы A равняется 4.

Приведение матрицы к ступенчатому виду

Ранг ступенчатой матрицы равняется количеству её ненулевых строк. То есть все, что нам нужно сделать – это привести матрицу к соответствующему виду, например, с помощью элементарных преобразований, которые, как мы уже упомянули выше, не меняют ее ранг.

Пример
Найдем ранг матрицы B ниже. Мы не берем слишком сложный пример, т.к. наша основная цель – это просто продемонстрировать применение метода на практике.

Решение
1. Сначала вычтем из второй строки удвоенную первую.

2. Теперь отнимем из третьей строки первую, умноженную на четыре.

Таким образом, мы получили ступенчатую матрицу, в которой количество ненулевых строк равняется двум, следовательно ее ранг, также, равен 2.

Ранг матрицы и способы его вычисления

Рангом матрицы называется наивысший порядок отличных от нуля миноров. Его обозначают через или .

СВОЙСТВА РАНГА МАТРИЦЫ

1. Ранг матрицы равен нулю только для нулевой матрицы. В других случаях ранг матрицы равен некоторому положительном числу.

2. Ранг прямоугольной матрицы не превышает меньшего из двух чисел и т.е. .

3. Для квадратной матрицы -го порядка только тогда, когда матрица невырожденная.

4. В случае квадратной матрицы если то определитель матрицы равен нулю.

При нахождении ранга матрицы, как правило, нужно вычислять большое количество определителей. Чтобы облегчить задачу студентам давным-давно найдены элементарные преобразования с помощью которых можно слегка поменяв вид матрицы без вычисления определителей посчитать ранг.

ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ МАТРИЦЫ

1. Транспонирование, т.е. замена каждой строки столбцом с тем же номером и наоборот.

2. Перестановка двух строк или двух столбцов.

3. Умножение всех элементов строки или столбца на любое число не равное нулю.

4. Добавление всех элементов строки или столбца соответствующих элементов параллельного ряда, умноженного на одно и то же число.

Матрицы, полученные одна из второй элементарными преобразованиями называются эквивалентными. Эквивалентные матрицы не равны друг другу, но при элементарных преобразованиях матрицы ее ранг не меняется. Если матрицы и эквивалентны то это записывается так:

Рассмотрим два основных метода нахождения ранга матрицы.

Первый метод –- метод окантовки — заключается в следующем:

Если все миноры 1-го порядка, т.е. элементы матрицы равны нулю, то .

Если хоть один из миноров 1-го порядка не равен нулю, а все миноры 2-го порядка равны нулю то .

Если минор 2-го порядка отличен от нуля то исследуем миноры 3-го порядка. Таким образом находят минор -го порядка и проверяют, не равны ли нулю миноры -го порядка.

Если все миноры -го порядка равны нулю, то ранг матрицы равен числу . Такие миноры -го порядка, как правило, находят путем «окантовки» минора -го порядка.

Второй метод определения ранга матрицы заключается в применении элементарных преобразований матрицы при возведении ее к диагональному виду. Ранг такой матрицы равно числу отличных от нуля диагональных элементов.

Рассмотрим примеры применения каждого метода.

—————————————————

Пример 1.

Задание. Найти ранг матрицы методом окантовки.

Решение. Матрица содержит ненулевые элементы миноры 1-го порядка, следовательно ее ранг может быть равен единице. Согласно правила ранг матрицы не превышает трем . Минор 2-го порядка

равен нулю, но следующий минор

отличен от нуля. Окантовывая минор второго порядка проверим третий: для этого разложим его по третьей колонке

Рассмотрим минор четвертого порядка, окантовывает настоящее

Он равен нулю, поскольку последняя строка нулевой.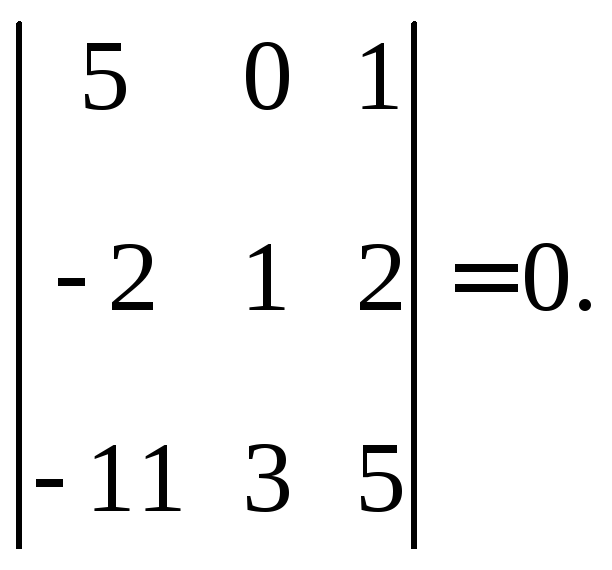 Остается вычислить еще один минор

Искомый ранг матрицы равен четырем (). На примере можно видеть, что выбор окантовки не всегда можно удачно выбрать и нужно числить большое количество миноров.

—————————————————

Пример 2.

Задание. Найти ранг матрицы .

Решение.

1.Переставим четвертый столбец на первое место, а все остальные сместим вправо.

2. Превратим в ноль все элементы в первой строке после . Для этого к столбцам добавим первый умноженный на соответственно.

3. Третий столбец поделим на . К четвертого и пятого столбцов добавим третий, умноженный на .

4. До пятого столбца добавим четвертый, умноженный на .

5. Переставим третий и четвертый столбцы на второе и третье места, а второй столбец на место четвертого.

В исходной матрицы вычеркнут последний столбец с нулевыми элементами

Ранг эквивалентной матрицы равен четырем, а следовательно и . Можно заметить, что матрицы в первом и втором примерах эквивалентные между собой (имеют одинаковые ранги).

—————————————————————

Ставки пособий — Компенсация

Вниманию пользователей АТ. Чтобы получить доступ к меню на этой странице, выполните следующие действия. 1. Пожалуйста, выключите режим автоматических форм. 2. Нажмите Enter, чтобы развернуть пункт главного меню («Здоровье», «Преимущества» и т. д.). 3. Чтобы войти и активировать ссылки подменю, нажмите стрелку вниз. Теперь вы сможете использовать вкладку или стрелку вверх или вниз по параметрам подменю, чтобы получить доступ/активировать ссылки подменю.

Введите текст поискаКнопка для начала поиска

• карта сайта [a-z]

ВА » Администрация по выплате пособий ветеранам » Компенсация » Ставки пособий

 

Ставки пособий

Доступ к текущим ставкам

Выберите программу компенсации ниже, чтобы просмотреть текущие ставки.

Исторические ставки также связаны со страницей текущих ставок.

• Текущие ставки компенсационных выплат ветеранам
• Специальная ежемесячная компенсация (SMC) Текущие ставки
• Компенсация от иждивенцев (DIC) Текущие ставки
• Текущие ставки DIC для родителей
• Автомобильное пособие, пособие на одежду и почетные ставки
• Врожденные дефекты (расщепление позвоночника, дети женщин-ветеранов Вьетнама) Показатели

Узнайте больше о ставках компенсации VA

• Как VA рассчитывает ставки компенсации
• Корректировка стоимости жизни (COLA)
• Комбинированные рейтинги

Как VA рассчитывает компенсационные ставки

Сумма базового пособия варьируется в зависимости от того, насколько вы инвалидны. VA принимает решение о серьезности вашей инвалидности на основании доказательств, которые вы предоставляете в рамках своего заявления, или которые VA получает из ваших военных документов.

VA оценивает инвалидность от 0% до 100% с шагом 10% (например, 10%, 20%, 30% и т. д.). См. раздел «Комбинированные рейтинги» ниже для получения информации о том, как VA рассчитывает процент инвалидности для нескольких видов инвалидности.

В некоторых случаях вам могут быть выплачены дополнительные суммы, если:

• У вас очень серьезная инвалидность или потеря конечностей
• у вас есть супруг(а), ребенок(и) или родитель(и) на иждивении
• у вас супруг(а) с серьезной инвалидностью

Корректировки на стоимость жизни (COLA)

Периодически VA вносит коррективы в стоимость жизни (COLA) в компенсационные и пенсионные пособия для VA, чтобы гарантировать, что покупательная способность пособий VA не будет подорвана инфляцией. В соответствии с федеральным законом корректировки стоимости жизни для компенсаций и пенсий VA составляют тот же процент, что и для пособий по социальному обеспечению. Вы можете узнать больше о COLA на веб-странице COLA Администрации социального обеспечения.

Комбинированные рейтинги

Если VA обнаружит, что у ветерана несколько видов инвалидности, VA использует приведенную ниже таблицу комбинированных рейтингов для расчета комбинированного рейтинга инвалидности. Рейтинги инвалидности не суммируются, а это означает, что если у ветерана одна инвалидность оценивается в 60%, а вторая инвалидность составляет 20%, общий рейтинг не составляет 80%. Это связано с тем, что последующие оценки инвалидности применяются к уже инвалидному ветерану, поэтому 20% инвалидности применяются к ветерану, инвалидность которого уже составляет 60%. Ниже вы найдете шаги, предпринимаемые VA для комбинирования рейтингов более чем одной инвалидности, и примеры использования таблицы комбинированных рейтингов, иллюстрирующие, как рассчитываются комбинированные рейтинги.

1. Инвалидность сначала располагается в точном порядке их серьезности, начиная с наибольшей инвалидности, а затем комбинируется с использованием Комбинированной таблицы оценок ниже
2. Степень одной инвалидности будет указана в левой колонке, а степень другой — в верхней строке, в зависимости от того, что подходит
3. Цифры, появляющиеся в пространстве, где пересекаются столбец и строка, представляют собой объединенное значение двух
4. Это комбинированное значение округляется до ближайших 10%
5. Если имеется более двух ограничений, общее значение для первых двух будет найдено, как описано выше для двух ограничений
6. Точное суммарное значение (пока без округления), совмещенное со степенью третьей инвалидности
7. Этот процесс продолжается для последующих инвалидностей, и окончательное число округляется до ближайших 10%

Примеры объединения двух видов инвалидности

Если ветеран имеет 50-процентную инвалидность и 30-процентную инвалидность, общее значение будет равно 65 процентам, но 65 процентов должны быть преобразованы в 70 процентов, чтобы представить окончательную степень инвалидности. инвалидность.

Точно так же, с инвалидностью 40 процентов и другой инвалидностью 20 процентов, общее значение равно 52 процентам, но 52 процента необходимо преобразовать в ближайшую степень, кратную 10, что составляет 50 процентов.

Пример объединения трех инвалидностей

Если есть три инвалидности, оцениваемые в 60 процентов, 40 процентов и 20 процентов соответственно, объединенное значение для первых двух будет найдено напротив 60 и менее 40 и составит 76 процентов. Эти 76 будут находиться в левом столбце, а рейтинг 20 — в верхнем ряду. Пересечение этих двух оценок равно 81. Таким образом, итоговая оценка будет округлена до 80%.

Таблица I. Комбинированные рейтинги Таблица
[10 в сочетании с 10 равно 19]

	10	20	30	40	50	60	70	80	90
19	27	35	43	51	60	68	76	84	92
20	28	36	44	52	60	68	76	84	92
21	29	37	45	53	61	68	76	84	92
22	30	38	45	53	61	69	77	84	92
23	31	38	46	54	62	69	77	85	92
24	32	39	47	54	62	70	77	85	92
25	33	40	48	55	63	70	78	85	93
26	33	41	48	56	63	70	78	85	93
27	34	42	49	56	64	71	78	85	93
28	35	42	50	57	64	71	78	86	93
29	36	43	50	57	65	72	79	86	93
30	37	44	51	58	65	72	79	86	93
31	38	45	52	59	66	72	79	86	93
32	39	46	52	59	66	73	80	86	93
33	40	46	53	60	67	73	80	87	93
34	41	47	54	60	67	74	80	87	93
35	42	48	55	61	68	74	81	87	94
36	42	49	55	62	68	74	81	87	94
37	43	50	56	62	69	75	81	87	94
38	44	50	57	63	69	75	81	88	94
39	45	51	57	63	70	76	82	88	94
40	46	52	58	64	70	76	82	88	94
41	47	53	59	65	71	76	82	88	94
42	48	54	59	65	71	77	83	88	94
43	49	54	60	66	72	77	83	89	94
44	50	55	61	66	72	78	83	89	94
45	51	56	62	67	73	78	84	89	95
46	51	57	62	68	73	78	84	89	95
47	52	58	63	68	74	79	84	89	95
48	53	58	64	69	74	79	84	90	95
49	54	59	64	69	75	80	85	90	95
50	55	60	65	70	75	80	85	90	95
51	56	61	66	71	76	80	85	90	95
52	57	62	66	71	76	81	86	90	95
53	58	62	67	72	77	81	86	91	95
54	59	63	68	72	77	82	86	91	95
55	60	64	69	73	78	82	87	91	96
56	60	65	69	74	78	82	87	91	96
57	61	66	70	74	79	83	87	91	96
58	62	66	71	75	79	83	87	92	96
59	63	67	71	75	80	84	88	92	96
60	64	68	72	76	80	84	88	92	96
61	65	69	73	77	81	84	88	92	96
62	66	70	73	77	81	85	89	92	96

Таблица I – Таблица комбинированных характеристик (продолжение)

	10	20	30	40	50	60	70	80	90
63		67	70	74	78	82	85	89	93	96
64	68	71	75	78	82	86	89	93	96
65	69	72	76	79	83	86	90	93	97
66	69	73	76	80	83	86	90	93	97
67	70	74	77	80	84	87	90	93	97
68	71	74	78	81	84	87	90	94	97
69	72	75	78	81	85	88	91	94	97
70	73	76	79	82	85	88	91	94	97
71	74	77	80	83	86	88	91	94	97
72	75	78	80	83	86	89	92	94	97
73	76	78	81	84	87	89	92	95	97
74	77	79	82	84	87	90	92	95	97
75	78	80	83	85	88	90	93	95	98
76	78	81	83	86	88	90	93	95	98
77	79	82	84	86	89	91	93	95	98
78	80	82	85	87	89	91	93	96	98
79	81	83	85	87	90	92	94	96	98
80	82	84	86	88	90	92	94	96	98
81	83	85	87	89	91	92	94	96	98
82	84	86	87	89	91	93	95	96	98
83	85	86	88	90	92	93	95	97	98
84	86	87	89	90	92	94	95	97	98
85	87	88	90	91	93	94	96	97	99
86	87	89	90	92	93	94	96	97	99
87	88	90	91	92	94	95	96	97	99
88	89	90	92	93	94	95	96	98	99
89	90	91	92	93	95	96	97	98	99
90	91	92	93	94	95	96	97	98	99
91	92	93	94	95	96	96	97	98	99
92	93	94	94	95	96	97	98	98	99
93	94	94	95	96	97	97	98	99	99
94	95	95	96	96	97	98	98	99	99

ЧИСЛЕННЫЙ ВЫЧИСЛ ХАРАКТЕРИСТИЧЕСКИХ ЗНАЧЕНИЙ ВЕЩЕСТВЕННОЙ СИММЕТРИЧНОЙ МАТРИЦЫ (Технический отчет)

ЧИСЛЕННЫЙ ВЫЧИСЛ ХАРАКТЕРИСТИЧЕСКИХ ЗНАЧЕНИЙ ВЕЩЕСТВЕННОЙ СИММЕТРИЧНОЙ МАТРИЦЫ (Технический отчет) | ОСТИ. GOV

перейти к основному содержанию

• Полная запись
• Другое связанное исследование

Авторов:

Гивенс, В.

Дата публикации:

1954-03-01

Исследовательская организация:

Национальная лаборатория Ок-Ридж.

Идентификатор ОСТИ:

4412175

Номер(а) отчета:

ОРНЛ-1574

Номер АНБ:

НСА-08-002936

Номер контракта с Министерством энергетики:  

W-7405-ENG-26

Тип ресурса:

Технический отчет

Отношение ресурсов:

Прочая информация: ориг. Дата получения: 31-DEC-54

Страна публикации:

США

Язык:

Английский

Тема:

ФИЗИКА; СОБСТВЕННЫЕ ЗНАЧЕНИЯ; МАТЕМАТИКА; МАТРИЦЫ; ЦИФРЫ

---

Форматы цитирования

• MLA
• АПА
• Чикаго
• БибТекс

Гивенс В. ЧИСЛЕННОЕ ВЫЧИСЛЕНИЕ ХАРАКТЕРИСТИЧЕСКИХ ЗНАЧЕНИЙ ВЕЩЕСТВЕННОЙ СИММЕТРИЧНОЙ МАТРИЦЫ . США: Н. П., 1954. Веб. дои: 10.2172/4412175.

Копировать в буфер обмена

Гивенс, В. ЧИСЛЕННОЕ ВЫЧИСЛЕНИЕ ХАРАКТЕРИСТИЧЕСКИХ ЗНАЧЕНИЙ ВЕЩЕСТВЕННОЙ СИММЕТРИЧНОЙ МАТРИЦЫ . Соединенные Штаты. https://doi.org/10.2172/4412175

Копировать в буфер обмена

Гивенс, В. 1954. «ЧИСЛЕННЫЙ ВЫЧИСЛ ХАРАКТЕРИСТИЧЕСКИХ ЗНАЧЕНИЙ ВЕЩЕСТВЕННОЙ СИММЕТРИЧНОЙ МАТРИЦЫ». Соединенные Штаты. https://doi.org/10.2172/4412175. https://www.osti.gov/servlets/purl/4412175.

Копировать в буфер обмена

@статья{osti_4412175,
title = {ЧИСЛЕННОЕ ВЫЧИСЛЕНИЕ ХАРАКТЕРИСТИЧЕСКИХ ЗНАЧЕНИЙ ВЕЩЕСТВЕННОЙ СИММЕТРИЧНОЙ МАТРИЦЫ},
автор = {Гивенс, В.},
abstractNote = {},
дои = {10.2172/4412175},
URL-адрес = {https://www.osti.gov/biblio/4412175}, журнал = {},
номер =,
объем = ,
место = {США},
год = {1954},
месяц = ​​{3}
}

Копировать в буфер обмена

---

Посмотреть технический отчет (7,90 МБ)

https://doi.