Калькулятор решение тригонометрических уравнений онлайн: Решение тригонометрических уравнений | Онлайн калькулятор

Тригонометрический калькулятор решает тригонометрические функции онлайн

Калькулятор онлайн на нашем сайте легко и быстро решает тригонометрические функции, вам не понадобится таблица тригонометрических функций, вы можете навсегда забыть, что такое таблица Брадиса! Online калькулятор позволяет решать и самые простые задачи (например, найти косинус или синус угла), и сложные выражения с использованием обратных и гиперболических функций тригонометрии.

Кнопки калькулятора для решения тригонометрических функций

Тригонометрический калькулятор может осуществлять вычисления как в градусах, так и в радианах. Таким образом, найти косинус угла можно вне зависимости от единицы измерения, в которой он задан. Это очень удобно и экономит массу времени при ёмких расчётах. Прежде чем приступить к вычислениям, нужно на панели управления указать, какая единица измерения углов будет использоваться: градусы (Deg) или радианы (Rad).

Выбор единицы измерения угла

Обратите внимание, что в одной операции нельзя использовать разные единицы измерения углов, другими словами выражение «сумма синус 30 градусов и косинус пи =» будет посчитано неверно!

Простейшие тригонометрические функции

Простейшие тригонометрические функции: синус — sin (α), косинус — cos (β) и тангенс — tan (y). Рядом указаны их обозначения так, как они используются в калькуляторе (в зарубежной литературе тангенс сокращенно обозначается tan, в русской — tg).

Кнопки калькулятора: Простые тригонометрические функции

Функция косинуса является чётной, поэтому её значение для отрицательного угла будет положительным. Синус, тангенс и котангенс — нечётные тригонометрические функции, соответственно, значения тригонометрических функции для отрицательных углов также будут отрицательными.

Онлайн калькулятор сам учитывает чётность тригонометрических функций при умножении и делении. Вам не потребуется постоянно обращать внимание на соблюдение правила знаков.

Пример вычислений с простыми тригонометрическими функциями

Происхождение термина «синус» — история интересная. Первыми это понятие ввели индусы. На санскрите звучит как «ардхаджива», в переводе означает «ардха» — половина, «джива» — тетива лука (которую напоминает хорда). Позднее перешли на короткое название — «джива».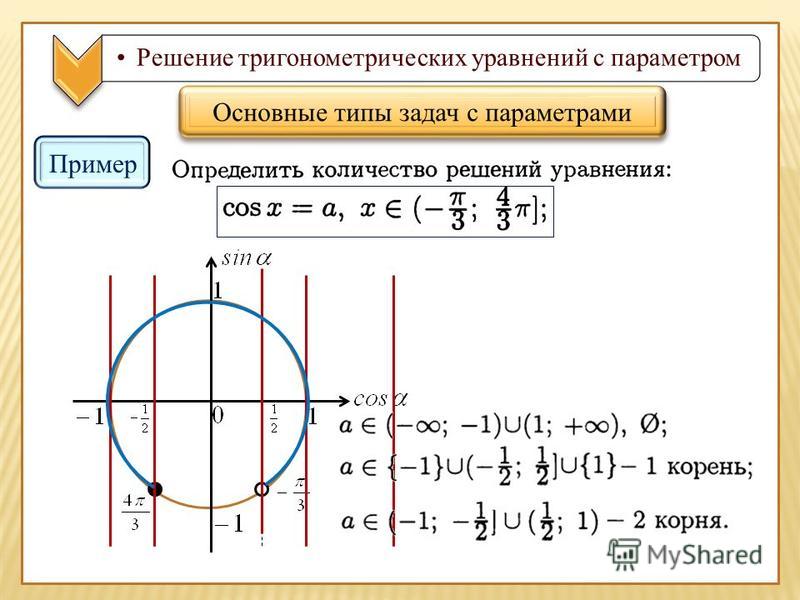 Арабские математики и астрономы, перенявшие знания по тригонометрии от индийцев, транскрибировали слово арабскими буквами, получилось «джиба». В силу особенностей арабского языка слово стали произносить как «джайб» (что значит «выпуклость», «пазуха»). При переводе арабских тестов на латынь «джайб» перевели дословно: на латинском «выпуклость, пазуха» обозначалось словом «синус». Именно так мы до сих пор называем линию синуса.

Обратные тригонометрические функции

Обратные тригонометрические функции: арксинус — asin(), арккосинус — acos() и арктангенс atan().

Кнопки калькулятора: Обратные тригонометрические функции

Если не вдаваться в формулы и подробности относительно единичной окружности, то обратные тригонометрические функции можно объяснить на простом примере: арккосинус x — это угол, косинус которого равен x. Обратные тригонометрические функции являются многозначными, и одному значению аргумента принадлежит множество значений самой функции.

Пример выражения с обратными тригонометрическими функциями

Гиперболические функции

Гиперболические функции: гиперболический синус — sinh(), гиперболический косинус — cosh () и гиперболический тангенс tanh (). Гиперболические (круговые) функции — семейство элементарных тригонометрических функций, выраженных через экспоненту.

Кнопки калькулятора: Гиперболические тригонометрические функции

Пример решения гиперболической функции

Обратные гиперболические функции: гиперболический арксинус — asinh(), гиперболический арккосинус — acosh() и гиперболический арктангенс — atanh().

Кнопки калькулятора: Обратные гиперболические функции

Пример решения обратной гиперболической функции

Если вам понравился онлайн калькулятор тригонометрических функций:

• добавьте его в закладки, он вам ещё не раз пригодится!
• сохраните и поделитесь этой страничкой в социальных сетях. Бесплатный калькулятор онлайн — это самое простое вычисление тригонометрических функций!
• порекомендуйте его тем, кому может понадобиться калькулятор тригонометрических функций, доступный в режиме онлайн!

Калькулятор Инструкция — обзор всех функций калькулятора и общая справка, как пользоваться калькулятором.

Исследовательский проект «Визуализированная алгоритмизация тригонометрических уравнений с отбором корней на C#» • Наука и образование ONLINE

Автор: Георгий Михайлович Васильев

Место работы/учебы (аффилиация): Международный образовательный комплекс «Гармония — школа №97», г.Ижевск, 10 класс

С каждым годом информационные технологии всё сильнее проникают в нашу жизнь. Если в 2006 году количество принятых вакансий IT сферы составило всего 41 тысячу, то 2021 это число увеличилось до невообразимых 240 тысяч. То есть за какие-то 15 лет информационные технологии развились настолько, что необходимость квалифицированных специалистов растёт в геометрической прогрессии.

Конечно же, информационный прогресс не может не повлиять на жизнь населения многих стран, в том числе и на детей. Дети нового поколения рождаются в веке информационных технологий, со всех сторон они окружены различными устройствами, которые так или иначе упрощают нашу жизнь. Но как это сказывается на самом поколении? Кто-то скажет, что оно потеряно, и вырастут лишь одни лоботрясы и лентяи, однако на практике подрастающие дети сильно заинтересованы окружающими их технологиями.

В качестве доказательства можно привести рейтинг результатов Единого Государственного Экзамена по предмету «Информатика и ИКТ», напрямую связанного с информационными технологиями. В 2010 его выбрали 62652 человека (≈7% от общего количества сдающих), а в 2020 уже 83610 (≈14% от общего количества сдающих). Несмотря на невысокое численное повышение сдающих, процентное соотношения возросло в целых 2 раза. Объясняется это понижением общего количества подрастающего поколения в 2020 году, из-за чего экзамен в этом году сдавало на 33% меньше выпускников.

Ещё 20-30 лет назад каждый школьник мечтал о собственной ЭВМ, способной в миг решить за них любую задачу из алгебры или геометрии. С массовым внедрением калькуляторов, эти мечты частично осуществились, ведь сейчас каждый школьник может не только ждать и надеяться, что такое устройство появится, но и может запрограммировать его сам. Программирование преподаётся во многих школах России, существует множество курсов и возможностей самому осуществлять собственные мечты в реальность, это и заманивает столько новых людей в IT сферу.

С другой стороны, такие приложения, как например, PhotoMath, способное вычислять примеры, решать уравнения и неравенства практически любой сложности, уже созданы и многие считают, что незачем изобретать уже изобретённый велосипед. Но не стоит забывать, что приложения не всесильны, и даже команда лучших разработчиков и математиков могут упустить некоторые типы заданий, которые не могут быть решены иным приложением.

При использовании PhotoMath, я столкнулся с проблемой отсутствия возможности задавать числовой промежуток при решении тригонометрических уравнений, что не позволяло быстро и точно проверить собственные ответы.

Поэтому мне пришла идея написать собственный «калькулятор», который помог бы студентам и школьникам с решением и проверкой этих уравнений.

Проблема: можно ли запрограммировать решение тригонометрических уравнений с возможностью отбора корней,  и на каком языке программирования это будет лучше всего реализовать.

Объект: программирование и один из разделов математики – тригонометрия.

Предмет исследования: тригонометрические уравнения из ЕГЭ.

Цель: написать программу для решения максимально возможного количества тригонометрических уравнений с возможностью отбора корней.

Задачи:

1. Проанализировать существующие виды тригонометрических уравнений из ЕГЭ за последние 10 лет.
2. Провести сравнительный анализ подходящих языков программирования.
3. Создать оконную оболочку для записи уравнения.
4. Написать универсальный код для решения тригонометрических уравнений

Методы: теоретический анализ и синтез, классификация и обобщение  материала, сравнение наиболее подходящих языков программирования.

Решатель тригонометрических уравнений — онлайн-калькулятор триггеров

Поиск инструмента

Найдите инструмент в dCode по ключевым словам:

Просмотрите полный список инструментов dCode

Решатель тригонометрических уравнений

Инструмент / решатель для решения одного или нескольких тригонометрических уравнений, уравнений с неизвестными переменными и cos, sin, tan и т. д.

Результаты

Решатель тригонометрических уравнений — dCode

Метки: Символьные вычисления

Поделиться

dCode и другие

dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Решение триггерного уравнения

Тригонометрическое уравнение для решения (по одному в строке)
2cos(x)=pi/4
Переменные

Набор областей решения

R (действительные числа) Z (целые числа) C (сложные)

Форсировать результаты как числовые значения

См.

также: Решатель уравнений — Решатель неравенств — Решатель дифференциальных уравнений

Ответы на вопросы (FAQ)

Что такое тригонометрическое уравнение?

Тригонометрическое уравнение — это математическое выражение с равенством двух элементов, содержащее неизвестные переменные и тригонометрические функции (cos, sin, tan и т. д.).

Пример: $ \cos(x) = sin(\pi) $

Как решить тригонометрическое уравнение?

dCode автоматически решает тригонометрические уравнения (с = символ равенства) и вычисляет значения неизвестных.

Поддерживаются все тригонометрические функции: sin() , cos() , tan() , а также тригонометрические обратные функции acos() , arcsin() и так далее. а также гиперболические функции cosh() , sinh() и т. д.

Пример: $ \sin(x) = 0 $ возвращает решение $ x = 0 $ (радиан)

Некоторые уравнения будет иметь бесконечное число решений (по модулю $\pi$ или $2\pi$ или с константами $c_i$)

Все углы указаны в радианах.

Как решить несколько тригонометрических уравнений?

Несколько триггерных уравнений с одинаковыми переменными можно комбинировать с помощью логического оператора И : && или ⋀ .

Кроме того, любой новый возврат линии будет рассматриваться как новое уравнение.

Как шаг за шагом решить триггерное уравнение?

Решатель dCode не отображает шаги расчета, поскольку они отражают не шаги человеческого мышления, а шаги машинного мышления (побитовые двоичные вычислительные операции), далекие от ручного разрешения. dCode позволяет проверить результат.

Исходный код

dCode сохраняет за собой право собственности на исходный код «Решателя тригонометрических уравнений». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Решатель тригонометрических уравнений», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Тригонометрического уравнения». Функции Solver (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, сценарий или доступ к API для «Решателя тригонометрических уравнений» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!

Напоминание: dCode можно использовать бесплатно.

Cite dCode

Копирование и вставка страницы «Решатель тригонометрических уравнений» или любых ее результатов разрешено, если вы цитируете dCode!
Цитировать как источник (библиографию):
Средство решения тригонометрических уравнений на dCode.fr [онлайн-сайт], получено 30 октября 2022 г., https://www.dcode.fr/trig-equation-solver

Резюме

• Решение тригонометрического уравнения
• Что такое тригонометрическое уравнение?
• Как решить тригонометрическое уравнение?
• Как решить несколько тригонометрических уравнений?
• Как шаг за шагом решить триггерное уравнение?

Similar pages

• Differential Equation Solver
• Inequality Solver
• Equation Solver
• Math Expression Simplifier
• Polynomial Factorization
• Boolean Minterms and Maxterms
• Gaussian Elimination
• DCODE’S TOOLS LIST

Support

• Paypal
• Patreon
• More

 

Forum/Help

Keywords

equation,trig,trigonometric,trigonometry,equality,equal,unknown,variable,cos,sin,tan

Links

▲

Решатель тригонометрических уравнений — онлайн-калькулятор триггеров

Поиск инструмента

Найдите инструмент в dCode по ключевым словам:

Просмотрите полный список инструментов dCode

Решатель тригонометрических уравнений

Инструмент / решатель для решения одного или нескольких тригонометрических уравнений, уравнений с неизвестными переменными и cos, sin, tan и т. д. dCode и многое другое

dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Решение триггерного уравнения

Тригонометрическое уравнение для решения (по одному в строке)
2cos(x)=pi/4
Переменные

Набор областей решения

R (действительные числа) Z (целые числа) C (сложные)

Преобразовать результаты в числовые значения

См. также: Решатель уравнений — Решатель неравенств — Решатель дифференциальных уравнений

Ответы на вопросы (FAQ)

Что такое тригонометрическое уравнение?

Тригонометрическое уравнение — это математическое выражение с равенством двух элементов, содержащее неизвестные переменные и тригонометрические функции (cos, sin, tan и т. д.).

Пример: $ \cos(x) = sin(\pi) $

Как решить тригонометрическое уравнение?

dCode автоматически решает тригонометрические уравнения (с символом равенства = ) и вычисляет значения неизвестных.

Поддерживаются все тригонометрические функции: sin() , cos() , tan() , а также тригонометрические обратные функции acos() , arcsin() и так далее. а также гиперболические функции cosh() , sinh() , и т. д.

Пример: $ \sin(x) = 0 $ возвращает решение $ x = 0 $ (радиан)

Некоторые уравнения могут иметь бесконечное число решения (по модулю $\pi$ или $2\pi$ или с константами $c_i$)

Все углы указаны в радианах.

Как решить несколько тригонометрических уравнений?

Несколько триггерных уравнений с одинаковыми переменными можно комбинировать с помощью логического оператора И : && или ⋀ .

Кроме того, любой новый возврат линии будет рассматриваться как новое уравнение.

Как шаг за шагом решить триггерное уравнение?

Решатель dCode не отображает шаги расчета, поскольку они отражают не шаги человеческого мышления, а шаги машинного мышления (побитовые двоичные вычислительные операции), далекие от ручного разрешения. dCode позволяет проверить результат.

Исходный код

dCode сохраняет за собой право собственности на исходный код «Решателя тригонометрических уравнений». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Решатель тригонометрических уравнений», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Тригонометрического уравнения». Функции Solver (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т.