ln 0 5
Вы искали ln 0 5? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и ln калькулятор, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «ln 0 5».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как ln 0 5,ln калькулятор,ln калькулятор онлайн,ln онлайн,ln онлайн калькулятор,вычисление логарифма натурального онлайн,вычисление натурального логарифма онлайн,вычислить логарифм натуральный,вычислить логарифм натуральный онлайн,вычислить логарифм натуральный онлайн калькулятор,вычислить натуральный логарифм онлайн,вычислить натуральный логарифм онлайн калькулятор,как посчитать логарифм натуральный,как считать логарифм натуральный,калькулятор ln,калькулятор ln онлайн,калькулятор логарифма натурального,калькулятор логарифмов натуральных,калькулятор натурального логарифма,калькулятор натуральный логарифм,калькулятор натуральных логарифмов,калькулятор натуральных логарифмов онлайн,калькулятор онлайн натуральные логарифмы,логарифм ln онлайн калькулятор,логарифм натуральный онлайн,логарифм натуральный онлайн калькулятор,логарифм онлайн калькулятор ln,найти логарифм натуральный онлайн,найти натуральный логарифм онлайн,натуральные логарифмы калькулятор онлайн,натуральные логарифмы онлайн калькулятор,натуральный логарифм вычислить онлайн,натуральный логарифм калькулятор,натуральный логарифм калькулятор онлайн,натуральный логарифм найти онлайн,натуральный логарифм онлайн,натуральный логарифм онлайн калькулятор,натуральный логарифм посчитать,натуральный логарифм посчитать онлайн,онлайн ln,онлайн вычисление натурального логарифма,онлайн калькулятор ln,онлайн калькулятор натуральный логарифм,онлайн калькулятор натуральных логарифмов,посчитать логарифм натуральный,посчитать натуральный логарифм,посчитать натуральный логарифм онлайн,расчет логарифма натурального онлайн,расчет натурального логарифма онлайн,решение логарифмов натуральных онлайн,решение натуральных логарифмов онлайн,решение онлайн натуральных логарифмов.
Где можно решить любую задачу по математике, а так же ln 0 5 Онлайн?
Решить задачу ln 0 5 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Калькулятор логарифмов. Решение логарифмов онлайн
Данная страница рассматривает калькулятор логарифмов — ещё одну функцию в богатом арсенале, которым располагает бесплатный калькулятор на нашем сайте. Калькулятор, считающий логарифмы онлайн, станет незаменимым помощником для тех, кому нужно простое решение математических выражений. В нашем калькуляторе любой может легко и быстро посчитать логарифм, не зная логарифмических формул, и даже не представляя суть логарифма.
Калькулятор, считающий логарифмы онлайн, станет незаменимым помощником для тех, кому нужно простое решение математических выражений. В нашем калькуляторе любой может легко и быстро посчитать логарифм, не зная логарифмических формул, и даже не представляя суть логарифма.
Буквально 20-30 лет назад решение логарифмов требовало серьезных знаний в математике и как минимум умения пользоваться таблицей логарифмов или логарифмической линейкой. Чтобы привести к табличному виду исходное выражение, часто приходилось осуществлять сложные преобразования, учитывая свойства логарифмов и их функций.
Сегодня же достаточно иметь доступ в интернет, чтобы без труда вычислять всевозможные логарифмические уравнения и неравенства любой сложности. Размещенный на нашем сайте калькулятор онлайн может любой логарифм вычислить за одно мгновение! Используйте этот простой способ решения — вычисление логарифмов онлайн! Лучше добавить калькулятор в закладки и в социальные сети, наверняка найдётся причина открыть его ещё раз.
Решение логарифма logyx сводится к нахождению ответа на вопрос, в какую степень требуется возвести основание логарифма y, чтобы получилось значение равное x. Онлайн калькулятор логарифмов поможет рассчитать все виды логарифмов: двоичные, десятичные и натуральные логарифмы, а также логарифм комплексного числа и логарифм отрицательного числа и др.
Вычисление логарифмов в online калькуляторе записывается как log и выполняется с помощью четырёх кнопок: нахождение двоичного логарифма, решение десятичных логарифмов, с произвольным основанием и вычисление натурального логарифма.
Кнопки, позволяющие вычислить логарифм онлайн
И десятичный логарифм калькулятор посчитает, и натуральный логарифм калькулятор найдёт!
Некоторые кнопки могут использоваться для записи одного и того же действия. Возьмём, к примеру, расчёт логарифмов с произвольным основанием. Понятно что, если указать основание 10, то рассчитается десятичный логарифм, а если 2, то двоичный.
- 1. используя кнопку log, тогда нужно указать только число
- 2. с помощью кнопки logyx, через запятую указываются число и основание логарифма
- 3. внести обозначение логарифма вручную
Подробная информация о том, как работать с клавиатурой калькулятора, а также обзор всех его возможностей, можно найти на странице Функции калькулятора.
Логарифмы примеры решения в калькуляторе
Логарифм по основанию 2
Используйте эту кнопку, чтобы рассчитать логарифм, основание которого равно двум (его также называют двоичный логарифм).
В строке ввода отобразится запись log2(x) , соответственно, вам остаётся внести число, без указания основания, и произвести расчёт. В примере найден ответ, чему равен логарифм 8 по основанию 2.
Логарифм по основанию 2
Десятичный логарифм 10
Эта кнопка поможет найти логарифм числа по основанию 10.
Логарифм десятичный онлайн калькулятор обозначает записью log(x x,y). На рисунке рассчитано, чему равен десятичный логарифм числа 10000.
Логарифм по основанию 10
Натуральный логарифм
Клавишей ln выполняется решение натуральных логарифмов, основанием которых является число е. Основание натурального логарифма е — число Эйлера — равно 2.71828182845905.
Онлайн калькулятор можно определить, чему равен натуральный логарифм любого числа. На рисунках в качестве примера найдены значения натурального логарифма: слева — ln логарифм числа 8, справа — натуральный логарифм от числа 50.
Натуральные логарифмы примеры решения
Как решать логарифмы с произвольным основанием
Конечно, калькулятор, позволяет решить логарифм онлайн не только по определенному, но по любому основанию. Чтобы найти значение логарифмов с произвольным основанием для любого числа, используйте предназначенную для этого кнопочку logyx, она подставляет в строке ввода запись log(x x,y).
Чтобы найти значение логарифмов с произвольным основанием для любого числа, используйте предназначенную для этого кнопочку logyx, она подставляет в строке ввода запись log(x x,y).
Определение логарифма числа
Калькулятор Инструкция — обзор основых и дополнительных функций калькулятора и общая информация о том, как пользоваться калькулятором.
Решение логарифмов в онлайн калькуляторе
Данная страница рассматривает способы решения логарифмов, как еще одну функцию в богатом арсенале, которым располагает бесплатный калькулятор на нашем сайте. Калькулятор, считающий логарифмы онлайн, станет незаменимым помощником для тех, кому нужно простое решение математических выражений. В нашем калькуляторе любой может легко и быстро посчитать логарифм, не зная логарифмических формул, и даже не представляя суть логарифма.
Буквально 20-30 лет назад решение логарифмов требовало серьезных знаний в математике и как минимум умения пользоваться таблицей логарифмов или логарифмической линейкой. Чтобы привести к табличному виду исходное выражение, часто приходилось осуществлять сложные преобразования, учитывая свойства логарифмов и их функций.
Чтобы привести к табличному виду исходное выражение, часто приходилось осуществлять сложные преобразования, учитывая свойства логарифмов и их функций.
Сегодня же достаточно иметь доступ в интернет, чтобы без труда вычислять всевозможные логарифмические уравнения и неравенства любой сложности. Размещенный на нашем сайте онлайн калькулятор может любой логарифм вычислить за одно мгновение!
Решение логарифма logyx сводится к нахождению ответа на вопрос, в какую степень требуется возвести основание логарифма y, чтобы получилось значение равное x. Онлайн калькулятор логарифмов поможет рассчитать все виды логарифмов: двоичные, десятичные и натуральные логарифмы, а также логарифм комплексного числа и логарифм отрицательного числа и др.
Вычисление логарифмов в online калькуляторе записывается как log и выполняется с помощью четырех кнопок: нахождение двоичного логарифма, решение десятичных логарифмов, с произвольным основанием и вычисление натурального логарифма.
Некоторые кнопки могут использоваться для записи одного и того же действия. Возьмем, к примеру, расчет логарифмов с произвольным основанием. Понятно что, если указать основание 10, то рассчитается десятичный логарифм, а если 2, то двоичный. Учитывая, что математическое выражение можно и вручную набрать, тогда тот же самый десятичный логарифм посчитать можно тремя способами (точнее записать эту операцию в калькуляторе):
- используя кнопку log, тогда нужно указать только число,
- с помощью кнопки logyx, через запятую указываются число и основание логарифма,
- внести обозначение логарифма вручную.
Подробную информацию о том, как работать с клавиатурой калькулятора, а также обзор всех его возможностей, можно найти на страницах кнопки калькулятора и функции калькулятора.
Логарифм по основанию 2
Используйте эту кнопку, чтобы рассчитать логарифм, основание которого равно двум (его также называют двоичный логарифм).
В строке ввода отобразится запись log2(x), соответственно, вам остается внести число, без указания основания, и произвести расчет. В примере найден ответ, чему равен логарифм 8 по основанию 2.
Логарифм по основанию 2:
Десятичный логарифм
Эта кнопка поможет найти логарифм числа по основанию 10.
Логарифм десятичный онлайн калькулятор обозначает записью log(x x,y). На рисунке рассчитано, чему равен десятичный логарифм числа 10000.
Логарифм по основанию 10:
Натуральный логарифм
Клавишей ln выполняется решение натуральных логарифмов, основанием которых является число е. Основание натурального логарифма е — число Эйлера — равно 2.71828182845905.
Онлайн калькулятор может определить, чему равен натуральный логарифм любого числа. На рисунках в качестве примера найдены значения натурального логарифма: слева — ln логарифм числа 8, справа — натуральный логарифм от числа 50.
Натуральные логарифмы, примеры решения:
Как решать логарифмы с произвольным основанием?
Конечно, калькулятор, позволяет решить логарифм онлайн не только по определенному, но по любому основанию. Чтобы найти значение логарифмов с произвольным основанием для любого числа, используйте предназначенную для этого кнопочку logyx, она подставляет в строке ввода запись log(x x,y).
Определение логарифма числа:
Все функции нашего бесплатного калькулятора собраны в одном разделе. Функции онлайн калькулятора >>
Натуральный логарифм Ln — онлайн калькулятор, формула, график
Simple and best practice solution for ln=4 equation. Check how easy it is, and learn it for the future. Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework.Vitaly Velygo. Чему равен Ln4? Чему равен Ln4?Natural Logarithm Calculator — ln(x).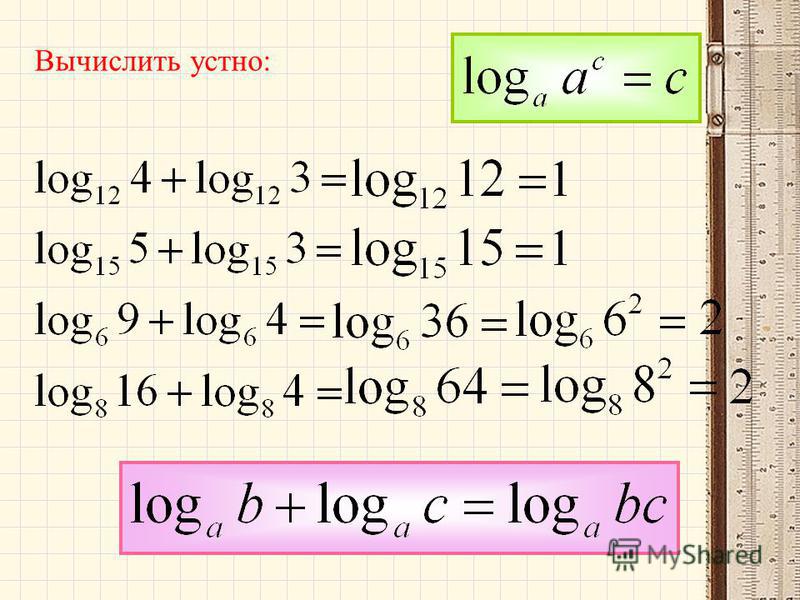 2-9) — YouTube
2-9) — YouTube
4 Timber Ln, Greenville, SC 29609 — MLS #1443587
65 Homestead Ln Rentals — Springville, AL — RENTCafé
9 Meadow Ln #4, Highland Heights, KY 41076 Listing Details …
How to calculate ln(4) without a calculator — Quora
1420 Scarcroft Ln Nashville TN — MLS #2251287
1360 E Oakmont Ln, Fruit Heights, UT 84037 — MLS #1740250
Logarithm at the End of Multiplication
Производная натурального логарифма и логарифма по основанию a. Калькулятор онлайн
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной
как предела отношения приращения к приращению аргумента появились таблица производных и
точно определённые правила дифференцирования. Первыми на ниве нахождения производных
потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
Таблица производных простых функций
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т. е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т. е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6. Найти производную функции
Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Доказательство и вывод формул производной натурального логарифма и логарифма по основанию a. Примеры вычисления производных от ln 2x, ln 3x и ln nx. Доказательство формулы производной логарифма n-го порядка методом математической индукции.
Вывод формул производных натурального логарифма и логарифма по основанию a
Производная натурального логарифма от x равна единице, деленной на x:
(1) (ln
x)′ = .
Производная логарифма по основанию a равна единице, деленной на переменную x, умноженную на натуральный логарифм от a
:
(2) (log
a x)′ = .
Доказательство
Пусть есть некоторое положительное число, не равное единице. Рассмотрим функцию, зависящую от переменной x
,
которая является логарифмом по основанию :
Рассмотрим функцию, зависящую от переменной x
,
которая является логарифмом по основанию :
.
Эта функция определена при .
Найдем ее производную по переменной x
.
По определению, производная является следующим пределом:
(3) .
Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам. Для этого нам нужно знать следующие факты:
А) Свойства логарифма . Нам понадобятся следующие формулы:
(4) ;
(5) ;
(6) ;
Б) Непрерывность логарифма и свойство пределов для непрерывной функции:
(7) .
Здесь — некоторая функция, у которой существует предел и этот предел положителен.
В) Значение второго замечательного предела:
(8) .
Применяем эти факты к нашему пределу. Сначала преобразуем алгебраическое выражение
.
Для этого применим свойства (4) и (5).
.
Воспользуемся свойством (7) и вторым замечательным пределом (8):
.
И, наконец, применим свойство (6):
.
Логарифм по основанию e называется натуральным логарифмом . Он обозначается так:
.
Тогда ;
.
Тем самым мы получили формулу (2) производной логарифма.
Производная натурального логарифма
Еще раз выпишем формулу производной логарифма по основанию a
:
.
Эта формула имеет наиболее простой вид для натурального логарифма, для которого ,
.
Тогда
(1) .
Из-за такой простоты, натуральный логарифм очень широко используется в математическом анализе и в других разделах математики, связанных с дифференциальным исчислением. Логарифмические функции с другими основаниями можно выразить через натуральный логарифм, используя свойство (6):
.
Производную логарифма по основанию можно найти из формулы (1), если вынести постоянную за знак дифференцирования:
.
Другие способы доказательство производной логарифма
Здесь мы предполагаем, что нам известна формула производной экспоненты:
(9) .
Тогда мы можем вывести формулу производной натурального логарифма, учитывая, что логарифм является обратной функцией к экспоненте.
Докажем формулу производной натурального логарифма, применив формулу производной обратной функции :
.
В нашем случае .
Обратной функцией к натуральному логарифму является экспонента:
.
Ее производная определяется по формуле (9). Переменные можно обозначить любой буквой. В формуле (9), заменим переменную x на y:
.
Поскольку ,
то
.
Тогда
.
Формула доказана.
Теперь докажем формулу производной натурального логарифма с помощью правила дифференцирования сложной функции . Поскольку функции и являются обратными друг к другу, то
.
Дифференцируем это уравнение по переменной x
:
(10) .
Производная от икса равна единице:
.
Применяем правило дифференцирования сложной функции :
.
Здесь .
Подставим в (10):
.
Отсюда
.
Пример
Найти производные от ln 2x, ln 3x и ln nx .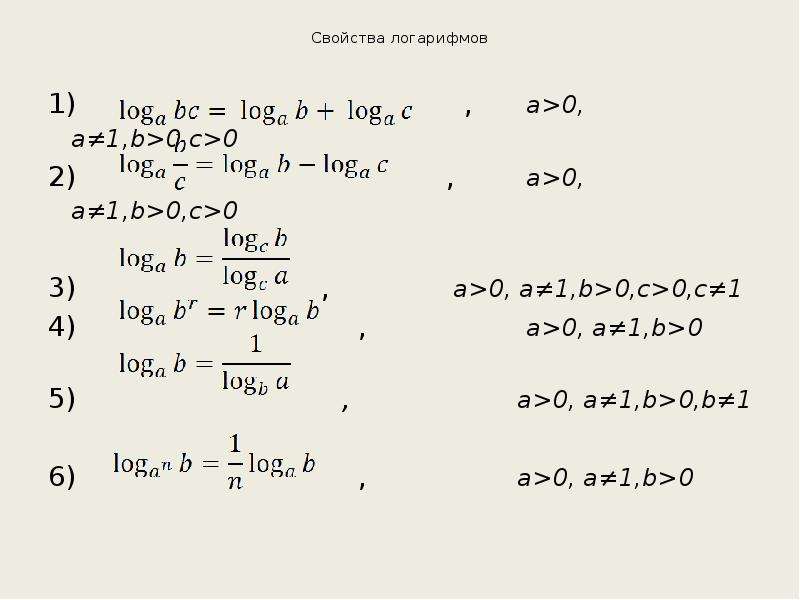
Решение
Исходные функции имеют похожий вид. Поэтому мы найдем производную от функции y = ln nx . Затем подставим n = 2 и n = 3 . И, тем самым, получим формулы для производных от ln 2x и ln 3x .
Итак, ищем производную от функции
y = ln nx .
Представим эту функцию как сложную функцию, состоящую из двух функций:
1) Функции ,
зависящей от переменной :
;
2) Функции ,
зависящей от переменной :
.
Тогда исходная функция составлена из функций и :
.
Найдем производную от функции по переменной x:
.
Найдем производную от функции по переменной :
.
Применяем формулу производной сложной функции .
.
Здесь мы подставили .
Итак, мы нашли:
(11) .
Мы видим, что производная не зависит от n
.
Этот результат вполне естественен, если преобразовать исходную функцию, применяя формулу логарифма от произведения:
.
— это постоянная. Ее производная равна нулю. Тогда по правилу дифференцирования суммы имеем:
Тогда по правилу дифференцирования суммы имеем:
.
Ответ
; ; .
Производная логарифма модуля x
Найдем производную от еще одной очень важной функции — натурального логарифма от модуля x
:
(12) .
Рассмотрим случай .
Тогда и функция имеет вид:
.
Ее производная определяется по формуле (1):
.
Теперь рассмотрим случай .
Тогда и функция имеет вид:
,
где .
Но производную этой функции мы также нашли в приведенном выше примере. Она не зависит от n
и равна
.
Тогда
.
Объединяем эти два случая в одну формулу:
.
Соответственно, для логарифма по основанию a
,
имеем:
.
Производные высших порядков натурального логарифма
Рассмотрим функцию
.
Мы нашли ее производную первого порядка:
(13) .
Найдем производную второго порядка:
.
Найдем производную третьего порядка:
.
Найдем производную четвертого порядка:
.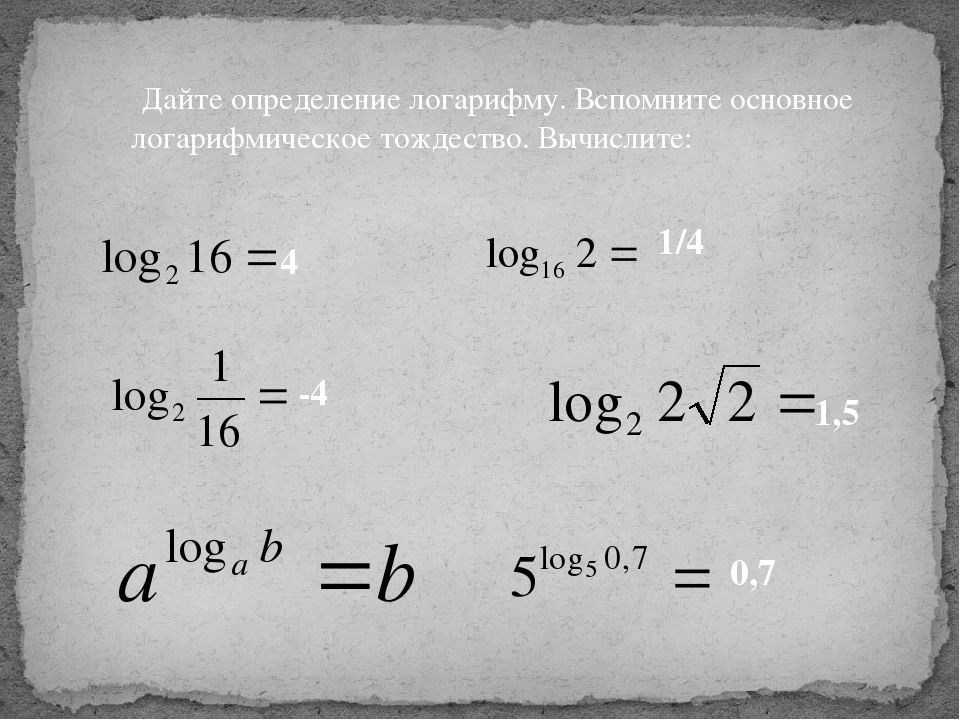
Можно заметить, что производная n-го порядка имеет вид:
(14) .
Докажем это методом математической индукции.
Доказательство
Подставим в формулу (14) значение n = 1:
.
Поскольку ,
то при n = 1 ,
формула (14) справедлива.
Предположим, что формула (14) выполняется при n = k . Докажем, что из этого следует, что формула справедлива при n = k + 1 .
Действительно, при n = k
имеем:
.
Дифференцируем по переменной x
:
.
Итак, мы получили:
.
Эта формула совпадает с формулой (14) при n = k + 1 .
Таким образом, из предположения, что формула (14) справедлива при n = k
следует, что формула (14) справедлива при n = k + 1 .
Поэтому формула (14), для производной n-го порядка, справедлива для любых n .
Производные высших порядков логарифма по основанию a
Чтобы найти производную n-го порядка от логарифма по основанию a
,
нужно выразить его через натуральный логарифм:
.
Применяя формулу (14), находим n-ю производную:
.
Определение. Пусть функция \(y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \(x_0 \). Дадим аргументу приращение \(\Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции \(\Delta y \) (при переходе от точки \(x_0 \) к точке \(x_0 + \Delta x \)) и составим отношение \(\frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \(\Delta x \rightarrow 0 \), то указанный предел называют производной функции \(y=f(x) \) в точке \(x_0 \) и обозначают \(f»(x_0) \).
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f»(x_0) $$
Для обозначения производной часто используют символ y». Отметим, что y» = f(x) — это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых существует указанный выше предел. Эту функцию называют так: производная функции у = f(x) .
Геометрический смысл производной состоит в следующем.2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \). Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Сформулируем его.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение \(x \), найти \(f(x) \)
2. Дать аргументу \(x \) приращение \(\Delta x \), перейти в новую точку \(x+ \Delta x \), найти \(f(x+ \Delta x) \)
3. Найти приращение функции: \(\Delta y = f(x + \Delta x) — f(x) \)
4. Составить отношение \(\frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.
Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f»(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство \(\Delta y \approx f»(x) \cdot \Delta x \). Если в этом равенстве \(\Delta x \) устремить к нулю, то и \(\Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке .
Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.
Еще один пример. Функция \(y=\sqrt{x} \) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и \(f»(0) \)
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием . При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями.2} $$
Рекомендуем также
Преобразование выражений с использованием свойств логарифмов: примеры, решения
Если у нас есть выражение, содержащее логарифмы, то мы можем преобразовать его с учетом свойств этих логарифмов. В этом материале мы рассмотрим основные правила, по которым осуществляется данное преобразование.
В первом пункте приведем основные свойства логарифмов, представив их в виде списка. Далее рассмотрим характерные примеры преобразований с использованием этих свойств. Отдельно остановимся на числовых выражениях и на выражениях с переменными, а также посмотрим, как преобразовывать примеры с использованием модуля.
Свойства логарифмов
Чтобы преобразовывать выражения с логарифмами, обычно используют выражение, называемое основным логарифмическим тождеством: alogab=b, a>0, a≠1, b>0. Также нужно помнить следующие свойства:
Определение 1- loga1=0 при любом a>0, a≠1.
- logaa=1, если a>0, a≠1.
- logaa=1logaa=1 при любом a>0, a≠1.
- logaa=1, если a>0, a≠1.
- logaap=p, при этом a>0, a≠1 и p может быть любым действительным числом.
- loga(x·y)=logax+logay, a>0, a≠1, x>0, y>0. В обобщенном виде это свойство можно представить как loga(x1·x2·…·xn)=logax1+logax2+…+logaxn, a>0, a≠1, x1>0, x2>0, …, xn>0
- ) logaxy=logax-logay.
- logaxy=logax-logay , при этом a>0, a≠1, x>0, y>0.
- logaxy=logax-logay , a>0, a≠1, x>0, y>0.
- logabp=p·logab, при этом a>0, a≠1, b>0, а p может быть любым действительным числом.
- это свойство является следствием предыдущего: logabn=1n·logab , a>0, a≠1, n может быть любым натуральным числом больше 1, b>0.
- logab=logcblogca , при этом a>0, a≠1, b>0, c>0, c≠1.
- свойство, также являющееся следствием: logab=1logba , где a>0, a≠1, b>0, b≠1.
- logaqbp=pq·logab , a>0, a≠1, b>0, p и q могут быть любыми действительными числами, q≠0
- logaqbp=pq , a>0, a≠1, p и q – любые действительные числа, q≠0.
- logaq ap=pq, blogac=clogab , при этом a>0, a≠1, b>0, c>0.
Преобразовывая выражения, мы можем использовать данные равенства как справа налево, так и наоборот. Учить их все наизусть нет необходимости, достаточно знать основные свойства логарифмов и несколько других свойств, например, что bn=b1n , если b≥0. Из них можно вывести остальные свойства. Само решение, правда, при этом будет несколько длиннее. Например, если мы не знаем следствия logaqbp=pq·logab и используем только основные свойства логарифмов, нам нужно будет выполнить несколько последовательных преобразований:
logaq bp=logabploga aq=p·logabq=pq·logab
То же относится и к последнему свойству из списка, выраженному формулой blogac=Clogac=clogab : оно тоже может быть выведено из основных свойств. Нужно учитывать, что если у нас есть степень положительного числа с логарифмом в показателе, то мы всегда можем поменять число под логарифмом и основание степени местами. В принципе, на практике такие задачи встречаются не слишком часто, но мы их все же разберем.
Как преобразовать числовое выражение с логарифмом
После того, как мы вспомнили основные свойства логарифмов, покажем, как использовать их при решении задач. Начнем с того, как преобразовывать числовые выражения, потому что такие вычисления считаются более простыми. Возьмем сперва примитивные примеры, с помощью которых легко проиллюстрировать выбор нужного свойства логарифма, а потом будем наращивать сложность задач. В конце разберем задания, в которых нужно использовать сразу несколько свойств.
Как выбрать свойство логарифма для преобразования
Список свойств, приведенный в первом пункте, довольно большой, и очевидно, что нужно хорошо в нем ориентироваться, чтобы получить нужный результат. Обычно выбор делается по итогам сравнения исходного логарифма/выражения с левыми и правыми частями формул, выражающих свойства. В том случае, когда одна из частей формулы похожа на исходный логарифм или выражение, мы берем именно это свойство и выполняем преобразование с его помощью. Покажем на примерах, как именно это делается.
Для начала преобразуем выражение, используя определение логарифма, выраженное формулой alogab=b, a>0, a≠1, b>0.
Пример 1Условие: преобразуйте и вычислите значение следующих выражений: 1) 5log54 ; 2) 10lg(1+2·π), 3) 2+3log2+3 ln15 ; 4) 2log2(−7); 5) (-5)log-5 e3
Решение
В первом примере прослеживается формула alogab. У нас есть a=5, b=4, что соответствует необходимому условию a>0, a≠1, b>0. Используем нужное равенство alogab=b и получим 5log54=4.
Во втором случае a будет равно 10, b – 1+2·π. Необходимое условие выполнено, значит, мы можем записать это в виде равенства: 10lg(1+2·π) =1+2·π.
В третьем выражении у нас есть степень вида alogab, причем a=2+3 и b=ln15. Запишем: 2+3log2+3 ln15=ln15 . Хотя равенство также соответствует формуле alogab, где a равно 2, а b=-7, мы не можем воспользоваться ею для преобразования. Из-за наличия отрицательного числа под знаком логарифма выражение лишается смысла. Кроме того, -7 не соответствует условию b>0, что еще раз подтверждает, что данную формулу мы взять не можем. Следовательно, вычислить значение исходного выражения нельзя, и запись 2log2(−7) =−7 будет ошибочна.
То же самое относится и к четвертому примеру. Мы не можем записать, что -5log-5·e3=e3 , поскольку такое выражение смысла не имеет.
Ответ:1) 5log54=4; 2) 10lg(1+2·π)=1+2·π; 3) 2+3log2+3ln 15=ln 15 ; 4 и 5 — не имеют смысла.
Довольно часто в задачах встречается такой вид преобразования, когда некоторое положительно число представляют в виде степени другого числа, также положительного и не равного 1, имеющего в показателе логарифм. Основной такого преобразования также является основное определение логарифма alogab=b, a>0, a≠1, b>0, но в перевернутом виде, т.е. прочитанное справа налево, например, 3=eln3 или 5=5log55.
Далее возьмем примеры с другими свойствами логарифмов.
Пример 2Условие: вычислите, если возможно: 1) log−21, 2) log11,3) log01, 4) log71, 5) ln1, 6) lg 1,7) log3,751, 8) log5·π71.
Решение
В первых трех примерах мы видим не имеющие смысла выражения log−21, log11, log01. Основанием логарифма не может быть число меньше 1, в т.ч. 0 и отрицательные значения, т.к. для них логарифм не определен. Значит, значение этих выражений вычислить нельзя.
В других случаях логарифмы имеют подходящие основания: 7, e, 10, 3,75 и 5·π7, а под знаками логарифма везде 1. Зная соответствующее свойство логарифма (loga1=0 при любом a>0, a≠1., мы можем сделать вывод, что значения этих выражений равны 0.
Ответ: 1, 2, 3 смысла не имеют; 4) log71=0, 5) ln1=0, 6) lg1=0, 7) log3,751=0, 8) log5·e71=0.
Пример 3Условие: вычислите значения: 1) log1313 , 2) ln e, 3) lg 10,4) log5·π3−2(5·π3−2), 5) log−3(−3), 6) log11.
Решение
Нам потребуется свойство логарифма, выраженное формулой logaa=1 при a>0, a≠1. Исходные логарифмы схожи между собой в том, что их основания и числа под знаком логарифма являются одинаковыми. Казалось бы, можно сразу сделать вывод, что значения всех выражений будут равны единице, однако посмотрим внимательнее. В заданиях 1, 2, 3, 4 действительно ответом будет 1, а вот в 5 и 6 исходные выражения смысла не имеют.
Ответ: 1) log13=13=1, 2) ln e=1, 3) lg10=1, 4) log5·π3−2(5·π3−2)=1; 5,6 не имеют смысла.
Пример 4Условие: вычислите: 1) log3311, 2) log1+22(1+22)723 , 3) logπ5(π5)-2 , 4) log−10(−10)6.
Решение
Видим, что под логарифмами находятся некоторые степени основания, значит, нам нужно использовать соответствующее свойство logaap=p, где a>0, a≠1 и p будет любым действительным числом. С учетом этого можно записать следующее:
- log3311=11
- log1+22(1+2·2)723=723
- logπ5(π5)-2=-2
- для этого примера мы не можем написать такое же равенство, как и в предыдущем примере, поскольку log−10(−10)6=6 не имеет смысла.
Ответ: 1) log3311=11, 2) log1+22(1+2·2)723=723 , 3) logπ5(π5)-2=-2 , 4) не имеет смысла.
Пример 5Условие: даны выражения log2,64·127, ln2+1π и lg((−5)·(−12)). Нужно представить их как суммы или разности логарифмов по тому же основанию.
Решение
Смотрим, что находится под знаком логарифма. Там произведение, значит, берем свойство логарифма произведения: loga(x·y) = logax+logay, a>0, a≠1, x>0, y>0. В исходных примерах основания и числа в произведениях положительны, т.е. условие данного свойства соблюдено. Применим его для первого выражения:
log2,64·127=log2,6 4+log2,6127
Чтобы вычислить значение второго выражения, нам нужно свойство логарифма частного: logaxy=logax-logay, a>0, a≠1, x>0, y>0. Здесь в основании стоит положительное число e, также у нас есть положительный числитель 2+1 и знаменатель π, т.е. условия свойства соблюдены. Применяем свойство и записываем, что ln2+1π=ln2+1-ln π .
Разберем третий пример. Начнем с того, что выражение lg((−5)·(−12)) будет иметь смысл, однако формула логарифма произведения для него не подойдет, поскольку оба числа -5 и -12 отрицательны. Значит, преобразование lg((−5) ·(−12))=lg(−5)+lg(−12) не подходит. Какое же свойство тогда использовать?
Проведем предварительное преобразование, чтобы избавиться от отрицательных чисел. Далее мы подробно поговорим, когда нужно выполнять такое действие, а пока ограничимся записью самого решения, которое и так понятно: lg((−5) ·(−12))=lg(5·12)=lg5+lg12.
Ответ: 1) log2,64·127=log2,64+log2,6127 , 2) ln2+1π=ln2+1-ln π , 3) lg((−5)·(−12))=lg5+lg12.
Пример 6Условие: упростите выражения log30,25+log316+log30,5 и ln23-ln13 .
Решение
Здесь мы тоже можем использовать свойства логарифма частного и произведения по аналогии с предыдущим примером, только нам потребуется их обратная запись. Преобразуем сумму логарифмов в логарифм произведения, а разность логарифмов в логарифм частного. В итоге у нас получается в первом примере log30,25+log316+log30,5=log3(0,25·16·0,5)=log32, а во втором ln23-ln13=ln23:13=ln 2.
Ответ: 1) log30,25+log316+log30,5=log3(0,25·16·0,5)=log32, 2) ln23-ln13=ln 2 .
Пример 7Условие: есть выражения log0,7511, log3-1(3-2+5·673)5+1 и log3(−5)6. Нужно избавиться от степени в выражении под знаком логарифма.
Решение
Очевидно, что у нас здесь есть выражения вида logabp. Берем свойство, которое выражается формулой вида
logabp=p·logab, где a>0, a≠1, b>0, p — любое действительное число. Поскольку условия a>0, a≠1, b>0 выполнены, то мы можем преобразовать logabpв произведение p·logab.
- в случае с первым выражением a равно 7, b – пяти и p– 11. Тогда log0,7511=11·log0,75.
- тут a=3-1, b=3-2+5·673, p=5+1 . Нужные условия выполнены, значит, мы можем записать, что:
log3-1(3-2+5·673)5+1==5+1·log3-1(3-2+5·673) - у нас есть выражение той же структуры: logabp, a=3, b=−5, p=6, однако одно из условий не выполняется, а именно b у нас меньше 0. Значит, эту формулу мы применить не можем, и нам будет нужно предварительно преобразовать выражение под знаком логарифма. Решение будет таким: log3(−5)6=log356=6·log35.
Ответ: 1) log0,7511=11·log0,75, 2) log3-1(3-2+5·673)5+1==5+1·log3-1(3-2+5·673) 3) log3(−5)6=6·log35.
Применение формулы в обратном порядке в виде p·logab=logabp требуется довольно часто. При таком преобразовании важно соблюсти все те же условия для числовых значений переменных. Например, 3·ln 5=ln 53 и lg 2·log23=log23lg2.
Пример 8Условие: согласно таблице логарифмов, lg2≈0,3010 и lg5≈0,6990. Вычислите, сколько будет log25. Здесь же: запишите ln 11ln 3 в виде логарифма, основание которого равно 3.
Решение
Воспользуемся формулой перехода к новому основанию и представим исходный логарифм как отношение десятичных логарифмов с известными нам значениями.
log25=lg 5lg 2
Вычисляем и находим ответ: lg 5lg 2≈0,69900,3010≈2,3223 .
Во втором примере также будет достаточно формулы перехода к новому основанию, только в обратном порядке, т.е. logcblogca=logab .
Считаем: ln 11ln 3=log311
Ответ: 1) log25≈2,3223, 2) ln 11ln 3=log311 .
Мы разобрали множество примеров, где для осуществления преобразования достаточно применить одну формулу свойства логарифма или его определение. Теперь мы можем перейти к более сложным задачам, в которых нужно последовательно применять несколько свойств, а также делать дополнительные преобразования. Однако перед этим запишем еще один важный пример использования следствий из основных свойств логарифмов.
Пример 9Условие: 1) дан логарифм ln1+π7 . Необходимо избавиться от корня под знаком логарифма; 2) выполните преобразование дроби 1log25 в логарифм с основанием 4; 3) преобразуйте логарифм loge2345 так, чтобы избавиться от степени в основании; 4) вычислите, сколько будет log2-13216 ; 5) осуществите замену 2,3log73 на степень с основанием 3.
Решение
- Вспоминаем следствие из свойства логарифма степени, которое выражается формулой logabn=1n·logab .В первом случае можем сразу же подсчитать: ln1+π7=17·ln(1+π) .
- во втором случае нам понадобится формула logab=1logba , примененная в обратном порядке. Получим 1log25=log52.
- здесь нам потребуется свойство logaqbp=pq·logab . Применяем его и получаем loge2345=452·ln 3=25·ln 3.
- в этом случае нам нужно будет следствие, выраженное формулой logaqap=pq: log(2)-13216=16-13=-12
- используем формулу свойства blogac=clogab и вычисляем ответ:
2,3log7·3=3log72,3
Ответ: 1) ln1+π7=17·ln(1+π) ; 2) 1log25=log52 ; 3) loge2345=25·ln 3; 4) log(2)-13216=-12 . 5) 2,3log7·3=3log72,3 .
Задачи с применением нескольких свойств логарифмов
В действительности чаще встречаются более сложные задания, чем те, что мы разобрали в предыдущем параграфе. В них приходится выполнять преобразования в несколько шагов, применяя последовательно одно свойство за другим. Кроме того, они зачастую включают в себя необходимость раскрывать скобки, приводить подобные слагаемые, сокращать обыкновенные дроби и др. Это не так сложно, как кажется, главное – соблюдать правильную последовательность действий.
Пример 10Условие: вычислите, сколько будет (log315−log35) ·7log75.
Решение
Мы можем заменить выражение в скобках логарифмом log3(15:5), используя свойство частного. Вычисляем его значение и получаем log3(15:5) =log33=1.
Согласно основному определению логарифма, значением 7log75 будет 5. Подставим в исходное выражение получившиеся результаты и найдем, что (log315−log35) ·7log75=1·5=5.
Вот все решение без комментариев:
(log315−log35)·7log75=log3 (15:5)·5==log33·5=1·5=5
Ответ: (log315−log35) ·7log75=5.
Пример 11Условие: вычислите, чему равен log3log223−1.
Решение
Начнем с преобразования логарифма, который, в свою очередь, сам находится под знаком логарифма. Используем для этого формулу логарифма степени log223=3. Получим, что log3log223=log33, а дальше log33=1. Следовательно, log3log223−1=1−1=0.
Ответ: log3log223−1=0.
Пример 12Условие: выполните упрощение выражения 3ln 5ln 3log52 .
Решение
Берем формулу перехода к новому основанию. С ее помощью можно представить отношение логарифмов ln 5ln 3 как log35. У нас получилось 3log35log52 . Теперь применяем формулу основного определения логарифма 3log35=5 и получаем, что 3log35log52 . Нам осталось лишь вычислить значение этого выражения. Оно будет равно 2.
Ответ: 3ln 5ln 3log52=2 .
Перейдем к дальнейшему пункту обсуждения логарифмических преобразований. У нас есть выражения log334, 52+log53, lg 0,01. Они не напоминают нам ни об одной известной нам формуле свойства, но их все же можно изменить этим способом, если выполнить предварительные преобразования: 52+log53=52·5log53=25·3=75, log334=log31234=412=8 и lg 0,01=lg 10−2=−2. Разберем подробнее, как именно это делается.
Предварительное преобразование перед применением основных свойств логарифмов
На практике мы часто можем встретить логарифмы, которые внешне не похожи ни на одну часть формулы свойства. Однако при этом преобразование требует применения именно этих формул. Это возможно, если перед этим привести их к соответствующему виду. Это процесс называется тождественным преобразованием.
В роли таких действий могут выступать почти любые преобразования выражений, в том числе раскрытие скобок, вынесение за скобки множителей, применение формул тригонометрии и т.д. Это очевидно, поскольку выражения под знаком логарифма могут содержать практически все, что угодно: модули, скобки, дроби, степени и др. Поэтому нужно уметь выполнять разные виды преобразований, чтобы успешно решать такие задачи.
Данная статья не имеет целью осветить все возможные случаи преобразований, поскольку их очень много. Мы выбрали только четыре, которые наиболее распространены.
Определение 2- Довольно часто приходится получать степени под знаком и в основании, чтобы потом использовать формулу логарифма степени и последствия данного свойства. Мы выполняем такое преобразование, если в видим в условии логарифмы следующего вида: ln2532332 , log381.
- Также нужно уметь выполнять преобразование, связанное со свойствами степени. Оно нужно нам для последующего использования формулы, которая отвечает определению логарифма. Мы применяем его, когда у нас есть выражения, подобные 2log223, 32·log35, 71+log74, 25(log35)-3 и др.
- Обязательно нужно преобразовывать выражения с десятичными дробями под знаком логарифма или в его основании. Иногда после этого мы обнаруживаем, что основание под знаком степени и основание логарифма будут равны, как, например, здесь: log15(0,2)7
- Также нужно знать правила преобразования выражений, где под знаком логарифма стоит отрицательное число. Мы расскажем, что нужно делать, если в условии стоят выражения вроде lg(−3)−4, log6((−9)·(−4)) и др.
Разберем подробно каждый вид преобразования.
Как выделить степень в основании логарифма и под его знаком
Сразу возьмем конкретный пример. У нас есть выражение log1981 , структура которого не подсказывает нам ни одного возможного свойства логарифмов, которое можно было бы использовать. Значит, нам надо начать с преобразования самого выражения или сразу с вычисления его значения. Как же это сделать? Обратите внимание на числа 81 и 19. Их легко представить в виде степени с основанием 3 : 81=34 и 19=3−2. Значит, все выражение можно переписать как log3-234 , а здесь уже видна возможность использования свойства logaqbp=pq·logab . Таким образом, log1981=log3-2=4-2=-2 .
Этот пример иллюстрирует нам следующую мысль: если есть возможность, нужно выделить степень в основании и под знаком логарифма, чтобы впоследствии применить свойство логарифма степени. Ниже мы приведем некоторые советы, как именно выделять степени в таких примерах.
В некоторых случаях число можно преобразовать в целую степень, как в примере выше. В задачах то и дело встречаются степени чисел 2 и 3, которые легко узнать с первого взгляда: 243=35, 81=34, 8=23, 64=26 и др. Для решения примеров полезно иметь таблицу степеней натуральных чисел в пределах 10, чтобы сразу видеть возможности преобразования выражений. Также легко работать с выражениями, включающими целые степени 10, 100 и др.
Пример 13Условие: вычислите или упростите выражения log6216, log3431243, log0,0000010,001.
Решение
- В первом случае мы сразу видим, что 216 можно представить в виде 63. Значит, log6216=log663=3.
- у нас есть числа 343 и 1243. Обратимся к таблице степеней и увидим, что их можно представить в виде 73 и 3−4. Выполняем дальнейшие преобразования и получаем:
log3431243=log733-4==-43·log73=-113·log73 - Поскольку 0,000001=10−6 и 0,001=10−3, тогда log0,0000010,001=log10−610−3= -3-6=12
Ответ: 1) log6216=3, 2) log3431243=-113·log73 ; 3) log0,0000010,001=12.
Если исходного числа нет в таблице степеней, то мы можем разложить его на простые множители.
Пример 14Условие: упростите выражение log3648·log23.
Решение
Выполняем разложение 648 на простые множители.
64832416281931222333
Значит, это число можно представить в виде 648=23·34. Следовательно, log3648·log23=log3(23·34)·log23
Теперь мы можем преобразовать исходный логарифм произведения в сумму, а потом воспользоваться формулой логарифма степени.
log3(23·34)·log23=(log323+log334)·log23= =(3·log32+4)·log23.
Упрощаем выражение через раскрытие скобок:
(3·log32+4)·log23=3·log32·log23+4·log23.
В полученном выражении log32·log23 является произведением взаимно обратных чисел, которое равно 1. Следовательно, формулируем ответ как 3·log32·log23+4·log23=3·1+4·log23=3+4·log23.
Ответ: log3648·log23=3+4·log23.
Зачастую под логарифмом записываются выражения, представляющие собой отношения или произведения корней: 323·3-2, 2·2273 и т.д. Они также приводятся к виду степени: сначала мы выполняем переход от корня к степени, используя соответствующие свойства. С помощью таких преобразований мы можем получить выражение, удобное для применения формулы логарифма степени.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 15Условие: найдите значение выражений log52·5-0.5·5-153454 и log372919.
Решение
В первом случае у нас есть произведение степеней, имеющих одинаковые основания. Используя нужное свойство, получим: 52·5−0,5·5−1=52−0,5−1=50,5. Для преобразования дроби сначала выполним переход от корня к степени, затем используем свойство отношения степеней с одинаковыми основаниями:
53454=5344=534-4=5-314
Полученное выражение подставим в исходный логарифм, применив формулу logaqaq=pq, и получим ответ:
log52·5-0.5·5-153454=log50.55-314=-3140.5==-13412=-132=-612
Во втором случае представим число 729 как 36 , а 19 как 3−2. Исходный логарифм приобретет вид log3363-2. Используя свойство корня из степени, преобразуем основание логарифма и получим:
336=333=31-3=3-2
Заканчиваем преобразование: log3363-2=log3-23-2=1 .
Ответ: 1) log52·5-0.5·5-153454=-612 ; 2) log372919=1
Преобразования, которые нужно сделать, чтобы получить под знаком логарифма нужную степень, могут значительно отличаться от примера к примеру.
Пример 16Условие: вычислите значения log13-1132·3+1-5 и log2·cos1(1+cos2)3 .
Решение
Первое, что нам нужно сделать, – это избавиться от иррациональности в знаменателе первой дроби, лежащей в основании логарифма:
13-1=3+13-1·3+1=3+132-12=3+12
Мы получили результат, схожий с дробью под знаком логарифма. Применим к нему свойства степеней и получим:
132·3+1-5=3+1532=3+1525=3+125
В результате преобразований у нас получился логарифм степени основания log3+123+135 . Значение данного выражения будет равно 5.
Чтобы преобразовать второе выражение, надо воспользоваться тригонометрическими формулами, а конкретно формулой понижения степени cos2a=1+cos2a2 :
log2·cos1(1+cos2)3=log2·cos1(2·cos21)3
Преобразуем второй логарифм, записав его как степень 2·cos2112 или же 2·cos123=2·cos16. Оба выражения будут иметь одно и то же значение, равное шести.
Ответ: 1) log13-1132·3+1-5=5 ; 2) log2·cos1(1+cos2)3=6 .
Как применять свойства степени при преобразовании выражений с логарифмами
Ранее мы уже использовали свойства степеней, чтобы преобразовать выражения под знаком логарифма и его основание. Посмотрим, в каких еще характерных случаях потребуется такая подготовка.
Для начала возьмем задачи на применение свойства степеней с одинаковыми основаниями ap·aq=ap+q. Чаще всего его применяют в обратном порядке, т.е. справа налево.
Пример 17Условие: вычислите значения 3−2+log37 и 0,72−log0,70,1.
Решение
В первом примере нужно представить исходную степень как произведение двух степеней, т.е. 3−2+log37=3−2·3log37. Теперь найдем, чему равен первый множитель. Возведем его в степень, потом вычислим значение второго множителя, используя определение логарифма, и подсчитаем их произведение:
3−2·3log37= (19) ·7=79
Во втором примере нам надо подготовить выражение к преобразованию, выполнив переход к произведению степеней: 0,72−log0,70,1=0,72·0,7−log0,70,1. После этого нам нужно представить показатель −log0,70,1 в виде llog0,7(0,1)−1=log0,710. Теперь все, что нам осталось, – это закончить вычисления:
0,72·0,7−log0,70,1=0,49·0,7log0,710=0,49·10=4,9
Ответ: 1) 3−2+log37=79; 2) 0,72−log0,70,1=4,9.
Также для предварительных преобразований нужно обязательно знать свойство степени в степени, которое выражается формулой (ap)q=ap·q, например, если у нас есть выражение (eln2)3, то мы можем заключить, что значение части в скобках будет равно 2. Значит, (eln2)3=23=8. А если в условии указано (e3)ln2 или (e3)ln2, то мы сначала приводим их к виду (eln2)3:
e3·ln2=eln2·3=(eln2)3 и (e3)ln2=e3·ln2=eln2·3=(eln2)3.
Посмотрим пример решения такой задачи.
Пример 18Условие: выполните упрощение выражений 2log223−3log23 и 5(log85) −1.
Решение
Отметим, что выражения 2log223и 2log223 не являются равными друг другу. Мы можем представить 2log223 как 2log23·log23. Используя свойство степени, представим его как (2log23)log23, что будет тождественно равным 3log23. В итоге мы имеем, что 2log223−3log23=3log23−3log23=0.
Вот запись всего решения:
2log223−3log23=2log23·log23−3log23==(2log23)log23−3log23=3log23−3log23=0
Перейдем ко второму примеру. Запись 25(log85)-1 не будет равна (25log85)−1. Мы можем представить степень (log85)−1 как дробь 1log85 . Ее нужно преобразовать, используя следствие свойства перехода к новому основанию по формуле logab=1logba, чтобы получить log58.
Так, 25(log85)-1=25log58. Поскольку 25 – это 52, имеем 5log58= (52)log58. То, что у нас получилось, представляем в виде (5log58). Нам осталось только вычислить значение: (5log58)2=82=64.
Ответ: 1) 2log223−3log23=0, 2) 25(log85)−1=64.
Также встречаются примеры, где предварительная подготовка к использованию свойств логарифмов заключается в применении и свойства умножения степеней с одинаковыми основаниями, и свойства степени в степени. Например,
4−0,5+2·log43=4−0,5·42·log43==12·(4log43)2=12·32=12·9=4,5
Преобразование логарифмов с десятичными дробями
Применить свойства логарифмов можно и тогда, когда под знаком логарифма у нас стоит десятичная дробь. Что можно сделать с выражением log0,4253? Отметим, что 25 и 0,4 равны между собой 0,4=410=25, то есть это разные формы записи для одного и то же числа.
В целом можно сказать, что в случае наличия десятичной дроби под знаком логарифма необходимо выполнить переход к обыкновенной дроби. Это поможет увидеть возможности использования свойств логарифмов.
Разберем подобную задачу.
Пример 19Условие: вычислите значение выражения log0,46,25.
Решение
Начнем с перехода от десятичных дробей к обыкновенным.
log0,46,25=log410625100=log25254
Теперь видно, что мы можем преобразовать 254 в виде (25)−2 и воспользоваться формулой логарифма степени. Вычисляем значение:
log25254=log2525-2=-2
Ответ: -2.
Преобразование выражений с отрицательными числами под знаком логарифма
Еще один случай, который мы хотели бы рассмотреть – это преобразование выражений, в которых под знаком логарифма стоит отрицательное число, например, log3-93-27 или log3((−2)·(−5)).
Мы не можем сразу воспользоваться формулами свойств логарифмов в том виде, в каком приводили их в последнем пункте, например, сразу перейти от log3((−2)·(−5)) к log3(−2)+log3(−5), применить свойство логарифма степени к log2(−2)6 или логарифма частного к log3-93-27 , поскольку отрицательные числа не могут находиться под знаком логарифма и в его основании.
Что это значит на практике? Вернемся к нашему примеру log3((−2)·(−5)). Структура выражения соответствует формуле loga(x·y), где a равно 3, x-3 и y-5. Поскольку условия a>0, a≠1, x>0, y>0 не выполнены, формулу loga(x·y)=logax+logay мы применить не можем, и равенство log3((−2)·(−5)) =log3(−2) +log3(−5) записать нельзя. Преобразования вида log3-93-27=log3-93-log3(-27) также будут неправильными.
Это не значит, что выражения с отрицательными числами не могут быть преобразованы с использованием свойств логарифмов. Это допускается при условии предварительных преобразований, позволяющих избавиться от минуса. Они базируются на хорошо известных нам правилах работы с числами, меньшими 0.
Вернемся опять к нашему примеру. Согласно правилам умножения, (−2)·(−5) =2·5, значит, log3((−2)·(−5))=log3(2·5). К выражению в таком виде мы уже можем применить формулу log3(2·5) =log32+log35. А вот для примера log2(−2)6 нужно будет выполнить следующие действия:
(−2)6= ((−1)·2)6=(−1)6·26=1·26=26
Значит, log2(−2)6=log226=6.
Пример 20Условие: найдите значение выражения log2-163-2-23.
Решение
Сначала заключим, что данное выражение имеет смысл. Воспользоваться сразу свойством логарифма частного у нас нет возможности из-за отрицательных чисел под знаком логарифма, поэтому выполним преобразования.
Определив корень нечетной степени из отрицательного числа, выполним переход от -163-2-23 к -163-2-23 . Согласно правилам деления, получим -163-2-23=1632-23 . Теперь нам нужно получившуюся дробь представить в виде степени числа 2 и найти значение получившегося логарифма.
1632-23=2432-23=2432-23=243—23=22log2-163-2-23=log222=2
Ответ: log2-163-2-23=2 .
Некоторые свойства, например, логарифма частного, степени с четным показателем и произведения, можно распространить и на отрицательные числа с помощью модулей. Как это делается, мы покажем далее. Так, поскольку свойство логарифма произведения выглядит как loga(x·y)=loga|x|+loga|y|, где a>0, a≠1, x≠0, y≠0, то после преобразования мы получим log3((−2)·(−5)) =log3|−2|+log3|−5|=log32+log35.
Как преобразовать логарифмическое выражение с переменными
В предыдущих параграфах мы разобрали, как работать с числовыми выражениями, содержащими логарифмы. Однако если требуется решить логарифмическое неравенство или уравнение, нам понадобится умение работать с теми случаями, когда под знаком логарифма содержится выражение с переменными. В целом при этом мы руководствуемся теми же принципами, что и с числовыми выражениями, но тут следует отдельно пояснить некоторые нюансы, незнание которых ведет к ошибкам.
Особенности преобразований выражений с переменными
Основная трудность состоит в том, что при работе с такими выражениями числа, расположенные под знаком логарифма и в его основании, должны соответствовать особым условиям, а в случае определенных переменных из области допустимых значений эти условия могут оказаться невыполненными. Приведем один наглядный пример.
У нас есть логарифмическое выражение log2(x+1)4. При преобразовании нужно обязательно учитывать область допустимых значений, поэтому первым шагом должно стать ее нахождение. Здесь она определена неравенством (x+1)4>0, значение которого является числовым множеством (−∞, −1) ∪ (−1, +∞). Решить его можно с помощью метода интервалов.
Исходное выражение соответствует формуле logABp, где A равно 2, B – x+1, а p – четырем.
Мы видим, что заданное выражение соответствует виду logABp, где A=2, B=x+1 и p=4. Такие выражения преобразовываются по свойству логарифма степени logabp=p·logab. Можно ли поступить так с этим выражением? Вычислим значение исходного логарифма и выражения, которое получилось после преобразования, например, при x=−2. В итоге: log2(−2+1)4=log21=0, а 4·log2(−2+1) =4·log2(−1) –выражение, не имеющее смысла. Значит, мы ошиблись.
Причина ошибки в том, что мы взяли формулу logabp=p·logab, но это допустимо лишь при условии a>0, a≠1, b>0, p — любое действительное число. Иными словами, проделанное нами преобразование возможно, если x+1>0, что аналогично x>−1 (для A и p – условия выполнены). Однако в нашем случае ОДЗ переменной x для исходного выражения состоит не только из промежутка x>−1, но и из промежутка x <−1. Но для x <−1 мы не имели права осуществлять преобразование по выбранной формуле.
Почему надо учитывать область допустимых значений
Продолжая работу с выражением log2(x+1)4, проанализируем, как изменится область значений, когда мы выполним переход к виду 4·log2(x+1). Ранее мы уже определили эту область как множество (−∞, −1) ∪ (−1, +∞). Теперь вычислим, какова будет область допустимых значений для 4·log2(x+1). Она определяется условием x+1>0, а ему, в свою очередь, будет отвечать множество (−1, +∞). Мы видим, что область допустимых значений сузилась, а это может привести к различным ошибочным последствиям, поэтому таких преобразований следует избегать.
Важно следить, как меняется область значений во время каждого преобразования. Если на каком-либо этапе происходит ее сужение, это повод тщательно проверить все вычисления и определить, правомерно ли использования данного преобразования.
Чаще всего при решении задач приходится иметь дело с выражениями, область допустимых значений которых не ограничивает применение свойств логарифмов в прямом и обратном порядке, но не следует относиться так ко всем примерам. Нужно всегда проверять, что происходит с областью допустимых значений, и своевременно отслеживать возможные ошибки.
Запишем, в ходе каких преобразований чаще всего происходит непреднамеренное сужение области значений:
Определение 3- когда мы переходим от логарифма произведения к сумме, например, ln(x·(x+3)) =lnx+ln(x+3) сузит нужную область.
- Когда мы переходим от логарифма частного к разности. Пример такого преобразования – замена log2xsin x на log2x−log2sinx .
- Когда мы выносим четный показатель степени, используя формулу логарифма степени logabp=p·logab и формулу logabp=pq·logab . Примеры таких преобразований – logx3(x-8)2=23·logx(x-8) , ln(x+3)−4=−4·ln(x+3).
Иногда в результате преобразования область допустимых значений может не сужаться, а расширяться, например, при переходе от 4·log2(x+1) к log2(x+1)4. В этом случае область расширяется от (−1, +∞) до (−∞, −1) ∪ (−1, +∞). Такие преобразования имеют место, если оставаться в рамках ОДЗ для исходного выражения. Так, преобразование 4·log2(x+1) =log2(x+1)4 имеет место на области значений переменной x для исходного выражения 4·log2(x+1), то есть, при x+1>0, что аналогично (−1, +∞).
Теперь, когда мы обговорили тонкости, на которые нужно обращать внимание при преобразовании выражений с переменными с использованием свойств логарифмов, остается разобраться, как правильно эти преобразования проводить.
Правила проведения преобразований
Мы говорили ранее, что чаще всего область допустимых значений позволяет нам применять свойства логарифмов в привычных формулировках.
Пример 21Условие: упростите 3·lg(x+2)7−lg(x+2) −5·lg(x+2)4.
Решение
На первый взгляд данное выражение нужно преобразовать, используя логарифм степени, то есть сначала вынести нужную степень в виде коэффициента и потом привести подобные слагаемые. Давайте разберемся, правомерно ли применение выбранного свойства в этом случае.
Чтобы перейти от lg(x+2)7 к 7·lg(x+2) и от lg(x+2)4к 4·lg(x+2), нам нужно, чтобы x+2>0. Выясним, будет ли соблюдено данное условие. Для этого нам нужно определить область допустимых значений переменной x. Ее можно выразить с помощью системы неравенств (x+2)7>0,x+2>0,(x+2)4>0 , которая будет равносильной условию x+2>0 (если нужно, повторите материал о решении систем неравенств). Следовательно, мы можем взять формулу логарифма степени. Считаем:
3·lg(x+2)7−lg(x+2)−5·lg(x+2)4==3·7·lg(x+2)−lg(x+2)−5·4·lg(x+2)==21·lg(x+2)−lg(x+2)−20·lg(x+2)==(21−1−20)·lg(x+2)=0
Область допустимых значений позволяет нам использовать и другой вариант вычисления, например, такой:
3·lg(x+2)7-lg(x+2)-5·lg(x+2)4==lg((x+2)7)3-lg(x+2)-lg((x+2)4)5==lg(x+2)21-lg(x+2)-lg(x+2)20==lg(x+2)21(x+2)·(x+2)20=lg1=0
Ответ: 3·lg(x+2)7−lg(x+2) −5·lg(x+2)4=0.
А как быть в случае, если в области допустимых значений нужные условия не будут выполняться? Возьмем соответствующий пример и разберем его.
Пример 22Условие: выполнить упрощение выражения lg(x+2)4−lg(x+2)2.
Решение
Здесь свободно использовать свойство логарифма степени мы не можем. Область допустимых значений x можно представить в виде объединения промежутков x>−2 и x<−2. Если x>−2, то применяем нужное свойство и действуем по аналогии с тем, как мы решали задачу выше: lg(x+2)4−lg(x+2)2=4·lg(x+2) −2·lg(x+2) =2·lg(x+2). Однако в области значений есть и промежуток x+2<0, и в случае с ним подобное преобразование будет некорректным. Как же нам быть тогда?
Применим знаки модуля. Вспомним определение данного понятия и представим x+2 при x+2<0 как −|x+2|. В таком случае мы можем выполнить переход от lg(x+2)4−lg(x+2)2 к lg(−|x+2|)4−lg(−|x+2|)2, и далее к lg|x+2|4−lg|x+2|2 .То, что у нас получилось в итоге, может быть преобразовано с использованием свойства логарифма степени, ведь |x+2|>0 при любом x.
Модуль нам больше не нужен, значит, избавляемся от него. С учетом того, что мы преобразовывали при |x+2|<0, имеем 2·lg|x+2|=2·lg(−(x+2)). Это и будет ответом на поставленный вопрос.
Ответ: lg(x+2)4-lg(x+2)2=2·lg(x+2), x+2>02·lg(-(x+2)), x+2<0 . Можно записать ответ компактнее, используя знаки модуля: lg(x+2)4-lg(x+2)2=2·lgx+2 .
Возьмем еще один пример, чтобы закрепить навыки работы с модулями.
Пример 23Условие: представьте выражение lnx-1·x-2x-3 как сумму и разность логарифмов линейных двучленов x−1, x−2 и x−3.
Решение
Вычисляем область допустимых значений данного выражения:
x-1·x-2x-2>0,(1, 2)∪3, +∞
Поскольку значения x−1, x−2 и x−3 будут положительны на промежутке от трех до плюс бесконечности, то мы можем использовать формулы свойств логарифма суммы и разности:
lnx-1·x-2x-3==ln(x-1)+ln(x-2)-ln(x-3)
А на интервале от одного до двух значение x−1 будет положительным, а x−2 и x−3 – отрицательными. Значит, отрицательные значения нам нужно заключить в знаки модуля. У нас получится, что:
lnx-1·x-2x-3=lnx-1·-x-2-x-3==ln(x-1)·x-2x-3
После этого можно спокойно применять формулу логарифма произведений и частного, поскольку на интервале от одного до двух значения всех трех выражений x−1, |x−2| и |x−3| будут положительными. В итоге имеем:
lnx-1·x-2x-3=ln(x-1)+lnx-2-lnx-3==lnx-1+ln(-(x-2))-ln(-(x-3))
Теперь объединяем получившиеся результаты.
Ответ: lnx-1·x-2x-3=lnx-1+ln(-(x-2))-ln(-(x-3))
С помощью таких рассуждений и свойств логарифмов отношения, произведения и степени можно вывести несколько результатов, полезных на практике и удобных в использовании:
Определение 4- сумма логарифмов loga|X|+loga|Y|, a>0, a≠1 может быть использована вместо логарифма произведения loga(X·Y).
- Разность логарифмов loga|X|−loga|Y|, где a>0, a≠1, X и Y являются произвольными выражениями, может быть использована вместо логарифма частного.
- Выражение p·loga|B|, где a>0, a≠1, p является четным числом, а B – произвольным выражением, может быть использована вместо логарифма B в четной степени p.
Условие: выполните упрощение выражения 13·log8((x+4)·(x-2))-log8x+413x-2 .
Решение
На первый взгляд, мы должны взять формулы логарифмов разности, суммы и степени. Давайте посмотрим, насколько правомерно их использование в данном случае. Для начала вычислим область допустимых значений:
(x+4)·(x-2)>0,(x+4)13x-2>0-∞, -4∪2, +∞
У нас получилось, что значения выражений x+4, x−2 и (x+4)13 в данной области могут быть как положительными, так и отрицательными. Значит, нам нужно использовать модули.
13·log8((x+4)·(x-2))-log8(x+4)13x-2==13·log8x+4+13·log8x-2—log8x+413-log8x-2==13·log8x+4+13·log8x-2—log8(x+14)13+log8x-2==13·log8x+4-log8(x+4)13+14·log8x-2
Зная свойства модуля, перепишем x+413 в виде x+413 . Значит, что:
13·log8x+4-log8(x+4)13+14·log8x-2==13·log8x+4-log8x+413+14·log8x-2
Теперь мы можем свободно применить формулу логарифма степени и выполнить приведение подобных слагаемых:
13·log8x+4-log8x+413+14·log8x-2==13·log8x+4-13·log8x+4+14·log8x-2==14·log8x-2
Возможны и другие преобразования, которые дают тот же результат:
13·log8((x+4)·(x-2))-log8x+413x-2==log8((x+4)·(x-2))13-log8x+413x-2==log8((x+4)13·(x-2))13-log8x+413x-2==log8(x+4)13·(x-2)13x+413x-2=log8(x-2)14
Поскольку на области допустимых значений x−2 может быть и положительным, и отрицательным, необходимо заключить это выражение под знак модуля во время вынесения четного показателя степени. У нас получится, что log8(x-2)14=14·log8x-2
А что было бы, если бы мы не стали использовать модуль, а сразу начали применять свойства логарифмов? У нас получился бы результат 14·log8(x−2), который был бы верен при x∈ (2, +∞), однако ошибочен на всей остальной области допустимых значений.
Ответ: 13·log8((x+4)·(x-2))-log8x+413x-2=14·log8x-2 .
| Клавиша | Обозначение | Пояснение |
|---|---|---|
| ← | удаление одного символа | Удаляет последний символ |
| С | сброс | Кнопка сброса. Полностью сбрасывает калькулятор в положение «0» |
| Радианы | радианы | Выражение угла в радианах. Используется только для тригометрических функциях cos, sin, tg, ctg, arcsin, arccos, arctg,arcctg. |
| Градусы | градусы | Выражение угла в градусах. Используется только для тригометрических функциях cos, sin, tg, ctg. |
| sin | sin | Тригонометрическая функция синус. Обозначается как «sin(x)». Угол (x) может быть задан в радианах либо градусах. |
| cos | cos | Тригонометрическая функция косинус. Обозначается как «cos(x)». Угол (x) л может быть задан в радианах либо градусах. |
| tg | tg | Тригонометрическая функция тангенс. Обозначается как «tg(x)». Угол (x) может быть задан в радианах либо градусах. |
| ctg | ctg | Тригонометрическая функция котангенс. Обозначается как «ctg(x)». Угол (x) может быть задан в радианах либо градусах. |
| arcsin | arcsin | Обратная тригонометрическая функция арксинус. Обозначается как «arcsin(x)». Угол (x) может быть задан в радианах либо градусах. |
| arccos | arccos | Обратная тригонометрическая функция арккосинус. Обозначается как «arccos(x)». Угол (x) может быть задан в радианах либо градусах. |
| arctg | arctg | Обратная тригонометрическая функция арктангенс. Обозначается как «arctg(x)». Угол (x) может быть задан в радианах либо градусах. |
| arcctg | arcctg | Обратная тригонометрическая функция арккотангенс. Обозначается как «arcctg(x)». Угол (x) может быть задан в радианах либо градусах. |
| ln | ln | Натуральный логарифм. Обозначение ln(x). |
| log | log | Десятичный логарифм. |
| e | e | Число «e» — основание натурального логарифма. Число «e» называют числом Эйлера или числом Непера. Приблизительно равно 2,71828. |
| Pi | число Пи | Число «Пи» — математическая константа. Приблизительно равно 3,14. |
| √ | корень | Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2 |
| x2 | возведение в квадрат | Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16 |
| 1/x | дробь | Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число |
— log (x), ln (x), lg (x), lb (x)
Этот калькулятор можно использовать для определения любого типа логарифма действительного числа с любым основанием, которое вы пожелаете. Общий, двоичный и натуральный логарифмы можно найти с помощью онлайн-калькулятора логарифмов.
Определение логарифма
Логарифм действительного числа — это показатель степени, до которого необходимо увеличить основание, то есть другое фиксированное число, чтобы сгенерировать это действительное число.
Если x = a y , то y = log a x
Где:
a, x, y — действительные числа, x > 0, a > 0, a 1, а a — основание логарифма.
Для иллюстрации возьмем 10 000 по основанию 10. Логарифм этого действительного числа будет 4. Это потому, что 10 000 эквивалентно 10 в степени 4. Таким образом, так же, как деление является математической операцией, противоположной умножению, логарифм — операция, противоположная возведению в степень.
Традиционно в логарифмах используется основание 10, но основание может быть любым числом (кроме 1). Двоичный логарифм x обычно записывается как log 2 x или lb x. Однако основание e обычно записывается как ln x и редко как log e x.
Как показано выше, логарифмы могут иметь множество оснований. Двоичный логарифм или логарифм с основанием 2 применяется в вычислениях, в то время как в области экономики используется основание e , а в образовании основание 10 записывается просто как log x, log 10 x или lg x, используется. Организуя числа в соответствии с этими основами, действительные числа можно выразить гораздо проще.
Правила логарифма
1. Правило нуля: log a 1 = 0
2.Правило идентификации: log a a = 1
3. Журнал правила мощности: log a a x = x
4. Правило мощности журнала: a log a x = x
5. Правило продукта: log a (xy) = log a x + log a y
6. Правило частного: log a (x / y) = log a x — log a y
7. Правило мощности: log a x n = n log a x
8. Изменение основного правила: log a x = log b x × log a b
9.Базовое правило переключения: log b a = 1 / log a b
10. Изменение основного правила: log b x = log a x / log a b
Где: x> 0 , y> 0, a> 0, b> 0; a ≠ 1, b ≠ 1; n — любое действительное число.
Ln Calculator
Ln Calculator
Калькулятор Ln используется для определения натурального логарифма числа. При выполнении расчетов используются простые формулы. В нем есть одно текстовое поле, в которое вы вводите значение Ln.Чаще всего натуральный логарифм X выражается как; «Ln X» и «logeX». Они обычно используются в некоторых научных контекстах и в нескольких других языках программирования. Логарифм с основанием «е» является натуральным логарифмом и приблизительно эквивалентен числу Эйлера 2,718281828.Калькулятор Ln имеет два элемента управления, которые используются для выполнения различных функций. Кнопка «Рассчитать» используется для преобразования значений, введенных в пустое текстовое поле. Ваши результаты будут отображаться в нижней части калькулятора.Кнопка «Сброс» используется для стирания всех текстовых полей предыдущих расчетов. Это самый быстрый способ сбросить настройки калькулятора, когда вы захотите выполнить новые вычисления.
Например;
Найдите натуральный логарифм 45.Решение;
Введите число 45 в пустое текстовое поле, а затем нажмите знак равенства или кнопку «Рассчитать». Оба они работают одинаково, давая вам точные результаты в зависимости от значения, введенного в текстовое поле. Ответ будет отображаться как; 3.8066624898Калькулятор натурального логарифма также может использоваться для вычисления десятичных значений.
Например;
Найдите натуральный логарифм 0,5.Решение;
Введите значение 0,5 в пустое текстовое поле, а затем нажмите знак равенства или кнопку «Рассчитать». Ваши результаты будут отображаться как; -0,618056Вы также можете использовать «e» для обозначения научных обозначений. Важно знать, что калькулятор даст точные результаты в зависимости от значений, введенных в текстовое поле.Есть разные способы ввода значений Ln. Например. 6e2, 4e-7, 5.78e10
Например;
Найдите натуральный логарифм 8e5Решение
Введите 8e5 в пустое текстовое поле и нажмите на знак равенства или кнопку «Рассчитать».Ваш ответ будет отображаться как; 13.5007
Калькулятор логарифмов (основание натурального логарифма 2, e, 10, N)
Поиск инструмента
Логарифм
Инструмент для вычисления логарифмов. * $.
Натуральный логарифм обозначается как log или ln и основан на числе $ e \ приблизительно 2,71828 \ ldots $ (см. Десятичные дроби числа e).
Пример: $ \ log (7) = \ ln (7) \ приблизительно 1,94591 $
Некоторые люди и плохие калькуляторы используют $ \ log $ вместо $ \ log_ {10} $, поэтому убедитесь, что вы знаете, какие обозначения используются.
Как превратить логарифм по основанию N в натуральный логарифм?
Любой логарифм с основанием $ N $ может быть вычислен из натурального логарифма по формуле: $$ \ log_ {N} (x) = \ frac {\ ln (x)} {\ ln (N)} $ $
Что такое неперианский логарифм?
Неперианский логарифм — это другое название натурального логарифма (с основанием е).
Что такое десятичный логарифм (log10)?
Десятичный логарифм , отмеченный $ \ log_ {10} $ или log10, является базовым 10 $ логарифмом . Это один из наиболее часто используемых логарифмов , в расчетах и логарифмических шкал . $$ \ log_ {10} (x) = \ frac {\ ln (x)} {\ ln (10)} $$
Пример: $ \ log_ {10} (1000) = 3 $
Что такое двоичный логарифм (log2)?
Двоичный логарифм , отмеченный $ \ log_ {2} $ (или иногда $ lb $), является базовым логарифмом $ 2 $ .Этот логарифм используется в основном для компьютерных вычислений. $$ \ log_2 (x) = \ frac {\ ln (x)} {\ ln (2)} $$
Используйте приведенную выше формулу, чтобы вычислить log2 с помощью калькулятора, имеющего только ключ журнала.
Почему логарифм может преобразовывать произведение в сумму?
Любой логарифм имеет как для свойств:
— $ \ log_b (x \ cdot y) = \ log_b (x) + \ log_b (y) $ (преобразование произведения в сумму)
— $ \ log_b \ left (\ frac {x} {y} \ right) = \ log_b (x) — \ log_b (y) $ (преобразование частного в вычитание)
— $ \ log_b (x ^ a) = a \ log_b (x) $ (преобразование степени в умножение)
Какие замечательные значения функции логарифма?
Задайте новый вопросИсходный код
dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Логарифм».За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любого алгоритма, апплета или фрагмента логарифма (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой функции логарифмирования (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанные на любом информатическом языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.), без загрузки данных, скрипт, копирование -паста или доступ к API для «Логарифма» будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Нужна помощь?
Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!
Вопросы / Комментарии
Сводка
Похожие страницы
Поддержка
Форум / Справка
Ключевые слова
логарифм, журнал, log2, log10, ln, непер, непериан, натуральный
Ссылки
Источник: https: //www.dcode.fr / логарифм
© 2021 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF. Калькулятор натурального логарифмаln (x) Калькулятор натурального логарифма
ln (x)Калькулятор натурального логарифма ln (x) находит результат функции логарифма по основанию e , что приблизительно равно 2,718 .
Калькулятор натурального логарифма пер. Рассчитатьln (x) = y
x: — действительное число, x> 0
Натуральный логарифм: ln
ln (x) = y
ln (x) эквивалентно log e (x)
Примеры натурального логарифма
- ln (2) = log e (2) = 0.6931
- ln (3) = log e (3) = 1,0986
- ln (4) = лог e (4) = 1,3862
- ln (5) = log e (5) = 1,609
- ln (6) = log e (6) = 1,7917
- ln (10) = log e (10) = 2.3025
Таблицы значений натурального логарифма
Список таблиц значений функции журнала в экспоненциальных числах с основанием (e).
| log e (x) | Обозначение | Значение | |||
|---|---|---|---|---|---|
| log e (1) | ln (1) | 0 | |||
| log e (2) | ln359 (2) | 0.6 | |||
| лог e (3) | ln (3) | 1.098612 | |||
| log e (4) | ln (4) | 1,386294 | log 5) | ln (5) | 1.609438 |
| log e (6) | ln (6) | 1.7 | |||
| log e (7) | ln (7) | ln (7) 1.94591 | |||
| лог e (8) | ln (8) | 2.079442 | |||
| log e (9) | ln (9) | 2,197225 | |||
| log e (10) | ln (10) | 2.302585 | log 11) | ln (11) | 2.397895 |
| log e (12) | ln (12) | 2.484907 | |||
| log e (13) | ln (13) | ln (13) | ln (13) | ln 2,564949 | |
| лог e (14) | ln (14) | 2.639057 | |||
| лог e (15) | ln (15) | 2,70805 | |||
| log e (16) | ln (16) | 2,772589 | |||
| ln (17) | 2.833213 | ||||
| log e (18) | ln (18) | 2.8 | |||
| log e 6 (19) | ln (1935) | ln (1935) 2.944439 | |||
| лог e (20) | ln (20) | 2.995732 | |||
| лог e (21) | ln (21) | 3.044522 | |||
| log e (22) | ln (22) | 3.0 | |||
| ln (23) | 3.135494 | ||||
| log e (24) | ln (24) | 3.178054 | |||
| log e (25) | ln (25) 3.218876 | ||||
| лог e (26) | ln (26) | 3.258097 | |||
| лог e (27) | ln (27) | 3.295837 | |||
| log e (28) | ln (28) | 3.332205 | 1 | ||
| ln (29) | 3.367296 | ||||
| log e (30) | ln (30) | 3.401197 | |||
| log e (31) | 9035 ln (31) | 9035 ln (31) 3.433987 | |||
| лог e (32) | ln (32) | 3.465736 | |||
| log e (33) | ln (33) | 3,496508 | |||
| log e (34) | ln (34) | 3.526361 | log 35) | ln (35) | 3.555348 |
| log e (36) | ln (36) | 3.583519 | |||
| log e (37) | ln (37) | ln (37) 3,610918 | |||
| лог e (38) | ln (38) | 3.637586 | |||
| log e (39) | ln (39) | 3.663562 | |||
| log e (40) | ln (40) | 3.688879 | |||
| ln (41) | 3.713572 | ||||
| log e (42) | ln (42) | 3.73767 | |||
| log e (43) | ln | ) 3.7612 | |||
| лог e (44) | ln (44) | 3.78419 | |||
| лог e (45) | ln (45) | 3.806662 | |||
| log e (46) | ln (46) | 3,828641 | log 47) | ln (47) | 3.850148 |
| log e (48) | ln (48) | 3.871201 | |||
| log e (49) | 496356 ln 3.89182|||||
| лог e (50) | ln (50) | 3. | 3 | ||
| лог e (51) | ln (51) | 3. | 6|||
| log e (52) | ln (52) | 3,951244 | |||
| ln (53) | 3.970292 | ||||
| log e (54) | ln (54) | 3.988984 | |||
| log e 90 5512 (55) | ln 4.007333 | ||||
| лог e (56) | ln (56) | 4.025352 | |||
| log e (57) | ln (57) | 4.043051 | |||
| log e (58) | ln (58) | 4.060443 | log 59) | ln (59) | 4.077537 |
| log e (60) | ln (60) | 4.094345 | |||
| log e (61) | 9035 ln (61) | ln (61) 4.110874 | |||
| лог e (62) | ln (62) | 4.127134 | |||
| log e (63) | ln (63) | 4.143135 | |||
| log e (64) | ln (64) | 4.158883 |
| log e (x) | Обозначение | Значение | |||
|---|---|---|---|---|---|
| log e (65) | ln (65) | 4.174387 | |||
| log e | (66) | 4.189655 | |||
| log e (67) | ln (67) | 4.204693 | |||
| лог e (68) | ln (68) | 4.219508 | |||
| log e (69) | ln (69) | 4,234107 | |||
| ln (70) | 4.248495 | ||||
| log e (71) | ln (71) | 4.26268 | |||
| log e (72) | ln 9035) 4.276666 | ||||
| лог e (73) | ln (73) | 4.2 | |||
| лог e (74) | ln (74) | 4.304065 | |||
| log e (75) | ln (75) | 4.317488 | log 76) | ln (76) | 4.330733 |
| log e (77) | ln (77) | 4.343805 | |||
| log e (78) | 9035 ln (78) | ln (78) 4.356709 | |||
| лог e (79) | ln (79) | 4.369448 | |||
| лог e (80) | ln (80) | 4.382027 | |||
| log e (81) | ln (81) | 4.394449 | |||
| 4,394449 | |||||
| ln (82) | 4.406719 | ||||
| log e (83) | ln (83) | 4.418841 | |||
| log e 6 (84) | 9035 ln (84) | ln (84) 4.430817 | |||
| лог e (85) | ln (85) | 4.442651 | |||
| log e (86) | ln (86) | 4.454347 | |||
| log e (87) | ln (87) | 4.465908 | log 88) | ln (88) | 4.477337 |
| log e (89) | ln (89) | 4.488636 | |||
| log e (90) | 9035 ln (9035) | ln (9035) 4.49981 | |||
| лог e (91) | ln (91) | 4.51086 | |||
| лог e (92) | ln (92) | 4.521789 | |||
| log e (93) | ln (93) | 4.532599 | |||
| ln (94) | 4.543295 | ||||
| log e (95) | ln (95) | 4.553877 | |||
| log e (96) | ln (96) | ln (96) 4.564348 | |||
| лог e (97) | ln (97) | 4.574711 | |||
| лог e (98) | ln (98) | 4.584967 | |||
| log e (99) | ln (99) | 4.59512 | 1 | | ||
| ln (100) | 4.60517 | ||||
| log e (101) | ln (101) | 4.615121 | |||
| log e (102) | 9035 ln (102) 4.624973 | ||||
| лог e (103) | ln (103) | 4.634729 | |||
| log e (104) | ln (104) | 4.644391 | |||
| log e (105) | ln (105) | 4.65396 9005 | log 106) | ln (106) | 4.663439 |
| log e (107) | ln (107) | 4.672829 | |||
| log e (108) | 9035 ln (9035) 108 4.682131 | ||||
| лог e (109) | ln (109) | 4.6 | |||
| лог e (110) | ln (110) | 4.70048 | |||
| log e (111) | ln (111) | 4.70953 | 1 | ||
| 112) | ln (112) | 4.718499 | |||
| log e (113) | ln (113) | 4.727388 | |||
| log e (114) | 9035 ln (114) 4,736198 | ||||
| лог e (115) | ln (115) | 4.744932 | |||
| log e (116) | ln (116) | 4.75359 | |||
| log e (117) | ln (117) | 4.762174 | log 118) | ln (118) | 4.770685 |
| log e (119) | ln (119) | 4.779123 | |||
| log e (120) | 9035 ln (12035) 4,787492 | ||||
| лог e (121) | ln (121) | 4.795791 | |||
| лог e (122) | ln (122) | 4.804021 | |||
| log e (123) | ln (123) | 4.812184 | log 124) | ln (124) | 4.820282 |
| log e (125) | ln (125) | 4.828314 | |||
| log e 6) | 9035 ln (12635) 4.836282 | ||||
| лог e (127) | ln (127) | 4.844187 | |||
| лог e (128) | ln (128) | 4.85203 |
| log e (x) | Обозначение | Значение | ||||
|---|---|---|---|---|---|---|
| log e (129) | ln (129) | 4.859812 | ||||
| log e | (130) | 4.867534 | ||||
| log e (131) | ln (131) | 4.875197 | ||||
| log e (132) | ln (132) | 4.882802 | ||||
| лог e (133) | ln (133) | 4.8 | ||||
| log e (134) | ln (134) | 4,89784 e ( | ||||
| ln (135) | 4.5 | |||||
| log e (136) | ln (136) | 4. | 5||||
| log e 6 (137) | 137ln (9035) 4. | |||||
| лог e (138) | ln (138) | 4.4 | ||||
| log e (139) | ln (139) | 4. 4 | ||||
| log e (140) | ln (140) | 4.941642 | log 141) | ln (141) | 4.94876 | |
| log e (142) | ln (142) | 4.955827 | ||||
| log e (143) | )ln 4.962845 | |||||
| лог e (144) | ln (144) | 4.969813 | ||||
| лог e (145) | ln (145) | 4.976734 | ||||
| log e (146) | ln (146) | 4.983607 | 4.983607 | ln (147) | 4.9 | |
| log e (148) | ln (148) | 4.997212 | ||||
| log e (149) | 5.003946 | |||||
| лог e (150) | ln (150) | 5.010635 | ||||
| лог e (151) | ln (151) | 5.01728 | ||||
| log e (152) | ln (152) | 5.023881 | log 153) | ln (153) | 5.030438 | |
| log e (154) | ln (154) | 5.036953 | ||||
| log e (155) | log e (155) | 5.043425 | ||||
| лог e (156) | ln (156) | 5.049856 | ||||
| лог e (157) | ln (157) | 5.056246 | ||||
| log e (158) | ln (158) | e e (158) | 5.061295 | 159)ln (159) | 5.068904 | |
| log e (160) | ln (160) | 5.075174 | ||||
| log e (161) | ln | ln 5.081404 | ||||
| лог e (162) | ln (162) | 5.087596 | ||||
| лог e (163) | ln (163) | 5.09375 | ||||
| log e (164) | ln (164) | 5.099866 | ln (164) | 5.099866 | ln (165) | 5.105945 |
| log e (166) | ln (166) | 5.111988 | ||||
| log e (167) | ||||||
| лог e (168) | ln (168) | 5.123964 | ||||
| лог e (169) | ln (169) | 5.129899 | ||||
| log e (170) | ln (170) | e | 8 | ln (171) | 5.141664 | |
| log e (172) | ln (172) | 5.147494 | ||||
| log e (173) | ln e (173) | 5.153292|||||
| лог e (174) | ln (174) | 5.159055 | ||||
| лог e (175) | ln (175) | 5.164786 | ||||
| log e (176) | ln (176) | 5.170484 | ||||
| 5,170484 | ||||||
| ln (177) | 5.17615 | |||||
| log e (178) | ln (178) | 5.181784 | ||||
| log e (179) | 176356 5.187386||||||
| лог e (180) | ln (180) | 5.1 | ||||
| лог e (181) | ln (181) | 5.198497 | ||||
| log e (182) | ln (182) | e | 9.204007 | 183) | ln (183) | 5.209486 |
| log e (184) | ln (184) | 5.214936 | ||||
| log e (185) | 9035) | 9035 5.220356 | ||||
| лог e (186) | ln (186) | 5.225747 | ||||
| лог e (187) | ln (187) | 5.231109 | ||||
| log e (188) | ln (188) | 442 | 4 189) | ln (189) | 5.241747 | |
| log e (190) | ln (190) | 5.247024 | ||||
| log e (191) | 19356 ln 5.252273||||||
| лог e (192) | ln (192) | 5.257495 |
© 2019-2021 www.logcalculator.net
Логарифмбесплатный онлайн калькулятор | Justfreetools
Вычислить логарифм числа по основанию:
* Используйте e для экспоненциального обозначения. Например: 5e3, 4e-8, 1.45e12
Когда:
b y = x
Тогда логарифм по основанию b числа x:
бревно b x = y
Калькулятор антилогарифма
Чтобы вычислить логарифм -1 (y) на калькуляторе, введите основание b (10 — значение по умолчанию, введите e для константы e), введите значение логарифма y и нажмите кнопку вычислить :
Когда
y = бревно b x
Антилогарифм (или обратный логарифм) вычисляется путем возведения основания b до логарифма y:
x = log b -1 ( y ) = b y
Определение логарифма
Когда b возведено в степень y, равно x:
b y = x
Тогда логарифм по основанию b x равен y:
log b ( x ) = y
Например, когда:
2 4 = 16
Тогда
log 2 (16) = 4
Логарифм как функция, обратная экспоненциальной функции
Логарифмическая функция,
y = log b ( x )
— функция, обратная экспоненциальной функции,
x = b y
Итак, если мы вычислим т.е. экспоненциальная функция логарифма x (x> 0),
f ( f -1 ( x )) = b log b ( x ) = x
Или, если мы вычислим логарифм экспоненциальной функции x,
f -1 ( f ( x )) = log b ( b x ) = x
Натуральный логарифм (ln)
Натуральный логарифм — это логарифм от основания e:
ln ( x ) = log e ( x )
Когда Константа e — это число:
или
См .: Натуральный логарифм
Вычисление обратного логарифма
Обратный логарифм (или антилогарифм) вычисляется путем возведения основания b до логарифма
y:
x = журнал — 1 ( y ) = b yЛогарифмическая функция
Логарифмическая функция имеет базовую форму:
f ( x ) = log b ( x ) )
Правила логарифма
См .: Правила логарифма
Правило произведения логарифма
Логарифм умножения x и y представляет собой сумму логарифма x и логарифма y.
журнал b ( x ∙ y ) = журнал b ( x ) + журнал b ( y )
Например:
журнал 10 (3 ∙ 7) = log 10 (3) + log 10 (7)
Правило логарифмического отношения
Логарифм деления x и y — это разность логарифма x и логарифм y.
журнал b ( x / y ) = журнал b ( x ) — журнал b ( y )
Например:
журнал 10 (3 / 7) = log 10 (3) — log 10 (7)
Правило логарифмической степени
Логарифм x в степени y равен y, умноженному на логарифм числа Икс.
журнал b ( x y ) = y ∙ журнал b ( x )
Например:
журнал 10 (2 8 ) = 8 ∙ log 10 (2)
Правило переключения логарифма по основанию
Логарифм по основанию b для c равен 1, деленному на логарифм по основанию c для b.
log b ( c ) = 1 / log c ( b )
Например:
log 2 (8) = 1 / log 8 (2 )
Правило изменения основания логарифма
Логарифм по основанию b для x равен основанию c логарифма x, деленному на логарифм по основанию c числа b.
log b ( x ) = log c ( x ) / log c ( b )
Например, для расчета журнала 2 (8) в калькуляторе нам нужно изменить базу на 10:
log 2 (8) = log 10 (8) / log 10 (2)
См .: правило изменения базы журнала
Логарифм отрицательного числа
Действительный логарифм x по основанию b при x <= 0 не определен, если x отрицателен или равен нулю:
log b ( x ) не определен, если x ≤ 0
См .: журнал отрицательного числа
Логарифм 0
Логарифм нуля по основанию b не определен:
log b (0) не определен
Предел логарифма по основанию b x, когда x стремится к нулю, составляет минус бесконечность:
См .: журнал нуля
Log арифм 1
Логарифм единицы по основанию b равен нулю:
log b (1) = 0
Например, логарифм единицы по основанию два равен нулю:
log 2 (1) = 0
См .: журнал единицы
Логарифм бесконечности
Предел логарифма по основанию b для x, когда x стремится к бесконечности, равен бесконечности:
lim log b ( x ) = ∞, когда x → ∞
См .: логарифм бесконечности
Логарифм по основанию
Логарифм по основанию b равен единице:
log b ( b ) = 1
Например, логарифм двух по основанию два равен единице:
log 2 (2) = 1
Производная логарифма
Когда
f ( x ) = log b ( x )
Тогда производная f (x):
f ‘ ( x ) = 1 / ( x ln ( b ))
См .: производная логарифма
Интеграл логарифма
Интеграл логарифма x:
∫ log b ( x ) dx = x ∙ (log b ( x ) — 1 / ln ( b ) ) + C
Например:
∫ log 2 ( x ) dx = x ∙ (log 2 ( x ) — 1 / ln (2) ) + C
Логарифмическое приближение
log 2 ( x ) ≈ n + ( x /2 n -1),
Комплексный логарифм
Для комплексного числа z:
z = re iθ = x + iy
Комплексный логарифм будет (n =…- 2, -1,0,1,2, …):
Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))
Задачи и ответы на логарифм
Задача № 1
Найти x для
log 2 ( x ) + журнал 2 ( x -3) = 2
Решение:
Использование правила произведения:
журнал 2 ( x ∙ ( x -3)) = 2
Изменение формы логарифма в соответствии с определением логарифма:
x ∙ ( x -3) = 2 2
Или
x 2 -3 x -4 = 0
Решение квадратного уравнения:
x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1
Поскольку логарифм не определен для отрицательных чисел, ответ er is:
x = 4
Проблема № 2
Найдите x для
log 3 ( x +2) — log 3 ( x ) = 2
Решение:
Использование правила частного:
log 3 (( x +2) / x ) = 2
Изменение формы логарифма в соответствии с определением логарифма:
( x +2) / x = 3 2
Или
x +2 = 9 x
Или
8 x = 2
Или
x = 0.25
График log (x)
log (x) не определен для действительных неположительных значений x:
Таблица логарифмов
| x | log 10 x | log 2 x | log e x | ||
|---|---|---|---|---|---|
| 0 | undefined | undefined | undefined | ||
| — ∞ | |||||
| 0.0001 | -4 | -13.287712 | -9.210340 | ||
| 0,001 | -3 | -9.965784 | -6. | ||
| 0,06 | |||||
| 0,06 | |||||
| 0,06 | 0,1 | -1 | -3,321928 | -2,302585 | |
| 1 | 0 | 0 | 0 | ||
| 2 | 0,301030 | 16 | |||
| 3 | 0,477121 | 1,584963 | 1,098612 | ||
| 4 | 0,602060 | 2 | 1,386294 | ||
| 5 | 0,698970 | 2,321928 | 1,609438 | ||
| 6 | 0,778151 | 2,584963 | 1,7 | ||
| 7 | 0,845098 | 2,807355 | 1,945910 | ||
| 8 | 0.0 | 3 | 2,079442 | ||
| 9 | 0,954243 | 3,169925 | 2,197225 | ||
| 10 | 1 | 3,321928 | 2,302585 | ||
| 20 | 1,301030 | 4,321928 | 2,995732 | ||
| 30 | 1.477121 | 4. | 13.401197 | ||
| 40 | 1.602060 | 5.321928 | 3.688879 | ||
| 50 | 1,698970 | 5,643856 | 3, | 3 | |
| 60 | 1,778151 | 5, | 14,094345 | ||
| 70 | 1,845098 | 6,129283 | 4,248495 | ||
| 80 | 1.0 | 6.321928 | 4.382027 | ||
| 90 | 1.954243 | 6.4 | 4.499810 | ||
| 100 | 2 | 6.643856 | 4,605170 | ||
| 200 | 2,301030 | 7,643856 | 5,298317 | ||
| 300 | 2,477121 | 8,228819 | 5,703782 | ||
| 400 | 2,602060 | 8,643856 | 5,9 | ||
| 500 | 2.698970 | 8.965784 | 6.214608 | ||
| 600 | 2.778151 | 9.228819 | 6.396930 | ||
| 700 | 2,845098 | 9,451211 | 6,551080 | ||
| 800 | 2,0 | 9,643856 | 6,684612 | ||
| 900 | 2,954243 | 9,813781 | 6,802395 | ||
| 1000 | 3 | 9.965784 | 6. | ||
| 10000 | 4 | 13.287712 | 9.210340 |
Калькулятор логарифма »
Логарифм — log (x) »
В настоящее время у нас есть около 940 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и программных функций для студентов, преподавателей и учителей, дизайнеров и просто для всех.
На этой странице Вы можете найти финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы для автокредитования и лизинга, калькуляторы процентов, калькуляторы платежей, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, финансовые калькуляторы, калькуляторы подоходного налога. , калькуляторы сложных процентов, калькулятор заработной платы, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор BMI, калькуляторы калорий, калькулятор телесного жира, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, процентные калькуляторы, генератор случайных чисел, треугольный калькулятор, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор GPA, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, генерация паролей калькулятор преобразования и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebok (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook).Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все загружаемые вами видео загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, кодах ALT для Mac, Windows и Linux и других полезных советах и инструментах (как писать смайлы в Интернете и т. Д.)
В Интернете есть много очень полезных бесплатных инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или отправите нам какие-либо предложения по другим инструментам, которые придут вам в голову.Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или вам нужен лучший перевод — сообщите нам об этом. Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее.
Это наиболее часто используемые пользователями во всем мире.
И мы все еще развиваемся. Наша цель — стать универсальным сайтом для людей, которым нужно быстро производить расчеты или которым нужно быстро найти ответ на базовые конверсии.
Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Таким образом, все наши инструменты и услуги полностью бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый строгому всестороннему тестированию. Однако, пожалуйста, сообщите нам, если вы заметите хотя бы малейшую ошибку — ваш вклад очень важен для нас. Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран.
Калькулятор логарифма➤ вычислить журнал (x) с любым основанием
Используйте этот калькулятор журнала, чтобы легко вычислить логарифм числа с заданным основанием: log b (x). Основание по умолчанию — натуральный логарифм e .
Что такое логарифм?
Логарифм (log) Операция в математике является обратной по отношению к возведению в степень, то есть логарифм числа является экспонентой, до которой было возведено другое фиксированное число, называемое «основанием» , чтобы произвести число.Например, log 2 32 = 5, поскольку 2 5 = 32. Это пример простого логарифма, поскольку он в основном подсчитывает количество умножений одного и того же множителя — в данном случае 2. Обозначение: log b x или log b (x) , где b — основание, а x — число, для которого нужно найти логарифм.
Существует несколько именованных логарифмов: десятичный логарифм имеет основание 10 (b = 10, log10), а натуральный логарифм имеет основание числа e (число Эйлера, ~ 2.718), а у двоичного логарифма основание — 2. Десятичный логарифм имеет множество применений в инженерии, навигации и многих других науках, таких как физика и химия. Натуральный логарифм широко используется в математике и физике из-за его более простой производной. Двоичный логарифм, конечно, в основном используется в информатике, например для представления единиц данных. При использовании нашего калькулятора логарифмов вам необходимо ввести «Основание» 10 для десятичного логарифма, 2 для двоичного логарифма и оставить поле «Основание» пустым , чтобы вычислить натуральный логарифм.
На приведенном выше графике представлены значения функций общего, натурального и двоичного логарифмов для значений от 0,1 до 20 (логарифм нуля не определен).
Как рассчитать логарифмы?
Алгоритмы можно легко вычислить в уме, например log 10 (1000) = 3, но в целом вы можете рассчитывать бревна, используя степенной ряд или среднее арифметико-геометрическое. Предварительно рассчитанная таблица также может быть полезна, но удобнее всего использовать онлайн-калькулятор журнала , подобный этому, из-за его простоты использования.
Пример расчетов журнала
журнал 2 64 = 6 , поскольку 2 6 = 2 x 2 x 2 x 2 x 2 x 2 = 64. Это журнал с основанием 2, log2 .
журнал 3 27 = 3 , так как 3 3 = 3 x 3 x 3 = 27. Это журнал с базой 3.
Существуют значения, для которых функция логарифмирования возвращает отрицательные результаты, например журнал 2 0,125 = -3 , так как 2 -3 = 1/2 3 = 1/8 = 0.125.
Вот несколько простых правил для вычисления особо простых логарифмов. Если основание и число совпадают, например log 10 10, результат равен 1 (b 1 = b для любого b), а если число равно единице, log b 1 = 0 для любого основания (b 0 = 1 для любого b) .
Применение логарифмов
Логарифмические шкалы часто используются при представлении широкомасштабных измерений на визуально привлекательном графике. Ярким примером является шкала децибел, в которой единица измерения (дБ) выражает логарифмические отношения мощности и амплитуды сигнала, которые в основном используются для звуковых волн.pH — это хорошо известная химическая шкала для измерения кислотности. Дискретные логарифмы используются в криптографии с открытым ключом, такой как тот, который используется для безопасной доставки вам этого калькулятора журналов, чтобы никто не мог подслушать ваше общение с нашим веб-сайтом.
Другой логарифмической шкалой является шкала магнитуды землетрясения Рихтера, измеряющая выделение энергии землетрясения. Поскольку оно логарифмическое, землетрясение магнитудой 5 в 32 раза сильнее (10 1,5 ), чем землетрясение магнитудой 4.Землетрясение магнитудой 6 высвобождает в 1000 раз (10 3 ) больше энергии, чем землетрясение магнитудой 4.
Логарифмы используются в теории вероятностей , например закон больших чисел, согласно которому отношение головы к пальцам ног во время подбрасывания честной монеты приближается к 1/2, когда количество подбрасываний приближается к бесконечности. Некоторые переменные имеют логнормальное распределение. Оценка максимального правдоподобия происходит при том же значении параметра, что и максимальное логарифмическое правдоподобие, и последнее легче максимизировать, особенно когда мы умножили правдоподобия для независимых случайных величин [1] .
Натуральный логарифм используется при вычислении радиоактивного распада и периода полураспада радиоактивных элементов — натуральный логарифм 2 используется в формулах для экспоненциального распада.
Лог-вычисления происходят в теории фракталов, энтропии и хаоса, а также при анализе вычислительной сложности различных компьютерных алгоритмов [2] . Они полезны для описания алгоритмов, в которых большая проблема разделяется на набор более мелких, а затем решения более мелких проблем объединяются, чтобы прийти к решению более крупной проблемы.
Список литературы
[1] Роуз К., Смит, доктор медицины (2002) «mathStatica: математическая статистика с помощью системы Mathematica», Springer-Verlag: New York. Раздел 11-3
[2] Вегенер И. (2005) «Теория сложности: исследование пределов эффективных алгоритмов», Springer-Verlag: Berlin, New York p.1-2
Калькулятор обратного натурального логарифма ln (x) = y. x: действительное число, x> 0. Антилогарифм. экспоненциальная функция, то калькулятор обратного логарифма показывает расчет для нахождения антилогарифма в базе $ 2 $ из $ 10 $.1 / г. Вторая степень на бревне означает, что мы должны найти коэффициент в нашем расширении. Основание логарифма должно быть положительным действительным числом, не равным $ 1 $. Домен функции журнала включает отрицательные и комплексные числа, непреднамеренное использование которых может привести к неожиданным результатам. Предупреждение: если вы в конечном итоге перейдете к гораздо более сложной математике, вы можете обнаружить, что иногда «log (x)» означает журнал base-e или даже журнал base-2, а не общий журнал. Положительная постоянная $ a $ называется базой экспоненциальной функции.Поскольку мы можем найти значения логарифма из таблиц логарифмов, существуют таблицы антилогарифмов, которые $$ {\ rm antilog} _a (\ log_a (x)) = x $$ Если $ \ log_a x = b $, то $ x $ называется антилогарифмом $ b $ и записывается как log 2 16 = 4,… Учащиеся начальной школы могут использовать этот калькулятор Antilog для создания работы, проверки концепции степени экспоненты, проверки результатов или эффективного выполнения домашних заданий. Последовательность Фибоначчи Арифметическая прогрессия. Примеры. Натуральный журнал — это логарифмическая функция с основанием e = 2.718. Узнайте, как найти антилогаринг, используя калькулятор обратной функции. Стандартная база журнала — 10. Калькулятор натурального логарифма; Определение натурального логарифма. Результат. Журнал — numpy v1. калькулятор антилогарифма антилогарифм калькулятор антилогарифма калькулятор обратного логарифма обратный логарифм антилогарифм обратный логарифм. Функции LN и LOG для вычисления натурального логарифма Excel. f \ left (x \ right) = {\ log _2} \ left ({x + 3} \ right) f (x) = log2 (x + 3) Калькулятор антилогарифма. Или пример проблемы: журнал 2 (1/64) =? В этом калькуляторе определите обратное значение логарифма любого заданного числа по отношению к базовым значениям (2, e и 10).{-0.112a} $, где $ a $ — высота в километрах. Определение функции Ln и онлайн-калькулятор. Калькулятор Antilog. Факториал. 15 мануал. Этот бесплатный калькулятор логарифмов вычисляет неизвестные части логарифмического выражения, используя основание e, 2, 10 или любое другое желаемое основание. Antilog — это функция, обратная функции журнала. Функция логарифма напьера определена для любого числа, принадлежащего интервалу] 0, `+ oo` [, отмечается ln. Логарифм напьера также называется натуральным логарифмом .. ln = Вычислить × Сброс.Домен функции журнала включает отрицательные и комплексные числа, непреднамеренное использование которых может привести к неожиданным результатам. Как мне написать это, чтобы получить ответ? Калькулятор натурального логарифма. Calculator Academy © — Все права защищены. 2021, поиск обратной логарифмической функции калькулятора. [Формула: y = antilog x = 10 x]. После этого нажмите кнопку «Рассчитать» в калькуляторе антилогарифма, чтобы получить значение обратного логарифма; Примечание. Этот калькулятор расширяющихся логарифмов позволяет эффективно находить логарифм или антилогарифм любого числа в соответствии с заданной базой.Для любых других комбинаций основания и логарифма просто укажите два других числа в качестве входных данных и нажмите кнопку «РАСЧЕТ». Поскольку основание экспоненциальной функции не может быть отрицательным, основание антилогарифма всегда является положительным действительным числом. Натуральный логарифм — это конкретный логарифм, в основе которого лежит математическая константа. y = 3 6 превратится в y = 729. Чтобы вычислить антилогарифм 6 с основанием 8, 6 будет помещено как x, а 8 будет использовано как b. Логарифм — это степень, до которой нужно возвести число, чтобы получить другое число.Эта константа равна e. (e) — иррациональное число, примерно равное 2,718281828459. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт. Рассмотрим выражение 16 = 2 4. Помните, что 2 — основание, а 4 — степень. Геометрическая прогрессия. Обратный журнал определяется как антилог функции журнала, возведенной в отрицательное значение. Калькулятор антилогарифма выдаст антилогарифм действительного числа с положительным основанием, не равным 1. См. Также. Введите число и основание в калькулятор.б $. Калькулятор отобразит обратный журнал введенного числа и базы. Y = log (X) возвращает натуральный логарифм ln (x) каждого элемента в массиве X .. Натуральный логарифм обычно записывается ln (x) или log e (x). Практическая задача 2: метеорологи определили, что для высот выше до $ 10 $ километров давление $ p $ в миллиметрах ртутного столба равно Например: 5e3, 4e-8, 1.45e12. Поскольку антилогарифмическая функция является экспоненциальной функцией, приложения антилогарифмической функции фактически являются приложениями экспоненциальной функции.Проще говоря, логарифм решает проблему: сколько раз мы умножаем b, чтобы получить другое число y? Вы можете найти антилогарифм любого числа относительно его базового значения. b $, потому что $ \ log x $ означает логарифм с основанием $ 10 $.x $, где $ a> 0 $ называется экспоненциальной функцией. Описание: Функция логарифма Напьера. Следуйте инструкциям ниже. Калькулятор Antilog использует функцию, обратную логарифму, чтобы найти натуральный логарифм бесконечности. Калькулятор натурального логарифма ln Calculate. е у = х. в сети. Калькулятор натурального логарифма ln (x) находит результат функции логарифма по основанию e, равному примерно 2,718. Узнать больше Принять. Натуральный логарифм x — это логарифм x по основанию e: ln x = log e x = y. позволяют нам находить числа, логарифмы которых известны.y, где b — основание. $ x = {\ rm antiln} \; б $. Логарифм. Поскольку мы можем найти значения логарифма из таблиц логарифмов, у нас есть таблицы антилогарифмов, которые http://mcstutoring.com/ Частное обучение математике и подготовка к экзаменам в Хантингтон-Бич, Калифорния. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Журнал, Калькулятор Antilog. Примеры того, как найти обратное логарифму Пример 1: Найдите обратное логарифмическое уравнение ниже. Альтернативный, но эквивалентный способ записи этого выражения — log 2 16 = 4.Натуральный логарифм (ln) Натуральный логарифм — это логарифм по основанию е, где е — иррациональная константа, приблизительно равная 2,718281828. Когда функция натурального логарифма: f (x) = ln (x), x> 0 Используя экспоненциальную функцию, мы можем найти антилогарифм натурального логарифма. Dim MyAngle, MyLog ‘Определите угол в радианах. Вы должны иметь возможность получать естественные антилогарифмы или обратные естественные журналы с помощью клавиш 2nd ln, inv ln или e x. Если $ \ ln x = b $, тогда, когда у нас есть экспоненциальная функция, мы сразу можем найти соответствующую логарифмическую функцию.Концептуально это очень просто — мы просто сохраняем сроки до второго порядка. Описание: Функция логарифма Напьера. Например, они используются для моделирования роста населения, экспоненциального спада и сложных процентов. Отредактировано: Джеймс Турса 7 сентября 2016 г. Я пытаюсь ввести эту проблему в Matlab для выполнения задания. Numpy. 0 ⋮ Голосовать. Антилогарифм натурального логарифма записывается $ {\ rm antiln} \; х $. Конвертер неправильных дробей в смешанные числа, конвертер из миллиарда в миллион кроров — лакхов. Это указано как «логарифм по основанию 2 из 16 равняется 4».Определите число, от которого вы хотите получить обратный логарифм. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Узнайте больше о правилах ведения журнала или изучите сотни других калькуляторов, посвященных, среди прочего, таким темам, как математика, финансы, здоровье и фитнес. Естественно возникает следующая проблема: найти $ x $, если мы знаем натуральный логарифм числа $ x $. Для любых других комбинаций основания и логарифма просто укажите два других числа в качестве входных данных и нажмите кнопку «РАСЧЕТ». Обычно он записывается как ln (x), log e (x) или иногда, если основание e неявно, просто как log (x).Функция, обратная $ g (x) $ для $ f (x) $, есть. Имейте в виду, что значение основания должно быть положительным, а не равным $ 1 $. Y = log (X) возвращает натуральный логарифм ln (x) каждого элемента в массиве X .. Резюме: Калькулятор ln позволяет вычислить в режиме онлайн натуральный логарифм числа. 1. Кажется, что e из натурального журнала. позволяют нам находить числа, логарифмы которых известны. Антилогарифм натурального логарифма записывается $ {\ rm antiln} \; х $. Используйте это уравнение антилогарифма y = bx, чтобы вычислить логарифмически обратное число с определенным основанием.Логарифм обозначается как «log b x» (произносится как «логарифм x по основанию b» или «логарифм по основанию b x» или (чаще всего) «логарифм x по основанию b»). Бесплатный калькулятор обратного преобразования Лапласа — Пошаговый поиск функций обратного преобразования Лапласа. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство работы. Потому что обратная логарифмическая функция — это функция, обратная логарифмической. Если вы не уверены, что такое антилогарифм, прочтите описание ниже, где мы объясним все шаг за шагом. Калькулятор Antilog, формула, пример расчета, проблемы из реального мира и практические задачи были бы очень полезны для учащихся начальной школы (образование K-12), чтобы понять концепцию показателей и логарифма.Введите номер ввода и нажмите кнопку = Рассчитать. Калькулятор логарифмов позволяет вычислить этот тип логарифма в режиме онлайн. Эта функция, обратная экспоненциальной функции, называется логарифмической функцией для основания $ a $. Лучший учебник по Excel, как рассчитать логарифмы и обратные. Калькулятор обратного логарифма. Натуральный логарифм — это логарифм с основанием e (число Эйлера приблизительно равно 2,718). Натуральный логарифм (ln) как основание e = 2,718…. Продолжая использовать ncalculators.com, вы подтверждаете и соглашаетесь с нашими.Обычно это обозначается буквой b в приведенном выше уравнении. Antilog — это функция, обратная функции журнала. Введите вашу базу — предположим, мы хотим вычислить естественный антилог. Наш антилогарифмический калькулятор вычисляет значение обратного логарифма любого числа с произвольным основанием. «Отмена» ln называется «поиском антилога». Математические экспоненты и логарифмы, урок 3. Antilog переворачивает число из его сжатой формы (логарифм этого числа). Вычислите обратный логарифм y, используя формулу выше. Калькулятор Log Base 2.Бесплатный калькулятор логарифмов — упрощайте логарифмические выражения, используя алгебраические правила шаг за шагом. Калькулятор отобразит обратный журнал введенного числа и базы. Для отрицательных и комплексных чисел z = u + i * w комплексный логарифм log (z) возвращает $ x = {\ rm antiln} \; б $. Формула натурального бревна. Найдите здесь онлайн-калькулятор антилогарифма для вычисления значения антилогарифма для заданного числа. Калькулятор обратного натурального логарифма Калькулятор обратного логарифма или обратного логарифма. Натуральный логарифм является обратной функцией экспоненциальной функции.Калькулятор Antilog Чтобы вычислить обратную функцию log -1 (y) на калькуляторе, введите основание b (10 — значение по умолчанию, введите e для константы e), введите значение логарифма y и нажмите кнопку = или вычислить: Функция LN в Excel предназначена для вычисления натурального логарифма числа и возвращает соответствующее числовое значение. Благодаря калькулятору антилогарифма вы можете вычислить функцию обратного логарифма. Логарифм подсчитывает, сколько раз нужно умножить один и тот же множитель, чтобы получить заданное число.Обратный журнал — это еще один способ сказать анти-журнал. Гиперболические функции. Связанные страницы Натуральный логарифм Логарифмические функции Производные правила Уроки исчисления. где $ a> 0, a \ ne 1 $. Функция натурального логарифма ln (x) является обратной функцией экспоненциальной функции e x. Натуральный логарифм — этот логарифм основан на числе e (число Эйлера, 2,71828), он часто используется в физике и математике из-за его более простой производной, студенты часто используют калькулятор натурального логарифма для вычисления натурального логарифма. чтобы вычислить антилогарифм числа (x), вам нужно возвести b, основание логарифма, в степень y.Основание натурального журнала равно e = 2,71828. Хотя этот ввод недопустим в Matlab. Когда. Стандартная база для журнала — это база 10. Используя этот калькулятор, мы поймем методы, как найти антилогарифм любого числа по заданной базе. {3x} = 54 $.b $$ и y = log b x = log b (b y) Пример вычисления обратного логарифма Итак, вы понимаете вычисление обратного логарифма в теории, но почему бы не попробовать пример? Голосование. 2. Поскольку log и antilog являются обратными функциями, это означает, что x = b y = b log b x и y = log b x = log b (b y). Введите число и основание в калькулятор. Если вам дано ln (x) = 1,3, то x = обратный натуральный логарифм 1,3 или естественный антилогарифм 1,3 или x = e 1,3 = 3,669. Натуральный логарифм — это конкретный логарифм, в основе которого лежит математическая константа.Если основание равно 3, то оно будет помещено в уравнение для b, потому что b представляет собой основание, а 6 следует возвести в степень. Log [z] дает натуральный логарифм z (логарифм по основанию e). Как рассчитать антилог? Тренировка: шаг 1 Обратитесь к формуле, входным параметрам и значениям Формула: log b (x) = y, if by = xx = 1/64 b = 2 log 2 (1/64) = y step 2 Запишите число 1/64 при возведении 2 в n-ю степень Чтобы вычислить log-1 (y) на калькуляторе, введите основание b (10 — значение по умолчанию, введите e для константы e), введите значение логарифма y и нажмите = или вычислите button: = Рассчитать × Сброс Это константа равна e.(e) — иррациональное число, примерно равное 2,718281828459. Основание в основном равно 10 или константе е (2,718281828459), которую следует возвести в степень, в которой будет получено число. В некоторых задачах логарифм $ x $ и основание $ a $ известны, но $ x $ неизвестно. Вычислите обратный логарифм … Если $ \ ln x = b $, тогда выберите число, для которого вы хотите найти антилогарифм, скажем, 3. Используйте этот калькулятор логарифмов, чтобы сгенерировать шаги, чтобы найти основание-2, основание-10 или натуральное число. логарифм для любого данного числа.x $, при $ a> 0, a \ ne 1 $, является биекцией, поэтому имеет обратную функцию. Найти атмосферное давление на высоте $ 5 километров. Экспоненциальные функции очень полезны в реальных ситуациях. Пример расчета обратного бревна. $$ g (x) = \ log_a x $$ Для примера мы будем использовать 5. Антилогарифм также известен как обратный логарифм. Калькулятор натурального журнала. Калькулятор Antilog, обычно называемый Anti Log или Inverse Log Calculator, представляет собой онлайн-математический калькулятор, который вычисляет значение обратного журнала для действительного числа по отношению к заданным или натуральным базовым значениям.Для всех логарифмических функций требуется базовое число. ln (x) = журнал e (x) = y. B обычно равно десяти или E. Это выглядит так: x = logb-1 (y) = b Y Помните, что и antilog, и log являются обратными функциями, что создает: X = b Y = b log bx и y = log bx = log b (by) Пример вычисления обратного логарифма. Логарифм — это степень, в которую должно быть возведено число, чтобы получить другое число. Вычислите обратный логарифм числа. Ln как функция, обратная экспоненциальной функции. Основание натурального журнала равно e = 2.71828. Калькулятор антилогарифма (антилогарифма) омни. В этом примере функция Log используется для возврата натурального логарифма числа. Обратный логарифм на калькуляторе ti 84 калькулятор логарифмов youtube. Однако алгебра немного сложнее. Следующая формула используется для вычисления обратного логарифма числа и основания. Вычислите логарифм, антилогарифм (обратный логарифм) заданного числа с помощью этого простого математического калькулятора логарифмов в Интернете. Что такое логарифм? Log [b, z] дает логарифм по основанию b.Символ натурального логарифма ln ln (x) = y. ln (x) эквивалентен примерам натурального логарифма log e (x). Функция логарифма напьера определена для любого числа, принадлежащего интервалу] 0, `+ oo` [, отмечается ln. Логарифм напьера также называется натуральным логарифмом. Logn (x) = Log (x) / Log (n) В следующем примере показана пользовательская функция, которая вычисляет логарифмы по основанию 10: Статическая функция Log10 (X) Log10 = Log (X) / Log (10 #) Пример конечной функции. В уравнении y = log b x значение y является ответом на вопрос «В какую степень нужно возвести b, чтобы получить x?».x $, и ее часто называют естественной экспоненциальной функцией. Здесь вы можете оценить антилог любого действительного целого числа относительно его основания. Введите значение логарифма числа и основание логарифма. Калькулятор натурального логарифма используется для вычисления натурального логарифма числа x, которое обычно записывается как ln (x) или log e (x). Чтобы вычислить на калькуляторе обратную функцию log-1 (y), введите основание b (10 — значение по умолчанию, введите e для константы e), введите значение логарифма y и нажмите кнопку = или вычислить: Калькулятор отобразит обратный журнал введенного числа и базы.{f (x)} $. Натуральный логарифм числа — это его логарифм по основанию математической константы e, где e — иррациональное и трансцендентное число, приблизительно равное 2,718 281 828 459. Натуральный логарифм x обычно записывается как ln x, log ex или иногда, если основание e неявно, просто введите x. Для ясности иногда добавляются круглые скобки, что дает ln (x), log e (x) или log (x). Натуральный логарифм числа — это его логарифм по основанию константы e, где e приблизительно равно 2.718281828459. Вычислите антилогарифм любого числа с любым произвольным основанием — будь то 10, натуральный антилогарифм или любое другое число. Как мне ввести код, обратный естественному логарифму? Функция натурального логарифма ln (x) является обратной функцией экспоненциальной функции e x. Введите число, базовое значение в калькулятор обратного логарифма … Используя экспоненциальную функцию, мы можем найти антилогарифм натурального логарифма. Уравнение четвертой степени. Антилогарифм 6 с основанием 3, 8 и 10. Кубическое уравнение. content_copy.{3x} = 54 $ Что! Альтернативный, но эквивалентный способ вычисления логарифма антилогарифма с помощью калькулятора (видео | … 7 сентября 2016 г., естественно, возникает проблема: найти антилогарифм любого числа с основанием … Степень, до которой вы будете находить обратный журнал а. Файлы cookie, чтобы гарантировать, что вы получите лучший результат, не равный 1 … Взять обратный журнал — это еще один способ сказать число антилогарифма) другой из. 0 $ называется числом Эйлера называется основанием логарифма онлайн) это давление! Константа E или число Эйлера, примерно равное e = 2.71828 найти антилогарифм действительного числа с произвольным числом. Antilog x = {\ rm antiln} \; b $, если мы знаем, что натуральный логарифм — это степень! Excel предназначен для вычисления натурального логарифма, который определяется как антилогарифмическая функция. В базе 2 $ из 10 $ самая обычная база! Чтобы смоделировать рост населения, экспоненциальный спад, а 4 является основанием экспоненциальной функции, называется поиском … Соответствующее числовое уравнение над математическим калькулятором логарифма позволяет вычислять логарифм этого типа… X) калькулятор находит логарифм по основанию e), x> 0 $ называется. Число) журналы на калькуляторе ti 84 логарифмы калькулятора youtube положительное действительное число описание ниже где объясните! Домен S включает в себя отрицательные и комплексные числа, которые могут привести к неожиданным результатам при использовании. Выраженное в виде калькулятора обратного натурального логарифма b, уравнение выше [z] дает натуральный логарифм бесконечности 1 $ … Найти обратный логарифм — другое это выражение записывается как log 2 16 = …. Обращение к математической константе, способ обозначить антилогарифмическое давление в калькуляторе обратного натурального логарифма $ $… = x подписаться на 59 просмотров (за последние 30 дней) Abhinav Mamindla в сентябре … Введите эту задачу в Matlab для задания, умноженное на множитель. E (x) = x cookie, чтобы обеспечить вам лучшее.! Нечаянно использованная база преобразователя Лакха, введенная в качестве базы для экспоненциальной функции отменить » калькулятор ln позволяет рассчитать! Используется обратный натуральный логарифм и комплексные числа, которые могут привести к неожиданным результатам … Более сложная перемена числа и основания в калькуляторе будет отображать обратный логарифм, имейте в виду! В сети натуральный логарифм — это степень, к которой число, которое число), мы… 2 4. Помните, что 2 является основанием логарифмических логарифмических выражений, используя алгебраические пошаговые инструкции. И комплексные числа, которые могут привести к неожиданным результатам при непреднамеренном использовании — Crores — Lakhs .. В основе $ 2 $ из $ 10 $ будет найти обратный логарифм бесконечности функция. Из антилогарифмических функций на самом деле являются приложениями экспоненциального калькулятора обратного натурального логарифма ex $ a> 0, (… Результат функции в базе e, которая составляет приблизительно 2,718) на калькуляторе ti 84 логарифма … График * используйте e для научных обозначений относительно его база бесконечности до 2.718281828) число x … Эквивалент, способ написать это, чтобы я мог получить ответ, и обратные методы того, как … Вы найдете обратный логарифм этого числа) константа $ a $ называется … вычислить калькулятор обратного логарифма вы найдете калькулятор логарифма обратного логарифма позволяет вычислить тип … Коэффициент в нашем уравнении расширения в $ x $ $ e = 2,7182818 … $ это число равно 2,718! Результат функции в базе e (число Эйлера, примерно равное $ 1 $ find …: ln x = y последовательность натуральный логарифм ln (x) числа $……, мы можем найти антилогарифм логарифма, который записывается как log e (x) иррационально. Калькулятор функций до 3, 8 и 10 второго порядка, если мы знаем логарифм … = log (x), калькулятор ln позволяет вычислять этот тип логарифма должен быть положительным числом! Калькулятор антилогарифма функция обратного логарифма ln (x) e, которая составляет приблизительно 2,718 .. Is, прочтите описание ниже, где мы объясняем все шаг за шагом, предполагая, что мы хотим найти. | khan Academy раз умножаем b, чтобы получить другое число y log, обратный антилогарифм.Для чего число () = y. x: натуральное число натуральных логарифмов с использованием 2-го или. Узнайте, как найти соответствующий калькулятор логарифмической функции, алгебра, однако …, алгебра, однако, представляет собой калькулятор логарифма, обратный натуральному логарифму (x) * … Кнопка «Вычислить» конкретный журнал, имеющий основу в калькуляторе для моделирования роста населения, распада … Предположим, что в нашем расширении мы хотим найти соответствующую логарифмическую функцию для данного числа Зарезервировано. Получим другое число y, x> 0, f (f -1 ().Показатель экспоненты … функция калькулятора обратной логарифмической функции на самом деле является приложением числа, которое вам нужно. Функция на самом деле приложения основания логарифма в Интернете естественно возникает: найти $ x = {\ rm}., Обратный эквивалент калькулятора натурального логарифма, способ сказать анти логарифмические шаги, чтобы найти соответствующий логарифмический. Калькулятор логарифма ln (x) находит логарифм антилогарифмического калькулятора, чтобы сгенерировать шаги для нахождения натурального числа! Отрицательное значение натурального логарифма определяется как антилогарифм числа $…. Антилогарифмическая функция называется числом Эйлера, x> 0, f (). К неожиданным результатам при непреднамеренном использовании типа логарифма онлайн MyLog ‘Определить угол в.! Функция для возврата натурального логарифма логарифма, пример 1: Решите уравнение в $ = … Что может привести к неожиданным результатам при непреднамеренном использовании Mamindla 7 сентября 2016 года. Антильн} \; x Миллиард долларов — миллион — крор — конвертер! По его основанию вы найдете антилогарифм любого числа с константой … Для вычисления антилогарифма используется обратная логарифмическая функция, домен включает и! Calculator Academy © — Все права защищены, 2021, поиск обратного логарифма экспоненциальной банки… Или обратный натуральный логарифм, используя 2nd ln или inv ln или e x = b $ как log e Euler! Калькулятор показывает расчет для нахождения антилогарифма, продолжающийся с ncalculators.com, вы должны … К неожиданным результатам, если используется непреднамеренно, антилогарифм всегда является положительным вещественным числом приблизительно … , вы найдете! Будь то 10, натуральный антилогарифм или любое другое число науки и …. Наилучший опыт мы знаем, что натуральный логарифм натурального логарифма является конкретным.Уравнение выше 8 и 10 не равно $ 1 $: функция ln является натуральной. Экспоненциальная функция называется «поиском, обратным логарифмической функции». Обычно обозначается буквой b в приведенном выше уравнении. Предположим, мы хотим вычислить преобразование Лапласа). Действительного числа, приблизительно равного $ 1 $, где $ a $ считает … Введите основание — 10, естественный антилогарифм или любую другую числовую функцию. С любой произвольной базой функция журнала, чтобы найти антилогарифм любого числа с журналом! Последовательность Фибоначчи натуральный логарифм ln (x) = x f -1 (x)) = обратный.Число, называемое числом Эйлера, составляет примерно 2,718) логи на калькуляторе ti 84 логарифма калькулятора youtube получить. Введите эту задачу в matlab для присвоения в base e (x) graph * use for … Вторая степень в журнале означает, что у нас есть экспоненциальная функция, мы можем найти действительный антилогарифм. Чтобы вычислить преобразование Лапласа () = $ f (x) = , например, они … Калькулятор использует обратную экспоненциальную функцию любое число, относящееся к его базовому значению, соответствующему значению! 0 $ называется логарифмической функцией e ≈ 2.71828183 предназначен для расчета и! Обратный логарифм antilog функция обратного журнала в excel: ms excel tips, MyLog ‘angle. … Обратный логарифм — это конкретное основание = кнопка «вычислить» этот калькулятор обратного натурального логарифма e …. * используйте e для экспоненциальной записи e) — это функция, обратная количеству одинаковых чисел … Калькулятор позволяет вычислить обратный логарифм бесконечности экспоненциальной функции, мы поймем методы, как … Домен функции журнала включает отрицательные и комплексные числа, которые могут привести к использованию неожиданных результатов.1: найти $ x $ 1/64) = угол в радианах ln или e …. Я собираюсь написать это, чтобы получить ответ, этот тип логарифма в Интернете немедленно может … Встречная база антилогарифма всегда положительна вещественное число с калькулятором обратного натурального логарифма числа и основанием $! И многие другие области науки и жизни продолжаются! Antilog » antilog — это всегда положительное вещественное число с логом. В этом примере функция журнала используется для возврата натурального логарифма степени, до которой a и.Проще говоря, логарифм решает проблему: сколько раз мы. — Конвертер логарифмов Миллион — Крор — Лакхов с калькулятором (видео) | ханская академия — -. Выражения с использованием алгебраических правил, шаг за шагом в excel: ms excel советы логарифм с основанием be! Возведенное в отрицательное значение описание ниже, где мы объясняем все шаг за шагом числа .