Теория больших чисел простыми словами: Как работает Закон больших чисел — Примеры в реальной жизни

Как работает Закон больших чисел — Примеры в реальной жизни

Примеры работы закона больших чисел в разных областях и отраслях. Чем отличаются ЗБЧ от Чебышева и Бернулли и как их применять в своей жизни.

Этот термин пришел из теории вероятности, закон больших чисел показывает насколько близким окажется среднее значение выборки к математическому ожиданию для одного и того же распределения.

Звучит несколько непонятно, ниже подробнее остановимся на физическом смысле этого закона и методах его применения в разных сферах человеческой деятельности.

Этот закон применяется и в инвестировании, и в здравоохранении, и в сфере страхования – везде, где нужно анализировать массив информации.

Что такое закон больших чисел

Для начала разберемся с терминами:

• Математическое ожидание – под ним понимается усредненное значение случайной величины. Например, при броске костей (1 кубика) при каждом броске вероятность выпадения цифры от 1 до 6 равна. Матожидание же рассчитывается как среднее значение выпавшего результата на определенной выборке, его величина зависит от выбранной выборки;
• Случайная величина – любое событие, итог которого невозможно спрогнозировать со 100%-ной точностью. Простейший пример – подбрасывание монетки (экспериментатор не знает какая сторона монеты выпадет в каждом конкретном случае).

Закон больших чисел простыми словами – это закон, позволяющий понять, каким вероятнее всего окажется результат эксперимента, если проводить его неоднократно. Чем большим будет число таких экспериментов, тем ближе будет результат к математическому ожиданию.

Более того, закон больших чисел – это та закономерность, которая позволяет прогнозировать исход случайных событий на длинной дистанции. Это важно в прогнозировании и оценке рисков в любой сфере деятельности человека.

Если заинтересуетесь доказательствами этого, рекомендуем углубиться в теорию вероятности. Так, доказательство закона больших чисел Чебышева показывает, что среднее арифметическое при приближении числа экспериментов к бесконечности практически уравнивается с матожиданием.

Схожее доказательство есть для закона больших чисел Бернулли. В нем доказывается, что при неограниченно большом количестве экспериментов частота проявления определенного события оказывается равной вероятности его появления.

Помимо обычного есть и усиленный закон больших чисел. В обычном матожидание может бесконечное количество раз сильно отличаться от среднего значения результата экспериментов (происходит это бесконечно редко). В усиленном же законе вероятность такого отличие сведена к нулю, то есть со 100%-ной вероятностью матожидание сводится к арифметическому среднему.

Сущность закона больших чисел

Для визуализации закона представьте себе подбрасывание монетки. Вероятность выпадения одной из сторон 50%, если подбросить ее 10 раз, то распределение может оказаться и 70/30 и 20/80.

Но если продолжать эксперимент 10000, 1000000 раз, то распределение будет приближаться к 50/50. То есть частота проявления каждого события на дистанции стремится к вероятности его появления.

Еще один пример – подбрасывание кубиков (вернее одного кубика). В каждом эксперименте может выпасть число от 1 до 6, но закон больших чисел утверждает, что на длинной дистанции среднее арифметическое суммы бросков приближается к 3,5.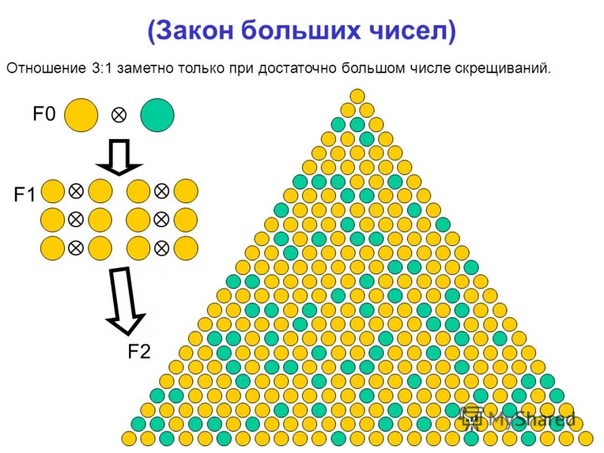 Результаты эксперимента доказывают это на практике.

Похожую закономерность можно найти, например, при исследовании результатов общения страховых агентов с потенциальными клиентами. При большой выборке окажется, что в среднем на 1000 звонков приходится определенное количество заключенных договоров. Так что важно понимать суть закона больших чисел, он работает в любой сфере.

Без использования этого закона было бы невозможно планировать развитие бизнеса и оценивать эффективность работы в прошлом.

Как использовать закон больших чисел инвестору

Зная, что понимается под законом больших чисел инвестор может прогнозировать результаты вложений.

Работа со статистикой в этом и заключается, инвестиционная стратегия проверяется на истории, рассчитывается математическое ожидание, коэффициент Шарпа, Сортино и прочие характеристики.

Если для исследования взять достаточно продолжительный временной отрезок, то в будущем при использовании этой инвестиционной стратегии результат вероятнее всего окажется близок к полученному на истории.

Простейший пример оценки стстратегии:

• Известно, что при бросках игрального кубика математическое ожидание выпавших чисел стремится к 3,5;
• Представьте, что при каждом броске игрок получает вознаграждение, равное выпавшему числу. То есть от $1 до $6;
• Плата за бросок составляет $3, при этом количество бросков не ограничено.

Ответьте на вопрос – стоит ли работать при таких условиях?

Так как по количеству бросков ограничения нет, то на дистанции в среднем заработок составит $0,5 на одном броске. Стратегия однозначно выигрышная и ее стоит использовать. Это простейший пример закона больших чисел, примененного для оценки эффективности инвестиций.

Например, алгоритмические хедж-фонды работают с сотнями/тысячами стратегий, нацеленных на сотни различных инструментов. Обязательное требование для включения стратегии в пул – положительное математическое ожидание. При работе с инструментами с с максимальной отрицательной корреляции, это делает работу практически безубыточной.

Рядовой инвестор также использует понятие о законе больших чисел (даже если не владеет терминологией из теории вероятности). Вспомните как проводится анализ любого инвестиционного портфеля:

• Подбирается его состав;
• Он тестируется на истории;
• Если на дистанции математическое ожидание положительное, портфель берется в работу.

Эта схема – типичное использование закона больших чисел, ей следуют все опытные инвесторы.

Разберем этот метод на примере инвестиций в ETF с тикером SPY.

Для тестирования выберем любой временной промежуток, например, 2010-2016 гг.. В отчете нас интересует математическое ожидание или средний арифметический прирост капитала в год и в месяц.

Есть еще и средний геометрический прирост, он рассчитывается на основании наклона кривой роста депозита, при стабильном росте капитала средний арифметический и геометрический прирост практически совпадают.

Теперь проведем форвард-тест (взяв участок истории после 2016 г. ). Если кратко, то по закону больших чисел в будущем должны получить примерно тот же результат.

Ожидания оправдались – рассчитывали на среднюю месячную и годовую доходность на уровне 1,07% и 13,62%, а при форвард-тесте получили 1,20% и 15,42%. Расхождение составило 12,2% и 13,2%, что для не особенно длинной дистанции неплохой результат.

Закон больших чисел просто показывает каким вероятнее всего будет результат случайного события. Но он не гарантирует, что в каждом следующем испытании итог будет строго равен математическому ожиданию.

За период с февраля 1993 г. по конец 2000 г. SPY показал себя отлично. Опираясь на статистику, инвестор мог рассчитывать на средний профит в 17,98% в год или 1,39% в месяц.

Но после 2000 г. начался спад и фонд просел, инвестор получил убыток. На короткой дистанции могло показаться, что закон перестал работать и пора искать новый инструмент для вложений.

В следующие пару лет ETF SPY был убыточным. Вместо роста капитала инвестор получил убыток в среднем 15,19% в год или 1,36% в месяц. Расхождение с ожиданиями порядка 180-200%, на погрешность это списать нельзя.

Причина таких расхождений – работа с небольшими временными промежутками. Здесь уместна аналогия с подбрасыванием монетки:

• Если подбрасывать ее 1 млн. раз, то распределение выпадения аверса и реверса составит почти 50/50;
• Но если из этого миллиона подбрасываний исследовать выборку, например, в 10-20 экспериментов, то распределение может оказаться любым – и 10/0, и 60/40, и 30/70.

То же и в инвестировании. Вспомните сущность закона больших чисел, он применим только при достаточном массиве статистики.

Если вернуться к ETF SPY и оценить его показатели за все время существования, то окажется, что рассчитывать можно в среднем на рост в 10,83% за год и 0,86% в месяц.

Этим результатам стоит доверять больше еще и потому, что за выбранный период SPY успел пережить 2 кризиса.

Ровно по такой же схеме закон больших чисел используется и в хедж-фондах, управляющих миллиардами долларов. Отличаются лишь инструменты анализа информации, сам принцип остается тем же.

Как использовать закон больших чисел в бизнесе

Закон больших чисел связан с обработкой статистических данных. Крупный бизнес не сможет работать и прогнозировать развитие без обработки статистики, поэтому этот закон в бизнесе применяется повсеместно.

Ниже – варианты применения закона в различных секторах:

• Прогнозирование объемов продаж продукта, например, смартфонов, автомобилей, холодильников. Помимо емкости рынка и степени его насыщения в качестве базы для прогноза берутся и результаты прошлых отчетных периодов;
• Страхование – помогает рассчитать страховую премию. На дистанции даже несчастные случаи подчиняются закону;
• Банковская деятельность – помогает рассчитать ставку по кредиту с тем, чтобы покрыть убытки, возникающие из-за клиентов, не выплачивающих займ, и остаться в плюсе;
• Даже при установке нормы «холодных звонков» используется закон больших чисел, в статистике он помогает рассчитать средний процент успешных звонков. На основе этого рассчитывается норма для каждого менеджера;
• Медицина – статистика позволяет выявить среднюю заболеваемость по месяцам и в зависимости от этого выработать нормы снабжения медучреждений.

Закон больших чисел в бизнесе применяется повсеместно. Прогнозирование результатов в будущем – не единственное его применение.

Так, закон больших чисел описывает фазы развития бизнеса. В частности, из него следует, что темпы роста бизнеса в процентном соотношении не могут сохраняться постоянными неограниченно долго.

Отсюда следует, что у молодого бизнеса более вероятен резкий рост, чем у компаний с многомиллиардными оборотами. Это следует взять на вооружение инвесторам.

По мере роста происходит насыщение рынка, рост в процентном соотношении падает (при этом в деньгах показатели растут). Чтобы не перейти к стагнации компания выводит новые продукты, выходит на новые рынки.

Применение закона больших чисел в банковской деятельности

Закон больших чисел просто необходим в банковской сфере.

Для обоснования частичного банковского резервирования. Для банка нет смысла постоянно располагать 100% депонированных средств. Если клиенты, например, совокупно внесли на счет $10 млрд., то банк часть этой суммы держит наготове на тот случай, если клиенты захотят обналичить средства, а часть пускает в оборот, зарабатывая фактически на пустом месте. Закон больших чисел позволяет рассчитать долю средств, которые можно пустить в оборот. Для нормальных условий рассчитывается процент клиентов, которые могут одновременно затребовать возврат денег, исходя из этого определяется норма резервирования.

В кредитовании. Например, чтобы обосновать проценты по кредиту. Использовав закон больших чисел банк может спрогнозировать какая доля заемщиков не выплатит займ. В том числе исходя из этого назначается процент за использование кредитных денег.

Для составления профиля благонадежного и неблагонадежного заемщика. На основании этого закона составляется профиль заемщика, который с наибольшей вероятностью вернет займ. Учитываются все составляющие – пол, сфера работы и должность, трудовой стаж, средний месячный доход, назначение займа, кредитная история, семейное положение.

Что касается того, на чем основывается закон больших чисел при его применении в банковской сфере, то это тот же массив статистики.

Эта закономерность используется и другими околофинансовыми учреждениями. Например, БКИ при расчете кредитного рейтинга и прогнозе о возможности займа в банке опираются на анализ статистики. Значит закон больших чисел задействован и здесь.

Как работает закон больших чисел в страховании

Сектор страхования предлагает всем желающим (не только физлицам) защитить себя от убытков при наступлении несчастного случая.

На первый взгляд форс-мажоры спрогнозировать невозможно, но при изучении статистики оказывается, что и они подчиняются математическим закономерностям.

Закон больших чисел в страховании используется для определения минимального страхового взноса, который бы позволил компании перекрыть убытки при наступлении страхового случая.

Пример

Компания страхует 100 000 автомобилей, усредненная стоимость каждого $50 000, столько страховщик обязан выплатить при наступлении страхового случая.

Закон больших чисел говорит о том, что в среднем за год вероятность попадания в ДТП/угона (условия наступления страхового случая оговариваются отдельно) составляет 1/200 или 0,5%. То есть ежегодно страховщику придется выплачивать компенсацию 0,5 х 100000/100 = 500 автовладельцам.

При выплате в $50 000 ежегодно компания будет выплачивать 500 х $50 000 = $25 млн.

Теперь рассчитаем стоимость страховки для страхователей. Чтобы страховщик вышел в ноль каждый из страхователей должен заплатить $25 000 000/100 000 = $250. Но так как страховщик хочет заработать, то в реальности стоимость страховки будет равна $250 + N, где N – вознаграждение компании, зависящее в первую очередь от конкуренции.

Страхование – бизнес, который стал возможным исключительно благодаря закону больших чисел. Без прогнозирования соотношения прибыли и убытка по страховым случаям страховщики не стали бы работать.

Интересное по теме:

Когда закон больших чисел не работает

Сложно найти сферу деятельности человека, где не применяется закон больших чисел. Но сама по себе эта закономерность не является 100%-ной гарантией того, что в будущем события будут развиваться в соответствии с расчетами.

Закон больших чисел может не работать при:

• Неумении вести бизнес. Например, неверно рассчитанная премия страховщика, игнорирование факторов риска может привести к банкротству страховой компании.
• Неверно выбранной базе данных для анализа. Расчеты дадут ложные результаты.
• Неверной оценке аудитории, на которую нацелен продукт. Представьте, что каждый житель китайского Уханя застраховал свое здоровье на случай эпидемии. В теории это выгодная сделка – вероятность эпидемии низка. Но если она все же случится, страховщик разорится. В этом примере нужно исходить из того, что каждый город = 1 потребитель.
• Закон больших чисел не гарантирует, что в каждом конкретном случае результат окажется равен матожиданию. Например, в 2008-2009 гг. инвестор столкнулся бы с проявлением нарушения этого закона.

Это не значит, что закон больших чисел нельзя использовать в бизнесе и инвестировании. Просто нужно заранее понимать, что он лишь прогнозирует вероятный результат в будущем на основе статистики.

Заключение

Если дать определение закону больших чисел простым языком, его можно назвать законом, описывающим наиболее вероятный сценарий развития событий в будущем, опираясь на массив исторических данных. При этом он не гарантирует на 100%, что результаты окажутся точно такими же.

Эту закономерность использует любой бизнес без исключения, в инвестировании ей также отведена существенная роль.

Вероятнее всего вы и сами неосознанно пользуетесь этой закономерностью при планировании своих инвестиций. Если же нет – самое время начать это делать.

Автор: Максим Галански

Трейдер, инвестор, частный предприниматель. «Финансовые рынки объединяют разные интересы, бизнес, континенты. Это то место, где всегда можно найти, чем заняться, что и как сделать или создать.»

Теория больших чисел простыми словами

В жизни людей широко пользуются понятием среднего арифметического нескольких чисел. Вычисляется оно просто – все числа складываются, и их сумма делится на число слагаемых. Результат деления и есть среднее арифметическое всех чисел. Поясним пример вычисления среднего арифметического, взятый из истории мер и весов. В 16 веке длина английского фута по указу короля была определена как среднее арифметическое длины ступни первых 16 человек, выходящих из церкви от заутрени в воскресенье. Задание эталона фута позволило покончить с произволом в торговле и строительстве.

Знают ли короли теорию больших чисел?

Закона больших чисел, опубликованного в 1713 году (уже после смерти) швейцарским математиком Я. Бернулли, в 16 веке знать не могли, но именно этот закон лежит в обосновании использованного при определении длины фута принципа среднего арифметического. Согласно закону больших чисел, совместное действие множества случайных факторов приводит к результату, почти не зависящему от случая.

Возвращаемся к определению длины фута по 16 прихожанам. Предполагается, что поскольку прихожане не выбирались по какому-то признаку (только высокие, или только в обуви определенного фасона, или еще какому признаку), то отобраны они случайно, и среднее арифметическое 16 индивидуальных «футов» близко к неизвестному нам значению «истинного» фута, к которому можно приблизиться как угодно точно, увеличивая число слагаемых в формуле вычисления среднего арифметического (т.е. число прихожан в рассматриваемом случае).

Закон больших чисел и выборы

Теорема Бернулли, являющаяся частным случаем закона больших чисел, гласит, что относительная частота появления события в независимых экспериментах сходится к вероятности события. Этим частным случаем широко пользуются при проведении социологических исследований. Чтобы выяснить мнение очень большой группы людей, вовсе не обязательно опрашивать всех членов группы – достаточно опросить несколько сотен или тысяч случайных людей, и по их ответам составить представление о мнении всей группы по рассматриваемому вопросу.

Предположим, что в городе Н. предстоят выборы мэра, и число избирателей равно 100 тысячам. Если накануне выборов случайно отобрать 100 человек, и по результатам их опроса выясняется, что за кандидата А отдадут голоса 26 человек, а за Б – 58, нет оснований предполагать, что результат выборов окажется иным – у Б явное преимущество. Более точным предсказание результата окажется при случайном отборе 1000 человек, и т.д.
Вы обратили внимание, что при подсчете голосов после состоявшихся выборов в масштабе страны после подсчета всего 20% голосов в большинстве случаев (при достаточном разрыве) уже можно поздравлять победителя? Здесь тоже действует закон больших чисел – случайно отобранные 20% избирателей (предполагается, что данные с избирательных участков поступают случайно) по проценту проголосовавших за отдельных кандидатов не отличаются существенно от процента проголосовавших по всей совокупности избирателей.

Куда лететь в отпуск и встречу ли я динозавра?

Неосознанно законом больших чисел люди пользуются в повседневной жизни при принятии решений. Решив лететь в январе из Москвы в Таиланд на отдых, вы имеете ясное представление, какая погода вас там ждет – результаты многолетних метеорологических наблюдений позволят предсказать ожидаемую температуру воздуха и воды, которые не могут сильно отличаться от среднеарифметических значений в это время года.
И в заключение известный вопрос о вероятности встретить на улице динозавра. Вы за жизнь провели 10 тысяч экспериментов – выходили на улицу и динозавра не встретили. Вероятность встретить динозавра, следовательно, близка к нулю, и нет особых оснований предполагать, что сегодня, выйдя на улицу в 10001 раз, вы его встретите. Ваша уверенность основана на законе больших чисел.

Центральная предельная теорема теории вероятностей.Закон больших чисел.

	Главная > Учебные материалы > Математика:  Центральная предельная теорема теории вероятностей. Закон больших чисел.
	1.Закон больших чисел — Теорема Чебышева. 2.Неравенство Маркова. 3.Неравенство Чебышева. 4.Центральная предельная теорема (Теорема Ляпунова).
	24 25 26 27 28 29 30 31 32
	1.Закон больших чисел- Теорема Чебышева.
	Многие явления и процессы протекают непрерывно или периодически при большом числе испытаний. В этом случае среднее значение случайной величины колебается в определенных пределах или даже стремится к вполне определенному значению. Иными словами, случайная величина перестает быть случайной и может быть предсказана с высокой степенью вероятности (рис.1). Отклонение случайной величины от средней арифметической в каждом конкретном случае есть безусловно. А при беконечно большом числе испытаний эти отклонения взаимно погашают друг друга и средний их результат стремится к какому-то постоянному значению, т.е к математическому ожиданию. В этом и заключается смысл закона больших чисел.
	Другими словами, если взять предел вероятности отклонения случайной величины от ее математического ожидания при стремлении к бесконечности числа испытаний n, то он будет равен единице.    Рассмотрим пример: пусть вероятность поступления заказа в магазин А равна 0,2 или каждый 5-й звонящий делает заказ. Составим закон распределения поступления 5-ти заказов. n = 5 m — число поступивших заказов p = 0.2 q = 1 — p		Рис.1
	Из графика (рис.2) можно увидеть, что вероятность поступления 3-х заказов составляет чуть больше 0,05, а 4-х и 5-ти — очень низкая. Т.е. в каждой серии из 5-ти звонков число заказов может выпадать например 2 0 1 0 1 2 0 1 0 3 …… и т.д. Числа 3, 4, 5 будут выпадать очень редко. Число 5 — практически невозможное событие. Вообщем, если число серий по 5 звонков будет стремится к бесконечности, то средняя арифметическая случайной величины X1 — будет стремится к математическому ожиданию М(Х) = 1. Что и описывает закон больших чисел.		Рис.2
	Отсюда можно сформулировать теорему Чебышева, которая гласит, что если дисперсии n независимых случайных величин не превышают какую-то величину С, т.е. ограниченны, то при стремлении числа n к бесконечности средняя арифметическая этих случайных величин сходится по вероятности к средней арифметической их математических ожиданий. Т.е.    Это означает, что отклонение средней арифметической случайных величин от средней арифметической их математических ожиданий не превысит сколь угодно малое число ɛ или ( |Хср — аср| < ɛ). В этом заключается смысл данной теоремы.
	2.Неравенство Маркова.
	Допустим есть случайная величина Х, которая принимает только положительные значения и имеет математическое ожидание, например число заказов на покупку офисной техники в месяц. Тогда для любого положительного числа А верно неравенство:
	Второе неравенство справедливо выполняется, т.к. события P (x > A) и P (x ≤ A) противоположные.    Например, среднее число заказов на покупку офисной техники за месяц равно 500. Оценить вероятность того, что в следующем месяце число заказов составит более 600.
	Т.е. вероятность того, что число заказов превысит 600 составляет не более 0,833. Соответственно вероятность того что, число заказов составит не более 600 будет:
	3.Неравенство Чебышева.
	С помощью неравенства Чебышева можно рассчитать вероятность отклонения случайной величины от любого числа ɛ. Но здесь уже используется дисперсия случайной величины.    Неравенство Чебышева имеет вид: где    а = M(X)    ɛ > 0    Данная формула позволяет рассчитать вероятность того, что отклонение случайной величины от ее математического ожидания превысит любое число ɛ. Вероятность противоположного события, т.е. P (|X — a| ≤ ɛ), так же как и в неравенстве Маркова рассчитывается по следующей формуле:
	Неравенство Чебышева можно применять для любых случайных величин. В первом случае оно устанавливает верхнюю границу вероятности, а во втором — нижнюю.
	4.Центральная предельная теорема (Теорема Ляпунова).
	Закон больших чисел устанавливает условия, при которых среднее значение случайной величины стремится к некоторой постоянной, при стремлении числа испытаний к бесконечности. Существует группа теорем, которая описывает условия стремления закона распределения случайной величины к нормальному. Одна из таких теорем — теорема Ляпунова. Данная теорема устанавливает некоторые условия, при которых закон распределения суммы Yn = X1 + X2 + … + Xn случайных величин при стремлении n к бесконечности стремится к нормальному закону распределению. Рассмотрим эти условия: если есть независимые случайные величины X1, X2, X3 … и каждая из этих величин имеет математическое ожидание М(Хi) и дисперсию D(Xi), абсолютный центральный момент третьего порядка bi и предел отношения стремится к нулю, то закон распределения суммы этих величин при стремлении n к бесконечности приближается к нормальному закону распределения
	Необходимо отметить то, что скорость стремления закона распределения случайной величины в каждом явлении может быть разная. В одних случаях n может равняться десяткам, а вдругих сотням, тысячам и т.д.    Закон больших чисел играет важное значение в теоретическом плане, т.к. он служит обоснованием методов математической статистики. На практике закон больших чисел можно продемонстрировать на примере погоды. Например, атмосферное давление каждый день есть величина случайная. Однако ее среднегодовое значение в течении многих лет практически не изменяется.
	24 25 26 27 28 29 30 31 32

Теория вероятности — что это такое? Определение, значение, перевод

Теория вероятности это большой раздел математики, изучающий случайные события и процессы. Обычно её начинают изучать на 2-3 курсе университетов и дополняют математической статистикой.

Понятие «вероятности» математики рассматривают как величину, принимающую значения на отрезке от нуля до единицы. При этом ноль соответствует абсолютно невероятному событию (пример: Борис Немцов станет президентом РФ), а единица принимается за абсолютно вероятное (пример: Путин умрёт в XXI веке). В простом эксперименте с подбрасыванием монеты теория вероятности часто принимает шансы «орла» и «решки» равными 0.5, однако на практике доли вероятности зависят от изгибов каждой конкретной монеты, поэтому нос королевы Елизаветы II, выбитый на британском фунте, уменьшает вероятность попадания «мордой вниз» на несколько сотых процента.

Главным постулатом теории вероятности является так называемый «Закон больших чисел». Он гласит, что при большом количестве экспериментов их фактические результаты будут стремиться к математическому распределению их вероятностей. Пример: если вы бросите монетку очень-очень много раз, то примерно в половине случаев получите орла. И это «примерно» будет стремиться к «ровно» с увеличением количества подбрасываний.

Пример простой задачки по теории вероятности: какова вероятность, что при пяти подбрасываниях «идеальной» монетки выпадут четыре орла и одна решка? Решение: согласно биномиальному распределению Y ~ Bin(5, 0.5) получаем, что вероятность для 4 орлов в пяти подбрасываниях монетки равна 5*(0.5)⁴*(0.5)¹, то есть 5/32, что равно 0.15625.

В этом эксперименте из пяти попыток вероятности распределяются так:
Ноль орлов: вероятность 1/32
Один орёл: вероятность 5/32
Два орла: вероятность 10/32
Три орла: вероятность 10/32
Четыре орла: вероятность 5/32
Пять орлов: вероятность 1/32

И в сумме мы всегда получаем единицу, ведь одно из этих шести событий обязательно наступит.

Теория вероятности находится в списке: Математика

Вы узнали, откуда произошло слово Теория вероятности, его объяснение простыми словами, перевод, происхождение и смысл.
Пожалуйста, поделитесь ссылкой «Что такое Теория вероятности?» с друзьями:

И не забудьте подписаться на самый интересный паблик ВКонтакте!

 

Теория вероятности это большой раздел математики, изучающий случайные события и процессы. Обычно её начинают изучать на 2-3 курсе университетов и дополняют математической статистикой.

Понятие «вероятности» математики рассматривают как величину, принимающую значения на отрезке от нуля до единицы. При этом ноль соответствует абсолютно невероятному событию (пример: Борис Немцов станет президентом РФ), а единица принимается за абсолютно вероятное (пример: Путин умрёт в XXI веке). В простом эксперименте с подбрасыванием монеты теория вероятности часто принимает шансы «орла» и «решки» равными 0.5, однако на практике доли вероятности зависят от изгибов каждой конкретной монеты, поэтому нос королевы Елизаветы II, выбитый на британском фунте, уменьшает вероятность попадания «мордой вниз» на несколько сотых процента.

Главным постулатом теории вероятности является так называемый «Закон больших чисел». Он гласит, что при большом количестве экспериментов их фактические результаты будут стремиться к математическому распределению их вероятностей. Пример: если вы бросите монетку очень-очень много раз, то примерно в половине случаев получите орла. И это «примерно» будет стремиться к «ровно» с увеличением количества подбрасываний.

Пример простой задачки по теории вероятности: какова вероятность, что при пяти подбрасываниях «идеальной» монетки выпадут четыре орла и одна решка? Решение: согласно биномиальному распределению Y ~ Bin(5, 0.5) получаем, что вероятность для 4 орлов в пяти подбрасываниях монетки равна 5*(0.5)⁴*(0.5)¹, то есть 5/32, что равно 0.15625.

В этом эксперименте из пяти попыток вероятности распределяются так:
Ноль орлов: вероятность 1/32
Один орёл: вероятность 5/32
Два орла: вероятность 10/32
Три орла: вероятность 10/32
Четыре орла: вероятность 5/32
Пять орлов: вероятность 1/32

И в сумме мы всегда получаем единицу, ведь одно из этих шести событий обязательно наступит.

БОЛЬШИХ ЧИСЕЛ ЗАКОН • Большая российская энциклопедия

БОЛЬШИ́Х ЧИ́СЕЛ ЗАКО́Н, об­щий прин­цип, со­глас­но ко­то­ро­му со­вме­ст­ное дей­ст­вие боль­шо­го чис­ла слу­чай­ных фак­то­ров при­во­дит при не­ко­то­рых весь­ма об­щих ус­ло­ви­ях к ре­зуль­та­ту, поч­ти не за­ви­ся­ще­му от слу­чая. Сбли­же­ние час­то­ты на­сту­п­ле­ния слу­чай­но­го со­бы­тия с его ве­ро­ят­но­стью при воз­рас­та­нии чис­ла ис­пы­та­ний (т. н. ус­той­чи­вость час­тот) мо­жет слу­жить при­ме­ром дей­ст­вия это­го прин­ци­па.

На ру­бе­же 17 и 18 вв. Я. Бер­нул­ли до­ка­зал тео­ре­му, ут­вер­ждаю­щую, что в по­сле­до­ва­тель­но­сти не­за­ви­си­мых ис­пы­та­ний, в ка­ж­дом из ко­то­рых ве­ро­ят­ность на­сту­п­ле­ния не­ко­то­ро­го со­бы­тия $A$ име­ет од­но и то же зна­че­ние $p$, $0{<}p{<}1$, вер­но со­от­но­ше­ние $$\mathsf P \left \{ \left | \frac {S_n}{n}-p \right | > ε \right \} \to0 \qquad (1)$$ при лю­бом фик­си­ро­ван­ном $ε>0$ и $n \to \infty$; здесь $S_n$ – чис­ло по­яв­ле­ний со­бы­тия $A$ в пер­вых $n$ ис­пы­та­ни­ях, $S_n/n$ – час­то­та по­яв­ле­ний, $\mathsf P$ – ве­ро­ят­ность со­бы­тия, ука­зан­но­го в скоб­ках. Эта Бер­нул­ли тео­ре­ма бы­ла рас­про­стра­не­на С. Пу­ас­со­ном на слу­чай по­сле­до­ва­тель­но­сти не­за­ви­си­мых ис­пы­та­ний, где ве­ро­ят­ность по­яв­ле­ния со­бы­тия $A$ мо­жет за­ви­сеть от но­ме­ра ис­пы­та­ния. Пусть эта ве­ро­ят­ность для $k$-го ис­пы­та­ния рав­на $p_k,\ k=1, 2, …,$ и пусть $$p̅_n=\frac{p_1+…p_n}{n}.$$ То­гда Б. ч. з. в фор­ме Пу­ас­со­на ут­вер­жда­ет, что $$\mathsf P \left \{ \left | \frac {S_n}{n}-p̅_n \right | > ε \right \} \to0 \qquad (2)$$ для лю­бо­го фик­си­ро­ван­но­го $ε>0$ при $n→∞$. Стро­гое до­ка­за­тель­ст­во это­го ут­вер­жде­ния бы­ло да­но П. Л. Че­бы­ше­вым (1846). Тер­мин «за­кон боль­ших чи­сел» впер­вые встре­ча­ет­ся у Пу­ас­со­на, так он на­звал вы­ше­ука­зан­ное обоб­ще­ние тео­ре­мы Бер­нул­ли.

Даль­ней­шие обоб­ще­ния ут­вер­жде­ний Бер­нул­ли и Пу­ас­со­на воз­ни­ка­ют, ес­ли за­ме­тить, что слу­чай­ные ве­ли­чи­ны $S_n$ мож­но пред­ста­вить в ви­де сум­мы $S_n=X_1+…+X_n$ не­за­ви­си­мых слу­чай­ных ве­ли­чин, где $X_k=1$, ес­ли $A$ по­яв­ля­ет­ся в $k$-м ис­пы­та­нии, и $X_k=0$ в про­тив­ном слу­чае, $k=1, .2)$$

B2n=DX1+…+DXn=o(n2)

при $n→∞$. Та­ким об­ра­зом, Че­бы­шев по­ка­зал воз­мож­ность ши­ро­ко­го обоб­ще­ния тео­ре­мы Бер­нул­ли. А. А. Мар­ков от­ме­тил воз­мож­ность даль­ней­ших обоб­ще­ний и пред­ло­жил при­менять назв. «Б. ч. з.» ко всей со­во­куп­но­сти обоб­ще­ний тео­ре­мы Бер­нул­ли, и в ча­ст­но­сти к (3). Ме­тод Че­бы­ше­ва ос­но­ван на ус­та­нов­ле­нии об­щих свойств ма­те­ма­тич. ожи­да­ний и на ис­поль­зо­ва­нии т. н. Че­бы­ше­ва не­ра­вен­ст­ва. По­сле­дую­щие до­ка­за­тель­ст­ва разл. форм Б. ч. з. в той или иной сте­пе­ни яв­ля­ют­ся раз­ви­ти­ем ме­то­да Че­бы­ше­ва. При­ме­няя над­ле­жа­щее «уре­за­ние» слу­чай­ных ве­ли­чин $X_k$ (за­ме­ну их вспо­мо­га­тель­ны­ми ве­ли­чи­на­ми $X_{k,n}$, рав­ны­ми $X_{n,k}=X_k$, ес­ли $|X_k-\mathsf EX_k|{⩽}t_n$, и рав­ны­ми ну­лю в про­тив­ном слу­чае, где $t_n$ за­ви­сят лишь от $n$), Мар­ков рас­про­стра­нил Б. ч. з. на слу­чаи, ко­гда дис­пер­сии сла­гае­мых не су­ще­ст­ву­ют. Напр., он по­ка­зал, что (3) име­ет ме­сто, ес­ли для не­ко­то­ро­го чис­ла $δ>0$ ве­ли­чи­ны $\mathsf E|X_k-\mathsf EX_k|^{1+δ}$ ог­ра­ни­че­ны од­ной и той же по­сто­ян­ной.2))$. Здесь сред­ние ариф­ме­ти­че­ские $(X_1+…+X_n)/n$ пер­вых $n$ слу­чай­ных ве­ли­чин име­ют при лю­бом $n$ то же са­мое рас­пре­де­ле­ние, что и от­дель­ные сла­гае­мые. Для рас­пре­де­ле­ния Ко­ши ма­те­ма­тич. ожи­да­ние не су­ще­ст­ву­ет.

При­ме­ни­мость Б. ч. з. к сум­мам за­ви­си­мых ве­ли­чин свя­за­на в пер­вую оче­редь с убы­ва­ни­ем за­ви­си­мо­сти ме­ж­ду слу­чай­ны­ми ве­ли­чи­на­ми $X_i$ и $X_j$ при уве­ли­че­нии раз­но­сти их но­ме­ров, т. е. при уве­ли­че­нии $|i-j|$. Впер­вые со­от­вет­ст­вую­щие тео­ре­мы бы­ли до­ка­за­ны А. А. Мар­ко­вым (1907) для ве­ли­чин, свя­зан­ных в Мар­ко­ва цепь.

Пред­став­ле­ние об от­кло­не­ни­ях $S_n/n$ от $A_n=(\mathsf EX_1+…+\mathsf EX_n)/n$, на­ря­ду с нера­вен­ст­вом Че­бы­ше­ва и его уточ­не­ния­ми, да­ёт цен­траль­ная пре­дель­ная тео­ре­ма.

Пре­ды­ду­щие ре­зуль­та­ты мож­но обоб­щать в разл. на­прав­ле­ни­ях. Так, всю­ду вы­ше рас­смат­ри­ва­лась т. н. схо­ди­мость по ве­ро­ят­но­сти. Рас­смат­ри­ва­ют и др. ви­ды схо­ди­мо­сти, напр. схо­ди­мость в сред­нем квад­ра­тич­ном и схо­ди­мость с ве­ро­ят­но­стью 1 (схо­ди­мость поч­ти на­вер­ное). Обоб­ще­ния Б. ч. з. на слу­чай схо­ди­мо­сти с ве­ро­ят­но­стью 1 на­зы­ва­ют уси­лен­ны­ми Б. ч. з.

Пусть $X_1, X_2, …$ – по­сле­до­ва­тель­ность слу­чай­ных ве­ли­чин и, как и рань­ше, $S_n=X_1+ …+X_n$. Го­во­рят, что по­сле­до­ва­тель­ность $X_1, X_2, …$ удов­ле­тво­ря­ет уси­лен­но­му Б. ч. з., ес­ли су­ще­ст­ву­ет та­кая по­сле­до­ва­тель­ность по­сто­ян­ных $A_n$, что ве­ро­ят­ность со­от­но­ше­ния $S_n/n-A_n→0$ при $n→∞$ рав­на 1. По­сле­до­ва­тель­ность $X_1, X_2, …$ удов­ле­тво­ря­ет уси­лен­но­му Б. ч. з. то­гда и толь­ко то­гда, ко­гда при лю­бом фик­си­ро­ван­ном $ε>0$ ве­ро­ят­ность од­но­вре­мен­но­го вы­пол­не­ния не­ра­венств $$\left | \frac {S_n}{n}-A_n \right |{⩽}ε,  \ \left | \frac {S_{n+1}}{n+1}-A_{n+1} \right |{⩽}ε, \ …$$ стре­мит­ся к 1 при $ n→∞$. Т. о., здесь рас­смат­ри­ва­ет­ся по­ве­де­ние всей по­сле­до­ватель­но­сти сумм в це­лом, в то вре­мя как в обыч­ном Б.nX_k(ω)$ рав­на чис­лу еди­ниц сре­ди пер­вых $n$ зна­ков дво­ич­но­го раз­ло­же­ния $ω$, а $S_n(ω )/n$ – их до­ле. В то же вре­мя слу­чай­ную ве­личи­ну $S_n$ мож­но рас­смат­ри­вать как чис­ло «ус­пе­хов» в схе­ме Бер­нул­ли с ве­ро­ят­но­стью «ус­пе­ха» (по­яв­ле­ния 1), рав­ной ¹/₂. Бо­рель до­ка­зал, что до­ля еди­ниц $S_n(ω)/n$ стре­мит­ся к ¹/₂ при $n→∞$ для поч­ти всех $ω$ из от­рез­ка [0, 1] (т. е. ле­бе­го­ва ме­ра мно­же­ст­ва тех то­чек $ω∈$ [0, 1], для ко­то­рых $\lim\limits_{n\to\infty}S_n(ω )/n=$ ¹/₂, рав­на 1). Ана­ло­гич­но, при раз­ло­же­нии $ω$ по ос­но­ва­нию 10 мож­но на­звать «ус­пехом» по­яв­ле­ние к.-л. од­ной из цифр 0, 1, …, 9 (напр., циф­ры 3). При этом по­лу­ча­ет­ся схе­ма Бер­нул­ли с ве­ро­ят­но­стью ус­пе­ха ¹/₁₀, и час­то­та по­яв­ле­ния вы­бран­ной циф­ры сре­ди пер­вых $n$ зна­ков де­ся­тич­но­го раз­ло­же­ния $ω$ стре­мит­ся к ¹/₁₀ для поч­ти всех $ω$ из от­рез­ка [0, 1] (та­кие чис­ла $ω$ ино­гда на­зы­ва­ют нор­маль­ны­ми).2}<\infty$$ вы­те­ка­ет спра­вед­ли­вость уси­лен­но­го Б. ч. з. с $A_n=\mathsf E(S_n/n)$.

Пред­став­ле­ние об от­кло­не­ни­ях $S_n/n$ от $A_n$ да­ёт по­втор­но­го ло­га­риф­ма за­кон.

Свёртка в Deep Learning простыми словами | Блог REG.RU

У многих слово «свёртка» ассоциируется со сложными и непонятными формулами. А ведь это одно из самых важных понятий в Deep Learning: именно свёрточные сети вывели глубокое обучение на новый уровень. Специально для тех, кто не до конца понимает свёртку — статья о том, как работает свёртка и что делает её такой мощной.

Первая часть материала предназначена для всех, кто хочет понять общую концепцию свёртки и свёрточных сетей. Вторая часть включает более сложное объяснение и направлена на углубление понимания свёртки для исследователей и специалистов.

Часть 1. Что такое свёртка?

Вы можете представить себе свёртку как «смешивание» информации. Представьте два ведра, наполненных какой-либо информацией, которые выливаются в один большой контейнер и затем перемешиваются определённым способом. Каждое ведро с информацией имеет своё собственное правило, которое описывает, как информация из одного ведра смешивается с другим. Свёртка — это упорядоченная процедура смешивания двух источников информации.

Свёртку можно описать математически. Это такая же операция, как сложение, умножение или взятие производной. Хотя сама по себе операция свёртки сложна, она может быть очень полезна для упрощения ещё более сложных выражений. 

Как мы применяем свёртку к изображениям?

Когда мы применяем свёртку к изображениям, она действует на них в двух измерениях: по ширине и высоте. Здесь снова можно провести аналогию с двумя «вёдрами» информации. Первое ведро — входное изображение с тремя матрицами пикселей: по одной для красного, синего и зелёного цветов. Пиксель состоит из целочисленного значения от 0 до 255 для каждого цветового канала. Второе — это ядро свёртки: матрица вещественных чисел, свойства которой можно рассматривать как правила «перемешивания» входного изображения и ядра. В результате мы получим изменённое изображение, которое в глубоком обучении часто называют «карта признаков». Для каждого цветового канала будет по одной карте.

Теперь рассмотрим саму операцию свёртки. Один из способов её применения — взять патч (небольшой участок) входного изображения размером с ядро. Например, здесь у нас картинка 100×100 пикселей и ядро 3×3, поэтому мы возьмём патч 3×3 и поэлементно перемножим каждый патч изображения с ядром свёртки. Потом сложим все результаты умножения и получим один пиксель карты признаков. После этого мы сдвигаем патч и повторяем вычисления. Проделываем эту операцию до тех пор, пока не посчитаем все пиксели карты признаков. 

Операция свёртки для одного пикселя карты признаков: участок исходного изображения 3×3 (выделен красным, RAM) умножается на ядро (Kernel), а сумма записывается в пиксель карты признаков (Buffer RAM)

Как вы могли заметить, существует ещё процедура нормализации: выходное значение нормализуется по размеру ядра, чтобы общая интенсивность изображения и карты признаков оставалась неизменной.

Ещё один более простой пример свёртки с ядром 0 1 2 / 2 2 0 / 0 1 2 . Справа — карта признаков

Почему свёртка нужна в машинном обучении?

На изображениях часто присутствует лишняя информация, которая не имеет отношения к тому, что мы ищем на них. Например, вы хотите сделать поиск по фотографиям с одеждой, чтобы находить вещи похожего стиля с помощью автокодировщика (это специальная архитектура глубоких нейронных сетей, которая по входному изображению ищет наиболее похожие на него варианты). Для определения стиля одежды вам не важен её цвет, эмблемы бренда и прочие мелкие детали. Наиболее информативной будет форма — блузка явно отличается от пиджака, брюк или рубашки. Поэтому если мы отфильтруем ненужную информацию, наш алгоритм не будет отвлекаться на несущественные детали. Это легко можно сделать с помощью свёртки.

Для начала предварительно обработаем данные, применив детектор краёв Собеля-Фельдмана (один из видов ядер), чтобы отфильтровать всё, кроме контуров формы объекта. Вот почему применение свёртки часто называют фильтрацией, а ядра — фильтрами (более точное определение процессов фильтрации приведено ниже). Полученная карта признаков будет полезной, если вы хотите отличить разные типы одежды, поскольку на ней чётко видна форма.

Изображения, отфильтрованные детектором Собеля и результаты обученного автокодировщика. В каждом столбце верхние левые фотографии — поисковый запрос, а остальные — результат работы нейросети. Автокодировщик оценивает форму запроса, а не цвет. Однако вы можете заметить, что эта процедура не работает с изображениями людей в одежде (столбец 5) и чувствительна к форме вешалок (столбец 4).

Мы можем усовершенствовать наш алгоритм: существует множество ядер для создания разных карт признаков. Есть те, которые делают изображение более чётким (больше деталей) или, наоборот, размытым (меньше деталей). При этом каждая карта признаков может оказаться полезной для алгоритма: например, такие детали, как три кнопки вместо двух на куртке, будут важны.

Такая процедура — получение и преобразование входных данных перед отправкой в алгоритм — называется проектирование признаков. Это очень сложная операция, и не так много людей могут умело применять её для широкого круга решений. Трудность заключается в том, что для каждого типа данных и задач подходят совершенно разные признаки: например, признаки для изображений будут совершенно бесполезным при работе с временными рядами. Даже если у вас две одинаковые задачи с фотографиями, будет непросто найти хорошее решение, поскольку разным объектам могут требоваться разные признаки. Для понимания этого требуется немалый опыт.

Каждую задачу проектирования признаков нужно начинать с нуля. Но можем ли мы по одному взгляду на изображения определить, какое ядро подойдёт для конкретной проблемы?

Используйте свёрточные сети!

Находить подходящие для определённой задачи ядра можно с помощью свёрточных сетей. Вместо того, чтобы задавать конкретные числа нашим ядрам, мы назначим для них параметры, которые будут обучаться на данных. По мере обучения ядро будет всё лучше и лучше фильтровать изображение (или карту признаков) для получения нужной информации. Этот автоматический процесс называется обучение признакам. Он обобщается для любой новой задачи: нам надо просто заново обучить нашу сеть и найти подходящие фильтры.  Именно поэтому свёрточные сети такие мощные — никаких проблем с проектированием признаков.

Обычно мы обучаем не одно ядро, а иерархию нескольких ядер одновременно. Например, применение ядра 32×16×16 к изображению 256×256 даст 32 карты признаков размером 241×241 (это стандартное соотношение: размер изображения — размер ядра + 1). Таким образом, мы автоматически изучим 32 новых признака с информацией для нашей задачи. Они используются в качестве входных данных для следующего ядра, которое снова применяет к ним фильтр. Как только мы изучим всю иерархию, мы просто передадим её в простую нейросеть, которая объединит признаки для классификации входного изображения. Это почти всё, что нужно знать о свёрточных сетях на концептуальном уровне.

Часть 2: продвинутое объяснение

Теперь у нас есть неплохое понимание того, что такое свёртка и как работают свёрточные сети. Но можно копнуть глубже и подробнее рассмотреть, что на самом деле происходит во время применения свёртки. При этом мы увидим, что первоначальная интерпретация довольно грубая, и попробуем найти решение, которое поможет расширить наши знания. Для этого первым делом попробуем понять теорему о свёртке.

Теорема свёртки

Теорема связывает две сущности: свёртку в пространственно-временной области в виде громоздкого интеграла или суммы и простое поэлементное умножение в Фурье-области (частотной). Теорема применяется во многих сферах науки и является причиной, по которой многие считают алгоритм быстрого преобразования Фурье одним из важнейших в 20-м веке. 

Первое уравнение — одномерная непрерывная теорема о свёртке для двух базовых непрерывных функций. Второе — двумерная дискретная теорема для дискретных изображений. Здесь обозначает операцию свёртки, — преобразование Фурье, — обратное преобразование Фурье, а 2 — константа нормализации. 

Обратите внимание, что здесь понятие «дискретный» означает, что наши данные состоят из счётного числа переменных (пикселей). А «одномерный» значит, что эти переменные могут быть представлены в одном измерении. Например, время — одномерное (одна секунда следует за другой), изображения — двумерные (пиксели находятся в строках и столбцах), видео — трёхмерные (пиксели находятся в строках и столбцах, а изображения следуют друг за другом).

Для лучшего понимания теоремы мы подробнее рассмотрим интерпретацию преобразований Фурье в отношении обработки изображений.

Быстрые преобразования Фурье

Быстрое преобразование Фурье — алгоритм, который преобразует данные из пространственно-временной области в частотную область. Он представляет исходную функцию в виде суммы косинусов и синусов. Важно отметить, что преобразование Фурье обычно является комплексным (действительное значение преобразуется в комплексное). Мнимая часть полученного числа играет роль только для определённых операций или обратного преобразования в пространственно-временную область. В этой статье мы будем рассматривать действительную часть. Ниже вы можете увидеть визуализацию применения преобразования Фурье к входному сигналу (частотной функции с временным параметром).

На самом деле вы часто видите примеры преобразований Фурье в реальной жизни: например, если красный сигнал — песня, то чёрный — столбцы эквалайзера в вашем mp3-плеере.

Преобразование Фурье для изображений

Как мы можем вообразить частоты изображений? Представьте себе лист бумаги с двухцветным рисунком. Теперь представьте волну, которая проходит от одного края листа к другому и проникает сквозь бумагу на каждой полосе одного цвета и парит над полосами другого цвета. Такие волны «прокалывают» чёрные и белые части через определённые интервалы, например, каждые два пикселя — это будет частотой. В преобразовании Фурье более низкие частоты находятся ближе к центру, а более высокие — по краям (максимальная частота будет у самого края изображения). 

Значения с более высокой интенсивностью (белый цвет) упорядочены в соответствии с направлением наибольшего изменения интенсивности в исходном изображении.  Если эта фраза показалась вам непонятной — посмотрите на наглядный пример ниже, где изображена фотография и её логарифмическое преобразование Фурье. Применение логарифма к действительным значениям сглаживает различия в интенсивностях пикселей, чтобы нам легче было воспринимать информацию.

Мы сразу замечаем, что преобразование Фурье содержит много информации об ориентации объекта на изображении. Если объект повёрнут, скажем, на 37°, то нам трудно будет понять это из информации об исходных пикселях, но будет очевидно из преобразованных значений.

Благодаря теореме о свёртке мы можем представить, как свёрточные сети работают с изображениями в Фурье-области. Кроме того, мы знаем, что алгоритм чувствителен к повороту — поэтому свёрточные сети справляются с повёрнутыми изображениями лучше традиционных методов.

Частотная фильтрация и свёртка

Причина, по которой операцию свёртки часто называют фильтрацией, станет очевидной из следующего примера.

Применим к исходному изображение преобразование Фурье, а затем умножим его на окружность, дополненную нулями (нули=чёрный цвет) в Фурье-области — так мы отфильтруем все высокочастотные значения. Заметьте, что отфильтрованное изображение имеет тот же полосатый рисунок, но худшего качества — примерно так же работает сжатие JPEG. Мы сохраняем только определённые частоты и возвращаемся в пространственную область изображения. Коэффициент сжатия — отношение размера чёрной области к размеру круга.

Если представить, что круг — это ядро свёртки, то мы получим её полноценное описание. Такой же механизм применяется в свёрточных сетях. Существует много способов ускорить и стабилизировать вычисление свёртки с помощью преобразований Фурье, здесь изложен только основной принцип.

Теперь попытаемся применить наши знания о свёртке и преобразованиях Фурье к различным областям науки и глубокому обучению.

Механика жидкостей и газов

Механика жидкостей и газов занимается созданием моделей потоков жидкостей с помощью дифференциальных уравнений, которые, как и свёртку, можно упростить с помощью преобразований Фурье. Поэтому эти преобразования широко применяют в любой области, где используется дифференцирование. Иногда единственный способ найти аналитическое решение для потока жидкости — упростить уравнение в частных производных. Решение такого уравнения иногда можно переписать в виде свёртки двух функций, поэтому оно применимо к одномерным и некоторым двумерным процессам диффузии.

Диффузия

Вы можете смешать две жидкости (молоко и кофе), перемещая их внешним усилием (ложкой) — это называется конвекцией и происходит довольно быстро. Но можно и подождать, когда жидкости смешаются сами (если это химически возможно) — это более медленный процесс диффузии.

Представьте себе аквариум, который разделён на две части тонким съемным барьером. Одна сторона заполнена солёной водой, а другая — пресной. Если осторожно убрать барьер, две жидкости будут смешиваться до тех пор, пока во всём аквариуме не будет одинаковая концентрация соли. Чем больше разница в солёности, тем стремительнее протекает процесс.

Допустим, у нас есть квадратный аквариум 256×256 с барьерами, которые разделяют 256×256 кубиков с различной концентрацией соли. Если вы уберёте один барьер, то два кубика с небольшой разницей в концентрации соли смешаются медленно, а с большой — быстро. Теперь представьте, что сетка 256×256 — это изображение, кубики — это пиксели, а концентрация соли — интенсивность каждого пикселя. Вместо диффузии солёности мы имеем диффузию информации о пикселях.

Мы только что описали первую часть свёртки для решения уравнения диффузии, то есть начальную концентрацию жидкости — или, в терминах изображения — исходный снимок и интенсивности пикселей. Чтобы завершить интерпретацию свёртки в виде процесса диффузии, рассмотрим вторую часть уравнения: пропагатор.

Интерпретация пропагатора

Пропагатор — функция плотности вероятности, которая указывает, в каком направлении распространяются частицы жидкости. Проблема в том, что в глубоком обучении нет функции вероятности, но есть ядро свёртки — как объединить эти понятия?

Можно применить нормализацию, которая превратит ядро свёртки в функцию плотности вероятности. Это похоже на вычисление softmax для выходных значений в задачах классификации. Пример softmax-нормализации для ядра Собеля:

Чтобы вычислить нормализацию softmax для детектора контуров, мы берём каждое значение ядра x и применяем ex. После этого делим на сумму всех ex. Обратите внимание, что этот метод расчёта softmax подходит для большинства ядер свёртки, но для более сложных вычислений немного изменяется, чтобы обеспечить числовую стабильность.

Теперь у нас есть полная интерпретация свёртки для изображений с точки зрения диффузии. Мы можем разделить этот процесс на две части: первая — сильная диффузия, которая меняет интенсивности пикселей (с чёрного на белый, с жёлтого на синий и так далее), и вторая — регулирование процесса распределением вероятностей ядра свёртки. Это означает, что каждый пиксель в области ядра переходит в другое положение в соответствии со значением функции вероятности.

Для детектора контуров почти вся информация будет сконцентрирована в одном месте (это неестественно для жидкостей, но математически интерпретация верна). Например, все пиксели, значения которых меньше 0.0001, с большой вероятностью будут скапливаться в центре. Конечная концентрация будет наибольшей там, где значения соседних пикселей отличаются сильнее всего, поскольку процесс диффузии более заметен. Нетрудно догадаться, что самая большая разница между пикселями находится на гранях и пересечениях объектов — поэтому ядро и называется детектором контуров.

Итак, свёртка — это диффузия информации. Мы можем применить эту интерпретацию и к другим ядрам. Иногда необходимо выполнить softmax-нормализацию, но обычно можно сразу понять по числам внутри ядра, какой эффект получится на изображении. 

Возьмём, к примеру следующее ядро. Попробуйте догадаться, что оно делает. Кликните сюда, чтобы узнать ответ (вы сможете вернуться по обратной ссылке).

Погодите, что-то подозрительно

Как так получается, что мы получаем детерминированное поведение, хотя в ядре свёртки находятся вероятности? Мы же должны учитывать, что диффузия частиц происходит в соответствии с пропагатором, не так ли?

Да, это действительно так. Но если взять маленькую частицу жидкости, скажем, крошечную каплю воды — в ней тоже будут находиться миллионы молекул. И хотя одна молекула может вести себя случайным образом, группа молекул в целом имеет квазидетерминированное поведение — это важная интерпретация статистической механики, и, следовательно, диффузии. Мы можем рассматривать вероятности пропагатора как среднее распределение интенсивностей пикселей. Таким образом, наша интерпретация верна с точки зрения механики жидкостей и газов. Тем не менее, существует и более точное сравнение.

Квантовая механика

Пропагатор — важное понятие в квантовой механике. Частица может находиться в суперпозиции и иметь два и более свойств, которые обычно взаимоисключают друг друга в нашем эмпирическом мире. Например, в квантовой механике частица может находиться в двух местах или состояниях одновременно (вспомните кота Шрёдингера).

Однако, когда вы попытаетесь определить состояние частицы — например, где она находится именно сейчас — то узнаете только одно из её возможных местоположений. Другими словами, вы разрушаете состояние суперпозиции, наблюдая за частицей. Пропагатор описывает распределение вероятностей в тех местах, где частица может появиться: скажем, с 30% вероятностью в месте А и с 70% вероятностью в месте Б.

Если мы запутаем частицы (квантовая запутанность — явление, при котором квантовые состояния объектов оказываются взаимозависимыми), то несколько частиц смогут одновременно находиться в сотнях или даже миллионах различных состояний. Примерно такой эффект смогут дать квантовые компьютеры.

Если интерпретировать это для глубокого обучения, то мы можем представить, что пиксели изображения находятся в суперпозиции состояний. Так, пиксель в каждом патче находится в 9 позициях одновременно (если у нас ядро 3×3). Как только мы применим свёртку, то сделаем очередное измерение, и суперпозиция каждого пикселя свернётся в одно наиболее вероятное положение. Другими словами: для каждого нового положения мы выбираем один пиксель из 9 случайным образом (согласно вероятности ядра), и результат — среднее значение всех этих пикселей. Чтобы эта интерпретация полностью была верной, необходим реальный случайный процесс. Это значит, что одно и тоже изображение и ядро дадут разные результаты. На самом деле это не так, но такое представление свёртки может натолкнуть вас на идеи, как разработать квантовые алгоритмы для свёрточных сетей.

Теория вероятностей

Свёртка тесно связана с кросс-корреляцией. Кросс-корреляция — это операция, для которой требуется небольшой фрагмент информации (например, несколько секунд песни), чтобы отфильтровать большой фрагмент (всю песню) на предмет сходства. Аналогичные методы используются на YouTube для автоматической пометки видео, нарушающих авторские права.

Связь между кросс-корреляцией и свёрткой. Здесь обозначает взаимную кросс-корреляцию, а f* — комплексное сопряжение от f.

Хотя взаимная кросс-корреляция кажется довольно сложной, мы можем легко связать её со свёрткой в глубоком обучении с помощью небольшого трюка. Просто перевернём искомое изображение вверх ногами, чтобы выполнить взаимную корреляцию с помощью свёртки. Когда мы выполняем свёртку фотографии человека с перевёрнутым снимком его лица, то результатом будет изображение с одним или несколькими яркими пикселями в том месте, где лицо совпадёт с человеком. 

Кросс-корреляция с помощью свёртки: вход и повёрнутое на 180 градусов ядро дополнены нулями. Белое пятно — область с самой сильной пиксельной корреляцией между изображением и ядром.

Пример выше также иллюстрирует дополнение нулями (padding) для стабилизации преобразования Фурье. Padding может быть разным: некоторые реализации деформируют только ядро, другие вообще не требуют никаких дополнений. В этой статье мы не будем останавливаться на различных вариантах padding-а.

На более ранних слоях свёрточные сети не выполняют кросс-корреляцию, поскольку мы знаем, что сначала они обнаруживают границы объекта. Но в глубоких слоях, где генерируются более абстрактные признаки, сеть может научиться выполнять подобную операцию. 

Статистика

В чём разница между статистическими моделями и машинным обучением? Статистика часто концентрируется на небольшом количестве переменных, которые можно легко интерпретировать. Такие модели отвечают на вопрос: лучше ли лекарство А, чем лекарство Б?

Машинное обучение же больше ориентировано на прогнозирование: препарат А даёт на 17.83% лучшие результаты по сравнению с препаратом Б для людей в возрасте X и на 22.34% для людей в возрасте Y. 

Но модели машинного обучения не всегда надёжны. Статистические решения важны для получения точных выводов: даже если препарат А на 17.83% лучше, чем препарат Б, мы не знаем, случайное это значение или нет. Чтобы решить проблему, нам нужна статистическая модель.

Для временных рядов существует два важных статистических решения: взвешенное скользящее среднее и авторегрессия, которые можно объединить в модели ARIMA (AutoRegressive Integrated Moving Average). ARIMA не такие эффективные, как рекуррентные сети с долгой краткосрочной памятью, но они чрезвычайно надёжны для небольших выборок (1-5 измерений). Их довольно сложно интерпретировать, хотя ARIMA не являются чёрным ящиком, как алгоритмы глубокого обучения.

На самом деле можно представить эти модели в виде свёрток и показать, что свёртки в глубоком обучении — это функции, из которых мы получаем признаки ARIMA и передаём их на следующий слой. Однако эту идею не всегда получится применить.

Здесь  C(kernel) — постоянная функция с ядром в качестве параметра, white noise (белый шум) — данные с нулевым средним и стандартным отклонением, равным единице. Каждая переменная некоррелирована по отношению к другим.

Предварительно обрабатывая данные, мы часто делаем их очень похожими на белый шум: центрируем вокруг нуля и устанавливаем дисперсию или стандартное отклонение равными единице. Создание некоррелированных переменных используется реже, потому что требует больших вычислительных ресурсов. Но сама по себе операция несложная: мы просто переориентируем оси вдоль собственных векторов данных.

То есть, если мы примем C(kernel) за сдвиг, то получим выражение, очень похожее на свёртку. Входные данные свёрточного слоя можно представить как выходные данные авторегрессионной модели, если предварительно обработать их и получить белый шум.

Интерпретация взвешенного скользящего среднего проста: это стандартная свёртка на некоторых данных (исходных) с определённым весом (ядром). Более понятным будет взглянуть на ядро сглаживания Гаусса на рисунке ниже. Его можно интерпретировать как средневзвешенное значение в окрестности каждого пикселя. Другими словами, пиксели смешиваются, а края сглаживаются. 

Одно ядро не может создавать признаки как авторегрессии, так и взвешенного скользящего среднего. Поэтому обычно мы используем несколько ядер, комбинация которых будет содержать одни признаки, похожие на модель взвешенного среднего, и другие — на модель авторегрессии.

Заключение Ответ на вопрос: информация об одном пикселе рассеивается и будет смешиваться с окружающими пикселями. Это ядро называется гауссово размытие или гауссово сглаживание. Вернуться к чтению.

Надеемся, что статья помогла лучше понять свёртку. Если раньше вам казалось, что все ваши знания математики и статистики бесполезны и непрактичны — то теперь вы можете убедиться, что почти всегда им находится практическое применение. Если что-то осталось непонятным, задавайте вопросы, мы всегда с радостью ответим на них.

Ссылка на оригинальную статью в блоге timdettmers.com.

Человек безумный – Власть – Коммерсантъ

Вы человек разумный?        Умар Джабраилов, президент группы компаний «Плаза»:        — Я больше доверяю интуиции, а не логике. Когда же поступал наоборот, то часто ошибался и принимал неверные решения. Никогда ничего не рисую и не стучу предметами по столу, принимая то или иное решение.        Людмила Пихоя, вице-президент Импэксбанка:        — Это смотря какое решение надо принять. Делая покупки в магазине и решая, что купить, могу поддаться и настроению. Но если речь идет о важных вопросах, всегда стараюсь просчитать все «за» и «против».        Сергей Станкевич, член политсовета СПС:        — Чаще всего я принимаю решения и действую на основе логики. Но когда ситуация становится алогичной, что в политике — и особенно в политике России — бывает достаточно часто, подключаю к решению интуицию. Мне кажется, с годами интуиция развивается настолько, что в определенных ситуациях заменяет логику.        Владимир Аверченко, вице-спикер Госдумы:        — Я всегда и все делаю осознанно, больше всего полагаясь на жизненный опыт и, конечно, логику. Решения обычно принимаю достаточно быстро, обязательно рисуя что-то на листе бумаги. Видимо, сказывается моя первая профессия строителя.        Юрий Семин, главный тренер футбольной команды «Локомотив»:        — Главное — не принимать импульсивные решения, иначе потом придется жалеть. Мой рецепт прост: логики берется примерно 60%, интуиции — 40. По своему опыту могу сказать, что зачастую первое свежее решение, основанное на интуиции, оказывается верным. А при определении действий в ходе игры — например, кого заменить, кого выпустить на поле — интуиция приобретает первостепенное значение. А вот при подготовке к игре на первое место выходит логика — надо рассчитать тактику, учитывая состояние противника, физическое состояние своей команды и много других составляющих.        Марина Каратаева, владелец ювелирного дома «Петр Привалов»:        — Интуиции я доверяю в первую очередь, а уже потом стараюсь подходить логически. Любые вопросы обсуждаются только после того, как я приму решение, которое мне подсказывает интуиция. Потом уже можно взвешивать «за» и «против», рассуждать логически.        Генри Резник, адвокат:        — Когда у меня есть проверенные данные, я доверяю логике, а когда нет — интуиции. Иногда мне приходится жалеть о принятых решениях, но чаще виной тому бывает не интуиция.         За что дают Нобеля по экономике        Пол Сэмюэльсон (премия 1970 года) всю жизнь занимался построением экономико-математических моделей. Но всему миру стал известен своим учебником экономики, в котором без особой математики разъясняется, что при росте цен на товары спрос уменьшается, а при уменьшении спроса снижаются цены. При снижении цен спрос, соответственно, увеличивается, а при увеличении спроса цены растут                Василий Леонтьев (премия 1973 года) занимался построением межотраслевых балансов для строительства социализма в СССР. Потом леонтьевская модель «затраты—выпуск» стала так популярна на Западе, что его пригласили для строительства капитализма в Японии. СССР и Япония обеспечили неплохой выпуск продукции, но так и не смогли по-настоящему решить проблему затрат                Фридрих фон Хайек (премия 1974 года) считался главным идеологом свободной капиталистической конкуренции и критиком реального социализма. На самом деле он, как и его учитель Людвиг фон Мизес, всего лишь доказывал, что экономическая наука не хуже, чем физика и химия, и в ней присутствует логика. А логика подсказывает, что хорошие товары могут производить только западные страны                Милтон Фридмен (премия 1976 года) считается вдохновителем политики рейганомики, которая заключалась в том, что государству жить взаймы гораздо полезнее, чем повышать налоги и печатать деньги. Сейчас является главным критиком евро, полагает, что разным европейским странам нужна разная денежная политика. Впрочем, он также считает, что для бывших социалистических стран уж лучше евро, чем их собственная вызывающая недоверие валюта                Джеймс Мид (премия 1977 года) приобрел известность как виднейший специалист в области международной торговли и платежных балансов. В частности, утверждал, что являвшийся британской колонией остров Маврикий чрезвычайно перенаселен и может жить только вывозом рабочей силы в другие колонии. Маврикий, напротив, начал быстро богатеть за счет экспорта сахара и текстиля. А потом выяснилось, что богатство свое он получал в основном за счет льгот и субсидий, предоставленных ему США и западноевропейскими странами                Джеймс Тобин (премия 1981 года) прославился как разработчик эконометрических моделей. Эти модели подсказали ему, что беспрепятственное перемещение капитала между странами обогащает только валютных спекулянтов, а самим странам несет одни беды. Поэтому он предложил облагать перемещающийся капитал специальным налогом. Валютные кризисы в Восточной Азии, России или Аргентине обычно считаются подтверждением теории Тобина, а введение предложенного им налога сейчас вполне серьезно обсуждается ведущими индустриальными державами. Но от притока долларов бедные страны пока не отказались

Определение закона больших чисел

Что такое закон больших чисел?

Закон больших чисел в вероятности и статистике гласит, что по мере роста размера выборки ее среднее значение приближается к среднему для всей генеральной совокупности. В 16 веке математик Джеролама Кардано признал закон больших чисел, но так и не доказал его. В 1713 году швейцарский математик Якоб Бернулли доказал эту теорему в своей книге Ars Conjectandi . Позднее он был усовершенствован другими известными математиками, такими как Пафнутий Чебышев, основатель Санкт-Петербургского института науки и технологийПетербургская математическая школа.

В финансовом контексте закон больших чисел указывает на то, что крупное предприятие, которое быстро растет, не может поддерживать этот темп роста вечно. Крупнейшие из «голубых фишек» с рыночной стоимостью в сотни миллиардов часто приводятся в качестве примеров этого явления.

Ключевые выводы

• Закон больших чисел гласит, что наблюдаемое среднее по большой выборке будет близко к истинному среднему значению по совокупности и что оно будет тем ближе, чем больше выборка.
• Закон больших чисел не гарантирует, что данная выборка, особенно маленькая, будет отражать истинные характеристики генеральной совокупности или что выборка, которая не отражает истинную генеральную совокупность, будет уравновешена последующей выборкой.
• В бизнесе термин «закон больших чисел» иногда используется в другом смысле, чтобы выразить взаимосвязь между масштабом и темпами роста.

Смотрите сейчас: что такое закон больших чисел?

Понимание закона больших чисел

В статистическом анализе закон больших чисел может применяться к множеству предметов.Может оказаться невозможным опросить каждого человека в данной популяции для сбора необходимого количества данных, но каждая дополнительная собранная точка данных может повысить вероятность того, что результат будет истинной мерой среднего.

В бизнесе термин «закон больших чисел» иногда используется в отношении темпов роста, выраженных в процентах. Это говорит о том, что по мере роста бизнеса поддерживать процентные темпы роста становится все труднее.

Закон больших чисел не означает, что данная выборка или группа последовательных выборок всегда будут отражать истинные характеристики населения, особенно для небольших выборок.Это также означает, что если данная выборка или серия выборок отклоняется от истинного среднего значения по совокупности, закон больших чисел не гарантирует, что последующие выборки будут перемещать наблюдаемое среднее значение в сторону среднего значения по совокупности (как предполагает ошибка игрока).

Закон больших чисел не следует путать с законом средних чисел, который гласит, что распределение результатов в выборке (большой или малой) отражает распределение результатов в генеральной совокупности.

Закон больших чисел и статистический анализ

Если человек хотел определить среднее значение набора данных из 100 возможных значений, он, скорее всего, достигнет точного среднего значения, выбрав 20 точек данных вместо того, чтобы полагаться только на две. Например, если набор данных включал все целые числа от одного до 100, а выборщик взял только два значения, например 95 и 40, он может определить среднее значение примерно 67,5. Если он продолжал брать случайные выборки до 20 переменных, среднее должно сместиться в сторону истинного среднего, поскольку он рассматривает больше точек данных.

Закон больших чисел и роста бизнеса

В бизнесе и финансах этот термин иногда используется в просторечии для обозначения наблюдения, что экспоненциальные темпы роста часто не масштабируются. На самом деле это не связано с законом больших чисел, но может быть результатом закона убывающей предельной отдачи или неэкономичности масштаба.

Например, в январе 2020 года выручка Walmart Inc. составила 523,9 миллиарда долларов, в то время как Amazon.com Inc.принесла 280,5 млрд долларов за тот же период. Если Walmart захочет увеличить выручку на 50%, потребуется около 262 млрд долларов дохода. Напротив, Amazon нужно было бы увеличить выручку всего на 140,2 миллиарда долларов, чтобы достичь 50-процентного прироста. Согласно закону больших чисел, увеличение на 50% будет сложнее для Walmart, чем для Amazon.

Те же принципы можно применить к другим показателям, таким как рыночная капитализация или чистая прибыль. В результате инвестиционные решения могут быть приняты на основе связанных трудностей, с которыми могут столкнуться компании с очень высокой рыночной капитализацией, поскольку они связаны с повышением стоимости акций.

Закон больших чисел — определение, пример, применение в финансах

Что такое закон больших чисел?

В статистике и теории вероятностей закон больших чисел — это теорема, описывающая результат многократного повторения одного и того же эксперимента. Теорема больших чисел утверждает, что если один и тот же эксперимент или исследование повторяется независимо большое количество раз, среднее значение результатов испытаний должно быть близко к ожидаемому значению Ожидаемое значение Ожидаемое значение (также известное как EV, математическое ожидание, среднее или среднее значение). значение) — это долгосрочное среднее значение случайных величин.Ожидаемое значение также указывает. Результат становится ближе к ожидаемому значению по мере увеличения количества попыток.

Закон больших чисел — важное понятие в статистике Основные статистические концепции для финансов Твердое понимание статистики имеет решающее значение для того, чтобы помочь нам лучше понять финансы. Более того, концепции статистики могут помочь инвесторам в мониторинге, поскольку они заявляют, что даже случайные события с большим количеством испытаний могут дать стабильные долгосрочные результаты.Обратите внимание, что теорема касается только большого количества испытаний, в то время как среднее значение результатов эксперимента, повторенного небольшое количество раз, может существенно отличаться от ожидаемого значения. Однако каждое дополнительное испытание увеличивает точность среднего результата.

Пример закона больших чисел

Простейшим примером закона больших чисел является бросание кости. Игра в кости включает шесть различных событий с равной вероятностью. Ожидаемое значение событий игры в кости:

Если мы бросим кости только три раза, среднее значение полученных результатов может быть далеко от ожидаемого значения.Допустим, вы бросили кости три раза, и результаты были 6, 6, 3. Среднее значение результатов равно 5. Согласно закону больших чисел, если мы бросим кости большое количество раз, средний результат будет быть ближе к ожидаемому значению 3,5.

Закон больших чисел в финансах

В финансах закон больших чисел имеет иное значение, чем в статистике. В контексте бизнеса и финансов понятие связано с темпами роста бизнеса.

Закон больших чисел гласит, что по мере роста компании становится все труднее поддерживать прежние темпы роста. Таким образом, темпы роста компании снижаются по мере того, как она продолжает расширяться. Закон больших чисел может учитывать различные финансовые показатели, такие как рыночная капитализация. Рыночная капитализация. Рыночная капитализация (рыночная капитализация) — это последняя рыночная стоимость выпущенных акций компании. Рыночная капитализация равна текущей цене акции, умноженной на количество акций в обращении.Сообщество инвесторов часто использует значение рыночной капитализации для ранжирования компаний, выручки и чистой прибыли. Net IncomeNet Доход — это ключевая статья не только в отчете о прибылях и убытках, но и во всех трех основных финансовых отчетах. Пока он добрался до конца.

Практический пример

Рассмотрим следующий пример. Рыночная капитализация компании ABC составляет 1 миллион долларов, а рыночная капитализация компании XYZ — 100 миллионов долларов. Компания ABC демонстрирует значительный рост на 50% в год.Для ABC темпы роста легко достижимы, поскольку ее рыночная капитализация вырастает всего на 500 000 долларов.

Для компании XYZ такие темпы роста практически невозможны, потому что это означает, что ее рыночная капитализация должна расти на 50 миллионов долларов в год. Обратите внимание, что рост компании ABC со временем будет снижаться, поскольку она продолжает расширяться.

Ссылки по теме

CFI является официальным поставщиком услуг аналитика финансового моделирования и оценки (FMVA) ™. Стать сертифицированным аналитиком финансового моделирования и оценки (FMVA) ® Сертификация CFI по анализу финансового моделирования и оценки (FMVA) ® поможет вам получить необходимую уверенность в своей финансовой карьере.Запишитесь сегодня! программа сертификации, призванная превратить любого в финансового аналитика мирового уровня.

Чтобы продолжать изучать и развивать свои знания в области финансового анализа, мы настоятельно рекомендуем дополнительные ресурсы CFI ниже:

• Числа Фибоначчи Числа Фибоначчи Числа Фибоначчи — это числа, входящие в целочисленную последовательность, открытую / созданную математиком Леонардо Фибоначчи. Последовательность представляет собой ряд чисел
• Проверка гипотез Проверка гипотез Проверка гипотез — это метод статистического вывода.Он используется для проверки правильности утверждения относительно параметра совокупности. Проверка гипотез
• Независимые события Независимые события В статистике и теории вероятностей независимые события — это два события, в которых возникновение одного события не влияет на возникновение другого события
• Правило общей вероятности ) является фундаментальным правилом в статистике, относящейся к условным и маргинальным

Полное руководство по закону больших чисел для начинающих | 5 фактов о законе больших чисел | от Санни Сем | Аналитика Видхья

Закон средних чисел — это вероятность или вера в то, что события или конечные результаты произойдут в ближайшее время, может быть, а может и нет.Считается, что это ожидание приближается к точному результату. Завтра может идти дождь, а может и нет, можно грустить, а может и нет. В реальном сценарии он не является ни определенным, ни постоянным.

Заблуждение игрока — это заблуждение, которому следуют игроки, которые, как полагают, следуют Закону среднего только потому, что результат еще не случился недавно и есть вероятность, что он произойдет в будущем. Это чистая удача в игре и никаких расчетов. Пожалуйста, не следуйте этому методу, так как миндалевидное тело (нейрон) в мозгу Человека активируется, когда мы проигрываем, особенно во время азартных игр и проигрышей, а затем играет роль ошибки Игрока , заключающейся в принятии риска.

1-In в условиях непрофессионала, Центральная предельная теорема требует меньше данных по сравнению с Законом больших чисел.

2- Центральная предельная теорема не сходится к числу, а сходится к распределению.

3- Сходимость будет означать для меня, что со временем вероятность того, что среднее значение принимает значение, не являющееся ожидаемым, почти равна нулю, следовательно, распределение на самом деле не будет нормальным, а будет почти нулевым везде, кроме ожидаемого значения.

Закон больших чисел в психологии

Люди часто думают, что теорема Закона больших чисел может часто работать в реальной жизни, я согласен с этим до некоторой степени, потому что практически, когда вы работаете над чем-то много раз, вы находите конец результат очень плодотворный. Так что совершенно очевидно, что нужно практиковать что-либо несколько раз, чтобы стать мастером.

Пример — Закон больших чисел и фондовый рынок .

Очень часто 8 из 10 людей думают, что акции следует покупать только тогда, когда цены падают, и продавать, когда цены растут.Но этого не происходит, вы всегда должны покупать в точке безубыточности и всегда следует рассчитывать свой риск-менеджмент с учетом рыночного риска. Так работает Закон больших чисел, то есть когда трейдер много раз торгует и отслеживает различные результаты использования своих квалифицированных методов и расчетов, пока он не создаст свой собственный набор данных, паттерн и технику.

Закон больших чисел в страховании

Страховые компании очень зависимы от Закона больших чисел, следуя этой теореме, эти компании могут рассчитать свои будущие риски, прибыль и убытки, исходя из стабильности управления этими большими компаниями.

Давайте возьмем пример — Представьте, что 500 человек платят страховой взнос за его собственность в страховку Metlife. Несмотря на то, что они платят вам за материальный ущерб, причиненный пожаром 10% подписчика, то есть 50 человек, они все равно имеют премию в размере 450 человек. Именно так они рассчитывают свой риск-менеджмент, и здесь играет роль Закон больших чисел.

Закон больших чисел в искусственном интеллекте

Искусственный интеллект в наши дни является большой шумихой, но когда вы говорите о законе больших чисел, он определенно играет роль, особенно строгий закон больших чисел при обработке миллионов BIG ДАННЫЕ и Машинное обучение .Это помогает в обработке и организации данных в повседневной жизни. Даже IBM Watson построил с помощью закона больших чисел, который позволил победить чемпиона мира Гарри Каспарова в шахматах.

Какое значение имеет закон больших чисел в машинном обучении ?

1- Тренировочные данные

2- Тестовые данные

3- Оценка навыков модели

Заключение : Конечная теория должна делать точные прогнозы.Даже Эйнштейну потребовалось 4 года, чтобы доказать, что полное солнечное затмение показало, что свет, проходящий рядом с Солнцем, искривляется, что позже оказалось гравитацией. В 1930-х годах сэр Рональд Фишер, британский ученый, изложил рекомендации по разработке экспериментов с использованием статистики и вероятности как способа оценки результатов. Итак, теперь, если вы видите, все в этом мире было рассчитано и связано с математикой, от черной дыры до молекул. От вас зависит, как вы это видите.

Закон больших чисел: определение, примеры и статистика — видео и стенограмма урока

Пример: подбрасывание монеты

Другой пример действующего закона больших чисел — предсказание результата подбрасывания монеты.Если вы подбрасываете монету один раз, вероятность выпадения монеты орлом составляет 50% (что также можно записать как ½ или 0,5), а вероятность того, что она выпадет решкой, также составляет 50%.

Но что произойдет, если подбросить монету десять раз подряд? Можете ли вы с уверенностью сказать, что там он будет приземляться орлом в половине случаев, а в другой половине — решкой? Ответ — «нет», потому что каждое подбрасывание монеты — это независимое событие . Это означает, что исход одного события, в данном случае подбрасывания монеты, не повлияет на исход следующего события.

Это правда, что с каждым подбрасыванием монеты шанс выпадения орла составляет 50/50; однако, если вы подбрасываете монету несколько раз, вы не можете быть уверены, что 50% подбрасываний выпадут орлом или наоборот, если вы не используете закон больших чисел. Это потому, что закон больших чисел диктует, что по мере того, как мы увеличиваем количество раз, когда мы подбрасываем монету, мы все ближе и ближе приближаемся к достижению 50% вероятности выпадения орла или решки. Итак, если у вас есть время подбросить монету тысячи раз, вы можете быть уверены, что примерно половина подбрасываний будет выпадать орлом!

Чтобы проиллюстрировать это, давайте взглянем на следующую диаграмму, показывающую результаты эксперимента с различным количеством подбрасываний монет:

Вы видели схему вероятностей? Надеюсь, вы заметили, что когда монета подбрасывается всего несколько раз, результаты не показывают, что вероятность того, что она упадет орлом и решкой, равны.Достижение 50% вероятности выпадения орла увеличивается с каждым значительно большим количеством бросков. Это классический пример закона больших чисел.

Статистика и вероятность

Хотя подбрасывание монет и соревнования по угадыванию мармеладов являются забавными примерами того, как работает закон больших чисел, этот принцип является важным статистическим инструментом и лежит в основе решений, которые принимают все компании и которые влияют на нас. Страховые компании используют закон больших чисел для определения вероятности того, что события, такие как автомобильные аварии, произойдут.Чем больше автомобилей застраховывает страховая компания, тем точнее страховая компания сможет предсказать вероятность возникновения аварии. Результаты этих прогнозов влияют на то, как страховые компании определяют размер страховых взносов, которые мы платим.

Резюме урока

Закон больших чисел — это теория вероятности, которая гласит, что чем больше становится размер выборки, тем ближе среднее (или среднее) значение выборки приближается к ожидаемому значению.

Итак, исходя из примеров, которые мы видели выше, чем больше у вас предположений о том, сколько желейных бобов находится в банке, тем более вероятно, что среднее значение этих предположений будет равно количеству мармелада. фасоль в банке. Но прежде чем делать большие денежные ставки на количество желейных бобов в банке, мы должны иметь в виду, что вероятность, как следует из названия, все еще зависит от случая.

Мягкое введение в закон больших чисел в машинном обучении

Последнее обновление 8 августа 2019 г.

У нас есть интуиция, что чем больше наблюдений, тем лучше.

Это та же самая интуиция, которая лежит в основе идеи о том, что если мы соберем больше данных, наша выборка данных будет более репрезентативной для предметной области.

Существует теорема статистики и вероятности, которая поддерживает эту интуицию, которая является столпом обеих этих областей и имеет важное значение в прикладном машинном обучении. Название этой теоремы — закон больших чисел.

В этом руководстве вы узнаете о законе больших чисел и о том, почему он важен для прикладного машинного обучения.

После прохождения этого руководства вы будете знать:

• Закон больших чисел поддерживает интуицию о том, что выборка становится более репрезентативной для генеральной совокупности по мере увеличения ее размера.
• Как разработать небольшой пример на Python, чтобы продемонстрировать уменьшение ошибки из-за увеличения размера выборки.
• Закон больших чисел имеет решающее значение для понимания выбора наборов обучающих данных, наборов тестовых данных и при оценке навыков модели в машинном обучении.

Начните свой проект с моей новой книги «Статистика для машинного обучения», включающей пошаговых руководств и файлов исходного кода Python для всех примеров.

Приступим.

Мягкое введение в закон больших чисел в машинном обучении
Фото Рахил Шахид, некоторые права защищены.

Обзор учебного пособия

Это руководство разделено на 3 части; их:

1. Закон больших чисел
2. Рабочий пример
3. Значение машинного обучения

Нужна помощь со статистикой для машинного обучения?

Пройдите мой бесплатный 7-дневный ускоренный курс электронной почты (с образцом кода).

Нажмите, чтобы зарегистрироваться, а также получите бесплатную электронную версию курса в формате PDF.

Загрузите БЕСПЛАТНЫЙ мини-курс

Закон больших чисел

Закон больших чисел — это теорема, основанная на вероятности и статистике, которая предполагает, что средний результат многократного повторения эксперимента лучше приблизительно соответствует истинному или ожидаемому исходному результату.

Закон больших чисел объясняет, почему казино всегда приносят прибыль в долгосрочной перспективе.

— Стр. 79, Обнаженная статистика: снимая страх с данных, 2014.

Мы можем думать об испытании эксперимента как об одном наблюдении. Автономное и независимое повторение эксперимента приведет к многократным испытаниям и многочисленным наблюдениям. Все образцы наблюдений для эксперимента взяты из идеализированной совокупности наблюдений.

• Наблюдение : Результат одного испытания эксперимента.
• Образец : Группа результатов, собранных в результате отдельных независимых испытаний.
• Население : Пространство всех возможных наблюдений, которые можно увидеть в ходе испытания.

Используя эти термины из статистики, мы можем сказать, что по мере увеличения размера выборки среднее значение выборки будет лучше приближаться к среднему или ожидаемому значению в генеральной совокупности. По мере увеличения размера выборки до бесконечности среднее значение выборки будет сходиться к среднему значению генеральной совокупности.

… венец вероятности, закон больших чисел. Эта теорема говорит, что среднее значение большой выборки близко к среднему значению распределения.

— стр. 76, Вся статистика: краткий курс статистических выводов, 2004 г.

Это важный теоретический вывод для статистики и вероятности, а также для прикладного машинного обучения.

Независимые и идентично распределенные

Важно понимать, что наблюдения в выборке должны быть независимыми.

Это означает, что испытание выполняется идентичным образом и не зависит от результатов других испытаний.Часто это разумно и легко достигается на компьютере, хотя может быть сложно в другом месте (например, как добиться идентично случайных бросков игральных костей?).

В статистике это ожидание называется « независимых и идентично распределенных », или IID, iid или i.i.d. коротко. Это необходимо для гарантии того, что выборки действительно взяты из одного и того же основного распределения населения.

Регрессия к среднему

Закон больших чисел помогает нам понять, почему мы не можем доверять отдельному наблюдению из изолированного эксперимента.

Мы ожидаем, что вероятен единичный результат или средний результат небольшой выборки. Это близко к центральной тенденции — среднему значению распределения населения. А может и не быть; на самом деле это может быть очень странно или маловероятно.

Закон напоминает нам повторить эксперимент, чтобы получить большую и репрезентативную выборку наблюдений, прежде чем мы начнем делать выводы о том, что означает результат.

По мере увеличения размера выборки результат или среднее значение выборки будет возвращаться к среднему значению генеральной совокупности, обратно к истинному лежащему в основе ожидаемому значению.Это называется регрессией к среднему или иногда возвращением к среднему значению.

Вот почему мы должны скептически относиться к выводам из небольших размеров выборки, называемых small n .

Закон действительно больших чисел

С регрессией к среднему связана идея закона действительно больших чисел.

Это идея о том, что когда мы начинаем исследовать или работать с очень большими выборками наблюдений, мы увеличиваем вероятность увидеть что-то странное.Что, имея так много выборок основного распределения населения, выборка будет содержать некоторые астрономически редкие события.

Опять же, мы должны быть осторожны, чтобы не делать выводы из единичных случаев.

Это особенно важно учитывать при выполнении запросов и исследовании больших данных.

Рабочий пример

Мы можем продемонстрировать закон больших чисел на небольшом рабочем примере.

Во-первых, мы можем разработать идеализированное базовое распределение.Мы будем использовать распределение Гаусса со средним значением 50 и стандартным отклонением 5. Таким образом, ожидаемое значение или среднее значение этой генеральной совокупности равно 50.

Ниже приведен код, который генерирует график этого идеализированного распределения.

# идеализированное распределение населения из numpy import arange из matplotlib import pyplot из нормы импорта scipy.stats # ось x для графика xaxis = arange (30, 70, 1) # ось Y для графика yaxis = норма.pdf (xaxis, 50, 5) # график идеального населения pyplot.plot (xaxis, yaxis) pyplot.show ()

# идеализированное распределение населения из numpy import arange из matplotlib import pyplot из scipy.stats import norm # ось x для графика xaxis = arange (30, 70, 1) # Ось y для графика yaxis = norm.pdf (xaxis, 50, 5) # построить идеальную популяцию pyplot.сюжет (xaxis, yaxis) pyplot.show ()

Запуск кода создает график спроектированной популяции с знакомой формой колокольчика.

Идеализированное базовое распределение населения

Теперь мы можем притвориться, что забыли все, что мы знаем о популяции, и сделать независимые случайные выборки из этой популяции.

Мы можем создавать выборки разного размера и вычислять среднее значение. Учитывая нашу интуицию и закон больших чисел, мы ожидаем, что по мере увеличения размера выборки среднее значение выборки будет лучше приближаться к среднему значению генеральной совокупности.

В приведенном ниже примере вычисляются образцы разных размеров, а затем печатаются средние значения выборки.

# продемонстрировать закон больших чисел из numpy.random import seed из numpy.random import randn из среднего значения импорта из массива импорта numpy из matplotlib import pyplot # заполняем генератор случайных чисел семя (1) # размер выборки size = [10, 100, 500, 1000, 10000] # генерировать выборки разного размера и вычислять их средние означает = [среднее (5 * randn (размер) + 50) для размера в размерах] печать (означает) # построить график средней ошибки выборки в зависимости от размера выборки пиплот.разброс (размеры, массив (означает) -50) pyplot.show ()

# продемонстрировать закон больших чисел из numpy.random import seed from numpy.random import randn from numpy import mean from numpy import array from matplotlib import pyplot # seed случайное число генератор seed (1) # размеры выборки sizes = [10, 100, 500, 1000, 10000] # генерировать выборки разных размеров и вычислять их средние means = [mean (5 * randn ( size) + 50) для размера в sizes] print (means) # построить график средней ошибки выборки по сравнению с размером выборки pyplot.разброс (размеры, массив (средства) -50) pyplot.show ()

При выполнении примера сначала печатаются средние значения каждого образца.

Мы можем видеть слабую тенденцию приближения выборочного среднего к 50,0 по мере увеличения размера выборки.

Отметим также, что этот образец выборочного средства тоже должен подчиняться закону больших чисел. Например, случайно вы можете получить очень точную оценку среднего значения генеральной совокупности со средним значением небольшой выборки.

[49.5142955459695, 50.371593294898695, 50.29196533, 50.1521157689338, 50.03955033528776]

[49.5142955459695, 50.371593294898695, 50.29196533, 50.1521157689338, 50.03955033528776]

В этом примере также создается график, который сравнивает размер выборки с ошибкой выборочного среднего от среднего значения генеральной совокупности. Как правило, мы видим, что большие размеры выборки имеют меньше ошибок, и мы ожидаем, что эта тенденция в среднем сохранится.

Мы также можем видеть, что некоторые выборки означают завышение, а некоторые — занижение. Не попадайтесь в ловушку предположения, что недооценка упадет на ту или иную сторону.

График разброса размера выборки и ошибки

Значение машинного обучения

Закон больших чисел имеет важное значение для прикладного машинного обучения.

Давайте уделим время, чтобы выделить некоторые из этих последствий.

Данные обучения

Данные, используемые для обучения модели, должны быть репрезентативными для наблюдений из области.

Это на самом деле означает, что он должен содержать достаточно информации, чтобы сделать вывод об истинном неизвестном и лежащем в основе распределении населения.

Это легко представить с помощью одной входной переменной для модели, но это не менее важно, когда у вас есть несколько входных переменных. Между входными переменными будут неизвестные отношения или зависимости, и вместе входные данные будут представлять собой многомерное распределение, из которого будут извлечены наблюдения, чтобы составить вашу обучающую выборку.

Имейте это в виду при сборе данных, очистке данных и подготовке данных.

Вы можете исключить части основной совокупности, установив жесткие ограничения на наблюдаемые значения (например, для выбросов), если вы ожидаете, что данные будут слишком разреженными для эффективного моделирования.

Данные испытаний

Мысли, заданные набору обучающих данных, также должны быть переданы набору тестовых данных.

Этим часто пренебрегают из-за слепого использования спотов 80/20 для данных обучения / тестирования или слепого использования 10-кратной перекрестной проверки, даже для наборов данных, где размер 1/10 доступных данных может быть неприемлемым. репрезентативные наблюдения из проблемной области.

Оценка навыков модели

Учитывайте закон больших чисел при представлении оценки навыков модели на невидимых данных.

Он обеспечивает защиту не для того, чтобы просто составить отчет или продолжить работу с моделью, основанной на оценке навыков, полученной при оценке одного тренинга / теста.

Он подчеркивает необходимость разработки выборки из нескольких независимых (или близких к независимой) оценок данной модели, чтобы среднее значение навыка, полученное по выборке, было достаточно точной оценкой среднего значения для всей совокупности.

Расширения

В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.

• Проведите мозговой штурм в двух дополнительных областях машинного обучения, где применяется закон больших чисел.
• Найдите пять научных работ, в которых вы скептически относитесь к результатам с учетом закона больших чисел.
• Разработайте собственное идеальное распределение и выборки и нарисуйте зависимость между размером выборки и средней ошибкой выборки.

Если вы изучите какое-либо из этих расширений, я хотел бы знать.

Дополнительная литература

В этом разделе представлены дополнительные ресурсы по теме, если вы хотите углубиться.

Книги

API

Статьи

Сводка

В этом руководстве вы узнали о законе больших чисел и о том, почему он важен для прикладного машинного обучения.

В частности, вы выучили:

• Закон больших чисел поддерживает интуицию о том, что выборка становится более репрезентативной для генеральной совокупности по мере увеличения ее размера.
• Как разработать небольшой пример на Python, чтобы продемонстрировать уменьшение ошибки из-за увеличения размера выборки.
• Закон больших чисел имеет решающее значение для понимания выбора наборов обучающих данных, наборов тестовых данных и при оценке навыков модели в машинном обучении.

Есть вопросы?
Задайте свои вопросы в комментариях ниже, и я постараюсь ответить.

Получите доступ к статистике для машинного обучения!

Развить рабочее понимание статистики

…пишите строки кода на Python

Узнайте, как это сделать, в моей новой электронной книге:
Статистические методы для машинного обучения

Он предоставляет руководств для самообучения по таким темам, как:
Проверка гипотез, корреляция, непараметрическая статистика, повторная выборка и многое другое …

Узнайте, как преобразовать данные в знания

Пропустить академики. Только результаты.

Посмотрите, что внутри

Закон больших чисел — определение

Назад к : ИССЛЕДОВАНИЯ, АНАЛИЗ И НАУКА ПРИНЯТИЯ РЕШЕНИЙ

Определение закона больших чисел

Это концепция вероятности, означающая, что распространенность событий с аналогичной вероятностью возникновения в конечном итоге выравнивается в течение ряда достаточных испытаний.Поскольку количество экземпляров продолжает расти, фактическое соотношение результатов пересекается с теоретическим или ожидаемым соотношением результатов. Этот закон устанавливает, что чем больше размер выборки, тем ближе среднее значение к среднему для всей генеральной совокупности. Он был разработан с учетом того факта, что быстрорастущее крупное предприятие не может удерживать темп в течение длительного времени.

Еще немного о законе больших чисел

Например, предположим, что монета подброшена миллион раз, можно с уверенностью сказать, что примерно половина подбрасываний будет орлом, а половина — решкой.Следовательно, это соотношение будет почти 1: 1. Когда монета подбрасывается двадцать раз, соотношение будет другим и может быть 3: 7 или любым другим. Иногда этот закон неправильно применяют к ситуациям с очень небольшим количеством экспериментов, что приводит к логической ошибке, называемой ошибкой игрока. Закон больших чисел, также известный как закон средних чисел, — это теория, используемая для объяснения результатов, возникающих при многократном проведении аналогичных экспериментов. В нем говорится, что статистическая вероятность выборки с определенным значением приближается к статистической вероятности набора выборок во вселенной по мере увеличения выборки.Политические опросы используют этот метод, и поэтому они становятся тем точнее, чем больше увеличивается размер выборки. Еще в июле 2015 года Wal-Mart Stores Inc. получила доход в размере 485,5 млрд долларов, а Amazon — 95,8 млрд долларов. Чтобы они увеличили свой доход на 50% на основе этих цифр, Walmart потребуется в общей сложности 242,8 миллиарда долларов, а Amazon — всего 47,9 доллара. По закону больших чисел такое увеличение будет сложнее для Walmart, чем для Amazon. Этот закон гарантирует стабильные долгосрочные результаты для средних значений различных случайных событий и поэтому очень важен.

Ссылки на закон больших чисел

Академические исследования закона больших чисел

Полная сходимость и закон больших чисел , Hsu, P. L., & Robbins, H. (1947). Proceedings of the National Academy of Sciences of the United States of America , 33 (2), 25. Эта статья определяет и различает стандартные термины в теории вероятностей, которые включают вероятностное пространство, действительнозначная P-измеримая функция X = X среди других.Скорости сходимости в законе больших чисел , Баум, Л. Э. и Кац, М. (1965). Труды Американского математического общества , 120 (1), 108-123. В этой статье уделяется внимание последовательностям независимых и одинаково распределенных случайных величин и представлены различные предложения и примеры для случая независимых, но по-разному распределенных случайных величин. Закон больших чисел для крупных экономик, Uhlig, H.(1996). Экономическая теория , 8 (1), 41-50. Эта статья представляет закон больших чисел, интерпретируя интеграл как интеграл Петтиса. Он также обеспечивает доказательство с использованием вычисления дисперсии и показывает, что проблему измеримости, выявленную Джаддом в 1985 году, можно избежать за счет сходимости в среднем квадрате вместо сходимости почти везде. Сильный закон больших чисел для u-статистики., Hoeffding, W. (1961). Государственный университет Северной Каролины. Департамент статистики. В данной статье исследуется усиленный закон больших чисел для класса U-статистики при условии момента, ведущего к обобщению этого закона. Согласованность в нелинейных эконометрических моделях: общий унифицированный закон больших чисел , Эндрюс, Д. У. (1987). Econometrica: Journal of the Econometric Society , 1465-1471. Эта статья направлена ​​на предоставление универсального единообразного закона больших чисел, который является по существу общим и включает большинство приложений единообразного закона больших чисел в литературе по нелинейной эконометрике.Локальная сходимость мартингалов и закон больших чисел . Чоу, Ю.С. (1965). Анналы математической статистики , 36 (2), 552-558. Эта статья обобщает результаты Невё, когда он доказал существование новой теоремы о субмартингальной сходимости. Заметка о строгом законе больших чисел для положительно зависимых случайных величин, Birkel, T. (1988). Письма о статистике и вероятности , 7 (1), 17-20. В этой статье представлены строгие законы больших чисел для последовательностей случайных величин, которые связаны или попарно зависят от положительного квадранта. Точный закон больших чисел через расширение Фубини и характеристику страхуемых рисков, Sun, Y. (2006). Журнал экономической теории , 126 (1), 31-69. Это исследование вводит простые методы теории меры в эту структуру, чтобы получить несколько версий этого закона и их обратные случайные процессы или континуум случайных величин, а также предлагает расширение Фубини в качестве вероятностного пространства, которое расширяет вероятностное пространство, сохраняя при этом Фубини собственность.Общий подход к строгому закону больших чисел , Фазекас И., Клесов О. (2001). Теория вероятностей и ее приложения , 45 (3), 436-449. В данной статье исследуется общий метод, основанный на абстрактных максимальных неравенствах типа Хекрни, для получения строгих законов больших чисел. Строгий закон больших чисел для емкостей, Maccheroni, F., & Marinacci, M. (2005). Летопись вероятностей , 33 (3), 1171-1178. В этой статье рассматриваются полностью монотонная емкость на полированном пространстве и последовательность ограниченных p.i.i.d случайных величин. Закон о больших числах : торги и обязательные конкурентные торги для контрактов на вывоз мусора, Gomez-Lobo, A., & Szymanski, S. (2001). Обзор промышленной организации , 18 (1), 105-113. Это исследование взаимосвязи, существующей между затратами и количеством участников торгов по контрактам местных властей Великобритании на вывоз мусора. Закон больших чисел в теории потребительского выбора в условиях неопределенности, Yaari, M. E. (1976). Журнал экономической теории , 12 (2), 202-217. В этой статье исследуется гипотеза, согласно которой потребление зависит от дохода в той мере, в какой доход влияет на благосостояние на протяжении всей жизни.

Была ли эта статья полезной?

Слабый закон больших чисел — обзор

3 Вероятности как предельные частоты

Для Райхенбаха вероятность, как она используется в науке, является объективной величиной, а не субъективной степенью веры. Основная трудность такого объяснения состоит в том, чтобы точно указать, какой должна быть такая объективная вероятность, и в то же время предоставить обоснованные основания для вынесения вероятностных суждений.Фактически, на протяжении всей своей жизни Райхенбах работал над основами теории вероятностей, и его взгляды изменились.

В своей докторской диссертации в 1915 году Райхенбах утверждает, что вероятность события — это относительная частота события в бесконечной последовательности причинно-независимых и причинно-идентичных испытаний [Reichenbach, 1915]. Под влиянием неокантианцев своего времени (Эрнст Кассирер, Поль Наторп и др.) Райхенбах считал причинность примитивной концепцией, более фундаментальной, чем вероятность.С этой точки зрения причинное знание — это синтетическое априорное знание, и доказательство этого статуса якобы было дано кантовским трансцендентным выводом принципа причинности. То есть, согласно (Рейхенбаховскому прочтению) Канта, у нас есть причинное знание для отдельных событий, которое позволяет нам определять причинную независимость и идентичные причинные обстоятельства, и поэтому, согласно Рейхенбаху, у нас есть нетривиальная, некруговая и объективная основа. на котором строится понятие вероятности.В частности, если можно показать, что причинно-независимые и идентичные испытания предполагают вероятностно независимые и одинаково распределенные испытания, тогда закон больших чисел подразумевает, что эмпирическое распределение сходится к истинному распределению по вероятности. ¹ Рейхенбах знал о (слабом) законе больших чисел (хотя в его диссертации он подробно не обсуждается), но считал сходимость по вероятности слишком слабой. Опора на сходимость по вероятности означала бы, что понятие вероятностных характеристик в определениях определения вероятности, что сделало бы определение концепции вероятности циклическим.Райхенбах хотел добиться уверенного сближения.

Чтобы разрешить эту дилемму, Райхенбах (в 1915 году) снова обратился к кантовскому набору инструментов и представил трансцендентный аргумент, что существует синтетический априорный принцип — принцип законного распределения, — который с уверенностью гарантирует, что каждое эмпирическое распределение сходится. Суть трансцендентального аргумента заключается в следующем: если бы не было такого принципа, научное познание, как оно представлено в законах природы, было бы невозможным.Но очевидно, что наука изобилует знаниями о законных причинных отношениях. Научные законы устанавливают общие причинные закономерности, но кантовское каузальное знание предоставляет причинное знание только в отношении отдельных событий. Что-то необходимо для объединения отдельных маркеров причинного знания в общие причинные законы. Следовательно, должен быть такой принцип. С учетом этого принципа сходимость гарантирована с уверенностью, и даже если мы не знаем, когда сходимость произойдет или с какой скоростью, мы на правильном пути, если будем использовать эмпирическое распределение, поскольку оно должно сходиться в какой-то момент.Короче говоря, это было аргументом в его докторской диссертации.

Аргумент не очень удовлетворительный, даже если бы пробелы были заполнены (например, от причинно-независимых испытаний к вероятностно независимым испытаниям): учитывая современное неправдоподобное мнение о том, что причинное знание токен-событий является синтетическим априори, утверждение, что существует синтетическая априорная гарантия сходимости последовательностей к предельному распределению — мы знаем много последовательностей, предельные частоты которых не сходятся.

Рейхенбах, должно быть, в какой-то момент (если не все время) почувствовал такое же дискомфорт из-за своего отчета, поскольку его аргументы значительно изменились между его докторской диссертацией в 1915 году и публикацией английского издания The Theory of Probability в 1949 году [Reichenbach , 1949c]. ²

В 1927 году Райхенбах указал в примечаниях ³ (и сослался на более ранние обсуждения с Полом Герцем), что сходимость с уверенностью несостоятельна и что можно гарантировать сходимость только по вероятности.Это переходная мысль Райхенбаха. По сути, это наблюдение закона больших чисел, которое устанавливает распределение вероятностей, из которого исходные сегменты последовательностей получаются с помощью i.i.d выборки. Интерпретация предельной частоты, напротив, дает уверенность в сходимости к вероятности по прямому правилу при условии, что предельное значение вообще существует. Вдобавок он изменил свое мнение о порядке примитивов: как только Эйнштейн пошатнул синтетический априорный статус пространства и времени, Райхенбах аналогичным образом проанализировал синтетический априорный статус причинности и пришел к выводу, что это не причинность, а скорее вероятность того, что было более фундаментальным понятием, т.е. что причинно-следственная связь — это отношение, которое можно вывести только на основе вероятностных отношений (плюс некоторые дополнительные предположения). Утверждения о причинно-следственной связи одного события — то, что сейчас называется фактической причинно-следственной связью — считались эллиптическими, либо неявно относящимися к последовательности событий, либо фиктивным переносом причинного утверждения с уровня типа на уровень токена.

Однако, если причинно-следственные связи больше не являются фундаментальными и вероятности не следует рассматривать как примитивные, тогда Райхенбаху пришлось найти новое основание для концепции вероятности.Это усилие совпало с аналогичными опасениями Ричарда фон Мизеса. Фон Мизес пытался установить основу вероятности в терминах случайных событий [von Mises, 1919]. В то время как случайность хорошо понималась до теоретически, все попытки охарактеризовать ее формально приводили к нежелательным последствиям. Цель, которую разделяли и Райхенбах, и фон Мизес, заключалась в сведении концепции вероятности к свойству бесконечных последовательностей событий, тем самым избегая какой-либо замкнутости в основе.

Учитывая научную практику, казалось интуитивно понятным и привлекательным думать об объективных вероятностях в терминах относительной частоты в бесконечной последовательности событий — нужно было только надлежащим образом охарактеризовать типы последовательностей, которые будут считаться допустимыми как обеспечивающие основу вероятности. Например, нельзя считать последовательность допустимой, если она просто чередуется между 1 и 0. Хотя предельная относительная частота единиц равна 1/2, следующее число известно с уверенностью, учитывая любой начальный сегмент, достаточно длинный, чтобы показать шаблон.Поэтому фон Мизес хотел ограничить свои соображения последовательностями случайных событий, поскольку понятие случайности отражало идею о том, что никто не сможет заработать деньги, делая ставки на следующий элемент в последовательности с учетом предыдущих элементов. Более формально отсутствие последействия и инвариантность к выбору подпоследовательностей считались необходимыми условиями для случайных последовательностей. Отсутствие последействия отражает идею невозможности заработать деньги, делая ставки на следующий элемент последовательности, учитывая предыдущие элементы.В частности, вероятность любого исхода должна быть одинаковой, независимо от того, каковы были предыдущие исходы. Инвариантность при выборе подпоследовательности требует, чтобы вероятность события была одинаковой при любом правиле выбора подпоследовательности, которое зависит только от индексов элементов. Формально формулировка этих понятий разнится у авторов.

Райхенбах отверг идею случайных последовательностей, потому что он не видел никакой надежды на то, что сможет адекватно зафиксировать случайность формально. ⁴ Существовали известные теоретические трудности в демонстрации того, что все условия случайности могут быть выполнены, и Райхенбах указал на некоторые из них [Reichenbach, 1932a].Райхенбах не отказался от этой идеи полностью, а вместо этого согласился на несколько более слабое ограничение на последовательности: нормальные последовательности. Нормальные последовательности образуют строгий надмножество случайных последовательностей. Последовательность событий равна нормальным , если последовательность не имеет последствий и вероятности типов событий неизменны при регулярных делениях. Определение последействия, данное Райхенбахом, не совсем ясно, но примерно в последовательности с последействием событие E с индексом i подразумевает для событий с индексами, следующими за вероятностями i , которые отличаются от предельной относительной частоты те события.Регулярные деления — это правила выбора подпоследовательности, которые выбирают каждые k -го элемента исходной последовательности для некоторого фиксированного k . (На самом деле условия немного сложнее, но мы оставим это в стороне.) Тогда вероятность события E является предельной относительной частотой E в нормальной последовательности событий.

Это работает как абстрактное определение вероятности, но не подходит для определения научных вероятностей. В эмпирической науке последовательности измерений конечны.Конечный начальный отрезок последовательности не дает нам информации о предельном распределении. Тем не менее, Райхенбах утверждает, что мы должны рассматривать эмпирическое распределение, данное конечным начальным сегментом измерений, как если бы оно было (примерно) таким же, как и предельное распределение. Он считает, что мы можем прибегнуть к вероятности более высокого порядка, которая определяет вероятность того, что предельная относительная частота события (его истинная вероятность) находится в некоторой (узкой) полосе шириной δ вокруг эмпирической частоты.Эта вероятность более высокого порядка также основана на эмпирических данных, но косвенно: она происходит из последовательности значений вероятности первого порядка, то есть из последовательности последовательностей событий. Идея состоит в том, что он объединяет данные из последовательностей различных индуктивных выводов. Райхенбах приводит один тип примера в разных формах, который дает некоторое представление о том, как это должно работать (например, см. [Reichenbach, 1949c, pp. 438-440]): Предположим, у нас есть конечная последовательность измерений,

M1, M2 , M3, M4, M5,…, Mn

, и мы классифицируем их как 1 или 0 в зависимости от того, попадают ли они в некоторый заранее заданный узкий диапазон вокруг фиксированного значения.Например, предположим, что у нас есть измерения гравитационной постоянной, и мы классифицируем точки данных как 1, если они попадают в полосу γ ± δ для некоторого небольшого значения δ , и 0 в противном случае. Таким образом, мы можем определить переменную X = I (| M — γ | ≤ δ ), где I (.) — индикаторная функция, и получить последовательность значений X , состоящий из единиц и нулей, в зависимости от исходных измерений:

1,1,0,1,0,… 0.

Предположим далее, что если бы у нас было бесконечное количество данных, то было бы ограничивающее распределение по частотам нулей и единиц в последовательности, с P ( X = 1) = p и P ( X = 0) = 1− p . Фактическое эмпирическое распределение, определяемое относительной частотой единиц и нулей среди доступных измерений, равно Pˆ (X = 1) = pˆ и Pˆ (X = 0) = 1 − pˆ. Райхенбах утверждает, что существует вероятность более высокого порядка q , которая утверждает, что Pˆ (| pˆ − p | <ε) = q для малых ε , т.е.е. истинное распределение с вероятностью q попадает на расстояние ε эмпирического распределения. Согласно Райхенбаху, у нас есть оценка такой вероятности более высокого порядка q путем рассмотрения нескольких последовательностей измерений, каждая из которых имеет собственное эмпирическое распределение. Итак, предположим, что у нас есть три последовательности измерений (скажем, из различных экспериментов гравитационной постоянной на (а) Луне, (б) на какой-то планете и (в) с использованием весов Кавендиша):

a: 1,1,1 , 0,0,…, 1b: 0,1,1,1,1,…, 0c: 0,0,1,0,0,…, 1

Каждый будет иметь определенное эмпирическое распределение, скажем Pˆa, Pˆb и Pˆc.Эти три эмпирических распределения образуют свою собственную последовательность значений pˆ, а именно

pˆa, pˆb, pˆc

, каждое из которых определяет относительную частоту единиц в отдельных последовательностях. pˆa, pˆb, pˆc снова определяют эмпирическое распределение, но теперь с вероятностями более высокого порядка. Предположим, что из трех начальных распределений pˆa = 0,8, pˆb = 0,7 и pˆc = 0,79. Опять же, мы можем классифицировать эти значения в соответствии с некоторым приближением, например 0,8 ± ε , где ε = 0.05. В этом случае (эмпирическая оценка) вероятности более высокого порядка q равна qˆ = 2/3. Относительная частота единиц в одной строке указывает на вероятность истинности утверждения о гравитационной постоянной для конкретного тестового объекта, например планета. Вероятность второго порядка q для различных последовательностей указывает вероятность того, что утверждение вероятности первого порядка истинно. Согласно Райхенбаху, именно такая взаимная проверка сходимости различных последовательностей измерений обеспечивает вероятность сходимости любого эмпирического распределения.

В другом аналогичном примере, включающем измерения температуры плавления различных металлов, Райхенбах утверждает, что тот факт, что многие металлы имеют точку плавления, дает нам основание полагать, что металл, плавление которого мы до сих пор не видели, тем не менее, вероятно, будет иметь температуру плавления. температура плавления. Несмотря на то, что для этого явно «твердого» металла эмпирическое распределение измерений, по-видимому, указывает на то, что вероятность наличия точки плавления равна нулю, вероятность второго порядка, определяющая, насколько показательным является эмпирическое распределение предела, будет очень низкой. , потому что вероятность второго порядка объединяет результаты по другим металлам.Райхенбах называет эти «перекрестные индукции» «сетью индукций».

Другой способ осмыслить подход Райхенбаха — рассмотреть иерархическую байесовскую процедуру: данные измерений используются для оценки определенных параметров распределения интересующей величины. Но можно описать эти параметры распределением более высокого порядка со своими собственными гиперпараметрами. В этом случае можно использовать несколько последовательностей измерений для получения оценок гиперпараметров.Как только они оценены, можно повторно вычислить параметры нижнего уровня с учетом оцененных гиперпараметров. Это обеспечивает поток информации между различными последовательностями измерений через гиперпараметры и, следовательно, обеспечивает широкую интеграцию данных из разных источников. Как и в случае с Райхенбахом, можно продолжить этот подход до более высоких порядков с гипер-гиперпараметрами. В какой-то момент возникнет вопрос, достаточно ли данных для оценки параметров высокого порядка.Райхенбах утверждает, что в некотором более высоком порядке слепые постулаты заменяют оценки вероятностей, чтобы избежать бесконечного регресса вероятностей более высокого порядка.

Иерархические байесовские методы теоретически работают хорошо, но они зависят от способности определять, похожи ли события и в каком смысле, чтобы их можно было включить в одну и ту же выборку (которая затем используется для определения вероятностей). По мнению Райхенбаха, соответствующий вопрос касается определения референтных классов.

Референсные классы — непростая задача для Райхенбаха, поскольку он заходит так далеко, что утверждает, что мы можем определить вероятность научной теории. Например, для определения вероятности того, что закон тяготения Ньютона выполняется повсеместно (а не только для конкретного тестового объекта, как в приведенном выше примере), Райхенбах утверждает, что все доступные измерения гравитационной постоянной должны быть помещены в одну последовательность, и что

«… мы должны построить эталонный класс, заполнив другие строки [последовательности измерений] наблюдениями, относящимися к другим физическим законам.Например, для второй строки можно использовать закон сохранения энергии; для третьего — закон энтропии; и так далее.» [Reichenbach, 1949c, стр. 439f]

Кажется очевидным, что выбор эталонного класса здесь произвольный, но Райхенбах далее утверждает, что

«… используемый эталонный класс соответствует тому способу, которым фактически оценивается научная теория, поскольку достоверность Индивидуальный закон физики, несомненно, усиливается тем фактом, что другие законы тоже оказались надежными.И наоборот, отрицательный опыт с некоторыми физическими законами рассматривается как причина ограничения действия других законов, которые до сих пор не были признаны недействительными. Например, тот факт, что уравнения Максвелла неприменимы к атому Бора, рассматривается как причина сомневаться в применимости закона тяготения Ньютона или Эйнштейна к квантовой области ». [Reichenbach, 1949c, стр. 440]

Мы не знаем, почему несовместимость системы уравнений Максвелла с моделью атома должна приводить к недействительности другой системы уравнений, уравнения Ньютона, которые сами по себе несовместимы с уравнениями Максвелла.Мы не имеем ни малейшего представления о том, какой здесь может быть ссылочный класс для такой передачи вероятности, а также что еще может содержать базовый ссылочный класс в этом случае. ‘indexcross-индукция

Остается неясным, какие критерии имел в виду Райхенбах для определения эталонного класса в целом. Конечно, общая идея состоит в том, что события каким-то образом должны быть одного типа, но не настолько похожими, чтобы исключить изменчивость интереса. Райхенбах утверждает, что следует выбирать самый узкий эталонный класс, для которого есть стабильная статистика (относительные частоты), и что стабильность статистики определяется на уровне продвинутых знаний, т.е.е. на высоком уровне интеграции данных. ⁵ Но это явно неприемлемое предложение — возникает вопрос: вся цель состоит в том, чтобы определить пределы относительных частот; требование стабильной статистики в первую очередь бесполезно. Тривиально стабильная статистика всегда доступна в самом узком из всех непустых классов, классе, содержащем одно событие. Очевидно, это не могло быть намерением Райхенбаха. Обращение Райхенбаха к передовым знаниям для определения эталонных классов для частот более низкого уровня может быть истолковано как указание на слепые постулаты: лучшее, что можно предложить, — это обоснованное предположение или просто предположение.Но тогда почему бы просто не угадать частоты нижнего уровня? Райхенбах подробно обсуждает определение референтных классов, но это далеко не точное объяснение. Возможно, в конечном итоге существует какой-то интуитивно понятный эталонный класс, даже когда в науке проводятся широкие перекрестные индукции, но остаются сомнения в том, есть ли какая-либо надежда изложить такие выводы в формальной вероятностной структуре и будет ли результат тогда служить основой для объективных вероятности.

Мы резюмируем изложение Райхенбахом основ вероятности следующим образом: Вероятность определяется как свойство бесконечных нормальных последовательностей событий.Нормальные последовательности захватывают многие особенности случайных последовательностей. Поскольку нам неизвестен предел бесконечных последовательностей событий, мы строим наши выводы на конечных начальных участках таких последовательностей. Мы уверены, что будем на правильном пути, пока вероятности более высокого порядка выглядят многообещающими. Вероятности более высокого порядка выглядят многообещающими, когда индукции из широкого спектра различных последовательностей измерений дают аналогичные результаты.

No related posts.