Чистый синус или модифицированный меандр
09-03-2013
Графики чистого синуса и меандра на экране осциллографа
Что такое «чистый синус» электропитания, и зачем он нужен? Давайте разбираться.
Качество электроэнергии, поставляемой в наши дома, отвечает определенным требованиям. Один из важных показателей качества — вид графика напряжения. График напряжения электрического сигнала в сети должен иметь правильную синусоидальную форму. Для такого графика часто используют определение «чистый синус».
В случае отключения сетевого электропитания используются источники бесперебойного питания. Однако далеко не все ИБП обеспечивают электропитание правильной синусоидальной формы.
Вид графика напряжения выходного сигнала источника бесперебойного питания зависит от типа и конструкции данного устройства.
Большинство обычных компьютерных ИБП генерируют на выход сигнал, называемый «модифицированный синус» или «меандр».
Различные типы графиков выходного сигнала, полученные с помощью осциллографа, представлены на следующем рисунке.
Методы аппроксимации графика чистого синуса
В этом разделе мы ознакомимся с различными методами аппроксимации графика чистого синуса, применяемыми на практике.
График напряжения в форме правильной синусоиды на следующих рисунках представлен красным цветом. Графики напряжения, имеющие приближенную к синусоиде форму, представлены другим цветом.
Самым простым приближением является график меандра. Меандр — простая ломаная линия, в данном случае имеющая форму прямоугольника в каждом полупериоде графика синуса. График простого меандра представлен на рисунке 1. На практике преобразователи такого типа не используются по причине резкого изменения значения напряжения в точках пересечения нулевого значения напряжения.
Для снижения негативных эффектов применяется преобразование типа «меандр» с дополнительными «паузами» в точках смены полярности сигнала. График такого модифицированного меандра представлен на рисунке 2.
Более совершенные методы аппроксимации графика синусоиды напряжения позволяют получать график с большим количеством «ступенек». Такой подход позволяет снизить амплитуду перехода на следующую ступень и ближе подойти к графику «чистого синуса». Такой график носит название «модифицированный синус» и представлен на рисунке 3.
Когда нужен «чистый синус», а когда достаточно и «модифицированного»
Различные электроприборы и электрооборудование имеют разные требования к качеству электропитания. Ряд устройств корректно работает только с сигналом «чистый синус», другие приборы могут без проблем использовать электропитание в форме «модифицированного синуса».
Не критичны к форме графика напряжения и могут использовать «модифицированный синус» следующие приборы:
- нагревательные приборы;
- компьютеры;
- бытовые приборы, имеющие импульсные источники питания.
Требуют использования питания форме чистого синуса следующие приборы:
- электродвигатели;
- котлы отопления;
- циркуляционные и погружные насосы;
- компрессоры;
- приборы и оборудование, имеющие трансформаторные источники питания;
- приборы и оборудование, чувствительные к электрическим помехам в сети.
Отклонения от правильной синусоидальной формы напряжения приводят к перегреву такого оборудования, повышенному трению и биению подвижных частей конструкции, к возможным авариям и поломкам.
Использование источников питания с модифицированным синусом выходного сигнала приводит к существенному сокращению срока эксплуатации приборов, имеющих трансформаторные источники питания или электродвигатели.
ИБП с чистым синусом для питания котлов отопления
Для правильного и безопасного электропитания газовых котлов отопления необходимо использовать только ИБП с синусоидальной формой сигнала.
В конструкцию современного котла отопления входят: электронный блок управления, циркуляционные насосы, насосы или компрессоры для обогащения воздухом горючей смеси. Все эти устройства требуют правильного синусоидального электропитания.
Использование источников бесперебойного питания с формой сигнала в виде модифицированного синуса приведет к сбоям в работе электронного блока и повышенному износу и перегреву насосов котла отопления.
Надёжные российские источники бесперебойного питания компании БАСТИОН представлены в разделе Бесперебойное питание.
Читайте также по теме
- Молниезащита здания и электросети
- Перенапряжение в сети и защита от перенапряжения
- Выбираем стабилизатор напряжения для холодильника
- Регуляторы напряжения
- TEPLOCOM Space Technology – космические технологии в ваших руках!
- Стабилизатор напряжения TEPLOCOM для газовых котлов
- Многофункциональное реле напряжения АЛЬБАТРОС РНТ-63А
- Выбираем стабилизатор напряжения для всего дома
Синус и косинус
Главная / i / t
Синус
Каждый знает знает, что есть в школьной математике такое слово как синус, косинус, тангенс и котангенс, но все ли действительно понимают что это такое? В этой статье будет правильно и главное максимально просто рассказано об этом.
Если посмотреть в школьный учебник по геометрии за 7-9 класс, то там будет написано следующее:
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе
Чтобы понять что это значит, надо взять треугольник, в котором один угол будет 90°, т.е. прямоугольный треугольник. Сторона ВС называется катетом противолежащим углу А, сторона АС называется катетом прилежащим к углу А. Сторона АВ лежащая против угла 90° — это гипотенуза, она является всегда самой длиной стороной прямоугольного треугольника.
Тогда для того, чтобы вычислить синус угла А, надо найти противолежащую этому углу А сторону — в нашем рисунке это будет сторона ВС, измерить эту сторону, затем измерить самую длинную сторону АВ (гипотенузу) и разделить длину ВС на длину АВ. И тогда получившееся число будет синусом угла А.
Например, нам надо приближенно вычислить синус 30°, начертим прямоугольный треугольник и измерим противолежащую углу в 30° сторону ВС и сторону АВ.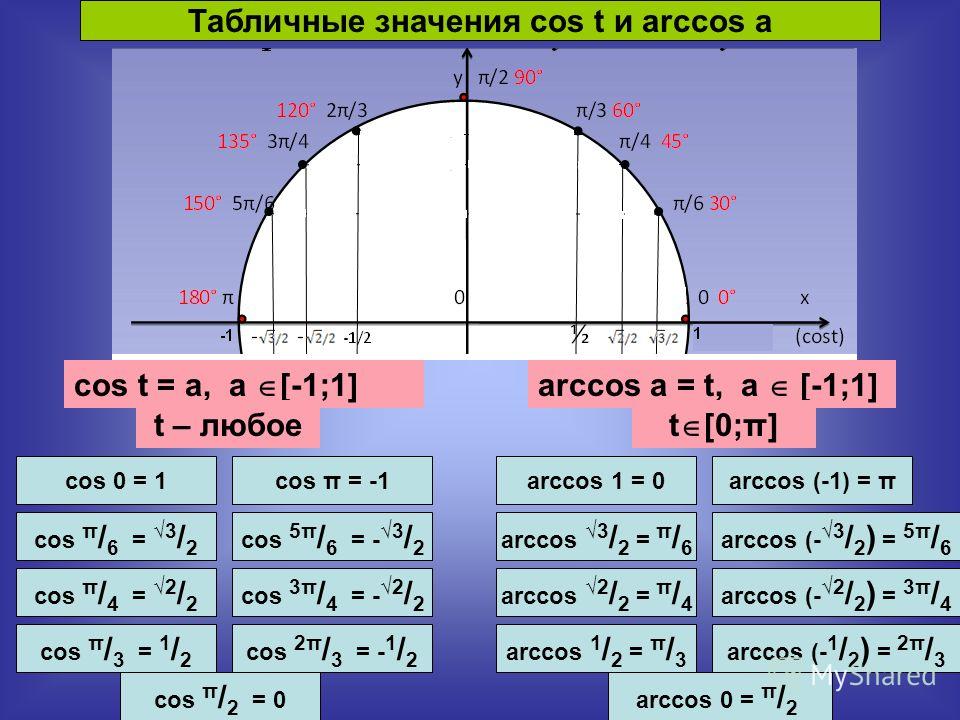
После измерения выяснилось, что катет BC=5 см, а гипотенуза AB=10 см. Делим 5 на 10 и получаем 0.5 — это и будет синус 30°. Стороны могли бы быть какой угодно длины, например, 7 см и 14 см, или 6,8 см и 3,4 см, но, если угол А равен 30°, а угол С будет 90°, то синус все равно будет около 0,5.
Точное значение синуса, косинуса, тангенса и котангенса таким способом определить не удастся, потому что невозможно начертить идеальный треугольник и абсолютно правильно его измерить, но это и не понадобится, для школьных задач просто нужно будет помнить только значения основных углов этих функций — 30°, 45° и 60°. Таблица с точными значениями синуса и косинуса этих углов будет дана ниже.
Вычисленные синусы любых углов меньших 90° (и не только синусы) можно легко проверить с помощью калькулятора. Для этого достаточно начертить произвольный прямоугольный треугольник, измерить в нем угол, противолежащий ему катет и гипотенузу, разделить длину измеренного катета на длину измеренной гипотенузы и записать получившееся число.
Проверим полученное приближенное значение синуса: возьмем инженерный калькулятор или его инженерную версию в компьютере (только надо поставить единицу измерения — градус, а не радиан), и попробовать вычислить на калькуляторе синус того же угла, что и был в треугольнике; то получиться должно примерно то же число.
Вычисленный нами синус 45° очень похож на то, что нам показывает калькулятор, значит мы все правильно посчитали.
То же попробуем с углом 60°.
И синус 60° вычислен правильно: наши вычисления и показания калькулятора очень близки.
Косинус
С синусом вроде бы все. Теперь нужно разобраться с косинусом. Формальное определение косинуса:
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе
В силу простой симметрии косинус очень похож на синус — надо только делить на сторону АВ не противолежащую сторону BC, а прилежащую к углу А сторону АС.
Как вычислить приближенно cos 45° изображено на следующем рисунке.
Проверим полученный результат на калькуляторе.
Попробуем вычислить cos 60°
Здесь cos 60° на калькуляторе полностью совпал с нашим результатом. Действительно, всегда, когда в прямоугольном треугольнике есть угол 30° или 60°, катет, лежащий напротив угла 30°, будет равен половине гипотенузы (этот же катет будет являться прилежащим к углу 60°), поэтому sin 30° и cos 60° всегда будут равны 0.5.
Все точные значения синуса и косинуса, которые следует знать указаны в следующей таблице.
Надеюсь, что удалось понять почему синус и косинус 45° оказались одинаковыми.
Калькулятор синуса
- Главная
- Расчет
- Математика
- Калькулятор синуса
Калькулятор синуса
Результат:
| sin(X): | 0 |
Что такое синус?
Синус — это тригонометрическая функция. В прямоугольном треугольнике синус угла x определяется как отношение стороны, противоположной углу, к гипотенузе.
$$sin\, x = {противоположные \над гипотенузой}$$
Рассмотрим прямоугольный треугольник, показанный ниже.
В этом треугольнике прямой угол лежит в точке B. Мы хотим найти синус x. Сторона, противолежащая углу x, равна АВ, а гипотенуза — АС. Следовательно,
$$sin\, x\, =\, {противоположно \над гипотенузой} \,=\,{AB\над AC}$$
Свойства функции синуса
Ниже приведены некоторые свойства функции синуса.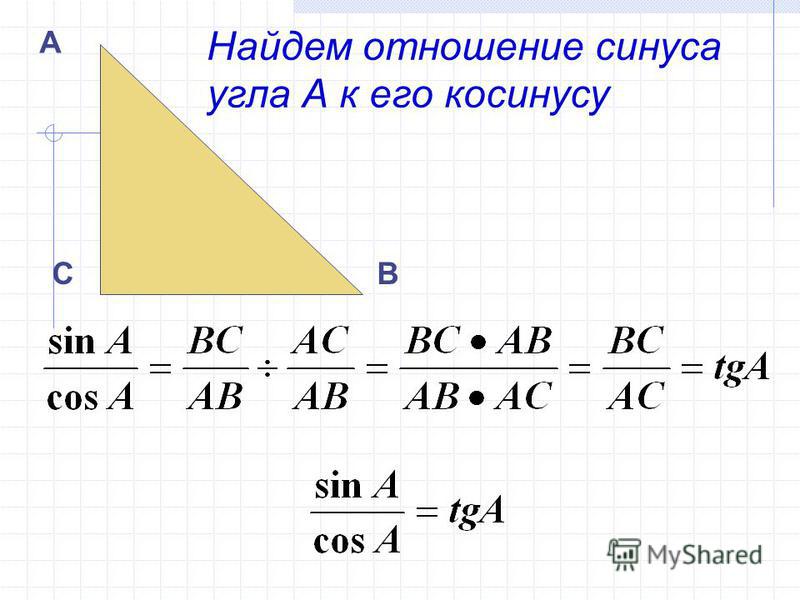
Угол – Обозначается переменной x или θ, это параметр, для которого вычисляется значение синуса.
Домен — значения угла x, для которых мы можем вычислить sin(x). Это значение изменяется от -инфинитива до +инфинитива.
Диапазон – Значения, между которыми лежит sin(x) любого угла x. Это значение равно -1≤ sin(x) ≤1.
Период – Горизонтальная длина одного полного цикла функции синуса. Период для sin(x) составляет 2π радиан или 360⁰.
Ниже приведен график функции синуса.
Функция синуса периодична по своей природе с периодом 2π радиан (или 360⁰). Это означает, что график повторяется каждые 2π радиан. На приведенном выше графике ось x обозначает угол, а ось y обозначает синус этого угла.
Из графика видно, что sin(x) изменяется от 0 до +1, а затем падает до -1. Оттуда снова идет вверх. Он достигает значения +1 при π/2 радианах и -1 при 3π/2 радианах.
Значения sin(x)
Ниже приведены некоторые часто используемые значения sin(x).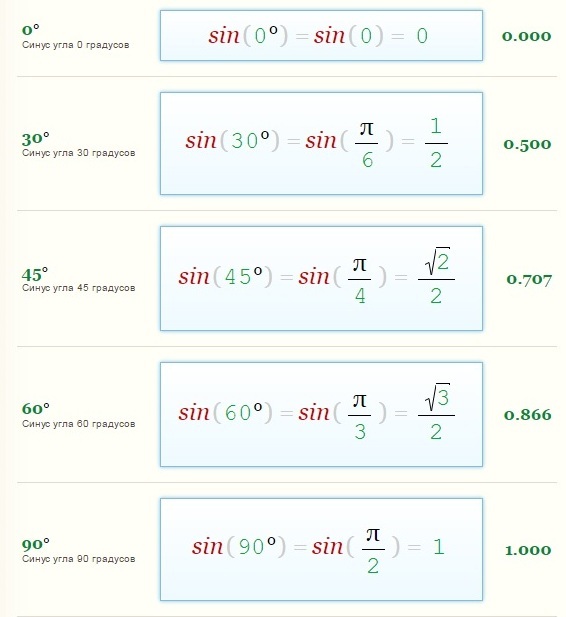
| Угол x в градусах | Угол x в радианах | Грех(х) |
|---|---|---|
| 0 | 0 | 0 |
| 30 | $$π\over6$$ | $$1\over2$$ |
| 45 | $$π\over4$$ | $$1\over√2$$ |
| 60 | $$π\over3$$ | $$√3\более2$$ |
| 90 | $$π\over2$$ | 1 |
| 120 | $$2π\over3$$ | $$√3\более2$$ |
| 135 | $$3π\over4$$ | $$1\over√2$$ |
| 150 | $$5π\over6$$ | $$1\over2$$ |
| 180 | № | 0 |
| 270 | $$3π\over2$$ | -1 |
| 360 | 2π | 0 |
Значение sin(x) может быть положительным или отрицательным, в зависимости от того, где находится угол x в четырех квадрантах.
Например, sin(150⁰) является положительным, тогда как sin(270⁰) отрицательным.
Это было проиллюстрировано ниже.
| Квадрант | x в градусах | x в радианах | Знак синуса | Диапазон значений sin |
|---|---|---|---|---|
| 1 | от 0⁰ до 90⁰ | $$0\, to\, {π\over2}$$ | + | 0 |
| 2 | от 90⁰ до 180⁰ | $${π\over2}\, to\, π$$ | + | 0 |
| 3 | от 180⁰ до 270⁰ | $$π\, to\, {3π\over2}$$ | — | -1 |
| 4 | от 270⁰ до 360⁰ | $${3π\over2}\, до\, 2π$$ | — | -1 |
Если угол x не лежит в пределах от 0⁰ до 360⁰ (или от 0 до 2π радиан), его можно выразить как кратное, сумму или разность одного из указанных выше углов, а затем определить его синусоидальное значение.
Формула синуса
Для вычисления sin(x) из прямоугольного треугольника используется следующая формула:
$$sin\, x = {противоположная \по гипотенузе}$$ мы хотим вычислить синус угла в калькуляторе.
Это можно сделать, используя приближение ряда Тейлора для функции синуса, когда угол x выражен в радианах. Формула такова; 99\over9!} — …$$
Чем больше членов, тем точнее приближение.
Области применения
Тригонометрические функции, такие как функция синуса, могут использоваться для моделирования нескольких реальных сценариев, таких как электрические токи, приливы и радиоволны. Реальные задачи, связанные с гармоническим движением, можно решить, используя функцию синуса, например, распространение звуковых волн в среде. Формула греха также часто используется для решения тригонометрических задач или доказательства тригонометрических тождеств.
В этом разделе мы рассмотрим несколько примеров задач, связанных с использованием формулы синуса.
Ответ: Эту проблему можно представить следующим образом.
Лестница обозначается AC, длину которой нам нужно узнать. Стена обозначается AB.
Используя формулу синуса, мы можем вычислить длину лестницы.
SIN 0,43633 = 0,43633 — 0,013845 + 0,000132 — 0 + 0 -…
SIN0,43633 = 0,422617
Отсюда, SIN 25⁰,0,422217
. угла, который не лежит между 0⁰ и 360⁰.Ответ: Угол 540⁰ не лежит между 0⁰ и 360⁰. Мы пытаемся уменьшить значение этого угла, убрав все полные обороты на 360⁰.
Итак, 540⁰ = 360⁰ + 180⁰.
Удаление одного полного оборота показывает нам, что sin 540⁰ эквивалентен sin 180⁰.
Из графика синусов, а также из таблицы приведенных значений видно, что sin 180⁰ = 0,
Отсюда sin 540⁰ = 0,
См. также:
- Косинус 0 Калькулятор
- Калькулятор касательной
- Калькулятор арксинуса
- Калькулятор Arccos
- Калькулятор арктангенса
- Калькулятор тригнометрии
Делиться:
Калькулятор синуса
Калькулятор синуса
| грех | ° рад | ||
| Результат: | |||
Калькулятор обратного синуса
| грех -1 | |||
| Результат: | |||
| °рад | |||
Калькулятор синуса
Калькулятор тригонометрического синуса используется для вычисления синуса нескольких значений.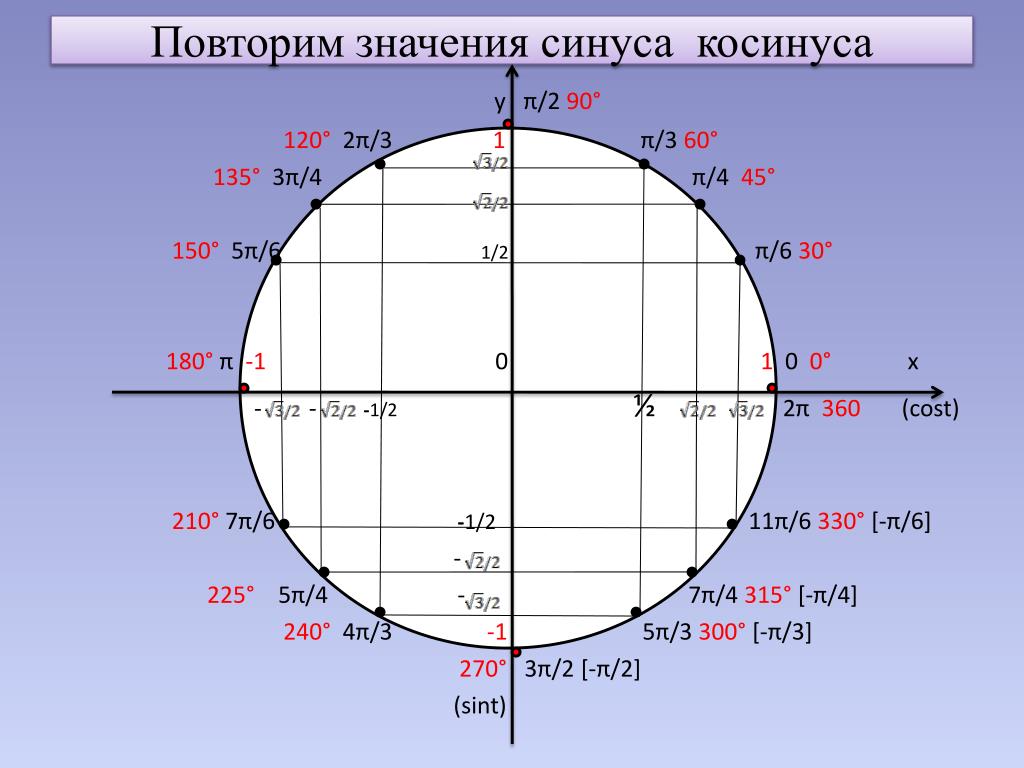
Он был специально разработан для предоставления точных результатов в зависимости от значений, введенных в текстовые поля. Калькулятор синусов имеет одно текстовое поле и два элемента управления, которые выполняют разные функции. Первый шаг — ввести значение sin (x) в пустое текстовое поле. Выберите тип угла, который может быть выражен в градусах Цельсия (°) или в радианах (рад).
После этого нажмите знак равенства (=) или кнопку «Рассчитать», чтобы выполнить расчет. Результаты будут отображаться на нижней платформе калькулятора под двумя элементами управления. Кнопка «Сброс» используется для удаления всех предыдущих вычислений из текстовых полей. Это самый быстрый способ очистки калькулятора всякий раз, когда вы хотите выполнить новые вычисления.
Калькулятор синуса может выполнять только одно преобразование за раз, что означает, что вам придется скоординировать кнопки «Рассчитать» и «Сброс» в ситуациях, когда у вас есть несколько значений. Этот калькулятор использует определенные формулы при проведении расчетов.
Он надежен, поскольку дает точные результаты в течение секунды.
Например,
Вычислить Sin 30°
Раствор
Введите 30 в первое текстовое поле и выберите градусы в качестве типа угла. Нажмите знак равенства или кнопку «Рассчитать», чтобы выполнить расчет.
Результат будет; 0,5.
Если вычислить Sin в радианах, то результат будет таким: -0,98803162
Калькулятор обратного синуса
Выполняет функцию, противоположную калькулятору синусов, поскольку используется для определения значения в процентах или радианах.
Сначала введите значение, полученное в Калькуляторе синуса, чтобы определить результат в градусах или радианах.
Например,
Найдите обратный синус 0,5
Раствор
Вы вводите 0,5 в пустое текстовое поле и нажимаете знак равенства или кнопку «Рассчитать», чтобы выполнить расчет.