Калькулятор сложение и вычитание деление и умножение: Онлайн калькулятор. Сложение, вычитание, умножение и деление столбиком

Восьмеричный калькулятор онлайн

Если вам необходимо произвести математические операции в восьмеричной системе счисления воспользуйтесь нашим восьмеричным онлайн калькулятором:

+−×÷ANDORXOR =

Просто введите восьмеричные числа, выберите операцию и получите результат.

Калькулятор может производить следующие действия:

• сложение +
• вычитание −
• умножение ×
• деление ÷
• логическое И (AND)
• логическое ИЛИ (OR)
• исключающее ИЛИ (XOR)

Сложение в восьмеричной системе счисления

Сложение двух восьмеричных чисел производится столбиком, как и в десятичной системе, но по следующим правилам:

class=»krest»>

+	0	1	2	3	4	5	6	7
0	0	1	2	3	4	5	6	7
1	1	2	3	4	5	6	7	10
2	2	3	4	5	6	7	10	11
3	3	4	5	6	7	10	11	12
4	4	5	6	7	10	11	12	13
5	5	6	7	10	11	12	13	14
6	6	7	10	11	12	13	14	15
7	7	10	11	12	13	14	15	16

Пример

Для примера сложим 777 и 15:

+		7	7	7
			1	5
	1	0	1	4

777₈ + 15₈ = 1014₈

(511₁₀ + 13₁₀ = 524₁₀)

Вычитание в восьмеричной системе счисления

Вычитание восьмеричных чисел производится столбиком. Правила вычитания обратны правилам сложения (см. таблицу выше).

Пример

Для примера вычтем из числа 1014 число 777:

–	1	0	1	4
		7	7	7
			1	5

1014₈ − 777₈ = 15₈

(524₁₀ − 511₁₀ = 13₁₀)

Умножение чисел в восьмеричной системе счисления

Умножение восьмеричных чисел производится в столбик по следующим правилам:

×	0	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7
2	0	2	4	6	10	12	14	16
3	0	3	6	11	14	17	22	25
4	0	4	10	14	20	24	30	34
5	0	5	12	17	24	31	36	43
6	0	6	14	22	30	36	44	52
7	0	7	16	25	34	43	52	61

Пример

Для примера перемножим числа 777 и 15:

×			7	7	7
				1	5
+		4	7	7	3
		7	7	7
	1	4	7	6	3

777₈ × 15₈ = 14763₈

(511₁₀ × 13₁₀ = 6643₁₀)

Деление чисел в восьмеричной системе счисления

Деление восьмеричных чисел выполняется по тому же принципу, что и деление десятичных, например:

Пример

Для примера разделим число 720 на 4:

720₈ ÷ 4₈ = 164₈

(464₁₀ ÷ 4₁₀ = 116₁₀)

См.

также

Калькулятор комплексных чисел: сложение, вычитание, деление, умножение

Виды калькуляторов

Чтобы быстро и правильно выполнить операцию с комплексными числами, воспользуйтесь данным онлайн калькулятором, для этого необходимо:

• ввести в ячейки калькулятора вещественную и мнимую части каждого числа;
• выбрать из списка операцию, которую необходимо произвести;
• нажать кнопку. Через считанные секунды вы получите точный ответ.

Числа вида a+bi называются комплексными (мнимыми) числами, где a,b — вещественные (или действительные) числа, i — мнимая единица — число, для которого выполняется равенство: i² = -1, т.е. мнимая единица в квадрате является отрицательным числом, равным -1. Комплексные числа расширяют понятие действительного числа, позволяют в удобной форме описывать математические модели всевозможных прикладных процессов.

Комплексное число z можно представить в алгебраической, тригонометрической или показательной (экспоненциальной) форме.

1. Алгебраическая запись: z = a + bi, где a и b являются вещественными числами, причем, a — действительная часть, bi — мнимая, i — мнимая единица.

2. Тригонометрическая запись: z = r (cos + i sin φ), где r — модуль комплексного числа, z — расстояние от точки на комплексной плоскости до начала координат.

Модуль комплексного числа — вещественное число |z|, равное корню квадратному из суммы квадратов вещественных чисел (a и b): r = |z| = √a² + b²

Аргумент комплексного числа z — угол φ, образованный радиус-вектором точки, соответствующей комплексному числу. Значение аргумента находится в диапазоне (-π…π], для всех целых k определяется с точностью 2πk: φ = Аrg (z) = arctg (b/a). Для z, равного нулю, аргумент не определен.

3. Для сокращения Эйлер ввел Показательную запись: z = rе^iφ

Действия над комплексными числами

1. Сложение: z1 + z2 = (а1 + а2) + (b1 + b2) i, где z1 = а1 + b1i; z2 = а2 + b2i. При сложении комплексных чисел складываются их реальные и мнимые части, причем, сумма не изменится от перемены мест слагаемых.

2. Вычитание: z1 — z2 = (а1 — а2) + (b1 — b2) i. При вычитании комплексных чисел вычитаются их реальные и мнимые части.

3. Умножение: z1z2 = (а1а2 — b1b2) + (а1b2 + а2b1) i, зная что i*i=-1. Умножение комплексных чисел выполняется по правилам умножения многочленов.

4. Деление: z1 / z2 = (a + bi) / (c + di) = (ac + bd) / (c2 + d2) + ((bc — ad) / (c2 + d2)) i, где z1 = a + bi; z2 = c + di. Деление выполняется путем умножения числителя и знаменателя на выражение, сопряженное знаменателю.

5. Возведение в целую степень. Для возведения комплексного числа во вторую степень можно записать степень, как произведение двух множителей и выполнить операцию умножения по правилу умножения многочленов. Для возведения комплексного числа в большую степень проще воспользоваться показательной формой:

zⁿ = rⁿe^inφ полученной из формулы Муавра: (cos (х) + isin (х))ⁿ = cos (nх) + isin (nх).

6. Вычисление корня n-ой степени: , где k — целое число в диапазоне 0…n-1

Предыдущая Онлайн калькулятор модуль комплексного числа

Двоичный калькулятор — сложение, вычитание, умножение, деление

Создано Филиппом Маусом

Отзыв Стивена Вудинга

Последнее обновление: 11 марта 2022 г.

Содержание:

• Что такое арифметические двоичные операции?
• Двоичное сложение
• Двоичное вычитание
• Двоичное умножение
• Двоичное деление
• Как пользоваться двоичным калькулятором?
• Часто задаваемые вопросы

Двоичный калькулятор упрощает выполнение арифметических двоичных операций. Это объясняет как вычислять двоичное сложение, вычитание, умножение и деление . Калькулятор выполняет все расчеты в знаковом и беззнаковом представлении.

Что такое арифметические двоичные операции?

Двоичные числа представляют собой чисел с основанием 2 , состоящих только из цифр 0 и 1 . Они представляют собой строку битов, которая может представлять только два логических состояния: включено или выключено.

Так как нас учат арифметическим операциям, таким как сложение и вычитание, основанным на десятичной системе, двоичные арифметические операции могут сначала показаться немного сложными. Но к концу этой статьи вы увидите, что это не так уж и сложно! И двоичные числа обладают замечательным свойством, позволяющим выполнять операции, ограниченные только этой системой счисления, такие как битовые сдвиги и побитовые операции И, ИЛИ и XOR.

Двоичные числа можно преобразовывать в десятичные числа и обратно. Мы представляем отрицательные значения двоичных чисел в так называемом дополнении до двух со знаком, в котором первый бит указывает на знак числа, 0 означает отрицательное значение, а 1 положительное.

Двоичное сложение

Основой для рабочего двоичного арифметического калькулятора является двоичное сложение. Двоичное сложение работает очень похоже на десятичное сложение . Есть 4 основных правила:

• 0 + 0 = 0
• 0 + 1 = 1
• 1 + 0 = 1
• 1 + 1 = 0 (перенести 1 на следующий бит)

Применение этих правил, начиная с самого правого (наименее значимого) бита, позволяет легко складывать двоичные числа. См. пример ниже для дальнейшего объяснения:

Двоичное вычитание

Двоичное вычитание может быть выполнено двумя различными способами:

• Метод заимствования эквивалентен процедуре десятичного вычитания.
• Метод дополнения заменяет вычитаемое его двойным дополнением, а затем выполняет двоичное сложение, как показано выше.

В этой статье показан только метод заимствования, для которого применяются следующие правила:

• 0 — 0 = 0
• 0 — 1 = 1 (заимствовать 1 из следующего бита)
• 1 — 0 = 1
• 1 — 1 = 0

Опять же, мы начинаем с самого правого, наименее значащего бита и продвигаемся влево.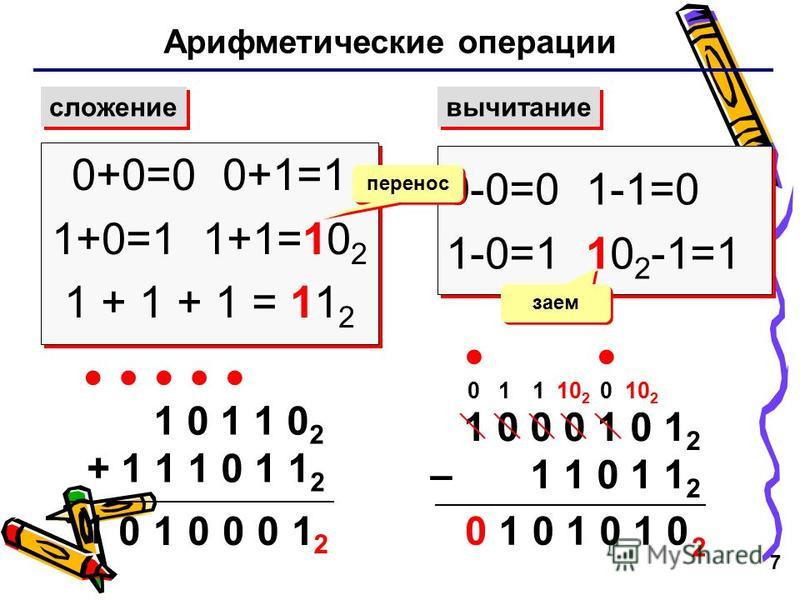 Мы покажем, как вычислить двоичное вычитание в следующем примере:

Двоичное умножение

Двоичное умножение очень похоже на десятичное длинное умножение , только проще, так как мы работаем только с цифрами 0 и 1 . Он основан на концепции бинарного сложения. Еще раз, есть четыре основных правила, но на этот раз нам не нужно носить с собой или брать взаймы:

• 0 * 0 = 0
• 0 * 1 = 0
• 1 * 0 = 0
• 1 * 1 = 1

См. ниже пример двоичного арифметического калькулятора для умножения:

Двоичное деление

Двоичное деление сильно следует за десятичным делением . Процедура состоит из шагов двоичного умножения и двоичного вычитания. Начиная слева (старший бит), исследуется, можно ли разделить текущую цифру делимого на делитель. Если да, то 1 отмечается в этой позиции частного; если нет, то 0 . Остаток процесса деления сохраняется, и к нему добавляется следующая цифра. Эта процедура повторяется до тех пор, пока не будет достигнут самый правый (самый младший бит).

В качестве примера, давайте разделим 101010 (делимое) на 110 (делитель):

Не каждое двоичное деление работает идеально с остатком 0 . Вот почему двоичный калькулятор представит результат двоичного деления с остатком 9.0026 в двоичной и десятичной системе.

Как пользоваться двоичным калькулятором?

Вы знаете как работают двоичные сложения, вычитания, умножения и деления , но эти операции могут быть довольно запутанными и запутанными для больших двоичных чисел. Но не волнуйтесь, для этого и существует двоичный калькулятор! Итак, давайте посмотрим, как его использовать. В качестве примера вычтем двоичный эквивалент десятичного числа 38 из 115 . Чтобы преобразовать двоичное число в десятичное и наоборот, используйте этот инструмент.

1. Выберите двоичное представление . Это количество битов вашего ввода, и ваш результат будет представлен. Учтите, что операции сложения и умножения, скорее всего, будут иметь результат с более значащими битами, чем входные числа.

• Наше большее входное число 1110011 ( 115 в десятичном формате) имеет 7 значащих битов, и мы выполняем вычитание, поэтому 8 битов достаточно.

2. Введите ваши двоичные числа в соответствующие поля. Помните о порядке ввода, так как вычитание и деление чувствительны к этому.

• Мы хотим вычесть 38 из 115 , поэтому первый ввод будет 1110011 , а второй ввод будет 100110 .

3. Выберите арифметическую двоичную операцию , которую вы хотите выполнить.

• Для нас это Вычитание .

3. Результат вашей арифметической двоичной операции представлен в двоичной и десятичной системе.

• Двоичный: 0100 1101
• Десятичный: 77

Если ваш двоичный результат имеет значение 1 в старшем разряде и может быть понят как положительный результат в записи без знака или отрицательный результат в записи со знаком, будут отображены оба результата.

Часто задаваемые вопросы

Как вычислять двоичные числа?

Двоичные числа позволяют производить те же арифметические вычисления, что и числа из десятичной системы . Сложение, вычитание, умножение и деление легко выполняются с двоичными числами. Кроме того, могут быть выполнены побитовых операций, таких как сдвиг битов, логическое И, ИЛИ и XOR .

Как добавить двоичные числа?

Двоичное сложение работает аналогично десятичному сложению . Начиная с младшего бита, добавьте значения бита из каждого слагаемого. Если оба слагаемых имеют значение 1 в этом бите, перенесите 1 в следующий старший бит результата.

Как рассчитать двоичное вычитание?

Двоичное вычитание можно вычислить двумя способами:

• Метод заимствования подобен методу десятичного вычитания. Начиная с младшего бита, вычесть значение вычитаемого из уменьшаемого бита . В случае, если первое 1 , а второе 0 , заимствуйте 1 из следующего старшего бита.
• Метод дополнения выполняет сложение уменьшаемого и дополнения до двух вычитаемого.

Каковы преимущества двоичных операций?

Двоичные и побитовые операции широко применяются из-за их преимуществ в производительности и потребности в памяти . Сюда могут входить регистров процессоров, встроенных систем, передачи данных, а также видео- и аудиокодеков 9.0026 .

Как сложить 3 и 10 в двоичном формате?

Чтобы сложить двоичные числа 3 и 8 , выполните следующие действия:

1. Преобразуйте числа из десятичных в двоичные : 0011 и 1010 .
2. Складываем значения четвертого бита: 1 + 0 = 1 .
3. Складываем значения третьего бита: 1 + 1 = 0 , переносим 1 на следующий бит.
4. Складываем значения второго бита: 0 + 0 + 1 перенос = 1 .
5. Складываем значения первого бита: 0 + 1 = 1 .
6. Ваша сумма 1101 или 13 в десятичной системе.

Филип Маус

Входные данные

Двоичное представление

Вы можете записывать двоичные числа, содержащие не более 8 цифр. Вам не нужно вводить лидирующие нули.

Номер 1

Номер 2

Арифметическая операция

Операция

Проверьте 10 аналогичных двоичных калькуляторов 1️0️

Двождаемое сложение. Действие. Действие.

---

 

Шестнадцатеричный калькулятор используется для сложения, вычитания, умножения и деления двух шестнадцатеричных чисел.

 

Что такое шестнадцатеричное число?

Шестнадцатеричное число — это число, выраженное в шестнадцатеричной позиционной системе счисления с основанием 16, в которой используются шестнадцать символов: цифры от 0 до 9 и буквы A, B, C, D, E, F. Где A, B, C, D, E и F представляют собой однобитовые представления десятичного значения от 10 до 15. В шестнадцатеричном формате используется четырехбитное двоичное кодирование. Это означает, что каждая цифра в шестнадцатеричном формате равна четырем цифрам в двоичном формате. Octal использует трехбитную двоичную систему.

Hexadecimal: 0 1 2 3 4 5 6 7 8 9 A B C D E F

Десятичный: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

HEX Дополнение

Сложение шестнадцатеричных чисел аналогично сложению десятичных чисел. Единственным отличием являются добавленные цифры A, B, C, D, E и F. Может быть удобно преобразовать шестнадцатеричные числа в десятичную систему, когда значения больше числа 9. Ниже приведен пример шестнадцатеричного сложения.

В приведенном выше примере E + 7 в десятичной форме равно 14 + 7 = 21. 21 в десятичной форме равно 15 в шестнадцатеричном формате. Как и при десятичном сложении, 1 переносится на следующий столбец. В следующем столбце получается 1 + B (11) + 5 = 17 в десятичном виде и 11 в шестнадцатеричном. Перенесите 1 в последний столбец, в результате чего 1 + 6+ E (14) = 21 в десятичном виде и 14 в шестнадцатеричном. Это дает результат 1515 в шестнадцатеричном формате.

 

Вычитание шестнадцатеричного числа

Вычитание шестнадцатеричного числа может быть рассчитано так же, как десятичное вычитание, но большая разница заключается в том, что при заимствовании в шестнадцатеричном формате «1» представляет собой 16-значное число, а не 10-значное число. Это связано с тем, что столбец, из которого заимствуется, в 16 раз больше в шестнадцатеричном формате, чем в 10 раз в десятичном. Ниже приведен пример шестнадцатеричного вычитания.

В первом столбце 7 меньше, чем E, или 15 в десятичной системе. Поэтому нам нужно заимствовать из следующего столбца. Это уменьшает 5 до 4 и дает 1 или 16 десятичных чисел в первом столбце, т. е. 16 десятичных + 7 десятичных — E или 14 десятичных = 9.