Калькулятор степенные корни: Онлайн калькулятор: Корень и степень

Содержание

Реферат «Извлечение квадратных корней без микрокалькулятора»

Научно-практическая конференция «Секция математики»

Извлечение квадратных корней без калькулятора

Выполнила:

Мыздрикова Анна

Ученица 8 класса Г

МБОУ «Гимназия № 22»

(Алтайский край, г.Барнаул)

Руководитель:

Нежибецкая Елена Викторовна

Учитель математики

Барнаул — 2017

Оглавление

Введение ….…………………………………………….………………………………………………….. 4

Глава 1. Способ разложения на простые множители ………………………………. 5

Глава 2. Способ использования таблицы квадратов двузначных чисел …. 6

Глава 3. Формула Древнего Вавилона ………………………………………………………… 7

Глава 4. Через решение уравнения ……………….…………………………………………… 8

Глава 5 Способ отбрасывания полного квадрата ……….…………………………..….. 9

Глава 6. Метод Ньютона……………………………………………………………………………… 10

Глава 7. Геометрический метод …………….……………………………………..……………. 11

Глава 8. Графический метод ………………………………………………………..……………. 12

Глава 9. Метод вещественного анализа функции у=√х ……………………… 13

Глава 10. Канадский метод …………………………………………………………………………. 10

Глава 11. Метод вычетов нечётного числа ……………………………………………….. 14

Заключение …………………………………………………………………..……………………… 19 — 20

Список литературы …………………………….……………………………………………………….. 21

Приложения ……………………………………………………………………………………………. 22 — 27

Актуальность исследования : распространение алгоритмов извлечения корней среди учащихся, что особенно актуально при сдаче экзаменов, где запрещён калькулятор , а также использовать эти знания при работе с квадратным корнем.

Цель работы: изучить все известные способы извлечения квадратных корней без калькулятора и отобрать самые рациональные для практического применения.

Задачи:

1. Проанализировать путём соцопроса умение учащихся, преподавателей и родителей извлекать квадратные корни без калькулятора.

2. Изучить всю найденную литературу по данному вопросу

3. Рассмотреть особенности каждого найденного способа и описать его алгоритм.

4. Оценить все найденные способы, и выбрать самый лучший.

5. Познакомить с результатами полученных исследований одноклассников и создать буклет – памятку по самым интересным алгоритмам.

Гипотеза: Существует не менее двух-трёх способов извлечения квадратных корней без калькулятора.

Объект исследования: Квадратный корень.

Предмет исследования: особенности способов извлечения квадратных корней без калькулятора.

Методы исследования:

1. Анализ опроса по изучаемой теме.

2. Поиск способов и алгоритмов.

3. Сравнение найденных способов и выявление их преимущества и недостатков.

4. Подтверждение правильности разных способов на практике.

Введение

При изучении темы квадратных корней по алгебре, которая в одно и то же время «переплеталась» с изучением теоремы Пифагора по геометрии, на уроках и дома приходилось часто пользоваться калькулятором и таблицей квадратов. Но не всегда эти предметы были под рукой. И уже тогда возник вопрос, как же быть в этих случаях, когда на экзаменах пользование калькулятором запрещено. Таблица квадратов целых чисел не всегда поможет(к примеру корень из 5,7,3).

Все знают, что извлечь квадратный корень без калькулятора – это очень сложно. В том случае если калькулятора нет под рукой, прибегают к методу подбора или стараются вспомнить данные из таблицы квадратов целых чисел, но это не всегда помогает. И в эту ситуацию попадали многие из нас. Я решила что выучить всю таблицу квадратов двузначных чисел у меня не получится, да и калькулятор пронести на экзамен тоже не получится. Но а найти какие-нибудь простые способы вычисления квадратного корня у меня точно получится.

Глава 1. Способ разложения на простые множители

Для извлечения квадратного корня можно разложить число на простые множители и извлечь квадратный корень из произведения.

3136│2 7056│2

1568│2 3528│2

784│2 1764│2

392│2 882│2

196│2 441│3

98│2 147│3

49│7 49│7

7│7 7│7

√3136 = √2²∙2²∙2²∙7² = 2∙2∙2∙7 = 56 √3136 = √2²∙2²∙3²∙7² = 2∙2∙3∙7 = 84

Многие ребята принимают его почти успешно. Извлечение корня таким способом очень трудоемкая задача и не все с этой задачей справляются. К примеру, попробуем извлечь корень из числа 567890, при разложении на простые множители получается вот такая запись : 567890 | 2

283945 | 5

56789 | ? (56789)

И как же быть с этим примером? Ведь считать в уме столь большие числа не получится. А ответ мы так и не получили. Поэтому способ не сильно нам поможет. И без помощи калькулятора нам не обойтись.

Глава 2. Способ использования таблицы квадратов

двузначных чисел

Этот способ очень прост, и даёт очень точный ответ (до десятых). Но для этого метода понадобится таблица квадратов. (Таблицу можно найти в интернете и во всех учебниках за 8 класс также таблица прилагается на экзамене в качестве справочного материала. )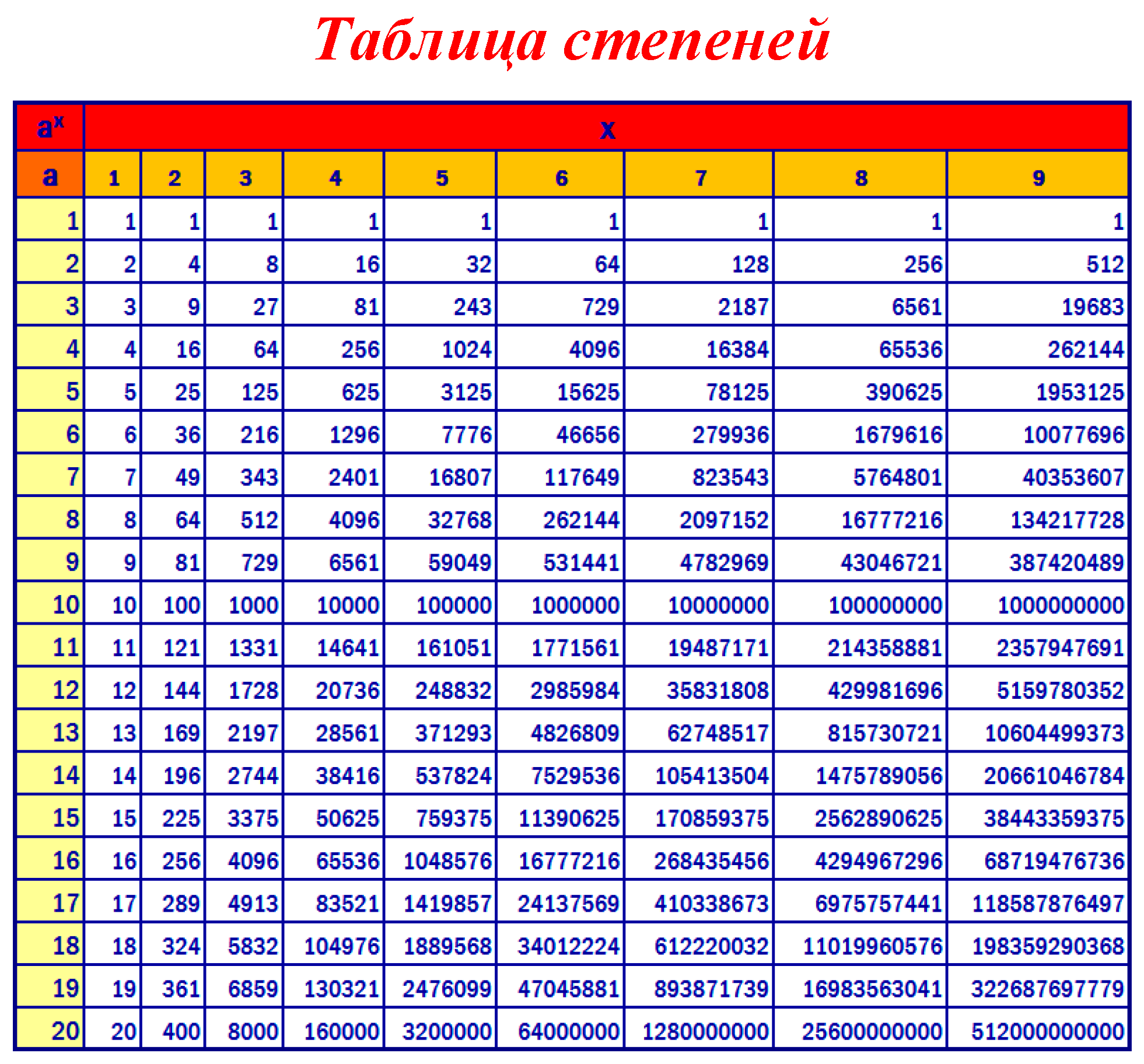

Всё очень просто: закройте две последние цифры числа, в таблице и найдите нужное вам, не превосходящее подкоренное число, и далее действуйте по правилам этой таблицы.

Рассмотрим на примере. Найдём значение √74.

Закрываем две последние цифры у всех чисел в таблице и находим близкие для 74 – таких только два 7396 и 7569. Но 75 – это уже много.

Значит, остаётся только одно – 7396.

Левый столбик даёт ответ 8 (это целых), а верхняя строчка 6 (это десятых). Значит √74≈ 8.6. Проверим на МК √74 ≈ 8.60232526704.

Быстро, удобно, а главное очень просто. И этот способ точно пригодиться на экзамене, но корень больше 100 этим способом уже не получиться извлеч.

Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня из числа х.

Число х они представляли в виде суммы а²+ b, где а²_{ближайший к числу х точный квадрат натурального числа а и пользовались формулой:}

Глава 3. Формула Древнего Вавилона

Извлечём с помощью этой древней формулы корень квадратный из числа 28:

Ответ с помощью МК = 5.29150262212. Как уже видно ответ совпал. Этот способ хорош и прост, но также как и все методы имеет несколько минусов:

Нужно запомнить формулу , и без знания полных квадратов вычислить будет очень сложно.

Глава 4. Через решение уравнения

Способ этот дает возможность вычислить значение корня с точностью до одного — двух знаков после запятой, а, при желании, достичь и большей точности. В чем его суть рассмотрим на примере и попробуем вычислить значение корня 17.Сначала определим границы искомого корня в целых числах. Легко догадаться, что это числа 16 = 4² и 25 = 5², поэтому √16 < √17 < √25 и 4 < √17 < 5.

Пусть х – это та разница, на которую отличны друг от друга √16 и √17,

следовательно √17 = 4 + х. Возведем в квадрат обе части полученного уравнения (√17) ² = (4 + х)² и раскроем скобки при помощи формулы суммы квадрата:

17 = (4 + х)²

= 16 + 8х + х².

Так как мы рассчитываем получить результат с точностью до десятых или до сотых, а х² явно достаточно малая дробь, то ей вполне можно пренебречь.

В результате приходим к простому линейному уравнению 17 = 16 + 8х.

Решив его, получаем значение: х = 0,125. Значит √ 17 ≈ 4 + 0,125 ≈ 4,125 .

На самом деле, при расчете на калькуляторе, значение этого корня равно 4,1231056, то есть погрешность при нашем расчете составила 0,0018944 – это менее двух тысячных. Не правда ли, вполне приличная точность!

Но если все же решение задач по математике требует еще большей точности, то можно достичь ее тем же способом, просто продолжив вычисления с уже полученным значением корня.

Глава 6. Способ отбрасывания полного квадрата

( только у четырехзначных чисел)

Сразу стоит уточнить, что этот способ применим только для извлечения квадратного корня из точного квадрата, а алгоритм нахождения зависит от величины подкоренного числа.

1) Извлечение корней до числа 75² = 5625

Например: √¯3844 = √¯ 3700 + 144 = 37 + 25 = 62.

Число 3844 представим в виде суммы, выделив из этого числа квадрат 144, затем выделенный квадрат отбрасываем, к числу сотен первого слагаемого (37) прибавляем всегда 25. Получим ответ 62.

Так можно извлекать только квадратные корни до числа 75² =5625!

2) Извлечение корней после числа 75² = 5625

Как же устно извлечь квадратные корни из чисел больше 75² =5625?

Например: √7225 = √7000 + 225 = 70 + √225 = 70 + 15 = 85.

Поясним,7225 представим в виде суммы 7000 и выделенного квадрата 225. Затем к числу сотен прибавить квадратный корень из 225, равный 15.

Получим ответ 85.

Возможно,этот способ мало изучен или имеет какие – то исключения.

Он достаточно сложен в запоминании из – за двойственности алгоритма и применим только для четырёхзначных чисел точных корней, но я проработала множество примеров и убедилась в его правильности. Кроме всего этот способ доступен тем, кто уже запомнил наизусть квадраты чисел от11 до 29, ведь без их знания он будет бесполезен.

Глава 7. Метод Ньютона

Этот приближенный метод извлечения квадратного корня без использования калькулятора разработал Исаак Ньютон, но открыл его ещё раньше (около 100 г. н.э.) один из математиков древнего мира Герон Александрийский. Метод этот (известный как метод Ньютона) заключается в следующем:

Пусть а₁ — первое приближение числа √ х (в качестве а₁ можно брать значения квадратного корня из натурального числа — точного квадрата,

не превосходящего х) .

Следующее, более точное приближение а₂ числа √ х найдется по формуле.

Третье, еще более точное приближение

и так далее до любой точности

(n+1) — е приближение √ х найдется по формуле

Нахождение приближенного значения числа√2 методом Ньютона дает следующие результаты: а₁= 1,4; а₂= 1,41; а₃= 1,415.

Указанный способ Герона позволяет извлекать квадратный корень из большого числа с любой точностью, правда с существенным недостатком: громоздкость вычислений.

Глава 8. Геометрический метод

(с использованием циркуля и измерительной линейки с прямым углом или угольника)

Прежде всего стоит заметить, что использование этого метода обещает значительные погрешности, которые могут зависеть и от чистоты построения чертежей, и от точности измерительных инструментов.

Этот метод предполагает знание двух теорем геометрии:

а) Нахождение высоты прямоугольного треугольника, опущенной из прямого угла ( h = √ a∙b)

, но если

, то

[9],[7]

б) Свойство вписанного угла, опирающегося на диаметр окружности ĿАВС= 90º

А подробнее это можно описать так: Положите перед собой чистый лист, циркуль и карандаш с линейкой. Попробуем геометрическим способом извлечь квадратный корень числа 7. Работаем в сантиметрах.

Начертим отрезок АС = АН + НС, то есть АС = 1+ 7 = 8(см)

Найдём середину АС – точку О (АО = ОС) и при помощи циркуля построим окружность с центром О и радиусом ОС и отметим точку Н на отрезке АС так, что АН = 1 см. и построим перпендикуляр НВ в точке Н к отрезку АС.

Измерим длину полученного отрезка ВН. Получили 2 см и 6 мм.

Этот результат и будет примерно равен √7.

Вывод: геометрическим способом нашли результат √7 ≈ 2,6

Минусы этого способа сразу понятны: неточность в измерениях и построении, однако его можно применять в ситуациях недоступности калькулятора и отсутствия клеточной бумаги, что тоже иногда может спасти ситуацию.

Глава 8. Графический метод.

Он полностью основан на графическом решении уравнения b= х², полученном из √ b= х путём возведения в квадрат первого. С алгоритмом решения этого уравнения знаком каждый школьник: Построим на клеточной бумаге в одной системе координат два графика функций у = b и у = х². Найдём точку пересечения в первой четверти системы координат. Абсцисса этой точки и будет соответствовать значению квадратного корня из числа b.

Например, поработаем с √11

Решим графически уравнение 11= х².

у =11 – прямая, параллельная оси абсцисс, а у = х² — классическая парабола.

При построении на клеточной бумаге х = 3,3, а точное вычисление МК = 3,3166.

Какие же неудобства и трудности испытывают при применении такого способа решения данной проблемы:

Предварительная подготовка — построение графика параболы.

Ограничение размером тетрадного листа (о чём сразу предупреждали), поэтому невозможно извлечение чисел, больших 40, так как длина тетрадного листа 40 клеток. Неточность в построении кривых линий и получение больших погрешностей, в отличие от других методов.

Глава 9. Метод вещественного анализа

элементарной функции у = √х

Полностью такой же, как и предыдущий, но только рассматривается другой график. Все плюсы и минусы этих методов очень схожи.

Глава 10. Канадский метод

Этот быстрый метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность – не более двух – трёх знаков после запятой. Вот их формула:

√ X = √ S + (X — S) / (2 √ S), гдеX — число, из которого необходимо извлечь квадратный корень, а S — число ближайшего точного квадрата.

Давайте попробуем извлечь квадратный корень из 75

X = 75, S = 81. Это означает, что √ S = 9.

Просчитаем по этой формуле √75: √ 75 = 9 + (75 — 81) / (2∙ 9)
√ 75 = 9 + ( — 6/18 ) = 9 — 0,333 = 8,667

Метод несложный и удобный.

Глава 11. Метод вычетов нечётного числа

Он заключается в том, чтобы последовательно вычитать нечётные числа 1,3,5,7 и т.д. пока не дойдете до нуля, а затем подсчитать число вычитаний. Это и будет ответ.
Например, чтобы получить квадратный корень из 36 и 121 это:

36 — 1 = 35 — 3 = 32 — 5 = 27 — 7 = 20 — 9 = 11 — 11 = 0 [7]

Общее количество вычитаний = 6, поэтому квадратный корень из 36 = 6.

121 — 1 = 120 — 3 = 117- 5 = 112 — 7 = 105 — 9 = 96 —11 = 85 – 13 = 72 — 15 = 57 – 17 = 40 —19 = 21 — 21 = 0

Общее количество вычитаний = 11, поэтому √121 = 11.

Российские учёные называют этот метод арифметическим извлечением квадратного корня, а за глаза «методом черепахи» из-за его медлительности.
Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее. В то же время такой способ вполне доступен детям, решающим простейшие математические задачи, требующие извлечения квадратного корня. Попробуйте извлечь квадратный корень из числа, например, 5963364 этим способом и вы поймёте, что он «работает», безусловно, без погрешностей для точных корней, но очень — очень длинный в решёнии.

Заключение

Приложение 1

Литература и сайты Интернета:

1. Мордкович А.Г. Алгебра, 8 класс, учебник — Москва, Мнемозина, 2005г

2. Пичугин Л.Ф. За страницами учебника алгебры. Книга для учащихся 7- 9 классов средней школы. – Москва, Просвещение, 1990 г.

3. Ткачева М.В. Домашняя математика. Книга для учащихся 8 класса учебных заведений. – Москва, Просвещение, 1994г.

4. http://festival.1september.ru

5. http://translate.google.ru/translate

6. http://www.murderousmaths.co.uk/books/sqroot.htm

7. http://www.life123.com/question/Square-Root-without-a-Calculator

8. http://www.megabotan.ru/pages/

9. http://ru.wikipedia.ord /wiki /teorema/

Представим, что 29 = 25 + 4 =5²+ 4 = 5²(1+ 4/25) = 5²(1+ 0,16), тогда

√29 = √5²( 1 + 0,16) и отсюда 0,16 = х.

Осталось применить формулу степенного ряда:

√1 + х =1 + (1/2)х — (1/2) (1/4) х² + (1/2) (1/4) (3/6) х³ — (1/2) (1/4) (3/6) (5/8)х4 +

Для начала мы договоримся, число из которого нужно извлечь корень это площадь квадрата.   Первое, что нужно сделать — составить таблицу:
x | x² | x²- (x-1)² |
1 | 1² = 1 | 1- 0 = 1 |
2 | 2² = 4 | 4 -1= 3 |
3 | 3² = 9 | 9 – 4 = 5 |
4 | 4² = 16 | 16 — 9 =7 |
5 | 5² = 25 | 25 -16 = 9 |
6 | 6² = 36 | 36 – 25 = 11 |
7 | 7² = 49 | 49 -36 =13 |
8 | 8² = 64 | 64 – 49 = 15 |
9 | 9² = 81 | 81- 64 =17 |
10 | 10²=100 | 100 — 81=19 | .
Обратите внимание на правую часть таблицы, например, 25-16=9. Если к результату прибавить 1 и разделить на 2, то получим квадрат из 25 (9+1):2=5.      А если отнять 1 и снова разделить на 2, то получим квадрат из 16 (9-1):2= 4!!!
Теперь напишем формулу. Пусть a — площадь малого квадрата, b — площадь большого квадрата, c — разность сторон, x — сторона большого квадрата,           x=(b-a-c²):2c
Пример: a=9, b=2809, c=50, x=(2809-9+50²):2∙50, x=(2800+2500):100, x=5300:100, корень из 2809 это 53!
Снова обратимся к правой части таблицы. Числа постоянно увеличиваются на два — 1; 3; 5… Очевидно, что это арифметическая прогрессия. К тому же, если складывать эти числа, то рано или поздно получим число, из которого нужно извлечь корень. Тогда к последнему слагаемому прибавить 1 и разделить на 2, корень будет найден!

Пример №1: Нужно извлечь корень из 16. 1+3+5+7=16 16=16! Последнее слагаемое было 7, пишем (7+1):2=4. Корень из 16 равен 4. А можно просто сосчитать, сколько чисел мы сложили, это и будет ответом! 1 — первое число, 3 — второе число, 5 — третье число, 7 — четвертое число, значит ответ 4! Но если сумма чисел окажется больше, чем число, из которого извлекаете корень, тогда последнее слагаемое считать не надо, вам останется, лишь подобрать десятые, сотые доли. [8]

Приложение 7

Схема подбора целочисленных значений катетов для ряда от √2 до √98 при использовании логического метода с использованием теоремы Пифагора:

(Результаты моих исследований)

Для √50 – два варианта решения: катеты 7 и 1; катеты 5 и 5.

Библиотека Sympy: символьные вычисления в Python

Что такое SymPy? Это библиотека символьной математики языка Python. Она является реальной альтернативой таким математическим пакетам как Mathematica или Maple и обладает очень простым и легко расширяемым кодом. SymPy написана исключительно на языке Python и не требует никаких сторонних библиотек.

Документацию и исходный код этой библиотеки можно найти на ее официальной странице.

Первые шаги с SymPy

Используем SymPy как обычный калькулятор

В библиотеке SymPy есть три встроенных численных типа данных: Real, Rational и Integer. С Real и Integer все понятно, а класс Rational представляет рациональное число как пару чисел: числитель и знаменатель рациональной дроби. Таким образом, Rational(1, 2) представляет собой 1/2, а, например, Rational(5, 2) — соответственно 5/2.

import sympy as sym
a = sym.Rational(1, 2) # дает 1/2
a * 2 # дает 1

Библиотека SymPy использует библиотеку mpmath, что позволяет производить вычисления с произвольной точностью. Таким образом, ряд констант (например, пи, e), которые в данной библиотеке рассматриваются как символы, могут быть вычислены с любой точностью.

sym.pi**2 # результат pi**2
sym.pi.evalf() # результат 3.14159265358979
(sym.pi + sym.exp(1)).evalf() # результат 5.85987448204884

Как можно заметить, функция evalf() дает на выходе число с плавающей точкой.

В SymPy есть также класс, представляющий такое понятие в математике, как бесконечность. Он обозначается следующим образом: oo.

sym.oo > 99999 # результат True
sym.oo + 1 # результат oo

Символы

В отличие от ряда других систем компьютерной алгебры, в SymPy можно в явном виде задавать символьные переменные. Это происходит следующим образом:

x = sym.Symbol('x')
y = sym.Symbol('y')

После их задания, с ними можно производить различные манипуляции.

x + y + x - y # результат 2*x
(x + y) ** 2 # результат (x + y)**2

С символами можно производить преобразования с использованием некоторых операторов языка Python. А именно, арифметических (+, -`, ``*, **) и логических (&, |, ~) .

Библиотека SymPy позволяет задавать форму вывода результатов на экран. Обычно мы используем формат такого вида:

sym.init_printing(use_unicode=False, wrap_line=True)

Алгебраические преобразования

SymPy способна на сложные алгебраические преобразования. Здесь мы рассмотрим наиболее востребованные из них, а именно раскрытие скобок и упрощение выражений.

Раскрытие скобок

Чтобы раскрыть скобки в алгебраических выражениях, используйте следующий синтаксис:

sym. expand((x + y) ** 3)

?³+3?²?+3??²+?³

3 * x * y ** 2 + 3 * y * x ** 2 + x ** 3 + y ** 3

?³+3?²?+3??²+?³

При помощи ключевого слова можно добавить поддержку работы с комплексными переменными, а также раскрытие скобок в тригонометрических функциях.

sym.expand(x + y, complex=True)#результат re(?)+re(?)+?im(?)+?im(?)
sym.expand(sym.cos(x + y), trig=True)
# результат −sin(?)sin(?)+cos(?)cos(?)

Упрощение выражений

Если вы хотите привести выражение к более простому виду (возможно, сократить какие-то члены), то используйте функцию simplify.

sym.simplify((x + x * y) / x) # результат y + 1

Также надо сказать, что для определенных видов математических функций существуют альтернативные, более конкретные функции для упрощения выражений. Так, для упрощения степенных функций есть функция powsimp, для тригонометрических —trigsimp, а для логарифмических — logcombine, radsimp.

Вычисления

Вычисления пределов

Для вычисления пределов в SymPy предусмотрен очень простой синтаксис, а именно limit(function, variable, point). Например, если вы хотите вычислить предел функции f(x), где x -> 0, то надо написать limit(f(x), x, 0).

sym. limit(sym.sin(x) / x, x, 0) # результат 1

Также можно вычислять пределы, которые стремятся к бесконечности.

sym.limit(x, x, sym.oo) # результат oo
sym.limit(1 / x, x, sym.oo) # результат 0
sym.limit(x ** x, x, 0) # результат 1

Дифференцирование

Для дифференцирования выражений в SymPy есть функция diff(func, var). Ниже даны примеры ее работы.

sym.diff(sym.sin(x), x) # результат cos(?)
sym.diff(sym.sin(2 * x), x) # результат 2cos(2?)
sym.diff(sym.tan(x), x)

tan²(?)+1

Проверим результат последней функции при помощи определения производной через предел.

sym.limit((sym.tan(x + y) - sym.tan(x)) / y, y, 0)

tan²(?)+1 Результат тот же.

Также при помощи этой же функции могут быть вычислены производные более высоких порядков. Синтаксис функции будет следующим: diff(func, var, n). Ниже приведено несколько примеров.

sym.diff(sym.sin(2 * x), x, 1) # результат 2cos(2?)
sym.diff(sym.sin(2 * x), x, 2) # результат −4sin(2?)
sym.diff(sym.sin(2 * x), x, 3) # результат −8cos(2?)

Разложение в ряд

Для разложения выражения в ряд Тейлора используется следующий синтаксис: series(expr, var).

sym.series(sym.cos(x), x)

1−?²/2+?⁴/24+?(?⁶)

sym.series(1/sym.cos(x), x)

1+?²/2+5?⁴/24+?(?⁶)

Интегрирование

В SymPy реализована поддержка определенных и неопределенных интегралов при помощи функции integrate(). Интегрировать можно элементарные, трансцендентные и специальные функции. Интегрирование осуществляется с помощью расширенного алгоритма Риша-Нормана. Также используются различные эвристики и шаблоны. Вот примеры интегрирования элементарных функций:

sym. integrate(sym.sin(x), x) # результат −cos(?)
sym.integrate(sym.log(x), x) # результат ?log(?)−?

Также несложно посчитать интеграл и от специальных функций. Возьмем, например, функцию Гаусса:

sym.integrate(sym.exp(-x ** 2) * sym.erf(x), x)

Результат вычисления можете посмотреть сами. Вот примеры вычисления определенных интегралов.

sym.integrate(x**3, (x, -1, 1)) # результат 0
sym.integrate(sym.sin(x), (x, 0, sym.pi / 2)) # результат 1
sym.integrate(sym.cos(x), (x, -sym.pi / 2, sym.pi / 2)) 
# результат 2

Также можно вычислять определенные интегралы с бесконечными пределами интегрирования (несобственные интегралы).

sym.integrate(sym.exp(-x), (x, 0, sym.oo)) # результат 1

Решение уравнений

При помощи SymPy можно решать алгебраические уравнения с одной или несколькими переменными. Для этого используется функция solveset().

sym.solveset(x ** 4 - 1, x) # результат {−1,1,−?,?}

Как можно заметить, первое выражение функции solveset() приравнивается к 0 и решается относительно х. Также возможно решать некоторые уравнения с трансцендентными функциями.

sym. solveset(sym.exp(x) + 1, x) # результат {?(2??+?)|?∈ℤ}

Системы линейных уравнений

SymPy способна решать широкий класс полиномиальных уравнений. Также при помощи данной библиотеки можно решать и системы уравнений. При этом переменные, относительно которых должна быть разрешена система, передаются в виде кортежа во втором аргументе функции solve(), которая используется для таких задач.

solution = sym.solve((x + 5 * y - 2, -3 * x + 6 * y - 15), (x, y))
solution[x], solution[y] # результат (-3, 1)

Факторизация

Другим мощным методом исследования полиномиальных уравнений является факторизация многочленов (то есть представление многочлена в виде произведения многочленов меньших степеней). Для этого в SymPy предусмотрена функция factor(), которая способна производить факторизацию очень широкого класса полиномов.

f = x ** 4 - 3 * x ** 2 + 1
sym.factor(f)

(?²−?−1)(?²+?−1)

sym.factor(f, modulus=5)

(?−2)²(?+2)²

Булевы уравнения

Также в SymPy реализована возможность решения булевых уравнений, что по сути означает проверку булевого выражения на истинность. Для этого используется функция satisfiable().

sym. satisfiable(x & y) # результат {x: True, y: True}

Данный результат говорит нам о том, что выражение (x & y) будет истинным тогда и только тогда, когда x и y истинны. Если выражение не может быть истинным ни при каких значениях переменных, то функция вернет результат False.

sym.satisfiable(x & ~x) # результат False

Линейная алгебра

Матрицы

Матрицы в SymPy создаются как экземпляры класса Matrix:

sym.Matrix([[1, 0], [0, 1]])

[10] [01]

В отличие от NumPy, мы можем использовать в матрицах символьные переменные:

x, y = sym. symbols('x, y')
A = sym.Matrix([[1, x], [y, 1]])
A

[1 ?] [? 1]

И производить с ними разные манипуляции:

A**2

[??+1 2?] [2? ??+1]

Дифференциальные уравнения

При помощи библиотеки SymPy можно решать некоторые обыкновенные дифференциальные уравнения. Для этого используется функция dsolve(). Для начала нам надо задать неопределенную функцию. Это можно сделать, передав параметр cls=Function в функцию symbols().

f, g = sym.symbols('f g', cls=sym.Function)

Теперь f и g заданы как неопределенные функции. мы можем в этом убедиться, просто вызвав f(x).

f(x) # результат ?(?)
f(x).diff(x, x) + f(x)

?(?)+?²/??²?(?)

Теперь решим следующее дифференциальное уравнение:

sym.dsolve(f(x).diff(x, x) + f(x), f(x))
# результат ?(?)=?1sin(?)+?2cos(?)

Чтобы улучшить решаемость и помочь этой функции в поиске решения, можно передавать в нее определенные ключевые аргументы. Например, если мы видим, что это уравнение с разделяемыми переменными, то мы можем передать в функцию аргумент hint='separable'.

sym. dsolve(sym.sin(x) * sym.cos(f(x)) + sym.cos(x) * sym.sin(f(x)) * f(x).diff(x), f(x), hint='separable') 
# результат [Eq(f(x), -acos(C1/cos(x)) + 2*pi), Eq(f(x), 
#            acos(C1/cos(x)))]

Калькулятор степеней и корней степеней

Этот калькулятор требует использования браузеров с поддержкой Javascript и поддержкой . Этот калькулятор предназначен для вычисления степеней (также известных как экспоненты или индексы) и корней степени любого числа. В некоторых случаях, как в случае с мэйнфреймами и мини-компьютерами, наши расчеты корней мощностей являются очень близкими приближениями. Введите целевое число и нажмите «Рассчитать». И степени, и значения степенных корней вычисляются до 18 цифр.

Вы можете нажать «Очистить значения», чтобы сделать другое.

Отрицательная мощность обратна множеству. Например, если набор равен 5 в степени 2 (или 5 в квадрате, или 5², или 5 * 5), обратная величина равна 1 / (5 * 5).

Силы и корни власти
Требуемый ввод данных
Введите значение
Введите значение мощности
Результаты расчетов
Расчетный корень мощности
Расчетная мощность

Версия 1.

1.9

Оставьте нам вопрос или комментарий на Facebook
	Поиск или просмотр нашего сайта

Калькулятор корня — определение | Решение шаг за шагом

Здесь вы можете использовать наш калькулятор корня для вычисления n-го корня любого числа. Корень n-й степени любого числа также называют корневой степенью, и CalCon позволяет вычислить его с помощью интерактивного калькулятора на этой странице или путем загрузки приложений из магазина Play и App. Это довольно просто, потому что все, что вам нужно ввести, это мощность корня и число, чей корень вы ищете.

Ниже мы дадим краткий теоретический обзор того, что такое корень в математике, как он оценивается и вычисляется, затем, как оценить квадратный корень, краткий обзор того, что такое кубический корень, и многое другое. Кроме того, проверьте некоторые из наших связанных калькуляторов по этой теме, чтобы помочь вам с кубическим корнем или квадратным корнем. Проверьте также другие калькуляторы, такие как «Процент», «Разница в процентах» или какой-нибудь калькулятор, связанный с геометрией. 9{1/n}

 x = \sqrt [1/n] {y}

И в конце, в виде логарифмов

 \log_y(x) = n

В выражении \sqrt[n]{ a} , натуральное число n называется показателем степени, степенью корня или индексом, а a называется подкоренным числом. Чаще всего используются квадратные и кубические корни, и о них мы кое-что скажем позже.

На множестве действительных чисел корни с четным показателем степени (второй, четвертый, шестой и т. д.) действительны только для нуля и положительного числа. Для отрицаний определение четного корня требует введения мнимой единицы (комплексных чисел).

В алгебре определение корней распространяется на нецелые показатели степени и комплексные числа. Однако корень комплексного числа нельзя однозначно определить как его логарифм.

Как найти рут?

Поиск корней в математике — это обратная задача возведения в степень. Существуют разные корни: корни второй степени, корни третьей степени, корни четвертой степени и т. д. Это зависит от того, в какой степени число изначально было усилено. Корень обозначается символом: √ — квадратный корень, т. е. корень второй степени; если корень имеет степень больше второй, то соответствующая степень присваивается над знаком корня. Число под знаком корня является подкоренным выражением.

Основные правила

При нахождении корня есть несколько правил, которые помогут вам не ошибиться:

Четный корень (если степень 2, 4, 6, 8 и т. д.) отрицательного числа НЕ существует. Если подкоренное выражение отрицательное, но требуется нечетный корень (3, 5, 7 и т. д.), результат будет отрицательным.

Корень любой степени единицы всегда равен единице: \sqrt{1} = 1 .

Корень из нуля равен нулю: \sqrt{0} = 0 .

Оценка корня

Один из самых простых способов найти квадратный корень — использовать специальную таблицу. С помощью таблицы можно найти квадрат любого числа от 10 до 9.9. При этом в строках таблицы указаны значения десятков, в столбцах – значения единиц. Ячейка, которая находится на пересечении столбца и строки, содержит двузначный квадрат. Например, чтобы возвести в квадрат 63, нужно найти строку 6 и столбец 3. На пересечении находим ячейку 3969.

Так как извлечение корня противоположно возведению в квадрат, то для выполнения этого действия нужно сделать обратное: сначала , найдите ячейку с числом, радикал которого вы хотите вычислить, а затем определите ответ по значениям столбца и строки. В качестве примера рассмотрим вычисление квадратного корня из 169..

Аналогично можно найти кубические корни и -й степени с помощью соответствующих таблиц.

Удобство этого метода заключается в его простоте и отсутствии дополнительных расчетов. Однако недостатки очевидны: метод можно использовать только для ограниченного диапазона значений (число должно быть в диапазоне от 100 до 9801). Кроме того, это не сработает, если указанного номера нет в таблице.

Оценка квадратного корня

Наиболее распространенными корнями являются квадратные, где n = 2, и кубическое, где n = 3. Вычисление квадратных корней и n ^th корней довольно интенсивно. Это требует оценки, проб и ошибок. Существуют более точные способы оценки квадратных корней, но мы упростим и представим метод, который не требует значительного понимания сложных математических понятий. Оценить √a:

Оценить b
Разделить по б . Остановитесь, если c возвращено с точностью до нужного десятичного разряда.
Среднее b и c и результатом будет новое предположение
Повторите второй шаг

Например, найдите 3 знака после запятой

Сначала нам нужно угадать: 5,125, тогда:

27 \дел 5,125 = 5,268

\ гидроразрыв {5 125 + 5 268} {2} = 5 197

27 \дел 5,197 = 5,195

\фракция {5,195+5,197}{2} = 5,196

27 \дел 5 196 = \mathbf{5 196}

Таким образом, результат, округленный до трех знаков после запятой, равен 5196.

Оценка n-го корня

Вычисление n ^th корней может быть выполнено с использованием аналогичного метода, с некоторыми изменениями относительно n . Оценить более высокие корни n ^th сложно, даже если использовать калькулятор для промежуточных шагов. Простой метод приведен ниже с примером. Оценить ⁿ √a следуйте следующей форме:

Оцените b
Разделите a на б ^н-1 . Остановиться, если возвращенное число c точно соответствует требуемому десятичному разряду.
Среднее значение уравнения: [b × (n-1) + c] / n
Повторите второй шаг

Найдите ⁸ √15 до 3 знаков после запятой 900 24

Время угадывать: 1.432 97 = 1403

\фракция {1403 \cdot 7+1388}{8} = 1402

Тогда должно быть ясно, что дальнейшее продолжение приведет к числу, которое будет округлено до 1,403, что делает 1,403 окончательной оценкой с точностью до 3 знаков после запятой. В заключение, это итеративный процесс.

Квадрат, Куб, Четвертый, n-й корень

Что касается квадратного корня, то существует несколько других методов, с помощью которых можно вычислить корни, и некоторые из известных:

Метод догадки и проверки (объяснение выше)
Метод усреднения
Метод повторного вычитания
Метод простой факторизации (подробнее см.
No related posts.