tablica istinnosti ru
tablica istinnosti ruВы искали tablica istinnosti ru? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и алгебра логика калькулятор онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «tablica istinnosti ru».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как tablica istinnosti ru,алгебра логика калькулятор онлайн,алгебра логика онлайн калькулятор,алгебра логики калькулятор,алгебра логики калькулятор онлайн,алгебра логики онлайн,алгебра логики онлайн калькулятор,алгебра логики онлайн решение,алгебра логики решение онлайн,алгебра логики упростить выражение онлайн,булева алгебра калькулятор онлайн,булева алгебра онлайн,булева алгебра онлайн калькулятор,булевы функции онлайн калькулятор,булевых функций онлайн калькулятор,дискретная математика калькулятор онлайн,дискретная математика онлайн калькулятор,дискретная математика упростить выражение онлайн,днф и кнф онлайн,днф и кнф онлайн калькулятор,днф онлайн,днф онлайн калькулятор,доказать равносильность логических выражений онлайн,и таблица истинности,информатика упростить логическое выражение онлайн калькулятор,калькулятор алгебра логика,калькулятор алгебра логики,калькулятор алгебры логики,калькулятор алгебры логики онлайн,калькулятор булевой алгебры онлайн,калькулятор булевых функций,калькулятор булевых функций онлайн,калькулятор днф и кнф онлайн,калькулятор истинности,калькулятор истинности онлайн,калькулятор кнф онлайн,калькулятор логики,калькулятор логики онлайн,калькулятор логические операции,калькулятор логический,калькулятор логических выражений,калькулятор логических выражений онлайн,калькулятор логических выражений онлайн упрощение,калькулятор логических операций,калькулятор логических функций,калькулятор логических функций онлайн,калькулятор мат логика,калькулятор математической логики,калькулятор математической логики онлайн,калькулятор онлайн алгебра логика,калькулятор онлайн истинности,калькулятор онлайн сднф,калькулятор онлайн таблицы истинности,калькулятор онлайн упрощение логических выражений,калькулятор сднф,калькулятор сднф и скнф онлайн,калькулятор скнф и сднф онлайн,калькулятор таблиц истинности онлайн,калькулятор таблица истинности,калькулятор таблица истинности онлайн калькулятор,калькулятор таблицы истинности,калькулятор таблицы истинности онлайн,калькулятор упростить логическое выражение,калькулятор упрощение логических выражений онлайн,карта карно онлайн калькулятор,карты карно калькулятор онлайн,карты карно онлайн калькулятор,карты карно онлайн решение,карты карно решение онлайн,кнф и днф онлайн,кнф и днф онлайн калькулятор,кнф онлайн,логика алгебра онлайн калькулятор,логические выражения калькулятор онлайн,логические выражения онлайн,логические выражения онлайн калькулятор,логические выражения онлайн упростить,логические выражения упростить онлайн,логические операции калькулятор,логические операции калькулятор онлайн,логические операции онлайн,логические операции онлайн калькулятор,логические схемы онлайн,логические уравнения онлайн,логический калькулятор,логический калькулятор онлайн,мат логика калькулятор,мат логика онлайн,математическая логика калькулятор онлайн,математическая логика онлайн,математическая логика онлайн калькулятор,мднф онлайн,минимизация булевых функций онлайн,минимизация логических функций калькулятор онлайн,минимизация логических функций онлайн,минимизация логических функций онлайн калькулятор,минимизация онлайн,минимизация функции онлайн,минимизировать функцию онлайн,многочлен жегалкина онлайн калькулятор,онлайн алгебра логики,онлайн калькулятор алгебра логика,онлайн калькулятор алгебра логики,онлайн калькулятор алгебры логики,онлайн калькулятор булевой алгебры,онлайн калькулятор булевых функций,онлайн калькулятор дискретная математика,онлайн калькулятор днф,онлайн калькулятор истинности,онлайн калькулятор логики,онлайн калькулятор логические выражения,онлайн калькулятор логические операции,онлайн калькулятор логический,онлайн калькулятор логических выражений,онлайн калькулятор логических выражений упрощение,онлайн калькулятор логических функций,онлайн калькулятор математической логики,онлайн калькулятор полином жегалкина,онлайн калькулятор сднф,онлайн калькулятор таблиц истинности,онлайн калькулятор таблица истинности,онлайн калькулятор таблицы истинности,онлайн калькулятор упростить логическое выражение,онлайн калькулятор упростить логическое выражение информатика,онлайн калькулятор упрощение логических выражений,онлайн кнф,онлайн логические операции,онлайн логические схемы,онлайн логические уравнения,онлайн мат логика,онлайн математическая логика,онлайн минимизация,онлайн минимизация логических функций,онлайн минимизация функции,онлайн построение таблиц истинности,онлайн построение таблицы истинности,онлайн преобразование логических выражений,онлайн решение алгебра логики,онлайн решение карты карно,онлайн решение логических выражений,онлайн решение логических уравнений,онлайн решение таблиц истинности,онлайн решение таблицы истинности,онлайн сднф,онлайн составление таблиц истинности,онлайн составление таблицы истинности,онлайн упростите логическое выражение,онлайн упрощение логических выражений,онлайн упрощение логических функций,онлайн упрощение формул логики,полином жегалкина калькулятор онлайн,полином жегалкина онлайн,полином жегалкина онлайн калькулятор,построение онлайн таблиц истинности,построение онлайн таблиц истинности логических выражений,построение таблиц истинности логических выражений онлайн,построение таблиц истинности онлайн,построение таблицы истинности онлайн,построить логическое выражение по таблице истинности онлайн,построить логическую схему онлайн,построить онлайн таблицу истинности,построить таблицу истинности для логического выражения онлайн,построить таблицу истинности онлайн,преобразование логических выражений онлайн,привести к днф функцию онлайн,привести функцию к днф онлайн,решение алгебра логики онлайн,решение карты карно онлайн,решение логических выражений онлайн,решение логических операций онлайн,решение логических уравнений онлайн,решение онлайн логических выражений,решение онлайн таблица истинности,решение таблиц истинности онлайн,решение таблицы истинности онлайн,решить логическое уравнение онлайн,сднф и скнф онлайн,сднф и скнф онлайн калькулятор,сднф и скнф онлайн калькулятор с решением,сднф калькулятор,сднф калькулятор онлайн,сднф онлайн,сднф онлайн калькулятор,сднф по таблице истинности онлайн,скнф и сднф онлайн,скнф и сднф онлайн калькулятор,скнф онлайн,скнф упрощение онлайн,сократить днф онлайн,сокращение логических выражений онлайн,составить логическую схему онлайн,составить таблицу истинности,составить таблицу истинности онлайн,составить таблицу истинности онлайн с решением,составление таблиц истинности онлайн,составление таблицы истинности онлайн,составьте таблицу истинности,таблица истинности,таблица истинности калькулятор,таблица истинности калькулятор онлайн,таблица истинности логических операций онлайн,таблица истинности логических операций онлайн калькулятор,таблица истинности онлайн,таблица истинности онлайн калькулятор,таблица истинности онлайн решение,таблица истинности решение онлайн,таблица истинности ру,таблица истинности это,таблицы истинности калькулятор онлайн,таблицы истинности онлайн,таблицы истинности онлайн калькулятор,таблицы истинности онлайн решение,таблицы истинности решение онлайн,упростите логическое выражение онлайн,упростить выражение алгебра логики онлайн,упростить выражение дискретная математика онлайн,упростить выражение онлайн алгебра логики,упростить выражение онлайн дискретная математика,упростить логические выражения онлайн,упростить логическое выражение калькулятор,упростить логическое выражение калькулятор онлайн,упростить логическое выражение онлайн,упростить логическое выражение онлайн калькулятор,упростить логическое выражение онлайн калькулятор информатика,упростить логическое выражение онлайн калькулятор с решением,упростить логическую функцию онлайн,упростить формулу логики онлайн,упрощение булевых функций онлайн,упрощение логических выражений информатика онлайн калькулятор,упрощение логических выражений калькулятор онлайн,упрощение логических выражений онлайн,упрощение логических выражений онлайн калькулятор,упрощение логических выражений онлайн калькулятор информатика,упрощение логических функций онлайн,упрощение логического выражения онлайн,упрощение скнф онлайн,упрощение формул логики онлайн.
Решить задачу tablica istinnosti ru вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Построение СКНФ и СДНФ по таблице истинности
- СКНФ
- СДНФ
Нормальной форме логической формулы не свойственна эквивалентность, отрицание формул неэлементарного типа и знаки импликации.
Выделяют такие виды формы нормального типа:
- КНФ (конъюнктивная нормальная форма), где подразумевается конъюнкция того или иного количества дизъюнкций, как пример, ;
- ДНФ (дизъюнктивная нормальная форма), где осуществляется дизъюнкция конъюнкций, как пример, .
СКНФ
Совершенная КНФ является разновидностью конъюнктивной нормальной формы, удовлетворяющей такие условия:
- отсутствие одинаковых элементарных дизъюнкций;
- дизъюнкции не содержат одинаковые переменные;
- все дизъюнкции содержат каждую переменную из входящих в конъюнктивную НФ такого типа.
Построение СКНФ согласно таблице истинности
Если функция равна нулю, то в случае каждого набора записывают сумму, причем с отрицанием берутся те переменные, которые равны единице.
СДНФ
Совершенная ДНФ является разновидностью дизъюнктивной нормальной формы, удовлетворяющей следующие условия:
- отсутствие одинаковых элементарных конъюнкций;
- конъюнкции не свойственно обладать одинаковыми переменными;
в случае любой конъюнкции элементарного типа имеет место быть переменная, входящая в такую нормальную дизъюнктивную форму. При этом в одинаковом порядке.
При этом в одинаковом порядке.
Все формулы булевого типа, которые не относятся к тождественно ложным, могут быть представлены в совершенной разновидности ДНФ, при этом в единственном возможном варианте.
Построение СДНФ согласно таблице истинности
Если функция соответствует единице, то в случае каждого набора записывается произведение, причем с отрицанием берутся те переменные, которые равны нулю.
Нахождение СКНФ и СДНФ: примеры
Пример
Согласно таблице истинности записать логическую функцию:
Рисунок 1.
Решение:
Прибегнем к правилу построения совершенной ДНФ
Рисунок 2.
Получаем такую СДНФ
Задействовав правило её построения:
Рисунок 3.
Получаем СКНФ:
Пример
Представить функцию как СДНФ и СКНФ, при том, что она задаётся таблицей истинности.
Рисунок 4.
РешениеДля начала нужно записать логическую функцию в СДНФ. Чтобы упростить решение, добавляем к таблице столбец. Прибегнув к правилу составления СДНФ, вводим знак отрицания для переменных с нулевым значением. Инвертирование нулевых значений переменных имеет большое значение, поскольку без этого значения конъюнкций будут преобразованы в нули ключевой функции.
Прибегнув к правилу составления СДНФ, вводим знак отрицания для переменных с нулевым значением. Инвертирование нулевых значений переменных имеет большое значение, поскольку без этого значения конъюнкций будут преобразованы в нули ключевой функции.
Рисунок 5.
Вычисленные конъюнкции из вспомогательного столбца необходимо объединить знаком дизъюнкции и получим необходимую логическую функцию, имеющую вид совершенной конъюнктивной формы нормального типа:
Запишем логическую функцию в СКНФ.
Прибегнув к правилу, по которому составляется СКНФ, нужно помнить о введения знака отрицания для переменных с единицей. Инвертирование единичных значений имеет большое значение, поскольку без этого значения дизъюнкций будут преобразованы в единицы ключевой функции.
Рисунок 6.
Вычисленные дизъюнкции из вспомогательного столбца необходимо объединить знаком конъюнкции, так как таким образом и можно получить необходимую логическую функцию, имеющую вид совершенной нормальной формы конъюнктивного типа.
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Устройства хранения информации Алфавитный подход к оценке количества информации. Формула Хартли Информационные процессы и информация Прикладное программное обеспечение Архитектура персонального компьютера
Формула Хартли Информационные процессы и информация Прикладное программное обеспечение Архитектура персонального компьютера
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Генератор таблиц истинности— Мгновенное создание таблиц логической истинности
Генератор таблиц истинности — Мгновенное создание таблиц логической истинности
Логический инструмент для создания таблицы истинности онлайн
Введите логическое выражение
Поделиться
Твитнуть
Как использовать ?
- Введите свое логическое выражение в поле поиска
- Используйте буквы для переменных, символы для логических операторов
- Нажмите кнопку «Получить таблицу истинности»
- Таблица истинности будет отображаться
- Нажмите кнопку «Расширенная таблица истинности» для операций с пропозициональной логикой
| Оператор | Символ для ввода | Пример |
|---|---|---|
| ИЛИ | | | А | Б | С |
| И | и | А и В и С |
| НЕ | ! | ! А |
| И-НЕ (И + НЕ) 9 Б |
Таблица истинности
Таблица истинности представляет собой представление логического выражения в табличном формате. Он в основном используется в математике и информатике.
Он в основном используется в математике и информатике.
Представление выполняется с использованием двухзначной логики — 0 или 1. Вы также можете ссылаться на них как на True (1) или False (0). Он используется для просмотра выходного значения, сгенерированного из различных комбинаций входных значений.
Символы логических вентилей
Эти входные значения представляют собой различные переменные и символы (обычно называемые ЛОГИЧЕСКИМИ ВОРОТАМИ). Ниже приведены ВОРОТ и символы
- И (символически: &)
- ИЛИ (символически: +)
- НЕ (символически: !)
- НО (обозначает: НЕ ИЛИ)
- НЕ-И (Обозначает: Не-И)
Примеры таблиц истинности
В каждой таблице истинности каждое утверждение обычно представлено двоичной цифрой или переменной. Для лучшего понимания взгляните на приведенные ниже примеры.
Для лучшего понимания взгляните на приведенные ниже примеры.
Таблица истинности шлюза OR
| Символ | А | Б | А+В |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 0 | 1 | 1 | |
| 1 | 1 | 1 |
Таблица истинности шлюзов И
| Символ | А | Б | АБ |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 1 |
Таблица истинности логических элементов NAND
| Символ | А | Б | !(А. Б) Б) |
|---|---|---|---|
| 0 | 0 | 1 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
Таблица истинности шлюза NOR
| Символ | А | Б | !(А+В) |
|---|---|---|---|
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 0 |
Таблица истинности шлюза НЕ
| Символ | А | !А |
|---|---|---|
| 0 | 1 | |
| 1 | 0 |
Генератор таблиц истинности
Таблица истинности представляет собой математическую таблицу и основу для всех вычислительных нужд.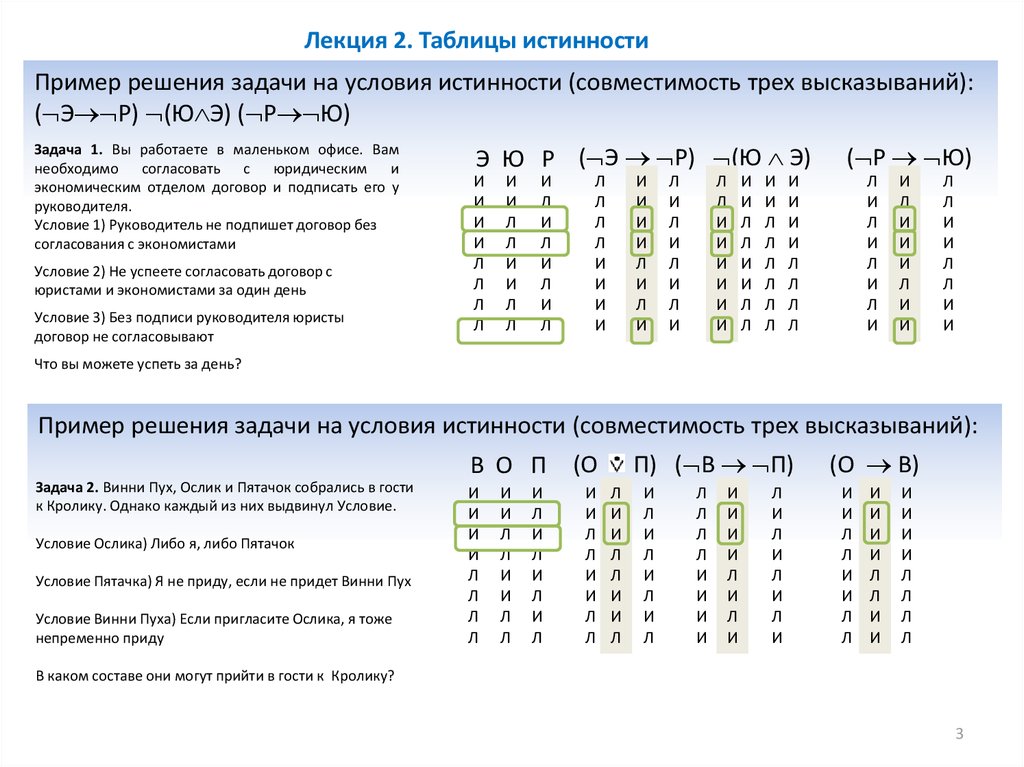 Он используется, чтобы выяснить, истинно ли пропозициональное выражение для всех допустимых входных значений.
Он используется, чтобы выяснить, истинно ли пропозициональное выражение для всех допустимых входных значений.
Создание таблицы истинности включает в себя простую логику, но иногда это может замедлить работу, особенно когда вы работаете над последним проектом. Это когда вы можете использовать генератор таблиц истинности.
Генератор таблиц истинности — это онлайн-инструмент, который используется для мгновенного создания логических таблиц истинности. Вы можете вводить логические операторы в различных форматах и получать точные результаты в виде символов логической логики.
Расширенная таблица истинности
Этот инструмент генерирует таблицы истинности для формул пропозициональной логики. Вы можете вводить логические операторы в нескольких различных форматах. Например, пропозициональная формула p ∧ q → ¬r может быть записана как р/\ q -> ~г, как p и q => не r, или как p && q -> !r. Связки ⊤ и ⊥ можно вводить как T и F.
FAQ
Таблица, показывающая все возможные комбинации переменных в выражении в символьной логике с их окончательным результатом как истинным или ложным.
Таблица истинности представляет собой разбивку логической функции путем перечисления всех возможных значений, которые может получить функция.
0 представляет false в булевых логических выражениях. 1 считается Истинным. .
Генератор таблиц истинности с заключением
Краткое руководство по логическим операторам
Первым шагом в создании таблицы истинности является перевод вашего аргумента на язык символической логики. Вот шпаргалка по логическому переводу, чтобы помочь.
| Символ | Альтернатива | Название | Синд | Английские соединения |
| ~ | ! | Тильда | Отрицание (НЕ) | это не тот случай, что А; не А; неверно, что А |
| & | &&, /\ | Амперсанд | Союз (И) | А и В; А, но Б; А еще Б; А пока Б; А кроме того Б; А однако Б; А тем не менее Б; А еще Б; А тем не менее Б; А также Б; А хотя Б; оба а и Б; А дополнительно В; А кроме того В |
| v | ||, \/ | Клин | Разъединение (OR) | A или B; A кроме B |
| ⊃ | > | Подкова | Условное (IF) | если A, то B; В только если А; А является необходимым условием для В; B — необходимое условие для A; B при условии, что A; В при условии, что А; А подразумевает, что Б; В при условии, что А; B в случае, если A |
| ≡ | ==, = | Тройной стержень | Биусловный (IFF) | A тогда и только тогда, когда B; А на всякий случай, что Б; А является необходимым и достаточным условием для В; A эквивалентен B |
Что такое таблица истинности?
Таблица истинности — это таблица, которую можно использовать для работы с логическими утверждениями. Википедия говорит, что:
Таблица истинности — это математическая таблица, используемая в логике, особенно в связи с булевой алгеброй, булевыми функциями и исчислением высказываний, в которой излагаются функциональные значения логических выражений для каждого из их функциональных аргументов, то есть для каждой комбинации значений, принимаемых их логическими переменными. В частности, таблицы истинности можно использовать, чтобы показать, является ли пропозициональное выражение истинным для всех законных входных значений, то есть логически верным.
Но это не очень полезно, если вы еще не логик. По сути, таблица истинности показывает все возможные входы и выходы логического утверждения.
Что такое оператор символьной логики?
Оператор символьной логики — это способ представления логического аргумента с помощью символов. Итак, вы можете написать что-то вроде этого:
Итак, вы можете написать что-то вроде этого:
Я человек или я робот, и у меня есть процессор вместо мозга.
во что-то вроде этого:
H v (R & C)
Чтобы перевести это в символическую логику, мы превратили каждый из атомарных операторов оператора в однобуквенные константы, а такие слова, как или и и , в соответствующие логические операторы ( v и и ). Вы можете найти список всех логических операторов здесь.
Теперь, когда у нас есть оператор символьной логики, мы можем сгенерировать для него таблицу истинности. Для этого введите его в калькулятор. Вы должны увидеть вывод, подобный этому: В самом верху есть смайлик с большим пальцем вверх, указывающий, что утверждение правильно сформировано. Если вы добавите ошибку в оператор (например, замените «&» на «&&»), она исчезнет, и вы увидите сообщение об ошибке. Также есть кнопка «Prettify» для замены таких операторов, как 9.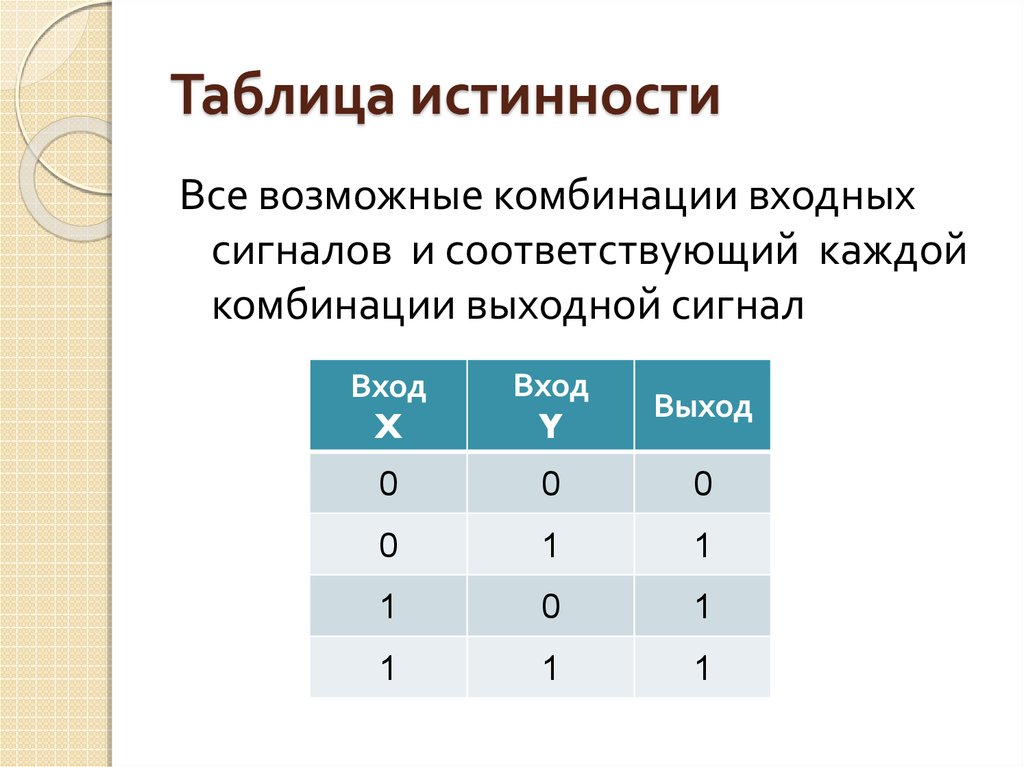 0493 > или = с более красивыми версиями. Далее вы увидите индикаторы, показывающие, что оператор является непредвиденным обстоятельством . Это просто означает, что утверждение может быть либо истинным, либо ложным, в зависимости от того, являются ли входные данные (идентификаторы) истинными или ложными. Утверждения также могут быть тавтологиями (утверждение всегда истинно, независимо от входных данных) или противоречиями (всегда ложно). Например, A v ~A — это тавтология, потому что если вы переведете это на английский язык, то получится, что «A истинно или ложно», что, конечно, всегда верно, независимо от того, что такое A. A & ~A — это противоречие, потому что оно говорит, что «A истинно и ложно», и невозможно, чтобы что-то было одновременно и истинным, и ложным. Наш пример является случайным, потому что я могу быть ни человеком, ни роботом, или я могу быть роботом, но не иметь ЦП вместо мозга.
0493 > или = с более красивыми версиями. Далее вы увидите индикаторы, показывающие, что оператор является непредвиденным обстоятельством . Это просто означает, что утверждение может быть либо истинным, либо ложным, в зависимости от того, являются ли входные данные (идентификаторы) истинными или ложными. Утверждения также могут быть тавтологиями (утверждение всегда истинно, независимо от входных данных) или противоречиями (всегда ложно). Например, A v ~A — это тавтология, потому что если вы переведете это на английский язык, то получится, что «A истинно или ложно», что, конечно, всегда верно, независимо от того, что такое A. A & ~A — это противоречие, потому что оно говорит, что «A истинно и ложно», и невозможно, чтобы что-то было одновременно и истинным, и ложным. Наш пример является случайным, потому что я могу быть ни человеком, ни роботом, или я могу быть роботом, но не иметь ЦП вместо мозга.
Наконец, у нас есть таблица истинности для нашего утверждения. Каждый компонент нашего заявления разбит на столбец таблицы. Столбец главного оператора выделен; это «вывод» оператора. Давайте попробуем использовать его! Во-первых, мы должны определить, каково значение каждого идентификатора. Я человек, я не робот, и у меня нет процессора вместо мозга, так что H верно, R ложно, и C тоже ложно. В таблице мы можем найти строку, в которой каждый из наших идентификаторов имеет значение, которое мы определили: И мы видим, что в этой строке основной оператор истинен, что означает, что утверждение истинно!
Каждый компонент нашего заявления разбит на столбец таблицы. Столбец главного оператора выделен; это «вывод» оператора. Давайте попробуем использовать его! Во-первых, мы должны определить, каково значение каждого идентификатора. Я человек, я не робот, и у меня нет процессора вместо мозга, так что H верно, R ложно, и C тоже ложно. В таблице мы можем найти строку, в которой каждый из наших идентификаторов имеет значение, которое мы определили: И мы видим, что в этой строке основной оператор истинен, что означает, что утверждение истинно!
Как пользоваться таблицей истинности?
Подведение итогов, составление и использование таблицы истинности:
- Преобразование вашего утверждения в символьную логику
- Вставьте ваше утверждение в калькулятор для создания таблицы истинности
- Найдите строку в таблице, в которой значения идентификаторов совпадают ваши входные значения
- Прочтите значение в главном столбце оператора (выделено), чтобы увидеть результат!
Часто задаваемые вопросы
Трудны ли таблицы истинности?
Таблицы истины поначалу могут показаться немного пугающими, но как только вы научитесь ими пользоваться, они станут очень простыми.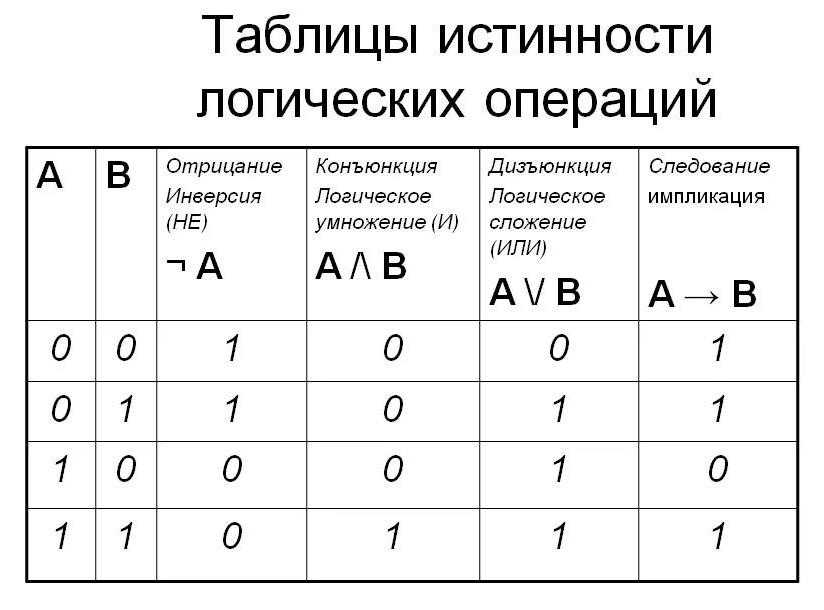

 0)
0)