Калькулятор треугольников онлайн: Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Стороны равнобедренного треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Зная стороныдва угла и сторонудве стороны и уголпрямоугольный треугольникравнобедренный треугольникравносторонний треугольникоснование и высоту

сторонывысоту и сторонусторону и уголвысоту и угол

Сторона треугольника a

Сторона треугольника b

Равнобедренный треугольник имеет две равные по значению боковые стороны a и основание b. Это позволяет рассчитать любые параметры треугольника, необходимые для решения задачи. Периметр равнобедренного треугольника равен удвоенной боковой стороне в сумме с основанием. (рис.88.1) P=2a+b

Высота, проведенная к основанию равнобедренного треугольника, делит его на два конгруэнтных прямоугольных треугольника, с половиной основания в качестве второго катета и боковой стороной как гипотенузой. Такая высота одновременно является и медианой и биссектрисой. Найти ее можно по теореме Пифагора из прямоугольного треугольника. (рис. 2 )

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

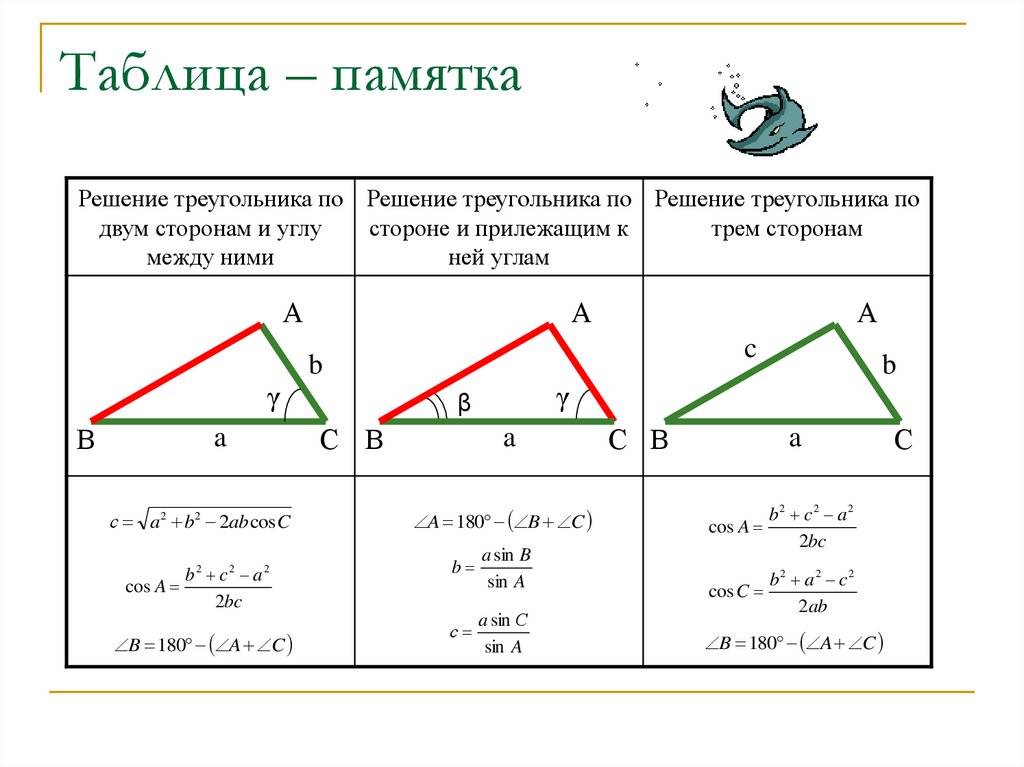
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

1. Три стороны треугольника.
2. Две стороны треугольника и угол между ними.
3. Две стороны и угол противостоящий к одному из этих сторон треугольника.
4. Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.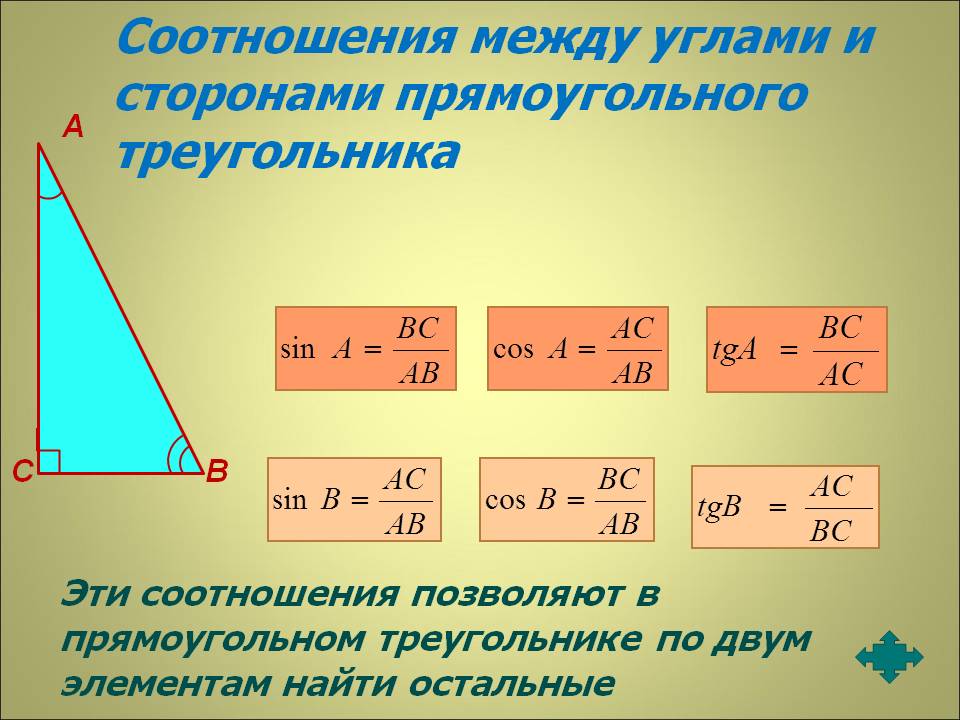 1). Найдем .

Решение:

Из теоремы косинусов имеем:

Откуда

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

Используя онлайн калькулятор для arcsin и arccos находим углы A и B:

И, наконец, находим угол C:

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Решение:

Найдем сторону c используя теорему косинусов:

Далее, из формулы

найдем cosA:

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

Пример 2. Известны две стороны треугольника ABC: и (Рис. 2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

Вычисления выше легко производить инженерным онлайн калькулятором.

Из формулы (3) найдем cosA:

Используя онлайн калькулятор для arcsin и arccos или инженерный онлайн калькулятор находим угол A:

Поскольку уже нам известны два угла то находим третий:

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Решение:

Так как, уже известны два угла, то можно найти третий:

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

Откуда

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

Ответ:

Калькулятор треугольника

Введите 3 значения, включая хотя бы одну сторону, в следующие 6 полей и нажмите кнопку «Рассчитать». Если в качестве единицы измерения угла выбран радиан, он может принимать такие значения, как пи/2, пи/4 и т. д.

Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, в которой встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединены тремя отрезками, называемыми ребрами. Треугольник обычно называют его вершинами. Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники, как правило, описываются на основе длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют одинаковую длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют одинаковую длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.

Засечки на ребрах треугольника — общепринятое обозначение, отражающее длину стороны, где одинаковое количество засечек означает одинаковую длину. Аналогичные обозначения существуют для внутренних углов треугольника, обозначаемых разным количеством концентрических дуг, расположенных в вершинах треугольника. Как видно из приведенных выше треугольников, длина и внутренние углы треугольника напрямую связаны, поэтому имеет смысл, что равносторонний треугольник имеет три равных внутренних угла и три стороны одинаковой длины. Обратите внимание, что треугольник, представленный в калькуляторе, показан не в масштабе; хотя он выглядит равносторонним (и имеет маркировку углов, которые обычно читаются как равные), он не обязательно является равносторонним и представляет собой просто изображение треугольника. При вводе фактических значений выходные данные калькулятора будут отражать форму входного треугольника.

Треугольники, классифицированные по их внутренним углам, делятся на две категории: прямоугольные и косоугольные. Прямоугольный треугольник — это треугольник, в котором один из углов равен 90°, и обозначается двумя отрезками, образующими квадрат в вершине, составляющей прямой угол. Самая длинная сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой. Любой треугольник, который не является прямоугольным, классифицируется как косоугольный и может быть либо тупоугольным, либо остроугольным. В тупоугольном треугольнике один из углов треугольника больше 90°, а в остроугольном треугольнике все углы меньше 90°, как показано ниже.

Факты, теоремы и законы треугольника

• Зная длины всех трех сторон любого треугольника, каждый угол можно вычислить с помощью следующего уравнения. Обратитесь к треугольнику выше, предполагая, что значения a, b и c известны.

Площадь треугольника

Существует несколько различных уравнений для расчета площади треугольника, в зависимости от того, какая информация известна. Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание, b и высота h . «Основание» относится к любой стороне треугольника, где высота представлена ​​длиной отрезка, проведенного от вершины, противоположной основанию, к точке на основании, образующей перпендикуляр.

Зная длину двух сторон и угол между ними, можно использовать следующую формулу для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному в калькуляторе выше. Учитывая а = 9, b = 7 и C = 30°:

Другой метод вычисления площади треугольника использует формулу Герона. В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат. Однако для этого требуется, чтобы длины трех сторон были известны. Опять же, в отношении треугольника, представленного в калькуляторе, если a = 3, b = 4 и c = 5:

Медиана, внутренний радиус и радиус описанной окружности

Медиана

Медиана треугольника определяется как длина отрезка, проходящего от вершины треугольника до середины противоположной стороны. Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек треугольника) треугольника. Обратитесь к приведенному ниже рисунку для пояснения.

Медианы треугольника представлены отрезками m _a , m _b и m _c . Длину каждой медианы можно рассчитать следующим образом:

Где a, b и c представляют длину стороны треугольника, как показано на рисунке выше.

Например, учитывая, что a=2, b=3 и c=4, медиана m _a может быть рассчитана следующим образом: круг, который поместится внутри заданного многоугольника, в данном случае треугольника. Внутренний радиус перпендикулярен каждой стороне многоугольника. В треугольнике внутренний радиус можно определить, построив две биссектрисы угла, чтобы определить центр треугольника. Внутренний радиус — это расстояние по перпендикуляру между центром вписанной стороны и одной из сторон треугольника. Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром вписанной стороны, поскольку центр вписанной стороны по определению равноудален от каждой стороны треугольника.

Для целей этого калькулятора внутренний радиус рассчитывается с использованием площади (Area) и полупериметра (s) треугольника по следующим формулам:

внутренний радиус =

с =

а+б+в 2

где a, b и c — стороны треугольника

Радиус окружности

Радиус окружности определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника. Центр этой окружности, где встречаются все серединные перпендикуляры каждой стороны треугольника, является центром описанной окружности треугольника и является точкой, от которой измеряется радиус описанной окружности.

Центр описанной окружности треугольника не обязательно должен находиться внутри треугольника. Стоит отметить, что у всех треугольников есть описанная окружность (окружность, проходящая через каждую вершину) и, следовательно, радиус описанной окружности.

Для целей данного калькулятора радиус описанной окружности рассчитывается по следующей формуле:

радиус описанной окружности =

а 2sin(A)

Где а — сторона треугольника, а А — угол, противоположный стороне а

Хотя сторона а и угол А используются, в формуле можно использовать любую из сторон и соответствующие им противоположные углы.

Калькулятор теорем треугольника

Фигура треугольника

Угол-бок-угол (ASA)

А = угол А
B = угол B
С = угол С
а = сторона а
b = сторона b
с = сторона с

P = периметр
с = полупериметр
К = площадь
r = радиус вписанной окружности
R = радиус описанной окружности

Использование калькулятора

Каждый вариант расчета, показанный ниже, имеет подпункты, перечисляющие последовательность методов, используемых в этом калькуляторе для расчета неизвестных значений угла и стороны, включая Сумма углов треугольника, закон синусов и Закон косинусов.

Это НЕ ЕДИНСТВЕННЫЕ последовательности, которые вы можете использовать для решения подобных проблем.

• См. также тригонометрические калькуляторы:
• Калькулятор закона косинусов
• Калькулятор закона синусов

Решение теорем о треугольниках

AAA is Angle, Angle, Angle

Указание трех углов треугольника не однозначно определяет один треугольник. Таким образом, задание двух углов треугольника позволяет вычислить только третий угол.

Зная размеры двух углов треугольника, вы можете вычислить размер третьего угла. Сумма будет равна 180° или π радиан.

C = 180° — A — B (в градусах)

C = π — A — B (в радианах)

AAS — Угол, Угол, Сторона

Дан размер 2 углов и 1 стороны, противоположной по заданным углам можно вычислить размеры оставшегося 1 угла и 2 сторон.

используйте Правило суммы углов, чтобы найти другой угол, затем

Используйте закон синусов, чтобы решить для каждой из двух других сторон.

ASA is Angle, Side, Angle

Зная размер 2 углов и размер стороны, которая находится между этими 2 углами, вы можете рассчитать размеры оставшегося 1 угла и 2 сторон.

используйте правило суммы углов, чтобы найти другой угол, затем

используйте закон синусов, чтобы решить для каждой из двух других сторон.

ASS (или SSA) — это угол, сторона, сторона

Учитывая размер двух сторон (a и c, где a < c) и размер угла A, который не находится между этими двумя сторонами, вы можете рассчитать размеры оставшихся 1 стороны и 2 углов в зависимости от следующих условий.

Для A ≥ 90° (A ≥ π/2) :

Если a ≤ c нет возможных треугольников

Пример:

Если a > c существует 1 возможное решение

• используйте закон синусов для решения угла C
• используйте правило суммы углов, чтобы найти другой угол, B
• используйте закон синусов для решения последней стороны, b
• Пример:
  

Для A < 90° (A < π/2) :

Если a ≥ c существует 1 возможное решение

• используйте закон синусов для решения угла C
• используйте правило суммы углов, чтобы найти другой угол, B
• используйте закон синусов для решения последней стороны, b
• Пример:
  

Если a < c , у нас есть 3 возможных ситуации. «Если sin(A) < a/c , есть два возможных треугольника, удовлетворяющих заданным условиям. Если sin(A) = a/c , есть один возможный треугольник. Если sin(A) > a/c , возможных треугольников нет.» ^[1]

sin(A) < a/c , возможны два треугольника

найти 2 возможных значения третьей стороны b = c*cos(A) ± √[ a ² — c ² sin ² (A) ] ^[1]

для каждого набор решений, используйте закон косинусов, чтобы решить для каждого из двух других углов

представить 2 полных решения

Пример:

sin(A) = a/c , есть один возможный треугольник

Используйте закон синусов для нахождения угла C

используйте правило суммы углов, чтобы найти другой угол, B

используйте закон синусов, чтобы найти последнюю сторону, b

Пример:

sin(A) > a/c , возможных треугольников нет

Уведомление об ошибке: sin(A) > a/c, поэтому нет ни решений, ни треугольника!

Пример:

SAS — это Side, Angle, Side

Зная размер двух сторон (c и a) и размер угла B между этими двумя сторонами, вы можете рассчитать размеры оставшихся 1 стороны и 2 углов. .

используйте закон косинусов, чтобы найти оставшуюся сторону, b

определите, какая сторона, a или c, наименьшая, и используйте закон синусов, чтобы найти размер противоположного угла, A или C соответственно. ^[2]

используйте правило суммы углов, чтобы найти последний угол .

Используйте закон косинусов, чтобы найти углы. Вы также можете использовать правило суммы углов, чтобы найти окончательный угол, когда вы знаете 2 из них.

Сумма углов треугольника

В градусах A + B + C = 180°

В радианах A + B + C = π треугольника, противоположного углам А, В и С соответственно; тогда закон синусов гласит:

a/sin A = b/sin B = c/sin C

Решение, например, для угла, A = sin ^-1 [ a*sin(B) / b ]

Закон косинусов

Если a, b и c — длины катетов треугольника, противоположных углам A, B и C соответственно; тогда закон косинусов гласит:

a ² = c ² + b ² — 2bc cos A, решение для cos A,   cos A = ( b ² + c ² — a ²

b ² = a ² + c ² — 2ca cos B, решение для cos B,   cos B = (c ² + a ² — b ²

c ² = b ² + a ² — 2ab cos C,   решение для cos C,   cos C = ( a ² + б ² — в ² ) / 2аб

Решение, например, для угла, A = cos ^-1 [ ( b ² + c ² — a ² ) / 2bc ]

Другие характеристики треугольника

Периметр треугольника, P = a + b + c

Полупериметр треугольника, s = 0,5 * (a + b + c)

Площадь треугольника, K = √[ s*(s-a)* (s-b)*(s-c)]

Радиус вписанной окружности в треугольник, r = √[ (s-a)*(s-b)*(s-c) / s ]

Радиус описанной окружности вокруг треугольника, R = (abc) / (4K)

Ссылки/дополнительная литература

[1] Вайсштейн, Эрик В.