Калькулятор умножение десятичных дробей онлайн: Онлайн калькулятор. Умножение столбиком

Перевести бесконечную периодическую дробь в обыкновенную дробь. Онлайн калькулятор.

С помощью нашего калькулятора вы сможете перевести бесконечную периодическую десятичную дробь перевести в обыкновенную дробь или смешанное число с подробным пошаговым решением.

Определение периодической дроби

Периодическая дробь — это бесконечная десятичная дробь в записи которой с определённого места бесконечно повторяется определённая группа цифр. Например 2.2(3), 0.(7). Цифры в скобках называются периодом дроби.

Виды периодических дробей

Чистая периодическая десятичная дробь — это дробь в записи которой после точки сразу идёт периодическая часть. Например 1.(5), 0.(14), 12.(3).

Смешанная периодическая десятичная дробь — это дробь в записи которой между точкой и периодической частью присутствует одна или более цифр. Например 4.14(3), 0.51(34).

Как перевести периодическую дробь в обыкновенную

Алгоритм зависит от вида периодической дроби, чистая или смешанная дробь.

Алгоритм перевода чистой периодической дроби в обыкновенную

С алгоритмом перевода лучше разбираться на примере, переведём периодическую чистую дробь 0.(23) в обыкновенную.

• 1) Нужно обозначить дробь за x. x = 0.(23)
• 2) Затем равенство умножить на такое число, чтобы период стал целым числом. Т.е. в данном случае на 100. 100x = 23.(23)
• 3) Вычтем исходное равенство из полученного. 100x-x=23.(23)-0.(23), 99x=23
• 4) Вычислить x. x=23/99

Алгоритм перевода смешанной периодической дроби в обыкновенную

С алгоритмом перевода лучше разбираться на примере, переведём периодическую смешанную дробь 0.9(6) в обыкновенную.

• 1) Нужно обозначить дробь за x. x = 0.9(6)
• 2) Затем равенство умножить на такое число, чтобы период стал целым числом. Т.е. в данном случае на 100. 100x = 96.(6)
• 3) Затем равенство умножить на такое число, чтобы числа до периода оказались в целой части. Т.е. в данном случае на 10. 10x = 9.(6)
• 4) Вычтем равенства. 100x-10x=96.(6)-9.(6), 90x=87
• 5) Вычислить x. x=87/90=29/30

Пример перевода бесконечной периодической десятичной дроби в обыкновенную дробь

Переведём дробь 0.5(3)

• 1) Обозначим дробь за x. x = 0.5(3)
• 2) Затем равенство умножить на такое число, чтобы период стал целым числом. Т.е. в данном случае на 100. 100x = 53.(3)
• 3) Затем равенство умножить на такое число, чтобы числа до периода оказались в целой части. Т.е. в данном случае на 10. 10x = 5.(3)
• 4) Вычтем равенства. 100x-10x=53.(3)-5.(3), 90x=48
• 5) Вычислить x. x=48/90=8/15

Переведём дробь 0.(1)

• 1) Обозначим дробь за x. x = 0.(1)
• 2) Затем равенство умножить на такое число, чтобы период стал целым числом. Т.е. в данном случае на 10. 10x = 1.(1)
• 3) Вычтем равенства. 10x-x=1.(1)-0.(1), 9x=1
• 4) Вычислить x. x=1/9

Перевести бесконечную периодическую десятичную дробь 2.7(013) в обыкновенную дробь
Перевести бесконечную периодическую десятичную дробь 25.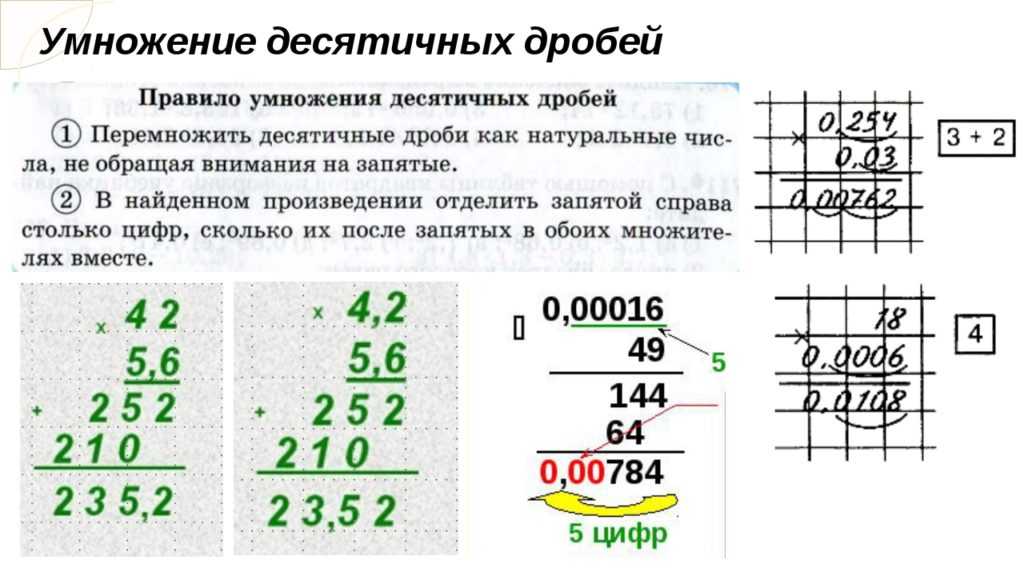 0(10) в обыкновенную дробь
Перевести бесконечную периодическую десятичную дробь 6.(7) в обыкновенную дробь
Перевести бесконечную периодическую десятичную дробь 12.(04) в обыкновенную дробь
Перевести бесконечную периодическую десятичную дробь 4.(13) в обыкновенную дробь

Похожие калькуляторы

Перевести десятичную дробь в обыкновенную

Привести дробь к новому знаменателю

Деление дробей

Умножение дробей

Преобразовать смешанную дробь в неправильную дробь

Преобразовать неправильная дробь в смешанную дробь

Сравнение дробей

Сложение дробей

Вычитание дробей

Приведение дробей к наименьшему общему знаменателю

Сократить дробь

Двоичный калькулятор онлайн

Если вам необходимо произвести математические операции над двоичными числами воспользуйтесь нашим двоичным онлайн калькулятором:

+−×÷ANDORXOR =

Просто введите целые двоичные числа, выберите операцию и получите результат.

Данный калькулятор может производить следующие действия над двоичными числами:

• сложение +
• вычитание −
• умножение ×
• деление ÷
• логическое И (AND)
• логическое ИЛИ (OR)
• исключающее ИЛИ (XOR)

Сложение двоичных чисел

Сложение двух двоичных чисел производится столбиком поразрядно. Начиная с младшего разряда (справа на лево), как и при сложении столбиком десятичных чисел. Но так как цифр всего две (0 и 1), их сложение происходит по следующим правилам:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 10

Пример

Для примера сложим 1011 и 101:

+		1	0	1	1
			1	0	1
	1	0	0	0	0

1011₂ + 101₂ = 10000₂

(11₁₀ + 5₁₀ = 16₁₀)

Вычитание двоичных чисел

Вычитание двоичных чисел производится аналогично сложению – столбиком, но по следующим правилам:

0 – 0 = 0

1 – 0 = 1

1 – 1 = 0

10 – 1 = 1

Пример

Для примера вычтем из числа 1011 число 101:

−	1	0	1	1
		1	0	1
		1	1	0

1011₂ − 101₂ = 110₂

(11₁₀ − 5₁₀ = 6₁₀)

Умножение двоичных чисел

Умножение двоичных чисел производится в столбик аналогично умножению в десятичной системе, но по следующим правилам:

0 × 0 = 0

0 × 1 = 0

1 × 0 = 0

1 × 1 = 1

Пример

Для примера перемножим числа 1011 и 101:

×			1	0	1	1
				1	0	1
+			1	0	1	1
		0	0	0	0
	1	0	1	1
	1	1	0	1	1	1

1011₂ × 101₂ = 110111₂

(11₁₀ × 5₁₀ = 55₁₀)

Деление двоичных чисел

Внешне деление двоичных чисел похоже на деление десятичных чисел, но тут есть свои нюансы: такое деление производится вычитанием делителя со сдвигом вправо, если остаток больше нуля. Чтобы понять этот процесс рассмотрим пример:

Пример

Для примера разделим число 11110 на 110:

11110₂ ÷ 110₂ = 101₂

(30₁₀ ÷ 6₁₀ = 5₁₀)

См. также

Десятичный калькулятор

Десятичный калькулятор с шагами выполняет основные математические операции с числами, в частности, с десятичными числами.

Формула и отображение пошаговых расчетов позволяют пользователю понять, как был рассчитан ответ, доказывая, что это надежный инструмент.

От базовых функций, таких как сложение и умножение, до небольших сложных операций, таких как логарифмирование десятичных чисел, этот калькулятор может выполнять все.

Как пользоваться этим инструментом?

Простой и понятный интерфейс делает его удобным в использовании. Вам нужно будет:

1. Введите десятичные числа.
2. Выберите операцию.
3. Нажмите кнопку Вычислить .

Давайте узнаем больше о десятичных числах.

Что такое десятичные числа?

Десятичные числа представляют собой смесь дробей и целых чисел. Целая часть числа отделяется от дроби десятичной точкой.

Пример десятичного числа 98,9 . 98 слева — это целое число. Затем идет десятичная точка, а в конце цифра 9 для дроби, которая на самом деле означает 9/10.

Вы можете преобразовать любую дробь в десятичную, используя калькулятор дроби в десятичную дробь.

Арифметические операции с десятичными числами

Для арифметических операций, таких как деление или вычитание, используйте калькулятор выше. Вы получите не только результат, но и шаги, которые могут быть очень полезны пользователям, которые хотят больше узнать о десятичных числах.

Оставайтесь с нами, чтобы учиться на примерах.

Как складывать или вычитать десятичные числа?

Техника сложения и вычитания десятичных чисел проста. Воспользуйтесь калькулятором, шучу????. Просто сложите целые числа с целыми числами и дробную часть с другой дробной частью.

Пример:

Добавьте следующие числа: 561,1 и 234,9 .

Решение:

Шаг 1: Напишите числа друг над другом.

    5 6 1 . 1

+ 2 3 4 . 9

__________

Шаг 2: Сложите числа.

    5 6 1 . 1

+ 2 3 4 . 9

__________

     7 9 6 . 0

Пример вычитания с использованием одних и тех же чисел.

После написания чисел начните вычитать. Возьмите один перенос слева направо. 1 справа станет 11. 

  5 6 1 . 1

— 2 3 4 . 9

__________

   3 2 6 . 2

Как делить или умножать десятичные числа?

Методы умножения или деления десятичных дробей немного отличаются от целых чисел. При умножении единственная разница заключается в размещении десятичной точки.

Для ясности см. следующий пример.

Пример:

Умножить 67,3 на 7,1 .

Решение:

Шаг 1: Умножьте числа.

6 7 . 3

х 7 . 1

_________

     6 7 3

4 7 1 1 x

_________
4 7 7 8 3

такое же количество цифр справа.

Есть 2 цифры, поэтому точка будет помещена после 2 цифр справа, например 477,83 .

При делении десятичных чисел нужно смотреть, является ли делитель целым числом или нет. Чтобы выполнить деление, это должно быть целое число.

Пример:

Разделить 5,76 на 0,3 .

Решение:

Шаг 1: Преобразовать десятичное число в целое.

Если мы хотим изменить делитель, те же изменения будут применены к делимому.

Умножьте оба значения на 10. 

5,76 x 10 = 57,6 , 0,3 x 10 = 3

Шаг 2: Теперь разделите.

Отсюда; 5,76/0,3 = 19,2

Это были основные четыре операции. Надеюсь это поможет.

Калькулятор длинного умножения — Как умножать десятичные числа

Умножьте два числа самостоятельно с помощью этого бесплатного калькулятора длинного умножения с шагами. Поэтому, если вы запутались в проблеме с длинным продуктом, следующее чтение — единственное возможное решение, чтобы понять это.

Сосредоточься!

Что такое длинное умножение?

В контексте арифметики:

«Произведение большого числа (множимое) на другое большое число (множитель) называется длинным умножением»

Как сделать длинное умножение?

Выполнение длинного умножения вручную фактически позволяет найти конечный продукт больших чисел. Алгоритм включает в себя следующие шаги:

• Перейдите к расположению разрядных значений в столбцах так, чтобы числа точно располагались друг над другом. Традиционная практика предполагает установку чисел с большим количеством цифр в верхней позиции

Примечание: Верхнее число называется множимым, а нижнее — множителем.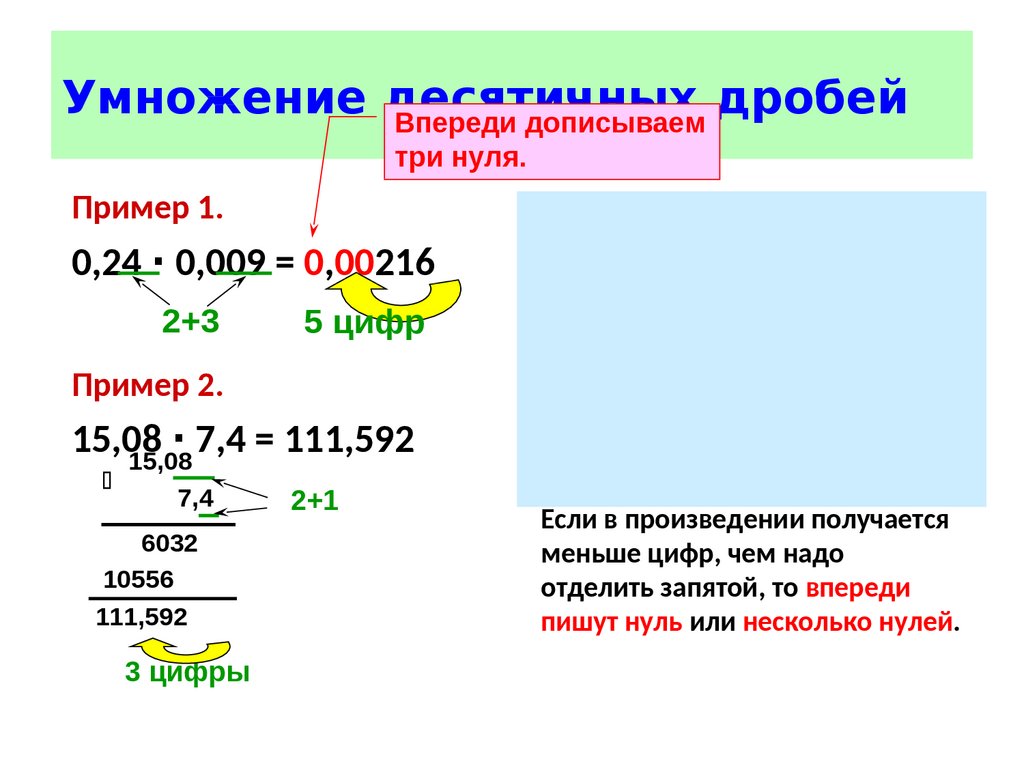

• Теперь пришло время запустить продукт. Просто умножьте число единиц в множителе на число единиц в множимом
  . Как только вы закончите с этим, напишите ответ под строкой. Имейте в виду, что если номер ответа представляет собой значение разряда десятков, запишите число единиц ниже и примите значение разряда десятков как перенос
.
• Проделайте тот же процесс справа налево и умножьте первое число множителя на все цифры множимого, одну за другой
• Когда вы закончите с единицами, пришло время перейти к разряду десятков в множителе. Теперь повторите тот же процесс до тех пор, пока вы не закончите умножение самой правой цифры множителя на все цифры множимого
.
• Теперь, когда вы закончите продукт, сделайте строку ниже и просто добавьте все столбцы один за другим, начиная справа налево. Помните, что это обычное сложение, которое вы также можете выполнить с помощью бесплатного калькулятора длинных сложений 9.0014

Кроме того, вы можете позволить этому длинному калькулятору умножения с десятичными дробями выполнять мгновенные вычисления для любой комбинации множимого и множителя.

Как умножать десятичные дроби?

Длинное умножение с десятичными знаками включает еще несколько правил, перечисленных ниже:

• Множитель и множитель содержат десятичные цифры. Теперь вам нужно посчитать десятичные разряды обоих этих чисел и посчитать их сумму
.
• После этого запишите числа без цифр и найдите их произведение так же, как мы обсуждали для целых чисел
• В конце, когда вы получите окончательный ответ, вспомните количество знаков после запятой, начните считать справа налево и остановитесь на числе, на котором счет заканчивается. Это то место, где вы должны поставить десятичную точку.

Здесь для мгновенных и точных вычислений у вас нет другого выбора, кроме этого бесплатного калькулятора умножения десятичных дробей.

Как долго умножать?

Лучший способ определить возрастание чисел — правильно использовать этот пошаговый калькулятор умножения с десятичными дробями. Но что касается полного понимания концепции, вы должны выполнить следующие ручные вычисления:

Пример № 01:

Решите следующую задачу на длинное умножение:

7633 x 65

Решение:

Переноска 2				3	1	1
Переноска 1				3	1	1
				7	6	3	3
х						6	5
+			3	8	1	6	5
+		4	5	7	9	8	х
=		4	9	6	1	4	5

Пример № 02:

Умножение в длину с десятичными дробями:

22,3 x 2,5

Решение:

Нести 2
Переноска 1			1	1
			2	2	3
х				2	5
+		1	1	1	5
+		4	4	6	х
=		5	5	7	5

Поскольку число 5575, а количество знаков после запятой равно 2, то окончательный ответ будет следующим:

55,75.

Например, этот бесплатный калькулятор частичных произведений позволит вам узнать, как умножать десятичные дроби без частичных произведений.

Как долго работает калькулятор умножения?

Приступайте к изучению того, как с помощью этого калькулятора умножения можно получить мгновенные произведения коротких и длинных целых чисел или десятичных дробей. Оставайтесь с ним!

Ввод:

• Введите множимое и множитель в соответствующие поля
• Теперь нажмите кнопку расчета

Вывод:

Бесплатный калькулятор умножения легко находит произведение двух целых или десятичных чисел

Часто задаваемые вопросы:

Кто изобрел длинное умножение?

Вавилоняне на самом деле изобрели умножение, и недавно математика в совершенстве овладела этой концепцией. И чтобы свести на нет любые ошибки в расчетах произведения, мы разработали этот бесплатный калькулятор длинного умножения с шагами.

No related posts.