Извлечение квадратных корней без калькулятора
Городская научно-практическая конференция школьников
«Интеллектуал»
Секция МАТЕМАТИКИ
«Извлечение квадратных корней без калькулятора»
Автор работы:
Каширина Елизавета Сергеевна
8 Б класс
МАОУ «СОШ № 93»
Руководитель:
Мартынюк Татьяна Владимировна,
учитель математики МАОУ «СОШ № 93»
г. Кемерово
2018 г.
Оглавление
Введение ……………………………………………………………………………… 2
Глава 1. Способ разложения на простые множители …………………………….….4
Глава 2. Способ использования таблицы квадратов двузначных чисел …….
.. ….5
Глава 3. Формула Древнего Вавилона ……………………………………………… ..6
Глава 4. Через решение уравнения ……………………………………………………7
Глава 5. Деление на пары через составление ребуса …………………….……………8
Глава 6. Геометрический метод ……………………………………………….…….12
Глава 7. Графический метод ………………………………………….………..……..13
Глава 8. Канадский метод ………………………………………………..…..………14
Глава 9.Метод вычетов нечетного числа ……………………………………………14
Глава 10.Другие методы …………………………………………………………………………………..15
Заключение …………………………………………………………………………….16
Список литературы ……………………………………….…………….…..…………17
Приложение 1…………………………………………………………………………..18
Введение
При изучении темы квадратных корней на уроках алгебры часто приходилось использовать таблицу квадратов и калькулятор. Извлекать квадратные корни приходилось и на уроках геометрии при изучении теоремы Пифагора, и при решении текстовых задач, в которых нужно было найти корни квадратного уравнения с большим дискриминантом.
Но не всегда под рукой был калькулятор и таблица квадратов. Уже тогда возникал вопрос, как же быть в тех случаях, когда на экзаменах ГИА и ЕГЭ использовать калькулятор запрещено. Кроме того таблица квадратов целых чисел не даёт ответ на такие вопросы, как, например, чему равен , , и др. даже приблизительно.
Все знают, что извлечь квадратный корень без калькулятора — это непосильная задача. В лучшем случае, в ситуации, когда решение задач требует извлечения корня, а калькулятора нет под рукой, прибегают к методу подбора и пытаются вспомнить данные из таблицы квадратов целых чисел, но это не всегда спасает. Сколько раз все попадали в подобные ситуации?
Как-то на уроке при изучении темы квадратных корней учительница математики показала, как в столбик можно извлекать квадратные корни. Вычислить корень можно с произвольной точностью, найти сколько угодно цифр в его десятичной записи, даже если он получается иррациональным. Алгоритм плохо запомнился, остались вопросы.
Я решила разобраться в этом приеме извлечения квадратного корня, стала работать над этим вопросом. Также я узнала, что извлекать корни люди научились задолго до изобретения «умной» техники, что существуют и другие способы извлечения квадратного корня. Мои вопросы и легли в основу исследования, которое для меня стало маленьким открытием. Исследуя эту тему, я нашла не один, а несколько способов решения данной проблемы.
Актуальность исследования обусловлена желанием углублить математические знания путем изучения простейших способов извлечения квадратных корней без калькулятора, распространить алгоритмы извлечения корней среди учащихся, что особенно актуально при сдаче экзаменов, где запрещено пользоваться калькулятором, а также использовать эти знания при работе с вычислениями корней на уроках математики в ситуациях отсутствия калькулятора.
Цель работы: изучить способы извлечения квадратных корней без калькулятора и отобрать самые рациональные для практического применения.
Задачи:
- Изучить всю найденную литературу по данному вопросу, научные статьи, исторические справки и работы современных учёных и исследователей.
- Рассмотреть найденные способы и описать их алгоритм.
- Познакомить с результатами полученных исследований одноклассников и друзей.
Гипотеза: Существует не менее двух-трёх способов извлечения квадратных корней без калькулятора.
Предмет исследования: извлечение квадратных корней без калькулятора.
Объект исследования: способы извлечения квадратных корней без калькулятора.
Глава 1. Способ разложения на простые множители
Для извлечения квадратного корня можно разложить число на простые множители и извлечь квадратный корень из произведения.
Этим способ принято использовать при решении заданий, связанных с извлечением квадратных корней, в школе.
Пример 1:
11025│5
2205│5
441│3
147│3
49│7
7│7
= = 3∙5∙7 = 105
Пример 2:
213444│2
106722│2
53361│3
17787│3
5929│11
539│11
49│7
7│7
= = 2∙3∙7∙11 = 462;
Многие применяют его успешно и считают единственным.
Извлечение корня разложением на множители довольно трудоёмкая задача, которая тоже не всегда приводит к желаемому результату. Попробуйте извлечь квадратный корень из числа 820836. Разложение на простые множители дает произведение 2∙2∙3∙3∙22801. А как быть дальше? С этой задачей сталкиваются все, и спокойно в ответе записывают остаток от разложения под знак корня. Методом проб и ошибок, подбором разложение, конечно, можно выполнить, если быть уверенным в том, что получится красивый ответ, но практика показывает, что очень редко предлагаются задания с полным разложением. Чаще бывает так, что корень до конца не извлечь.
Поэтому, этот способ лишь частично решает проблему извлечения квадратного корня без калькулятора.
Глава 2. Способ с применением таблицы квадратов
двузначных чисел
С этим способом мы познакомились на уроках математики. Способ очень прост в применении и даёт мгновенное извлечение квадратного корня из любых целых чисел от 1 до 100 с точностью до десятых без калькулятора.
Но для этого метода требуется наличие таблицы квадратов натуральных чисел от 10 до 99. (Она есть во всех учебниках алгебры 8 класса, и на экзамене ГИА предлагается в качестве справочного материала).
Откройте таблицу и проверьте скорость нахождения ответа. Но при использовании таблицы квадратов для извлечения квадратного корня нужно не перепутать, что крайний левый столбик определяет цифру, стоящую в разряде целых, а самая верхняя строчка – это десятые в ответе. А дальше всё просто: закройте две последние цифры числа в таблице и найдите нужное вам, не превосходящее 100 подкоренное число, и далее действуйте по правилам этой таблицы.
Пример 1: Найдём значение .
Решение: Мысленно отбрасываем две последние цифры у всех чисел в таблице и находим 57 или близкие к 57-ти – такое число одно 5776. Левый столбик даёт ответ 7 (это целые), а верхняя строчка 6 (это десятые). Значит ≈ 7,6. Проверим на микрокалькуляторе ≈ 7,549834.
Пример 2: Найдём значение .
Решение: Мысленно поставим запятые, отсчитав две последние цифры, у всех чисел в таблице и находим близкие для 89 – таких только два 88,36 и 90,25. Но 90,25 – это много, 88,36 ближе к 89. Значит, выбираем 8836.
Левый столбик даёт ответ 9 (это целые), а верхняя строчка 4 (это десятые). Значит ≈ 9,4. Проверим на микрокалькуляторе ≈ 9,43398113.
Быстро, просто, доступно на экзамене. Но сразу понятно, что корни, большие 100 мы уже этим способом извлечь не сможем. Способ удобен для заданий с маленькими корнями и при наличии таблицы.
Глава 3. Формула Древнего Вавилона
Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня из числа n.
Число n они представляли в виде суммы а2 + b, где а2 ближайший к числу n точный квадрат натурального числа а и пользовались формулой:
Извлечём с помощью этой древней формулы корень квадратный из числа 40:
Глава 4.
Через решение уравнения
На самом деле существует удобный способ нахождения квадратного корня «вручную» через решение уравнения, ведь математика — наука с многовековой историей, а калькуляторы были не всегда. Способ этот дает возможность вычислить значение корня с точностью до одного — двух знаков после запятой, а, при желании, достичь и большей точности. Звучит невероятно, но попробуйте испытать этот способ при вычислении квадратного корня.
Суть этого способа рассмотрим на примере и попробуем вычислить значение .
Сначала определим границы искомого корня в целых числах. Легко догадаться, что это числа 16 = 4² и 25 = 5²,
поэтому и .
Пусть х – это та разница, на которую отличны друг от друга и ,
следовательно = 4 + х.
Возведем в квадрат обе части полученного уравнения и раскроем скобки при помощи формулы суммы квадрата:
( ) ² = (4 + х)² ; 20 = (4 + х)² ; 20 = 16 + 8х + х².
Так как мы рассчитываем получить результат с точностью до десятых или до сотых, а х² явно достаточно малая дробь, то ей вполне можно пренебречь.
В результате приходим к простому линейному уравнению
20 = 16 + 8х.
Решив его, получаем значение х = 0,5.
Значит ≈ 4 + 0,5 ≈ 4,5 .
На самом деле, при расчете на калькуляторе, значение этого корня равно 4,47213595, то есть погрешность при нашем расчете составила 0,02786405. Не правда ли, вполне приличная точность!
Но если все же решение задач по математике требует еще большей точности, то можно достичь ее тем же способом, просто продолжив вычисления с уже полученным значением корня. Так что подобный способ вычисления квадратного корня необычайно точен и удобен, а погрешность вычисления зависит исключительно от вашего терпения и упорства.
Но и этот способ требует терпения и умения решать уравнения с использованием формул сокращённого умножения.
Глава 5. Извлечение квадратного корня в столбик
(деление на пары через составление ребуса)
Пример 1: Найдём значение .
1. Разбиваем число на пары справа налево:
5`54`13`16
2. Извлекаем квадратный корень из первой группы цифр слева — в нашем случае это 5 (ясно, что точно корень может не извлекаться, берем число, квадрат которого максимально близок к нашему числу, образованному первой группой цифр, но не превосходит его). В нашем случае это будет число 2. Записываем 2 в ответ — это старшая цифра корня.Так мы получаем первую цифру числа, которое является значением квадратного корня.
3. Возводим число, которое стоит уже в ответе ( это 2 ) в квадрат и вычитаем из первой слева группы цифр, т. е. из числа 5.
4. Находим разность первой группы и квадрата первой цифры (5 4 = 1).
4
1
5.Сносим следующие две цифры, т.е. приписываем справа следующую группу из двух цифр (54), получили число 154:
4
154
6. Удваиваем первую, найденную нами цифру (т. е. 2), записываем слева от
4 (2∙2 = 4):
4 4
154
7. Далее необходимо найти вторую цифру. Нам нужно к числу 4 справа приписать одну цифру (обозначим a), и число 4a умножить на a ( удвоенная первая цифра, найденная нами, становится цифрой десятков числа), то есть на ту же самую приписанную цифру. Результат должен быть как можно ближе к 154, но опять-таки не больше этого числа.
4a 4
a 154
В нашем случае это будет цифра 3 (так как 43∙ 3 = 129).
, ее записываем в ответ после 2. Это следующая цифра в десятичной записи нашего числа, которое является значением квадратного корня.
Число 129 подписываем под числом 154:
43 4
3 154
129 129
8. Находим разность (154 – 129 = 25).
9. Сносим следующую группу (получаем число 2513):
43 4
3 154
129 129
2513
10. Удваиваем число 23, получаем 46, записываем слева от 129:
43 4
3 154
129 46 129
2513
11.
Теперь необходимо найти третью цифру: 46 десятков в числе, при умножении которого на число единиц(обозначено буквой a), мы должны получить число меньшее 2513
43 4
3 154
129 46a 129
a 2513
(это цифра 5, так как 465∙5=2325).
5 третья цифра числа, которое является значением квадратного корня. Далее процесс повторяется. 12.Число 2325 подписываем под числом 2513:
43 4
3 154
129 465 129
5 2513
2325 2325
13.Находим разность (2513 – 2325 = 188).
14. Сносим следующую группу (получаем число 18816):
43 4
3 154
129 465 129
5 2513
2325 2325
18816
15. Удваиваем число 235, получаем 470, записываем слева от 2325:
43 4
3 154
129 465 129
5 2513
2325 470 2325
18816
16. Теперь необходимо найти четвёртую цифру: 470 десятков в числе, при умножении которого на число единиц(обозначено буквой a), мы должны получить число меньшее 18816 (или равное ему в случае, если –целое число, так как мы снесли последнюю группу чисел):
43 4
3 154
129 465 129
5 2513
2325 470a 2325
a 18816
(это цифра 4, так как 4704∙4 = 18816).
4 четвёртая цифра числа, которое является значением квадратного корня. 17.Число 18816 подписываем под числом 18816 и вычитаем:
43 4
3 154
129 465 129
5 2513
2325 4704 2325
4 18816
18816 18816
Этим же способом можно извлечь квадратный корень и из десятичной дроби. В случае десятичной дроби разбиваем его цифры на пары следующим образом: те, что стоят слева от десятичной запятой, группируем по две справа налево, а те, что правее – по две слева направо. Далее применяем этот же алгоритм, поставив в соответствующем месте запятую.
Способ почти универсальный, так как применим к любым числам, но составление ребуса (угадывание цифры на конце числа) требует логики и хороших вычислительных навыков столбиком.
Он трудоёмкий, но очень точный.
Глава 6. Геометрический метод
(с использованием циркуля и измерительной линейки с прямым углом или угольника)
Прежде всего стоит заметить, что использование этого метода обещает значительные погрешности, которые могут зависеть и от чистоты построения чертежей, и от точности измерительных инструментов.
Этот метод предполагает знание двух теорем геометрии :
а) Нахождение высоты прямоугольного треугольника, опущенной из прямого угла ( h =)
б) Свойство вписанного угла, опирающегося на диаметр окружности ∠АВС= 90º
А подробнее это можно описать так: Положите перед собой чистый лист, циркуль и карандаш с линейкой. Попробуем геометрическим способом извлечь квадратный корень числа 7. Работаем в сантиметрах.
Начертим отрезок АС = АН + НС, то есть АС = 1+ 7 = 8(см)
Найдём середину АС – точку О (АО = ОС) и при помощи циркуля построим окружность с центром О и радиусом ОС и отметим точку Н на отрезке АС так, что АН = 1 см , построим перпендикуляр НВ в точке Н к отрезку АС.
Измерим длину полученного отрезка ВН. Получили 2 см и 6 мм.
Этот результат и будет примерно равен .
Вывод: геометрическим способом нашли результат ≈ 2,6
Минусы этого способа сразу понятны: неточность в измерениях и построении, однако его можно применять в ситуациях недоступности калькулятора и отсутствия клеточной бумаги, что тоже иногда может спасти ситуацию.
Глава 7. Графический метод.
Графический метод извлечения квадратных корней наш учитель математики предлагает использовать для маленьких чисел, когда под рукой нет таблицы квадратов. Он полностью основан на графическом решении уравнения b= х², полученном из = х путём возведения в квадрат первого. С алгоритмом решения этого уравнения знаком каждый школьник: Построим на клеточной бумаге в одной системе координат два графика функций у = b и у = х². Найдём точку пересечения в первой четверти системы координат. Абсцисса этой точки и будет соответствовать значению квадратного корня из числа b.
Какие же неудобства и трудности испытывают при применении такого способа решения данной проблемы:
1)предварительная подготовка – построение графика параболы;
2) ограничение размером тетрадного листа (о чём сразу предупреждали), поэтому невозможно извлечение чисел, больших 40, так как длина тетрадного листа 40 клеток;
3) неточность в построении кривых линий и получение больших погрешностей, в отличие от других методов.
Глава 8. Канадский метод
Этот быстрый метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность : не более двух – трёх знаков после запятой. Вот их формула:
= + , где X — число, из которого необходимо извлечь квадратный корень, а S — число ближайшего точного квадрата.
Давайте попробуем извлечь квадратный корень из 75
X = 75, S = 81. Это означает, что = 9.
Просчитаем по этой формуле :
= 9 + = 9 – = 9 – 0,333 = 8,667
При детальном изучении этого метода легко можно доказать его сходство с вавилонским и поспорить за авторские права изобретения этой формулы, если такие есть в действительности.
Метод несложный и удобный.
Глава 9. Метод вычетов нечётного числа
Этот способ предлагает преподаватель математики одной из школ Вашингтона миссис Бруксбанк своим ученикам. Он заключается в том, чтобы последовательно вычитать нечётные числа 1,3,5,7 и т.д. пока не дойдете до нуля, а затем подсчитать число вычитаний. Это и будет ответ.
Например, чтобы получить квадратный корень из 36 и 121 это:
36 – 1 = 35 – 3 = 32 – 5 = 27 – 7 = 20 – 9 = 11 – 11 = 0
Общее количество вычитаний = 6, поэтому = 6.
121 – 1 = 120 – 3 = 117 – 5 = 112 – 7 = 105 – 9 = 96 – 11 = 85 – 13 =
=72 – 15 = 57 – 17 = 40 – 19 = 21 – 21 = 0
Общее количество вычитаний = 11, поэтому = 11.
Российские учёные называют этот метод арифметическим извлечением квадратного корня, а за глаза «методом черепахи» из-за его медлительности.
Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее.
В то же время такой способ вполне доступен детям, решающим простейшие математические задачи, требующие извлечения квадратного корня. Попробуйте извлечь квадратный корень из числа, например, 5963364 этим способом и вы поймёте, что он «работает», безусловно, без погрешностей для точных корней, но очень длинный в решении.
Глава 10. Другие методы
В ходе моего исследования я отыскала ещё несколько способов решения моей проблемы. Это метод степенных рядов высших степеней и метод определения путём составления таблицы. Изучив эти алгоритмы, я оценила их сложность и в некоторых местах непонимание, поэтому не стала глубоко изучать эти методы, понимая, что это уровень высшей математики или даже научной диссертации.
Если метод степенных рядов сложен в вычислении и запоминании огромной формулы, то метод таблицы так запутан, что его сложно даже пересказать, а тем более овладеть для практики.
Заключение
Во время работы я нашла не один, а нескольких способов извлечения квадратных корней.
В ходе исследования было выявлено, что современной науке известно много таких способов, начиная со способа математиков Древнего Вавилона и заканчивая способом степенных рядов сложных степеней из разделов высшей математики. Мною были изучены, описаны и отработаны на практике 9 способов. Работа по данной теме меня так увлекла, что я решила продолжить свои исследования уже за рамками своего проекта. В учебнике алгебры автор знакомит восьмиклассников с корнями третьей степени и других степеней, предлагая подождать с их изучением до 11 класса. Но мне стало очень интересно узнать и про эту новую для меня тему в математике. И в продолжение моего исследования я хочу разобрать те способы, которые пока мне сложно разобрать, и выяснить, существуют ли способы извлечения корня третьей степени без калькулятора.
Таким образом, хочу подвести итог проделанной работы и сделать вывод. На основании результатов данного исследования доказано, что науке известно много способов извлечения квадратного корня без калькулятора.
У всех способов различные алгоритмы и степень сложности вычислений, но не один из них не входит в школьный курс, так как относится к разделу высшей или прикладной математики. В ходе исследования были отработаны 9 способов, а их практическое применение доказало все недостатки и преимущества каждого из методов.
В ходе работы было доказано на практике, что умение извлекать корни без калькулятора не только полезно и актуально, но и очень увлекательно.
Список использованной литературы и сайты Интернета:
- Мордкович А.Г. Алгебра, 8 класс, учебник — Москва, Мнемозина, 2005г
- Пичугин Л.Ф. За страницами учебника алгебры. Книга для учащихся 7- 9 классов средней школы. – Москва, Просвещение, 1990 г.
- Ткачева М.В. Домашняя математика. Книга для учащихся 8 класса учебных заведений. – Москва, Просвещение, 1994г.
- http://festival.1september.ru
- http://ru.wikipedia.ord /wiki /teorema/
Приложение 1
Этот способ нахождения хорошо известен как российским учёным, так и зарубежной общественности.
Убедиться в этом легко, зайдя на любой научный или образовательный форум. Ссылки на этот способ почти во всех комментариях студентов и школьников. О нём пишут учёные и исследователи СНГ, Канады, Великобритании и Америки. Я разобрала несколько десятков примеров по этому способу, поэтому недостатка материала в изучении не испытывала. Предлагаю несколько примеров:
Извлечь квадратный корень 3. Кубический корень (извлечение без калькулятора)
До появления калькуляторов студенты и преподаватели вычисляли квадратные корни вручную. Существует несколько способов вычисления квадратного корня числа вручную. Некоторые из них предлагают только приблизительное решение, другие дают точный ответ.
Шаги
Разложение на простые множители
Разложите подкоренное число на множители, которые являются квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа – числа, из которых можно извлечь целый квадратный корень.
Множители – числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как √25 = 5, √36 = 6, √49 = 7. Квадратные множители – это множители, которые являются квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
- Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 – это квадратное число. Разделив 400 на 25, вы получите 16. Число 16 также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
- Записать это можно следующим образом: √400 = √(25 х 16).
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть √(а х b) = √a x √b.
Воспользуйтесь этим правилом и извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
- В нашем примере извлеките корень из 25 и из 16.
- √(25 х 16)
- √25 х √16
- 5 х 4 = 20
Если подкоренное число не раскладывается на два квадратных множителя (а так происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
- Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
- = √(49 х 3)
- = √49 х √3
- = 7√3
Если нужно, оцените значение корня. Теперь можно оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу.
- Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
- Этот метод также работает с большими числами. Например, рассмотрим √35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (√25 = 5) и 36 (√36 = 6). Таким образом, значение √35 расположено между 5 и 6. Так как значение √35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что √35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.
Еще один способ – разложите подкоренное число на простые множители .
Простые множители – числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
- Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, √45 = √(3 х 3 х 5). 3 можно вынести за знак корня: √45 = 3√5. Теперь можно оценить √5.
- Рассмотрим другой пример: √88.
- = √(2 х 44)
- = √ (2 х 4 х 11)
- = √ (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
- = 2√(2 х 11) = 2√2 х √11. Теперь можно оценить √2 и √11 и найти приблизительный ответ.
Вычисление квадратного корня вручную
При помощи деления в столбик
Этот метод включает процесс, аналогичный делению в столбик, и дает точный ответ. Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию.
Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70».- Для примера вычислим квадратный корень числа 780,14. Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде «7 80, 14». Это нормально, что первая слева цифра является непарной цифрой. Ответ (корень из данного числа) будете записывать справа сверху.
- Для первой слева пары чисел (или одного числа) найдите наибольшее целое число n, квадрат которого меньше или равен рассматриваемой паре чисел (или одного числа).
Другими словами, найдите квадратное число, которое расположено ближе всего к первой слева паре чисел (или одному числу), но меньше ее, и извлеките квадратный корень из этого квадратного числа; вы получите число n. Напишите найденное n сверху справа, а квадрат n запишите снизу справа.
- В нашем случае, первым слева числом будет число 7. Далее, 4
Вычтите квадрат числа n, которое вы только что нашли, из первой слева пары чисел (или одного числа).
Результат вычисления запишите под вычитаемым (квадратом числа n).- В нашем примере вычтите 4 из 7 и получите 3.
Снесите вторую пару чисел и запишите ее около значения, полученного в предыдущем шаге.
Затем удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».- В нашем примере второй парой чисел является «80». Запишите «80» после 3. Затем, удвоенное число сверху справа дает 4. Запишите «4_×_=» снизу справа.
Заполните прочерки справа.
- В нашем случае, если вместо прочерков поставить число 8, то 48 х 8 = 384, что больше 380. Поэтому 8 — слишком большое число, а вот 7 подойдет. Напишите 7 вместо прочерков и получите: 47 х 7 = 329. Запишите 7 сверху справа — это вторая цифра в искомом квадратном корне числа 780,14.
Вычтите полученное число из текущего числа слева. Запишите результат из предыдущего шага под текущим числом слева, найдите разницу и запишите ее под вычитаемым.
- В нашем примере, вычтите 329 из 380, что равно 51.
Повторите шаг 4. Если сносимой парой чисел является дробная часть исходного числа, то поставьте разделитель (запятую) целой и дробной частей в искомом квадратном корне сверху справа. Слева снесите вниз следующую пару чисел. Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
- В нашем примере следующей сносимой парой чисел будет дробная часть числа 780.14, поэтому поставьте разделитель целой и дробной частей в искомом квадратном корне сверху справа. Снесите 14 и запишите снизу слева. Удвоенным числом сверху справа (27) будет 54, поэтому напишите «54_×_=» снизу справа.
Повторите шаги 5 и 6. Найдите такое наибольшее число на место прочерков справа (вместо прочерков нужно подставить одно и тоже число), чтобы результат умножения был меньше или равен текущему числу слева.
- В нашем примере 549 х 9 = 4941, что меньше текущего числа слева (5114).
- В нашем примере 549 х 9 = 4941, что меньше текущего числа слева (5114).
Если для квадратного корня вам необходимо найти больше знаков после запятой, напишите пару нулей у текущего числа слева и повторяйте шаги 4, 5 и 6. Повторяйте шаги, до тех пор пока не получите нужную вам точность ответа (число знаков после запятой).
Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70».
Результат вычисления запишите под вычитаемым (квадратом числа n).
Понимание процесса
Рассмотрим первую пару цифр Sa числа S (Sa = 7 в нашем примере) и найдем ее квадратный корень. В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен S a (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa
- Допустим, что нужно разделить 88962 на 7; здесь первый шаг будет аналогичным: рассматриваем первую цифру делимого числа 88962 (8) и подбираем такое наибольшее число, которое при умножении на 7 дает значение меньшее или равное 8. То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8
Мысленно представьте квадрат, площадь которого вам нужно вычислить. Вы ищите L, то есть длину стороны квадрата, площадь которого равна S.
A, B, C — цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.- Пусть (10A+B)² = L² = S = 100A² + 2×10A×B + B² . Запомните, что 10A+B — это такое число, у которого цифра B означает единицы, а цифра A — десятки. Например, если A=1 и B=2, то 10A+B равно числу 12.(10A+B)² — это площадь всего квадрата, 100A² — площадь большого внутреннего квадрата, B² — площадь малого внутреннего квадрата, 10A×B — площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
Для усвоения данного метода представьте число, квадратный корень которого необходимо найти, как площадь квадрата S. В этом случае вы будете искать длину стороны L такого квадрата. Вычисляем такое значение L, при котором L² = S.
Задайте букву для каждой цифры в ответе. Обозначим через A первую цифру в значении L (искомый квадратный корень). B будет второй цифрой, C — третьей и так далее.
Задайте букву для каждой пары первых цифр.
Обозначим через S a первую пару цифр в значении S, через S b — вторую пару цифр и так далее.Уясните связь данного метода с делением в столбик.
Как и в операции деления, где каждый раз нас интересует только одна следующая цифра делимого числа, при вычислении квадратного корня мы последовательно работаем с парой цифр (для получения одной следующей цифры в значении квадратного корня).
A, B, C — цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.Если под рукой есть калькулятор, извлечь кубический корень из любого числа не составит никаких проблем. Но если калькулятора нет или вы просто хотите произвести впечатление на окружающих, извлеките кубический корень вручную. Большинству людей описываемый здесь процесс покажется довольно сложным, но с практикой извлекать кубические корни станет намного легче.
Перед тем как приступить к чтению данной статьи, вспомните основные математические операции и вычисления с числами в кубе.
Шаги
Часть 1
Извлечение кубического корня на простом примере
Запишите задачу. Извлечение кубического корня вручную похоже на деление в столбик, но с некоторыми нюансами. Сначала запишите задачу в определенной форме.
- Запишите число, из которого нужно извлечь кубический корень. Число разбейте на группы по три цифры, причем отсчет начните с десятичной запятой. Например, нужно извлечь кубический корень из 10. Напишите это число так: 10, 000 000. Дополнительные нули призваны повысить точность результата.
- Возле и над числом нарисуйте знак корня. Представьте, что это горизонтальная и вертикальная линии, которые вы рисуете при делении в столбик. Единственное отличие – это форма двух знаков.
- Над горизонтальной линией поставьте десятичную запятую. Сделайте это непосредственно над десятичной запятой исходного числа. 2 = 1. Таким образом, первый множитель равен сумме следующих чисел: 1200 + 60 + 1 = 1261. Запишите это число слева от вертикальной черты.
2 = 1. Таким образом, первый множитель равен сумме следующих чисел: 1200 + 60 + 1 = 1261. Запишите это число слева от вертикальной черты.Умножьте и вычтите. Умножьте последнюю цифру ответа (в нашем примере это 1) на найденный множитель (1261): 1*1261 = 1261. Запишите это число под 2000 и вычтите его из 2000. Вы получите 739 (это второй остаток).
Подумайте, является ли полученный ответ достаточно точным. Делайте это каждый раз, после того как завершите очередное вычитание. После первого вычитания ответ был равен 2, что не является точным результатом. После второго вычитания ответ равен 2,1.
- Чтобы проверить точность ответа, возведите его в куб: 2,1*2,1*2,1 = 9,261.
- Если вы считаете, что ответ достаточно точный, вычисления можно не продолжать; в противном случае проделайте еще одно вычитание.
Найдите второй множитель. Чтобы попрактиковаться в вычислениях и получить более точный результат, повторите действия, которые описаны выше.
{3}=729}
, то значение кубического корня из 600 лежит между 8 и 9. Поэтому используйте числа 512 и 729 в качестве верхнего и нижнего пределов ответа.
Оцените второе число. Первое число вы нашли благодаря знанию кубов целых чисел. Теперь целое число превратите в десятичную дробь, приписав к нему (после десятичной запятой) некоторую цифру от 0 до 9. Необходимо найти десятичную дробь, куб которой будет близок, но меньше исходного числа.
- В нашем примере число 600 находится между числами 512 и 729. Например, к первому найденному числу (8) припишите цифру 5. Получится число 8,5.
- В нашем примере: 8 , 5 ∗ 8 , 5 ∗ 8 , 5 = 614 , 1. {\displaystyle 8,5*8,5*8,5=614,1.}
Сравните куб полученного числа с исходным числом. Если куб полученного числа больше исходного числа, попробуйте оценить меньшее число. Если же куб полученного числа намного меньше исходного числа, оценивайте большие числа до тех пор, пока куб одного из них не превысит исходное число.
{3}=614,1}
. Исходное число 600 ближе к 592, чем к 614. Поэтому к последнему числу, которое вы оценили, припишите цифру, которая ближе к 0, чем к 9. Например, таким числом является 4. Поэтому возведите в куб число 8,44.
Если нужно, оцените другое число. Сравните куб полученного числа с исходным числом. Если куб полученного числа больше исходного числа, попробуйте оценить меньшее число. Короче говоря, нужно найти такие два числа, кубы которых чуть больше и чуть меньше исходного числа.
- В нашем примере 8 , 44 ∗ 8 , 44 ∗ 8 , 44 = 601 , 2 {\displaystyle 8,44*8,44*8,44=601,2} . Это чуть больше исходного числа, поэтому оцените другое (меньшее) число, например, 8,43: 8 , 43 ∗ 8 , 43 ∗ 8 , 43 = 599 , 07 {\displaystyle 8,43*8,43*8,43=599,07} . Таким образом, значение кубического корня из 600 лежит между 8,43 и 8,44.
Выполняйте описанный процесс до тех пор, пока не получите ответ, точность которого вас устроит. Оцените следующее число, сравните его с исходным, затем, если нужно, оцените другое число и так далее.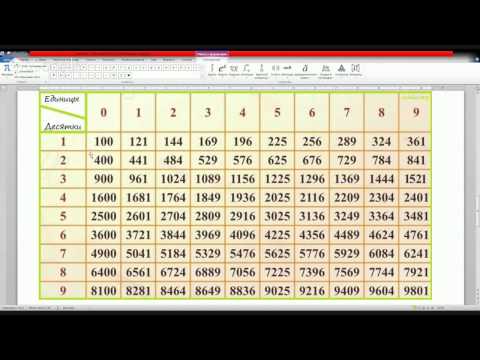
{3}=599,93}
, то есть результат меньше исходного числа менее чем на 0,1.
Корень n-ной степени из числа x — это такое неотрицательное число z, которое при возведении в n-ную степень превращается в x. Определение корня входит в список основных арифметических операций, с которыми мы знакомимся еще в детстве.
Математическое обозначение
«Корень» произошел от латинского слова radix и сегодня слово «радикал» используется как синоним данного математического термина. С 13-го века математики обозначали операцию извлечения корня буквой r с горизонтальной чертой над подкоренным выражением. В 16-веке было введено обозначение V, которое постепенно вытеснило знак r, однако горизонтальная черта сохранилась. Его легко набирать в типографии или писать от руки, но в электронных изданиях и программировании распространилось буквенное обозначение корня — sqrt. Именно так мы и будем обозначать квадратные корни в данной статье.
Квадратный корень
Квадратным радикалом числа x называется такое число z, которое при умножении на самого себя превращается в x.
Например, если мы умножим 2 на 2, то получим 4. Двойка в этом случае и есть квадратный корень из четырех. Умножим 5 на 5, получим 25 и вот мы уже знаем значение выражения sqrt(25). Мы можем умножить и – 12 на −12 и получить 144, а радикалом 144 будет как 12, так и −12. Очевидно, что квадратные корни могут быть как положительными, так и отрицательными числами.
Своеобразный дуализм таких корней важен для решения квадратных уравнений, поэтому при поиске ответов в таких задачах требуется указывать оба корня. При решении алгебраических выражений используются арифметические квадратные корни, то есть только их положительные значения.
Числа, квадратные корни которых являются целыми, называются идеальными квадратами. Существует целая последовательность таких чисел, начало которой выглядит как:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256…
Квадратные корни других чисел представляют собой иррациональные числа. К примеру, sqrt(3) = 1,73205080757… и так далее.
Это число бесконечно и не периодично, что вызывает некоторые затруднения при вычислении таких радикалов.
Школьный курс математики утверждает, что нельзя извлекать квадратные корни из отрицательных чисел. Как мы узнаем в вузовском курсе матанализа, делать это можно и нужно – для этого и нужны комплексные числа. Однако наша программа рассчитана для извлечения действительных значений корней, поэтому она не вычисляет радикалы четной степени из отрицательных чисел.
Кубический корень
Кубический радикал числа x — это такое число z, которое при умножении на себя три раза дает число x. Например, если мы умножим 2 × 2 × 2, то получим 8. Следовательно, двойка является кубическим корнем восьми. Умножим три раза на себя четверку и получим 4 × 4 × 4 = 64. Очевидно, что четверка является кубическим корнем для числа 64. Существует бесконечная последовательность чисел, кубические радикалы которых являются целыми. Ее начало выглядит как:
1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197, 2744…
Для остальных чисел кубические корни являются иррациональными числами.
В отличие от квадратных радикалов, кубические корни, как и любые нечетные корни, можно извлекать из отрицательных чисел. Все дело в произведении чисел меньше нуля. Минус на минус дает плюс – известное со школьной скамьи правило. А минус на плюс – дает минус. Если перемножать отрицательные числа нечетное количество раз, то результат будет также отрицательным, следовательно, извлечь нечетный радикал из отрицательного числа нам ничего не мешает.
Однако программа калькулятора работает иначе. По сути, извлечение корня – это возведение в обратную степень. Квадратный корень рассматривается как возведение в степень 1/2, а кубический – 1/3. Формулу возведения в степень 1/3 можно переиначить и выразить как 2/6. Результат один и тот же, но извлекать такой корень из отрицательного числа нельзя. Таким образом, наш калькулятор вычисляет арифметические корни только из положительных чисел.
Корень n-ной степени
Столь витиеватый способ вычисления радикалов позволяет определять корни любой степени из любого выражения.
Вы можете извлечь корень пятой степени из куба числа или радикал 19 степени из числа в 12 степени. Все это элегантно реализовано в виде возведения в степени 3/5 или 12/19 соответственно.
Рассмотрим пример
Диагональ квадрата
Иррациональность диагонали квадрата была известна еще древним греками. Они столкнулись с проблемой вычисления диагонали плоского квадрата, так как ее длина всегда пропорциональна корню из двух. Формула для определения длины диагонали выводится из и в конечном итоге принимает вид:
d = a × sqrt(2).
Давайте определим квадратный радикал из двух при помощи нашего калькулятора. Введем в ячейку «Число(x)» значение 2, а в «Степень(n)» также 2. В итоге получим выражение sqrt(2) = 1,4142. Таким образом, для грубой оценки диагонали квадрата достаточно умножить его сторону на 1,4142.
Заключение
Поиск радикала – стандартная арифметическая операция, без которой не обходятся научные или конструкторские вычисления. Конечно, нам нет нужды определять корни для решения бытовых задач, но наш онлайн-калькулятор определенно пригодится школьникам или студентам для проверки домашних заданий по алгебре или математическому анализу.
Размещенный на нашем сайте. Извлечение корня из числа часто используется в различных расчетах, а наш калькулятор — это отличный инструмент для подобных математических вычислений.
Онлайн калькулятор с корнями позволит быстро и просто сделать любые расчеты, содержащие извлечение корня. Корень третьей степени посчитает также легко, как и квадратный корень из числа, корень из отрицательного числа, корень из комплексного числа, корень из числа пи и т.д.
Вычисление корня из числа возможно вручную. Если есть возможность вычислить целый корень числа, то просто находим значение подкоренного выражения по таблице корней. В остальных случаях приближенное вычисление корней сводится к разложению подкоренного выражения на произведение более простых множителей, которые являются степенями и их можно убрать за знак корня, максимально упрощая выражение под корнем.
Но не стоит использовать такое решение корня. И вот, почему. Во-первых, придется потратить массу времени на подобные расчеты.
Числа в корне, а точнее сказать, выражения могут быть достаточно сложными, а степень не обязательно квадратичной или кубической. Во-вторых, не всегда устраивает точность таких вычислений. И, в-третьих, есть онлайн калькулятор корней, который сделает за вас любое извлечение корня в считанные секунды.
Извлечь корень из числа — значит найти такое число, которое при его возведении в степень n будет равно значению подкоренного выражения, где n — это степень корня, а само число — основание корня. Корень 2 степени называют простым либо квадратным, а корень третьей степени — кубическим, опуская в обоих случаях указание степени.
Решение корней в онлайн калькуляторе сводится лишь к написанию математического выражения в строке ввода. Извлечение из корня в калькуляторе обозначается как sqrt и выполняется с помощью трех клавиш — извлечение квадратного корня sqrt(x), извлечение корня кубического sqrt3(x) и извлечение корня n степени sqrt(x,y). Более детальная информация о панели управления представлена на странице .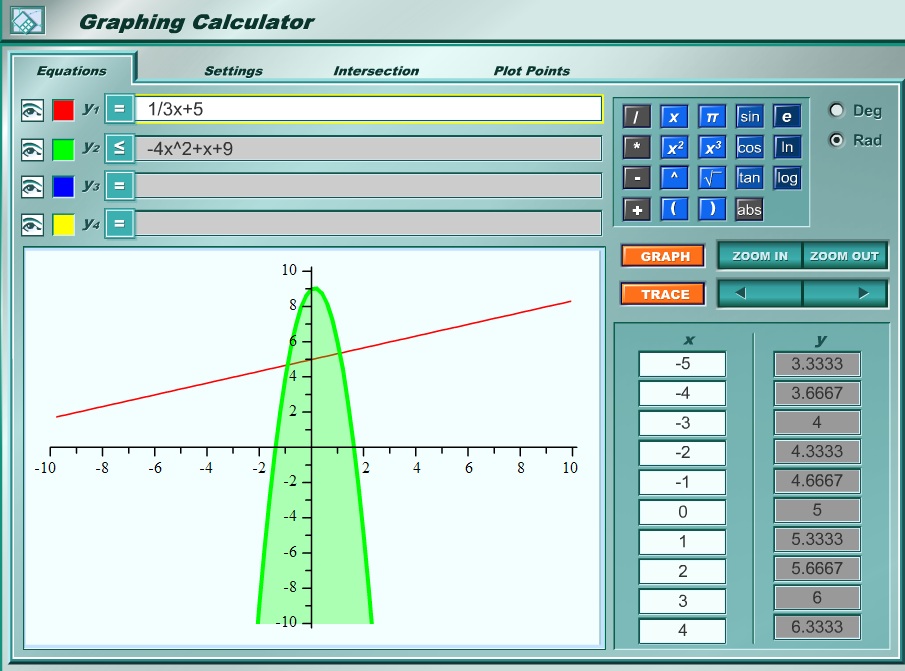
Извлечение квадратного корня
Нажатие этой кнопки вставит в строке ввода запись извлечения из квадратного корня: sqrt(x), вам нужно только внести подкоренное выражение и закрыть скобку.
Пример решения квадратных корней в калькуляторе:
Если под корнем отрицательное число, а степень корня четная, то ответ будет представлен в виде комплексного числа с мнимой единицей i.
Квадратный корень из отрицательного числа:
Корень третьей степени
Используйте эту клавишу, когда нужно извлечь кубический корень. Она вставляет в строке ввода запись sqrt3(x).
Корень 3 степени:
Корень степени n
Естественно, онлайн калькулятор корней позволяет извлекать не только квадратный и кубический корень из числа, но также корень степени n. Нажатие этой кнопки выведет запись вида sqrt(x x,y).
Корень 4 степени:
Точный корень n степени из числа можно извлечь только, если само число является точным значением степени n.
В противном же случае расчет получится приблизительным, хотя и очень близким к идеалу, так как точность вычислений онлайн калькулятора достигает 14 знаков после запятой.
Корень 5 степени с приблизительным результатом:
Корень из дроби
Вычислить корень калькулятор может из различных чисел и выражений. Нахождение корня дроби сводится к отдельному извлечению корня из числителя и знаменателя.
Квадратный корень из дроби:
Корень из корня
В случаях когда корень выражения находится под корнем, по свойству корней их можно заменить одним корнем, степень которого будет равняться произведению степеней обоих. Проще говоря, чтобы извлечь корень из корня, достаточно перемножить показатели корней. В приведенном на рисунке примере выражение корень третьей степени корня второй степени можно заменить одним корнем 6-ой степени. Указывайте выражение так, как вам удобно. Калькулятор в любом случае все рассчитает верно.
Пример, как извлечь корень из корня:
Степень в корне
Корень степени калькулятор позволяет рассчитать в одно действие, без предварительного сокращения показателей корня и степени.
Корень третьей степени можно вычислить и в программе MS Excel. Для этого введите в любую клетку «=» и выберите значок «вставка » (fx). Выберите в появившемся окошке функцию «СТЕПЕНЬ» и нажмите кнопку «Ок». В появившемся окошке введите значение числа, для которого необходимо вычислить корень третьей степени. В «Степень» введите число «1/3». Число 1/3 набирайте именно в таком виде – как обыкновенную . После этого нажмите кнопку «Ок». В той клетке таблицы, где создавалась , появится кубический корень из заданного числа.
Если корень третьей степени приходится вычислять постоянно, то немного усовершенствуйте описанный выше метод. В качестве числа, из которого требуется извлечь корень, укажите не само число, а клетку таблицы. После этого, просто каждый раз вводите в эту клетку исходное число – в клетке с формулой будет появляться его кубический корень.
Видео по теме
Обратите внимание
Заключение. В данной работе были рассмотрены различные методы вычисления значений кубического корня.
Полезный совет
Корни второй и третьей степени употребляются особенно часто и поэтому имеют специальные названия. Квадратный корень: В этом случае показатель степени обычно опускается, а термин «корень» без указания степени чаще всего подразумевает квадратный корень. Практическое вычисление корней Алгоритм нахождения корня n-ной степени. Квадратные и кубические корни обычно предусмотрены во всех калькуляторах.
Источники:
- корень третий степени
- Как извлечь квадратный корень в N степени в Excel
Операцию нахождения корня третьей степени обычно называют извлечением «кубического» корня, а заключается она в нахождении такого вещественного числа, возведение которого в куб даст значение равное подкоренному числу.
Lazarus: Калькулятор (2018-2019) [10 класс] — Школа N61 г.Ульяновска
Команда 1 «Северное сияние»
Файл для открытия проекта: Calkulator9.lpiКалькулятор умеет:
- Складывать, умножать, делить и вычитать числа подряд
- Возводить в любую степень
- Искать синус градусов
- Вычисляет квадратный корень
Планируется:
- Ввести функцию косинус
- Перенести из электронного вида в материальный
- Ввести корень любой степени
Команда 2 «Одуванчики»
Файл для открытия проекта: project1.lpiНаш калькулятор умеет:
- складывать
- вычитать
- умножать
- делить
- возводить числа в степень
Команда 3 «Клептоманка»
Файл для открытия проекта: project1.Команда «Клептоманка».
Модель калькулятора: «Apples 32»Что мы имеем:
- Мы создали прототип калькулятора
- Он умеет складывать, отнимать, умножать, делить и взводить числа в степень
- Главная его особенность — это креативный дизайн и название, с помощью которых будет возрастать желание им пользоваться и сделает вашу учебу только увлекательнее
Что мы не имеем:
- Калькулятор не может совершать вычисления в виде процентов, вывода из корня и из степени, и работать с дробными числами.
Что мы планировали в начале проекта:
- Создать калькулятор
- Чтобы он работал
- Чтобы хорошо работал
- И не ломался
- Заряжался от солнечной батареи
- Мы хотели, чтобы калькулятор появлялся из компьютера в виде облака и пользователь мог им пользоваться, нажимая на кнопочки прямо в воздухе
- Пользователь сам мог бы изменять цвет калькулятора в зависимости от своего настроения
Команда 4 «Белки»
Файл для открытия проекта: project1.Команда 5 «ПУМА»
Файл для открытия проекта: project1.lpiКалькулятор ПУМА
Нас окружают множество вещей, которыми мы пользуемся изо дня в день, без некоторых мы даже не представляем свою жизнь. В нашем 21 веке все намного проще, чем раньше. Калькуляторы есть в каждом телефоне, а телевизоры обладают таким потенциалом, о котором нельзя было и мечтать 20 лет назад. Но прогресс не стоит на месте. Нашей целью было создать максимально простой и удобный калькулятор.
Название нашего калькулятора — ПУМА.
П-простойМинимализм всегда остается в моде, поэтому в нашем калькуляторе нет ничего лишнего. Он имеет 10 кнопок, а также по задумке в нем есть кнопки синуса и косинуса, что делает задачу вычисления более простой.
У-уникальныйОн определенно является уникальным из-за того, что он имеет два экрана, на одном из которых, мы можем увидеть сам пример или задачу для вычислений, а на другом решение.
М-модныйЕще одной фишкой нашего калькулятора является его дизайн, цвет схож с окраской пумы, а также он имеет ушки, как у животного, это делает его более привлекательным и неповторимым.
А-актуальныйКалькулятор всегда будет нужен в подсчетах, ведь мы не всегда можем произвести сложные вычисления в уме и сделать это быстро и точно. Наш калькулятор делает вычисления без единой ошибки, и это является его огромным плюсом. Длина калькулятора 10 см, а ширина 6, это дает возможность носить такой прибор везде с собой.
И в заключение мы хотим сказать, что калькулятор в наши дни просто необходим, а с нашим калькулятором «ПУМА» жизнь станет намного лучше и удобнее. ПУМА это просто, уникально, модно, актуально.
Команда 6 «Шестерёнка»
Файл для открытия проекта: project1.lpiОписание калькулятора
Функции нашего устройства
- Сложение.
Сложение-одна из самых главных и основных функций любого калькулятора.
- Вычитание.
Вычитание по важности занимает тоже место ,что и сложение. Это одна из основных функций калькулятора. Мы используем её примерно с такой же периодичностью, что и сложение. Вычитание-операция обратная сложению. На письме обозначается знаком «-«.При наличии отрицательных чисел вычитание удобно рассматривать как разновидность сложения -сложение с отрицательным числом.
- Умножение.
Данная функция имеет очень большое значение в скорости подсчётов крупных числовых значений. Первый аргумент обычно называют множимым ,а второй множителем. Результат умножения двух аргументов называется из произведением. Ведь есть различные виды умножения:
- Умножение дробей
- Сокращённое умножение
- Умножение чисел
- Деление
Деление-функция обратная умножению.
- Возведение в степень
Эта функция непосредственно связана с умножением. Мы возводим в ту степень, сколько раз хотим умножить число само на себя.
Команда 7 «Анастасия Alone»
Файл для открытия проекта: project1.lpiКалькулятор О. Анастасии
Имеет базовые функции:
делит, умножает, складывает, вычитает (как целые, так и дробные числа). Также возводит числа в квадрат, вычисляет квадратный корень.
В перспективе:
вычисление синуса и косинуса.
Преимущества калькулятора:
- компактный,
- удобный в использовании,
- не загроможденный излишними кнопками,
- имеет все необходимые функции,
- безошибочно вычисляет запросы.
Команда 8 Проект
Файлы по проекту «Калькулятор», 2018-2019 год.
Вложения: шаблон Калькулятор [2018.10.15] [10 класс] 478 Кб шаблон Калькулятор [2018.11.07] [10 класс] 348 Кб шаблон Калькулятор [2018.11.08] [10 класс] 501 Кб calc_puma2_[2019.04.08].zip [10 класс, Лиза & Co] 127 Кб team1 Cеверное сияние.zip [10 класс, 2018.12.05 team1] 253 Кб team3 calc Клиптоманка.zip [10 класс, 2019.01.16 team3] 127 Кб team4 calc_belki Белки.zip [10 класс, 2019.01.30 team4] 127 Кб team6 calc_07 Шестерёнка.zip [10 класс, 2018.12.05 team6] 127 Кб team8 calc_N08.zip [10 класс, 2018.12.14 team8] 128 Кб Команда1 Cеверное сияние.docx [ ] 13 Кб Команда1 Cеверное сияние.zip [10 класс, 2019.05] 1137 Кб Команда2 Одуванчики 10л. [ ] 19 Кб Команда2 Одуванчики.zip [10 класс, 2019.05] 127 Кб Команда3 Клептоманка.docx [ ] 15 Кб Команда3 Клиптоманка.zip [10 класс, 2019.05] 127 Кб Команда4 Белки.zip [10 класс, 2019.05] 127 Кб Команда5 Пума.docx [ ] 13 Кб Команда5 Пума.zip [10 класс, 2019.05] 129 Кб Команда6 Шестерёнка 10Л.docx [ ] 16 Кб Команда6 Шестерёнка.zip [10 класс, 2019.05] 254 Кб Команда7 Огородникова.docx [ ] 12 Кб Команда7 Огородникова.zip [10 класс, 2019.05] 127 Кб Команда8 calc_N08.zip [10 класс, 2019.05] 128 Кб Огородникова.zip [10 класс, 2019.02.05] 127 Кб Калькулятор умножения квадратных корней
Дом Многочлены Нахождение наибольшего общего делителя Факторинг трехчленов Функция абсолютного значения Краткий обзор полиномов факторинга Решение уравнений с одним радикальным членом Добавление дробей Вычитание дробей Метод ФОЛЬГИ График составных неравенств Решение абсолютных неравенств Сложение и вычитание многочленов Использование наклона Решение квадратных уравнений Факторинг Свойства умножения показателей степени Завершение квадрата Решение систем уравнений методом подстановки Объединение подобных радикальных терминов Исключение с помощью умножения Решение уравнений Теорема Пифагора 1 Нахождение наименьших общих кратных Умножение и деление в научной записи Сложение и вычитание дробей Решение квадратных уравнений Сложение и вычитание дробей Умножение на 111 Добавление дробей Умножение и деление рациональных чисел Умножение на 50 Решение линейных неравенств с одной переменной Упрощение кубических корней, содержащих целые числа График составных неравенств Простые трехчлены как произведения двучленов Написание линейных уравнений в форме наклона-пересечения Решение линейных уравнений Линии и уравнения Пересечения параболы Функция абсолютного значения Решение уравнений Решение сложных линейных неравенств Комплексные числа Факторизация разности двух квадратов Умножение и деление рациональных выражений Сложение и вычитание радикалов Умножение и деление чисел со знаком Решение систем уравнений Факторизация противоположности GCF Умножение специальных многочленов Свойства показателей степени Научное обозначение Умножение рациональных выражений Сложение и вычитание рациональных выражений с отличающимися знаменателями Умножение на 25 Десятичные дроби в дроби Решение квадратных уравнений путем заполнения квадрата Частное правило для показателей степени Упрощение квадратных корней Умножение и деление рациональных выражений Независимые, противоречивые и зависимые системы уравнений Склоны Графические линии на координатной плоскости Графические функции Силы десяти Свойство нулевой мощности экспонентов Вершина параболы Рационализация знаменателя Тест факторизуемости для квадратных трехчленов Трехчленные квадраты Решение двухшаговых уравнений Решение линейных уравнений, содержащих дроби Умножение на 125 Свойства экспоненты Умножение дробей Сложение и вычитание рациональных выражений с одинаковым знаменателем Квадратные выражения — Заполнение квадратов Сложение и вычитание смешанных чисел с разными знаменателями Решение формулы для заданной переменной Факторинг трехчленов Умножение и деление дробей Умножение и деление комплексных чисел в полярной форме Уравнения мощности и их графики Решение линейных систем уравнений подстановкой Решение полиномиальных уравнений методом факторинга Законы показателей индекс casa mÃo Системы линейных уравнений Свойства рациональных показателей Мощность произведения и мощность частного Различия в факторинге идеальных квадратов Деление дробей Разложение полинома на множители путем нахождения GCF Графики линейных уравнений шагов факторинга Свойство умножения показателей степени Решение систем линейных уравнений с тремя переменными Решение экспоненциальных уравнений Нахождение НОК набора одночленов
- Expression
- Equation
- Inequality
- Contact us
- Simplify
- Factor
- Expand
- GCF
- LCM
- Solve
- Graph
- System
- Решение
- График
- Система
- Математический решатель на вашем сайте
Наших пользователей:
Поздравляем и благодарим за это замечательное программное обеспечение.
Натали Олив, МиссуриЯ использовал вашу программу для подготовки к экзамену по алгебре. Мне очень нравится пошаговый процесс решения и пояснения.
МБ, ИллинойсСамый ценный репетитор по алгебре, которого я когда-либо встречал. Он обслуживает не только основных учащихся, но и студентов, которые занимаются продвинутой алгеброй. Пошаговое решение задач, сопровождаемое объяснением каждого шага, делает эту программу бесценным математическим инструментом.
РГ, ФлоридаСтуденты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение может спасти им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?
Поисковые фразы, использованные 20 сентября 2013 г.:
- год 9 математические работы
- год 11 математика алгебра
- базовый тест на математические способности, текстовые задачи, версия для печати
- Рабочие листы по алгебраическим рассуждениям
- АЛГЕБРА ЛИНЕЙНАЯ РЕГРЕССИЯ 9 КЛАССА
- когда была изобретена алгебра?
- Алгебра для студентов 8 выпуск
- Египет математические мелочи
- Прентис Холл Математика Алгебра 2 Оклахома 906:40
- ответов к задаче по алгебре 2
- ti 83+ триггерных программы
- сложение дробей с отрицательными знаками
- ПАРАБОЛА фото
- как решить проблему с пропорциями?
- бесплатных печатных листов для теста ged
- общих вопросов о способностях и ответы на
- алгебра 2 читы
- Математические мелочи
- решение без радикальных выражений
- бесплатный репетитор по асимптотам
- Лучшее программное обеспечение
- как не провалить предварительную алгебру
- бесплатных рабочих листов по вычислению переменных выражений
- квадратные числа интерактивные
- aptitude papers скачать бесплатно
- наименьший общий знаменатель в Java
- недавняя бумага о способностях с ответом
- Макдугал Литтел интегрированная математика 3
- алгебра 1 читбук
- примеры математических мелочей для элементарного
- Упроститель математических уравнений
- квадратных корней
- ti-83 plus скачать прошивку
- Предварительная алгебра для 6 класса
- страница практики математика 6 класс
- Периметр прямоугольника равен 150 дюймам.
- Алгебра 1 сложение, вычитание, умножение или деление дробей
- Правила факторизации многочленов и трехчленов шпаргалка 906:40
- примеры вопросов по математике-тригонометрия
- наименьший общий знаменатель с переменными
- Математические листы для 3-го класса сложить вычесть
- Предварительная алгебра для 7-го класса + Северная Каролина + примеры тестов
- основные степени алгебры
- процентные математические листы для детей\
- уравнение зла
- проверка моих ответов на предварительную алгебру
- Прентис Холл Математика Алгебра видео домашнее задание
- как построить эллипс на графическом калькуляторе
- по алгебре, как найти значение силы?
- рабочих листов для печати показателей
- решить и построить график нелинейных уравнений
- сухие корни
- сумма квадратов первых 5 нечетных чисел
- алгебраическая замена
- ввод третьего корня в калькулятор
- апплет алгебры задач теней
- спиральная алгебра1 математическая книга онлайн 906:40
- бесплатных спутниковых тестов для печати
- как возвести в квадрат в excel
- перевести квадратные метры в погонные метры
- ti 89 сложная матрица
- примеров систем линейных неравенств в повседневной жизни
- загрузок калькулятора TI-84
- самое сложное уравнение
- самая старая математическая задача в мире
- как дела по алгебре 8 класс
- линейных уравнений на листе с одной переменной 906:40
- Как упростить выражения с двойным радикалом
- Решатель алгебры колледжа
- помогите решить проблему с распределительной собственностью
- Matlab нелинейный ODE
- онлайн-решатель проблем неравенства
- Математика Базовые навыки+сложение, вычитание, умножение, деление целых чисел
- детский сад 3 математика работает бесплатно
Метод- для получения наименьшего общего кратного
Теорема Пифагора- электронная книга ppt pdf 906:40
- полоса гетероперехода
- Алгоритм Рунге-Кутта с несколькими переменными matlab
- алгебра 2 решение радикалов
- ti 84 загрузки бесплатных игр
- скачать книги pdf бухгалтерия
- образец теста для математических тестов STAR для 8-го класса
Предыдущий Следующий
Мэтуэй | Популярные задачи
1 93-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92 Калькулятор умножения квадратных корней
Дом Точка Арифметические операции с числовыми дробями Умножение полинома на моном Решение линейного уравнения Решение линейных уравнений Решение неравенств Решение сложных неравенств Решение систем уравнений с помощью замены Упрощение дробей 3 Факторирование квадратичных уравнений Специальные продукты Запись дробей в процентах : Использование шаблонов для умножения двух двучленов Сложение и вычитание дробей Решение линейных неравенств Добавление дробей Решение систем уравнений — Экспоненциальные функции Целочисленные экспоненты Пример 6 Деление мономов Умножение может увеличивать или уменьшать число Графики горизонтальных линий Упрощение выражений, содержащих только мономы Десятичные числа Отрицательные числа Факторинг Вычитание многочленов Сложение и вычитание дробей Полномочия i Умножение и деление дробей Упрощение сложных дробей Нахождение координат точки Дроби и десятичные дроби Рациональные выражения Решение уравнений методом факторинга Наклон линии Процент введен Приведение рациональных выражений к наименьшим терминам Гипербола Стандартная форма уравнения прямой Умножение на 75 Решение квадратных уравнений с использованием квадратичной формулы Возведение продукта в степень Решение уравнений с логарифмическими условиями на каждой стороне Мономиальные коэффициенты Решение неравенств с использованием дробей и скобок Свойство деления квадратных и кубических корней Умножение двух чисел, близких к 100, но меньше Решение абсолютных неравенств Уравнения окружностей Проценты и десятичные дроби Интегральные показатели Линейные уравнения — положительные и отрицательные наклоны Умножение радикалов Факторинг специальных квадратных полиномов Упрощение рациональных выражений Сложение и вычитание непохожих дробей Графики линейных неравенств Линейные функции Решение квадратных уравнений с помощью квадратичной формулы Сложение и вычитание многочленов Функции сложения и вычитания Основные алгебраические операции и упрощение Упрощение сложных дробей Ось симметрии и вершины Факторирование многочленов с четырьмя членами Оценка простых формул Графические системы уравнений Научное обозначение Линии и уравнения Горизонтальные и вертикальные линии Решение уравнений методом факторинга Решение систем линейных неравенств Сложение и вычитание рациональных выражений с разными знаменателями Сложение и вычитание дробей Решение линейных уравнений Простые трехчлены как произведения двучленов Решение нелинейных уравнений с помощью факторинга Решение системы уравнений Экспоненциальные функции Вычисление площади кругов Стандартная форма квадратного уравнения Дискриминант Деление мономов с использованием правила частных Возведение разницы Изменение знака экспоненты Добавление дробей Полномочия радикальных выражений Этапы решения линейных уравнений Полные квадраты квадратичных выражений Дроби 1 Свойства отрицательных показателей Факторинг идеальных квадратных трехчленов Алгебра Решение квадратных уравнений с использованием свойства квадратного корня Деление рациональных выражений Квадратные уравнения с мнимыми решениями Факторинг трехчленов с использованием шаблонов
- Expression
- Equation
- Inequality
- Contact us
- Simplify
- Factor
- Expand
- GCF
- LCM
- Solve
- Graph
- System
- Solve
- Graph
- Система
- Математический решатель на вашем сайте
Калькулятор умножения квадратных корней
Похожие темы:
решения задач по алгебре бесплатно | формула превращения десятичных дробей в дроби | как конвертировать 2/3 | бесплатные ответы по алгебре | бесплатный тест по алгебре для 6-го класса | рабочий лист по алгебре 153 | игры на умножение и деление дробей | алгебра помогает в реальных жизненных ситуациях | рабочие листы по математике для 5 класса | предварительный решатель алгебры | выучить предварительную алгебру онлайн | конвертировать дроби в децимели | неоднородные уравнения в частных производных | предварительное алгебраическое решение уравнений с одной переменной листа
Автор Сообщение youngxectorianc Зарегистрирован: 16.
Источник: YoungHistorians.com
Размещено: вторник, 26 декабря, 11:35 Может ли кто-нибудь помочь мне с моими вопросами задания? Они основаны на калькуляторе умножения квадратных корней. Я прочитал несколько статей о квадратных уравнениях и умножающих матрицах, но это не помогло мне найти ответы на вопросы из моей домашней работы. Прошлой ночью я не мог уснуть, так как мне скоро нужно лечь спать. Но проблема в том, что сколько бы времени я ни тратил, мне кажется, что я просто не врубаюсь. Каждый вопрос ставит новый вызов, который кажется более сложным, чем покорение Эвереста! Мне нужна помощь как можно скорее. Наверх nxu Зарегистрирован: 25.10.2006
Откуда: Сибирь, Российская Федерация
Размещено: Четверг, 28 декабря, 10:05 Я действительно не знаю, почему Бог создал алгебру, но вы будете рады узнать, что кто-то также придумал Алгебратор! Да, Algebrator — это программа, которая может помочь вам решить математические задачи, о которых вы никогда не думали, что сможете. Наверх Mibxrus Зарегистрирован: 19.10.2002
Откуда: Ванкувер, Канада
Размещено: Суббота, 30 декабря, 07:08 Да, я согласен, Алгебратор — действительно полезный инструмент. Наверх Sr33vel Дата регистрации: 13.08.2007
Откуда: Иллинойс
Размещено: Понедельник, 01 января, 07:33 Кажется, эта вещь действительно хороша. Наверх Свиз Зарегистрирован: 10.03.2003
Откуда: Словения
Размещено: Понедельник, 01 января, 15:11 Я бы предложил использовать Алгебратор. Он не только поможет вам решить математические задачи, но и подробно покажет все необходимые шаги, чтобы вы могли лучше понять предмет. Наверх Xane Зарегистрирован: 16.04.2003
Откуда: пустоши между бессонницей и ясновидением
Размещено: Понедельник, 01 января, 18:09 Программное обеспечение — кусок пирога. Просто дайте ему 15 минут, и вы станете профессионалом в этом. Вы можете найти программное обеспечение здесь, https://алгебра1help.
y».
Выяснилось, что значения кубического корня можно находить с помощью метода итераций, также можно аппроксимировать кубический корень, возводить число в степень 1/3, искать значения корня третьей степени с помощью Microsoft Office Ecxel, задавая формулы в ячейках.
Операция извлечения арифметического корня любой степени n эквивалентна операции возведения в степень 1/n. Для практического вычисления кубического корня можно использовать несколько способов.
lpi
lpi
Это пожалуй, первая функция, нужная для многих видов вычислительных работ с цифрами и тригонометрическими функциями. Самая часто используемая функция ,начиная со школьной математики ,заканчивая подсчётами для погашения кредитов. На письме данная функция обозначается знаком «+».
Обозначается двоеточием и если дроби, то дробь переворачивается. Деление заменяет неоднократно повторенное вычитание.
docx
Это и сложно, и весело. 
Длина превышает с на 3 дюйма. Найдите длину и ширину.
09.2002 
Кто-нибудь, пожалуйста, направьте меня.
Он не только решает проблему, но также дает подробное описание того, как он пришел к этому решению. Всего наилучшего!
Я купил его несколько месяцев назад и могу сказать, что это главная причина, по которой я сдаю уроки математики. Я рекомендовал его своим друзьям, и они тоже считают его очень полезным. Я настоятельно рекомендую его, чтобы помочь вам с домашним заданием по математике.
Как я могу это получить? Я хотел бы попробовать это сам, как можно скорее. Ура! Теперь мне есть чем помочь!
