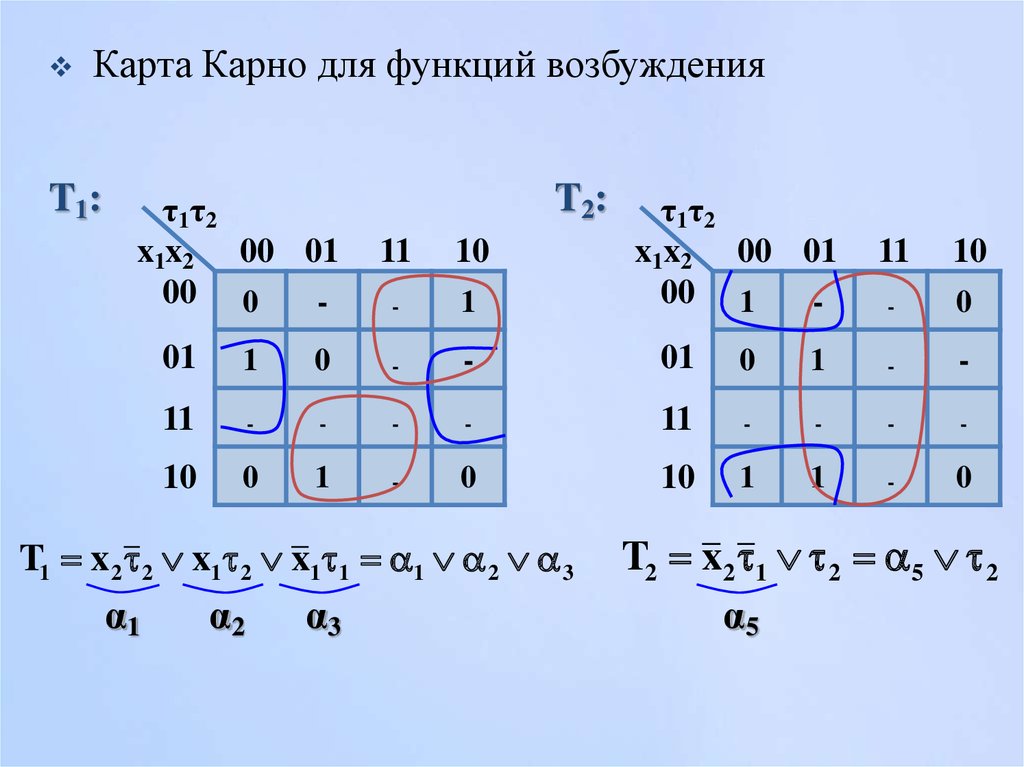
Карта карно онлайн: Схема логических элементов онлайн

Содержание

Минимизация логических функций — Мегаобучалка

Логические функции построенные по СДНФ или СКНФ оказываются достаточно сложными и требуют большого количества логических элементов. С целью упрощения принципиальных схем применяются методы минимизации логических функций такие как

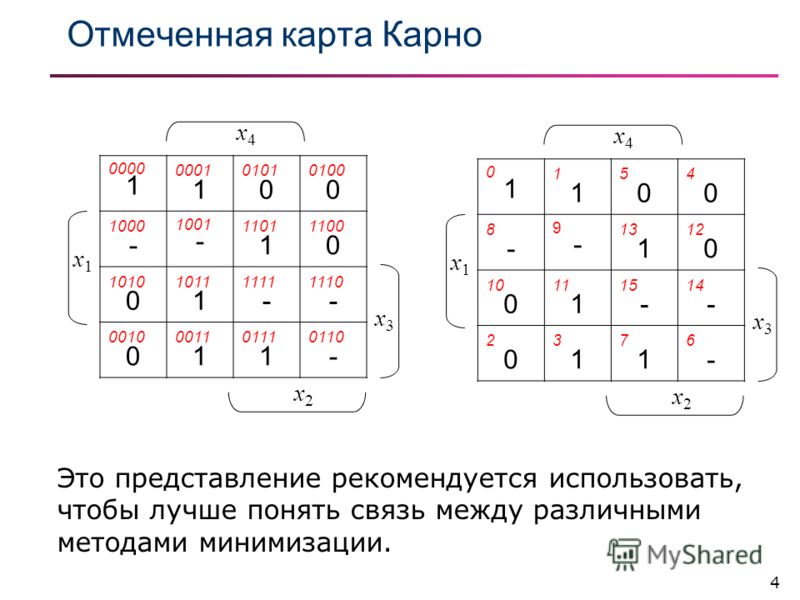
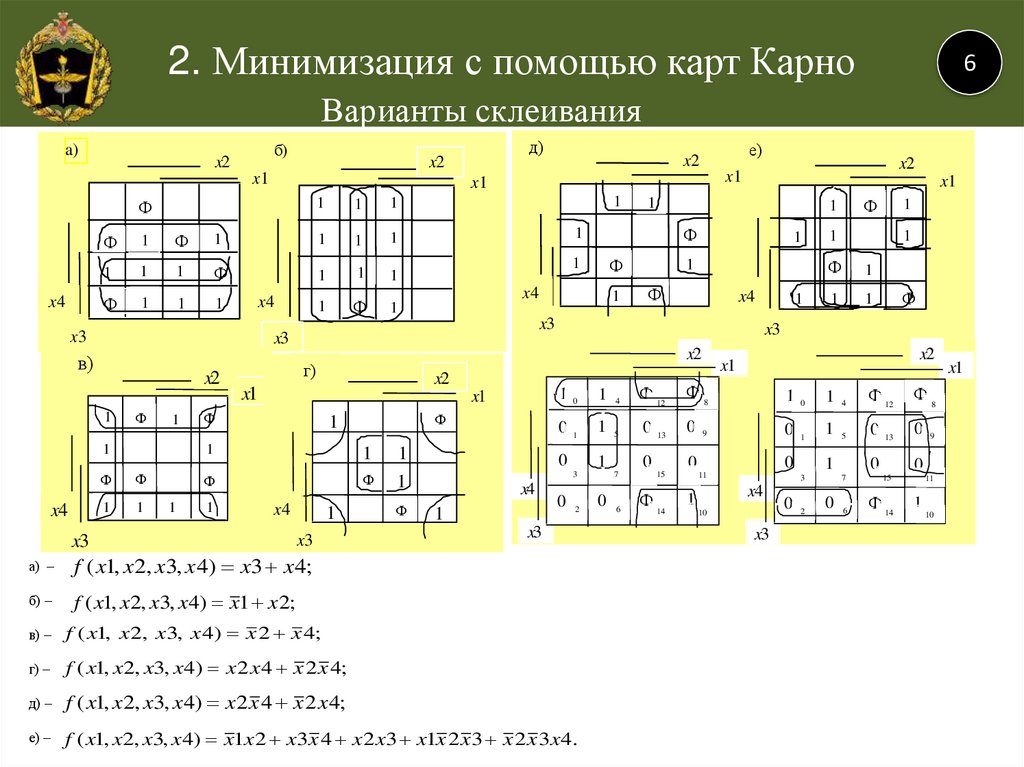
Метод карт Карно (карты минитермов)

Метод карт Вейча

Минтерм — выражение соответствующее минимальному поименованному участку карты (кодовое имя клетки)

Отличие методов заключается в различном расположении имен (кодов) клеток карты в последовательности определяемой рефлексным (циклическим ) кодом.

В каждую клетку внесен символ истинности или ложности соответствующий кодовому слову клетки.

Особенность циклического кода и карт является свойство соседства. Оно состоит в том , что каждое следующее (или предыдущее) значение кода отличается от имени своих соседей лишь одним признаком (прямой или обратной формой предикта.) Макстерм — кодовое имя максимального количества клеток с одним значением (истинно ) или (ложно).

(петля)

Любая булева функция представима как вввиде суммы минитермов (дизюнктивная форма), так и в виде произведения мастермов (конъюнктивная форма). Связующий терм (избыточная петля) применяется для устранения ложных сигналов в комбинационных цепях и нами рассматриваться не будут.

Минимизация логических функций методом диаграмм Вейча (карт Карно).

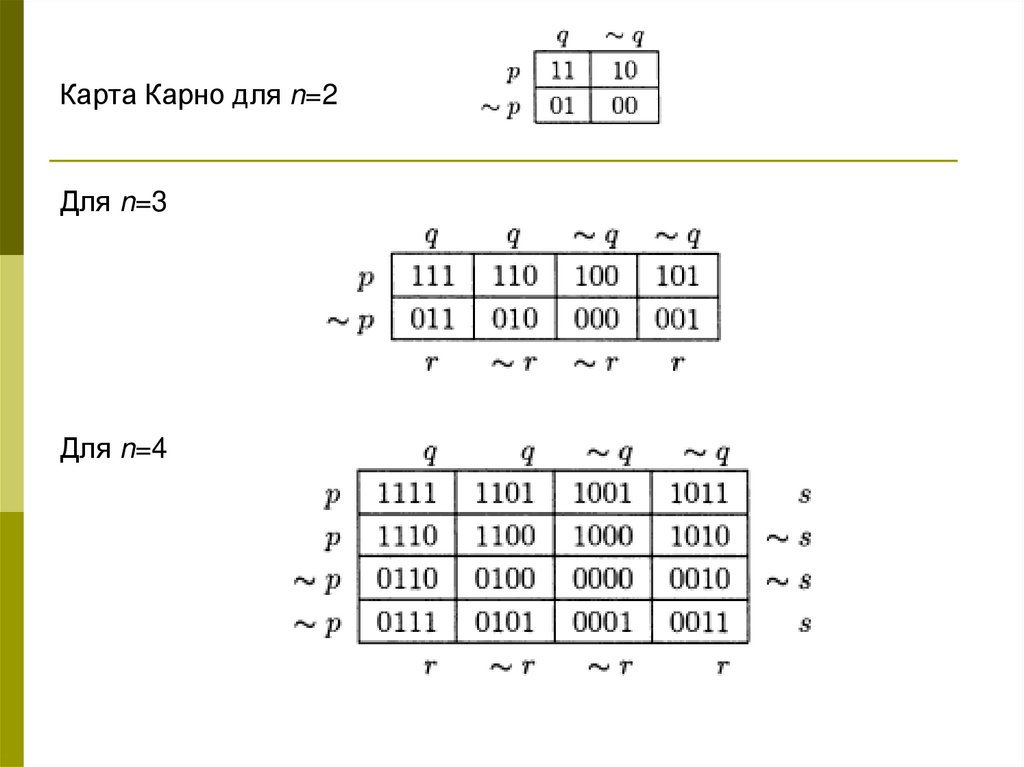
Карта для двух переменных

	х2
х1

Таблица истинности

Х2	Х1	выход

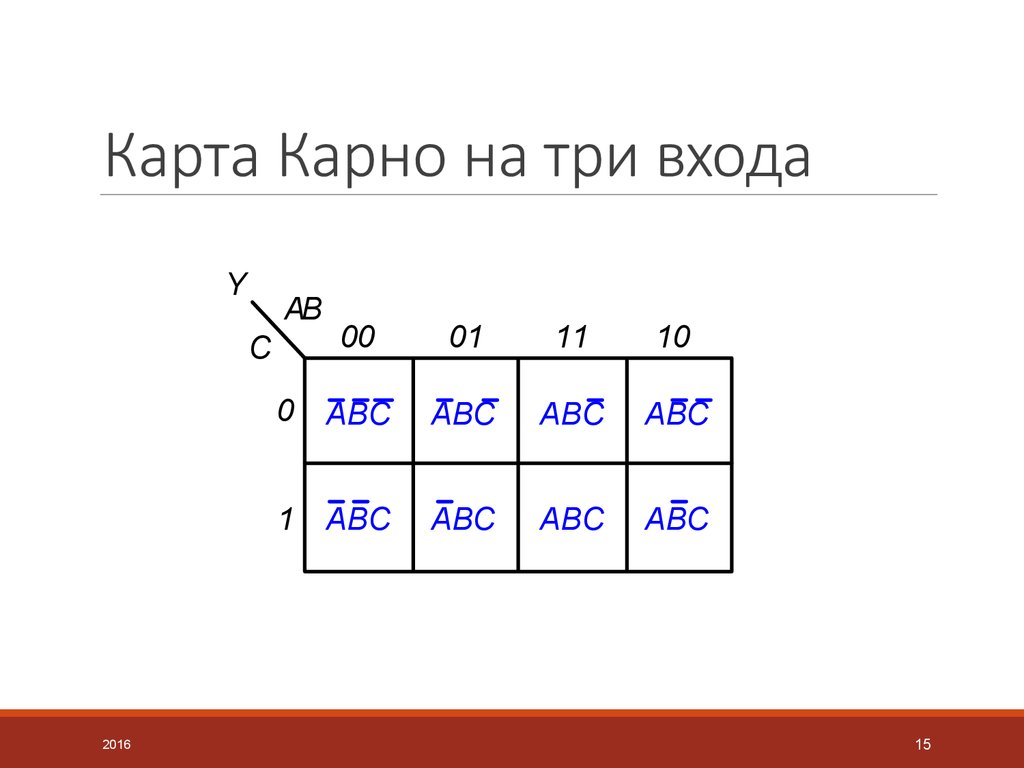
Карта для трех переменных

	х2
х1

		х3

Таблица истинности

х3	х2	х1	выход

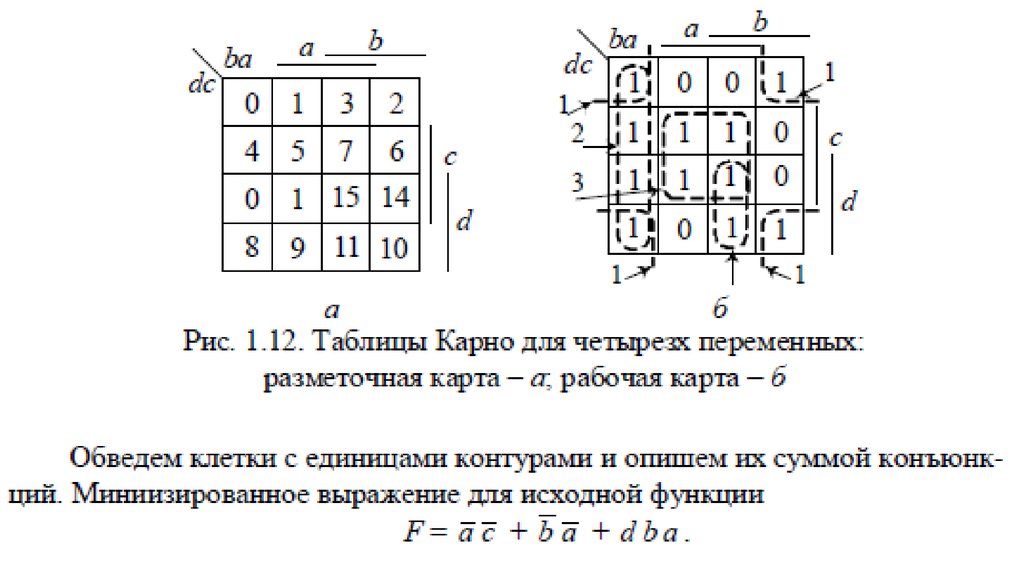
карта Карно для четырех переменных

	х1
х2
			х4

	.	.
		х3

карта Карно для пяти переменных

Данная карта состоит из двух карт Карно для четырех переменных

х5

	х1
х2
			х4

	.	.
		х3

	х1
х2
		х4

	. C

Пример

Пусть имеются три независимых параметра система считается исправной при выполнении следующего неравенства

В для нашей схемы карта Карно запишется в виде

	х2
х1

		х3

Выражение упростится до вида

Конструктивно исключен один из элементов И и три элемента Не кроме того вместо трехвходовых элементах схема контроля будет реализована на двухвходовых элементах.

Тоже выражение при реализации функции СКНФ

СКНФ

	х2
х1

		х3

	х2
х1

		х3

В нашем случае обе функции будут реализованы по одной схеме с использованием разных элементов Однако подобная симметрия не всегда возможна поэтому необходим Анализ как функции МКНФ так и функции МДНФ выбирается та схема которая содержит меньшее количество элементов.

. Результат минимизации может быть неоднозначен, и одной заданной таблице истинности могут соответствовать различные схемы.

Рассмотрим для примера функцию неравнозначности (ИСКЛЮЧАЮЩЕЕ ИЛИ). Ее таблица истинности следующая:

ИСКЛЮЧАЮЩЕЕ ИЛИ
x1	x2	F(x1,x2)

Уравнение по первой стандартной форме:

(3.5)

Уравнение по второй стандартной форме:

(3.6)

Преобразуем вторую скобку в уравнении 6 по принципу двойственности:

(3.7)

Рис. 3.3. Схемы по уравнениям 3.5 (а) и 3.7 (б)

Для построения схемы по уравнению 5 необходимы 2 элемента НЕ, два двухвходовых элемента И и один двухвходовый элемент ИЛИ.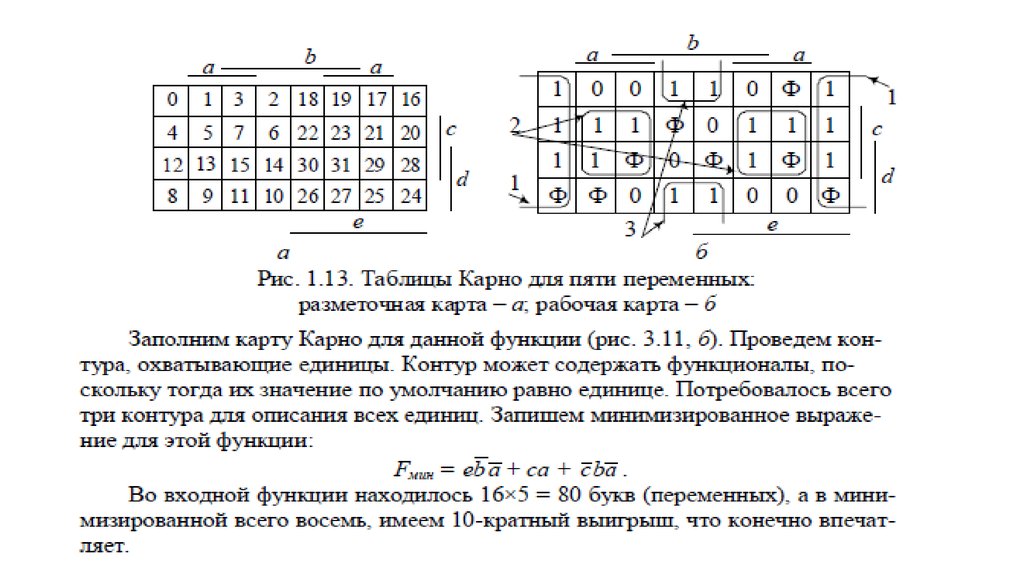 В схеме, построенной по уравнению 3. 7 на один элемент НЕ меньше (рис. 3.3 ).

Как было отмечено выше, существуют полные наборы логических функций, к которым относятся три функции ИЛИ, И, НЕ, функция ИЛИ-НЕ, функция И-НЕ. Все построенные нами схемы использовали полный набор функций ИЛИ, И, НЕ. Однако представляет интерес и имеет практическое значение использование для построения схем базовых логических элементов ИЛИ-НЕ и И-НЕ. Для построения схемы на элементах ИЛИ-НЕ (рис. 3.4 ) воспользуемся уравнением 3. 6. Преобразуем его по принципу двойственности:

Для построения схемы на элементах И-НЕ (рис. 3.4 б) преобразуем уравнение 5, избавляясь от операции логического сложения:

Рис. 3.4 . Схемы элемента ИСКЛЮЧАЮЩЕЕ ИЛИ на элементах
ИЛИ-НЕ (а) и И-НЕ (б)

Пример

Реализация системы управления и контроля за несколькими независимыми параметрами.

Построить систему контроля, удовлетворяющую этой зависимости с минимально возможным количеством элементов.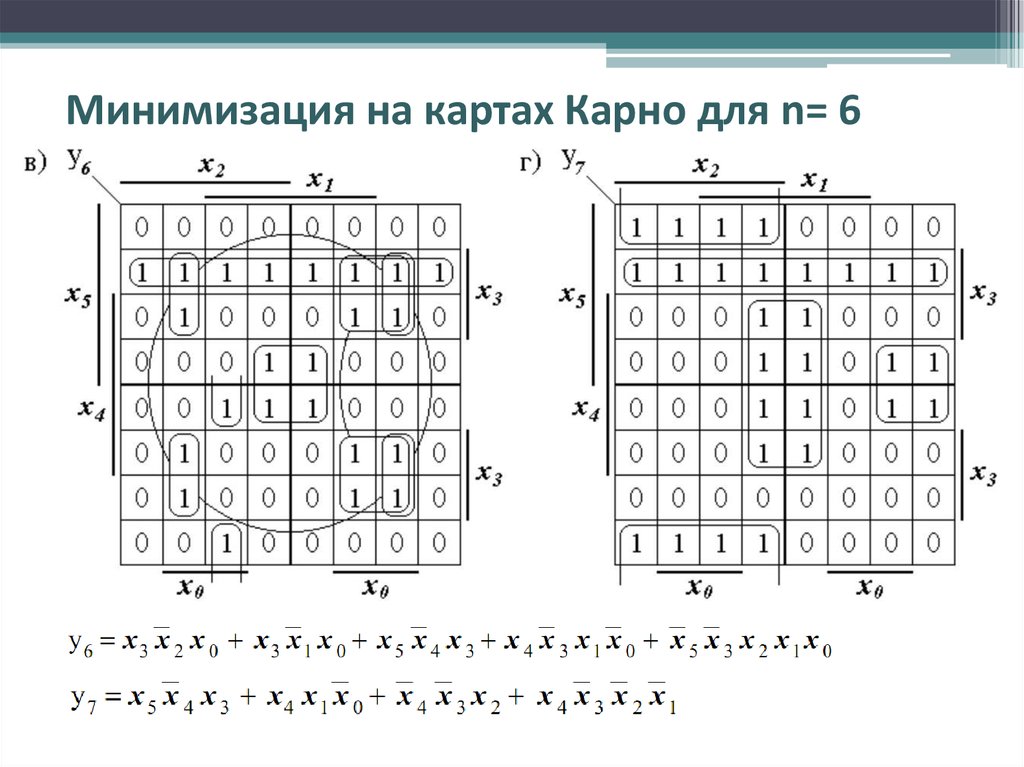

Вопросы для самопроверки

6.1. Сформулируйте правило перехода от таблицы истинности к первой стандартной форме. Приведите примеры. Запишите уравнение функции равнозначности в первой стандартной форме.

6.2. . Сформулируйте правило перехода от таблицы истинности ко второй стандартной форме. Приведите примеры. Запишите уравнение функции неравнозначности во второй стандартной форме.

6.3. Докажите, что уравнения функции ИСКЛЮЧАЮЩЕЕ ИЛИ, записанные в первой и второй стандартных формах преобразуются одна в другую.

6.4. Постройте схему устройства, описываемого уравнением, полученным в пункте 6.1.

6.5. Постройте схему элемента ИЛИ на элементах И-НЕ.

6.6. Постройте схему элемента И на элементах ИЛИ-НЕ.

6.7. Постройте схему элемента реализующего функцию равнозначности на элементах И-НЕ.

6.8. Постройте схему элемента реализующего функцию равнозначности на элементах ИЛИ-НЕ.

6.9. Постройте схему элемента ИСКЛЮЧАЮЩЕЕ ИЛИ на элементах И, ИЛИ, НЕ.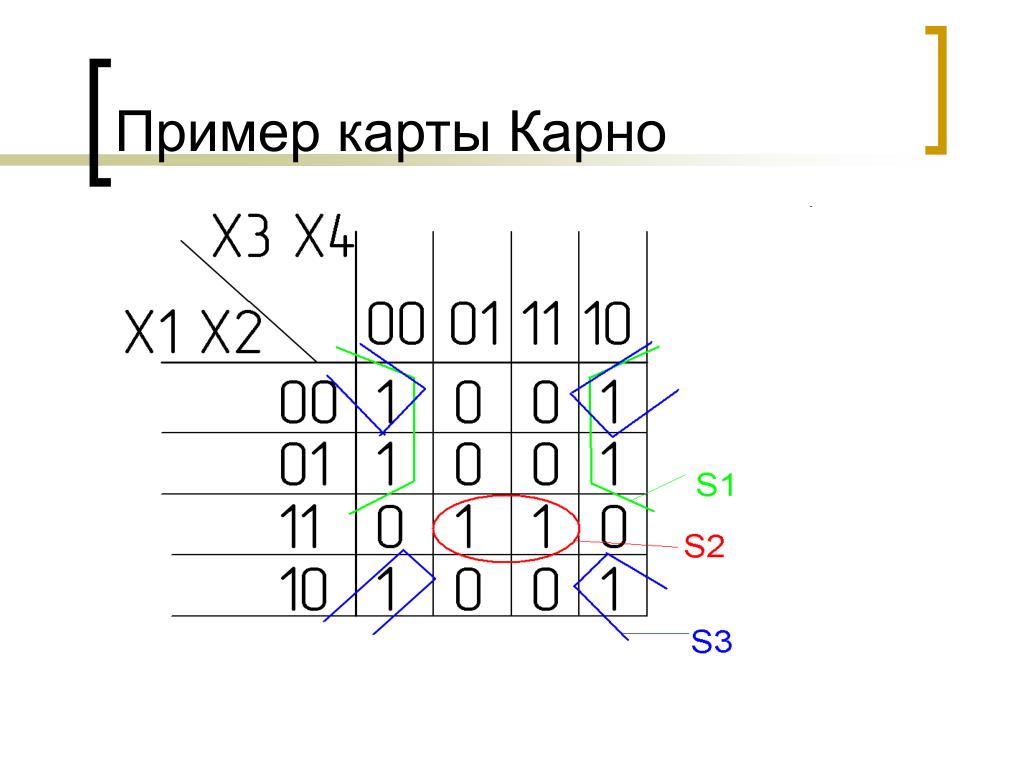

Лабораторная на тему Карта Карно

Лабораторная работа №2
Вариант 12
Задание:
1. Заполнить таблицу истинности для 3-х переменных в соответствии с вариантом задания:
a) Получить выражение в форме СДНФ;
b) Упростить полученное выражение, используя эквивалентные преобразования булевой алгебры;
c) Построить карту Карно;
d) Упростить по карте Карно.
f8=1,0,1,0,0,1,1,0Решение:
abcf800010010010101101000101111011110a) Для нахождения СДНФ нужно из таблицы истинности выделить лишь те строки, результат которых равен 1. Для данной функции набор строк будет следующим:
abcf80001010110111101Далее, для каждой строки выписываем конъюнкцию всех переменных по следующему алгоритму: если значение переменной в данной строке равно 1, то в конъюнкцию записываем саму переменную, а если равно 0, то – отрицание этой переменной. После этого все конъюнкции связываем в дизъюнкцию. В результате, СДНФ функции f8 имеет вид:f8=a&b&c∨a&b&c∨a&b&c∨a&b&cb) Упростим полученное выражение, используя эквивалентные преобразования булевой алгебры:
a&b&c∨a&b&c∨a&b&c∨a&b&c==a&b&c∨a&b&c∨a&b&c∨a&b&c∨a&b&c==a&c&b∨b∨a&b&c∨b&c&a∨a==a&c&1∨a&b&c∨b&c&1==a&c∨a&b&c∨b&c1. Закон идемпотентности
2. Закон дистрибутивности
3. Закон исключенного третьего
4. Свойство «1»

c) Строим карту Карно, используя таблицу истинности для функции f8:
a\bc000111100100110101d) После объединения соответствующих ячеек таблицы, упрощаем функцию f8:

f8=a&c∨a&b&c∨b&cРезультаты, полученные в пунктах b) и d) совпали.
2. Заполнить таблицу истинности для 4-х переменных в соответствии с вариантом задания:
a) Получить выражение в форме СДНФ;
b) Упростить полученное выражение, используя эквивалентные преобразования булевой алгебры;
c) Построить карту Карно;
d) Упростить по карте Карно.
f16=0,0,1,0,1,0,1,1,0,1,1,0,1,0,0,1Решение:
abcdf1600000000100010100110010010101001101011111000010011101011011011001110101110011111
a) Для нахождения СДНФ нужно из таблицы истинности выделить лишь те строки, результат которых равен 1. Для данной функции набор строк будет следующим:
abcdf160010101001011010111110011101011100111111Далее, для каждой строки выписываем конъюнкцию всех переменных по следующему алгоритму: если значение переменной в данной строке равно 1, то в конъюнкцию записываем саму переменную, а если равно 0, то – отрицание этой переменной.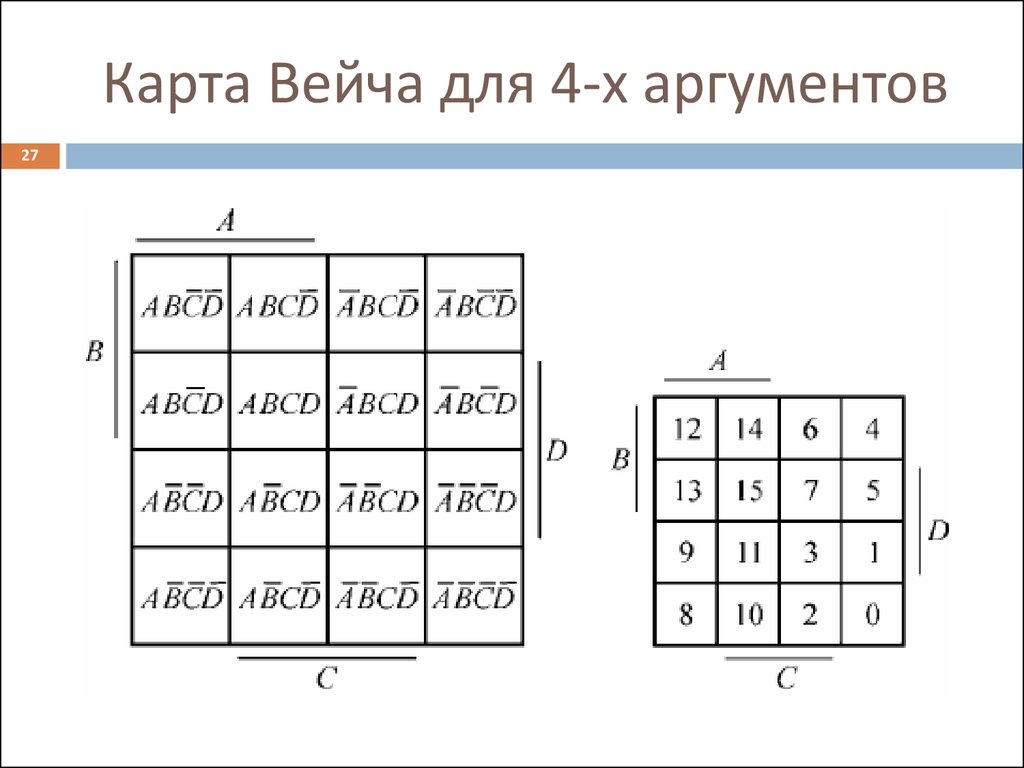 После этого все конъюнкции связываем в дизъюнкцию. В результате, СДНФ функции f8 имеет вид:f8=a&b&c&d∨a&b&c&d∨a&b&c&d∨a&b&c&d∨a&b&c&d∨∨a&b&c&d∨a&b&c&d∨a&b&c&db) Упростим полученное выражение, используя эквивалентные преобразования булевой алгебры:
a&b&c&d∨a&b&c&d∨a&b&c&d∨a&b&c&d∨a&b&c&d∨∨a&b&c&d∨a&b&c&d∨a&b&c&d==a&b&c&d∨a&…

Решатель карт Карно

Решатель карт Карно найдет k-карту с ответом суммы произведений и произведения сумм в трех типах форматов.

Общее решение [с использованием (+), (.), (‘)]
Решение VHDL [с использованием И, НЕ и ИЛИ]
Решение Verilog [с использованием (~), (|) и (&) ]

Получите карту Карно для 2,4,6 и даже 10 переменных в калькуляторе карт Карно.

Что такое карта Карно?

Эта карта, разработанная физиком Морисом Карно, находит решение двоичных выражений в графической форме и упрощает их без использования каких-либо законов или теорем.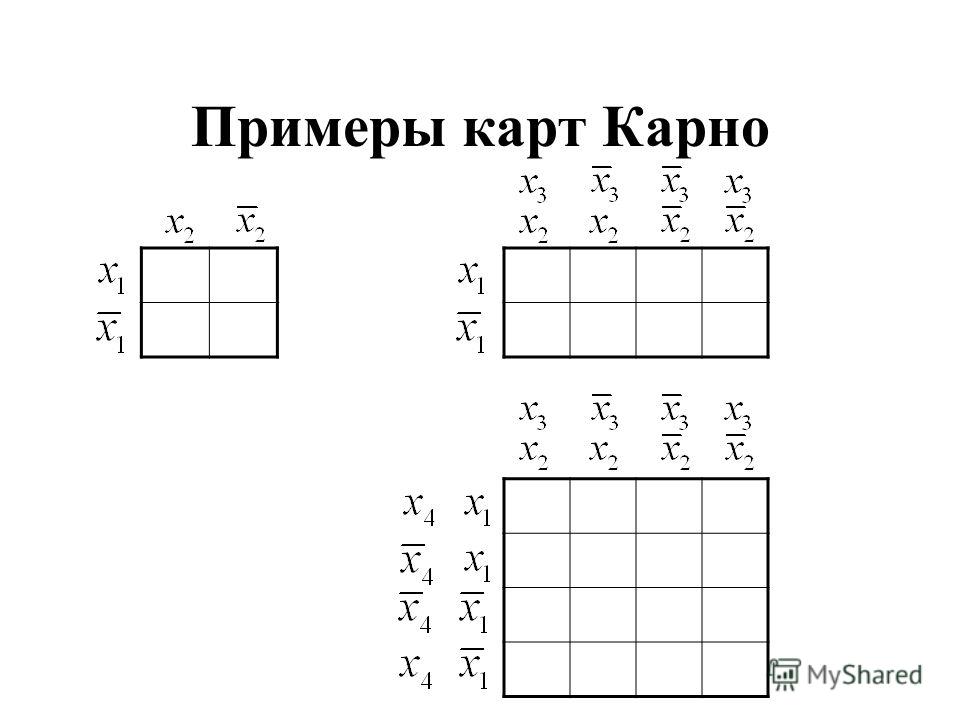

Формула для карты карно:

Карта формируется по правилам, но основным моментом карты является ее формула.

2 ⁿ где n представляет количество переменных. Эта формула расскажет о количестве отрисовываемых клеток/квадратов.

Цифры внутри ячейки представляют номер ячейки. Их предстоит запомнить. Уловка, чтобы запомнить эти числа, заключается в умножении двоичного числа строки и столбца для этой ячейки и нахождении его десятичного представления.

Например, 5 представляется как 101 в двоичном формате. Если вы найдете ячейку № 5 на карте и умножите ее номер столбца и строки, это также даст 101.

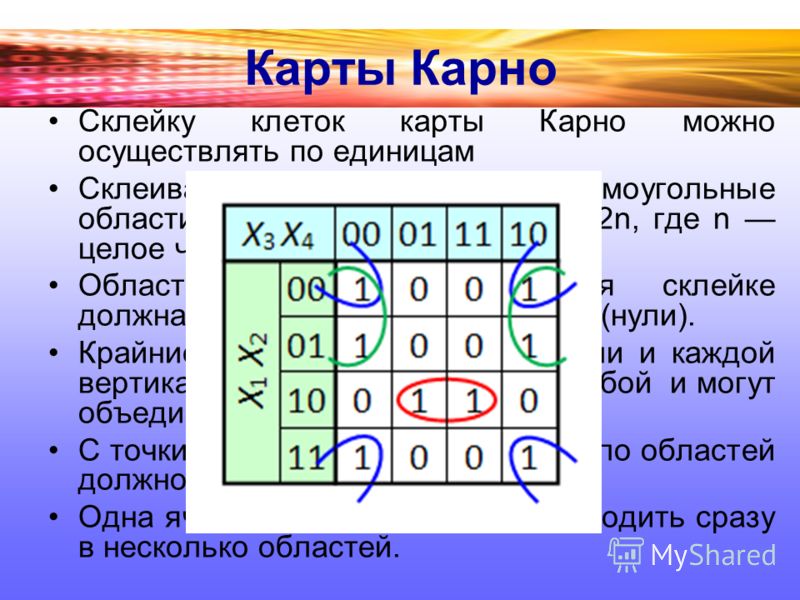
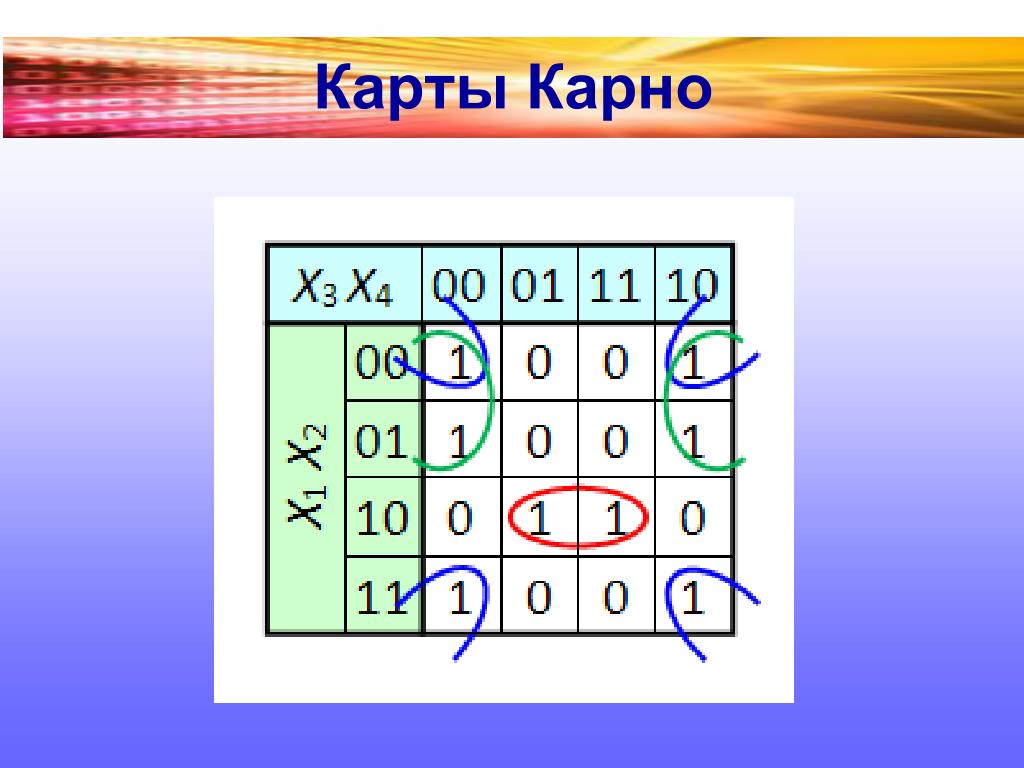
Правила для k-map:

Всегда используйте «1» для обозначения минтерма в ячейке.
Создание горизонтальных или вертикальных групп. Диагональная группировка не допускается.
Одна ячейка может входить в состав двух и более групп одновременно. Допускается перекрытие.
Создавайте группы парами, четверками или октетами. Короче, как можно больше. Попробуйте сделать октет. Если это невозможно, ищите четверку, а затем пару.

Ниже приведены примеры парной и четверной группировки.

Как сделать карту карно (k-map)?

Найдите количество переменных. Используйте число как показатель степени 2 и вычислите требуемые номера ячеек. Представьте minterms на 1 после определения местоположения ячеек.

Пример:

Создайте k-карту из следующих выражений и сформируйте группы.

F (A,B,C,D) = (4,12,6,14,8,10)

Решение:

Шаг 1: Найдите количество ячеек.

Имеется 4 переменные. Используя 4 как степень 2, мы получаем:

2 ⁴ = 16

Шаг 2: Сделайте ячейки.

Шаг 3: Найдите ячейки и поместите в них одну.

Шаг 4: Сделайте группы.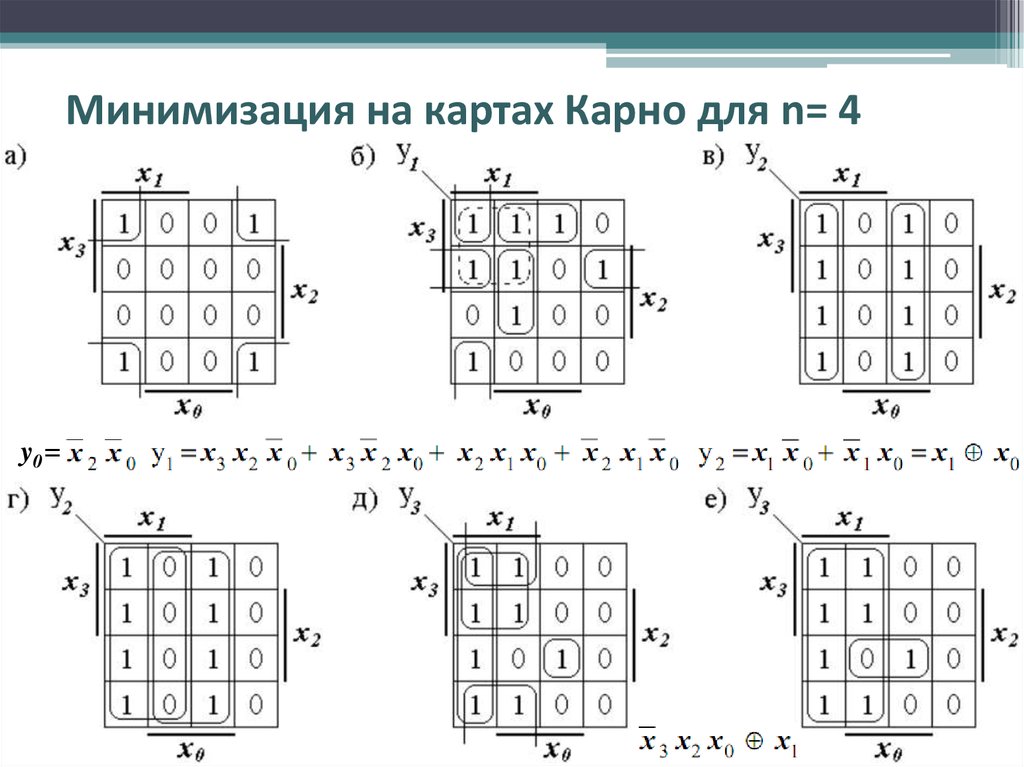

Формируется четверка и пара.

SOP и POS карты karnaugh:

Сумма произведений и произведение сумм — это методы представления логических выражений. Оба имеют свое применение в зависимости от ситуации.

Ключевые точки:

Minterms — это значения, дающие результат 1. Minterms представлены в SOP.

Максимальное количество членов приводит к нулям и включает все оставшиеся ячейки, кроме безразличных. Они используются в POS.

Неважно — это ячейки, представленные «x». Они часто используются для завершения групп.

Пара 1 и 0 отменяется.

Сумма произведений:

Все 0 означают дополнение переменной. Все единицы означают пустые или нормальные переменные. Переменные группы разделяются точкой (умножение), а группы разделяются плюсом (сложение).

Пример:

Найдите SOP этого логического выражения.

F(A,B,C,D) = m (0,6,8,13,14)
= d (2,4,10)

Решение:

Шаг 1: -карта.

Шаг 2: Разместите минтермс и пофиг.

Шаг 3: Создайте группы.

Образуются две четверки и одиночка. Как вы можете видеть, во втором квадрате значения безразличия равны 1,9.0005

Шаг 4: Запишите двоичное значение групп.

Шаг 5: Запишите сумму произведений.

F = (B’ .D’) + (C .D’) + (A .B .C’ .D)

Произведение сумм:
Среднее дополнение переменной со всеми единицами. Все нули означают пустую или нормальную переменную. Переменные группы разделяются суммой (сложением), а группы разделяются точкой (умножение).
Пример:
В предыдущем примере найдите произведение сумм.
Решение:
Шаг 1: После создания k-карты, как и раньше, введите 0 в качестве maxterms. Кроме того, инвертируйте дополнения.
Шаг 2: Создание групп.
Шаг 3: Запишите двоичные значения и отмените 1 и 0.

Шаг 4: Запишите произведение сумм.
F = (A + D’)(C’ + D’)(B + D’)(B’ + C + D)
Карты Карно онлайн | Ворота Видьялай
Minimization Of Boolean Expressions-

There are following two methods of minimizing or reducing the boolean expressions-

By using laws of Boolean Algebra
By using Karnaugh Maps also called as K Maps

В этой статье мы обсудим Karnaugh Maps или K Maps.

Карта Карно-

Карта Карно, также называемая K-картой, представляет собой графическое представление
, обеспечивающее систематический метод упрощения логических выражений.

Для логического выражения, состоящего из n переменных, количество ячеек, необходимых в K Map = 2 ⁿ ячеек.

Карта K с двумя переменными-

Карта K с двумя переменными строится для логического выражения, состоящего из двух переменных.
Количество ячеек, присутствующих в двух переменных K Map = 2 ² = 4 ячейки.
Итак, для булевой функции, состоящей из двух переменных, мы рисуем карту 2 x 2 K.

Две переменные K Map могут быть представлены как-

Здесь A и B — две переменные данной логической функции.

K-карта с тремя переменными-

K-карта с тремя переменными строится для логического выражения, состоящего из трех переменных.
Количество ячеек, присутствующих в трех переменных K Map = 2 ³ = 8 ячеек.
Итак, для булевой функции, состоящей из трех переменных, мы рисуем карту 2 x 4 K.

Карта K с тремя переменными может быть представлена как

Здесь A, B и C — три переменные данной логической функции.

K-карта с четырьмя переменными-

K-карта с четырьмя переменными строится для логического выражения, состоящего из четырех переменных.
Количество ячеек, присутствующих в четырех переменных K Map = 2 ⁴ = 16 ячеек.
Итак, для булевой функции, состоящей из четырех переменных, мы рисуем карту 4 x 4 K.

Карта K с четырьмя переменными может быть представлена как:

Здесь A, B, C и D — четыре переменные данной булевой функции.

Правила упрощения карты Карно-

Чтобы минимизировать заданную логическую функцию,
Мы рисуем K-карту в соответствии с количеством содержащихся в ней переменных.
Мы заполняем карту K нулями и единицами в соответствии с ее функцией.
Затем минимизируем функцию в соответствии со следующими правилами.

Правило-01:

Мы можем сгруппировать 0 с 0 или 1 с 1, но мы не можем сгруппировать 0 и 1 вместе.
X, представляющий безразличие, может быть сгруппирован как с 0, так и с 1.

ПРИМЕЧАНИЕ
Нет необходимости отдельно группировать X, т. е. их можно игнорировать, если все 0 и 1 уже сгруппированы.

Правило-02:

Группы могут перекрывать друг друга.

Правило-03:

Мы можем создать только группу, количество ячеек которой может быть представлено в степени 2.
Другими словами, группа может содержать только 2 ⁿ, т. е. 1, 2, 4, 8, 16 и так далее количество ячеек.
Пример-
Правило-04:
могут быть только любые горизонтальные или верные.
Мы не можем создавать группы диагональной или любой другой формы.

Правило-05:

Каждая группа должна быть как можно больше.
Пример-
Правило-06:
Опциональная группа и группировка угловой.
Пример противоположной группировки показан в Правиле-05.
Ниже показан пример группировки углов.

Пример —

Правило-07:

Групп должно быть как можно меньше.
Проблемы, основанные на карту Карно,
Проблема-01:
Минимизируйте следующую функцию Boolean-
F (A, B, C, D) = σm (0, 0,
F (A, B, C, D) = 1, 2, 5, 7, 8, 9, 10, 13, 15)

Решение-

Поскольку данное логическое выражение имеет 4 переменные, мы рисуем карту 4 x 4 K.
Заполняем ячейки K Map в соответствии с заданной булевой функцией.
Затем формируем группы в соответствии с указанными выше правилами.

Тогда имеем-

Теперь
F(A, B, C, D) +
+ AB
= AB (A’B’ + A’B + AB + AB’)C’D + (A’B’ + AB’)(C’D’ + CD’)
= BD + C’D + B’D’
Таким образом, минимизированное логическое выражение составляет
F (A, B, C, D) = BD + C’D + B’D ‘
Проблема-02:
. Минимизируйте следующую логическую функцию:
F(A, B, C, D) = Σm(0, 1, 3, 5, 7, 8, 9, 11, 13, 15)

Решение:

Поскольку данное логическое выражение имеет 4 переменные, мы рисуем карту 4 x 4K.
Заполняем ячейки K Map в соответствии с заданной булевой функцией.
Затем мы формируем группы в соответствии с вышеуказанными правилами.

Тогда имеем-

Теперь
F(A, B, C, D)
+
= (A’B’AB’) (C’D + CD) + (A’B’ + AB’)(C’D’ + C’D)
= D + B’C’

Таким образом, минимизированное логическое выражение равно:
F(A, B, C, D) = B’C’ + D

Задача-03:

Минимизация следующей булевой функции-
F(A, B, C, D) = Σm(1, 3, 4, 6, 8, 9, 11, 13, 15) + Σd(0, 2, 14)

Решение-

Поскольку данное логическое выражение имеет 4 переменные, мы рисуем карту 4 x 4 K.
Заполняем ячейки K Map в соответствии с заданной булевой функцией.
Затем формируем группы в соответствии с указанными выше правилами.

Тогда имеем-

Теперь,
F(A, B, C, D)
= (AB + AB’)(C’D + CD) + (A’B’ + AB’)(C ‘D + CD) + (A’B’ + AB’)(C’D’ + C’D) + (A’B’ + A’B)(C’D’ + CD’)
= AD + B’D + B’C’ + A’D’

Таким образом, минимизированное логическое выражение равно:
F(A, B, C, D) = AD + B’D + B’C’ + A ‘D’

Проблема-04:

Минимизация следующей логической функции-
F(A, B, C) = Σm(0, 1, 6, 7) + Σd(3, 5)

Решение-

Поскольку данное логическое выражение имеет 3 переменные, поэтому мы рисуем карту 2 x 4 K.
Заполняем ячейки K Map в соответствии с заданной булевой функцией.
Затем формируем группы в соответствии с указанными выше правилами.

Тогда имеем-

Теперь
F(A, B, C)
= A'(B’C’ + B’C) + A(BC + BC’)
= A’B’ + AB

Таким образом, минимизированное логическое выражение равно B, C) = AB + A’B’
ПРИМЕЧАНИЕ.
Можно отметить, что нет необходимости рассматривать четверную группу.
Это потому, что даже если мы рассмотрим эту группу, нам придется рассмотреть два других дуэта.
Итак, нет смысла рассматривать эту четверную группу.

Задача-05:

Минимизация следующей булевой функции-
F(A, B, C) = Σm(1, 2, 5, 7) + Σd(0, Σd(0, 6, 6) )

Решение-

Поскольку данное логическое выражение имеет 3 переменные, мы рисуем карту 2 x 4 K.
Заполняем ячейки K Map в соответствии с заданной булевой функцией.
Затем формируем группы в соответствии с указанными выше правилами.

Тогда имеем-

Теперь
F(A, B, C)
) + ‘C + A’04 = (A, B, C)
) + ‘C + A’04 = (A, B, C) A(B’C’ + B’C + BC + BC’) + (A + A’)(B’C’ + BC’)
= B’ + A + C’

Таким образом, минимизированное логическое значение выражение is-
F(A, B, C) = A + B’ + C’

Задача-06:

Минимизация следующей логической функции- , С) = Σm(0, 1, 6, 7) + Σd(3, 4, 5)

Решение-

Поскольку данное логическое выражение имеет 3 переменные, мы рисуем карту 2 x 4 K.
Заполняем ячейки K Map в соответствии с заданной булевой функцией.
Затем формируем группы в соответствии с указанными выше правилами.

Тогда имеем-

Теперь
F(A, B, C)
+ ‘C +
) = (A, B, C)
+ ‘C A’) А(В’С’ + В’С + ВС + ВС’)
= B ‘ + A
Таким образом, минимизированное логическое выражение составляет
F (A, B, C) = A + B’
Проблема-07:
следующая логическая функция:
F(A, B, C, D) = Σm(0, 2, 8, 10, 14) + Σd(5, 15)

Решение-
7
^{08 Поскольку данное логическое выражение имеет 4 переменные, мы рисуем карту 4 x 4 K. Заполняем ячейки K Map в соответствии с заданной булевой функцией.
Затем мы формируем группы в соответствии с вышеуказанными правилами.

Тогда имеем-

Теперь
F(A, B, C, D)
= (CB’AB +’AB + AB’)(C’D’ + CD’)
= ACD’ + B’D’

Таким образом, минимизированное логическое выражение равно
F(A, B, C, D) = ACD’ + B’D’

Задача-08:
Минимизация следующей логической функции-
F(A, B, C, D) = Σm(3, 4, 5, 7, 9, 13, 14, 15)

Решение-
4 переменных, поэтому мы рисуем карту 4 x 4K.
Заполняем ячейки K Map в соответствии с заданной булевой функцией.
Затем формируем группы в соответствии с указанными выше правилами.

Тогда имеем-

Теперь,
F(A, B, C, D)
= A’B(C’D’ + C’D) + (A’B’ + A’B)(CD) + (AB + AB’)(C ‘D) + AB(CD + CD’)
= A’BC’ + A’CD + AC’D + ABC

Таким образом, минимизированное логическое выражение равно
F(A, B, C, D) = A’BC’ + A’CD + AC’D + ABC
≥
Важно отметить, что мы не рассматриваем четверную группу, потому что мы все равно должны рассматривать дуэты.

Задача-09:
Рассмотрим следующую логическую функцию-
F(W, X, Y, Z) = Σm(1, 3, 4, 6, 9, 11, 12, 14)

Эта функция независима от ________ числа переменных. Заполнить бланк.

Решение-
Поскольку данное логическое выражение имеет 4 переменные, мы рисуем карту 4 x 4 K. No related posts.}