iMath Wiki — Минимизация булевых функций. Минимизирующие карты Карно. Метод Куайна-МакКласки
Ясно, что при разработке логических схем, немаловажной является задача минимизации количества используемых элементов (другими словами, логических операций).
В связи с этим, возникает задача минимизации логических функций в некотором классе формул. В частности, в классах ДНФ и КНФ.
- Минимальная ДНФ
- Такая ДНФ, которая содержит наименьшее общее число вхождений переменных по сравнению со всеми равносильными ей ДНФ.
- Минимальная КНФ
- Такая КНФ, которая содержит наименьшее общее число вхождений переменных по сравнению со всеми равносильными ей КНФ.
Процесс нахождения минимальных форм, собственно, и называется минимизацией. В простых случаях, для минимизации достаточно тождественных преобразований. В более сложных – используются специальные алгоритмы.
Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения.
\[ \;\overline{x_1}\;x_2x_3x_4 \vee \;\overline{x_1}\;x_2\;\overline{x_3}\;x_4 = \;\overline{x_1}\;x_2x_4 (x_3 \vee\;\overline{x_3}\;) = \;\overline{x_1}\;x_2x_4 \mathbin{\&}1 = \;\overline{x_1}\;x_2x_4. \]
Аналогично для КНФ:
\[ (\;\overline{x_1}\;\vee x_2\vee x_3\vee x_4) (\;\overline{x_1}\;\vee x_2\vee\;\overline{x_3}\;\vee x_4) = \;\overline{x_1}\;\vee x_2\vee x_4\vee x_3\;\overline{x_3}\; = \;\overline{x_1}\;\vee x_2\vee x_4\vee 0 = \;\overline{x_1}\;\vee x_2\vee x_4. \]
Возможность поглощения следует из очевидных равенств
\[ A \vee\;\overline{A}\; = 1 \]\[ A\;\overline{A}\; = 0. \]
Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск членов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей.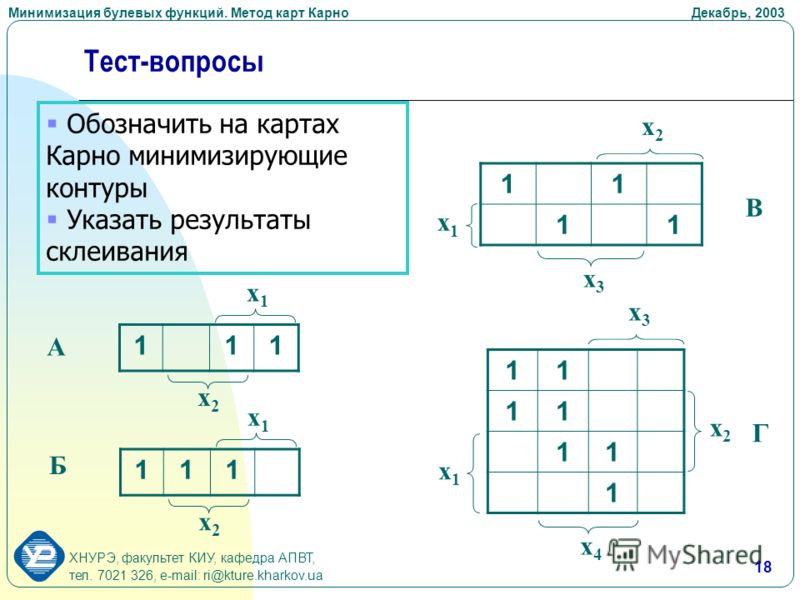 N\) различных элементарных членов.
N\) различных элементарных членов.
Элементарные члены СДНФ или СКНФ образуют структуру, топологически эквивалентную \(N\)-мерному кубу. Действительно, если рассматривать набор значений функции \(x_1,\,\ldots,\,x_N\) как \(N\)-мерный вектор \(\{x_1,\,\ldots,\,x_N\}\), мы получим набор точек, лежащих на ортах \(N\)-мерной системы координат, и удаленных друг от друга на \(1\). Другими словами, мы получим \(N\)-мерный гиперкуб с ребром \(1\).
Например, для функции двух переменных, заданной таблицей истинности:
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
можно построить эквивалентный ей квадрат:
001111000110Или, если обозначить вершины соответствующими элементарными конъюнкциями и выделить вершины, конъюнкции которых входят в СДНФ:
0x̅₁x₂1x₁x₂0x̅₁x̅₂1x₁x̅₂Или СКНФ:
0x₁∨x̅₂1x̅₁∨x̅₂0x₁∨x₂1x̅₁∨x₂Можно заметить, что члены, находящиеся на одной стороне квадрата, могут быть склеены. Соответственно, если составляется ДНФ, то операции производятся только над вершинами, в которых функция имеет значение \(1\) (по правилам построения СДНФ). Если же составляется КНФ, то над вершинами, в которых функция имеет значение \(0\) (по правилам построения СКНФ).
Соответственно, если составляется ДНФ, то операции производятся только над вершинами, в которых функция имеет значение \(1\) (по правилам построения СДНФ). Если же составляется КНФ, то над вершинами, в которых функция имеет значение \(0\) (по правилам построения СКНФ).
При этом, сохраняются переменные, значение которых на стороне постоянно.
В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.
Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации. Например, четыре члена, принадлежащие одной грани куба, объединяются в один с поглощением двух переменных:
\[ \;\overline{x_1}\;\;\overline{x_2}\;\;\overline{x_3}\; \vee x_1\;\overline{x_2}\;\;\overline{x_3}\; \vee \;\overline{x_1}\;\;\overline{x_2}\;x_3 \vee x_1\;\overline{x_2}\;x_3 =\]
\[ = \;\overline{x_2}\; (\;\overline{x_1}\;\;\overline{x_3}\; \vee\;\overline{x_1}\;x_3 \vee x_1\;\overline{x_3}\; \vee x_1x_3) = \;\overline{x_2}\; (\;\overline{x_1}\; \vee x_1)(\;\overline{x_3}\; \vee x_3) = \;\overline{x_2}\; \]
В общем случае можно сказать, что \(2^K\) членов, принадлежащие одной \(K\)–мерной грани гиперкуба, склеиваются в один член, при этом поглощаются \(K\) переменных.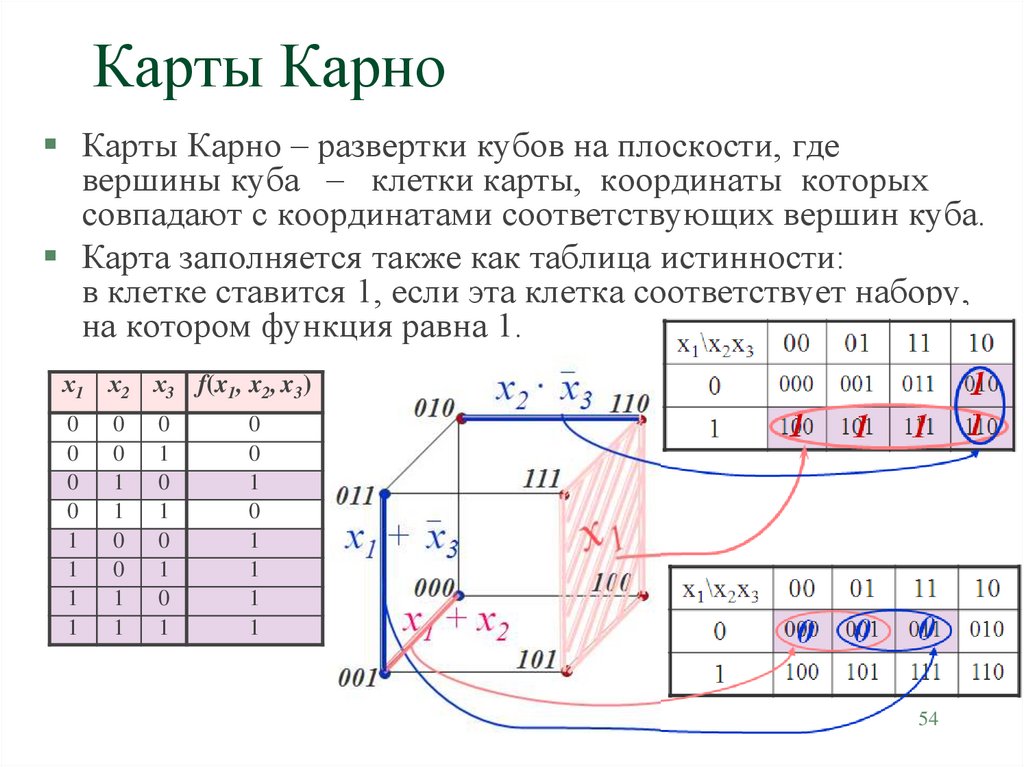 K\) смежных ячеек, и в результирующую ДНФ или КНФ входят только те переменные, которые неизменны в рамках данной группы. Общее число членов соответствует числу групп в карте Карно, а число неизменных переменных обратным образом зависит от количества элементов в группе. Как следствие, группы необходимо выбирать как можно более большими. Следует отметить, что одна комбинация переменных может входить в несколько групп.
K\) смежных ячеек, и в результирующую ДНФ или КНФ входят только те переменные, которые неизменны в рамках данной группы. Общее число членов соответствует числу групп в карте Карно, а число неизменных переменных обратным образом зависит от количества элементов в группе. Как следствие, группы необходимо выбирать как можно более большими. Следует отметить, что одна комбинация переменных может входить в несколько групп.
Для функций четырех переменных, требуется развертка 4-мерного гиперкуба. Карта Карно в таком случае имеет вид:
| \(00\) | \(f(0,0,0,0)\) | \(f(0,1,0,0)\) | \(f(1,1,0,0)\) | \(f(1,0,0,0)\) |
| \(01\) | \(f(0,0,0,1)\) | \(f(0,1,0,1)\) | \(f(1,1,0,1)\) | \(f(1,0,0,1)\) |
| \(11\) | \(f(0,0,1,1)\) | \(f(0,1,1,1)\) | \(f(1,1,1,1)\) | \(f(1,0,1,1)\) |
| \(10\) | \(f(0,0,1,0)\) | \(f(0,1,1,0)\) | \(f(1,1,1,0)\) | \(f(1,0,1,0)\) |
В данном случае, все крайние ячейки смежны друг другу.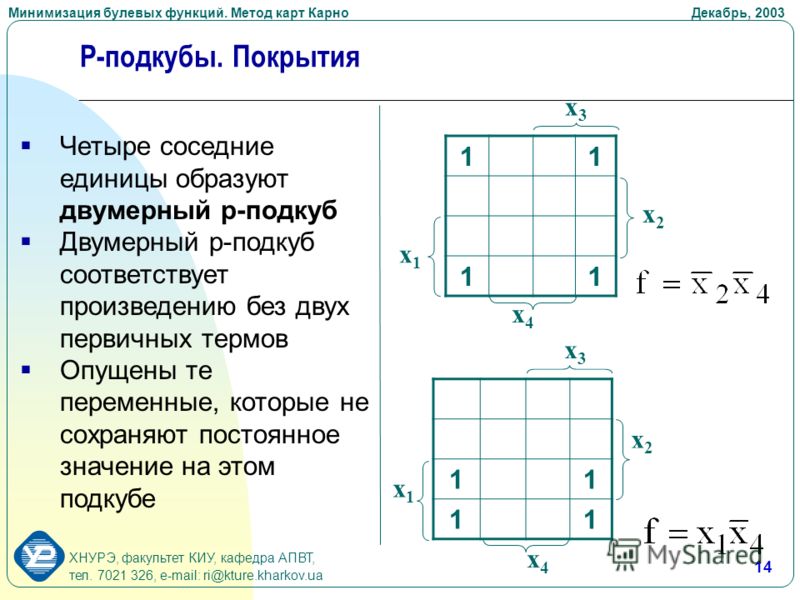 Это можно себе представить, натянув эту развертку на тор (“бублик”):
Это можно себе представить, натянув эту развертку на тор (“бублик”):
Возможно так же построение карт Карно для функций 5 и 6 переменных, однако работа с ними значительно затрудена. Для числа переменных, большего 6, использование карт Карно попросту непрактично.
Пример
Рассмотрим функцию, имеющую следующую таблицу истинности:
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Перепишем эту таблицу в виде карты Карно:
| 00 | 1 | 1 | 0 | 0 |
| 01 | 1 | 0 | 0 | 0 |
| 11 | 0 | 1 | 1 | 0 |
| 10 | 1 | 1 | 1 | 0 |
Легко выделяются три группы.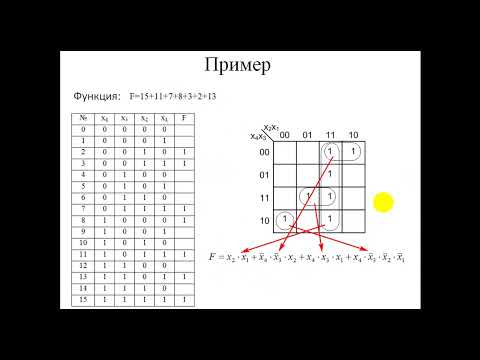 Исходя из этого, записывается ДНФ:
Исходя из этого, записывается ДНФ:
\(\;\overline{x_1}\;\;\overline{x_2}\;\;\overline{x_3}\;\)\(\vee\)\(\;\overline{x_1}\;\;\overline{x_4}\;\)\(\vee\)\({x_2}{x_3}\)
Метод Куайна-МакКласси строится на основе того же аппарата, что и карты Карно, однако оказывается более практичным для большего количества переменных.
Алгоритм заключается последовательной склейке, и затем редукции результата.
Склейка
Сначала элементарные члены совершенной формы записываются в двоичной форме в таблицу, где группируются по количеству единиц.
Затем, члены, которые отличаются одной переменной (одним битом), могут быть склеены. В таком случае единица заменяется на “-”. Очевидно, что склеены могут быть только члены из соседних групп
Члены, которые нельзя склеить, обозначаются звездочкой «*».
Полученные склеенные члены могут, в свою очередь, так же быть склеены. При этом “-” трактуется как “третье” значение.
Когда никакие члены больше не могут быть склеены, из членов, отмеченных “*”, составляется сокращенная форма, которая не обязательно минимальна.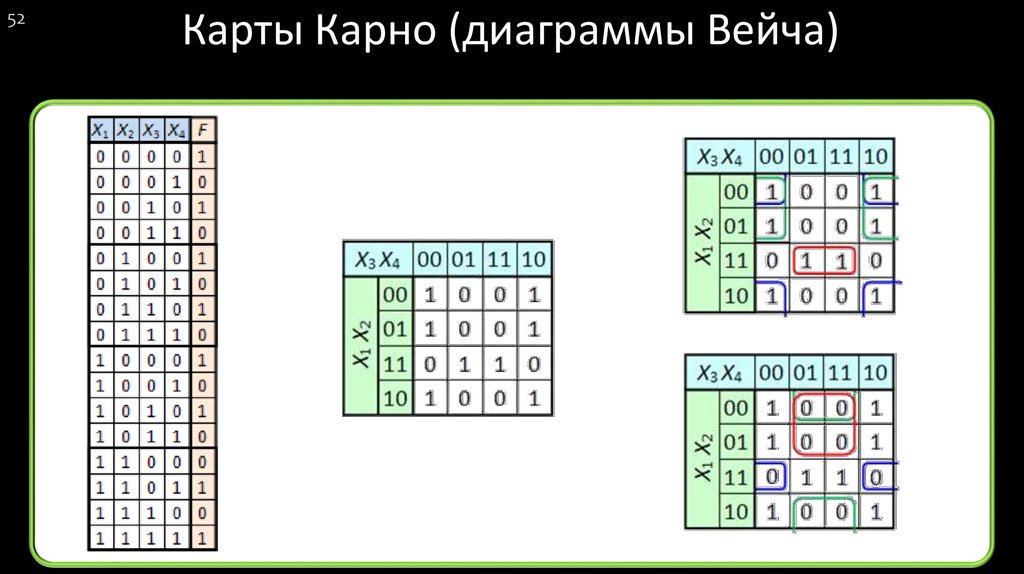 После этого производится редукция.
После этого производится редукция.
Редукция
Для редукции, составляется таблица, в строки которой включаются члены сокращенной формы, а в столбцы – члены совершенной.
В ячейках ставится отметка (например, крестик “×”), если соответствующий член сокращенной формы поглощает соответствующий член совершенной формы (т.е. если заголовок строки является частью заголовка столбца).
Выбираются столбцы, содержащие только один “×”. Соответсвтующие им члены сокращенной формы составляют
Если ядро не перекрывает все столбцы, то в минимальную форму так же включаются несколько членов сокращенной формы, не входящих в ядро, таким образом, чтобы члены минимальной формы перекрывали все столбцы таблицы.
Пример
Найдем минимальную форму функции
| 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 1 |
| 3 | 0 | 0 | 1 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 10 | 1 | 0 | 1 | 0 | 1 |
| 11 | 1 | 0 | 1 | 1 | 0 |
| 12 | 1 | 1 | 0 | 0 | 1 |
| 13 | 1 | 1 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 0 |
| 15 | 1 | 1 | 1 | 1 | 1 |
Члены СДНФ в двоичной нотации:
- 0000 = 0
- 0001 = 1
- 0010 = 2
- 0011 = 3
- 0101 = 5
- 0111 = 7
- 1000 = 8
- 1010 = 10
- 1100 = 12
- 1101 = 13
- 1111 = 15
Группировка:
0
- 0000 = 0
1
- 0001 = 1
- 0010 = 2
- 1000 = 8
2
- 0011 = 3
- 0101 = 5
- 1010 = 10
- 1100 = 12
3
- 0111 = 7
- 1101 = 13
4
- 1111 = 15
Склейка 1:
- 0, 1 = 000-
- 0, 2 = 00-0
- 0, 8 = -000
- 1, 3 = 00-1
- 1, 5 = 0-01
- 2, 3 = 001-
- 2,10 = -010
- 8,10 = 10-0
- 8,12 = 1-00
- 3,7 = 0-11
- 5,7 = 01-1
- 5,13 = -101
- 12,13 = 110-
- 7,15 = -111
- 13,15 = 11-1
Группировка 2:
- 0, 1 = 000-
- 2, 3 = 001-
- *12,13 = 110-
- 0, 2 = 00-0
- 1, 3 = 00-1
- 8,10 = 10-0
- 5,7 = 01-1
- 13,15 = 11-1
- 1, 5 = 0-01
- *8,12 = 1-00
- 3,7 = 0-11
- 0, 8 = -000
- 2,10 = -010
- 5,13 = -101
- 7,15 = -111
Склейка 2:
- *0,1,2,3 = 00–
- *0,2,8,10 = -0-0
- *5,7,13,15 = -1-1
- *1,3,5,7 = 0–1
Итого, члены сокращенной формы:
- 12,13 = 110-
- 8,12 = 1-00
- 0,1,2,3 = 00–
- 0,2,8,10 = -0-0
- 5,7,13,15 = -1-1
- 1,3,5,7 = 0–1
Редукция:
| 12,13 | × | × | |||||||||
| 8,12 | × | × | |||||||||
| 0,1,2,3 | × | × | × | × | |||||||
| 0,2,8,10 | × | × | × | ⊗ | |||||||
| 5,7,13,15 | × | × | × | ⊗ | |||||||
| 1,3,5,7 | × | × | × | × |
Кружком обведены члены ядра.
Ядро, таким образом, включает члены -0-0 и -1-1. Для получения минимальной формы, нам нужно перекрыть дополнительно столбцы 1, 3, 12. Для этого можно взять, например, 0,1,2,3 = 00– и 12,13 = 110-:
\[ f = \;\overline{x_2}\;\;\overline{x_4}\; \vee {x_2}{x_4} \vee \;\overline{x_1}\;\;\overline{x_2}\; \vee {x_1}{x_2}\;\overline{x_3}\; \]
Карта Карно:
| 00 | 1 | 1 | 1 | |
| 01 | 1 | 1 | 1 | |
| 11 | 1 | 1 | 1 | |
| 10 | 1 | 1 |
Минимизация функций с помощью карт Карно
Занятие 17. Тема «Минимизация функций с помощью карт Карно»
План лекции:
Понятие карты Карно
Виды карт Карно и метод их заполнение
Принципы склейки
Правило нахождения МДНФ и МКНФ
Понятие карты Карно
МДНФ – минимальная дизъюнктивная нормальная форма
МКНФ — минимальная конъюнктивная нормальная форма
Метод карт Карно позволяет быстро получить минимальные ДНФ и КНФ.
Карта Карно – это таблица, каждая клетка в ней соответствует набору переменных булевой функции в её таблице истинности. Строки и столбцы карты обозначаются таким образом, чтобы любые соседние клетки по строкам или по столбцам отличались бы между собой значением только одной переменной. Это сделано для того, чтобы было бы возможно применить закон склеивания.
Виды карт Карно и метод их заполнение
Карта Карно для 2-х переменных – квадратная таблица размером (4 ячейки)
х1 х2 | 0 | 1 |
0 | ||
1 |
Ячейки заполняются 0 или 1, полученные в последнем столбце таблицы истинности, соответствующие наборам 00, 01, 10, 11.
Карта Карно для 3-х переменных – прямоугольная таблица размером (8ячеек). Каждая ячейка соответствует наборам 000, 001, 010, 011, 100, 101, 110, 111.
х2х3 х1 | 00 | 01 | 11 | 10 |
0 | ||||
1 |
Любые две рядом расположенные клетки являются соседними. Клетки, находящиеся на границах одной строки или столбца, так же считаются соседними, то есть, клетки, которые будут соседними при скручивании карты в вертикальный и горизонтальный цилиндры.
Карта Карно для 4-х переменных – квадратная таблица размером (16 ячеек).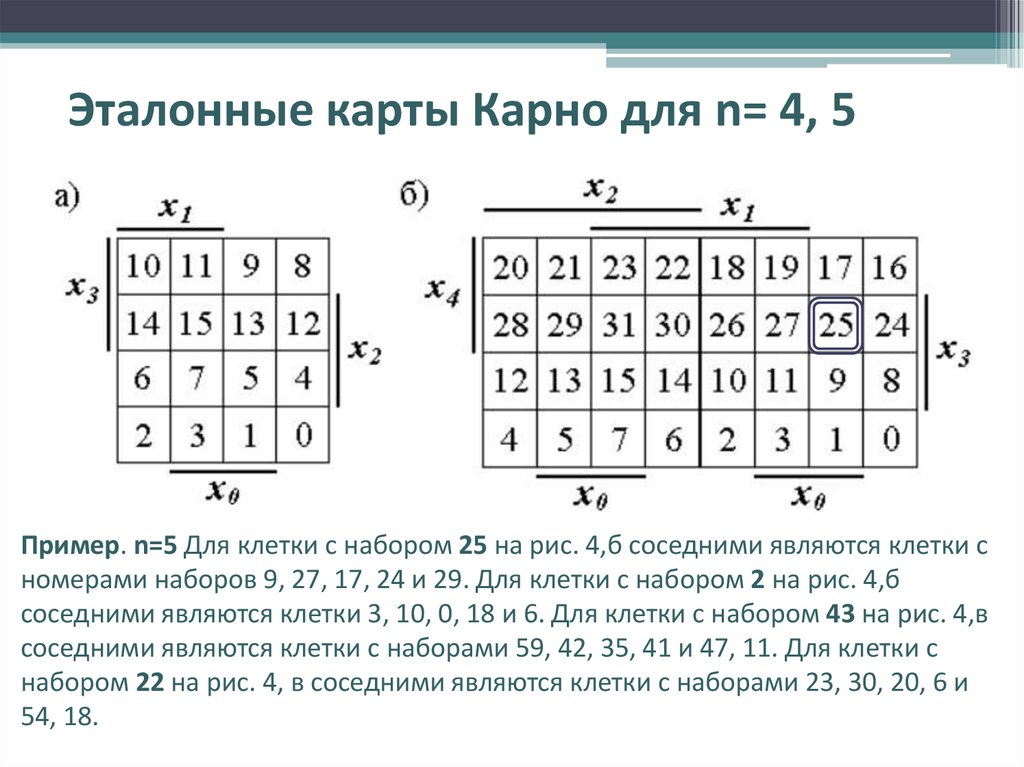 Каждая ячейка соответствует наборам 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.
Каждая ячейка соответствует наборам 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.
Карта Карно для 5-х переменных – прямоугольная таблица размером (32 ячейки).
Минимизация функций с помощью карт Карно или нахождение МДНФ (МКНФ) – это процесс склеивания одинаковых значений, стоящих в соседних ячейках.
Принципы склейки
Склейку клеток карты Карно можно осуществлять по единицам (если необходимо получить МДНФ) или по нулям (если требуется МКНФ).
Склеивать можно только прямоугольные области с числом единиц (нулей) 2n, где n — целое число.
Область, которая подвергается склейке, должна содержать только единицы (нули).
Крайние клетки каждой горизонтали и каждой вертикали также граничат между собой и могут объединяться в прямоугольники.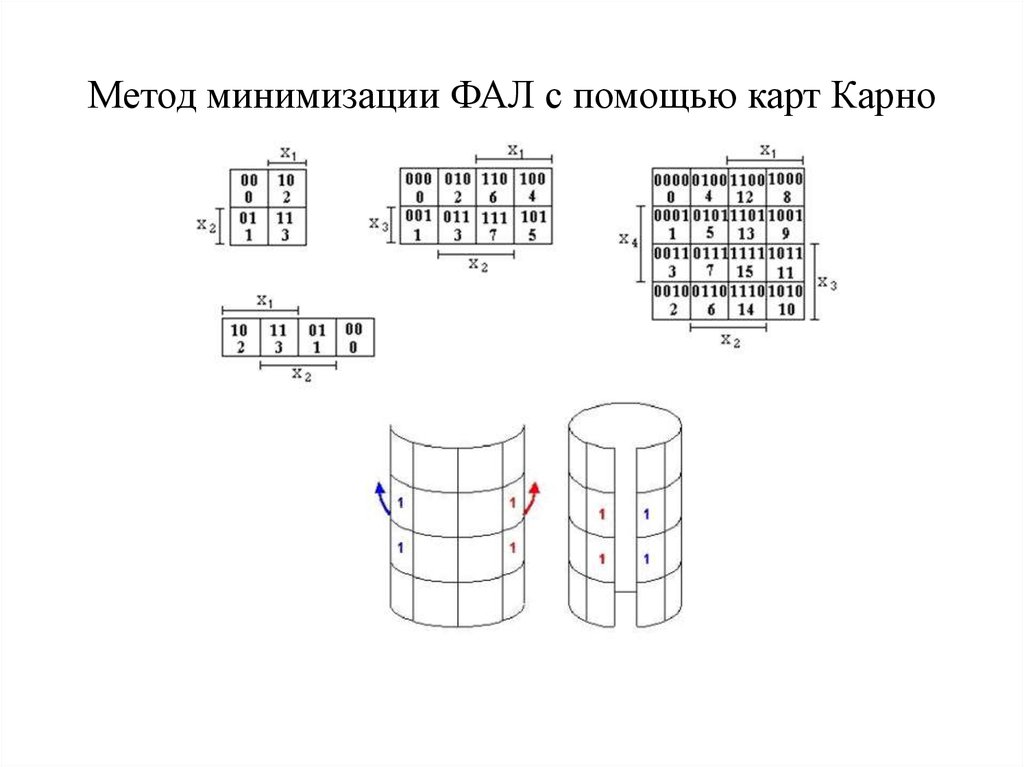 Следствием этого правила является смежность всех четырёх угловых ячеек карты Карно для N=4. Если во всех четырёх угловых ячейках стоят единицы (нули), они могут быть объединены в квадрат.
Следствием этого правила является смежность всех четырёх угловых ячеек карты Карно для N=4. Если во всех четырёх угловых ячейках стоят единицы (нули), они могут быть объединены в квадрат.
Все единицы (нули) должны попасть в какую-либо область.
С точки зрения МДНФ (МКНФ), число областей должно быть как можно меньше (каждая область представляет собой терм), а число клеток в области должно быть как можно больше (чем больше клеток в области, тем меньше переменных содержит терм).
Области могут пересекаться.
Область должна располагаться симметрично оси (оси располагаются через каждые четыре клетки) Несмежные области, расположенные симметрично оси, могут объединяться в одну.
Правило нахождения МДНФ (МКНФ).
Берём первую полученную область и смотрим, какие переменные не меняются в пределах этой области, выписываем конъюнкцию для МДНФ (дизъюнкцию для МКНФ) этих переменных; если неменяющаяся переменная нулевая, проставляем над ней инверсию для МДНФ (для МКНФ не ставим инверсию). Если переменная единичная, то не ставим инверсию для МДНФ (ставим инверсию для МКНФ). Берём следующую область, выполняем то же самое, что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией для МДНФ (дизъюнкции областей объединяем конъюнкцию для МКНФ).
Если переменная единичная, то не ставим инверсию для МДНФ (ставим инверсию для МКНФ). Берём следующую область, выполняем то же самое, что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией для МДНФ (дизъюнкции областей объединяем конъюнкцию для МКНФ).
Функции могут быть записаны не формулой, а аналитическим путем, то есть содержать номера наборов из таблицы истинности дизъюнктивно ( работает с 1) или конъюнктивно (& работает с 0). Например, Y= (1,4,8,10,12,14,15). Это означает, что карта Карно из 4-х переменных заполняется единицами в ячейках с номерами 1,4,8,10,12,14,15, а остальные ячейки заполняются нулями.
Пример.
x | y | z | B | ||||||
0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
Для нахождения МДНФ
— Составим карту для 3-х переменных и заполним ее 1 из последнего столбца таблицы истинности.
уz х | 00 | 01 | 11 | 10 |
0 | 1 | 1 | 1 | |
1 | 1 | 1 |
— Выделим покрытия по принципам склейки
— Для каждого покрытия составляем элементарную конъюнкцию, зачеркивая столбец с разными значениями и записывая оставшие переменные с инверсией, если все 0 и без инверсии, если все 1.
x y z x y z x y z
0 0 0 0 0 1 1 0 1
0 1 0 1 0 1 1 1 1
МДНФ: у=
Для нахождения МКНФ
— Составим карту для 3-х переменных и заполним ее 0 из последнего столбца таблицы истинности.
уz х | 00 | 01 | 11 | 10 |
0 | 0 | |||
1 | 0 | 0 |
— Выделим покрытия по принципам склейки
— Для каждого покрытия составляем элементарную дизъюнкцию, зачеркивая столбец с разными значениями и записывая оставшие переменные с инверсией, если все 1 и без инверсии, если все 0.
x y z x y z
1 0 0 0 1 1
1 1 0
МКНФ: у=
Задание для самостоятельного выполнения
составить карту Карно и найти МДНФ и МКНФ для следующих функций
а)
б)
Ответить на контрольные вопросы:
Что называется картой Карно?
Какие разновидности карт Карно есть?
Как заполняются карты Карно?
Для чего нужны принципы склейки?.
Чем отличается правило нахождения МДНФ от правила нахождения МКНФ?
Пользуясь этим и теоретическим материалом учебника М.С. Спирина «Дискретная математика» глава 4 п.4,6,3 стр.180, выполнить 1 задание.
Выполненное задание отправить на адрес электронной почты преподавателя. Имя файла – фамилия студента и номер занятия. (например Петров-17)
K-Map с 5 переменными в Digital Logic
Предварительное условие – присутствует в K-Map
Карта Карно или K-Map — это альтернативный способ записи таблицы истинности, который используется для упрощения логических выражений. До сих пор мы знакомы с K-Map с 3 переменными и K-Map с 4 переменными. Теперь давайте подробно обсудим K-карту с 5 переменными. Любое логическое выражение или функция, состоящая из 5 переменных, может быть решена с использованием K-карты с 5 переменными. K-карта для выражения с 5 переменными может быть обозначена двумя картами с 4 переменными, расположенными рядом друг с другом.
*** QuickLaTeX не может скомпилировать формулу: *** Сообщение об ошибке: Ошибка: Нечего показывать, формула пуста
2 5 = 32 ячейки для заполнения каждого минтерма. По мере увеличения числа переменных эффективность карты Карно снижается. Пусть булева функция с 5 переменными представлена в виде f (P Q R S T) , где P, Q, R, S и T — переменные, P — старшая битовая переменная, а T — наименее значащая битовая переменная. Структура такой K-карты для экспрессии SOP приведена ниже: Cell no. написанное, соответствующее каждой ячейке, можно понять из примера, описанного здесь:
Здесь для переменной P=0 имеем Q = 0, R = 1, S = 1, T = 1, т.е. (PQRST)=(00111) . В десятичной форме это эквивалентно 7 . Итак, для ячейки, показанной выше, соответствующая ячейка №. = 7. Аналогичным образом мы можем записать номера ячеек, соответствующие каждой ячейке, как показано на рисунке выше.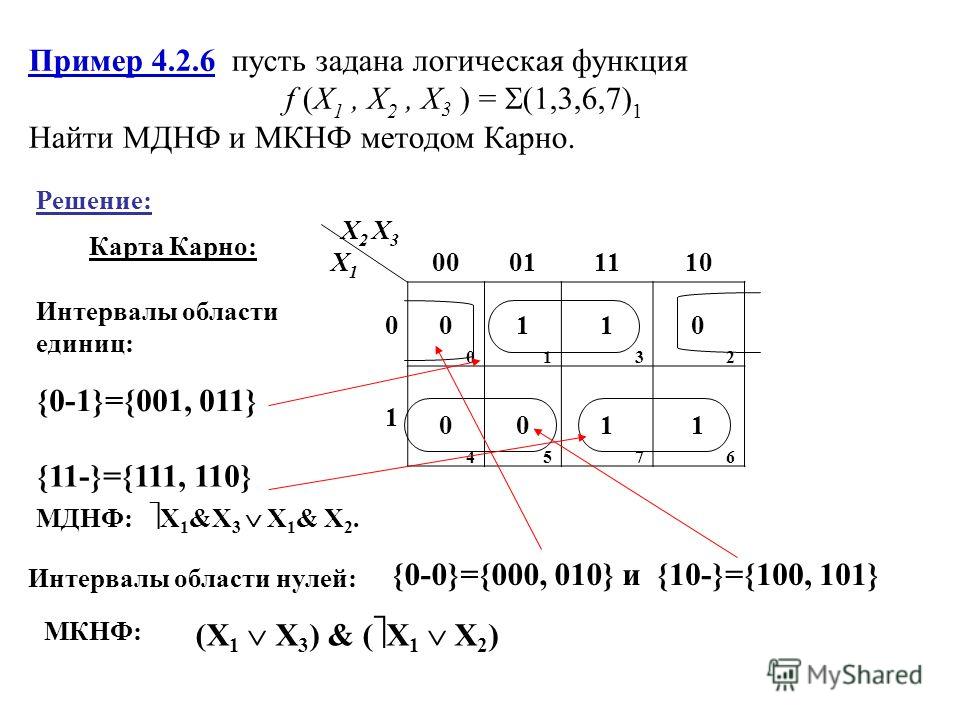 Теперь давайте обсудим, как использовать K-карту с 5 переменными для минимизации булевой функции.
Теперь давайте обсудим, как использовать K-карту с 5 переменными для минимизации булевой функции.
Правила, которым нужно следовать:
- Если функция задана в компактной канонической форме SOP (сумма произведений), то мы пишем «1» , соответствующий каждому минтерму (указанному в вопросе) в соответствующих номерах ячеек. Например: For мы напишем «1», соответствующее номерам ячеек (0, 1, 5, 7, 30 и 31).
- Если функция задана в компактной канонической форме POS (произведение сумм), то мы пишем «0» , соответствующее каждому максимальному термину (указанному в вопросе) в соответствующих номерах ячеек. Например: For мы напишем «0», соответствующий номерам ячеек (0, 1, 5, 7, 30 и 31).
Шаги, которые необходимо выполнить:
- Создайте вложенный куб максимально возможного размера, охватывающий все отмеченные 1 в случае SOP или все отмеченные 0 в случае POS на K-карте. Важно отметить, что каждый подкуб может содержать члены только в степени 2.
 Также вложенный куб ячеек возможен тогда и только тогда, когда в этом вложенном кубе для каждой ячейки мы удовлетворяем тому, что «m» число ячеек составляет соседних ячеек .
Также вложенный куб ячеек возможен тогда и только тогда, когда в этом вложенном кубе для каждой ячейки мы удовлетворяем тому, что «m» число ячеек составляет соседних ячеек . - Все Essential Prime Implicants (EPI) должны присутствовать в минимальных выражениях.
I. Решение SOP-функции: Для ясного понимания давайте решим пример минимизации SOP-функции 5 переменных K-карты, используя следующее выражение: В приведенной выше K-карте у нас есть 4 подкуба:
- Подкуб 1: Отмеченный красным содержит ячейки ( 0, 4, 8, 12, 16, 20, 24, 28)
- Подкуб 2: Отмеченный синим содержит ячейки (7, 23 )
- Подкуб 3: Отмеченный розовым цветом включает в себя ячейки (0, 2, 8, 10, 16, 18, 24, 26)
- Подкуб 4: Отмеченный желтым цветом содержит ячейки (24, 25, 26, 27)
Теперь, записывая минимальное выражение каждого из подкубов, мы будем искать литерал, общий для всех ячеек, присутствующих в этом подкубе.
- Подкуб 1 : [Tex]\bar T [/Tex]
- Подкуб 2 : [Tex]R [/Tex][Tex] Т[/Текс]
- Подкуб 3 : [Tex]\bar T [/Tex]
- Подкуб 4 : [Tex]Q [/Tex] 900 79
- Подкуб 1: Красный содержит ячейки (0, 4, 8, 12, 16, 20, 24, 28)
- Подкуб 2: 9 0006 Тот, что отмечен синим цветом, содержит ячейки (7, 23)
- Подкуб 3: Отмеченный розовым цветом содержит ячейки (0, 2, 8, 10, 16, 18, 24, 26)
- Подкуб 4: Тот, что отмечен желтым цветом содержит ячейки (24, 25, 26, 27)
- Подкуб 1 :
- Подкуб 2 : [Tex]+ \bar S [/Tex]
- 9 0005 Подкуб 3 :
- Подкуб 4 : [Tex ]+ R [/Tex]
- Для 5-переменной K-Map диапазон номеров ячеек будет от 0 до -1, т. е. от 0 до 31,
- Вышеупомянутый термин «Смежные ячейки» означает «любые две ячейки, отличающиеся только одной переменной».
- Пожалуйста, свяжитесь с нами, чтобы сообщить, что эта страница отсутствует, или используйте поле выше, чтобы продолжить поиск
- Наша страница «О нас» содержит дополнительную информацию о сайте, на котором вы находитесь, WhatIs.com.
- Посетите нашу домашнюю страницу и просмотрите наши технические темы
- коллизия в сети
В полудуплексной сети Ethernet коллизия возникает в результате попытки двух устройств в одной сети Ethernet передать…
- краеугольный камень домкрат
Гнездо трапецеидального искажения — это гнездовой разъем, используемый для передачи аудио, видео и данных. Он служит гнездом для подходящей вилки…
- инкапсуляция (объектно-ориентированное программирование)
В объектно-ориентированном программировании (ООП) инкапсуляция — это практика объединения связанных данных в структурированную единицу вместе с .
 ..
.. - Вредоносное ПО TrickBot
TrickBot — это сложное модульное вредоносное ПО, которое начиналось как банковский троян, а затем эволюционировало, чтобы поддерживать множество различных типов …
- Общая система оценки уязвимостей (CVSS)
Общая система оценки уязвимостей (CVSS) — общедоступная система оценки серьезности уязвимостей безопасности в …
- WPA3
WPA3, также известный как Wi-Fi Protected Access 3, является третьей итерацией стандарта сертификации безопасности, разработанного Wi-Fi …
- качественные данные
Качественные данные — это информация, которую невозможно подсчитать, измерить или выразить с помощью чисел.
- зеленые ИТ (зеленые информационные технологии)
Green IT (зеленые информационные технологии) — это практика создания и использования экологически устойчивых вычислительных ресурсов.

- Agile-манифест
The Agile Manifesto — это документ, определяющий четыре ключевые ценности и 12 принципов, в которые его авторы верят разработчикам программного обеспечения…
- опыт кандидата
Опыт кандидата отражает отношение человека к процессу подачи заявления о приеме на работу в компанию.
- непрерывное управление производительностью
Непрерывное управление эффективностью в контексте управления человеческими ресурсами (HR) представляет собой надзор за работой сотрудника …
- вовлечения сотрудников
Вовлеченность сотрудников — это эмоциональная и профессиональная связь, которую сотрудник испытывает к своей организации, коллегам и работе.
- распознавание голоса (распознавание говорящего)
Распознавание голоса или говорящего — это способность машины или программы принимать и интерпретировать диктовку или понимать и .

Наконец, минимальное выражение данной логической функции может быть выражается следующим образом: [Tex]\bar T [/Tex][Tex]R [/Tex][Tex]T [/Tex][Tex]\bar T [/Tex][Tex]Q [/Tex]
II. Решение функции POS: Теперь давайте решим пример минимизации функции POS для K-карты с 5 переменными, используя следующее выражение: В приведенной выше K-карте у нас есть 4 подкуба:
Теперь, записывая минимальное выражение каждого из подкубов, мы будем искать литерал, общий для всех ячеек, присутствующих в этом подкубе.
Наконец, минимальное выражение данной логической функции может быть выражено следующим образом:
ПРИМЕЧАНИЕ:
404: Страница не найдена
Страница, которую вы пытались открыть по этому адресу, похоже, не существует. Обычно это результат плохой или устаревшей ссылки. Мы извиняемся за любые неудобства.
Что я могу сделать сейчас?
Если вы впервые посещаете TechTarget, добро пожаловать! Извините за обстоятельства, при которых мы встречаемся. Вот куда вы можете пойти отсюда:
Вот куда вы можете пойти отсюда:
Поиск по категории
Сеть
Безопасность
ИТ-директор
HRSoftware
Отдел обслуживания клиентов

 Также вложенный куб ячеек возможен тогда и только тогда, когда в этом вложенном кубе для каждой ячейки мы удовлетворяем тому, что «m» число ячеек составляет соседних ячеек .
Также вложенный куб ячеек возможен тогда и только тогда, когда в этом вложенном кубе для каждой ячейки мы удовлетворяем тому, что «m» число ячеек составляет соседних ячеек . ..
..
