Уравнения и неравенства. Нестандартные методы решения
Уравнения и неравенства. Нестандартные методы решения
ОглавлениеОт авторовГлава I. Алгебраические уравнения и неравенства § 1.1. Разложение многочлена на множители 1.1.2. Применение формул сокращенного умножения. 1.1.3. Выделение полного квадрата. 1.1.4. Группировка. 1.1.5. Метод неопределенных коэффициентов. 1.1.6. Подбор корня многочлена по его старшему и свободному коэффициентам. 1.1.7. Метод введения параметра. 1.1.8. Метод введения новой неизвестной. 1.1.9. Комбинирование различных методов. § 1.2. Простейшие способы решения алгебраических уравнений § 1.3. Симметрические и возвратные уравнения 1.3.2. Симметрические уравнения четвертой степени. 1.3.3. Возвратные уравнения. 1.3.4. Уравнения четвертой степени с дополнительными условиями на коэффициенты. § 1.4. Некоторые искусственные способы решения алгебраических уравнений 1.  4.2. Угадывание корня уравнения.1.4.3. Использование симметричности уравнения. 1.4.4. Использование суперпозиции функций. 1.4.5. Исследование уравнения на промежутках действительной оси. § 1.5. Решение алгебраических неравенств 1.5.2. Метод интервалов. 1.5.3. Обобщенный метод интервалов. Глава II. Уравнения и неравенства, содержащие радикалы, степени, логарифмы и модули § 2.1. Уравнения и неравенства, содержащие неизвестную под знаком корня 2.1.4. Умножение уравнения или неравенства на функцию. § 2.2. Уравнения и неравенства, содержащие неизвестную в основании логарифмов 2.2.2. Переход к основанию, содержащему неизвестную. 2.2.3. Уравнения вида … 2.2.5. Неравенства вида … § 2.4. Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины 2.4.6. Использование свойств абсолютной величины. Глава III. Способ замены неизвестных при решении уравнений § 3.  1. Алгебраические уравнения§ 3.2. Рациональные уравнения § 3.3. Иррациональные уравнения 3.3.3. Сведение решения иррационального уравнения к решению тригонометрического уравнения. § 3.4. Уравнения вида § 3.5. Решение некоторых уравнений сведением их к решению систем уравнений относительно новых неизвестных Глава IV. Решение уравнений и неравенств с использованием свойств входящих в них функций § 4.1. Применение основных свойств функций 4.1.2. Использование ограниченности функций. 4.1.3. Использование монотонности. 4.1.4. Использование графиков. 4.1.5. Метод интервалов для непрерывных функций. § 4.2. Решение некоторых уравнений и неравенств сведением их к решению систем уравнений или неравенств относительно той же неизвестной 4.2.3. Использование ограниченности функций. 4.2.4. Использование свойств синуса и косинуса. 4.2.5. Использование числовых неравенств. § 4.3. Применение производной 4.3.2. Использование наибольшего и наименьшего значений функции.  4.3.3. Применение теоремы Лагранжа. Дополнения |
Задача 15 (С3). Рациональные неравенства. Методы решения уравнений и неравенств с модулем. — Математика (профильный)
На этом занятии мы рассмотрим интересные приемы решения рациональных неравенств, а также поговорим об уравнениях и неравенствах с модулем.
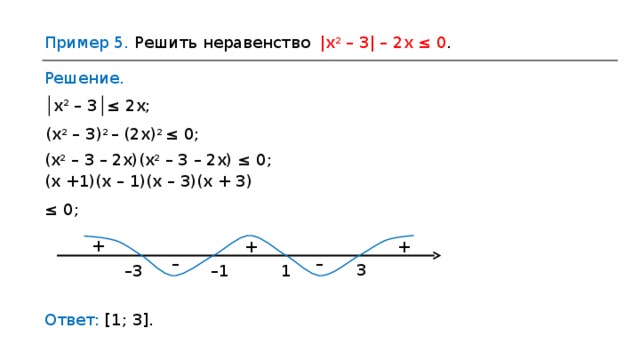
Конспект занятия «Задача 15 (С3). Рациональные неравенства. Методы решения уравнений и неравенств с модулем.»Решенте рациональных неравенств
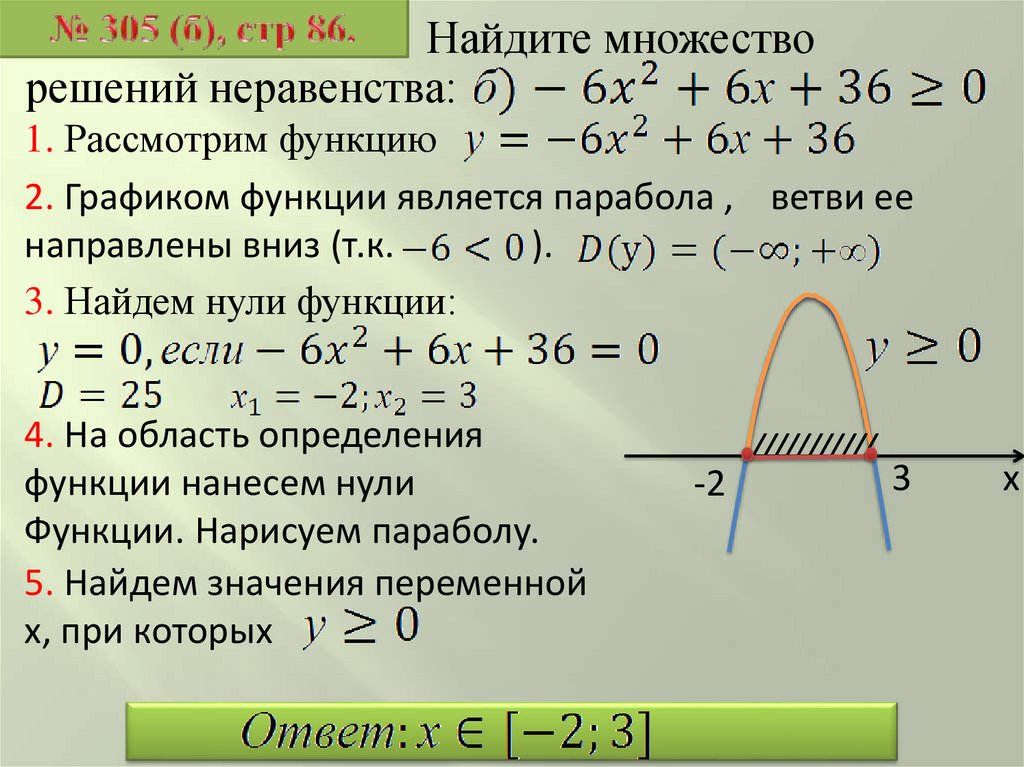
Рассмотрим стандартный приём решения рациональных неравенств, основанный на сведении данного неравенства к неравенству для многочлена, метод решения которого (метод интервалов) нам уже известен. Итак, рассмотрим рациональное неравенство
f (x) g (x), |
где f (x) и g (x) − рациональные функции, то есть функции, представимые в виде отношения многочленов.
Перенося обе части рационального неравенства в левую часть, представим её в виде отношения двух многочленов: (Такой вид неравенства называется стандартным.)
Привести неравенство к стандартному виду
Разложить на множители многочлены P (x) и Q (x
) (как мы знаем, для этого придётся решить уравнения P (x) = 0 и Q (x) = 0).Нули числителя, не совпадающие с нулями знаменателя, отметить на числовой оси точками, а нули знаменателя − кружочками (эти точки, очевидно, не входят в ОДЗ рациональной функции и потому они как будто «выколоты» из числовой оси).
Подставить мысленно в неравенство очень большое число (большее самого большого из корней числителя и знаменателя) для того, чтобы определить, какой знак имеет рациональная функция на самом правом интервале. Провести кривую знаков, проходя через все точки, отмеченные на числовой прямой, меняя или не меняя знак в зависимости от суммарной степени двучлена, отвечающего данной точке.
Записать ответ, обращая особое внимание на граничные точки, часть из которых может быть «выколота».
Таким образом, для нестрогих рациональных неравенств имеем по определению
|
Решение неравенств, содержащих выражение под знаком модуль
Основные способы решений неравенств с модулем во многом совпадают с методами решения аналогичных уравнений. Только, решая неравенства с модулем (как, впрочем, и неравенства вообще), нужно очень внимательно совершать равносильные переходы и следить не только за тем, чтобы не приобрести новые решения, но и за тем, чтобы не потерять уже имеющиеся.
Стандартный путь решения неравенств с модулем заключается в том, что координатная прямая разбивается на промежутки, границами этих промежутков являются нули подмодульных выражений, а затем неравенство решается на каждом из промежутков.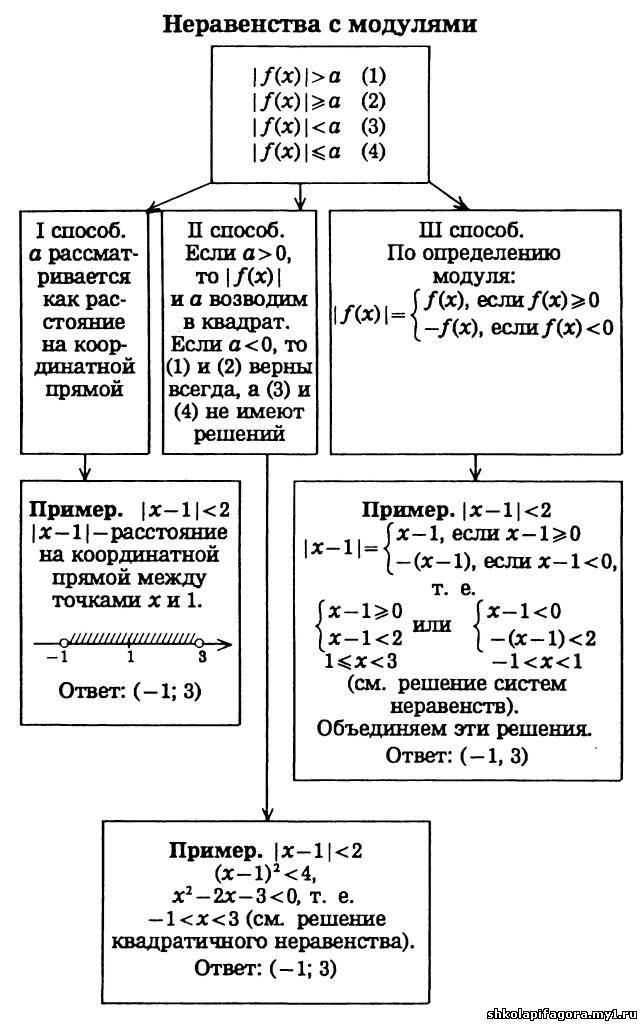
Этот метод работает всегда. Нужно понимать, что раскрытие модуля по определению неизменно приводит к цели. Конечно же, этот метод не является оптимальным: в условиях ЕГЭ, где важен не только результат, но и то время, которое потрачено на его получение. Рассмотрим методы, не связанные с поиском нулей функций, стоящих под знаком модуля.
Решение неравенств с модулем:
1) |x+a|≤b⇔−(b+a)≤x≤b−a, где a0,b0a0,b0
2) |x+a|≥b⇔x≤−(a+b) или x≥−(a−b), где a0,b0a0,b0
3) x2≤a2⇔|x|≤a, a0 ⇔ −a≤x≤a
4) x2≥a2⇔|x|≥a,a0⇔x≤−a или x≥a .
5) |f(x)|⇔f2(x)2⇔(f(x)−k)⋅(f(x)+k)⇔f2(x)⇔(f(x)−k)⋅(f(x)+k)
6) Неравенства вида |f1(x)|+|f2(x)|≤|f3(x)| содержащие алгебраическую сумму двух и более модулей, решают
разобьем числовую ось точками, в которых обращаются в нуль выражения, стоящие под знаком модуля.
выбирая на этих промежутках контрольные точки, проверяем, удовлетворяется ли на них заданное неравенство или нет.
ответом к задаче служит объединение промежутков, где выполняется данное неравенство.
Задачи к теме:
Решите неравенство
Решите неравенство
Решите неравенство
Решите неравенство
Решите неравенство
Решить неравенство:
Решить неравенство:
Решить неравенство:
Решить неравенство:
Задание 1
(2 балла)
Задание 2
(2 балла)
Задание 3
(3 балла)
Проверить правильность выполнения заданий вы можете в автоматическом режиме в разделе домашние задания на странице с курсом «Математика (профильный) Подготовка к ЕГЭ, (бывшая С) 2016»
Следующий урок на тему »
Задача 18 (С 5) Параметры.
Уравнения с параметром.»
Предыдущий урок на тему » Задача 15 (С 3). Показательные и логарифмические неравенства.»
Четверть 2 — Модуль 4_Решение задачи, связанной с системой линейных неравенств с двумя переменными.pdf — 88 8 НЕ Математика Четверть 2 — Модуль 4 РЕШЕНИЕ
Предварительный просмотр неформатированного текста: 88
8 НЕ Математика
Четверть 2 — Модуль 4 РЕШЕНИЕ ПРОБЛЕМЫ С УЧАСТИЕМ СИСТЕМЫ
ЛИНЕЙНЫХ НЕРАВЕНСТВ В ДВУХ
ПЕРЕМЕННЫЕ 8
Математика
Четверть 2 — Модуль 4
Решение проблемы, связанной с системой линейных
Неравенство в двух переменных Департамент образования ● Республика Филиппины 8 Альтернативный способ доставки
Четверть 2 — Модуль 4: Решение задачи, связанной с системой линейных неравенств в
Две переменные
Первое издание
Республиканский закон 8293, раздел 176 гласит: «Никакое авторское право не действует ни в
Работа правительства Филиппин. Однако предварительное одобрение
государственное учреждение или учреждение, в котором создается произведение, необходимы для
использование такой работы для получения прибыли.
Такое агентство или учреждение может, среди прочего,
поставить в качестве условия выплату роялти.
Заимствованные материалы (например, песни, рассказы, стихи, картинки, фотографии,
имена, товарные знаки и т. д.), включенные в эту книгу, принадлежат их соответствующим
правообладатели. Были приложены все усилия, чтобы найти и получить разрешение на
использовать эти материалы от соответствующих владельцев авторских прав. Издатель и
авторы не представляют и не претендуют на право собственности на них.
Опубликовано Министерством образования — Отделение города Гингуг.
Начальник отдела: Джеснар Демс С. Торрес, доктор философии, CESO VI
Команда разработчиков модуля
Сценарист: Ромео К. Намбатак мл. Рецензент: Ма. Кристина Б. Гальго, Рина Т. Куахотор Иллюстратор: Джей Майкл А. Калипусан Художник-макет: Джей Майкл А. Калипусан Группа управления
Председатель: Джеснар Демс С. Торрес, доктор философии, CESO VI Сопредседатель: Коннибель К. Нистал, суперинтендант школьного отдела OIC, офис школьного суперинтенданта Паблито Б.
Альтубар
Главные члены CID: Ma. Кристина Б. Гальго, EPS
Химая Б. Синатао, менеджер LRMDS
Джей Майкл А. Калипусан, PDO II
Мерси М. Кахарян, библиотекарь II Напечатано на Филиппинах
Департамент образования — Отдел города Гингуг
Адрес офиса:
Брги. 23, Национальное шоссе, город Джингуг
Телефакс:
088 328 0108/ 088328 0118
Адрес электронной почты:
[email protected] Эта страница намеренно пуста Содержание
О чем этот модуль…………………………………………… ……………………………………..я
Что мне нужно знать………………………………………………….. …………………………………………. ..я
Как извлечь уроки из этого модуля……………………………………. …………………………………я
Иконки этого модуля…………………………………………… …………………………………………. ….ii
Что я знаю ……………………………………….. ………………………………………
…. ………….iii
Урок 1:
Решение задачи, связанной с системными линейными неравенствами, в двух
переменные……………………………………………………………………………………..1
Что внутри…………………………………………………………………………..1
Мероприятие 1: …………………………………………………………………………….1
Что мне нужно знать ……………………………………………… …………………………………………4
Что нового ………………………………………… …………………………………………. 4
Занятие 2: ……………………………….……………………………………………4
Что это такое: ………………………………………………………. …………………………..5
Что еще: ………………………….. ……………………………….. …………………………..9Чему я научился……………………………………………………………12
Мероприятие 3: ……………………………………………………………………12
Обобщение ………………………………………………………. …………………………..13
Что я могу сделать: ……………………………………… …………………………..
…………….13
Краткое содержание …………………………………………. …………………………………………. …………….14
Оценка: (После теста)……………………………………. …………………………… 15
Ключ к ответу ………………………………………………………. …………………………………………. ……..18
Использованная литература …………………………………………. …………………………………………. ………….23 О чем этот модуль
Этот модуль предоставит вам возможность углубить свои
понимание решения задач, связанных с системой линейных неравенств в двух
переменные, это также поможет вам расширить свое понимание, чтобы узнать, как эти
системы используются для решения реальных жизненных проблем и принятия решений. Что мне нужно знать
В конце этого модуля вы должны уметь:
1. решать текстовые задачи с участием систем линейных неравенств с двумя переменными.
(M8AL-IIb-2) Как извлечь уроки из этого модуля
Для достижения цели, указанной выше, соблюдайте следующее:
1.
Внимательно прочитайте все уроки.
2. Не торопитесь проходить каждый урок.
3. Ответьте на предварительный тест честно, цель предварительного теста — определить
ваши предварительные знания, прежде чем идти через уроки и мероприятия.
4. Если вам трудно понять уроки и задания, пожалуйста, сделайте
сделать перерыв. Перерывы между уроками и мероприятиями дадут вам
какое-то место, где вы можете хорошо усвоить урок.
5. Если вам нужна дополнительная информация об уроке, вы можете воспользоваться Интернетом. i Иконки этого модуля
Что мне нужно
Знать Эта часть содержит цели обучения, которые
созданы для того, чтобы вы учились по ходу
модуль. Что я знаю Это оценка вашего уровня
знания по рассматриваемому предмету,
предназначена специально для оценки предшествующих связанных
Знания What’s In Эта часть связывает предыдущий урок с тем
текущего. Что нового Введение в новый урок через
различные мероприятия, прежде чем он будет представлен
вам Что это? Это обсуждение деятельности как
способ углубить свое открытие и
понимание концепции.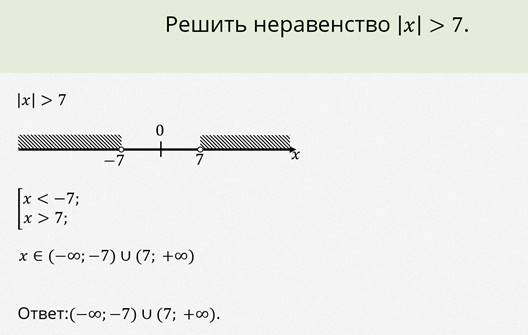
Более того, это последующие действия, которые
предназначен для вашей дальнейшей практики, чтобы
освоить компетенции. Что у меня есть
Выученные действия, предназначенные для обработки того, что у вас есть
урока Что я могу сделать Это задачи, которые предназначены для
продемонстрировать свои навыки и полученные знания,
и применяются в реальных проблемах и
ситуации. ii Что я знаю I. Предварительная оценка
Инструкция: прочитайте и ответьте на вопросы ниже. Выберите букву лучшего
ответ из предложенных вариантов.
1. Какой из следующих символов является правильным для «меньше чем»?
а. <
б. > в. ≤ д. ≥ 2. Какой из следующих символов означает «больше чем»?
а. <
б. > в. ≤ д. ≥ 3. Какая нижеприведенная фраза является правильным значением символа неравенства «≤»?
а.
б.
в.
д. Меньше или равно
Больше или равно
Меньше, чем
больше 4. Что из следующего лучше всего описывает систему линейных неравенств в двух
переменные?
а. у > 0 б. 2х + у = -1 в. х + 5у = 5
3х – у = — 1 д. 3х – у > 1
x+y<3 5. Как правильно перевести фразу «трижды сумма y и 5 меньше 10»?
а.
3(у + 5) < 10б. 2(у + 5) < 10 в. 3(у + 5) ≤ 10 дней. 3( y + 5) ≥ 10 6. Переведите вербальное высказывание «Мария средний балл в академическом
испытуемых составляет не менее 82 %». (Подсказка: x = средний балл Марии в академическом
предмет).
а. х < 82 б. х > 82 в. х ≥ 82 д. x ≤ 82 7. Что из следующего является правильным переводом выражения «Стоимость
книга может быть больше или равна 300 филиппинским песо ?
(Подсказка: x = представляет книгу)
а.
б.
в.
д. х < 300
х > 300
х ≤ 300
x ≥ 300 8. Какой математический символ соответствует выражению «Мэри должна прочитать
минимум 5 книг за лето для ее филиппинского класса»? (Подсказка: M =
представляет собой количество книг)
а. М < 5
б. М > 5
III в. М ≤ 5
д. М ≥ 5
9. Какой математический символ эквивалентен выражению «миссис. Чай
в ее классе будет не более 30 учеников»?
(Подсказка: C = представлять студента)
а.
б.
в.
д. С< 30
С>30
С ≤ 30
C ≥ 30 10. Что из следующего является эквивалентной словесной фразой неравенства,
2п + 5 > 8?
а.
б.
в.
д. Дважды число, увеличенное на пять, больше восьми
Дважды число, увеличенное на пять, меньше восьми
Дважды число, увеличенное на пять, больше или равно восьми
Дважды число, умноженное на пять, меньше или равно восьми.
11. Мисс Лопес заказала пиццу и хлебные палочки для школьной вечеринки и имеет
бюджет не более 810.00 Php. Коробка пиццы стоит 130 песо.
хлебные палочки стоят 70 песо. Запишите линейное неравенство в стандартной форме для
эта ситуация.
а. 130x + 70y ˂ 810
б. 130x + 70y ≤ 810 в. 130x + 70y ≥ 810
д. 130x + 70y > 810 12. Майкл собирает деньги для своей баскетбольной лиги. Он продает шоколадные батончики.
по 25 филиппинских песо за штуку и шоколадные мятные леденцы по 35 филиппинских песо за штуку. Если Майкл хочет
чтобы собрать более 1500,00 филиппинских песо, напишите неравенство, показывающее количество
шоколадных батончиков b и количество мятных конфет m, которые он должен продать.
а. 25.00б + 35.00м > 1500.00
б. 25.00б + 35.00м ˂ 1500.00 в. 25.00м + 35.00б > 1500.00
д. 25,00 м + 35,00 бат ˂ 1500,00 13. Педро нужно накопить не менее 1000 филиппинских песо на возвращение домой. он работает 2
работы, зарабатывая 80 песо в час в качестве официанта и 250 песо в час в качестве репетитора. Он только
успевает поработать за 14 часов до возвращения домой.
Какая система неравенств
ниже правильно модели для возвращения на родину?
а. х + у ≥ 250
х + у ≤ 80
б. х + у ≥ 1000
80x + 250y ≤ 14 в.в. 80x + 250y ≤ 1000
х + у ≤ 14
д. 80x + 250y ≥ 1000
х + у ≤ 14
14. Вы можете работать в общей сложности не более 41 часа в неделю на двух своих работах.
Уборка дома оплачивается 50 песо в час, а ваша работа по продажам оплачивается 80 песо в час.
час. Вам необходимо зарабатывать не менее 2500 филиппинских песо в неделю, чтобы оплачивать счета.
Напишите систему неравенств, наилучшим образом описывающую данную ситуацию.
а. 50x + 80y ≥ 2500
х + у ≤ 41
б. 50x + 80y ≤ 2500
х + у ˂ 41
в. х + у ≤ 2500
50x + 80y ˂ 41
д. 50x + 80y ≤ 2500
х + у ≤ 41
15. Лифт в торговом центре имеет грузоподъемность 1350 кг. Предположим, что в среднем
ребенок весит около 25 кг, а взрослый весит 60 кг. Сколько возможно
количество детей и взрослых, которым разрешается подниматься на лифте без
превышает его возможности?
а. (10 детей, 15 взрослых)
б. (30 детей, 15 взрослых) c.(5 детей, 24 взрослых)
г.
(2 детей, 25 взрослых) v vi Урок 1 Урок Решение проблем с вовлечением
Система линейных неравенств
в двух переменных
Что в этом уроке, вам предоставляется возможность использовать свои предыдущие знания и навыки в
решение системы линейных неравенств графически. Вам также даются разнообразные мероприятия
обработать полученные знания и навыки, углубить понимание решения
задача с системой линейных неравенств с двумя переменными и переводом
проблема в математический символ. Мероприятие № 1
Описание: Это упражнение позволит вам вспомнить, как решать системные линейные задачи.
неравенства с двумя переменными и перевести словесную фразу в
математическая фраза.
А. Решите графически каждую из следующих систем линейных неравенств.
Приведите не менее 3 упорядоченных пар, удовлетворяющих обоим неравенствам.
Первый сделан для тебя.
1. х+у≥2
x–y≤1 (0, 4), (2, 4) и (-2, 6) удовлетворяют обоим
неравенства 1 1. x>1
у>1 2. х+у˂3
ух+5 3. у > 2х + 1
y˂x+1 2 B. Перевести словесную фразу в математическую фразу.
Номер один
сделанно для тебя. Дополните неравенство, добавив недостающее слагаемое.
1. Дважды число
увеличено на 2 больше
чем семь 2x + 2 >7 2. В два раза число уменьшилось
на 2 меньше семи(x
представить в виде числа) 2−27 3. пять плюс пять раз a
число больше или
равно девяти. (x представляют
как число) + 594. Карл средний балл по математике
составляет не менее 85%. (С=
представлять
как
Карлс
средняя оценка) C 5. Джозеф и Мэй провели
более 12 000 рублей в
их отпуск в Маниле. (Икс
«=»
представлять Иосифа и
расходы Мэя) x 6. Разница между A
и B не менее 30 A− 85 30 7. Г-н Лорето Камю ежемесячно L
зарплата не более Php
40 000. (L = представляет г.
Лорето Камю ежемесячно
зарплата)
8. Допустимая вместимость
грузовик с грузом находится на
большинство двухтонн. (T представляют
как грузоподъемность грузовых автомобилей) 2 9. 3 раза число больше
больше или равно восьми. 3 10. Цена мобильного телефона
составляет не менее десяти тысяч (C
представляет собой цену на
мобильный телефон) C 3 8 Что мне нужно знать Вы когда-нибудь задавались вопросом, как бизнесмены получают прибыль? Как родители финансируют
свои доходы на еду, образование, одежду и другие нужды? Как пользователи мобильных телефонов
выбрать лучший план оплаты? Как студенты тратят свои суточные или путешествуют
из дома в школу?
Узнать ответы на эти вопросы и определить огромное
применения систем линейных неравенств с двумя переменными и решение задачи
включение системы линейных неравенств через этот модуль.
Что нового Занятие № 2
Описание:В этом упражнении вы сможете использовать линейные неравенства с двумя переменными.
представить реальную ситуацию и найти возможные решения
линейное неравенство с двумя переменными и начертите его график.
Указания: Используйте приведенную ниже ситуацию, чтобы ответить на следующие вопросы.
Нимфа живет рядом с морским курортом. Во время летних каникул она продает
сувенирные изделия, такие как браслеты и ожерелья из местных ракушек. каждыйбраслет
стоит 85 филиппинских песо, в то время как каждое ожерелье стоит 115 филиппинских песо.
Браслеты и ожерелья на сумму 15 000 песо. 1. Заполните таблицу ниже
Количество
браслет продан Стоимость Кол-во
продано ожерелий 1 1 2 2 3 3 4 4 5 5 10 10 15 15 4 Общая стоимость 20 20 25 25 30 30 40 40 50 50 60 60 70 70 80 80 2. Сколько будет общая сумма продажи Нимфы, если она продаст 5 браслетов и 5
ожерелья? А если она продаст 10 браслетов и 20 ожерелий? 3. Какое математическое выражение будет представлять общий объем продаж браслетов и ожерелий? Опишите математическое утверждение,
затем постройте график для конкретного случая, когда Nimfa продает в общей сложности
15000р.
4. Нимфа хочет, чтобы общий объем продаж составил не менее 15 000 филиппинских песо. Что
математическое утверждение будет представлять это? Опишите
математическое утверждение, затем график. Что это решение задачи, связанной с системой линейных неравенств с двумя переменными
Многие студенты находят проблемы реальной жизни более сложными. В решении проблемы
включая систему линейных неравенств, есть много шагов, чтобы найти решение.
1. Прочтите вопрос правильно
2. Сформулируйте неравенства на основе заданного вопроса.
3. Преобразовать данные неравенства в виде отрезка наклона, тогда
4. Следуйте шагам решения системы линейных неравенств с двумя переменными
графически. 5 При формулировании неравенств всегда помните следующее: > is
больший
чем
является
более
чем
превышает
кончено
выше
является
больше
чем
является
дольше
чем
является
выше
чем < меньше чем
находится под
меньше, чем
является
меньше
чем
ниже
является
короче
чем
ниже
ниже, чем ≥
больший
больше или равно
к
по крайней мере
не меньше
чем
не находится под
имеет минимум
ценить
больше чем
или равно ≤ меньше или
равно
самое большее
является
нет
больший
чем
делает
нет
превосходить
имеет
а
максимум
ценить
больше не
чем решение системных линейных неравенств словесных задач
1.
Топливо от бензоколонки А стоит 30 филиппинских песо за литр и от бензоколонки Б.
стоит 50р за литр. У мистера Суаве есть не более 200 филиппинских песо на топливо.
Напишите и начертите систему линейных неравенств.
Решение:
Пусть x = топливо от бензонасоса A
y = топливо от бензонасоса B
У мистера Суаве есть максимум 200 филиппинских песо, чтобы потратить на топливо, поэтому
форма неравенства:
30x + 50 лет ≤ 200
При покупке топлива отрицательные числа не учитываются:
х≥0
y≥0 6 Поскольку и x, и y больше нуля, то включается ноль.
Итак, можно сформулировать систему:
30x + 50y ≤ 200
х≥0
у≥0
График 3-х неравенств Топливо из насоса B (y литров) 30x + 50 y ≤ 200 30x + 50y ≤ 200 Топливо из насоса A (x литров) Топливо из насоса B (y литров) x≥0 x≥0 Топливо из насоса A (x литров) Топливо от насоса B (y литров) y≥0 y≥0 Топливо от насоса A (x литров)
7 График системы 30x + 50y ≤ 20
х≥0
y≥0 Топливо из насоса B (y литров) p Топливо из насоса A (x литров) Топливо из насоса B (y литров) Решение системы РЕШЕНИЕ Топливо из насоса A (x литров) Любые координаты из этой области удовлетворяют неравенству .
Например, (3, 2)
и (2,2) и т.д.
3x + 5y ≤ 20
х≥0
у≥0 8 Проверка
(3, 2) (2, 2) 3x + 5y ≤ 20 3x + 5y ≤ 20 30(3) + 50(2) ≤ 200
90 + 100 ≤ 200
190≤ 200Истинно 30(2) + 50(2) ≤ 200
60 + 100≤ 200
160≤ 200Истинно x ≥ 0x ≥ 0
3≥0 верно 2≥0 верно y ≥ 0y ≥ 0
2≥0 Верно 2≥0 Верно Следовательно, Mr.Suave может покупать следующие виды топлива у разных топливных насосов.
не потратив не более 200.
3 литра топлива от насоса А и 2 литра от насоса В
2 литра топлива из насоса A и 2 литра из насоса B. Что еще?
Тея покупает почву и растения для своего сада. Растения стоят 100 филиппинских песо каждое.
и стоимость почвы 40,00 филиппинских песо за мешок. Она хочет купить как минимум 5 растений. Она
не может потратить более 1000,00 Php. а. Представьте данное с помощью любых переменных.
Пусть х = количество растений
y = мешки с землей b. Напишите систему линейных неравенств, наилучшим образом описывающую ситуацию.
100x + 40y ≤ 1000
х≥5 9в. Нарисуйте график отдельных линейных неравенств, чтобы смоделировать все возможные решения задачи.
ситуация Количество мешков с почвой (y) 100x + 40y ≤ 1000 Количество растений (x)
Примечание. На этот раз мы никогда не будем использовать отрицательное число, потому что
нельзя купить отрицательное количество растений и мешок с землей. Количество мешков с почвой (y) x≥5 Количество растений (x) 10 количество мешков с почвой (y) 100x + 40y ≤ 1000
х≥5 100х + 40у ≤ 100 х≥5
количество растений (x) Перекрывающиеся области – это
решения системы
д. Приведите не менее двух возможных решений системы.
Все упорядоченные пары, найденные в перекрывающейся области, являются решениями. е. Никаких отрицательных чисел, потому что мы не можем покупать отрицательные предметы. 11 Чему я научился Задание № 3
Описание: Это задание расширит ваше понимание, чтобы узнать, как работает эта система.
используются при решении реальных жизненных проблем и принятии решений.
Указания: Ответьте на каждый из следующих вопросов. Покажите полное решение.
Пример:
Лифт в торговом центре имеет грузоподъемность 1350 кг. Предположим, что средний, a
ребенок весит около 25 кг, а взрослый весит 60 кг.
а. Напишите систему неравенств для данной ситуации, затем постройте график
множество решений системы.
25x + 60 лет ≤ 1350
х≥0
у≥0
б. Является ли заказанная пара (2 детей и 10 взрослых) решением проблемы
система?
Запасной (2, 10)
25x + 60 лет ≤ 1350
25(2) + 60(10) ≤ 1350
50 + 600 ≤ 1350
650 ≤ 1350 Правда x≥0
2 ≥ 0 Истинно y≥0
10 ≥ 0 Истинно Следовательно: Упорядоченная пара (2, 10) является решением системы
1. Сотрудники Математического клуба планируют провести мини-концерт в рамках своего фонда
поднимающий проект. Студенческие билеты будут продаваться по 25 филиппинских песо каждый, а билеты для нестудентов по 40 филиппинских песо каждый. Они должны продать не менее 120 билетов и
сделать не менее 4000 Php от общего объема продаж.
а. Напишите систему неравенств для данной ситуации, затем начертите график
множество решений системы
б. Приведите одну упорядоченную пару, удовлетворяющую системе неравенств.
Покажите, что эта пара удовлетворяет условиям задачи. 12 2. Еженедельный бюджет матери на рыбу и курицу составляет не более 1200 филиппинских песо.
Примечание
что 1 килограмм рыбы стоил 60 песо, а 1 килограмм курицы стоил песо.
120.
а. Напишите систему неравенств для данной ситуации и нарисуйте график
множество решений системы.
б. Определите, является ли упорядоченная пара (10, 7) решением системы.
3. Билеты на спектакль стоят 250 песо для взрослых и 200 песо для детей.
спонсор шоу собрал общую сумму не более 44 000 песо
от более чем 150 взрослых и детей, которые смотрели спектакль.
а. Какие математические утверждения представляют данную ситуацию?
б. Нарисуйте и опишите график математических утверждений.
в. Назовите 4 возможных номера взрослых и детей, которые смотрели
играть. Обоснуйте свои ответы. Обобщение
В вашей собственной концепции и понимании предыдущей темы вы
изучили, создайте простую процедуру решения проблемы, связанной с
системы линейных неравенств с двумя переменными. Что я могу сделать
Цель: Чтобы применить полученные знания в реальных жизненных ситуациях, вам будет предложено практическое задание.
что продемонстрирует ваше понимание.
Ситуация Ваша мама хочет на ужин курицу-гриль и тилапию. Вы узнали
эта курица продается по 150 песо за килограмм, а тилапия продается по цене песо
100р за килограмм. Сколько возможных килограмм каждого предмета ваша мать
купит, если общая стоимость не превысит 450 песо? Направление: Вы делаете budg…
Просмотр
Полный документ
интегрированная математика 1 — Google Suche
AlleBilderVideosShoppingMapsNewsBücher
suchoptionen
Integrated Math, Course 1, Student Edition
Buch
4 | Khan Academywww.khanacademy.org › math › math2
Курс математики 1, который часто преподается в 9й класс, охватывает линейные уравнения, неравенства, функции и графики; Системы уравнений и неравенств …
Решение уравнений и неравенств · Основы алгебры · Работа с единицами измерения
[PDF] Интегрированный математический курс 1 – Объединенный школьный округ Чино-Вэлли
www.
chino.k12.ca.us › cms › lib › Domain › Int Math 1- УЧЕБНИК
Глава 0 Подготовка к интегрированной математике I. Глава 1 Выражения, уравнения и функции. Глава 2 Линейные уравнения. Глава 3 Линейные функции.
Integrated Math 1 — Mr. Math Blog
www.mrmathblog.com › Integrated-math-1
Модули первого семестра 1–12 · Решение линейных систем с помощью графика — модуль 11.1 · Решение систем с помощью подстановки — модуль 11.2 (Часть 1) · Метод замены с …
Бесплатная версия для студентов Easy Access — интегрированная математика
bim.easyaccessmaterials.com › …
Бесплатная версия для студентов Easy Access — интегрированная математика. Выберите книгу. Математика больших идей: интегрированная математика I · Математика больших идей: интегрированная математика …
Интегрированная математика 1 IM1 Алгебра — Решение одно- и двухшаговых уравнений
www.youtube.com › смотреть
10.09.2013 · Интегрированная математика 1 IM1 Алгебра — Решение одно- и двухшаговых уравнений.
Посмотреть позже. Делиться. Копировать …
Dauer: 20:26
Прислан: 10.09.2013
Большие идеи Математика Интегрированная математика I — 1-е издание — Решения и …
quizlet.com › объяснения › учебники-решения › большие идеи -math-integrate…
Найти пошаговые решения и ответы на Big Ideas Math Integrated Mathematics I — 9781680331127, а также тысячи… Глава 1 Стандарты оценки.
[PDF] Обзор курса Integrated Math 1 — Средняя школа Коронадо
chs.coronadousd.net › Академические курсы › Предложения по выбору › Integ…
Обзор курса Integrated Math 1. Интегрированная математика 1 — это первый курс из трех курсов, включая интегрированный.
McGraw Hill Integrated I, 2012 — 9780076638581 — Mathleaks
mathleaks.com › исследование › mcgraw-hill-integrated-mat…
Подготовка к интегрированной математике I · Предварительное тестирование · 1. План решения задач · 2. Вещественные числа · 3.