Линейный коэффициент корреляции Пирсона — statanaliz.info
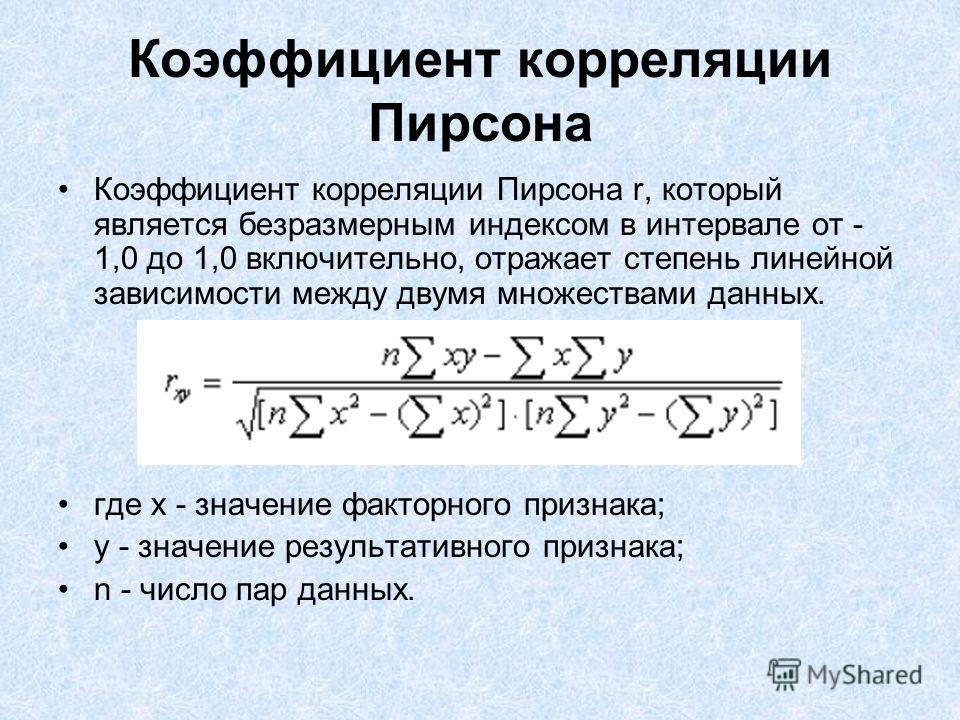
Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.
Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.
Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.
Далее будет рассматриваться только линейная корреляция. На диаграмме рассеяния (график корреляции) изображена взаимосвязь двух переменных X и Y.
Пунктиром показаны средние.
При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего. Это прямая или положительная корреляция. Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.
Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.
Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?
Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии.
Там эту проблему обходят через возведение каждого отклонения в квадрат.
Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.
Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число). Большая положительная ковариация говорит о прямой взаимосвязи между переменными. Обратная взаимосвязь дает отрицательную ковариацию. Если количество совпадающих по знаку отклонений примерно равно количеству не совпадающих, то ковариация стремится к нулю, что говорит об отсутствии линейной взаимосвязи.
Таким образом, чем больше по модулю ковариация, тем теснее линейная взаимосвязь. Однако значение ковариации зависит от масштаба данных, поэтому невозможно сравнивать корреляцию для разных переменных.
Можно определить только направление по знаку. Для получения стандартизованной величины тесноты взаимосвязи нужно избавиться от единиц измерения путем деления ковариации на произведение стандартных отклонений обеих переменных. В итоге получится формула коэффициента корреляции Пирсона.
Показатель имеет полное название линейный коэффициент корреляции Пирсона или просто коэффициент корреляции.
Коэффициент корреляции показывает тесноту линейной взаимосвязи и изменяется в диапазоне от -1 до 1. -1 (минус один) означает полную (функциональную) линейную обратную взаимосвязь. 1 (один) – полную (функциональную) линейную положительную взаимосвязь. 0 – отсутствие линейной корреляции (но не обязательно взаимосвязи). На практике всегда получаются промежуточные значения. Для наглядности ниже представлены несколько примеров с разными значениями коэффициента корреляции.
Таким образом, ковариация и корреляция отражают тесноту линейной взаимосвязи. Последняя используется намного чаще, т.
к. является относительным показателем и не имеет единиц измерения.
Диаграммы рассеяния дают наглядное представление, что измеряет коэффициент корреляции. Однако нужна более формальная интерпретация. Эту роль выполняет квадрат коэффициента корреляции r2, который называется коэффициентом детерминации, и обычно применяется при оценке качества регрессионных моделей. Снова представьте линию, вокруг которой расположены точки.
Линейная функция является моделью взаимосвязи между X иY и показывает ожидаемое значение Y при заданном X. Коэффициент детерминации – это соотношение дисперсии ожидаемых Y (точек на прямой линии) к общей дисперсии Y, или доля объясненной вариации Y. При r = 0,1 r2 = 0,01 или 1%, при r = 0,5 r2 = 0,25 или 25%.
Выборочный коэффициент корреляции
Коэффициент корреляции обычно рассчитывают по выборке.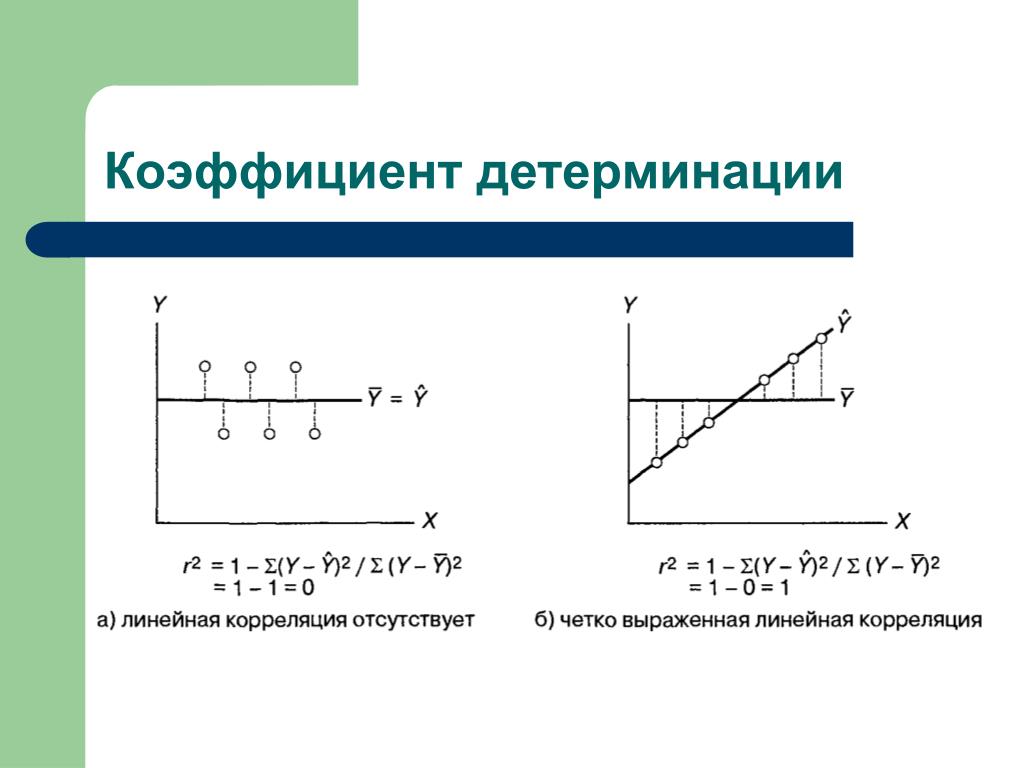
Значит, у аналитика в распоряжении не истинное значение, а оценка, которая всегда ошибочна. Если выборка была репрезентативной, то истинное значение коэффициента корреляции находится где-то относительно недалеко от оценки. Насколько далеко, можно определить через доверительные интервалы.
Согласно Центральное Предельной Теореме распределение оценки любого показателя стремится к нормальному с ростом выборки. Но есть проблемка. Распределение коэффициента корреляции вблизи придельных значений не является симметричным. Ниже пример распределения при истинном коэффициенте корреляции ρ = 0,86.
Предельное значение не дает выйти за 1 и, как бы «поджимает» распределение справа. Симметричная ситуация наблюдается, если коэффициент корреляции близок к -1.
В общем рассчитывать на свойства нормального распределения нельзя. Поэтому Фишер предложил провести преобразование выборочного коэффициента корреляции по формуле:
Распределение z для тех же r имеет следующий вид.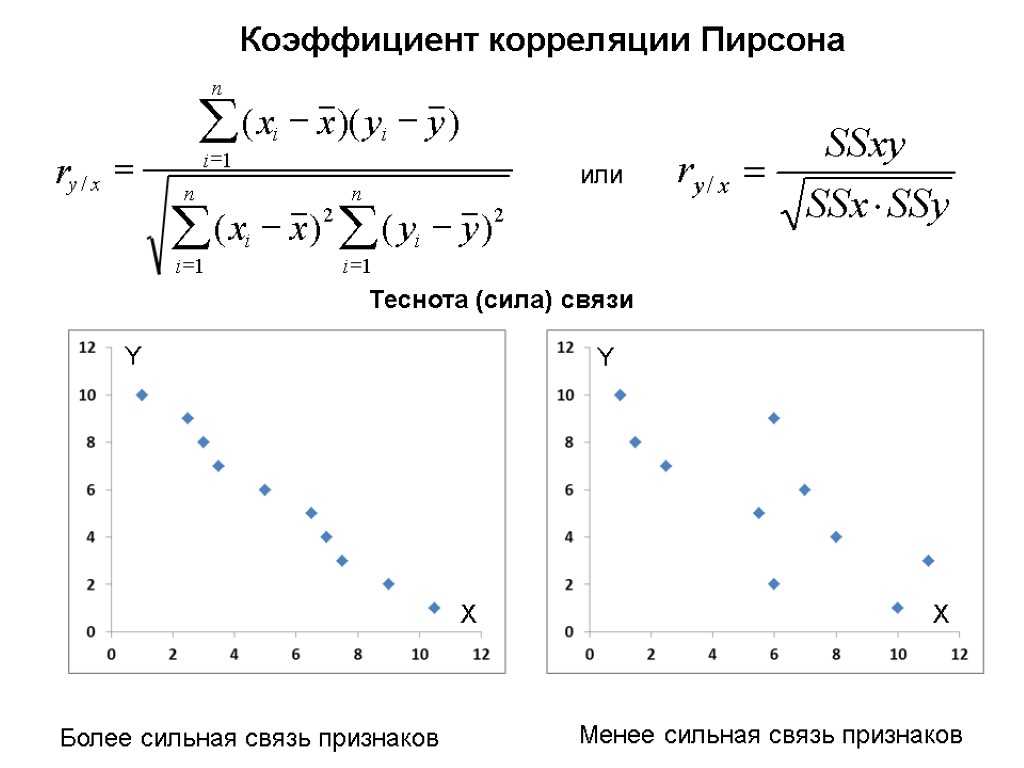
Намного ближе к нормальному. Стандартная ошибка z равна:
Далее исходя из свойств нормального распределения несложно найти верхнюю и нижнюю границы доверительного интервала для z. Определим квантиль стандартного нормального распределения для заданной доверительной вероятности, т.е. количество стандартных отклонений от центра распределения.
cγ – квантиль стандартного нормального распределения;
N-1 – функция обратного стандартного распределения;
γ – доверительная вероятность (часто 95%).
Затем рассчитаем границы доверительного интервала.
Нижняя граница z:
Верхняя граница z:
Теперь обратным преобразованием Фишера из z вернемся к r.
Нижняя граница r:
Верхняя граница r:
Это была теоретическая часть. Переходим к практике расчетов.
Как посчитать коэффициент корреляции в Excel
Корреляционный анализ в Excel лучше начинать с визуализации.
На диаграмме видна взаимосвязь двух переменных. Рассчитаем коэффициент парной корреляции с помощью функции Excel КОРРЕЛ. В аргументах нужно указать два диапазона.
Коэффициент корреляции 0,88 показывает довольно тесную взаимосвязь между двумя показателями. Но это лишь оценка, поэтому переходим к интервальному оцениванию.
Расчет доверительного интервала для коэффициента корреляции в Excel
В Эксель нет готовых функций для расчета доверительного интервала коэффициента корреляции, как для средней арифметической. Поэтому план такой:
— Делаем преобразование Фишера для r.
— На основе нормальной модели рассчитываем доверительный интервал для z.
— Делаем обратное преобразование Фишера из z в r.
Удивительно, но для преобразования Фишера в Excel есть специальная функция ФИШЕР.
Стандартная ошибка z легко подсчитывается с помощью формулы.
Используя функцию НОРМ.
СТ.ОБР, определим квантиль нормального распределения. Доверительную вероятность возьмем 95%.
Значение 1,96 хорошо известно любому опытному аналитику. В пределах ±1,96σ от средней находится 95% нормально распределенных величин.
Используя z, стандартную ошибку и квантиль, легко определим доверительные границы z.
Последний шаг – обратное преобразование Фишера из z назад в r с помощью функции Excel ФИШЕРОБР. Получим доверительный интервал коэффициента корреляции.
Нижняя граница 95%-го доверительного интервала коэффициента корреляции – 0,724, верхняя граница – 0,953.
Надо пояснить, что значит значимая корреляция. Коэффициент корреляции статистически значим, если его доверительный интервал не включает 0, то есть истинное значение по генеральной совокупности наверняка имеет тот же знак, что и выборочная оценка.
Несколько важных замечаний
1. Коэффициент корреляции Пирсона чувствителен к выбросам.
Одно аномальное значение может существенно исказить коэффициент. Поэтому перед проведением анализа следует проверить и при необходимости удалить выбросы. Другой вариант – перейти к ранговому коэффициенту корреляции Спирмена. Рассчитывается также, только не по исходным значениям, а по их рангам (пример показан в ролике под статьей).
2. Синоним корреляции – это взаимосвязь или совместная вариация. Поэтому наличие корреляции (r ≠ 0) еще не означает причинно-следственную связь между переменными. Вполне возможно, что совместная вариация обусловлена влиянием третьей переменной. Совместное изменение переменных без причинно-следственной связи называется ложная корреляция.
3. Отсутствие линейной корреляции (r = 0) не означает отсутствие взаимосвязи. Она может быть нелинейной. Частично эту проблему решает ранговая корреляция Спирмена, которая показывает совместный рост или снижение рангов, независимо от формы взаимосвязи.
В видео показан расчет коэффициента корреляции Пирсона с доверительными интервалами, ранговый коэффициент корреляции Спирмена.
↓ Скачать файл с примером ↓
Поделиться в социальных сетях:
Коэффициент корреляции онлайн
где x·y, x, y — средние значения выборок; σ(x), σ(y) — среднеквадратические отклонения.Кроме того, коэффициент линейной парной корреляции Пирсона может быть определен через коэффициент регрессии b: , где σ(x)=S(x), σ(y)=S(y) — среднеквадратические отклонения, b — коэффициент перед x в уравнении регрессии
y=a+bx.
Другие варианты формул:
или
Кxy — корреляционный момент (коэффициент ковариации)
Для нахождения линейного коэффициента корреляции Пирсона необходимо найти выборочные средние x и y, и их среднеквадратические отклонения σx = S(x), σy = S(y):
Линейный коэффициент корреляции указывает на наличие связи и принимает значения от –1 до +1 (см.
Геометрический смысл коэффициента корреляции: rxy показывает, насколько различается наклон двух линий регрессии: y(x) и х(у), насколько сильно различаются результаты минимизации отклонений по x и по y. Чем больше угол между линиями, то тем больше rxy.
Знак коэффициента корреляции совпадает со знаком коэффициента регрессии и определяет наклон линии регрессии, т.е. общую направленность зависимости (возрастание или убывание). Абсолютная величина коэффициента корреляции определяется степенью близости точек к линии регрессии.
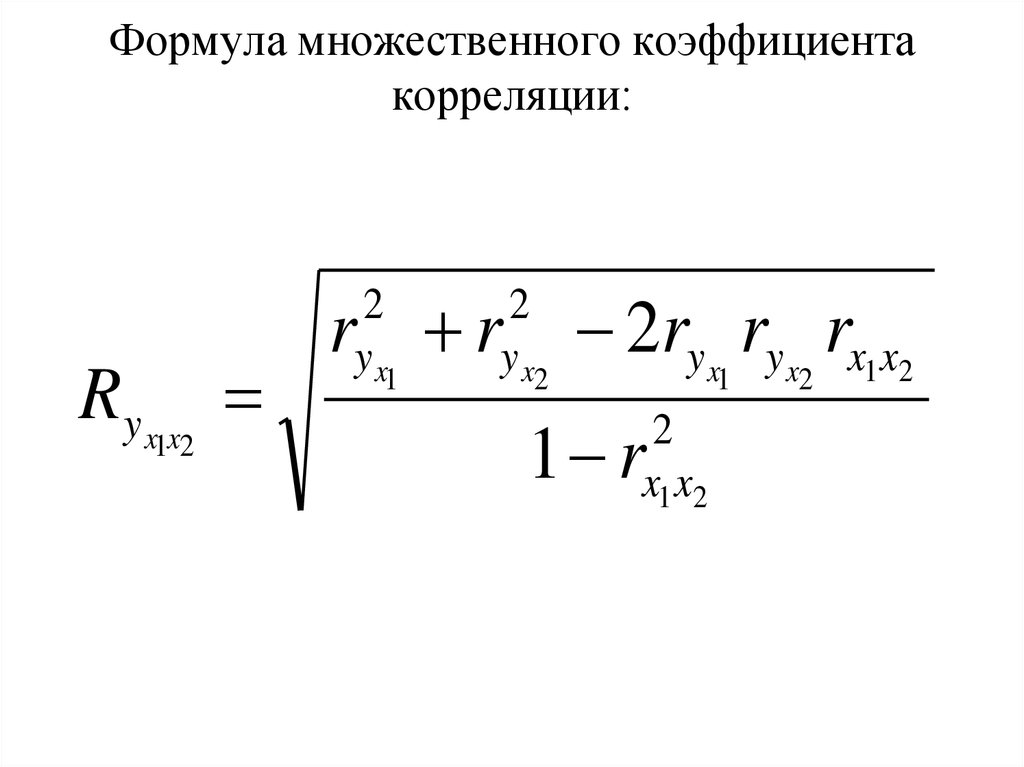
Свойства коэффициента корреляции
- |rxy| ≤ 1;, -1≤x≤1
- если X и Y независимы, то rxy=0, обратное не всегда верно;
- если |rxy|=1, то Y=aX+b, |rxy(X,aX+b)|=1, где a и b постоянные, а ≠ 0;
- |rxy(X,Y)|=|rxy(a1X+b1, a2X+b2)|, где a1, a2, b1, b2 – постоянные.
Поэтому для проверки направления связи выбирается проверка гипотезы при помощи коэффициента корреляции Пирсона с дальнейшей проверкой на достоверность при помощи
- Решение онлайн
- Видеоинструкция
- Оформление Word
- Типовые задачи
Инструкция. Укажите количество исходных данных.
Полученное решение сохраняется в файле Word (см. Пример нахождения уравнения регрессии). Также автоматически создается шаблон решения в Excel. Подробнее.
Количество строк
(исходных данных)
Заданы итоговые значения величин (∑x, ∑x2, ∑xy, ∑y, ∑y2)
Типовые задания (см. также нелинейная регрессия)
Типовые задания
Исследуется зависимость производительности труда y от уровня механизации работ x (%) по данным 14 промышленных предприятий. Статистические данные приведены в таблице.
1) Найти оценки параметров линейной регрессии у на х. Построить диаграмму рассеяния и нанести прямую регрессии на диаграмму рассеяния.
2) На уровне значимости α=0.05 проверить гипотезу о согласии линейной регрессии с результатами наблюдений.
3) С надежностью γ=0.95 найти доверительные интервалы для параметров линейной регрессии.
Пример. На основе данных, приведенных в Приложении 1 и соответствующих Вашему варианту (таблица 2), требуется:
- Рассчитать коэффициент линейной парной корреляции и построить уравнение линейной парной регрессии одного признака от другого. Один из признаков, соответствующих Вашему варианту, будет играть роль факторного (х), другой – результативного (y). Причинно-следственные связи между признаками установить самим на основе экономического анализа. Пояснить смысл параметров уравнения.
- Определить теоретический коэффициент детерминации и остаточную (необъясненную уравнением регрессии) дисперсию. Сделать вывод.
- Оценить статистическую значимость уравнения регрессии в целом на пятипроцентном уровне с помощью F-критерия Фишера. Сделать вывод.
- Выполнить прогноз ожидаемого значения признака-результата y при прогнозном значении признака-фактора х, составляющим 105% от среднего уровня х.
Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал с вероятностью 0,95.
Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал с вероятностью 0,95.
y = ax + b
Средние значения
Дисперсия
Среднеквадратическое отклонение
Коэффициент корреляции Связь между признаком Y фактором X сильная и прямая (определяется по шкале Чеддока).
Уравнение регрессии Коэффициент регрессии: k = a = 4.01
Коэффициент детерминации
R 2 = 0.99 2 = 0.97, т.е. в 97% случаев изменения х приводят к изменению y. Другими словами — точность подбора уравнения регрессии — высокая. Остаточная дисперсия: 3%.
| x | y | x2 | y2 | x·y | y(x) | (yi-y)2 | (y-y(x))2 | (x-xp)2 |
| 1 | 107 | 1 | 11449 | 107 | 103. 19 |
333.06 | 14.5 | 30.25 |
| 2 | 109 | 4 | 11881 | 218 | 107.2 | 264.06 | 3.23 | 20.25 |
| 3 | 110 | 9 | 12100 | 330 | 111.21 | 232.56 | 1.47 | 12.25 |
| 4 | 113 | 16 | 12769 | 452 | 115.22 | 150.06 | 4.95 | 6.25 |
| 5 | 120 | 25 | 14400 | 600 | 119.23 | 27.56 | 0.59 | 2.25 |
| 6 | 122 | 36 | 14884 | 732 | 123.24 | 10.56 | 1.55 | 0.25 |
| 7 | 123 | 49 | 15129 | 861 | 127. 26 |
5.06 | 18.11 | 0.25 |
| 8 | 128 | 64 | 16384 | 1024 | 131.27 | 7.56 | 10.67 | 2.25 |
| 9 | 136 | 81 | 18496 | 1224 | 135.28 | 115.56 | 0.52 | 6.25 |
| 10 | 140 | 100 | 19600 | 1400 | 139.29 | 217.56 | 0.51 | 12.25 |
| 11 | 145 | 121 | 21025 | 1595 | 143.3 | 390.06 | 2.9 | 20.25 |
| 12 | 150 | 144 | 22500 | 1800 | 147.31 | 612.56 | 7.25 | 30.25 |
| 78 | 1503 | 650 | 190617 | 10343 | 1503 | 2366. 25 | 66.23 | 143 |
Примечание: значения y(x) находятся из полученного уравнения регрессии:
y(1) = 4.01*1 + 99.18 = 103.19
y(2) = 4.01*2 + 99.18 = 107.2
... ... ...
H0: rxy = 0, нет линейной взаимосвязи между переменными;
H1: rxy ≠ 0, есть линейная взаимосвязь между переменными;
Для того чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции нормальной двумерной случайной величины при конкурирующей гипотезе H1 ≠ 0, надо вычислить наблюдаемое значение критерия (величина случайной ошибки): По таблице Стьюдента находим tтабл (n-m-1;α/2) = (10;0.025) = 2.228
Поскольку Tнабл > tтабл, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.
Интервальная оценка для коэффициента корреляции (доверительный интервал)
r — Δr ≤ r ≤ r + Δr
Δr = ±tтаблmr = ±2.228 • 0.0529 = 0.118
0.986 — 0.118 ≤ r ≤ 0.986 + 0.118
Доверительный интервал для коэффициента корреляции: 0.868 ≤ r ≤ 1
Анализ точности определения оценок коэффициентов регрессии
Sa=0.2152
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 7
(122.4;132.11)
1) t-статистика
Статистическая значимость коэффициента регрессии подтверждается (18.63>2.228).
Статистическая значимость коэффициента регрессии подтверждается (62.
62>2.228).
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими (tтабл=2.228):
(a — tтабл·Sa; a + tтабл·S a)
(3.6205;4.4005)
(b — tтабл·Sb; b + tтабл·Sb)
(96.3117;102.0519)
2) F-статистики
Fkp = 4.96. Поскольку F > Fkp, то коэффициент детерминации статистически значим (см. критерий Фишера).
см. также Корреляционный анализ. Примеры решения задач.
Пример №2
1. Расчет средних значений x, y:
x =
∑xi
n
=
660.6
11
= 60.05
y =
∑yi
n
=
333.
94
11
= 30.36
x·y =
∑xi·yi
n
=
19952.07
11
= 1813.82
2. Расчет дисперсий:
S2(x) =
xi2
n
— x2 =
40337.2
11
— 60.052 = 60.47
S2(y) =
yi2
n
— y2 =
10329.52
11
— 30.362 = 17.43
3. Расчет среднеквадратических отклонений:
S(x) =
√
S2(x)
=
√
60.47
= 7.78
S(y) =
√
S2(y)
=
√
17.
43
= 4.17
4. Расчет линейного коэффициента корреляции Пирсона:
rxy =
x·y — x·y
S(x)·S(y)
=
1813.82-60.05·30.36
7.78·4.17
= -0.2872
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < rxy < 0.3: слабая;
0.3 < rxy < 0.5: умеренная;
0.5 < rxy < 0.7: заметная;
0.7 < rxy < 0.9: высокая;
0.9 < rxy < 1: весьма высокая;
В нашем примере связь между признаком Y фактором X слабая и обратная.
| x | y | x2 | y2 | x·y | y(x) | (yi-y)2 | (y-y(x))2 |
68. 5
| 22.39 | 4692.25 | 501.31 | 1533.72 | 29.06 | 63.49 | 44.44 |
| 75.7 | 29.24 | 5730.49 | 854.98 | 2213.47 | 27.95 | 1.25 | 1.67 |
| 52.7 | 32.92 | 2777.29 | 1083.73 | 1734.88 | 31.49 | 6.56 | 2.04 |
| 60.2 | 33.52 | 3624.04 | 1123.59 | 2017.9 | 30.34 | 10 | 10.14 |
| 62.3 | 30.98 | 3881.29 | 959.76 | 1930.05 | 30.01 | 0.39 | 0.94 |
| 48.3 | 37.17 | 2332.89 | 1381.61 | 1795.31 | 32.17 | 46.4 | 25 |
56. 5
| 32.12 | 3192.25 | 1031.69 | 1814.78 | 30.91 | 3.1 | 1.47 |
| 65.9 | 31.76 | 4342.81 | 1008.7 | 2092.98 | 29.46 | 1.97 | 5.3 |
| 56.2 | 28.48 | 3158.44 | 811.11 | 1600.58 | 30.95 | 3.53 | 6.11 |
| 51.1 | 23.17 | 2611.21 | 536.85 | 1183.99 | 31.74 | 51.67 | 73.42 |
| 63.2 | 32.19 | 3994.24 | 1036.2 | 2034.41 | 29.87 | 3.36 | 5.37 |
| 660.6 | 333.94 | 40337.2 | 10329.52 | 19952.07 | 333.94 | 191.71 | 175.9 |
Значимость линейного коэффициента корреляции Пирсона.
tнабл = rxy·
√
n-2
√
1-rxy2
= 0.2872·
√
9
√
1-0.28722
= 0.9
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=n-m-1=11-1-1=9 находим tкрит: tкрит(n-m-1;α/2) = tкрит(9;0.025) = 2.262, где m=1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции Пирсона признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл < tкрит, то принимаем гипотезу о равенстве 0 коэффициента корреляции.
Другими словами, коэффициент корреляции статистически — не значим
В парной линейной регрессии t2r = t2b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
Интервальная оценка для линейного коэффициента корреляции Пирсона
(
rxy — tкрит·
1-rxy2
√
n
;
rxy + tкрит·
1-rxy2
√
n
)
Доверительный интервал для коэффициента корреляции
(
0.29 — 2.262·
1-0.292
√
11
;
0.
29 + 2.262·
1-0.292
√
11
)
Доверительный интервал для линейного коэффициента корреляции Пирсона: r(-0.9129;0.3386)
Перейти к онлайн решению своей задачи
Результат:
10.2: Коэффициент линейной корреляции
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 543
- Анонимный
- LibreTexts
Цели обучения
Чтобы узнать, что такое коэффициент линейной корреляции, как его вычислить и что он говорит нам о связи между двумя переменными \(x\) и \(y\)
Рисунок \(\PageIndex{1}\) иллюстрирует линейные отношения между двумя переменными \(x\) и \(y\) различной силы.
Наглядно видно, что в ситуации на панели (а) \(х\) может служить полезным предиктором \(у\), он будет менее полезен в ситуации, показанной на панели (б), и в ситуации, показанной на панели (б), В ситуации с панелью (с) линейная зависимость настолько слаба, что практически отсутствует. Коэффициент линейной корреляции — это число, вычисленное непосредственно из данных, которые измеряют силу линейной связи между двумя переменными \(x\) и \(y\).
Определение: коэффициент линейной корреляции
Коэффициент линейной корреляции для набора \(n\) пар \(x\) чисел в выборке это число \(r\), заданное формулой
. Коэффициент линейной корреляции обладает следующими свойствами, показанными на рисунке \(\PageIndex{2}\)
- Значение \(r\) лежит между \(−1\) и \(1\) включительно.
- Знак \(r\) указывает направление линейной зависимости между \(x\) и \(y\):
- Размер \(|r|\) указывает на силу линейной зависимости между \(x\) и \(y\):
- Если \(|r|\) близко к \(1\) (то есть, если \(r\) близко к \(1\) или \(−1\)), то линейная связь между \ (x\) и \(y\) сильно.
- Если \(|r|\) близко к \(0\) (то есть, если \(r\) близко к \(0\) и любого знака). тогда линейная связь между \(x\) и \(y\) слабая.
- Если \(|r|\) близко к \(1\) (то есть, если \(r\) близко к \(1\) или \(−1\)), то линейная связь между \ (x\) и \(y\) сильно.
так что
\[ r= \dfrac{SS_{xy}}{\sqrt{SS_{xx}SS_{yy}}}=\dfrac{2,44,583}{\sqrt{(46,916)(1690,916)}}=0,868 \ не число \]
Число количественно определяет то, что визуально видно из рисунка. \(\PageIndex{2}\) вес имеет тенденцию к линейному увеличению с высотой (\(r\) положительное значение), и хотя соотношение не идеальное, оно достаточно сильное (\( г\) близко к \(1\)).
Рисунок \(\PageIndex{2}\): коэффициент линейной корреляции \(r\) . Обратите особое внимание на панель (f), которая показывает совершенно детерминированную связь между \(x\) и \(y\), но \(f=0\), поскольку связь не является линейной. (В данном конкретном случае точки лежат на верхней половине круга.)Пример \(\PageIndex{1}\)
Вычислить коэффициент линейной корреляции для пар роста и веса, показанных на рисунке \(\PageIndex{2}\).
2\)»> 336025
Ключевые выводы
- Коэффициент линейной корреляции измеряет силу и направление линейной зависимости между двумя переменными \(x\) и \(y\).
- Знак коэффициента линейной корреляции указывает направление линейной зависимости между \(x\) и \(y\).
- Когда \(r\) близко к \(1\) или \(-1\), линейная зависимость сильна; когда он близок к \(0\), линейная зависимость слабая.
Эта страница под названием 10.2: Коэффициент линейной корреляции распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Anonymous с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Аноним
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 3,0
- Программа OER или Publisher
- Издатель, имя которого нельзя называть
- Показать оглавление
- нет
- Теги
- коэффициент линейной корреляции
- источник@https://2012books. lardbucket.org/books/beginning-statistics
lardbucket.org/books/beginning-statisticsКоэффициенты корреляции: положительный, отрицательный и нулевой
Коэффициенты корреляции — это индикаторы силы линейной связи между двумя разными переменными, x и y. Коэффициент линейной корреляции больше нуля указывает на положительную связь. Значение меньше нуля означает отрицательную связь. Наконец, нулевое значение указывает на отсутствие связи между двумя переменными x и y.
В этой статье объясняется значение коэффициентов линейной корреляции для инвесторов, как рассчитать ковариацию для акций и как инвесторы могут использовать корреляцию для прогнозирования рынка.
Основные выводы:
- Коэффициенты корреляции используются для измерения силы линейной зависимости между двумя переменными.
- Коэффициент корреляции больше нуля указывает на положительную связь, а значение меньше нуля указывает на отрицательную связь.
- Нулевое значение указывает на отсутствие связи между двумя сравниваемыми переменными.
- Отрицательная корреляция, или обратная корреляция, является ключевой концепцией создания диверсифицированных портфелей, способных лучше противостоять волатильности портфеля.
- Вычисление коэффициента корреляции занимает много времени, поэтому данные часто вводятся в калькулятор, компьютер или статистическую программу, чтобы найти коэффициент.
Понимание корреляции
Коэффициент корреляции ( ρ ) — это мера, определяющая степень, в которой движение двух разных переменных связано. Наиболее распространенный коэффициент корреляции, генерируемый корреляцией продукта-момента Пирсона, используется для измерения линейной зависимости между двумя переменными. Однако при нелинейной зависимости этот коэффициент корреляции не всегда может быть подходящей мерой зависимости.
Возможный диапазон значений коэффициента корреляции составляет от -1,0 до 1,0. Другими словами, значения не могут превышать 1,0 или быть меньше -1,0. Корреляция -1,0 указывает на идеальную отрицательную корреляцию, а корреляция 1,0 указывает на идеальную положительную корреляцию.
Если коэффициент корреляции больше нуля, это положительная связь. И наоборот, если значение меньше нуля, это отрицательная связь. Нулевое значение указывает на отсутствие связи между двумя переменными.
При интерпретации корреляции важно помнить, что если две переменные коррелированы, это не означает, что одна является причиной другой.
Корреляция и финансовые рынки
На финансовых рынках коэффициент корреляции используется для измерения корреляции между двумя ценными бумагами. Например, когда две акции движутся в одном направлении, коэффициент корреляции положительный. И наоборот, когда две акции движутся в противоположных направлениях, коэффициент корреляции отрицательный.
Если коэффициент корреляции двух переменных равен нулю, между переменными нет линейной зависимости. Однако это только для линейной зависимости. Возможно, что переменные имеют сильную криволинейную связь. Когда значение ρ близко к нулю, обычно между -0,1 и +0,1, говорят, что переменные не имеют линейной связи (или имеют очень слабую линейную связь).
Например, предположим, что цены на кофе и компьютеры наблюдают и обнаруживают корреляцию +0,0008. Это означает, что между двумя переменными нет корреляции или взаимосвязи.
Инвестопедия / Хьюго ЛинРасчет ρ
Перед определением корреляции необходимо рассчитать ковариацию двух рассматриваемых переменных. Далее требуется стандартное отклонение каждой переменной. Коэффициент корреляции определяется путем деления ковариации на произведение стандартных отклонений двух переменных.
Стандартное отклонение — это мера разброса данных по сравнению со средним значением. Ковариация — это мера того, как две переменные изменяются вместе. Однако его величина неограничена, поэтому его трудно интерпретировать. Нормализованная версия статистики рассчитывается путем деления ковариации на произведение двух стандартных отклонений. Это коэффициент корреляции.
Корреляция «=» р «=» крышка ( Икс , Д ) о Икс о Д \text{Корреляция}=\rho=\frac{\text{cov}(X,Y)}{\sigma_X\sigma_Y} Корреляция=ρ=σXσYcov(X,Y)
Положительная корреляция
Положительная корреляция — когда коэффициент корреляции больше 0 — означает, что обе переменные движутся в одном направлении.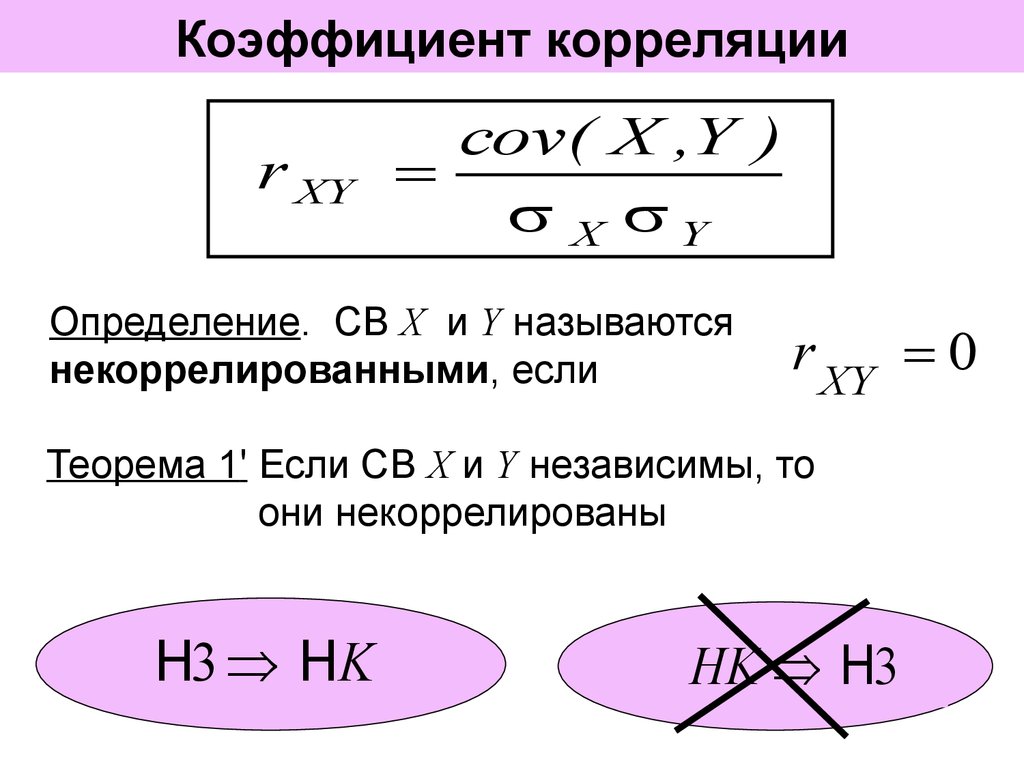
Когда ρ равно +1, это означает, что две сравниваемые переменные имеют совершенно положительную связь; когда одна переменная движется вверх или вниз, другая переменная движется в том же направлении с той же величиной.
Чем ближе значение ρ к +1, тем сильнее линейная связь. Например, предположим, что значение цен на нефть напрямую связано с ценами на авиабилеты с коэффициентом корреляции +0,95. Связь между ценами на нефть и стоимостью авиабилетов имеет очень сильную положительную корреляцию, поскольку значение близко к +1. Так, если цена на нефть снижается, стоимость авиабилетов также снижается, а если цена на нефть растет, то снижаются и цены на авиабилеты.
На приведенной ниже диаграмме мы сравниваем один из крупнейших банков США, JPMorgan Chase & Co. (JPM), с биржевым фондом Financial Select SPDR (ETF) (XLF). Как вы понимаете, JPMorgan Chase & Co. должна иметь положительную корреляцию с банковской отраслью в целом. Мы видим, что коэффициент корреляции в настоящее время составляет 0,9.
8, что свидетельствует о сильной положительной корреляции. Показание выше 0,50 обычно свидетельствует о положительной корреляции.
Понимание корреляции между двумя акциями (или одной акцией) и ее отраслью может помочь инвесторам оценить, как акции торгуются по сравнению с аналогами. Все типы ценных бумаг, включая облигации, секторы и ETF, можно сравнивать с коэффициентом корреляции.
Отрицательная корреляция
Отрицательная (обратная) корреляция возникает, когда коэффициент корреляции меньше 0. Это указывает на то, что обе переменные движутся в противоположном направлении. Короче говоря, любое значение от 0 до -1 означает, что две ценные бумаги движутся в противоположных направлениях. Когда ρ равно -1, говорят, что отношение абсолютно отрицательно коррелировано.
Короче говоря, если одна переменная увеличивается, другая переменная уменьшается с той же величиной (и наоборот). Однако степень отрицательной корреляции между двумя ценными бумагами может меняться со временем (и почти никогда они не всегда точно коррелируют).
Примеры отрицательной корреляции
Например, предположим, что проводится исследование для оценки взаимосвязи между наружной температурой и счетами за отопление. В исследовании делается вывод, что существует отрицательная корреляция между ценами на счета за отопление и температурой наружного воздуха. Коэффициент корреляции рассчитывается равным -0,9.6. Эта сильная отрицательная корреляция означает, что при понижении температуры снаружи растут цены на счета за отопление (и наоборот).
Когда дело доходит до инвестирования, отрицательная корреляция не обязательно означает, что ценных бумаг следует избегать. Коэффициент корреляции может помочь инвесторам диверсифицировать свой портфель, включив в него несколько инвестиций, имеющих отрицательную или низкую корреляцию с фондовым рынком. Короче говоря, при снижении риска волатильности в портфеле иногда противоположности притягиваются.
Например, предположим, что у вас есть сбалансированный портфель в размере 100 000 долларов, который вложен на 60% в акции и на 40% в облигации.
В год сильных экономических показателей компонент акций вашего портфеля может принести доход в размере 12%, а компонент облигаций может принести доход -2%, потому что процентные ставки растут (что означает, что цены на облигации падают).
Таким образом, общая доходность вашего портфеля составит 6,4% ((12% x 0,6) + (-2% x 0,4). В следующем году, когда экономика заметно замедлится и процентные ставки будут снижены, ваш портфель акций может принести -5 %, в то время как доходность вашего портфеля облигаций может составлять 8 %, что дает вам общую доходность портфеля в размере 0,2 %.
Что, если бы вместо сбалансированного портфеля ваш портфель состоял на 100 % из акций? Используя те же предположения о доходности, ваш портфель, полностью состоящий из акций, будет иметь доходность 12% в первый год и -5% во второй год. Эти цифры явно более волатильны, чем доходность сбалансированного портфеля в 6,4% и 0,2%.
Коэффициент линейной корреляции
Коэффициент линейной корреляции – это число, рассчитанное на основе заданных данных, которое измеряет силу линейной связи между двумя переменными: x и y.
Знак коэффициента линейной корреляции указывает направление линейной зависимости между x и y. Когда r (коэффициент корреляции) близок к 1 или −1, линейная зависимость сильна; когда он близок к 0, линейная зависимость слабая.
Даже для небольших наборов данных вычисления коэффициента линейной корреляции могут быть слишком длинными, чтобы выполнять их вручную. Таким образом, данные часто вводятся в калькулятор или, что более вероятно, в компьютер или статистическую программу для нахождения коэффициента.
Коэффициент Пирсона
Как расчет коэффициента Пирсона, так и базовая линейная регрессия позволяют определить линейную связь между статистическими переменными. Однако эти два метода различаются. Коэффициент Пирсона — это мера силы и направления линейной связи между двумя переменными без предположения о причинно-следственной связи. Коэффициент Пирсона показывает корреляцию, а не причинно-следственную связь. Коэффициенты Пирсона варьируются от +1 до -1, где +1 представляет собой положительную корреляцию, -1 представляет отрицательную корреляцию, а 0 представляет отсутствие связи.
Простая линейная регрессия описывает линейную зависимость между переменной отклика (обозначается y) и независимой переменной (обозначается x) с использованием статистической модели. Статистические модели используются для прогнозирования.
Упростите линейную регрессию, вычислив корреляцию с помощью программного обеспечения, такого как Excel.
В финансах, например, корреляция используется в нескольких анализах, включая расчет стандартного отклонения портфеля. Поскольку это занимает много времени, корреляцию лучше всего рассчитывать с помощью программного обеспечения, такого как Excel. Корреляция объединяет статистические понятия, а именно дисперсию и стандартное отклонение. Дисперсия — это дисперсия переменной вокруг среднего значения, а стандартное отклонение — это квадратный корень из дисперсии.
Поиск корреляции с помощью Excel
Существует несколько методов расчета корреляции в Excel. Самый простой — получить два набора данных рядом и использовать встроенную формулу корреляции:
Investopedia.
comЕсли вы хотите создать корреляционную матрицу для ряда наборов данных, в Excel есть подключаемый модуль анализа данных, который находится на вкладке «Данные» в разделе «Анализ».
Выберите таблицу возвратов. В этом случае наши столбцы имеют заголовки, поэтому мы хотим установить флажок «Ярлыки в первой строке», чтобы Excel знал, что их следует рассматривать как заголовки. Затем вы можете выбрать вывод на тот же лист или на новый лист.
Investopedia.comКак только вы нажмете Enter, данные будут созданы автоматически. Вы можете добавить текст и условное форматирование, чтобы очистить результат.
Investopedia.comКоэффициент линейной корреляции Часто задаваемые вопросы
Что такое коэффициент линейной корреляции?
Коэффициент линейной корреляции — это число, рассчитанное на основе заданных данных, которое измеряет силу линейной связи между двумя переменными, x и y.
Как найти коэффициент линейной корреляции?
Корреляция объединяет несколько важных и связанных статистических понятий, а именно дисперсию и стандартное отклонение.
2)]}}
r=[n∑x2−(∑x)2][n∑y2−(∑y)2)]n(∑xy)−(∑x)(∑y)
Вычисления слишком длительны, чтобы выполнять их вручную, а программное обеспечение, такое как Excel или статистическая программа, являются инструментами, используемыми для расчета коэффициента.
Что понимается под линейной корреляцией?
Коэффициент корреляции – это значение от -1 до +1. Коэффициент корреляции +1 указывает на идеальную положительную корреляцию. Когда переменная x увеличивается, переменная y увеличивается. Когда переменная x уменьшается, переменная y уменьшается. Коэффициент корреляции -1 указывает на полную отрицательную корреляцию. По мере увеличения переменной x переменная z уменьшается. Когда переменная x уменьшается, переменная z увеличивается.
Как найти коэффициент линейной корреляции на калькуляторе?
Графический калькулятор необходим для расчета коэффициента корреляции. Следующие инструкции предоставлены Statology.
Шаг 1. Включите диагностику
Вам нужно будет сделать этот шаг только один раз на вашем калькуляторе.
После этого вы всегда можете начать с шага 2 ниже. Если вы этого не сделаете, r (коэффициент корреляции) не будет отображаться при запуске функции линейной регрессии.
- Нажмите [2], а затем [0], чтобы войти в каталог вашего калькулятора. Прокрутите, пока не увидите «диагностика включена».
- Нажимайте клавишу ввода, пока на экране калькулятора не появится надпись «Готово».
Важно повторить: вам никогда не придется делать это снова, если вы не перезагрузите свой калькулятор.
Шаг 2: введите данные
Введите свои данные в калькулятор, нажав [STAT], а затем выбрав 1:Редактировать. Чтобы упростить задачу, вы должны ввести все свои «данные x» в L1 и все ваши «данные y» в L2.
Шаг 3: Расчет!
После того, как вы введете свои данные, вы перейдете к [STAT], а затем к меню CALC вверху. Наконец, выберите 4:LinReg и нажмите Enter.
Вот и все! Готово! Теперь вы можете просто считать коэффициент корреляции прямо с экрана (это r).