Производная от sinx 2: найти производную функции y=sin x/2

Содержание

Основные правила дифференцирования

Производная суммы (разности) равна сумме (разности) производных

(f(x)±g(x))′=f′(x)±g′(x)

Производная произведения

(f(x)·g(x))′=f′(x)·g(x)-f(x)·g(x)′/g2(x)

Производная частного

(f(x)/g(x))′=f′(x)·g(x)+f(x)·g(x)′

Производная сложной функции равна произведению производной внешней функции на производную внутренней функции

f(g(x))′=f′(g(x))·g′(x)

Физический смысл производной

Если материальная точка движется прямолинейно и её координата изменяется в зависимости от времени по закону x(t), то мгновенная скорость данной точки равна производной функции. v(t)=x′(t)

Геометрический смысл производной

Напомним, что уравнение прямой, не параллельной осям координат, можно записать в виде y=kx+b, где k – угловой коэффициент прямой. Коэффициент k равен тангенсу угла наклона между прямой и положительным направлением оси Ох.

k=tgα

Производная функции f(x) в точке х0 равна угловому коэффициенту k касательной к графику в данной точке:

f′(x0)=k

Следовательно, можем составить общее равенство:

f′(x0)=k=tgα

На рисунке касательная к функции f(x) возрастает, следовательно, коэффициент k>0. Так как k>0, то f′(x0)=tgα>0. Угол α между касательной и положительным направлением Ох острый.

На рисунке касательная к функции f(x) убывает, следовательно, коэффициент k<0, следовательно, f′(x0)=tgα<0.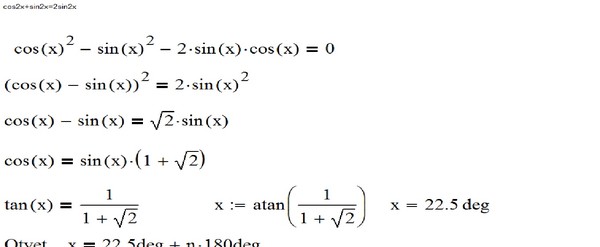 Угол α между касательной и положительным направлением оси Ох тупой.

На рисунке касательная к функции f(x) параллельна оси Ох, следовательно, коэффициент k=0, следовательно, f′(x0)=tgα=0. Точка x0, в которой f′(x0)=0, называется экстремумом.

Производная так же применяется для нахождения промежутков возрастания и убывания функции:

Если f′(x)>0 на промежутке, то функция f(x) возрастает на этом промежутке.

Если f′(x)<0 на промежутке, то функция f(x) убывает на этом промежутке.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!

«Производная функции» — Алгебра, 10 класс

Перед вами вопросы теста, правильный ответ только 1. Время на прохождение теста не ограничено, правильные ответы будут отображаться после нажатия на кнопку результатов (внизу).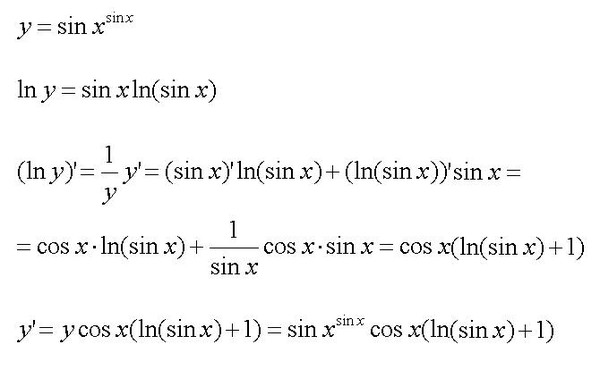

Алгебра10 класс 10.01.2022 0 965

Результаты авторизованых пользователей

Название теста	Дата	Результат	Пользователь
Математика / Тест с ответами: “Умножение многочлена на многочлен”	03-27-2023 09:41:36 pm	7/20	Aiza Min
Медицина / Тест с ответами: “Кишечные инфекции”	03-27-2023 08:15:43 pm	13/20	Татьяна Владимировна Панченко
Психология / Тест с ответами: “Основы психологии”	03-27-2023 05:56:24 pm	12/20	кусь кусь
Литература / Тест с ответами: “История болезни” М.Зощенко	03-27-2023 03:44:37 pm	17/20	EvMeyIngisc
Литература / Тест с ответами: “История болезни” М.Зощенко	03-27-2023 03:37:46 pm	10/20	EvMeyIngisc

Все результаты

#1. Вычислите (cosx)’=

A. -sinx

B. -cosx

C. sinx

#2. Вычислите (10x)’=

A. x

B. 1

C. 10

#3. Вычислите (lnx)’=

A. 1/x

B. 1

C. 0

#4. Вычислите (kx+b)’=

A. x+b

B. k

C. k+b

#5. Функция f называется возрастающей на некотором промежутке

A. если x2 > x1, то f(x2) > f(x1)

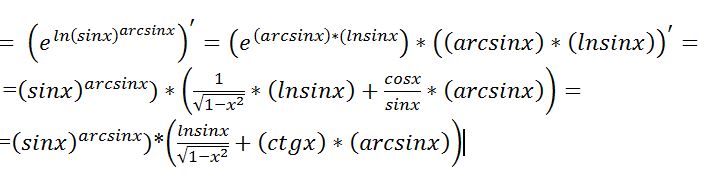B. если x2 > x1, то f(x2)=f(x1)

C. если x2 > x1, то f(x2) < f(x1)

#6. Вычислите (5)’=

A. x

B. 5

C. 0

#7. Вычислите (√8)’=

A. 1

B. 4

C. 0

#8. Прямая, проходящая через начало координат, касается графика функции y=f(x) в точке (-2;10). Вычислите f ´(-2)

A. 6

B. -5

C. -6

#9. Функция f называется убывающей на некотором промежутке

A.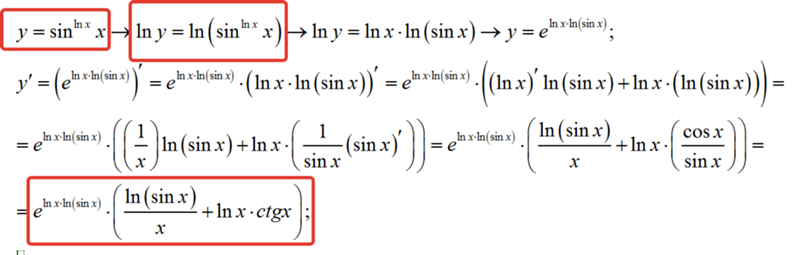 если x2 > x1, то f(x2)=f(x1)

B. если x2 > x1, то f(x2) > f(x1)

C. если x2 > x1, то f(x2) < f(x1)

#10. Чему равен угловой коэффициент прямой y=-2x+3

A. -2

B. 3

C. 2

#11. Функция y=4x²+ 23 на отрезке [-2006; 2006] имеет наименьшее значение при х, равном

A. 23

B. 0

C. -2005

#12. Установите соответствие между функцией и ее производнойcos 2x

A. -4 cos 2x

B. -2 sin 2х

б) -2 sin 2х

#13. Функцией называется

A. множество всех значений, которые может принимать функция

B. множество всех точек (x; f(x)) на координатной плоскости, где x принадлежит D

C. закон, по которому каждому значению x из множества D ставится в соответствие одно определенное число y

#14. Укажите точку максимума функции f(x), если f´ (x)=(x+6)(x-4)

A. 6

B. 5

C. -6

#15. Установите соответствие между функцией и ее производнойsin (x/2)

A. 1/2 cos (х/2)

B. -sin (x/2)

б) -sin (x/2)

#16. Установите соответствие между функцией и ее производной2 cos (x/2)

A. 1/2 cos (х/2)

B. -sin (x/2)

б) -sin (x/2)

#17. Вычислите (ax2+bx+c)’=

A. ax+b

B. 2ax+b

C. ax+b+c

#18. Вычислите (7×5)’

A. 35×4

35x

B. 35x

C. 7x

#19. Вычислите (sinx)’=

A. -cosx

B. sinx

C. cosx

#20. Вычислите (x5)’=

A. 5

B. 5x

C. 5×4

Показать результаты

Оцените тест после прохождения!

Нажмите на звезду, чтобы оценить!

Средняя оценка 4 / 5. Количество оценок: 1

Оценок пока нет. Поставьте оценку первым.

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

2)$ этим методом.

Кто-нибудь может мне помочь!

исчисление
производные

$\endgroup$

$\begingroup$

Вы недостаточно старались. 2),$$ как вы хотели. 9(2).

ПУБЛИКАЦИЯ СУРЫ-ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — ДИФФЕРЕНЦИРУЕМОСТЬ И МЕТОДЫ ДИФФЕРЕНЦИАЦИИ-УПРАЖНЕНИЕ 10.4

20 видео

Аб Падхаи каро бина адс ке

адхорукоки аватари Д.Н.

Обновлено: 27-06-2022

Текст Решение

Ответ

Правильный ответ: cosx2

Похожие видео

Найдите производную от xsin.

32539808