Коэффициент стьюдента для 4 измерений: Коэффициенты Стьюдента — Лабораторный практикум

Коэффициент стьюдента

Число прямых измерений всегда конечно. Поэтому средняя квадратичная погрешность заведомо меньше истинной абсолютной погрешности. Чтобы получить близкое к реальности значение абсолютной погрешности, нужно увеличить среднюю квадратичную погрешность, умножив ее на коэффициент Стьюдента . В теории Стьюдента рассчитаны значения этого коэффициента в зависимости от доверительной вероятности α и числа измерений n. С ростом доверительной вероятности, то есть надежности значения абсолютной погрешности, коэффициент Стьюдента увеличивается. А с ростом числа измерений, увеличивающим надежность самих результатов измерения, коэффициент Стьюдента уменьшается. Ниже приведены значения коэффициента Стьюдента для доверительной вероятности α = 0,95.

n	2	3	4	5	6
tα (n)	12,71	4,303	3,182	2,776	2,571
n	7	8	9	10	20
tα (n)	2,447	2,365	2,306	2,262	2,093

Отметим, что запись результата измерения в форме (7) означает, что значение измеренной величины x с заданной вероятностью α не выйдет за пределы интервала (x_ср – Δx, x_ср + Δx). Поэтому абсолютную погрешность Δx

часто называют полушириной доверительного интервала.

Результат косвенного измерения есть результат расчета по заданной формуле. Оценка относительной погрешности результата расчета уже описана выше. Относительная погрешность рассчитывается по формуле (2), если величины, полученные в результаты прямых измерений, входят в заданную формулу в качестве множителей или делителей.

Для примера рассмотрим косвенное измерение объема прямого цилиндра высоты

h с диаметром d. Объем такого цилиндра можно вычислить по формуле

Для вычисления объема цилиндра по формуле (9) нужно иметь результаты измерения его диаметра и высоты. Пусть в результате прямых измерений получены значения диаметра и высоты цилиндра в соответствии с (7):

В этом случае известны и относительные погрешности значений диаметра и высоты цилиндра:

и

Прежде, чем приступать к вычислению объема, оценим относительную погрешность результата вычисления по формуле (9). В эту формулу входят четыре величины (числа). Два числа из них пришли из математики и являются, а скорее считаются, абсолютно точными: это числа 4 и π. Но число 4 – конечное число, а число

π – является бесконечной непериодической дробью. Как это будет показано, можно взять округленное значение числа π с таким количеством значащих цифр, что это число практически не внесет никакой погрешности в окончательный результат расчета значения объема цилиндра.

Таким образом, источниками погрешности являются значения диаметра и высоты цилиндра. Обе эти величины входят множителями в формулу (9), но диаметр входит множителем два раза (в квадрате), а высота – один раз. Следовательно, подстановка этих величин в формулу (9) приведет к сложению двух относительных погрешностей диаметра и одной относительной погрешности высоты. Согласно формуле (2), относительная погрешность объема составит

Как видим, наибольший вклад в относительную погрешность объема цилиндра вносит неточность измерения диаметра цилиндра.

Поэтому для уменьшения погрешности результата необходимо именно диаметр цилиндра измерить с как можно большей точностью.

Чтобы число π не внесло дополнительную погрешность в результат вычисления объема, нужно взять его значение с относительной погрешностью, много меньшей погрешностей диаметра и высоты цилиндра. Поскольку, как нам известно, точность числа зависит от количества значащих цифр в нем, нужно взять столько цифр числа π, чтобы их количество на одну цифру превышало бы максимальное число значащих цифр в средних значениях диаметра и высоты. Вот запись округленного числа π, содержащая 7 значащих цифр: π = 3,141593.

Теперь, взяв число π с необходимым количеством значащих цифр, можно выполнить расчет среднего значения объема цилиндра по формуле (9):

После этого нужно выполнить расчет относительной погрешности значения объема по формуле (14). Затем вычислить абсолютную погрешность объема по формуле

Значение этой погрешности нужно округлить, оставив только две значащие цифры. Затем нужно уточнить запись среднего значения объема, сопоставив его с величиной абсолютной погрешности (16). Число, обозначающее среднее значение объема, нужно округлить, оставив в нем все цифры вплоть до разряда, являющегося последним в окончательной записи абсолютной погрешности. Записываем результат измерений в виде суммы округленного среднего значения и абсолютной погрешности:

Например, мы получили следующие величины: среднее значение = 3867,395 мм³, = 4,258 мм³. Округляем значение до двух значащих цифр, получаем = 4,3 мм³. Вторая значащая цифра находится в разряде десятых долей миллиметра. Значит, последней оставленной цифрой в записи должна быть цифра 3, стоящая в этом же разряде. Первой отбрасываемой цифрой является 9 ˃ 5, следовательно, нужно добавить 1 к оставленной тройке. В итоге получим: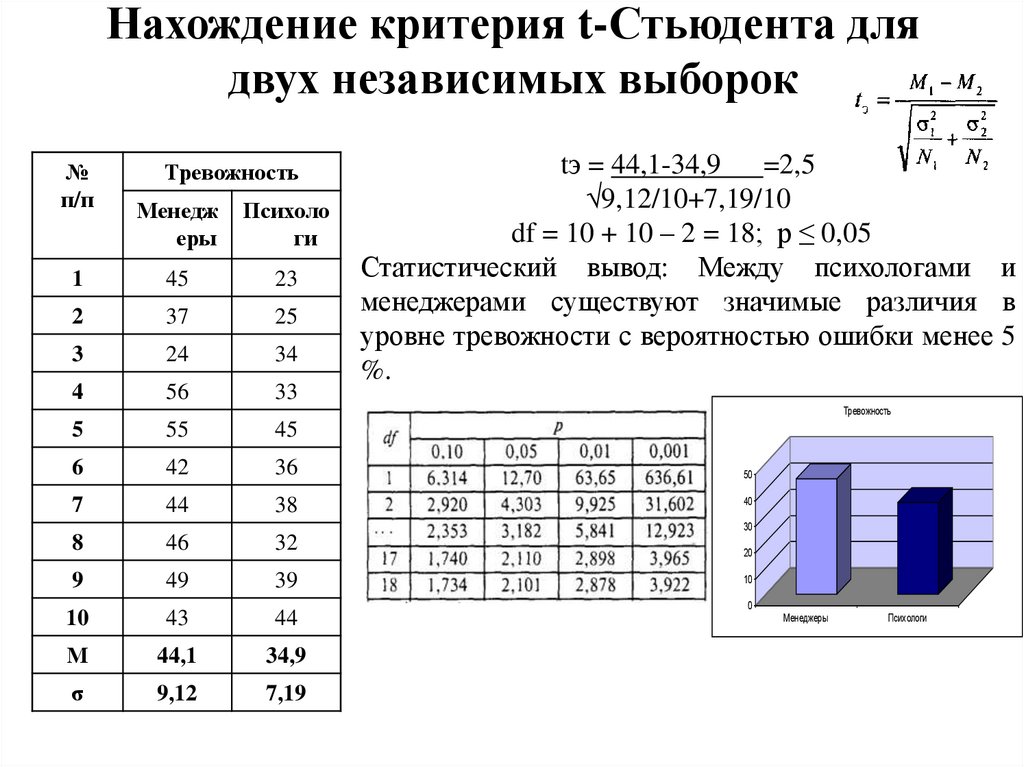

V = (3867,4 4,3) мм³ = (3,8674 0,0043) мм³ = (3,8674 0,0043) = (3,8674 0,0043) . Окончательно:

с относительной погрешностью, равной

КОЕ-ЧТО ИЗ МАТЕМАТИКИ

Для успешного освоения предлагаемого курса физики нужно вспомнить, что такое вектор и как с ним работать, поскольку в описании физической реальности нельзя обойтись без векторных величин. Многие физические величины являются векторами.

Вектор можно изобразить в виде направленного отрезка определенной длины.

Вектор имеет две характеристики: модуль (абсолютную величину или просто величину) и направление. Каждая из этих характеристик может быть постоянной или изменяться независимо от другой.

Векторы складываются по правилу треугольника, как это показано на рисунке.

При умножении вектора на число получается новый вектор, который направлен в ту же сторону, что и старый, если число положительное, и в противоположную сторону, если число отрицательное.

Модуль нового вектора равен произведению модуля старого вектора на модуль этого числа.

При умножении вектора на число 0, получается нулевой вектор, не имеющий ни величины, ни направления.

Любой вектор можно спроецировать на ось координат. Проекция вектора на ось координат равна произведению модуля этого вектора на косинус угла между вектором и осью. Если угол острый, то его косинус и соответственно проекция вектора положительны. Если угол тупой, то его косинус и соответственно проекция вектора отрицательны. Если вектор перпендикулярен оси, то его проекция на эту ось равна нулю.

α

0

Любой вектор можно представить в виде суммы трех его составляющих по осям координат:

где , , и – проекции вектора, а – единичные векторы (орты) соответствующих осей координат.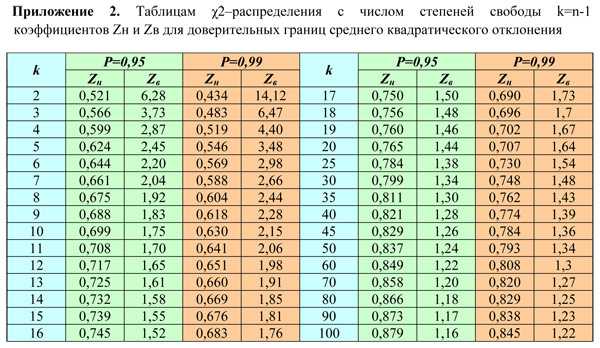

Вектор равен сумме трех векторов , , , каждый из которых направлен вдоль своей оси координат.

0

Допустим некоторая векторная физическая величина, например скорость , изменилась с течением времени. Тогда изменение скорости тоже будет вектором:

Для нахождения вектора это векторное равенство перепишем по-другому

и найдем этот вектор по правилу треугольника. Откладываем из одной точки два вектора и . По правилу треугольника строим вектор . Обратите внимание, какой физический смысл здесь раскрывается: Вектор изменения скорости соединяет конец первого вектора с концом второго, то есть показывает, как изменился вектор скорости (увеличился или уменьшился и в какую сторону повернулся).

Существуют два разных умножения вектора на вектор: скалярное и векторное.

Результатом скалярного произведения вектора на вектор является число, равное произведению модуля первого вектора на модуль второго и на косинус угла между ними:

или равное сумме одноименных проекций этих векторов на оси координат:

Скалярное умножение обозначается точкой.

Результатом векторного произведения вектора на вектор является вектор. Векторное умножение обозначается косым крестиком. Например, вектор равен векторному произведению векторов и :

Вектор перпендикулярен векторам и и его направление определяется по правилу буравчика (правого винта), как это показано на рисунке. Буравчик вращается от первого вектора в сторону второго вектора . Если векторы – множители поменять местами, то вектор изменит направление на противоположное.

Модуль вектора равен произведению модуля первого вектора на модуль второго и на синус угла между ними:

α

Если два вектора параллельны, то их векторное произведение равно нулевому вектору .

Для успешного освоения предлагаемого курса физики нужно также вспомнить основы математического анализа и, как минимум, уметь найти производную от комбинации элементарных функций и взять табличный интеграл.

Напомню определение производной. Пусть некоторая физическая величина, например вектор скорости, меняется с течением времени. Тогда время t является независимой переменной, то есть аргументом (играет роль x из математики). А скорость является зависимой переменной, то есть функцией (играет роль y из математики). Производной называется предел

Если , то и Существует обозначение для величины, которая стремится к 0, но не равна 0. Эта величина называется бесконечно малой. Все дело в том, что она не имеет конкретного значения. Зато она всегда меньше любого сколь угодно малого числа, какое бы мы ни назвали. Для такой бесконечно малой величины существует обозначение: . Это выражение называется дифференциалом и является в данном случае бесконечно малым промежутком времени. – бесконечно малое приращение вектора скорости. Имеем дробь:

которая обладает всеми свойствами дроби из математики, за исключением того, что ее значение нельзя получить обычным делением числителя на знаменатель, а нужно перейти к пределам и раскрыть получившуюся неопределенность. Для любой функции в математике это все проделано и сведено в правила взятия производной от элементарной функции.

Например, некоторое тело движется так, что модуль его скорости зависит от времени по уравнению:

где и – константы. Найдем производную от модуля скорости по времени:

Как Вы вероятно помните, эта производная является ускорением.

Настоятельно рекомендую каждую производную от функции y по аргументу x, которая встретится Вам в физике, обозначать только такой дробью:

Для успешного освоения предлагаемого курса физики нужно также вспомнить, что такое степень и логарифм. Степенью называется двухуровневое выражение вида , нижняя и верхняя части которого неравнозначны.

Показатель степени

Степень

b

a

Основание степени

Для удобства обозначим эту степень буквой у. Имеем равенство

где а – основание степени у, а b – показатель степени у. Чтобы выразить а и b из этого равенства, нужно применить разные правила.

Основание а степени у равно корню из этой степени:

а показатель b степени у равен логарифму этой степени по основанию а:

Итак, показатель степени и логарифм степени – это практически одно и то же.

Чтобы убедиться, проверьте тождество:

и левая и правая части которого равны у.

Страница не найдена

Размер:

AAA

Цвет: C C C

Изображения Вкл. Выкл.

Обычная версия сайта

RUENBY

Гомельский государственный
медицинский университет

• Университет
  • Университет
  • История
  • Руководство
  • Устав и Символика
  • Воспитательная деятельность
  • Организация образовательного процесса
  • Международное сотрудничество
  • Система менеджмента качества
  • Советы
  • Факультеты
  • Кафедры
  • Подразделения
  • Первичная профсоюзная организация работников
  • Издания университета
  • Гордость университета
  • Выпускник-2021
  • Первичная организация «Белорусский союз женщин»
  • Одно окно
  • ГомГМУ в международных рейтингах
  • Структура университета
• Абитуриентам
  • Приёмная комиссия
  • Университетская олимпиада по биологии
  • Целевая подготовка
  • Заключение, расторжение «целевого» договора
  • Льготы для молодых специалистов
  • Архив проходных баллов
  • Карта и маршрут проезда
  • Порядок приёма на 2023 год
  • Специальности
  • Контрольные цифры приёма в 2022 году
  • Стоимость обучения
  • Информация о ходе приёма документов
  • Приём документов и время работы приёмной комиссии
  • Порядок приёма граждан РФ, Кыргызстана, Таджикистана, Казахстана
  • Горячая линия по вопросам вступительной кампании
• Студентам
  • Первокурснику
  • Расписание занятий
  • Расписание экзаменов
  • Информация для студентов
  • Студенческий клуб
  • Спортивный клуб
  • Общежитие
  • Нормативные документы
  • Практика
  • Стоимость обучения
  • Безопасность жизнедеятельности
  • БРСМ
  • Профком студентов
  • Учебный центр практической подготовки и симуляционного обучения
  • Многофункциональная карточка студента
  • Анкетирование студентов
• Выпускникам
  • Интернатура и клиническая ординатура
  • Докторантура
  • Аспирантура
  • Магистратура
  • Распределение
• Врачам и специалистам
  • Профессорский консультативный центр
  • Факультет повышения квалификации и переподготовки
• Иностранным гражданам
  • Факультет иностранных студентов
  • Стоимость обучения
  • Регистрация и визы
  • Полезная информация
  • Правила приёма
  • Информация о возможностях и условиях приема в 2022 году
  • Официальные представители ГомГМУ по набору студентов
  • Страхование иностранных граждан
  • Приём на Подготовительное отделение иностранных граждан
  • Прием иностранных граждан для обучения на английском языке / Training of foreign students in English
  • Повышение квалификации и переподготовка для иностранных граждан
• Научная деятельность
  • Направления научной деятельности
  • Научно-педагогические школы
  • Студенчеcкое научное общество
  • Инновационные технологии в ГомГМУ
  • Научно-исследовательская часть
  • Научно-исследовательская лаборатория
  • Конкурсы, гранты, стипендии
  • Работа комитета по этике
  • Научные мероприятия
  • В помощь исследователю
  • Диссертационный совет
  • «Горизонт Европа»
  • Патенты
  • Инструкции на метод
  • Совет молодых ученых
  • Госпрограмма (ЧАЭС)

• Главная

t Распределение

t Распределение (также известное как t-распределение Стьюдента ) это распределение вероятностей, которое используется для оценки населения параметры, когда размер выборки мал и/или когда население дисперсия неизвестна.

Зачем использовать дистрибутив t?

Согласно в центральная предельная теорема, выборочное распределение статистики (например, выборочное среднее) будет следовать за нормальное распределение, при условии, что объем выборки достаточно велик. Поэтому, когда мы Зная стандартное отклонение совокупности, мы можем вычислить z-показатель и используйте нормальное распределение для оценки вероятности с выборочным средним.

Но размеры выборки иногда малы, и часто мы не знаем стандартное отклонение населения. При возникновении любой из этих проблем статистики полагаются на распределение t статистика (также известная как t оценка ), значения которых определяются как:

т = [ х — мк ] / [ s / sqrt( n ) ]

, где x — выборочное среднее, μ — среднее значение генеральной совокупности, s — стандартное отклонение выборки, а n — размер образца. Распределение t статистика называется т раздача или Студенческое распределение t .

Распределение t позволяет нам проводить статистический анализ определенных данных наборы, не подходящие для анализа, с использованием нормального распределения.

Степени свободы

На самом деле существует множество различных распределений t. Особая форма распределения t определяется его степени свободы . Степени свободы относятся к количеству независимых наблюдений в наборе данных.

При оценке среднего балла или доли по одной выборке число независимых наблюдений равно выборке размер минус один. Следовательно, распределение статистики t из выборки размера 8 будут описаны t-распределением, имеющим 8 — 1 или 7 степеней свободы. Точно так же распределение т статистика от выборки размера 16 будут описаны t-распределением, имеющим 16 — 1 или 15 степеней свободы.

Для других применений можно вычислить степени свободы иначе. Мы будем описывать эти вычисления по мере их появления.

Объявление

Свойства распределения t

Распределение t имеет следующие свойства:

• Дисперсия всегда больше 1, хотя и близко к 1, когда имеется много степеней свободы.
• С бесконечными степенями свободы, распределение t такое же, как стандартное нормальное распределение.

Когда использовать распределение t

Распределение t можно использовать с любой статистикой, имеющей форму колокола распределение (т. е. приблизительно нормальное). Разумно предположить, что выборочное распределение статистики будет иметь форму колокола при выполнении любого из следующих условий.

• Размер выборки больше 40 без выбросов.

Распределение t следует использовать с небольшими выборками из популяции, которые не являются приблизительно нормальными.

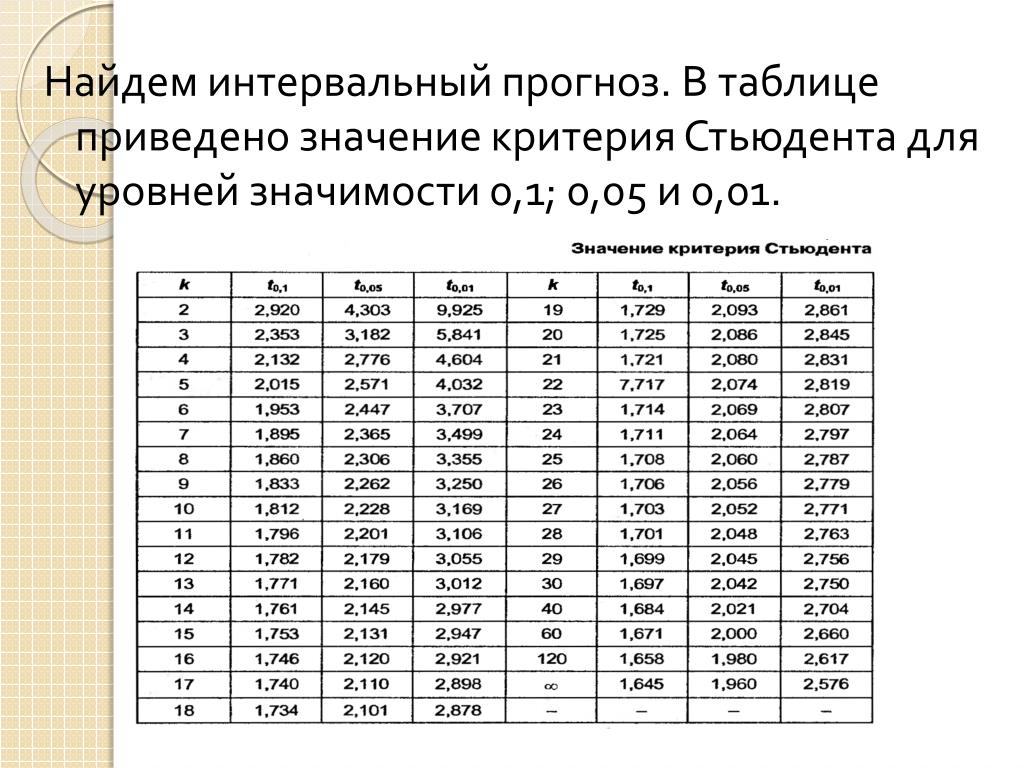
Вероятность и распределение Стьюдента t

нормальное (или близкое к нормальному) распределение, выборочное среднее может быть преобразуется в t-статистику с использованием уравнения, представленного на начало этого урока. Мы повторяем это уравнение ниже:

т = [ х — мк ] / [ с / sqrt ( п ) ]

где x — выборочное среднее, мк — среднее значение генеральной совокупности, s — стандартное отклонение выборки, n — размер выборки и степени свободы равны n — 1.

Статистику t, полученную в результате этого преобразования, можно связать с уникальный кумулятивная вероятность. Эта кумулятивная вероятность представляет вероятность обнаружения выборочное среднее значение меньше или равно x, дана случайная выборка размера и .

Чтобы найти вероятность, связанную с t-статистикой, используйте таблицу t-распределения (приведенную в приложении к большинству вводные статистические тексты), графический калькулятор, онлайн-калькулятор распределения t, такой как Stat Trek Калькулятор распределения T.

Калькулятор T-распределения

Калькулятор T-распределения решает распространенные статистические задачи на основе распределение. Калькулятор вычисляет кумулятивные вероятности на основе простых входы.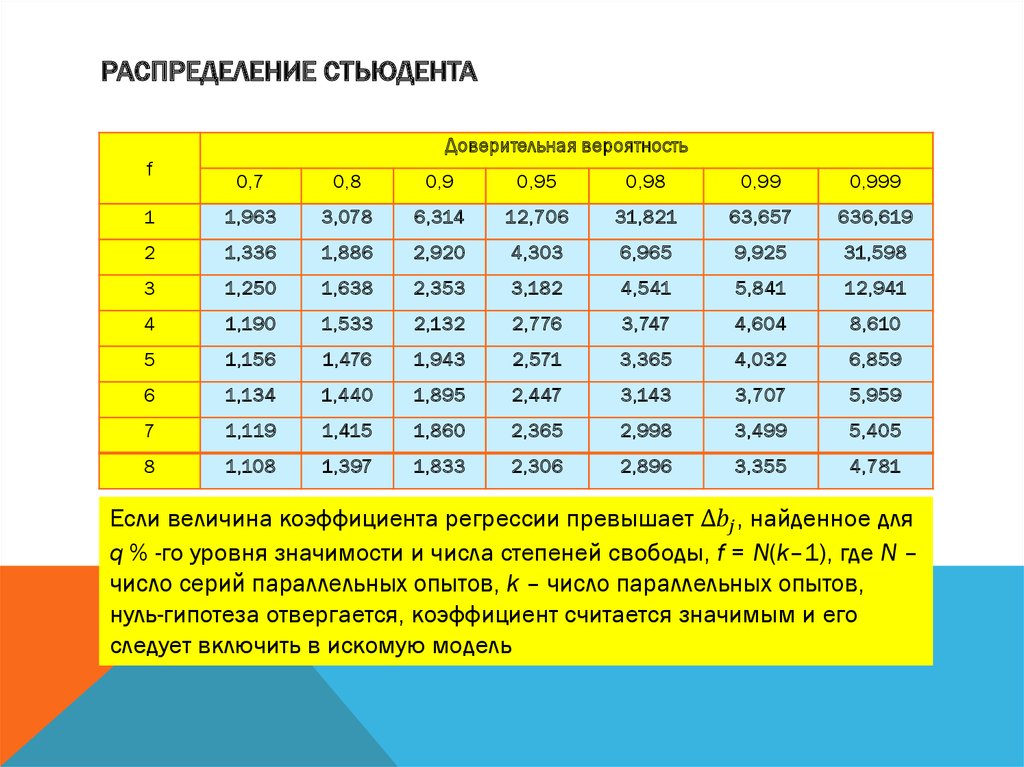 Четкие инструкции приведут вас к точному решению, быстро и без труда. Если что-то непонятно, часто задаваемые вопросы и примеры проблем давать прямые пояснения. калькулятор бесплатный. Его можно найти в Stat Trek Главное меню на вкладке Инструменты статистики. Или вы можете нажать кнопку ниже.

Калькулятор распределения T

Обозначения и t-статистика

Статистики используют t _α для представляют статистику t, которая имеет кумулятивная вероятность из (1 — а). Например, предположим, что нас интересует статистика t, имеющая кумулятивная вероятность 0,95. В этом примере α будет равно (1 — 0,95) или 0,05. Мы бы назвали статистику t t _0,05

Конечно, значение t _0,05 зависит от номера степеней свободы. Например, при 2 степенях свободы t _0,05 равно 2,92; но при 20 степенях свободы t _0,05 равно до 1,725.

Примечание: Поскольку распределение t симметрично относительно нулевого среднего, верно следующее.

т _α = — т _{1 — альфа} А также t _{1 — альфа} = — t _α

Таким образом, если t _0,05 = 2,92, то t _0,95 = -2,92.

Проверьте свои знания

Задача 1

Acme Corporation производит лампочки. Генеральный директор утверждает, что средний Acme лампочка горит 300 дней. Исследователь случайным образом выбирает 15 луковиц для тестирования. Отобранные луковицы хранятся в среднем 290 дней со стандартным отклонением 50 дней. Если утверждения генерального директора были правдой, какова вероятность того, что 15 случайно выбранных лампы имеют средний срок службы не более 290 дней?

Примечание: Есть два способа решить эту проблему, используя Калькулятор распределения T. Оба подхода представлены ниже. Решение А является традиционным подход. Требуется вычислить статистику t на основе данных, представленных в описание проблемы. Затем вы используете калькулятор T-распределения, чтобы найти вероятность. Решение Б проще. Вы просто вводите данные о проблеме в Калькулятор T-распределения. Калькулятор вычисляет статистику «за сцены», и отображает вероятность. Оба подхода дают точно тот же ответ.

Решение A

Первое, что нам нужно сделать, это вычислить t-статистику на основе по следующему уравнению:

т = [ х — мк ] / [ с / sqrt ( п ) ]
t = ( 290 — 300 ) / [ 50 / sqrt ( 15 ) ]
т = -10 / 12,909945 = — 0,7745966

где x — выборочное среднее, мк — среднее значение генеральной совокупности, s — стандартное отклонение выборки, а n — размер образца.

Теперь мы готовы использовать калькулятор T-распределения. Поскольку мы знаем статистику t, мы выбираем «t score» из случайной переменной.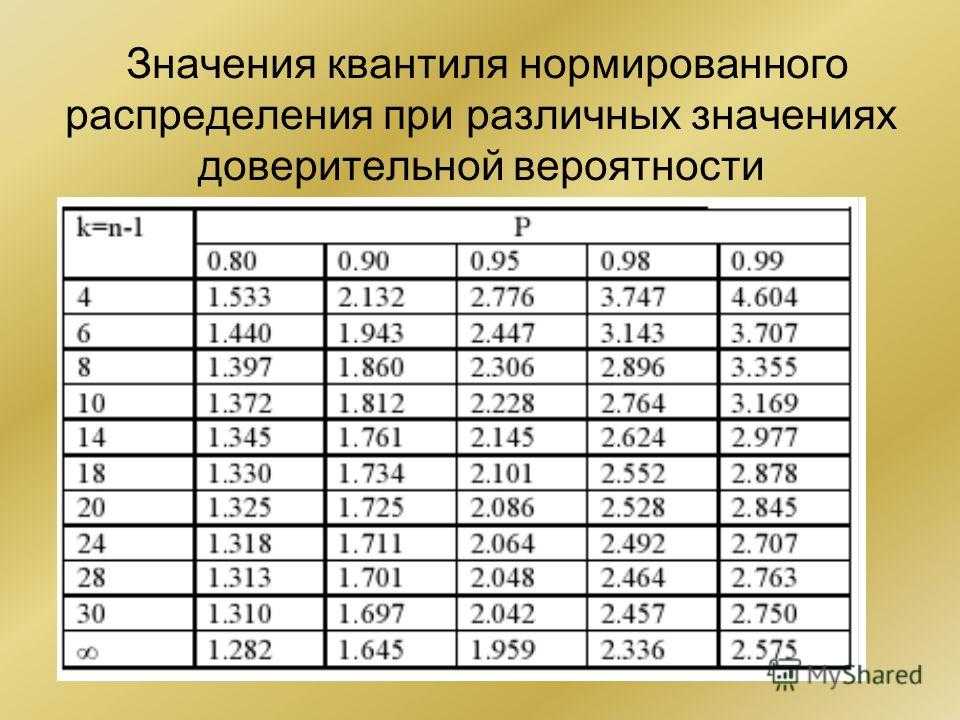 выпадающий список. Затем вводим следующие данные:

• Статистика t равна — 0,7745966.

Калькулятор показывает кумулятивную вероятность: 0,22573.

Значит, если истина срок службы лампочки был 300 дней, есть около Вероятность того, что средний срок службы 15 случайно выбранных лампочек составит 22,6 %. быть меньше или равно 290 дням.

Решение B:

На этот раз мы не будем вычислять t-статистику вручную; Т Калькулятор распределения сделает эту работу за нас. Мы выбираем «средний балл» из раскрывающегося списка «Случайная переменная». коробка. Затем вводим следующие данные:

• Стандартное отклонение выборки равно 50.

Калькулятор показывает кумулятивную вероятность: 0,22573.

Следовательно, существует 22,6%-ная вероятность того, что средняя выбранная лампочка перегорит в течение 290 дней.

Задача 2

Предположим, что баллы по IQ-тесту распределены нормально, а среднее значение генеральной совокупности равно 100. Предположим, случайным образом выбраны и протестированы 20 человек. Стандартное отклонение в выборочная группа — 15 человек. Какова вероятность того, что средний балл теста в группа выборки будет не более 110?

Решение:

Чтобы решить эту задачу, мы не будем вычислять t-статистику; Т Калькулятор распределения сделает эту работу за нас. Мы выбираем «средний балл» из раскрывающегося списка «Случайная переменная». коробка. Затем вводим следующие данные:

• Стандартное отклонение выборки равно 15,
.

Мы вводим эти значения в Калькулятор T распределения.

Калькулятор показывает кумулятивную вероятность: 0,99616. Следовательно, существует Вероятность того, что среднее значение по выборке не превысит 110, составляет 99,6 %.

Последний урок Следующий урок

Нормальное распределение данных

Горячая математика

А нормальное распределение является общим распределение вероятностей . Он имеет форму, которую часто называют «кривой колокола».

Многие повседневные наборы данных обычно имеют нормальное распределение: например, рост взрослых людей, баллы за тест, данный большому классу, ошибки в измерениях.

Нормальное распределение всегда симметрично относительно среднего.

стандартное отклонение является мерой того, насколько разбросан нормально распределенный набор данных. Это статистика, которая говорит вам, насколько близко все примеры собраны вокруг среднего значения в наборе данных. Форма нормального распределения определяется средним значением и стандартным отклонением. Чем круче кривая колокола, тем меньше стандартное отклонение. Если примеры разбросаны далеко друг от друга, колоколообразная кривая будет намного более плоской, что означает большое стандартное отклонение.

В общем о 68 % площади под кривой нормального распределения лежит в пределах одного стандартного отклонения от среднего.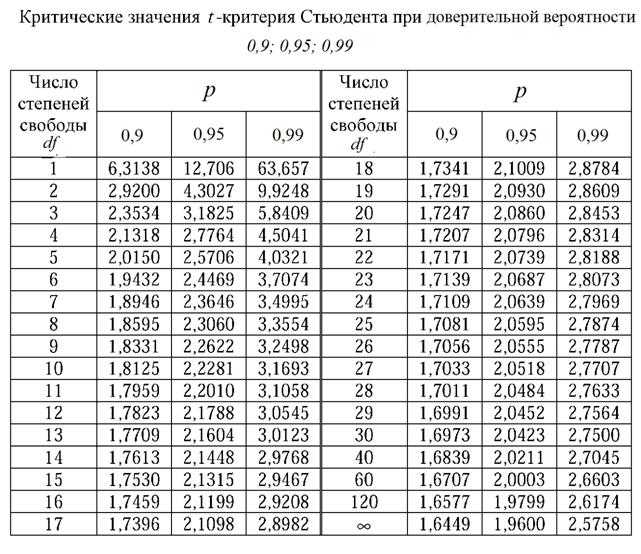

То есть, если Икс ¯ это среднее и о — стандартное отклонение распределения, тогда 68 % значения попадают в диапазон между ( Икс ¯ − о ) а также ( Икс ¯ + о ) . На рисунке ниже это соответствует области, заштрихованной розовым цветом.

О 95 % значений лежат в пределах двух стандартных отклонений от среднего, то есть между ( Икс ¯ − 2 о ) а также ( Икс ¯ + 2 о ) .

(На рисунке это сумма розовой и синей областей: 34 % + 34 % + 13,5 % + 13,5 % знак равно 95 % . )

О 99,7 % значений лежат в пределах трех стандартных отклонений от среднего, то есть между ( Икс ¯ − 3 о ) а также ( Икс ¯ + 3 о ) .

(Розовая, синяя и зеленая области на рисунке.)

(Обратите внимание, что эти значения являются приблизительными.)

Пример 1:

Набор данных обычно распределяется со средним значением 5 . Какой процент данных меньше, чем 5 ?

Нормальное распределение симметрично относительно среднего. Таким образом, половина данных будет меньше среднего, а половина данных будет больше среднего.

Следовательно, 50 % процент данных меньше, чем 5 .

Пример 2:

Срок службы полностью заряженной батареи сотового телефона обычно распределяется со средним значением 14 часов со стандартным отклонением 1 час. Какова вероятность того, что батарея прослужит не менее 13 часы?

Среднее значение 14 и стандартное отклонение 1 .

50 % нормального распределения лежит правее среднего, поэтому 50 % время, батарея будет работать дольше, чем 14 часы.

Интервал от 13 к 14 часов представляет собой одно стандартное отклонение слева от среднего значения. Итак, о 34 % времени, батарея будет длиться между 13 а также 14 часы.

Следовательно, вероятность того, что батарея проработает не менее 13 часов около 34 % + 50 % или же 0,84 .

Пример 3:

Средний вес ягоды малины 4.4 гм со стандартным отклонением 1,3 гм. Какова вероятность того, что случайно выбранная ягода малины будет весить не менее 3.1 г, но не более 7,0 гм?

Среднее значение 4.4 и стандартное отклонение 1,3 .

Обратите внимание, что

4.4 − 1,3 знак равно 3.1

а также

4.4 + 2 ( 1,3 ) знак равно 7,0

Итак, интервал 3.1 ≤ Икс ≤ 7,0 на самом деле находится между одним стандартным отклонением ниже среднего и 2 стандартные отклонения выше среднего.

В нормально распределенных данных около 34 % значений лежат между средним значением и одним стандартным отклонением ниже среднего, и 34 % между средним значением и одним стандартным отклонением выше среднего.

Кроме того, 13,5 % значений лежат между первым и вторым стандартными отклонениями выше среднего.

Складывая площади, получаем 34 % + 34 % + 13,5 % знак равно 81,5 % .

Следовательно, вероятность того, что случайно выбранная малина будет весить не менее 3.1 г, но не более 7,0 гм это 81,5 % или же 0,815 .

Пример 4:

В городе есть 330 000 взрослые люди. Их высоты нормально распределены со средним 175 см и дисперсия 100 см ² .Сколько людей, по вашему мнению, будут выше 205 см?

дисперсия набора данных 100 см ² .