Коэффициент стьюдента
Число прямых измерений всегда конечно. Поэтому средняя квадратичная погрешность заведомо меньше истинной абсолютной погрешности. Чтобы получить близкое к реальности значение абсолютной погрешности, нужно увеличить среднюю квадратичную погрешность, умножив ее на коэффициент Стьюдента . В теории Стьюдента рассчитаны значения этого коэффициента в зависимости от доверительной вероятности α и числа измерений n. С ростом доверительной вероятности, то есть надежности значения абсолютной погрешности, коэффициент Стьюдента увеличивается. А с ростом числа измерений, увеличивающим надежность самих результатов измерения, коэффициент Стьюдента уменьшается. Ниже приведены значения коэффициента Стьюдента для доверительной вероятности α = 0,95.
n | 2 | 4 | 5 | 6 | |
tα (n) | 12,71 | 4,303 | 3,182 | 2,776 | 2,571 |
n | 7 | 8 | 9 | 10 | 20 |
tα (n) | 2,447 | 2,365 | 2,306 | 2,262 | 2,093 |
Отметим, что запись
результата измерения в форме (7) означает,
что значение измеренной величины x с заданной вероятностью α не выйдет за
пределы интервала (xср – Δx, xср + Δx). Поэтому абсолютную погрешность Δx
Поэтому абсолютную погрешность Δx
часто называют полушириной доверительного интервала.
Результат косвенного измерения есть результат расчета по заданной формуле. Оценка относительной погрешности результата расчета уже описана выше. Относительная погрешность рассчитывается по формуле (2), если величины, полученные в результаты прямых измерений, входят в заданную формулу в качестве множителей или делителей.
Для примера рассмотрим косвенное измерение объема прямого цилиндра высоты
Для вычисления объема цилиндра по формуле (9) нужно иметь результаты измерения его диаметра и высоты. Пусть в результате прямых измерений получены значения диаметра и высоты цилиндра в соответствии с (7):
В этом случае известны и относительные погрешности значений диаметра и высоты цилиндра:
и
Прежде, чем
приступать к вычислению объема, оценим
относительную погрешность результата
вычисления по формуле (9). В эту формулу
входят четыре величины (числа). Два числа
из них пришли из математики и являются,
а скорее считаются, абсолютно точными:
это числа 4 и π.
Но число 4 – конечное число, а число π – является бесконечной непериодической
дробью. Как это будет показано, можно
взять округленное значение числа π с таким количеством значащих цифр, что
это число практически не внесет никакой
погрешности в окончательный результат
расчета значения объема цилиндра.
В эту формулу
входят четыре величины (числа). Два числа
из них пришли из математики и являются,
а скорее считаются, абсолютно точными:
это числа 4 и π.
Но число 4 – конечное число, а число π – является бесконечной непериодической
дробью. Как это будет показано, можно
взять округленное значение числа π с таким количеством значащих цифр, что
это число практически не внесет никакой
погрешности в окончательный результат
расчета значения объема цилиндра.
Таким образом, источниками погрешности являются значения диаметра и высоты цилиндра. Обе эти величины входят множителями в формулу (9), но диаметр входит множителем два раза (в квадрате), а высота – один раз. Следовательно, подстановка этих величин в формулу (9) приведет к сложению двух относительных погрешностей диаметра и одной относительной погрешности высоты. Согласно формуле (2), относительная погрешность объема составит
Как видим, наибольший
вклад в относительную погрешность
объема цилиндра вносит неточность
измерения диаметра цилиндра.
Чтобы число π не внесло дополнительную погрешность в результат вычисления объема, нужно взять его значение с относительной погрешностью, много меньшей погрешностей диаметра и высоты цилиндра. Поскольку, как нам известно, точность числа зависит от количества значащих цифр в нем, нужно взять столько цифр числа π, чтобы их количество на одну цифру превышало бы максимальное число значащих цифр в средних значениях диаметра и высоты. Вот запись округленного числа π, содержащая 7 значащих цифр: π = 3,141593.
Теперь, взяв число π с необходимым количеством значащих цифр, можно выполнить расчет среднего значения объема цилиндра по формуле (9):
После этого нужно выполнить расчет относительной погрешности значения объема по формуле (14). Затем вычислить абсолютную погрешность объема по формуле
Значение этой
погрешности нужно округлить, оставив
только две значащие цифры. Затем нужно
уточнить запись среднего значения
объема, сопоставив его с величиной
абсолютной погрешности (16). Число,
обозначающее среднее значение объема,
нужно округлить, оставив в нем все цифры
вплоть до разряда, являющегося последним
в окончательной записи абсолютной
погрешности. Записываем результат
измерений в виде суммы округленного
среднего значения и абсолютной
погрешности:
Затем нужно
уточнить запись среднего значения
объема, сопоставив его с величиной
абсолютной погрешности (16). Число,
обозначающее среднее значение объема,
нужно округлить, оставив в нем все цифры
вплоть до разряда, являющегося последним
в окончательной записи абсолютной
погрешности. Записываем результат
измерений в виде суммы округленного
среднего значения и абсолютной
погрешности:
Например, мы
получили следующие величины: среднее
значение = 3867,395 мм3, = 4,258 мм3.
Округляем значение до двух значащих цифр, получаем = 4,3 мм Окончательно:
Окончательно:
с относительной погрешностью, равной
КОЕ-ЧТО ИЗ МАТЕМАТИКИ
Для успешного освоения предлагаемого курса физики нужно вспомнить, что такое вектор и как с ним работать, поскольку в описании физической реальности нельзя обойтись без векторных величин. Многие физические величины являются векторами.
Вектор можно изобразить в виде направленного отрезка определенной длины. Вектор имеет две характеристики: модуль (абсолютную величину или просто величину) и направление. Каждая из этих характеристик может быть постоянной или изменяться независимо от другой.Векторы складываются по правилу треугольника, как это показано на рисунке.
При
умножении вектора на число получается
новый вектор,
который направлен в ту же сторону, что
и старый, если число положительное, и в
противоположную сторону, если число
отрицательное.
При умножении вектора на число 0, получается нулевой вектор, не имеющий ни величины, ни направления.
Любой вектор можно спроецировать на ось координат. Проекция вектора на ось координат равна произведению модуля этого вектора на косинус угла между вектором и осью. Если угол острый, то его косинус и соответственно проекция вектора положительны. Если угол тупой, то его косинус и соответственно проекция вектора отрицательны. Если вектор перпендикулярен оси, то его проекция на эту ось равна нулю.
α
0
Любой вектор можно представить в виде суммы трех его составляющих по осям координат:
где
,
,
и – проекции вектора, а – единичные векторы (орты) соответствующих
осей координат.
Вектор равен сумме трех векторов , , , каждый из которых направлен вдоль своей оси координат.
0
Допустим некоторая векторная физическая величина, например скорость , изменилась с течением времени. Тогда изменение скорости тоже будет вектором:
Для нахождения вектора это векторное равенство перепишем по-другому
и найдем этот
вектор по правилу треугольника.
Откладываем из одной точки два вектора и
. По правилу треугольника строим вектор
.
Обратите внимание, какой физический
смысл здесь раскрывается: Вектор изменения
скорости соединяет конец первого вектора с концом
второго, то есть показывает, как изменился вектор скорости (увеличился или уменьшился
и в какую сторону повернулся).
По правилу треугольника строим вектор
.
Обратите внимание, какой физический
смысл здесь раскрывается: Вектор изменения
скорости соединяет конец первого вектора с концом
второго, то есть показывает, как изменился вектор скорости (увеличился или уменьшился
и в какую сторону повернулся).
Существуют два разных умножения вектора на вектор: скалярное и векторное.
Результатом скалярного произведения вектора на вектор является число, равное произведению модуля первого вектора на модуль второго и на косинус угла между ними:
или равное сумме одноименных проекций этих векторов на оси координат:
Скалярное умножение
обозначается точкой.
Результатом векторного произведения вектора на вектор является вектор. Векторное умножение обозначается косым крестиком. Например, вектор равен векторному произведению векторов и :
Вектор перпендикулярен векторам и и его направление определяется по правилу буравчика (правого винта), как это показано на рисунке. Буравчик вращается от первого вектора в сторону второго вектора . Если векторы – множители поменять местами, то вектор изменит направление на противоположное.
Модуль вектора равен произведению модуля первого вектора на модуль второго и на синус угла между ними:
α
Если два вектора
параллельны, то их векторное произведение
равно нулевому вектору
.
Для успешного освоения предлагаемого курса физики нужно также вспомнить основы математического анализа и, как минимум, уметь найти производную от комбинации элементарных функций и взять табличный интеграл.
Напомню определение производной. Пусть некоторая физическая величина, например вектор скорости, меняется с течением времени. Тогда время t является независимой переменной, то есть аргументом (играет роль x из математики). А скорость является зависимой переменной, то есть функцией (играет роль y из математики). Производной называется предел
Если
,
то и Существует обозначение для величины,
которая стремится к 0, но не равна 0. Эта
величина называется бесконечно малой.
Все дело в том, что она
не имеет конкретного значения.
Зато она всегда меньше любого сколь
угодно малого числа, какое бы мы ни
назвали. Для такой бесконечно малой
величины существует обозначение:
. Это выражение называется дифференциалом и является в данном случае бесконечно
малым промежутком времени. – бесконечно малое приращение вектора
скорости. Имеем дробь:
Это выражение называется дифференциалом и является в данном случае бесконечно
малым промежутком времени. – бесконечно малое приращение вектора
скорости. Имеем дробь:
которая обладает всеми свойствами дроби из математики, за исключением того, что ее значение нельзя получить обычным делением числителя на знаменатель, а нужно перейти к пределам и раскрыть получившуюся неопределенность. Для любой функции в математике это все проделано и сведено в правила взятия производной от элементарной функции.
Например, некоторое тело движется так, что модуль его скорости зависит от времени по уравнению:
где и – константы. Найдем производную от модуля скорости по времени:
Как Вы вероятно помните, эта производная является ускорением.
Настоятельно рекомендую каждую производную от функции y по аргументу x, которая встретится Вам в физике, обозначать только такой дробью:
Для успешного
освоения предлагаемого курса физики
нужно также вспомнить, что такое степень и логарифм. Степенью называется двухуровневое
выражение вида
,
нижняя и верхняя части которого
неравнозначны.
Степенью называется двухуровневое
выражение вида
,
нижняя и верхняя части которого
неравнозначны.
Показатель степени
Степень
b
a
Основание степени
Для удобства обозначим эту степень буквой у. Имеем равенство
где а – основание степени у, а b – показатель степени у. Чтобы выразить а и b из этого равенства, нужно применить разные правила.
Основание а степени у равно корню из этой степени:
а показатель b степени у равен логарифму этой степени по основанию а:
Итак, показатель
степени и логарифм степени – это
практически одно и то же.
Чтобы убедиться, проверьте тождество:
и левая и правая части которого равны у.
Коэффициенты Стьюдента
Число измерений N | Надежность Р | ||||||
0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 0,95 | 0,99 | |
2 | 1,00 | 1,38 | 2,0 | 3,1 | 6,3 | 12,7 | 637 |
3 | 0,82 | 1,06 | 1,5 | 1,9 | 2,9 | 4,3 | 35 |
4 | 0,77 | 0,98 | 1,3 | 1,6 | 2,4 | 3,2 | 12,9 |
5 | 0,74 | 0,94 | 1,2 | 1,5 | 2,1 | 2,8 | 8,6 |
6 | 0,73 | 0,92 | 1,2 | 1,5 | 2,0 | 2,6 | 6,9 |
7 | 0,72 | 0,91 | 1,1 | 1,4 | 1,9 | 2,4 | 6,0 |
8 | 0,71 | 0,90 | 1,1 | 1,4 | 1,9 | 2,4 | 5,4 |
9 | 0,71 | 0,89 | 1,1 | 1,4 | 1,9 | 2,3 | 5,0 |
10 | 0,70 | 0,88 | 1,1 | 1,4 | 1,8 | 2,3 | 4,8 |
2.
 2. Расчет случайной погрешности
2. Расчет случайной погрешностиПри обработке прямых измерений результаты наблюдений и вычислений удобно оформлять в виде табл. 2.
Таблица 2
Расчет среднего значения и случайной погрешности по методу Стьюдента
№ | ai | ai | ai2 | | P | tPN | aсл | |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
1 | ||||||||
2 | ||||||||
3 |
В колонке 1указывается номер опыта
по порядку (обычно проводится 3-7
измерений).
В колонке 2 записываютсязначения измеряемой величины.
В колонку 3вноситсясреднее значениеизмеряемой величины, рассчитанное по формуле:
. (1)
В колонке 4представленыотклонениякаждого значенияизмеряемой величины от среднего:
. (2)
Каждый результат, полученный по последней формуле, возводится в квадрат и заносится в колонку 5.
В колонке 6следует расположитьсреднеквадратичную погрешность , рассчитанную по формуле:
. (3)
Она характеризует разброс средних значений измеряемой величины. Среднеквадратичная погрешность тем больше, чем сильнее измеренные величины отличаются друг от друга.
В колонку 7заносится значение
доверительной вероятности (или надежности)
Обычно достаточно выбрать значениеР= 0,95 (или, что то же самое, 95%).
Коэффициент Стьюдента, учитывающий заданную доверительную вероятность и число измерений tPN ,находится по табл. 1 и располагаетсяв колонке 8.
Случайная погрешностьрассчитывается по формуле
aсл=tPN S(4)
и заносится в колонку 9.
2.3. Учет систематических погрешностей
К учитываемым систематическим погрешностям относятся погрешности средств измерения и погрешности отсчета.
В форме абсолютных погрешностейзадаются погрешности линеек, штангенциркулей, секундомеров, термометров и т.п. Абсолютная погрешность средства измерения в этом случае может быть вычислена по формуле
, (5)
где - цена деления прибора.
В форме приведенных погрешностейзадаются пределы допускаемых погрешностей
электроизмерительных приборов,
манометров. Этим приборам присваиваются
классы точности.Класс точностиравен пределу допускаемой приведенной
погрешности, выраженной в процентах,
которая определяется по формуле
Этим приборам присваиваются
классы точности.Класс точностиравен пределу допускаемой приведенной
погрешности, выраженной в процентах,
которая определяется по формуле
,
где ап—нормирующее значениеприбора илипредел измерений;
— предел допускаемой приведенной погрешности прибора в процентах от нормирующего значения;
аси— абсолютная погрешность прибора.
Пользуясь этой формулой, можно определить абсолютную погрешность измерительного прибора:
. (6)
Полная абсолютная погрешностьпрямых измерений рассчитывается по формуле
. (7)
Чаще всего случайная погрешность и погрешность средств измерения — величины разных порядков; в таких случаях меньшей погрешностью пренебрегают. Например, если , то
{(r+1)/2}}\) для \(-\infty
Кстати, распределение \(t\) впервые было обнаружено человеком по имени В.С. Госсет. Он открыл для себя этот дистрибутив, когда работал на ирландской пивоварне. Поскольку он публиковался под псевдонимом Стьюдент, распределение \(t\) часто называют распределением Стьюдента \(t\).
Если оставить в стороне историю, приведенное выше определение, вероятно, не особенно информативно. Давайте попробуем почувствовать распределение \(t\) с помощью моделирования. Давайте случайным образом сгенерируем 1000 стандартных нормальных значений (\(Z\)) и 1000 значений хи-квадрат(3) (\(U\)). Затем приведенное выше определение говорит нам, что если мы возьмем эти случайно сгенерированные значения, вычислим:
\(T=\dfrac{Z}{\sqrt{U/3}}\)
и создадим гистограмму из 1000 результирующих значений \(T\), мы должны получить гистограмму, которая выглядит как \( t\) распределение с 3 степенями свободы. Итак, вот подмножество результирующих значений одного такого моделирования:
| ROW | З | ЧИСЛО (3) | Т(3) |
|---|---|---|---|
| 1 | -2,60481 | 10. 2497 2497 | -1,4092 |
| 2 | 2,92321 | 1,6517 | 3,9396 |
| 3 | -0,48633 | 0,1757 | -2,0099 |
| 4 | -0,48212 | 3,8283 | -0,4268 |
| 5 | -0,04150 | 0,2422 | -0,1461 |
| 6 | -0,84225 | -0,0903 | -4,8544 |
| 7 | -0,31205 | 1,6326 | -0,4230 |
| 8 | 1.33068 | 5.2224 | 1.0086 |
| 9 | -0,64104 | 0,9401 | -1.1451 |
| 10 | -0,05110 | 2,2632 | -0,0588 |
| 11 | 1.61601 | 4,6566 | 1.2971 |
| 12 | 0,81522 | 2,1738 | 0,9577 |
| 13 | 0,38501 | 1.8404 | 0,4916 |
| 14 | -1,63426 | 1. 1265 1265 | -2,6669 |
| …и так далее… | |||
| 994 | -0,18942 | 3.5202 | -0,1749 |
| 995 | 0,43078 | 3,3585 | 0,4071 |
| 996 | -0,14068 | 0,6236 | -0,3085 |
| 997 | -1,76357 | 2,6188 | -1,8876 |
| 998 | -1.02310 | 3.2470 | -0,9843 |
| 999 | -0,93777 | 1.4991 | -1,3266 |
| 1000 | -0,37665 | 2.1231 | -0,4477 |
Обратите внимание, например, в первой строке:
\(T(3)=\dfrac{-2.60481}{\sqrt{10.2497/3}}=-1.4092\)
‘
7 Здесь как выглядит результирующая гистограмма 1000 случайно сгенерированных значений \(T(3)\) с наложенной стандартной кривой \(N(0,1)\):
-9-6-303600150200250ЧастотаГистограмма кривой TNormalN(0,1)Среднее значение — 0StDev — 1N — 1000T
Хммм.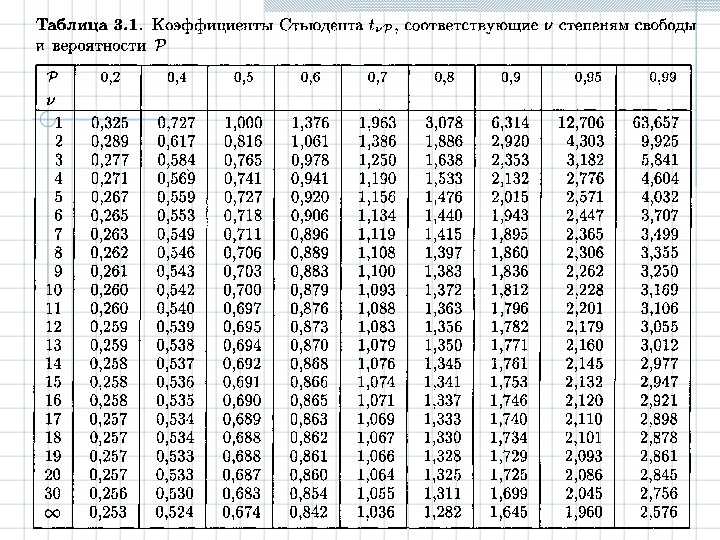 \(t\)-распределение похоже на стандартное нормальное распределение. Используя приведенную выше формулу для p.d.f. \(T\), мы можем построить кривую плотности различных \(t\) случайных величин, скажем, когда \(r=1, r=4\) и \(r=7\), чтобы увидеть, что это действительно так:
\(t\)-распределение похоже на стандартное нормальное распределение. Используя приведенную выше формулу для p.d.f. \(T\), мы можем построить кривую плотности различных \(t\) случайных величин, скажем, когда \(r=1, r=4\) и \(r=7\), чтобы увидеть, что это действительно так:
На самом деле это выглядит так, как если бы степени свободы \(r\) увеличивается, кривая плотности \(t\) становится все ближе и ближе к стандартной нормальной кривой. Давайте подытожим то, что мы узнали в нашем небольшом исследовании о характеристиках t дистрибутив :
- Поддержка выглядит как \(-\infty
- Распределение вероятностей симметрично относительно \(t=0\). (Так и есть!)
- Распределение вероятностей похоже на колокол. (Так и есть!)
- Кривая плотности выглядит как стандартная нормальная кривая, но хвосты \(t\)-распределения «тяжелее», чем хвосты нормального распределения.
 То есть мы с большей вероятностью получим экстремальные \(t\)-значения, чем экстремальные \(z\)-значения.
То есть мы с большей вероятностью получим экстремальные \(t\)-значения, чем экстремальные \(z\)-значения.- По мере увеличения степеней свободы \(r\) \(t\)-распределение приближается к стандартному нормальному \(z\)-распределению. (Так и есть!)
Как вы скоро увидите, нам нужно будет искать \(t\)-значения, а также вероятности относительно \(T\) случайных величин, довольно часто в статистике 415. Поэтому нам лучше убедиться, что мы уметь читать \(t\) таблицу.
Если вы посмотрите на Таблицу VI в конце вашего учебника, вы найдете то, что выглядит как типичная \(t\) таблица. Вот как выглядит верхняя часть Таблицы VI (ну, за вычетом штриховки, которую я добавил): 9{(r+1) / 2}} d w\]
\[P(T \leq-t)=1-P(T \leq t)\]
| P ( T ≤ т ) | |||||||
| 0,60 | 0,75 | 0,90 | 0,95 | 0,975 | 0,99 | 0,995 | |
| р | т 0,40 ( р ) | т 0,25 ( р ) | т 0,10 ( р ) | т 0,05 ( р ) | т 0,025 ( р ) | т 0,01 ( р ) | т 0,005 ( р ) |
| 1 | 0,325 | 1. 000 000 | 3.078 | 6.314 | 12.706 | 31.821 | 63,657 |
| 2 | 0,289 | 0,816 | 1,886 | 2,920 | 4.303 | 6,965 | 9,925 |
| 3 | 0,277 | 0,765 | 1,638 | 2,353 | 3,182 | 4,541 | 5.841 |
| 4 | 0,271 | 0,741 | 1,533 | 2,132 | 2,776 | 3,747 | 4.604 |
| 5 | 0,267 | 0,727 | 1,476 | 2,015 | 2,571 | 3,365 | 4. 032 032 |
| 6 | 0,265 | 0,718 | 1.440 | 1,943 | 2,447 | 3,143 | 3,707 |
| 7 | 0,263 | 0,711 | 1,415 | 1,895 | 2,365 | 2,998 | 3,499 |
| 8 | 0,262 | 0,706 | 1,397 | 1,860 | 2,306 | 2,896 | 3,355 |
| 9 | 0,261 | 0,703 | 1,383 | 1,833 | 2,262 | 2,821 | 3.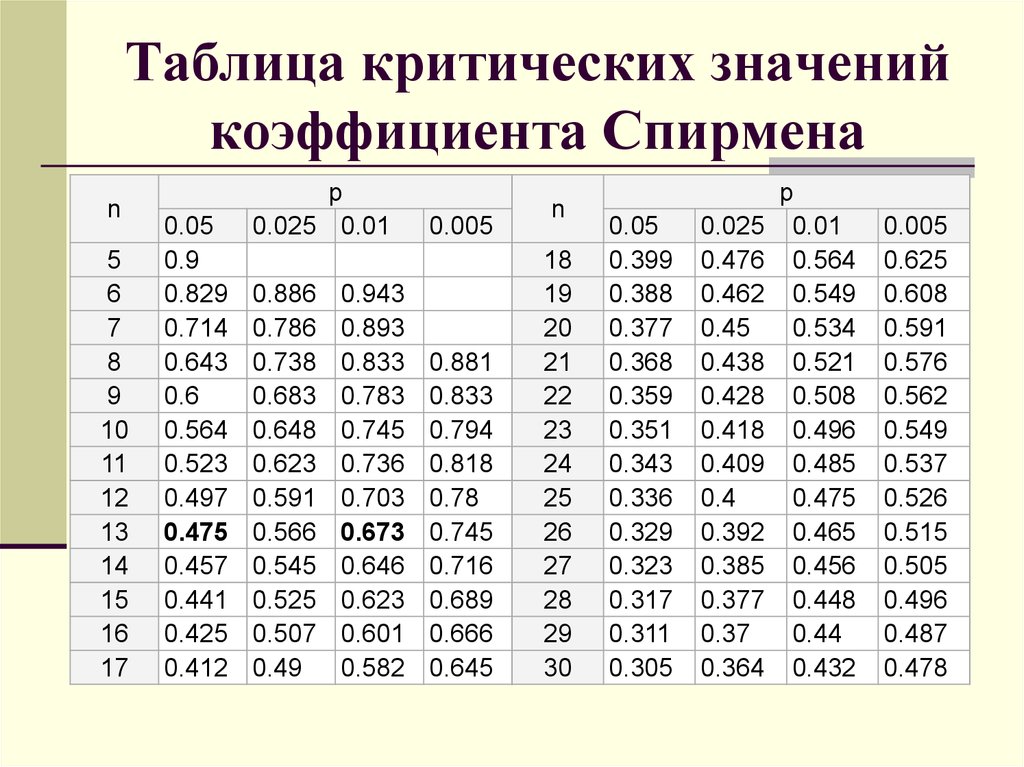 250 250 |
| 10 | 0,260 | 0,700 | 1,372 | 1,812 | 2,228 | 2,764 | 3,169 |
\(t\)-таблица похожа на таблицу хи-квадрат тем, что внутри \(t\)-таблицы (заштрихованной фиолетовым цветом ) содержится \(t\)- значения для различных кумулятивных вероятностей (заштрихованы красным цветом ), таких как 0,60, 0,75, 0,90, 0,95, 0,975, 0,99 и 0,995, а также для различных распределений \(t\) с \(r\) степенями свободы (заштрихованы в синий ). Строка, заштрихованная зеленым цветом , указывает верхнюю \(\альфа\) вероятность, которая соответствует \(1-\альфа\) кумулятивной вероятности. Например, если вас интересует кумулятивная вероятность 0,60 или верхняя вероятность 0,40, вам нужно найти значение \(t\) в первом столбце.
Давайте воспользуемся \(t\)-таблицей, чтобы прочитать несколько вероятностей и \(t\)-значений из таблицы:
Давайте рассмотрим еще несколько примеров.
Пусть \(T\) следует \(t\)-распределению с \(r=8\) ф.р. Какова вероятность того, что абсолютное значение \(T\) меньше 2,306?
Решение
Расчет вероятности очень похож на расчет, который мы должны сделать для обычной случайной величины. Во-первых, переписав вероятность через \(T\) вместо абсолютного значения \(T\), мы получим:
\(P(|T|<2,306)=P(-2,306 Затем мы должны переписать вероятность в терминах кумулятивных вероятностей, которые мы действительно можем найти, то есть: \(P(|T|<2,306)=P(T<2,306)-P(T<-2,306)\) Графически искомая вероятность выглядит примерно так: Но \(t\)-таблица не содержит отрицательных \(t\)-значений, поэтому нам придется воспользоваться симметрией \(T\)-распределения. То есть: >\(P(|T|<2,306)=P(T<2,306)-P(T>2,306)\) Можете ли вы найти необходимые \(t\)-значения на \(t \)-стол? 30602.306
30602.306 Р ( Т ≤ т ) 0,60 0,75 0,90 0,95 0,975 0,99 0,995 р т 0,40 ( р ) т 0,25 ( р ) т 0,10 ( р ) т 0,05 ( р ) т 0,025 ( р ) т 0,01 ( р ) т 0,005 ( р ) 1 0,325 1.  000
000 3,078 6.314 12.706 31.821 63,657 2 0,289 0,816 1,886 2,920 4.303 6,965 9,925 3 0,277 0,765 1,638 2,353 3.182 4,541 5,841 4 0,271 0,741 1,533 2,132 2,776 3,747 4,604 5 0,267 0,727 1,476 2,015 2,571 3,365 4.032 6 0,265 0,718 1.440 1,943 2,447 3,143 3,707 7 0,263 0,711 1,415 1,895 2,365 2,998 3,499 8 0,262 0,706 1,397 1,860 2,306 2,896 3,355 9 0,261 0,703 1,383 1,833 2,262 2,821 3.  250
250 10 0,260 0,700 1,372 1,812 2,228 2,764 3,169 P ( T ≤ t ) 0,60 0,75 0,90 0,95 0,975 0,99 0,995 р т 0,40 ( р ) т 0,25 ( р ) т 0,10 ( р ) т 0,05 ( р ) т 0,025 ( р ) т 0,01 ( р ) т 0,005 ( р ) 1 0,325 1.000 3,078 6.314 12.706 31.821 63,657 2 0,289 0,816 1,886 2,920 4.  303
303 6,965 9,925 3 0,277 0,765 1,638 2,353 3,182 4,541 5,841 4 0,271 0,741 1,533 2,132 2,776 3,747 4,604 5 0,267 0,727 1,476 2,015 2,571 3,365 4.032 6 0,265 0,718 1.440 1,943 2,447 3,143 3,707 7 0,263 0,711 1,415 1,895 2,365 2,998 3,499 8 0,262 0,706 1,397 1,860 2,306 2,896 3,355 9 0,261 0,703 1,383 1,833 2,262 2,821 3.  250
250 10 0,260 0,700 1,372 1,812 2,228 2,764 3,169
Таблица \(t\) говорит нам, что \(P(T<2,306)=0,975\) и \(P(T>2,306)=0,025\). Следовательно:
\(P(|T|>2,306)=0,975-0,025=0,95\)
Что такое \(t_{0,05}(8)\)?
Решение
Значение \(t_{0,05}(8)\) — это значение \(t_{0,05}\), такое, что вероятность того, что \(T\) случайная величина с 8 степенями свободы больше, чем значение \(t_{0,05}\) равно 0,05. То есть:
T(8)0t0.050.05Можете ли вы найти значение \(t_{0.05}\) в таблице \(t\)?
| P ( T ≤ t ) | |||||||
| 0,60 | 0,75 | 0,90 | 0,95 | 0,975 | 0,99 | 0,995 | |
| р | т 0,40 ( р ) | т 0,25 ( р ) | т 0,10 ( р ) | т 0,05 ( р ) | т 0,025 ( р ) | т 0,01 ( р ) | т 0,005 ( р ) |
| 1 | 0,325 | 1. 000 000 | 3,078 | 6.314 | 12.706 | 31.821 | 63,657 |
| 2 | 0,289 | 0,816 | 1,886 | 2,920 | 4.303 | 6,965 | 9,925 |
| 3 | 0,277 | 0,765 | 1,638 | 2,353 | 3,182 | 4,541 | 5,841 |
| 4 | 0,271 | 0,741 | 1,533 | 2,132 | 2,776 | 3,747 | 4,604 |
| 5 | 0,267 | 0,727 | 1,476 | 2,015 | 2,571 | 3,365 | 4.032 |
| 6 | 0,265 | 0,718 | 1.440 | 1,943 | 2,447 | 3,143 | 3,707 |
| 7 | 0,263 | 0,711 | 1,415 | 1,895 | 2,365 | 2,998 | 3,499 |
| 8 | 0,262 | 0,706 | 1,397 | 1,860 | 2,306 | 2,896 | 3,355 |
| 9 | 0,261 | 0,703 | 1,383 | 1,833 | 2,262 | 2,821 | 3. 250 250 |
| 10 | 0,260 | 0,700 | 1,372 | 1,812 | 2,228 | 2,764 | 3,169 |
| P ( T ≤ т ) | |||||||
| 0,60 | 0,75 | 0,90 | 0,95 | 0,975 | 0,99 | 0,995 | |
| р | т 0,40 ( р ) | т 0,25 ( р ) | т 0,10 ( р ) | т 0,05 ( р ) | т 0,025 ( р ) | т 0,01 ( р ) | т 0,005 ( р ) |
| 1 | 0,325 | 1.000 | 3,078 | 6.314 | 12.706 | 31. 821 821 | 63,657 |
| 2 | 0,289 | 0,816 | 1,886 | 2,920 | 4.303 | 6,965 | 9,925 |
| 3 | 0,277 | 0,765 | 1,638 | 2,353 | 3,182 | 4,541 | 5,841 |
| 4 | 0,271 | 0,741 | 1,533 | 2,132 | 2,776 | 3,747 | 4,604 |
| 5 | 0,267 | 0,727 | 1,476 | 2,015 | 2,571 | 3,365 | 4.032 |
| 6 | 0,265 | 0,718 | 1.440 | 1,943 | 2,447 | 3,143 | 3,707 |
| 7 | 0,263 | 0,711 | 1,415 | 1,895 | 2,365 | 2,998 | 3,499 |
| 8 | 0,262 | 0,706 | 1,397 | 1,860 | 2,306 | 2,896 | 3,355 |
| 9 | 0,261 | 0,703 | 1,383 | 1,833 | 2,262 | 2,821 | 3. 250 250 |
| 10 | 0,260 | 0,700 | 1,372 | 1,812 | 2,228 | 2,764 | 3,169 |
Мы определили, что вероятность того, что \(T\) случайная величина с 8 степенями свободы больше значения 1,860, равна 0,05. 92}\)
следует распределению хи-квадрат с \(n-1\) степенями свободы. Мы также узнали, что \(Z\) и \(U\) независимы. Следовательно, используя определение случайной величины \(T\), мы получаем:
Это результирующая величина, то есть:
\(T=\dfrac{\bar{X}-\mu}{ s/\sqrt{n}}\)
, что поможет нам в Stat 415 использовать среднее из случайной выборки, то есть \(\bar{X}\), с уверенностью узнать что-то о население означает \(\mu\).
Т-распределение | Введение в статистику
Что такое
t -распределение?Распределение t- описывает стандартизированные расстояния выборочных средних значений от средних значений генеральной совокупности, когда стандартное отклонение генеральной совокупности неизвестно, а наблюдения происходят из нормально распределенной генеральной совокупности.
Распределение
t- совпадает с распределением Стьюдента t ?Да.
В чем основное различие между
t- и z-распределения?Стандартное нормальное или z-распределение предполагает, что известно стандартное отклонение генеральной совокупности. Распределение t- основано на стандартном отклонении выборки.
t -Распределение по сравнению с нормальным распределением t -распределение аналогично нормальному распределению. Он имеет точное математическое определение. Вместо того, чтобы углубляться в сложную математику, давайте посмотрим на полезные свойства т-9.Распределение 0005 и почему оно важно для анализа.
Вместо того, чтобы углубляться в сложную математику, давайте посмотрим на полезные свойства т-9.Распределение 0005 и почему оно важно для анализа.
- Как и нормальное распределение, распределение t- имеет гладкую форму.
- Как и нормальное распределение, распределение t- является симметричным. Если вы подумаете о том, чтобы сложить его пополам в среднем, каждая сторона будет одинаковой.
- Подобно стандартному нормальному распределению (или z-распределению), распределение t- имеет нулевое среднее значение.
- Нормальное распределение предполагает, что стандартное отклонение генеральной совокупности известно. 9Распределение 0004 t- не делает этого предположения.
- Распределение t- определяется степенями свободы . Они связаны с размером выборки.
- Распределение t- наиболее полезно для небольших размеров выборки, когда неизвестно стандартное отклонение генеральной совокупности или и то, и другое.

- По мере увеличения размера выборки распределение t- становится более похожим на нормальное распределение.
Рассмотрим следующий график, на котором сравниваются три t- распределений со стандартным нормальным распределением:
Рис. 1: Три t-распределения и стандартное нормальное (z-) распределение.
Все распределения имеют плавную форму. Все симметричны. У всех среднее нулевое.
Форма распределения t- зависит от степеней свободы. Кривые с большим количеством степеней свободы выше и имеют более тонкие хвосты. Все три распределения t- имеют «более тяжелые хвосты», чем z-распределение.
Вы можете видеть, что кривые с большим количеством степеней свободы больше похожи на z-распределение. Сравните розовую кривую с одной степенью свободы с зеленой кривой для z-распределения. Распределение t- с одной степенью свободы короче и имеет более толстые хвосты, чем z-распределение. Затем сравните синюю кривую с 10 степенями свободы с зеленой кривой для z-распределения. Эти два дистрибутива очень похожи.
Затем сравните синюю кривую с 10 степенями свободы с зеленой кривой для z-распределения. Эти два дистрибутива очень похожи.
Общепринятое эмпирическое правило заключается в том, что для размера выборки не менее 30 можно использовать z-распределение вместо т- раздача. На рисунке 2 ниже показано распределение t- с 30 степенями свободы и z-распределение. На рисунке используется зеленая кривая из пунктирных линий для z, так что вы можете видеть обе кривые. Это сходство является одной из причин, по которой z-распределение используется в статистических методах вместо распределения t , когда размеры выборки достаточно велики.
Рис. 2: z-распределение и t-распределение с 30 степенями свободы
Хвосты для тестов гипотез и распределения
t Когда вы выполняете t -тест, вы проверяете, является ли ваша тестовая статистика более экстремальным значением, чем ожидалось для распределения t-.
Для двустороннего теста вы смотрите на оба хвоста распределения. На рисунке 3 ниже показан процесс принятия решения для двустороннего теста. Кривая представляет собой распределение t- с 21 степенью свободы. Значение из распределения t- с α = 0,05/2 = 0,025 равно 2,080. Для двустороннего теста вы отклоняете нулевую гипотезу, если статистика теста больше, чем абсолютное значение эталонного значения. Если значение тестовой статистики находится либо в нижнем хвосте, либо в верхнем хвосте, вы отклоняете нулевую гипотезу. Если тестовая статистика находится в пределах двух контрольных линий, вы не можете отвергнуть нулевую гипотезу.
Рисунок 3: Процесс принятия решения для двустороннего теста
Для одностороннего теста вы смотрите только на один хвост распределения. Например, на рис. 4 ниже показан процесс принятия решения для одностороннего теста. Кривая снова представляет собой распределение t- с 21 степенью свободы. Для одностороннего теста значение из распределения t- с α = 0,05 равно 1,721. Вы отклоняете нулевую гипотезу, если статистика теста больше опорного значения. Если тестовая статистика ниже контрольной линии, вы не можете отвергнуть нулевую гипотезу.
Для одностороннего теста значение из распределения t- с α = 0,05 равно 1,721. Вы отклоняете нулевую гипотезу, если статистика теста больше опорного значения. Если тестовая статистика ниже контрольной линии, вы не можете отвергнуть нулевую гипотезу.
Рисунок 4: Процесс принятия решения для одностороннего теста
Как использовать таблицу
t-Большинство людей используют программное обеспечение для выполнения расчетов, необходимых для t -тестов. Но во многих книгах по статистике по-прежнему приводятся таблицы t-, поэтому понимание того, как пользоваться таблицей, может быть полезным. Шаги ниже описывают, как использовать типичный стол t-.
- Определите, предназначена ли таблица для двусторонних или односторонних тестов. Затем решите, какой у вас тест: односторонний или двусторонний. Столбцы для 9Таблица 0004 t- определяет различные альфа-уровни.


 То есть мы с большей вероятностью получим экстремальные \(t\)-значения, чем экстремальные \(z\)-значения.
То есть мы с большей вероятностью получим экстремальные \(t\)-значения, чем экстремальные \(z\)-значения.
