Методическая разработка урока по геометрии в 9 классе по теме Синус, косинус, тангенс по учебнику Л.С. Атанасяна и др. М., Просвещение, 2014
Методическая разработка урока геометрии в 9 классе
по теме « Синус, косинус, тангенс»
Учебник: «Геометрия» 7-9 класс. Авт.: Л.С. Атанасян, В.Б. Бутузов и др.;М.,Просвещение, 2014
План урока
Организационный момент
Актуализация знаний.
Объяснение нового материала.
Физкультминутка
Закрепление нового материала.
Подведение итогов урока.
Домашнее задание.
Тип урока:
Урок ознакомления с новым материалом (1 час)
Цели урока:
1. Образовательные
-углубить изученные в 8 классе сведения о синусе, косинусе и тангенсе угла;
-сформировать понятия «тригонометрический круг»;
-ввести понятие синуса, косинуса и тангенса для углов от 0º до 180º;
-научить использовать определение синуса, косинуса и тангенса при решении задач.
-повторить основное тригонометрическое тождество ( доказательство запланировано на следующий урок)
2. Развивающие:
-развитие мышления учащихся: учить детей анализировать, выделять главное;
-развитие сенсорной сферы: развитие глазомера, развитие формы и точности;
-развитие навыков самоконтроля.
3. Воспитательные:
-развитие нравственных качеств личности: ответственности, дисциплинированности, аккуратности, требовательности к себе, умения работать в коллективе.
Ход урока.
Организационный момент (сведения из истории).
Введение (зарождение тригонометрии)
Впервые график тригонометрической функции — синусоида была вычерчена в конце 30-х годов XVII в. французским математиком Робельвалем.. Волновые процессы находят проявление во многих областях физики и технике, и для описания их используется тригонометрическая функция. В физике изучаются: механические колебания, электромагнитные колебания в контуре, переменный ток, звуковые волны и т.
д. При изучении колебаний пружинного и математического маятников вводится понятия амплитуды, фазы, циклической чистоты.
Актуализация знаний
Повторение – мать учения (Сведения из курса 8 класса)
Что называется синусом, косинусом, тангенсом острого угла прямоугольного треугольника? Какое равенство называют основным тригонометрическим тождеством? Чему равны значения синуса, косинуса и тангенса для углов 30 , 45 и 60 градусов ?
3 Изучение нового материала
Введем прямоугольную систему координат Оху . Построим полуокружность радиуса 1 с центром в начале координат, расположенном в I и II четвертях Назовем ее единичной полуокружностью
Выполнить в тетрадях рисунок 290 (страница 252 учебника)
Дать новые определения синуса, косинуса и тангенса для любого угла а из промежутка от 0º до 180º . Подчеркнуть, какие значения могут принимать синус, косинус и тангенс для угла а из промежутка от 0º до 180º . Вывести, используя единичную полуокружность, основное тригонометрическое тождество.
Записать формулы приведения, объяснить их смысл, используя единичную полуокружность
4.Физкультминутка
5 Закрепление нового материала.
Тест
1. Синус – это:
a) абсцисса точки, лежащей на единичной полуокружности; b) ордината точки, лежащей на единичной полуокружности; с) угол между осью Ох и осью Оy.
2. Выберите из списка значения, которые может принимать sina 1; 1,0001; 2; 0,0001; 2,0001:
a) 1; 2; 1,0001; b) 1; 0,0001; с) 1,0001; 0,0001; 2,0001.
3. Выберите из списка значения, которые может принимать cos: -1; 1; 0,5; -0,5; 1,5.
a) 1; 0,5; 1,5; b) 1; 0,5; -0,5; с) -1; 1; 0,5; -0,5.
4. Чему равен tga, если sina=0; cosa=1?
a)не определен; b)) tga = 0; с) tga = 1.
5 Чему равен cosa , если угол a — прямой?
a) 0; b) 1; с) 90⁰.’
6. Выберите из списка значения, по которым можно утверждать, что угол a острый: cosa = 0,03; sina=0,03 cosa = — 0,03; sina=-0.
03
a) sina = 0.03 или sina =-0.03 b) cosa= — 0,03 или cosa = 0,03; с) cosa = 0,03.
7. Если угол a — тупой, то
a)0 < cosa < 1; b)cosa ˃ 1; с) -1
Письменная работа в классе № 1013 в, № 1014 б, № 1015 в
Подведение итогов урока. Выставление оценок.
Рефлексия.
-Достигли цели?
Введены определения синуса, косинуса и тангенса для углов промежутка от 0º до 180º , основного тригонометрического тождества, даны некоторые формулы приведения;
научились использовать определение синуса, косинуса и тангенса при решении задач.
Какие выводы сделали?
-Вывели понятие синуса, косинуса, тангенса используя единичную полуокружность,
-Объяснили смысл некоторых формул приведения, вспомнили основное тригонометрическое тождество.
-Как мы это делали?
-Обсуждали
-Анализировали
Домашнее задание.
П.93. № 1013а; № 1014а (по желанию № 1015 а )
Адрес публикации: https://www.
prodlenka.org/metodicheskie-razrabotki/291844-metodicheskaja-razrabotka-uroka-po-geometrii-
Видеоурок по алгебре 10 класс тема Числовые функции
Тригонометрические формулы
Решение тригонометрических уравнений и неравенств
Предел последовательности. Предел функции
Производная
Применение непрерывности и производной
Применение производной к использованию функций
Показать все темы
7 8 9 10 11
Поделиться
0
0
05:40
В первом уроке мы вспомним основные положения по теме “Числовая функция” и методы исследования функции, пройденные в курсе алгебры: какие значения может принимать функция y=f(x), какова область её допустимых значений, при каких условиях функция будет возрастающей или убывающей, четной или нечетной, ограниченной или неограниченной.
Графики Тангенса: что это такое и как их использовать
Графики Тангенса — это тип графика, который помогает найти функцию касательной для заданного диапазона углов.
Они обычно представлены в виде ряда точек, соединенных линиями, и могут использоваться для определения конкретных углов и соответствующих значений их касательных.
Они показывают отношение между тангенсом угла и самим углом. Тангенс угла – это отношение длины стороны, противолежащей углу, к длине стороны, прилежащей к углу.
Диаграмма тангенса обычно рисуется как ряд точек, соединенных линиями, что позволяет легко идентифицировать определенные углы и соответствующие значения тангенсов.
Что такое диаграммы Тангенса и что они показывают
Они помогают найти функцию касательной для заданного диапазона углов. Тангенс угла – это отношение длины стороны, противолежащей углу, к длине стороны, прилежащей к углу.
Тангенс диаграммы показывает отношение между тангенсом угла и самим углом.
Как используются диаграммы Tan
Они показывают связь между тангенсом угла и самим углом, что может быть полезно при решении задач, связанных с тригонометрией.
Чтобы использовать диаграмму тангенса, вам сначала нужно определить угол, для которого вы хотите найти тангенс. Затем найдите соответствующую точку на графике и прочтите значение по оси Y. Это тангенс этого угла.
Конкретные применения Tan-графов в задачах тригонометрии
Тан-графы могут быть применены к множеству тригонометрических задач.
Некоторые специальные приложения включают нахождение тангенса заданного угла, решение задач, связанных с обратными тригонометрическими функциями, и нахождение точного значения тригонометрической функции.
Танграф может быть особенно полезен при решении задач, связанных с обратными тригонометрическими функциями.
Обратные тригонометрические функции применяются для нахождения углов, когда известно значение соответствующей тригонометрической функции.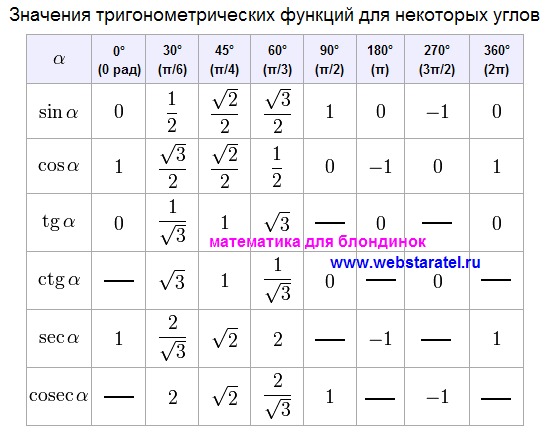
График тангенса можно использовать для определения угла, соответствующего заданному значению касательной, просто рисуя линии от начала координат до различных точек на кривой. Это выгодно с точки зрения правильного и быстрого решения вопросов.
Кроме того, график тангенса можно использовать для нахождения точного значения тригонометрической функции. Когда вы знаете значение угла и соответствующий ему тангенс, вы можете использовать график тангенса, чтобы найти точное значение тригонометрической функции.
Как можно использовать тангенс-график для решения задачи, связанной с тригонометрией?
При решении задачи, связанной с тригонометрией, вы можете использовать график тангенса, чтобы найти точное значение тригонометрической функции.
Когда вы знаете значение угла и соответствующий ему тангенс, вы можете использовать график тангенса, чтобы найти точное значение тригонометрической функции.
Это может быть полезно при решении сложных задач по тригонометрии.
Например, допустим, что вам дано уравнение y = sin(x) + 1. Вы знаете, что тангенс х равен 45 градусам, и вы хотите найти значение тангенса y, когда тангенс х равен 45 градусов. Вы можете использовать график загара, чтобы найти точное значение y.
Сначала определите угол, который соответствует 45 градусам на графике тангенса. Затем найдите соответствующую точку на графике и прочтите значение по оси Y.
Это значение тангенса у, когда тангенс х равен 45 градусам. Следовательно, y = sin(45 градусов) + 1 = 0,72 + 1 = 1,72.
Диаграмма тангенса может помочь в точном и эффективном решении проблем.
Их также можно использовать для нахождения точного значения тригонометрической функции, что может оказаться полезным при решении сложных тригонометрических задач.
Насколько важно понимать, как использовать tan-графы при решении задач по тригонометрии?
Необходимость понимать, как использовать тангенс-график при решении задач по тригонометрии, невозможно переоценить.
Танграфы являются важным инструментом для правильного разрешения тригонометрических ситуаций.
С помощью диаграммы тангенса можно легко определить угол, соответствующий заданному значению касательной. Это может помочь вам решить проблемы правильно и быстро.
Кроме того, график тангенса можно использовать для нахождения точного значения тригонометрической функции.
Когда вы знаете значение угла и соответствующий ему тангенс, вы можете использовать график тангенса, чтобы найти точное значение тригонометрической функции.
Таким образом, для точного и эффективного решения тригонометрических задач необходимо понимание того, как использовать диаграммы тангенса.
Заключение
Танграф может использоваться в различных задачах тригонометрии и особенно полезен при решении задач, связанных с обратными тригонометрическими функциями.
С помощью диаграммы тангенса можно легко определить угол, соответствующий заданному значению тангенса, что может быть полезно при решении сложных задач тригонометрии.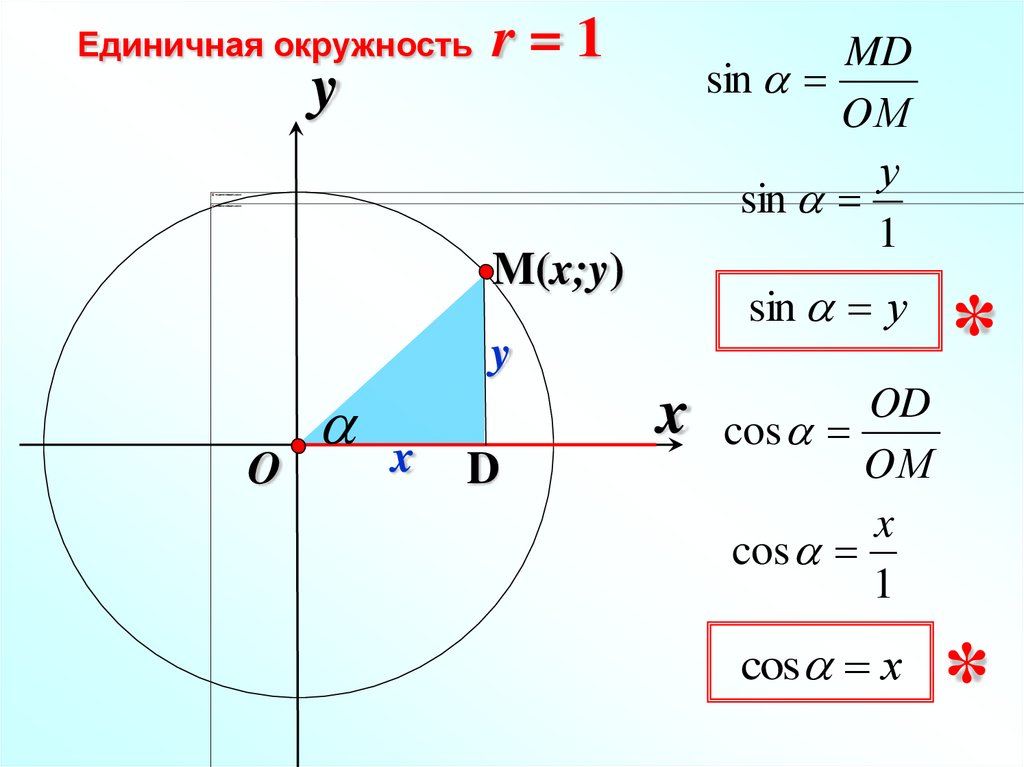
Кроме того, график тангенса можно использовать для нахождения точного значения тригонометрической функции.
Зная значение угла и соответствующий ему тангенс, можно использовать график тангенса, чтобы найти точное значение тригонометрической функции.
Понимание того, как использовать тангенс-график, необходимо для точного и эффективного решения тригонометрических задач.
Диаграмма тангенса — ценный инструмент, который можно использовать в различных задачах тригонометрии. Если вы понимаете, как их использовать, они могут помочь в точном и эффективном решении проблем.
Итак, в следующий раз, когда вы столкнетесь с проблемой тригонометрии, не забудьте свериться со своим верным графиком загара!
Обязательно ознакомьтесь с другими статьями в SchoolOnline, зайдя на нашу страницу GCSE Maths Foundation, чтобы узнать больше о математике!
Часто задаваемые вопросы
Загар y x или x y?
Когда координаты выражаются дробью, они называются тета.
Тангенс тета равен y относительно x, когда эти переменные заменены на y и x.
Что делает функция загара?
Функция тангенса принимает угол в радианах и возвращает отношение длины противоположной стороны к длине соседней стороны.
Почему он называется тангенсом?
Слово «тангенс» происходит от латинского слова «tangens», что означает «касание». Это потому, что линия, которая касается кривой только в одной точке, называется касательной.
Как найти тангенс угла?
Есть несколько способов найти тангенс угла. Самый распространенный метод — использовать калькулятор, но вы также можете использовать таблицу значений или график тангенса.
Что является обратной функцией тангенса?
Обратной функцией тангенса является функция арктангенса. Эта функция принимает отношение и возвращает угол в радианах, который имеет это отношение.
Каково применение функции касательной?
Функция тангенса имеет множество приложений в математике, физике и технике.
Он используется для расчета таких вещей, как амплитуда волны, скорость и ускорение. Он также используется в навигации и астрономии.
Как построить график функции тангенса?
Касательную функцию можно построить вручную или с помощью компьютерной программы. Чтобы построить график функции вручную, вам нужно будет использовать таблицу значений или график тангенса. Если вы используете компьютерную программу, вам нужно будет ввести уравнение в программу, а затем построить график.
Как рассчитывается тангенс?
Тангенс угла – это отношение длины противолежащей стороны к длине прилежащей стороны. Это можно рассчитать с помощью калькулятора, таблицы значений или графика тангенса.
Котангенс стремится к положительной бесконечности слева от нуля и к отрицательной бесконечности справа?
Нет, функция котангенса не стремится к положительной или отрицательной бесконечности (влево или вправо) от нуля. Функция котангенса не определена в нуле, но она стремится к бесконечности, когда угол приближается к нулю слева или справа.
Является ли тангенс полиномом?
Нет, функция тангенса не является многочленом. Это иррациональное число, которое не может быть выражено как рациональное число.
Какова область определения функции касательной?
Область определения функции тангенса — все действительные числа, кроме нуля. Это связано с тем, что функция тангенса не определена в нуле.
Каков диапазон функции касательной?
Диапазон функции тангенса — все действительные числа.
Значение Tan 0 градусов: периодичность с решенными примерами
0
Сохранить
Скачать публикацию в формате PDF В тригонометрии значение тангенса 0 градусов равно нулю. Функция тангенса является периодической функцией и является одной из шести основных тригонометрических функций. Тангенс функции угла определяется как отношение синуса и косинуса этого угла в прямоугольном треугольнике. Касательная функция угла также определяется как отношение противолежащей стороны к прилежащей по отношению к углу прямоугольного треугольника.
Значение Tan 0 представляет собой отношение sin 0 к cos 0. Это значение tan 0 может быть получено либо из других тригонометрических функций, либо из единичного круга.
Значение тангенса 0 градусов получается из отношения sin 0 градусов к cos 0 градусов и равно нулю. Это значение выражается для угла в градусах. Мы также можем представить это значение, когда угол берется в радианах. Мы преобразуем меру угла из градусов в радианы, умножая значение градуса на отношение π/180. Таким образом, ноль градусов эквивалентен нулю радиан. Итак, у нас есть значение tan 0 градусов = tan 0 радиан = 0
Методы определения значения тангенса 0 градусовЗначение тангенса 0 можно найти следующими способами:
- Тангенс 0 градусов с помощью единичной окружности
- Тангенс 0 градусов с помощью тригонометрических функций
\(tan\theta\) определяется как отношение \(sin\theta\) к \(cos\theta\).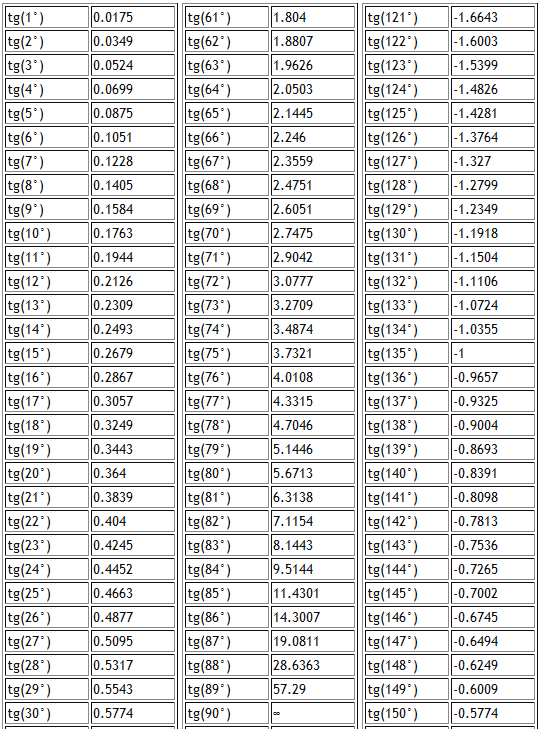
В единичном круге абсцисса, т. Е. Координата x, представляет значение cos, а ордината, т. е. координата y, представляет значение sin. Теперь, чтобы получить значение тангенса, мы просто делим соответствующее значение sin на значение cos, т. е. ординату на абсциссу.
На приведенном выше изображении дан единичный круг, где мы видим, что отмечены стандартные углы для sin и cos. Теперь, чтобы найти значение tan 0, мы просто находим отношение sin 0 к cos 0.
Таким образом, \( \tan0=\frac{\sin0}{\cos0}=\frac{0}{1}= 0 \)
Tan 0 Степень с использованием тригонометрических функцийЗдесь мы используем различные тригонометрические тождества, чтобы получить значение tan 0.
- \( \tan\theta=\frac{1}{\cot\theta} \) 9{\circ} \). Значения, соответствующие стандартным углам для тангенса \(\theta\), приведены в таблице ниже.
В приведенной выше таблице мы видим, что вычисляются значения, соответствующие функции y=tan x.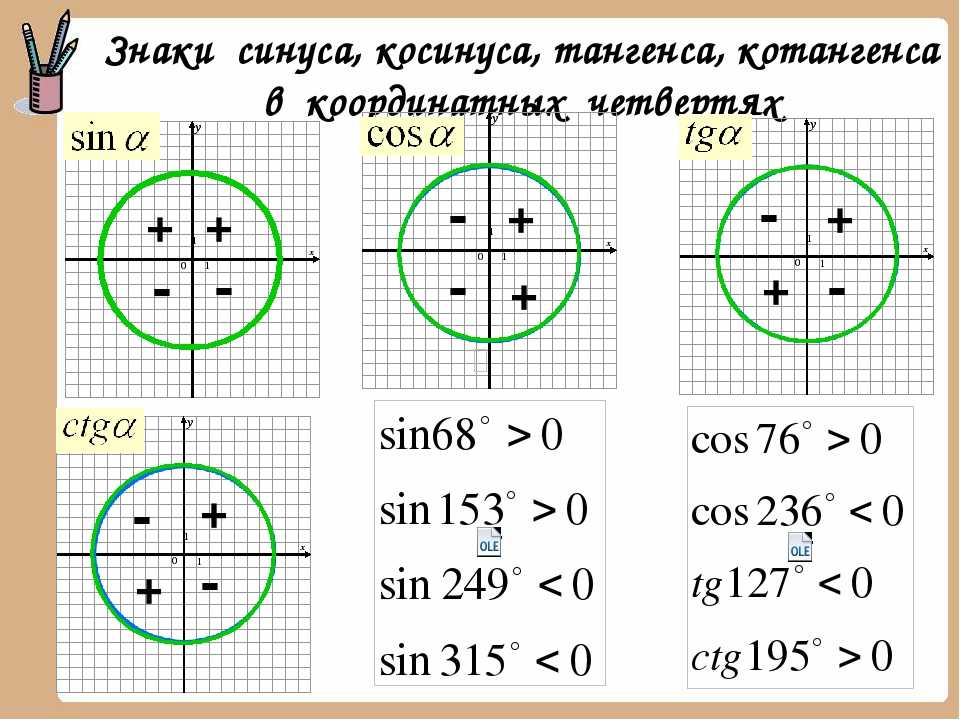
{\circ} \) или \ (\пи\) 9{\circ}}=\frac{1\left(1-0\right)}{\frac{1}{2}}=\frac{2\times1}{1}=2 \)
Если хотите чтобы набрать хороший балл на экзамене по математике, то вы находитесь в правильном месте. Здесь вы получите еженедельную подготовку к тестам, живые уроки и серию экзаменов. Загрузите приложение Testbook прямо сейчас, чтобы подготовить умную и высокорейтинговую стратегию к экзамену.
Часто задаваемые вопросы о Tan 0 DegreeВ.1 Какое значение имеет Tan 0?
Ответ 1 Значение тангенса 0 равно 0,
Q.2 Что такое tan 0 на единичном круге?
Ответ 2 На единичной окружности тангенс o равен sin o, деленному на cos o, где o/1=1.
Q.3 Как найти тангенс 0 треугольника?
Ответ 3 Мы находим отношение sin 0 к cos 0, чтобы получить тангенс 0.
В.4. Тангенс 0 не определен?
Ответ 4 Нет, тангенс 0 не является неопределенным.