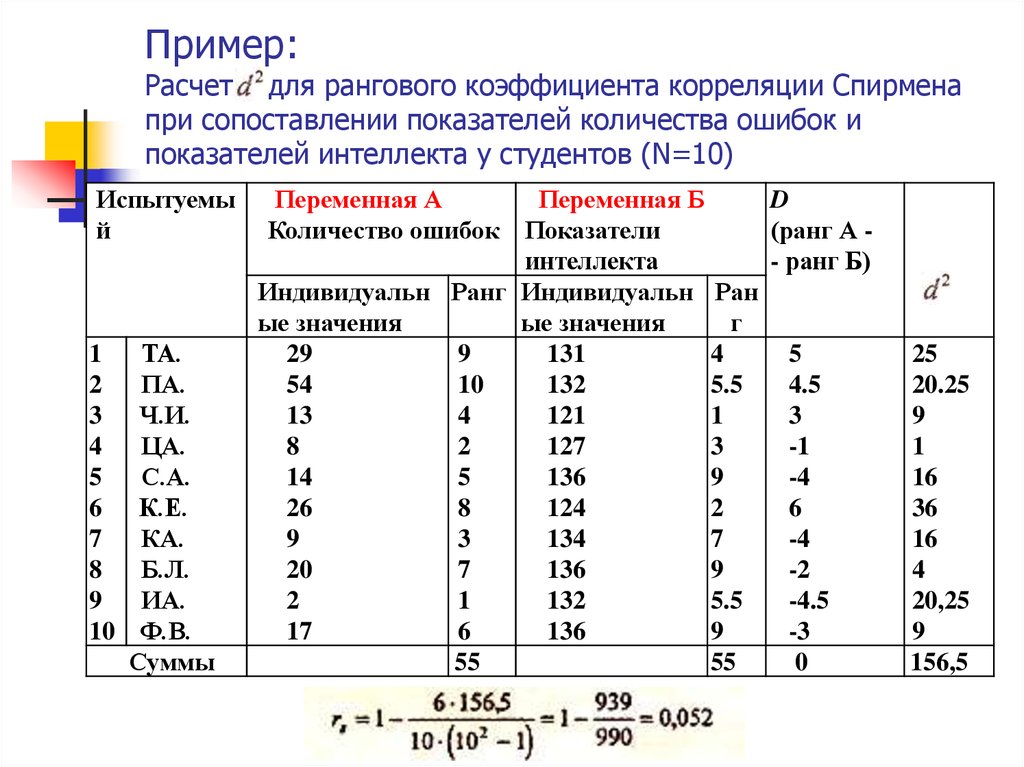
Коэффициент конкордации онлайн
Коэффициент конкордации является мерой согласованности мнений экспертов.,
где , Li — число связок (видов повторяющихся элементов) в оценках i-го эксперта, tl — количество элементов в l-й связке для i-го эксперта (количество повторяющихся элементов). Если нет связанных рангов, то Ti равно нулю.Назначение сервиса. С помощью онлайн-калькулятора производится расчет коэффициента конкордации, а также делается вывод о его значимости.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Инструкция. Укажите Число факторов и Число экспертов. Полученное решение сохраняется в файле Word.
Число факторов
Число экспертов
Пример. Шесть экспертов (n=6) ранжируют пять (m=5) элементов (X1, X2, …, X3) по их важности. Результаты сведены в таблицу. Определить суммарную ранжировку этих элементов и коэффициент конкордации. Проверить значимость коэффициента конкордации, если табличное значение χ20,01(4) для 1% уровня значимости и 4 степеней (k = n-1=5-1=4) свободны равно 13,277.
Шесть экспертов (n=6) ранжируют пять (m=5) элементов (X1, X2, …, X3) по их важности. Результаты сведены в таблицу. Определить суммарную ранжировку этих элементов и коэффициент конкордации. Проверить значимость коэффициента конкордации, если табличное значение χ20,01(4) для 1% уровня значимости и 4 степеней (k = n-1=5-1=4) свободны равно 13,277.
Таблица — Расчет коэффициента конкордации
| Эксперты ↓ Факторы→ | 1 | 2 | 3 | 4 | 5 | 6 | rj | di | d2 |
| 1 | 2 | 3 | 1 | 2 | 1 | 1 | 10 | -8 | 64 |
| 2 | 1 | 1 | 3 | 3 | 4 | 2 | 14 | -4 | 16 |
| 3 | 3 | 2 | 2 | 1 | 2 | 3 | 13 | -5 | 25 |
| 4 | 4 | 5 | 4 | 5 | 3 | 4 | 25 | 7 | 49 |
| 5 | 5 | 4 | 5 | 4 | 5 | 5 | 28 | 10 | 100 |
Анализ строки rj (суммы рангов, полученных элементом Xj от всех экспертов) показывает, что наименьшее значение эта сумма имеет для первого элемента.
 Этому элементу приписывается ранг 1. Ранг 2 имеет 3-й элемент, ранг 3 имеет 2-й элемент, ранги 4 и 5 имеют 4-й и 5-й элементы соответственно.
Этому элементу приписывается ранг 1. Ранг 2 имеет 3-й элемент, ранг 3 имеет 2-й элемент, ранги 4 и 5 имеют 4-й и 5-й элементы соответственно.
Коэффициент конкордации W=254/360=0,71.
Значение χ2 = N·(m-l)·W=6·(5-l)·0,71=17,04, т.к. χ2> χ20,01 (χ 20,01(4) =13,27), следовательно, коэффициент значим, согласованность удовлетворительна.

Пример №2.
Цель решения задачи: использование полученной информации для определения путей качественного совершенствования продукции, оценки технического уровня, конкурентоспособности холодильников на рынке, обоснования цен, надбавок (скидок) с цен с учетом технического уровня продукции, выявления новых секторов рынка холодильников.
Задание. Произвести экспертную оценку технических параметров холодильников по степени значимости их для потребителей.
Исходные данные
Технические параметры холодильников:
1. Объем камеры м3.
2. Количество камер шт.
3. Энергопотребление.
4. Наличие системы Hoy Frost.
5. Дизайн.
6. Бренд.
Число факторов n= 6
Число экспертов m= 4
- Решение
- Видео решение
Этап 1. Создание экспертной комиссии.
В экспертную группу вошло 4 эксперта.
Этап 2. Сбор мнений специалистов путем анкетного опроса.
Оценку степени значимости технических параметров холодильника для потребителей эксперты производят путем присвоения им рангового номера. Фактору, которому эксперт дает наивысшую оценку, присваивается ранг 1. Если эксперт признает несколько факторов равнозначными, то им присваивается одинаковый ранговый номер. На основе данных анкетного опроса составляется сводная матрица рангов.
Этап 3. Составление сводной матрицы рангов.
Таблица 1
Матрица рангов
| № п/п | Технические параметры холодильника | Единица измерения | Эксперты | |||
| 1 | 2 | 3 | 4 | |||
| 1 | Объем камеры (x1) | м3 | 3 | 4 | 5 | 4 |
| 2 | Бренд (x2) | - | 5 | 6 | 3 | 4 |
| 3 | Количество камер (x3) | Шт.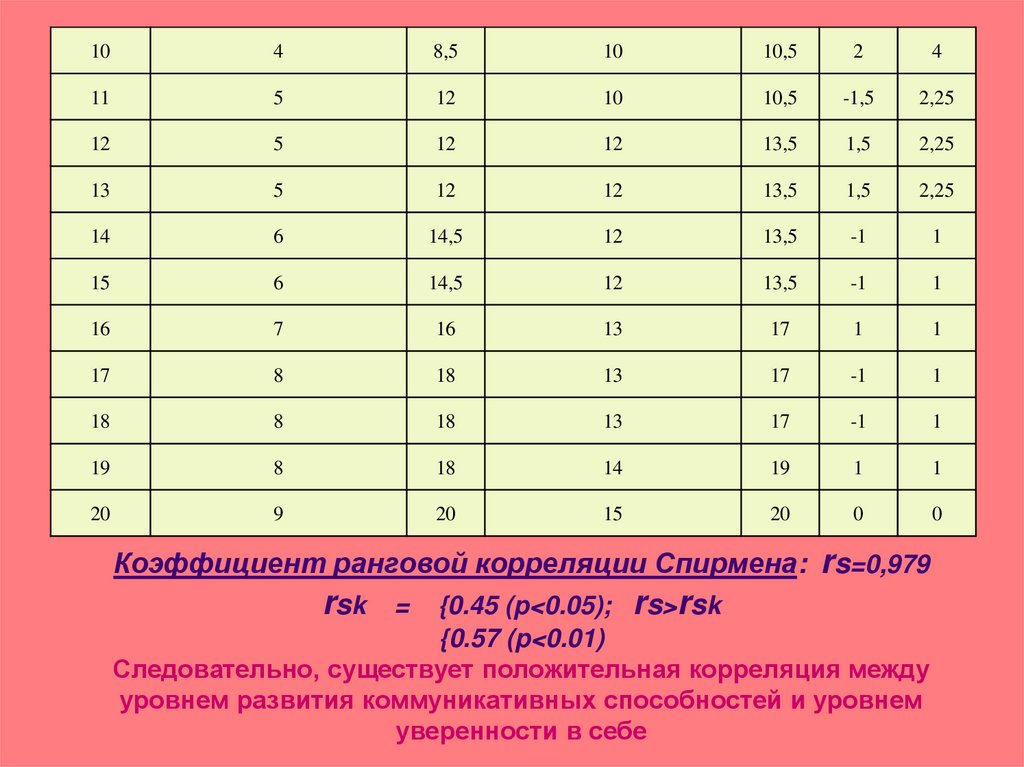
| 4 | 3 | 1 | 3 |
| 4 | Наличие систем Hoy Frost (x4) | - | 1 | 1 | 3 | 1 |
| 5 | Энергопотребление (x | Вт. | 6 | 5 | 6 | 6 |
| 6 | Дизайн (x6) | - | 2 | 2 | 2 | 2 |
Переформирование рангов производится в табл.
 2, 3
2, 3
Таблица 2
| Номера мест в упорядоченном ряду | 1 | 2 | 3 | 4 | 5 | 6 |
| Расположение факторов по оценке эксперта | 1(x3) | 2(x6) | 3(x2) | 3(x4) | 5(x1) | 6(x5) |
| Новые ранги | 1 | 2 | 3,5 | 3,5 | 5 | 6 |
Таблица 3
| Номера мест в упорядоченном ряду | 1 | 2 | 3 | 4 | 5 | 6 |
| Расположение факторов по оценке эксперта | 1(x4) | 2(x6) | 3(x3) | 4(x1) | 4(x2) | 6(x5) |
| Новые ранги | 1 | 2 | 3 | 4,5 | 4,5 | 6 |
 4).
4).
Матрица рангов
Таблица 4
| Эксперты Факторы | 1 | 2 | 3 | 4 | Сумма рангов | Δ | |
| x1 | 3 | 4 | 5 | 4,5 | 16,5 | 2,5 | 6,25 |
| x2 | 5 | 6 | 3,5 | 4,5 | 19 | 5 | 25 |
| x3 | 4 | 3 | 1 | 3 | 11 | -3 | 9 |
| x4 | 1 | 1 | 3,5 | 1 | 6,5 | -7,5 | 56,25 |
| x5 | 6 | 5 | 6 | 6 | 23 | 9 | 81 |
| x6 | 2 | 2 | 2 | 2 | 8 | -6 | 36 |
| Σ | 21 | 21 | 21 | 21 | 84 | S = 213,5 | |
Проверка правильности составления матрицы на основе исчисления контрольной суммы:
.
Сумма по столбцам матрицы равны между собой и контрольной суммы, значит матрица составлена правильно.
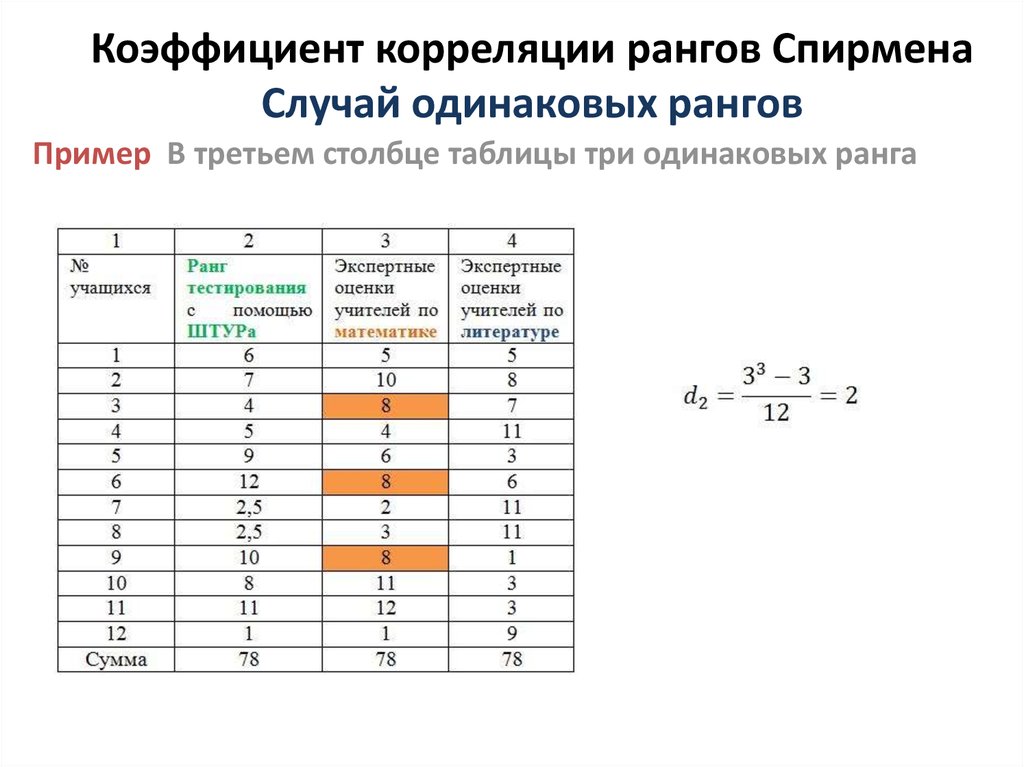
В данном примере факторы по значимости распределились следующим образом (табл. 5).
Таблица 5 — Расположение факторов по значимости
| Факторы | x4 | x6 | x3 | x1 | x2 | x5 |
| Сумма рангов | 6,5 | 8 | 11 | 16,5 | 19 | 23 |

Рис. 1. Гистограмма и полигон распределения сумм рангов
Гистограмма (рис. 1) позволяет сделать следующие выводы:
1. Наибольшее значение для потребителей имеют фактор x4 (наличие систем Hoy Frost) и фактор x6 (дизайн).
2. Вторая группа по значимости включает в себя один фактор x3 (количество камер).
3. Третья группа включает в себя факторы x1 (объем камеры), x2 (бренд), x5 (энергопотребление).
Итак, важнейшими для потребителей являются следующие технические параметры холодильников: x4, x6, x3.
Этап 5. Оценка средней степени согласованности мнений всех экспертов.
Воспользуемся коэффициентом конкордации для случая, когда имеются связанные ранги (одинаковые значения рангов в оценках одного эксперта)
,
где , Li — число связок (видов повторяющихся элементов) в оценках i-го эксперта, tl — количество элементов в l-й связке для i-го эксперта (количество повторяющихся элементов).
S = 213,5 (см. табл. 6.4), n = 6, m = 4,
(в оценках 3-его эксперта одна связка, повторяется ранг «3,5» 2 раза),
, (в оценках 4-ого эксперта одна связка, повторяется ранг «4,5» 2 раза),
, (если нет связанных рангов, то Ti равно нулю)
.
W = 0.774 говорит о наличии высокой степени согласованности мнений экспертов. На высокую степень согласованности мнений экспертов указывает и полигон распределения сумм рангов (рис. 6.1). Ломанная и прямая линии близко расположены друг к другу.
Этап 6. Оценка значимости коэффициента конкордации.
Для этой цели исчислим критерий согласования Пирсона: , .
Вычисленный сравним с табличным значением для числа степеней свободы K = n-1 = 6-1 = 5 и при заданном уровне значимости α = 0,05.
Так как расчетный 15,471 > табличного = 11,07, то W = 0.744 — величина не случайная, а потому полученные результаты по оценке качественных свойств холодильников по степени их значимости для потребителей имеют смысл и могут использоваться в дальнейших исследованиях.
Этап 7. Подготовка решения экспертной комиссии.
Была поставлена задача выяснить, какие технические параметры холодильников в наибольшей степени интересуют потребителей.
В результате проведенного исследования на основе экспертных оценок выяснилось, что важнейшими качественными свойствами являются: наличие систем, дизайн и количество камер. Следовательно, качественное совершенствование холодильников должны идти по пути улучшения этих свойств (исходя из требований НТП).
Себестоимость, цены, доплата к ценам на изделия улучшенного качества и скидки с цен на холодильники должны строиться с учетом вышеперечисленных качественных свойств.
На основе получения суммы рангов (табл. 4) можно вычислить показатели весомости рассмотренных технических параметров холодильников для потребителя с тем, чтобы их можно было учитывать при оценке технического уровня холодильников. Для этого произведем следующие вычисления. Сначала по каждому параметру вычислим величины, обратные сумме рангов, то есть
; ;
; ; .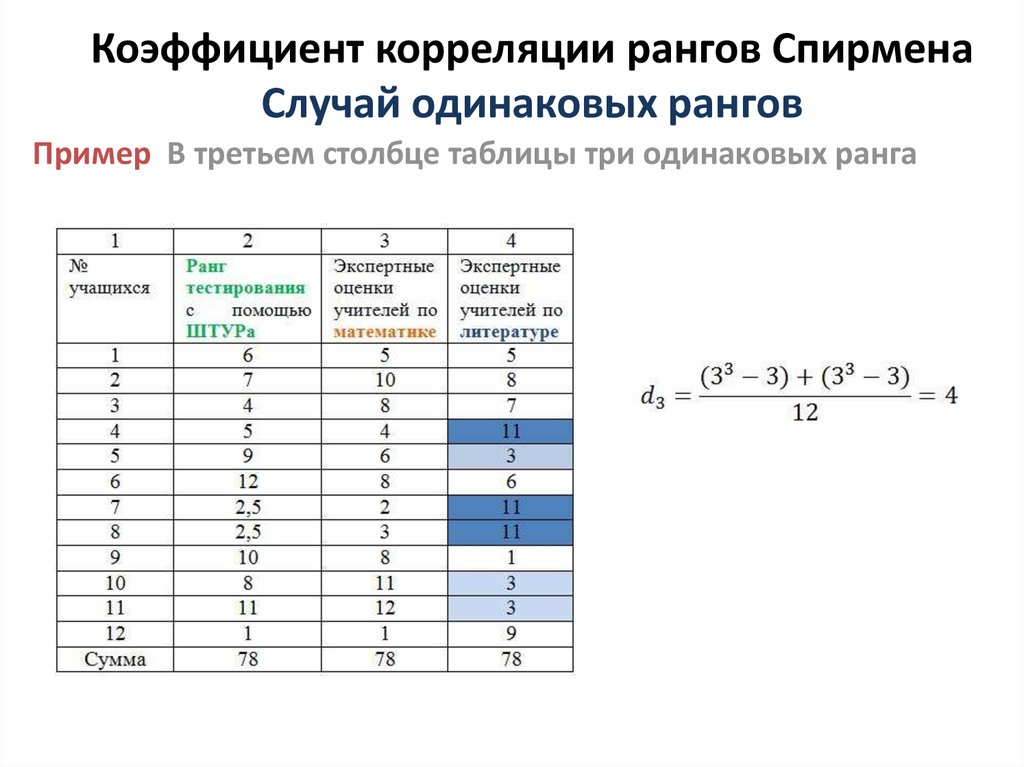
Это делается для того, чтобы привести в соответствие содержание сумм рангов коэффициентам весомости. Расположим полученные числа по мере убывания, сложим их, взвесим каждое число в полученной сумме, которую примем равной 1 (табл. 6).
Таблица 6
| Технические параметры | Величины, обратные сумме рангов | Коэффициенты весомости параметров |
| x4 x6 x3 x1 x2 x5 | 0,15
0,12 0,09 0,06 0,05 0,04 | 0,29
0,23 0,18 0,12 0,10 0,08 |
Онлайн калькулятор: Коэффициент корреляции Спирмена
РаботаСтатистика
Расчет коэффициента ранговой корреляции Спирмена.
Калькулятор ниже вычисляет коэффициент ранговой корреляции Спирмена между двумя случайными величинами. Теоретическая часть, чтобы не отвлекаться от калькулятора, традиционно размещается под ним.
Коэффициент корреляции Спирмена
Изменения случайных величин
| X | Y | ||
|---|---|---|---|
51020501001000
Изменения случайных величин
Импортировать данныеОшибка импорта
Данные
Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: -50.5;-50.5
Загрузить данные из csv файла
Точность вычисления
Знаков после запятой: 4
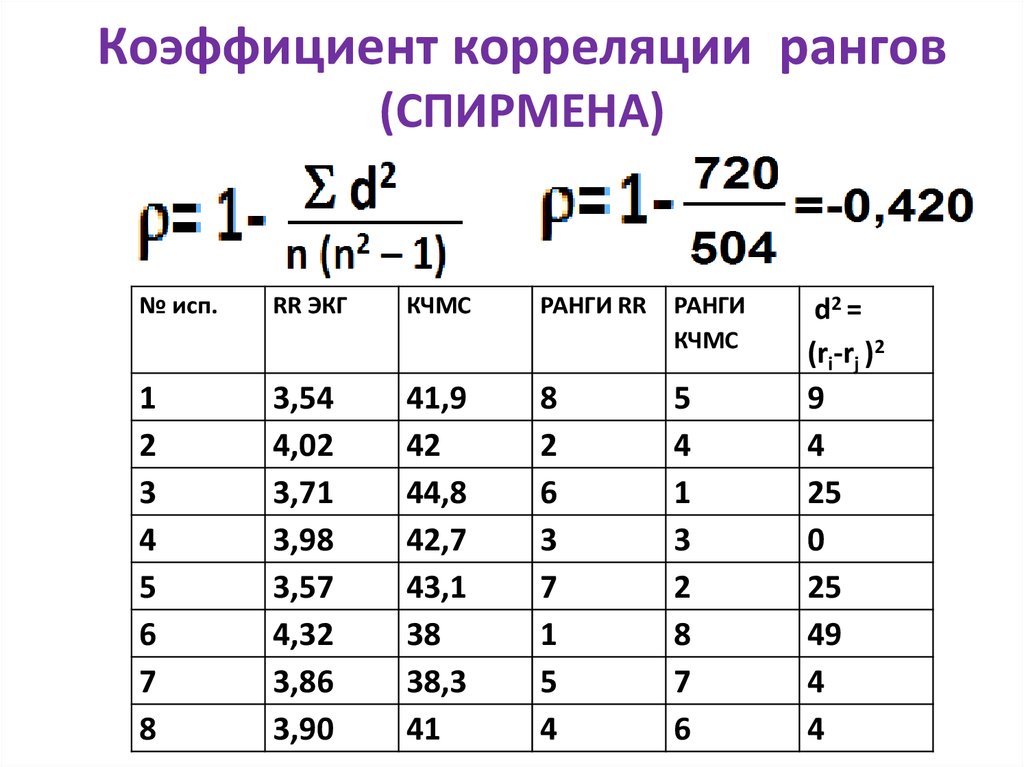
Коэффициент корреляции Спирмена
Метод расчета коэффициента ранговой корреляции Спирмена на самом деле описывается очень просто.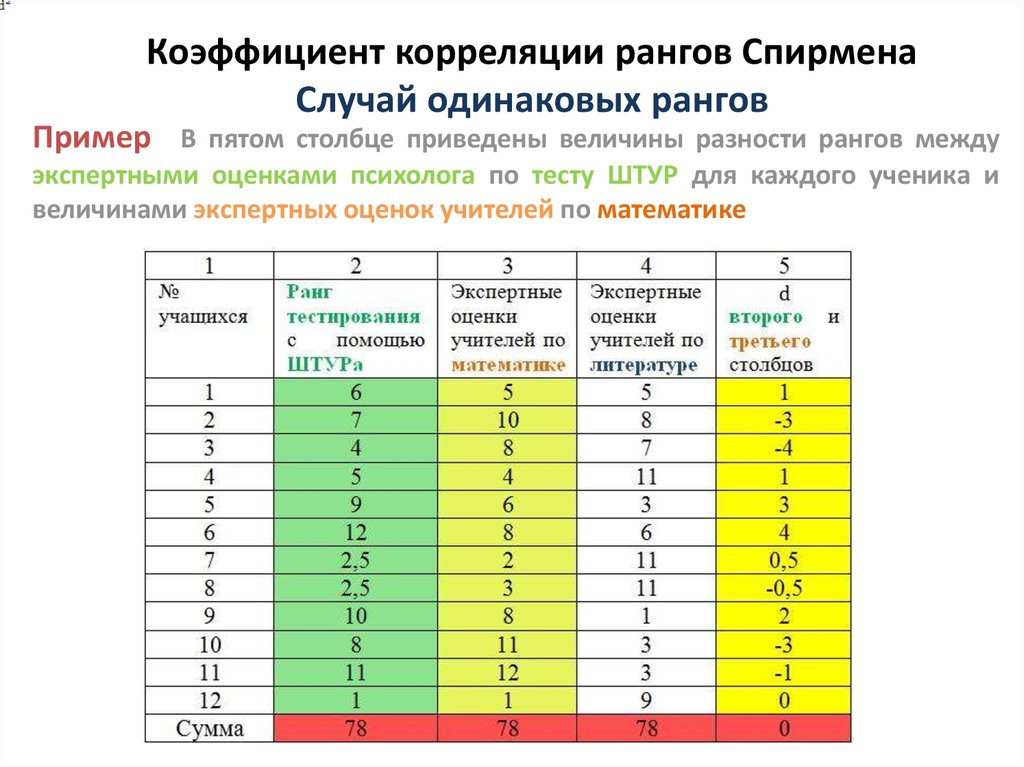 Это тот же самый Коэффициент корреляции Пирсона, только рассчитанный не для самих результатов измерений случайных величин, а для их ранговых значений.
Это тот же самый Коэффициент корреляции Пирсона, только рассчитанный не для самих результатов измерений случайных величин, а для их ранговых значений.
То есть,
Осталось только разобраться, что такое ранговые значения и для чего все это нужно.
Если элементы вариационного ряда расположить в порядке возрастания или убывания, то рангом элемента будет являться его номер в этом упорядоченном ряду.
Например, пусть у нас есть вариационный ряд {17,26,5,14,21}. Отсортируем его элементы в порядке убывания {26,21,17,14,5}. 26 имеет ранг 1, 21 — ранг 2 и т.д. Вариационный ряд ранговых значений будет выглядеть следующим образом {3,1,5,4,2}.
То есть, при расчете коэффициента Спирмена исходные вариационные ряды преобразуются в вариационные ряды ранговых значений, после чего к ним применяется формула Пирсона.
Есть одна тонкость — ранг повторяющихся значений берется как среднее из рангов. То есть для ряда {17, 15, 14, 15} ряд ранговых значений будет выглядеть как {1, 2.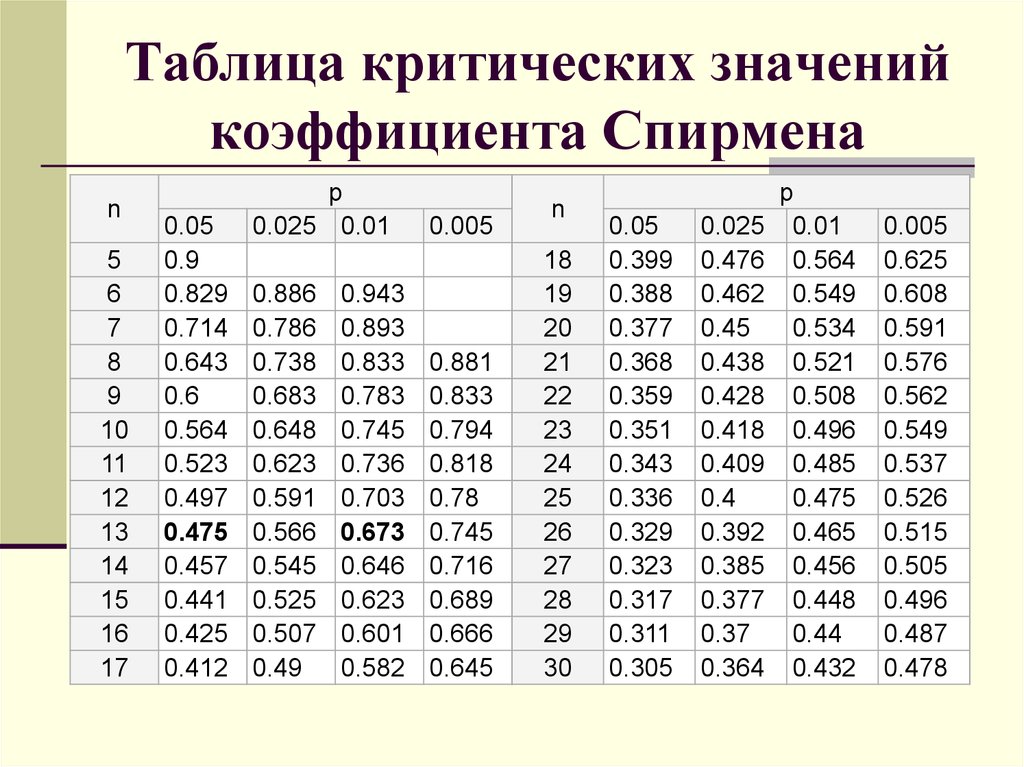 5, 4, 2.5}, так как первый элемент равный 15 имеет ранг 2, а второй — ранг 3, и .
5, 4, 2.5}, так как первый элемент равный 15 имеет ранг 2, а второй — ранг 3, и .
Если же повторяющихся значений нет, то есть все значения ранговых рядов — числа из диапазона от 1 до n, формулу Пирсона можно упростить до
Ну и кстати, эта формула чаще всего и приводится как формула расчета коэффицента Спирмена.
В чем же суть перехода от самих значений к их ранговым значениям?
А суть в том, что исследуя корреляцию ранговых значений можно установить насколько хорошо зависимость двух переменных описывается монотонной функцией.
Знак коэффициента указывает на направление связи между переменными. Если знак положительный, то значения Y имеют тенденцию увеличиваться при увеличении значений X; если знак отрицательный, то значения Y имеют тенденцию уменьшаться при увеличении значений X. Если коэффициент равен 0, то никакой тенденции нет. Если же коэффициент равен 1 или -1, то зависимость между X и Y имеет вид монотонной функции — то есть, при увеличении X, Y также увеличивается, либо наоборот, при увеличении X, Y уменьшается.
То есть, в отличие от коэффициента корреляции Пирсона, который может выявить только линейную зависимость одной переменной от другой, коэффициент корреляции Спирмена может выявить монотонную зависимость, там, где непосредственная линейная связь не выявляется.
Поясню на примере. Предположим, что мы исследуем функцию y=10/x.
У нас есть следующие результаты измерений X и Y
{{1,10}, {5,2}, {10,1}, {20,0.5}, {100,0.1}}
Для этих данных коэффициент корреляции Пирсона равен -0.4686, то есть связь слабая либо отсутствует. А вот коэффициент корреляции Спирмена строго равен -1, что как бы намекает исследователю, что Y имеет строгую отрицательную монотонную зависимость от X.
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Коэффициент корреляции Пирсона
- • Коэффициент Танимото
- • Аппроксимация функции одной переменной
- • Аппроксимация функции одной переменной методом наименьших квадратов с дополнительными условиями
- • Биномиальное распределение.
 Функция плотности вероятности, кумулятивная функция распределения, математическое ожидание и дисперсия
Функция плотности вероятности, кумулятивная функция распределения, математическое ожидание и дисперсия - • Раздел: Статистика ( 32 калькуляторов )
корреляция коэффициент корреляции коэффициент корреляции Спирмена Статистика теория вероятности
PLANETCALC, Коэффициент корреляции Спирмена
Timur2020-11-03 14:19:28
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Калькулятор коэффициента корреляции — включая ковариацию и этапы расчета
Калькулятор корреляции и калькулятор ковариации вычисляет корреляцию и проверяет значимость результата.
Информация
Что такое ковариация?
Ковариация проверяет взаимосвязь между двумя переменными.
Диапазон ковариации не ограничен от отрицательной бесконечности до положительной бесконечности. Для независимых переменных ковариация равна нулю .
Положительная ковариация — изменения идут в одном направлении, при увеличении одной переменной обычно увеличивается и вторая переменная, а при уменьшении одной переменной обычно уменьшается и вторая переменная.
Отрицательная ковариация — противоположное направление, при увеличении одной переменной обычно уменьшается вторая переменная, а при уменьшении одной переменной обычно увеличивается вторая переменная.
Как рассчитать ковариацию
Формула ковариации:
Cov(X,Y) = E[(X-E[X])(Y-E[Y])]
Cov(X,Y) = E[XY]-E(X)E[Y ]
S XY — выборочная ковариация между X и Y.
| S XY = | 08 -в) |
| н — 1 |
Что такое корреляция?
Можно сказать, что существует корреляция между двумя переменными или статистическая связь, когда значение одной переменной может хотя бы частично предсказывать значение другой переменной.
Корреляция представляет собой стандартизированную ковариацию, диапазон корреляции находится в диапазоне от -1 до 1.
Корреляция игнорирует вопрос о причине и следствии, зависит ли X от Y или Y зависит от X, или обе переменные зависят от третьей переменной Z.
Аналогично к ковариации для независимых переменных корреляция равна нулю .
Положительная корреляция — изменения идут в одном направлении, при увеличении одной переменной обычно увеличивается и вторая переменная, а при уменьшении одной переменной обычно уменьшается и вторая переменная.
Отрицательная корреляция — противоположное направление, при увеличении одной переменной обычно уменьшается вторая переменная, а при уменьшении одной переменной обычно увеличивается вторая переменная.
Идеальная корреляция — Когда вы знаете значение одной переменной, вы можете вычислить точное значение второй переменной. Для совершенной положительной корреляции r = 1, а для совершенной отрицательной корреляции r = -1.
Что такое коэффициент корреляции Пирсона?
Коэффициент корреляции Пирсона — это тип корреляции, который измеряет линейную связь между двумя переменными
Как рассчитать корреляцию Пирсона?
Формула корреляции Пирсона для населения
| ρ XY = | E[(X-E[X])(Y-E[Y])] |
| σ 9030 7 X σ Y |
Население Пирсон формула корреляции — с использованием ковариации 0022
Образец формулы корреляции Пирсона
| r = | Σ(x i — x̄)(y i — ȳ) |
| √(Σ(x i — х̄) 2 Σ(у я — ȳ) 2 ) |
Пример формулы корреляции Пирсона — с использованием ковариации
Допущения
- Непрерывные переменные — Две переменные являются непрерывными (отношение или интервал).

- Выбросы — Значение выборочной корреляции чувствительно к выбросам. Мы проверяем выбросы на парном уровне, на остатках линейной регрессии,
- Линейность — линейная связь между двумя переменными, корреляция — это размер эффекта линейности. (обычно используемый размер эффекта f 2 получен из R 2 (r и R одинаковы)
- Нормальность — Двумерное нормальное распределение. Вместо проверки двумерной нормальности мы вычисляем линейную регрессию и проверяем нормальность остатков.
- Гомоскедастичность , однородность дисперсии — дисперсия остатков постоянна и не зависит от независимых переменных X 308 = 0, независимые переменные, и X и Y имеют двумерное нормальное распределение или размер выборки большой, то вы можете использовать t-критерий.
Когда ρ 0 ≠ 0, выборочное распределение не будет симметричным, поэтому вы не можете использовать t-распределение. В этом случае для преобразования распределения следует использовать преобразование Фишера.
После использования преобразования выборочное распределение стремится к нормальному распределению.Что такое ранговый коэффициент корреляции Спирмена?
Коэффициент ранговой корреляции Спирмена — это непараметрическая статистика, которая измеряет монотонную связь между двумя переменными.
Что такое монотонная ассоциация? когда одна переменная увеличивается, обычно увеличивается и вторая переменная, или когда одна переменная увеличивается, обычно вторая переменная уменьшается.
Вы можете использовать ранговую корреляцию Спирмена, когда две переменные не соответствуют предположениям корреляции Пирсона. как в следующих случаях:- Порядковые дискретные переменные
- Нелинейные данные
- Распределение данных не является двумерным нормальным.
- Данные содержат выбросы
- Данные не соответствуют предположению о гомоскедастичности. Дисперсия остатков не постоянна.
Как рассчитать ранговую корреляцию Спирмена?
Ранжируйте данные отдельно для каждой переменной, а затем вычислите корреляцию Пирсона ранжированных данных.

Наименьшее значение получает 1, второе — 2 и т. д. Даже при обратном ранжировании, когда наибольшее значение равно 1, результатом будет то же значение корреляции.Данные связей
Когда данные содержат повторяющиеся значения, каждое значение получает среднее значение рангов. В приведенном ниже примере значение 8 рангов равно 4 и 5, следовательно, оба значения получат средний ранг: (4 + 5)/2 = 4,5 .
Пример
Данные
РангиX Y 7,3 7 900 19 8 6,6 5,4 5,4 2,7 3,7 8 9,9 9,1 11 X Y 3 4 4.5 3 2 90 019 2 1 1 4,5 5 6 6 Допущения
- Порядковый/непрерывный — Две переменные должны быть порядковыми или непрерывными (отношение или интервал).

- Монотонная ассоциация
Распределение
Когда ρ 0 ≠ 0, распределение несимметрично, в этом случае инструмент будет использовать нормальное распределение по преобразованию Фишера.
Когда ρ 0 = 0, у вас есть несколько вариантов:- Автоматически — использует t-критерий и использует преобразование Фишера для доверительного интервала.
- T — распределение — использовать t-критерий и доверительный интервал с t-распределением
- Z — распределение — использовать преобразование Фишера для z-критерия и доверительного интервала.
- Точное — актуально только для ранговой корреляции Спирмена, когда размер выборки мал, t-распределение или распределение по z недостаточно хороши в качестве аппроксимации, поэтому следует использовать точное значение, взятое из предварительно рассчитанного таблице, в этом случае значение p следующего списка будет точным:
[0,25,0,1,0,05,0,025,0,01,0,005,0,0025,0,001,0,0005]
Любое значение p между ними является только экстраполяцией, но обычно не меняет результат, поскольку все общие уровни значимости, перечисленные выше, являются точными.

 Функция плотности вероятности, кумулятивная функция распределения, математическое ожидание и дисперсия
Функция плотности вероятности, кумулятивная функция распределения, математическое ожидание и дисперсия Некоммерческое (академическое) использование этого программного обеспечения бесплатно. Единственное, что просят взамен — цитировать этот софт при использовании результатов в публикациях.
Некоммерческое (академическое) использование этого программного обеспечения бесплатно. Единственное, что просят взамен — цитировать этот софт при использовании результатов в публикациях. , (2017), Spearman Rank Correlation (v1.0.3) in Free Statistics Software (v1.2.1), Office for Research Development and Education, URL https: //www.wessa.net/rwasp_spearman.wasp/
, (2017), Spearman Rank Correlation (v1.0.3) in Free Statistics Software (v1.2.1), Office for Research Development and Education, URL https: //www.wessa.net/rwasp_spearman.wasp/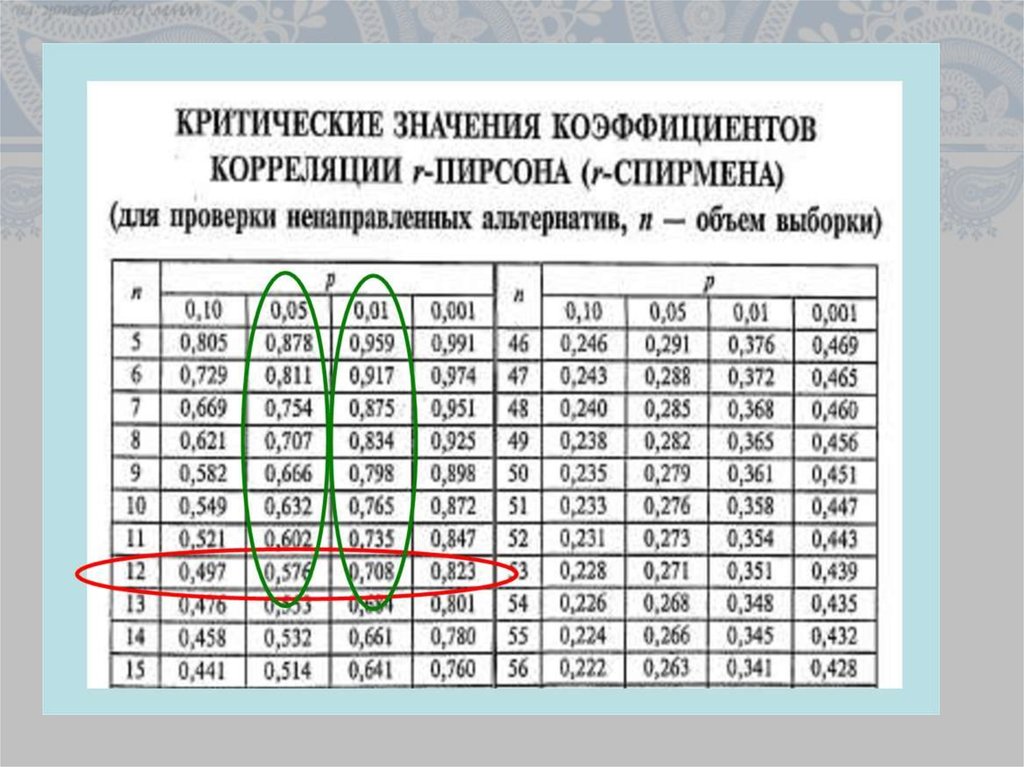 (2023), Бесплатное статистическое программное обеспечение, Управление исследований, развития и образования,
(2023), Бесплатное статистическое программное обеспечение, Управление исследований, развития и образования,  Мы прилагаем разумные усилия для предоставления точной и своевременной информации
и периодически обновлять информацию и программное обеспечение без предварительного уведомления. Мы
не давать никаких гарантий или заявлений
в отношении точности или полноты такой информации (или программного обеспечения), и не предполагает
ответственности или ответственности за ошибки или упущения в содержании этого веб-сайта
сайт или какие-либо программные ошибки в онлайн-приложениях. Вы используете этот веб-сайт НА СВОЙ СОБСТВЕННЫЙ РИСК. Ни при каких обстоятельствах и
ни по какой правовой теории мы не несем ответственности перед вами или любым другим
лицо для любого прямого, косвенного, специального, случайного, образцового или
косвенный ущерб, возникающий в результате вашего доступа к этому веб-сайту или его использования.
Мы прилагаем разумные усилия для предоставления точной и своевременной информации
и периодически обновлять информацию и программное обеспечение без предварительного уведомления. Мы
не давать никаких гарантий или заявлений
в отношении точности или полноты такой информации (или программного обеспечения), и не предполагает
ответственности или ответственности за ошибки или упущения в содержании этого веб-сайта
сайт или какие-либо программные ошибки в онлайн-приложениях. Вы используете этот веб-сайт НА СВОЙ СОБСТВЕННЫЙ РИСК. Ни при каких обстоятельствах и
ни по какой правовой теории мы не несем ответственности перед вами или любым другим
лицо для любого прямого, косвенного, специального, случайного, образцового или
косвенный ущерб, возникающий в результате вашего доступа к этому веб-сайту или его использования. net Дом
net Дом