Как не заучивать формулы приведения
Как не заучивать формулы приведения.
При решении тригонометрических уравнений или совершении тригонометрических преобразований первым делом нужно минимизировать количество различных аргументов тригонометрических функций. Для этого нужно все углы привести к углам первой четверти, воспользовавшись формулами приведения. Я хочу познакомить вас с мнемоническим правилом, которое позволяет не заучивать формулы приведения. Это правило в шутку называется «Лошадиное правило».
В этом ВИДЕОУРОКЕ я расскажу, как пользоваться этим правилом: приводить тригонометрическую функцию произвольного угла к углу первой четверти, освободив себя от необходимости запоминать формулы приведения:
Итак, «лошадиное правило» звучит так:
Если мы откладываем угол от вертикальной оси, лошадь говорит «да» (киваем головой вдоль оси OY) и приводимая функция меняет свое название: синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс.
Если мы откладываем угол от горизонтальной оси, лошадь говорит «нет» (киваем головой вдоль оси OХ) и приводимая функция не меняет свое название.
Знак правой части равенства совпадает со знаком приводимой функции, стоящей в левой части равенства.
Приведу несколько примеров использования формул приведения:
1. Найти значение выражения:
1. Выделим целую часть в дроби :
2. Так как период функции равен , выделим «холостые обороты»:
Теперь наш аргумент находится в пределах от нуля до , и самое время применить «лошадиное правило»:
Чтобы попасть в точку, соответствующую углу поворота на , мы сначала совершаем поворот на радиан, а потом из этой точки откладывает угол радиан:
Мы отложили угол от горизонтальной оси (лошадь говорит «нет») — не меняет свое названия, угол расположен в третьей четверти, в которой косинус отрицателен, следовательно приводимая функция отрицательна. Получаем:
Получаем:
2. Найти значение выражения:
Разберемся по отдельности с каждой функцией:
— мы сначала совершаем поворот на радиан, а затем откладываем угол 1 радиан от вертикальной оси в отрицательном направлении и попадаем в третью четверть:
Следовательно, приводимая функция меняет свое название, приводимая функция больше нуля (тангенс угла третьей четверти больше нуля): .
:
Сначала совершаем поворот на радиан, а затем из этой точки двигаемся на 1 радиан в отрицательном направлении. Откладываем угол 1 радиан от горизонтальной оси (синус не меняет свое название) и попадаем во вторую четверть, в которой синус больше нуля:
.
:
Сначала совершаем поворот на радиан, а затем из этой точки двигаемся на 1 радиан в положительном направлении. Откладываем угол 1 радиан от горизонтальной оси (косинус не меняет свое название) и попадаем в третью четверть, в которой косинус меньше нуля:
Вернемся к исходному примеру:
Ответ: 0
И.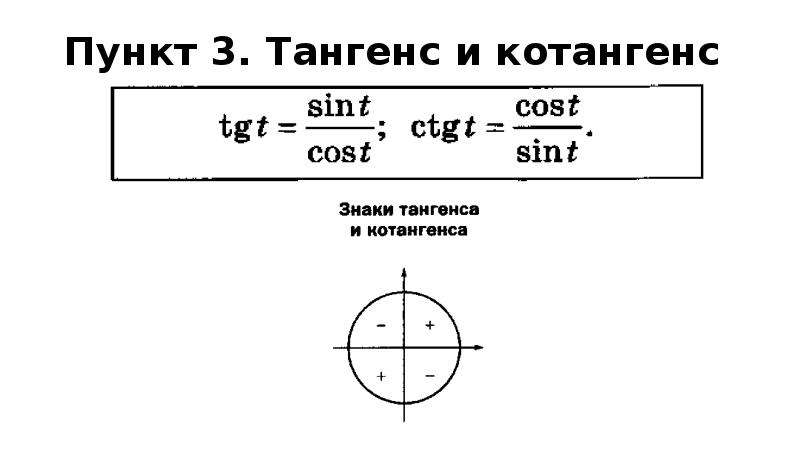 В. Фельдман, репетитор по математике.
В. Фельдман, репетитор по математике.
Купить видеокурс «ВСЯ ТРИГОНОМЕТРИЯ. Часть В и С1»
Формулы приведение
Тригонометрия.Формулы приведения.
Формулы приведения не нужно учить их нужно понять. Понять алгоритм их вывода. Это очень легко!
Возьмем единичную окружность и расставим все градусные меры (0°; 90°; 180°; 270°; 360°) на ней.
Разберем в каждой четверти функции sin(a) и cos(a).
Запомним, что функцию sin(a) смотрим по оси Y, а функцию cos(a) по оси X.
В первой четверти видно, что функция sin(a)>0, потому что ось Y положительна в этой четверти.
И функция cos(a)>0, потому что ось X положительна в этой четверти.
Первую четверть можно описать через градусную меру, как (90-α) или (360+α).
Во второй четверти видно, что функция sin(a)>0, потому что ось Y положительна в этой четверти.
А функция cos(a)<0, потому что ось X отрицательна в этой четверти.
Вторую четверть можно описать через градусную меру, как (90+α) или (180-α).
В третьей четверти видно, что функции sin(a)<0 и cos(a)<0, потому что ось Y и X отрицательны в этой четверти.
Третья четверть можно описать через градусную меру, как (180+α) или (270-α).
В четвертой четверти видно, что функция sin(a)<0, потому что ось Y отрицательна в этой четверти.
А функция cos(a)>0, потому что ось X положительна в этой четверти.
Четвертую четверть можно описать через градусную меру, как (270+α) или (360-α).
Теперь рассмотрим сами формулы приведения.
Запомним простой алгоритм:
1. Четверть. (Всегда смотрите в какой вы четверти находитесь).
2. Знак. (Относительно четверти смотрите положительны или отрицательный функции косинуса или синуса).
3. Если у вас есть в скобочках (90° или π/2) и (270° или 3π/2), то функция меняется.
И так начнем разбирать по четвертям данный алгоритм.
Выясни чему будет равно выражение cos(90-α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции косинуса положительный.
3. В скобочках есть (90° или π/2), то функция меняется с косинуса на синус.
Будет cos(90-α) = sin(α)
Выясни чему будет равно выражение sin(90-α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции синуса положительный.
3. В скобочках есть (90° или π/2), то функция меняется с синуса на косинус.
Будет sin(90-α) = cos(α)
Выясни чему будет равно выражение cos(360+α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции косинуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет cos(360+α) = cos(α)
Выясни чему будет равно выражение sin(360+α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(360+α) = sin(α)
Выясни чему будет равно выражение cos(90+α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции косинуса отрицательный.
3. В скобочках есть (90° или π/2), то функция меняется с косинуса на синус.
Будет cos(90+α) = -sin(α)
Выясни чему будет равно выражение sin(90+α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции синуса положительный.
3. В скобочках есть (90° или π/2), то функция меняется с синуса на косинус.
Будет sin(90+α) = cos(α)
Выясни чему будет равно выражение cos(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции косинуса отрицательный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет cos(180-α) = cos(α)
Выясни чему будет равно выражение sin(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
Четверть вторая.
2. Во второй четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(180-α) = sin(α)
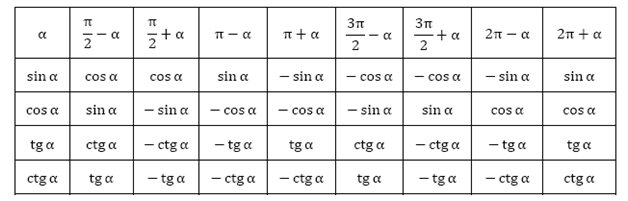
Рассуждаю про третью и четвертую четверть подобным образом составим таблицу:
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Как изменить амплитуду, период и положение графика тангенса или котангенса ies
Исследуйте Книга Купить На Amazon
Вы можете преобразовать график для тангенса и котангенса по вертикали, изменить период, сдвинуть график по горизонтали или сдвинуть его по вертикали. Тем не менее, вы должны выполнять каждое преобразование по одному шагу за раз.
Например, для графика
выполните следующие действия:
Нарисуйте родительский график для касательной.
Уменьшить или растянуть родительский граф.

Вертикальное сжатие составляет 1/2 для каждой точки этой функции, поэтому каждая точка на касательном родительском графике вдвое меньше.
Увидеть вертикальные изменения для графиков тангенса и котангенса сложнее, но они есть. Сконцентрируйтесь на том, что родительский граф имеет
точек., который в преобразованной функции становится
Как вы можете видеть на рисунке, граф действительно вдвое меньше!
График y = (1/2)tan x .
Изменить период.
Константа 1/2 не влияет на период. Почему? Потому что она стоит перед функцией касательной, которая влияет только на вертикальное, а не горизонтальное движение.
Сдвиг графика по горизонтали и вертикали.
Этот график не сдвигается по горизонтали, так как внутри группирующих символов (круглых скобок) функции не добавляется константа. Таким образом, вам не нужно ничего делать горизонтально. -1 в конце функции — это сдвиг по вертикали, перемещающий график вниз на одну позицию.
 На рисунке показан преобразованный граф
На рисунке показан преобразованный графПри необходимости укажите домен и диапазон преобразованной функции.
Поскольку диапазоном функции тангенса являются все действительные числа, преобразование его графика не влияет на диапазон, а только на домен. Область определения функции тангенса состоит не только из действительных чисел из-за асимптот. Однако домен функции из примера не был затронут преобразованиями. Где n — целое число,
Теперь, когда вы нарисовали основы, вы можете построить график функции с изменением периода, как в функции
В нем много пи. Расслабляться! Вы знаете, что на этом графике есть изменение периода, потому что вы видите число в скобках, которое умножается на переменную. Эта константа изменяет период функции, что, в свою очередь, изменяет расстояние между асимптотами. Чтобы график правильно отображал это изменение, вы должны вынести эту константу за скобки. Совершайте трансформацию шаг за шагом:
Нарисуйте исходный график для котангенса.

Уменьшить или растянуть родительский граф.
Никакая константа не умножается снаружи функции; поэтому вы не можете применять усадку или растяжение.
Найти изменение периода.
Вы вычёркиваете
, который влияет на период. Функция теперь читает
Период котангенса родительской функции равен пи. Следовательно, вы должны разделить число пи на коэффициент периода, в данном случае на 2 числа пи. Этот шаг дает вам период для преобразованной функции котангенса:
, так что вы получите период 1/2 для преобразованной функции. График этой функции начинает повторяться с 1/2, что отличается от пи/2, поэтому будьте осторожны, когда маркируете свой график.
Этот период не является дробью числа пи; это просто рациональное число. Когда вы получаете рациональное число, вы должны изобразить его как таковое. На рисунке показан этот шаг.
График y ( x ) = кроватка 2pi x показывает период 1/2.

Определите горизонтальное и вертикальное смещение.
Поскольку вы уже учли постоянную периода, вы можете видеть, что сдвиг по горизонтали составляет 1/4 влево. На следующем рисунке это преобразование показано на графике.
Никакая константа не добавляется и не вычитается из этой функции снаружи, поэтому график не испытывает вертикального смещения.
Преобразованный граф y ( x ) = кроватка 2pi ( x + 1/4).
При необходимости укажите домен и диапазон преобразованной функции.
Горизонтальный сдвиг влияет на домен этого графика. Чтобы найти первую асимптоту, установите
(устанавливая сдвиг периода равным исходной первой асимптоте). Вы обнаружите, что x = –1/4 – это ваша новая асимптота. График повторяется каждые 1/2 радиана из-за его периода. Итак, домен
., где n
Эту статью можно найти в категории:
- Предварительное исчисление,
Давайте изучим графики функций тангенса и котангенса
¶График \(y=\tan(t)\).
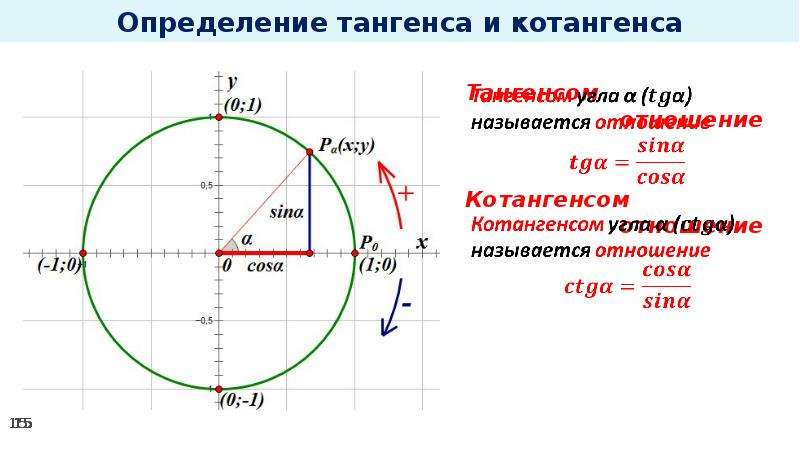
Изучение влияния факторной идентичности \(\tan(t)=\frac{\sin(t)}{\cos(t)}\) на поведение функции тангенса даст нам много информации о graph \(y=\tan(t)\text{.}\) Давайте сделаем некоторые начальные наблюдения.
Везде есть \(t\)-перехват \(\sin(t)=0\text{.}\) Это дает нам следующие \(t\)-перехваты.
\begin{уравнение*} …,\,(-2\pi,0),\,(-\pi,0),\,(0,0),\,(\pi,0),\,(2\pi,0 ),\,… \end{уравнение*}
Вертикальная асимптота при каждом значении \(t\), где \(\cos(t)=0\text{.}\) Это дает нам следующие вертикальные асимптоты.
\begin{уравнение*} …,\,t=-\frac{5\pi}{2},\,t=-\frac{3\pi}{2},\,t=-\frac{\pi}{2} ,\,t=\frac{\pi}{2},\,t=\frac{3\pi}{2},\,t=\frac{5\pi}{2},\,… \end{уравнение*}
\(y\)-координата точки на графике \(y=\tan(t)\) равна \(1\) или \(-1\) при каждом значении \(t\) где функции синуса и косинуса имеют равные или противоположные значения. Это дает нам следующие моменты.
\begin{уравнение*} .
 ..,\,\влево(-\frac{5\pi}{4},-1\вправо),\,\влево(-\frac{3\pi}{4},1\вправо),\ ,\left(-\frac{\pi}{4},-1\right),\,\left(\frac{\pi}{4},1\right),\,\left(\frac{3 \pi}{4},-1\вправо),\,\влево(\frac{5\pi}{4},1\вправо),\,…
\end{уравнение*}
..,\,\влево(-\frac{5\pi}{4},-1\вправо),\,\влево(-\frac{3\pi}{4},1\вправо),\ ,\left(-\frac{\pi}{4},-1\right),\,\left(\frac{\pi}{4},1\right),\,\left(\frac{3 \pi}{4},-1\вправо),\,\влево(\frac{5\pi}{4},1\вправо),\,…
\end{уравнение*}
Давайте продолжим и построим то, что мы обсуждали до сих пор. Это показано на рисунке 16.5.1.
Рисунок 16.5.1. Точки и асимптоты для графика \(y=\tan(t)\)Знак значения тангенса может меняться только тогда, когда \(t\) перемещается из одного квадранта в другой. На рис. 16.5.1 это происходит на асимптотах и \(t\)-перехватах. Мы можем использовать этот факт, чтобы сделать вывод о поведении функции, когда \(t\) приближается к асимптоте с любой стороны, что дает нам график функции, показанный на рисунке 16.5.2.
Мы должны сделать так, чтобы в отличие от функций синуса и косинуса период \(y=\tan(t)\) составлял всего \(\pi\text{.}\)
График \(y=\cot(t)\).
Изучение влияния факторной идентичности \(\cot(t)=\frac{\cos(t)}{\sin(t)}\) на поведение функции котангенса даст нам много информации о graph \(y=\cot(t)\text{. }\) Давайте сделаем некоторые начальные наблюдения.
}\) Давайте сделаем некоторые начальные наблюдения.
Везде есть \(t\)-перехват \(\cos(t)=0\text{.}\) Это дает нам следующие \(t\)-перехваты.
\begin{уравнение*} …,\,\влево(-\frac{5\pi}{2},0\вправо),\,\влево(-\frac{3\pi}{2},0\вправо),\, \left(-\frac{\pi}{2},0\right),\,\left(\frac{3\pi}{2},0\right),\,\left(\frac{5\ pi}{2},0\вправо),\,\влево(\frac{7\pi}{2},0\вправо),\,… \end{уравнение*}
Вертикальная асимптота при каждом значении \(t\), где \(\sin(t)=0\text{.}\) Это дает нам следующие вертикальные асимптоты.
\begin{уравнение*} …,\,t=-2\pi,\,t=-\pi,\,t=0,\,t=\pi,\,t=2\pi,\,t=3\pi, \,… \end{уравнение*}
\(y\)-координата точки на графике \(y=\cot(t)\) равна \(1\) или \(-1\) при каждом значении \(t\) где функции синуса и косинуса имеют равные или противоположные значения. Это дает нам следующие моменты.
\begin{уравнение*} …,\,\влево(-\frac{5\pi}{4},-1\вправо),\,\влево(-\frac{3\pi}{4},1\вправо),\ ,\left(-\frac{\pi}{4},-1\right),\,\left(\frac{\pi}{4},1\right),\,\left(\frac{3 \pi}{4},-1\вправо),\,\влево(\frac{5\pi}{4},1\вправо),\,.
 ..
\end{уравнение*}
..
\end{уравнение*}
Давайте продолжим и построим то, что мы обсуждали до сих пор. Это показано на рисунке 16.5.3.
Знак значения котангенса может меняться только тогда, когда \(t\) перемещается из одного квадранта в другой. На рис. 16.5.3 это происходит на асимптотах и \(t\)-перехватах. Мы можем использовать этот факт, чтобы сделать вывод о поведении функции, когда \(t\) приближается к асимптоте с любой стороны, что дает нам график функции, показанный на рисунке 16.5.4.
Рисунок 16.5.4. \(y=\cot(t)\)Следует отметить, что, как и у функции тангенса, период \(y=\cot(t)\) равен \(\pi\text{.}\)
Давайте двигаться дальше и обсудить графические преобразования, произведенные над \(y=\tan(t)\) и \(y=\cot(t)\text{.}\)
Период функции тангенса или котангенса.
Как и в случае с функцией синуса и косинуса, если \(\omega\) ненулевая константа, не равная \(1\) или \(-1\text{,}\), то график \ (y=\tan(\omega t)\) или \(y=\cot(\omega t)\) будут отличаться от периодов графиков \(y=\tan(t)\) и \( y=\cot(t)\text{.
Пример 16.5.5.
Нарисуйте три периода функции \(y=\tan(2t)\text{.}\)
Решение
Мы видим, что \(\omega=2\text{,}\) поэтому период этой функции равен \(\frac{\pi}{2}\text{.}\)
Когда есть нет смещения по горизонтали, функция касательной имеет вертикальные асимптоты по половине периода как слева, так и справа от оси \(y\). В данном случае это означает, что и \(t=-\frac{\pi}{4}\), и \(t=\frac{\pi}{4}\) являются вертикальными асимптотами. Каждый раз, когда мы перемещаемся на один полный период влево или вправо от вертикальной асимптоты, мы сталкиваемся с другой вертикальной асимптотой. Это означает, что и \(t=-\frac{3\pi}{4}\), и \(t=\frac{3\pi}{4}\) являются вертикальными асимптотами. Эти вертикальные асимптоты показаны на рисунке 16.
Существует \(t\)-отрезок на полпути между каждой парой асимптот. В четверти периода слева от каждого \(t\)перехвата находится точка с \(y\)-координатой \(-1\text{.}\) В четверти периода справа от на каждом \(t\)-перехвате есть точка с \(y\)-координатой \(1\text{.}\). Все эти точки добавлены на график на рисунке 16.5.7.
Рисунок 16.5.7. Точки и асимптоты для графика \(y=\tan(2t)\)Осталось только соединить точки таким образом, чтобы продемонстрировать асимптотическое поведение функции. Это показано на рисунке 16.5.8.
Рисунок 16.5.8. Точки и асимптоты для графика \(y=\tan(2t)\)Пример 16.5.9.
Нарисуйте три периода функции \(y=\cot\left(\frac{\pi}{3}\right)\text{.}\)
Решение
Начнем с того, что \(\frac{t}{3}=\frac{1}{3}t\text{,}\) поэтому \(\omega=\frac{1}{3} \text{. }\) Период для \(y=\cot\left(\frac{pi}{3}\right)\) получен ниже.
}\) Период для \(y=\cot\left(\frac{pi}{3}\right)\) получен ниже.
\begin{выравнивание*} \ гидроразрыва {\ пи} {\ абс {\ омега}} \ amp = \ гидроразрыва {\ пи} {\ гидроразрыва {1} {3}} \\ \amp=\frac{\pi}{1} \cdot \frac{3}{1} \end{align*}
При отсутствии смещения по горизонтали ось \(y\) представляет собой вертикальную асимптоту графика функции котангенса. Каждый раз, когда мы перемещаемся на один полный период влево от вертикальной асимптоты, мы сталкиваемся с другой вертикальной асимптотой. В данном случае это означает, что \(t=-3\pi\text{,}\) \(t=3\pi\text{,}\) и \(t=6\pi\) также являются вертикальными асимптотами. Эти вертикальные асимптоты показаны на рисунке 16.5.10. Обратите внимание, что масштаб по оси \(t\) равен \(\frac{3\pi}{2}\text{.}\). Это потому, что \(\frac{3\pi}{2}\) составляет половину периода.
Рисунок 16.5.10. Вертикальные асимптоты для графика \(y=\cot\left(\frac{\pi}{3}\right)\) На полпути между каждой парой асимптот есть \(t\)-отрезок. В четверти периода слева от каждого \(t\)перехвата находится точка с \(y\)-координатой \(1\text{. }\) В четверти периода справа от каждого \(t\)-перехват есть точка с \(y\)-координатой \(-1\text{.}\) Все эти точки были добавлены на график на рисунке 16.5.7.
}\) В четверти периода справа от каждого \(t\)-перехват есть точка с \(y\)-координатой \(-1\text{.}\) Все эти точки были добавлены на график на рисунке 16.5.7.
Осталось только соединить точки таким образом, чтобы продемонстрировать асимптотическое поведение функции. Это показано на рисунке 16.5.12.
Рисунок 16.5.12. \(y=\cot\left(\frac{\pi}{3}\right)\)Горизонтальный сдвиг функции тангенса или котангенса.
Как и для любой другой функции, ненулевая константа \(h\) в выражении \(y=\tan(\omega(t-h))\) или \(y=\cot(\omega(t-h))\) влияет на горизонтальный сдвиг \(\abs{h}\) относительно их родительской функции (\(y=\tan(\omega t)\) или \(y=\cot(\omega t)\)). Когда \(h\) положителен, сдвиг вправо, а когда \(h\) отрицателен, сдвиг влево.
Например, \(y=\tan\left(t-\frac{\pi}{3}\right)\) лежит \(\frac{\pi}{3}\) справа от \(y =\tan(t)\), тогда как \(y=\tan\left(t+\frac{\pi}{3}\right)\) лежит \(\frac{\pi}{3}\) слева из \(y=\tan(t)\text{.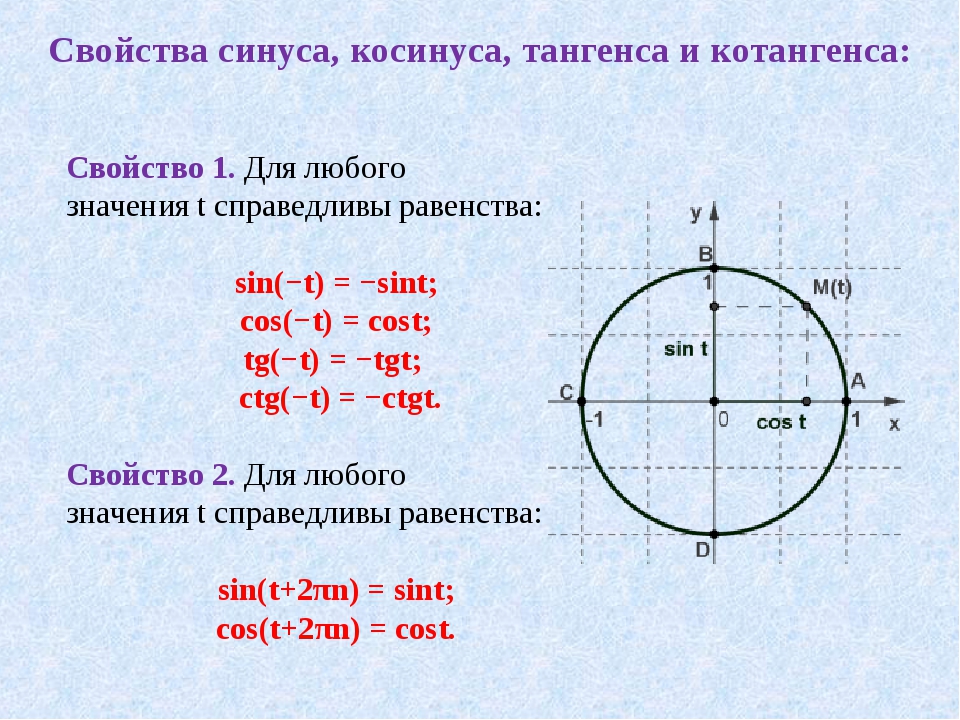 }\)
}\)
Давайте посмотрим на пару примеров графического процесса при горизонтальном смещении.
Пример 16.5.13.
Эскиз трех периодов функции \(y=\tan\left(t-\frac{\pi}{3}\right)\text{.}\)
Решение
Функция \(y=\tan(t)\) имеет вертикальную асимптоту в точке \(t=-\frac{3\pi}{2}\text{,}\) \(t=-\frac {\pi}{2}\text{,}\) \(t=\frac{\pi}{2}\text{,}\) и \(t=\frac{3\pi}{2}\ text{.}\) Функция \(y=\tan\left(t-\frac{\pi}{3}\right)\) лежит \(\frac{\pi}{3}\) справа функции \(y=\tan(t)\text{.}\) Влияние, которое это оказывает на расположение вертикальных асимптот графика \(y=\tan\left(t-\frac{\pi {3}\right)\) вычисляется ниже
\begin{выравнивание*} t\amp=-\frac{3\pi}{2}+\frac{\pi}{3}\\ t\amp=-\frac{7\pi}{6} \end{выравнивание*}
\begin{выравнивание*} t \ amp = — \ frac {\ pi} {2} + \ frac {\ pi} {3} \\ т \ амп = — \ гидроразрыва {\ пи} {6} \end{выравнивание*}
\begin{выравнивание*} t \ amp = — \ frac {\ pi} {2} + \ frac {\ pi} {3} \\ t\amp=-\frac{5\pi}{6} \end{выравнивание*}
\begin{выравнивание*} t \ amp = — \ frac {\ pi} {2} + \ frac {\ pi} {3} \\ t\amp=-\frac{11\pi}{6} \end{align*}
Другим способом, которым мы могли бы вычислить расположение этих вертикальных асимптот, является применение сдвига к \(t=\frac{\pi}{2}\) (в результате получается \(t= \frac{5\pi}{6})\), а затем многократно добавляя или вычитая полную точку (в данном случае \(\pi\)) к \(\frac{5\pi}{6}\text{. }\)
}\)
Независимо от стратегии определения вертикальных асимптот, в данном случае они равны \(t=-\frac{7\pi}{6}\text{,}\) \(t=-\frac{\pi {6}\text{,}\) \(t=\frac{5\pi}{6}\text{,}\) и \(t=\frac{11\pi}{6}\text{ .}\) Эти асимптоты показаны на рисунке 16.5.14. Обратите внимание, что средняя точка между каждой парой последовательных асимптот также была определена. Это точки, в которых касательные кривые будут пересекать ось \(t\).
Рисунок 16.5.14. Асимптоты для графика \(y=\tan\left(t-\frac{\pi}{6}\right)\)На полпути между каждой парой асимптот есть \(t\)-отрезок. В четверти периода слева от каждого \(t\)перехвата находится точка с \(y\)-координатой \(-1\text{.}\) В четверти периода справа от на каждом \(t\)-перехвате есть точка с \(y\)-координатой \(1\text{.}\). Все эти точки добавлены на график на рис. 16.5.15.
Рисунок 16.5.15. Точки и асимптоты для графика \(y=\tan\left(t-\frac{\pi}{6}\right)\) Все, что осталось сделать, это соединить точки таким образом, чтобы продемонстрировать асимптотику поведение функции. Это показано на рисунке 16.5.16.
Это показано на рисунке 16.5.16.
Пример 16.5.17.
Эскиз трех периодов функции \(y=\cot\left(2t+\frac{\pi}{2}\right)\text{.}\)
Решение
Начнем с того, что период этой функции равен \(\frac{\pi}{2}\text{.}\). вдали от \(t\) и \(\frac{\pi}{2}\text{.}\) Это делается ниже.
\begin{уравнение*} \ кроватка \ влево (2t + \ frac {\ pi} {2} \ справа) = \ кроватка \ влево (2 \ влево (t + \ frac {\ pi} {4} \ вправо) \ вправо) \end{уравнение*}
Теперь мы можем видеть сдвиг влево на \(\frac{\pi}{4}\text{.}\)
Линии \(t=-\frac{\pi}{2}\ text{,}\) \(t=0\text{,}\) \(t=\frac{\pi}{2}\text{,}\) и \(t=\pi\) все вертикальны асимптоты для функции \(y=\cot(2t)\text{.}\) Функция \(y=\cot\left(2t+\frac{\pi}{2}\right)\) лежит \(\ frac{\pi}{4}\) слева от \(y=\cot(2t)\text{,}\), поэтому он имеет вертикальные асимптоты \(t=-\frac{3\pi}{4 }\text{,}\) \(t=-\frac{\pi}{4}\text{,}\) \(t=\frac{\pi}{4}\text{,}\) и \(t=\frac{3\pi}{4}\text{. }\) Эти асимптоты показаны на рисунке 16.5.18. Обратите внимание, что средняя точка между каждой парой последовательных асимптот также была определена. Это точки, в которых касательные кривые будут пересекать ось \(t\).
}\) Эти асимптоты показаны на рисунке 16.5.18. Обратите внимание, что средняя точка между каждой парой последовательных асимптот также была определена. Это точки, в которых касательные кривые будут пересекать ось \(t\).
На полпути между каждой парой асимптот есть \(t\)-перехват. В четверти периода слева от каждого \(t\)перехвата находится точка с \(y\)-координатой \(-1\text{.}\) В четверти периода справа от на каждом \(t\)-перехвате есть точка с \(y\)-координатой \(1\text{.}\). Все эти точки добавлены на график на рис. 16.5.19.
Рисунок 16.5.19. Точки и асимптоты для графика \(y=\cot\left(2t+\frac{\pi}{2}\right) \)Осталось только соединить точки таким образом, чтобы продемонстрировать асимптотическое поведение функции. Это показано на рисунке 16.5.20.
Рисунок 16.5.20. \(y=\cot\left(2t+\frac{\pi}{2}\right) \)вертикальных растяжений, сжатий, отражений и сдвигов.
Вертикальные растяжения, сжатия, отражения и сдвиги работают точно так же для функций тангенса и котангенса, как и для любой другой функции. А именно:
А именно:
График \(y=A \tan(t)\text{,}\) \(A \neq 0\text{,}\) \(A \neq \pm 1\text{,}\ ) является либо вертикальным растяжением, либо вертикальным сжатием графика \(y=\tan(t)\text{.}\) Если \(\abs{A} \gt 1\text{,}\) эффект является отклонением от оси \(t\) в \(A\text{.}\) Если \(\abs{A} \lt 1\text{,}\) эффект представляет собой вертикальный сжатие по оси \(t\) в \(\abs{A}\text{.}\) Кроме того, если \(A \lt 0\text{,}\) кривые \(y =\tan(t)\) отражаются поперек оси \(t\).
График \(y=\tan(t)+k\text{,}\) \(k \neq 0\text{,}\) является вертикальным сдвигом графика \(y=\tan (t)\text{.}\) Когда \(k \gt 0\text{,}\) сдвиг вверх на \(k\text{.}\) Когда \(k \lt 0\text{, }\) сдвиг вниз на \(\abs{k}\text{.}\)
Давайте рассмотрим пример.
Пример 16.5.21.
Зарисовать три периода функции \(y=-3\cot(t)+2\text{.}\)
Решение
Говоря словами, графические преобразования, затрагивающие родительскую функцию \(y=\cot(t)\), являются растяжением в \(3\text{,}\) раз отражения через \(t \)-ось и, наконец, сдвиг вверх на \(2\text{. }\)
}\)
При построении графика \(y=\cot(t)\text{,}\) между каждой парой последовательных пар асимптот есть три ключевые точки. Точки слева направо имеют вид
\begin{equation*} (t,1),\,\,(t,0),\,\,(t,-1). \end{equation*}
На графике \(y=-3\cot(2)+2\) эти точки становятся
\begin{equation*} (t,3(1)+2),\,\,(t,3(0)+2),\,\,(t,3(-1)+2) \end{equation*}
, которые упрощаются до
\begin{equation*} (t,5),\,\,(t,2),\,\,(t,-2). \end{уравнение*}
Поскольку в горизонтальном направлении изменений нет, мы знаем, что \(t=-\pi\text{,}\) \(t=0\text{,}\) \(t=\pi\text{ ,}\) и \(t=2\pi\) — вертикальные асимптоты функции. Эти асимптоты и вышеупомянутые точки представлены на рисунке 16.5.22.
Рисунок 16.5.22. Точки и асимптоты для графика \(y=-3\cot(t)+2\)Все, что осталось сделать, это соединить точки таким образом, чтобы продемонстрировать асимптотическое поведение функции. Это показано на рисунке 16.5.23.
Рисунок 16.5.23. \(у=-3\кот(т)+2\)Упражнения Упражнения
Нарисуйте три периода каждой функции.
1.
\(у=\кроватка(3т)\)
Решение
Единственным преобразованием, затрагивающим функцию \(y=\cot(t)\), является изменение периода. Новый период равен \(\frac{\pi}{3}\text{.}\) Строки \(t=-\frac{\pi}{3}\text{,}\) \(t=0 \text{,}\) \(t=\frac{\pi}{3}\text{,}\) и \(t=\frac{2\pi}{3}\) будут вертикальными асимптотами для график. На полпути между каждой последовательной парой асимптот кривая будет пересекать ось \(t\). В четверти периода левее каждого \(t\)-перехвата находится точка с \(y\)-координатой \(1\) и в четверти периода правее каждого \(t\) )-перехват есть точка с \(y\)-координатой \(-1\text{.}\) Все это показано на рисунке 16.5.24.
Рисунок 16.5.24. Точки и асимптоты для графика \(y=\cot(3t)\)Все, что осталось сделать, это соединить точки таким образом, чтобы продемонстрировать асимптотическое поведение функции. Это показано на рисунке 16.5.24.
Рисунок 16.5.25. \(y=\cot(3t)\)2.
\(y=\tan\left(t-\frac{\pi}{8}\right)\)
Решение
Единственным преобразованием, затрагивающим график \(y=\tan(t)\), является сдвиг вправо \(\frac{\pi}{8}\text{. }\) Эффект этого на вертикальных асимптотах вычисляется ниже.
}\) Эффект этого на вертикальных асимптотах вычисляется ниже.
\begin{выравнивание*} t\amp=-\frac{3\pi}{2}+\frac{\pi}{8}\\ t\amp=-\frac{11\pi}{8} \end{выравнивание*}
\begin{выравнивание*} t \ amp = — \ frac {\ pi} {2} + \ frac {\ pi} {8} \\ t\amp=-\frac{3\pi}{8} \end{выравнивание*}
\begin{выравнивание*} t\amp=\frac{\pi}{2}+\frac{\pi}{8}\\ t\amp=\frac{5\pi}{8} \end{выравнивание*}
\begin{выравнивание*} t\amp=\frac{3\pi}{2}+\frac{\pi}{8}\\ t\amp=-\frac{13\pi}{8} \end{align*}
На полпути между каждой последовательной парой асимптот кривая пересекает ось \(t\). В четверти периода слева от каждого \(t\)-перехвата находится точка с \(y\)-координатой \(-1\) и в четверти периода справа от каждого \(t \)-перехват есть точка с \(y\)-координатой \(1\text{.}\) Все это показано на рисунке 16.5.26.
Рисунок 16.5.26. Точки и асимптоты для графика \(y=\tan\left(t-\frac{\pi}{8}\right)\) Все, что осталось сделать, это соединить точки таким образом, чтобы продемонстрировать асимптотику поведение функции. Это показано на рисунке 16.5.27.
Это показано на рисунке 16.5.27.
3.
\(y=\frac{2}{3}\cot(t)-2\)
Решение
Все модификации графика \(y=\cot(t)\) выполняются в вертикальном направлении. Происходит вертикальное сжатие в \(\frac{2}{3}\) с последующим сдвигом вниз в 2,9 раза.0005
При построении графика \(y=\cot(t)\text{,}\) между каждой парой последовательных пар асимптот есть три ключевые точки. Точки слева направо имеют вид
\begin{equation*} (t,1),\,\,(t,0),\,\,(t,-1). \end{equation*}
На графике \(y=y=\frac{2}{3}\cot(t)-2\) эти точки становятся
\begin{equation*} (t,\frac{2}{3}(1)-2),\,\,(t,\frac{2}{3}(0)-2),\,\,(t,\frac{ 2}{3}(-1)-2) \end{equation*}
, которые упрощаются до
\begin{equation*} (t,-\frac{4}{3}),\,\,(t,-2),\,\,(t,-\frac{8}{3}). \end{уравнение*}
Давайте построим наши асимптоты, \(t=-\pi\text{,}\) \(t=0\text{,}\) \(t=\pi\text{,}\) и \(t=2\pi\text{.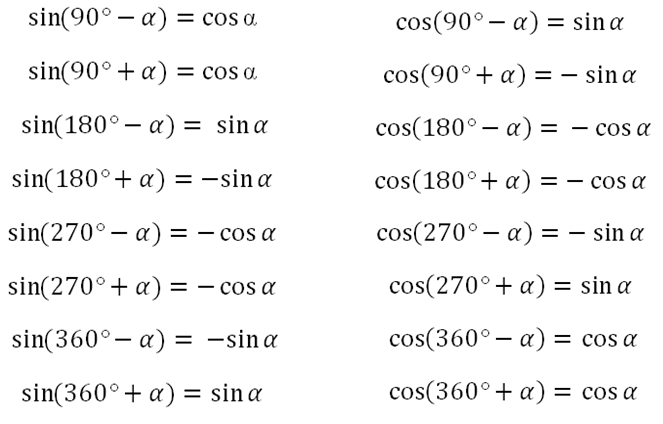 }\) Давайте также нанесем точки, о которых говорилось выше. Это показано на рисунке 16.5.28.
}\) Давайте также нанесем точки, о которых говорилось выше. Это показано на рисунке 16.5.28.
Все, что осталось сделать, это соединить точки таким образом, чтобы продемонстрировать асимптотическое поведение функции . Это показано на рисунке 16.5.29.
Рисунок 16.5.29. \(y=\frac{2}{3}\cot(t)-2\)4.
\(y=-\tan\left(3\left(t+\frac{\pi}{6}\right)\right)\)
Решение
Начнем с того, что период равен \(\frac{\pi}{3}\text{.}\)
Линии \(y=-\frac{3\pi}{2}\ text{,}\) \(y=-\frac{\pi}{2}\text{,}\) \(y=\frac{\pi}{2}\text{,}\) и \( y=\frac{3\pi}{2}\) — все вертикальные асимптоты для графика \(y=\tan(t)\text{.}\). Все эти линии должны быть сжаты по направлению к \(y \) по оси в \(\frac{1}{3}\text{.}\) Результирующие вертикальные асимптоты для графика \(y=\tan(3t)\) равны \(y=-\ frac{\pi}{2}\text{,}\) \(y=-\frac{\pi}{6}\text{,}\) \(y=\frac{\pi}{6}\ text{,}\) и \(y=\frac{\pi}{2}\text{. }\) Все эти строки сдвинуты влево на \(\frac{\pi}{6}\) на график \(y=-\tan\left(3\left(t+\frac{\pi}{6}\right)\right)\text{.}\) Эффект, который это оказывает на вертикальные асимптоты, вычисляется ниже.
}\) Все эти строки сдвинуты влево на \(\frac{\pi}{6}\) на график \(y=-\tan\left(3\left(t+\frac{\pi}{6}\right)\right)\text{.}\) Эффект, который это оказывает на вертикальные асимптоты, вычисляется ниже.
\begin{выравнивание*} t \ amp = — \ frac {\ pi} {2} — \ frac {\ pi} {6} \\ t\amp=-\frac{2\pi}{3} \end{выравнивание*}
\begin{выравнивание*} t \ amp = — \ frac {\ pi} {6} — \ frac {\ pi} {6} \\ т \ амп = — \ гидроразрыва {\ пи} {3} \end{выравнивание*}
\begin{выравнивание*} t\amp=\frac{\pi}{6}-\frac{\pi}{6}\\ т\ампер=0 \end{выравнивание*}
\begin{выравнивание*} t\amp=\frac{\pi}{2}-\frac{\pi}{6}\\ т \ амп = \ гидроразрыва {\ пи} {3} \end{align*}
Давайте построим вертикальные асимптоты. Это показано на рисунке 16.5.30.
Рисунок 16.5.30. Асимптоты для графика \(y=-\tan\left(3\left(t+\frac{\pi}{6}\right)\right)\) Существует кривая, пересекающая ось \(t\) на полпути между каждой парой последовательных асимптот. На графике \(y=\tan(t)\) есть точка в четверти периода слева от каждого \(t\)-перехвата с \(y\)-координатой \(1 \) и точка на четверть периода справа от каждого \(t\)-перехвата с \(y\)-координатой \(1\text{. }\) Поскольку функция, которую мы рисуем, имеет отрицательный знак перед выражением касательной, точки с \(y\)-координатой \(1\) попадут левее \(t\)-перехвата, а точки с \(y\)-координатой )-координата \(-1\) будет падать правее \(t\)-перехватов. Эти точки были добавлены на график на рисунке 16.5.31.
}\) Поскольку функция, которую мы рисуем, имеет отрицательный знак перед выражением касательной, точки с \(y\)-координатой \(1\) попадут левее \(t\)-перехвата, а точки с \(y\)-координатой )-координата \(-1\) будет падать правее \(t\)-перехватов. Эти точки были добавлены на график на рисунке 16.5.31.
Осталось только соединить точки способом, демонстрирующим асимптотическое поведение функции. Это показано на рисунке 16.5.32.
Рисунок 16.5.32. Точки и асимптоты для графика \(y=-\tan\left(3\left(t+\frac{\pi}{6}\right)\right)\)5.
\(y=\cot\left(\frac{t}{2}-\frac{\pi}{4}\right)-3\)
Решение
Сначала заметим, что \(\frac{t}{2}=\frac{1}{2}t\text{,}\), поэтому значение \(\omega\) равно \(\frac {1}{2}\text{.}\) Период рассчитывается ниже.
\begin{выравнивание*} \ гидроразрыва {\ пи} {\ абс {\ омега}} \ amp = \ гидроразрыва {\ пи} {\ гидроразрыва {1} {2}} \\ \amp=\frac{\pi}{1} \cdot \frac{2}{1}\\ \амп=2\пи \end{align*}
Прежде чем мы сможем установить сдвиг по горизонтали, нам нужно разложить \(\frac{1}{2}\) как на \(t\), так и на \(\frac{\pi}{ 4}\text{. }\) Это делается ниже.
}\) Это делается ниже.
\begin{уравнение*} \cot\left(\frac{t}{2}-\frac{\pi}{4}\right)-3=\cot\left(\frac{1}{2}\left(t-\frac{ \pi}{2}\справа)\справа)-3 \end{equation*}
Теперь мы можем видеть, что имеет место сдвиг вправо \(\frac{\pi}{2}\text{.}\)
Строки \(y=-2\pi\text{,}\) \(y=0\text{,}\) \(y=2\pi\text{,}\) и \(y= 4\pi\) все вертикальные асимптоты на графике \(y=\cot\left(\frac{t}{2}\right)\text{.}\) На графике \(y=\cot\ left(\frac{t}{2}-\frac{\pi}{4}\right)-3\) все эти асимптоты нужно сдвинуть вправо на \(\frac{\pi}{2}\text {.}\) Результирующие асимптоты равны \(y=-\frac{3\pi}{2}\text{,}\) \(y=\frac{\pi}{2}\text{,}\ ) \(y=\frac{5\pi}{2}\text{,}\) и \(y=\frac{9\pi}{2}\text{.}\) Эти асимптоты представлены на рис. 16.5.33.
Рисунок 16.5.33. Асимптоты для графика \(y=\cot\left(\frac{t}{2}-\frac{\pi}{4}\right)-3\) Между асимптотами через равные промежутки в один- четверть периода координаты \(y\) немодифицированной функции котангенса следуют схеме \(1\text{,}\) \(0\text{,}\) \(-1\text{.

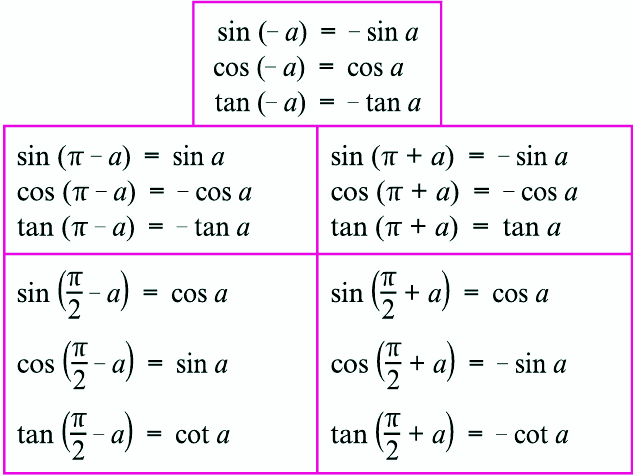
 На рисунке показан преобразованный граф
На рисунке показан преобразованный граф
 ..,\,\влево(-\frac{5\pi}{4},-1\вправо),\,\влево(-\frac{3\pi}{4},1\вправо),\ ,\left(-\frac{\pi}{4},-1\right),\,\left(\frac{\pi}{4},1\right),\,\left(\frac{3 \pi}{4},-1\вправо),\,\влево(\frac{5\pi}{4},1\вправо),\,…
\end{уравнение*}
..,\,\влево(-\frac{5\pi}{4},-1\вправо),\,\влево(-\frac{3\pi}{4},1\вправо),\ ,\left(-\frac{\pi}{4},-1\right),\,\left(\frac{\pi}{4},1\right),\,\left(\frac{3 \pi}{4},-1\вправо),\,\влево(\frac{5\pi}{4},1\вправо),\,…
\end{уравнение*}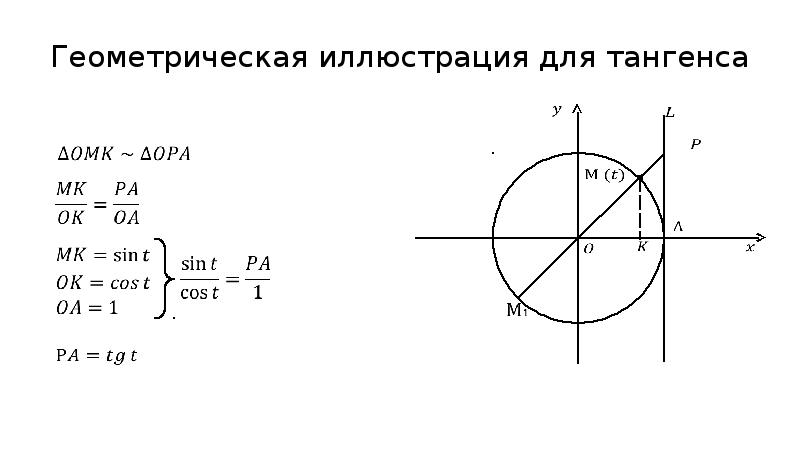 ..
\end{уравнение*}
..
\end{уравнение*}