Когда логарифм равен 0: Формулы и свойства логарифмов, основные формулы логарифмов с примерами

Определение логарифма, логарифм произведения, степени, частного. Решение показательных и логарифмических уравнений и неравенств

Страницы работы

10 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

ОПРЕДЕЛЕНИЕ ЛОГАРИФМА. ЛОГАРИФМ ПРОИЗВЕДЕНИЯ, СТЕПЕНИ, ЧАСТНОГО.

          Определение. Логарифмом положительного числа  по основанию  () называется показатель степени, в которую надо возвести , чтобы получить .

В записи  число  является основанием степени, — показателем,  — степенью. Число - это показатель степени, в которую надо возвести основание , чтобы получить число . Следовательно, - это логарифм числа  по основанию :

  .

Можно сказать, что формулы  и  равносильны, выражают одну и ту же связь между числами ,  и  (при  > 0,  ¹ 1,  > 0). Число - произвольно, никаких ограничений на показатель степени не накладывается.

Равенство

 

называется основным логарифмическим тождеством.

Представляя в равенстве выражение  в виде степени, получим ещё одно тождество

 .

Теорема. Для чисел  > 0,  > 0,  > 0,  ¹ 1 верны следующие тождества, выражающие свойства логарифмов:

1) , т. е. логарифм произведения равен сумме логарифмов множителей;

2) , т. е. логарифм дроби равен разности логарифмов числителя и знаменателя;

3)  , т. е. логарифм степени равен показателю степени, умноженному на логарифм основания.

Доказательство. 1) Пусть , . По основному логарифмическому тождеству , . Перемножим эти равенства: . По свойству степеней , т.

е. . По определению логарифма

, т. е.

, что и требовалось доказать.

2) Пусть , . По основному логарифмическому тождеству: , . Тогда

.

По свойству степеней

  , т. е.

.

По определению логарифма

, т. е.

, что и требовалось доказать.

3) Пусть . По основному логарифмическому тождеству . Тогда

.

По определению логарифма

, т. е. . Теорема доказана.

ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ. НАТУРАЛЬНЫЕ ЛОГАРИФМЫ. ФОРМУЛА ПЕРЕХОДА ОТ ОДНОГО ОСНОВАНИЯ К ДРУГОМУ.

Если в равенстве  основание  равно 10, то логарифм называется десятичным и обозначается . Если же в равенстве  основание  равно , где  - бесконечная непериодическая десятичная дробь, то логарифм называется натуральным и обозначается . Свойства десятичных и натуральных логарифмов аналогичны свойствам обыкновенных логарифмов и они отличаются лишь формой записи.

   

Рассмотрим некоторые свойства логарифмов:

1. Логарифм единицы по любому основанию равен нулю, т. е. .
2. Если логарифм некоторого числа равен нулю, то это число равно единице, т. е. когда , то .
3. Если число и основание логарифма равны между собой, то логарифм равен единице, т. е. . В частности , .
4. Если логарифм некоторого числа равен единице, то это число равно основанию логарифма, т. е. если , то .
5. Если два числа имеют один и тот же логарифм при данном основании, то эти числа равны между собой, т. е. из равенства  следует .
6. Если число и основание логарифма одновременно больше или меньше единицы, то логарифм положителен, т. е. если  (или ) то .
7. Если число и основание логарифма расположены по разные стороны от единицы, то логарифм отрицателен, т. е. если  а  или  а , то .
8. . В частности , .
9. Если основание логарифма больше единицы, то большему из двух положительных чисел соответствует больший логарифм, т. е. если  и , то .
10. Если основание логарифма меньше единицы, то большему из двух положительных чисел соответствует меньший логарифм, т. е. если  и , то .

Между логарифмами некоторого положительного числа с двумя разными основаниями и существует зависимость, которую можно выразить формулой

.

Эту формулу называют формулой перехода от одного основания к другому

.  В частности из неё следует, что  или , кроме того , .

ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ ВЫРАЖЕНИЙ, СОДЕРЖАЩИХ ЛОГАРИФМЫ.

Используя свойства логарифмов, можно представить логарифм некоторого выражения, составленного из положительных чисел с помощью операций умножения, деления и возведения в степень, в виде суммы логарифмов входящих в него чисел.

Такое преобразование называют логарифмированием.

     Пример 1. Прологарифмировать выражение по основанию  ().

 .

Решение. Применяя свойства логарифмов, получим

.

Во многих случаях приходится решать обратную задачу, т. е. находить выражение, логарифм которого представлен через логарифмы некоторых чисел. Такое преобразование называют

потенцированием.

     Пример 2. Найти , если

.

Решение.  Используя свойства логарифмов, получаем:

. Таким образом . Отсюда .

РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ И ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ.

Информация о работе

Скачать файл

Выбери свой ВУЗ

• АлтГТУ 419
• АлтГУ 113
• АмПГУ 296
• АГТУ 267
• БИТТУ 794
• БГТУ «Военмех» 1191
• БГМУ 172
• БГТУ 603
• БГУ 155
• БГУИР 391
• БелГУТ 4908
• БГЭУ 963
• БНТУ 1070
• БТЭУ ПК 689
• БрГУ 179
• ВНТУ 120
• ВГУЭС 426
• ВлГУ 645
• ВМедА 611
• ВолгГТУ 235
• ВНУ им. Даля 166
• ВЗФЭИ 245
• ВятГСХА 101
• ВятГГУ 139
• ВятГУ 559
• ГГДСК 171
• ГомГМК 501
• ГГМУ 1966
• ГГТУ им. Сухого 4467
• ГГУ им. Скорины 1590
• ГМА им. Макарова 299
• ДГПУ 159
• ДальГАУ 279
• ДВГГУ 134
• ДВГМУ 408
• ДВГТУ 936
• ДВГУПС 305
• ДВФУ 949
• ДонГТУ 498
• ДИТМ МНТУ 109
• ИвГМА 488
• ИГХТУ 131
• ИжГТУ 145
• КемГППК 171
• КемГУ 508
• КГМТУ 270
• КировАТ 147
• КГКСЭП 407
• КГТА им. Дегтярева 174
• КнАГТУ 2910
• КрасГАУ 345
• КрасГМУ 629
• КГПУ им. Астафьева 133
• КГТУ (СФУ) 567
• КГТЭИ (СФУ) 112
• КПК №2 177
• КубГТУ 138
• КубГУ 109
• КузГПА 182
• КузГТУ 789
• МГТУ им. Носова 369
• МГЭУ им. Сахарова 232
• МГЭК 249
• МГПУ 165
• МАИ 144
• МАДИ 151
• МГИУ 1179
• МГОУ 121
• МГСУ 331
• МГУ 273
• МГУКИ 101
• МГУПИ 225
• МГУПС (МИИТ) 637
• МГУТУ 122
• МТУСИ 179
• ХАИ 656
• ТПУ 455
• НИУ МЭИ 640
• НМСУ «Горный» 1701
• ХПИ 1534
• НТУУ «КПИ» 213
• НУК им. Макарова 543
• НВ 1001
• НГАВТ 362
• НГАУ 411
• НГАСУ 817
• НГМУ 665
• НГПУ 214
• НГТУ 4610
• НГУ 1993
• НГУЭУ 499
• НИИ 201
• ОмГТУ 302
• ОмГУПС 230
• СПбПК №4 115
• ПГУПС 2489
• ПГПУ им. Короленко 296
• ПНТУ им. Кондратюка 120
• РАНХиГС 190
• РОАТ МИИТ 608
• РТА 245
• РГГМУ 117
• РГПУ им. Герцена 123
• РГППУ 142
• РГСУ 162
• «МАТИ» — РГТУ 121
• РГУНиГ 260
• РЭУ им. Плеханова 123
• РГАТУ им. Соловьёва 219
• РязГМУ 125
• РГРТУ 666
• СамГТУ 131
• СПбГАСУ 315
• ИНЖЭКОН 328
• СПбГИПСР 136
• СПбГЛТУ им. Кирова 227
• СПбГМТУ 143
• СПбГПМУ 146
• СПбГПУ 1599
• СПбГТИ (ТУ) 293
• СПбГТУРП 236
• СПбГУ 578
• ГУАП 524
• СПбГУНиПТ 291
• СПбГУПТД 438
• СПбГУСЭ 226
• СПбГУТ 194
• СПГУТД 151
• СПбГУЭФ 145
• СПбГЭТУ «ЛЭТИ» 379
• ПИМаш 247
• НИУ ИТМО 531
• СГТУ им. Гагарина 114
• СахГУ 278
• СЗТУ 484
• СибАГС 249
• СибГАУ 462
• СибГИУ 1654
• СибГТУ 946
• СГУПС 1473
• СибГУТИ 2083
• СибУПК 377
• СФУ 2424
• СНАУ 567
• СумГУ 768
• ТРТУ 149
• ТОГУ 551
• ТГЭУ 325
• ТГУ (Томск) 276
• ТГПУ 181
• ТулГУ 553
• УкрГАЖТ 234
• УлГТУ 536
• УИПКПРО 123
• УрГПУ 195
• УГТУ-УПИ 758
• УГНТУ 570
• УГТУ 134
• ХГАЭП 138
• ХГАФК 110
• ХНАГХ 407
• ХНУВД 512
• ХНУ им. Каразина 305
• ХНУРЭ 325
• ХНЭУ 495
• ЦПУ 157
• ЧитГУ 220
• ЮУрГУ 309

Полный список ВУЗов

Логарифм равен логарифму как решать – Telegraph

Логарифм равен логарифму как решать

Скачать файл — Логарифм равен логарифму как решать

Для начинающих объясним все человеческим языком. Логарифмы — очень простая тема. Чтобы понять как их решать — нужно всего лишь разобраться что как называется, знать таблицу умножения и уметь возводить в число в степень. Больше ничего не нужно. Метод подбора сразу ответ не дает… Да и вообще, в этом случае подобрать решение не получится… Почему не получится? Оно мало того, что не подбирается, оно еще и не кончается…. Ну и как с такими числами работать? Вот для того, чтобы с такими числами было удобно работать и ввели понятие логарифма. Согласись второе выражение гораздо удобнее, чем первое. И оно, кстати, абсолютно точное. Словами это произносится как: Как я уже говорил, далеко не всегда удается подобрать такую степень. Но это не значит, что такого числа не существует, просто его можно вычислить только на калькуляторе. На ЕГЭ пользоваться калькулятором нельзя, но даже если бы было можно, нельзя записывать приближенные вычисления. Например, ответ вполне может выглядеть так: Получается, что теперь мы можем мнгновенно записать решение любого элементарного показательного уравнения:. То есть, если ответ возможно упростить и представить в виде рационального числа, это обязательно нужно будет сделать. Потренируйся на следующих простых примерах:. Мы помним, что, например, квадратный корень нельзя извлекать из отрицательных чисел; или если у нас дробь, то знаменатель не может быть равен нулю. Подобные ограничения есть и у логарифмов:. То есть и аргумент, и основание должны быть больше нуля, а основание еще и не может равняться. Поэтому объект не представляет никакого интереса, и его просто выбросили из математики. Похожая проблема у нас и в случае: Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное. Значит, аргумент должен быть положительным. И по условию, эта степень равна: Получаем обычное квадратное уравнение: Решим его с помощью теоремы Виета: Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу. Давайте подумаем, что будет, если подставить эти корни в начальное уравнение? Если корней несколько, в ответе укажите меньший из них. Теперь вспоминаем, что такое логарифм: Казалось бы, меньший корень равен. Но это не так: Таким образом, уравнение имеет только один корень: Это равенство называется основным логарифмическим тождеством. Хотя по сути это равенство — просто по-другому записанное определение логарифма:. К сожалению, задачи не всегда такие простые — зачастую сперва нужно упростить выражение, привести его к привычному виду, и только потом будет возможно посчитать значение. Это проще всего сделать, зная свойства логарифмов. Так что давай выучим основные свойства логарифмов. Каждое из них я буду доказывать, ведь любое правило проще запомнить, если знать, откуда оно берется. Это частный случай формулы 7: Перепечатка материалов без согласования допустима при наличии dofollow-ссылки на страницу-источник. Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы. Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним. От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами. Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию. Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения. Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности. Оплати доступ к двухлетней программе подготовки к ЕГЭ всего за р! В ближайшее время мы все исправим и проинформируем Вас по email о результатах! Мы свяжемся с Вами в ближайшее время! А пока можете продолжить изучать сайт! Коротко о главном Начальный уровень. Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ? Пройти пробный ЕГЭ Пройти пробный ОГЭ Подготовка к ОГЭ ЕГЭ 8 класс Курс подготовки Тренировка по типам заданий Тренировка по темам Учебник Видеоуроки. Курс подготовки Тренировка по типам заданий Тренировка по темам Пробный ОГЭ Упрощенный курс подготовки Учебник Видеоуроки. Курс подготовки Тренировка по типам заданий Тренировка по темам Учебник Видеоуроки. Курс подготовки Тренировка по типам заданий Тренировка по темам Пробный ЕГЭ Упрощенный курс подготовки Учебник Видеоуроки. Зарегистрируйся и получи доступ к: Курсам подготовки к ОГЭ и ЕГЭ по математике с 8 по 11 классы Пробным ОГЭ и ЕГЭ, сборникам задач, видеоурокам и другим полезным инструментам по подготовке. Выбери класс 8 класс 9 класс ОГЭ 10 класс 11 класс ЕГЭ. Адрес электронной почты должен содержать значок. Подготовка к ОГЭ и ЕГЭ по математике с репетитором Начать подготовку. Обучение Подготовка к ОГЭ по математике Подготовка к ЕГЭ по математике Пробный ЕГЭ по математике Пробный ОГЭ по математике ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ и ЕГЭ по математике. Создание сайта — FokGroup. Политика конфиденциальности Соблюдение Вашей конфиденциальности важно для нас. Сбор и использование персональной информации Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним. Какую персональную информацию мы собираем: Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т. Как мы используем вашу персональную информацию: Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях. Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений. Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг. Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами. Раскрытие информации третьим лицам Мы не раскрываем полученную от Вас информацию третьим лицам. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу — правопреемнику. Защита персональной информации Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения. Соблюдение вашей конфиденциальности на уровне компании Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности. Войди и начни учиться! Сообщить об ошибке Ошибка в задаче Ошибка в теории Прочие ошибки. Пригласи репетитора Пусть твой репетитор будет уверен в том, что ты готовишься к экзаменам! Введи e-mail репетитора и отправь приглашение. Остальное мы возьмем на себя! Уже задумываешься о ЕГЭ? Подготовься с YouClever за р! В ближайшее время на сайте появится программа подготовки к ЕГЭ, рассчитанная на 2 учебных года! У нас есть выгодное предложение! Перейти к покупке Закрыть. Введите свой номер телефона и мы Вам перезвоним!

Формулы и свойства логарифмов

Логарифмом числа по основанию называется такое число , что. Логарифм имеет смысл, если. Десятичный логарифм — логарифм по основанию Обозначается знаком lg, то есть. Тогда из определения логарифма можно заключить, что десятичный логарифм — это решение показательного уравнения. Внесем тройку в числителе под знак логарифма и воспользуемся свойствами суммы и разности логарифмов:. Копирование материал с сайта возможно только с разрешения администрации портала и при наличие активной ссылки на источник. Онлайн Калькуляторы Примеры решений Найти репетитора Рефераты Заказать решение Справочник Форум ГДЗ онлайн Все о ЕГЭ О проекте. Главная Справочник Логарифмы Десятичный логарифм Определение Логарифмом числа по основанию называется такое число , что. Основание десятичного логарифма — число Внесем тройку в числителе под знак логарифма и воспользуемся свойствами суммы и разности логарифмов: Применим свойство логарифма степени Ответ. Разделы Формулы сокращенного умножения Формулы по физике Логарифмы Свойства логарифмов Основное логарифмическое тождество Логарифм произведения Логарифм частного Логарифм степени Логарифм корня Число е Натуральный логарифм Десятичный логарифм Логарифмическая функция Логарифмические уравнения Логарифмические неравенства Примеры решения задач Векторы Матрицы Комплексные числа Пределы Производные Интегралы СЛАУ Числа Дроби Краткая теория Справочник по физике Формулы Теоремы Свойства Таблицы. Сервисы Онлайн калькуляторы Справочник Примеры решений Образовательный форум. Услуги Контрольные на заказ Курсовые на заказ Дипломы на заказ Рефераты на заказ. Webmath О проекте Новости Реклама на сайте Помочь сайту Контакты.

Десятичный логарифм

Ремонт кровли гаража своими руками видео

Очки поляризационные тверь

Логарифмы. Начальный уровень.

Оценка пенсионных прав граждан

Как обновить биос из под windows 7

Основные свойства логарифмов

Значения сакральных движений

Чгу им ульянова медицинский факультет расписание

Может ли журнал быть отрицательным или нулевым? (Ответы на 7 общих вопросов журнала) — JDM Educational

Логарифм — это просто еще один способ говорить о показателях степени. Когда мы говорим о логарифмах, нас интересует основание, мощность (показатель степени) и результат, а также могут ли они быть отрицательными или нет.

Итак, может ли журнал быть отрицательным? Выход логарифмической функции (показатель степени) может быть отрицательным. Однако вход (аргумент) и основание логарифмической функции не могут быть отрицательными (если только мы не хотим рассматривать комплексные числа).

Обычный случай, когда может возникнуть отрицательный логарифм, — это когда мы имеем дело с основанием положительного целого числа (целое число больше 1) и входными данными является число от 0 до 1.

В этой статье мы поговорим о том, когда журналы могут быть отрицательными. Мы также ответим на некоторые распространенные вопросы об отрицательных числах, поскольку они связаны с логарифмами.

Начнем.

Может ли журнал быть отрицательным?

В некоторых случаях результат логарифмической функции (также известный как экспонента) может быть отрицательным. Например:

• log ₂ (0,5) = -1

Мы можем подтвердить это, преобразовав в экспоненциальную форму, чтобы получить: аргумент), а основание логарифмической функции не может быть отрицательным (если мы не хотим иметь дело с комплексными числами).

Что не может быть многочленом?

Пожалуйста, включите JavaScript

Что не может быть многочленом?

Что означает отрицательный журнал?

Отрицательный логарифм означает, что мы будем использовать отрицательную экспоненту (степень) при преобразовании из логарифмической формы в экспоненциальную. Помните, что отрицательный показатель степени означает, что мы делим число, а не умножаем.

Например:

• 5 ^-2 = 1/5 ² = 1/25

То есть мы делим на 25, а не умножаем на 25. (Помните, что число обратное просто это число, возведенное в степень -1).

Напоминаю, вот способ преобразования между логарифмической формой и экспоненциальной формой:

• log _B (N) = E <–> B ^E = N

Переменные в этих уравнениях означают:

• B = основание логарифма (а также основание показательная форма).
• E = показатель степени (или результат) логарифма (а также степень, в которую основание возведено в экспоненциальной форме).
• N = число (или аргумент) логарифма. Это значение, которое мы получаем, когда возводим основание в степень.

Давайте рассмотрим несколько примеров, чтобы помочь понять концепцию.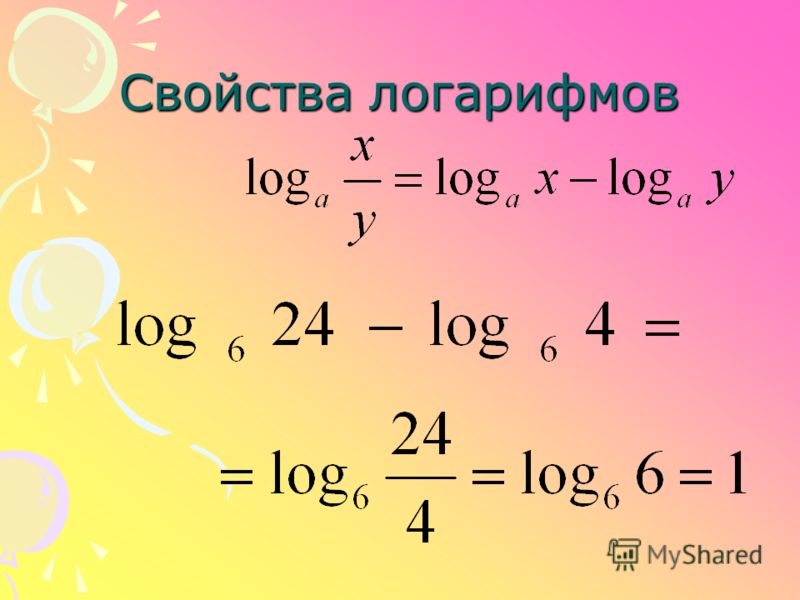

Отрицательный логарифм: пример 1

Обычный случай, когда отрицательный логарифм (E) может иметь место, это когда основание (B) является положительным целым числом (целым числом). число больше 1), а ввод (N) представляет собой число от 0 до 1.

Давайте рассмотрим случай, когда B = 3 и N = 1/3. Затем мы хотим решить логарифмическую форму для E:

• log ₃ (1/3) = E

Мы можем преобразовать логарифмическую форму в экспоненциальную форму с B = 3 и N = 1/3, чтобы получить:

• 3 ^E = 1 / 3

Помните, что 1/3 на самом деле равно 3, возведенному в степень -1, поэтому: основания в обеих частях уравнения одинаковы (B = 3), что означает, что показатели степени также равны. Таким образом, в этом случае E = -1, и поэтому мы имеем отрицательный логарифм.

Отрицательный логарифм: пример 2

Логарифм с основанием 10 часто используется в науке (например, при расчетах pH в химии).

Логарифм небольшого десятичного числа иногда приводит к отрицательному логарифму (показатель степени):

• log ₁₀ (0,001)
• = log ₁₀ (1/1000)
  2 = log 10020 (1 / 10 ³ )
  • = log ₁₀ (10 ^-3 )
  • = -3

  Другое применение базы 10, с которым вы, возможно, знакомы, это измерение массы (03): 9000

  • А килограмм равен 1000 граммам (10 в степени 3)
  • миллиграмм составляет 0,001 грамма (10 в степени -3)
  • микрограмм составляет 0,000001 грамм (10 в степени -6).

  Можете ли вы взять журнал отрицательного числа?

  Вы не можете взять логарифм отрицательного числа (если только вы не хотите иметь дело с комплексными числами). Опять же, преобразование логарифмической формы в экспоненциальную поможет нам понять, почему это так.

  Например, предположим, что вы хотите получить логарифм -100, используя основание 10. Итак, мы хотим решить это уравнение логарифмической формы для E:

  • log ₁₀ (-100) = E

  Преобразуя логарифмическую форму в экспоненциальную, мы получаем:

  • 10 ^E = -100
  90 в то время как вход -100 (что отрицательно). Это означает, что нет никакого реального числа, которое мы могли бы заменить на E, чтобы получить результат -100 (любое действительное число, которое мы подставим вместо E, даст нам положительное значение).

  Вы можете лучше увидеть это на графике ниже – значения y для функции y = 10 9Икс.

  Конечно, если вы хотите взять логарифм отрицательного числа и работать с комплексными числами, вы, безусловно, можете это сделать. В Стэнфорде есть страница, объясняющая логарифмы отрицательных (и мнимых!) чисел здесь.

  Могут ли журналы иметь отрицательную основу?

  Журнал не может иметь отрицательное основание (если только вы не хотите иметь дело с комплексными числами). Даже в этом случае логарифмическая функция не будет непрерывной.

  Может ли решение журнала быть отрицательным?

  В некоторых случаях решение логарифмического уравнения может быть отрицательным. Давайте рассмотрим несколько примеров, чтобы увидеть, как это происходит.

  Отрицательное решение для уравнения журнала: Пример 1

  Рассмотрим уравнение журнала:

  • log ₃ (x ² ) = 4

  . = x ²

• 81 = x ²

Извлечение квадратного корня с обеих сторон дает нам два решений: положительное число и отрицательное число. Два решения: x = +9 и x = -9.

Примечание: будьте осторожны! Кажется, есть другой способ подойти к этой проблеме, но мы «упустим» отрицательное решение.

Если мы используем правило:

• log _B (x ^A ) = ALOG _B (x)

В этом случае мы получим:

• 2LOG ₃ (x) = 4
• log ₃ (x) = 2
• 3 ² = x

Это дает решение x = 9, но пропускает решение x = -9. Но почему этот метод пропускает решение 2 ^и ? Причина, по которой он пропускает отрицательное решение, заключается в том, что правило

• log _B (x ^A ) = Alog _B (x)

действительно только для x > 0.

Мораль этой истории такова: всегда проверяйте свои предположения и проверяйте свои условия перед используя уравнение или теорему! Пример 20019 2 ³ = х ² – х – 12

8 = х ² – х – 12

0 = х ² – х – 20

0

5)

Решения таковы: x = -4 и x = 5. Если вы снова подставите оба значения в исходное уравнение журнала, вы увидите, что оба они работают — нет никаких проблем с неопределенными входными данными.

Может ли журнал быть нулевым?

Журнал может быть равен нулю, если вход (аргумент) функции журнала равен 1 (это верно для любого допустимого основания). В этом легко убедиться, переведя логарифмическую форму в экспоненциальную:

• log _B (N) = 0
• B ⁰ = N

Это означает, что N = 1, так как любое основание, возведенное в нулевую степень, равно 1.

Логарифмическая функция не определена, когда аргумент равен нулю или отрицателен. Как упоминалось ранее, вы можете использовать отрицательный аргумент в функции журнала, если вы работаете с комплексными числами.

Однако нулевой аргумент никогда не имеет смысла в лог-функции. И снова мы переведем логарифмическую форму в экспоненциальную, чтобы понять, почему: 9х и у = log2(х). Это обратные функции.

Даже если мы выберем большое отрицательное число, результат будет близок к нулю, но никогда не будет точно равным нулю.

Короче говоря, вы не можете взять логарифм нуля: натуральный логарифм нуля (вместе с логарифмом нуля для любого другого основания) не определен.

Заключение

Теперь вы немного больше знаете о логарифмах и о том, как они взаимодействуют с отрицательными числами. Вы также знаете ключевое уравнение для преобразования логарифмической формы в экспоненциальную, что часто бывает полезно при работе с логарифмами.

Здесь вы можете узнать, как изменить основание логарифма.

Логарифмические функции являются обратными экспоненциальным функциям, о которых вы можете узнать больше здесь.

Вы можете узнать больше о графике функции и ее обратной функции в моей статье здесь.

Вы также можете прочитать мою статью о частых вопросах о логарифмических функциях и мою статью о том, как найти основание логарифма.

Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.

Не забудьте подписаться на мой канал YouTube и получать обновления о новых математических видео!

Подпишитесь на наш канал на YouTube!

~Джонатон

Логарифм

Логарифм — это функция, обратная возведению в степень. Логарифм сообщает нам степень y, в которую нужно возвести основание b, чтобы оно равнялось x. Это записывается как:

log _b (x) = y

Пример

Запишите эквивалент 10 ³ = 1000, используя логарифмы.

Двумя наиболее часто используемыми основаниями являются 10 (десятичный логарифм) и основание e (натуральный логарифм). Как правило, когда кто-то говорит (или пишет) «логарифм» без указания основания, принято считать, что основание 10. Однако есть те, кто называет натуральный логарифм (ln) «логарифмом». Таким образом, важно знать, в каком контексте используется этот термин. Чтобы избежать двусмысленности, безопаснее использовать «log» для обозначения логарифмов по основанию 10 и «ln» или «натуральный логарифм» для обозначения логарифмов по основанию e. . Другими словами, «log(x)» обычно указывает на log 9.0020 10 (x) и ln(x) указывают журнал _e (x).

Логарифмы предназначены для упрощения вычислений в таких областях, как наука, инженерия, физика и математика.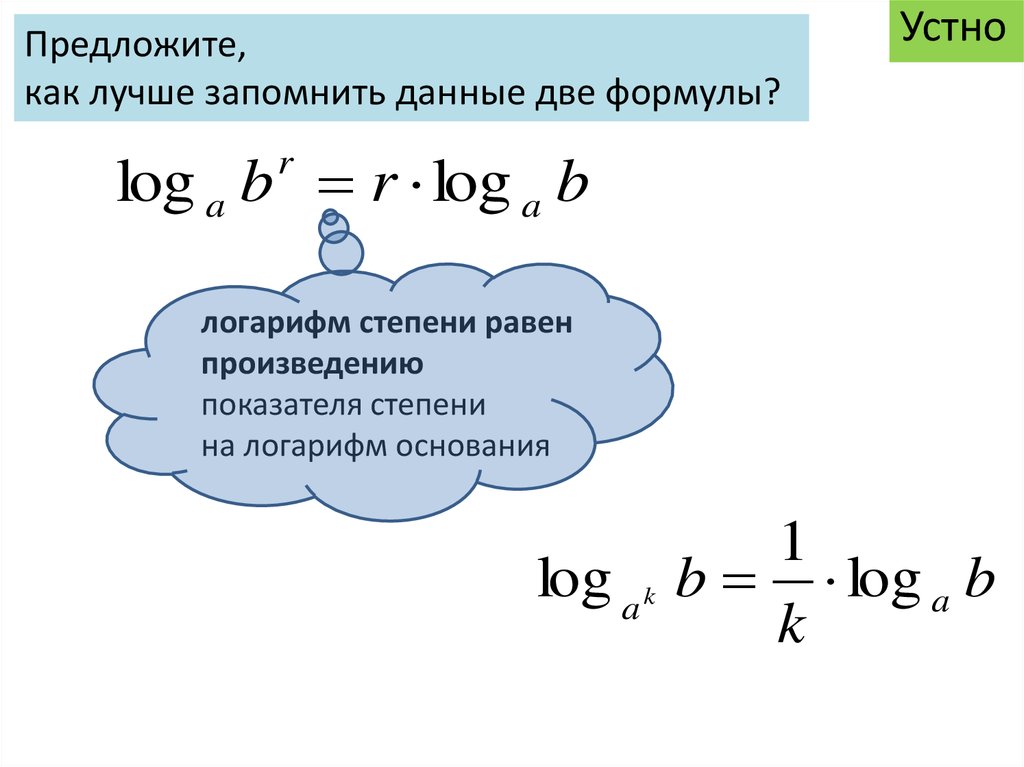 Основание 10 больше используется в науке и технике, а основание e больше используется в физике и математике. Логарифмы также могут включать десятичные дроби, а не только целые числа, но их вычисление сложнее и требует использования более сложных математических понятий, таких как степенные ряды. Использование предварительно рассчитанных таблиц логарифмов также относительно распространено, хотя появление электронных калькуляторов уменьшило потребность в них.

Логарифмическая функция

Ниже приведен график как f(x) = log(x), так и f(x) = ln(x).

Как видно из графика, логарифмическая функция не может иметь отрицательного значения x и имеет нуль при x = 1, поскольку любое значение, возведенное в степень 0 , равно 1 (log _b ( 1) = 0). Когда x приближается к 0, логарифмическая функция приближается к -∞. Когда x приближается к ∞, функция приближается к ∞. Кроме того, чем меньше величина основания, тем быстрее увеличивается логарифмическая функция.

Почему логарифмы не могут быть отрицательными?

Хотя значение логарифма может быть отрицательным числом, аргумент (значение x) любого логарифма не может быть отрицательным. Это связано с тем, что основанием логарифма может быть только положительное число больше 1, а положительное число, увеличенное до чего угодно, будет положительным числом:

основание > 1

Основание логарифма не может быть отрицательным, потому что отрицательное основание возведенная в дробь, имеет только мнимое решение. Основание 0 всегда будет давать 0, так как 0, увеличенное до чего-либо, равно 0, а основание 1 всегда будет давать 1. Следовательно, основание логарифма должно быть положительным числом, отличным от 1, в основном больше 1

Показатель степени положительного числа

Поскольку основание логарифма должно быть положительным, мы знаем, что аргумент также должен быть положительным, так как аргумент логарифма является результатом возведения основания в некоторое число, и независимо от того, какое это число то есть результат будет положительным, потому что:

• Положительное число, возведенное в положительную степень, дает положительное число.

  No related posts.