Когда определитель равен нулю: Свойства определителя матрицы | Мозган калькулятор онлайн

1.3. Свойства определителей

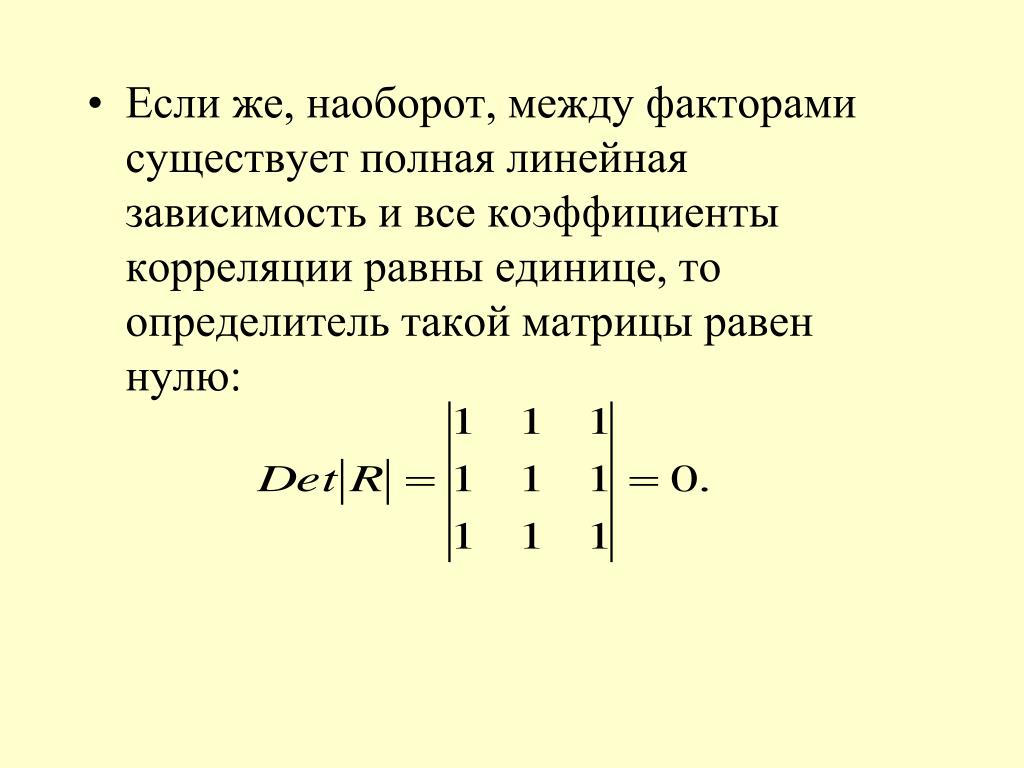
	1.3. Свойства определителей			Высшая математика > 1. Элементы линейной алгебры > 1.3. Свойства определителей
	Определение 1 Матрица, полученная из данной матрицы  заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной по отношению к данной, и обозначается: .   Свойство 1 Определитель транспонированной матрицы равен определителю исходной.   Свойство 2 Если в определителе поменять местами две строки (столбца), то определитель поменяет знак.   Свойство 3  Определитель с двумя пропорциональными (в частности, равными) строками (столбцами) равен нулю.   Свойство 4 Если в определителе строка (столбец) целиком состоит из нулей, то определитель равен нулю.   Свойство 5 Общий множитель всех элементов какой либо строки (столбца) можно вынести за знак определителя.   Свойство 6 Правило сложения определителей: , т.е. если каждый элемент некоторой строки (столбца) представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, причем в одном из них соответствующая строка (столбец) состоит из первых слагаемых, а в другом — из вторых слагаемых, остальные же строки (столбцы) — те же, что и в исходном определителе.   Свойство 7 Определитель не изменится, если ко всем элементам одной строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и тоже число: .   Определение 2 Верхней треугольной матрицей называется матрица вида: .   Определение 3 Нижней треугольной матрицей называется матрица вида: .   Определение 4 Диагональной матрицей называется матрица вида: . Свойство 8 Определитель диагональной, треугольной (верхней и нижней) матрицы равен произведению диагональных элементов.   Определение 5 Минором элемента определителя  называется определитель, получаемый из данного определителя вычеркиванием -ой строки и-ого столбца. Обозначается: . Замечание 1 Минор — это определитель, порядок которого на единицу меньше, чем у исходного.   Определение 6 Алгебраическим дополнением элемента определителя  называется число: , где  — соответствующий минор.   Пример 1 Дан определитель: . Вычислить  и   Решение Так как нужно вычислить минор и алгебраическое дополнение элемента , вычеркиваем в определителе вторую строку и третий столбец: . Тогда: , . Замечание 2 Так как знак перед минором в алгебраическом дополнении определяется только местом элемента в определителе, то правило выбора знаков выглядит следующим образом: .   Теорема разложения Определитель равен сумме произведений элементов какой — либо строки (столбца) на их алгебраические дополнения. Это означает, что если взять в определителе -ую строку, то его величину можно вычислить по следующей формуле: . Такой способ вычисления определителя называется разложением его по элементам -ой строки (аналогично определяется разложение определителя по элементам -ого столбца).   Пример 2 Вычислить определитель: , разложив его по элементам первого столбца.   Решение 1 способ . 2 способ Используя 7-ое свойство, обратим некоторые элементы первого столбца в ноль. Это упростит вычисление определителя. Умножим первую строку на (-3) и прибавим ко второй строке, затем умножим первую строку на (-7) и прибавим к третьей строке: . Заметим, что вторая строка имеет общий множитель (-2), а третья — (-1). Поэтому, применяя дважды 5-ое свойство, получим: . В первом столбце остался лишь один элемент, отличный от нуля. Тогда, разложив определитель по элементам первого столбца, получим: .   Свойство 10 Сумма произведений элементов какой — либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю. Например, сумма произведений элементов первой строки определителя на алгебраические дополнения соответствующих элементов второй строки равна нулю: .
gif»>

Определитель (детерминант) – многочлен от элементов квадратной матрицы.

(обозначается ∆, det a, |a|, d)

При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.

Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.

Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.

Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).

Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.

Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.

3. (Практика) 2х2, 3х3, 4х4

4. Обратная матрица A^-1= 1/|A|*A^Т˳

A˳ = Матрица миноров * на матрицу знаков

Матрица миноров – посредством нахождения каждого определителя.

Для проверки A* A^-1 = E

5. В том случае, если определитель матрицы равен нулю – обратной матрицы не существует.

6. (практика) Ранг матрицы — максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.

Если ранг матрицы равен r, то любые m:n > r строк или столбцов этой матрицы будут линейно зависимы.

Если A — квадратная матрица, определитель которой = 0 , то строки и столбцы этой матрицы линейно зависимы.

Пусть ранг матрицы = r, тогда максимальное количество линейно независимых строк (столбцов) этой матрицы равно r.

Найти можно по «Методу окаймляющих миноров» или с помощью «элементарных преобразований».

СЛАУ

7. Система линейных алгебраических уравнений — это система уравнений вида, где

X1, x2, …, xn — неизвестные, которые надо определить. A11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными.

Система является…

однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.

квадратной, если m=n

совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой.

Решение системы — совокупность чисел c₁, c₂, …, c_n, таких что подстановка каждого в систему обращает все её уравнения в тождества.

Совместная система может иметь одно или более решений.

8. СЛАУ совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы.

Система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных. (это и есть теорема Кронекера-Капелли)

9. Решать можно школьным методом (выражение одной переменной через другую и подстановка в выражение), сложением и вычитанием строк, матричным методом (см. вопрос 10), с помощью теоремы Крамера (см. вопрос 11) или Гаусса (см. вопрос 12).

10. (практика)Матричный метод – решение с помощью обратной матрицы (A^-1) Подходит только для невырожденных (det≠0).

AX = B, значит Х=В/А=В* A^-1 (как найти A^-1 смотри 4-й вопрос)

11. (практика) Метод Крамера (det≠0)

1. Записываем коэффициенты при Х в виде матрицы.

2. Рассчитываем det матрицы.

3. Заменяем 1-ю (потом 2-ю и 3-ю строку) на столбец свободных членов,

рассчитываем их det-ты.

4. Находим иксы по формуле:

12.(практика) Метод Гаусса

1. Записываем уравнения в расширенную матрицу

2. Элементарные преобразования (перестановка строк (столбцов), складывание вычитание строк (столбцов))

3. Главная цель – привести к ступенчатому виду (под диагональю 0-ли)

4. Подстановка в нижнее уравнение Х и решение снизу-вверх.

13. Система называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0) (рисунок к 10-му вопросу). Имеет ненулевое решение, когда ранг её матрицы коэффициентов при переменных меньше числа переменных, т.е. при rang A˂ n.

14. (практика) Метод: 1. Записать в виде матрицы, отдельно Х, отдельно коэффициенты, отдельно свободные члены (0-ли) 2. Привести к ступенчатому виду (элементарные преобразования).

3. Найти ранг системы и кол-во решений(n—rang). N – кол-во переменных.

4. Переписать в виде уравнений и выразить из них любую переменную.

5. Подставить 1-цу в переменную, найти остальные. Записать в табличку.

6. Ответ записать в виде вектора.

ВЕКТОРЫ

15. N-мерным вектором называется последовательность чисел. Эти числа называются координатами вектора. Число координат вектора n называется размерностью вектора.

Вектор записывается в виде строки или столбца:

Существуют: нулевой вектор (все цифры = 0), единичные векторы специального вида (одно из чисел единица). Векторы можно: умножать на число, складывать, перемножать, находить модуль вектора. При сложении, умножении – можно менять местами, выносить за скобки.

Сложение:

Перемножение:

Умножение на число: λA=(λ*a₁, λ*a₂,…, λ*a_n)

Модуль вектора: . (То есть записать так вектор и перемножить его по свойству, получится число)

16. Арифметическое n— мерное векторное пространство — это множество всех арифметических n-мерных векторов, а также их суммы и произведения на числа. Обозначается «V».

Аксиомы:

1)сумма любых двух элементов из V и произведение скаляра и произвольного элемента из V являются некоторыми элементами из V. (выводится из определения векторного пространства (см. вверх)).

2)сложение любых трёх элементов из V подчиняется сочетательному закону (или как ещё говорят — векторное сложение ассоциативно): .

3)сложение любых двух элементов из V подчиняется переместительному закону (векторное сложение коммутативно):

4)существует такой элемент из V (нулевой вектор), что для любого верно

5)для любого элемента из V существует такой элемент из V, сумма которого с исходным элементом равна

6) (обратить внимание – вектор ТОЛЬКО СО СТРЕЛКОЙ, остальные – числа)

7)

8)

9)

17. Длина = модулю вектора (см. 15 вопрос, в конце). Скалярное произведение (см. 15 вопрос). Ортогональность(перпендикулярность): Если выполняется – перпендикулярны.

18. Система векторов A₁, A₂,…,A_n называется линейно зависимой, если существует ненулевой набор чисел λ₁, λ₂,. ..,λ_n, при котором линейная комбинация векторов λ₁*A₁+λ₂*A₂+…+λ_n*A_n равна нулевому вектору. Условие: все λ≠0. Если λ=0, то система линейно независима. Эквивалентные системы – системы, которые можно выразить друг через друга. Их ранги равны. Эквивалентные преобразования – изменение нумерации вектора, удаление нулевого вектора, удаление линейной комбинации векторов, умножение на число, прибавление к одному вектору линейную комбинацию других векторов системы.

Что значит иметь определитель равный нулю? | by Mathphye

6 min read

·

5 января

Определитель, равный нулю, означает , что матрица является сингулярной матрицей. Матрица является вырожденной, если она не имеет обратной, что означает, что ее нельзя использовать для решения систем линейных уравнений.

Это может быть проблемой, когда вы пытаетесь решить систему линейных уравнений с использованием обратной матрицы и обнаруживаете, что обратная сингулярная матрица не определена. Вы можете сделать вывод, что «решения нет» и остановимся на этом.

Однако можно найти другой способ решения системы уравнений, когда определитель равен нулю, без прямого использования обратной матрицы.

Почему нельзя найти обратную матрицу, если определитель равен нулю?

Напомним, что определитель матрицы — это числовое значение, которое можно вычислить из элементов матрицы. Определитель матрицы используется в различных областях математики и физики для решения задач, связанных с матрицами. Его отношение к обратной матрице зависит от следующей эквивалентности, где обратная матрица существует только в том случае, если определитель отличен от нуля, поскольку это означает деление на ноль:

Геометрически мы можем интерпретировать определитель матрицы как площадь (для матриц 2×2) или объем (для 3×3 и т. д.) между всеми векторами. Если один вектор равен нулю или компланарен другим, то он не будет вносить вклад в «высоту» объема, и определитель будет равен нулю.

Аналогичным примером зависимой переменной может быть стол с четырьмя ножками, который может стоять, даже если отсутствует одна ножка. Хотя технически возможно, чтобы зависимый вектор вносил некоторый вклад, в этом нет необходимости, поскольку его можно заменить линейной комбинацией других векторов. Каждая нога может быть смоделирована как сила в линейном уравнении, а уравнения основаны на законах Ньютона.

Матрица обычно преобразует один набор характеристик в другой. Это происходит плавно, когда существует однозначное соответствие, также известное как биективное отображение. Однако если определитель матрицы равен нулю, это означает, что биективного отображения нет.

При биективном отображении информация преобразуется из одного пространства в другое, аналогично переводу между языками. Исходное преобразование можно отменить с помощью взаимно-однозначного сопоставления, аналогичного кодированию и декодированию сообщения, путем отслеживания исходного преобразования во внешней таблице (например, Розеттский камень преобразования).

В этом случае определитель отличен от нуля.

В системах уравнений каждая строка представляет собой уравнение или ограничение, а каждый столбец представляет переменную, которую необходимо отобразить. Для каждой переменной нам нужно одно уравнение. Если уравнений больше, чем переменных, мы не сможем удовлетворить их все одновременно. С другой стороны, если переменных больше, чем уравнений, у нас не будет достаточно уравнений, чтобы свести переменные к однозначному результату.

Проблемы возникают при отображении «многие к одному» или «один ко многим», так как в этих случаях определитель равен нулю.

Это связано с тем, что может быть невозможно однозначно определить исходный набор характеристик из преобразованного набора или наоборот. Другими словами, информация может быть не сохранена или необратима при преобразовании.

От многих к одному, может быть интерпретировано как проекция, кодировщик или суммирование, это процесс конвергенции. Это может дать вам корреляцию с вектором.

> Решение. В этом случае, чтобы найти решение, нам нужно определить дополнительные ограничения, в основном функцию стоимости, чтобы оптимизировать лучшее решение.

От одного ко многим, можно интерпретировать как генератор или декодер. это расходящийся процесс. Мы могли бы сгенерировать множество художественных рисунков, имеющих одинаковый стиль, поскольку степень свободы вывода не выше, чем входная, по крайней мере, в детерминированном процессе.

> Решение. В этом случае нам нужно не лучшее решение для данных, а лучшая система или модель для описания основного поведения для правильного создания данных с помощью этой модели.

Чтобы найти желаемое решение на техническом уровне, вы можете применить инверсию Мура-Пенроуза. Этот метод представляет собой процесс оптимизации, который минимизирует среднеквадратичную ошибку/значение за счет сокращения «многих» вариантов до одного. Для этого вам в основном нужно будет умножить обе части уравнения на транспонированную матрицу, а затем решить как обычно.

Эта концепция может быть трудной для понимания , но ее легко реализовать . Вот почему я даю больше контекста и объяснений, а не просто пишу формулы. Я надеюсь, что некоторые из ключевых идей останутся с вами.

Почему этот трюк с умножением на транспонированную матрицу работает? Короче говоря, это проекция, которая избавляется от неортогонального направления, и поскольку ближайшая точка к исходной точке содержится в ортогональной линии к нулевому пространству, вы получаете минимизацию.

Далее я приведу пример того, как обрабатывать определитель, равный нулю, в ситуации, когда столбцов больше, чем строк. Так как конкретный пример с реальным приложением мог бы быть пока этот рассказ я напишу отдельно.

Спойлер: Это связано с тросовыми роботами и статическим равновесием. В общем, для задач, которые являются «статически неопределенными». То есть количество неизвестных больше, чем количество уравнений.

Вот я играл с таким «роботом» 🤣 получилось не очень, но с этим многому научился.

Определитель — Линейная алгебра | Elevri

Линейная алгебра

Определитель

Определитель – это скалярное представление матрицы, определяемое специальным вычислением. Геометрическая интерпретация заключается в том, что это масштабный коэффициент для линейного преобразования, которое представляет матрица. Он также говорит о том, имеет ли система линейных уравнений, которую представляет матрица, единственное решение или нет.

Содержание

Почему это называется правилом Крамера?

В 1750 году Габриэль Крамер опубликовал статью с изложением известного метода, который сегодня носит его имя: Правило Крамера . Швейцарский гений понял, что определителей можно использовать для решения систем линейных уравнений.

В возрасте всего 18 лет Крамер получил докторскую степень в Женевском университете. Учебное заведение было настолько впечатлено способностями молодого математика, что для него создали новую должность сопредседателя кафедры математики в университете.

Как оказалось, это был умный ход со стороны Университета, от которого выиграла вся Женева.

Крамер оставался в университете до конца своей жизни, где он реформировал систему образования, чтобы математика преподавалась на французском языке, а не только на латыни, таким образом охватив более широкую аудиторию.

Каково определение определителя?

Определитель матрицы представляет собой скалярное значение, обозначаемое или . Чтобы существовать, матрица должна быть квадратной, и если она квадратная, то раскрывает информацию о решениях системы уравнений, которую составляет матрица.

Если определитель равен нулю, то у данной системы либо бесконечно много решений, либо их нет вообще. Все остальные значения означают, что существует единственное решение.

Для матриц, определители которых равны нулю, мы можем быть уверены, что либо существует бесконечное число решений, либо ни одного из них. Более того, ненулевой определитель всегда будет давать единственное решение.

Значение определителя также тесно связано с обратной матрицей. Тогда и только тогда, когда матрица имеет ненулевой определитель, она обратима, и мы можем использовать определитель, чтобы найти обратную матрицу.

Кроме того, определитель дает коэффициент масштабирования линейного преобразования, описываемого матрицей.

Как найти определитель квадратной матрицы?

Чтобы найти определитель квадратной матрицы (он должен быть квадратным), мы можем использовать такие методы, как формула Лейбница или разложение Лапласа, которые всегда будут работать. Однако есть короткие пути, которые мы можем использовать в определенных случаях.

Если — матрица, ее определитель можно быстро найти по следующей формуле:

В случае, если мы имеем дело с матрицей, используем следующую формулу:

Подробнее об определителе

Введение

Определитель является скаляром и отмечен:

Определитель может быть введен как поздно, так и рано в курсе линейной алгебры. Что касается того, что это такое, студентов традиционно сначала знакомят с тем, как вычисляется определитель, а затем с практической связью и ее геометрической интерпретацией.

Мы делаем наоборот.

Практическая связь

Определитель показывает, имеет ли линейная система уравнений решения. Помните три случая; единственное решение , бесконечно много решений или нет решений .

Если определитель равен нулю, система имеет «бесконечное множество решений» или «нет решений».

Если определитель отличен от нуля, система имеет единственное решение.

Геометрическая интерпретация

Определитель геометрически интерпретируется как масштабный коэффициент для линейного преобразования, с которым, к сожалению, обычно не знаком новичок, когда необходимы вычисления определителя.

Короче говоря, каждое умножение матриц является линейным преобразованием, но с практической точки зрения можно сказать, что линейное преобразование — это матрица, которая умножается на вектор для получения желаемого результата.

Простым примером может быть линейное преобразование, которое поворачивает по часовой стрелке на угол и удваивает свою длину. Тогда масштабный коэффициент, то есть определитель, будет равен .

Определитель 2×2

Определение определителя -матрицы формирует основу для вычисления определителя -матрицы.

Пусть:

откуда определение определителя:

Определитель 3×3

Алгоритм вычисления определителя -матрицы выполняется с использованием суммы трех -определителей. Мы получаем их, расширяя одну строку или столбец в определителе (называемый расширением кофактора ).

Пусть:

и тогда применимо, что определитель равен:

где мы сделали разложение первой строки, потому что скаляры каждой -матрицы — это просто элементы из первой строки.

Теперь рассмотрим, как делается расширение. Рассмотрим определитель:

Мы начнем с расширения вдоль первой строки и начнем с первого элемента:

Расширение затем происходит путем выбора строки и столбца текущего элемента для извлечения оставшихся элементов в виде -детерминанта, умноженного на :

Переходим к следующему элементу по первой строке и получаем:

Обратите внимание, что расширение вокруг идет со знаком минус! Мы скоро вернемся к этому.

Теперь мы продолжаем расширять следующий и последний элемент: .

Обратите внимание, что элемент идет со знаком плюс!

Теперь мы закончим вычисление, используя определение -определителя:

Который завершает формулу для -определителя, а также алгоритм, облегчающий запоминание определения вместо того, чтобы заучивать формулу наизусть (что-то, что требуется для продвижения со статусом новичка).

Альтернативная формула

Приведенный выше метод можно легко аналогично распространить на более крупные матрицы, поэтому мы начали с него. Однако существует альтернативный алгоритм, применимый к -детерминанту, который визуально напоминает определение -детерминанта:

Если мы расширим это мышление, мы получим метод, который работает, но работает только для вычисления -детерминантов. Метод называется Правило Сарру .

nxn определитель

Вычисление определителя, вне зависимости от размерности матрицы, производится аналогично -определителю — можно выразить в виде алгоритма для каждого -определителя. Но прежде чем мы это сделаем, мы объясним, почему элемент в вычислении -детерминанта имел знак минус.

Рассмотрим -матрицу . В этом случае каждый извлеченный элемент в своем определителе несет с собой знак плюс или минус в зависимости от его положения в соответствии со следующим «шахматным шаблоном»:

Это означает, что для -определителя скрытый знак для каждого элемента следующим образом:

Например, если бы мы выбрали расширение по второму столбцу, сумма произведений была бы:

Обратите внимание, что знаки плюс и минус, записанные в указанных выше определителях, не должны использоваться ни в каких вычислениях, но теперь они сделано только в образовательных целях.

Общая форма разложения вдоль линии (кофакторное разложение) для определителя -матрицы может быть записана как:

где — каждый элемент в выбранной строке , и — кофактор , который является -детерминантом другие элементы, которые не делят строку или столбец с соответствующим .

Алгоритм для определителя nxn

1. Выберите строку или столбец, которые необходимо разложить в произведение суммы матричных элементов и -определителей

2. Для каждого элемента в выбранной строке/столбце:
   \begin{enumerate}

3. Извлечь элемент со знаком плюс или минус, который он несет, и умножить на -детерминант элементов, которые не разделяют строку или столбец с выделенным элементом

4. Повторять до тех пор, пока не будут извлечены все элементы в выбранной строке/столбце

\item Повторять вышеуказанные шаги до тех пор, пока последняя сумма произведений не будет содержать только -детерминанты.
\конец{перечислить}
Алгоритм показывает, что вычисление определителя может быть чрезвычайно трудоемким, если размерность велика.

Однако обратите внимание на преимущество извлечения строки или столбца, число элементов которых равно нулю! Это означает, что сумма разработанного продукта значительно снижается. Например, как в:

Если определитель, который вы вычисляете, не хватает 0-элементов или их недостаточно, чтобы значительно упростить вычисление, вы можете, как Гаусс-Жордан, сократить строку матрицы определителя без изменения определителя. Эти и другие функции обсуждаются в следующем разделе.

Сопряжение к матрице

Сопряжение к матрице основано на кофакторных разложениях . Это становится интересным в теореме для выражения , если обратное существует. Наше определение сопряженной матрицы:

Если -матрица и является кофактором , то отсюда следует, что матрица:

называется кофакторной матрицей матрицы A. Транспонирование этой матрицы называется примыкает к матрице и обозначается как .

Используя сопряженную матрицу , мы можем очень легко выразить, существует ли обратная, используя следующую теорему, которую мы оставляем недоказанной.

Если обратимая матрица, то:

Сейчас мы покажем все это на примерах. Пусть следующая обратимая матрица:

, кофакторы которой становятся:

и, таким образом, матрица кофакторов и сопряженная матрица становятся следующими:

Определяющие свойства

детерминантную матрицу перед расширением строки, чтобы максимизировать количество 0-элементов.

Для каждой -матрицы применяется следующее:

• Если матрица является результатом умножения скаляра на строку или столбец в матрице , то:

• Если матрица является результатом двух строк или столбцов, поменявшихся местами в , применяется следующее:

• Если матрица является результатом умножения строки или столбца матрицы на другую строку или столбец, то:

Доказательство первого и третьего пункта — хорошее упражнение для новичка, прямого доказательства -детерминанта и -детерминанта достаточно, чтобы убедиться. Чтобы создать устойчивое математическое доказательство, рекомендуется доказательство по индукции.

Второй пункт следует из определения определителя с «шахматной» схемой символов в предыдущем разделе.

С помощью предыдущего утверждения мы можем получить следующее утверждение:

Пусть — -матрица.

• Если две строки или столбца равны, то:

• Если строку или столбец можно уменьшить до 0, то:

• Если является скаляром, то:

  9 0233

Теперь мы готовы к самой запоминающейся теореме для студентов, которая основана на последних теоремах и доказательствах, которые мы представили для того, как обратимая матрица может быть уменьшена по строкам до:

Квадратная матрица обратима тогда и только тогда, когда .

Предположим, что построчно можно свести к , тогда:

Предположим противное, что нельзя построчно свести к , но к . Это означает, что необратимо, потому что по крайней мере две строки в линейно зависимы, и мы получаем по крайней мере одну нулевую строку в . Одна нулевая строка дает:

Другая полезная теорема для арифметики:

Если и — квадратные матрицы одинаковой размерности, то:

Следующее утверждение применимо к обратному:

Если матрица обратима, то применяется:

Помните, что . Тогда у нас есть:

Поскольку , у нас есть:

Мы заканчиваем этот раздел, связывая теорему, которая вводится с обратными и линейными системами уравнений, а также наши идеи с определителем.

Пусть -матрица. Тогда применяются следующие утверждения:

• Сокращенная ступенчатая форма строки для is

• может быть выражена как произведение элементарных матриц

• обратим

• имеет только тривиальное решение 003

• Вектор-столбцы линейно независимы

• Векторы-строки линейно независимы. Правило Крамера — это утверждение, которое, прежде всего, облегчает выражение решения, так как у нас нет чисел в матрице.

  Правило Крамера Если это линейная система уравнений с уравнениями и переменными, то система имеет единственное решение тогда и только тогда, когда , после чего решение может быть выражено как:

  где матрица где столбец в заменено на .

  Для визуалов

  Анимации и пояснения от 3blue1brown нравятся многим, особенно тем, кто лучше всего учится с помощью видео.

  No related posts.