Формулы приведения. Бесплатный видеоурок — материалы для подготовки к ЕГЭ по Математике
Применять формулы приведения — легко! Их не надо зубрить наизусть. И не надо тащить на экзамен шпаргалки, рискуя спалиться. Надо всего лишь запомнить два правила, о которых вы узнаете, посмотрев этот ролик. Это так просто, что даже лошадка поймет! 🙂 Посмотри и передай друзьям.
Часто в задачах встречаются выражения вида а также или — то есть такие, где к аргументу прибавляется нечетное число, умноженное на или целое число, умноженное на Они упрощаются с помощью формул приведения.
Запомните: формулы приведения, от слова «привести». К привидениям, то есть к призракам и прочим глюкам, эти формулы отношения не имеют : -)
Эти формулы называются так потому, что с их помощью можно привести выражения к более простым.
Например,
Зубрить наизусть формулы приведения не нужно.
1) Если в тригонометрической формуле к аргументу прибавляется (или вычитается из него) — в общем, угол, лежащий на вертикальной оси, — функция меняется на кофункцию. Синус меняется на косинус, косинус на синус, тангенс на котангенс и наоборот.
Если же мы прибавляем или вычитаем — в общем, то, что лежит на горизонтальной оси, — функция на кофункцию не меняется.
Это легко запомнить. Если прибавляемый угол лежит на вертикальной оси — вертикально киваем головой, говорим: «Да, да, меняется функция на кофункцию». Если прибавляемый угол лежит на горизонтальной оси — горизонтально мотаем головой, говорим: «Нет, нет, не меняется функция на кофункцию».
Это первая часть правила. Теперь вторая.
2) Знак получившегося выражения такой же, каким будет знак тригонометрической функции в левой его части, при условии, что аргумент мы берем из первой четверти.
Упростим, например, выражение Функция меняется на кофункцию — и в результате получится синус.
Посмотрим, как формулы приведения применяются в задачах ЕГЭ по математике.
1. Найдите значение выражения:
Ответ: 11.
2. Вычислите:
Ответ: 4.
3. Вычислите:
Мы упростили выражения в скобках.
Ответ: — 24.
4. Найдите значение выражения:
Ответ: 4.
5. Упростите выражение:
Ответ: 2.
6. Найдите значение выражения:
Решение:
Используя формулы приведения, получим
Ответ: 0,4.
7.
Решение:
cos cos cos
Снова формула приведения.
Ответ: -12.
8. Найдите значение выражения:
Решение:
Мы применили одну из формул приведения.
Ответ: 42.
9. Найдите значение выражения:
Решение:
Воспользуемся формулами приведения:
Также мы применили основное тригонометрическое тождество. Сумма квадратов синуса и косинуса угла альфа равна единице.
Ответ: 9,5.
Спасибо за то, что пользуйтесь нашими материалами. Информация на странице «Формулы приведения» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена: 07.04.2023
Как решать формулы приведения. Формулы приведения
Определение. Формулами приведения называют формулы, которые позволяют перейти от тригонометрических функций вида к функциям аргумента . С их помощью синус, косинус, тангенс и котангенс произвольного угла можно привести к синусу, косинусу, тангенсу и котангенсу угла из интервала от 0 до 90 градусов (от 0 до радиан). Таким образом, формулы приведения позволяют нам переходить к работе с углами в пределах 90 градусов, что, несомненно, очень удобно.
С их помощью синус, косинус, тангенс и котангенс произвольного угла можно привести к синусу, косинусу, тангенсу и котангенсу угла из интервала от 0 до 90 градусов (от 0 до радиан). Таким образом, формулы приведения позволяют нам переходить к работе с углами в пределах 90 градусов, что, несомненно, очень удобно.
Формулы приведения:
Для использования формул приведения существует два правила.
1. Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется
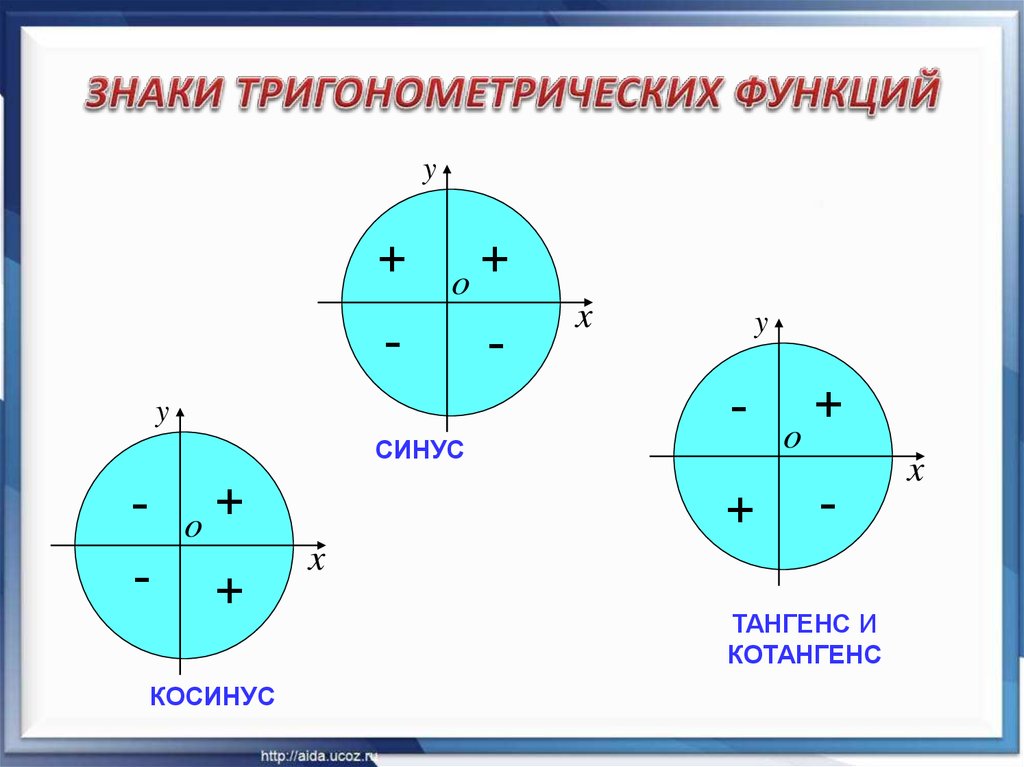
Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет
2. Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс». Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».
На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.
Пример:
Вычислить
Воспользуемся формулами приведения:
Sin(150˚) находится во второй четверти, по рисунку видим что знак sin в этой четверти равен «+». Значит у приведенной функции тоже будет знак «+». Это мы применили второе правило.
Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.
Они относятся к разделу «тригонометрия» в математике. Суть их заключается в приведении тригонометрических функций углов к более «простому» виду. О важности их знания написать можно много. Этих формул аж 32 штуки!
Не пугайтесь, учить их не надо, как и многие другие формулы в курсе математики. Лишней информацией голову забивать не нужно, необходимо запоминать «ключики» или законы, и вспомнить или вывести нужную формулу проблемой не будет. Кстати, когда я пишу в статьях «… нужно выучить!!!» – это значит, что действительно, это необходимо именно выучить.
Кстати, когда я пишу в статьях «… нужно выучить!!!» – это значит, что действительно, это необходимо именно выучить.
Если вы с формулами приведения не знакомы, то простота их вывода вас приятно удивит – есть «закон», при помощи которого это легко сделать. И любую из 32 формул вы напишите за 5 секунд.
Перечислю лишь некоторые задачи, которые будут на ЕГЭ по математике, где без знания этих формул есть большая вероятность потерпеть фиаско в решении. Например:
– задачи на решение прямоугольного треугольника, где речь идёт о внешнем угле, да и задачах на внутренние углы некоторые из этих формул тоже необходимы.
– задачи на вычисление значений тригонометрических выражений; преобразования числовых тригонометрических выражений; преобразования буквенных тригонометрических выражений.
– задачи на касательную и геометрический смысл касательной, требуется формула приведения для тангенса, а также другие задачи.
– стереометрические задачи, по ходу решения не редко требуется определить синус или косинус угла, который лежит в пределах от 90 до 180 градусов.
И это лишь те моменты, которые касаются ЕГЭ. А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.
Так что же к чему приводится и как оговоренные формулы упрощают для нас решение задач?
Например, вам нужно определить синус, косинус, тангенс или котангенс любого угла от 0 до 450 градусов:
угол альфа лежит пределах от 0 до 90 градусов
* * *
Итак, необходимо уяснить «закон», который здесь работает:
1. Определите знак функции в соответствующей четверти.
Напомню их:
2. Запомните следующее:
функция изменяется на кофункцию
функция на кофункцию не изменяется
Что означает понятие — функция изменяется на кофункцию?
Ответ: синус меняется на косинус или наоборот, тангенс на котангенс или наоборот.
Вот и всё!
Теперь по представленному закону запишем несколько формул приведения самостоятельно:
Данный угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:
Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:
Угол лежит в первой четверти, синус в первой четверти положителен. Не меняем функцию на кофункцию, так как у нас 360 градусов, значит:
Вот вам ещё дополнительное подтверждение того, что синусы смежных углов равны:
Угол лежит во второй четверти, синус во второй четверти положителен. Не меняем функцию на кофункцию, так как у нас 180 градусов, значит:
Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.
***
В статье на решение был отмечен такой факт – синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём.
Данная статья посвящена подробному изучению тригонометрических формул приведения. Дан полный список формул приведения, показаны примеры их использования, приведено доказательство верности формул. Также в статье дано мнемоническое правило, которое позволяет выводить формулы приведения, не запоминая каждую формулу.
Yandex.RTB R-A-339285-1
Формулы приведения. Список
Фомулы приведения позволяют приводить основные тригонометрические функции углов произвольной величины к функциям углов, лежащих в интервале от 0 до 90 градусов (от 0 до π 2 радиан). Оперировать углами от 0 до 90 градусов гораздо удобнее, чем работать со сколь угодно большими значениями, поэтому формулы приведения широко применяются при решении задач тригонометрии.
Прежде, чем мы запишем сами формулы, уточним несколько важных для понимания моментов.
- Аргументами тригонометрических функций в формулах приведения являются угды вида ± α + 2 π · z , π 2 ± α + 2 π · z , 3 π 2 ± α + 2 π · z . Здесь z — любое целое число, а α — произвольный угол поворота.
- Не обязательно учить все формулы приведения, количество которых довольно внушительно. Существует мнемоническое правило, которо позволяет легко вывести нужную формулу. Речь о мнемоническом правиле пойдет позже.
Теперь перейдем непосредственно к формулам приведения.
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов. запишем все формулы в виде таблицы.
Формулы приведения
sin α + 2 π z = sin α , cos α + 2 π z = cos α t g α + 2 π z = t g α , c t g α + 2 π z = c t g α sin — α + 2 π z = — sin α , cos — α + 2 π z = cos α t g — α + 2 π z = — t g α , c t g — α + 2 π z = — c t g α sin π 2 + α + 2 π z = cos α , cos π 2 + α + 2 π z = — sin α t g π 2 + α + 2 π z = — c t g α , c t g π 2 + α + 2 π z = — t g α sin π 2 — α + 2 π z = cos α , cos π 2 — α + 2 π z = sin α t g π 2 — α + 2 π z = c t g α , c t g π 2 — α + 2 π z = t g α sin π + α + 2 π z = — sin α , cos π + α + 2 π z = — cos α t g π + α + 2 π z = t g α , c t g π + α + 2 π z = c t g α sin π — α + 2 π z = sin α , cos π — α + 2 π z = — cos α t g π — α + 2 π z = — t g α , c t g π — α + 2 π z = — c t g α sin 3 π 2 + α + 2 π z = — cos α , cos 3 π 2 + α + 2 π z = sin α t g 3 π 2 + α + 2 π z = — c t g α , c t g 3 π 2 + α + 2 π z = — t g α sin 3 π 2 — α + 2 π z = — cos α , cos 3 π 2 — α + 2 π z = — sin α t g 3 π 2 — α + 2 π z = c t g α , c t g 3 π 2 — α + 2 π z = t g α
В данном случае формулы записаны с радианами. Однако можно записать их и с использованием градусов. Достаточно только перевести радианы в градусы, заменив π на 180 градусов.
Однако можно записать их и с использованием градусов. Достаточно только перевести радианы в градусы, заменив π на 180 градусов.
Примеры использования формул приведения
Покажем, как пользоваться формулами приведения и как указанные формулы применяются при решении практических примеров.
Угол под знаком тригонометрической функции можно представить не одним, а множеством способов. Например, аргумент тригонометрической функции может быть представлен в видах ± α + 2 π z , π 2 ± α + 2 π z , π ± α + 2 π z , 3 π 2 ± α + 2 π z . Продемонстрируем это.
Возьмем угол α = 16 π 3 . Это угол можно записать так:
α = 16 π 3 = π + π 3 + 2 π · 2 α = 16 π 3 = — 2 π 3 + 2 π · 3 α = 16 π 3 = 3 π 2 — π 6 + 2 π
В зависимости от представления угла используется соответствующая формула приведения.
Возьмем тот же угол α = 16 π 3 и вычислим его тангенс
Пример 1. Использование формул приведения
α = 16 π 3 , t g α = ?
Представим угол α = 16 π 3 в виде α = π + π 3 + 2 π · 2
Этому представлению угла будет соответствовать формула приведения
t g (π + α + 2 π z) = t g α
t g 16 π 3 = t g π + π 3 + 2 π · 2 = t g π 3
Воспользовавшись таблицей, укажем значение тангенса
Теперь используем другое представление угла α = 16 π 3 .
Пример 2. Использование формул приведения
α = 16 π 3 , t g α = ? α = — 2 π 3 + 2 π · 3 t g 16 π 3 = t g — 2 π 3 + 2 π · 3 = — t g 2 π 3 = — (- 3) = 3
Наконец, для третьего представления угла запишем
Пример 3. Использование формул приведения
α = 16 π 3 = 3 π 2 — π 6 + 2 π t g 3 π 2 — α + 2 π z = c t g α t g α = t g (3 π 2 — π 6 + 2 π) = c t g π 6 = 3
Теперь приведем пример на использование формул приведения посложнее
Пример 4. Использование формул приведения
Представим sin 197 ° через синус и косинус острого угла.
Для того, чтобы можно было применять формулы приведения, нужно представить угол α = 197 ° в одном из видов
± α + 360 ° · z , 90 ° ± α + 360 ° · z , 180 ° ± α + 360 ° · z , 270 ° ± α + 360 ° · z . Согласно условию задачи, угол должен быть острым. Соответственно, у нас есть два способа для его представления:
197 ° = 180 ° + 17 ° 197 ° = 270 ° — 73 °
Получаем
sin 197 ° = sin (180 ° + 17 °) sin 197 ° = sin (270 ° — 73 °)
Теперь посмотрим на формулы приведения для синусов и выберем соответствующие
sin (π + α + 2 πz) = — sinα sin (3 π 2 — α + 2 πz) = — cosα sin 197 ° = sin (180 ° + 17 ° + 360 ° · z) = — sin 17 ° sin 197 ° = sin (270 ° — 73 ° + 360 ° · z) = — cos 73 °
Мнемоническое правило
Формул приведения много, и, к счастью, нет необходимости заучивать их наизусть.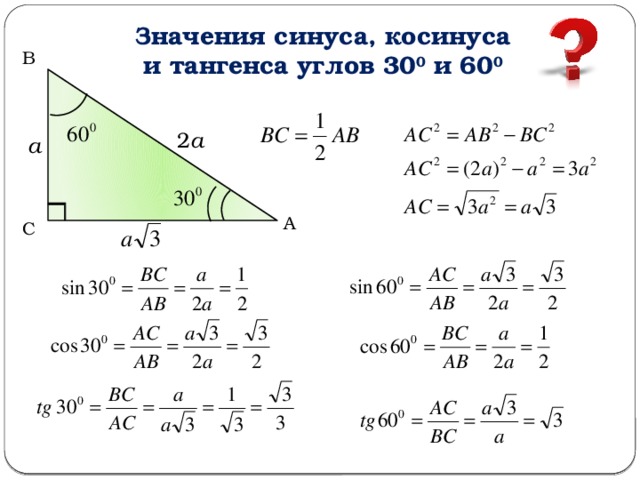 Существуют закономерности, по которым можно выводить формулы приведения для разных углов и тригонометрических функций. Эти закономерности называются мнемоническим правилом. Мнемоника — искусство запоминания. Мнемоническое правило состоит из трех частей, или содержит три этапа.
Существуют закономерности, по которым можно выводить формулы приведения для разных углов и тригонометрических функций. Эти закономерности называются мнемоническим правилом. Мнемоника — искусство запоминания. Мнемоническое правило состоит из трех частей, или содержит три этапа.
Мнемоническое правило
1. Аргумент исходной функции представляется в одном из видов
± α + 2 πz π 2 ± α + 2 πz π ± α + 2 πz 3 π 2 ± α + 2 πz
Угол α должен лежать в пределах от 0 до 90 градусов.
2. Определяется знак исходной тригонометрической функции. Такой же знак будет иметь функция, записываемая в правой части формулы.
3. Для углов ± α + 2 πz и π ± α + 2 πz название исходной функции остается неизменным, а для углов π 2 ± α + 2 πz и 3 π 2 ± α + 2 πz соответственно меняется на «кофункцию». Синус — на косинус. Тангенс — на котангенс.
Чтобы пользоваться мнемоническим праилом для формул приведения нужно уметь определять знаки тригонометрических функций по четвертям единичной окружности.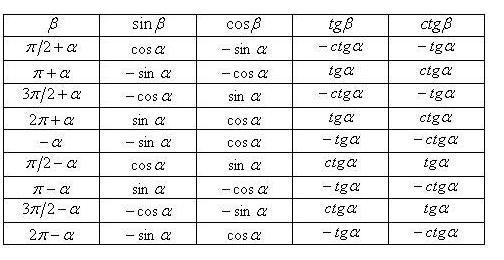 Разберем примеры применения мнемонического правила.
Разберем примеры применения мнемонического правила.
Пример 1. Использование мнемонического правила
Запишем формулы приведения для cos π 2 — α + 2 πz и t g π — α + 2 πz . α — улог первой четверти.
1. Так как по условию α — улог первой четверти, мы пропускаем первый пункт правила.
2. Определим знаки функций cos π 2 — α + 2 πz и t g π — α + 2 πz . Угол π 2 — α + 2 πz также является углом первой четверти, а угол π — α + 2 πz находится во второй четверти. В первой четверти функция косинуса положительна, а тангенс во второй четверти имеет знак минус. Запишем, как будут выглядеть искомые формулы на этом этапе.
cos π 2 — α + 2 πz = + t g π — α + 2 πz = —
3. Согласно третьему пункту для угла π 2 — α + 2 π название функции изменяется на конфуцию, а для угла π — α + 2 πz остается прежним. Запишем:
cos π 2 — α + 2 πz = + sin α t g π — α + 2 πz = — t g α
А теперь заглянем в формулы, приведенные выше, и убедимся в том, что мнемоническое правило работает.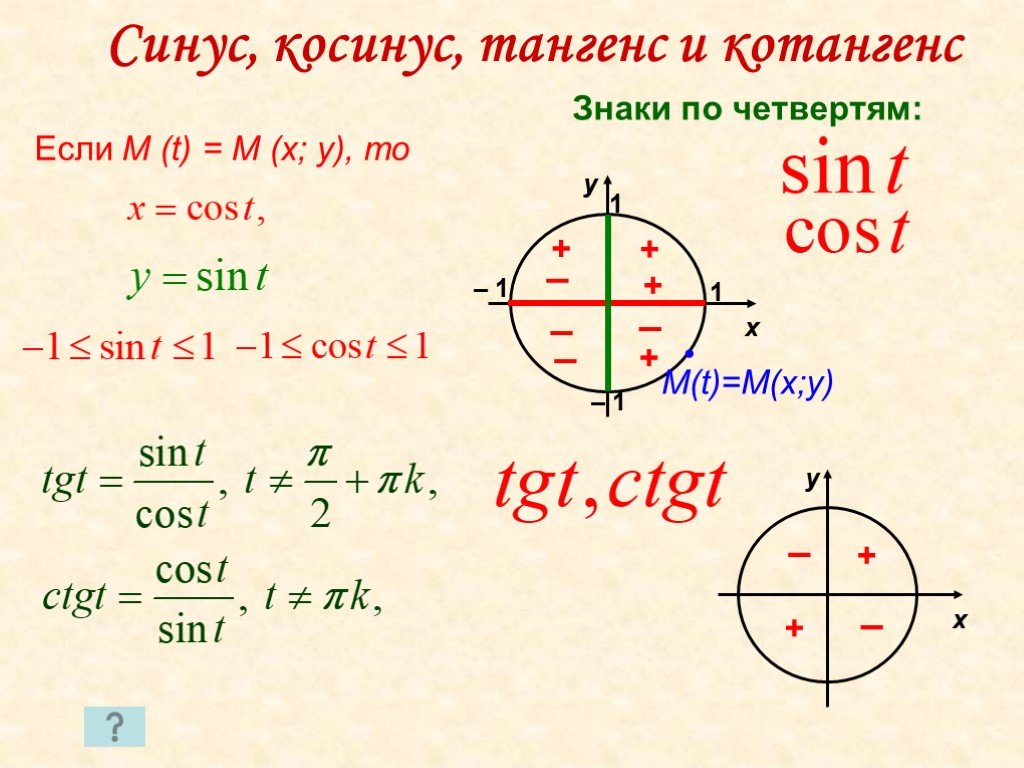
Рассмотрим пример с конкретным углом α = 777 ° . Приведем синус альфа к тригонометрической функции острого угла.
Пример 2. Использование мнемонического правила
1. Представим углол α = 777 ° в необходимом виде
777 ° = 57 ° + 360 ° · 2 777 ° = 90 ° — 33 ° + 360 ° · 2
2. Исходный угол — угол первой четверти. Значит, синус угла имеет положительный знак. В итоге имеем:
3. sin 777 ° = sin (57 ° + 360 ° · 2) = sin 57 ° sin 777 ° = sin (90 ° — 33 ° + 360 ° · 2) = cos 33 °
Теперь рассмотрим пример, который показывает, как важно правильно определить знак тригонометрической функции и правильно представить угол при использовании мнемонического правила. Повторим еще раз.
Важно!
Угол α должен быть острым!
Вычислим тангенс угла 5 π 3 . Из таблицы значений основных тригонометрических функций можно сразу взять значение t g 5 π 3 = — 3 , но мы применим мнемоническое правило.
Пример 3. Использование мнемонического правила
Представим угол α = 5 π 3 в необходимом виде и воспользуемся правилом
t g 5 π 3 = t g 3 π 2 + π 6 = — c t g π 6 = — 3 t g 5 π 3 = t g 2 π — π 3 = — t g π 3 = — 3
Если же представить угол альфа в виде 5 π 3 = π + 2 π 3 , то результат применениея мнемонического правила будет неверным.
t g 5 π 3 = t g π + 2 π 3 = — t g 2 π 3 = — (- 3) = 3
Неверный результат обусловлен тем, что угол 2 π 3 не явдяется острым.
Доказательство формул приведения основывается на свойствах периодичности и симметричности тригонометрических функций, а также на свойстве сдвига на углы π 2 и 3 π 2 . Доказательство справедливости всех формул приведения иожно проводить без учета слагаемого 2 πz , так как оно обозначает изменение угла на целое число полных оборотов и как раз отражает свойство периодичности.
Первые 16 формул следуют напрямую из свойств основных тригонометрических функций: синуса, косинуса, тангенса и котанганса.
Приведем доказательство формул приведения для синусов и косинусов
sin π 2 + α = cos α и cos π 2 + α = — sin α
Посмотрим на единичную окружность, начальная точка которой после повоторота на угол α перешла в точку A 1 x , y , а после поворота на угол π 2 + α — в точку A 2 . Из обеих точек проведем перпендикуляры к оси абсцисс.
Два прямоугольных треугольника O A 1 H 1 и O A 2 H 2 равны по гипотенузе и прилежащим к ней углам.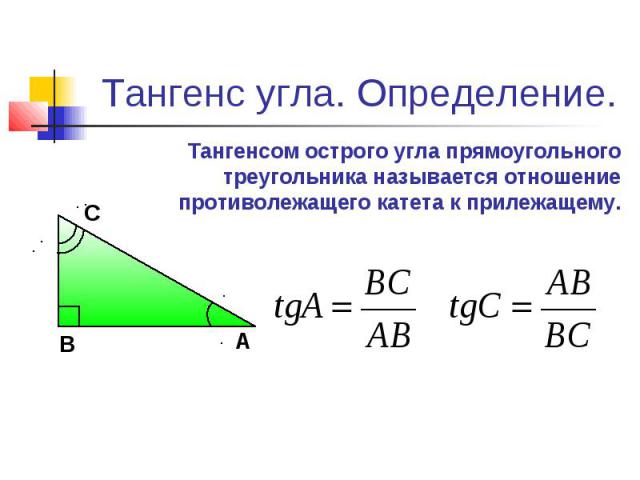 Из расположения точек на окружности и равенства треугольников можно сделать вывод о том, что точка A 2 имеет координаты A 2 — y , x . Используя определения синуса и косинуса, запишем:
Из расположения точек на окружности и равенства треугольников можно сделать вывод о том, что точка A 2 имеет координаты A 2 — y , x . Используя определения синуса и косинуса, запишем:
sin α = y , cos α = x , sin π 2 + α = x , cos π 2 + α = y
sin π 2 + α = cos α , cos π 2 + α = — sin α
С учетом основных тождеств тригонометрии и только что доказанного, можно записать
t g π 2 + α = sin π 2 + α cos π 2 + α = cos α — sin α = — c t g α c t g π 2 + α = cos π 2 + α sin π 2 + α = — sin α cos α = — t g α
Для доказательства формул приведения с аргументом π 2 — α его необходимо представить в виде π 2 + (- α) . Например:
cos π 2 — α = cos π 2 + (- α) = — sin (- α) = sin α
В доказательстве используются свойства тригонометрических функций с аргументами, противоположными по знаку.
Все остальные формулы приведения можно доказать на базе записанных выше.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Тема урока
- Изменение синуса, косинуса и тангенса при возрастании угла.

Цели урока
- Познакомиться с новыми определениями и вспомнить некоторые уже изученные.
- Познакомится с закономерностью изменений значений синуса косинуса и тангенса при возрастании угла.
- Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
- Воспитательные — посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.
Задачи урока
- Проверить знания учащихся.
План урока
- Повторение ранее изученного материала.
- Задачи на повторение.
- Изменение синуса, косинуса и тангенса при возрастании угла.
- Практическое применение.
Повторение ранее изученного материала
Начнем с самого начала и вспомним то что будет полезно освежить в памяти. Что же такое синус, косинус и тангенс и к какому разделу геометрии относятся эти понятия.
Тригонометрия — это такое сложное греческое слово: тригонон — треугольник, метро — мерять. Стало быть по-гречески это означает: мерятся треугольниками.
Предмети > Математика > Математика 8 класс
Урок и презентация на тему: «Применение формул приведения при решении задач»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
1С: Школа. Интерактивные задания на построение для 7-10 классов
1С: Школа. Решаем задачи по геометрии. Интерактивные задания на построение в пространстве для 10–11 классов
Что будем изучать:
1. Немного повторим.
2. Правила для формул приведения.
3. Таблица преобразований для формул приведения.
4. Примеры.
Повторение тригонометрических функций
Ребята, с формулами привидения вы уже сталкивались, но так их еще не называли.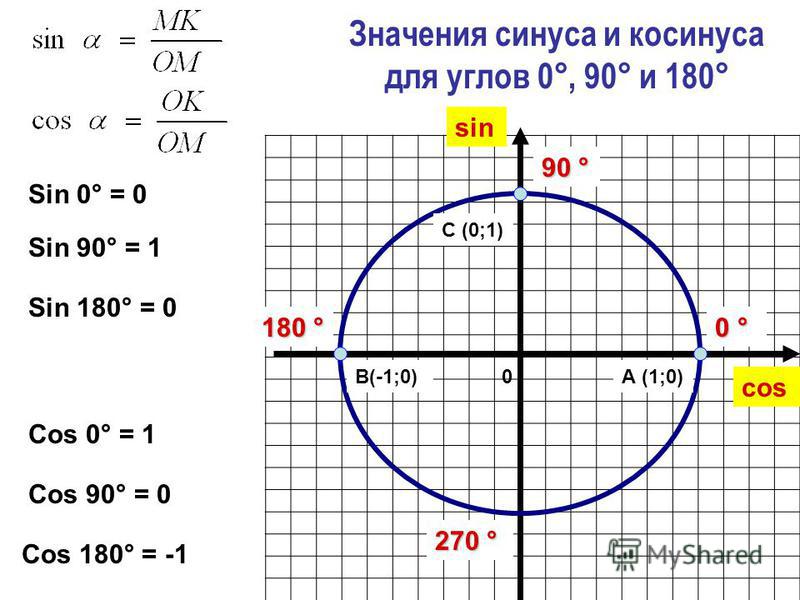 Как думаете: где?
Как думаете: где?
Посмотрите на наши рисунки. Правильно, когда вводили определения тригонометрических функций.
Правило для формул приведения
Давайте введем основное правило: Если под знаком тригонометрической функции содержится число вида π×n/2 + t, где n – любое целое число, то нашу тригонометрическую функцию можно привести к более простому виду, которая будет содержать только аргумент t. Такие формулы и называют формулами привидения.
Вспомним некоторые формулы:
- sin(t + 2π*k) = sin(t)
- cos(t + 2π*k) = cos(t)
- sin(t + π) = -sin(t)
- cos(t + π) = -cos(t)
- sin(t + π/2) = cos(t)
- cos(t + π/2) = -sin(t)
- tg(t + π*k) = tg(x)
- ctg(t + π*k) = ctg(x)
формул привидения очень много, давайте составим правило по которому будем определять наши тригонометрические функции при использовании формул привидения :
- Если под знаком тригонометрической функции содержатся числа вида: π + t, π — t, 2π + t и 2π — t, то функция не изменится, то есть, например, синус останется синусом, котангенс останется котангенсом.

- Если под знаком тригонометрической функции содержатся числа вида: π/2 + t, π/2 — t,
3π/2 + t и 3π/2 — t, то функция изменится на родственную, т. е. синус станет косинусом, котангенс станет тангенсом. - Перед получившийся функцией, надо поставить тот знак, который имела бы преобразуемая функция при условии 0
Эти правила применимы и когда аргумент функции задан в градусах!
Так же мы можем составить таблицу преобразований тригонометрических функций:
Примеры применения формул приведения
1.Преобразуем cos(π + t). Наименование функции остается, т.е. получим cos(t). Далее предположим, что π/2
2. Преобразуем sin(π/2 + t). Наименование функции изменяется, т.е. получим cos(t). Далее предположим что 0 sin(t + π/2) = cos(t)
3. Преобразуем tg(π + t). Наименование функции остается, т.е. получим tg(t). Далее предположим, что 0
4. Преобразуем ctg(270 0 + t). Наименование функции изменяется, то есть получим tg(t). Далее предположим что 0
Далее предположим что 0
Задачи с формулами приведения для самостоятельного решения
Ребята, преобразуйте самостоятельно, используя наши правила:
1) tg(π + t),
2) tg(2π — t),
3) ctg(π — t),
4) tg(π/2 — t),
5) ctg(3π + t),
6) sin(2π + t),
7) sin(π/2 + 5t),
8) sin(π/2 — t),
9) sin(2π — t),
10) cos(2π — t),
11) cos(3π/2 + 8t),
12) cos(3π/2 — t),
13) cos(π — t).
PDF БОЛЬШЕ ТРИГОНОМЕТРИИ Обзор модуля В этом модуле вы научитесь строить графики функций синуса, косинуса и тангенса. Вы также узнаете, как изменения в стандартном уравнении могут изменить амплитуду и период графика. Пифагорейское тождество будет доказано, а затем использовано для нахождения тригонометрических значений.  График характеристических кривых тригонометрических функций — синуса, косинуса и тангенса Тригонометрические функции можно изобразить в виде графика в прямоугольной системе координат путем нанесения точек, координаты которых принадлежат функции. В таблице ниже показаны значения функции синуса для критических значений θ , где 0 ≤ θ ≤ 2π. Каждое из этих значений можно соединить в пары и нанести на график с помощью точек на 9-й шкале.0028 xy -плоскость, позволив « θ » разместить на оси x и отобразить sin θ на оси y следующим образом: Если все значения в таблице отобразить таким образом, получится следующий стандартный график sin θ : Поскольку областью определения синуса являются действительные числа, график y = sin θ рисуется путем повторения части, показанной на графике выше.  Часть графика y = sin θ показана ниже: Часть графика y = sin θ показана ниже:Синусоидальная функция имеет период 2π, потому что синусоида повторяется каждые 2π единицы. Максимальное значение функции равно 1, а минимальное значение функции равно –1. Средняя линия функции – это горизонтальная линия посередине между максимальным и минимальным значениями функции. Для y = sin θ , средней линией является линия y = 0 (горизонтальная ось). Амплитуда функции равна половине разницы между максимальным и минимальным значениями. Амплитуда функции y = sin θ равна 1. Обратите внимание, что синусоидальная функция имеет значение 0 всякий раз, когда θ кратно π. Таким образом, sin 0, sin π, sin 2π, sin 3π…, все имеют значения 0. График функции косинуса рисуется так же, как график функции синуса. В таблице ниже показаны значения функции косинуса для критических значений θ , где 0 ≤ θ ≤ 2π. Если изобразить все значения в таблице, то получится стандартный график косинуса: Чтобы изобразить эти функции на графическом калькуляторе, используя радианы, установите режим в радианы. Введите следующие параметры:
Нажмите клавишу y = и введите функцию, график которой вы хотите изобразить, то есть y = sin x или y = cos x .  Чтобы изобразить эти функции на графическом калькуляторе с использованием градусов, установите режим на градусы. Введите следующие параметры:
График функции тангенса также можно построить, нанеся точки. В таблице ниже показаны значения функции тангенса для критических значений θ , где 0 ≤ θ ≤ 2π. Обратите внимание, что для θ существуют значения, при которых функция тангенса не определена. График имеет вертикальные асимптоты при этих значениях. Следующие диаграммы служат характеристическими кривыми для наших графиков для всех углов от 0 до 2π (от 0 до 360). Кривые синусов, косинусов и касательных (06:08) S топ! Перейдите к вопросам 1–8 по этому разделу, затем вернитесь, чтобы перейти к следующему разделу.  Вариации тригонометрических функций Как и в случае с другими функциями, изменения в уравнении родительского графика могут повлиять на внешний вид графика. Изучим изменения амплитуды и периода характеристических графиков синуса и косинуса, исследуя графики y = A sin( Bx ) и y = A cos( Bx ). Амплитуда ( А ) Значение A влияет на амплитуду. Это значение определяет максимальное и минимальное вертикальные значения функции. В характеристической кривой y = sin θ амплитуда равна A = 1. С настройками окна вашего калькулятора, установленными для значений, используемых для нахождения характеристических кривых в первой части этого единицу, введите следующее уравнение в и посмотреть их графики:
Первой кривой для построения графика была характеристическая кривая для y = sin θ . Вторая кривая для y = 3sin θ находится за пределами экрана по вертикали, потому что при амплитуде «3» она достигает своих y -максимального и y -минимального значений 3 и –3 за пределами калькулятора. настройки окна для Ymin и Ymax. (Чтобы увидеть всю эту кривую, вы можете соответствующим образом настроить эти параметры). График третьей кривой достигает максимального и минимального значения и соответственно. Важной особенностью всех кривых является то, что все они достигают своих максимальных и минимальных значений при θ = и , и все три пересекают ось x в точках 0, π и 2π. 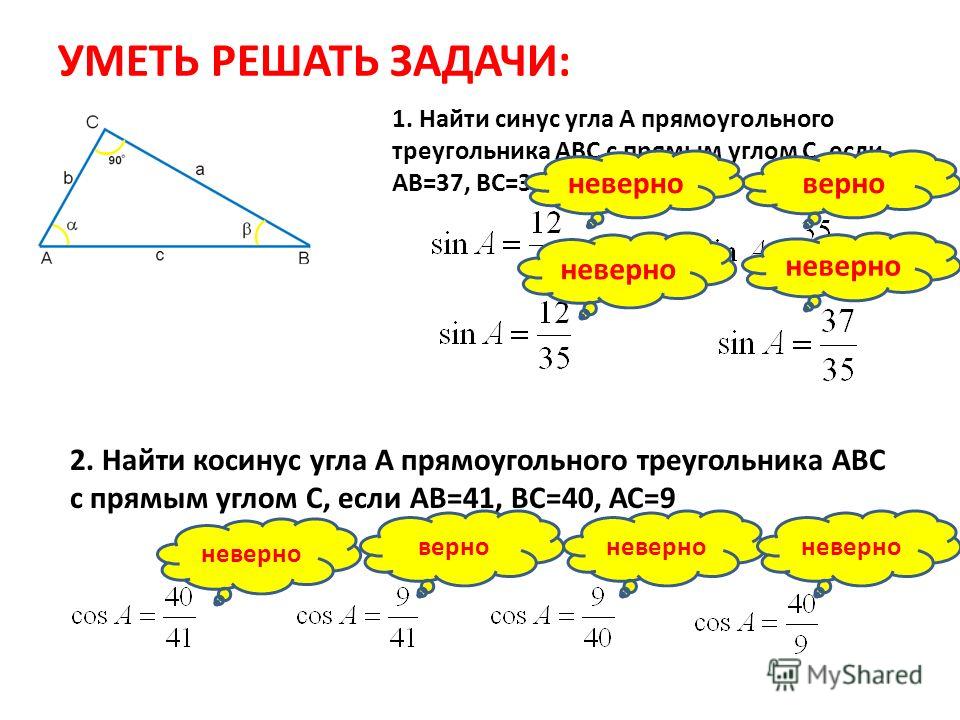 Изменение амплитуды тригонометрической кривой «растягивает» кривую по вертикали, но не влияет на значения θ , где она будет принимать максимальное, минимальное и нулевое значения. Изменение амплитуды тригонометрической кривой «растягивает» кривую по вертикали, но не влияет на значения θ , где она будет принимать максимальное, минимальное и нулевое значения.Когда A отрицательное значение, график представляет собой отражение по оси x ( y = sin θ отображается красным, а y = –sin θ показан синим цветом). Амплитуда обеих этих функций равна 1, так как амплитуда | А |. В функции y = A cos θ амплитуда работает аналогично функции y = A sin θ . Касательная функция не имеет амплитуды, потому что у нее нет максимального или минимального значения. В функции y = A tan θ , изменения A влияют на крутизну графика. Частота и период Следующим компонентом стандартного уравнения является значение «B», «Частота» и «Период», который равен . На их характеристических графиках каждое тригонометрическое соотношение демонстрирует один полный «цикл» или «период» от 0 до 2π с «частотой», равной единице. Оба эти значения можно отрегулировать, изменив значение « B ” в стандартном уравнении. На их характеристических графиках каждое тригонометрическое соотношение демонстрирует один полный «цикл» или «период» от 0 до 2π с «частотой», равной единице. Оба эти значения можно отрегулировать, изменив значение « B ” в стандартном уравнении.Введите следующие уравнения в свой калькулятор и просмотрите каждый график.
Когда Y 2 отображается на графике, между 0 и 2π появляются две полные косинусные кривые. Для Y 2 = cos(2 x ), значение B = 2. Таким образом, оно проходит 2 раза от 0 до 2π. Период функции = = π. Таким образом, он совершает один полный цикл каждые π единиц. Если ввести третье уравнение в Y 3 например: Y 3 = cos(0,5 x ) и просмотреть его график, появится только первая половина характеристической кривой косинуса. Для функции y = A tan( Bx ), частота равна B . Период указан потому, что период загара x равен π вместо 2π. Кривые синусов, косинусов и касательных (продолжение) (11:50) S топ! Перейдите к вопросам № 9–17 , чтобы заполнить этот модуль. 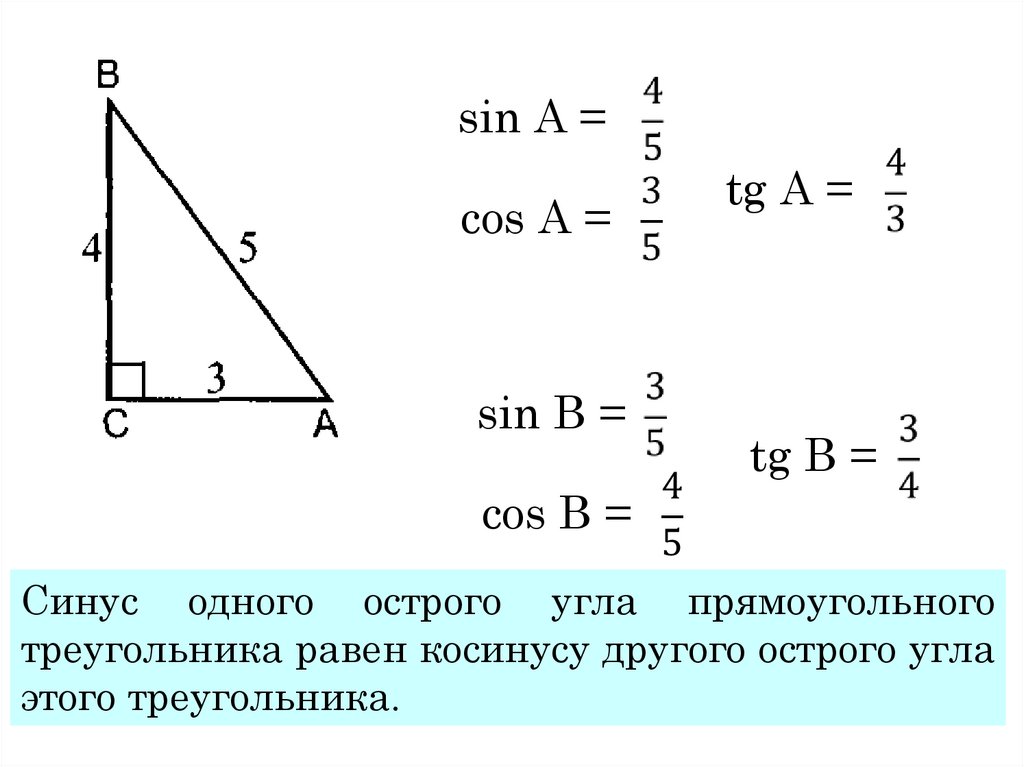 Тождество Пифагора Тождество — это любое уравнение, истинное для каждого числа в области определения уравнения. Тождество, включающее тригонометрические выражения, называется тригонометрическим тождеством. Важным тригонометрическим тождеством является пифагорейское тождество. Пифагорейское тождество можно проверить, используя единичный круг и теорему Пифагора. Помните из предыдущего раздела, что прямоугольный треугольник можно вписать в окружность следующим образом. Для угла в стандартном положении конечная сторона угла в единичной окружности попадает в точку, координата x которой является косинусом угла, а координата y — синусом угла, то есть cos θ = x и sin θ = y . Уравнение единичного круга равно х 2 + у 2 = 1.
Тождество Пифагора: cos 2 θ + sin 2 θ = 1, Тождество Пифагора, чтобы найти значения других тригонометрических функций. Имейте в виду, что знаки триггерных функций различны в каждом квадранте. Изучите иллюстрацию ниже. Стоп! Перейдите к вопросам №18–28, чтобы заполнить этот блок. |
Определение фазового сдвига функции синуса или косинуса
Все ресурсы Precalculus
12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept
Precalculus Помощь » Графики и обратные тригонометрические функции » График функций синуса и косинуса » Найти фазовый сдвиг функции синуса или косинуса
Найти фазовый сдвиг функции .
Возможные ответы:
Правильный ответ:
Объяснение:
В формуле
.
представляет фазовый сдвиг.
Вставив то, что мы знаем, мы получим:
.
Упрощенно, тогда фаза .
Сообщить об ошибке
Пожалуйста, выберите лучший ответ из следующих вариантов.
Опишите фазовый сдвиг следующей функции:
Возможные ответы:
Сдвиг вверх на радиан.
Сдвиг влево на радиан.
Вертикальное растяжение в радианах.
Сдвиг вниз на радиан.
Правильный ответ:
Сдвиг влево на радиан.
Объяснение:
Поскольку добавляется в скобках, произойдет сдвиг по горизонтали. Цель состоит в том, чтобы сохранить ноль в круглых скобках, чтобы вы сместили радианы влево.
Цель состоит в том, чтобы сохранить ноль в круглых скобках, чтобы вы сместили радианы влево.
Сообщить об ошибке
Какое уравнение даст этот график?
Возможные ответы:
Правильный ответ:
Пояснение:
Это график синуса, но сдвинутый вправо на единицы. Чтобы отразить этот сдвиг, следует вычесть из x.
Таким образом получается
.
Сообщить об ошибке
Какое уравнение даст этот синусоидальный график?
Возможные ответы:
Правильный ответ:
Объяснение:
Амплитуда графика равна 2, но он сдвинут вниз на 1:
С точки зрения уравнения это ставит 2 перед грехом и -1 в конце.
Это облегчает понимание того, что график начинается [находится в 0], где .
Фазовый сдвиг вправо или .
Сообщить об ошибке
Напишите уравнение синусоидального графика с максимумом в и минимумом в .
Возможные ответы:
Правильный ответ:
Пояснение:
Для написания этого уравнения полезно начертить график:
Указав точки максимума и минимума, мы видим, что этот график сдвинут вверх на 1 и имеет амплитуду 2.
Расстояние от точки максимума до точки минимума равно половине длины волны. В этом случае длина волны равна . Это означает, что полная длина волны равна , а частота равна 1,9.0009
Этот эскиз показывает, что график начинается слева от оси Y. Чтобы выяснить, где именно, вычтите из максимальной координаты x :
.
Наше уравнение будет иметь вид, где A — амплитуда, f — частота, h — сдвиг по горизонтали, а k — сдвиг по вертикали.
Этот график имеет уравнение
.
Сообщить об ошибке
Напишите уравнение косинуса с максимумом в и минимумом в .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы написать это уравнение, полезно начертить график:
Пунктирная линия находится в точке , где достигается максимум и, следовательно, где начинается график. Это означает, что график сдвинут вправо.
Расстояние от максимума до минимума равно половине всей длины волны. Вот .
Поскольку половина длины волны равна , это означает, что полная длина волны равна , поэтому частота равна всего 1,
Амплитуда равна 3, потому что график идет симметрично от -3 до 3.
Уравнение будет иметь вид, где A — амплитуда, f — частота, h — сдвиг по горизонтали, а k — сдвиг по вертикали.
Это уравнение равно
.
Сообщить об ошибке
Напишите уравнение для синуса с максимумом в и минимумом в .
Возможные ответы:
Правильный ответ:
Объяснение:
Уравнение будет иметь вид, где A — амплитуда, f — частота, h — сдвиг по горизонтали, а k — сдвиг по вертикали.
Чтобы написать уравнение, полезно начертить график:
Из построения максимума и минимума видно, что график находится в центре с амплитудой 3.
Расстояние от максимума до минимум составляет половину длины волны. Для этого графика это расстояние равно .
Это означает, что общая длина волны равна 1, а частота равна 1.
График начинается за точкой максимума. Чтобы определить это значение x, вычтите из x-координаты максимума:
Наше уравнение:
.




 Асимптота — это воображаемая линия, к которой график приближается, но никогда не касается. Обратите внимание, что график касательной будет иметь асимптоту при всех половинных значениях π, таких как и т. д. Функция пересекает x — ось в нуле, на полпути между асимптотами. Таким образом, функция касательной будет пересекать ось x всякий раз, когда θ кратно π. Таким образом, тангенс 0, тангенс π, тангенс 2π, тангенс 3π…, все имеют значения 0. Поскольку график повторяется каждые π радиан, период функции тангенса равен π. Функция тангенса не имеет высоты, так как у нее нет ни максимального, ни минимального значения.
Асимптота — это воображаемая линия, к которой график приближается, но никогда не касается. Обратите внимание, что график касательной будет иметь асимптоту при всех половинных значениях π, таких как и т. д. Функция пересекает x — ось в нуле, на полпути между асимптотами. Таким образом, функция касательной будет пересекать ось x всякий раз, когда θ кратно π. Таким образом, тангенс 0, тангенс π, тангенс 2π, тангенс 3π…, все имеют значения 0. Поскольку график повторяется каждые π радиан, период функции тангенса равен π. Функция тангенса не имеет высоты, так как у нее нет ни максимального, ни минимального значения. 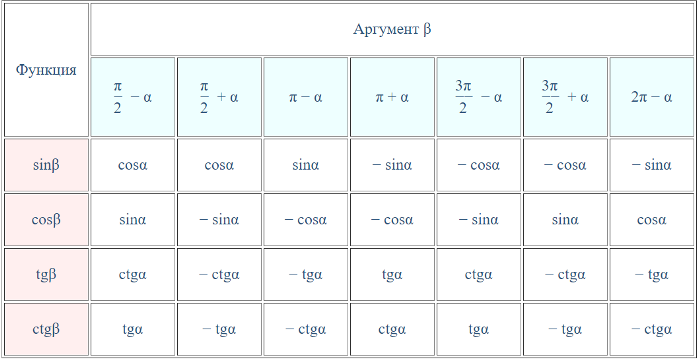
 Значение В = 0,5. Следовательно, значение « B » — частота — определяет, сколько характеристических кривых появится в стандартном окне просмотра от 0 до 2π. Период функции Y = cos(0,5 x ) можно найти, заменив 0,5 на B в выражении . Период функции будет = = 4π. Таким образом, он совершает один полный цикл каждые 4π единиц.
Значение В = 0,5. Следовательно, значение « B » — частота — определяет, сколько характеристических кривых появится в стандартном окне просмотра от 0 до 2π. Период функции Y = cos(0,5 x ) можно найти, заменив 0,5 на B в выражении . Период функции будет = = 4π. Таким образом, он совершает один полный цикл каждые 4π единиц.