Геометрия Равенство векторов
Материалы к уроку
Конспект урока
. Равенство векторов
|
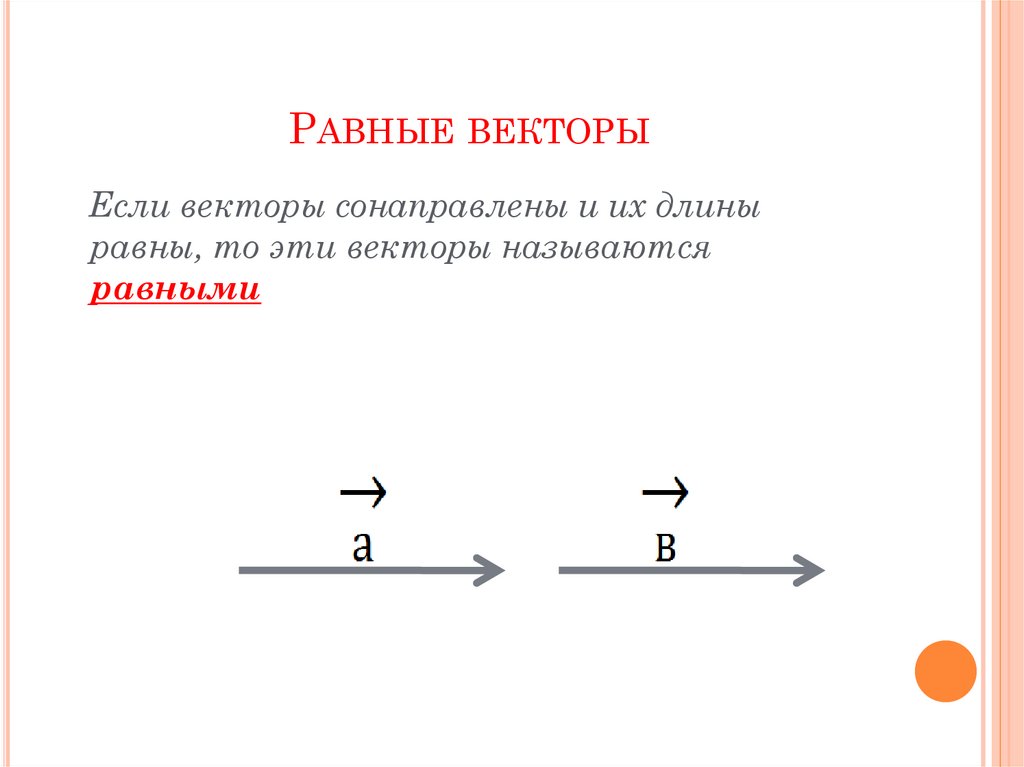
Введем определение равных векторов. Векторы называются равными, если они сонаправлены и их длины равны.
|
Текст Равенство векторов Определение: Векторы называются равными, если они сонаправлены и их длины равны.
|
|
Для примера рассмотрим прямоугольный параллелепипед. Векторы АВ и ЕС, отмеченные на параллелепипеде, равны, так как они сонаправлены и их длины равны. |
Рисунок параллелепипеда с выделенными векторами АВ и ЕС
|
|
А на этом рисунке векторы АВ и СМ неравны, так как они сонаправлены, но их длины неравны. |
Рисунок параллелепипеда с выделенными векторами
|
|
На этом параллелепипеде векторы АН и ОК так же неравны, так как нарушено условие сонаправленности. |
Рисунок параллелепипеда с выделенными векторами
|
|
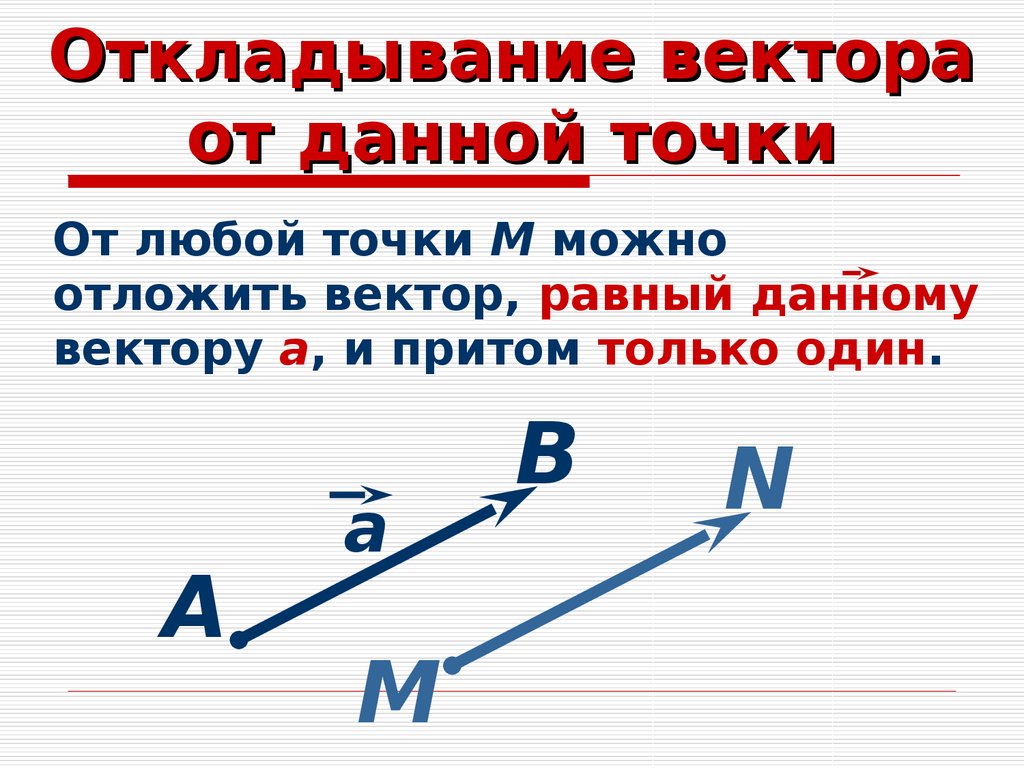
Если точка М – начало вектора а, то говорят, что вектор а отложен от точки М. |
Рисунок вектора с началом в точке М
|
|
Докажем, что от любой точки пространства можно отложить вектор, равный данному, и притом только один. Вспомним определения: Векторы называются равными, если они сонаправлены и их длины равны. Если векторы коллинеарны и при этом их лучи сонаправлены, то эти векторы называются сонаправленными. Пусть нам дан вектор а и точка М. Проведем через вектор а и точку М плоскость. В этой плоскости построим вектор МК, равны вектору а. Очевидно, что вектор МК – искомый вектор. Из построения следует, что этот вектор единственный с началом в точке М и равный вектору а.
|
Текст
|
|
Решим задачу № 323. На рисунке изображен тетраэдр АВСD, ребра которого все равны. Точки М, N, P и Q – середины сторон AB, AD, DC, BC. Необходимо выписать все пары равных векторов, изображенных на рисунке, и определить вид четырехугольника МNPQ. |
Текст Задача № 323 Дано: точки М, N, P,Q – середины сторон AB, AD, DC, BC; AB=AD= DC=BC=DD=AC; Задание: а) выписать пары равных векторов; б) определить вид четырехугольника MNHQ . Рисунок тетраэдра с серединами сторон из условия задачи
|
|
Векторы равны, если они сонаправлены и их длины равны. Из условия задачи знаем, что точка Р середина DC,значит, отрезки DP и PC равны. Векторы DP и PC сонаправлены, а, значит, эти векторы равны. NP-средняя линия треугольника ADC, значит, NP равно половинеAC и параллельно AC; MQ-средняя линия тр. Значит, NP равно MQ, NP параллельно MQ. Из рисунка видим, что они сонаправленны. Векторы PN и QM равны. PQ-средняя линия треугольника DВC; PQ равно половине DB и параллельно DB; NM-средняя линия треугольника ADB, MN равно половине DB и параллельно DB. Делаем вывод, что вектор QP равен вектору MN.
|
Рисунок прежний |
|
Пары равных векторов: MN и QP, PN и QM, DP и PC.
|
Рисунок прежний
|
|
Определим вид четырехугольника МNPQ. По условию все ребра тетраэдра равны, значит, он правильный и скрещивающиеся ребра в нем перпендикулярны. Имеем: NP параллельно АС и параллельно QM. MN параллельно DB и параллельно QP. Отрезки MN, QP, PN и QM равны. Учитывая перпендикулярность DB и АС, можно сделать вывод, что MNPQ — квадрат. Задача решена.
|
Рисунок прежний
|
Комментарий: сценарий хороший)
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Равные вектора.
Навигация по странице:
- Определение равных векторов
- Условие равенства векторов
- Примеры задач на равенство векторов
- плоские задачи
- пространственные задачи
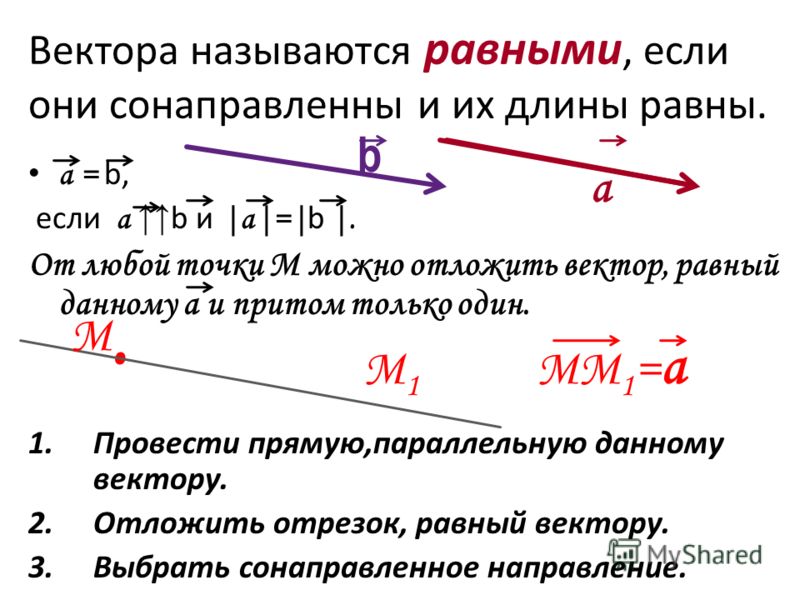
Определение. Вектора a и b называются равными, если они имеют одинаковую длину, лежат на параллельных прямых или на одной прямой, и направлены в одном направлении. (рис. 1).
Вектора a и b называются равными, если они имеют одинаковую длину, лежат на параллельных прямых или на одной прямой, и направлены в одном направлении. (рис. 1).
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b, если a↑↑b и |a| = |b|.
Условие равенства векторов.Вектора равны, если их координаты равны.
| рис. 1 |
Примеры плоских задач на равенство векторов
Пример 1. Определить какие из векторов равны a = {1; 2}, b = {1; 2}, c = {3; 2}.
Решение:
a = b — так как их координаты равны,
a ≠ c — так как их координаты не равны,
b ≠ c — так как их координаты не равны.
Пример 2. При каком значении параметра n вектора a = {1; 8;} и b = {1; 2n} равны.
Решение:
Проверим равенство компонентов векторов
ax = bx = 1
ay = by => 8 = 2n => n = 8/2 = 4
Ответ: при n = 4 вектора a и b равны.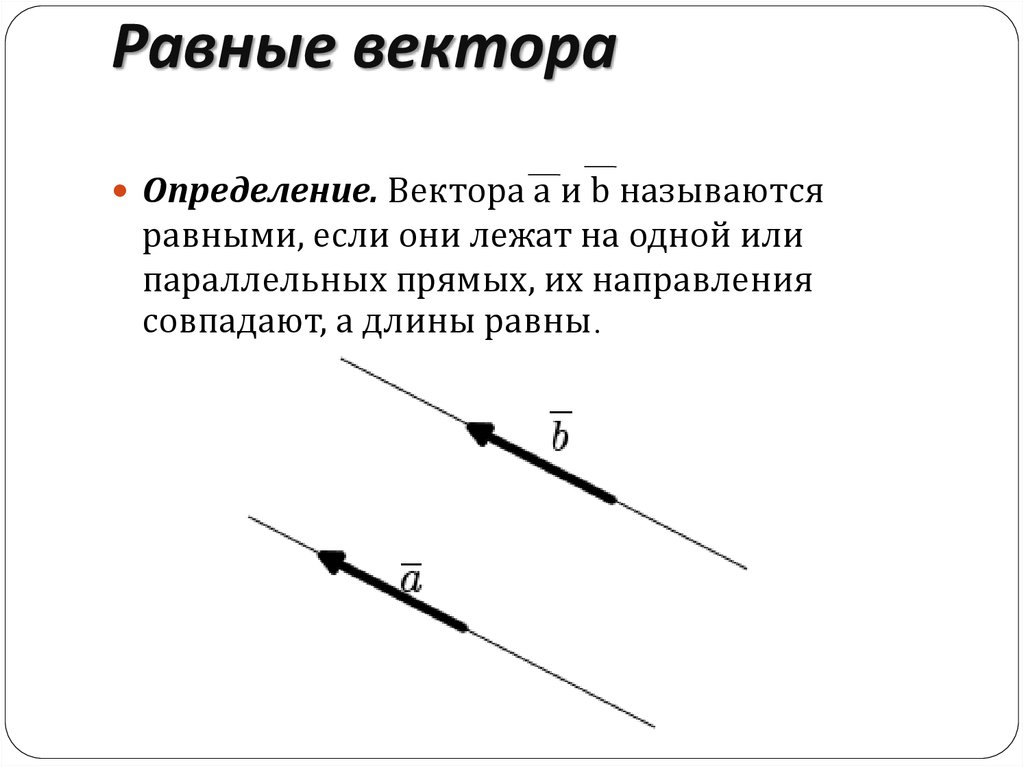
Примеры пространственных задач на равенство векторов
Пример 3. Определить какие из векторов равны a = {1; 2; 4}, b = {1; 2; 2}, c = {1; 2; 4}.
Решение:
a = c — так как их координаты равны,
b ≠ c — так как их координаты не равны.
Пример 4. При каком значении параметра n вектора a = {1; 2; 4} и b = {1; 2; 2n} равны.
Решение:
Проверим равенство компонентов векторов
ax = bx = 1
ay = by = 2
az = bz => 4 = 2n => n = 4/2 = 2
Ответ: при n = 2 вектора a и b равны.
Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису
Онлайн калькуляторы с векторами
Онлайн упражнения с векторами на плоскости
Онлайн упражнения с векторами в пространстве
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Математика и наука были изобретены людьми для описания и
понимать окружающий мир. На этом слайде мы показываем три примера, в которых два вектора
по сравнению.
Векторы обычно обозначаются на рисунках стрелкой.
Длина стрелки указывает величину и
кончик стрелки указывает направление. Вектор
помечены буквой в алфавитном порядке
буква с линией сверху, чтобы отличить ее от скаляра.
Наши шрифты для веб-печати не поддерживают эту запись, поэтому мы будем использовать
жирная буква для вектора. Пример №1: у нас есть два вектора с одинаковым направлением, но величины (или длины векторов) различны. Вектор и не равен вектору b в этом примере. Этот пример кажется довольно просто, потому что то же правило применимо и к скалярам; если величина разная, количества не равны. Объект весом 50 фунтов не равен объекту весом 25 фунтов. Пример №2: Этот пример немного сложнее.
В этом случае у нас есть два вектора с
одинаковые по величине, но направления разные. Вектор и не равен вектору b в этом примере. Если бы вектор был
скорости, это говорит нам о том, что автомобиль, движущийся со скоростью 45 миль в час на северо-восток
окажется в другом месте, чем другая машина, также движущаяся со скоростью 45 миль в час
строго на восток. За один час они оба пройдут 45 миль, но места
будет другим. Пример №3: В этом примере у нас есть два вектора одинаковой длины. и одинаковое направление. Вектор равен вектору b . Чтобы два вектора были равны, они должны иметь как модуль, так и направления равны. Виды деятельности: Экскурсии с гидом Навигация ..
|
линейная алгебра — Каковы условия равенства двух векторов?
В обычной математической формулировке общих векторов, т. е. как элементов векторного пространства, векторы не имеют такой вещи, как «позиции», как и обычные числа. Вам не нужна «позиция», чтобы сказать, что температуры, измеренные в двух разных точках комнаты, равны, поэтому пара векторов, которые применяются в двух разных точках, также не нуждаются в «позициях», чтобы называть их «равный».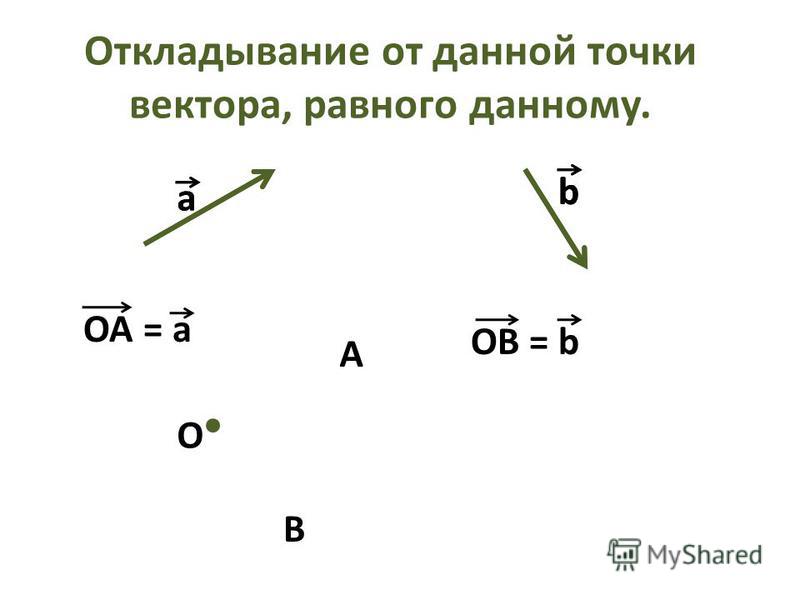
Важным свойством векторов является то, что вы можете «добавлять» их от до «позиций» или лучше, точек . В частности, если $P$ — точка, а $\mathbf{v}$ — вектор, то $P + \mathbf{v}$ — другая точка, удаленная от нее на $|\mathbf{v}|$, и от $P$ к направлению, закодированному в $\mathbf{v}$. Покоординатно, если $P = (P_x, P_y)$ и $\mathbf{v} = \langle v_x, v_y \rangle$, то $P + \mathbf{v} = (P_x + v_x, P_y + v_y)$.
В контексте физики такие векторы, как сила и скорость, которые не непосредственно имеют единиц (или физического измерения) позиции, конечно, не могут быть добавлены к позициям, но в конечном счете они относятся к ним каким-то другим более косвенным образом, который все еще согласуется с этим, часто предполагая комбинации с другими векторами, и константы, которые при умножении изменяют свою физическую размерность. Конечно, в вашем случае оба вектора и имеют такие единицы, поэтому имеет смысл говорить о них именно так, но важно помнить о таких вещах, как сила, скорость и т.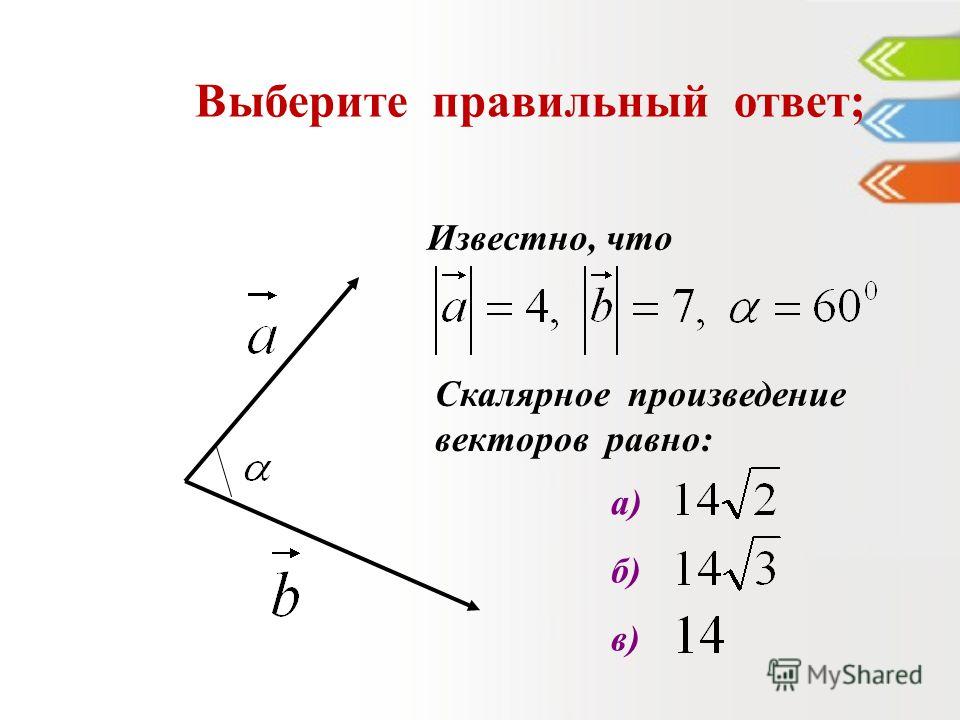 д.
д.
В геометрическом контексте сказать, что «вектор является нормальным», означает на самом деле сказать, что сегмент , созданный применением этого вектора, является нормальным к поверхности в данной точке, то есть сегмент $\overline{PQ} $ с $Q = P + \mathbf{v}$, когда $P$ — искомая точка на поверхности. Другой, эквивалентный способ, который является более прямо «векторным», состоит в том, что вектор нормальен к плоскости, если вектор нормальен к любому вектору, который переводит точку на плоскости в любую другую точку на плоскости, и для криволинейных поверхностей конечно, естественное продолжение обоих из них через касательную плоскость.
Так почему два вектора равны? Вообще говоря, любые два математических объекта равны , если все характеризующие данные между ними идентичны. Для векторов релевантными характеристиками являются величина и направление, хотя последнее довольно сложно сформулировать, поэтому часто проще вместо этого с самого начала характеризовать их декартовыми компонентами, а именно.


 И
И
 ABC, MQ равно половине AC и параллельно AC;
ABC, MQ равно половине AC и параллельно AC;
 Заметим, что существуют некоторые величины и процессы в
наш мир, которые зависят от направления , в котором
они происходят, и есть некоторые величины, которые не зависят
по направлению.
Математики и ученые называют количество
который зависит от направления a количество векторов . Количество
которая не зависит от направления, называется скалярной величиной .
А
векторное количество
имеет две характеристики: величина и направление .
При сравнении
две векторные величины одного и того же типа, вы должны сравнить обе
величина и направление.
Заметим, что существуют некоторые величины и процессы в
наш мир, которые зависят от направления , в котором
они происходят, и есть некоторые величины, которые не зависят
по направлению.
Математики и ученые называют количество
который зависит от направления a количество векторов . Количество
которая не зависит от направления, называется скалярной величиной .
А
векторное количество
имеет две характеристики: величина и направление .
При сравнении
две векторные величины одного и того же типа, вы должны сравнить обе
величина и направление.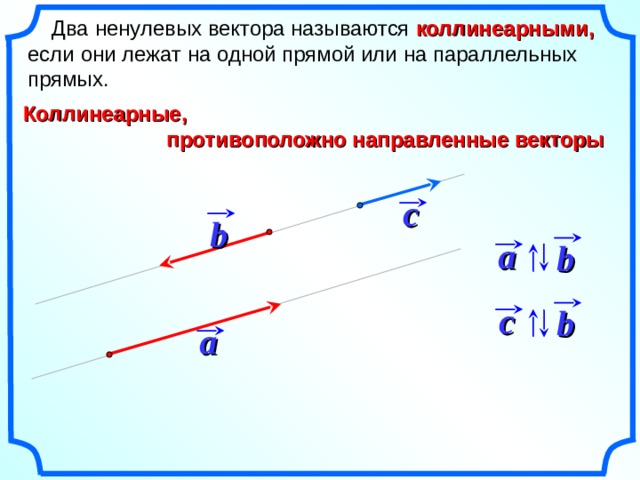 Мы будем сравнивать два вектора, и и б . Это могут быть силы, скорости или ускорения;
это действительно не имеет значения.
Мы будем сравнивать два вектора, и и б . Это могут быть силы, скорости или ускорения;
это действительно не имеет значения.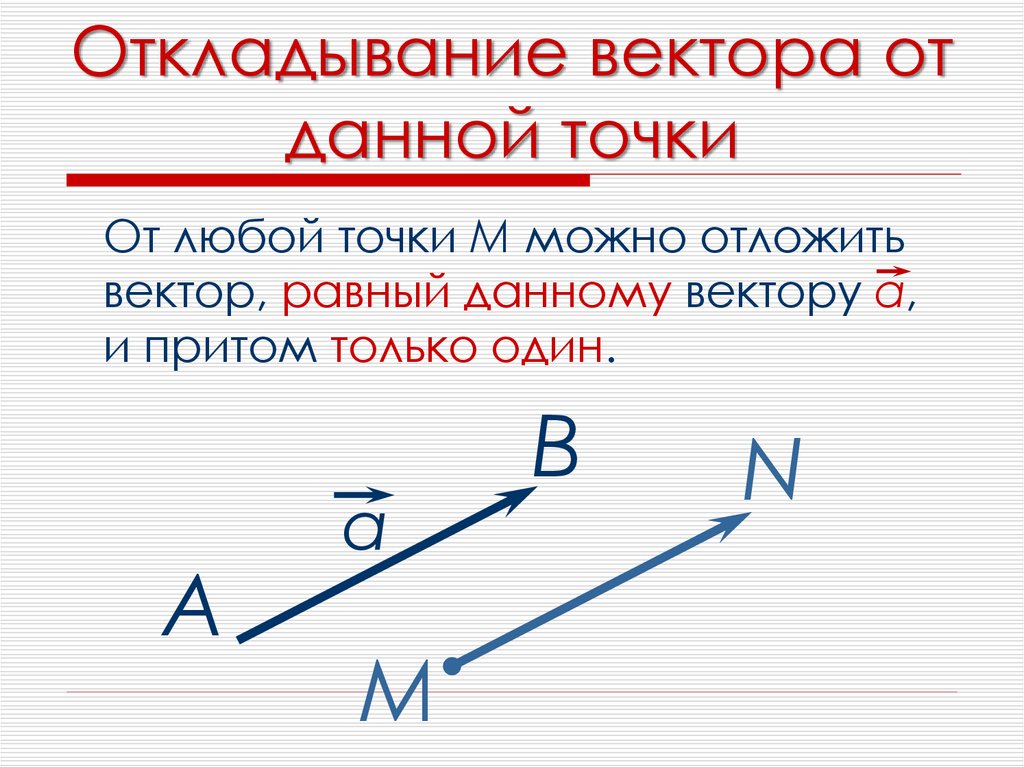 Через два часа они будут еще дальше друг от друга.
Через два часа они будут еще дальше друг от друга.