|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного… История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации… Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства… Интересное: Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются… Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны. Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
Крестьянин купил корову, козу, овцу и свинью, заплатив 1325р. Два летчика вылетели одновременно из одного города в два различных пункта. Кто из них долетит до места назначения быстрее, если первому из них нужно пролететь вдвое большее расстояние, но за то он летит в два раза быстрее, чем второй?
Тур
· 9.1 Сумма двух чисел равна 80, а их разность равна 8. Найдите эти числа. · 9.2 Найдите сумму: 1+2+3+…+181– 96– 97 –…– 1. · 9.3 Во сколько раз километр больше миллиметра? Тур · 10.1 Ваня раскладывает на столе камешки на расстоянии 2 см один от другого. Сколько камешков он разложил на протяжений 10 см? · 10. · 10.3 На складе имеются гвозди в ящиках по 24, 23, 17 и 16 кг. Можно ли отправить со склада 100 кг гвоздей, не распечатывая ящики? · 10.4 Как, имя пятилитровую банку и девятилитровое ведро, набрать из реки ровно три литра воды? · 10.5 Два Муравья отправились в гости к Стрекозе. Один всю дорогу прополз, а второй первую половину пути ехал на Гусенице, что было в два раза медленнее, чем ползти, а вторую половину скакал на Кузнечике, что было в два раза быстрее. Какой Муравей придет в гости первым, если они вышли одновременно? Тур · 11.1 Известно, что 4 персика, 2 груши и яблоко вместе весят 550 г, а персик, 3 груши и 4 яблока вместе весят 450 г. · 11.2 Какой цифрой оканчивается произведение всех нечетных чисел от 1 до 51? · 11.3 Сумма цифр двузначного числа равна 12. Если цифру десятков умножить на 2, а цифру единиц на 3 и сложить оба произведения, то в результате получится 29. Найдите это число. · 11.4 Расстояние между двумя велосипедистами, едущими по шоссе, равно 35 км. Скорость одного равна 12 км/ч, а скорость другого – 15 км/ч. Какое расстояние будет между ними через 2 часа? · 11.5 Разделите фигуру на восемь равных частей: Тур · 12.1 Как, используя цифру 5, представить все числа от 0 до 10 включительно. · 12.2 Костя разложил на столе 5 камешков на расстоянии 3 см один от другого. Какое расстояние то первого камешка до второго? · 12.3 В трех ящиках находятся мука, крупа и сахар. · 12.4 Три курицы снесли за три дня три яйца. Сколько яиц снесут 12 куриц за 12 дней? · 12.5 Поезд проходит мост длиной 450 метров за 45 секунд, а мимо светофора за 15 секунд. Найдите длину поезда и его скорость. Тур · 13.1 В магазин привезли 141 л масла в бидонах по 10 л и по 13 л. Сколько было всего бидонов? · 13.2.Найдите сумму: 1 + 3 + 5 +…+ 97 + 99. · 13.3 Шесть карасей тяжелее, чем десять лещей, но легче, чем пять окуней. Что тяжелее: 2 карася или 3 леща? · 13.4 Сумма двух последовательных чисел равна 75. Найдите эти числа. · 13.5.Разделите фигуру на 6 равных частей: Тур · 14.1 Два всадника едут навстречу друг к другу: один проезжает 12 км в час, а другой на 3 км больше. · 14.2 В пакете 3кг600г крупы. Как разделить крупу на три части: две по 800 г и 2 кг, сделав три взвешивания на чашечных весах, имея одну гирю в 200г? · 14.3 Если учащихся посадить по одному человеку на стул, то семерым не хватит места. Если на каждый стул посадить по два человека, то останутся свободными пять стульев. Сколько было учащихся и сколько было стульев? · 14.4 Дочери 10 лет, а матери 36 лет. Через сколько лет мать будет вдвое старше дочери? · 14.5.Разделите фигуру на пять равных частей: Тур · 15.1 В магазин привезли 223л масла в бидонах по 10 л и по 17 л. Сколько было бидонов? · 15.2 В одном ряду 8 камешков на расстоянии 2 см один от другого. В другом ряду 15 камешков на расстоянии 1 см один от другого. Какой ряд длиннее? · 15. · 15.4 Сумма двух последовательных четных чисел равна 150. Найдите эти числа? · 15.5 Из двух пунктов, расстояние между которыми 100 км, выехали одновременно навстречу друг другу два всадника. Скорость первого всадника 15 км/ч, а второго – 10 км/ч. Вместе с первым всадником выбежала собака, скорость которой 20 км/ч. Встретив второго всадника, она повернула назад и побежала к первому, добежав до него, снова повернула и так бегала до тех пор, пока всадники не встретились. Сколько километров пробежала собака? Тур · 16.1 Когда отцу было 27 лет, сыну было 3 года. Сейчас сыну в три раза меньше лет, чем отцу. Сколько лет каждому из них? · 16.2 Как набрать из озера восемь литров воды, имея девятилитровое и пятилитровое ведро? · 16.3 Установите закономерность в числовой последовательности 253, 238, 223, 208, 193, …и запишите еще три числа. · 16.4 Встретились три друга: Белов, Чернов и Рыжов. Один из них – блондин, другой – брюнет, а третий – рыжий. Брюнет сказал Белову: «Ни у одного из нас цвет волос не соответствует фамилии». Какой цвет у каждого из них? · 16.5 Разделите фигуру на две равные части: Тур · 17.1 Сумма четырех последовательных четных чисел равна 196. Найдите эти числа. · 17.2 Пять лет назад брату и сестре вместе было 8 лет. Сколько лет им будет вместе через пять лет? · 17.3 Если к половине денег прибавить 80 долларов, то получится 3/4 имеющихся денег. Сколько денег в наличии? · 17.4 В ящике 100 черных и 100 белых шаров. Какое наименьшее число шаров надо вытащить, не заглядывая в ящик, чтобы среди них наверняка было два шара одного цвета? · 17.5.Разделите фигуру на четыре равные части: Тур · 18. · 18.2 Что быстрее: проехать весь путь на велосипеде или половину пути проехать на мотоцикле, а во вторую половину пройти пешком, если скорость мотоциклиста в два раза больше скорости велосипедиста, а скорость велосипеда, в свою очередь, в два раза больше скорости пешехода? · 18.3 Если к числу учеников класса прибавить столько же и еще половину первоначального количества учеников, то получится 100. Сколько учеников класса? · 18.4 На острове коренными жителями являются Лжецы, которые всегда лгут, и Рыцари, которые всегда говорят правду. Человек говорит: «Я – лжец». Может ли он быть коренным жителем острова? · 18.5.Используя цифру 3 пять раз, знаки действий и скобки, представьте все числа от 0 до 11 включительно. Тур · 19.1 Сейчас шесть часов вечера. Какая часть суток прошла? Какая осталась? Какую часть составляет оставшаяся часть суток от прошедшей? · 19. · 19.3 В ящике 100 белых, 100 красных, 100 синих, 100 черных шаров. Какое наименьшее число шаров надо вытащить, не заглядывая в ящик, чтобы среди них было не меньше, чем 3 шара одного цвета? · 19.4 Какую цифру надо поставить вместо буквы А в запись числа А37, чтобы оно делилось: а) на 6; б) на 9? · 19.5 Разделите фигуру на четыре равные части: Тур · 20.1 Найдите наибольшее число, при делении которого на 31 в частном получаем 30. · 20.2 Пятилитровый бидон и трехлитровая банка наполнены молоком. Как разделить молоко пополам, имея пустое восьмилитровое ведро? · 20.3 Кирпич весит 2 кг и еще полкирпича. Сколько весит один кирпич? · 20.4 О каждом из трех островитян А, В и С известно, что он либо Рыцарь, либо Лжец. · 20.5.Расшифруйте пример, если одинаковые цифры заменены одинаковыми буквами: ОДИН + ОДИН _______ МНОГО Тур · 21.1 Замените * в записи числа *43* цифрами, возможно и различными, но такими, чтобы оно делилось на 45. · 21.2 Расстояние между автомобилями в полдень было 20 км, скорость одного из них 40 км/ч, а другого – 60 км/ч. Какое расстояние будет между ними через 1 час? · 21.3 Сколько сейчас времени, если до конца суток осталось3/5 времени, прошедшего от начала суток? · 21.4 В ящике 100 черных и 100 белых шаров. Какое наименьшее число шаров надо вытащить, не заглядывая в ящик, чтобы среди них наверняка было 2 шара белого цвета? · 21.
Тур
· 22.1 Найдите наименьшее трехзначное число, кратное трем, такое, чтобы первая его цифра была 7. · 22.2 Произведением четырех простых последовательных чисел оканчивается нулем. Что это за числа? Найдите их произведение. · 22.3 Трехзначное число 5АА разделили на однозначное число и в остатке получили 8. Найдите делимое, делитель и частное. · 22.4 В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом находится между кувшином и сосудом с квасом, в банке – не лимонад и не вода. Стакан находится около банки и сосуда с молоком. Как распределены эти жидкости по сосудам? · 22.5.Разделите фигуру на две такие равные фигуры, чтобы из них было можно сложить квадрат: Тур · 23. · 23.2 Является ли число 19961994 + 19941994 простым? · 23.3 Когда у пастуха спросили, сколько у него овец, то он ответил, что 60 овец пьют воду, а остальные 0,6 всех овец пасутся. Сколько же всего овец? · 23.4 В трех коробках лежат шары: в первой – два белых, во второй – два черных, а в третьей – один белый и один черный. На коробках написано: ББ, ЧЧ и БЧ, но содержимое каждой из них не соответствует надписи. Как, вытащив только один шар, определить содержимое каждой из коробок? · 23.5 Расшифруйте пример: ПОДАЙ — ВОДЫ _________ ПАША Тур · 24.1 Напишите наибольшее пятизначное число, кратное 9, такое, чтобы его первой цифрой была 3, а все остальные цифры были бы различны. · 24.2 На одной чаше весов лежит кусок мыла, а на другой ¾ такого же куска и еще ¾ кг. Сколько весит весь кусок? · 24.3 Что быстрее: проехать весь путь на велосипеде или 2/3 пути на мотоцикле, что в два раза быстрее, чем на велосипеде, а 1/3 часть пути пешком, что в два раза медленнее? · 24.4 О жителях некоторого острова известно, что каждый из них либо Рыцарь, либо Лжец. (Рыцарь всегда говорит правду, Лжец всегда лжет.) А высказывает утверждение: «Я – Лжец, а В – не Лжец». Кто из островитянин Рыцарь, а кто Лжец? · 24.5 Используя цифру 7 четыре раза, знаки действий и скобки, представьте все числа от 0 до 10. Тур · 25.1 Замените * в записи числа 72*3* цифрами так, чтобы это число делилось без остатка на 45. · 25.2 Плоскость окрашена в два цвета. Докажите, что найдутся две точки, отстоящие друг от друга на расстоянии 1 см, окрашенные одинаково. · 25.3 Кошка весит 0,5 кг и еще 0,8 всего своего веса. Сколько весит кошка? · 25.4 Мальчик каждую букву своего имени заменил порядковым номером этой буквы в русском алфавите. Получилось число 510141. Как звали мальчика? · 25.5.Раздели фигуру на шесть равных частей: Тур · 26.1 Если из некоторого трехзначного числа вычесть 7, то полученная разность будет делиться на 7, если вычесть 8, то полученная разность будет делиться на 8, если вычесть 9, то разность будет делиться на 9. Найдите наименьшее такое число. · 26.2 Расстояние между двумя городами 320 км. Из этих городов одновременно выходят навстречу друг другу два поезда, причем скорость одного из них 45 км/ч, а другого – 35км/ч. Одновременно с первым поездом вылетел почтовый голубь и со скоростью 50 км/ч полетел навстречу второму поезду, встретив его, он повернулся назад и полетел навстречу первому ит. · 26.3 Как разложить 80 тетрадей на две стопки так, чтобы число тетрадей одной из них составляло 60% числа тетрадей в другой? · 26.4 В сенате заседают 100 сенаторов. Каждый из них либо продажен, либо честен. Известно, что: 1) по крайней мере один из сенаторов является честным; Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой. Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… |
Интеллектуальная игра по общепрофессиональным дисциплинам
1. Министерство образования и науки Калужской области Государственное бюджетное образовательное учреждение среднего
профессионального образования«Сосенский радиотехнический техникум»
представляет
интеллектуальную игру по общепрофессиональным дисциплинам
для студентов вторых курсов
2. БОЙ 1 «МНОЖЕСТВА и ОТОБРАЖЕНИЯ»
3. «1 раунд»
Мадемуазель Рембо любит домашних животных.Известно, что у нее не менее трех животных. Все ее
животные, кроме двух — собаки; все кроме двух —
кошки; все кроме двух — попугаи; все, кроме собак,
кошек и попугаев — тараканы. Опишите множество
животных у мадемуазель Рембо.
4. «1 раунд»
У мадемуазель Рембо одна кошка, одна собака,один попугай и нет тараканов.

5. «2 раунд»
В люстре 5 лампочек. Переключатель имеет 6положений, при которых горит разное количество
лампочек: от 0 до 5. Однажды несколько лампочек
перегорело. Может ли человек, не знающий схемы
работы переключателя, определить множество
перегоревших лампочек?
«2 раунд»
Способ
определения
множества
перегоревших лампочек таков. Следует
испробовать все шесть положений и отметить
лампочки, которые не загорались ни при
каких положениях. Они, и только они
являются перегоревшими.
«3 раунд»
В комнате находятся 12 человек. Некоторые из
них всегда говорят правду, а остальные всегда лгут.
Каждый сказал по фразе. Первый сказал: «Здесь нет
ни одного правдивого человека», второй: «Здесь не
более одного правдивого человека», третий: «Здесь
не более двух правдивых людей», и т. д.,
двенадцатый: «Здесь не более одиннадцати
правдивых людей». Определите, кто из них
принадлежит множеству правдивых людей.

«3 раунд»
Нетрудно понять, что если кто-то из присутствующих
сказал правду, то и следующие за ним также сказали правду,
а если кто-то из присутствующих солгал, то и все,
говорившие перед ним, также солгали. Заметим также, что
первый заведомо солгал, а последний сказал правду. Таким
образом, последние k человек сказали правду, а первые 12-k
солгали. Первой прозвучавшей правдой было «Здесь не
более k правдивых людей», это сказал человек, говоривший
(12-k+1)-м по порядку, а судя по тому, что он сказал, он
говорил (k+1) -м. Поэтому ( 12-k)+1=k+1, откуда k=6.
Итак, первые шесть человек — лжецы, последние шесть
составляют в этой комнате множество правдивых людей.
«4 раунд»
Число 222122111121 получается, если в
некотором слове заменить буквы на их
номера в русском алфавите. Какое это слово?
«4 раунд»
Из цифр 1 и 2 можно составить следующие
числа, соответствующие буквам в алфавите:
1, 2, 11, 12, 21, 22, т. е. буквам А, Б, Й, К, У, Ф.

Единственное осмысленное слово в данном
случае: ФУФАЙКА
«5 раунд»
Опишите множество, являющееся
пересечением множества четных чисел и
множества чисел, делящихся на 5.
«5 раунд»
Это — множество чисел, делящихся на 10.
«6 раунд»
Опишите множество четырехугольников,
являющихся одновременно
прямоугольниками и ромбами.
«6 раунд»
Это — множество квадратов.
«7 раунд»
В
Монреале
80% жителей
знают
французский язык и 70% — английский.
Сколько процентов жителей знают оба языка,
если каждый житель знает хотя бы один из
этих языков?
«7 раунд»
По условию 20% жителей Монреаля не
знают французского языка, но знают
английский, а 30% не знают английского, но
знают французский. Поэтому 50% знают
лишь один язык и 50% жителей знают оба
языка.
«8 раунд»
Среди математиков каждый седьмой —
философ, а среди философов каждый десятый
— математик. Кого больше — философов или
математиков?
«8 раунд»
Рассмотрим
множество
философов,
являющихся математиками.
 Пусть их число
Пусть их числоравно n, тогда математиков 7n, а философов
10n. Значит, философов больше, чем
математиков.
«9 раунд»
В классе 40% мальчиков. Математический
кружок посещают 40% учеников, при этом
40% участников математического кружка
составляют девочки. Какая часть мальчиков
посещает математический кружок?
«9 раунд»
Пусть N — число учеников, тогда
мальчиков 2N/5, и столько же участников
кружка.
Мальчики
составляют
3/5
кружковцев, т. е. их 6N/25; так как
6N/25:2N/5= 0,6,
то
60%
мальчиков
посещают кружок. При решении полезно
нарисовать диаграмму Эйлера—Венна.
«10 раунд»
Учитель задал на уроке замысловатую
задачу. В результате количество мальчиков,
решивших эту задачу, оказалось равным
количеству девочек, ее не решивших. Кого в
классе больше — решивших задачу или
девочек?
«10 раунд»
Множество учеников класса разбивается на
4 подмножества: Мр — мальчики, решившие
задачу, Мн — мальчики, не решившие ее, Др
— девочки, решившие задачу, и Дн —
девочки, не решившие ее.
 Так как количество
Так как количестворешивших равно Мр
Др, а количество
девочек равно Др
Дн, то (поскольку Мр
=Дн) эти количества равны.
«11 раунд»
Из 100 студентов колледжа 28 изучают
английский язык, 42 — французский, 30 —
немецкий, 8 — английский и немецкий, 10 —
английский и французский, 5 — немецкий и
французский, 3 — все три языка. Сколько
студентов не изучает ни одного языка?
Сколько
студентов
изучает
только
французский язык?
Нарисуем диаграмму
Эйлера—Венна в виде
трех
кругов,
соответствующих
изучающим каждый из
языков, и начнем ее
заполнять, начиная с
конца списка в условиях
задачи. Получим картину.
Видно,
что
только
французский
язык
изучают 30 человек, а ни
одного языка — 20.
«11 раунд»
«12 раунд»
Является ли отображением следующее
соответствие для множества живущих людей?
Каждому человеку ставится в соответствие
его дочь.
«12 раунд»
Нет, поскольку не у всех живущих людей
есть дочь.

«13 раунд»
Является ли отображением следующее
соответствие для множества живущих людей?
Каждому человеку ставится в соответствие
его мать.
«13 раунд»
Да, поскольку у всех людей есть (или была)
мать.
«14 раунд»
Участникам математической олимпиады
было предложено пять задач. Является ли
функцией соответствие, сопоставляющее
каждому участнику номера решенных им
задач?
«14 раунд»
Нет, поскольку некоторым участникам
может сопоставляться несколько номеров.
«15 раунд»
Два города назовем эквивалентными, если
количество жителей одного отличается от
количества жителей другого не более, чем на
5000 человек.
Является это отношение отношением
эквивалентности?
«15 раунд»
Это отношение не транзитивно (для
доказательства достаточно рассмотреть три
города с числом жителей 5 000, 10 000 и 15
000).
33. БОЙ 2 «ЛОГИКА»
«1 раунд»Как называется наука,
изучающая законы и формы мышления?
«1 раунд»
Логика
«2 раунд»
Повествовательное предложение,
в котором что-то утверждается или
отрицается называется
«2 раунд»
Высказывание
«3 раунд»
Константа,
которая обозначается «1»
в алгебре логики называется
«3 раунд»
Истина
«4 раунд»
Какое из следующих высказываний
являются истинными?
А) город Париж — столица Англии;
Б) 3+5=2+4;
В) II + VI = VIII;
Г) томатный сок вреден.

«4 раунд»
В) II + VI = VIII
«5 раунд»
Объединение двух высказываний в одно
с помощью союза «и» называется
«5 раунд»
конъюнкция
«6 раунд»
Чему равно значение логического
выражения (1v1)&(1v0)?
«6 раунд»
1
«7 раунд»
Какая из логических операций не является
базовой?
А) конъюнкция;
Б) дизъюнкция;
В) инверсия;
Г) эквивалентность.
«7 раунд»
Г) эквивалентность
«8 раунд»
Графическое изображение логического
выражения называется
«8 раунд»
Схема
«9 раунд»
Объединение двух высказываний в одно
с помощью оборота «если…,
то…» называется
«9 раунд»
Импликация
«10 раунд»
Таблица, содержащая все возможные
значения логического выражения, называется
«10 раунд»
Таблица истинности
«11 раунд»
Символом F обозначено одно из указанных ниже
логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
XYZF
0110
1111
0011
Какое выражение соответствует F?
1) X /\ ¬Y /\ ¬Z
2) ¬X /\ ¬Y /\ Z
3) ¬X \/ ¬Y \/ Z
4) X \/ ¬Y \/ ¬Z
«11 раунд»
X \/ ¬Y \/ ¬Z
«12 раунд»
Укажите, какое логическое выражение
равносильно выражению
A \/ ¬( ¬B \/ ¬C):
1) ¬A \/ B \/ ¬C
2) A \/ (B /\ C)
3) A \/ B \/ C
4) A \/ ¬B \/ ¬C
«12 раунд»
A \/ (B /\ C)
«13 раунд»
Девять школьников, остававшихся в классе на перемене, были вызваны к
директору.
 Один из них разбил окно в кабинете. На вопрос директора, кто
Один из них разбил окно в кабинете. На вопрос директора, ктоэто сделал, были получены следующие ответы:
Володя: «Это сделал Саша».
Аня: «Володя лжет!»
Егор: «Маша разбила».
Саша: «Аня говорит неправду!»
Рома: «Разбила либо Маша, либо Нина…»
Маша: «Это я разбила!»
Нина: «Маша не разбивала!»
Коля: «Ни Маша, ни Нина этого не делали».
Олег: «Нина не разбивала!»
Кто разбил окно, если известно, что из этих девяти высказываний истинны
только три?
«13 раунд»
Нина
«14 раунд»
В языке запросов поискового сервера для обозначения логической операции
«ИЛИ» используется символ «|», а для логической операции
«И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц
некоторого сегмента сети Интернет.
Запрос Найдено страниц
(в тысячах)
Крейсер | Линкор 7000
Крейсер 4800
Линкор 4500
Какое количество страниц (в тысячах) будет найдено по запросу
Крейсер & Линкор ?
Считается, что все запросы выполнялись практически одновременно, так что
набор страниц, содержащих все искомые слова, не изменялся за время
выполнения запросов.

«14 раунд»
2300
«15 раунд»
Какое из приведенных имен удовлетворяет
логическому условию
¬ (первая буква гласная → вторая буква гласная) /\ последняя буква гласная
1)
2)
3)
4)
ИРИНА
МАКСИМ
АРТЕМ
МАРИНА
«15 раунд»
ИРИНА
«16 раунд»
Сколько различных решений имеет
уравнение
J /\ ¬K /\ L /\ ¬M /\ (N \/ ¬N) = 0
где J, K, L, M, N – логические переменные?
В ответе не нужно перечислять все
различные наборы значений J, K, L, M и N,
при которых выполнено данное равенство. В
качестве ответа Вам нужно указать
количество таких наборов.
«16 раунд»
30
«17 раунд»
Запишите логическую функцию,
описывающую состояние логической схемы:
1
A
B
&
«17 раунд»
¬(¬A \/ A /\B)
68. БОЙ 3 «ЭЛЕМЕНТЫ ТЕОРИИ и ПРАКТИИ КОДИРОВАНИЯ»
«1 раунд»Числа 11012 и 110112 записаны в двоичной
системе счисления. Чему равна их сумма в
этой системе? А в десятичной
«1 раунд»
В двоичной системе счисления имеем
11012+110112=1010002, что соответствует
числу 13 + 27 = 40
«2 раунд»
Для
передачи
сигналов
на
флоте
используются
специальные
сигнальные
флаги, вывешиваемые в одну линию
(последовательность
важна).

Какое
количество различных сигналов может
передать корабль при помощи четырех
сигнальных флагов, если на корабле имеются
флаги трех различных видов (флагов каждого
вида неограниченное количество)?
«2 раунд»
34=3*3*3*3=81
73. Министерство образования и науки Калужской области Государственное бюджетное образовательное учреждение среднего
профессионального образования«Сосенский радиотехнический техникум»
представляет
интеллектуальную игру по общепрофессиональным дисциплинам
для студентов вторых курсов
Методическое пособие по теме «Решение нестандартных математических задач в 5-6 классах»
Методическое пособие по теме
«Решение нестандартных математических задач в 5-6 классах»
Борошко Виктория Викторовна,
зам. директора по ВР, учитель математики и информатики
СПГАХЛ им.Б.В.Иогансона
Решение задач на расстановку скобок и знаков.
1)Как нужно расставить знаки «+» в записи 1234567, чтобы получилась сумма, равная 100?
2)Как нужно расставить знаки «+» в записи 987654321, чтобы получилась сумма, равная 99?
3)При помощи любых арифметических действий составьте число 100 из пяти единиц.
4) В записи, состоящей из восьми восьмерок, поставьте между некоторыми цифрами знак сложения так, чтобы получилось выражение, значение которого равно 1000.
5)Используя ровно пять раз цифру 3, знаки действий и скобки, представьте все целые числа от 0 до 11.
6)Используя ровно пять раз цифру 5, знаки действий и скобки, представьте все целые числа от 0 до 10.
7)Используя ровно четыре раза цифру семь, знаки действий и скобки, представьте все целые числа от 0 до 10.
8)Записаны двадцать пять пятерок: 55555…..55. Поставьте между некоторыми цифрами знак сложения так, чтобы сумма равнялась 1000.
9)Между цифрами 1,2,3,4,5,6,7,8 и 9, написанными в указанном порядке, поставьте знаки сложения и умножения так, чтобы полученное выражение имело значение 100. Использовать скобки нельзя. Между любыми двумя соседними цифрами должен стоять знак действия.
Использовать скобки нельзя. Между любыми двумя соседними цифрами должен стоять знак действия.
10)Расставьте между цифрами знаки действий и скобки так, чтобы в результате вычисления в каждой строке получилась 1. В некоторых случаях между цифрами можно ничего не ставить.
1 2 3 = 1
1 2 3 4 = 1
1 2 3 4 5 = 1
1 2 3 4 5 6 = 1
1 2 3 4 5 6 7 = 1
1 2 3 4 5 6 7 8 = 1
1 2 3 4 5 6 7 8 9 = 1
Решение задач с числами.
11)Выписаны подряд все числа от 1 до 99. Сколько раз написана цифра 5?
12)Найти сумму 1+2+3+…+98+99
13)Вычислить 2−1+4−3+6−5 +98−97+100−99
14)Установите закономерность в числовой последовательности и запишите еще два числа:0, 3, 8, 15, 24…
15)Установите закономерность в числовой последовательности и запишите еще два числа: 10, 8, 11, 9, 12, 10, 13…
16)Установите закономерность в числовой последовательности и запишите еще три числа: 15, 29, 56, 109, 214…
17)Задумано трехзначное число, у которого с любым из чисел 543, 142 и 562 совпадает один из разрядов, а два других не совпадают. Какое число задумано?
Какое число задумано?
18)Докажите что число 7777+1 не делится на 5.
19)Все натуральные числа от 1 до 100 разбиты на две группы: четные и нечетные. Определите, в какой из групп сумма всех цифр, использованных для записи числе, больше и на сколько?
20)Натуральные числа от 1 начинают выписывать подряд. Какая цифра стоит на 1992-м месте?
21)Сумма восьми чисел равна 1998. Одно из этих чисел 998. Это число заменили на 899. Какой будет новая сумма?
22)В стозначном числе 12345678901234567890…1234567890 вычеркнули все цифры, стоящие на нечетных местах. В полученном пятидесятизначном числе вновь вычеркнули все цифры, стоящие на нечетных местах. Вычеркивание продолжалось до тех пор, пока ничего не осталось. Какая цифра была вычеркнута последней?
23)На какую цифру оканчивается число 2100?
24)На какую цифру оканчивается число 3100?
25)Расставьте числа 1, 1, 2, 2, 3, 3, 4, 4, в таком порядке, чтобы между единицами оказалась одна цифра, между двойками – две, между тройками – три, а между четверками – четыре цифры.
Решение задач на переливания, взвешивания и перекладывания.
26)В мешке 24 кг гвоздей. Как, имя только чашечные весы без гирь, отмерить 9 кг гвоздей?
27)Из трех монет одна фальшивая, она легче остальных. За сколько взвешиваний на чашечных весах без гирь можно определить, какая именно монета фальшивая?
28)Среди 12 монет имеется одна фальшивая. Известно, что фальшивая монета отличается от настоящих, но неизвестно — легче она или тяжелее. Все настоящие монеты имеют одинаковую массу. С помощью трех взвешиваний на чашечных весах без гирь выделите фальшивую монету и одновременно установите, легче она или тяжелее остальных.
29)Имеется 10 мешков монет. В девяти мешках монеты настоящие (вес одной монеты 10г.), а в одном – фальшивые (вес одной монеты – 11 г.) Как одним взвешиванием на точных электронных весах определить в каком мешке фальшивые монеты?
30)В восьмилитровом бидоне находится молоко. Как при помощи пятилитрового бидона и трехлитровой банки отмерить 4 литра молока?
31)Как из восьмилитрового ведра, наполненного молоком, отлить один литр с помощью трехлитровой банки и пятилитрового бидона?
32)Как, имя пятилитровую банку и девятилитровое ведро, набрать из реки ровно три литра воды?
33)В шестилитровом ведре содержится четыре литра кваса, а в семилитровом – шесть литров. Как разделить весь имеющийся квас пополам, используя эти ведра и пустую трехлитровую банку?
Как разделить весь имеющийся квас пополам, используя эти ведра и пустую трехлитровую банку?
34)В трех кучках находится 22, 14 и 12 орехов. Требуется путем трех перекладываний уровнять число орехов в каждой кучке, соблюдая при этом условие: из любой кучки разрешается перекладывать в другую лишь столько орехов, сколько их в этой второй кучке.
35)Положите на стол три кучки спичек. В одну кучку положите 11 спичек, в другую – 7, в третью – 6. Перекладывая спички из любой кучки в любую другую, нужно за три операции сравнять все три кучки, чтобы в каждой было по 8 спичек. К любой кучке разрешается добавлять столько спичек, сколько в ней есть.
Решение задач на перемещения.
36)От потолка комнаты вертикально вниз по стене ползли две мухи. Спустившись до пола, они поползли обратно. Первая муха ползла в оба конца с одной и той же скоростью, а вторая хотя и поднималась в двое медленнее первой, но зато спускалась в двое быстрее. Какая из мух раньше приползет обратно?
37)Два Муравья отправились в гости к Стрекозе. Один всю дорогу прополз, а второй первую половину пути ехал на Гусенице, что было в два раза медленнее, чем ползти, а вторую половину скакал на Кузнечике, что было в десять раз быстрее. Какой Муравей первым придет в гости, если они вышли одновременно?
Один всю дорогу прополз, а второй первую половину пути ехал на Гусенице, что было в два раза медленнее, чем ползти, а вторую половину скакал на Кузнечике, что было в десять раз быстрее. Какой Муравей первым придет в гости, если они вышли одновременно?
38)Два летчика вылетели одновременно из одного города в два различных пункта. Кто из них долетит до места назначения быстрее, если первому из них нужно пролететь вдвое большее расстояние, но зато он летит в два раза быстрее, чем второй?
39)Что быстрее: проехать весь путь на велосипеде или половину пути проехать на мотоцикле, а вторую половину пройти пешком, если скорость мотоцикла в два раза больше скорости велосипеда, а скорость велосипеда, в свою очередь, в два раза больше скорости пешехода?
40)Путь от дома до школы Буратино проделал пешком, обратно он двигался той же дорогой, но первую половину пути он проехал на собаке, а вторую половину пути – на черепахе. Известно, что скорость собаки в четыре раза больше, а скорость черепахи – в два раза меньше, чем скорость, с которой Буратино шел пешком в школу. На каой путь – из дома до школы или из школы до дома – затратил Буратино больше времени?
На каой путь – из дома до школы или из школы до дома – затратил Буратино больше времени?
Решение логических задач.
(найти соответствие)
41)В трех ящиках находятся мука, крупа и сахар. На первом из них написано «Крупа», на втором – «Мука», на третьем – «Крупа или сахар». Известно, что содержимое ящиков не соответствует надписи. В каком ящике что находится?
42)На улице, став в кружок беседуют четыре девочки: Аня, Валя, Галя и Надя. Девочка в зеленом платье (не Аня и не Валя) стоит между девочкой в голубом платье и Надей. Девочка в белом платье стоит между девочкой в розовом и Валей. Какое платье носит каждая из девочек?
43)Алеша, Боря и Витя учатся в одном классе. Один ездит домой из школы на автобусе, другой – на трамвае, третий – на троллейбусе. Алеша однажды после уроков пошел проводить друга до автобусной остановки. Когда мимо проходил троллейбус, третий друг крикнул из окна: «Боря, ты забыл в школе дневник!». Кто на чем ездит домой.
Кто на чем ездит домой.
44)Встретились три друга: Белов, Чернов и Рыжов. «Волосы одного из нас белые, другого — черные, третьего –рыжие, но ни у кого цвет волос не соответствует фамилии», — заметил черноволосый. «Ты прав», – подтвердил Белов. Какие у кого волосы?
45)Три подруги вышли в белом, зеленом и синем платьях. Их туфли были одного из тех же трех цветов. Известно, что только у Ани цвета платья и туфель совпали. Ни платье, ни туфли Вали не были белыми. Наташа была в зеленых туфлях. Определите цвет платья и туфель каждой из подруг.
46)На одном заводе работают три друга: слесарь, токарь и сварщик. Их фамилии: Борисов, Иванов и Семенов. У слесаря нет ни братьев, ни сестер, он самый младший из друзей. Семенов старше токаря и женат на сестре Борисова. Назовите фамилии слесаря, токаря и сварщика соответственно.
47)В очереди за билетами в кино стоят друзья: Юра, Миша, Володя, Саша и Олег. Известно, что Юра купит билет раньше, чем Миша, но позже Олега. Володя и Олег не стоят рядом, А Саша не находится рядом ни с Олегом, ни с Юрой, ни с Володей. Кто за кем стоит?
Володя и Олег не стоят рядом, А Саша не находится рядом ни с Олегом, ни с Юрой, ни с Володей. Кто за кем стоит?
48)В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшинов и сосудом с квасом, в банке не лимонад и не вода. Стакан стоит около банки и сосуда с молоком. В какой сосуд налита каждая из жидкостей?
49)Коля, Боря, Вова и Юра заняли в соревновании первые четыре места, причем никакие два мальчика не делили между собой какие-нибудь места. Коля не занял ни первое, ни четвертое место. Боря занял второе место, а Вова не был последним. Какое место занял каждый из мальчиков?
50)На столе лежат в ряд четыре фигуры: треугольник, ромб, круг и квадрат. Цвета этих фигур: зеленый, желтый, синий, красный. В каком порядке лежат фигуры и каков цвет каждой из них, если фигура красного цвета лежит между зеленой и синей. Справа от желтой фигуры лежит ромб, круг лежит правее треугольника и ромба, причем треугольник лежит с краю, и, наконец, фигура синего цвета не лежит рядом с фигурой желтого цвета?
(некоторые из высказываний ложны)
51)В тетради написано 100 утверждений:
В этой тетради ровно одно ложное утверждение.
В этой тетради ровно два ложных утверждений.
…
В этой тетради ровно сто ложных утверждений.
Какое из этих утверждений верно.
52)Придя с работы домой, мама обнаружила, что ее любимая вазочка разбита. « Кто это сделал?»- обратилась она к детям.
Саша сказал: «Я не разбивал. Вазу разбил Олег».
Олег сказал: « Это сделал не я. Это сделал Саша».
Маша сказала: « Я вазочку не разбивала. И Олег не разбивал».
Определите, кто разбил вазу, если известно, что у каждого из детей одно утверждение верно, а другое ложно.
53)Один из попугаев А, В, и С всегда говорит правду, другой всегда врет, а третий – хитрец, он иногда говорит правду, а иногда врет. На вопрос: «Кто В?» они ответили:
А: — Лжец.
В: — Я хитрец!
С: — Абсолютно честный попугай.
Кто из попугаев лжец, а кто хитрец?
54)До Царя дошла весть, что кто-то из трех богатырей убил Змея Горыныча. Приказал Царь им явиться ко двору. Молвили богатыри:
Приказал Царь им явиться ко двору. Молвили богатыри:
Илья Муромец: — Змея убил Добрыня Никитич.
Добрыня Никитич: — Змея убил Алеша Попович.
Алеша Попович: — Я убил змея.
Известно, что только один богатырь сказал правду, а двое других слукавили. Кто убил змея?
55)До царя Гороха дошла молва, что наконец кто-то убил Змея Горыныча. Царь догадался, что это дело рук или Ильи Муромца, или Добрыни Никитича, или Алеши Поповича. Пригласил их ко двору, стал расспрашивать. Трижды каждый богатырь речь держал. И сказали они так:
Илья Муромец: «Я не убивал Змея Горыныча. Я в заморские страны уезжал. А змея Горыныча убил Алеша Попович.»
Добрыня Никитич: «Змея Горыныча убил Алеша Попович. Но я если бы и убил, то не сознался бы. Много еще нечистой силы осталось!»
Алеша Попович: «Нея убил Змея Горыныча. Я давно ищу, какой бы подвиг совершить. И взаправду Илья Муромец в заморские страны уезжал.»
Потом царь Горох узнал, что дважды каждый богатырь правду говорил, а один раз соврал.
Так кто же убил Змея Горыныча?
56)За круглый стол сели семь братьев-гномов. Гномы всегда говорят правду всем старшим братьям, а младшим всегда врут. Каждый гном сказал своему правому соседу: «все здесь присутствующие говорят мне только неправду». В каком порядке сидят гномы?
57)За круглым столом сидят восемь человек, каждый из которых либо рыцарь, либо лжец. Рыцари всегда говорят правду, а лжецы – всегда лгут . На вопрос, кто их соседи, каждый из них ответил : « Мои соседи – лжец и рыцарь». Сколько среди них было лжецов ?
58)В стране Рыцарей и Лжецов живут рыцари, все высказывания которых правдивы, и лжецы – каждое высказывание которых – ложь. И еще в этой стране бывают гости, в большинстве своем, — нормальные люди, с которыми особенно трудно: они могут говорить правду, но могут и солгать. Однажды, прогуливаясь по стране рыцарей и лжецов, я встретил человека, который сказал о себе: «Я – лжец». Кем был тот человек, которого я встретил?
59)В одной сказочной стране поблизости один от другого находятся города А и В. Все жители города А говорят только правду, а жители города В всегда лгут. Жители этих городов ходят друг к другу в гости. Путешественник попал в один из этих городов, но не знает, в какой. Как он может, задав один вопрос первому попавшемуся жителю, узнать, в каком городе он находится?
Все жители города А говорят только правду, а жители города В всегда лгут. Жители этих городов ходят друг к другу в гости. Путешественник попал в один из этих городов, но не знает, в какой. Как он может, задав один вопрос первому попавшемуся жителю, узнать, в каком городе он находится?
60)В конференции участвовало 100 человек – химики и алхимики. Каждому был задан вопрос: « Если не считать Вас, то кого больше среди остальных участников – химиков или алхимиков?» когда опросили 51 участника, и все ответили, что алхимиков больше, опрос прервался. Алхимики всегда лгут, а химики всегда говорят правду. Сколько химиков среди участников?
(пересечение и объединение множеств)
61)Каждая семья, живущая в нашем доме, выписывает или газету, или журнал, или и то и другое вместе. 75 семей выписывают газету, а 27 семей выписывают журнал. И лишь 13 семей выписывают и журнал и газету. Сколько семей живет в нашем доме?
62)Из 40 учащихся нашего классаи32 любят молоко, 21 – лимонад, а 15 и молоко и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?
Сколько ребят в нашем классе не любят ни молоко, ни лимонад?
63)12 моих одноклассников любят читать детективы, 18 –фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?
64)В воскресенье 19 учеников нашего класса побывали в планетарии, 10 – в цирке и 6 – на стадионе. Планетарий и цирк посетили 5 учеников; планетарий и стадион – 3, цирк и стадион – 1. Сколько учеников в нашем классе, если никто не успел посетить все три места, а три ученика не посетили ни одного места?
65)В ясельной группе 11 деток любят манную кашу, 13 – гречневую и 7 малышей – перловую. Четверо любят и манную кашу, и гречневую, 3 – манную и перловую, 6 – гречневую и перловую, а двое с удовольствием «уплетают» все три вида каши. Сколько детей в этой группе, если в ней нет ни одного ребенка, вовсе не любящего кашу?
66)В одном классе 25 учеников. Из них 7 любят груши, 11- черешню. Двое любят груши и черешню; 6 – груши и яблоки; 5 – яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?
Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?
67)Из 100 человек 85 знают английский язык, 80 – испанский, 75 – немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три иностранных языка?
68)Из сотрудников фирмы 16 побывали во Франции, 10 – в Италии, 6 – в Англии. В Англии и Италии – 5, в Англии и Франции – 6, во всех странах – побывали 5 сотрудников. Сколько человек посетили Италию и Францию, если всего в фирме работает 19 человек и каждый из них побывал хотя бы в одной из названных стран?
69)В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике – 12; по истории – 23. По русскому и математике – 4; по математике и истории – 9;по русскому и истории — 5. Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?
70)Получил я посылку от своих друзей из Сочи с яблоками и грушами. Одни плоды были большие, другие маленькие. Да и по цвету они отличались: часть была желтого цвета, часть – зеленого. Среди плодов не было маленьких груш и не было маленьких зеленых яблок. Яблок было 25. Груш было 17. Больших плодов было 32. Желтых плодов было 28. Зеленых яблок было на 2 больше, чем зеленых груш. Сколько больших желтых яблок было в этой посылке?
Одни плоды были большие, другие маленькие. Да и по цвету они отличались: часть была желтого цвета, часть – зеленого. Среди плодов не было маленьких груш и не было маленьких зеленых яблок. Яблок было 25. Груш было 17. Больших плодов было 32. Желтых плодов было 28. Зеленых яблок было на 2 больше, чем зеленых груш. Сколько больших желтых яблок было в этой посылке?
(сколько надо взять?)
71)В коробке лежат 10 красных и 10 синих воздушных шариков. Продавец, не глядя, достает по одному шарику. Сколько шариков надо вытащить, чтобы среди вынутых из коробки шариков обязательно нашлись два шарика одного цвета?
72)В коробке лежат семь красных и пять синих карандашей. Из коробки в темноте берут карандаши. Сколько надо взять карандашей, чтобы среди них было не менее двух красных и трех синих?
73)В пакете перемешали конфеты трех сортов, неразличимых на ощупь. Какое наименьшее число конфет надо взять наугад из пакета, чтобы среди взятых конфет обязательно были хотя бы две одного сорта?
74)В ящике лежат 10 красных, 8 синих и 4 желтых карандаша. Из ящика в темноте берут карандаши. Какое наименьшее число карандашей надо взять, чтобы среди них заведомо было:
Из ящика в темноте берут карандаши. Какое наименьшее число карандашей надо взять, чтобы среди них заведомо было:
а) не менее 4 карандашей одного цвета;
б) не менее 6 карандашей одного цвета;
в) хотя бы 1 карандаш каждого цвета;
г) не менее 6 синих карандашей?
75)В темной кладовой в беспорядке лежат ботинки: 10 пар черных и 10 пар коричневых. Сколько ботинок надо взять, чтобы среди них оказалась хотя бы одна пара (левый и правый ботинок) одного цвета? В темноте нельзя отличить не только цвет ботинка, но и левый от правого.
Решение задач, решаемых с конца.
76)Задумано число, к нему прибавлена 1, сумма умножена на 2, произведение разделено на 3 и от результата отнять 4. Получилось 6. Какое число задумано?
77)Женщина собрала в саду яблоки. Чтобы выйти из сада, ей пришлось пройти через четыре двери, каждую из которых охранял свирепый стражник, отбиравший половину яблок. Домой она принесла 10 яблок. Сколько яблок досталось стражникам?
Сколько яблок досталось стражникам?
78)У моста через речку встретились лодырь и черт. Лодырь пожаловался на свою бедность. В ответ черт предложил: « Я могу тебе помочь. Каждый раз, как ты перейдешь этот мост, у тебя деньги удвоятся. Но каждый раз, перейдя мост, ты должен будешь отдать мне 24 копейки.» Три раза проходил лодырь мост, а когда заглянул в кошелек, там стало пусто. Сколько денег было у лодыря?
79)Мама положила на стол сливы и сказала детям, чтобы они, вернувшись из школы, разделили их поровну. Первой пришла Аня, взяла треть сли и ушла. Потом вернулся из школы Боря, взял треть оставшихся слив и ушел. Затем пришел Витя и взял 4 сливы – треть от числа слив, которые он увидел. Сколько слив оставила мама?
80)В ящик лежат лимоны. Сначала из него взяли половину всех лимонов и половину лимона, затем половину остатка и еще половину лимона, наконец, половину нового остатка и опять половину лимона. После этого в ящике остался 31 лимон. Сколько лимонов было в ящике вначале?
Разные задачи.
81)На скотном дворе гуляли гуси и поросята. Мальчик сосчитал количество голов, их оказалось 30, затем сосчитал, сколько всего ног, их оказалось 84. Можно ли узнать, сколько гусей и сколько поросят было на скотном дворе?
82)В клетке находятся фазаны и кролики. Известно, что в клетке 35 голов и 94 ноги. Сколько в клетке фазанов и сколько кроликов?
83)На поляне ребята пасут жеребят. Если пересчитать ноги ребят и жеребят, то будет 74, а если считать головы, то 22. Сколько на лугу жеребят?
84)Если учащихся посадить по одному человеку на стул, то семерым не хватит места. Если на каждый стул посадить по два человека, то останутся свободными пять стульев. Сколько было учащихся и сколько стульев?
85)На поляне паслись ослы. К ним подошло несколько ребят. Если на каждого осла сядут по одному мальчику, то двум из них не хватит ослов. Если же на каждого осла сядут по два мальчика, то один осел будет лишний. Сколько ослов и сколько мальчиков было на поляне?
86)Учитель задал на уроке сложную задачу. В результате количество мальчиков, решивших задачу, оказалось равно количеству девочек, ее не решивших. Кого в классе больше – решивших задачу или девочек?
В результате количество мальчиков, решивших задачу, оказалось равно количеству девочек, ее не решивших. Кого в классе больше – решивших задачу или девочек?
87)Один биолог открыл удивительную разновидность амеб. Каждая из них через минуту делится на две. В пробирку биолог кладет одну амебу, и ровно через час вся пробирка оказывается заполненной амебами. Сколько потребовалось бы времени, чтобы вся пробирка заполнилась амебами, если бы в нее положили не одну амебу, а две?
88)В гости пришло шесть человек в галошах разного размера. Расходились по одному, и некоторые надевали галоши большего размера. Сколько могло остаться гостей, не сумевших надеть галоши?
89)Винни-Пух, Пятачок, Кролик и ослик Иа-Иа съели 70 бананов, причем каждому сколько-то досталось. Винни-Пух съел больше каждого из остальных, а Кролик и Пятачок вместе съели 45 бананов. Сколько бананов досталось ослику?
90)Путешественник хочет пересечь пустыню за 6 дней. Известно, что один человек способен взять с собой припасов на 4 дня. Он не сможет преодолеть весь путь в одиночку, но он может взять с собой носильщиков. Сколько человек он должен взять с обой и как организовать путешествие, чтобы благополучно пересечь пустыню и все носильщики вернулись домой?
Он не сможет преодолеть весь путь в одиночку, но он может взять с собой носильщиков. Сколько человек он должен взять с обой и как организовать путешествие, чтобы благополучно пересечь пустыню и все носильщики вернулись домой?
Решение математических ребусов.
91)
92)ТРИ+ДВА=ПЯТЬ
93)НАУКА+УЧЕБА=РАБОТА
94)СИНИЦА+СИНИЦА=ПТИЧКИ
95)РАЙОН+РАЙОН=ГОРОД
96)ДРАМА+ДРАМА=ТЕАТР
97)БАРБОС+БОБИК=СОБАКИ
98)КОШКА+КОШКА+КОШКА=СОБАКА
99)АИСТ+АИСТ+АИСТ+АИСТ=СТАЯ
100)ПАРУС+ПАРУС+ПАРУС+ПАРУС=РЕГАТА
Используемая литература.
1. Газета «Математика» приложение к газете «Первое сентября» №№ 28, 38,39,40, 1996г.
2. Библиотечка «Первого сентября» Математика № 4, 2005г.
3. Библиотечка «Первого сентября» Математика № 35 2010г.
4. Задачи по математике для внеклассной работы в V-VIклассах. , В.Ю.Сафонова — М.МИРОС, 1993г.
, В.Ю.Сафонова — М.МИРОС, 1993г.
5. Математический кружок 6-7 классы./ Спивак А.В. — МЦНМО, 2009г.
6. Занимательная математика на уроках в 5-11 классах./ Гаврилова Т.Д. — Учитель, 2008г.
7. Весенний турнир Архимеда. / под. ред. Чулкова П.В. — МЦНМО, 2009г.
8. Математика. Задачи на развитие математического мышления 5-6 классы./Чулков П.В. — Издат-школа, 2000г.
9. Математическая шкатулка. /Нагибин Ф.Ф., Канин Е.С. — Просвещение, 1984г.
10. Математика. Сборник задач. /Смыкалова Е.В. — СМИО Пресс, 2007г.
«Решение нестандартных математических задач в 5-6 классах»
Урок математики по теме «Решение нестандартных математических задач в 5-6 классах» Телегаева Валентина Юрьевна зам. директора по ВР, учитель математики Решение задач на расстановку скобок и знаков. 1)Как нужно расставить знаки «+» в записи 1234567, чтобы получилась сумма, равная 100? 2)Как нужно расставить знаки «+» в записи 987654321, чтобы получилась сумма, равная 99? 3)При помощи любых арифметических действий составьте число 100 из пяти единиц. 4) В записи, состоящей из восьми восьмерок, п…
4) В записи, состоящей из восьми восьмерок, п…
Поделитесь с коллегами:
Начало формы
Конец формы
Урок математики по теме
«Решение нестандартных математических задач в 5-6 классах»
Телегаева Валентина Юрьевна
зам. директора по ВР, учитель математики
Решение задач на расстановку скобок и знаков.
1)Как нужно расставить знаки «+» в записи 1234567, чтобы получилась сумма, равная 100?
2)Как нужно расставить знаки «+» в записи 987654321, чтобы получилась сумма, равная 99?
3)При помощи любых арифметических действий составьте число 100 из пяти единиц.
4) В записи, состоящей из восьми восьмерок, поставьте между некоторыми цифрами знак сложения так, чтобы получилось выражение, значение которого равно 1000.
5)Используя ровно пять раз цифру 3, знаки действий и скобки, представьте все целые числа от 0 до 11.
6)Используя ровно пять раз цифру 5, знаки действий и скобки, представьте все целые числа от 0 до 10.
7)Используя ровно четыре раза цифру семь, знаки действий и скобки, представьте все целые числа от 0 до 10.
8)Записаны двадцать пять пятерок: 55555…..55. Поставьте между некоторыми цифрами знак сложения так, чтобы сумма равнялась 1000.
9)Между цифрами 1,2,3,4,5,6,7,8 и 9, написанными в указанном порядке, поставьте знаки сложения и умножения так, чтобы полученное выражение имело значение 100. Использовать скобки нельзя. Между любыми двумя соседними цифрами должен стоять знак действия.
10)Расставьте между цифрами знаки действий и скобки так, чтобы в результате вычисления в каждой строке получилась 1. В некоторых случаях между цифрами можно ничего не ставить.
1 2 3 = 1
1 2 3 4 = 1
1 2 3 4 5 = 1
1 2 3 4 5 6 = 1
1 2 3 4 5 6 7 = 1
1 2 3 4 5 6 7 8 = 1
1 2 3 4 5 6 7 8 9 = 1
Решение задач с числами.
11)Выписаны подряд все числа от 1 до 99. Сколько раз написана цифра 5?
12)Найти сумму 1+2+3+…+98+99
13)Вычислить 2−1+4−3+6−5 +98−97+100−99
14)Установите закономерность в числовой последовательности и запишите еще два числа:0, 3, 8, 15, 24…
15)Установите закономерность в числовой последовательности и запишите еще два числа: 10, 8, 11, 9, 12, 10, 13…
16)Установите закономерность в числовой последовательности и запишите еще три числа: 15, 29, 56, 109, 214…
17)Задумано трехзначное число, у которого с любым из чисел 543, 142 и 562 совпадает один из разрядов, а два других не совпадают. Какое число задумано?
Какое число задумано?
18)Докажите что число 7777+1 не делится на 5.
19)Все натуральные числа от 1 до 100 разбиты на две группы: четные и нечетные. Определите, в какой из групп сумма всех цифр, использованных для записи числе, больше и на сколько?
20)Натуральные числа от 1 начинают выписывать подряд. Какая цифра стоит на 1992-м месте?
21)Сумма восьми чисел равна 1998. Одно из этих чисел 998. Это число заменили на 899. Какой будет новая сумма?
22)В стозначном числе 12345678901234567890…1234567890 вычеркнули все цифры, стоящие на нечетных местах. В полученном пятидесятизначном числе вновь вычеркнули все цифры, стоящие на нечетных местах. Вычеркивание продолжалось до тех пор, пока ничего не осталось. Какая цифра была вычеркнута последней?
23)На какую цифру оканчивается число 2100?
24)На какую цифру оканчивается число 3100?
25)Расставьте числа 1, 1, 2, 2, 3, 3, 4, 4, в таком порядке, чтобы между единицами оказалась одна цифра, между двойками — две, между тройками — три, а между четверками — четыре цифры.
Решение задач на переливания, взвешивания и перекладывания.
26)Из трех монет одна фальшивая, она легче остальных. За сколько взвешиваний на чашечных весах без гирь можно определить, какая именно монета фальшивая?
27)Среди 12 монет имеется одна фальшивая. Известно, что фальшивая монета отличается от настоящих, но неизвестно — легче она или тяжелее. Все настоящие монеты имеют одинаковую массу. С помощью трех взвешиваний на чашечных весах без гирь выделите фальшивую монету и одновременно установите, легче она или тяжелее остальных.
28)Имеется 10 мешков монет. В девяти мешках монеты настоящие (вес одной монеты 10г.), а в одном — фальшивые (вес одной монеты — 11 г.) Как одним взвешиванием на точных электронных весах определить в каком мешке фальшивые монеты?
29)В восьмилитровом бидоне находится молоко. Как при помощи пятилитрового бидона и трехлитровой банки отмерить 4 литра молока?
30)Как из восьмилитрового ведра, наполненного молоком, отлить один литр с помощью трехлитровой банки и пятилитрового бидона?
31)Как, имя пятилитровую банку и девятилитровое ведро, набрать из реки ровно три литра воды?
32)В шестилитровом ведре содержится четыре литра кваса, а в семилитровом — шесть литров. Как разделить весь имеющийся квас пополам, используя эти ведра и пустую трехлитровую банку?
Как разделить весь имеющийся квас пополам, используя эти ведра и пустую трехлитровую банку?
33)В трех кучках находится 22, 14 и 12 орехов. Требуется путем трех перекладываний уровнять число орехов в каждой кучке, соблюдая при этом условие: из любой кучки разрешается перекладывать в другую лишь столько орехов, сколько их в этой второй кучке.
34)Положите на стол три кучки спичек. В одну кучку положите 11 спичек, в другую — 7, в третью — 6. Перекладывая спички из любой кучки в любую другую, нужно за три операции сравнять все три кучки, чтобы в каждой было по 8 спичек. К любой кучке разрешается добавлять столько спичек, сколько в ней есть.
Решение задач на перемещения.
35)От потолка комнаты вертикально вниз по стене ползли две мухи. Спустившись до пола, они поползли обратно. Первая муха ползла в оба конца с одной и той же скоростью, а вторая хотя и поднималась в двое медленнее первой, но зато спускалась в двое быстрее. Какая из мух раньше приползет обратно?
36)Два Муравья отправились в гости к Стрекозе. Один всю дорогу прополз, а второй первую половину пути ехал на Гусенице, что было в два раза медленнее, чем ползти, а вторую половину скакал на Кузнечике, что было в десять раз быстрее. Какой Муравей первым придет в гости, если они вышли одновременно?
Один всю дорогу прополз, а второй первую половину пути ехал на Гусенице, что было в два раза медленнее, чем ползти, а вторую половину скакал на Кузнечике, что было в десять раз быстрее. Какой Муравей первым придет в гости, если они вышли одновременно?
37)Два летчика вылетели одновременно из одного города в два различных пункта. Кто из них долетит до места назначения быстрее, если первому из них нужно пролететь вдвое большее расстояние, но зато он летит в два раза быстрее, чем второй?
38)Что быстрее: проехать весь путь на велосипеде или половину пути проехать на мотоцикле, а вторую половину пройти пешком, если скорость мотоцикла в два раза больше скорости велосипеда, а скорость велосипеда, в свою очередь, в два раза больше скорости пешехода?
39)Путь от дома до школы Буратино проделал пешком, обратно он двигался той же дорогой, но первую половину пути он проехал на собаке, а вторую половину пути — на черепахе. Известно, что скорость собаки в четыре раза больше, а скорость черепахи — в два раза меньше, чем скорость, с которой Буратино шел пешком в школу. На каой путь — из дома до школы или из школы до дома — затратил Буратино больше времени?
На каой путь — из дома до школы или из школы до дома — затратил Буратино больше времени?
Решение логических задач.
(найти соответствие)
40)В трех ящиках находятся мука, крупа и сахар. На первом из них написано «Крупа», на втором — «Мука», на третьем — «Крупа или сахар». Известно, что содержимое ящиков не соответствует надписи. В каком ящике что находится?
41)На улице, став в кружок беседуют четыре девочки: Аня, Валя, Галя и Надя. Девочка в зеленом платье (не Аня и не Валя) стоит между девочкой в голубом платье и Надей. Девочка в белом платье стоит между девочкой в розовом и Валей. Какое платье носит каждая из девочек?
42)Алеша, Боря и Витя учатся в одном классе. Один ездит домой из школы на автобусе, другой — на трамвае, третий — на троллейбусе. Алеша однажды после уроков пошел проводить друга до автобусной остановки. Когда мимо проходил троллейбус, третий друг крикнул из окна: «Боря, ты забыл в школе дневник!». Кто на чем ездит домой.
43)Встретились три друга: Белов, Чернов и Рыжов. «Волосы одного из нас белые, другого — черные, третьего -рыжие, но ни у кого цвет волос не соответствует фамилии», — заметил черноволосый. «Ты прав», — подтвердил Белов. Какие у кого волосы?
«Волосы одного из нас белые, другого — черные, третьего -рыжие, но ни у кого цвет волос не соответствует фамилии», — заметил черноволосый. «Ты прав», — подтвердил Белов. Какие у кого волосы?
44)Три подруги вышли в белом, зеленом и синем платьях. Их туфли были одного из тех же трех цветов. Известно, что только у Ани цвета платья и туфель совпали. Ни платье, ни туфли Вали не были белыми. Наташа была в зеленых туфлях. Определите цвет платья и туфель каждой из подруг.
45)На одном заводе работают три друга: слесарь, токарь и сварщик. Их фамилии: Борисов, Иванов и Семенов. У слесаря нет ни братьев, ни сестер, он самый младший из друзей. Семенов старше токаря и женат на сестре Борисова. Назовите фамилии слесаря, токаря и сварщика соответственно.
46)В очереди за билетами в кино стоят друзья: Юра, Миша, Володя, Саша и Олег. Известно, что Юра купит билет раньше, чем Миша, но позже Олега. Володя и Олег не стоят рядом, А Саша не находится рядом ни с Олегом, ни с Юрой, ни с Володей. Кто за кем стоит?
Кто за кем стоит?
47)В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшинов и сосудом с квасом, в банке не лимонад и не вода. Стакан стоит около банки и сосуда с молоком. В какой сосуд налита каждая из жидкостей?
48)Коля, Боря, Вова и Юра заняли в соревновании первые четыре места, причем никакие два мальчика не делили между собой какие-нибудь места. Коля не занял ни первое, ни четвертое место. Боря занял второе место, а Вова не был последним. Какое место занял каждый из мальчиков?
49)На столе лежат в ряд четыре фигуры: треугольник, ромб, круг и квадрат. Цвета этих фигур: зеленый, желтый, синий, красный. В каком порядке лежат фигуры и каков цвет каждой из них, если фигура красного цвета лежит между зеленой и синей. Справа от желтой фигуры лежит ромб, круг лежит правее треугольника и ромба, причем треугольник лежит с краю, и, наконец, фигура синего цвета не лежит рядом с фигурой желтого цвета?
(некоторые из высказываний ложны)
50)В тетради написано 100 утверждений:
В этой тетради ровно одно ложное утверждение.
В этой тетради ровно два ложных утверждений.
…
В этой тетради ровно сто ложных утверждений.
Какое из этих утверждений верно.
51)Придя с работы домой, мама обнаружила, что ее любимая вазочка разбита. « Кто это сделал?»- обратилась она к детям.
Саша сказал: «Я не разбивал. Вазу разбил Олег».
Олег сказал: « Это сделал не я. Это сделал Саша».
Маша сказала: « Я вазочку не разбивала. И Олег не разбивал».
Определите, кто разбил вазу, если известно, что у каждого из детей одно утверждение верно, а другое ложно.
52)Один из попугаев А, В, и С всегда говорит правду, другой всегда врет, а третий — хитрец, он иногда говорит правду, а иногда врет. На вопрос: «Кто В?» они ответили:
А: — Лжец.
В: — Я хитрец!
С: — Абсолютно честный попугай.
Кто из попугаев лжец, а кто хитрец?
53)До Царя дошла весть, что кто-то из трех богатырей убил Змея Горыныча. Приказал Царь им явиться ко двору. Молвили богатыри:
Илья Муромец: — Змея убил Добрыня Никитич.
Добрыня Никитич: — Змея убил Алеша Попович.
Алеша Попович: — Я убил змея.
Известно, что только один богатырь сказал правду, а двое других слукавили. Кто убил змея?
54)До царя Гороха дошла молва, что наконец кто-то убил Змея Горыныча. Царь догадался, что это дело рук или Ильи Муромца, или Добрыни Никитича, или Алеши Поповича. Пригласил их ко двору, стал расспрашивать. Трижды каждый богатырь речь держал. И сказали они так:
Илья Муромец: «Я не убивал Змея Горыныча. Я в заморские страны уезжал. А змея Горыныча убил Алеша Попович.»
Добрыня Никитич: «Змея Горыныча убил Алеша Попович. Но я если бы и убил, то не сознался бы. Много еще нечистой силы осталось!»
Алеша Попович: «Нея убил Змея Горыныча. Я давно ищу, какой бы подвиг совершить. И взаправду Илья Муромец в заморские страны уезжал.»
Потом царь Горох узнал, что дважды каждый богатырь правду говорил, а один раз соврал.
Так кто же убил Змея Горыныча?
55)За круглый стол сели семь братьев-гномов. Гномы всегда говорят правду всем старшим братьям, а младшим всегда врут. Каждый гном сказал своему правому соседу: «все здесь присутствующие говорят мне только неправду». В каком порядке сидят гномы?
Гномы всегда говорят правду всем старшим братьям, а младшим всегда врут. Каждый гном сказал своему правому соседу: «все здесь присутствующие говорят мне только неправду». В каком порядке сидят гномы?
56)За круглым столом сидят восемь человек, каждый из которых либо рыцарь, либо лжец. Рыцари всегда говорят правду, а лжецы — всегда лгут . На вопрос, кто их соседи, каждый из них ответил : « Мои соседи — лжец и рыцарь». Сколько среди них было лжецов ?
57)В стране Рыцарей и Лжецов живут рыцари, все высказывания которых правдивы, и лжецы — каждое высказывание которых — ложь. И еще в этой стране бывают гости, в большинстве своем, — нормальные люди, с которыми особенно трудно: они могут говорить правду, но могут и солгать. Однажды, прогуливаясь по стране рыцарей и лжецов, я встретил человека, который сказал о себе: «Я — лжец». Кем был тот человек, которого я встретил?
58)В одной сказочной стране поблизости один от другого находятся города А и В. Все жители города А говорят только правду, а жители города В всегда лгут. Жители этих городов ходят друг к другу в гости. Путешественник попал в один из этих городов, но не знает, в какой. Как он может, задав один вопрос первому попавшемуся жителю, узнать, в каком городе он находится?
Жители этих городов ходят друг к другу в гости. Путешественник попал в один из этих городов, но не знает, в какой. Как он может, задав один вопрос первому попавшемуся жителю, узнать, в каком городе он находится?
59)В конференции участвовало 100 человек — химики и алхимики. Каждому был задан вопрос: « Если не считать Вас, то кого больше среди остальных участников — химиков или алхимиков?» когда опросили 51 участника, и все ответили, что алхимиков больше, опрос прервался. Алхимики всегда лгут, а химики всегда говорят правду. Сколько химиков среди участников?
(пересечение и объединение множеств)
60)Каждая семья, живущая в нашем доме, выписывает или газету, или журнал, или и то и другое вместе. 75 семей выписывают газету, а 27 семей выписывают журнал. И лишь 13 семей выписывают и журнал и газету. Сколько семей живет в нашем доме?
61)Из 40 учащихся нашего классаи32 любят молоко, 21 — лимонад, а 15 и молоко и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?
62)12 моих одноклассников любят читать детективы, 18 -фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?
Сколько учеников в нашем классе?
63)В воскресенье 19 учеников нашего класса побывали в планетарии, 10 — в цирке и 6 — на стадионе. Планетарий и цирк посетили 5 учеников; планетарий и стадион — 3, цирк и стадион — 1. Сколько учеников в нашем классе, если никто не успел посетить все три места, а три ученика не посетили ни одного места?
64)В ясельной группе 11 деток любят манную кашу, 13 — гречневую и 7 малышей — перловую. Четверо любят и манную кашу, и гречневую, 3 — манную и перловую, 6 — гречневую и перловую, а двое с удовольствием «уплетают» все три вида каши. Сколько детей в этой группе, если в ней нет ни одного ребенка, вовсе не любящего кашу?
65)В одном классе 25 учеников. Из них 7 любят груши, 11- черешню. Двое любят груши и черешню; 6 — груши и яблоки; 5 — яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?
66)Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три иностранных языка?
Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три иностранных языка?
67)Из сотрудников фирмы 16 побывали во Франции, 10 — в Италии, 6 — в Англии. В Англии и Италии — 5, в Англии и Франции — 6, во всех странах — побывали 5 сотрудников. Сколько человек посетили Италию и Францию, если всего в фирме работает 19 человек и каждый из них побывал хотя бы в одной из названных стран?
68)В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике — 12; по истории — 23. По русскому и математике — 4; по математике и истории — 9;по русскому и истории — 5. Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?
69)Получил я посылку от своих друзей из Сочи с яблоками и грушами. Одни плоды были большие, другие маленькие. Да и по цвету они отличались: часть была желтого цвета, часть — зеленого. Среди плодов не было маленьких груш и не было маленьких зеленых яблок. Яблок было 25. Груш было 17. Больших плодов было 32. Желтых плодов было 28. Зеленых яблок было на 2 больше, чем зеленых груш. Сколько больших желтых яблок было в этой посылке?
Да и по цвету они отличались: часть была желтого цвета, часть — зеленого. Среди плодов не было маленьких груш и не было маленьких зеленых яблок. Яблок было 25. Груш было 17. Больших плодов было 32. Желтых плодов было 28. Зеленых яблок было на 2 больше, чем зеленых груш. Сколько больших желтых яблок было в этой посылке?
(сколько надо взять?)
70)В коробке лежат 10 красных и 10 синих воздушных шариков. Продавец, не глядя, достает по одному шарику. Сколько шариков надо вытащить, чтобы среди вынутых из коробки шариков обязательно нашлись два шарика одного цвета?
71)В коробке лежат семь красных и пять синих карандашей. Из коробки в темноте берут карандаши. Сколько надо взять карандашей, чтобы среди них было не менее двух красных и трех синих?
72)В пакете перемешали конфеты трех сортов, неразличимых на ощупь. Какое наименьшее число конфет надо взять наугад из пакета, чтобы среди взятых конфет обязательно были хотя бы две одного сорта?
73)В ящике лежат 10 красных, 8 синих и 4 желтых карандаша. Из ящика в темноте берут карандаши. Какое наименьшее число карандашей надо взять, чтобы среди них заведомо было:
Из ящика в темноте берут карандаши. Какое наименьшее число карандашей надо взять, чтобы среди них заведомо было:
а) не менее 4 карандашей одного цвета;
б) не менее 6 карандашей одного цвета;
в) хотя бы 1 карандаш каждого цвета;
г) не менее 6 синих карандашей?
74)В темной кладовой в беспорядке лежат ботинки: 10 пар черных и 10 пар коричневых. Сколько ботинок надо взять, чтобы среди них оказалась хотя бы одна пара (левый и правый ботинок) одного цвета? В темноте нельзя отличить не только цвет ботинка, но и левый от правого.
Решение задач, решаемых с конца.
75)Задумано число, к нему прибавлена 1, сумма умножена на 2, произведение разделено на 3 и от результата отнять 4. Получилось 6. Какое число задумано?
76)Женщина собрала в саду яблоки. Чтобы выйти из сада, ей пришлось пройти через четыре двери, каждую из которых охранял свирепый стражник, отбиравший половину яблок. Домой она принесла 10 яблок. Сколько яблок досталось стражникам?
77)У моста через речку встретились лодырь и черт. Лодырь пожаловался на свою бедность. В ответ черт предложил: « Я могу тебе помочь. Каждый раз, как ты перейдешь этот мост, у тебя деньги удвоятся. Но каждый раз, перейдя мост, ты должен будешь отдать мне 24 копейки.» Три раза проходил лодырь мост, а когда заглянул в кошелек, там стало пусто. Сколько денег было у лодыря?
Лодырь пожаловался на свою бедность. В ответ черт предложил: « Я могу тебе помочь. Каждый раз, как ты перейдешь этот мост, у тебя деньги удвоятся. Но каждый раз, перейдя мост, ты должен будешь отдать мне 24 копейки.» Три раза проходил лодырь мост, а когда заглянул в кошелек, там стало пусто. Сколько денег было у лодыря?
78)Мама положила на стол сливы и сказала детям, чтобы они, вернувшись из школы, разделили их поровну. Первой пришла Аня, взяла треть сли и ушла. Потом вернулся из школы Боря, взял треть оставшихся слив и ушел. Затем пришел Витя и взял 4 сливы — треть от числа слив, которые он увидел. Сколько слив оставила мама?
79)В ящик лежат лимоны. Сначала из него взяли половину всех лимонов и половину лимона, затем половину остатка и еще половину лимона, наконец, половину нового остатка и опять половину лимона. После этого в ящике остался 31 лимон. Сколько лимонов было в ящике вначале?
Разные задачи.
80)На скотном дворе гуляли гуси и поросята. Мальчик сосчитал количество голов, их оказалось 30, затем сосчитал, сколько всего ног, их оказалось 84. Можно ли узнать, сколько гусей и сколько поросят было на скотном дворе?
Можно ли узнать, сколько гусей и сколько поросят было на скотном дворе?
81)В клетке находятся фазаны и кролики. Известно, что в клетке 35 голов и 94 ноги. Сколько в клетке фазанов и сколько кроликов?
82)На поляне ребята пасут жеребят. Если пересчитать ноги ребят и жеребят, то будет 74, а если считать головы, то 22. Сколько на лугу жеребят?
83)Если учащихся посадить по одному человеку на стул, то семерым не хватит места. Если на каждый стул посадить по два человека, то останутся свободными пять стульев. Сколько было учащихся и сколько стульев?
84)На поляне паслись ослы. К ним подошло несколько ребят. Если на каждого осла сядут по одному мальчику, то двум из них не хватит ослов. Если же на каждого осла сядут по два мальчика, то один осел будет лишний. Сколько ослов и сколько мальчиков было на поляне?
85)Учитель задал на уроке сложную задачу. В результате количество мальчиков, решивших задачу, оказалось равно количеству девочек, ее не решивших. Кого в классе больше — решивших задачу или девочек?
86)Один биолог открыл удивительную разновидность амеб. Каждая из них через минуту делится на две. В пробирку биолог кладет одну амебу, и ровно через час вся пробирка оказывается заполненной амебами. Сколько потребовалось бы времени, чтобы вся пробирка заполнилась амебами, если бы в нее положили не одну амебу, а две?
Каждая из них через минуту делится на две. В пробирку биолог кладет одну амебу, и ровно через час вся пробирка оказывается заполненной амебами. Сколько потребовалось бы времени, чтобы вся пробирка заполнилась амебами, если бы в нее положили не одну амебу, а две?
87)В гости пришло шесть человек в галошах разного размера. Расходились по одному, и некоторые надевали галоши большего размера. Сколько могло остаться гостей, не сумевших надеть галоши?
88)Винни-Пух, Пятачок, Кролик и ослик Иа-Иа съели 70 бананов, причем каждому сколько-то досталось. Винни-Пух съел больше каждого из остальных, а Кролик и Пятачок вместе съели 45 бананов. Сколько бананов досталось ослику?
89)Путешественник хочет пересечь пустыню за 6 дней. Известно, что один человек способен взять с собой припасов на 4 дня. Он не сможет преодолеть весь путь в одиночку, но он может взять с собой носильщиков. Сколько человек он должен взять с обой и как организовать путешествие, чтобы благополучно пересечь пустыню и все носильщики вернулись домой?
Решение математических ребусов.
90)
91)ТРИ+ДВА=ПЯТЬ
92)НАУКА+УЧЕБА=РАБОТА
93)СИНИЦА+СИНИЦА=ПТИЧКИ
94)РАЙОН+РАЙОН=ГОРОД
95)ДРАМА+ДРАМА=ТЕАТР
96)БАРБОС+БОБИК=СОБАКИ
97)КОШКА+КОШКА+КОШКА=СОБАКА
98)АИСТ+АИСТ+АИСТ+АИСТ=СТАЯ
99)ПАРУС+ПАРУС+ПАРУС+ПАРУС=РЕГАТА
Используемая литература.
1. Газета «Математика» приложение к газете «Первое сентября» №№ 28, 38,39,40, 1996г.
2. Библиотечка «Первого сентября» Математика № 4, 2005г.
3. Библиотечка «Первого сентября» Математика № 35 2010г.
4. Занимательная математика на уроках в 5-11 классах./ Гаврилова Т.Д. — Учитель, 2008г.
5. Математика. Задачи на развитие математического мышления 5-6 классы./Чулков П.В. — Издат-школа, 2000г.
6. Математическая шкатулка. /Нагибин Ф.Ф., Канин Е.С. — Просвещение, 1984г.
7. Математика. Сборник задач. /Смыкалова Е.В. — СМИО Пресс, 2007г.
задач — Полный курс алгебры
Навыки
в н
A L G E B R A
Содержание | Дом
10
Примеры
Проблемы
ЗАДАЧИ СЛОВА требуют практики перевода словесного языка на алгебраический язык. См. Урок 1, Задача 8. Тем не менее, текстовые задачи делятся на разные типы. Ниже приведены некоторые примеры.
См. Урок 1, Задача 8. Тем не менее, текстовые задачи делятся на разные типы. Ниже приведены некоторые примеры.
Пример 1. x ± b = c . Все проблемы, подобные следующей, в конечном итоге приводят к уравнению в такой простой форме.
Джейн потратила 42 доллара на обувь. Это было на 14 долларов меньше, чем в два раза больше, чем она потратила на блузку. Сколько стоила блузка?
Раствор. У каждой задачи со словами есть неизвестный номер. В этой задаче это цена блузки. Всегда позволяйте x представлять неизвестное число. То есть пусть x ответьте на вопрос.
Пусть х , то сколько она потратила на блузку. В задаче указано, что «Это», то есть 42 доллара США, было на 14 долларов меньше, чем удвоенное x .
Вот уравнение:
| 2 x − 14 | = | 42. |
| 2 x | = | 42 + 14 (Урок 9) |
| = | 56. | |
| x | = | 56 2 |
| = | 28. | |
Блузка стоит 28 долларов.
Пример 2. В классе b мальчиков. Это в три с лишним раза больше, чем у девочек. Сколько девочек в классе?
Решение. Опять же, пусть x представляет собой неизвестное число, которое вас просят найти: Пусть x будет количеством девочек.
(Хотя b неизвестно — это идея определенного числа — это не то, что вас просят найти.)
Задача утверждает, что «Это» — b — в три раза больше, чем в четыре раза x :
| 4 x + 3 | = | б . | ||
| Следовательно, | ||||
| 4 х | = | б − 3 | ||
| x | = | б − 3 4 | . | |
Решение здесь не числовое, потому что оно будет зависеть от значения b . Это тип «буквального» уравнения, который очень распространен в алгебре.
Пример 3. Целое равно сумме частей.
Сумма двух чисел равна 84, и одно из них на 12 больше другого. Какие два числа?
Решение. В этой задаче нас просят найти два числа. Поэтому пусть х будет одним из них.
Пусть x будет первым числом.
Тогда другое число будет еще 12, x + 12.
В задаче указано, что их сумма равна 84:
= 84
Линия размером x + 12 является группирующим символом, называемым vinculum . Это избавляет нас от написания скобок.
У нас есть:
| 2 x | = | 84 − 12 |
| = | 72. | |
| х | = | 72 2 |
| = | 36. | |
Это первый номер. Следовательно, другой номер
х + 12 = 36 + 12 = 48.
Сумма 36 + 48 равна 84.
Пример 4. Сумма двух последовательных чисел равна 37. Что это такое?
Решение . Два последовательных числа подобны 8 и 9 или 51 и 52.
Пусть x будет первым числом. Тогда число после него будет x + 1.
Задача утверждает, что их сумма равна 37:
= 37
| 2 x | = | 37 − 1 |
| = | 36. | |
| x | = | 36 2 |
| = | 18. | |
Два числа 18 и 19.
Пример 5. Одно число на 10 больше другого. Сумма удвоенного меньшего плюс трехкратного большего равна 55. Какие это два числа?
Сумма удвоенного меньшего плюс трехкратного большего равна 55. Какие это два числа?
Решение. Пусть x будет меньшим числом.
Тогда большее число будет на 10 больше: x + 10.
Проблема гласит:
| 2 х + 3( х + 10) | = | 55. |
| Это означает | ||
| 2 x + 3 x + 30 | = | 55. Урок 14. |
| 5 x | = | 55 — 30 = 25. |
| x | = | 5. |
Это меньшее число. Большее число на 10 больше: 15.
Пример 6. Разделите 80 долларов между тремя людьми так, чтобы у второго было в два раза больше, чем у первого, а у третьего было на 5 долларов меньше, чем у второго.
Решение .
Пусть x будет суммой, которую получит первый человек.
Тогда второй получает в два раза больше, 2 x .
А третий получает на 5 долларов меньше, 2 x − 5.
Их сумма $80:
| 5 х | = | 80 + 5 |
| x | = | 85 5 |
| = | 17. | |
Столько получает первый человек. Поэтому второй получает
| 2 x | = | 34. |
| И третий получает | ||
| 2 x − 5 | = | 29. |
Сумма 17, 34 и 29 на самом деле равна 80.
Пример 7. Нечетные числа. Сумма двух последовательных нечетных чисел равна 52. Какие два нечетных числа?
Решение . Во-первых, четное число кратно 2: 2, 4, 6, 8 и т. д. В алгебре принято представлять четное число как 2 n , где под вызовом переменной n подразумевается, что n будет принимать целочисленные значения: n = 0, 1, 2, 3, 4 и так далее.
Нечетное число на 1 больше (или на 1 меньше), чем четное число. Итак, мы представляем нечетное число как 2 n + 1.
.Пусть 2 n + 1 будет первым нечетным числом. Тогда в следующем будет еще 2 — это будет 2 n + 3. Задача утверждает, что их сумма равна 52:
| 2 n + 1 + 2 n + 3 | = | 52. |
Теперь мы решим это уравнение для n , а затем заменим решение на 2 n + 1, чтобы найти первое нечетное число. У нас есть:
У нас есть:
| 4 п + 4 | = | 52 |
| 4 п | = | 48 |
| п | = | 12. |
Следовательно, первое нечетное число равно 2 · 12 + 1 = 25. Следующее число равно 27. Их сумма равна 52.
Проблемы
Задача 1. У Джули есть 50 долларов, что на восемь долларов больше, чем у Джона. Сколько у Джона? (Сравните пример 1.)
Во-первых, что вы позволите представлять x ?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
Неизвестное число — сколько у Джона.
Что такое уравнение?
2 х + 8 = 50.
Вот решение:
х = 21
долларов СШАЗадача 2. Карлотта потратила на рынке 35 долларов. Это на семь долларов меньше, чем в три раза больше, чем она потратила в книжном магазине; сколько она там потратила?
Вот уравнение.
3 х — 7 = 35
Вот решение:
х = 14
долларов СШАЗадача 3. Есть b черных шариков. Это в четыре раза больше, чем количество красных шариков. Сколько красных шариков? (Сравните пример 2.)
Вот уравнение.
2 х + 4 = б
Вот решение:
| х = | б − 4 2 |
Задача 4. Джанет потратила 100 долларов на книги. Это было на тысяч долларов меньше, чем в пять раз больше, чем она потратила на обед. Сколько она потратила на обед?
Вот уравнение.
5 х — к = 100
Вот решение:
| х = | 100 + к 5 |
Задача 5. Целое равно сумме частей.
Сумма двух чисел равна 99, и одно из них на 17 больше другого. Какие два числа? (Сравните пример 3.)
Вот уравнение.
Вот решение:
| x | = | 41 |
| x + 17 | = | 58 |
Задача 6. Класс из 50 учеников делится на две группы; в одной группе на восемь меньше, чем в другой; сколько в каждой группе?
Вот уравнение.
Вот решение:
| x | = | 29 |
| x − 8 | = | 21 |
Задача 7. Сумма двух чисел равна 72, и одно из них в пять раз больше другого; какие два числа?
Сумма двух чисел равна 72, и одно из них в пять раз больше другого; какие два числа?
Вот уравнение.
х + 5 х = 72.
Вот решение:
х = 12, 5 х = 60,
Задача 8. Сумма трех последовательных чисел равна 87; кто они такие? (Сравните пример 4.)
Вот уравнение.
Вот решение:
28, 29, 30.
Задача 9. Группа из 266 человек состоит из мужчин, женщин и детей. Мужчин в четыре раза больше, чем детей, и вдвое больше, чем женщин. Сколько каждого из них?
(Чему вы приравняете x — количеству мужчин, женщин или детей?)
| Пусть х | = | Количество детей. Затем |
| 4 x | = | Количество мужчин.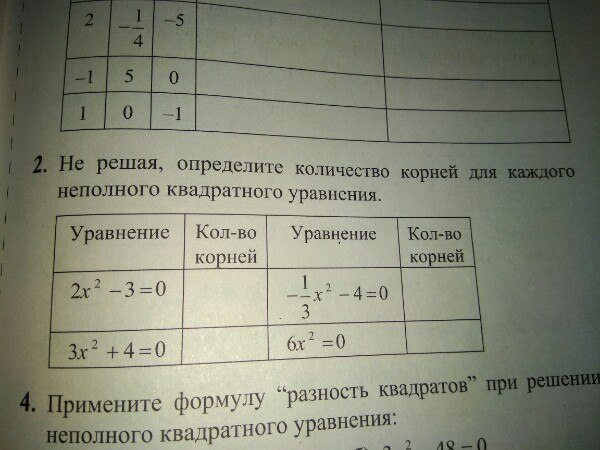 И И |
| 2 x | = | Количество женщин. |
| Вот уравнение: | ||
х + 4 х + 2 х = 266
Вот решение:
х = 38, 4 х = 152, 2 х = 76,
Задача 10. Разделите 79 долларов между тремя людьми так, чтобы у второго было в три раза больше, чем у первого, а у третьего было на два доллара больше, чем у второго. (Сравните пример 6.)
Вот уравнение.
Вот решение:
11 долларов США, 33 долларов США, 35 долларов США.
Задача 11. Разделите 15,20 доллара между тремя людьми так, чтобы у второго было на один доллар больше, чем у первого, а у третьего было на 2,70 доллара больше, чем у второго.
Вот уравнение.
Вот решение:
3,50 доллара США, 4,50 доллара США, 7,20 доллара США.
Задача 12. Два последовательных нечетных числа таковы, что первое, умноженное на три, больше второго в 5 раз. Что это за два нечетных числа?
(см. пример 7, где мы представляем нечетное число как 2 n + 1.)
Решение . Пусть первое нечетное число будет 2 н + 1.
Тогда следующий будет 2 n + 3 — потому что будет еще 2.
Задача утверждает, то есть уравнение:
| 3(2 n + 1) | = | 2(2 н + 3) + 5. | |
| Это означает: | |||
| 6 п + 3 | = | 4 п + 6 + 5. | |
| 2 нет | = | 8. | |
| п | = | 4. | |
Следовательно, первое нечетное число равно 2 · 4 + 1 = 9. Следующее число равно 11.
Следующее число равно 11.
И это верное решение, потому что согласно задаче:
3 · 9 = 2 · 11 + 5.
Следующий урок: неравенства
Содержание | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
3.1 Использование стратегии решения задач — Элементарная алгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Подходите к словесным задачам с позитивным настроем
- Используйте стратегию решения проблем со словами
- Решить числовые задачи
Приготовься 3.1
Прежде чем приступить к работе, пройдите этот тест на готовность.
Переведите «6 меньше чем в два раза x » в алгебраическое выражение.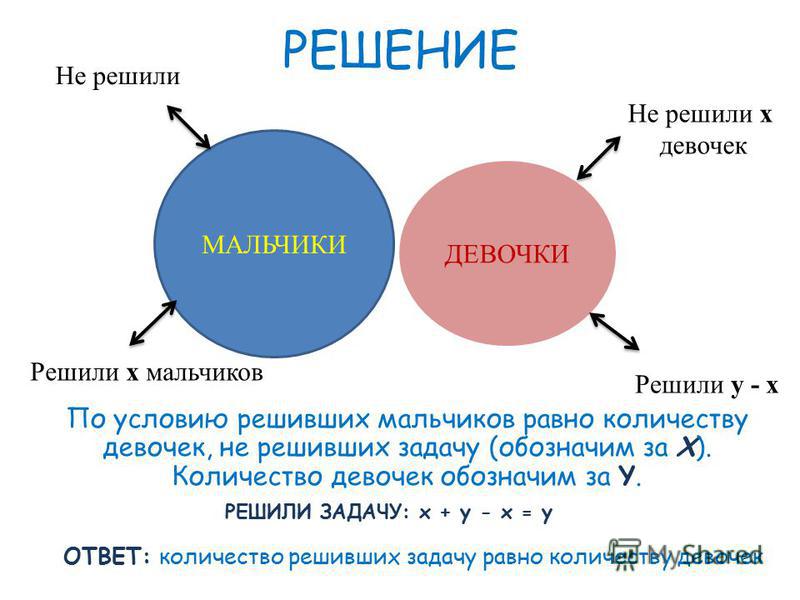
Если вы пропустили эту проблему, просмотрите пример 1.26.
Приготовься 3.2
Решите: 23x=24,23x=24.
Если вы пропустили эту проблему, просмотрите пример 2.16.
Решите: 3x+8=14,3x+8=14.
Если вы пропустили эту проблему, просмотрите пример 2.27.
Подходите к задачам со словами с позитивным настроем
«Если вы думаете, что можете… или думаете, что не можете… вы правы» — Генри Форд
Мир полон текстовых задач! Позволит ли мой доход арендовать эту квартиру? Сколько пунша мне нужно сделать для вечеринки? Бриллиант какого размера я могу позволить себе купить своей девушке? Должен ли я лететь или ехать на воссоединение моей семьи?
Сколько денег мне нужно, чтобы заправить машину бензином? Сколько чаевых следует оставлять в ресторане? Сколько носков взять с собой в отпуск? Индейку какого размера мне нужно купить на ужин в честь Дня Благодарения, а затем, во сколько мне нужно поставить ее в духовку? Если мы с сестрой купим маме подарок, сколько каждый из нас заплатит?
Теперь, когда мы можем решать уравнения, мы готовы применить наши новые навыки для решения текстовых задач. Знаете ли вы кого-нибудь, у кого в прошлом был негативный опыт решения проблем со словами? Были ли у вас когда-нибудь такие мысли, как у студента ниже?
Знаете ли вы кого-нибудь, у кого в прошлом был негативный опыт решения проблем со словами? Были ли у вас когда-нибудь такие мысли, как у студента ниже?
Рисунок 3.2 Негативные мысли могут стать препятствием на пути к успеху.
Когда мы чувствуем, что у нас нет контроля, и продолжаем повторять негативные мысли, мы возводим барьеры на пути к успеху. Нам нужно успокоить наши страхи и изменить наши негативные чувства.
Начните с чистого листа и начните мыслить позитивно. Если мы возьмем на себя управление и поверим, что можем добиться успеха, мы сможем решать текстовые задачи! Прочитайте положительные мысли на рис. 3.3 и произнесите их вслух.
Рисунок 3.3 Позитивные мысли — первый шаг к успеху.
Подумайте о чем-то помимо школы, что вы можете делать сейчас, но не могли 3 года назад. Это вождение автомобиля? Катание на сноуборде? Готовите изысканную еду? Говорите на новом языке? Ваш прошлый опыт решения задач со словами случился, когда вы были моложе, — теперь вы стали старше и готовы к успеху!
Использование стратегии решения задач Word
Мы рассмотрели перевод английских фраз в алгебраические выражения с использованием некоторых основных математических терминов и символов. Мы также перевели английские предложения в алгебраические уравнения и решили некоторые текстовые задачи. Словесные задачи применяли математику к повседневным ситуациям. Мы переформулировали ситуацию в одном предложении, присвоили переменную, а затем написали уравнение для решения задачи. Этот метод работает, пока ситуация знакома и математика не слишком сложна.
Мы также перевели английские предложения в алгебраические уравнения и решили некоторые текстовые задачи. Словесные задачи применяли математику к повседневным ситуациям. Мы переформулировали ситуацию в одном предложении, присвоили переменную, а затем написали уравнение для решения задачи. Этот метод работает, пока ситуация знакома и математика не слишком сложна.
Теперь мы расширим нашу стратегию, чтобы использовать ее для успешного решения любой текстовой задачи. Мы перечислим стратегию здесь, а затем воспользуемся ею для решения некоторых задач. Ниже мы суммируем эффективную стратегию решения проблем.
Как
Используйте стратегию решения проблем для решения задач Word.
- Шаг 1. Прочтите проблему. Убедитесь, что все слова и идеи понятны.
- Шаг 2. Определите , что мы ищем.
- Шаг 3. Имя то что мы ищем. Выберите переменную для представления этого количества.

- Шаг 4. Переведите число в уравнение. Может быть полезно переформулировать проблему в одном предложении со всей важной информацией. Затем переведите английское предложение в алгебраическое уравнение.
- Шаг 5. Решите уравнение, используя хорошие методы алгебры.
- Шаг 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл.
- Шаг 7. Ответьте на вопрос полным предложением.
Пример 3.1
Пилар купила кошелек на распродаже за 18 долларов, что составляет половину первоначальной цены. Какова была первоначальная цена кошелька?
Решение
Шаг 1. Прочтите проблему. Прочитайте задачу два или более раз, если это необходимо. Поищите незнакомые слова в словаре или в Интернете.
- В этой задаче понятно, о чем идет речь? Каждое слово знакомо?
Шаг 2. Определите , что вы ищете. Вы когда-нибудь заходили в спальню, чтобы что-то взять, а потом забывали, что искали? Трудно найти что-то, если вы не уверены, что это такое! Прочитайте задачу еще раз и найдите слова, которые говорят вам, что вы ищете!
Определите , что вы ищете. Вы когда-нибудь заходили в спальню, чтобы что-то взять, а потом забывали, что искали? Трудно найти что-то, если вы не уверены, что это такое! Прочитайте задачу еще раз и найдите слова, которые говорят вам, что вы ищете!
- В этой задаче слова «какова была первоначальная цена кошелька» говорят нам, что нам нужно найти.
Шаг 3. Назовите то, что мы ищем. Выберите переменную для представления этого количества. Мы можем использовать любую букву для переменной, но выбираем ту, которая позволяет легко запомнить, что она представляет.
- Пусть p=p= первоначальная цена кошелька.
Шаг 4. Преобразуйте в уравнение. Может быть полезно переформулировать проблему в одном предложении со всей важной информацией. Переведите английское предложение в алгебраическое уравнение.
Внимательно перечитайте задачу, чтобы увидеть, как связана данная информация. Часто есть одно предложение, которое дает эту информацию, или может помочь написать одно предложение со всей важной информацией. Ищите слова-подсказки, которые помогут перевести предложение на алгебраический язык. Переведите предложение в уравнение.
Часто есть одно предложение, которое дает эту информацию, или может помочь написать одно предложение со всей важной информацией. Ищите слова-подсказки, которые помогут перевести предложение на алгебраический язык. Переведите предложение в уравнение.
| Решите уравнение. | |
| Умножьте обе стороны на 2. | |
| Упрощение. |
Шаг 6. Проверьте ответ в задаче, чтобы убедиться, что он имеет смысл. Мы решили уравнение и нашли, что p = 36, p = 36, что означает, что «первоначальная цена» составляла 36 долларов.
Проверьте ответ в задаче, чтобы убедиться, что он имеет смысл. Мы решили уравнение и нашли, что p = 36, p = 36, что означает, что «первоначальная цена» составляла 36 долларов.
- Имеет ли значение $36 в задаче? Да, потому что 18 — это половина от 36, а кошелек продавался за половину первоначальной цены.
Шаг 7. Ответьте на вопрос полным предложением. Задача задавалась вопросом: «Какова была первоначальная цена кошелька?»
- Ответ на вопрос: «Первоначальная цена кошелька составляла 36 долларов».
Если бы это было домашнее задание, наша работа могла бы выглядеть так:
Пилар купила сумочку на распродаже за 18 долларов, что составляет половину первоначальной цены. Какова была первоначальная цена кошелька?
Пусть p=p= первоначальная цена. | |
| 18 составляет половину первоначальной цены. | |
| Умножьте обе стороны на 2. | |
| Упрощение. | |
| Чек. Является ли 36 долларов разумной ценой для кошелька? | |
| Да. | |
| Является ли 18 половиной 36? | |
| 18=?12⋅3618=?12⋅36 | |
| 18=18✓18=18✓ | |
| Первоначальная цена кошелька составляла 36 долларов. |
Попытайся 3.1
Хоакин купил книжный шкаф на распродаже за 120 долларов, что составляло две трети первоначальной цены. Какова была первоначальная цена книжного шкафа?
Попытайся 3.2
Две пятых песен в плейлисте Мариэль — кантри. Если в плейлисте 16 песен в стиле кантри, сколько всего песен в плейлисте?
Давайте попробуем этот подход на другом примере.
Пример 3.2
Джинни и ее одноклассники сформировали учебную группу. Девочек в исследуемой группе было на три больше, чем юношей более чем в два раза. В учебной группе было 11 девочек. Сколько мальчиков было в учебной группе?
Решение
| Шаг 1. Прочтите проблему. | |
| Шаг 2. Определите , что мы ищем. | Сколько мальчиков было в учебной группе? |
| Шаг 3. Имя. Выберите переменную для представления количества мальчиков. | Пусть n=n= число мальчиков. |
| Шаг 4. Переведите. Переформулируйте проблему в одном предложении со всей важной информацией. | |
| Преобразовать в уравнение. | |
Шаг 5. Решите уравнение. | |
| Вычтите 3 с каждой стороны. | |
| Упрощение. | |
| Разделите каждую сторону на 2. | |
| Упрощение. | |
| Шаг 6. Проверка. Во-первых, разумен ли наш ответ? Да, иметь 4 мальчиков в учебной группе кажется нормальным. В задаче говорится, что девочек было на 3 больше, чем мальчиков. Если есть четыре мальчика, получается одиннадцать девочек? Дважды 4 мальчика равно 8. Трое больше 8 равно 11. | |
| Шаг 7. Ответьте на вопрос. | В учебной группе было 4 мальчика. |
Попытайся 3.3
Гильермо купил учебники и тетради в книжном магазине. Учебников было в 3 раза больше, чем тетрадей. Он купил 7 учебников. Сколько тетрадей он купил?
Попытайся 3.4
На этой неделе Джерри разгадывал судоку и кроссворды. Количество решенных им судоку в восемь раз превышает количество кроссвордов более чем в два раза. Он решил 22 головоломки судоку. Сколько кроссвордов он разгадал?
Количество решенных им судоку в восемь раз превышает количество кроссвордов более чем в два раза. Он решил 22 головоломки судоку. Сколько кроссвордов он разгадал?
Решить числовые задачи
Теперь, когда у нас есть стратегия решения задач, мы будем использовать ее для решения нескольких различных типов текстовых задач. Первый тип, над которым мы будем работать, — это «задачи с числами». Задачи с числами дают некоторые подсказки об одном или нескольких числах. Мы используем эти подсказки, чтобы написать уравнение. Проблемы с числами обычно не возникают каждый день, но они являются хорошим введением в практику стратегии решения проблем, описанной выше.
Пример 3.3
Разница между числом и шестью равна 13. Найдите число.
Решение
| Шаг 1. Прочтите проблему. Все ли слова знакомы? | |
Шаг 2. Определите , что мы ищем. Определите , что мы ищем. | номер |
| Шаг 3. Имя. Выберите переменную для представления числа. | Пусть n=n= число. |
| Шаг 4. Переведите. Не забывайте искать слова-подсказки, такие как «разница… между… и…» | |
| Переформулируйте проблему одним предложением. | |
| Преобразовать в уравнение. | |
| Шаг 5. Решите уравнение. | |
| Упрощение. | |
| Шаг 6. Проверка. | |
| Разница 19а 6 это 13. Это проверка! | |
| Шаг 7. Ответьте на вопрос. | Число 19. |
Попытайся 3,5
Разница числа и восьмерки равна 17. Найдите число.
Попытайся 3,6
Разница числа и одиннадцати равна −7,−7. Найдите число.
Найдите число.
Пример 3.4
Сумма удвоенного числа и семи равна 15. Найдите число.
Решение
| Шаг 1. Прочтите проблему. | |
| Шаг 2. Определите , что мы ищем. | номер |
| Шаг 3. Имя. Выберите переменную для представления числа. | Пусть n=n= число. |
| Шаг 4. Переведите. | |
| Переформулируйте проблему одним предложением. | |
| Преобразовать в уравнение. | |
| Шаг 5. Решите уравнение. | |
| Вычтите по 7 с каждой стороны и упростите. | |
| Разделите каждую сторону на 2 и упростите. | |
Шаг 6. Проверка. Проверка. | |
| Сумма удвоенных 4 и 7 равна 15? | |
| 2⋅4+7≟1515=15✓2⋅4+7≟1515=15✓ | |
| Шаг 7. Ответьте на вопрос. | Число 4. |
Вы заметили, что мы пропустили некоторые шаги при решении этого уравнения? Если вы еще не готовы пропустить эти шаги, запишите столько, сколько вам нужно.
Попытайся 3,7
Сумма четырех умноженных на число и два равна 14. Найдите число.
Попытайся 3,8
Сумма трех чисел, умноженных на семь, равна 25. Найдите число.
Некоторые задачи с числовыми словами требуют от нас найти два или более чисел. Может показаться заманчивым назвать их все разными переменными, но до сих пор мы решали уравнения только с одной переменной. Чтобы избежать использования более одной переменной, мы будем определять числа в терминах одной и той же переменной. Обязательно внимательно прочитайте задачу, чтобы узнать, как все числа соотносятся друг с другом.
Обязательно внимательно прочитайте задачу, чтобы узнать, как все числа соотносятся друг с другом.
Пример 3,5
Одно число на пять больше другого. Сумма чисел равна 21. Найдите числа.
Решение
| Шаг 1. Прочтите проблему. | ||
| Шаг 2. Определите , что мы ищем. | Ищем два номера. | |
| Шаг 3. Имя. Нам нужно назвать два номера, и для каждого нужно имя. | ||
| Выберите переменную для представления первого числа. | Пусть n=1stn=1st число. | |
| Что мы знаем о втором числе? | Одно число на пять больше другого. | |
| n+5=2ndn+5=2-й номер | ||
Шаг 4. Перевести. Переформулируйте проблему одним предложением со всей важной информацией. Переформулируйте проблему одним предложением со всей важной информацией. | Сумма чисел 1 st и 2 nd равна 21. | |
| Преобразовать в уравнение. | ||
| Подставьте переменные выражения. | ||
| Шаг 5. Решите уравнение. | ||
| Объедините похожие термины. | ||
| Вычтите 5 с обеих сторон и упростите. | ||
| Раздели на 2 и упрости. | ||
| Найдите и второе число. | ||
| Шаг 6. Проверка. | ||
| Эти номера учитываются в проблеме? | ||
| Одно число на 5 больше другого? | 13≟8+513≟8+5 | |
Тринадцать 5 больше 8? Да. | 13=13✓13=13✓ | |
| Сумма двух чисел равна 21? | 8+13≟218+13≟21 | |
| 21=21✓21=21✓ | ||
| Шаг 7. Ответьте на вопрос. | Цифры 8 и 13. |
Попытайся 3,9
Одно число на шесть больше другого. Сумма чисел равна двадцати четырем. Найдите числа.
Попытайся 3.10
Сумма двух чисел равна пятидесяти восьми. Одно число на четыре больше другого. Найдите числа.
Пример 3,6
Сумма двух чисел равна четырнадцати. Одно число на четыре меньше другого. Найдите числа.
Решение
 Проверка.
Проверка. Попытайся 3.11
Сумма двух чисел минус двадцать три. Одно число на семь меньше другого. Найдите числа.
Попытайся 3.12
Сумма двух чисел равна −18.−18. Одно число на 40 больше другого. Найдите числа.
Пример 3,7
Одно число в десять раз больше другого. Их сумма равна единице. Найдите числа.
Решение
Шаг 1. Прочтите проблему. Прочтите проблему. | ||
| Шаг 2. Определите , что вы ищете. | Ищем два номера. | |
| Шаг 3. Имя. | ||
| Выберите переменную. | Пусть x=1stx=1-е число. | |
| Одно число в 10 раз больше другого. | 2x+10=2nd2x+10=2-й номер | |
| Шаг 4. Перевести. | ||
| Переформулируйте одним предложением. | Их сумма равна единице. | |
| Сумма двух чисел равна 1. | ||
| Преобразовать в уравнение. | ||
| Шаг 5. Решите уравнение. | ||
| Объедините похожие термины. | ||
Вычтите 10 с каждой стороны. | ||
| Разделите каждую сторону на 3. | ||
| Шаг 6. Проверка. | ||
| Является ли число десять больше, чем удвоенное −3, равно 4? | 2(−3)+10≟42(−3)+10≟4 | |
| −6+10≟4−6+10≟4 | ||
| 4=4✓4=4✓ | ||
| Их сумма равна 1? | −3+4≟1−3+4≟1 | |
| 1=1✓1=1✓ | ||
| Шаг 7. Ответьте на вопрос. | Числа -3 и 4. |
Попытайся 3.13
Одно число в восемь раз больше другого. Их сумма равна минус четырем. Найдите числа.
Попытайся 3.14
Одно число в три раза больше другого. Их сумма равна −5,−5. Найдите числа.
Некоторые задачи с числами включают последовательные целые числа. Последовательные целые числа — это целые числа, следующие непосредственно друг за другом. Примеры последовательных целых чисел:
.1,2,3,4-10,-9,-8,-7150,151,152,1531,2,3,4-10,-9,-8,-7150,151,152,153
Обратите внимание, что каждое число на единицу больше, чем предшествующее ему число. Итак, если мы определим первое целое число как n , следующее последовательное целое число будет n+1.n+1. Следующий за ним на единицу больше, чем n+1,n+1, поэтому это n+1+1,n+1+1, то есть n+2.n+2.
n1 целое числоn+12-е целое число подрядn+23-е целое число подряд . . . и т. д.n1 целое числоn+12-е целое число подрядn+23-е целое число подряд . . . и т.д.
Пример 3,8
Сумма двух последовательных целых чисел равна 47. Найдите числа.
Найдите числа.
Решение
| Шаг 1. Прочтите проблему. | ||
| Шаг 2. Определите , что вы ищете. | два последовательных целых числа | |
| Шаг 3. Назовите каждое число. | Пусть n=1stn=1-е целое число. | |
| n+1=n+1= следующее последовательное целое число | ||
| Шаг 4. Перевести. | ||
| Переформулируйте одним предложением. | Сумма целых чисел равна 47. | |
| Преобразовать в уравнение. | ||
| Шаг 5. Решите уравнение. | ||
| Объедините похожие термины. | ||
Вычтите по 1 с каждой стороны. | ||
| Разделите каждую сторону на 2. | ||
| Шаг 6. Проверка. | ||
| 23+24≟4747=47✓23+24≟4747=47✓ | ||
| Шаг 7. Ответьте на вопрос. | Два последовательных целых числа 23 и 24. |
Попытайся 3.15
Сумма двух последовательных целых чисел равна 95,95. Найдите числа.
Попытайся 3.16
Сумма двух последовательных целых чисел равна −31,−31. Найдите числа.
Пример 3,9
Найдите три последовательных целых числа, сумма которых равна −42,−42.
Решение

Попытайся 3.17
Найдите три последовательных целых числа, сумма которых равна -9.6.−96.
Попытайся 3.18
Найдите три последовательных целых числа, сумма которых равна −36,−36.
Теперь, когда мы работали с последовательными целыми числами, мы расширим нашу работу, включив в нее последовательные четные и последовательные нечетные целые числа. Последовательные четные числа — это четные целые числа, следующие непосредственно друг за другом. Примеры последовательных четных целых чисел:
Последовательные четные числа — это четные целые числа, следующие непосредственно друг за другом. Примеры последовательных четных целых чисел:
18,20,2264,66,68-12,-10,-818,20,2264,66,68-12,-10,-8
Обратите внимание, что каждое целое число на 2 больше предыдущего числа. Если мы назовем первый n , то следующий n+2.n+2. Следующим будет n+2+2n+2+2 или n+4.n+4.
n1steven integern+22-е последовательное четное целоеn+43-е последовательное четное целое . . . и т.д.n1steven integern+22ndstrengtheven integern+43rdstrengtheven integer . . . и т.д.
Последовательные нечетные числа — это нечетные целые числа, следующие непосредственно одно за другим. Рассмотрим последовательные нечетные целые числа 77, 79 и 81.
77,79,81n,n+2,n+477,79,81n,n+2,n+4
n1нечетное целое числоn+22-е последовательное нечетное целое числоn+43-е последовательное нечетное целое число . . . и т.д.n1нечетное целое числоn+22-е последовательное нечетное целое числоn+43-е последовательное нечетное целое число . . . и т. д.
. . и т.д.n1нечетное целое числоn+22-е последовательное нечетное целое числоn+43-е последовательное нечетное целое число . . . и т. д.
Не кажется ли вам странным прибавлять 2 (четное число) для перехода от одного нечетного целого числа к другому? Получится ли у вас нечетное или четное число, если мы прибавим 2 к 3? до 11? до 47?
Независимо от того, запрашивает ли задача последовательные четные или нечетные числа, ничего другого делать не нужно. Схема остается той же — чтобы перейти от одного нечетного или одного четного целого числа к следующему, прибавьте 2.
.Пример 3.10
Найдите три последовательных четных целых числа, сумма которых равна 84.
Решение
| Шаг 1. Прочтите проблему. | |
| Шаг 2. Определите , что мы ищем. | три последовательных четных целых числа |
Шаг 3. Назовите целые числа. Назовите целые числа. | Пусть n=1stn=1st четное целое число. n+2=2ndn+2=2-е последовательное четное целое число n+4=3rdn+4=третье последовательное четное целое число |
| Шаг 4. Перевести. | |
| Переформулируйте одним предложением. | Сумма трех четных целых чисел равна 84. |
| Преобразовать в уравнение. | n+n+2+n+4=84n+n+2+n+4=84 |
| Шаг 5. Решите уравнение. | |
| Объедините похожие термины. | n+n+2+n+4=84n+n+2+n+4=84 |
| Вычтите 6 с каждой стороны. | 3n+6=843n+6=84 |
| Разделите каждую сторону на 3. | 3n=783n=78 |
| n=261 целое число+22-е целое число26+228n+43-е целое число26+430n=261 целое число+22-е целое число26+228n+43-е целое число26+430 | |
Шаг 6. Проверка. Проверка. | |
| 26+28+30=?8484=84✓26+28+30=?8484=84✓ | |
| Шаг 7. Ответьте на вопрос. | Три последовательных целых числа: 26, 28 и 30. |
Стол 3.1
Попытайся 3.19
Найдите три последовательных четных целых числа, сумма которых равна 102.
Попытайся 3.20
Найдите три последовательных четных целых числа, сумма которых равна −24,−24.
Пример 3.11
Супружеская пара вместе зарабатывает 110 000 долларов в год. Жена зарабатывает на 16 000 долларов меньше, чем в два раза больше, чем зарабатывает ее муж. Что зарабатывает муж?
Решение
| Шаг 1. Прочтите проблему. | ||
Шаг 2. Определите , что мы ищем. | Сколько зарабатывает муж? | |
| Шаг 3. Имя . | ||
| Выберите переменную для представления суммы заработка мужа. | Пусть h=h= сумма заработка мужа. | |
| Жена зарабатывает на 16 000 долларов меньше, чем вдвое больше. | 2ч-16,0002ч-16,000 сумма, которую зарабатывает жена. | |
| Шаг 4. Переведите. | Вместе муж и жена зарабатывают 110 000 долларов. | |
| Переформулируйте проблему в одном предложении с всей важной информацией. | ||
| Преобразовать в уравнение. | ||
| Шаг 5. Решите уравнение. | ч + 2 ч — 16 000 = 110 000 | |
| Объедините похожие термины. | 3 часа — 16 000 = 110 000 | |
Добавьте 16 000 с обеих сторон и упростите. | 3 ч = 126 000 | |
| Разделите каждую сторону на 3. | ч = 42 000 | |
| $42 000 сумма мужа | ||
| 2 часа − 16 000 сумма заработка жены | ||
| 2(42 000) − 16 000 | ||
| 84 000 − 16 000 | ||
| 68 000 | ||
| Шаг 6. Проверка. | ||
| Если жена зарабатывает 68 000 долларов, а муж зарабатывает 42 000 долларов, получается, что общая сумма составляет 110 000 долларов? Да! | ||
| Шаг 7. Ответьте на вопрос. | Муж зарабатывает 42 000 долларов в год. |
Попытайся 3.21
По данным Национальной ассоциации автомобильных дилеров, средняя стоимость автомобиля в 2014 году составляла 28 500 долларов. Это было на 1500 долларов меньше, чем в 6 раз больше, чем в 1975 году. Какова была средняя стоимость автомобиля в 1975 году?
Это было на 1500 долларов меньше, чем в 6 раз больше, чем в 1975 году. Какова была средняя стоимость автомобиля в 1975 году?
Попытайся 3,22
Данные переписи населения США показывают, что средняя цена нового дома в США в ноябре 2014 года составляла 280,9 долларов США.00. Это было на 10 700 долларов больше, чем в 14 раз по сравнению с ценой в ноябре 1964 года. Какова была средняя цена нового дома в ноябре 1964 года?
Раздел 3.1 Упражнения
Практика ведет к совершенству
Используйте слова «подход» к проблемам с позитивным настроем
В следующих упражнениях подготовьте описанные списки.
1.
Перечислите пять позитивных мыслей, которые вы можете сказать себе, и которые помогут вам решать проблемы со словами с позитивным настроем. Вы можете скопировать их на лист бумаги и положить в начало тетради, где вы сможете часто их читать.
2.
Перечислите пять негативных мыслей, которые вы говорили себе в прошлом и которые будут мешать вашему прогрессу в решении текстовых задач. Вы можете написать каждое из них на маленьком листе бумаги и разорвать его, чтобы символически уничтожить негативные мысли.
Использование стратегии решения задач Word
В следующих упражнениях решите, используя стратегию решения текстовых задач. Не забудьте написать полное предложение, чтобы ответить на каждый вопрос.
3.
Две трети детей четвертого класса — девочки. Если в классе 20 девочек, сколько всего детей в классе?
4.
Три пятых членов школьного хора составляют женщины. Если в хоре 24 женщины, то каково общее количество участников хора?
5.
У Захари 25 компакт-дисков с музыкой в стиле кантри, что составляет пятую часть его коллекции компакт-дисков. Сколько дисков у Закари?
Сколько дисков у Закари?
6.
Четвертая часть конфет в пакете M&M’s красная. Сколько конфет в мешке, если 23 красные конфеты?
7.
В школьном клубе 16 девочек. Девочек в четыре раза больше, чем мальчиков. Найдите количество мальчиков.
8.
В Стае 645 18 детенышей разведчиков. Количество разведчиков в три раза больше, чем количество взрослых лидеров, более чем в пять раз. Найдите количество взрослых лидеров.
9.
Хуонг организует книги в мягкой и твердой обложке для распродажи подержанных книг в своем клубе. Количество книг в мягкой обложке на 12 меньше, чем в три раза больше, чем в твердой обложке. У Хуонга было 162 книги в мягкой обложке. Сколько было книг в твердом переплете?
10.
Джефф выстраивает детские и взрослые велосипеды в магазине велосипедов, где он работает. Количество детских велосипедов на девять меньше, чем количество велосипедов для взрослых, и в три раза меньше. Есть 42 взрослых велосипеда. Сколько детских велосипедов?
Количество детских велосипедов на девять меньше, чем количество велосипедов для взрослых, и в три раза меньше. Есть 42 взрослых велосипеда. Сколько детских велосипедов?
11.
Филип ежемесячно платит 1620 долларов за аренду. Эта сумма на 120 долларов больше, чем вдвое больше, чем его брат Пол платит за аренду. Сколько Павел платит за аренду?
12.
Марк только что купил внедорожник за 54 000 долларов. Это на 7400 долларов меньше, чем вдвое меньше, чем его жена заплатила за свою машину в прошлом году. Сколько жена заплатила за машину?
13.
Лори инвестировала 46 000 долларов в акции и облигации. Сумма, вложенная в акции, на 8000 долларов меньше суммы, вложенной в облигации, в три раза. Сколько Лори вложил в облигации?
14.
В прошлом году Эрика заработала на двух работах в общей сложности 50 450 долларов. Сумма, которую она заработала на своей работе в магазине, составила 1250 долларов, что более чем в три раза превышает сумму, которую она заработала на своей работе в колледже. Сколько она зарабатывала на своей работе в колледже?
Сумма, которую она заработала на своей работе в магазине, составила 1250 долларов, что более чем в три раза превышает сумму, которую она заработала на своей работе в колледже. Сколько она зарабатывала на своей работе в колледже?
Решить числовые задачи
В следующих упражнениях решите задачу с числовыми словами.
15.
Сумма числа и восьми равна 12. Найдите число.
16.
Сумма числа и девяти равна 17. Найдите число.
17.
Разница числа и 12 равна трем. Найдите число.
18.
Разница числа и восьмерки равна четырем. Найдите число.
19.
Сумма трех чисел, умноженных на восемь, равна 23. Найдите число.
20.
Сумма удвоенного числа и шести равна 14. Найдите число.
21.
Разница удвоенного числа и семи равна 17. Найдите число.
22.
Разница четырехкратного числа и семи равна 21. Найдите число.
23.
Сумма числа, умноженная на три, равна 12. Найдите число.
24.
Сумма числа, умноженного на шесть и восемь, равна 30. Найдите число.
25.
Одно число на шесть больше другого. Их сумма равна 42. Найдите числа.
26.
Одно число на пять больше другого. Их сумма равна 33. Найдите числа.
27.
Сумма двух чисел равна 20. Одно число на четыре меньше другого. Найдите числа.
28.
Сумма двух чисел равна 27. Одно число на семь меньше другого. Найдите числа.
29.
Сумма двух чисел равна −45.−45. Одно число на девять больше другого. Найдите числа.
30.
Сумма двух чисел равна −61,−61. Одно число на 35 больше другого. Найдите числа.
31.
Сумма двух чисел равна −316.−316. Одно число на 94 меньше другого. Найдите числа.
32.
Сумма двух чисел равна −284.−284. Одно число на 62 меньше другого. Найдите числа.
33.
Одно число на 14 меньше другого. Если их сумму увеличить на семь, получится 85. Найдите числа.
34.
Одно число на 11 меньше другого. Если их сумму увеличить на восемь, получится 71. Найдите числа.
35.
Одно число на пять больше другого. Если их сумму увеличить на девять, получится 60. Найдите числа.
36.
Одно число на восемь больше другого. Если их сумму увеличить на 17, получится 95. Найдите числа.
37.
Одно число в два раза больше другого. Их сумма равна −5,−5. Найдите числа.
38.
Одно число в шесть раз больше другого, чем в пять раз. Их сумма равна шести. Найдите числа.
39.
Сумма двух чисел равна 14. Одно число в два раза меньше другого в три раза. Найдите числа.
40.
Сумма двух чисел равна нулю. Одно число на девять меньше другого в два раза. Найдите числа.
41.
Сумма двух последовательных целых чисел равна 77. Найдите целые числа.
42.
Сумма двух последовательных целых чисел равна 89. Найдите эти числа.
43.
Сумма двух последовательных целых чисел равна −23,−23. Найдите целые числа.
Найдите целые числа.
44.
Сумма двух последовательных целых чисел равна −37,−37. Найдите целые числа.
45.
Сумма трех последовательных целых чисел равна 78. Найдите эти числа.
46.
Сумма трех последовательных целых чисел равна 60. Найдите эти числа.
47.
Найдите три последовательных целых числа, сумма которых равна −36,−36.
48.
Найдите три последовательных целых числа, сумма которых равна −3,−3.
49.
Найдите три последовательных четных целых числа, сумма которых равна 258.
50.
Найдите три последовательных четных целых числа, сумма которых равна 222.
51.
Найдите три последовательных нечетных числа, сумма которых равна 171.
52.
Найдите три последовательных нечетных целых числа, сумма которых равна 291.
53.
Найдите три последовательных четных целых числа, сумма которых равна −36,−36.
54.
Найдите три последовательных четных целых числа, сумма которых равна −84,−84.
55.
Найдите три последовательных нечетных целых числа, сумма которых равна −213,−213.
56.
Найдите три последовательных нечетных целых числа, сумма которых равна −267,−267.
Математика на каждый день
57.
Цена со скидкой Пэтти заплатила 35 долларов за кошелек на распродаже на 10 долларов дешевле первоначальной цены. Какова была первоначальная цена кошелька?
58.
Цена со скидкой Трэвис купил пару ботинок на распродаже на 25 долларов дешевле первоначальной цены. Он заплатил 60 долларов за ботинки. Какова была первоначальная цена ботинок?
59.
Покупка оптом Мин потратил 6,25 доллара на пять книг с наклейками, чтобы подарить своим племянникам. Найдите стоимость каждой книги с наклейками.
60.
Покупка оптом Алисия купила упаковку из восьми персиков за 3,20 доллара. Найдите стоимость каждого персика.
61.
Цена до уплаты налога с продаж Том заплатил 1166,40 долларов за новый холодильник, включая налог в размере 86,40 долларов. Сколько стоил холодильник?
62.
Цена до уплаты налога с продаж Кенджи заплатил 2279 долларов за новый набор для гостиной, включая налог в размере 129 долларов. Сколько стоил комплект гостиной?
Сколько стоил комплект гостиной?
Письменные упражнения
63.
Каков был ваш предыдущий опыт решения текстовых задач?
64.
Когда вы начинаете решать задачу со словами, как вы решаете, что должна представлять переменная?
65.
Что такое последовательные нечетные целые числа? Назовите три последовательных нечетных целых числа от 50 до 60.
66.
Что такое последовательные четные целые числа? Назовите три последовательных четных целых числа в диапазоне от −50−50 до −40,−40.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.
ⓑ Если большинство ваших чеков было:
…уверенно. Поздравляем! Вы достигли своих целей в этом разделе! Подумайте об учебных навыках, которые вы использовали, чтобы вы могли продолжать их использовать. Что вы сделали, чтобы обрести уверенность в своих способностях делать эти вещи? Быть конкретной!
Что вы сделали, чтобы обрести уверенность в своих способностях делать эти вещи? Быть конкретной!
…с некоторой помощью. Это нужно решать быстро, так как темы, которые вы не освоили, становятся выбоинами на вашем пути к успеху. Математика последовательна — каждая тема основывается на предыдущей работе. Прежде чем двигаться дальше, важно убедиться, что у вас есть прочная основа. Кого вы можете попросить о помощи? Ваши одноклассники и преподаватель являются хорошими ресурсами. Есть ли в кампусе место, где есть репетиторы по математике? Можно ли улучшить свои учебные навыки?
… нет, я не понимаю! Это очень важно, и вы не должны игнорировать это. Вам нужно немедленно обратиться за помощью, иначе вы будете быстро разбиты. Как можно скорее обратитесь к инструктору, чтобы обсудить вашу ситуацию. Вместе вы можете придумать план, как получить необходимую вам помощь.
9.1 Использование стратегии решения задач — Предварительная алгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Подходите к словесным задачам с позитивным настроем
- Используйте стратегию решения задач для словесных задач
- Решение числовых задач
Приготовься 9.
 1
1Прежде чем приступить к работе, пройдите этот тест на готовность.
Переведите «6“6 меньше, чем в два раза х“х» в алгебраическое выражение.
Если вы пропустили эту проблему, просмотрите пример 2.25.
Приготовься 9.2
Решите: 23x=24,23x=24.
Если вы пропустили эту проблему, просмотрите пример 8.16.
Приготовься 9.3
Решите: 3x+8=14,3x+8=14.
Если вы пропустили эту проблему, просмотрите пример 8.20.
Подходите к проблемам со словами с позитивным настроем
В мире полно текстовых задач. Сколько денег мне нужно, чтобы заправить машину бензином? Сколько дать чаевых официанту в ресторане? Сколько носков взять с собой в отпуск? Насколько большую индейку мне нужно купить на ужин в честь Дня Благодарения и во сколько мне нужно поставить ее в духовку? Если мы с сестрой купим маме подарок, сколько каждый из нас заплатит?
Теперь, когда мы можем решать уравнения, мы готовы применить наши новые навыки для решения текстовых задач. Знаете ли вы кого-нибудь, у кого в прошлом был негативный опыт решения проблем со словами? Были ли у вас когда-нибудь мысли, как у ученика на рис. 9.2?
Знаете ли вы кого-нибудь, у кого в прошлом был негативный опыт решения проблем со словами? Были ли у вас когда-нибудь мысли, как у ученика на рис. 9.2?
Рисунок 9.2 Негативные мысли о проблемах со словами могут стать препятствием на пути к успеху.
Когда мы чувствуем, что у нас нет контроля, и продолжаем повторять негативные мысли, мы возводим барьеры на пути к успеху. Нам нужно успокоить наши страхи и изменить наши негативные чувства.
Начните с чистого листа и начните мыслить позитивно, как ученик на рис. 9.3. Прочитайте положительные мысли и произнесите их вслух.
Рисунок 9.3 Когда дело доходит до текстовых задач, позитивный настрой — это большой шаг к успеху.
Если мы возьмем на себя управление и поверим, что сможем добиться успеха, мы сможем справиться с текстовыми задачами.
Подумайте о том, что вы можете сделать сейчас, но не могли сделать три года назад. Будь то вождение автомобиля, катание на сноуборде, приготовление изысканной еды или говорение на новом языке, вы смогли изучить и освоить новый навык. Проблемы со словами ничем не отличаются. Даже если в прошлом вы боролись с текстовыми задачами, вы приобрели много новых математических навыков, которые помогут вам добиться успеха сейчас!
Проблемы со словами ничем не отличаются. Даже если в прошлом вы боролись с текстовыми задачами, вы приобрели много новых математических навыков, которые помогут вам добиться успеха сейчас!
Использование стратегии решения задач Word
В предыдущих главах вы переводили словосочетания в алгебраические выражения, используя базовый математический словарь и символы. С тех пор вы увеличили свой математический словарный запас, поскольку узнали больше об алгебраических процедурах, и у вас было больше практики перевода слов в алгебру.
Вы также перевели словесные предложения в алгебраические уравнения и решили некоторые текстовые задачи. Словесные задачи применяли математику к повседневным ситуациям. Вы должны были переформулировать ситуацию в одном предложении, назначить переменную, а затем написать уравнение, которое нужно решить. Этот метод работает до тех пор, пока ситуация вам знакома и математика не слишком сложна.
Теперь мы разработаем стратегию, которую вы сможете использовать для решения любой текстовой задачи. Эта стратегия поможет вам добиться успеха в решении текстовых задач. Мы продемонстрируем стратегию при решении следующей задачи.
Эта стратегия поможет вам добиться успеха в решении текстовых задач. Мы продемонстрируем стратегию при решении следующей задачи.
Пример 9.1
Пит купил рубашку на распродаже за 18 долларов, 18 долларов, что составляет половину первоначальной цены. Какова была первоначальная цена рубашки?
Решение
Шаг 1. Прочтите проблему. Убедитесь, что вы понимаете все слова и идеи. Возможно, вам придется прочитать задачу два или более раз. Если есть слова, которые вы не понимаете, поищите их в словаре или в Интернете.
- В этой задаче вы понимаете, о чем идет речь? Вы понимаете каждое слово?
Шаг 2. Определите , что вы ищете. Трудно найти что-то, если вы не уверены, что это такое! Прочитайте задачу еще раз и найдите слова, которые говорят вам, что вы ищете!
- В этой задаче слова «какова была первоначальная цена рубашки» говорят вам о том, что вы ищете: первоначальная цена рубашки.

Шаг 3. Назовите то, что вы ищете. Выберите переменную для представления этого количества. Вы можете использовать любую букву для переменной, но может помочь выбрать ту, которая поможет вам запомнить, что она представляет.
- Пусть p=p= первоначальная цена рубашки
Шаг 4. Преобразуйте в уравнение. Может помочь сначала переформулировать проблему в одном предложении со всей важной информацией. Затем переведите предложение в уравнение.
Шаг 5. Решите уравнение, используя хорошие методы алгебры. Даже если вы сразу знаете ответ, использование алгебры лучше подготовит вас к решению задач, на которые нет очевидных ответов.
| Напишите уравнение. | |
| Умножьте обе стороны на 2. | |
Упрощение. |
Шаг 6. Проверьте ответ в задаче и убедитесь, что он имеет смысл.
- Мы обнаружили, что p=36,p=36, , что означает, что исходная цена была $36.$36. Имеет ли значение $36$36 смысл в задаче? Да потому что 1818 это половина 36,36, и рубашка продавалась за половину первоначальной цены.
Шаг 7. Ответьте на вопрос полным предложением.
- Проблема с вопросом: «Какова была первоначальная цена рубашки?» Ответ на вопрос: «Первоначальная цена рубашки была 36 долларов. 36 долларов.
Если бы это было домашнее задание, наша работа могла бы выглядеть так:
Попытайся 9.
 1
1Хоакин купил книжный шкаф на распродаже за 120 долларов, 120 долларов, что составляло две трети первоначальной цены. Какова была первоначальная цена книжного шкафа?
Попытайся 9.2
Две пятых людей в столовой центра для престарелых — мужчины. Если 1616 мужчин, сколько всего людей в столовой?
Перечислим шаги, которые мы предприняли для решения предыдущего примера.
Стратегия решения проблем
- Шаг 1. Прочитайте слово задача. Убедитесь, что вы понимаете все слова и идеи. Возможно, вам придется прочитать задачу два или более раз. Если есть слова, которые вы не понимаете, поищите их в словаре или в Интернете.
- Шаг 2. Определите , что вы ищете.
- Шаг 3. Имя то, что вы ищете. Выберите переменную для представления этого количества.
- Шаг 4. Переведите число в уравнение. Может быть полезно сначала переформулировать проблему в одном предложении, прежде чем переводить.

- Шаг 5. Решите уравнение, используя хорошие методы алгебры.
- Шаг 6. Проверьте ответ в задаче. Убедитесь, что это имеет смысл.
- Шаг 7. Ответьте на вопрос полным предложением.
Давайте применим этот подход к другому примеру.
Пример 9.2
Яш принес на пикник яблоки и бананы. Количество яблок было на три больше, чем вдвое больше, чем количество бананов. Яш привез на пикник 1111 яблок. Сколько бананов он принес?
Решение
| Шаг 1. Прочтите проблему. | |
| Шаг 2. Определите , что вы ищете. | Сколько бананов он принес? |
| Шаг 3. Назовите то, что вы ищете. Выберите переменную для представления количества бананов. | Пусть b=количество банановb=количество бананов |
Шаг 4. Перевести. Переформулируйте проблему в одном предложении со всей важной информацией. Перевести. Переформулируйте проблему в одном предложении со всей важной информацией. Перевести в уравнение. | |
| Шаг 5. Решите уравнение. | |
| Вычтите по 3 с каждой стороны. | |
| Упрощение. | |
| Разделите каждую сторону на 2. | |
| Упрощение. | |
| Шаг 6. Проверка: Во-первых, разумен ли наш ответ? Да, взять четыре банана на пикник кажется разумным. В задаче говорится, что яблок было на три больше, чем бананов. Если есть четыре банана, получается одиннадцать яблок? Дважды 4 банана равно 8. На три больше 8 равно 11. | |
| Шаг 7. Ответьте на вопрос. | Яш принес на пикник 4 банана. |
Попытайся 9.3
Гильермо купил учебники и тетради в книжном магазине. Учебников было на 33 больше, чем тетрадей. Он купил 55 учебников. Сколько тетрадей он купил?
Учебников было на 33 больше, чем тетрадей. Он купил 55 учебников. Сколько тетрадей он купил?
Попытайся 9.4
На этой неделе Джерри разгадывал судоку и кроссворды. Количество решенных им судоку на семь больше, чем количество кроссвордов. Он решил 1414 головоломок судоку. Сколько кроссвордов он разгадал?
В разделе «Решение налогов с продаж, комиссий и скидок» мы научились преобразовывать и решать основные процентные уравнения и использовать их для решения налоговых и комиссионных приложений. В следующем примере мы применим нашу стратегию решения проблем к большему количеству применений процентов.
Пример 9.3
Премия Нга по страхованию автомобиля увеличилась на 60, 60 долларов, что составило 8%8% от первоначальной стоимости. Какова была первоначальная стоимость премии?
Решение
Шаг 1. Прочтите проблему. Помните, если есть слова, которые вы не понимаете, поищите их. Помните, если есть слова, которые вы не понимаете, поищите их. | |
| Шаг 2. Определите , что вы ищете. | первоначальная стоимость премиум |
| Шаг 3. Имя. Выберите переменную для представления первоначальной стоимости премии. | Пусть c=первоначальная стоимостьc=первоначальная стоимость |
| Шаг 4. Перевести. Переформулируйте одним предложением. Переведите в уравнение. | |
| Шаг 5. Решите уравнение. | |
| Разделите обе части на 0,08. | |
| Упрощение. | с=750с=750 |
| Шаг 6. Проверка: Разумен ли наш ответ? Да, премия в размере 750 долларов США по автострахованию является разумной. Теперь давайте проверим нашу алгебру. 8% от 750 равно 60? | |
Шаг 7. Ответьте на вопрос. Ответьте на вопрос. | Первоначальная стоимость премии Нга составляла 750 долларов. |
Попытайся 9,5
Арендная плата Пилар увеличилась на 4%.4%. Увеличение составило $38.$38. Какова была первоначальная сумма арендной платы Пилар?
Попытайся 9,6
Стив откладывает 12%12% от своей зарплаты каждый месяц. Если он сэкономил 504 504 доллара в прошлом месяце, сколько будет его зарплата?
Решаем задачи с числами
Теперь переведем и решим задачи с числами. В числовых задачах вам даются некоторые подсказки об одном или нескольких числах, и вы используете эти подсказки для построения уравнения. Проблемы с числами обычно не возникают каждый день, но они являются хорошим введением в практику стратегии решения проблем. Не забывайте искать ключевые слова, такие как разница , из , и .
Пример 9.4
Разница между числом и шестью составляет 13,13. Найдите число.
Решение
| Шаг 1. Прочтите проблему. Вы понимаете все слова? | |
| Шаг 2. Определите , что вы ищете. | номер |
| Шаг 3. Имя. Выберите переменную для представления числа. | Пусть n=числоn=число |
| Шаг 4. Перевести. Переформулируйте одним предложением. Перевести в уравнение. | |
| Шаг 5. Решите уравнение. Добавьте 6 к обеим сторонам. Упростить. | |
| Шаг 6. Проверка: Разница между 19 и 6 равна 13. Это проверка. | |
Шаг 7. Ответьте на вопрос. | Число 19. |
Попытайся 9,7
Разница между числом и восьмеркой составляет 17,17. Найдите число.
Попытайся 9,8
Разница числа и одиннадцати равна −7,−7. Найдите число.
Пример 9,5
Сумма удвоенного числа и семи равна 15,15. Найдите число.
Решение
| Шаг 1. Прочтите проблему. | |
| Шаг 2. Определите то, что вы ищете. | номер |
| Шаг 3. Имя. Выберите переменную для представления числа. | Пусть n=числоn=число |
| Шаг 4. Перевести. Переформулируйте проблему одним предложением. Перевести в уравнение. | |
| Шаг 5. Решите уравнение. | |
Вычтите по 7 с каждой стороны и упростите. | |
| Разделите каждую сторону на 2 и упростите. | |
| Шаг 6. Проверка: сумма удвоенных 4 и 7 равна 15? | |
| Шаг 7. Ответьте на вопрос. | Число 4. |
Попытайся 9,9
Сумма четырех умноженных на число и два равна 14,14. Найдите число.
Попытайся 9.10
Сумма трех чисел, умноженных на семь, равна 25,25. Найдите число.
В некоторых задачах с числовыми словами нужно найти два или более чисел. Может показаться заманчивым назвать их все разными переменными, но до сих пор мы решали уравнения только с одной переменной. Определим числа через ту же переменную. Обязательно внимательно прочитайте задачу, чтобы узнать, как все числа соотносятся друг с другом.
Пример 9,6
Одно число на пять больше другого. Сумма чисел равна двадцати одному. Найдите числа.
Найдите числа.
Решение
| Шаг 1. Прочтите проблему. | ||
| Шаг 2. Определите , что вы ищете. | Вы ищете два номера. | |
| Шаг 3. Имя. Выберите переменную для представления первого числа. Что вы знаете о втором числе? Перевести. | Пусть n=1-е число n=1-е число Одно число на пять больше другого. x+5=2-е числоx+5=2-е число | |
| Шаг 4. Перевести. Переформулируйте проблему одним предложением со всей важной информацией. Перевести в уравнение. Замените переменные выражения. | Сумма чисел 21. Сумма 1-го числа и 2-го числа 21. | |
Шаг 5. Решите уравнение. | ||
| Объедините похожие термины. | ||
| Вычтите пять с обеих сторон и упростите. | ||
| Раздели на два и упрости. | ||
| Найдите и второе число. | ||
| Замена n = 8 | ||
| Шаг 6. Проверка: | ||
| Эти номера учитываются в проблеме? Одно число на 5 больше другого? Тринадцать, 5 больше, чем 8? Да. Сумма двух чисел равна 21? | | |
| Шаг 7. Ответьте на вопрос. | Цифры 8 и 13. |
Попытайся 9.11
Одно число на шесть больше другого. Сумма чисел равна двадцати четырем. Найдите числа.
Найдите числа.
Попытайся 9.12
Сумма двух чисел равна пятидесяти восьми. Одно число на четыре больше другого. Найдите числа.
Пример 9,7
Сумма двух чисел равна четырнадцати. Одно число на четыре меньше другого. Найдите числа.
Решение
| Шаг 4. Перевести. Пишите одним предложением.  Перевести в уравнение. Замените переменные выражения. | Сумма двух чисел равна минус четырнадцать. | |
| Шаг 5. Решите уравнение. | ||
| Объедините похожие термины. | ||
| Добавьте по 4 с каждой стороны и упростите. | ||
| Разделить на 2. | ||
| Подставьте n=−5n=−5, чтобы найти число 2 и . | ||
| Шаг 6. Проверка: | ||
| Является ли -9 на четыре меньше, чем -5? Их сумма равна −14? | | |
| Шаг 7. Ответьте на вопрос. | Числа -5 и -9. |
Попытайся 9.
 13
13Сумма двух чисел минус двадцать три. Одно число на 77 меньше другого. Найдите числа.
Попытайся 9.14
Сумма двух чисел минус восемнадцать. Одно число на 4040 больше другого. Найдите числа.
Пример 9,8
Одно число в десять раз больше другого. Их сумма равна единице. Найдите числа.
Решение
| Шаг 1. Прочтите проблему. | ||
| Шаг 2. Определите , что вы ищете. | две цифры | |
| Шаг 3. Имя. Выберите переменную. Одно число в десять раз больше другого. | Пусть х = 1 ст номер 2 х + 10 = 2 й номер | |
Шаг 4. Перевести. Переформулируйте одним предложением. Переформулируйте одним предложением. | Их сумма равна единице. | |
| Преобразование в уравнение | ||
| Шаг 5. Решите уравнение. | ||
| Объедините похожие термины. | ||
| Вычтите 10 с каждой стороны. | ||
| Разделите каждую сторону на 3, чтобы получить первое число. | ||
| Подставьте, чтобы получить второе число. | ||
| Шаг 6. Проверка. | ||
| 4 десять больше, чем удвоенное −3? Их сумма равна 1? | | |
| Шаг 7. Ответьте на вопрос. | Числа -3 и 4. |
Попытайся 9.15
Одно число в восемь раз больше другого. Их сумма равна минус четырем. Найдите числа.
Попытайся 9.16
Одно число в три раза больше другого. Их сумма равна минус пяти. Найдите числа.
Последовательные целые числа — это целые числа, которые следуют непосредственно друг за другом. Некоторые примеры последовательных целых чисел:
.…1,2,3,4,……1,2,3,4,…
…−10,−9,−8,−7,…. ..−10,−9,−8,−7,…
…150,151,152,153,……150,151,152,153,…
Обратите внимание, что каждое число на единицу больше, чем предыдущее. Итак, если мы определим первое целое число как n,n, следующее последовательное целое число будет n+1.n+1. Следующий за ним на единицу больше, чем n+1,n+1, поэтому это n+1+1,n+1+1 или n+2.n+2.
n1-е целое числоn+12-е последовательное целое числоn+23-е последовательное целое числоn1-е целое числоn+12-е последовательное целое числоn+23-е последовательное целое число
Пример 9,9
Сумма двух последовательных целых чисел равна 47,47. Найдите числа.
Найдите числа.
Решение
| Шаг 1. Прочтите проблему. | ||
| Шаг 2. Определите , что вы ищете. | два последовательных целых числа | |
| Шаг 3. Имя. | Пусть n = 1 st целое число n + 1 = следующее последовательное целое число | |
| Шаг 4. Перевести. Переформулируйте одним предложением. Перевести в уравнение. | ||
| Шаг 5. Решите уравнение. | ||
| Объедините похожие термины. | ||
| Вычтите по 1 с каждой стороны. | ||
Разделите каждую сторону на 2. | ||
| Подставьте, чтобы получить второе число. | ||
| Шаг 6. Проверка: | | |
| Шаг 7. Ответьте на вопрос. | Два последовательных целых числа 23 и 24. |
Попытайся 9.17
Сумма двух последовательных целых чисел равна 95,95. Найдите числа.
Попытайся 9.18
Сумма двух последовательных целых чисел равна −31,−31. Найдите числа.
Пример 9.10
Найдите три последовательных целых числа, сумма которых равна 42,42.
Решение
| Шаг 1. Прочтите проблему. | ||
Шаг 2. Определите , что вы ищете. Определите , что вы ищете. | три последовательных целых числа | |
| Шаг 3. Имя. | Пусть n = 1 st целое число n + 1 = 2 nd последовательное целое число n + 2 = 3 rd последовательное целое число | |
| Шаг 4. Перевести. Переформулируйте одним предложением. Перевести в уравнение. | ||
| Шаг 5. Решите уравнение. | ||
| Объедините похожие термины. | ||
| Вычтите 3 с каждой стороны. | ||
| Разделите каждую сторону на 3. | ||
| Подставьте, чтобы получить второе число. | ||
Подставьте, чтобы получить третье число. | ||
| Шаг 6. Проверка: | | |
| Шаг 7. Ответьте на вопрос. | Три последовательных целых числа: 13, 14 и 15. |
Попытайся 9.19
Найдите три последовательных целых числа, сумма которых равна 96,96.
Попытайся 9.20
Найдите три последовательных целых числа, сумма которых равна −36,−36.
Раздел 9.1 Упражнения
Практика делает совершенным
Используйте стратегию решения задач для текстовых задач
В следующих упражнениях используйте стратегию решения задач для решения текстовых задач. Отвечай полными предложениями.
1.
Две трети детей четвертого класса — девочки. Если девочек 2020, сколько всего детей в классе?
Если девочек 2020, сколько всего детей в классе?
2.
Три пятых членов школьного хора составляют женщины. Если 2424 женщины, то каково общее количество участников хора?
3.
У Захари 2525 компакт-дисков с музыкой в стиле кантри, что составляет пятую часть его коллекции компакт-дисков. Сколько дисков у Закари?
4.
Четвертая часть конфет в пакете красного цвета. Если красных конфет 2323, сколько конфет в мешке?
5.
В школьном клубе 1616 девочек. Число девочек на 44 человека более чем в два раза превышает количество мальчиков. Найдите количество мальчиков в клубе.
6.
В отряде 645.645 1818 молодых скаутов. Количество скаутов — 33 человека, что более чем в пять раз превышает количество взрослых лидеров. Найдите количество взрослых лидеров.
7.
Ли выносит посуду и стаканы из посудомоечной машины. Количество блюд на 88 меньше количества стаканов. Если блюд 99, то сколько стаканов?
8.
Количество щенков на витрине зоомагазина на двенадцать меньше, чем количество собак в магазине. Если на витрине 66 щенков, сколько собак в магазине?
9.
После 33 месяцев диеты Лиза потеряла 12%12% своего первоначального веса. Она потеряла 2121 фунт. Какой был первоначальный вес Лизы?
10.
Триша получила прибавку к своей недельной зарплате на 6%6%. Повышение составляло 30-30 долларов в неделю. Какова была ее первоначальная недельная зарплата?
11.
Тим оставил чаевые в размере 9 долларов США на счет в ресторане на 50 долларов США. Сколько процентов чаевых он оставил?
12.
Рашид оставил чаевые в размере 15 долларов 15 долларов за счет ресторана в размере 75 долларов 75 долларов. Сколько процентов чаевых он оставил?
13.
Юки купила платье на распродаже за $72.$72. Цена продажи составила 60%60% от первоначальной цены. Какова была первоначальная цена платья?
14.
Ким купила пару туфель на распродаже за 40,50$. 40,50$. Цена продажи составила 45%45% от первоначальной цены. Какова была первоначальная цена обуви?
Решите числовые задачи
В следующих упражнениях решите каждую числовую задачу.
15.
Сумма числа и восьмерки равна 12,12. Найдите число.
16.
Сумма числа и девяти равна 17,17. Найдите число.
17.
Разница числа и двенадцати составляет 3,3. Найдите число.
18.
Разница между числом и восьмеркой составляет 4,4. Найдите число.
19.
Сумма трех чисел, умноженных на восемь, равна 23,23. Найдите число.
20.
Сумма удвоенного числа и шести равна 14,14. Найдите число.
21.
Разница удвоенного числа и семи составляет 17,17. Найдите число.
22.
Разница четырехкратного числа и семи составляет 21,21. Найдите число.
23.
Трижды умножить сумму числа и девяти на 12,12. Найдите число.
24.
Сумма шести чисел, умноженных на восемь, равна 30,30. Найдите число.
25.
Одно число на шесть больше другого. Их сумма сорок два. Найдите числа.
26.
Одно число на пять больше другого. Их сумма тридцать три. Найдите числа.
Их сумма тридцать три. Найдите числа.
27.
Сумма двух чисел равна двадцати. Одно число на четыре меньше другого. Найдите числа.
28.
Сумма двух чисел равна двадцати семи. Одно число на семь меньше другого. Найдите числа.
29.
Число в два раза больше другого числа. Их сумма равна минус пяти. Найдите числа.
30.
Одно число в шесть раз больше другого, чем в пять раз. Их сумма равна шести. Найдите числа.
31.
Сумма двух чисел равна четырнадцати. Одно число в два раза меньше другого в три раза. Найдите числа.
32.
Сумма двух чисел равна нулю. Одно число на девять меньше другого в два раза. Найдите числа.
33.
Одно число на четырнадцать меньше другого. Если их сумму увеличить на семь, получится 85,85. Найдите числа.
Если их сумму увеличить на семь, получится 85,85. Найдите числа.
34.
Одно число на одиннадцать меньше другого. Если их сумму увеличить на восемь, получится 71,71. Найдите числа.
35.
Сумма двух последовательных целых чисел равна 77,77. Найдите целые числа.
36.
Сумма двух последовательных целых чисел равна 89,89. Найдите целые числа.
37.
Сумма двух последовательных целых чисел равна −23,−23. Найдите целые числа.
38.
Сумма двух последовательных целых чисел равна −37,−37. Найдите целые числа.
39.
Сумма трех последовательных целых чисел равна 78,78. Найдите целые числа.
40.
Сумма трех последовательных целых чисел равна 60,60. Найдите целые числа.
41.
Найдите три последовательных целых числа, сумма которых равна −36,−36.
42.
Найдите три последовательных целых числа, сумма которых равна −3,−3.
Математика на каждый день
43.
Покупки Пэтти заплатила 35 долларов 35 долларов за кошелек на распродаже на 10 долларов 10 долларов дешевле первоначальной цены. Какова была первоначальная цена кошелька?
44.
Покупки Трэвис купил пару ботинок на распродаже за 25 долларов 25 долларов дешевле первоначальной цены. Он заплатил 60$60 за ботинки. Какова была первоначальная цена ботинок?
45.
Покупки Мин потратил 6,25 долларов 6,25 долларов на 55 книг с наклейками, чтобы подарить своим племянникам. Найдите стоимость каждой книги с наклейками.
46.
Покупки Алисия купила упаковку из 88 персиков за 3,20 доллара. 3,20 доллара. Найдите стоимость каждого персика.
47.
Покупки Том заплатил 1166,40 долларов 1166,40 долларов за новый холодильник, включая налог 86,40 долларов 86,40 долларов. Сколько стоил холодильник до вычета налогов?
48.
Покупки Кенджи заплатил 2279 долларов 2279 долларов за новый набор для гостиной, включая налог 129 долларов 129 долларов. Какова была цена гостиной до вычета налогов?
Письменные упражнения
49.
Напишите несколько предложений о своих мыслях и мнениях о текстовых задачах. Являются ли эти мысли положительными, отрицательными или нейтральными? Если они отрицательные, как вы могли бы изменить свой образ мышления, чтобы стать лучше?
50.
Когда вы начинаете решать задачу со словами, как вы решаете, что должна представлять переменная?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.
ⓑ Если большинство ваших чеков:
…уверенно. Поздравляем! Вы достигли целей в этом разделе. Подумайте об учебных навыках, которые вы использовали, чтобы вы могли продолжать их использовать. Что вы сделали, чтобы обрести уверенность в своих способностях делать эти вещи? Быть конкретной.
…с некоторой помощью. Это нужно решать быстро, потому что темы, которые вы не осваиваете, становятся выбоинами на вашем пути к успеху. В математике каждая тема основывается на предыдущей работе. Прежде чем двигаться дальше, важно убедиться, что у вас есть прочная основа. Кого вы можете попросить о помощи? Ваши одноклассники и преподаватель являются хорошими ресурсами. Есть ли в кампусе место, где есть репетиторы по математике? Можно ли улучшить свои учебные навыки?
… нет, я не понимаю! Это предупреждающий знак, и вы не должны его игнорировать. Вы должны немедленно обратиться за помощью, иначе вы быстро будете поражены. Как можно скорее обратитесь к инструктору, чтобы обсудить вашу ситуацию. Вместе вы можете придумать план, как получить необходимую вам помощь.
Вы должны немедленно обратиться за помощью, иначе вы быстро будете поражены. Как можно скорее обратитесь к инструктору, чтобы обсудить вашу ситуацию. Вместе вы можете придумать план, как получить необходимую вам помощь.
7.9 Возрастные задачи — Алгебра среднего уровня
Одним из приложений линейных уравнений является так называемая проблема возраста. При решении возрастных задач, как правило, сравнивают возраст двух разных людей (или объектов) как в настоящем, так и в будущем (или прошлом). Целью этих задач обычно является определение текущего возраста каждого субъекта. Поскольку в этих задачах может быть много информации, для организации и решения можно использовать диаграмму. Пример такой таблицы ниже.
| Человек или объект | Текущий возраст | Изменение возраста |
|---|---|---|
Джоуи на 20 лет моложе Бекки. Через два года Бекки будет вдвое старше Джоуи. Заполните таблицу возрастных проблем, но не решайте.
Через два года Бекки будет вдвое старше Джоуи. Заполните таблицу возрастных проблем, но не решайте.
- Первое предложение говорит нам, что Джоуи на 20 лет моложе Бекки (это текущий возраст)
- Второе предложение говорит нам о двух вещах:
- Изменение возраста Джоуи и Бекки составляет плюс два года
- Через два года Бекки будет вдвое старше Джои через два года
| Человек или объект | Текущий возраст | Изменение возраста (+2) |
|---|---|---|
| Джоуи (Дж.) | Б − 20 | Б – 20 + 2 Б – 18 |
| Бекки (Б) | Б | Б = 2 |
Использование этого последнего утверждения дает нам решение уравнения:
В + 2 = 2 (В — 18)
Кармен старше Дэвида на 12 лет. Пять лет назад сумма их возрастов равнялась 28. Сколько им сейчас?
- Первое предложение говорит нам, что Кармен старше Дэвида на 12 лет (это текущий возраст)
- Второе предложение говорит нам, что возраст Кармен и Дэвида изменился пять лет назад (−5)
Заполнение таблицы дает нам:
| Человек или объект | Текущий возраст | Изменение возраста (−5) |
|---|---|---|
| Кармен (К) | Д + 12 | Д + 12 − 5 Д + 7 |
| Дэвид (D) | Д | Д − 5 |
Последнее утверждение дает нам уравнение для решения:
Пять лет назад сумма их возрастов была 28
Следовательно, возраст Кармен равен возрасту Дэвида (13) + 12 лет = 25 лет.
Сумма возрастов Николь и Кристин равна 32 годам. Через два года Николь будет в три раза старше Кристин. Сколько им сейчас лет?
- Первое предложение говорит нам, что сумма возрастов Николь (N) и Кристин (K) равна 32 годам. Таким образом, N + K = 32, что означает, что N = 32 − K или
K = 32 − N ( мы будем использовать эти уравнения, чтобы исключить одну переменную в нашем окончательном уравнении) - Второе предложение говорит нам, что изменение возраста Николь и Кристен произойдет через два года (+2)
Заполнение таблицы дает нам:
| Человек или объект | Текущий возраст | Изменение возраста (+2) |
|---|---|---|
| Николь (Н) | Н | Н + 2 |
| Кристин (К) | 32 − N | (32 – С.ш.) + 2 34 – С.ш. |
Последнее утверждение дает нам уравнение для решения:
Через два года Николь будет в три раза старше Кристин
Если Николь 25 лет, то Кристин 32 − 25 = 7 лет .
Луизе 26 лет. Ее дочери Кармен 4 года. Через сколько лет Луиза будет вдвое старше дочери?
- Первое предложение говорит нам, что Луизе 26 лет, а ее дочери 4 года
- Вторая строка сообщает нам, что изменение возраста Кармен и Луизы должно быть рассчитано ()
Заполнение таблицы дает нам:
| Человек или объект | Текущий возраст | Изменение возраста |
|---|---|---|
| Луиза (L) | ||
| Дочь (Д) |
Последнее утверждение дает нам уравнение, которое нужно решить:
Через сколько лет Луиза будет вдвое старше своей дочери?
Через 18 лет Луиза будет вдвое старше своей дочери.
Для вопросов с 1 по 8 напишите уравнения, определяющие отношения.
- Рик на 10 лет старше своего брата Джеффа. Через 4 года Рик будет вдвое старше Джеффа.

- Отец старше сына в 4 раза. Через 20 лет отец будет вдвое старше сына.
- Пэт на 20 лет старше своего сына Джеймса. Через два года Пэт будет вдвое старше Джеймса.
- Диана на 23 года старше своей дочери Эми. Через 6 лет Дайан будет вдвое старше Эми.
- Фред на 4 года старше Барни. Пять лет назад сумма их возрастов равнялась 48 годам.
- Джон в четыре раза старше Марты. Пять лет назад сумма их возрастов равнялась 50.
- Тим на 5 лет старше Джоанн. Через шесть лет сумма их возрастов будет 79..
- Джек вдвое старше Лейси. Через три года сумма их возрастов будет 54.
Решите вопросы с 9 по 20.
- Сумма возрастов Джона и Марии равна 32 годам. Четыре года назад Джон был вдвое старше Марии.
- Сумма возрастов отца и сына равна 56. Четыре года назад отец был в 3 раза старше сына.
- Сумма возрастов деревянной и бронзовой таблички составляет 20 лет. Четыре года назад бронзовая табличка была вдвое моложе деревянной.

- Мужчине 36 лет, а его дочери 3 года. Через сколько лет мужчина будет в 4 раза старше своей дочери?
- Возраст Боба вдвое больше, чем у Барри. Пять лет назад Боб был в три раза старше Барри. Найдите возраст обоих.
- Кувшину 30 лет, а вазе 22 года. Сколько лет назад кувшин был вдвое старше вазы?
- Мардж вдвое старше Консуэло. Сумма их возрастов семь лет назад равнялась 13. Сколько им лет сейчас?
- Сумма возрастов Джейсона и Мэнди составляет 35 лет. Десять лет назад Джейсон был вдвое старше Мэнди. Сколько им сейчас лет?
- Серебряная монета на 28 лет старше бронзовой. Через 6 лет серебряная монета будет вдвое старше бронзовой. Найдите текущий возраст каждой монеты.
- Сумма возрастов Клайда и Венди равна 64 годам. Через четыре года Венди будет в три раза старше Клайда. Сколько им сейчас лет?
- Дивану 12 лет, а столу 36 лет. Через сколько лет стол будет вдвое старше дивана?
- Отец в три раза старше сына, а дочь на 3 года младше сына.
 Если сумма всех трех возрастов 3 года назад была 63 года, найдите настоящий возраст отца.
Если сумма всех трех возрастов 3 года назад была 63 года, найдите настоящий возраст отца.
Ключ ответа 7.9
Решение словесных вопросов о неравенстве
(Сначала вы можете прочитать Введение в неравенства и их решение.)
Сэм и Алекс играют в одной футбольной команде.
В прошлую субботу Алекс забил на 3 гола больше, чем Сэм, но вместе они забили меньше 9 голов.
Какое возможное количество голов забил Алекс?
Как их решить?
Хитрость заключается в том, чтобы разбить решение на две части:
Превратите английский в алгебру.
Затем используйте алгебру для решения.
Превращение английского языка в алгебру
Превратить английский язык в алгебру поможет:
- Сначала прочитать полностью
- При необходимости сделайте набросок
- Назначить букв для значений
- Найдите или разработайте формулы
Мы также должны записать то, что на самом деле запрашивается , чтобы мы знали, куда мы идем и когда мы прибыли!
Лучший способ изучить это на примере, поэтому давайте попробуем наш первый пример:
Сэм и Алекс играют в одной футбольной команде.

В прошлую субботу Алекс забил на 3 гола больше, чем Сэм, но вместе они забили меньше 9 голов.
Какое возможное количество голов забил Алекс?
Буквы присвоения:
- количество забитых Алексом голов: A
- количество забитых Сэмом голов: S
Мы знаем, что Алекс забил на 3 гола больше, чем Сэм, поэтому: A = S + 3
И мы знаем, что вместе они забили меньше 9голов: S + A < 9
Нас спрашивают, сколько голов мог забить Алекс: A
Решите:
Начните с: S + A < 9
3 A + 3, поэтому:
S + (S + 3) < 9Упростить: 2S + 3 < 9
Вычесть 3 с обеих сторон: 2S < 9 − 3
Упростить: 2900
Разделить обе части на 2: S < 3
Сэм забил меньше 3 голов, что означает, что Сэм мог забить 0, 1 или 2 гола.
Алекс забил на 3 гола больше, чем Сэм, поэтому Алекс мог забить 3, 4 или 5 голов .
Проверить:
- Если S = 0, то A = 3 и S + A = 3, и 3 < 9 верно
- Когда S = 1, тогда A = 4 и S + A = 5, и 5 < 9 верно
- Когда S = 2, то A = 5 и S + A = 7, а 7 < 9правильно
- (Но когда S = 3, то A = 6 и S + A = 9, а 9 < 9 неверно)
Еще много примеров!
Пример: Из 8 щенков девочек больше, чем мальчиков.
Сколько девочек-щенков может быть?
Назначить Буквы:
- Количество девушек: г
- количество мальчиков: б
Мы знаем, что есть 8 щенков, поэтому: g + b = 8, что можно преобразовать в
b = 8 − g
Мы также знаем, что девочек больше, чем мальчиков, поэтому:
g > b
Нас спрашивают о количестве щенков-девочек: g
Решите:
Начните с : g > b
b = 8 − g , поэтому: g > 8 − g
Прибавить g к обеим сторонам: g + g > 8
Упростить:
Разделите обе стороны на 2: г > 4
Таким образом, может быть 5, 6, 7 или 8 девочек-щенков.
Может ли быть 8 девочек-щенков? Тогда не было бы мальчиков вообще, и вопрос не ясен на этот счет (иногда такие вопросы).
Проверка
- Когда g = 8, тогда b = 0 и g > b верно (но допустимо ли b = 0?)
- Если g = 7, тогда b = 1 и g > b верно
- Если g = 6, тогда b = 2 и g > b верно
- Если g = 5, тогда b = 3 и g > b верно
- (Но если g = 4, то b = 4 и g > b неверно)
Быстрый пример:
Пример: Джо участвует в гонке, где он должен ездить на велосипеде и бежать.
Он проехал 25 км на велосипеде, а затем пробежал 20 км. Его средняя скорость бега составляет половину его средней скорости езды на велосипеде.
Джо завершает гонку менее чем за 2,5 часа, что можно сказать о его средней скорости?
Назначить буквы:
- Средняя скорость работы: с
- Итак, средняя скорость езды на велосипеде: 2 с
Формулы:
- Скорость = Расстояние Время
- Который можно переставить на: Время = Расстояние Скорость
Нас спрашивают его средние скорости: с и 2с
Гонка делится на две части:
1.
 Велоспорт
Велоспорт- 91 км Расстояние = 25 км
- Средняя скорость = 2 с км/ч
- Итак, Время = Расстояние Средняя скорость = 25 2 с часов
2. Бег
- Расстояние = 20 км
- Средняя скорость = с км/ч
- Время = Расстояние Средняя скорость = 20 с часов
Джо завершает гонку менее чем за 2½ часа
- Общее время < 2½
- 25 2 с + 20 с < 2½
Решение:
Start с: 25 2S + 20 S <2½
Умножение все термины на 2S: 25 + 40 <5S
Символ.
Разделите обе части на 5: 13 < s
Поменяйте стороны местами: s > 13
Значит, его средняя скорость бега больше 13 км/ч, а его средняя скорость езды на велосипеде больше 26 км/ч
В этом примере мы используем сразу два неравенства:
Пример: Скорость
v м/с мяча, брошенного прямо вверх, определяется выражением v = 20 − 10t , где t — время в секундах.
В какие моменты времени скорость будет от 10 м/с до 15 м/с?
Буквы:
- скорость в м/с: v
- время в секундах: t
Формула:
- v = 20 − 10t
Нас просят время T , когда V составляет от 5 до 15 м/с:
10 10 <20 - 10t <15 Решай: СТАРЬ С. 10 <20 - 10t <15 Вычитание 20 из каждого: 10 — 20 <20 - 10t - 20 <15 - 20 Упрощение: -10 <-10t <-5 Разделите каждый на 10: −1 < −t < −0,5 Замените знаки и обратные неравенства: 1 > t > 0,5 Лучше сначала показать меньшее число Таким образом, скорость будет между 10 м/с и 15 м/с между 0,5 и 1 секундой после. И достаточно жесткий пример для завершения: Сделайте набросок: мы не знаем размеров столов, только их площадь, они могут подойти идеально или нет! Назначить Буквы: Формула для периметра 2(Ш + Д) , и мы знаем, что это 16 м Мы также знаем, что площадь прямоугольника равна произведению ширины на длину: Площадь = Ш × Д И площадь должна быть больше или равна 7: Нас спрашивают о возможных значениях W и L Решим: Начнем с: W × L ≥ 7 − 9 W × L ≥ 7 − 9 W L 0 : 8 − W) ≥ 7 Расширить: 8W − W 2 ≥ 7 Перенесем все члены в левую часть: W 2 − 8W + 7 ≤ 0 Это квадратное неравенство. Перенесем числовой член − 7 в правую часть неравенства: W 2 − 8W ≤ −7 квадрат в левой части неравенства и уравновесить это, добавив такое же значение к
правая часть неравенства: W 2 − 8W + 16 ≤ −7 + 16 Упростить: (W − 4) 2 ≤ 9 Извлечь квадратный корень из обеих частей неравенства: − −3 4 ≤ 3 Да, у нас есть два неравенства, потому что 3 2 = 9 И (−3) 2 = 9 Прибавьте 4 к обеим частям каждого неравенства: 1≤W Таким образом, ширина должна быть между 1 м и 7 м (включительно), а длина 8-ширина . Проверить: МНОГО примеров! В алгебре у нас часто возникают словесные вопросы, например: В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр. Сколько игр сыграл Алекс? Как их решить? Хитрость заключается в том, чтобы разбить решение на две части: Превратите английский в алгебру. Затем используйте алгебру для решения. Превратить английский язык в алгебру поможет: Вы также должны записать то, что на самом деле запрашивается , чтобы вы знали, куда вы идете и когда вы прибыли! Также ищите ключевые слова: добавить, итого, сумма, увеличить, больше, вместе, вместе, плюс, более минус, меньше, разность, меньше, меньше, меньше умножить, раз, произведение, коэффициент разделить, частное, на, вне, отношение, отношение, процент, скорость Некоторые формулировки могут быть сложными, из-за чего трудно думать «правильно», например: $ Теперь … это: S − 2 = A или должно быть: S = A − 2 или должно быть: S = 2 − A Правильный ответ: S = A − 2 ( S − 2 = A — распространенная ошибка, так как вопрос пишется «Сэм… на 2 меньше… Алекс») Теперь… это: 2D = C или должно быть: D = 2C Теперь хорошенько подумайте! Правильный ответ: D = 2C ( 2D = C — распространенная ошибка, так как вопрос пишется «дважды…собаки…кошки») Давайте начнем с действительно простого примера , чтобы мы увидели, как это делается: Превратите английский в алгебру: Эскиз: Буквы: Формула для площади прямоугольника: A = w × h Нас спрашивают о площади. Решите: A = w × h = 12 × 5 = 60 м 2 Площадь 60 квадратных метров . Теперь давайте попробуем пример из верхней части страницы: Превратите английский в алгебру: Буквы: Мы знаем, что Сэм сыграл на 4 игры больше, чем Алекс, поэтому: S = A + 4 И мы знаем, что вместе они сыграли 12 игр: S + A = 12 Нас спрашивают, сколько игр, в которые играл Алекс: A Решите: Начните с: S + A = 12 S = A + 4 , поэтому мы можем Упростить: 2A + 4 = 12 Вычесть 4 из обеих частей: 2A = 12 − 4 Упростить: 2A = 8 Разделить обе части на 2: A = 4 Это означает, что Алекс сыграл 4 игры в теннис. Проверка: Сэм сыграл на 4 игры больше, чем Алекс, поэтому Сэм сыграл 8 игр.
Вместе они сыграли 8 + 4 = 12 игр. Да! Чуть более сложный пример: Алекс, работая в одиночку, может сделать 10 штук за 30 дней. Сколько времени потребуется Сэму, работающему одному, чтобы сделать 10 столов? Превратите английский в алгебру: Буквы: 12 дней Алекса и Сэма — это 10 столов, поэтому: 12a + 12s = 10 30 дней одного Алекса — это тоже 10 столов: 30a = 10 Нас спрашивают, сколько времени займет Сэм сделать 10 столов. Решите: 30a = 10 , значит, курс Алекса (столов в день): a = 10/30 = 1/3 Начнем с: 12a + 12s = 10
,
поэтому поменяйте местами: 0,5 < t < 1 Пример: прямоугольная комната вмещает как минимум 7 столов, каждый из которых имеет площадь 1 квадратный метр.
 Периметр комнаты 16 м.
Периметр комнаты 16 м.
Какой может быть ширина и длина комнаты? Ее можно решить разными способами, здесь мы решим ее, заполнив квадрат:
Ее можно решить разными способами, здесь мы решим ее, заполнив квадрат: Решение словесных вопросов
Пример: Сэм и Алекс играют в теннис.

Превращение английского языка в алгебру
Когда вы видите Подумай + − × ÷ увеличить или уменьшить геометрия
формулы Скорость, скорость расстояние
формулы Как долго, дни, часы, минуты, секунды время Мыслить ясно
Пример: У Сэма на 2 доллара меньше, чем у Алекса.
 Как мы запишем это в виде уравнения?
Как мы запишем это в виде уравнения? Пример: на нашей улице собак вдвое больше, чем кошек. Как мы запишем это в виде уравнения?
Примеры
Пример: прямоугольный сад размером 12 м на 5 м, какова его площадь?

Пример: Сэм и Алекс играют в теннис. В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр. Сколько игр сыграл Алексей?
заменить «A + 4» на S: (A + 4) + A = 12
Пример: Алекс и Сэм тоже строят столы.
Вместе они делают 10 столов за 12 дней.
Упрощение: 4 + 12S = 10
Вычитание 4 с обеих сторон: 12S = 6
Разделите обе стороны на 12: S = 6/12
Упрощение: S = 1/2
, что означает что скорость Сэма составляет полстола в день (быстрее, чем у Алекса!)
Таким образом, 10 столов займут у Сэма всего 20 дней.
Интересно, Сэму нужно платить больше?
И еще пример «подстановки»:
Пример: Дженна усердно тренируется, чтобы пройти отбор на Национальные игры.
У нее регулярный еженедельный распорядок: в некоторые дни она тренируется по пять часов в день, а в остальные дни — по 3 часа.
Всего она тренируется 27 часов в неделю. Сколько дней она тренируется по пять часов?
Буквы:
- Количество «5-часовых» дней: д
- Количество «3-х часовых» дней: e
Мы знаем, что в неделе семь дней, поэтому: d + e = 7
И она тренируется 27 часов в неделю, из них d 5 часов в день и e 3 часа в день: 5d + 3e = 27
Нас спрашивают, сколько дней она тренируется по 5 часов: d
Решите:
+
= 7
Итак: e = 7 − d
Подставим это в 5d + 3e = 27 5d + 3(7−d) = 27
2= 1 9 d 9 900
Вычесть 21 с обеих сторон: 5d − 3d = 6
Упростить: 2d = 6
Разделите обе части на 2: d = 3
Количество «5-часовых» дней равно 3
Проверка : Она тренируется по 5 часов 3 дня в неделю, поэтому тренироваться по 3 часа в день в остальные 4 дня недели.
3 × 5 часов = 15 часов плюс 4 × 3 часа = 12 часов дает в сумме 27 часов
Несколько примеров из геометрии:
Пример: Площадь круга 12 мм
2 , каков его радиус?Буквы:
- Используйте A для области: A = 12 мм 2
- Используйте r для радиуса
А формула площади такова: A = π r 2
Нас спрашивают о радиусе.
Решите:
Нам нужно изменить формулу, чтобы найти площадь
Начните с: A = π r 2
Поменяйте местами стороны: π r 20 = A
Разделите обе стороны на π : R 2 = A / π
Квадратный корень с обеих сторон: R = √ (A / π)
Теперь мы можем использовать формула: r = √(12/ π)
И получаем: r = 1,954 (на 3 знака)
Пример: куб имеет объем 125 мм
3 , какова площадь его поверхности?Сделать быстрый набросок:
Буквы:
- Используйте V для тома
- Используйте A для Зоны
- Используйте s для длины стороны куба
Формулы:
- Объем куба: V = s 3
- Площадь поверхности куба: A = 6s 2
Нас спрашивают о площади поверхности.
Решите:
Сначала вычислите s , используя формулу объема:
Начните с: V = S 3
СОЗДАЯ СТОРОНА: S 3 = V
Корень Куба с обеих сторон: S = ∛ (V )
и мы получаем: с = ∛ = ∛ = ∛ = ∛ = ∛ = ∛ = ∛ = ∛ = ∛ = ∛ = ∛ = ∛ = ∛ = ∛ = ∛ = ∛ = ∛ = ∛ = ∛ = ∛ = ∛ ∛. (125 ) = 5
Теперь мы можем рассчитать площадь поверхности:
СТАРЬ С: A = 6S 2
И мы получаем: A = 6 (5) 2
2
999999 А = 6 × 25 = 150 мм 2Пример про Деньги:
Пример: Джоэл работает в местной пиццерии. Когда он работает сверхурочно, он зарабатывает в 1¼ раза больше обычной ставки.
Одну неделю Джоэл работал 40 часов по обычной ставке, а также работал сверхурочно 12 часов. Если Джоэл в общей сложности заработал 660 долларов за эту неделю, какова его нормальная ставка?
Письма:
- Обычная ставка Джоэла: $N в час
Формулы:
- Джоэл работает 40 часов за N долларов в час = 40N долларов
- Когда Джоэл работает сверхурочно, он зарабатывает в 1¼ раза больше обычной ставки = 1,25 N долларов в час
- Джоэл работает 12 часов за 1,25 н.
 долл. США в час = (12 × 1¼ Н) = 15 н. долл. США
долл. США в час = (12 × 1¼ Н) = 15 н. долл. США - И вместе он заработал 660 долларов, так что:
$40N + $(12 × 1¼N) = $660
Нас спрашивают об обычной ставке Джоэла в $N.
Решите:
Начните с 40N $ + (12 × 1¼N) = 660 $
Упростите: 40N $ + 15N = 660 $
Упростите больше: $ 55N = 660 $
Разделите обе стороны на 55: $ n = $ 12
, так что нормальная ставка Джоэла составляет 12 долларов США в час
. составляет 12 долларов в час, поэтому его ставка сверхурочных составляет 1¼ × 12 долларов в час = 15 долларов в час. Таким образом, его обычная заработная плата 40 × 12 = 480 долларов плюс оплата сверхурочных 12 × 15 = 180 долларов дает нам в сумме 660
долларов.Подробнее о деньгах, с этими двумя примерами, связанными со сложными процентами
Пример: Алекс кладет в банк 2000 долларов под сложные проценты в размере 11% годовых. Сколько он будет стоить через 3 года?
Это формула сложных процентов:
Поэтому мы будем использовать эти буквы:
- Приведенная стоимость PV = 2000 долларов
- Процентная ставка (в виде десятичной дроби): r = 0,11
- Количество периодов: n = 3
- Будущая стоимость (значение, которое мы хотим): FV
Нас спрашивают о будущем значении: FV
Решите:
Начните с: FV = PV × (1+r) n
9000 Что мы знаем: 29 FV0 9000 2000 долл. США × (1+0,11) 3
США × (1+0,11) 3 Расчет: FV = 2000 долл. США × 1,367631
Расчет: FV = 2735,26 долл. США (с точностью до 3 центов) 900
Пример: Роджер положил 1000 долларов на сберегательный счет. Начисленные проценты начислялись ежегодно по той же ставке. Через девять лет депозит Роджера вырос до 1551,33 доллара 9.1026
Какова была годовая процентная ставка по сберегательному счету?
Формула сложных процентов:
С:
- Приведенная стоимость PV = $1,000
- Процентная ставка (значение, которое мы хотим): r
- Количество периодов: n = 9
- Будущая стоимость: FV = $1551,33
Нас спрашивают о процентной ставке: r
Решите:
Начните с: FV = PV × (1+r) n
Put in what we know: $1,551.33 = $1000 × (1+r) 9
Swap sides: $1000 × (1+r) 9 = $1,551.33
Divide both sides by 1000: (1+r) 9 = 1 551,33 долл. США / 1 000 долл. США
США / 1 000 долл. США
Упрощение: (1+R) 9 = 1,55133
9 -й корень: 1+R = 1,55133 39 ().
Рассчитать: 1+r = 1,05
Рассчитать: r = 0,05 = 5%
Таким образом, годовая процентная ставка составляет 5%
Чек : 1000 долл. США × (1,05) 9 = 1000 долл. США × 1,55133 = 1551,33 долл. США
И пример вопроса о соотношении:
Пример: В начале года соотношение мальчиков и девочек в классе было 2 : 1
Но сейчас, спустя полгода, из класса ушли четыре мальчика и две новые девочки. Соотношение мальчиков и девочек теперь 4 : 3
Сколько сейчас всего учеников?
Буквы:
- Количество мальчиков сейчас: b
- Количество девушек сейчас: г
Коэффициент тока составляет 4: 3
B G = 4 3
, который может быть перестроен до 3B = 4G
В начале года. 4) 90 030 мальчиков и 90 029 (г — 2) 90 030 девочек, а соотношение было 2 : 1 90 003 90 002 95 412 б + 4 91 043 91 086 г — 2 91 087 = 2 1
4) 90 030 мальчиков и 90 029 (г — 2) 90 030 девочек, а соотношение было 2 : 1 90 003 90 002 95 412 б + 4 91 043 91 086 г — 2 91 087 = 2 1
Которое можно преобразовать в b + 4 = 2(g − 2)
Нас спрашивают, сколько всего учеников сейчас: b + g
Решите :
Начало с: B + 4 = 2 (g — 2)
Упрощение: B + 4 = 2G — 4
Выбросы 4 с обеих сторон: B = 2G — 8
Умножаем обе части на 3 (получаем 3b): 3b = 6g − 24
Remember 3b = 4g : 4g = 6g − 24
Subtract 6g from both sides : −2g = − 24
Разделите обе части на −2: г = 12
Есть 12 девочек !
И 3b = 4g , поэтому b = 4g/3 = 4 × 12 / 3 = 16 , значит, 16 мальчиков
Итак, теперь в классе 12 девочек и 16 мальчиков, что составляет Всего 28 студентов .
Чек
В настоящее время насчитывается 16 мальчиков и 12 девочек, поэтому соотношение мальчиков и девочек составляет 16 : 12 = 4 : 3
В начале года было 20 мальчиков и 10 девочек, поэтому соотношение было 20 : 10 = 2 : 1
А теперь немного квадратных уравнений:
Пример: Произведение двух последовательных четных целых чисел равно 168. Что это за целые числа?
Последовательно означает одно за другим. А их даже , так что они могут быть 2 и 4, или 4 и 6 и т. д.
Мы назовем меньшее целое число n , поэтому большее целое число должно быть n+2
И нам говорят, что произведение (то, что мы получаем после умножения) равно 168, поэтому мы знаем:
n(n + 2) = 168
Нас просят ввести целые числа
Решить:
Начать с: n(n + 2) ) = 168
Развернуть: n 2 + 2n = 168
Вычесть 168 с обеих сторон: n 2 + 2n − 168 = 0
Это квадратное уравнение, и есть много способов его решения. Используя Решатель квадратных уравнений, мы получаем -14 и 12.
Используя Решатель квадратных уравнений, мы получаем -14 и 12.
Проверка -14: -14(-14 + 2) = (-14)×(-12) = 168 ДА
Проверка 12: 12( 12 + 2) = 12×14 = 168 ДА
Итак, есть два решения: −14 и −12 — одно, 12 и 14 — другое.
Примечание: мы могли бы также попробовать «угадать и проверить»:
- Мы могли бы попробовать, скажем, n=10: 10(12) = 120 НЕТ (слишком маленький)
- Далее мы можем попробовать n=12: 12(14) = 168 ДА
Но если мы не будем помнить, что умножение двух отрицательных чисел дает положительное, мы можем упустить из виду другое решение (−14)×(−12).
А:
Пример: Вы архитектор. Ваш клиент хочет, чтобы комната была в два раза длиннее, чем ее ширина. Они также хотят веранду шириной 3 метра вдоль длинной стороны.
У вашего клиента есть 56 квадратных метров красивой мраморной плитки, чтобы покрыть всю площадь.
Какой длины должна быть комната?
Давайте сначала сделаем эскиз, чтобы все получилось правильно!:
Буквы:
- длина комнаты: L
- ширина комнаты: Ш
- Общая площадь включая веранду: А
Мы знаем:
- ширина комнаты равна половине ее длины: Ш = ½Д
- общая площадь равна (ширине комнаты + 3), умноженной на длину: А = (Ш+3) × Д = 56
Нас спрашивают о длине комнаты: L
Решите:
Начните с: (W + 3) × L = 56
Подставьте W = ½L : (½L0 + 3) × l = 56
Упрощение: ½L 2 + 3L = 56
Умножение все термины на 2: L 2 + 6L = 112
112 3939: обоих SITES : SITES : : : SITES.

 Коза, свинья и овца вместе стоят 425р., корова, свинья и овца стоят вместе 1225р., а коза и свинья стоят вместе 275р. Найдите цену каждого животного.
Коза, свинья и овца вместе стоят 425р., корова, свинья и овца стоят вместе 1225р., а коза и свинья стоят вместе 275р. Найдите цену каждого животного. 2 На поляне паслись ослы. К ним подошло несколько ребят. Если на каждого осла сядут по одному мальчику, то двум из них не хватит ослов. Если же на каждого осла сядут по два мальчика, то один осел будет лишний. Сколько ослов и сколько мальчиков было на поляне?
2 На поляне паслись ослы. К ним подошло несколько ребят. Если на каждого осла сядут по одному мальчику, то двум из них не хватит ослов. Если же на каждого осла сядут по два мальчика, то один осел будет лишний. Сколько ослов и сколько мальчиков было на поляне? Сколько весят персик, груша и яблоко вместе?
Сколько весят персик, груша и яблоко вместе? На первом из них написано «Крупа», на втором – «Мука», на третьем – «Крупа или сахар». Известно, что содержимое ящиков не соответствует надписи. В каком ящике что находится?
На первом из них написано «Крупа», на втором – «Мука», на третьем – «Крупа или сахар». Известно, что содержимое ящиков не соответствует надписи. В каком ящике что находится? На каком расстоянии друг от друга они будут через два часа после встречи?
На каком расстоянии друг от друга они будут через два часа после встречи? 3 Как из восьмилитрового ведра, наполненного молоком, отлить 1 литр с помощью трехлитровой банки и пятилитрового бидона?
3 Как из восьмилитрового ведра, наполненного молоком, отлить 1 литр с помощью трехлитровой банки и пятилитрового бидона?
 1 Является ли число 1234535 + 711 простым?
1 Является ли число 1234535 + 711 простым? 2 Установите закономерность в числовой последовательности и запишите еще три числа: 15, 29, 56, 109, 214, … .
2 Установите закономерность в числовой последовательности и запишите еще три числа: 15, 29, 56, 109, 214, … . А говорит: «Мы все лжецы». В говорит: «Ровно один из нас Лжец». Можно ли определить, кто такой В – Рыцарь или Лжец? Можно ли определить, кто такой С?
А говорит: «Мы все лжецы». В говорит: «Ровно один из нас Лжец». Можно ли определить, кто такой В – Рыцарь или Лжец? Можно ли определить, кто такой С? 5.Разрежте фигуру на четыре равные части и сложите из этих частей квадрат с квадратным отверстием посередине:
5.Разрежте фигуру на четыре равные части и сложите из этих частей квадрат с квадратным отверстием посередине: 1 Числа 100 и 90 разделили на одно и то же число. В первом случае получили в остатке 4, а в другом – 18. Какое число было делителем?
1 Числа 100 и 90 разделили на одно и то же число. В первом случае получили в остатке 4, а в другом – 18. Какое число было делителем?

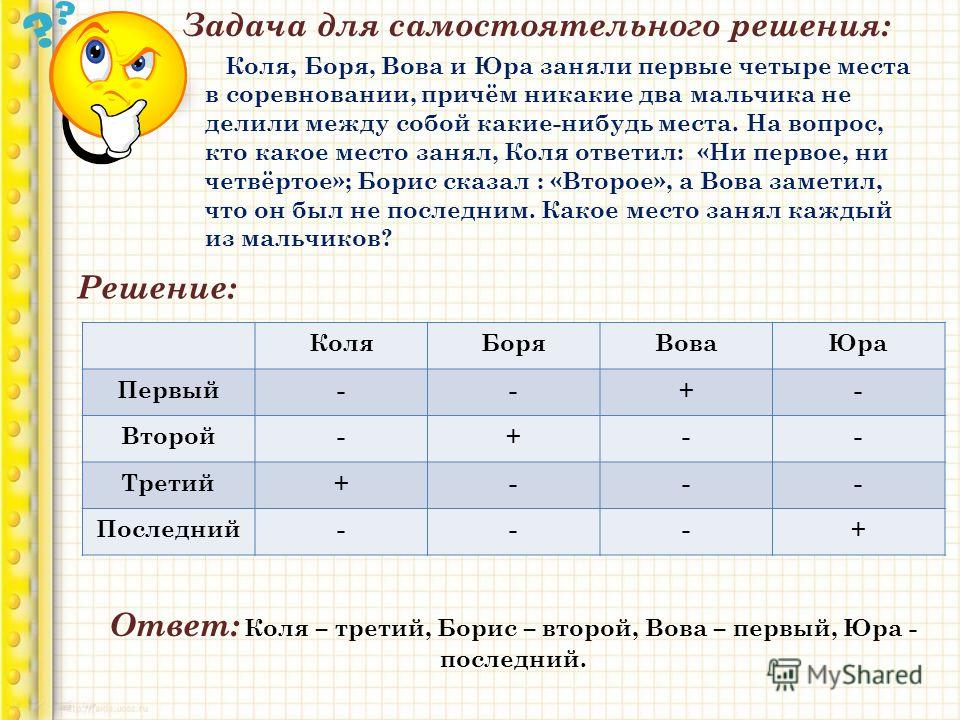 д. Какое расстояние пролетит голубь до момента встречи поездов.
д. Какое расстояние пролетит голубь до момента встречи поездов. ..
..