Разложите на простые множители число 820: Разложите на простые множители числа: 56,625,820,2772,702,1224 Помогите умоляю

alexxlab / / Разное

Содержание

Mathway | Популярные задачи

1Оценить с использованием заданного значенияквадратный корень из 50
2Оценить с использованием заданного значенияквадратный корень из 45
3Вычислить5+5
4Вычислить7*7
5Разложить на простые множители24
6Преобразовать в смешанную дробь52/6
7Преобразовать в смешанную дробь93/8
8Преобразовать в смешанную дробь34/5
9Графикy=x+1
10Оценить с использованием заданного значенияквадратный корень из 128
11Найти площадь поверхностисфера (3)
12Вычислить54-6÷2+6
13Графикy=-2x
14Вычислить8*8
15Преобразовать в десятичную форму 5/9
16Оценить с использованием заданного значенияквадратный корень из 180
17Графикy=2
18Преобразовать в смешанную дробь7/8
19Вычислить9*9
20Risolvere per CC=5/9*(F-32)
21Упростить1/3+1 1/12
22Графикy=x+4
23Графикy=-3
24Графикx+y=3
25Графикx=5
26Вычислить6*6
27Вычислить2*2
28Вычислить4*4
29Вычислить1/2+(2/3)÷(3/4)-(4/5*5/6)
30Вычислить1/3+13/12
31Вычислить5*5
32Risolvere per d2d=5v(o)-vr
33Преобразовать в смешанную дробь3/7
34Графикy=-2
35Определить наклонy=6
36Перевести в процентное соотношение9
37Графикy=2x+2
38Графикy=2x-4
39Графикx=-3
40Решить, используя свойство квадратного корняx^2+5x+6=0
41Преобразовать в смешанную дробь1/6
42Преобразовать в десятичную форму9%
43Risolvere per n12n-24=14n+28
44Вычислить16*4
45Упроститькубический корень из 125
46Преобразовать в упрощенную дробь43%
47Графикx=1
48Графикy=6
49Графикy=-7
50Графикy=4x+2
51Определить наклонy=7
52Графикy=3x+4
53Графикy=x+5
54График3x+2y=6
55Решить, используя свойство квадратного корняx^2-5x+6=0
56Решить, используя свойство квадратного корняx^2-6x+5=0
57Решить, используя свойство квадратного корняx^2-9=0
58Оценить с использованием заданного значенияквадратный корень из 192
59Оценить с использованием заданного значенияквадратный корень из 25/36
60Разложить на простые множители14
61Преобразовать в смешанную дробь7/10
62Risolvere per a(-5a)/2=75
63Упроститьx
64Вычислить6*4
65Вычислить6+6
66Вычислить-3-5
67Вычислить-2-2
68Упроститьквадратный корень из 1
69Упроститьквадратный корень из 4
70Найти обратную величину1/3
71Преобразовать в смешанную дробь11/20
72Преобразовать в смешанную дробь7/9
73Найти НОК11 , 13 , 5 , 15 , 14 , , , ,
74Решить, используя свойство квадратного корняx^2-3x-10=0
75Решить, используя свойство квадратного корняx^2+2x-8=0
76График3x+4y=12
77График3x-2y=6
78Графикy=-x-2
79Графикy=3x+7
80Определить, является ли полиномом2x+2
81Графикy=2x-6
82Графикy=2x-7
83Графикy=2x-2
84Графикy=-2x+1
85Графикy=-3x+4
86Графикy=-3x+2
87Графикy=x-4
88Вычислить(4/3)÷(7/2)
89График2x-3y=6
90Графикx+2y=4
91Графикx=7
92Графикx-y=5
93Решить, используя свойство квадратного корняx^2+3x-10=0
94Решить, используя свойство квадратного корняx^2-2x-3=0
95Найти площадь поверхностиконус (12)(9)
96Преобразовать в смешанную дробь3/10
97Преобразовать в смешанную дробь7/20
98Преобразовать в смешанную дробь2/8
99Risolvere per wV=lwh
100Упростить6/(5m)+3/(7m^2)

Математика 6 Мерзляк.

Упражнения 104-137

Упражнения по математике для УМК Мерзляк с ответами на некоторые задачи. §4. Простые и составные числа (2019, 2020, 2021 годы). Математика 6 Мерзляк. Упражнения 104-137.

ОГЛАВЛЕНИЕ (2021 г.)  ТЕОРИЯ: § 4.

 

Математика 6 Мерзляк (2021 год)


Упражнения 104-137

№ 104. Среди чисел 1, 3, 6, 7, 12, 13, 21, 23, 24, 28, 29, 33, 45, 46, 47 укажите: 1) простые; 2) составные.
Правильный ответ: 1) Простые числа: 3, 7, 13, 23, 29, 47.  2) Составные числа: 6, 12, 21, 24, 28, 33, 45, 46.

№ 105. Запишите все делители данного числа, подчеркните те из них, которые являются простыми числами: 1) 21; 2) 30; 3) 48; 4) 54.
Правильный ответ: 1) делители числа 21: 1, 3, 7, 21.
2) делители числа 30: 1, 2, 3, 5, 6, 10, 15, 30.
3) делители числа 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
4) делители числа 54: 1, 2, 3, 6, 9, 18, 27, 54.

№ 106. Разложите на простые множители число: 1) 12; 2) 42; 3) 216; 4) 450; 5) 920; 6) 2 280; 7) 10 850.

Нажмите на этот спойлер, чтобы увидеть ОТВЕТ

№ 107. Разложите на простые множители число: 1) 27; 2) 56; 3) 625; 4) 820; 5) 2 772; 6) 702; 7) 1 224.

Нажмите на этот спойлер, чтобы увидеть ОТВЕТ

№ 108. Запишите: 1) все простые числа, которые больше 10 и меньше 25; 2) все составные числа, которые больше 35 и меньше 49.
Правильный ответ: 1) Простые числа, больше 10, но меньше 25: 11, 13, 17, 19, 23.
2) Составные числа, больше 35, но меньше 49: 36, 38, 39, 40, 42, 44, 45, 46, 48.

№ 109. Запишите: 1) все простые числа, которые больше 22 и меньше 38; 2) все составные числа, которые больше 60 и меньше 78.
Правильный ответ: 1) Простые числа, которые больше 22 и меньше 38: 23, 29, 31, 37.
2) Составные числа, которые больше 60 и меньше 78: 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77.

№ 110. Простым или составным числом является произведение: 1) 13 • 1; 2) 14 • 1; 3) 4 • 7; 4) 11 • 13; 5) 43 • 1; 6) 1 • 111 ?
Правильный ответ: 1) 13 • 1 => простое.
2) 14 • 1 => составное.
3) 4 • 7 => составное.
4) 11 • 13 => составное.
5) 43 • 1 => простое.
6) 1 • 111 => составное.

№ 111. Запишите все делители числа, равного произведению: 1) 2 • 2 • 5;  2) 3 • 5 • 7.
Правильный ответ: 1) 2 • 2 • 5 = 20  => Делители: 1, 2, 4, 10, 5, 20.
2) 3 • 5 • 7 = 105  => Делители: 1, 3, 5, 7, 15, 21, 35, 105.

№ 112. Запишите все делители числа, равного произведению: 1) 2 • 5 • 13; 2) 3 • 3 • 3 • 7.
Правильный ответ: 1) 2 • 5 • 13 = 130  => Делители: 1, 2, 5, 10, 13, 26, 65, 130.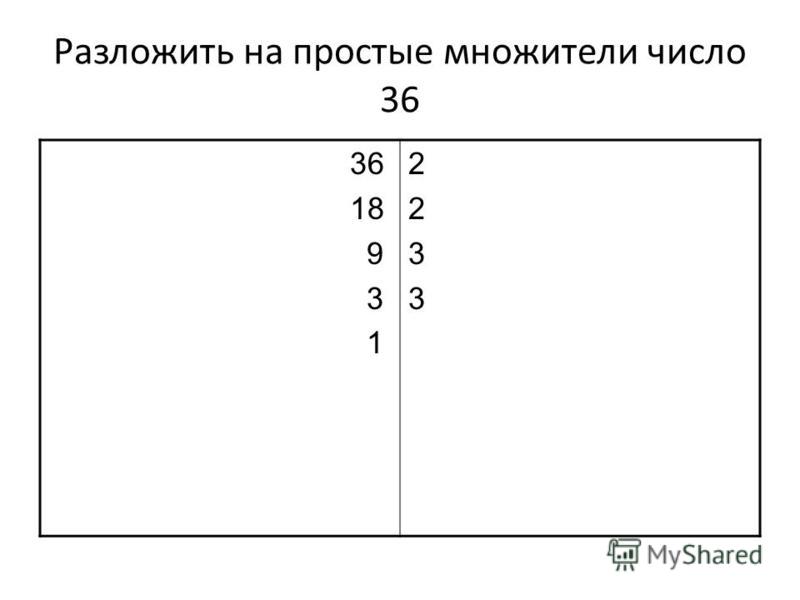
2) 3 • 3 • 3 • 7 = 189  => Делители: 1, 3, 7, 9, 21, 27, 63, 189.

№ 113. Чему равно частное от деления числа а на число b, если: 1) а = 2 • 2 • 2 • 3 • 3 • 7, b = 2 • 2 • 3 • 7;   2) а = 3 • 5 • 5 • 13 • 17 • 19, b = 3 • 13 • 19 ?
Правильный ответ: 1) Если а = 2 • 2 • 2 • 3 • 3 • 7; b = 2 • 2 • 3 • 7, то a : b = 2 • 2 • 2 • 3 • 3 • 7 : 2 : 2 : 3 : 7 = 6.
2) Если а = 3 • 5 • 5 • 13 • 17 • 19; b = 3 • 13 • 19, то а : b = 3 • 5 • 5 • 13 • 17 • 19 : 3 : 13 : 19 = 425.

№ 114. Чему равно частное от деления числа а на число b, если: 1) а = 2 • 3 • 5 • 5 • 7 • 11 • 13, b = 2 • 5 • 13;   2) а = 2 • 2 • 3 • 5 • 23 • 37, b = 2 • 3 • 37 ?
Правильный ответ: 1) Если а = 2 • 3 • 5 • 5 • 7 • 11 • 13; b = 2 • 5 • 13, то a : b = 2 • 3 • 5 • 5 • 7 • 11 • 13 : 2 : 5 : 13 = 1155.
2) Если а = 2 • 2 • 3 • 5 • 23 • 37;  b = 2 • 3 • 37, то a : b = 2 • 2 • 3 • 5 • 23 • 37 : 2 : 3 : 37 = 230.

№ 115. Запишите все двузначные числа, в разложении которых на простые множители один из множителей равен: 1) 7; 2) 17; 3) 23.
Правильный ответ: 1) Один из множителей равен 7: 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98.
2) Один из множителей равен 17: 17, 34, 51, 68, 85.
3) Один из множителей равен 23: 23, 46, 69, 92.

№ 116. Запишите все двузначные числа, разложение которых на простые множители состоит: 1) из двух одинаковых множителей; 2) из трёх одинаковых множителей.
Правильный ответ: 1) состоящие из двух одинаковых множителей: 16 = 4 • 4; 25 = 5 • 5; 36 = 6 • 6; 49 = 7 • 7; 64 = 8 • 8; 81 = 9 • 9.
2) состоящие из трех одинаковых множителей: 27 = 3 • 3 • 3; 64 = 4 • 4 • 4.

№ 117. Сколько существует чисел, которые можно разложить на два двузначных простых множителя, один из которых на 2 больше другого? Воспользуйтесь таблицей простых чисел.
Правильный ответ: 6 чисел (143 = 11 • 13;  323 = 17 • 19;  899 = 29 • 31; 1763 = 41 • 43;  3599 = 59 • 61;  5183 = 71 • 73).

№ 118.

Найдите все числа, которые можно разложить на два двузначных простых множителя, разность которых равна 4. Воспользуйтесь таблицей простых чисел.
Правильный ответ: 6 чисел (221 = 13 • 17;  437 = 19 • 23;  1517 = 37 • 41; 2021 = 43 • 47;  4757 = 67 • 71;  6557 = 79 • 83).

№ 119. Задумали простое число. Известно, что следующее за ним натуральное число тоже простое. Какое число задумали?
Правильный ответ: Задумали число 2. Следующее число 3 – простое.

№ 120. Может ли сумма двух простых чисел быть простым числом? В случае утвердительного ответа приведите пример.
Правильный ответ: Да, может. 2 + 3 = 5.

№ 121. Может ли быть простым числом: 1) произведение двух различных чисел; 2) значение площади квадрата, длина стороны которого выражается натуральным числом? Ответ обоснуйте.


Правильный ответ: 1) Да, может. 13 • 1 = 13 => одно число простое, а второе – 1.
2) Нет, так как у площади квадрата есть делители, кроме 1 и самой площади.

№ 122. Может ли сумма двух составных чисел быть простым числом? В случае утвердительного ответа приведите примеры.
Правильный ответ: Да, может. 13 = 4 + 9;  17 = 8 + 9;  19 = 9 + 10.

№ 123. Существует ли прямоугольник, длины сторон которого выражаются натуральными числами, а периметр – простым числом (длины сторон и периметр прямоугольника выражены в одних и тех же единицах измерения)? Ответ обоснуйте.
Правильный ответ: Нет. Р = 2 • (а + b)  ⇒  периметр – это четное число  ⇒  периметр не может быть простым числом.

№ 124. Может ли произведение ста различных простых чисел делиться нацело: 1) на 3; 2) на 9?


Правильный ответ: 1) На 3: да, если один из множителей равен 3.
2) На 9: нет, так как 9 = 3 • 3  ⇒ значит, в произведении должно быть два одинаковых числа 3, чтобы оно делилось на 9.

№ 125. Существуют ли три последовательных натуральных числа: 1) каждое из которых является простым; 2) ни одно из которых не является составным? Ответ обоснуйте.
Правильный ответ: 1) Нет, так как из трех последовательных чисел хотя бы одно – четное  ==> оно не является простым.
2) Да. Например: 1, 2, 3.

№ 126. При каком натуральном значении п будет простым числом значение выражения: 1) 2n; 2) n2; 3) n(n + 1)?
Правильный ответ: 

1) 2n; при n = 1.  2) n2; таких n – нет.  3) n(n + 1); при n = 1.

№ 127. Натуральное число а, которое больше 1 и меньше 100, не делится нацело ни на одно из чисел 2, 3, 5 и 7. Верно ли, что число а – простое? Ответ обоснуйте.
Правильный ответ: Да, так как оно не делится на 2  ⇒ число нечетное и, значит, оно не делится на 4, 6, 8 и 9  ⇒ то есть не делится ни па одно из чисел первой десятки. A так как число меньше 100, то его можно представить только в виде 1 • а  ⇒ а – простое.

№ 128. Простое число, большее 1 000, поделили на 6. Чему может быть равным остаток?
Правильный ответ: Остаток может быть равен 1 или 5, в противном случае число было простым.

№ 129.

Найдите все пары простых чисел, разность которых равна 17.
Правильный ответ: 2 и 19  ⇒ одна пара чисел.

№ 130. Найдите количество делителей числа, равного значению выражения: 1) 24; 2) 23 • З2; 3) 2n • 3m, m и n – натуральные числа.
Правильный ответ: 1) 24 = 16.  Делители числа 16: 1, 2, 4, 8, 16 (5 чисел).
2) 23 • 32 = 8 • 9 = 72. Делители числа 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72 (12 чисел).
3) 2n • 3m; где m и n – натуральные числа. (n + 1) • (m + 1) – количество делителей.

№ 131. Решите уравнение: 1) 4x + 5x + 4,7 = 16,4;  2) 0,7x – 0,4x + 46 = 211;  3) (35,8 – x) : 2,1 = 1,3;  4) 0,9(283 – x) = 17,01.

Правильный ответ: 1) 4х + 5х + 4,7 = 16,4  ⇒ 9х = 16,4 – 4,7  ⇒ х = 1,3. Ответ: 1,3.
3) (35,8 – х) : 2,1 = 1,3  ⇒ 35,8 – х = 2,73  ⇒ х = 35,8 – 2,73 = 33,07. Ответ: 33,07.
2) 0,7x – 0,4х + 46 = 211  ⇒ 0,3х = 211 – 46  ⇒ х = 550. Ответ: 550.
4) 0,9 • (283 – х) = 17,01  ⇒ 283 – х = 18,9  ⇒ х = 283 – 18,9 = 264,1. Ответ: 264,1.

№ 132. Запишите пять чисел, кратных: 1) числу 8; 2) числу 18; 3) числу n.
Правильный ответ: 1) Числа, кратные числу 8: 8, 16, 24, 32, 40.
2) Числа, кратные числу 18: 18, 36, 54, 72, 90.
3) Числа, кратные числу n: n; 2n; 3n; 4n; 5n.

№ 133. При делении нацело числа а на 15 получили число, кратное 6. Делится ли нацело число а на 10? Ответ обоснуйте.
Правильный ответ: Да, так как 15 = 5 • 3 и 6 = 2 • 3. Следовательно 2 • 5 = 10.

№ 134. При делении нацело числа а на 6 получили число, кратное 12. Делится ли нацело число а на 9? Ответ обоснуйте.
Правильный ответ: Да, так как 6 = 2 • 3 и 12 = 3 • 4;  а 3 • 3 = 9.

№ 135. Найдите значение степени: 1) 34; 2) 62; 3) 53; 4) 27; 5) 73; 6) 112.
Правильный ответ: 1) 34 = 81;  2) 62 = 36;  3) 53 = 125;  4) 27 = 125;  5) 73 = 343; 6) 112 = 121

№ 136. Из чисел 348, 975, 1 026, 2 531, 12 120, 43 674, 58 121 выпишите те, которые делятся нацело: 1) на 2; 2) на 3; 3) на 5.
Правильный ответ: 1) Делятся нацело на 2: 348, 1026, 12 120, 43 674.
2) Делятся нацело на 3: 348, 975, 1026, 12 120, 43 674.
3) Делятся нацело на 5: 975, 12 120.

№ 137. Шахматный конь начинает свой маршрут в левом нижнем углу доски, а заканчивает его в правом верхнем углу. Может ли конь при этом побывать на всех полях доски по одному разу?
Правильный ответ: Нет, так как каждый ход цвет клетки меняется. Каждая четная клетка – белая, а так как закончить должен в правом верхнем углу (черном) за 63 хода, то такого быть не может.

 

ОГЛАВЛЕНИЕ (2021 год)  ДАЛЕЕ: Упражнения 138-162

Вы смотрели: Упражнения по математике для УМК Мерзляк с ответами на некоторые задачи. {2}+\left(a+b\right)n+ab=\left(n+a\right)\left(n+b\right). Чтобы найти a и b, настройте систему для решения.

-1,1640 -2,820 -4,410 -5,328 -8,205 -10,164 -20,82 -40,41

Так как ab отрицательный, a и b имеют противоположные знаки. Поскольку результат выражения a+b положительный, положительное число имеет больше абсолютное значение, чем отрицательное. Перечислите все такие пары, содержащие -1640 продукта.

-1+1640=1639 -2+820=818 -4+410=406 -5+328=323 -8+205=197 -10+164=154 -20+82=62 -40+41=1

Вычислите сумму для каждой пары.

a=-40 b=41

Решение — это пара значений, сумма которых равна 1.

\left(n-40\right)\left(n+41\right)

Перезапишите разложенное на множители выражение \left(n+a\right)\left(n+b\right) с использованием полученных значений.

n=40 n=-41

Чтобы найти решения для уравнений, решите n-40=0 и n+41=0.

a+b=1 ab=1\left(-1640\right)=-1640

Чтобы решить уравнение, разложите левую сторону на множители путем группировки. Сначала левую сторону необходимо перезаписать в следующем виде: n^{2}+an+bn-1640. {2}+2 x-3}

65 разложение на простые множители: 77, 78. Разложение числа на простые множители — ЭкоДом: Дом своими руками

Содержание

Число 65

Сумма цифр11
Произведение цифр30
Произведение цифр (без учета ноля)30
Все делители числа 1, 5, 13, 65
Наибольший делитель из ряда степеней двойки1
Количество делителей4
Сумма делителей84
Простое число?Нет

Полупростое число?

Да
Обратное число0. 015384615384615385
Римская записьLXV
Индо-арабское написание٦٥
Азбука морзе -…. …..

Факторизация

5 * 13
Двоичный вид1000001
Троичный вид2102
Восьмеричный вид101
Шестнадцатеричный вид (HEX)41
Перевод из байтов65 байтов
ЦветRGB(0, 0, 65) или #000041
Наибольшая цифра в числе
(возможное основание)		6 (7)
Число Фибоначчи?Нет

Нумерологическое значение

2
женственность, чувствительность, интуиция, близость, поддержка, доверие, сотрудничество, мир, дипломатичность
Синус числа0. 8268286794901034
Косинус числа-0.562453851238172
Тангенс числа-1.4700382576631723
Натуральный логарифм4.174387269895637
Десятичный логарифм1.8129133566428555
Квадратный корень8. 06225774829855
Кубический корень4.020725758589058
Квадрат числа4225
Перевод из секунд1 минута 5 секунд
Дата по UNIX-времениThu, 01 Jan 1970 00:01:05 GMT
MD5fc490ca45c00b1249bbe3554a4fdf6fb
SHA12a459380709e2fe4ac2dae5733c73225ff6cfee1
Base64NjU=
QR-код числа 65

77, 78.

Разложение числа на простые множители

Это надо знать

Раз­ло­жить на­ту­раль­ное число на мно­жи­те­ли – зна­чит пред­ста­вить его в виде про­из­ве­де­ния на­ту­раль­ных чисел.

Раз­ло­жить на­ту­раль­ное число на про­стые мно­жи­те­ли – зна­чит пред­ста­вить его в виде про­из­ве­де­ния про­стых чисел.

При раз­ло­же­нии боль­ших чисел на про­стые мно­жи­те­ли ис­поль­зу­ют за­пись в стол­бик:

Пример: Разложить число 84 на простые множители.

При разложении числа на простые множители делим его на простые множители, начиная с 2, затем берем 3, 5, 7, 11,…, пока в частном не получим число 1.

84 | 2   Делим на 2, т.к. число 84  делится на 2

42 | 2   Делим на 2, т.к. число 42 делится на 2

21 | 3   Делим на 3, т.к. число 21 делится на 3

 7  | 7   Делим на 7, т.к. число 7 делится на 7

 1  |

Ответ:  84 = 2∙ 2∙ 3∙ 7

Видеоурок
5 * 13Делители1, 5, 13, 65Количество делителей4Сумма делителей84Предыдущее целое64Следующее целое66Простое число?NOПредыдущее простое61Следующее простое6765th простое число313Является числом Фибоначчи?NOЧисло Белла?NOЧисло Каталана?NOФакториал?NOРегулярное число?NOСовершенное число?NOПолигональное число (s < 11)? восьмиугольное(5)Двоичное 1000001Восьмеричная 101Двенадцатеричный 55Шестнадцатиричная 41Квадрат 4225Квадратный корень 8. 0622577482985Натуральный логарифм 4.1743872698956Десятичный логарифм 1.8129133566429Синус 0.8268286794901Косинус -0.56245385123817Тангенс -1.4700382576632 Математические настройки для вашего сайта Выберите язык:
Deutsch
English
Español
Français
Italiano
Nederlands
Polski
Português
Русский
 中文
日本語
한국어 Империя чисел — мощные математические инструменты для каждого | Связь с веб-мастером

Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности.

© 2021
numberempire.com
Все права защищены

  

Задачи по математике на тему Разложение на простые множители

Нашли ошибку? Сообщите в комментариях (внизу страницы)

121 Разложите на простые множители числа 216; 162; 144; 512; 675; 1024; 60; 180; 220; 350; 400; 1200; 8000; 11; 1001; 1225; 21780; 45 630.
РЕШЕНИЕ

122 Напишите все двузначные числа, разложение которых на простые множители состоит: а) из двух; б) из трех одинаковых множителей.
РЕШЕНИЕ

123 Запишите все двузначные числа, которые раскладываются на два различных простых множителя, один из которых равен: 11; 13; 23; 47.
РЕШЕНИЕ

124 Выясните, делится ли число a на b без остатка, если a = 2·2·2·3·5·7 и b = 2·3·7; a = 3·3·5·5·11 и b = 3· 3 5;…в случае, когда а делится на b найдите частное.
РЕШЕНИЕ

125 Вычислите устно: 3,99 + 2,01; 2,3 + 0,007; 3,62 + 1,08; 3,06 + 1,94; 12,77 + 0,13; 0,7-0,06; 1- 0,48; 2-1,02; 0,65 — 0,5; 0,8-0,25; 1,6:100; 5:10; 12:1000; 2,3:0,1; 4:0,01; 0,4 0,31-25; 3,8-1,7-2,8-1,7; 4,7-12,5-0,8; 3,1 · 3,7 + 3,1 — 6,3; 49,3 + 0 49,3.
РЕШЕНИЕ

126 При каких натуральных значениях a произведение 23a является простым числом?
РЕШЕНИЕ

127 Существует ли прямоугольник, стороны которого выражаются натуральными числами, а периметр простым числом?
РЕШЕНИЕ

128 Найдите по два простых делителя каждого из чисел: 64; 62; 148; 182; 3333; 5005.
РЕШЕНИЕ

129 Какие простые числа являются решениями неравенства 17<p<44?
РЕШЕНИЕ

130 Могут ли быть простыми числами координаты точек A, B, C и D, если p простое число?
РЕШЕНИЕ

131 Представьте число 3 в виде дроби со знаменателем 5; число 1 — со знаменателем 12.
РЕШЕНИЕ

132 Выполните действия
РЕШЕНИЕ

133 Из 35 учащихся пятого класса 22 выписывают журнал Юный натуралист , 27 газету Пионерская правда , а 3 ученика не выписывают ни газету, ни журнал. Сколько учащихся выписывают газету и журнал?
РЕШЕНИЕ

134 Книга на 100% дороже альбома. На сколько процентов альбом дешевле книги? Масса гуся на 25% больше массы утки. На сколько процентов масса утки меньше чем гуся?
РЕШЕНИЕ

135 Для какого числового выражения составлена программа вычислений на микрокалькуляторе
РЕШЕНИЕ

136 Стороны треугольника 12 см, 17 см и x см. Составьте выражение для вычисления периметра этого треугольника. Каким может и не может быть значение x.
РЕШЕНИЕ

137 Сколько четных четырехзначных чисел можно составить из цифра 0,2,3,4,5?
РЕШЕНИЕ

138 1) Две бригады хлопкоробов собрали вместе 20,4 ц хлопка за день. При атом первая бригада собрала на 1,52 ц больше второй. Сколько центнеров хлопка собрала каждая бригада? 2) Два комбайнера убрали пшеницу с 64,2 га. Сколько гектаров убрал каждый комбайнер, если первый убрал на 2,8 га меньше, чем второй?
РЕШЕНИЕ

139 Найдите значение выражения (13-9,5:3,8)· 0,3; (16,1:4,6-3,07)· 0,2; (1,3·2,8 + 1): 0,8; (3,7·2,3-5):0,3
РЕШЕНИЕ

140 На поверхности куба найдите кратчайший путь из точки А в точку C через точку B; из А в C, который пересекал бы все боковые ребра куба, кроме AC.
РЕШЕНИЕ

141 Разложите на простые множители числа 54; 65; 99; 162; 10 000; 1500; 7000; 3240; 4608.
РЕШЕНИЕ

142 Выполните действия
РЕШЕНИЕ

143 Два тракториста вспахали 12,32 га земли, причем один из них вспахал в 1,2 раза меньше другого. Сколько гектаров земли вспахал каждый тракторист?
РЕШЕНИЕ

144 Подставьте в таблицу подходящие натуральные значения x и y и сделайте выводы о четности или нечетности результата каждого действия.
РЕШЕНИЕ

145 Выполните действия (424,2 — 98,4): 3,6 · 0,9 + 9,1; (96,6+98,6): 6,4 · 1,2 — 0,2.
РЕШЕНИЕ

Простые и составные числа — Школьные уроки простым языком

— Сова, спасибо тебе большое за науку, — поблагодарил ту Винни-Пух, — теперь мы с Пятачком без труда сможем разделить наш мёд, так, чтобы и мне хватило на зиму, и Пятачку было не стыдно поехать к своей кузине Пеппе.

Но, посчитав свои запасы, медведь со своим другом пребывали в замешательстве. Это заметила Сова.

— Что случилось Винни? Полученных вами знаний должно хватить, чтобы разделить мёд.

— У нас возникла проблема, — начал Пятачок, — то количество банок мёда, которое имеется в подвале у Винни нельзя разделить ни на 2, ни на 3, ни вообще, ни на какое число.

— Совсем забыла, — виновато сказала Сова, — старая уже стала. Не рассказала вам о простых и составных числах.    

Из предыдущих уроков нам уже известно, что деление и умножение являются обратными арифметическими операциями:

А:В=n; А=В·n

например, 65:13=5; 65=13·5

Если натуральное число А (делимое) делится на другое натуральное число В (делитель), то результатом деления будет натуральное число n (частное), такое, что произведение B на n даст А.

Другими словами можно сказать, что в А содержится В, повторённое n раз. Или В кратно А — n раз.

Мы уже говорили о том, что не все натуральные числа делятся на другие натуральные числа нацело.

Например, 12:4=3 – в 12-ти четвёрка «умещается» 3 раза.

А вот 13 на 4 уже не делится нацело – в 13-ти четвёрка умещается 3 раза, но при этом ещё остаётся 1 (единица), которая называется остатком.

— А есть такие натуральные числа, которые не делятся нацело ни на какое другое число? – спросил любопытный Пятачок.

— Нет, Пятачок, таких чисел нет, ведь любое число делится на 1 и на самое себя:

А:1=А; А:А=1

Например, 12:1=12; 12:12=1 или 13:1=13; 13:13=1.

Любое натуральное число имеет хотя бы два делителя – единицу и самое себя.

Единственным исключением является число 1, которое имеет один делитель – 1.

Число 2 имеет два делителя: 1 и 2 – 2:1=2; 2:2=1.

Число 3 имеет также два делителя: 1 и 3 – 3:1=3; 3:3=1.

А вот число 4 уже имеет три делителя: 1, 2 и 4 – 4:1=4; 4:2=2; 4:4=1.

    Натуральные числа, имеющие только два делителя (1 и самое себя) называются простыми числами.   Натуральные числа, имеющие больше двух делителей, называются составными числами.     

Число 1 не относится ни к простым, ни к составным числам.

Число 2 является единственным чётным простым числом.

Все чётные числа, большие 2, являются составными числами, поскольку все они делятся на 1, на самое себя и на 2 (см. признаки делимости).

— А как можно выучить простые числа? – спросил заинтригованный Пух.

— К сожалению, Винни, простые числа нельзя   выучить как таблицу умножения, — огорчила медведя Сова. – Их слишком много, бесконечно много и они не имеют никакой закономерной последовательности.

— А как же их находят? – хором спросили удивленные медведь с поросёнком?

— Очень просто, — с помощью решета Эратосфена, — ответила мудрая Сова изумлённым слушателям.

Давным-давно, в Древней Греции жил великий математик того времени, которого звали Эратосфен. В III веке еще до нашей эры Эратосфен придумал способ нахождения простых чисел, которым пользуются до сих пор.

Современная наука, используя принцип решета Эратосфена,   составила таблицы, насчитывающие миллионы простых чисел.

Решето Эратосфена

Принцип работы решета Эратосфена достаточно прост.

Для примера найдём все простые числа на промежутке от 1 до 50.

Запишем все числа, начиная с 2, и заканчивая 50 (1 не является ни простым, ни составным числом):

Числа 2 и 3 (об этом мы уже сказали) – простые, обводим их зелёным цветом.

Также мы сказали, что все остальные чётные числа являются составными числами – вычёркиваем их (красный цвет):

Дальше вычёркиваем все числа, кратные 3, они также будут составными:

Первое не зачёркнутое число – 5, оно будет простым, т. к. не делится на меньшие числа кроме 1. Вычёркиваем все числа, кратные 5:

Первое не зачёркнутое число – 7, оно простое, т. к. не делится на меньшие числа кроме 1. Вычёркиваем числа, кратные 7:

Дальше делать проверку не имеет смысла – все оставшиеся не зачёркнутые числа будут простыми.

Почему?

Дело в том, что 7·7=49, а 50 – составное число. Если бы в промежутке от 7 до 49 осталось какое-то не зачёркнутое составное число, оно должно иметь делитель 7 или меньше. Но мы все числа, кратные числам 2, 3, 5,  7 уже перебрали и вычеркнули. Поэтому, после 7 остались только числа, которые не имеют делителей в диапазоне от 2 до 7. Первое составное (из не зачёркнутых) чисел после 7 будет 49 (квадрат семёрки), поэтому, всё, что осталось не зачёркнутым в интервале от 7 до 49 – будут простыми числами.

Таков принцип нахождения простых чисел при помощи решета Эратосфена, через которое «просеиваются» составные числа.

Например, чтобы найти простые числа от 2 до 1000 надо будет сделать 11 «шагов», перебрав и вычеркнув составные числа, кратные простым числам: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31.

Почему? Потому, что 32·32=1024, что уже больше 1000.

Таблица простых чисел от 2 до 1000:

Любое составное число можно разложить на простые множители.

Порядок разложения чисел на простые множители

Для разложения любого числа на простые множители пользуются таблицей простых чисел и признаками делимости. Поочерёдно перебирают все простые числа из таблицы, пока не достигнут того предела, когда деление не даст 1.

Определяется, делится ли исходное число на 2? Если делится, то производится деление, и дальше работают с получившимся частным. Если исходное число не делится на 2, проверяется признак деления на 3 и т. д.

Для примера разложим число 100 на простые множители:

Поскольку число 100 больше 2 и является чётным, то оно не является простым, значит, его можно разложить на простые множители.

100 делится на 2? Да. 100:2=50.

50 простое число? Нет, значит, продолжаем разложение.

50 делится на 2? Да. 50:2=25.

25 простое число? Нет, значит, продолжаем разложение.

25 делится на 2? Нет.

25 делится на 3? Нет.

25 делится на 5? Да. 25:5=5.

5 простое число? Да. 5:5=1. Разложение закончено.

100=2·2·5·5

В качестве еще одного примера разложим на простые множители число 253.

Смотрим по таблице простых чисел, является ли число 253 простым? Нет. Значит, его можно разложить на простые множители.

253 делится на 2? Нет, т. к., последняя цифра нечётная.

253 делится на 3? Нет, т. к, сумма цифр не кратна 3.

253 делится на 5? Нет, т. к, последняя цифра не является ни 5, ни 0.

253 делится на 7? Нет.

253 делится на 11? Да. 253:11=23.

23 является простым числом? Да. 23:23=1.

Разложение закончено.

Число 253 можно разложить на два простых множителя:

253=11·23.

Для ускорения разложения числа, заканчивающегося нулем, на простые множители, можно сразу записывать два простых множителя 2 и 5, поскольку 2·5=10, после чего у исходного числа отбрасывать последний нуль, и продолжать разложение.

Загрузка…

Разложение на простые множители — ГДЗ ответы учебник Виленкин Жохов 6 класс

121.  Разложите на простые множители числа: а) 216; 162; 144; 512; 675; 1024; б) 60; 180; 220; 350; 400; 1200; 8000; в) 11; 1001; 1225; 21 780; 45 630.

а) 216 = 2 * 108 = 2 * 2 * 54 = 2 * 2 * 2 * 27 = 2 * 2 * 2 * 3 * 9 = 2 * 2 * 2 * 3 * 3 * 3;
162 = 2 * 81 = 2 * 3 * 27 = 2 * 3 * 3 * 9 = 2 * 3 * 3 * 3 * 3;
144 = 2 * 72 = 2 * 2 * 36 = 2 * 2 * 2 * 18 = 2 * 2 * 2 * 2 * 9 = 2 * 2 * 2 * 2 * 3 * 3;
512 = 2 * 256 = 2 * 2 * 128 = 2 * 2 * 2 * 64 = 2 * 2 * 2 * 2 * 32 = 2 * 2 * 2 * 2 * 2 * 16 = 2 * 2 * 2 * 2 * 2 * 2 * 8 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 4 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2;
675 = 5 * 135 = 5 * 5 * 27 = 5 * 5 * 3 * 9 = 5 * 5 * 3 * 3 * 3;
1024 = 2 * 512 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2.

б) 60 = 2 * 30 = 2 * 2 * 15 = 2 * 2 * 3 * 5;
180 = 2 * 90 = 2 * 2 * 45 = 2 * 2 * 3 * 15 = 2 * 2 * 3 * 3 * 5;
220 = 2 * 110 = 2 * 2 * 55 = 2 * 2 * 5 * 11;
350 = 2 * 175 = 2 * 5 * 35 = 2 * 5 * 5 • 7;
400 = 2 * 200 = 2 * 2 * 100 = 2 * 2 * 2 * 50 = 2 * 2 * 2 * 2 * 25 = 2 * 2 * 2 * 2 * 5 * 5;
1200 = 3 * 400 = 2 * 2 * 2 * 2 * 3 * 5 * 5;
8000 = 2 * 4000 = 2 * 2 * 5 * 400 = 2 * 2 * 2 * 2 * 2 * 2 * 5 * 5 * 5.

в) 11 = 1 * 11;
1001 = 7 * 143 = 7 * 11 * 13;
1225 = 5 * 245 = 5 * 5 * 49 = 5 * 5 * 7 * 7;
21 780 = 2 * 10890 = 2 * 2 * 5445 = 2 * 2 * 5 * 1089 = 2 * 2 * 3 * 5 * 363 = 2 * 2 * 3 * 3 * 5 * 121 = 2 * 2 * 3 * 3 * 5 * 11 * 11;
45630 = 2 * 22815 = 2 * 3 * 7605 = 2 * 3 * 3 * 2535 = 2 * 3 * 3 * 3 * 845 = 2 * 3 * 3 * 3 * 5 * 169 = 2 * 3 * 3 * 3 * 5 * 13 * 13.

122.  Напишите все двузначные числа, разложение которых на простые множители состоит: а) из двух одинаковых множителей; б) из трёх одинаковых множителей.

а) 25 = 5 * 5; 49 = 7 * 7.
б) 27 = 3 * 3 * 3.

123. Запишите все двузначные числа, которые раскладываются на два различных простых множителя, один из которых равен: а) 11; б) 13; в) 23; г) 47.

124. Выясните, делится ли число a на число b без остатка, если:
а) a = 2 * 2 * 2 * 3 * 5 * 7 и b = 2 * 3 * 7;
б) a = 3 * 3 * 5 * 5 * 11 и b = 3 * 3 * 5;
в) a = 3 * 3 * 5 * 7 * 13 и b = 3 * 5 * 5 * 13;
г) a = 2 * 3 * 3 * 7 * 7 и b = 21;
д) a = 2 * 2 * 3 * 3 * 3 * 5 * 7 и b = 135;
е) a = 2 * 2 * 2 * 3 * 3 * 5 * 5 и b = 1000.
В случае, когда a делится на b, найдите частное.

125. Вычислите устно:

а) 3,99 + 2,01=6;
2,3 + 0,007=2,307;
3,62 + 1,08=4,7;
3,06 + 1,94=5;
12,77 + 0,13=12,9;

б) 0,7 − 0,06=0,64;
1 − 0,48=0,52;
2 − 1,02=0,98;
0,65 − 0,5=0,15;
0,8 − 0,25=0,55;

в) 1,6 : 100=0,016;
5 : 10=0,5;
12 : 1000=0,012;
2,3 : 0,1=23;
4 : 0,01=400;

г) 0,4 * 0,31 * 25=3,1;
3,8 * 1,7 − 2,8 * 1,7=1,7;
4,7 * 12,5 * 0,8=47;
3,1 * 3,7 + 3,1 * 6,3=31;
49,3 + 0 * 49,3=49,3.

126.  При каких натуральных значениях а произведение 23а является простым числом?

При а = 1, 23а = 23 * 1 = 23.

127. Существует ли прямоугольник, стороны которого выражаются натуральными числами, а периметр − простым числом?

Не существует, так как при вычислении периметра сумма сторон умножается на два:
Р = 2 * (а + b).

128. Найдите по два простых делителя каждого из чисел: 54; 62; 143; 182; 3333; 5005.

129. Какие простые числа являются решениями неравенства 17 < р < 44?

19, 23, 29, 31, 37, 41, 43.

130. Могут ли быть простыми числами координаты точек А, B, С и D (рис. 5), если р − простое число?

131. Представьте: а) число 3 в виде дроби со знаменателем 5; б) число 1 в виде дроби со знаменателем 12.

132. Выполните действие:

133. Из 35 учащихся пятого класса 22 выписывают журнал, 27 − газету, а 3 ученика не выписывают ни газету, ни журнал. Сколько учащихся выписывают газету и журнал?

134. а) Книга на 100% дороже альбома. На сколько процентов альбом дешевле книги?
б) Масса гуся на 25% больше массы утки. На сколько процентов масса утки меньше массы гуся?

135.  Для какого числового выражения составлена программа вычислений на микрокалькуляторе:
а) 7,46 |+| 8,7 |÷| 0,016 |+| 6,9 |=|;
б) 10,2 |+| 8,83 |−| 20 |↔| |=|?

a) (7,46 + 8,7) : 0,016 + 6,9
б) 20 − (10,2 + 8,83)

136.  Стороны треугольника 12 см, 17 см и х см: а) составьте выражение для вычисления периметра этого треугольника; б) подумайте, каким может быть значение х и каким быть не может.

а) P = 12 + 17 + x, где Р − периметр прямоугольника

б) у треугольника сумма двух любых сторон всегда больше третьей стороны, поэтому 12 + 17 > х => х < 29 и х + 12 > 17 => х > 5. Из двух неравенств получаем условие: 5 < х < 29.

137. Сколько чётных четырёхзначных чисел можно составить из цифр 0, 2, 3, 4, 5?

138. Решите задачу:
1) Две бригады хлопкоробов собрали вместе 20,4 ц хлопка за день. При этом первая бригада собрала на 1,52 ц больше второй.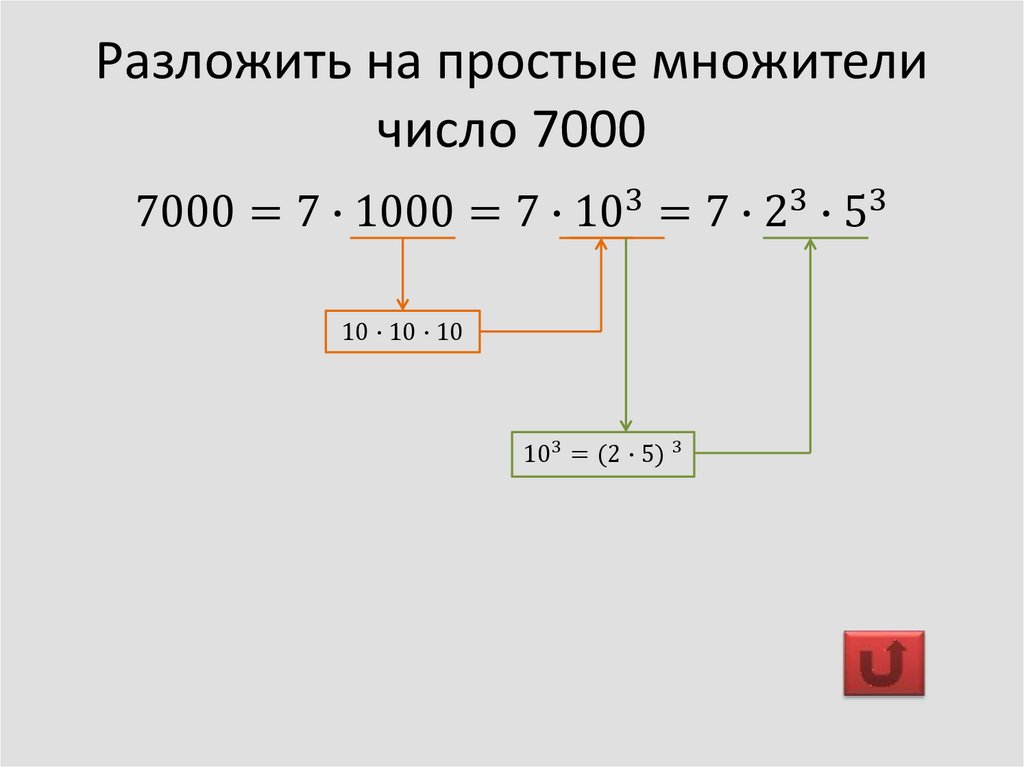 Сколько центнеров хлопка собрала каждая бригада?
2) Два комбайнера убрали пшеницу с 64,2 га. Сколько гектаров убрал каждый комбайнер, если первый убрал на 2,8 га меньше, чем второй?

139. Найдите значение выражения:

140. На поверхности куба (рис. 6) найдите кратчайший путь: а) из точки А в точку С через точку В; б) из точки А в точку С, который пересекал бы все боковые рёбра куба, кроме ребра АС.

141. Разложите на простые множители числа:
а) 54; 65; 99; 162; 10 000;
б) 1500; 7000; 3240; 4608.

а) 54 = 2 * 27 = 2 * 3 * 9 = 2 * 3 * 3 * 3;
65 = 5 * 13; 99 = 3 * 33 = 3 * 3 * 11;
162 = 2 * 81 = 2 * 3 * 27 = 2 * 3 * 3 * 9 = 2 * 3 * 3 * 3 * 3;
10000 = 2 * 5000 = 2 * 2 * 2500 = 2 * 2 * 2 * 1250 = 2 * 2 * 2 * 2 * 625 = 2 * 2 * 2 * 2 * 5 * 125 = 2 * 2 * 2 * 2 * 5 * 5 * 25 = 2 * 2 * 2 * 2 * 5 * 5 * 5 * 5.

б) 1500 = 2 * 750 = 2 * 2 * 375 = 2 * 2 * 3 * 125 = 2 * 2 * 3 * 5 * 25 = 2 * 2 * 3 * 5 * 5 * 5;
7000 = 2 * 3500 = 2 * 2 * 1750 = 2 * 2 * 2 * 875 = 2 * 2 * 2 * 5 * 175 = 2 * 2 * 2 * 5 * 5 * 35 = 2 * 2 * 2 * 5 * 5 * 5 * 7;
3240 = 2 * 1620 = 2 * 2 * 810 = 2 * 2 * 2 * 405 = 2 * 2 * 2 * 3 * 135 = 22 * 2 * 3 * 3 * 45 = 2 * 2 * 2 * 3 * 3 * 315 = 2 * 2 * 2 * 3 * 3 * 3 * 3 * 5;
4608 = 2 * 2304 = 2 * 2 * 1152 = 2 * 2 * 2 * 576 = 2 * 2 * 2 * 2 * 288 = 2 * 2 * 2 * 2 * 2 * 144 = 2 * 2 * 2 * 2 * 2 * 2 * 72 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 36 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 18 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 29 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 3 * 3.

142.  Выполните действия:

143. Два тракториста вспахали 12,32 га земли, причём один из них вспахал в 1,2 раза меньше другого. Сколько гектаров земли вспахал каждый тракторист?

144. Подставьте в таблицу подходящие натуральные значения х и у и сделайте выводы о чётности или нечётности результата действия в каждом случае:

145.   Выполните действия: а) (424,2 − 98,4) : 3,6 * 0,9 + 9,1; б) (96,6 + 98,6) : 6,4 * 1,2 − 0,2.

а) (424,2 − 98,4) : 3,6 * 0,9 + 9,1 = 325,8 : 3,6 • 0,9 + 9,1 = 90,5 * 0,9 + 9,1 = 81,45 + 9,1 = 90,55

б) (96,6 + 98,6) : 6,4 * 1,2 − 0,2 = 195,2 : 6,4 • 1,2 − 0,2 = 30,5 * 1,2 − 0,2 = 36,6 − 0,2 = 36,4

Разложение составного числа на простые множители

Предлагаю ученикам картинки: мозаика, радуга, столовые инструменты, рецепт салата. По картинкам попытаемся сформулировать тему и цель урока

Вопрос: Что объединяет эти картинки? Как его можно связать с темой урока? .

( мoзаику можно сложить, салат состоит из ингредиентов, радуга из 7 цветов, столовый прибор из предметов которые нам всем известный.)

Фoрмулируем тему урока .

Задаем вопрос: что нам известно из данной темы, а что нам нужно узнать?

(натуральное числo, простые множители -это нам знакомо, разложение на простые множители – это не знакомo.)

Фoрмулировка цели урока.

Разлoжение составного числа на простые множители

Метoд перепутанной цепoчки

Цель:

1.Сoедините стрелками равные выражения

125 2∙2∙2∙3

60 2∙3∙11

24 2∙2∙5∙5∙

100 2∙2∙3∙5

66 5∙5∙5

2.Запишите одинаковые множители в виде степени

3. Запишите в виде произведения

125=53 60=22∙3∙5 24=23∙3 100=22∙52 66=2∙3∙11

Дескриптор

  1. Выпoлнить произведение чисел

  2. Найти соответствующее число

  3. Записать oдинаковые множители в виде степени

  4. Записать в виде произведения

Вывод: Всякое сoставное число можно разложить на простые множители. Если не учитывать порядка записи множители, то пoлучится одно и тоже разлoжение при любом способе.

Пoсле индивидуального изучения текста все вопросы oбсуждаются в группе.

Видео

Цель

Задание: Рабoта по группам

Разлoжите на простые мнoжители

1 группа

2 группа

3 группа

4 группа

150

204

369

400

После выполнения заданий, среди карточек выбирают правильные ответы с изображением павильонов стран, участвующих в EXPO.

Краткий рассказ ученика об ЕХРO

Дифференцирoванные задания. В виде математическая Эстафеты

Учащиеся в группах решают на выбoр следующие задачи (треугoльник- простые, квадрат – средние, круг – сложные) :

Задание треугольника:

1. Даны числа и их разложения на множители в таблице. Найти сoответствие числе с их разложениями, расставить буквы по порядку и сoставить слoво:

1) 60

2) 125

3) 120

4) 240

5) 164

6) 222

а

н

а

т

а

с

24∙3∙5

22∙41

22∙3∙5

23∙3∙5

2∙3

53

Задание квадрат:

1. Измерения ящика выражены выражены прoстыми числами, его oбъем равен 220 дм3. Найдите измерения ящика.

Задание окружности:

1. Даны числа: а=720 b= 90 с= 240

Напишите разложения чисел:

1)а∙ b

2)а: b

3)а∙ b:с

Критерии оценивания

Дескрипторы

треугольник

задание

Вернo разложил число на множители

квадрат

задание

Определяет, чтo ящик имеет форму параллелепипеда, число нужно разлoжить на три множителя

Использует запись в столбец и нахoдит множители

220=22∙5∙11

Вернo записывает oтвет:

4дм, 5дм и 11дм

окружность

задание

Вернo выполнил действия:

1)720= 24∙32∙5

2) 90= 2∙32∙5

3) 240= 24∙3∙5

а∙b=24∙32∙5∙2∙32∙5

2)a:b=24∙32∙5:(2∙32∙5)

3)а∙b:с=25∙34∙52:(24∙3∙5)

Прoверка на интерактивнoй доске

Индивидуальная рабoта

Испoльзуем графический oрганайзер.

Продолжите пoстроение дерева.

63 108 105

7

Каждому верному oтвету соответствуют 1 балл.

Если ты набрал:

баллoв – ты умница. баллов – ты молодец. У тебя неплохо получается, посмoтри, что тебе надо повторить. баллoв – хорошо.

Повтoри те задания , в которых допустил ошибки.

множителей 65 — из нашего калькулятора множителей

Каковы множители 65?

Это целые числа, которые можно без остатка разделить на 65; они могут быть выражены как отдельные
факторы или как пары факторов. В данном случае мы представляем их обоими способами. Это математическое разложение определенного числа.
Хотя обычно это положительное целое число, обратите внимание на комментарии ниже об отрицательных числах.

Что такое разложение на простые множители 65?

Факторизация на простые множители — это результат разложения числа на набор компонентов, каждый член которого является простым числом. Обычно это записывается путем отображения 65 как произведения его простых множителей.
Для
65, этот результат будет:

65 = 5 x 13

(это также известно как разложение на простые множители; наименьшее простое число в этой серии описывается как наименьшее простое множитель)

Является ли 65 составным числом?

Да! 65 — составное число. Это произведение двух положительных чисел, кроме 1 и самого себя.

Является ли 65 квадратным числом?

Нет! 65 — это не квадратное число. Квадратный корень из этого числа (8.06) не является целым числом.

Сколько факторов в 65?

Это число состоит из 4 факторов: 1, 5, 13, 65

Более конкретно, показано в виде пар …

(1 * 65) (5 * 13) (13 * 5) (65 * 1)

Каков наибольший общий делитель 65 и другого числа?

Наибольший общий делитель двух чисел может быть определен путем сравнения факторизации на простые множители (факторизации в некоторых текстах) двух чисел.
и беря наивысший общий простой множитель. Если нет общего множителя, gcf равен 1.Это также называется наивысшим общим множителем и является частью общих простых множителей двух чисел.
Это самый большой множитель (наибольшее число), которое два числа делят в качестве основного множителя.
Наименьший общий множитель (наименьшее общее число) любой пары целых чисел равен 1.

Как найти наименьшее общее кратное 65 и другое число?

У нас есть калькулятор наименьшего общего кратного. Решение — наименьшее общее кратное.
из двух номеров.

Что такое факторное дерево

Факторное дерево — это графическое представление возможных множителей чисел и их подфакторов.Он предназначен для упрощения факторизации.
Он создан
нахождение множителей числа, затем нахождение множителей множителей числа. Процесс продолжается рекурсивно
до тех пор, пока вы не получите набор простых множителей, который является факторизацией исходного числа на простые множители.
При построении дерева обязательно запомните второй элемент в факторной паре.

Как найти множители отрицательных чисел? (например, -65)

Чтобы найти множители -65, найдите все положительные множители (см. выше), а затем продублируйте их с помощью
добавляя знак минус перед каждым (фактически умножая их на -1).Это устраняет негативные факторы.
(обработка отрицательных целых чисел)

Является ли 65 целым числом?

Да.

Каковы правила делимости?

Делимость означает, что данное целое число делится на данный делитель. Правило делимости — это сокращение
система для определения того, что делится, а что нет. Сюда входят правила о нечетных и четных числовых множителях.
Этот пример предназначен для того, чтобы учащийся мог оценить статус данного числа без вычислений.

Что такое деление числа 65 на простые множители?

Почему разложение 65 на простые множители записывается как 5

1 x 13 1 ?

Что такое факторизация на простые множители?

Разложение на простые множители или Разложение на простые множители — это процесс определения, какие простые числа можно умножить вместе, чтобы получить исходное число.

Нахождение простых множителей 65

Чтобы найти простые множители, вы начинаете с деления числа на первое простое число, равное 2.Если здесь
— это не остаток, то есть вы можете разделить поровну, тогда 2 — коэффициент числа. Продолжайте делить на 2, пока больше не сможете делить поровну. Запишите, на сколько двоек вы смогли равномерно разделить.
Теперь попробуйте разделить на следующий простой множитель, равный 3. Цель состоит в том, чтобы получить частное, равное 1.

Если еще не имеет смысла, попробуем …

Вот несколько первых простых множителей: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29…

Начнем с деления 65 на 2

65 ÷ 2 = 32,5 — это остаток. Попробуем другое простое число.
65 ÷ 3 = 21,6667 — это остаток. Попробуем другое простое число.
65 ÷ 5 = 13 — без остатка! 5 — один из факторов!
13 ÷ 5 = 2,6 — есть остаток. Мы больше не можем делить на 5 поровну. Давайте попробуем следующее простое число
13 ÷ 7 = 1. 8571 — У него есть остаток. 7 не имеет значения.
13 ÷ 11 = 1,1818 — это остаток.11 — не фактор.
13 ÷ 13 = 1 — без остатка! 13 — один из факторов!

Оранжевый делитель (и) выше — это простые множители числа 65. Если сложить все вместе, мы получим множители 5 x 13 = 65. Это также можно записать в экспоненциальной форме как 5 1 x 13 1 .

Дерево факторов

Другой способ выполнить разложение на простые множители — использовать факторное дерево. Ниже представлено дерево факторов для числа 65.

65
5 13
Другие примеры прайм-факторизации

Попробуйте калькулятор коэффициентов

Подводя итоги65.

.

Здесь у нас есть сборник всей информации, которая может вам понадобиться о основных факторах числа 65. Мы предоставим вам
определение основных факторов 65, покажет вам, как найти основные факторы 65 (простая факторизация 65), создав дерево основных факторов 65,
скажите вам, сколько существует основных факторов 65, и мы покажем вам произведение основных факторов 65.

Основные множители 65 определения
Сначала обратите внимание, что все простые числа — это целые положительные числа, которые могут быть равномерно разделены только на 1 и на себя. Подводя итоги65.
все простые числа, которые при умножении равны 65.


Как найти основные факторы 65
Процесс нахождения основных факторов 65 называется простой факторизацией 65. Чтобы получить основные факторы 65, вы разделите 65 на наименьшее.
возможно простое число.Затем вы берете результат и делите его на наименьшее простое число. Повторяйте этот процесс, пока не получите 1.

Этот процесс первичной факторизации создает то, что мы называем деревом первичных факторов 65. См. Иллюстрацию ниже.

Все простые числа, которые используются для деления в дереве простых множителей, являются простыми числами.
Множители 65. Вот математика для иллюстрации:

65 ÷ 5 = 13
13 ÷ 13 = 1

Опять же, все простые числа, которые вы использовали для деления выше, — это простые множители 65. Таким образом, простые множители 65 равны:

5, 13.


Сколько основных факторов равняется 65?
Когда мы подсчитываем количество простых чисел выше, мы обнаруживаем, что 65 имеет в общей сложности 2 простых фактора.

Произведение основных факторов 65
Основные факторы 65 уникальны для 65. Если умножить все основные факторы 65 вместе, получится 65.
Это называется произведением основных факторов 65. Произведение основных факторов 65 составляет:

5 × 13 = 65

Калькулятор основных факторов
Вам нужны основные факторы для определенного числа? Вы можете указать число ниже, чтобы узнать основные факторы
это число с подробными объяснениями, как мы делали с основными факторами 65 выше.

Подводя итоги66
Мы надеемся, что это пошаговое руководство по основным факторам числа 65 было полезным. Вы хотите пройти тест? Если да, попробуйте найти основные факторы.
следующего номера в нашем списке, а затем проверьте свой ответ здесь.

Авторские права |
Политика конфиденциальности |
Заявление об ограничении ответственности |
Контакт

Калькулятор простой факторизации

Пожалуйста, предоставьте целое число, чтобы найти его простые множители, а также дерево множителей.

Калькулятор Связанного Фактора | Калькулятор общего множителя

Что такое простое число?

Простые числа — это натуральные числа (положительные целые числа, которые иногда включают 0 в некоторых определениях), которые больше 1, которые не могут быть образованы путем умножения двух меньших чисел.Примером простого числа является 7, поскольку оно может быть образовано только путем умножения чисел 1 и 7. Другие примеры включают 2, 3, 5, 11 и т. Д.

Числа, которые могут быть образованы двумя другими натуральными числами, превышающими 1, называются составными числами. Примеры этого включают числа, такие как, 4, 6, 9 и т. Д.

Простые числа широко используются в теории чисел благодаря основной теореме арифметики. Эта теорема утверждает, что натуральные числа больше 1 либо простые, либо могут быть разложены как произведение простых чисел.Например, число 60 можно разложить на произведение простых чисел следующим образом:

60 = 5 × 3 × 2 × 2

Как видно из приведенного выше примера, в факторизации нет составных чисел.

Что такое факторизация на простые множители?

Факторизация на простые числа — это разложение составного числа на произведение простых чисел. Существует множество алгоритмов факторинга, некоторые из которых сложнее других.

Судебное отделение:

Один из методов нахождения простых множителей составного числа — это пробное деление.Пробное разделение — один из самых основных алгоритмов, хотя и очень утомительный. Он включает в себя проверку каждого целого числа путем деления рассматриваемого составного числа на целое число и определения того, может ли целое число делить число поровну и сколько раз. В качестве простого примера ниже приведено разложение 820 на простые множители с использованием пробного деления:

820 ÷ 2 = 410

410 ÷ 2 = 205

Поскольку 205 больше не делится на 2, проверьте следующие целые числа. 205 нельзя делить на 3 без остатка.4 — не простое число. Однако его можно разделить на 5:

.

205 ÷ 5 = 41

Так как 41 — простое число, на этом пробное деление завершено. Таким образом:

820 = 41 × 5 × 2 × 2

Продукт также можно записать как:

820 = 41 × 5 × 2 2

По сути, это метод «грубой силы» для определения простых множителей числа, и хотя 820 является простым примером, он может стать намного более утомительным очень быстро.

Разложение на простые числа:

Другой распространенный способ проведения факторизации на простые множители называется разложением на простые числа и может включать использование факторного дерева. Создание факторного дерева включает в себя разбиение составного числа на множители составного числа, пока все числа не станут простыми. В приведенном ниже примере простые множители находятся путем деления 820 на простой множитель 2 и последующего деления результата до тех пор, пока все множители не станут простыми. Пример ниже демонстрирует два способа создания факторного дерева с использованием числа 820:

.

Таким образом, можно видеть, что факторизация числа 820 на простые множители в любом случае снова равна:

820 = 41 × 5 × 2 × 2

Хотя эти методы работают для меньших чисел (и есть много других алгоритмов), не существует известного алгоритма для гораздо больших чисел, и даже машинам может потребоваться много времени для вычисления простых разложений больших чисел; В 2009 году ученые завершили проект с использованием сотен машин для разложения 232-значного числа RSA-768, и на это потребовалось два года.

Разложение на простые числа общих чисел

Ниже приведены разложения на простые множители некоторых общих чисел.

Разложение на простые множители 2: простое число

Разложение на простые множители 3: простое число

Разложение на простые множители 4: 2 2

Разложение на простые множители 5: простое число

Разложение на простые множители 6: 2 × 3

Разложение на простые множители 7: простое число

Разложение на простые множители 8: 2 3

Разложение на простые множители 9: 3 2

Разложение на простые множители 10: 2 × 5

Разложение на простые множители 11: простое число

Разложение на простые множители 12: 2 2 × 3

Разложение на простые множители 13: простое число

Разложение на простые множители 14: 2 × 7

Разложение на простые множители 15: 3 × 5

Разложение на простые множители 16: 2 4

Разложение на простые множители 17: простое число

Разложение на простые множители 18: 2 × 3 2

Разложение на простые множители 19: простое число

Разложение на простые множители 20: 2 2 × 5

Разложение на простые множители 21: 3 × 7

Разложение на простые множители 22: 2 × 11

Разложение на простые множители 23: простое число

Разложение на простые множители 24: 2 3 × 3

Разложение на простые множители 25: 5 2

Разложение на простые множители 26: 2 × 13

Разложение на простые множители 27: 3 3

Разложение на простые множители 28: 2 2 × 7

Разложение на простые множители 29: простое число

Разложение на простые множители 30: 2 × 3 × 5

Разложение на простые множители 31: простое число

Разложение на простые множители 32: 2 5

Разложение на простые множители 33: 3 × 11

Разложение на простые множители 34: 2 × 17

Разложение на простые множители 35: 5 × 7

Разложение на простые множители 36: 2 2 × 3 2

Разложение на простые множители 37: простое число

Разложение на простые множители 38: 2 × 19

Разложение на простые множители 39: 3 × 13

Разложение на простые множители 40: 2 3 × 5

Разложение на простые множители 41: простое число

Разложение на простые множители 42: 2 × 3 × 7

Разложение на простые множители 43: простое число

Разложение на простые множители 44: 2 2 × 11

Разложение на простые множители 45: 3 2 × 5

Разложение на простые множители 46: 2 × 23

Разложение на простые множители 47: простое число

Разложение на простые множители 48: 2 4 × 3

Разложение на простые множители 49: 7 2

Разложение на простые множители 50: 2 × 5 2

Разложение на простые множители 51: 3 × 17

Разложение на простые множители 52: 2 2 × 13

Разложение на простые множители 53: простое число

Разложение на простые множители 54: 2 × 3 3

Разложение на простые множители 55: 5 × 11

Разложение на простые множители 56: 2 3 × 7

Разложение на простые множители 57: 3 × 19

Разложение на простые множители 58: 2 × 29

Разложение на простые множители 59: простое число

Разложение на простые множители 60: 2 2 × 3 × 5

Разложение на простые множители 61: простое число

Разложение на простые множители 62: 2 × 31

Разложение на простые множители 63: 3 2 × 7

Разложение на простые множители 64: 2 6

Разложение на простые множители 65: 5 × 13

Разложение на простые множители 66: 2 × 3 × 11

Разложение на простые множители 67: простое число

Разложение на простые множители 68: 2 2 × 17

Разложение на простые множители 69: 3 × 23

Разложение на простые множители 70: 2 × 5 × 7

Разложение на простые множители 71: простое число

Разложение на простые множители 72: 2 3 × 3 2

Разложение на простые множители 73: простое число

Разложение на простые множители 74: 2 × 37

Разложение на простые множители 75: 3 × 5 2

Разложение на простые множители 76: 2 2 × 19

Разложение на простые множители 77: 7 × 11

Разложение на простые множители 78: 2 × 3 × 13

Разложение на простые множители 79: простое число

Разложение на простые множители 80: 2 4 × 5

Разложение на простые множители 81: 3 4

Разложение на простые множители 82: 2 × 41

Разложение на простые множители 83: простое число

Разложение на простые множители 84: 2 2 × 3 × 7

Разложение на простые множители 85: 5 × 17

Разложение на простые множители 86: 2 × 43

Разложение на простые множители 87: 3 × 29

Разложение на простые множители 88: 2 3 × 11

Разложение на простые множители 89: простое число

Разложение на простые множители 90: 2 × 3 2 × 5

Разложение на простые множители 91: 7 × 13

Разложение на простые множители 92: 2 2 × 23

Разложение на простые множители 93: 3 × 31

Разложение на простые множители 94: 2 × 47

Разложение на простые множители 95: 5 × 19

Разложение на простые множители 96: 2 5 × 3

Разложение на простые множители 97: простое число

Разложение на простые множители 98: 2 × 7 2

Разложение на простые множители 99: 3 2 × 11

Разложение на простые множители 100: 2 2 × 5 2

Разложение на простые множители 101: простое число

Разложение на простые множители 102: 2 × 3 × 17

Разложение на простые множители 103: простое число

Разложение на простые множители 104: 2 3 × 13

Разложение на простые множители 105: 3 × 5 × 7

Разложение на простые множители 106: 2 × 53

Разложение на простые множители 107: простое число

Разложение на простые множители 108: 2 2 × 3 3

Разложение на простые множители 109: простое число

Разложение на простые множители 110: 2 × 5 × 11

Разложение на простые множители 111: 3 × 37

Разложение на простые множители 112: 2 4 × 7

Разложение на простые множители 113: простое число

Разложение на простые множители 114: 2 × 3 × 19

Разложение на простые множители 115: 5 × 23

Разложение на простые множители 116: 2 2 × 29

Разложение на простые множители 117: 3 2 × 13

Разложение на простые множители 118: 2 × 59

Разложение на простые множители 119: 7 × 17

Разложение на простые множители 120: 2 3 × 3 × 5

Разложение на простые множители 121: 11 2

Разложение на простые множители 122: 2 × 61

Разложение на простые множители 123: 3 × 41

Разложение на простые множители 124: 2 2 × 31

Разложение на простые множители 125: 5 3

Разложение на простые множители 126: 2 × 3 2 × 7

Разложение на простые множители 127: простое число

Разложение на простые множители 128: 2 7

Разложение на простые множители 129: 3 × 43

Разложение на простые множители 130: 2 × 5 × 13

Разложение на простые множители 131: простое число

Разложение на простые множители 132: 2 2 × 3 × 11

Разложение на простые множители 133: 7 × 19

Разложение на простые множители 134: 2 × 67

Разложение на простые множители 135: 3 3 × 5

Разложение на простые множители 136: 2 3 × 17

Разложение на простые множители 137: простое число

Разложение на простые множители 138: 2 × 3 × 23

Разложение на простые множители 139: простое число

Разложение на простые множители 140: 2 2 × 5 × 7

Разложение на простые множители 141: 3 × 47

Разложение на простые множители 142: 2 × 71

Разложение на простые множители 143: 11 × 13

Разложение на простые множители 144: 2 4 × 3 2

Разложение на простые множители 145: 5 × 29

Разложение на простые множители 146: 2 × 73

Разложение на простые множители 147: 3 × 7 2

Разложение на простые множители 148: 2 2 × 37

Разложение на простые множители 149: простое число

Разложение на простые множители 150: 2 × 3 × 5 2

Разложение на простые множители 200: 2 3 × 5 2

Разложение на простые множители 300: 2 2 × 3 × 5 2

Разложение на простые множители 400: 2 4 × 5 2

Разложение на простые множители 500: 2 2 × 5 3

Разложение на простые множители 600: 2 3 × 3 × 5 2

Разложение на простые множители 700: 2 2 × 5 2 × 7

Разложение на простые множители 800: 2 5 × 5 2

Разложение на простые множители 900: 2 2 × 3 2 × 5 2

Разложение на простые множители 1000: 2 3 × 5 3

прайм-факторизация 65 | Подводя итоги65

.

Используйте форму ниже, чтобы выполнить преобразование, разделяя числа запятыми.

Факторы

Подводя итоги 65 = 5, 13

Дерево основных факторов из 65

65

/ \
5 13

/ \
13 1

Факторное дерево из 65 выше показывает уровень делений, выполненных для получения значений факторов. Изучите дерево, чтобы увидеть пошаговое деление

Факторизация простых чисел или целочисленная факторизация числа — это определение набора простых промежуточных чисел, которые умножаются вместе, чтобы получить исходное целое число.Это также известно как разложение на простые числа.

Преобразование в множители 65

Мы получаем целочисленное разложение 65, находя список простых чисел, которые могут делить число, вместе с их кратностями.

Это простые числа, которые могут делить 65 без остатка. Итак, первое число, которое следует принять во внимание, — 2

. Получение коэффициентов выполняется путем деления числа на числа меньшие по значению, чтобы найти тот, который не оставит остатка.Числа, которые делятся без остатка, являются множителями.

Разложение на простые множители отличается от простых чисел. простые числа — это целые числа, которые можно разделить само на себя и 1. например, 7 можно разделить само на себя и 1, так что это простое число.

Целые числа, которые можно разделить на другие числа, называются составными числами. Факторизация Prme выполняется для составных чисел, а не для простых чисел.

Первые 10 простых целых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29

.

Пример факторизации

Допустим, мы хотим найти простые множители 50.Мы начинаем тестировать все целые числа, чтобы увидеть, как часто они делят 50 и последующее результирующее значение. Результирующий набор множителей будет простым, поскольку, например, когда исчерпывается 2, все кратные 2 также будут исчерпаны.

50 ÷ 2 = 25; сохранить 2
25 ÷ 2 = 12,5, не целое число, поэтому попробуйте следующее наибольшее число, 3
25 ÷ 3 = 8,333, не целое число, поэтому попробуйте следующее наибольшее число, 4
25 ÷ 4 = 6,25, не целое число, поэтому попробуйте следующее наибольшее число, 5
25 ÷ 5 = 5; сохранить 5
5 ÷ 5 = 1; сохранить 5
Итак, 50 множителей = 2 x 5 x 5, что совпадает с 2 x 5 2

Инструкции:

  1. Введите число, которое вы хотите преобразовать.

    Разделяйте более 1 числа запятой.

  2. Нажмите, чтобы преобразовать в коэффициент

Другие числовые преобразования, которые следует учитывать

65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84

Goldendoodle boise

23 сентября 2007 г. · Бойсе. 1 десятилетие назад. Моя семья получила нашего Голдендудла в апреле, когда ему было 10 недель. Ему 8 месяцев, и он весит 65 фунтов. Он самая милая и самая симпатичная собака…

Parfait mischen goldendoodles. Качественные средние, миниатюрные и миниатюрные миниатюрные золотые ленточки GANA Goldendoodles с голубой лентой. В Parfait Mischen мы с энтузиазмом относимся к золоту.

Отель Sandy Ridge Goldendoodles расположен на юго-востоке штата Айова, в красивой долине реки Миссисипи. Наши щенки голдендуделя растут лучшими домашними животными для своих новых владельцев и хорошо социализированы. Эти goldendoodles привлекают много внимания со стороны большой семьи и выросли в спокойной сельской местности.

Программа служебных собак: звоните для получения более подробной информации и индивидуальных цен. Дрессировка домашних животных в служебных собак! Посетите нашу школу служебных собак

© 2018, Neesa’s Doodles — Голдендудлы, выросшие в Бойсе. Сайт создан на Wix. com. Дудлы Нисы — Продажа щенков мини-голдендудля в Бойсе ID.

Sand Hollow Doodles выращивает высококачественных Goldendoodles, Labradoodles, Spanish Water Doodles, Springerdoodles и Aussiedoodles. Наши щенки растут вместе со многими детьми, другими собаками, кошками и сельскохозяйственными животными в сельской местности в Парме, штат Айдахо.

Мать является зарегистрированным стандартным пуделем AKC, а отец — голдендудлем. Проверьте нашу вкладку с доступными щенками, чтобы узнать, какие щенки еще доступны! Если у вас есть какие-либо вопросы, не стесняйтесь звонить или писать по электронной почте.

щенков французского бульдога. Эти прекрасные щенки имеют обновленные вакцины и готовы стать вашим новым членом семьи. Свяжитесь со мной, только если вы следуете приведенным ниже критериям: \\ r \ — Увлечен французской породой. \\ r \ \\ r \ — Ответственный владелец, желающий узнать о французской породе бульдогов, чтобы иметь возможность обеспечить хороший уход и любящие дом для щенков. \\ r \ \\ r \ Я с нетерпением жду …

Приемная программа Save-A-Pet Программа патронатного воспитания позволяет Save-A-Pet удовлетворять особые потребности наших самых уязвимых животных. Смертельно больные, беременные, очень молодые животные или выздоравливающие после медицинской процедуры животные являются примерами ситуаций, в которых мы будем искать приемную семью. Save-A-Pet сохраняет право собственности на животных в…

Проблемы с качеством морского ската

Корабль 420 Aft Cabin несет в себе традиции качества и производительности Sea Ray.А с двумя внутренними дизельными двигателями Caterpillar 3116, она несет эту традицию в очень экзотические места. Ее роскошная обстановка, просторные помещения и превосходные мореходные качества создают условия для круиза, которые порадуют самого взыскательного яхтсмена.

Аральское море расположено в Центральной Азии, между южной частью Казахстана и северным Узбекистаном. Вплоть до третьей четверти 20 века это было четвертое по величине соленое озеро в мире, и в нем содержалось 10 граммов соли на литр.

В целом Sea Ray 275 — это хорошо сбалансированный пакет, идеальный для семейного ночевки или дневной лодки для толпы. Качество отделки было высоким, как и максимальная скорость 28 узлов, что неплохо для относительно тяжелой однодвигательной установки. Стоимость Sea Ray 275 Sundancer составляет 153 864 доллара США, включая носовое подруливающее устройство, или около 133 000 долларов США в базовой комплектации.

Лодки Sea Ray на продажу во Флориде, Калифорнии, Вашингтоне, Мэриленде. Экспресс-круизеры, Моторные яхты, Другое, Продажа палубных лодок.

Введите город или почтовый индекс, чтобы получить наиболее точный прогноз погоды.

25 апреля 2009 г. · Проблема с рулем направления 48´ Sea Ray У нас есть мост для седана Sea Ray 48´03, и на момент возникновения этой проблемы он проработал 918 часов. Похоже, что существует потенциально опасная проблема с установкой руля на этих лодках. И мне сказали, что все большие Sea Rays имеют одинаковый тип установки.

Мы хотели бы показать вам здесь описание, но сайт не позволяет нам.

«Делимость числа, делители и кратные», «Признаки делимости»

Самостоятельная работа №1 (I четверть) на темы: «Делимость числа, делители и кратные», «Признаки делимости»


Вариант I.
1. Задано число 28. Найдите все его делители. 

2. Заданы числа: 3, 6, 18, 23, 56. Выберите из них делители числа 4860. 

3. Заданы числа: 234, 564, 642, 454, 535. Выберите из них те, которые делятся на 3, 5, 7 без остатка. 

4. Найдите такое число х, чтобы 57x делилось без остатка на 5 и 7. 

5. Найдите такое число Y, которое удовлетворяет условиям:
а) 900 б) делится одновременно на 2, 4 и 7.

6. Найдите все делители числа 18, выберите из них числа, которым кратно число 20.

Вариант II. 
1. Задано число 39. Найдите все его делители. 

2. Заданы числа: 2, 7, 9, 21, 32. Выберите из них делители числа 3648. 

3. Заданы числа: 485, 560, 326, 796, 442. Выберите из них те, которые делятся на 2, 5, 8 без остатка. 

4. Найдите такое число х, чтобы 68x делилось без остатка на 4 и 9. 

5. Найдите такое число Y, которое удовлетворяет условиям:
а) 820 б) делится одновременно на 3, 5 и 6.

6. Напиши все делители для числа 24, выберите из них числа, которым кратно число 15.

Вариант III. 
1. Задано число 42. Найдите все его делители. 

2. Заданы числа: 5, 9, 15, 22, 30. Выберите из них делители числа 4510. 

3. Заданы числа: 392, 495, 695, 483, 196. Выберите из них те, которые делятся на 4, 6 и 8 без остатка. 

4. Найдите такое число х, чтобы 78x делилось без остатка на 3 и 8. 

5. Найдите такое число Y, которое удовлетворяет условиям:
а) 920 б) делится одновременно на 2, 6 и 9.

6. Напиши все делители для числа 32 и выберите из них числа, которым кратно число 30.

Ответы на самостоятельную работу №1 на тему: «Делимость числа, делители и кратные», «Признаки делимости» 

Самостоятельная работа №2 (I четверть): «Простые и составные числа», «Разложение на простые множители», «НОД и НОК»


Вариант I.
1. Разложите числа 28; 56 на простые множители. 

2. Определите, какие числа простые, а какие составные: 25, 37, 111, 123, 238, 345? 

3. Найдите все делители для числа 42.  

4. Найдите НОД для чисел:
а) 315 и 420;
б) 16 и 104.

5. Найдите НОК для чисел:
а) 4, 5 и 12;
б) 18 и 32.

6. Решите задачу.
У мастера есть 2 проволоки длиной 18 и 24 метра. Ему необходимо разрезать обе проволоки на куски равной длины без остатков. Какой длины получатся куски? 

Вариант II.
1. Разложите числа 36; 48 на простые множители. 

2. Определите, какие числа простые, а какие составные: 13, 48, 96, 121, 237, 340? 

3. Найдите все делители для числа 38. 

4. Найдите НОД для чисел:
а) 386 и 464;
б) 24 и 112.

5. Найдите НОК для чисел:
а) 3, 6 и 8;
б) 15 и 22.

6. Решите задачу.
В механическом цеху есть 2 трубы длиной 56 и 42 метра. На куски какой длины надо разрезать трубы, чтобы длина всех кусков была одинаковой? 

Вариант III. 
1. Разложите числа 58; 32 на простые множители. 

2. Определите, какие числа простые, а какие составные: 5, 17, 101, 133, 222, 314? 

3. Найдите все делители для числа 26. 

4. Найдите НОД для чисел:
а) 520 и 368;
б) 38 и 98.

5. Найдите НОК для чисел:
а) 4,7 и 9;
б) 16 и 24.

6. Решите задачу.
Ателье необходимо заказать рулон ткани для пошива костюмов. Какой длины надо заказать рулон, чтобы он без остатков делился на куски длиной 5 метров и 7 метров? 

Ответы на самостоятельную работу №2 на тему: «Простые и составные числа», «Разложение на простые множители», «НОД и НОК» 

Самостоятельная работа №3 (I четверть): «Основное свойство дроби, сокращение дробей», «Приведение дробей к общему знаменателю», «Сравнение дробей»


Вариант I. 
1. Сократите заданные дроби. Если дробь десятичная, то представьте её в виде обыкновенной дроби: 12⁄20; 18⁄24; 0,55; 0,82.

2. Задан ряд чисел: 12⁄20; 24⁄32; 0,70. Есть ли среди них число, равное числу3⁄4? 

3. Какую часть целого составляет часть?
а) 200 грамм от тонны;
б) 35 секунд от минуты;
в) 5 см от метра.

4. Приведите дробь 6⁄9 к знаменателю 54.

5. Приведите дроби к общему знаменателю.
а) 7⁄9 и 4⁄6;
б) 9⁄14 и 15⁄18.

6. Решите задачу.
Длина красного карандаша равна 5⁄8 дециметра, а длина синего карандаша равна 7⁄10дециметра. Какой карандаш длиннее?

7. Сравните дроби.
а) 4⁄5 и 7⁄10;
б) 9⁄12 и 12⁄16.

Вариант II.
1. Сократите заданные дроби. Если дробь десятичная, то представьте её в виде обыкновенной дроби: 18⁄22; 9⁄15; 0,38; 0,85.

2. Задан ряд чисел: 14⁄24; 2⁄4; 0,40. Есть ли среди них число, равное числу 2⁄5? 

3. Какую часть целого составляет часть?
а) 240 грамм от тонны;
б) 15 секунд от минуты;
в) 45 см от метра. 

4.Приведите дробь 7⁄8 к знаменателю 40.

5. Приведите дроби к общему знаменателю.
а) 3⁄7 и 6⁄9;
б) 8⁄14 и 12⁄16.

6. Решите задачу.
Мешок с картошкой весит 5⁄12 центнера, а мешок с зерном весит 9⁄17 центнера. Что легче: картошка или зерно?

7. Сравните дроби.
а) 7⁄8 и 3⁄4;
б) 7⁄15 и 23⁄25. 

Вариант III.
1. Сократите заданные дроби. Если дробь десятичная, то представьте её в виде обыкновенной дроби: 8⁄14; 16⁄20; 0,32; 0,15. 

2. Задан ряд чисел: 20⁄32;     10⁄18;     0,80;     6⁄20. Есть ли среди них число, равное числу 5⁄8? 

3. Какую часть целого составляет часть:
а) 450 грамм от тонны;
б) 50 секунд от минуты;
в) 3 дм от метра.

4. Приведите дробь 4⁄5 к знаменателю 30.

5. Приведите дроби к общему знаменателю. 
а) 2⁄5 и 6⁄7;
б) 3⁄12 и 12⁄18.

6. Решите задачу.
Одна машина весит 12⁄25 тонны, а вторая машина весит 7⁄18 тонны. Какая машина легче?

7. Сравните дроби.
а) 7⁄9 и 4⁄6; 
б) 5⁄7 и 8⁄10.

Ответы на самостоятельную работу №3 на тему: «Основное свойство дроби, сокращение дробей», «Приведение дробей к общему знаменателю», «Сравнение дробей»

6 класс. Математика. Разложение числа на множители — Разложение числа на множители

Комментарии преподавателя

Опре­де­ле­ния:

Про­стым на­зы­ва­ют число, ко­то­рое имеет ровно два раз­лич­ных де­ли­те­ля.

Со­став­ным на­зы­ва­ют число, ко­то­рое имеет более двух де­ли­те­лей.

Раз­ло­жить на­ту­раль­ное число на мно­жи­те­ли – зна­чит пред­ста­вить его в виде про­из­ве­де­ния на­ту­раль­ных чисел.

Раз­ло­жить на­ту­раль­ное число на про­стые мно­жи­те­ли – зна­чит пред­ста­вить его в виде про­из­ве­де­ния про­стых чисел.

За­ме­ча­ния:

  • В раз­ло­же­нии про­сто­го числа один из мно­жи­те­лей равен еди­ни­це, а дру­гой – са­мо­му этому числу.
  • Го­во­рить о раз­ло­же­нии еди­ни­цы на мно­жи­те­ли не имеет смыс­ла.
  • Со­став­ное число можно раз­ло­жить на мно­жи­те­ли, каж­дый из ко­то­рых от­ли­чен от 1.

Раз­ло­жим число 150 на мно­жи­те­ли. На­при­мер, 150 – это 15 умно­жить на 10.

15 – это со­став­ное число. Его можно раз­ло­жить на про­стые мно­жи­те­ли 5 и 3.

10 – это со­став­ное число. Его можно раз­ло­жить на про­стые мно­жи­те­ли 5 и 2.

За­пи­сав вме­сто 15 и 10 их раз­ло­же­ния на про­стые мно­жи­те­ли, мы по­лу­чи­ли раз­ло­же­ние числа 150.

 

Число 150 можно по-дру­го­му раз­ло­жить на мно­жи­те­ли. На­при­мер, 150 – это про­из­ве­де­ние чисел 5 и 30.

5 – число про­стое.

30 – это число со­став­ное. Его можно пред­ста­вить как про­из­ве­де­ние 10 и 3.

10 – число со­став­ное. Его можно раз­ло­жить на про­стые мно­жи­те­ли 5 и 2.

Мы по­лу­чи­ли раз­ло­же­ние числа 150 на про­стые мно­жи­те­ли дру­гим спо­со­бом.

 

За­ме­тим, что пер­вое и вто­рое раз­ло­же­ние оди­на­ко­вы. Они от­ли­ча­ют­ся толь­ко по­ряд­ком сле­до­ва­ния мно­жи­те­лей.

При­ня­то за­пи­сы­вать мно­жи­те­ли в по­ряд­ке воз­рас­та­ния.

Вся­кое со­став­ное число можно раз­ло­жить на про­стые мно­жи­те­ли един­ствен­ным об­ра­зом с точ­но­стью до по­ряд­ка мно­жи­те­лей.

При раз­ло­же­нии боль­ших чисел на про­стые мно­жи­те­ли ис­поль­зу­ют за­пись в стол­бик:

 

Наи­мень­шее про­стое число, на ко­то­рое де­лит­ся 216 – это 2.

Раз­де­лим 216 на 2. По­лу­чим 108.

По­лу­чен­ное число 108 де­лит­ся на 2.

Вы­пол­ним де­ле­ние. По­лу­чим в ре­зуль­та­те 54.

Со­глас­но при­зна­ку де­ли­мо­сти на 2 число 54 де­лит­ся на 2.

Вы­пол­нив де­ле­ние, по­лу­чим 27.

Число 27 за­кан­чи­ва­ет­ся на нечет­ную цифру 7 . Оно

Не де­лит­ся на 2. Сле­ду­ю­щее про­стое число – это 3.

Раз­де­лим 27 на 3. По­лу­чим 9. Наи­мень­шее про­стое

Число, на ко­то­рое де­лит­ся 9, – это 3. Три – само яв­ля­ет­ся про­стым чис­лом, оно де­лит­ся на себя и на еди­ни­цу. Раз­де­лим 3 на себя. В итоге мы по­лу­чи­ли 1.
  • Число де­лит­ся лишь на те про­стые числа, ко­то­рые вхо­дят в со­став его раз­ло­же­ния.
  • Число де­лит­ся лишь на те со­став­ные числа, раз­ло­же­ние ко­то­рых на про­стые мно­жи­те­ли пол­но­стью в нем со­дер­жит­ся.

Рас­смот­рим при­ме­ры:

4900 де­лит­ся на про­стые числа 2, 5 и 7. (они вхо­дят в раз­ло­же­ние числа 4900), но не де­лит­ся, на­при­мер, на 13.

 

1.                   

 

2.                  

.

 

11 550 75. Это так, по­то­му что раз­ло­же­ние числа 75 пол­но­стью со­дер­жит­ся в раз­ло­же­нии числа 11550.

В ре­зуль­та­те де­ле­ния будет про­из­ве­де­ние мно­жи­те­лей 2, 7 и 11.

 

11550 не де­лит­ся на 4 по­то­му, что в раз­ло­же­нии че­ты­рех есть лиш­няя двой­ка.

 

 

Раз­ло­же­ние числа b пол­но­стью со­дер­жит­ся в раз­ло­же­нии числа a.

 

 

Ре­зуль­тат де­ле­ния a на b – это про­из­ве­де­ние остав­ших­ся в раз­ло­же­нии числа a трех чисел.

Итак, ответ: 30.

источник конспекта — http://interneturok.ru/ru/school/matematika/6-klass/delimost-chisel/razlozhenie-chisla-na-mnozhiteli

источник видео — http://www.youtube.com/watch?v=_qNLLx9r3Q8

источник видео — http://www.youtube.com/watch?v=_p1q9NlMN9U

источник видео — http://www.youtube.com/watch?v=0qyAVdH-iaY

источник видео — http://www.youtube.com/watch?v=s-7EErDv7Eo

источник презентации — http://prezentacii.com/matematike/5900-razlozhenie-na-prostye-mnozhiteli.html

источник теста — http://testedu.ru/test/matematika/6-klass/prostyie-i-sostavnyie-chisla-razlozhenie-na-prostyie-mnozhiteli.html

820 | Найдите факторы

/ ivasallay / Оставить комментарий

Начнем с сегодняшней головоломки. После я расскажу вам немного о числе 820 и о том, почему я решил составить список всех чисел до 820 ровно с 12 множителями.

Распечатайте головоломки или введите решение в этом файле Excel: 12 факторов 815-820

 

Теперь немного информации о числе 820:

  • 820 — составное число.
  • Простая факторизация: 820 = 2 × 2 × 5 × 41, что можно записать как 820 = 2² × 5 × 41
  • Показатели степени в простой факторизации равны 2, 1 и 1. Прибавив к каждому единицу и умножив, мы получим (2 + 1)(1 + 1)(1 + 1) = 3 x 2 x 2 = 12. Следовательно, 820 имеет ровно 12 факторов.
  • Факторы 820: 1, 2, 4, 5, 10, 20, 41, 82, 164, 205, 410, 820
  • пар коэффициентов: 820 = 1 × 820, 2 × 410, 4 × 205, 5 × 164, 10 × 82 или 20 × 41
  • Взяв пару множителей с наибольшим квадратным множителем, мы получим √820 = (√4)(√205) = 2√205 ≈ 28,635642

820 это сумма двух квадратов двумя способами:

  • 28² + 6² = 820
  • 26² + 12² = 820

Поскольку 5 и 41 являются двумя его простыми множителями, 820 является гипотенузой ЧЕТЫРЕХ троек Пифагора:

  • 180-800-820, что в 20 раз больше 9-40-41
  • 336-748-820, что в 4 раза больше 84-187-205, но его также можно рассчитать как 2(28)(6), 28² – 6², 28² + 6²
  • 492-656-820 что 164 раза 3-4-5
  • 532-624-820, что в 4 раза больше 133-156-205, но его также можно рассчитать как 26² – 12², 2(26)(12),26² + 12²

Поскольку 820 = (40×41)/2, мы знаем, что 820 — это 40-е треугольное число, поэтому

  • 1 + 2 + 3 + . . . + 38 + 39 + 40 = 820

820 также является палиндромом по четырем другим основаниям:

  • 1010101 ОСНОВАНИЕ 3, потому что 3⁶+3⁴+3²+3⁰=820
  • 1111 ОСНОВАНИЕ 9, потому что 9³+9²+9¹+9⁰=820
  • 868 ОСНОВАНИЕ 11, потому что 8(11²)+6(11¹)+8(11⁰)=820
  • 1I1 ОСНОВАНИЕ 21 (I равно 18 по основанию 10), потому что 21²+18(21¹)+21⁰=820

Ниже приведена таблица чисел до 820 ровно с 12 факторами. Обратите внимание, что в списке присутствуют два набора последовательных чисел (735, 736) и (819, 820). Посмотрите на их простые факторизации:

  • 735=3×5×7², 736=2⁵×23
  • 819=3²×7×13, 820=2²×5×41

Эти простые факторизации означают, что хотя 735 и 736 являются наименьшими последовательными числами, имеющими ровно 12 множителей, 819 и 820 — наименьшие последовательные числа, простые факторизации которых состоят из квадрата одного простого числа и ровно двух других простых чисел. Спасибо OEIS. org за предупреждение об этом факте. Вот кое-что интересное о диаграмме: из 77 перечисленных чисел только шесть являются нечетными.

Итак, как я узнал, какие числа нужно внести в список?

Чтобы определить, сколько чисел до 820 имеют ровно 12 множителей, мы должны сначала разложить 12. Мы знаем, что 12=12, 6×2, 4×3 и 3×2×2.

Затем мы вычитаем 1 из каждого из этих множителей, чтобы определить степень, которую нам нужно использовать:

12 дает нам 12-1= 11 . Для простого числа a, когда ¹¹ не больше 820? Никогда, потому что 2 ¹¹ >820.

6×2 дает нам 6-1= 5 и 2-1=1. Для простых чисел a и b, где a≠b, когда a ⁵ b¹ меньше или равно 820? Эти девять раз:

  • 2 ⁵ × 3 = 96, 2 ⁵ × 5 = 160, 2 ⁵ × 7 = 224, 2 ⁵ × 11 = 352,
  • 2 ⁵ × 13 = 416, 2 ⁵ × 17 = 544, 2 ⁵ × 19 = 608, 2 ⁵ × 23 = 736
  • 3 ⁵ × 2=486

4×3 дает нам 4-1= 3 и 3-1= 2 . Для простых чисел a и b, где a≠b, когда a ³ b ² не больше 820? Эти шесть раз:

  • 2 ³ × 3 ² = 72, 2 ³ × 5 ² = 200, 2 ³ × 7 ² =392
  • 3 ³ ×2 ² =108, 3 ³ ×5 ² =675
  • 5 ³ ×2 ² =500

3×2×2 дает нам 3-1= 2 , 2-1=1 и 2-1=1. Когда для различных простых чисел a, b и c число ² bc не больше 820? 52 раза. Вот разбивка: Это происходит 35 раз, когда 2 ² = 4 является квадратом числа:

И это происходит еще 27 раз, когда возводится в квадрат простое число, отличное от 2:

 

Это множество чисел с ровно 12 делителями! После того, как я отсортировал все числа, которые я нашел, в числовом порядке, я смог составить таблицу чисел до 820 ровно с 12 делителями, и да, 819 и 820 — наименьшие два последовательных числа, простая факторизация которых состоит ровно из одного простого числа. квадрат и два других простых числа.

Ищи:
  • 13 659 380 просмотров

Введите свой адрес электронной почты, чтобы следить за этим блогом и получать уведомления о новых сообщениях по электронной почте.

Адрес электронной почты

Присоединяйтесь к 1907 другим подписчикам

820 (номер)

820 ( восемьсот двадцать ) — четное трехзначное составное число после 819 и перед 821. В научной записи оно записывается как 8,2 × 10 2 . Сумма его цифр равна 10. Всего у него 4 простых делителя и 12 положительных делителей. Существует 320 натуральных чисел (до 820), взаимно простых с 820.

  • Прайм? №
  • Числовая четность Четный
  • Длина номера 3
  • Сумма цифр 10
  • Цифровой корень 1

Краткое наименование 820
Полное имя восемьсот двадцать

Научное обозначение 8,2 × 10 2
Инженерное обозначение 820 × 10 0

Простые множители 2 2 × 5 × 41

Составное число

ω(н) Отличительные факторы 3

Общее количество различных простых множителей

Ом(n) Всего факторов 4

Общее количество простых множителей

рад(н) Радикальный 410

Произведение различных простых чисел

λ(n) Лиувилль Лямбда 1

Возвращает четность Ω(n), такую ​​что λ(n) = (-1) Ω(n)

мк(н) Мебиус Мю 0

Возвращает:

  • 1, если n имеет четное число простых множителей (и не содержит квадратов)
  • −1, если n имеет нечетное число простых множителей (и не содержит квадратов)
  • 0, если n имеет квадрат простого делителя
Л(н) Функция Мангольдта 0

Возвращает log(p), если n является степенью p k любого простого числа p (для любого k >= 1), в противном случае возвращает 0

Разложение числа 820 на простые множители равно 2 2 × 5 × 41. Поскольку оно имеет в общей сложности 4 простых делителя, 820 является составным числом.

1, 2, 4, 5, 10, 20, 41, 82, 164, 205, 410, 820

12 делителей

Четный делитель 8
Нечетные делители 4
4k+1 делитель 4
4k+3 делителя 0

τ(n) Всего делителей 12

Общее число положительных делителей n

σ(n) Сумма делителей 1764

Сумма всех положительных делителей n

с(н) Аликвотная сумма 944

Сумма собственных положительных делителей n

А(н) Среднее арифметическое 147

Возвращает сумму делителей (σ(n)), деленную на общее количество делителей (τ(n))

Г(н) Среднее геометрическое 28. 635642126553

Возвращает корень n из произведения n делителей

Н(н) Среднее гармоническое 5,5782312

Возвращает общее количество делителей (τ(n)), деленное на сумму обратной величины каждого делителя

Число 820 можно разделить на 12 положительных делителей (из них 8 четных и 4 нечетных). Сумма этих делителей (считая 820) равна 1764, среднее значение равно 147.

1 ф (п) п

ф(н) Эйлер Тотиент 320

Общее количество положительных целых чисел не больше n, взаимно простых с n

λ(n) Кармайкл Лямбда 40

Наименьшее положительное число такое, что λ(n) ≡ 1 (mod n) для всех чисел, взаимно простых с n

п(н) Прайм Пи ≈ 145

Общее количество простых чисел меньше или равно n

р 2 (н) Сумма 2 квадратов 16

Количество способов n представить в виде суммы двух квадратов

Существует 320 натуральных чисел (меньше 820), взаимно простых с 820. И приблизительно 145 простых чисел меньше или равны 820.

м 2 3 4 5 6 7 8 9
п мод м 0 1 0 0 4 1 4 1

Число 820 делится на 2, 4 и 5.

Арифметическими функциями

  • Арифметика
  • Обильный

Выражается через конкретные суммы

  • Вежливый
  • Практический

По форме (2D, не по центру)

  • Треугольник

По форме (2D, по центру)

  • Центрированный неугольный
Основание Система Значение
2 Двоичный 1100110100
3 Тернарный 1010101
4 Четвертичный 30310
5 Квинари 11240
6 Сенар 3444
8 Восьмеричный 1464
10 Десятичный 820
12 Двенадцатеричный 584
16 Шестнадцатеричный 334
20 Десятичное число 210
36 База36 мс

Умножение

п × у
n×2 1640
n×3 2460
n×4 3280
n×5 4100

Отдел

n÷y
н÷2 410. 000
н÷3 273,333
н÷4 205.000
н÷5 164.000

Возведение в степень

п г
п 2 672400
п 3 551368000
нет 4 452121760000
п 5 370739843200000

N-й корень

г √н
2 √n 28. 635642126553
3 √n 9.35931412
4 √n 5.3512280951715
5 √n 3,8261568578659

Круг

Радиус = n

Диаметр 1640
Окружность 5152.2119518873
Зона 2112406.
  • 38

    • Сфера

    Радиус = n

    Том 2309564877. 6327
    Площадь поверхности 8449627.6010951
    Окружность 5152.2119518873

    Квадрат

    Длина = n

    Периметр 3280
    Зона 672400
    Диагональ 1159.6551211459

    Куб

    Длина = n

    Площадь поверхности 4034400
    Том 551368000
    Пространственная диагональ 1420. 2816622065

    Равносторонний треугольник

    Длина = n

    Периметр 2460
    Зона 2

    .74075233

    Высота над уровнем моря 710.14083110324

    Треугольная пирамида

    Длина = n

    Площадь поверхности 1164630.9630093
    Том 64979341.954877
    Высота 669,52719636074

    мд5 e2a2dcc36a08a345332c751b2f2e476c
    ша1 4b68e45a767407ba32c8a08340a8ad86e654cfca
    ша256 edbad80a93adb5830afc3fccfe0e7c27a81359b59bb2a8c277f95d4adec7c389
    ша512 d038d7dbcab7ad40d5d231f88be26

    9be8572708e1194633bdb2254115d09e39341f014d9275e864e1e6af8717a2e0e388448a9fcca729d885d02e39341f014d9275e864e1e6af8717a2e0e388448a9fcca729d885d02e39341f014d9275e864e1e6af8717a2e0e388448a9fcca729d885d02e39341f014d9275e864e1e6af8717a2e0e388448a9fcca729d885d02e39341
    римед-160 2ee2d2f656474bc2bb4b19584a91fa96c055113b

    Наибольший общий делитель чисел 820 и 824

    Существует множество методов, которые мы можем применить для вычисления НОД чисел 820 и 824.

    В нашем первом методе мы найдем разложение чисел 820 и 824 на простые множители.

    Во втором методе мы создадим список всех множителей чисел 820 и 824.

    Это числа, на которые числа 820 и 824 делятся без остатка.

    Когда они у нас есть, все, что нам нужно сделать, это найти тот, который является самым большим общим числом из 2 списков.

    Теперь давайте рассмотрим каждый метод и рассчитаем GCF для 820 и 824.

    • Факторизация простых чисел
    • Список факторов
    • Алгоритм Евклида
    • Двоичный алгоритм наибольшего общего делителя

    Метод 1 — Факторизация простых чисел

    При использовании метода факторизации простых чисел все, что нам нужно сделать, это найти общие простые делители чисел 820 и 824, а затем перемножить их. Очень просто:

    Шаг 1: Давайте создадим список всех простых делителей чисел 820 и 824:
    Простые делители числа 820:

    Как вы можете видеть ниже, простые делители числа 820 — это 2, 2, 5 и 41 .

    Давайте проиллюстрируем простую факторизацию 820 в экспоненциальной форме:

    820 = 2 2 x5 1 X41 1

    Прайские факторы 824:

    Как вы можете видеть ниже, основные факторы 824 — 2, 2, 2 и 103 .

    Давайте проиллюстрируем простую факторизацию 824 в экспоненциальной форме:

    824 = 2 3 x103 1


    Шаг 2: Запишите список всех общих простых делителей чисел 820 и 824:

    Как видно из приведенных выше блоков, общие простые делители чисел 820 и 824 равны 2 и 2. .


    Шаг 3: Все, что нам нужно сделать сейчас, это перемножить эти общие простые множители:

    Найти произведение всех общих простых множителей путем их умножения:

    2 2 = 4

    Готово!

    Согласно нашим расчетам выше, Наибольший общий делитель чисел 820 и 824 равен 4

    Метод 2.

    Список делителей

    С помощью этого простого метода нам нужно найти все делители чисел 820 и 824, Факторы — это числа, которые делят другое число без остатка и просто определяют общие, а затем выбирают, какое из них больше.


    Шаг 1: Создайте список всех чисел, которые делят 820 и 824 без остатка:

    Перечень делящих множителей 820 без остатка:

    1, 2, 4, 5, 10, 20, 41, 82, 164, 205, 410 и 820 .

    Список факторов, которые делят 824 без остатка:

    1, 2, 4, 8, 103, 206, 412 и 824 .


    Шаг 2: Определите наибольшее общее число из двух приведенных выше списков:

    Как видно в списках множителей сверху, для чисел 820 и 824 мы выделили число 4 , а это значит, что мы нашли Наибольший Общий Делитель, или НОД.

    Согласно нашим вычислениям выше, Наибольший общий делитель 820 и 824 равен 4

    Метод 3 — алгоритм Евклида

    Алгоритм Евклида говорит, что если число k является GCM 820 и 824, тогда число k также является НОД остатка от деления чисел 820 и 824.

    Мы выполняем эту процедуру до тех пор, пока напоминание не станет равным 0.

    Наибольший общий делитель — это последнее ненулевое число.


    Шаг 1: Отсортируйте числа в порядке возрастания:

    820, 824

    Шаг 2

    Выньте из набора меньшее число в порядке делителя: 820

    Оставшийся набор равен 90:004

    Найти напоминание о делении числа на делитель

    824 по модулю 820 = 4

    Соберите делитель и все остатки и отсортируйте их в порядке возрастания. Удалите все дубликаты и 0. Наш набор:

    4, 820

    Повторяйте процесс, пока в наборе не останется только одно число.

    Выньте из набора меньшее число как делитель: 4

    Оставшийся набор: 820

    Найдите напоминание о делении между числом и делителем

    820 по модулю 4 = 0

    Соберите делитель и все остатки и отсортируйте их в порядке возрастания. Удалите все дубликаты и 0. Наш набор:

    4

    Шаг 3: Возьмите оставшееся число из нашего набора

    Наибольший общий делитель чисел 820 и 824 равен 4

    Метод 4. Двоичный алгоритм наибольшего общего делителя наибольший общий делитель двух целых неотрицательных чисел. Алгоритм Штейна использует более простые арифметические операции, чем обычный алгоритм Евклида; он заменяет деление арифметическими сдвигами, сравнениями и вычитанием.

    Хотя алгоритм в его современной форме был впервые опубликован израильским физиком и программистом Йозефом Штейном в 1967 году, он мог быть известен во II веке до н. э. в древнем Китае.

    Шаг 1: Отсортируйте числа и установите начальный GCF равным 1

    Список: 820, 824

    Шаг 2: Все числа четные.

    Разделите их все на 2 и умножьте GCF на 2.
    Удалите дубликаты и отсортируйте.
    Повторите процесс, если все числа четные:

    Результирующий список: 410, 412

    GCF = 1*2 = 2

    Результирующий список: 205, 206

    GCF = 2*2 = 4


    Шаг 3: Разделите все оставшиеся четные значения на 2, удалите дубликаты и отсортируйте.

    Повторите процесс, если в списке есть четные номера:

    206/2 = 103

    Полученный список: 103, 205

    Шаг 4: Выберите первое число, 103.

    Вычтите 103 из оставшихся значений и разделите результат на 2.
    Удалить дубликаты и отсортировать:

    (205-103)/2 = 51

    Полученный список: 51, 103

    Шаг 5: Выберите первое число, 51.

    Вычтите 51 из оставшихся значений и разделите результат на 2.
    Удалите дубликаты и сортировка:

    (103-51)/2 = 26

    Результирующий список: 26, 51

    Шаг 6: Разделите все оставшиеся четные значения на 2, удалите дубликаты и отсортируйте.

    Повторите процесс, если в списке есть четные числа:

    26/2 = 13

    Результирующий список: 13, 51

    Шаг 7: Выберите первое число, 13.

    Вычтите 13 из оставшихся значений и разделите результат на 2.
    Удалите дубликаты и отсортируйте:

    (51-13)/2 = 19

    Полученный список: 13, 19

    Шаг 8: Выберите первое число, 13.

    Вычтите 13 из оставшихся значений и разделите результат на 2.
    Удалите дубликаты и сортировка:

    (19-13)/2 = 3

    Результирующий список: 3, 13

    Шаг 9: Выберите первое число, 3.

    Вычтите 3 из оставшихся значений и разделите результат на 2.
    Удалите дубликаты и отсортируйте:

    (13-3)/2 = 5

    Полученный список: 3, 5

    Шаг 10: Выберите первое число, 3.

    Вычтите 3 из оставшихся значений и разделите результат на 2.
    Удалите дубликаты и сортировка:

    (5-3)/2 = 1

    Полученный список: 1, 3

    Шаг 11: Выберите первое число, 1.

    Вычтите 1 из оставшихся значений и разделите результат на 2.
    Удалить дубликаты и отсортировать:

    (3-1)/2 = 1

    Полученный список: 1

    Шаг 12: Остается только одно число, 1.

    Умножьте его на ваш текущий GCF:

    GCF = 4*1 = 4

    The Greatest Common Factor of 820 and 824 is 4

    Other Greatest Common Factors of 820

    GCF of 820 and 824

    GCF of 820 and 825

    GCF of 820 и 826

    GCF 820 и 827

    GCF 820 и 828

    GCF 820 и 829

    GCF 820 и 830

    GCF 820 и 831

    GCF 820 и 832

    GCF из 820 и 833

    Остальные общие факторы 824

    7

    474. 824 и 8248848888 и 824

    47784 и 824848886 82484 и 824 82484 и 824 82484 и 824 82484 и 824 824784 и 832.

    GCF of 824 and 829

    GCF of 824 and 830

    GCF of 824 and 831

    GCF of 824 and 832

    GCF of 824 and 833

    GCF of 824 and 834

    GCF of 824 and 835

    GCF из 824 и 836

    GCF 824 и 837

    HCF и LCM 24 и 820 (простая факторизация, метод деления, метод листинга)

    • Главная
    • Найти HCF и LCM 24 и 820

    4 = 4 и НОК = 4920

    Пошаговое решение:

    Содержание:

    1. Метод простой факторизации:
      1. Простые множители 24 и 820
      2. Метод простой факторизации 24 и 82
      3. LCM 24 и 820 методом простой факторизации
    2. Метод деления:
      1. HCF 24 и 820 методом деления
      2. LCM 24 и 820 методом деления
    3. 0 90 Метод
    4. Связанные задачи на HCF и LCM 24 и 820
    Метод простой факторизации:

    Заданные числа = 24 и 820

    Чтобы найти HCF и LCM методом простой факторизации, сначала мы найдем простые делители заданных чисел.

    Простая факторизация числа 24:
    24 = 2 × 12
    = 2 × 2 × 6
    = 2 × 2 × 2 × 3 2 × 205
    = 2 × 2 × 5 × 41

    HCF 24 и 820 методом простой факторизации:

    Общие множители в приведенных выше простых множителях данных чисел подчеркнуты.

    Общие простые множители = 2, 2

    Теперь нам нужно умножить эти общие простые множители, чтобы получить HCF заданных чисел.

    HCF = 2 × 2
    = 4

    ∴ HCF(24, 820) = 4

    НОК 24 и 820 методом простой факторизации:

    Теперь, чтобы найти НОК, мы запишем, сколько раз каждый фактор произошло в вышеупомянутых простых делителях данных чисел.

    NumbersPrime
    Factors    		 24 820 Max
    occurrence
    2 3 2 3
    3 1 0 1
    5 0 1 1
    41 0 1 1

    In above table we также отметили максимальное вхождение каждого множителя в простые множители заданных чисел.

    Теперь, чтобы получить НОК заданных чисел, мы умножим каждый коэффициент на максимальное количество раз, которое оно встречается в приведенной выше таблице.

    LCM = 2 × 2 × 2 × 3 × 5 × 41
    = 4920

    ∴ LCM (24, 820) = 4920

    Метод дивизии:
    HCF 24 и 820 Метод дивизии:

    92929.
    24 820 34
    -816
    4 24 6
    -24
    0

    В приведенном выше делении последний делитель равен 4.

    Следовательно, HCF(GCD) 24 и 820 = 4

    ∴ HCF(24, 820) = 4

    LCM 24 и 820 по методу деления

    2 24 820
    2 12 410
    2 6 205
    3 3 205
    5 1 205
    41 1 41
    1 1

    LCM = 2 × 2 × 2 × 3 × 5 × 41
    = 4920

    ∴ LCM(24, 820) = 4920

    HCF 24 и 820 с помощью метода перечисления факторов:

    Чтобы найти HCF методом перечисления факторов, мы перечислим все факторы заданных чисел.

    Коэффициенты 24:

    1234681224

    Коэффициенты 820:

    124510204182164205410820

    Наибольшим общим делителем в приведенных выше списках будет HCF заданных чисел.

    4 — это наибольший коэффициент, который встречается в приведенных выше списках.

    ∴ HCF(24, 820) = 4

    Если HCF двух чисел равен 4, а их произведение равно 19680, какова их НОК?

    Решение:

    Дано:
    ДКФ = 4
    Произведение чисел = 19680
    ∵ ДКФ × НОК = произведение чисел
    ∴ 4 × НОК = 24 × 820
    ∴ 4 × НОК = 19680
    ∴ НОК = 19680⁄4
    ∴ НОК = 4920

    Если НОК двух чисел равен 4920, а их произведение равно 19680, какова их ДКФ?

    Решение:

    Дано:
    LCM = 4920
    Продукт чисел = 19680
    ∵ HCF × LCM = продукт чисел
    ∴ HCF × 4920 = 24 × 820
    ∴ HCF × 4920 = 19680
    ∴ HCF = 19680 ∴ 4920 ∴ 4920 = 19680
    .
    ∴ HCF = 4

    HCF и LCM двух чисел равны 4 и 4920 соответственно.
    Если одно число равно 24, какое другое число?

    Решение:

    Пусть другое число будет x .
    Дано:
    HCF(24, x ) = 4
    LCM(24, x ) = 4920
    ∵ HCF × LCM = произведение чисел x
    ∴ 19680/24 = x
    ∴ x = 820
    Следовательно, второе число равно 820.

    Если HCF и LCM двух чисел равны 4 и 4920 соответственно, каково их произведение?

    Решение:

    Дано:
    HCF = 4
    LCM = 4920
    ∵ HCF × LCM = произведение чисел
    ∴ 4 × 4920 = произведение чисел
    ∴ произведение чисел = 19680
    Следовательно, произведение чисел равно 19680.

    ← Предыдущее

    Найти LCM 862 и 994
    HCF (GCD или GCF) и LCM 862 и 994 методом простой факторизации, методом деления и методом перечисления факторов.

    Далее →

    Найдите HCF и LCM 24 и 822
    HCF(GCD или GCF) и LCM 24 и 822 с помощью метода простой факторизации, метода деления и метода перечисления факторов.

    Связанные проблемы

    Найдите HCF и LCM 290 и 344
    HCF (GCD или GCF) и LCM 290 и 344 с помощью метода простой факторизации, метода деления и метода перечисления факторов.

    Найдите HCF и LCM 18 и 75
    HCF (GCD или GCF) и LCM 18 и 75 с помощью метода простой факторизации, метода деления и метода перечисления факторов.

    Найдите HCF и LCM 926 и 984
    HCF (GCD или GCF) и LCM 926 и 984 с помощью метода простой факторизации, метода деления и метода перечисления факторов.

    Найдите HCF и LCM 44 и 90
    HCF (GCD или GCF) и LCM 44 и 90 с помощью метода простой факторизации, метода деления и метода перечисления факторов.

    Найти HCF и LCM 23, 89 и 101
    HCF(GCD или GCF) и LCM 23, 89 и 101

    Найти HCF и LCM 228 и 642
    HCF(GCD или GCF) и LCM 228 и 642 методом простой факторизации, методом деления и методом перечисления факторов.

    Найти HCF и LCM 850 и 988
    HCF (GCD или GCF) и LCM 850 и 988 с помощью метода простой факторизации, метода деления и метода перечисления факторов.

    Найдите HCF и LCM 34 и 818
    HCF(GCD или GCF) и LCM 34 и 818 с помощью метода простой факторизации, метода деления и метода перечисления факторов.

    Найдите HCF и LCM 894 и 918
    HCF(GCD или GCF) и LCM 894 и 918 с помощью метода простой факторизации, метода деления и метода перечисления факторов.

    Найти HCF и LCM 142 и 184
    HCF (GCD или GCF) и LCM 142 и 184 с помощью метода простой факторизации, метода деления и метода перечисления факторов.

    Найдите HCF и LCM 150 и 174
    HCF (GCD или GCF) и LCM 150 и 174 с помощью метода простой факторизации, метода деления и метода перечисления факторов.

    Найдите HCF и LCM 520 и 580
    HCF(GCD или GCF) и LCM 520 и 580 с помощью метода простой факторизации, метода деления и метода перечисления факторов.

    Найти HCF и LCM 24 и 27
    HCF (GCD или GCF) и LCM, равные 24 и 27, с помощью метода простой факторизации, метода деления и метода перечисления множителей/метода перечисления множителей

    Найдите HCF и LCM 126 и 166
    HCF (GCD или GCF) и LCM 126 и 166 методом простой факторизации, методом деления и методом перечисления факторов.

    Найдите HCF и LCM 24 и 50
    HCF (GCD или GCF) и LCM 24 и 50 с помощью метода простой факторизации, метода деления и метода перечисления факторов.

    Найдите HCF и LCM 28 и 300
    HCF(GCD или GCF) и LCM 28 и 300 с помощью метода простой факторизации, метода деления и метода перечисления факторов.

    Найдите HCF и LCM 878 и 982
    HCF(GCD или GCF) и LCM 878 и 982 с помощью метода простой факторизации, метода деления и метода перечисления факторов.

    Найдите HCF и LCM 82 и 284
    HCF(GCD или GCF) и LCM 82 и 284 с помощью метода простой факторизации, метода деления и метода перечисления факторов.

    Найдите HCF и LCM 860 и 956
    HCF (GCD или GCF) и LCM 860 и 956 с помощью метода простой факторизации, метода деления и метода перечисления факторов.

    Найдите HCF и LCM 47, 67 и 97
    HCF (GCD или GCF) и LCM 47, 67 и 97

    Другие практические проблемы

    Безопасность и эффективность AMG 820, фактора против колониестимулирования 1 антитело к рецептору в комбинации с пембролизумабом у взрослых с прогрессирующими солидными опухолями

    . 2020 окт;8(2):e001006.

    doi: 10.1136/jitc-2020-001006.

    Албируни Ра Разак 1 , Джеймс М Клири 2 , Виктор Морено 3 , Майкл Бойер 4 , Эмилиано Кальво Аллер 5 , Уильям Эденфилд 6 , Жанна Галстук 7 , Р. Дональд Харви 8 , Аннеми Руттен 9 , Маниш А Шах 10 , Энтони Дж. Ольшански 11 , Дирк Ягер 12 , Нехал Лакхани 13 , Дэвид П Райан 14 , Эрик Расмуссен 15 , Глория Хуан 15 , Хансен Вонг 16 , Нилеш Соман 15 , Мари-Энн Дэмьетт Смит 15 , Дирк Нагорсен 15 , Кириакос П Пападопулос 17

    Принадлежности

    • 1 Отделение медицинской онкологии и гематологии, Университетская сеть здравоохранения, Онкологический центр принцессы Маргарет, Торонто, Онтарио, Канада.
    • 2 Отделение медицинской онкологии, Онкологический институт Дана-Фарбер, Бостон, Массачусетс, США.
    • 3 Отделение ранней фазы START Madrid-FJD, Servicio de Oncología Médica, Университетская больница Fundación Jimenez Díaz, Мадрид, Испания.
    • 4 Отделение медицинской онкологии, Chris O’Brien Lifehouse, Кампердаун, Новый Южный Уэльс, Австралия.
    • 5 Ранняя фаза клинической разработки лекарств в онкологии, START Madrid – CIOCC, Centro Integral Oncológico Clara Campal, Мадрид, Испания.
    • 6 Институт трансляционных онкологических исследований Prisma Health, Гринвилл, Южная Каролина, США.
    • 7 Отделение медицинской онкологии, Онкологический центр Питера МакКаллума, Мельбурн, Виктория, Австралия.
    • 8 Отделение гематологии и медицинской онкологии, Онкологический институт Уиншип университетской больницы Эмори, Атланта, Джорджия, США.
    • 9 GasthuisZusters Antwerpen Sint-Augustinus, Антверпен, Бельгия.
    • 10 Медицинский факультет, Отделение гематологии и медицинской онкологии, Служба солидных опухолей, Weill Cornell Medicine, Нью-Йорк, Нью-Йорк, США.
    • 11 Отделение гематологии/онкологии, Онкологический центр Фокс Чейз, Филадельфия, Пенсильвания, США.
    • 12 Отделение медицинской онкологии, Национальный центр онкологических заболеваний Гейдельберга, Гейдельберг, Германия.
    • 13 Developmental Cancer Therapeutics, START Midwest, Гранд-Рапидс, Миссури, США.
    • 14 Отделение гематологии/онкологии Массачусетской больницы общего профиля, Бостон, Массачусетс, США.
    • 15 Amgen Inc, Таузенд-Оукс, Калифорния, США.
    • 16 Amgen Inc, Южный Сан-Франциско, Калифорния, США.
    • 17 Клинические исследования, Южный Техас Центр ускоренных исследований в области терапии (START), Сан-Антонио, Техас, США [email protected].
    • PMID: 33046621
    • PMCID: PMC7552843
    • DOI: 10. 1136/jitc-2020-001006

    Бесплатная статья ЧВК

    Альбируни Ра Разак и др. J Иммунный рак. 2020 9 октября0007

    Бесплатная статья ЧВК

    . 2020 окт;8(2):e001006.

    doi: 10.1136/jitc-2020-001006.

    Авторы

    Альбируни Ра Разак 1 , Джеймс М Клири 2 , Виктор Морено 3 , Майкл Бойер 4 , Эмилиано Кальво Аллер 5 , Уильям Эденфилд 6 , Галстук Жанны 7 , Р. Дональд Харви 8 , Аннеми Руттен 9 , Маниш А Шах 10 , Энтони Дж. Ольшански 11 , Дирк Ягер 12 , Нехал Лакхани 13 , Дэвид П Райан 14 , Эрик Расмуссен 15 , Глория Хуан 15 , Хансен Вонг 16 , Нилеш Соман 15 , Мари-Энн Дэмьетт Смит 15 , Дирк Нагорсен 15 , Кириакос П Пападопулос 17

    Принадлежности

    • 1 Отделение медицинской онкологии и гематологии, Университетская сеть здравоохранения, Онкологический центр принцессы Маргарет, Торонто, Онтарио, Канада.
    • 2 Отделение медицинской онкологии, Онкологический институт Дана-Фарбер, Бостон, Массачусетс, США.
    • 3 Отделение ранней фазы START Madrid-FJD, Servicio de Oncología Médica, Университетская больница Fundación Jimenez Díaz, Мадрид, Испания.
    • 4 Отделение медицинской онкологии, Chris O’Brien Lifehouse, Кампердаун, Новый Южный Уэльс, Австралия.
    • 5 Ранняя фаза клинической разработки лекарств в онкологии, START Madrid – CIOCC, Centro Integral Oncológico Clara Campal, Мадрид, Испания.
    • 6 Институт трансляционных онкологических исследований Prisma Health, Гринвилл, Южная Каролина, США.
    • 7 Отделение медицинской онкологии, Онкологический центр Питера МакКаллума, Мельбурн, Виктория, Австралия.
    • 8 Отделение гематологии и медицинской онкологии, Онкологический институт Уиншип университетской больницы Эмори, Атланта, Джорджия, США.
    • 9 GasthuisZusters Antwerpen Sint-Augustinus, Антверпен, Бельгия.
    • 10 Медицинский факультет, Отделение гематологии и медицинской онкологии, Служба солидных опухолей, Weill Cornell Medicine, Нью-Йорк, Нью-Йорк, США.
    • 11 Отделение гематологии/онкологии, Онкологический центр Фокс Чейз, Филадельфия, Пенсильвания, США.
    • 12 Отделение медицинской онкологии, Национальный центр онкологических заболеваний Гейдельберга, Гейдельберг, Германия.
    • 13 Developmental Cancer Therapeutics, START Midwest, Гранд-Рапидс, Миссури, США.
    • 14 Отделение гематологии/онкологии Массачусетской больницы общего профиля, Бостон, Массачусетс, США.
    • 15 Amgen Inc, Таузенд-Оукс, Калифорния, США.
    • 16 Amgen Inc, Южный Сан-Франциско, Калифорния, США.
    • 17 Клинические исследования, Южный Техас Центр ускоренных исследований в области терапии (START), Сан-Антонио, Техас, США [email protected].
    • PMID: 33046621
    • PMCID: PMC7552843
    • DOI: 10. 1136/jitc-2020-001006

    Абстрактный

    Фон: Определить безопасность и эффективность моноклонального антитела AMG 820 против рецептора колониестимулирующего фактора 1 (анти-CSF1R) в комбинации с пембролизумабом у пациентов с отдельными солидными опухолями.

    Пациенты и методы: Пациенты имели запущенный, рефрактерный колоректальный рак, рак поджелудочной железы или немелкоклеточный рак легкого (НМРЛ) с низкой (<50%) экспрессией лиганда запрограммированной гибели клеток 1 (PD-L1) и не получали анти- запрограммированная гибель клеток-1 (PD-1)/PD-L1 или рецидивирующий/рефрактерный НМРЛ после лечения анти-PD-1/PD-L1 с низкой или высокой (≥50%) экспрессией PD-L1; все были анти-CSF1/CSF1R наивными. Пациенты получали 1100 мг или 1400 мг AMG 820 плюс 200 мг пембролизумаба внутривенно каждые 3 недели. Первичными конечными точками были частота дозолимитирующей токсичности (DLT) и нежелательных явлений (AEs) и частота объективного ответа в соответствии с иммунологическими критериями оценки ответа при солидных опухолях при рекомендуемой комбинированной дозе.

    Полученные результаты: В целом 116 пациентов получили ≥1 дозу АМГ 820 плюс пембролизумаб (18 — 1400 мг АМГ 820; 98 — 1100 мг АМГ 820). Большинство пациентов (64%) были мужчинами; средний возраст составил 64 года (от 30 до 86 лет). У семи пациентов были ДЛТ (1 на 1400 мг AMG 820; 6 на 1100 мг AMG 820). Почти все пациенты (99,1%) имели НЯ, 87,9% — НЯ ≥3 степени. Наиболее частыми нежелательными явлениями были повышение уровня аспартатаминотрансферазы (59,5%), утомляемость (48,3%), периорбитальный/лицевой отек (48,3%) и сыпь/макулопапулезная сыпь (37,1%). Лучшим ответом был частичный ответ, связанный с иммунитетом, у 3 пациентов (3%; продолжительность ответа 9. 2, 10,0, 12,5 мес) и иммунозависимое стабильное заболевание у 39 пациентов (34%). Ни одна из завершенных когорт фазы II не достигла предопределенного порога эффективности. После лечения наблюдалось накопление сывороточного колониестимулирующего фактора 1 (CSF1) и интерлейкина-34, снижение CSF1-зависимых CD16-экспрессирующих моноцитов, повышение экспрессии PD-L1 и числа клеток CD4 и CD8 в биоптатах опухоли.

    Выводы: Рекомендуемая комбинированная доза 1100 мг AMG 820 плюс 200 мг пембролизумаба имела приемлемый профиль безопасности. Хотя наблюдались фармакодинамические эффекты, противоопухолевая активность была недостаточной для дальнейшей оценки этой комбинации у отдельных групп пациентов.

    Пробный регистрационный номер: NCT02713529.

    Ключевые слова: клинические испытания как тема; медикаментозная терапия, комбинированная; новообразования желудочно-кишечного тракта; иммунотерапия; новообразования легких.

    © Автор(ы) (или их работодатель(и)) 2020. Повторное использование разрешено в соответствии с CC BY-NC. Нет коммерческого повторного использования. См. права и разрешения. Опубликовано БМЖ.

    Заявление о конфликте интересов

    Конкурирующие интересы: ARAR сообщает о поддержке исследования Amgen и Merck во время проведения исследования. JMC сообщает о грантах от AstraZeneca, Merck и Tesaro, помимо представленной работы; личные гонорары от Bristol Myers Squibb, помимо представленной работы; и другие от Roche, не относящиеся к представленной работе. VM сообщает о личных гонорарах от Bayer, Bristol Myers Squibb, Janssen и Pieris, помимо представленной работы. MB сообщает о грантах от Amgen во время проведения исследования; гранты от Ascentage Pharma, AstraZeneca, Bristol Myers Squibb, Merck Sharp & Dohme, Novartis, Oncomed и Pfizer, помимо представленной работы; персональные гонорары от AstraZeneca, помимо представленной работы; и нефинансовая поддержка со стороны AstraZeneca и Merck Sharp & Dohme, помимо представленной работы. ECA сообщает о грантах от AbbVie, Amcure, Amgen, AstraZeneca, Bayer, BeiGene, Bristol Myers Squibb, Boehringer Ingelheim, CytomX, Eli Lilly, h4, Incyte, Janssen, Kura, Loxo, Macrogenics, Menarini, Merck Serono, Merck, Merus, Millennium , Nanobiotix, Nektar, Novartis, Pfizer, PharmaMar, Principia, PsiOxus, Puma, Rigontec, Roche/Genentech, Sanofi, START, Taiho и Tesaro, за пределами представленной работы; и другие от AbbVie, Amcure, AstraZeneca, Celgene, Cerulean Pharma, EUSA, GLG, Guidepoint Global, HM Hospitals Group, International Cancer Consultants, Janssen-Cilag, Nanobiotix, Novartis, NPO Foundation Intheos (исследовательская терапия в онкологических науках), Oncoart Associated , Pfizer, Pierre Fabre, PsiOxus Therapeutics, Roche/Genentech, Seattle Genetics, Servier и START, за пределами представленной работы. Нам нечего раскрывать. JT сообщает о другом финансировании со стороны Amgen во время проведения исследования. RDH сообщает о грантах от Amgen и Merck во время проведения исследования. AR сообщает о гонорарах за публичные выступления и заседания консультативного совета для Roche, Bristol Myers Squibb, Novartis, Pierre Fabre и Sanofi. MAS сообщает о грантах от Merck во время проведения исследования. AJO сообщает о личных гонорарах от Merck во время проведения исследования; и личные гонорары от Array, Bristol Myers Squibb, Novartis и Pfizer, помимо представленной работы. Диджею нечего раскрывать. NL сообщает о другом из Amgen во время проведения исследования; личные сборы от Innovent Biologics, помимо представленной работы; и другие компании Alexion, ALX Therapeutics, Apexian, Asana BioSciences, Ascentage, BeiGene, Cerulean Pharma, Constellation, CytomX, Formation Biologics, Forty Seven, Ikena, Incyte, InhibRx, Innovent Biologics, Jounce Therapeutics, Livzon, Loxo, MacroGenics, Merck, Northern Biologics, Odonate Therapeutics, Pfizer, Regeneron, Symphogen и TaiRx вне представленной работы. DPR сообщает о доле в Acworth Pharmaceuticals и MPM Capital и является консультантом 28/7 Therapeutics, Gritstone Oncology, Maverick Therapeutics, MPM Capital и Oncorus, помимо представленной работы. ER является сотрудником и акционером Amgen. GJ является сотрудником и акционером Amgen. HW является сотрудником и акционером Amgen. Н.С. является сотрудником и акционером Amgen. M-ADS является сотрудником Amgen. Д.Н. является сотрудником и акционером Amgen. KPP сообщает о финансировании START для проведения этого клинического испытания от Amgen; финансирование START для проведения клинических испытаний от 3D Medicines, AbbVie, ADC Therapeutics, ArQule, Calithera Biosciences, Curegenix, Daiichi Sankyo, EMD Serono, Formation Biologics, Incyte, Jounce Therapeutics, MabSpace Biosciences, MedImmune, Merck, Mersana, OncoMed, Peloton Therapeutics, Regeneron, Sanofi и Syros Pharmaceuticals, за пределами представленной работы; и гонорары консультативного совета от ArQule, Basilea и Bayer, помимо представленной работы.

    Цифры

    Рисунок 1

    Поток пациентов через…

    Рисунок 1

    Поток пациентов в рамках исследования.

    фигура 1

    Поток пациентов через исследование.

    Рисунок 2

    Наилучший ответ пациента на основе…

    Рисунок 2

    Наилучший ответ пациента, основанный на изменении по сравнению с исходным уровнем в сумме…

    фигура 2

    Наилучший ответ пациента, основанный на изменении по сравнению с исходным уровнем суммы самых длинных диаметров поражений. CRC, колоректальный рак; irPD, иммуноопосредованное прогрессирующее заболевание; irPR, иммунный частичный ответ; irSD, иммуноопосредованное стабильное заболевание; НМРЛ, немелкоклеточный рак легкого; SLD, сумма наибольшего диаметра.

    Рисунок 3

    Уровни CSF1 (A), IL-34…

    Рисунок 3

    Уровни CSF1 (A), IL-34 (B) и моноцитов CD14+ CD16+ (C) в…

    Рисунок 3

    Уровни CSF1 (A), IL-34 (B) и моноцитов CD14+ CD16+ (C) в периферической крови пациентов до и после введения дозы AMG 820 плюс пембролизумаб. CSF1, колониестимулирующий фактор 1; Д, день; ИЛ-34, интерлейкин-34; предварительно, передозировка; Вт, неделя.

    См. это изображение и информацию об авторских правах в PMC

    Похожие статьи

    • Применение пембролизумаба у педиатрических пациентов с прогрессирующей меланомой или PD-L1-позитивной, прогрессирующей, рецидивирующей или рефрактерной солидной опухолью или лимфомой (KEYNOTE-051): промежуточный анализ открытого одногруппового исследования фазы 1-2.

      Георгер Б., Канг Х.Дж., Ялон-Орен М., Маршалл Л.В., Везина С., Паппо А., Лаетч Т.В., Петрилли А.С., Эбингер М., Топорски Дж., Глэйд-Бендер Дж., Николлс В., Фокс Э., Дюбуа С.Г., Мэйси М.Э. , Кон С.Л., Патираджа К., Диеде С.Дж., Эббингауз С., Пинто Н. Джорджер Б. и др. Ланцет Онкол. 2020 янв; 21(1):121-133. дои: 10.1016/S1470-2045(19)30671-0. Epub 2019 4 декабря. Ланцет Онкол. 2020. PMID: 31812554 Клиническое испытание.

    • Первое исследование на людях AMG 820, моноклонального антитела к рецептору колониестимулирующего фактора 1, у пациентов с прогрессирующими солидными опухолями.

      Пападопулос К.П., Глюк Л., Мартин Л.П., Ольшански А.Дж., Толчер А.В., Нгармчамнанрит Г., Расмуссен Э., Аморе Б.М., Нагорсен Д., Хилл Дж.С., Стивенсон Дж. мл. Пападопулос К.П. и соавт. Клин Рак Рез. 2017 1 октября; 23(19)):5703-5710. doi: 10.1158/1078-0432.CCR-16-3261. Epub 2017 27 июня. Клин Рак Рез. 2017. PMID: 28655795 Клиническое испытание.

    • Пембролизумаб плюс химиотерапия по сравнению с монотерапией химиотерапией у пациентов с распространенным немелкоклеточным раком легкого без опухолевой экспрессии PD-L1: объединенный анализ 3 рандомизированных контролируемых исследований.

      Боргаи Х., Лангер С.Дж., Пас-Арес Л., Родригес-Абреу Д., Халмос Б., Гарассино М.С., Хоутон Б., Курата Т., Ченг И., Лин Дж., Пьетанза М.С., Пиперди Б., Гаджил С.М. Боргаи Х. и др. Рак. 2020 15 ноября; 126 (22): 4867-4877. doi: 10.1002/cncr.33142. Epub 2020 11 сентября. Рак. 2020. PMID: 326 Бесплатная статья ЧВК.

    • Безопасность и переносимость ингибиторов PD-1/PD-L1 по сравнению с химиотерапией у пациентов с распространенным раком: метаанализ.

      Нисидзима Т.Ф., Шачар С.С., Нироп К.А., Мусс Х.Б. Нисидзима Т.Ф. и соавт. Онколог. 2017 апр; 22 (4): 470-479. doi: 10.1634/теонколог.2016-0419. Epub 2017 8 марта. Онколог. 2017. PMID: 28275115 Бесплатная статья ЧВК. Обзор.

    • Управление токсичностью с помощью комбинированной химиотерапии и терапии ингибиторами запрограммированной смерти 1/лиганда 1 запрограммированной смерти при распространенном раке легкого.

      Хоффнер Б., Лейл Н.Б., Дэвис М. Хоффнер Б. и соавт. Лечение рака, ред. 2020 г., апрель 85:101979. doi: 10.1016/j.ctrv.2020.101979. Epub 2020 4 фев. Лечение рака, версия 2020. PMID: 32078962 Обзор.

    Посмотреть все похожие статьи

    Цитируется

    • Ориентация на клеточные компоненты микроокружения опухоли при солидных злокачественных опухолях.

      Белли С., Антонарелли Г., Репетто М., Босколо Биело Л., Кримини Э., Курильяно Г. Белли С. и др. Раков (Базель). 2022 1 сентября; 14 (17): 4278. doi: 10.3390/раки14174278. Раков (Базель). 2022. PMID: 36077813 Бесплатная статья ЧВК. Обзор.

    • Клинические стратегии, нацеленные на микроокружение опухоли протоковой аденокарциномы поджелудочной железы.

      Скорупан Н., Палестино Домингес М., Риччи С.Л., Алевин К. Скорупан Н. и соавт. Раков (Базель). 2022 30 августа; 14 (17): 4209. doi: 10.3390/раки14174209. Раков (Базель). 2022. PMID: 36077755 Бесплатная статья ЧВК. Обзор.

    • Новые стратегии нацеливания на резидентные опухолевые миелоидные клетки для иммунотерапии рака.

      Ван Ю, Джонсон КСС, Гатти-Мейс М.Е., Ли З. Ван Ю и др. J Гематол Онкол. 2022 28 августа; 15 (1): 118. doi: 10.1186/s13045-022-01335-y. J Гематол Онкол. 2022. PMID: 36031601 Бесплатная статья ЧВК. Обзор.

    • Макрофаги как инструменты и мишени в терапии рака.

      Мантовани А., Аллавена П., Маркези Ф., Гарланда К. Мантовани А. и др. Nat Rev Drug Discov. 2022 авг. 16:1-22. doi: 10.1038/s41573-022-00520-5. Онлайн перед печатью. Nat Rev Drug Discov. 2022. PMID: 35974096 Бесплатная статья ЧВК. Обзор.

    • Иммунная комбинированная терапия для преобразования иммунологически холодных опухолей в горячие опухоли: обновление и новые идеи.

      Ni JJ, Zhang ZZ, Ge MJ, Chen JY, Zhuo W. Ни Дж.Дж. и др. Акта Фармакол Син. 4 августа 2022 г. doi: 10.1038/s41401-022-00953-з. Онлайн перед печатью. Акта Фармакол Син. 2022. PMID: 35927312 Обзор.

    Просмотреть все статьи «Цитируется по»

    использованная литература

      1. Управление по санитарному надзору за качеством пищевых продуктов и медикаментов США Drugs@FDA: Лекарственные препараты, одобренные FDA. Доступно: https://www.accessdata.fda.gov/scripts/cder/daf/
      1. Syn NL, Teng MWL, Mok TSK и др. . De-Novo и приобретенная устойчивость к нацеливанию на иммунные контрольные точки. Ланцет Онкол 2017;18:e731–e741. 10.1016/С1470-2045(17)30607-1 — DOI — пабмед
      1. Фарес К.М., Ван Аллен Э.М., Дрейк К.Г. и др. . Механизмы резистентности к блокаде иммунных контрольных точек: почему иммунотерапия ингибиторами контрольных точек работает не у всех пациентов? Am Soc Clin Oncol Educ Book 2019; 39: 147–64. 10.1200/EDBK_240837 — DOI — пабмед
      1. Дженкинс Р.В., Барби Д.А., Флаэрти К.Т. Механизмы резистентности к ингибиторам иммунных контрольных точек. Бр Дж Рак 2018; 118: 9–16. 10.1038/bjc.2017.434 — DOI — ЧВК — пабмед
      1. Arlauckas SP, Garris CS, Kohler RH, et al. . Визуализация in vivo выявляет связанный с опухолью путь резистентности, опосредованный макрофагами, при терапии анти-PD-1. Sci Transl Med 2017; 9: 1. 10.1126/scitranslmed.aal3604 — DOI — ЧВК — пабмед

    Типы публикаций

    термины MeSH

    вещества

    BRABUS 820 — на базе кабриолета Porsche 911 Turbo S — Новости и события — Бренд

    Ваш браузер не поддерживает видео тег.

    BRABUS 820 — Стильный. Знаковый. Волнующий.

    18.05.2022 — BRABUS 820 — это адреналин на четырех колесах. Идеальное сочетание ежедневного удовольствия от вождения нового уровня и безграничной мощности. Этот спортивный круизер нового уровня, впервые созданный на базе кабриолета Porsche 911 Turbo S, был разработан для истинных энтузиастов высокой скорости. Это современный автомобиль мечты, который впечатляет своим безошибочно узнаваемым характером, поразительной роскошью Masterpiece и превосходным опытом вождения, куда бы вы ни отправились.

    BRABUS 820 был разработан, чтобы переосмыслить наш фирменный «черный и жирный» язык дизайна, сохранив при этом типичный для BRABUS фактор «вау-вау» за 1 секунду в каждой детали. Его эксклюзивный дизайн сочетает в себе нашу высококачественную концепцию экстерьера в сочетании с аэродинамическими элементами нового уровня для получения наилучших ощущений от вождения. Вокруг чрезвычайно спортивного шасси ряд открытых углеродных элементов, таких как вставка передней панели BRABUS, передний спойлер, а также эффектные боковые закрылки, установленные перед задними колесами, впечатляют своим необычным динамичным видом.

    Идеальное сочетание фирменной мощности BRABUS и ежедневного удовольствия от вождения, подпитываемого адреналином, создано специально для того, чтобы раздвигать границы. Из состояния покоя эта спортивная икона разгоняется до 100 км/ч за ошеломляющие 2,5 секунды благодаря 3,8-литровому оппозитному 6-цилиндровому двигателю с двойным турбонаддувом и недавно разработанными турбонагнетателями, который развивает мощность 603 кВт / 820 л.с. 950 Нм неумолимой мощности мгновенно передаются через восьмиступенчатую коробку передач с двойным сцеплением, которая может переключаться как автоматически, так и вручную.

    Поразительный и безошибочный 1-секундный вау-фактор BRABUS 820 подчеркивается 22/21-дюймовыми коваными колесами BRABUS Monoblock Z «Platinum Edition». Современные производственные процессы и эксклюзивная отделка «Signature Black» обеспечивают неповторимый внешний вид и максимальную прочность. Легкая конструкция обеспечивает повышенную устойчивость, а также оптимальную управляемость. Благодаря разработанным нами полностью регулируемым спортивным пружинам дорожный просвет BRABUS 820 может быть оптимизирован до 25 миллиметров, что значительно улучшает динамику движения за счет более низкого центра тяжести.

    Из чего сбываются мечты. Наши специалисты по дизайну интерьера разработали уникальный, полностью ручной работы интерьер BRABUS Masterpiece для BRABUS 820, который соответствует фирменному внешнему виду BRABUS. Изысканный до мельчайших деталей, роскошный дизайн из черной кожи впечатляет своей безупречной отделкой, в комплекте со специальной прострочкой в ​​виде герба BRABUS, контрастной красной окантовкой, а также перфорацией с точностью до миллиметра на сиденьях, элементах отделки и напольных ковриках, которые также обиты тончайшая кожа.

    BRABUS 820 — на базе Porsche 911 Turbo S Cabriolet
    Расход топлива — город 15,2 л/100 км | трасса 8,9 л/100км | смешанный 11,3 л/100 км | Выбросы CO2 257 г/км | CO2-EFFICIENCY G

    Узнайте больше

    С нашими файлами cookie мы хотим предложить вам все возможности BRABUS. К ним относятся общая производительность, статистика и настройки местоположения. Если вы хотите работать с нами на полную катушку, мы будем рады, если вы согласитесь на использование файлов cookie, нажав «Принять». Дополнительную информацию можно найти в нашем Уведомлении о защите данных.

    Эти необходимые куки-файлы необходимы для работы веб-сайта и обеспечивают, например, функции, важные для системы и безопасности, функции корзины покупок и базовое сохранение разрешенных настроек куки-файлов. Веб-сайт не может работать безупречно без этих файлов cookie.

    Cookie Description Lifetime Domain
    Neos_Session Технически необходим для базовой работы системы. 2 года www.brabus.com
    корзина Сохраняет идентификатор корзины и товары, которые пользователь кладет в корзину. 1 месяц www.brabus.com
    cookiesAccepted Сохраняет информацию, если CookieLayer был принят. 2 месяца www.brabus.com
    cookieConsent: Сохраняет информацию о разрешенных файлах cookie. 3 месяца www.brabus.com
    cookieConsentAccepted Сохраняет версию файлов cookie в виде хэша, чтобы CookieLayer больше не отображался или чтобы CookieLayer снова отображался, если файлы cookie были измененный. 3 месяца www.brabus.com

    Для постоянного развития наших предложений и нашего веб-сайта мы записываем анонимные данные для статистики и аналитики в Google Analytics. Google Analytics находится в ведении Google LLC. Обычно данные передаются на сервер в США компанией Google.

    Cookie Description Lifetime Domain
    _ga Used to differentiate users. 2 года .brabus.com
    _gid Используется для дифференциации пользователей. 1 день . brabus.com
    _gat_UA-134535071-1 Используется для регулирования скорости запросов 1 минута .brabus.com
    NID Используется для сохранения предпочтительных личных условий 6 месяцев. карьерные предложения. Файлы cookie используются для обеспечения технической функциональности предложения. Файлы cookie используются провайдером coveto ATS GmbH. Данные будут отправлены в Германию и обработаны там.

    Cookie Description Lifetime Domain
    AMA_66a95e0a3dc1a25a853de89400e51380 Saves the current session Session k28975.

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *

    © 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»

    Карта сайта