python — Алгоритм получения комбинации по проценту (неограниченной длины)
Например есть следующая комбинация (все возможные комбинации из цифр от 1 до 2 длиной 3).
111 - 0% 112 - 14% 121 - 28% 122 - 42% 211 - 57% 212 - 71% 221 - 85% 222 - 100%
Комбинации цифр где каждая цифра может иметь диапазон в данном случае например от 1 до 2 включительно. Мне надо получить именно комбинацию 71% (например 71% эта комбинация 212 если кому не понятно).
Я в результате 1-го года размышлений как это можно сделать естественно не генерируя заранее готовые комбинации и выбирая из них уже по % я придумал алгоритм основанный на процентах от процентах но он не подходит для работы с большими по длине комбинациями (например 10000000 длина где цифры от 0 до 9 включительно), максимум комфортно это 300-1000 знаков, как бы он подходит, но для этого мне надо брать число процента с 0-ми равное по длине больше чем текста на этой странице и при нормализации по следующему % у меня уйдет n-е количество минут а то и часов.
- python
- python-3.x
- математика
- комбинаторика
16
Попробую накидать схему на Вашем примере. Трехсимвольные комбинации из цифр 1 и 2. Таких комбинаций всего 8.
- Считаем, сколько процентов составляет одна комбинация.
c=100/7 - Имея проценты, например, 71%,находим номер этой комбинации
n = 71/c, номера начинаются с нуля. - Так как используются только две цифры, переводим полученный номер в двоичную запись и представляем строкой.
- каждую цифру в строке увеличиваем на значение младшей используемой цифры — в вашем случае на 1. А если бы использовались, например, цифры 6 и 7, то увеличивали бы на 6.
- Результат получен.
Кажется, должно работать…
1
А что тут год думать? заменяем цифры в порялке возрастания на 01.
3=27 значений, значит, 0.71*(27-1) = 18.46. Округляем до 18, в троичной системе счисления это 200, значит, переводя в ваши цифры, 311.
3
На степень b умножаем, округляем, b-ичную запись получаем.
Функция to_digits переводит число в цифры по заданной базе. Питон не поддерживает эту функциональность из коробки. Для скорости пришлось сделать «разделяй и властвуй»:
def to_digits(k, n, b):
def digits(k, n):
if n <= 256:
for _ in range(n):
yield 1 + k % b
k //= b
else:
n1 = n // 2
n2 = n - n1
k2, k1 = divmod(k, b ** n1)
yield from digits(k1, n1)
yield from digits(k2, n2)
return reversed(tuple(digits(k, n)))
t1, t2, t3 = input().split()
n = int(t1)
b = int(t2)
p = float(t3)
pn, pd = p.as_integer_ratio()
m = b ** n - 1
k = (m * pn + (100 * pd) // 2) // (100 * pd)
sep = '' if b < 10 else '_'
print(sep.
join(str(d) for d in to_digits(k, n, b)))
$ echo 3 2 71 | python strange-percents.py 212 $ echo 3 3 71 | python strange-percents.py 311 $ echo 3 9 71 | python strange-percents.py 745 $ echo 3 10 71 | python strange-percents.py 8_1_10 $ time echo 1166400 2 71 | python strange-percents.py 2122121222...1111212111 real 0m2.152s user 0m2.076s sys 0m0.020s $ time echo 1166400 2 86 | python strange-percents.py 2212221111...2121112222 real 0m2.166s user 0m2.076s sys 0m0.032s
11
математика — Список всевозможных комбинаций чисел из 7 цифр от 0 до 9 без возможности повтора
Правильно ли написан .bat? Проверьте, пожалуйста. Требуется список всевозможных комбинаций чисел из 7 цифр от 0 до 9 без возможности повтора.В блокнот скопируем семь строк
FOR /L %%i IN (0,1,9) DO echo 000%%i>> stat.txt FOR /L %%i IN (10,1,99) DO echo 00%%i>> stat.
txt
FOR /L %%i IN (100,1,999) DO echo 0%%i>> stat.txt
FOR /L %%i IN (1000,1,9999) DO echo %%i>> stat.txt
FOR /L %%i IN (10000,1,99999) DO echo %%i>> stat.txt
FOR /L %%i IN (100000,1,999999) DO echo %%i>> stat.txt
FOR /L %%i IN (1000000,1,9999999) DO echo %%i>> stat.txt
Сохрани как run.bat и затем — кликни по нему (запуск с правами админа).
Через время — файл с комбинациями будет лежать в той же папке или %system32%
- математика
- bat
- комбинаторика
- числа
- генерация-случайных-данных
8
Ну, раз Stanislav Volodarskiy дал ответ по поводу размещений, я скажу о сочетаниях 🙂
Вот файл, который выводит все 120 сочетаний из 7 цифр из 10 возможных:
@echo off
setlocal enableextensions
setlocal enabledelayedexpansion
for /L %%g in (6,1,9) do (
set x=%%g
set /A x=x-1
for /L %%f in (5,1,!x!) do (
set y=%%f
set /A y=y-1
for /L %%e in (4,1,!y!) do (
set z=%%e
set /A z=z-1
for /L %%d in (3,1,!z!) do (
set u=%%d
set /A u=u-1
for /L %%c in (2,1,!u!) do (
set v=%%c
set /A v=v-1
for /L %%b in (1,1,!v!) do (
set w=%%b
set /A w=w-1
for /L %%a in (0,1,!w!) do echo %%a%%b%%c%%d%%e%%f%%g
)
)
)
)
)
)
endlocal
А уж куда перенаправить его вывод — дело десятое 🙂
Если немного повозиться — можно написать и размещение.
.bat составлен неправильно. Он порождает 10 + 90 + 900 + 9000 + 90000 + 900000 + 9000000 = 10000000 комбинаций.
Речь о числе размещений A(n, k). Количество способов выбрать всевозможные размещения 7 из 10 цифр без повторов равно A(10, 7) = 10! / (10 - 7)! = 604800.
Числа не совпадают, следовательно .bat составлен неправильно.
3
Зарегистрируйтесь или войдите
Регистрация через Google
Регистрация через Facebook
Отправить без регистрации
Почта
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки
Вероятность с использованием перестановок и комбинаций
Результаты обучения
- Вычисление условной вероятности события
- Используйте теорему Байе для вычисления условной вероятности
- Рассчитать ожидаемое значение события
Мы можем использовать перестановки и комбинации, чтобы помочь нам ответить на более сложные вопросы вероятности.
примеры
Выбран 4-значный PIN-код. Какова вероятность того, что нет повторяющихся цифр?
Показать раствор
Попробуйте
Пример
В лотерее одного штата 48 шаров с номерами от 1 до 48 помещаются в автомат, и шесть из них вытягиваются случайным образом. Если шесть выпавших номеров совпадают с номерами, выбранными игроком, игрок выигрывает 1 000 000 долларов. В этой лотерее порядок выпадения номеров не имеет значения. Вычислите вероятность того, что вы выиграете приз в миллион долларов, если купите один лотерейный билет.
Показать раствор
Пример
В лотерее штата из предыдущего примера, если пять из шести выпавших номеров совпадают с номерами, выбранными игроком, игрок выигрывает второй приз в размере 1000 долларов. Вычислите вероятность того, что вы выиграете второй приз, если купите один лотерейный билет.
Показать раствор
Предыдущие примеры показаны в следующем видео.
примера
Вычислите вероятность случайного извлечения пяти карт из колоды и получения ровно одного туза.
Показать раствор
Пример
Вычислите вероятность случайного извлечения пяти карт из колоды и получения ровно двух тузов.
Показать раствор
Просмотрите следующее для дальнейшей демонстрации этих примеров.
Попробуйте
Давайте сделаем паузу, чтобы рассмотреть известную задачу теории вероятностей:
Предположим, у вас есть комната, полная 30 человек.
Какова вероятность того, что есть хотя бы один общий день рождения?
Угадайте ответ на приведенную выше задачу. Было ли ваше предположение довольно низким, около 10%? Это кажется интуитивным ответом (возможно, 30/365?). Давайте посмотрим, стоит ли нам прислушиваться к своей интуиции. Однако начнем с более простой задачи.
пример
Предположим, в комнате находятся три человека. Какова вероятность того, что у этих трех человек есть хотя бы один общий день рождения?
Показать раствор
Предположим, в комнате находятся пять человек. Какова вероятность того, что среди этих пяти человек есть хотя бы один общий день рождения?
Показать раствор
Предположим, в комнате 30 человек. Какова вероятность того, что среди этих 30 человек есть хотя бы один общий день рождения?
Показать раствор
Ниже подробно рассматривается проблема дня рождения.
Если вам нравится делать ставки, и если вы можете убедить 30 человек раскрыть свои дни рождения, вы можете выиграть немного денег, поспорив с другом, что в комнате будет по крайней мере два человека с одинаковым днем рождения в любое время. вы находитесь в комнате на 30 и более человек. (Конечно, вам нужно убедиться, что ваш друг не изучал вероятность!) Вы не гарантированно выиграете, но вы должны выигрывать более чем в половине случаев.
Это один из многих противоречивых результатов теории вероятностей; то есть это идет вразрез с нашими внутренними инстинктами.
Попробуйте
Предположим, в комнате находятся 10 человек. Какова вероятность того, что среди этих 10 человек есть хотя бы один общий день рождения?
, используя числа от 0 до 9, перечислите все 4-значные числа, которые в сумме дают 19
Математическое комбо
Ccccc Z.
список всех комбинаций из 4-значных чисел, которые в сумме дают 19используя все номера от 0 до 9
Подписаться І 2
Подробнее
Отчет
1 ответ эксперта
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Дэвид В. ответил 30.07.15
Репетитор
4.7 (89)
Опытный профессор
Об этом репетиторе ›
Об этом репетиторе ›
Ну, их 660.
Этот форум ответов не позволит мне «перечислить все 4-значные числа, которые в сумме дают 19»; он урежет список, когда он заполнится.
Однако вам следует рассмотреть некоторую логику, необходимую для определения того, что существует 660 возможностей:
— предположим, что первое число равно 0
— теперь предположим, что второе число равно 0
Сколько комбинаций осталось, чтобы в сумме получить 19? (как вы думаете, почему они выбрали 19?)
— предположим, что первое число равно 0
— теперь предположим, что второе число 1
Сколько комбинаций осталось, чтобы в сумме получить 19?
— предположим, что первое число равно 0
— теперь предположим, что второе число равно 2
Сколько комбинаций осталось, чтобы в сумме получить 19?
.
. .
Видите какую-то закономерность??
. . .
О,.., наблюдайте, когда первые два числа начинают увеличиваться (а последние два выглядят обратными значениям первых двух и, наконец, становятся 1 и 0 !! Эта диаграмма выглядит как треугольник.
Когда вы сложите все значения (не расстраивайтесь, их не так много), вы должны получить 660.
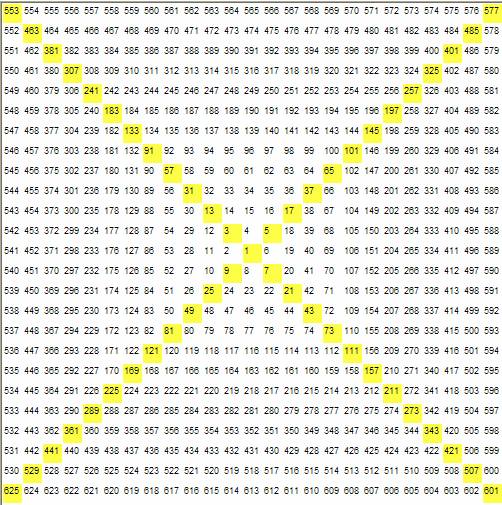
Чтобы увидеть образец и проверить некоторые работы, вот список (насколько Ответы Форум бокс позволяет):
1:0 1 9 9
2:0 2 8 9
3:0 2 9 8
4:0 3 7 9
5: 0 3 8 8
6: 0 3 9 7
7: 0 4 6 9
8: 0 4 7 8
9: 0 4 8 7
10: 0 4 9 6
11: 0 5 5 9
12: 0 5 6 8
13: 0 5 7 7
14: 0 5 8 6
15: 0 5 9 5
16: 0 6 4 9
17: 0 6 5 8
18: 0 6 6 7 1
: 0 6 7 6
20: 0 6 8 5
21: 0 6 9 4
22: 0 7 3 9
23: 0 7 4 8
24: 0 7 5 7
25: 0 7 6 6
26: 0 7 7 5
27: 0 7 8 4
28: 0 7 9 3
29: 0 8 2 9
30: 0 8 3 8
31: 0 8 4 7
32: 0 8 5 6
33: 0 8 6 5
34: 0 8 7 4
35: 0 8 8 3
36: 0 8 9 2
37: 0 9 1 9
38: 0 9 2 8
39: 0 9 0 1 3 1 7 7 40: 0 9 4 6
41: 0 9 5 5
42: 0 9 6 4
43: 0 9 7 3
44: 0 9 8 2
45: 0 9 9 1
46: 1 0 9 9 4
: 1 1 8 9
48: 1 1 9 8
49: 1 2 7 9
50: 1 2 8 8
51: 1 2 9 7
52: 1 3 6 9
53: 1 3 7 8
54: 1 3 8 7
55: 1 3 9 6
56: 1 4 5 9
57: 1 4 6 8
58: 1 4 7 7
59: 1 4 8 6
60: 1 4 9 5
61: 1 5 4 9
62: 1 5 5 8
63: 1 5 6 7
64: 1 5 7 6
65: 1 5 8 5
66: 1 5 9 4
67: 1 6 13 19 9 68: 1 6 4 8
69: 1 6 5 7
70: 1 6 6 6
71: 1 6 7 5
72: 1 6 8 4
73: 1 6 9 3
74: 1 7 2 7 9
: 1 7 3 8
76: 1 7 4 7
77: 1 7 5 6
78: 1 7 6 5
79: 1 7 7 4
80: 1 7 8 3
81: 1 7 9 2
82: 1 8 1 9
83: 1 8 2 8
84: 1 8 3 7
85: 1 8 4 6
86: 1 8 5 5
87: 1 8 6 4
88: 1 8 7 3
89: 1 8 8 2
90: 1 8 9 1
91: 1 9 0 9
92: 1 9 1 8
93: 1 9 2 7
94: 1 9 3 6
95: 1 9 13 15 96: 1 9 5 4
97: 1 9 6 3
98: 1 9 7 2
99: 1 9 8 1
100: 1 9 9 0
101: 2 0 8 9
102: 2 0 3 1 8 9031 : 2 1 7 9
104: 2 1 8 8
105: 2 1 9 7
106: 2 2 6 9
107: 2 2 7 8
108: 2 2 8 7
109: 2 2 19 13 10 90: 2 3 5 9
111: 2 3 6 8
112: 2 3 7 7
113: 2 3 8 6
114: 2 3 9 5
115: 2 4 4 9
116: 2 4 5 8
117: 2 4 6 7
118: 2 4 7 6
119: 2 4 8 5
120: 2 4 9 4
121: 2 5 3 9
1 9013 8 2 123: 2 5 5 7
124: 2 5 6 6
125: 2 5 7 5
126: 2 5 8 4
127: 2 5 9 3
128: 2 6 2 9
129: 2 1 90 3 3 : 2 6 4 7
131: 2 6 5 6
132: 2 6 6 5
133: 2 6 7 4
134: 2 6 8 3
135: 2 6 9 2
136: 7 13 19 19 30: 2 7 2 8
138: 2 7 3 7
139: 2 7 4 6
140: 2 7 5 5
141: 2 7 6 4
142: 2 7 7 3
143: 2 7 8 2
144: 2 7 9 1
145: 2 8 0 9
146: 2 8 1 8
147: 2 8 2 7
148: 2 8 3 6
1 9 13 5 2 150: 2 8 5 4
151: 2 8 6 3
152: 2 8 7 2
153: 2 8 8 1
154: 2 8 9 0
155: 2 9 0 8
156: 2 17 9 1 1 1 : 2 9 2 6
158: 2 9 3 5
159: 2 9 4 4
160: 2 9 5 3
161: 2 9 6 2
162: 2 9 7 1
163: 2 9 13 10 604: 3 0 7 9
165: 3 0 8 8
166: 3 0 9 7
167: 3 1 6 9
168: 3 1 7 8
169: 3 1 8 7
170: 3 1 9 6
171: 3 2 5 9
172: 3 2 6 8
173: 3 2 7 7
174: 3 2 8 6
175: 3 2 19 15 1906: 3 3 4 9
177: 3 3 5 8
178: 3 3 6 7
179: 3 3 7 6
180: 3 3 8 5
181: 3 3 9 4
182: 3 4 3 19 18013: 3 4 4 8
184: 3 4 5 7
185: 3 4 6 6
186: 3 4 7 5
187: 3 4 8 4
188: 3 4 9 3
189: 3 5 2 9 190:31 3 3 8
191: 3 5 4 7
192: 3 5 5 6
193: 3 5 6 5
194: 3 5 7 4
195: 3 5 8 3
196: 3 5 9 2
197: 3 6 1 9
198: 3 6 2 8
199: 3 6 3 7
200: 3 6 4 6
201: 3 6 5 5
1 9013 4 3 203: 3 6 7 3
204: 3 6 8 2
205: 3 6 9 1
206: 3 7 0 9
207: 3 7 1 8
208: 3 7 2 2 7
209: 3 1 7 1 3 3 : 3 7 4 5
211: 3 7 5 4
212: 3 7 6 3
213: 3 7 7 2
214: 3 7 8 1
215: 3 7 9 0
216: 7 8 13 12 12 900 3 8 1 7
218: 3 8 2 6
219: 3 8 3 5
220: 3 8 4 4
221: 3 8 5 3
222: 3 8 6 2
223: 3 8 7 1
224: 3 8 8 0
225: 3 9 0 7
226: 3 9 1 6
227: 3 9 2 5
228: 3 9 3 4
9 013 3 1 9 213 3 230: 3 9 5 2
231: 3 9 6 1
232: 3 9 7 0
.
. .
529: 8 0 2 9
530: 8 0 3 8
531: 8 0 4 7
532: 8 0 5 6
533: 8 0 5
534: 8 0 4
535: 8 0 5
534: 8 0 7 40131 535: 8 0 5
: 8 0 7 40131 533: 8 0 5
534: 8 4
533: 80 8 3
536: 8 0 9 2
537: 8 1 1 9
538: 8 1 2 8
539: 8 1 3 7
540: 8 1 4 6
541: 8 1 5 5 6
1 2: 4
543: 8 1 7 3
544: 8 1 8 2
545: 8 1 9 1
546: 8 2 0 9
547: 8 2 1 8
548: 8 2 2 7
549: 8 2 3 6
1 9013 550: 8 551: 8 2 5 4
552: 8 2 6 3
553: 8 2 7 2
554: 8 2 8 1
555: 8 2 9 0
556: 8 3 0 8
557: 8 50 3 1 7 1 1 : 8 3 2 6
559: 8 3 3 5
560: 8 3 4 4
561: 8 3 5 3
562: 8 3 6 2
563: 8 3 7 1
564: 8 3 13 10 5 90: 8 4 0 7
566: 8 4 1 6
567: 8 4 2 5
568: 8 4 3 4
569: 8 4 4 3
570: 8 4 5 2
571: 8 4 6 1
572: 8 4 7 0
573: 8 5 0 6
574: 8 5 1 5
575: 8 5 2 4
576: 8 5 3 3
1 9013 577: 2 8 578: 8 5 5 1
579: 8 5 6 0
580: 8 6 0 5
581: 8 6 1 4
582: 8 6 2 3
583: 8 6 3 2
584: 8 90 3 4 4 : 8 6 5 0
586: 8 7 0 4
587: 8 7 1 3
588: 8 7 2 2
589: 8 7 3 1
590: 8 7 4 0
591: 8 8 13 13 92 900 8 8 1 2
593: 8 8 2 1
594: 8 8 3 0
595: 8 9 0 2
596: 8 9 1 1
597: 8 9 2 0
598: 9 0 1 9
599: 9 0 2 8
600: 9 0 3 7
601: 9 0 4 6
602: 9 0 5 5
603: 9 0 13 4 604 : 9 0 7 3
605: 9 0 8 2
606: 9 0 9 1
607: 9 1 0 9
608: 9 1 1 8
609: 9 1 2 7
610: 9 1 13 16 90: 9 1 4 5
612: 9 1 5 4
613: 9 1 6 3
614: 9 1 7 2
615: 9 1 8 1
616: 9 1 9 0
617: 9 2 0 18 61813 9013 2 1 7
619: 9 2 2 6
620: 9 2 3 5
621: 9 2 4 4
622: 9 2 5 3
623: 9 2 6 2
624: 9 2 7 1
625: 9 2 8 0
626: 9 3 0 7
627: 9 3 1 6
628: 9 3 2 5
629: 9 3 3 4
3 1 634: 39 631: 9 3 5 2
632: 9 3 6 1
633: 9 3 7 0
634: 9 4 0 6
635: 9 4 1 5
636: 9 4 2 4
637: 61 3 90 3 3 3 : 9 4 4 2
639: 9 4 5 1
640: 9 4 6 0
641: 9 5 0 5
642: 9 5 1 4
643: 9 5 2 3
644: 9 5 13 1 2 900: 9 5 4 1
646: 9 5 5 0
647: 9 6 0 4
648: 9 6 1 3
649: 9 6 2 2
650: 96 3 1
651: 9 6 4 0
652: 9 7 0 3
653: 9 7 1 2
654: 9 7 2 1
655: 9 7 3 0
656: 9 8 0 2
6 8 1 1
658: 9 8 2 0
659: 9 9 0 1
660: 9 9 1 0
Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощь? Получите правильный ответ, быстро.
