Комбинаторика формулы: 2.03. Основные формулы комбинаторики

Комбинаторика. Формулы сложения и произведения. Примеры

1. Все что нужно знать к КР

По комбинаторике!

2. Формулы сложения и произведения

Сложение
-Когда использовать??
-Когда задача разбивается на
несколько непересекающихся
случаев!
Произведение
-Когда использовать??
-Когда задача разбивается на
несколько независимых
подзадач. Пусть количество
решений первой подзадачи X,
для ЛЮБОГО решения первой
подзадачи имеется Y решений
второй, тогда общее количество
X*Y

3. Примеры использования сложения и произведения

Сложение и произведение
Пусть имеется 3 синих, 4 красных, и 5 белых шаров, каким
количество способом можно вытащить 2 разноцветных шара?
Решение: Разбиваем задачу на непересекающиеся случаи
-Синий и красный 3*4=12 (так как для каждого из 3 синих, можем
вытянуть 4 красных)
-Синий и белый 3*5=15 (аналогично)
-Красный и белый 4*5=20
Ответ: 12+15+20=47

4.

Перестановки• Формула P(n)=n!
• Когда использовать?? Имеется n отличающихся между собой
объектов, и n позиций для них. Нужно расставить их на эти
позиции. НИКАКОЙ ВЫБОРКИ ОБЪЕКТОВ НЕТ!
• Объяснение формулы: На первое можно поставить любой из n
объектов, на следующее любой из оставшихся n-1, на следующее
n-2 и.т.д.
• Пример: Каким количеством способов можно расставить 10
людей в линию? 10!
Пример: Каким количеством способов можно перемешать колоду
из 52 карт? 52!

5. Размещение без повторений

• Формула A(n,m)=n!/(n-m)!
• Когда использовать?? Когда нужно выбрать из n различных
объектов m, и выставить их в определенном порядке, при этом
каждый объект может использоваться только 1 раз
• Объяснение формулы: На первую позицию можем поставить n
объектов, на вторую n-1, на третью n-2, на последнюю n-m+1,
n*(n-1)*(n-2)*…*(n-m+1)=n!/(n-m)!

6. Примеры

• Каким количеством способов можно выбрать в группе из 30
старосту и его помощника? A(30,2)=30!/(30-2)!=30*29=870
• Каким количеством способов 10 человек из 30 могут выстроится в
очередь к врачу? А(30,10)=30!/20!

7.

100

9. Сочетания

• Формула: С(n,k)=n!/(k!*(n-k)!)
• Когда использовать?? Из n различных объектов нужно выбрать
группу (в которой порядок не важен) из k объектов.
• Объяснение формулы: С(n,k)=A(n,k)/P(k) Если мы сначала решим
задачу, где нам важен порядок внутри группы, ответ будет А(n,k).
Однако все порядки отличающиеся лишь порядком элементов,
будут давать одну группу, а таких групп будет k! Для каждой
выборки

10. Примеры

• Сколькими способами можно выбрать 10 карт из 36? С(36,10)
• Сколькими способами можно выбрать 4 позиций из 10? С(10,4)
• Сколькими способами можно выбрать 8 карт из 36, чтобы там
были 2 короля и 2 туза? С(4,2)*С(4,2)*С(28,4) — Количество
способов выбрать 2 короля из 4, 2 туза из 4, и 4 любые карты из
оставшихся 28
• В турнире по шахматам, каждый игрок должен сыграть с каждым
ровно один раз, сколько партий будет сыграно в турнире из 14
человек? С(14,2) – Количество неупорядоченных пар шахматистов
и есть количество партий в турнире

11.

Задача Муавра• Формула F(n,k)=C(n+k-1,k-1)
• Когда использовать?? Либо когда у нас n ОДИНАКОВЫХ объектов,
раскладывается по k кучам, либо когда задача сводится к
нахождению решений уравнений x1+x2+…xk=n в целых числах,
когда каждый xi>=0
• Объяснение: Расположим между n шарами k-1 перегородок,
однозначно разбивающую группу на k групп. Всего позиций у нас
получается n+k-1, надо выбрать те, где будут стоять перегородки,
это количество C(n+k-1, k-1). Во втором случае мы как бы
раскидываем n единиц по иксам.

12. Примеры

• Сколькими способами можно купить 9 ручек, если в продаже
имеется 4? Пусть xi – количество ручек i x1+x2+x3+x4=9 ->Ответ
С(9+4-1,4-1)=С(12,3)
• Сколькими способами можно разделить 7 яблок и 4 груши на 3
человека? Будем по отдельности делить яблоки и груши, поделит
яблоки С(7+3-1,3-1) способов, а груш С(4+3-1,3-1) способов
(Стандартная задача Муавра, объекты – фрукты, люди — ящики).
-> Ответ С(9,2)*С(6,2)

13.

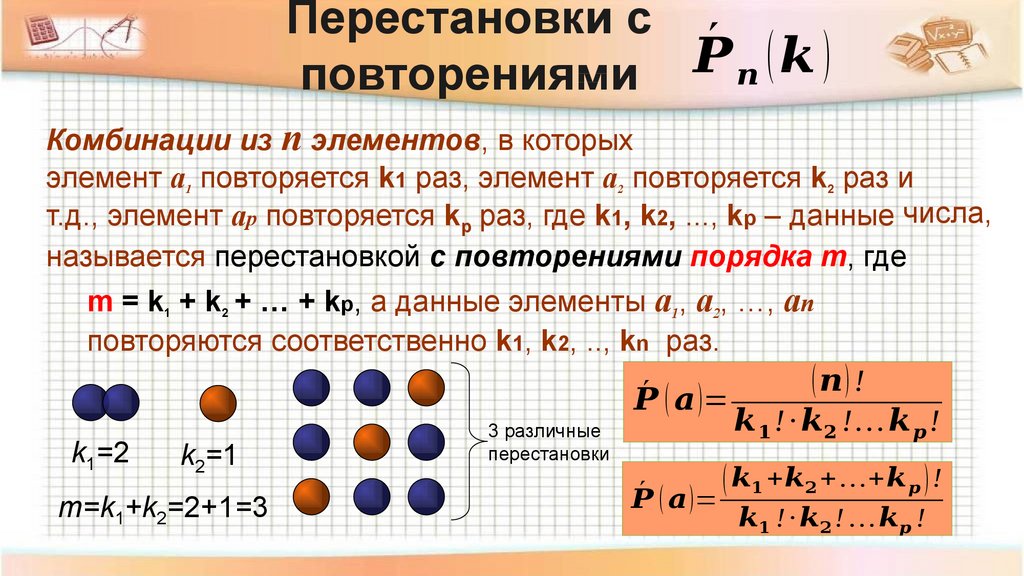Пример задач с ограничениями (было у нас в прошлом году на кр)• Каким количеством способом могут распределиться голоса на
выборах, если избирающих 450 человек, кандидатов 4, и
известно что победитель набрал более 2/3 голосов.
• Решение: Так как победитель набрал более 2/3, значит как
минимум 301 голос, отдадим их одну из 4 кандидатов, и
оставшиеся 149 голосов распределим по Муавру.
• Ответ: 4*С(149+4-1,4-1)=4*С(152,3)

14. Пример задач с ограничениями (было у нас в прошлом году на кр)

• Каким количеством способом могут распределиться голоса на
выборах, если избирающих 450 человек, кандидатов 4, и
известно что кандидат А набрал ровно половину голосов.
• Решение: Так как А набрал 225 голосов, отдадим их ему, а
оставшиеся распределим между 3 кандидатами по Муавру
• Ответ: С(225+3-1,3-1)=С(227,2)

15. Формула включений исключений

• Когда использовать?
1. Когда нужно найти объединение некоторых множеств, при этом
легко находятся их пересечения
2. 5 (От общего числа вычитаем
те, где нет X, те где нет Y, те где нет Z, прибавляем те где нет пар, и
вычитаем те, где нет всей тройки)

17. Задачи для решения (они из учебника Шварца ничего нового, но в конце презентации есть решения к ним)

18. Решение задачи 111

Введем систему координат, сейчас мы находимся в клетке (1,1,1)
надо попасть в (10,10,10). Мы сделаем это за 27 ходов, среди
которых 9 ходов это +1 по первой координате, 9 — +1 по второй и 9 +1 по третьей. То есть наш путь описывается последовательностью
из символов i, j,k, где каждого символа должно быть 9 штук.
Выберем позиции на которых будет i С(27,9) способами, из
оставшихся 18 выберем позиции, на которых будет j, на оставшиеся
автоматически попадут k.
Ответ С(27,9)*С(18,9)=27!/(9!*9!*9!)

19. Решение задачи 115

• Выберем позиции на которых будут стоять четные числа, это
можно сделать С(10,5) способами. Выбрав позиции для четных,
мы однозначно их расставляем в порядке возрастания, позиции
для нечетных тоже выбираются однозначно и числа в них
расставляются однозначно в порядке убывания
• Ответ: С(10,5)

20.

28
• Б) Она должна сделать 7 шагов, каждый шаг положительной
длины, сумма шагов равна 29. x1+x2+x3+x4+x5+x6+x7=29, но все х
положительные, значит задача с ограничениями, положим по
единице в каждый x получим x1+x2+x3+x4+x5+x6+x7=22. По
Муавру ответ C(22+7-1, 7-1)=C(28,6)

23. Решение задачи 194

• Всего решений этого уравнений в неотрицательных целых числах
С(n+3-1,3-1) способов. Вычтем те случаи в которых какая пара
совпала. То есть найдем количество решений уравнения 2*x+z=n.
Их n/2+1 штук ( округление вниз, не имеет никакого отношения к
комбинаторике, но не трудно убедиться). То есть мы вычитаем от
нашего решения 3*(n/2+1). Но возможен случай что все 3
переменные равны, его мы вычли 3 раза, надо 2 раза сложить.
Такой случай возможен только если n кратно трем.
• Ответ: При n кратном 3: С(n+2,2)-3*(n/2+1)+2
При n не кратном 3: С(n+2,2)-3*(n/2+1)

24. Решение задачи 199

• Если бы цветов каждого вида было бы бесконечно много, или хотя бы
больше 9, ответом была формула Муавра С(9+3-1,3-1). Однако нам нужно
вычесть лишние случаи, когда мы превысили лимит на какой-то вид роз.
Если мы превысили лимит на первый тип, то значит положили взяли его как
минимум 4 раза, и того количество способов это сделать С(5+3-1,3-1), второй
цветок чтобы превысить надо взять его минимум 5 раз, и того останется
всего выбор для 4 цветов С(4+3-1,3-1), а для третьего останется 3 С(3+3-1,31). Но возможен случай когда мы превысили лимит на первые цветка
одновременно (для остальных в данной задаче это невозможно), такой
способ 1.
• Ответ: С(11,2)-С(7,2)-С(6,2)-С(5,2)+1

25. Любите комбинаторику!

•И всем удачи на КР!
P.S. Если понравилась преза, подпишись на паблик https://vk.com/oproseswithlove

Комбинаторика и ее основные формулы – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД

Комбинаторикой называется область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих заданному множеству. 3_{27}=\frac{27!}{3!\cdot 24!}=\frac{27\cdot 26 \cdot 25}{1\cdot 2 \cdot3}=2925\).

При решении задач комбинаторики используют следующие правила:

Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.

Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана m · n способами.

Пример 5. Наряд студентки состоит из блузки, юбки и туфель. Девушка имеет в своем гардеробе четыре блузки, пять юбок и три пары туфель. Сколько нарядов может иметь студентка?

Решение: Пусть сначала студентка выбирает блузку. Этот выбор может быть совершен четырьмя способами, так как студентка имеет четыре блузки, затем пятью способами произойдет выбор юбки и тремя способами выбор туфель. По принципу умножения, получается: 4 · 5 · 3 = 60 нарядов (комбинаций).

Искусство решения проблем

Разбиение неотрицательного целого числа — это способ выразить его как неупорядоченную сумму других положительных целых чисел. Например, есть три раздела по 3: . Каждое из слагаемых представляет собой часть разбиения.

Функция разделения дает количество разделов . Существует точная формула для , открытая Г. Х. Харди, Дж. Э. Литтлвудом и Шринивасой Рамануджаном. Однако эта формула громоздка: неизвестно даже, при каких значениях числа разбиений четно, несмотря на наличие формулы! Более простой формулы не известно, и существование такой формулы сомнительно.

Плодотворным способом изучения номеров разделов является использование генерирующих функций. Производящая функция последовательности имеет вид . Разбиения также можно изучать с помощью тета-функции Якоби, в частности, тройного произведения Якоби. Подход производящей функции и подход тета-функции можно использовать для изучения многих вариантов статистической суммы, таких как количество способов записать число в виде суммы нечетных частей, или отдельных частей, или частей, эквивалентных , и т.

д. .

Содержание

• 1 Список разделов и значений функции распределения для малого
• 2 диаграммы Феррера
  • 2.1 Конъюгат
• 3 Генерирующие функции
• 4 Вариант
• 5 ресурсов
• 6 См. также

Список разделов и значений функции разделения для малого

Пустой раздел (без частей) является уникальным разделом , поэтому .

Уникальный раздел , так что .

, значит.

, значит.

, значит.

, значит.

Разделы часто записываются в виде кортежа , поэтому мы можем обозначать разделы как и . Это обозначение часто дополнительно сокращается до обозначения слов (путем опускания круглых скобок и запятых, поэтому становится ) или путем указания кратности с экспоненциальным обозначением (так становится ).

Используя это последнее обозначение, разделы равны и , поэтому . Можно продолжить это вычисление, чтобы найти , , , и так далее.

Диаграммы Феррерса

Диаграмма Феррерса — это способ геометрического представления разделов. Диаграмма состоит из рядов точек. Каждая строка представляет собой отдельное дополнение в разделе. Строки упорядочены в порядке невозрастания, так что строка с наибольшим количеством точек находится вверху, а строка с наименьшим количеством точек — внизу.

Например, 9 можно разделить на 4 + 3 + 1 + 1, что будет представлено следующей диаграммой Феррера:

4
3
1
1

Сопряжение

Сопряжение диаграммы Феррера формируется путем отражения диаграммы по ее диагонали (начинающейся в верхнем левом углу диаграммы). Это также можно интерпретировать как замену строк на столбцы. Например, рассмотрим наш предыдущий пример, но на этот раз давайте подсчитаем количество точек в каждом столбце:

	4	2	2	1
4
3
1
1

Исходное разбиение равно 4 + 3 + 1 + 1, а сопряженное — 4 + 2 + 2 + 1.

Создание функций

Генерирующие функции могут использоваться для решения некоторых проблем, связанных с разделами. Здесь мы выводим производящую функцию для числа разделов .

Рассмотрите возможность разбиения на слагаемые, равные 1. Производящая функция для этого такова, что существует только один способ представления в виде суммы единиц.

Рассмотрите возможность разделения чисел, используя только 2 в качестве слагаемых. Существует один способ разбить 0 на 2, ноль способов разбить 1 на 2, один способ разбить 2 на 2 и так далее. Следовательно, производящая функция для этого типа разбиения равна .

Таким же образом мы можем найти, что производящая функция для числа способов разбиения на слагаемые равна .

Теперь мы генерируем каждый раздел, выбирая некоторое количество частей равным 1, другое количество частей равным 2 и так далее. Таким образом, мы получаем производящую функцию для статистической суммы путем умножения производящих функций для разбиений только на 1, разбиений только на 2 и так далее.

Это дает нам выражение

.

Используя формулу суммы бесконечной геометрической последовательности, мы можем выразить это в более компактной форме

.

Вариант

Интересная теорема состоит в том, что количество разделов , состоящих только из последовательных положительных целых чисел , равно количеству нечетных делителей .

Доказательство: Пусть будет наименьшая часть в таком разделе и пусть будет количество частей. Тогда у нас есть

, так что

и, наконец,

.

Давайте на мгновение допустим в нашем разделе отрицательные целые числа и обозначим количество нечетных делителей . Теперь рассмотрим два возможных случая:

Случай 1: целое число.

Поскольку выражение в правой части должно быть целым числом, отсюда следует, что . Кроме того, чтобы быть целым числом, оно должно делиться на 2, что означает, что оно нечетное.

Следовательно, пока является нечетным делителем , мы можем найти последовательные целые числа, начиная с которых в сумме получается . Следовательно, в этом случае число решений равно .

Случай 2: не является целым числом.

Чтобы правая часть по-прежнему была целым числом, мы должны иметь некоторое нечетное целое число . Поскольку это не целое число, оно должно быть нечетным и, следовательно, должно быть четным. выражая в форме с быть нечетным целым числом, мы видим, что тогда и только тогда, когда , где любой нечетный делитель . В результате число решений и в этом случае равно .

Объединение двух случаев дает нам решение. Однако сюда входят разделы с отрицательными целыми числами. Однако, поскольку положительно, раздел с отрицательными целыми числами должен иметь вид:

Где . В результате мы можем сократить отрицательные целые числа с соответствующими аддитивными инверсиями, чтобы получить правильное разбиение. Подобие, мы можем перейти от допустимого раздела к разделу, содержащему отрицательные целые числа, добавляя все положительные целые числа перед наименьшим членом вместе с соответствующими аддитивными обратными.

В результате мы установили взаимное соответствие между действительными разбиениями с разбиениями, содержащими отрицательные целые числа.

Поскольку наш подсчет включает все возможные разделы, а количество допустимых разделов равно количеству разделов, содержащих отрицательные целые числа, количество допустимых разделов должно составлять ровно половину нашего первоначального подсчета. Следовательно, общее количество таких разделов равно , что является количеством нечетных делителей .

Ресурсы

• Разделение целых чисел Джозефом Лоренди
• Тета-функция Якоби Саймона Рубинштейна-Сальзедо
• Последовательность A000041 в OEIS — функция разделения

См. также

• Комбинаторика
• Теория чисел

Комбинаторные формулы | Apache OpenOffice Extensions

Комбинаторные формулы | Расширения Apache OpenOffice

Перейти к основному содержанию

Главное меню

Языки

Английский

Авторизоваться

×

Предупреждающее сообщение

Это расширение не обновлялось в последнее время.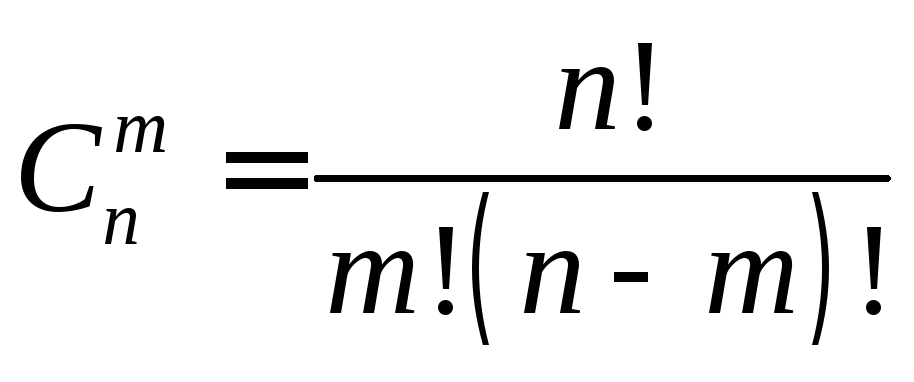 Это может не работать с последними версиями OpenOffice.

• Вид(активная вкладка)
• Выпуски

нейтральный

Расчет

https://www.dropbox.com/s/0jfn4mpku41pa12/Combinatorics-2.0.0.oxt?dl=0

http://kombinatorika.esagil.cz/prakticke-zalezitosti/home-page-for-extesions-com…

Пятница, 13 марта 2015 г. — 13:45

Неделя : Не отслеживается — Месяц : Не отслеживается — Год : Не отслеживается — График

Загрузить расширение

Независимая от системы версия — все выпуски

Совместимость с OpenOffice 4: Да

Отзывы пользователей:
Совместимость с OpenOffice 4. x?

• вверх

  50%

• вниз

  50%

Расширение

содержит макросы для создания формул:
Объединение
Варианты без повторения
Варианты с повторением
Факториал
После создания эти формулы можно использовать в других электронных таблицах, таких как Gnumeric, Excel, и все они совместимы с ECMA International.

Это также является целью данного выпуска. Это также причина для ограничения классов. Минимальный класс «k» 2 и максимальный 10-й

Максимально возможное «n» ограничено 32766 (тип данных INTEGER — комбинация, вариация и т.д.). Только 10 Факториал ограничен 10 («n» = «k»).

Другая цель — представить Факториал не так, как мы привыкли. Поэтому факториал оснащен подстановочным набором, а также потому, что расширение включает три примера приложений для фактириала.

Пользовательские значения вводятся непосредственно в макросы, но в контексте использования в других электронных таблицах требуется ручная модификация потенциала.