Образовательная платформа московских колледжей
Образовательная платформа московских колледжейРесурсы колледжей
- Главная
- Курсы
- Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика
Пройти курс
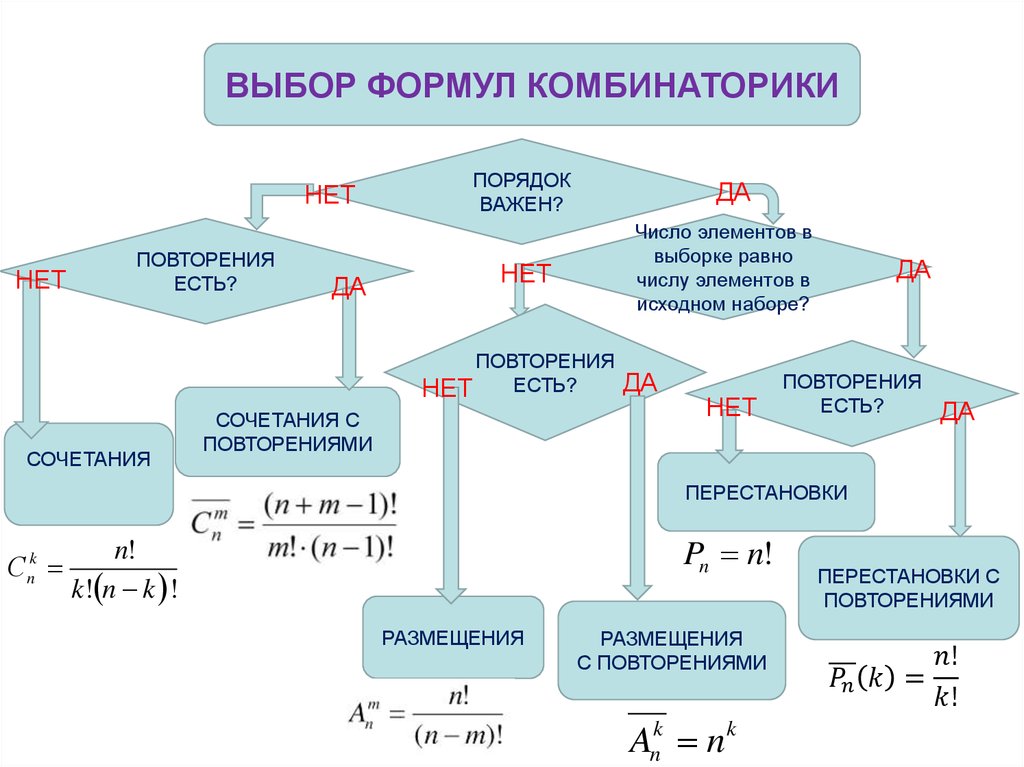
Раздел 1. Теория вероятностей. Тема 1.1. Комбинаторика
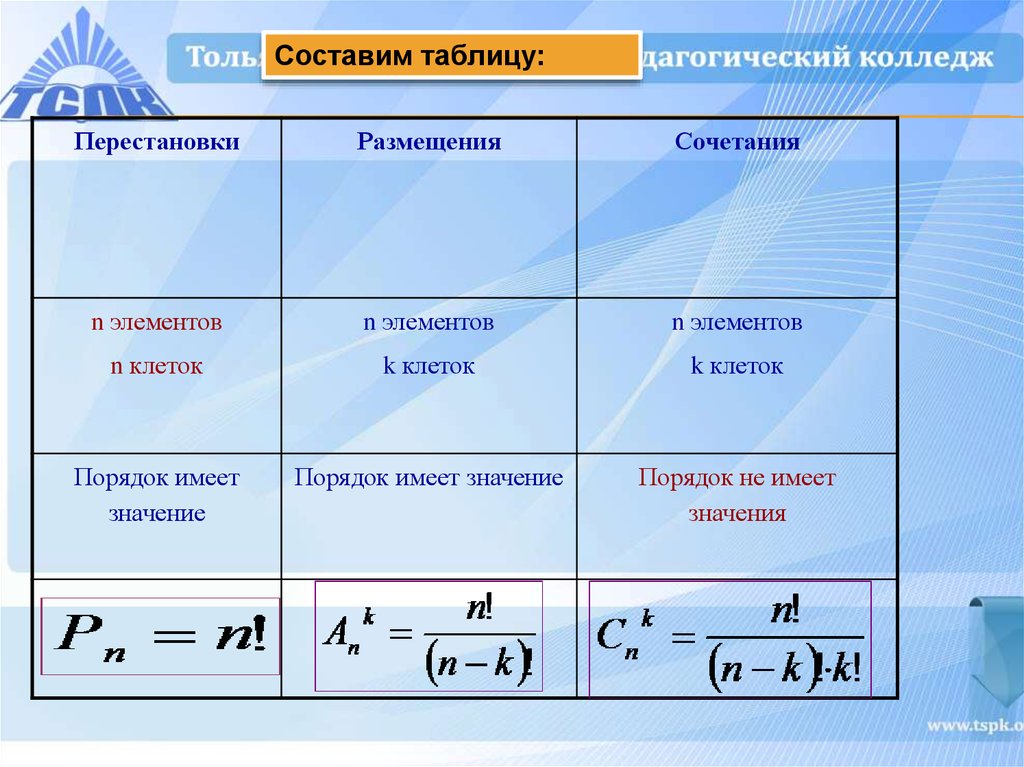
Правила комбинаторики. Сочетания. Размещения. Перестановки
Практическое занятие №1.
Раздел 1. Теория вероятностей. Тема 1.2. Основные понятия и теоремы теории вероятностей. Вероятность случайного события
Случайные события. Виды случайных событий. Вероятность случайного события. Классическое, статистическое и геометрическое определения вероятности события. Вероятность суммы событий. Вероятность произведения событий. Условная вероятность. Формула полной вероятности события. Формула Байеса
Практическое занятие №2. Классическое определение вероятности событий
Практическое занятие №3. Операции над вероятностями
Практическое занятие №4.
Раздел 1.
Теория вероятностей. Тема 1.3. Случайные величины
Дискретные случайные величины. Закон распределения. Числовые характеристики дискретной случайной величины: мода, медиана, математическое ожидание, дисперсия, среднеквадратическое отклонение Практическое занятие №8. Числовые характеристики ДСВ Виды распределений: биноминальное, геометрическое. Распределение Пуассона. Нормальное, равномерное распределение непрерывной случайной величины Практическое занятие №9. Виды распределений ДСВ. Числовые характеристики
Раздел 2.
Математическая статистика. Тема 2.1. Дискретный и интервальный вариационные ряды
Дискретный вариационный ряд. Интервальный вариационный ряд. Числовые характеристики вариационных рядов. Полигон и гистограмма Практическое занятие №10. Полигон и гистограмма. Числовые характеристики
Раздел 2. Математическая статистика. Тема 2.2. Проверка статистических гипотез
Практическое занятие №11. Проверка гипотезы о статистической значимости различий между величинами
Итоговое тестирование
Тест
Модуль
Теория вероятностей и математическая статистика
Занятие
Правила комбинаторики.
Сочетания. Размещения. Перестановки
Материалы
Презентация по теме «Правила комбинаторики. Сочетания. Размещения. Перестановки»
Скачать
Вопросы для самоконтроля
Скачать
НОУ ИНТУИТ | Лекция | Индукция и комбинаторика
< Лекция 11 || Лекция 2: 123
Аннотация: Метод математической индукции. Индукция по структуре объекта. Комбинаторика: число размещений, перестановок и сочетаний. Принцип включения и исключения
Ключевые слова: математическая индукция, доказательство, базис индукции, шаг индукции, неравенство, слово, индукция, дедукция, функция, список операций, глубина формулы, произвольное, комбинаторика, размещения, перестановки, сочетания, треугольник паскаля, биномиальные коэффициенты, бином Ньютона, принцип включения и исключения, тождество
Метод математической индукции
intuit.ru/2010/edi»> Математическая индукция — это весьма общий метод,
который позволяет доказывать утверждения, зависящие от целочисленных параметров. Его можно сформулировать следующим образом.Пусть P(n) — это некоторое утверждение, зависящее от целочисленного параметра n. Пусть, во-первых, утверждение P(n0) справедливо и пусть, во-вторых, для любого k >= n0 из справедливости P(k) следует справедливость P(k+1). Тогда утверждение P(n) справедливо для всех n >= n0.
Таким образом доказательство «по индукции» состоит из двух этапов.
- Базис (или основание) индукции состоит в доказательстве утверждения P(n0) для некоторого начального значения n0 ( обычно n0=1, но это не обязательно).
- Шаг индукции состоит в предположении справедливости P(n) при n=k >= n0 и доказательстве из этого предположения справедливости утверждения P(k+1) .
Рассмотрим несколько примеров применения метода математической индукции.
Пример 1. Доказать, что при n>= 1
Базис индукции. При n=1 имеем
.Шаг индукции. Допустим, что при n=k
Докажем тогда, что при n=k+1
Действительно,
Таким образом, наше утверждение выполненопри всех n>= 1.
Пример 2. Доказать, что для любого , и натурального n>= 2 выполнено неравенство (1+x)n > 1 +nx (это неравенство называют неравенством Бернулли).
- Базис индукции. При , учитывая, что , имеем (1+x)2=1 +2x +x2 > 1+2x.
- Шаг индукции. Допустим, что при n=k неравенство справедливо, т. е. (1+x)k > 1 +kx. Покажем, что тогда оно выполнено и при n=k+1. Действительно, так как 1+x > 0, то умножив обе части на 1+x > 0, получим (1+x)k(1+x)=(1+x) k+1 > (1+kx)(1+x)=1+ (k+1)x +kx2> 1+(k+1)x, что и требовалось.
е. (1+x)k > 1 +kx. Покажем, что тогда оно выполнено и при n=k+1. Действительно, так как 1+x > 0, то умножив обе части на 1+x > 0, получим (1+x)k(1+x)=(1+x) k+1 > (1+kx)(1+x)=1+ (k+1)x +kx2> 1+(k+1)x, что и требовалось.Отметим также, что приведенная формулировка принципа математической индукции
допускает разные эквивалентные варианты.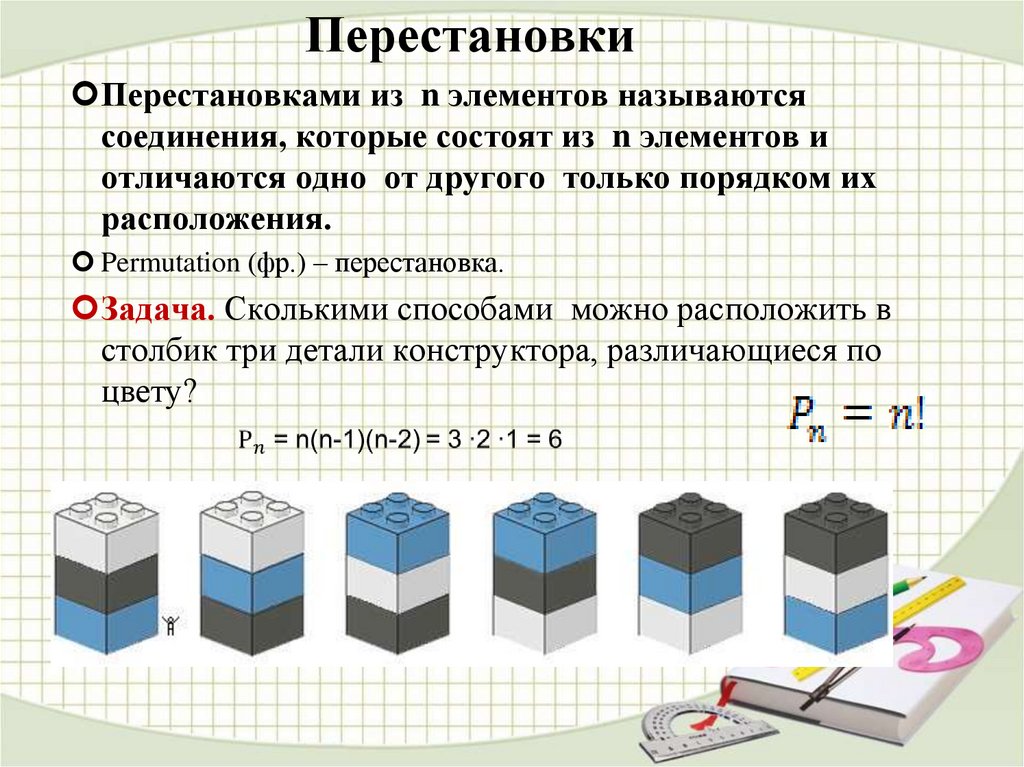
В ряде случаев мы будем использовать
вариант, в котором шаг индукции состоит в предположении справедливости P(n) при всех n <= k и доказательстве из этого
предположения справедливости утверждения P(k+1).
Такая формулировка будет использоваться, в частности, при доказательствах индукцией по построению объекта.
В дискретной математике и в информатике многие классы объектов определяются индуктивно. В таких определениях явно или неявно участвует некоторая функция, задающая «сложность» объекта, и индукция идет по значениям этой функции. На базисном шаге определяются объекты минимальной сложности (обычно они имеют сложность 0), а индукционный шаг определения заключается в том, что из объектов меньшей сложности с помощью некоторых операций (операторов, конструкций) строятся объекты большей сложности.
Для доказательства некоторого свойства объектов индуктивно определенного класса метод математической индукции применяется в следующем виде.
- Базис индукции состоит в проверке требуемого свойства у объектов минимальной сложности.
- Шаг индукции состоит в предположении справедливости доказываемого свойства
- у всех объектов класса, имеющих сложность <= k, и проверке того, что все объекты большей сложности (обычно, сложности k+1 ), получаемые из них с помощью используемых при определении класса операций, также обладают требуемым свойством.
Рассмотрим эту схему на примере простых арифметических выражений.
Пример 2.1.
Пусть V ={x, y, z} — множество переменных, O={+, -, *, / } — список операций.
Определим индуктивно множество выражений
( слов) в объединенном алфавите , называемых
арифметическими формулами. Одновременно будем определять меру сложности
этих формул, назывемую их глубиной.
Глубину формулы обозначим через .
- Базис индукции. Каждая переменная является арифметической формулой глубины 0, т.е. и d(v)=0.
- Шаг индукции. Пусть и — арифметические формулы глубины и , соответственно. Тогда выражения
- (а) ,
- (б) ,
- (в) ,
- (г) ,
также являются арифметическими формулами из и каждая из этих формул имеет глубину .
Пусть w=w1w2 … wn — произвольное слово в алфавите Скажем, что скобки в w расставлены правильно, если для каждого i <= n число левых скобок в слове w(i)=w1w2 … wi не меньше числа правых скобок, а во всем слове w число левых скобок равно числу правых.
Докажем, что в каждой арифметической формуле из
скобки расставлены правильно.
- Базис индукции. . Формула глубины 0 является переменной . В ней нет скобок и поэтому они расставлены правильно.
- Шаг индукции. Пусть утверждение справедливо для всех формул из глубины <= k и — произвольная формула глубины . Тогда она имеет одну из четырех форм (а), (б), (в) или (г). Предположим, что . Тогда из определения глубины следует, что и , и по индукционному предположению в обеих формулах и скобки расставлены правильно. Покажем, что и в скобки расставлены правильно. Пусть и . Тогда ,
здесь M= m1+m2 +3 и все символы vi, wj принадлежат алфавиту
Для каждого 1 < i <= m1+1 число левых скобок в t1 … ti на 1 больше числа левых скобок в v1… vi-1, и следовательно, больше числа
правых скобок в этом слове, так все они входят в v1… vi-1. Это же справедливо для слова t1t2 … tm1+2, заканчивающегося символом +.
При m1+2 < i < M
разница между числом левых и правых скобок в t1 … ti не меньше 1,
так как t1= (, а в и скобки расставлены правильно.
Во всем слове число левых и правых скобок совпадает, так как
к скобкам и добавилась одна левая и одна правая скобка.
Таким образом, в скобки расставлены правильно. Случаи (б), (в) и (г)
рассматриваются аналогично.
Это же справедливо для слова t1t2 … tm1+2, заканчивающегося символом +.
При m1+2 < i < M
разница между числом левых и правых скобок в t1 … ti не меньше 1,
так как t1= (, а в и скобки расставлены правильно.
Во всем слове число левых и правых скобок совпадает, так как
к скобкам и добавилась одна левая и одна правая скобка.
Таким образом, в скобки расставлены правильно. Случаи (б), (в) и (г)
рассматриваются аналогично.Задачи
Задача 2.1. Доказать, что
Задача 2.2. Доказать, что
Задача 2.3. Доказать, что
Задача 2.4. Доказать, что n различных прямых на плоскости разбивают ее на области,
которые можно закрасить белой и черной красками так, что смежные области
будут закрашены разными красками.
Задача 2.5. Найдите ошибку в следующем доказательстве «по индукции» утверждения:
для всех n >= 1 справедливо неравенство 3n > 3(n +1) +1 .
Доказательство Пусть для некоторого k >= 1 неравенство справедливо, т.е. 3k > 3(k +1) +1 (*). Докажем, что оно верно и для n=k+1, т.е. 3k+1 > 3(k+2) +1. Для этого заметим, что для любого k >= 1 верно неравенство 2 cdot 3k > 3. Прибавив его левую и правую часть к соответствующим частям неравенства (*), получим 3k + 2 x 3k > 3(k +1) +1+3 или 3 k+1 > 3(k+2) +1, что и требовалось. Установите, при каких n справедливо неравенство 3n > 3(n +1)+1.
Дальше >>
< Лекция 11 || Лекция 2: 123
Permutation and Combination — Aptitude Вопросы и ответы
Зачем мне учиться решать вопросы и ответы Aptitude в разделе «Перестановки и комбинации»?
Изучите и попрактикуйтесь в решении раздела вопросов и ответов Aptitude в разделе «Перестановка и комбинация», чтобы улучшить свои навыки, чтобы вы могли пройти собеседования, конкурсные экзамены и различные вступительные тесты (CAT, GATE, GRE, MAT, банковские экзамены, железнодорожные экзамены, д.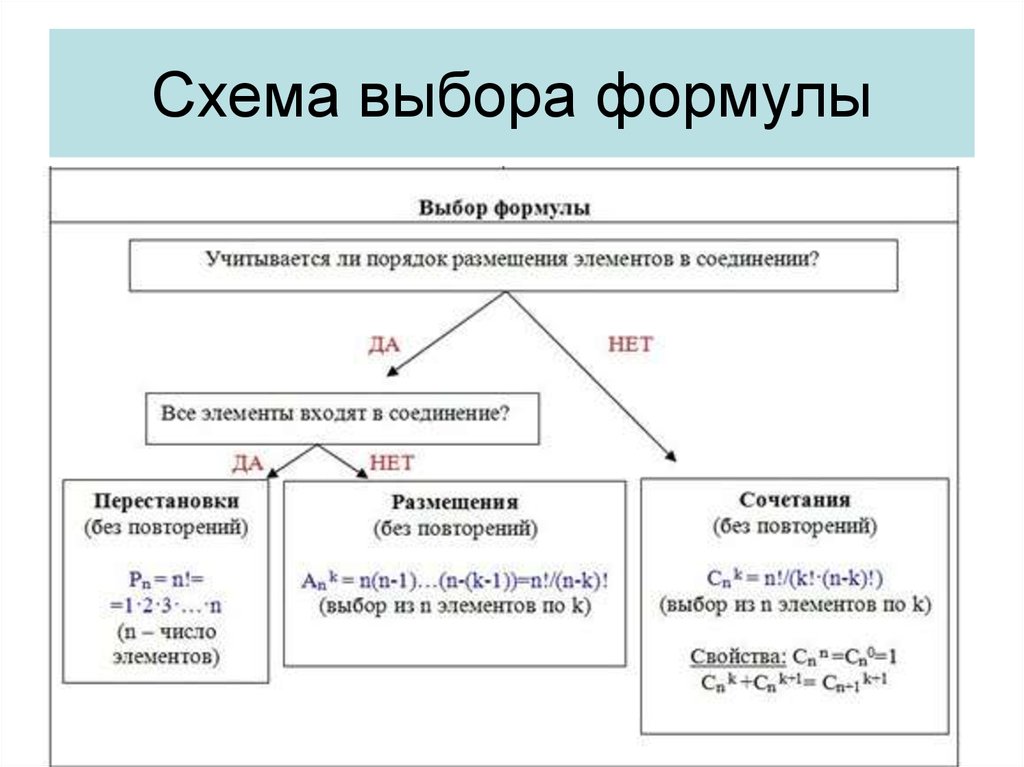
), с полной уверенностью.
Где я могу получить раздел вопросов и ответов Aptitude на тему «Перестановка и комбинация»?
IndiaBIX предоставляет вам множество вопросов и ответов Aptitude, основанных на «Перестановке и комбинации», а также полностью решенные примеры и подробные объяснения, которые будут легко понять.
Где я могу получить раздел о способностях по вопросам и ответам типа MCQ «Перестановка и комбинация» для собеседования (объективный тип, множественный выбор)?
Здесь вы можете найти вопросы и ответы Aptitude с несколькими вариантами ответов на основе «Перестановки и комбинации» для собеседований при приеме на работу и конкурсных экзаменов. Также даны вопросы объективного типа и типа «истина или ложь».
Как загрузить раздел вопросов и ответов Aptitude «Перестановка и комбинация» в формате PDF?
Вы можете загрузить раздел вопросов и ответов викторины Aptitude «Перестановка и комбинация» в виде файлов PDF или электронных книг.
Как решить задачи викторины на способности, основанные на «Перестановке и комбинации»?
Вы можете легко решать задачи викторины на определение способностей, основанные на «Перестановке и комбинации», выполняя данные упражнения, включая сокращения и приемы.
Упражнение: перестановка и комбинирование – общие вопросы
1.
Из группы из 7 мужчин и 6 женщин необходимо выбрать пять человек для формирования комитета таким образом, чтобы в комитете было не менее 3 мужчин. Сколькими способами это можно сделать?
Ни один из этих
Ответ: Вариант
Объяснение:
У нас может быть (3 мужчины и 2 женщины) или (4 мужчины и 1 женщина) или (только 5 мужчин).
| Необходимое количество путей | = ( 7 C 3 x 6 C 2 ) + ( 7 C 4 x 6 C 1 ) + ( 7 C 5 ). | |||||||||||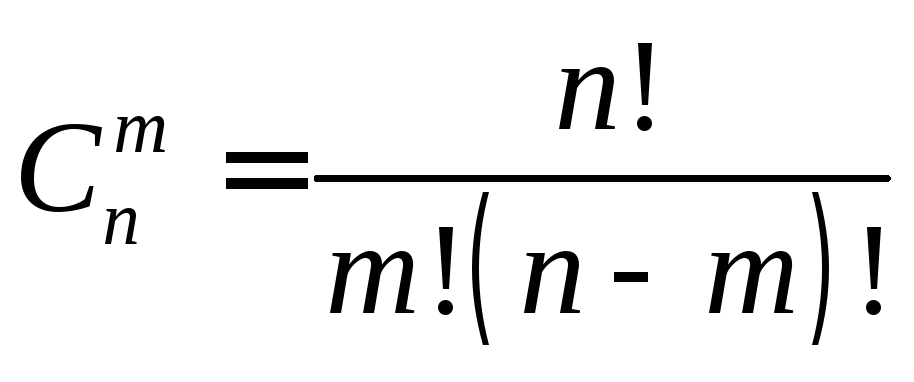
| ||||||||||||
| ||||||||||||
| = (525 + 210 + 21) | ||||||||||||
= 756. |
2.
Сколькими способами можно расставить буквы в слове «НАЧАЛО» так, чтобы гласные всегда совпадали?
Ни один из этих
Ответ: Вариант
Объяснение:
В слове «НАЧАЛО» 7 разных букв.
Когда гласные EAI всегда вместе, можно предположить, что они образуют одну букву.
Затем нам нужно расставить буквы LNDG (EAI).
Теперь 5 (4 + 1 = 5) букв можно составить 5! = 120 способов.
Гласные (EAI) можно расположить между собой по 3! = 6 способов.
Необходимое количество путей = (120 x 6) = 720.
Видео Пояснение: https://youtu.be/WCEF3iW3h3c
3.
Сколькими разными способами могут состоять буквы слова «КОРПОРАЦИЯ» устроить так, чтобы гласные всегда шли вместе?
Ответ: Вариант
Объяснение:
В слове «КОРПОРАЦИЯ» мы рассматриваем гласные OOAIO как одну букву.
Итак, у нас есть CRPRTN (OOAIO).
В нем 7 (6 + 1) букв, из которых R встречается 2 раза, а остальные разные.
| Количество способов расстановки этих букв = | 7! | = 2520. |
| 2! |
Теперь 5 гласных, в которых О встречается 3 раза, а остальные разные, можно расположить
| в | 5! | = 20 способов. |
| 3! |
Необходимое количество путей = (2520 x 20) = 50400.
Видео объяснение: https://youtu.be/o3fwMoB0duw
4.
Сколько слов из 7 согласных и 4 гласных можно ли образовать 3 согласных и 2 гласных?
Ни один из этих
Ответ: Вариант
Объяснение:
Количество способов выделения (3 согласных из 7) и (2 гласных из 4)
| = ( 7 С 3 х 4 С 2 ) | |||||||||
| |||||||||
= 210. |
Количество групп, в каждой из которых 3 согласных и 2 гласных = 210,
Каждая группа содержит 5 букв.
| Количество способов расположения 5 букв между собой | = 5! |
| = 5 х 4 х 3 х 2 х 1 | |
| = 120. |
Необходимое количество путей = (210 х 120) = 25200.
Видео Пояснение: https://youtu.be/dm-8T8Si5lg
5.
Сколькими способами можно составить буквы слова «ЛИДЕР» устроить?
Ни один из этих
Ответ: Опция
Объяснение:
Слово «ЛИДЕР» состоит из 6 букв, а именно 1L, 2E, 1A, 1D и 1R.
| Необходимое количество путей = | 6! | = 360. |
| (1!)(2!)(1!)(1!)(1!) |
Видео объяснение: https://youtu.be/2_2QukHfkYA
Мини-ИБП для Wi-Fi роутера
Бесперебойное резервное питание для существующих Wi-Fi роутеров
Игровые ноутбуки
Ознакомьтесь с новейшими игровыми ноутбуками 💻
Книги для вступительных экзаменов
Книги 📚 для вступительных экзаменов и собеседования
Лучшие Smart TV
Ознакомьтесь с новейшими Smart TV 🖥️
Расширение математики 1. Перестановки и комбинации
Перестановки и комбинации
Определения
Содержание
- 1 Определения
- 2 Принцип фундаментального подсчета
- 2,1 Пример 1
- 2,2 Раствор 1
- 2,3 Пример 2
- 2.4 Раствор 1
- 2,3 Пример 2
- 2.4 2
- 2,3 Пример 2
- 2. 4 2
- 2,3. Пример 3
- 3.2 Раствор 3
- 3.3 Пример 4
- 3.4 Раствор 4
- 3.5 Пример 5
- 3.6 Раствор 5
- 3.7 Пример 6
- 3,8 Решение 6
- 3.9 Пример 7
- 3.10 Решение 7
- 3.11 Пример 8
- 3.12 Решение 8
- 3,13 Пример
- 3,14 раствор
- 3,153887
- 3,14 раствор
- 3,15387
- 3,14.
- 3.18 Решение 11
- 4 Комбинации
- 4.1 Пример 12
- 4.2 Раствор 12
- 4.3. Пример 13
- 4.4 Раствор 13
- 4.5. Пример 140387
- 4.4.0387
- 4,7 Пример 15
- 4,8 раствор 15
- 4,9 Пример 16
- 4,10 Раствор 16
- 4,11 Пример 17
- 4.12 Решение 17
- 4.13 Пример 18
- 4.12 4.
- 4.13. Пример 18
- 4.13. к методам подсчета, используемым в дискретной математике. Перестановки и комбинации включают подсчет количества различных возможных вариантов выбора из набора объектов с учетом определенных ограничений и условий.
Теперь посмотрим, как различать перестановки и комбинации.
Определение : Перестановка — это выбор, в котором порядок выбора объектов важен, и повторение объектов не допускается. Например, выбор ABC отличается от выбора ACB как перестановки.
Определение: Комбинация — это выбор, в котором порядок выбора объектов не важен и повторение объектов не допускается. Например, выбор ABC аналогичен выбору ACB в виде комбинаций.
Чтобы подсчитать количество перестановок и комбинаций, мы, конечно, можем просто перечислить количество различных случаев, а затем просто подсчитать количество различных случаев. Однако этот метод становится утомительным, когда вы имеете дело с большими наборами объектов. Например, учитывая количество комбинаций 3 объектов, выбранных из группы из 10 различных объектов, для этого потребуется 120 различных случаев, которые, конечно, будет довольно утомительно перечислять.
Следовательно, нам необходимо ввести строгий и систематический метод для решения этих задач подсчета.Фундаментальный принцип счета
Этот принцип назван так из-за его важности для теории счета. По сути, этот принцип гласит, что;
, если есть Отдельные способы для выполнения и Q Отличные способы выполнения , а затем в общей сложности . .
Проще говоря, это означает, что при рассмотрении двух взаимоисключающих (независимых) событий общее количество способов выполнения обоих событий равно количеству способов выполнения первого, умноженному на количество способов выполнения второй. Этот принцип также может быть распространен на несколько различных событий. Рассмотрим пример ниже.
Пример 1 Если есть 3 способа добраться в Куала-Лумпур из Сиднея и 4 способа добраться из Куала-Лумпура в Токио, сколькими способами я могу добраться из Сиднея в Токио через.
Решение 1 Куала-Лумпур?Это простой пример фундаментального принципа счета. Рассмотрим приведенную ниже диаграмму (не то чтобы это не обязательно для вашего ответа, но очень помогает).
Итак, согласно фундаментальному принципу подсчета, количество способов добраться до Токио из Сиднея через. Куала-Лумпур дается
Количество путей
В следующем примере показана задача, в которой рассматриваемые случаи не являются независимыми, однако можно применить основной принцип подсчета.
Пример 2 Сколькими способами можно расставить на полке 3 разные книги?
Решение 2В этом вопросе мы снова используем фундаментальный принцип подсчета. Наш аргумент показан на диаграмме ниже.
Есть 3 способа поставить одну из этих книг на первое место, так как есть 3 возможные книги на выбор.
После того, как книга была удалена, есть 2 способа поместить книгу на вторую позицию, так как остается 2 книги на выбор. После того, как вторая книга удалена, остается 1 книга и, следовательно, 1 способ поместить книгу на это последнее место. Следовательно, количество способов расположить эти три книги на полке равно;Количество путей
Перестановки и обозначение факториала
Произведение всех положительных целых чисел, меньших или равных числу, например, обозначается и читается как «факториал». То есть
Итак, в качестве простых примеров у нас есть
, где
По определению, у нас есть это;
Функция факториала имеет область определения, равную неотрицательным целым числам. (Хотя в высшей математике бакалавриата оказывается способ рассмотреть функцию факториала для отрицательных целых чисел и дробных значений). Это обозначение особенно удобно при рассмотрении расположения в линиях или кругах.
Рассмотрим пример ниже.Пример 3 Сколькими способами могут сесть в ряд 6 девушек?
Решение 3В этом случае мы можем провести аналогичную аргументацию, как в примере 2, и выяснить, что ответ равен;
Количество путей
Однако это равно;
В общем случае при расположении отдельных объектов в ряд (повторения не допускаются) мы получаем, что количество расположений или перестановок этих объектов определяется как . Вот если бы у нас были объекты, не все различные, то это другое дело, и на самом деле для такого случая существует формула. Формула приведена ниже.
Если имеется объектов, из которых объектов неразличимы и одного типа, объектов неразличимы и другого типа, а объектов неразличимы и другого типа и т. д. , мы имеем, что количество расположений таких объектов в ряд определяется как,
Хотя это может быть не сразу очевидно, причина деления по значениям и просто исключить все перестановки подобные объекты между собой.
Рассмотрим приведенный ниже пример, иллюстрирующий использование этой формулы.Пример 4 Сколькими способами можно переставить буквы в слове МЛЕКОПИТАЮЩИЕ?
Раствор 4В этом примере мы отмечаем, что есть М и есть А, и что в сумме у нас есть буквы. Используя приведенную выше формулу, мы получаем, что количество расположений букв равно
.Предположим теперь, что мы хотим расположить объекты по кругу. Разница между этим и предыдущим случаем заключается в отсутствии определенной начальной и конечной точек. Из-за этого мы должны назначить один из размещаемых объектов в качестве нашей точки отсчета, и именно тогда мы можем расположить остальные объекты вокруг объекта, выбранного в качестве точки отсчета. Следовательно, при удалении объекта (поместить его в качестве точки отсчета) из общего числа объектов, подлежащих упорядочению, мы получим на один объект меньше, и тогда эти объекты должны быть расположены так же, как это было рассмотрено в примере 2.
Отсюда имеем, что ;Если имеется различных объектов, то общее количество способов, которыми эти объекты можно расположить по окружности, равно .
Пример 5 Сколькими способами можно расположить 5 супружеских пар вокруг круглого стола?
Раствор 5Так как супружеских пар 5, значит, есть и люди, которых можно устроить. Таким образом, общее количество аранжировок равно 9.0005
Предположим теперь, что у нас есть объекты среди тех, которые похожи, и еще один, похожий, и так далее. Число расположений вокруг круга теперь определяется как общее число расположений, деленное на расположение самих подобных объектов. Следовательно, мы имеем это;
Если есть объектов, из которых похожих и еще подобных и еще подобных и т. д., то общее количество расположений этих объектов по кругу равно
Теперь рассмотрим расположение предметов на ожерелье или цепочке для ключей.
Предположим, что мы такие, чтобы расположить отдельные бусины на ожерелье. Общее количество аранжировок равно общему количеству неограниченных аранжировок в круге, деленному на . Деление на связано с симметрией ожерелья, поскольку можно повернуть ожерелье и наблюдать точно такую же перестановку. Следовательно, мы имеем это;Дано предметов, каждый из которых индивидуален, количество расположений этих предметов на ожерелье определяется как,
До сих пор мы рассматривали расположение в ряды и круги, учитывая сходство между некоторыми объектами. Рассмотрим теперь количество расположений объектов при определенных условиях. Напомним, что перестановка объекта — это просто упорядоченный выбор или расположение. Таким образом, мы имеем, что
Количество перестановок объектов, выбирающих за раз, равно;
Обратите внимание, что для формула принимает вид
Таким образом, если кто-то выбирает все объекты в наборе, то общее количество перестановок равносильно размещению всех объектов в линию, что должно быть совершенно очевидным.
Кроме того, эта формула предполагает, что повторения не допускаются. Рассмотрим пример, иллюстрирующий использование этой формулы.Пример 6 Найдите количество расстановок букв в слове КОМПЛЕКС.
Решение 6Поскольку каждая буква различна, отсюда следует, что общее количество таких комбинаций равно
.Обратите внимание, что это точно так же, как и при использовании фундаментального принципа подсчета, здесь количество способов определяется как .
Теперь мы собираемся рассмотреть несколько примеров вопросов, которые включают перестановки при определенных условиях. Студенты, как правило, испытывают трудности в понимании используемых методов, поскольку каждый вопрос должен решаться сам по себе. Лучший способ освоить такие вопросы — подвергнуть себя как можно большему количеству примеров.
Пример 7 В скачках трифекта — это выбор первых трех борзых в скачках в правильном порядке.
Раствор 7 Сколькими способами это можно сделать, если есть 8 лошадей?В этом вопросе мы выбираем группу с важным порядком из набора . Использование формулы для перестановок дает
Пример 8 Сколькими способами можно расположить в ряд 5 девочек и 3 мальчиков, если:
а) мальчики должны сидеть рядом друг с другом?б) мальчики не должны сидеть рядом друг с другом?
Раствор 8а) Если мальчики должны сидеть рядом друг с другом, то мы можем рассматривать мальчиков как единое целое. Таким образом, используя эту технику, мы имеем общее количество объектов для перестановки в строке, общее число перестановок равно . Так вот, сами мальчики могут быть организованы вокруг себя внутри своего отряда, и это можно сделать разными способами. Таким образом, согласно фундаментальному принципу подсчета, общее количество способов расположить их таким образом равно 9.
0005b) Теперь, если мальчики НЕ должны сидеть рядом друг с другом, мы можем просто рассмотреть дополнительное событие .
Пусть изобразим мальчиков, сидящих рядом друг с другом, и изобразим мальчиков, не сидящих рядом друг с другом.
Пусть обозначает количество возможных вариантов .Отсюда имеем
Где дополнительное событие. Таким образом, у нас есть
То есть количество способов, которыми мальчики НЕ садятся рядом друг с другом, равно .
Примечание: Не попадайтесь в обычную ловушку перечисления случаев и последующего подсчета возможных договоренностей в каждом случае. Это бесполезно и утомительно. Если возможно, всегда сначала смотрите на дополнительное событие.
Пример 9 Сколькими способами можно расположить буквы слова ВСТРЕЧА, если гласные и согласные стоят попеременно?
Раствор 9Так как 3 гласных и 4 согласных, то все аранжировки имеют вид
, где C представляет согласную, а V представляет гласную.
Теперь сами гласные могут располагаться в своих собственных возможных позициях в общей сложности способами из-за того, что существует два А, и, таким образом, в этом случае нам нужно разделить между расположениями самих А. Согласные могут располагаться между собой в отведенных им позициях в общей сложности способами. Следовательно, общее количество аранжировок определяется выражением;
Следующий пример включает повторения.
Пример 10 Сколько существует различных автомобильных номерных знаков, если каждый из них содержит 3 согласные буквы алфавита, за которыми следуют три цифры?
Раствор 10Необходимо заполнить шесть мест. В первых трех местах может стоять согласная, а это означает, что одна из 21 возможных букв может встречаться в каждой из первых трех позиций. В последних трех позициях в каждую из позиций может входить по 10 возможных чисел.
Обратите внимание, что в этом случае допускаются повторы.Теперь мы рассмотрим вероятностный вопрос о перестановках. Напомним, что вероятность события определяется как
, где выборочное пространство представляет собой множество всех возможных исходов.
Пример 11 Мистер и миссис Смит и гости сидят за круглым обеденным столом. Найдите вероятность того, что два хоста вместе.
Раствор 11Итак, чтобы решить этот вопрос, нам нужно найти общее количество способов, которыми можно расположить людей, и это становится количеством элементов в пространстве выборки. Затем нам нужно найти нет. способов, которыми хозяева могут быть вместе.
Чтобы найти количество способов, которыми хозяева могут быть вместе, мы просто рассматриваем их как одну единицу, после чего у нас остается 7 объектов, а затем рассматриваем возможные перестановки вокруг круглого обеденного стола.
Напомним, что пара также может договориться между собой.Таким образом, мы имеем, что вероятность того, что хосты вместе, определяется выражением
Комбинации
Напомним, что комбинация — это выборка, в которой порядок объектов не важен. Количество комбинаций объектов, всех различных, взятых за раз, определяется как
и читается как «выбрать». Популярная альтернативная запись для этого:
Теперь мы рассмотрим несколько примеров, иллюстрирующих использование этой формулы.
Пример 12 В скачках quinella означает выбор первых двух лошадей в любом порядке. Найдите количество возможных вариантов квинеллы в скачках 8 лошадей, предполагая, что все лошади имеют равные шансы на победу.
Раствор 12Итак, мы выбираем по два из набора из восьми объектов, не обращая внимания на порядок. Это равно
Следовательно, существует 28 вариантов квинеллы.
Вопросы, связанные с комбинациями, могут подразумевать ограничения на возможные варианты выбора. Мы рассмотрим несколько примеров, чтобы проиллюстрировать некоторые возможные типы вопросов.
Пример 13 Сколькими способами можно выбрать комитет префектов мальчиков и девочек из группы мальчиков и девочек?
Раствор 13В этом вопросе мы выбираем из группы и затем выбираем из группы . В каждом случае порядок не важен. Обратите внимание, что мы умножим два на фундаментальный принцип подсчета. Количество таких комитетов префектов составляет 9.0005
Примечание: Студенты часто спрашивают, когда умножать результаты и когда их складывать (например, в приведенном выше примере мы умножали их). Как правило, результаты добавляются, если между двумя событиями есть соединение «и», а результаты добавляются, если между событиями есть соединение «или».
Рассмотрим пример ниже для примера «или».Пример 14 Найдите количество способов выбрать 3 буквы из букв слова УПРАЖНЕНИЕ.
Раствор 14Поскольку букв Е три, мы должны разбить это на падежи. Каждый случай классифицируется как один из следующих случаев: (1) нет двойных или троек, (2) присутствует один двойной или (3) присутствует один тройной. Этот прием особенно важен в Mathematics Extension 2.
Нет двойных или троек:
Мы должны выбрать три буквы из E , X , R , C , I , S. Количество способов сделать это равно
Только один двухместный номер:
Итак, у нас есть две Е в нашей тройке, и теперь нам нужно выбрать одну букву из букв X, R, C, I, S, так как мы не можем выбрать другую Е, так как это сделает ее тройкой, которая является отдельный случай. Количество способов сделать это равно
.Только один тройной:
Существует только один способ выбрать группу, содержащую три буквы E.
Так как других возможностей нет.Таким образом, общее количество комбинаций равно
Пример 15 Сколько диагоналей имеет -угольник (двусторонний многоугольник)?
Раствор 15Количество имеющихся диагоналей равно количеству способов, которыми мы можем выбрать две точки с неважным порядком, минус количество сторон. Это связано с тем, что при выборе двух точек у нас автоматически получается линия, проходящая через эти точки, и, таким образом, она представляет собой диагональ. Конечно, те линии, которые образуют стороны многоугольника, затем удаляются из общего подсчета. Таким образом, общее количество диагоналей равно 9.0005
Теперь мы рассмотрим несколько примеров, включающих как комбинации, так и перестановки. В этих примерах иногда можно с большим успехом использовать фундаментальный принцип счета.
Однако фундаментальный принцип подсчета не обязательно является самым простым способом решения каждой проблемы. Обратите внимание на приведенные ниже примеры. Опять же, лучший способ справиться с этими проблемами — решить их много.Кроме того, с этого момента во всех экзаменационных вопросах учащимся следует опасаться повторений. Студенты должны всегда спрашивать себя, разрешено ли повторение или нет. Часто на этот вопрос легко ответить, однако учащиеся все равно должны практиковать различие между ними.
Пример 16 Рассмотрим слово РИМАН. Сколько слов из 4 букв можно составить из ;
а) Нет.
б) один номер
c) обе N
Раствор 16а) Мы должны переставить четыре буквы из букв R , I , E , M , A. Всего способов
.Обратите внимание, что мы сначала выбираем 4 из 5 букв, а затем распределяем их соответствующим образом.
b) Здесь у нас уже есть одна N, что означает, что теперь мы должны выбрать три из R , I , E , M , A.
После того, как мы выбрали буквы, нам нужно расположить эти буквы соответствующим образом, включая N, который уже присутствует как один из четырех. Следовательно, общее количество способов равно;c) Здесь у нас уже есть две буквы N, и поэтому нам нужно выбрать две буквы из букв R, I, E, M, A. После того, как мы выбрали буквы, нам нужно переставить эти буквы с двумя буквами N. Имейте в виду, что в этом случае мы должны разделить общее количество перестановок на , так как N встречается дважды. Таким образом, общее количество таких договоренностей равно;
Пример 17 Сколькими способами можно распределить 6 разных книг между двумя учениками, если оба ученика получат хотя бы по одной книге?
Раствор 17Для этого вопроса мы составили таблицу, в которой указано количество книг, которые получает каждый учащийся, и количество возможных способов распределения книг в каждом случае.
Дело №. Кол-во книг у студента А Количество книг, которые есть у студента Б Количество способов получения книг 1 1 5 2 2 4 3 3 3 4 4 2 5 5 1 КОМБИНЕЗОН Таким образом, общее количество способов распространения книг равно 62.
Пример 18 Четыре семьи прибывают на курорт, где есть 4 мотеля.
а) Если нет ограничений на то, где они останавливаются, сколько существует различных вариантов размещения?
b) Если каждая семья останавливается в разных мотелях, сколько возможных вариантов размещения?
c) Две семьи являются близкими друзьями и хотят остановиться в одном мотеле.
4 2
Следовательно, нам необходимо ввести строгий и систематический метод для решения этих задач подсчета.
Куала-Лумпур?
После того, как книга была удалена, есть 2 способа поместить книгу на вторую позицию, так как остается 2 книги на выбор. После того, как вторая книга удалена, остается 1 книга и, следовательно, 1 способ поместить книгу на это последнее место. Следовательно, количество способов расположить эти три книги на полке равно;
Рассмотрим пример ниже.
Рассмотрим приведенный ниже пример, иллюстрирующий использование этой формулы.
Отсюда имеем, что ;
Предположим, что мы такие, чтобы расположить отдельные бусины на ожерелье. Общее количество аранжировок равно общему количеству неограниченных аранжировок в круге, деленному на . Деление на связано с симметрией ожерелья, поскольку можно повернуть ожерелье и наблюдать точно такую же перестановку. Следовательно, мы имеем это;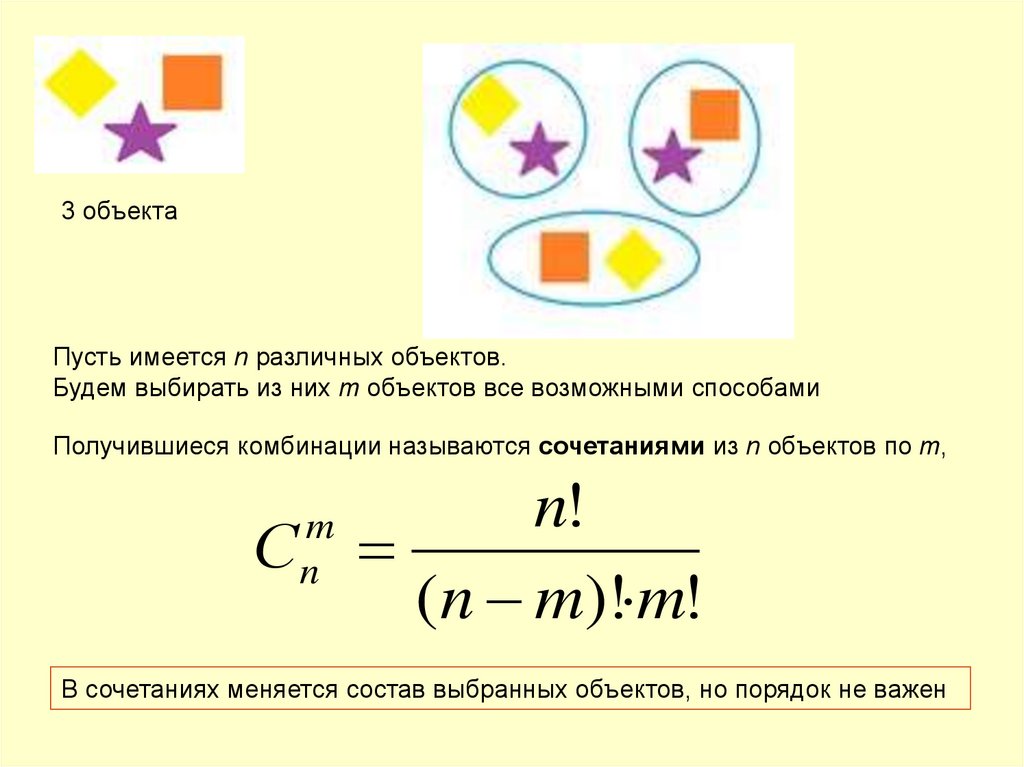
Кроме того, эта формула предполагает, что повторения не допускаются. Рассмотрим пример, иллюстрирующий использование этой формулы.
Сколькими способами это можно сделать, если есть 8 лошадей?
0005
Обратите внимание, что в этом случае допускаются повторы.
Напомним, что пара также может договориться между собой.
Рассмотрим пример ниже для примера «или».
Так как других возможностей нет.
Однако фундаментальный принцип подсчета не обязательно является самым простым способом решения каждой проблемы. Обратите внимание на приведенные ниже примеры. Опять же, лучший способ справиться с этими проблемами — решить их много.
После того, как мы выбрали буквы, нам нужно расположить эти буквы соответствующим образом, включая N, который уже присутствует как один из четырех. Следовательно, общее количество способов равно;
