Комбинаторные задачи примеры: Задачи по комбинаторике. Примеры решений

Примеры комбинаторных задач

Урок 26. Алгебра 9 класс ФГОС

На этом уроке вводиться определение комбинаторики. Рассматриваются примеры решения комбинаторных задач. Формулируется комбинаторное правило умножения и демонстрируется решение задач с его применением.

Конспект урока «Примеры комбинаторных задач»

Определение:

Комбинаторика — это раздел математики, который изучает, сколько различных комбинаций можно составить из заданных объектов.

Пример.

На семейном шахматном турнире Ульяна, Ярослава, Архип и Захар сыграли друг с другом только по одной партии. Сколько партий было сыграно?

Для краткости имена будем обозначать первой буквой.

Опишем состав партий, в которых принимала участие Ульяна. Получим 3 пары. Далее опишем состав партий, в которых участвовала Ярослава, но не принимала участия Ульяна. Так как пара Ульяна — Ярослава уже записана. Таким образом, получаем 2 новых пары. Запишем пары, в которые входит Архип, но не входят Ульяна и Ярослава. Получим только 1 пару. Других вариантов составления пар нет, так как все пары, куда входит Захар, уже составлены.

Итак, мы получили шесть различных пар, то есть было сыграно шесть партий.

Способ рассуждений, которым мы воспользовались при решении задачи, называют перебором возможных вариантов.

Пример.

Определить, сколько различных трёхзначных чисел можно составить, используя цифры 2, 6, 8 и 9. При этом цифры в числе не должны повторяться.

Первой цифрой числа может быть любая из данных цифр. Поставим на первое место, например, цифру 2. Тогда на втором месте могут стоять цифры 6, 8 или 9. Если на втором месте стоит цифра 6, то на третьем соответственно могут быть цифры 8 или 9. Так мы получим 2 числа: 268 и 269.

Если на втором месте стоит цифра 8, то на третьем может быть 6 или 9.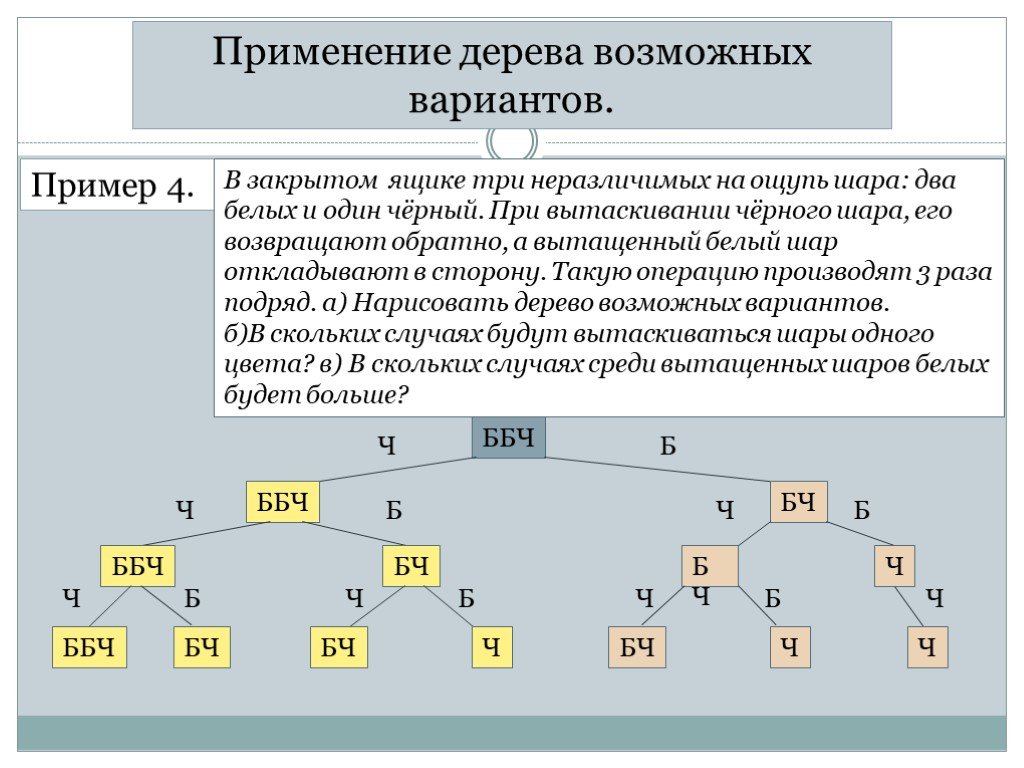

Также получим два числа.

И если на втором месте стоит 9, то третьей цифрой числа могут быть 6 или 8.

Аналогично можно расписать возможные варианты, если первой цифрой числа являются 6, 8 или 9.

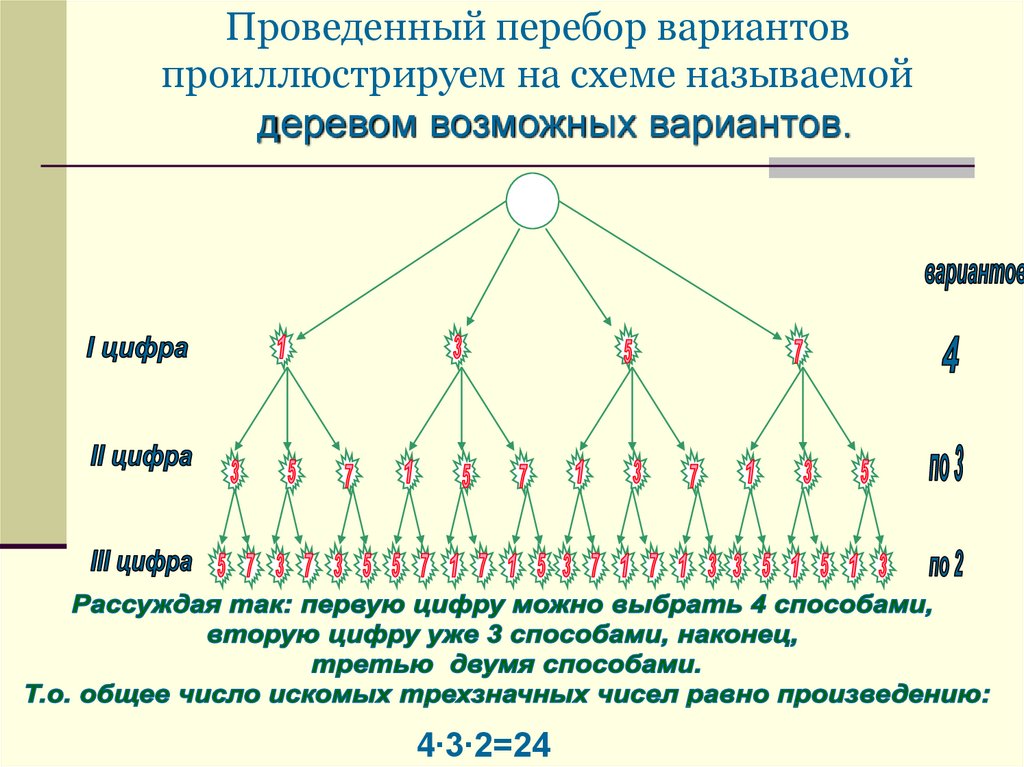
Схему, которую мы построили при решении задачи, называют деревом возможных вариантов.

Получили 24 различных трёхзначных числа.

Можно было по-другому решить задачу. Рассуждая так: первую цифру мы выбираем четырьмя способами, вторую тремя, так как после выбора первой осталось три цифры. А третью — двумя. Получаем, что общее количество искомых трёхзначных чисел равно двадцати четырём.

В данном случаи, воспользовались комбинаторным правилом умножения.

Комбинаторное правило умножения:

Пусть имеется n элементов и требуется выбрать из них один за другим k элементов. Если первый элемент можно выбрать  способами, после чего второй элемент можно выбрать  способами из оставшихся, затем третий элемент можно выбрать  способами из оставшихся и так далее, то число способов, которыми могут быть выбраны

k элементов, равно:

Пример.

На окружности отмечены 10 точек. Сколько можно провести незамкнутых не самопересекающихся девятизвенных линий с вершинами во всех этих точках?

Рассмотрим примеры линий, которые мы можем проводить. Возьмём некоторую точку. Чтобы все точки являлись вершинами ломанной, и эта линия была незамкнута и не самопересекающаяся, то второй точкой мы должны взять одну из соседних. Для удобства пронумеруем точки:

Чтобы найти количество различных таких линий, воспользуемся комбинаторным правилом умножения.

Первую точку мы можем выбрать 10 способами, вторую — 9, и так до девятой точки. Ну, а десятую точку мы выбираем 1 способом, так как она остаётся одна.

Вычислим количества линий:

Пример.

У маляра в наличии три банки с красками разного цвета. Ему нужно покрасить забор, состоящий из 10 досок так, чтобы любые две соседние доски были разных цветов, и при этом были использованы краски всех трёх цветов. Сколькими способами он может выполнить поручение?

При выборе цвета для первой доски у нас будет три варианта. Тогда вторую доску мы сможем окрасить в один из двух оставшихся цветов. И так далее.

Тогда, пользуясь комбинаторным правилом умножения, получим, что для определения количества способов выполнения поручения, необходимо вычислить значение выражения:

Предыдущий урок 25 Формула суммы первых n членов ГП

Следующий урок 27 Перестановки

Получите полный комплект видеоуроков, тестов и презентаций Алгебра 9 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Примеры комбинаторных задач.

9 класс

1. Примеры комбинаторных задач

9 класс
Тема урока:
Примеры комбинаторных задач
1 урок
В науке и на практике часто встречаются задачи,
решая которые приходится составлять различные
комбинации из конечного числа элементов и
подсчитывать число комбинаций.
Такие задачи получили название комбинаторных
задач, а раздел математики, в котором
рассматриваются эти задачи, называют
комбинаторикой.
2
Раздел математики,
в котором изучают
комбинаторные задачи,
называется
комбинаторикой
3
б
о
— раздел математики, в котором
изучаются вопросы о том, сколько
различных комбинаций,
подчинённых тем или иным
условиям, можно составить из
заданных объектов.
4
Термин «комбинаторика» происходит от
латинского слова «combina», что в переводе на
русский означает – «сочетать», «соединять».
Термин «комбинаторика»
был введён в
математический обиход
немецким философом,
математиком Лейбницем,
который в 1666 году
опубликовал свой труд
«Рассуждения о
комбинаторном искусстве».
06.04.2020
5
Познакомимся с некоторыми
приемами решения комбинаторных задач
решение методом перебора;
решение с помощью дерева возможных
вариантов;
решение с помощью комбинаторного
правила умножения;
решение с помощью таблиц;
решение с помощью графов.
6
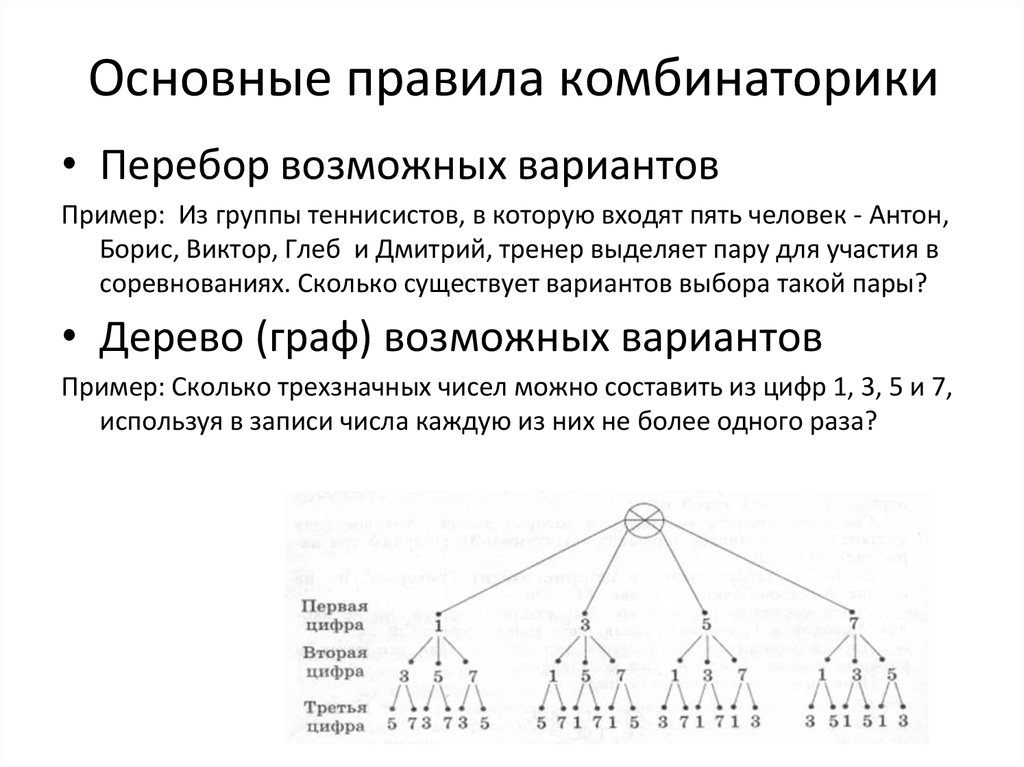
№715
У Ирины 5 подруг: Вера, Зоя, Марина, Полина
и Светлана. Она решила двух из них
пригласить в кино. Укажите все возможные
варианты выбора подруг. Сколько таких
вариантов?
Замечание. При решении для краткости будем
писать первые буквы имен.
7
Решение
Вера Зоя Марина Полина Света
Составим сначала все пары, в которые входит Вера.
ВЗ, ВМ, ВП, ВС Получим 4 пары.
Выпишем теперь пары, в которые входит Зоя, но не
входит Вера. ЗМ, ЗП, ЗС Таких пар три.
Далее составим пары, в которые входит Марина, но не
входят Вера и Зоя. МП, МС Их две.
Далее составим пары, в которые входит Полина.
Еще одна пара
ПС
Всего существует 4+3+2+1=10
Ответ:10 вариантов
8
Способ рассуждений, которым мы воспользовались при
решении задачи, называют перебором возможных
вариантов.
Рассмотрим еще одну задачу. На цветочной клумбе
сидели шмель, жук, бабочка и муха. Два насекомых
улетели. Какие пары насекомых могли улететь?
Укажите все возможные варианты. Сколько таких
вариантов?
ш
06.04.2020
м
ж
б
9
Решение
ш
ж
ж
б
ш
б
ж
м
б
м
Всего 3+2+1=6
ш
м
Ответ:6 вариантов
10
Приемы решения комбинаторных задач
метод перебора
Сколько двузначных чисел можно
составить, используя цифры 1; 4; 7?
Решение: Для того, чтобы не пропустить и не
повторить ни одного из чисел, будем выписывать
их в порядке возрастания:
11;14;17; (начали с 1)
41;44;47; (начали с 4)
71;74;77; (начали с 7)
Таким образом, из трёх данных цифр можно
составить всего 9 различных двузначных чисел.
Ответ: 9 чисел.
11
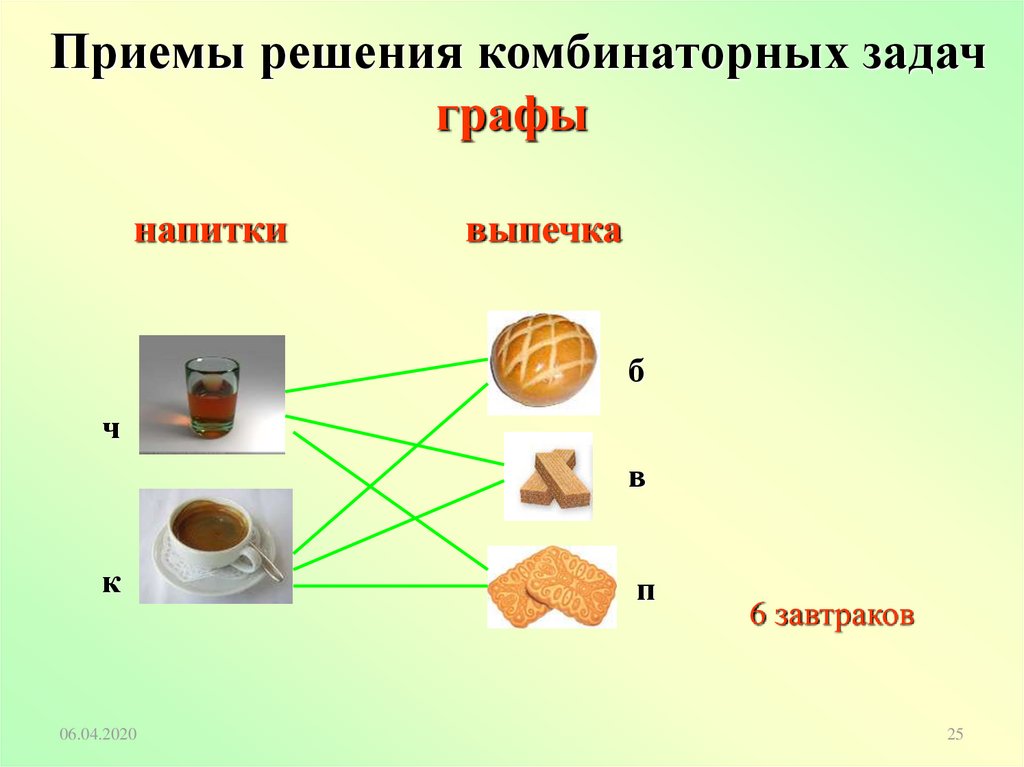
Решим аналогичную задачу о составлении трехзначных
чисел из цифр 1;4;7, так чтобы цифры не повторялись.
Для её решения построим схему — дерево возможных
вариантов.
число
4
1
4
7
7
1
4
7
7
7
1
1
4
4
1
Ответ: числа 147;174;417;471;714;741
6 чисел (вариантов)
Приемы решения комбинаторных задач
дерево возможных вариантов
12
Заметим, что ответ на вопрос, можно получить, не
выписывая сами числа. Будем рассуждать так.
Первую цифру можно выбрать тремя способами.
Так как после выбора первой цифры останутся две,
то вторую цифру можно выбрать двумя способами.
Остается приписать одну цифру. Следовательно,
общее число искомых трехзначных чисел равно
произведению
3 2 1 6
13
Мы нашли ответ на вопрос, используя так называемое
комбинаторное правило умножения
«Если объект А можно выбрать m способами,
а другой объект В можно выбрать k
способами, то объект «А и В» можно выбрать
m ∙ k способами».
14
комбинаторное правило умножения
У Куклы Светы 3 юбки и 5 кофт, удачно сочетающихся по
цвету. Сколько различных комбинаций одежды имеется у
Светы?
Решение. 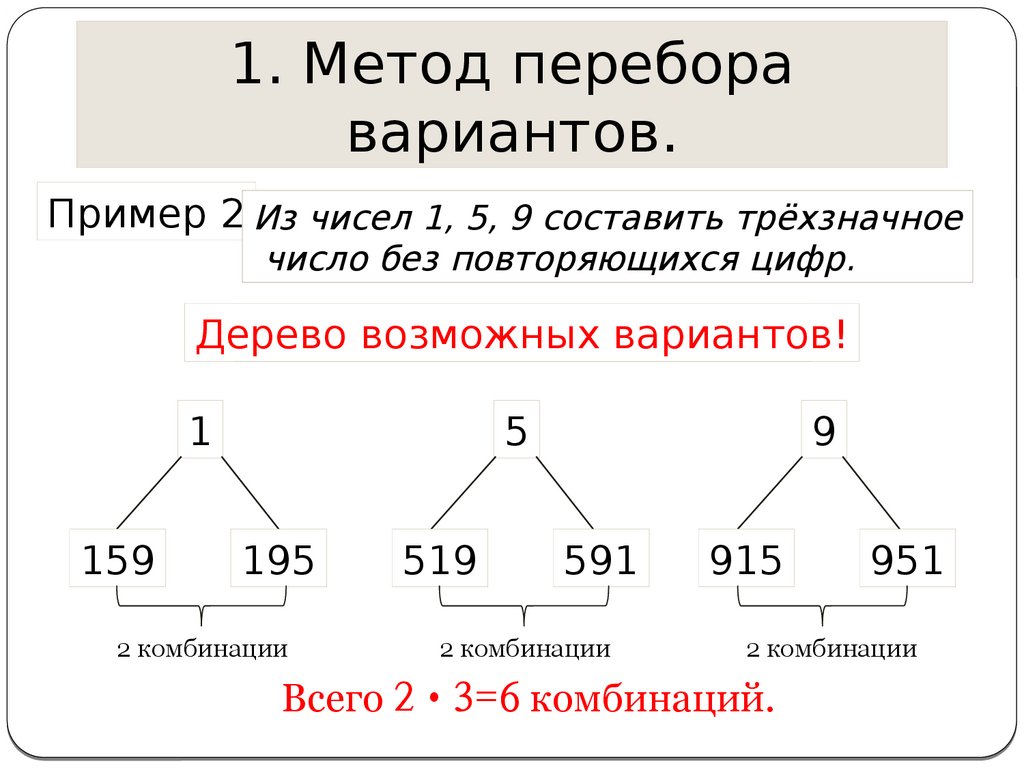3·5 = 15
15
Решите задачу, используя
дерево возможных вариантов
В класс пришли четыре новых ученика Миша, Катя,
Вася, Лиза. С помощью дерева возможных вариантов
покажи, все возможные варианты расположения
четырех учеников за одной партой. Сколько вариантов
выбора будет?
К
06.04.2020
М
В
Л
16
4 3 12
Решение
М
К
В
Л
Ответ: 12 вариантов
17
С помощью дерева возможных вариантов решите
задачу №714.
Обед
Борщ
Гуляш
Котлеты
Рассольник
Гуляш
Котлеты
Сосиски
Пельмени
Сосиски
Пельмени
Ответ : 2 4 8 ( вариантов )
06.04.2020
18
Приемы решения комбинаторных задач
задачи, решаемые с помощью таблиц
У Миши 4 ручки разного цвета и 3 блокнота
разного размера. Сколько различных наборов из
ручки и блокнота сможет составить Миша? Реши
задачу, составив таблицу.
б
с
з
м
с
ч
к
19
з
ч
к
с
б
с
м
12 различных наборов
20
Приемы решения комбинаторных задач
задачи, решаемые с помощью таблиц
Сколько четных двузначных чисел можно составить
из цифр 0,1,2,4,5,9?
0
2
4
1
10
12
14
2
20
22
24
4
40
42
44
5
50
9
90
52
92
Ответ:15 чисел (5·3)
54
94
21
б
о
ГРАФ – совокупность объектов со связями между
ними. Объекты представляются как вершины, или
узлы графа, а связи – как дуги, или ребра.
вершины
ребра
22
Пятеро друзей встретились после каникул и
обменялись рукопожатиями. Каждый, здороваясь,
пожал руку. Сколько всего было сделано
рукопожатий?
Ответ:10 рукопожатий
06.04.2020
23
Решите задачу, используя граф
Сколько различных завтраков, состоящих из 1
напитка и 1 вида выпечки, можно составить
из чая, кофе, булочки, печенья и вафель?
в
ч
б
п
к
06.04.2020
24
Приемы решения комбинаторных задач
графы
напитки
выпечка
б
ч
в
к
06.04.2020
п
6 завтраков
25
Эту же задачу можно решить, используя
дерево возможных вариантов
ч
б
06.04.2020
п
к
в
б
п
в
26
Решение задачи с помощью таблицы
Напитки
ч
Выпечка
06.04.2020
б
б
п
п
в
в
к
б
ч
ч
ч
к
п
в
к
к
27
Решите задачу, используя граф
Шесть семей уехали отдыхать в разные города. Приехав
к месту отдыха, они поговорили друг с другом по
телефону. Сколько звонков было сделано?
28
Закончи построение графа, соответствующего
данной задаче.
06.04.2020
29
Приемы решения комбинаторных задач
графы
Ответ:15 звонков
30
Приемы решения комбинаторных задач
задачи, решаемые с помощью таблиц
1
2
3
4
5
6
1
–
2
–
–
3
–
–
–
4
–
–
–
–
5
–
–
–
–
–
–
–
–
–
–
6
–
Ответ:15 звонков
31

32. Домашнее задание:

• п. 30
• № 716 (перебор), 720 (дерево), 723 (граф),
725 (таблица), 727 (умножение).
Приемы решения комбинаторных задач
дополнительные задачи
Задача 1
В магазине продают воздушные шары: красные,
желтые, зеленые, синие. Какие наборы можно
составить из двух разных шаров? Сколько наборов
у тебя получилось?
Задачи, решаемые
методом
организованного перебора
33
Задача 1
5 наборов
06. 04.2020
34
Приемы решения комбинаторных задач
Задача 2
В парке 4 пруда. Было решено засыпать песком
дорожки между ними так, чтобы можно было
пройти от одного пруда к другому кратчайшим
путем, т.е. не нужно было идти в обход.
Графы
Задание: покажи, какие дорожки надо сделать.
06.04.2020
35
Решение
06.04.2020
36
Приемы решения комбинаторных задач
В танцевальном кружке занимаются пять
девочек: Женя, Маша, Катя, Юля и Даша и
пять мальчиков: Олег, Вова, Стас, Андрей и
Иван. Сколько различных танцевальных пар
можно составить? Заполни таблицу.
Задачи, решаемые
с помощью таблиц
37
Женя
Маша
Катя
Юля
Даша
Олег
Олег
Женя
Олег
Маша
Олег
Катя
Олег
Юля
Олег
Даша
Вова
Вова
Женя
Вова
Маша
Вова
Катя
Вова
Юля
Вова
Даша
Стас
Стас
Женя
Стас
Маша
Стас
Катя
Стас
Юля
Стас
Даша
Андрей
Женя
Андрей
Маша
Андрей
Катя
Андрей
Юля
Андрей
Даша
Иван
Женя
Иван
Маша
Иван
Катя
Иван
Юля
Иван
Даша
Андрей
Иван
Ответ: 25 пар
38
Задачи, решаемые с помощью таблиц
На завтрак Миша может выбрать: плюшку, бутерброд,
пряник, или кекс, а запить он может: кофе, соком,
кефиром. Сколько возможных вариантов завтрака?
06.04.2020
Ответ:12 (4·3=12)
39
Существует много видов
комбинаторных задач, это лишь
некоторые из них.
Спасибо за внимание!
06.04.2020
Логинова Н.В. МБОУ «СОШ №16»
40

Некоторые задачи комбинаторной оптимизации

Содержание

• Проблема суммы подмножеств
• Проблема с разделом
• Недостатки этих примеров
• Раскраска графика
  • Генератор низкого давления LINDO

Здесь мы упомянем некоторые примеры задач моделирования в комбинаторике. используя линейные программы с бинарными переменными , то есть переменными, которые ограничены 0 или 1.

Задача о сумме подмножеств

Учитывая список чисел \(a_1, a_2, \ldots, a_n\) и целевую сумму \(s\), выберите некоторые числа так, чтобы их сумма была как можно ближе можно \(s\).

Мы можем смоделировать это как задачу целочисленного программирования с двоичная переменная \(x_i\) для каждого числа. Здесь «двоичный» означает, что \(x_i\) может принимать только значения 0 или 1; который в LINDO выражается добавлением INT xi после КОНЕЦ LP. (Переменные, которым разрешено принимать любое неотрицательное целочисленное значение, обозначается GIN xi — G означает «общий».)

Переменная \(x_i\) будет равна 1 или 0 в зависимости от того, какое число \(a_i\) среди избранных. Тогда сумма выбранного числа равны \(a_1 x_1 + \ldots + a_n x_n\). Таким образом, мы можем смоделировать несколько варианты этого вопроса как целочисленные программы:

Цена правильная

Если мы хотим, чтобы сумма была как можно ближе к можно \(s\), не переходя , мы можем решить:

Максимизируйте \(a_1 x_1 + \ldots + a_n x_n\)

при условии \[\ начало {выровнено} a_1 x_1 + \ldots + a_n x_n & \le s \\ x_1, \ldots, x_n & \in \{0,1\} \конец{выровнено} \]

Можем ли мы попасть внутрь \(k\)?

Здесь нас интересует только то, ограничения выполнимы, поэтому мы выбираем целевую функцию быть константой \(0\): это гарантирует, что LP не может быть неограниченный.

Развернуть \(0\)

при условии \[\ начало {выровнено} a_1 x_1 + \ldots + a_n x_n & \le s + k \\ a_1 x_1 + \ldots + a_n x_n & \ge s — k \\ x_1, \ldots, x_n & \in \{0,1\} \конец{выровнено}\]

Обратите внимание, что \(k\) — это параметр (т. е. число, которое нам нужно выбрать), а не переменная в LP.

Что ближе всего к нам?

Просто сделайте \(k\) переменной!

Минимизировать \(к\)

при условии \[\ начало {выровнено} a_1 x_1 + \ldots + a_n x_n & \le s + k \\ a_1 x_1 + \ldots + a_n x_n & \ge s — k \\ x_1, \ldots, x_n & \in \{0,1\} \конец{выровнено}\]

Проблема с разделом

Учитывая список чисел \(a_1, \ldots, a_n\), разделите их на два связки такие, что суммы чисел в каждой связке максимально близки насколько это возможно.

Минимизировать \(к\)

при условии \[\ начало {выровнено} a_1 x_1 + \ldots + a_n x_n & \le (a_1+\cdots+a_n)/2 + k \\ a_1 x_1 + \ldots + a_n x_n & \ge (a_1+\cdots+a_n)/2 — k \\ x_1, \ldots, x_n & \in \{0,1\} \конец{выровнено}\]

Недостатки этих примеров

Смысл этих простых примеров в том, что многие вопросы, которые кажутся очень комбинаторны и изначально не имеют ничего общего с линейными программирование может быть закодировано как линейная программа с двоичными переменными. Конечно, некоторые кодировки могут быть умнее других! те выше, не очень хороши: один из способов сказать, что расслабление эти проблемы слишком легко, то есть вся трудность задачи упаковывается в ограничение на переменные 0 или 1.

Например, ЛП для задачи о разбиении всегда имеет оптимальную решение \(k=0\), \(x_1=x_2=\ldots=x_n=0.5\), независимо от \(a_i\) есть!

Далее мы рассмотрим лучший пример кодирования комбинаторная задача как целочисленная линейная программа. У него больше интересные ограничения, захватывающие больше проблемы, и это расслабление не является тривиальным.

Раскраска графика

Граф — это просто набор вершин некоторые пары которых соединены ребрами . правильная раскраска графа есть присвоение цвета каждой вершине таким образом, что любые два вершинам, соединенным ребром, присваиваются разные цвета (но вершины, не соединенные напрямую ребром, могут быть назначены того же цвета). Мы можем моделировать правильные раскраски, используя линейные ограничения на бинарные переменные следующим образом:

Пусть \(v_1, v_2, \ldots, v_n\) вершины графа и пусть \(c_1, \ldots, c_m\) доступные цвета. Ввести переменную \(x_{ij}\) для каждых пара вершины \(v_i\) и цвета \(c_j\): \(x_{ij}\) будет равно 1, если \(v_i\) присвоен цвет \(c_j\) и 0, если нет. В терминах этих переменных мы можем выразить ограничения правильная окраска:

Каждой вершине должен быть присвоен цвет

Для каждого \(i\) имеем \(x_{i1} + x_{i2} + x_{im} = 1\).

Вершины, соединенные ребром, должны быть окрашены в разные цвета

Для каждой пары вершин \(v_{i_1}\) и \(v_{i_2}\), которые соединены ребром, и для каждого цвета \(c_j\) мы можем выразить, что \(v_{i_1}\) и \(v_{i_2}\) не могут быть оба цвета \(c_j\) через ограничение \(x_{i_1j} + x_{i_2j} \le 1\).

Если мы хотим выяснить, можно ли правильно раскрасить граф с помощью некоторых заданное количество цветов, то эти ограничения — все, что нам нужно. Что если мы хотим знать минимальное количество цветов в правильном раскраска? Хорошо, если в графе \(n\) вершин, а у вас минимум \(n\) доступных цветов, безусловно, можно найти правильная раскраска: просто задайте каждой вершине свой цвет! И по умно выбрав целевую функцию, мы можем найти минимум необходимое количество цветов (так называемые хроматический номер график).

Скажем, граф имеет 9 вершин, например. Тогда 9 цветов уж точно достаточно. Представьте, что для каждой раскраски графа составляется число чьи цифры — это просто количество использований каждого цвета. Для например, число \(000120303 = 120303\) означает, что только четыре цвета, которые мы фактически использовали, один раз, один дважды и два цвета три раз. В зависимости от того, как вы пронумеруете цвета, одна и та же окраска могли получить числа \(312030\), \(2331\) или \(1233\). Обратите внимание, что \(1233\) — это наименьшее число, которое может получить такая раскраска. (т. е. тот, кто использует четыре цвета, такое количество раз) может получить. Так как числа с большим количеством цифр всегда больше, чем числа с меньше цифр, если вы посмотрите на числа, связанные со всеми раскраски, наименьшая из них должна соответствовать раскраске с как можно меньше цветов! Итак, для нашего графика с 9{к-1}\) будет сведен к минимуму одновременно с уменьшением количества цветов. сведен к минимуму. Разумеется, минимальное значение этой целевой функции равно , а не минимальное количество цветов, необходимое для правильного окрашивания графика, но учитывая оптимальное решение \(x_{ij}\) вы можете легко понять сколько цветов он использовал: просто посчитайте, сколько \(j\) хотя бы один из \(x_{ij}\) равно 1.

Генератор низкого давления LINDO

Если вы читаете это на веб-сайте, ниже вы увидите форму, которая может сгенерировать эти LP в формате LINDO, учитывая описание вашего график. Если вы читаете это в формате PDF, остальная часть этого раздела будет выглядеть пустым.

Ребра графика:

Проверьте, можно ли раскрасить график с помощью цвета.

Найдите минимальное количество необходимых цветов.

Комбинаторная оптимизация | Engati

Что такое комбинаторная оптимизация?

Комбинаторная оптимизация — это раздел математической оптимизации, имеющий приложения в области искусственного интеллекта, теоретической информатики, прикладной математики, машинного обучения, разработки программного обеспечения и многих других областях.

Это связано с теорией сложности вычислений, теорией алгоритмов и исследованием операций.

Это процесс определения максимума или минимума для целевой функции, которая имеет дискретную область с большим пространством конфигураций.

Комбинаторная оптимизация в основном относится к методам, используемым для решения задач оптимизации, и, как правило, не предлагает рекомендаций о том, как преобразовать реальные проблемы в абстрактные математические вопросы и наоборот.

Вся область комбинаторной оптимизации в значительной степени берет свое начало в задачах теории графов, таких как раскраска ребер в неориентированных графах и паросочетания в двудольных графах.

Ранний прогресс в области комбинаторной оптимизации во многом связан с теоремами теории графов, а также их двойниками.

Когда впервые появилось линейное программирование, комбинаторная оптимизация стала применяться к таким задачам, как назначение, максимальный поток и транспортировка.

Сегодня комбинаторная оптимизация особенно используется для изучения алгоритмов, особенно тех, которые используются в искусственном интеллекте, машинном обучении и исследовании операций.

Источник: Википедия

‍

Что такое комбинаторная задача?

Задача комбинаторной оптимизации A представляет собой четверку (I, f, m, g)

Здесь

I — набор экземпляров.

Если экземпляр x ∈ I, , то f ( x ) является конечным множеством допустимых решений.

Если y является допустимым решением, например, x , то m ( x,y ) означает меру y . Это имеет тенденцию быть положительным реальным.

Целевая функция g либо мин., либо макс.

Цель состоит в том, чтобы найти оптимальное или возможное решение y например x с

m ( x,y ) = g { m | г’ ∈ f ( x )}

Каждая задача комбинаторной оптимизации имеет соответствующую ей задачу принятия решений и спрашивает, существует ли допустимое решение для некоторой конкретной меры m₀ .

‍

Для чего используется комбинаторная оптимизация?

Область комбинаторной оптимизации находится на переднем крае комбинаторики и теоретической информатики.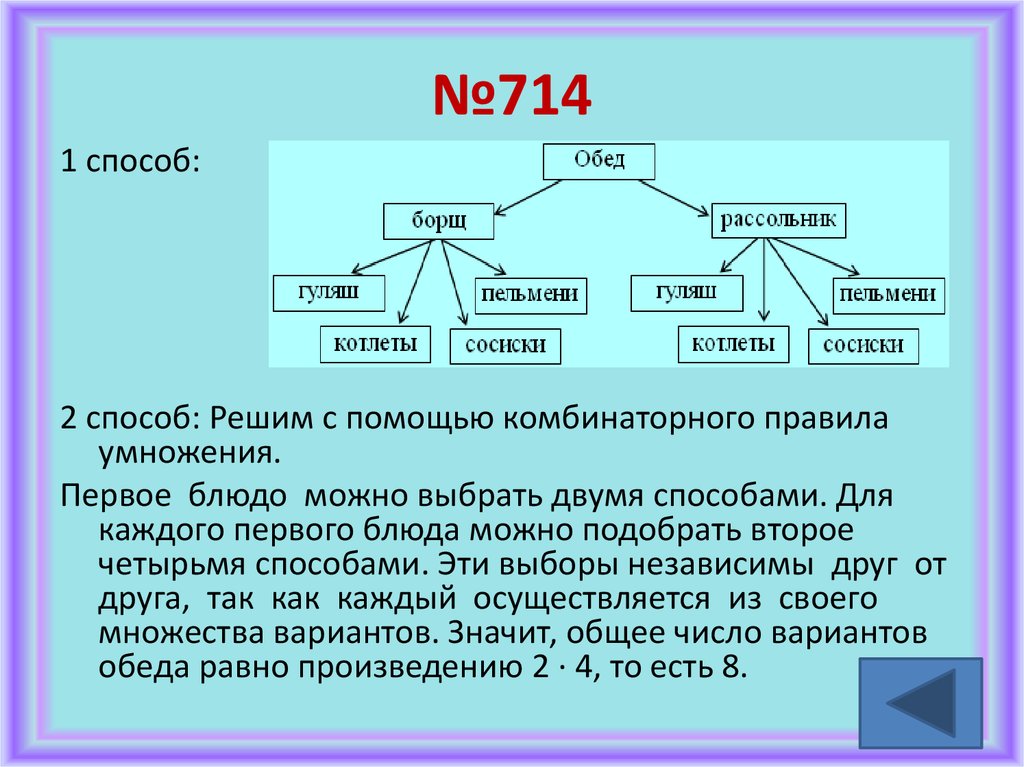 Комбинаторная оптимизация в основном используется для решения задач дискретной оптимизации с использованием комбинаторных методов. Эти задачи дискретной оптимизации в основном представляют собой задачи, направленные на поиск наилучшего возможного решения из конечного набора возможностей.

В компьютерных науках комбинаторная оптимизация используется для улучшения алгоритмов за счет использования математических методов с целью уменьшения размера набора доступных решений или даже ускорения самого поиска.

С комбинаторной точки зрения комбинаторная оптимизация используется для интерпретации особо сложных вопросов в терминах конечного множества объектов, о которых уже достаточно много известно, таких как множества, графы, многогранники и матроиды.

Что такое задачи комбинаторной оптимизации?

На практике задачи комбинаторной оптимизации (COP) обычно объединяют две или более подзадачи.

Некоторые примеры задач комбинаторной оптимизации:

Задача коммивояжёра (TSP)

Вероятно, это самая известная задача комбинаторной оптимизации. Он включает в себя полный граф на n вершинах с весовой функцией, определенной на ребрах. Цель этой задачи состоит в том, чтобы построить обход или обход, проходящий через каждую вершину, имеющую минимальный суммарный вес.

TSP считается сложной задачей комбинаторной оптимизации.

Задача о раскрое материала

Одномерная задача о раскрое материала направлена ​​на то, чтобы выяснить, как разрезать рулоны бумаги фиксированной ширины на заказы клиентов меньшей ширины, чтобы свести к минимуму потери.

Ее можно сформулировать как задачу целочисленного линейного программирования и решить с помощью генерации столбцов.

Проблемы упаковки

Эти проблемы можно считать дополнительными к задачам резки. Они стремятся максимально выгодно заполнить большое пространство меньшими формами.

Задачи геометрической упаковки возникают в одномерном, двухмерном и трехмерном измерениях.

Минимальное связующее дерево

Проблема минимального связующего дерева (задача MST) также является известной комбинаторной задачей. Это простая задача комбинаторной оптимизации (COP).

В связном неориентированном графе остовное дерево — это подграф, который является деревом и соединяет все вершины. Каждому ребру присваиваются веса, а минимальное остовное дерево — это остовное дерево, вес которого меньше или равен весу любого другого остовного дерева.

Проблема брака

В своей традиционной формулировке проблема брака направлена ​​на выявление набора из n пар из набора n мужчин и n женщин так, чтобы каждая пара состояла из одного мужчины и одна женщина и никакие два человека не предпочли бы друг друга своим партнерам. У каждой женщины есть иерархия предпочтений в отношении мужчин, и у каждого мужчины есть иерархия предпочтений в отношении женщин.

При наличии набора настроек для n мужчин и n женщин, существует ли решение? Как вы находите этот раствор?

Всегда будет существующее решение, это известно как Теорема Холла о браке. Такая задача известна как задача соответствия. Это один из немногих основных типов задач, для решения которых используется комбинаторная оптимизация.

‍

Что такое комбинаторные алгоритмы?

Два алгоритма, которые используются для решения задач комбинаторной оптимизации:

• Алгоритм Прима
• Алгоритм Крускала
  

Алгоритм Прима предлагает способ решения одной из простейших задач комбинаторной оптимизации. Это поможет вам найти минимальное остовное дерево на (взвешенном) графе.

Он использует тот факт, что tress являются графами с минимальной связностью и что графы имеют матроидную структуру. Это означает, что они восприимчивы к конкретным реализациям жадного алгоритма. Вот как это работает:

• Выберите вершину на графе
• Среди ребер, соединяющих выбранные вершины с остальной частью графа, выберите ребро с наименьшим весом (и связанную с ним вершину).

  No related posts.