Комплексные или комплексные числа: Национальный исследовательский университет «Высшая школа экономики»

Просто о сложном: комплексные числа

Комплексные числа всегда меня занимали. Как и с понятием экспоненты, большинство определений подпадали под одну из двух категорий:

• это математическая абстракция, всё упирается в формулы. Смиритесь.
• это используется в продвинутой физике, поверьте. Просто дождитесь университета.

Какой хороший способ привлечь деток к математике! Сегодня мы возьмем эту тему штурмом, используя наши любимые инструменты:

• Будем основываться на связях, а не на механических формулах.
• Рассмотрим комплексные числа как дополнение к нашей системе счисления, такому же, как ноль, дробные или отрицательные числа.
• Визуализируем идеи в графиках, чтобы лучше понять суть, а не просто изложим сухим текстом.

И наше секретное оружие: изучение по аналогии. Мы доберемся до комплексных чисел, начав с их предков, отрицательных чисел. Вот вам небольшое руководство:

Пока что смысла в этой таблице мало, но пусть она будет рядом. К концу статьи всё станет на свои места.

Давайте действительно поймем, что такое отрицательные числа

Отрицательные числа не так просты. Представьте, что вы — европейский математик в XVIII веке. У вас есть 3 и 4, и вы можете написать 4 – 3 = 1. Всё просто.

Но сколько будет 3 – 4? Что, собственно, это означает? Как можно отнять 4 коровы от 3? Как можно иметь меньше, чем ничего?

Отрицательные числа рассматривались как полная чушь, что-то, что «бросало тень на всю теорию уравнений» (Фрэнсис Масерес, 1759). Сегодня было бы полной чушью думать об отрицательных числах, как о чем-то нелогичном и неполезном. Спросите вашего учителя, нарушают ли отрицательные числа основы математики.

Что же произошло? Мы изобрели теоретическое число, которое обладало полезными свойствами. Отрицательные числа нельзя потрогать или ощутить, но они хорошо описывают определенные связи (как задолженность, например). Это очень полезная выдумка.

Вместо того, чтобы сказать «Я должен вам 30», и читать слова, чтобы понять в плюсе я или в минусе, я могу просто записать «-30», и знать, что это означает. Если я заработаю деньги и оплачу свои долги (-30 + 100 = 70), я смогу легко записать эту транзакцию несколькими символами. У меня останется +70.

Знаки плюса и минуса автоматически фиксируют направление — вам не нужно целое предложение, чтобы описать изменения после каждой транзакции. Математика стала проще, элегантнее. Стало не важно, являются ли отрицательные числа «осязаемыми» — у них есть полезные свойства, и мы пользовались ими, пока они крепко не вошли в наш обиход. Если кто-то из ваших знакомых еще не понял суть отрицательных чисел, теперь вы ему поможете.

Но не будем умалять человеческие страдания: отрицательные числа были настоящим сдвигом в сознании. Даже Эйлер, гений, открывший число е и много еще чего, не понимал отрицательные числа так же хорошо, как мы сегодня. Они рассматривались как «бессмысленные» результаты вычислений.

Странно требовать от детей, чтобы они спокойно понимали идеи, которые когда-то смущали даже самых лучших математиков.

Ввод мнимых чисел

С мнимыми числами та же история. Мы можем решать уравнения вроде этого целыми днями:

Ответами будут 3 и -3. Но представим, что какой-то умник приписал сюда минус:

Ну и ну. Такой вопрос заставляет людей съеживаться, первый раз видя его. Вы хотите вычислить квадратный корень из числа, меньшего, чем ноль? Это немыслимо! (Исторически реально существовали подобные вопросы, но мне удобнее представлять какого-то безликого умника, чтобы не вгонять в краску ученых прошлого).

Выглядит безумно, как в свое время выглядели и отрицательные числа, ноль и иррациональные числа (неповторяющиеся числа). В этом вопросе нет «реального» смысла, правда?

Нет, не правда. Так называемые «мнимые числа» нормальны настолько же, как и все другие (или настолько же ненормальные): они являются инструментом для описания мира. В том же духе, как мы представляем, что -1, 0.3 и 0 «существуют», давайте предположим, что существует некое число i, где:

Другими словами, вы умножаете i на себя же, чтобы получить -1. 2 = -1, которое можно записать так:

Какое преобразование x, применяемое дважды, превращает 1 в -1? Хм.

• Мы не можем умножить дважды положительное число, потому что результат будет положительным.
• Мы не можем умножить дважды отрицательное число, потому что результат опять будет положительным.

А как насчёт… вращения! Звучит, конечно, необычно, но что если представить х как «поворот 90 градусов», тогда применив х дважды, мы совершим поворот на 180 градусов на координатной оси, и 1 обернется в -1!

Вот это да! И если мы еще немного над этим поразмышляем, то мы можем совершить два оборота в противоположном направлении, и также перейти с 1 на -1. Это «отрицательное» вращение или умножение на -i:

Если мы дважды умножим на-i, то при первом умножении получим -i из 1, а при втором -1 из -i. Так что на самом деле существует два квадратных корня -1: i и -i.

Это довольно круто! У нас есть что-то вроде решения, но что оно означает?

• i — это «новая мнимая размерность» для измерения числа
• i (или -i) — это то, чем «становятся» числа при вращении
• Умножение на i — это вращение на 90 градусов против часовой стрелки
• Умножение на -i — это вращение на 90 градусов по часовой стрелке.
• Двойное вращение в любом из направлений дает -1: оно опять возвращает нас к «обычной» размерности положительных и отрицательных чисел (ось x).

Все числа 2-мерные. Да, это трудно принять, но древним римлянам было бы также трудно принять десятичные дроби или деление в столбик. (Как это так, между 1 и 2 есть еще числа?). Выглядит странно, как и любой новый способ мыслить в математике.

Мы спросили «Как превратить 1 в -1 в два действия?» и нашли ответ: повернуть 1 на 90 градусов дважды. Довольно странный, новый способ мыслить в математике. Но очень полезный. (Между прочим, эта геометрическая интерпретация комплексных чисел появилась только десятилетия спустя после открытия самого числа i).

Также, не забывайте, что принятие оборота против часовой стрелки за положительный результат — это сугубо человеческая условность, и всё могло бы быть совсем по-другому.

Поиск множеств

Давайте углубимся немного в детали. При умножении отрицательных чисел (как -1), вы получаете множество:

• 1, -1, 1, -1, 1, -1, 1, -1

Поскольку -1 не меняет размер числа, а только знак, вы получаете одно и то же число то со знаком «+», то со знаком «-». 2)и посмотрите на общее множество:

• X, Y, -X, -Y, X, Y, -X, -Y…

Точно, как отрицательные числа моделируют зеркальное отражение чисел, мнимые числа могут моделировать что угодно, что вращается между двумя измерениями «Х» и «Y». Или что угодно с циклической, круговой зависимостью — есть что-нибудь на примете?

Понимание комплексных чисел

Есть еще одна деталь для рассмотрения: может ли число быть и «реальным», и «мнимым»?

Даже не сомневайтесь. Кто сказал, что нам обязательно нужно поворачивать строго на 90 градусов? Если мы одной ногой станем на «реальную» размерность, а другой — на «мнимую», то будет выглядеть примерно так:

Мы находимся на отметке в 45 градусов, где вещественная и мнимая части одинаковы, и само число равно «1 + i». Это как хот-дог, где есть и кетчуп, и горчица — кто сказал, что нужно обязательно выбирать что-то одно?

По сути, мы можем выбрать любую комбинацию вещественной и мнимой части и сделать из всего этого треугольник. Угол становится «углом вращения». Комплексное число — это заумное название для чисел, в которых есть вещественная и мнимая части. Они пишутся, как «a + bi», где:

• a — вещественная часть
• b — мнимая часть

Неплохо. Но остается один последний вопрос: как «велико» комплексное число? Мы не можем измерить вещественную часть или мнимую отдельно, потому что мы упустим общую картину.

Давайте сделаем шаг назад. Размер отрицательного числа — это расстояние от нуля:

Это другой способ найти абсолютную величину. Но как измерить оба компонента на 90 градусах для комплексных чисел?

Это птица в небе… или самолет… Пифагор спешит на помощь!

Эта теорема выскакивает, где только можно, даже в числах, придуманных через 2000 лет после самой теоремы. Да, мы делаем треугольник, и его гипотенуза и будет равна расстоянию от нуля:

Хоть измерить комплексное число не так просто, как «просто опустить знак -», у комплексных чисел есть очень полезные применения. Давайте рассмотрим некоторые из них.

Реальный пример: Вращения

Мы не будем дожидаться университетского курса физики, чтобы попрактиковаться с комплексными числами. Мы займемся этим уже сегодня. Много можно рассказать на тему умножения комплексных чисел, но пока нужно понять главное:

• Умножение на комплексное число совершает вращение на его угол

Давайте посмотрим, как это работает. Представьте, что я на лодке, движусь с курсом 3 единицы на Восток каждые 4 единицы на Север. Я хочу изменить свой курс на 45 градусов против часовой стрелки. Каким будет мой новый курс?

Кто-то может сказать «Это просто! Вычислите синус, косинус, погуглите значение по тангенсу…и тогда…» Кажется, я сломал свой калькулятор…

Давайте пойдем более простым путем: мы идем по курсу 3 + 4i (не важно, какой тут угол, нам всё равно пока) и хотим повернуться на 45 градусов. Ну, 45 градусов это 1 + i (идеальная диагональ). Так что мы можем умножить наш курс на это число!

Вот в чем суть:

• Исходный курс: 3 единицы на Восток, 4 единицы на Север = 3 + 4i
• Вращение против часовой стрелки на 45 градусов = умножение на 1 + i

При умножении мы получаем:

Наш новый ориентир — 1 единица на Запад (-1 на Восток) и 7 единиц на Север, можете нарисовать координаты на графике и следовать им.

Но! Мы нашли ответ за 10 секунд, без всяких синусов и косинусов. Не было векторов, матриц, отслеживания, в каком квадранте мы находимся. Это была простая арифметика и немного алгебры для приведения уравнения. Мнимые числа отлично справляются с вращением!

Более того, результат такого вычисления очень полезен. У нас есть курс (-1, 7) вместо угла (atan(7/-1) = 98.13, и сразу ясно, что мы во втором квадранте. Как, собственно, вы планировали нарисовать и следовать указанному углу? Используя транспортир под рукой?

Нет, вы бы конвертировали угол в косинус и синус (-0.14 и 0.99), нашли бы примерное соотношение между ними (около 1 к 7) и набросали бы треугольник. И тут комплексные числа несомненно выигрывают — аккуратно, молниеносно, и без калькулятора!

Если вы похожи на меня, то это открытие покажется вам сногсшибательным. Если нет, боюсь, что математика вас совсем не зажигает. Уж извините!

Тригонометрия хороша, но комплексные числа значительно упрощают вычисления (вроде поиска cos(a + b)). Это только маленький анонс; в следующих статьях я предоставлю вам полное меню.

Лирическое отступление: некоторые люди думают примерно так: «Эй, ну не удобно же иметь курс Север/Восток вместо простого угла для следования судна!»

Правда? Ну хорошо, посмотрите на свою правую руку. Какой угол между основанием вашего мизинца и кончиком указательного пальца? Удачи с вашим способом вычисления.

А можно просто ответить «Ну, кончик находится на Х дюймов вправо и Y дюймов вверх» и с этим уже можно что-то сделать.

Комплексные числа стали ближе?

Мы пронеслись смерчем по моим базовым открытиям в области комплексных чисел. Посмотрите на самую первую иллюстрацию, теперь он должен стать более понятным.

Есть еще столько всего интересного в этих красивых, чудных числах, но мой мозг уже устал. Моя цель была проста:

• Убедить вас в том, что комплексные числа только рассматривались как «сумасшествие», а на деле они могут быть очень полезными (точно как и отрицательные числа)
• Показать, как комплексные числа могут упростить некоторые задачи вроде вращения.

Если я кажусь слишком озабоченным этой темой, то для этого есть причина. Мнимые числа годами были моей навязчивой идеей — недостаток понимания меня раздражал.

Сейчас я наконец-то дошел до этого долгожданного понимания, и мне не терпелось поделиться с вами. Но меня по-прежнему злит, что вы знакомитесь с этими замечательными, несложными приемами понимания в блоге какого-то безумного лунатика, а не в классе на уроке математики. Мы душим в себе вопросы и «пыхтим» над непонятными вещами, потому что не хотим искать, находить и делиться чистыми, абсолютно логичными объяснениями.

Но зажечь свечу лучше, чем пробираться сквозь кромешную тьму: вот мои мысли, и я уверен, что огонек зажжется и в умах моих читателей.

Эпилог: Но они по-прежнему довольно странные!

Я знаю, они и для меня всё еще выглядят странными. Я пытаюсь мыслить, как мыслил первый человек, открывший ноль.

Ноль — это такая странная идея, «что-то» представляет «ничего», и это никак не могли понять в Древнем Риме. То же самое и с комплексными числами — это новый способ мышления. Но и ноль, и комплексные числа значительно упрощают математику. Если бы мы никогда не внедряли странности вроде новых систем счисления, мы бы до сих пор считали всё на пальцах.

Я повторяю эту аналогию, потому что так легко начать думать, что комплексные числа «не нормальные». Давайте быть открытыми к новшествам: в будущем люди будут только шутить над тем, как кто-то вплоть до XXI века не верил в комплексные числа.

Перевод статьи «A Visual, Intuitive Guide to Imaginary Numbers»

Комплексные числа

Комплексное число это пара двух действительных чисел (x, y).
Мы можем представить комплексные числа, как точки в системе координат.
Пусть z — комплексное число.
z = (x, y)
x — это вещественная часть z, а y — это мнимая часть z.

Комплексные числа образуют $\mathbb{C}$ поле комплексных чисел.
Поле действительных чисел является его частью. {4n} = 1$Кратный 4
${4n, \ n \in \mathbb{Z}} = {4; 8; 12…}$

Полярная форма

Векторная форма комплексного числа это:

z = |z|(cosθ + isinθ) = |z|e^iθ
или
z = r(cos(θ) + i.sin(θ)) = r.e^i.θ

Здесь |z| — это модуль комплесного числа (совпадает с величиной OM), θ -это аргумент комплесного числа или фаза. Заштрихованный круг наверху означает модуль |z| комплексного числа z, а угол θ — аргумент комплексного числа.

Формулы Муавра

zⁿ = rⁿ[cos(n.θ) + i.sin(n.θ)]

$\sqrt[n]{z}=\sqrt[n]{r}(cos(\frac{\theta+2k\pi}{n})+i.sin(\frac{\theta+2k\pi}{n}))$
k = 0, 1, 2,…, n-1

Пишите на нашем форуме касательно комплексных чисел.

Комплексные числа

Выражение не имеет реального ответа. Символ i создан для представления и называется мнимой величиной . Так как , i ² = –1. Любое выражение, являющееся произведением действительного числа с на , называется чисто мнимым числом .

Пример 1

Упростите каждое из следующих действий.

3. (6 и )(4 и )

3. Это последнее выражение обычно пишется так, чтобы i не было ошибочно записано под радикалом.

4. (6 i )(4 i ) = 24 i ² = 24(–1) = –24

5. В этом последнем примере все мнимые значения должны были быть помещены в их « i‐ form», прежде чем можно будет сделать какое-либо упрощение. Обратите внимание, что

То есть правило произведения радикалов не выполняется (вообще) для мнимых чисел.

Когда i возводятся в степень, получается повторяющийся узор.

Когда i возводят в любую степень, результатом всегда будет 1, i , –1 или – i . Если показатель степени i разделить на 4, остаток указывает, какое из четырех значений является результатом.

Пример 2

Упростите каждое из следующих действий.

1. и ³⁴

2. и ⁹⁵

3. и ¹⁰⁸

4. и ⁵³

1. и ³⁴

   Так как 34 разделить на 4 дает в остатке 2, i ³⁴ = i ² = –1. Думайте об этом как , так что

2. и ⁹⁵

   Так как 95 разделить на 4 дает в остатке 3, i ⁹⁵ = i ³ = – i .

3. и ¹⁰⁸

   Так как 108 делится на 4 имеет нулевой остаток, i ¹⁰⁸ = i ⁰ = 1.

4. и ⁵³

   Так как 53 разделить на 4 дает остаток 1, i ⁵³ = i ¹ = i .

Комплексные числа и комплексно-сопряженные числа. Комплексное число — это любое выражение, представляющее собой сумму чисто мнимого числа и действительного числа. Комплексное число обычно выражается в форме, называемой a + bi , или стандартной форме, где a и b — реальные числа. Выражения a + bi и a – bi называются комплексно сопряженными. Комплексно-сопряженные числа используются для упрощения знаменателя при делении комплексных чисел. Это эквивалентно рационализации знаменателя при работе с дробями. Цель состоит в том, чтобы не получить комплексное число в знаменателе частного.

Арифметика с комплексными числами выполняется аналогично арифметике с полиномами. Ниже приведены определения арифметики с двумя комплексными числами, называемыми ( a + bi

) a n d ( c + di ).

Объединение подобных терминов и вынесение на множители i ,

Использование дистрибутива,

Упрощение знаменателя,

Пример 3

Найдите сумму, разность, произведение и частное (4 + 3 i ) и (5 – 4 i ).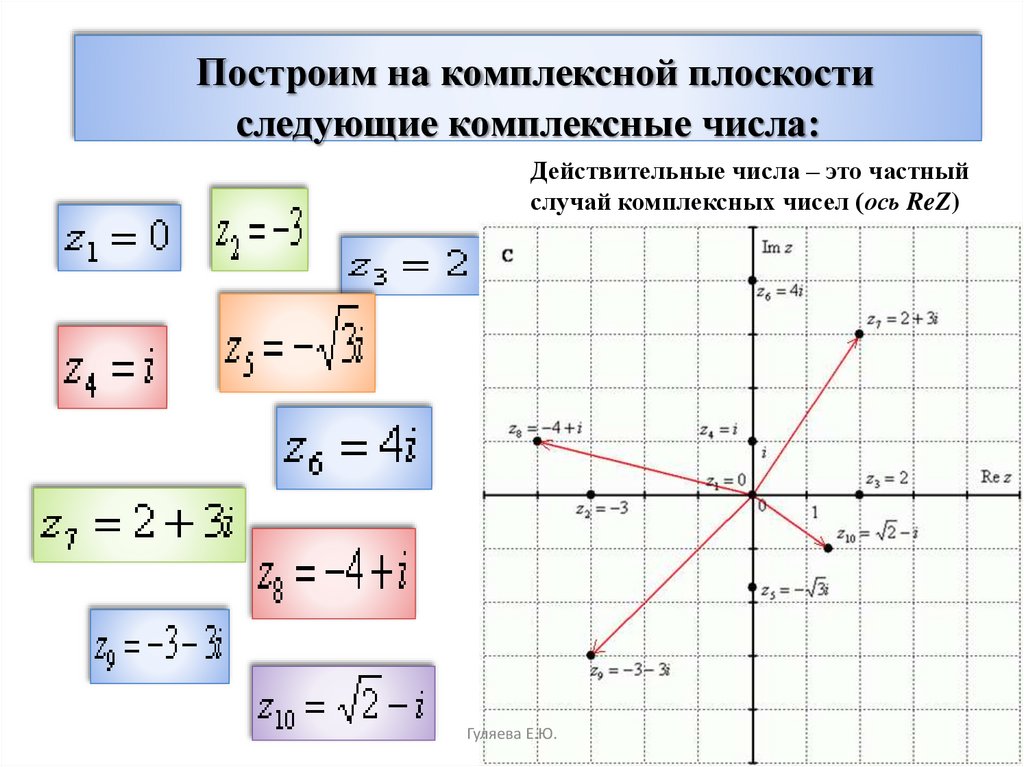

Частное: Рационализируйте знаменатель.

Пример 4

Упростить .

Поскольку 6 i равно 0 + 6 i , его комплексно-сопряженное число равно 0 – 6 i . Следовательно,

Комплексные числа (ответы на 7 часто задаваемых вопросов) – JDM Educational

Комплексные числа используются в алгебре, исчислении и других областях математики. Этот набор чисел часто вызывает некоторые вопросы о его природе по отношению к другим наборам.

Комплексные числа содержат набор действительных чисел, рациональных чисел и целых чисел. Итак, некоторые комплексные числа являются действительными, рациональными или целыми числами. Сопряжение комплексного числа часто используется для упрощения дробей или многочленов сомножителей, которые неприводимы в действительных числах. Модуль комплексного числа дает нам информацию о том, где находится комплексное число в координатной плоскости.

Конечно, комплексные числа не могут быть упорядочены как действительные числа, так как они находятся не на прямой, а во всей плоскости. Это связано с тем, что мнимая часть добавляет размерность 2 ^и , когда мы изображаем комплексные числа.

В этой статье мы поговорим о комплексных числах и ответим на некоторые распространенные вопросы об их природе. Мы также поговорим о сопряжении и модуле комплексного числа.

Начнем.

Может ли комплексное число быть действительным числом?

В некоторых случаях комплексное число может быть действительным числом, если его мнимая часть равна нулю (b = 0). Множество действительных чисел является подмножеством множества комплексных чисел.

Помните, что комплексное число имеет вид

a + bi

, где a и be — действительные числа (a — действительная часть, а b — мнимая часть комплексного числа).

Есть два особых случая комплексных чисел:

• Чистые мнимые числа (a = 0) : это дает нам число вида 0 + bi или просто bi, которое является чисто мнимым числом для любого отличного от нуля b. Некоторые примеры: i (a = 0, b = 1) и -2i (a = 0, b = -2).
• Действительные числа (b = 0) : это дает нам число вида a + 0i или просто a, которое является действительным числом для любого a. Некоторые примеры: 7 (a = 7, b = 0) и -5 (a = -5, b = 0).

Из частного случая 2 ^nd видно, что комплексное число является действительным числом, если его мнимая часть равна нулю (то есть b = 0). Эти числа имеют вид a + 0i.

В качестве альтернативы мы можем записать любое действительное число a как комплексное число, записав его как a + 0i.

На приведенной ниже диаграмме показано соотношение между комплексными, действительными и чисто мнимыми числами.

На этой диаграмме показано соотношение между комплексными, действительными и мнимыми числами.

Может ли комплексное число быть рациональным?

Комплексное число может быть рациональным, если его комплексная часть равна нулю (b = 0), а действительная часть рациональна (а рационально).   Это связано с тем, что множество рациональных чисел является подмножеством множества действительных чисел.

Одним из примеров является рациональное число ½, которое можно записать как ½ + 0i (a = ½, b = 0).

Другим примером является рациональное число -13/2, которое можно записать как -13/2 + 0i (a = -13/2, b = 0).

Обратите внимание, что комплексное число может иметь как a, так и b рациональные числа, но эти комплексные числа не являются рациональными числами, если b не равно нулю.

Например, ½ + (2/3)i имеет a = ½ и b = 2/3, оба числа рациональны. Однако само комплексное число ½ + (2/3)i не является рациональным.

Число (4/5)i имеет a = 0 и b = 4/5, оба числа рациональны. Однако (4/5)i не является рациональным числом.

На приведенной ниже диаграмме рациональные числа добавляются к диаграмме, показывающей взаимосвязь между комплексными, действительными и чисто мнимыми числами.

На этой диаграмме показаны отношения между комплексными, действительными и мнимыми числами, а также между рациональными числами.

Может ли комплексное число быть целым числом?

Комплексное число может быть целым, если его комплексная часть равна нулю (b = 0), а действительная часть является целым числом (a — целое число).   Это связано с тем, что множество целых чисел является подмножеством множества рациональных чисел (которое является подмножеством множества действительных чисел).

Одним из примеров является целое число 3, которое можно записать как 3 + 0i (a = 3, b = 0).

Другим примером является целое число -8, которое можно записать как -8 + 0i (a = -8, b = 0).

Обратите внимание, что комплексное число может иметь как целые числа a, так и b, но эти комплексные числа не являются целыми числами, если b не равно нулю.

Например, 2 + 5i имеет a = 2 и b = 5, которые являются целыми числами. Однако само комплексное число 2 + 5i не является целым числом.

Число 6i имеет a = 0 и b = 6, которые оба являются целыми числами. Однако 6i также не является целым числом.

На приведенной ниже диаграмме целые числа добавляются к диаграмме, показывающей взаимосвязь между комплексными, действительными и чисто мнимыми числами.

На этой диаграмме показаны отношения между комплексными, действительными и мнимыми числами, а также между рациональными числами и целыми числами.

Может ли комплексное число быть четным или нечетным?

Комплексное число может быть четным, если его действительная часть является четным целым числом, а мнимая часть равна нулю (a = 2n для некоторого целого числа n и b = 0).

Комплексное число может быть нечетным, если его действительная часть является нечетным целым числом, а мнимая часть равна нулю (a = 2n + 1 для некоторого целого числа n и b = 0).

Любое комплексное число с ненулевым b не может быть четным или нечетным (поскольку оно не является целым числом).

На этой диаграмме показаны отношения между комплексными, действительными и мнимыми числами, а также рациональными числами и целыми числами (как четными, так и нечетными).

Что такое сопряженное комплексное число?

Для комплексного числа a + bi его сопряженным (или комплексно-сопряженным) является a – bi.

Другими словами, найдите сопряженное комплексное число, оставьте действительную часть такой же, но возьмите противоположную (отрицательную) мнимую часть.

Например, сопряженное 2 + 3i равно 2 – 3i.

Сопряжение 8 – 6i равно 8 + 6i.

Сопряжение -4 – i равно -4 + i.

Сопряженное число 7i равно -7i (Сопряженное число любого чисто мнимого числа является противоположным (отрицательным) числа.)

Сопряженное число 5 равно 5 (Сопряженное число любого действительного числа является самим числом.)

Complex Number	Complex Conjugate
2 + 3i	2 – 3i
8 – 6i	8 + 6i
-4 – i	— 4 + i
7i	-7i
5	5

В этой таблице приведена выборка из
комплексных чисел и их сопряженных чисел. Обратите внимание, что действительная часть
остается неизменной,
, а мнимая часть
инвертируется при нахождении сопряженного
комплексного числа.

[таблица примерных комплексных чисел и сопряженных чисел]

Произведение любого комплексного числа и его сопряженного является действительным числом, так как:

• (a + bi)(a – bi)  [произведение комплексного числа и его сопряженный]
• а ² – аби + аби – б ² и ²   [ФОЛЬГА]
• а 2 2 б

  –

  ²   [объединить подобные термины]
• a ² + b ²   [поскольку i ² = -1, по определению мнимой единицы i]
903 900 числа, то таковы a ² и b ² , и такова их сумма, a ² + b ² .

Суть в том, что воображаемые части компенсируют друг друга, когда мы комбинируем одинаковые члены после того, как мы FOIL.

Комплексно-сопряженные числа часто используются для преобразования знаменателя комплексной дроби в действительное число.

Например, если у нас есть 1 / 2i, мы можем умножить на комплексное сопряжение -2i сверху и снизу дроби, чтобы получить:

• 1 / 2i [исходная дробь]
• (1* -2i) / (2i*-2i) [умножить на -2i сверху и снизу]
• -2i / -4i ²
• -2i / 4  [так как i ² = -1 , по определению мнимой единицы i]
• -i / 2

Эта дробь имеет в знаменателе действительное число.

Мы также можем использовать комплексные сопряжения для факторизации многочленов, неприводимых над действительными числами.

Например, f(x) = x ² + 1 неприводимо в действительных числах.

Однако мы можем разложить это как f(x) = (x + i)(x – i) в комплексных числах.

Обратите внимание, что i и -i комплексно-сопряженные.

Что такое модуль комплексного числа?

Модуль комплексного числа — это квадратный корень из суммы квадратов его действительной и мнимой частей. Итак, для комплексного числа z = a + bi модуль равен |z| = (a ² + b ² ) ^1/2 , которое является неотрицательным действительным числом.

Из-за обозначения |z|, которое обозначает модуль z, мы также используем фразу «абсолютное значение z», поскольку |z| сообщает нам расстояние от z до начала координат в комплексной плоскости.

Например, комплексное число z = 3 + 4i имеет модуль |z| = (3 ² + 4 ² ) ^1/2 = (9 + 16) ^1/2 = (25) ^1/2 = 5. Это означает, что если построить график z = 3 + 4i в комплексной плоскости, это расстояние 5 единиц от начала координат (точка 0 + 0i).

Обратите внимание, что модуль комплексного числа равен квадратному корню из произведения комплексного числа и его сопряженного. Итак, для комплексного числа z = a + bi:

• (a + bi)(a – bi) [произведение a + bi и его комплексно-сопряженное]
• a ² – abi + abi – b ² i ²   [ФОЛЬГА]
• a ² – b ² i ²   [объединить подобные термины] a

  20009 2 + B ² [с I ² = -1, по определению воображаемого блока I]

• (A ² + B ² ) ^{1 /2} [извлеките квадратный корень]
• |z| [по определению модуля z = a + bi]

Модуль комплексного числа подобен абсолютному значению в том, что он никогда не бывает отрицательным, и равен нулю только для комплексного числа 0 + 0i (a = 0 и b = 0).

Может ли комплексное число быть отрицательным?

Комплексное число не может быть отрицательным — эта идея отрицательного или положительного не имеет смысла для комплексных чисел.

Вещественное число может быть отрицательным, так как мы можем сравнить его положение с нулем на числовой прямой:

• Если действительное число находится слева от нуля на числовой прямой, оно отрицательно.
• Если действительное число находится справа от нуля на числовой прямой, оно положительно.

Однако мы не можем изобразить комплексные числа на линии, как мы можем изобразить действительные числа. Это потому, что есть дополнительное измерение: мнимая часть комплексного числа, или би.

В результате мы должны изобразить комплексное число на плоскости, а не на линии. Таким образом, понятие «слева или справа от нуля» теряет свое значение в двух измерениях.

Итак, не существует концепции «отрицательных» или «положительных» комплексных чисел, как для действительных чисел. Другими словами, мы не можем упорядочивать комплексные числа так, как упорядочиваем действительные числа.

При этом у нас все еще могут быть комплексные числа с отрицательной действительной частью (a < 0), отрицательной мнимой частью (b < 0) или с обеими (a < 0 и b < 0).

No related posts.