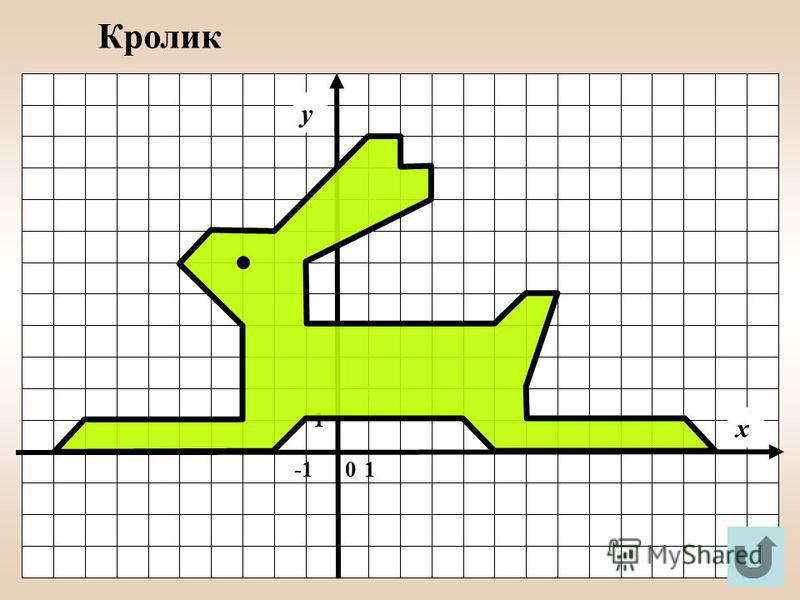
Рисунок по точкам с координатами
Рисунки по координатам с координатами
Рисунки на координатной плоскости
Система координат на плоскости рисунки
Декартова система координат на плоскости рисунки
Фигуры по точкам в системе координат
Построение фигур по точкам
Рисунки на координатной плоск
Декартова система координат на плоскости рисунки
Координатная плоскость с координатами
Декартова система координат на плоскости рисунки животных
Координатная плоскость рисунки животных с координатами
Рисунок на координатной плоскости с координатами
Фигурки на координатной плоскости
Рисунки на координатной плоскости
Рисунки по координатам с координатами
Декартова система координат на плоскости рисунки
Фигуры на координатной плоскости
Рестнуи по координатам
Математические рисунки с координатами
Рисование по координатам
Изображение на координатной плоскости
Рисунки по координатам кенгуру
Лось по координатам -2 2 -2 4
Фигуры на координатной прямой
Рисование по координатам сложные
Кумир чертежник слон 1068
Животные по координатным точкам
Координатная плоскость (-7, 5;4, 5) , (-8;5)
Прямоугольная система координат рисунок
Слоник на координатной плоскости 2 -3
Фигуры по координатным точкам
Слоник по координатным точкам
Рисунки на координатной плоскости 6 класс
Рисуем по координатам сложно
Лошадь по координатам
Рисунки на координатной плоскости
Кленовый лист по координатам
Координатные рисунки простые
Бабочка на координатной плоскости
Кумир чертежник собачка
Рисунки на координатной плоскости
Рисование по координатной
Попугай на координатной плоскости
Рисунки для чертежника
Построить фигуру по точкам
Ласточка по координатам
Координаты для рисования на плоскости
Рисунки на координатной плоскости
Рисунки на координатной плоскости
Рыба по координатам
Сердце по координатам
Бабочка на координатной плоскости
Симметричные рисунки
Рисунок в системе координат по точкам
Гриб по координатам
Симметричные рисунки карандашом
Построение координатной плоскости
Кумир чертежник слон
Рисунок на координатной плоскости с координатами
Рисунки по координатам Пикачу
Координатная плоскость рисунок зайца
Соединить по точкам
Рисунок по координатам космонавт
Чертежник задания
Медведь на координатной плоскости
Соединить по точкам и раскрасить
Пикачу обводить по точкам
Рисунки на координатной плоскости
Рисование по цифрам сложные
Соединить по точкам
Рисование по точкам с цифрами
Рисование по точкамсложне
Собачка по координатам
Рисование по точкам сложные
Комментарии (0)
Написать
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Рисунки по координатам легкие — 78 фото
Рисунки на координатной плоскости
Рисование по координатам
Рисунки по координатам с координатами
Рисунки поткоординатам
Рисунки на координатной плоскости
Координатная плоскость (1;-4) (1; -6)
Прямоугольная система координат рисунок
Гуси-лебеди координатная плоскость
Координатные рисунки
Рисунки на координальной плоскость
Рисунки на координатной плоскости
Рисунки на координатной плоскости
Координаты волка
Рисунок на координатной плоскости с координатами
Рисование фигур по координатам
Петух по координатам
Рисование по координатам
Фигуры по координатным точкам
Рисование по координатам
По точкам на координатной плоскости с координатами
Миллиметровка для рисования
Рисунок с координатами точек
Координаты для рисования животных
Декартова система координат на плоскости рисунки
Фигуры на координатной прямой
Рисунки на координатной плоскости
Симметричные фигуры
Рисунок по прямоугольной системе координат
Ракета по координатам
Верблюд по точкам на координатной
Рисунки на координатной плоскости
Изображение на координатной плоскости
По координатной плоскости
Рисунки на координатной плоскости сложные
Рисунки на координатной плоскости
Рисунки на координатной плоскости
Координаты фигуры
Рисунки на координатной оси
Фигура животного на координатной плоскости
Сложное координатное рисование
Рисунок из координатной плоскости
Бабочка по координатам
Рисунки на координатной плоскости
Прямоугольная система координат рисунок
Фигуры по координатным точкам
Рисунки на координатной плоскости сложные
Программа для рисования по координатам
Координатная плоскость (-7, 5;4, 5) , (-8;5)
Координатные плоскости (-1,-7),(-5,-3),(-5,-3)
Графический диктант по координатам
Слоник на координатной плоскости
Построение фигур на плоскости
Звезда на координатной плоскости
Фигура на координатной плоскости с координатами
Координатная плоскость рыбка -4 2 -3 4
Слоник на координатной плоскости
Координаты на плоскости
Летучая мышь по координатам
Рисунки на координатной плоскости лебедь
Координатный рисунок с координатами сложно
Страус по координатам
Рисунок с координатами точек
Информатика рисунок по координатам
Попугай на координатной плоскости с координатами
Информатика координаты для рисунка
Координатная плоскость Теремок
Рисунок на координатной плоскости с координатами
Кошечка на координатной плоскости
Заяц на координатной плоскости
Раскраска по координатам
Собачка по координатам
Рисунки на плоскости с координатами
Фигуры на координатной прямой
Координатная плоскость рисунок Орел
Петух по координатам
Бабочка по координатным точкам
Построить фигуру по точкам
Комментарии (0)
Написать
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
Объяснение урока: Отражения на координатной плоскости
В этом объяснителе мы научимся находить изображения точек, линий и фигур после их отражения в 𝑥- или 𝑦-ось на координатной плоскости.
Напомним, что геометрическое преобразование — это процесс, при котором одна геометрическая фигура (такая как точка, отрезок или фигура) преобразуется в другую.
Определение: преобразование
Преобразование преобразует каждую точку 𝑃 на плоскости в точку изображения 𝑃′ на той же плоскости.
Некоторыми хорошо известными типами преобразования являются перемещения, повороты и отражения. Здесь мы будем обсуждать только отражения.
Отражение на координатной плоскости берет геометрическую фигуру, такую как точка, отрезок или форма, и преобразует ее в конгруэнтную геометрическую фигуру, называемую изображением. В этом объяснении мы сосредоточимся на трех различных типах отражения на координатной плоскости:
- Отражение по оси 𝑥
- Отражение по оси 𝑦
- Размышление о происхождении
Мы рассмотрим каждый из них по очереди и рассмотрим несколько сопутствующих примеров.
Начнем с отражения по оси 𝑥. В дальнейшем будем использовать обозначение 𝑃(𝑥,𝑦) для обозначения общей точки на координатной плоскости.
Определение: отражение в 𝑥-оси
Отражение в картах 𝑥-оси 𝑃(𝑥,𝑦)→𝑃′(𝑥,−𝑦).
Другими словами, отражение на оси 𝑥 отображает точку 𝑃 на точку ее изображения 𝑃′, сохраняя 𝑥-координата та же самая и с изменением знака 𝑦-координаты. Эффект состоит в том, что положение 𝑃′ будет отражать 𝑃 на противоположной стороне оси 𝑥 (которая является линией с уравнением 𝑦=0) и на том же перпендикулярном расстоянии от оси 𝑥, что и 𝑃. Поскольку ось 𝑥 действует как зеркало, она называется линия отражения (или зеркальная линия).
Например, на диаграмме ниже показана точка 𝐴(2,3), отраженная на оси 𝑥, что дает ее изображение 𝐴′(2,−3). Точно так же точка 𝐵(−2,−1) имеет образ 𝐵′(−2,−(−1))=𝐵′(−2,1).
Обратите внимание, однако, что любая точка на оси 𝑥 останется неизменной при этом отражении, потому что она лежит на зеркальной линии.
Если нужно отразить более сложные геометрические фигуры, такие как отрезки линий или многоугольники, самый простой способ сделать это — отразить каждую отдельную конечную точку или вершину. Затем мы соединяем точки изображения в той же последовательности, в которой они появляются на исходном рисунке. В результате геометрическая фигура будет преобразована в его конгруэнтное зеркальное отражение на противоположной стороне зеркальной линии.
Давайте теперь рассмотрим пример, чтобы проверить, можем ли мы распознать отражение на оси 𝑥.
Пример 1. Определение пары треугольников, представляющих отражение на оси 𝑥
Какая пара треугольников представляет отражение на оси 𝑥?
Ответ
Напомним, что для общей точки 𝑃(𝑥,𝑦) отражение в картах оси 𝑥 𝑃(𝑥,𝑦)→𝑃′(𝑥,−𝑦).
В результате положение 𝑃′ будет отражать положение 𝑃 на противоположной стороне оси 𝑥. и на том же перпендикулярном расстоянии от оси 𝑥, что и 𝑃.
Поскольку это правило применяется к вершинам треугольников, то на диаграмме выше мы ожидаем, что пара отраженных треугольников появится один над другим,
по разные стороны от оси 𝑥 и на одинаковом перпендикулярном расстоянии от нее.
Если бы треугольник 𝐶 был одним из отраженных треугольников, то ось 𝑥 действовала бы как зеркало, давая изображение, показанное ниже.
Однако, поскольку такого треугольника нет, то 𝐶 не отразилось на оси 𝑥, поэтому отраженные треугольники должны быть 𝐴 и 𝐵. Хотя это должно быть очевидно из диаграммы, мы будем использовать определение отражения в 𝑥-ось, чтобы доказать это.
Читая схему, мы видим, что треугольник 𝐴 имеет вершины с координатами (−3,5), (−2,2) и (−5,3). Используя тот факт, что 𝑃(𝑥,𝑦)→𝑃′(𝑥,−𝑦), мы находим точки изображения следующим образом: (−3,5)→(−3,−5),(−2,2)→(−2,−2),(−5,3)→(−5,−3).
Легко проверить, что эти точки изображения являются точно вершинами, показанными для треугольника 𝐵. Более того, если бы мы начали с вершин треугольника 𝐵, мы бы обнаружили, что точки изображения являются вершинами треугольника 𝐴.
Мы заключаем, что пара треугольников 𝐴 и 𝐵 представляет собой отражение на оси 𝑥.
Далее мы рассмотрим отражение по оси 𝑦, которое очень похоже на отражение по оси 𝑥.
Определение: отражение в 𝑦-оси
Отражение в картах 𝑦-оси 𝑃(𝑥,𝑦)→𝑃′(−𝑥,𝑦).
Другими словами, отражение на оси 𝑦 отображает точку 𝑃 на точку ее изображения 𝑃′, меняя знак 𝑥-координаты с сохранением 𝑦-координаты. Эффект состоит в том, что положение 𝑃′ будет отражать 𝑃, на противоположной стороне оси 𝑦 (которая является линией с уравнением 𝑥=0) и на том же перпендикуляре расстояние от оси 𝑦 как 𝑃. Поскольку ось 𝑦 действует как зеркало, ее называют линией отражения (или зеркальной линией).
Например, на диаграмме ниже показана точка 𝐴(−1,3), отраженная по оси 𝑦, чтобы получить ее изображение 𝐴′(−(−1),3)=𝐴′(1,3). Точно так же точка 𝐵(4,−2) имеет образ 𝐵′(−4,−2).
Обратите внимание, однако, что любая точка на оси 𝑦 останется неизменной при этом отражении, потому что она лежит на зеркальной линии.
Вот пример с отражением по оси 𝑦.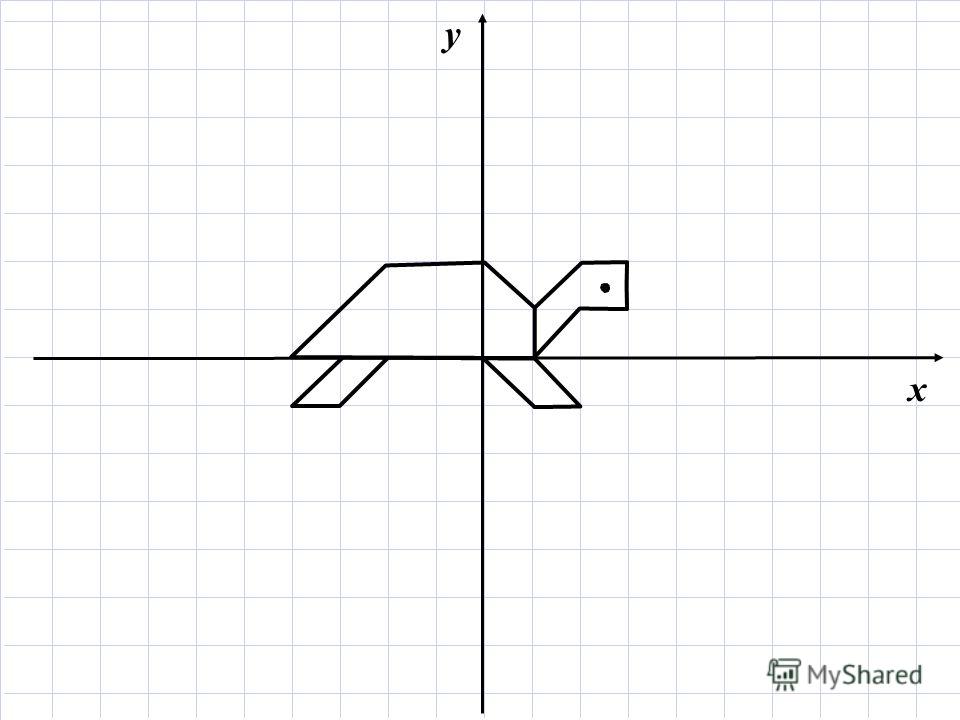
Пример 2. Нахождение координат вершин четырехугольника после отражения
Найти координаты изображений точек 𝐴,𝐵,𝐶 и 𝐷 после отражения по оси 𝑦.
Ответ
Напомним, что для общей точки 𝑃(𝑥,𝑦) отражение в картах оси 𝑦 𝑃(𝑥,𝑦)→𝑃′(−𝑥,𝑦).
Это означает, что он отображает точку 𝑃 в точку изображения 𝑃′, меняя знак 𝑥-координаты и сохраняя 𝑦-координату прежней.
Здесь наш первый шаг — считать координаты вершин четырехугольника. Затем мы можем использовать приведенное выше преобразование для разработки координаты соответствующих точек изображения.
Обратите внимание, что вершина 𝐴 имеет 𝑥-координату 8 и 𝑦-координату 6, поэтому ее можно записать как точку 𝐴(8,6). Точно так же мы получаем 𝐵(8,1), 𝐶(2,1) и 𝐷(2,6). Применение преобразования 𝑃(𝑥,𝑦)→𝑃′(−𝑥,𝑦) всем четырем вершинам дает 𝐴(8,6)→𝐴′(−8,6),𝐵(8,1)→𝐵′(−8,1),𝐶(2,1)→𝐶′(−2,1),𝐷( 2,6)→𝐷′(−2,6).
Помните, что отражение по оси 𝑦 берет геометрическую фигуру и отображает ее на конгруэнтное зеркальное отображение на противоположной стороне
𝑦-ось, причем каждая вершина изображения находится на том же перпендикулярном расстоянии от 𝑦-оси, что и соответствующая вершина
исходная фигура.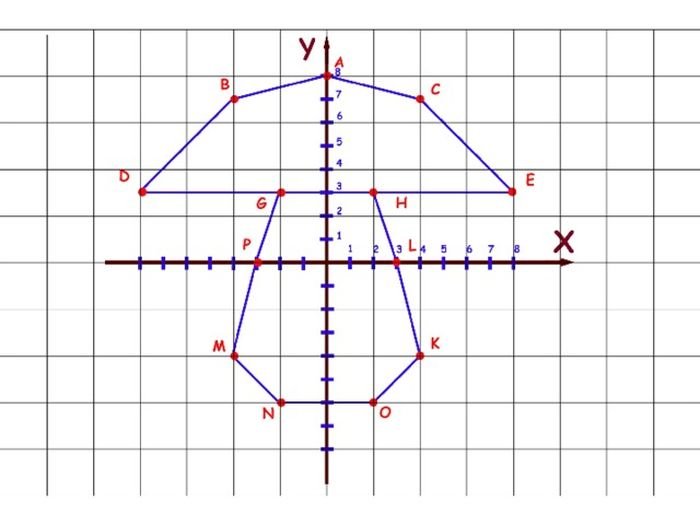 Нанеся указанные выше точки изображения и соединив их в правильном порядке, мы получим изображение четырехугольника, показанное на схеме ниже.
Нанеся указанные выше точки изображения и соединив их в правильном порядке, мы получим изображение четырехугольника, показанное на схеме ниже.
Таким образом, мы показали, что координаты образов точек 𝐴, 𝐵, 𝐶 и 𝐷 после отражения в оси 𝑦 равны 𝐴′(−8,6), 𝐵′(−8,1), 𝐶′(−2,1), и 𝐷′(−2,6).
Теперь вернемся к отражению по оси 𝑥. Всегда важно внимательно прочитать вопрос, чтобы применить правильное преобразование.
Пример 3. Решение задачи о точках, отраженных от оси 𝑥
Три точки 𝐴, 𝐵 и 𝐶 с координатами (1,3),(1,2) и (4,1) соответственно, отражаются по оси 𝑥 в точки 𝐴′, 𝐵′ и 𝐶′.
- Определите координаты точек 𝐴′, 𝐵′ и 𝐶′.
- Является ли величина угла 𝐴𝐵𝐶 меньше, больше или равна величине угла 𝐴′𝐵′𝐶′?
Ответ
Напомним, что для общей точки 𝑃(𝑥,𝑦) отражение в картах оси 𝑥
𝑃(𝑥,𝑦)→𝑃′(𝑥,−𝑦),
поэтому мы получаем изображение 𝑃′ из 𝑃, сохраняя 𝑥-координату той же и изменяя
знак 𝑦-координаты.
Часть 1
В первой части вопроса мы должны применить описанное выше преобразование к точкам 𝐴(1,3), 𝐵(1,2), и 𝐶(4,1); это даст нам координаты точек изображения. Таким образом, у нас есть 𝐴(1,3)→𝐴′(1,−3),𝐵(1,2)→𝐵′(1,−2),𝐶(4,1)→𝐶′(4,−1), как требуется.
Часть 2
Во второй части нам нужно сравнить меру угла 𝐴𝐵𝐶 с мерой угла 𝐴′𝐵′𝐶′. Это помогает обрисовать ситуацию, нарисовав треугольники для 𝐴𝐵𝐶 и 𝐴′𝐵′𝐶′ и выделив соответствующие углы, как показано на диаграмме ниже.
При отражении по оси 𝑥 треугольник 𝐴′𝐵′𝐶′ является зеркальным отражением треугольника 𝐴𝐵𝐶. Поскольку ∠𝐴′𝐵′𝐶′ треугольника 𝐴′𝐵′𝐶′ соответствует ∠𝐴𝐵𝐶 треугольника 𝐴𝐵𝐶, заключаем, что мера угла 𝐴𝐵𝐶 равна мере угла 𝐴′𝐵′𝐶′.
Отражение по оси 𝑥 и отражение по оси 𝑦 — два конкретных примера наиболее распространенного типа отражения:
отражение в линии. Во всех таких случаях прямая линия (называемая линией отражения или зеркальной линией) действует как зеркало, так что любая геометрическая фигура на
одна сторона линии будет преобразована в конгруэнтное зеркальное отражение на другой стороне линии.
Кроме того, отражение в линии имеет четыре ключевых свойства, которые мы проиллюстрируем на диаграмме ниже.
Здесь четырехугольник 𝐴𝐵𝐶𝐷 отразился в зеркальной линии, получив свое изображение, конгруэнтный четырехугольник 𝐴′𝐵′𝐶′𝐷′. Таким образом, изображение 𝐴′𝐵′𝐶′𝐷′ имеет точно такую же форму и размер, как исходный четырехугольник 𝐴𝐵𝐶𝐷, но был перевернут, и каждая вершина изображения находится на одинаковом перпендикулярном расстоянии от зеркала прямая как соответствующая вершина исходного четырехугольника.
Заметим также, что точка 𝐸, лежащая на зеркальной линии, не изменится при этом отражении, поэтому ее изображением будет она сама. Это верно вообще для любых точек, лежащих на зеркальной прямой.
Свойства: Отражение в линии
- Отражение сохраняет длину сегментов линии.
Например, длина 𝐴𝐵 равна длине 𝐴′𝐵′. - Отражение сохраняет меры углов.
Например, мера внутреннего угла в вершине 𝐴 совпадает с мерой внутреннего угла в вершине 𝐴′.
- Отражение сохраняет свойство промежуточности.
Например, поскольку вершина 𝐵 лежит между 𝐴 и 𝐶, то вершина 𝐵′ лежит между 𝐴′ и 𝐶′. - Отражение сохраняет параллелизм.
Например, поскольку 𝐵𝐶 параллельно 𝐴𝐷, то 𝐵′𝐶′ параллелен 𝐴′𝐷′.
Последний тип отражения, который мы здесь рассматриваем, — это размышление о происхождении. Это отличается от предыдущих двух типов, потому что включает в себя размышления о точка, а не линия. Однако, как мы увидим, его легко определить и описать. Напомним еще раз, что мы используем обозначение 𝑃(𝑥,𝑦) для обозначения общей точки на координатной плоскости.
Определение: размышление о происхождении
размышление о происхождении карты 𝑃(𝑥,𝑦)→𝑃′(−𝑥,−𝑦).
Другими словами, отражение относительно начала координат отображает точку 𝑃 на точку ее изображения 𝑃′, меняя знаки обеих ее координат.
Другой способ думать об отражении начала координат состоит в том, что оно отображает 𝑃 на свой образ 𝑃′, так что начало координат является средней точкой. из 𝑃𝑃′. Эффект состоит в том, что 𝑃 и 𝑃′ будут на одинаковом расстоянии от начала координат.
но по разные стороны от него по прямой.
из 𝑃𝑃′. Эффект состоит в том, что 𝑃 и 𝑃′ будут на одинаковом расстоянии от начала координат.
но по разные стороны от него по прямой.
Например, на приведенной ниже диаграмме точка 𝐴(3,1) отражена относительно начала координат, что дает ее изображение 𝐴′(−3,−1). Точно так же точка 𝐵(−2,4) имеет образ 𝐵′(2,−4). Отрезки между 𝐴 и 𝐴′, а также между 𝐵 и 𝐵′ нарисованы, чтобы показать, что в обоих случаях начало координат является их средней точкой.
Обратите внимание, что единственная точка, которая остается неизменной при этом отражении, — это само начало координат, потому что это точка, относительно которой отражаются все остальные точки.
Проще всего увидеть, как работает рефлексия о происхождении, на примере.
Пример 4: Нахождение координат точки после размышления о начале координат
Что из следующего представляет образ точки 𝐴(1,3) после размышления о начале координат?
- 𝐴′(1,−3)
- 𝐴′(−1,3)
- 𝐴′(−3,−1)
- 𝐴′(−3,1)
- 𝐴′(−1, −3)
Ответ
Напомним, что для общей точки 𝑃(𝑥,𝑦) отражение относительно карт начала координат
𝑃(𝑥,𝑦)→𝑃′(−𝑥,−𝑦).
Это означает, что он отображает точку 𝑃 на точку своего изображения 𝑃′, меняя знаки обеих ее координат.
Следовательно, мы должны применить это преобразование к точке 𝐴(1,3), чтобы получить ее изображение 𝐴′ следующим образом: 𝐴(1,3)→𝐴′(−1,−3).
Мы заключаем, что 𝐴′(−1,−3) представляет собой образ точки 𝐴(1,3) после размышления о начале координат, так что вариант Е правильный ответ.
Отражение относительно начала имеет интересное свойство, которое отличает его от отражения в линии. Это станет очевидным, когда мы посмотрим на его влияние. на треугольнике, как показано на следующей диаграмме.
Обратите внимание, что у исходного треугольника 𝐴𝐵𝐶 буквенные метки вершин расположены по часовой стрелке; то же самое верно и для его образа 𝐴′𝐵′𝐶′. Другими словами, ориентация вершин сохраняется. Это отличается от того, что происходит при отражении в линии, где порядок вершин сохраняется.
но направление маркировки (то есть по часовой стрелке или против часовой стрелки) меняется на противоположное.
Свойство: Отражение относительно начала координат
- Отражение относительно начала координат сохраняет ориентацию.
Например, если вершины многоугольника помечены по часовой стрелке, соответствующие метки вершин на изображении также будут упорядочены по часовой стрелке.
Наш последний пример поможет нам распознать размышления о происхождении.
Пример 5: Отражение треугольника относительно начала координат
Какой график представляет отражение треугольника 𝐴𝐵𝐶 относительно начала координат?
Ответ
Напомним, что для общей точки 𝑃(𝑥,𝑦) отражение относительно карт начала координат 𝑃(𝑥,𝑦)→𝑃′(−𝑥,−𝑦).
Следовательно, 𝑃′ будет иметь те же координаты, что и 𝑃, но с противоположными знаками, поэтому 𝑃 и 𝑃′
будет на том же расстоянии от начала координат, но по разные стороны от него по прямой. Вспомним также, что размышление о происхождении сохраняет ориентацию,
в то время как отражение на оси 𝑥 или оси 𝑦 нет.
Здесь нам нужно изучить графики один за другим, чтобы найти отражение о происхождении. В графе A треугольник 𝐴𝐵𝐶 и его изображение 𝐴′𝐵′𝐶′ находятся на противоположных сторонах оси 𝑦 с соответствующими вершинами на одном перпендикулярном расстоянии от оси 𝑦. Для каждой вершины 𝐴𝐵𝐶 ее образ в 𝐴′𝐵′𝐶′ имеет то же самое 𝑦-координата, но 𝑥-координата имеет противоположный знак. Мы распознаем это как отражение треугольника 𝐴𝐵𝐶 по оси 𝑦.
На графике B треугольник 𝐴𝐵𝐶 и его изображение 𝐴′𝐵′𝐶′ находятся по разные стороны от оси 𝑥, с соответствующими вершинами на одном и том же перпендикулярном расстоянии от оси 𝑥. Для каждой вершины 𝐴𝐵𝐶 ее образ в 𝐴′𝐵′𝐶′ имеет ту же 𝑥-координату, но 𝑦-координата имеет противоположный знак. Мы распознаем это как отражение треугольника 𝐴𝐵𝐶 на оси 𝑥.
В графе C треугольник 𝐴𝐵𝐶 и его изображение 𝐴′𝐵′𝐶′ находятся по разные стороны от начала координат. Соответствующие вершины
находятся на одном и том же расстоянии от начала координат, но по разные стороны от него по прямой. Для каждой вершины 𝐴𝐵𝐶 ее образ в
𝐴′𝐵′𝐶′ имеет те же координаты, но с противоположными знаками. Треугольник 𝐴𝐵𝐶 помечен против часовой стрелки и
так же и 𝐴′𝐵′𝐶′, поэтому ориентация вершин сохраняется, а также порядок. Мы признаем это отражением
треугольник 𝐴𝐵𝐶 относительно начала координат, поэтому граф C является правильным ответом.
Для каждой вершины 𝐴𝐵𝐶 ее образ в
𝐴′𝐵′𝐶′ имеет те же координаты, но с противоположными знаками. Треугольник 𝐴𝐵𝐶 помечен против часовой стрелки и
так же и 𝐴′𝐵′𝐶′, поэтому ориентация вершин сохраняется, а также порядок. Мы признаем это отражением
треугольник 𝐴𝐵𝐶 относительно начала координат, поэтому граф C является правильным ответом.
Интересно отметить, что на графике D фактически показан треугольник 𝐴𝐵𝐶, отраженный в наклонной вниз линии, которая проходит через начало координат в 45∘ как к оси 𝑥, так и к оси 𝑦. Эта линия имеет уравнение 𝑦=−𝑥, и мы нарисуем его ниже.
Однако, поскольку размышления этого типа выходят за рамки этого объяснения, мы не будем рассматривать их здесь более подробно.
Итак, мы показали, что граф C представляет собой отражение треугольника 𝐴𝐵𝐶 относительно начала координат.
Давайте закончим повторением некоторых ключевых понятий из этого объяснения.
Ключевые точки
- Отражение на координатной плоскости — это тип трансформации.
 Он принимает геометрическую фигуру, такую как точка, отрезок или фигура, и
преобразует его в конгруэнтную геометрическую фигуру, называемую изображением.
Он принимает геометрическую фигуру, такую как точка, отрезок или фигура, и
преобразует его в конгруэнтную геометрическую фигуру, называемую изображением. - При отображении геометрических фигур, таких как сегменты линий или многоугольники, самый простой способ сделать это — отразить каждую отдельную конечную точку или вершину, а затем соедините точки изображения в той же последовательности, в которой они появляются на исходном рисунке.
- Для общей точки 𝑃(𝑥,𝑦), отражение в картах оси 𝑥 𝑃(𝑥,𝑦)→𝑃′(𝑥,−𝑦). Эффект состоит в том, что положение 𝑃′ будет отражать положение 𝑃, на противоположной стороне от оси 𝑥 и на том же перпендикулярном расстоянии от оси 𝑥, что и 𝑃.
- Для общей точки 𝑃(𝑥,𝑦), отражение в картах оси 𝑦 𝑃(𝑥,𝑦)→𝑃′(−𝑥,𝑦). Эффект состоит в том, что положение 𝑃′ будет отражать это 𝑃, на противоположной стороне оси 𝑦 и на том же перпендикулярном расстоянии от оси 𝑦, что и 𝑃.
- Отражение в линии сохраняет длины отрезков, меры углов, свойство промежуточности и параллелизм.

- Для общей точки 𝑃(𝑥,𝑦) отражение относительно начала координат отображает 𝑃(𝑥,𝑦)→𝑃′(−𝑥,−𝑦). Эффект состоит в том, что 𝑃 и 𝑃′ будут на одном и том же расстоянии от начала координат, но по разные стороны от него по прямой.
- Отражение относительно начала сохраняет ориентацию.
Трансформации
День 1 Координаты точек на сетке
Декартовы координаты можно использовать для определения вашего местоположения на карте или графике. Плоскость декартовых координат, по сути, представляет собой две числовые линии (одну вертикальную и одну горизонтальную), которые пересекаются в фиксированной точке, называемой «начало координат », отмеченной на сетке точкой (0,0). Каждая из отдельных числовых линий называется осью .
Используя декартовы координаты, вы можете отметить точку
на графике, указав насколько далеко влево или вправо и вверх и вниз от исходной точки (0,0).
Координаты всегда записываются в определенном порядке:
- расстояние по горизонтали (влево-вправо) называется координатой X и всегда пишется первым,
- расстояние по вертикали (вверх-вниз) расстояние называется координатой Y и всегда пишется вторым.
Это называется « упорядоченная пара » ( пара номеров в специальном порядке ). Числа в упорядоченной паре разделяются запятой и заключаются в круглые скобки, чтобы отличить их от других точек. Например, на диаграмме ниже упорядоченная пара (4,3) находится на 3 единицы справа от начала координат и на 4 единицы выше начала координат.
Декартова плоскость разделена на четыре квадранта . Они пронумерованы от 1 до 4, начиная с правого верхнего угла и двигаясь против часовой стрелки (см. схему ниже).
| youtube.com/embed/r16I6LB2YbQ?wmode=opaque» frameborder=»0″ allowfullscreen=»»> | В квадранте I координаты x и y положительны; в квадранте II координата x отрицательна, а координата y положительна; в квадранте III оба отрицательные; а в квадранте IV x положительно, а y отрицательно. О точках, лежащих на оси (т. е. имеющих хотя бы одну координату, равную 0), говорят, что они не находятся ни в одном квадранте. Координаты вида ( x , 0) лежат на горизонтальной оси x , а координаты вида (0, y ) лежат на вертикальной оси y . Видео (слева) объясняет основы декартовой координатной плоскости, ключевую лексику, объясняет квадранты и способы построения координат. |
Перемещения на координатной плоскости0251 — это преобразование плоскости, при котором каждая точка фигуры перемещается на одинаковое расстояние в одном и том же направлении.
 Когда фигура переводится, она остается такой же или конгруэнтной.
Когда фигура переводится, она остается такой же или конгруэнтной. Когда мы ПЕРЕВОДИМ фигуру в координатной плоскости, мы прибавляем величину перемещения ко всем упорядоченным парам, из которых состоит фигура. Не забудьте:
- Назовите упорядоченные пары всех точек, составляющих фигуру
- Добавьте значение x перевода ко всем координатам x
- Добавьте значение y смещения ко всем координатам y
- Перепишите все новые упорядоченные пары и нарисуйте новую фигуру
| Вектор переноса A Вектор переноса — это вектор, задающий длину и направление конкретного переноса. Векторы на декартовой плоскости можно записать [x,y], что означает перевод x единиц по горизонтали и y единицы по вертикали. |
Отражения в координатной плоскости
Когда вы посмотрите в зеркало, вы видите свое отражение. В математике вы можете создавать зеркальные изображения фигур, отражая их по заданной линии.
Когда фигура отражается над заданной линией, результирующая фигура называется ее отражением. Отражение — это зеркальное отражение исходной фигуры, а линия отражения — это зеркало. Если бы вы могли сложить изображение по линии отражения, исходное изображение и его отражение идеально совпали бы.
| youtube.com/embed/ouNp8FtgiEE?wmode=opaque» frameborder=»0″ allowfullscreen=»»> |
Во втором видео игнорируйте раздел «Отражение в сегменте» (с 4:40 до 6:46). Несмотря на то, что это интересно и что-то, что вам нужно будет знать в конечном итоге, вы не будете проверять эту концепцию в 8-м классе в этом году. Хотя остальная часть видео очень полезна.
Обзор: (вы также можете просмотреть эти правила на изображении сверху)
Отражение по оси x (x,y) → (x,-y)
Отражение по оси Y (x,y) → (-x,y)
Отражение по диагонали линия через (1,1) или y=x равна
Отражение по диагональной линии через (-1,1) или y=-x равно (x,y )→(−y,−x)
Вращения в координатной плоскости
Когда фигуру поворачивают вокруг заданной точки, преобразование называется вращением. Фигура вращается против или по часовой стрелке вокруг неподвижной точки. Неподвижная точка называется «центром вращения».
Фигура вращается против или по часовой стрелке вокруг неподвижной точки. Неподвижная точка называется «центром вращения».
Примечание : для уклона центром вращения всегда будет исходная точка (0,0).
Правила вращения
Как показано на верхнем левом изображении и нижнем левом видеодисплее, существуют правила вращения в:
По часовой стрелке (CW)
Направление против часовой стрелки (CCW)
- Правило поворота на 90° вокруг начала координат (x,y)→(-y, x)
- Правило поворота на 180° вокруг начала координат: (x,y)→(−x,−y)
- Правило поворота на 270° вокруг начала координат начало координат (x,y)→(y, -x)
| youtube.com/embed/pqVKmLVIfl8?wmode=opaque» frameborder=»0″ allowfullscreen=»»> |
Dil ции в координатной плоскости Расширение делает фигуру больше или меньше, но имеет ту же форму, что и оригинал (см. рисунок справа). Другими словами, расширение похоже на , но не точно такое же, как в оригинале. Все расширения имеют центр и масштабный коэффициент . Центр является точкой отсчета для расширения (как точка схода на чертеже в перспективе), а масштабный коэффициент говорит нам, насколько фигура растягивается или сжимается. Чтобы расширить что-либо в координатной плоскости, умножьте каждую координату на коэффициент масштабирования (K). Это называется картирование. Если коэффициент масштабирования равен 0,5, то просто умножьте каждую исходную координату на 0,5. Изображение будет вдвое меньше исходной формы. |
| |


 Он принимает геометрическую фигуру, такую как точка, отрезок или фигура, и
преобразует его в конгруэнтную геометрическую фигуру, называемую изображением.
Он принимает геометрическую фигуру, такую как точка, отрезок или фигура, и
преобразует его в конгруэнтную геометрическую фигуру, называемую изображением.