делители, простота, двоичный вид, куб, квадрат
Укажите число, чтобы получить всю информацию о нем:
Случайное число
| Четность: |
Число 1521 является нечетным. |
| Сумма цифр: | 9 |
| Произведение цифр: | 10 |
| Количество цифр: | 4 |
| Все делители числа | 1 3 9 13 39 117 169 507 1521 |
| Количество делителей | 9 |
| Сумма делителей | 2379 |
| Простое число |
Составное число |
| Квадратный корень | 39 |
| Кубический корень | 11,5003150512302 |
| Квадрат | 2313441 |
| Куб | 3518743761 |
| Обратное число | 0,000657462195923734 |
| Предыдущее число: 1520 | Следующее число: 1522 |
Натуральное число 1521
является четырехзначным.
Оно записывается 4 цифрами.
Сумма цифр, из которых состоит число 1521, равна 9, а их произведение равно 10.
Число 1521 является нечетным.
Всего число 1521 имеет 9 делителей:
1,
3,
9,
13,
39,
117,
169,
507,
1521,
. Сумма делителей равна 2379. Куб числа 1521 равен 2313441, а квадрат составляет 3518743761.
Квадратный корень рассматриваемого числа равен 39. Кубический корень равен 11,5003150512302.
Число, которое является обратным к числу 1521, выглядит как 0,000657462195923734.
делители, простота, двоичный вид, куб, квадрат
Укажите число, чтобы получить всю информацию о нем:
Случайное число
| Четность: |
Число 39 является нечетным. |
| Сумма цифр: | 12 |
| Произведение цифр: | 27 |
| Количество цифр: | 2 |
| Все делители числа | 1 3 13 39 |
| Количество делителей | 4 |
| Сумма делителей | 56 |
| Простое число |
Составное число |
| Квадратный корень | 6,2449979983984 |
| Кубический корень | 3,39121144301417 |
| Квадрат | 1521 |
| Куб | 59319 |
| Обратное число | 0,0256410256410256 |
| Предыдущее число: 38 | Следующее число: 40 |
Натуральное число 39
является двузначным.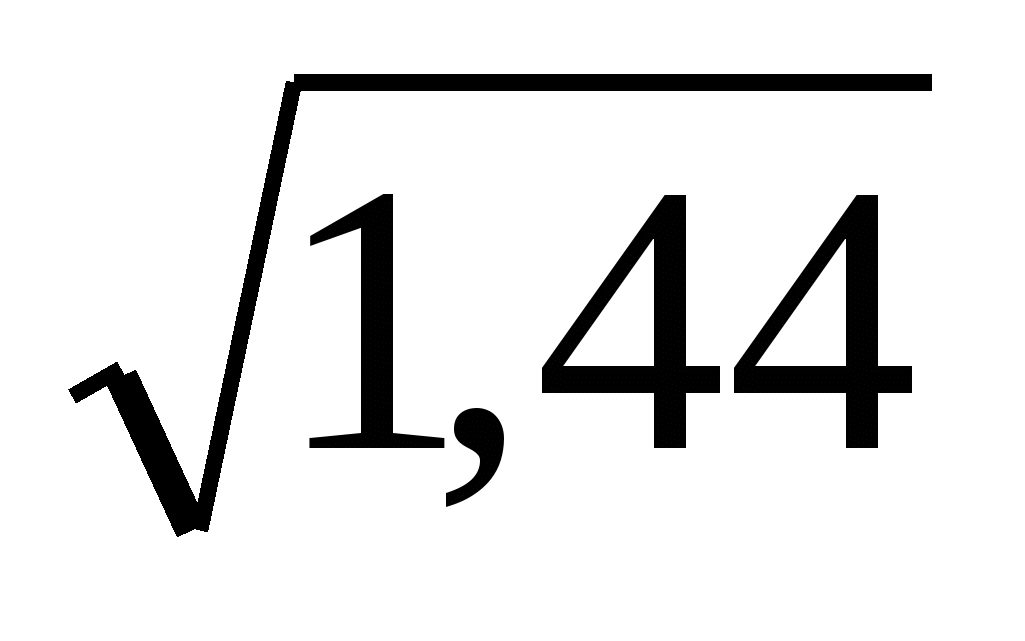
Квадратный корень из 1521 равен 39. Это потому, что умножая 39 само на себя, мы получаем 1521. 39 — это квадратный корень из 1521, а 1521 — это квадрат из 39. Квадратный корень из 1521 также может быть -39, потому что умножая -39 само на себя, мы также получаем 1521.
Таким образом, мы говорим, что квадратные корни из 1521 равны \( \pm39 \).
На изображении выше мы видим квадратный корень из 1521.
На изображении выше показан кубический корень из 1521.
Как вычислить квадратный корень из 1521 методом простой факторизацииМы выполняем простую факторизацию числа 1521 и получаем четыре множителя, т.е.
На изображении выше мы видим разложение числа 1521 на простые множители.
Затем мы объединяем их в группы по два и удаляем один элемент из группы, что и является нашим желаемым результатом.
\( \sqrt{1521}=\sqrt{3\times3\times13\times13}=\sqrt{\left(3\times3\right)\times\left(13\times13\right)}=3\times13 =39 \)
Как вычислить квадратный корень из 1521 методом деления в длинуСледующие шаги используются для получения корня квадратного из 1521 методом деления в длину.
Шаг 1 : Сначала мы соединяем цифры заданного числа, начиная с цифр справа, и помещаем горизонтальную черту над числами, обозначающими пары.
Шаг 2 : Затем мы находим число, которое при умножении дает произведение, меньшее или равное 15. Как мы знаем, 3 × 3 = 9 < 15. Итак, теперь полученная разность равна 6, а частное равно 3.
Шаг 3 : Далее мы опустим 21 и умножим частное на 2, и мы получим 6. Теперь 6 является начальной цифрой для нового делителя.
Шаг 4 : Этот процесс повторяется до тех пор, пока мы не получим ноль в качестве остатка.
Следовательно, квадратный корень из 1521 равен 39..
На изображении выше мы видим процесс деления числа 1521 в длину. Таким образом, мы получаем частное 39, которое является квадратным корнем из 39.
Следующие шаги должны быть использованы для нахождения квадратного корня из 1521 с использованием вавилонского метода.
Здесь мы допускаем ошибку для конечного результата, которая меньше 0,01. Другими словами, мы попытаемся найти значение квадратного корня для 1521 хотя бы с одним правильным десятичным знаком.
Шаг 1: Сначала разделите число (1521) на 2, чтобы получить первое приближение квадратного корня.
Первое предположение = 1521/2 = 760,5.
Шаг 2: Затем разделите 1521 на предыдущий результат. d = 1521/760,5 = 2,
Среднее значение (d) с шагом 1: (2 + 760,5)/2 = 381,25 (новое предположение).
Ошибка = новое предположение — предыдущее значение = 760,5 — 381,25 = 379,25.
379,25 > 0,01. Поскольку ошибка > точности, мы повторяем этот шаг снова.
Шаг 3: Далее делим 1521 на предыдущий результат. d = 1521/381,25 = 3,9895081967.
Среднее значение (d) со значением из шага 2: (3,9895081967 + 381,25)/2 = 192,6197540984 (новое предположение).
Ошибка = новое предположение — предыдущее значение = 381,25 — 192,6197540984 = 188,6302459016.
188,6302459016 > 0,01. Поскольку ошибка > точности, мы повторяем этот шаг снова.
Шаг 4: Затем разделите 1521 на предыдущий результат.
d = 1521/192,6197540984 = 7,8963863656.
Среднее значение (d) со значением из шага 3: (7,8963863656 + 192,6197540984)/2 = 100,258070232 (новое предположение).
Ошибка = новое предположение — предыдущее значение = 192,6197540984 — 100,258070232 = 92,3616838664.
92,3616838664 > 0,01. Поскольку ошибка > точности, мы повторяем этот шаг снова.
Шаг 5: Затем разделите 1521 на предыдущий результат. d = 1521/100,258070232 = 15,1708485559.
Среднее значение (d) со значением шага 4: (15,1708485559 + 100,258070232)/2 = 57.714459394 (новое предположение).
Ошибка = новое предположение — предыдущее значение = 100,258070232 — 57,714459394 = 42,543610838.
42,543610838 > 0,01. Поскольку ошибка > точности, мы повторяем этот шаг снова.
Шаг 6: Затем разделите 1521 на предыдущий результат. d = 1521/57,714459394 = 26,3538810893.
Среднее значение (d) со значением из шага 5: (26,3538810893 + 57,714459394)/2 = 42,0341702417 (новое предположение).
Ошибка = новое предположение — предыдущее значение = 57,714459394 – 42,0341702417 = 15,6802891523.
15,6802891523 > 0,01. Поскольку ошибка > точности, мы повторяем этот шаг снова.
Шаг 7: Разделите 1521 на предыдущий результат. d = 1521/42,0341702417 = 36,1848465488.
Среднее значение (d) со значением шага 6: (36,1848465488 + 42,0341702417)/2 = 39,1095083953 (новое предположение).
Ошибка = новое предположение — предыдущее значение = 42,0341702417 — 39,1095083953 = 2,9246618464.
2,9246618464 > 0,01. Поскольку ошибка > точности, мы повторяем этот шаг снова.
Шаг 8 : Разделите 1521 на предыдущий результат. d = 1521/39,1095083953 = 38,82332.
Среднее значение (d) со значением из шага 7: (38,82332 + 39,1095083953)/2 = 39,0001533143 (новое предположение).
Ошибка = новое предположение — предыдущее значение = 39,1095083953 — 39,0001533143 = 0,109355081.
0,109355081 > 0,01.
Поскольку ошибка > точности, мы повторяем этот шаг снова.
Шаг 9: Разделите 1521 на предыдущий результат. г = 1521/39,0001533143 = 38,9998466863.
Среднее значение (d) со значением шага 8: (38,9998466863 + 39,0001533143)/2 = 39,0000000003 (новое предположение).
Ошибка = новое предположение — предыдущее значение = 39,0001533143 — 39,0000000003 = 0,000153314.
0,000153314 <= 0,01. Поскольку ошибка <= точность, мы останавливаем итерации и используем 39,0000000003 в качестве квадратного корня.
Следовательно, мы получаем 39 как квадратный корень из 1521.
Является ли квадратный корень из 1521 рациональным или иррациональным? Число определяется как рациональное, если оно может быть выражено в форме p/q, где q не равно 0. Если число не является рациональным, оно называется иррациональным числом. Любые неконечные десятичные числа, которые имеют повторяющиеся числа после запятой, являются рациональными числами.
Здесь квадратный корень из 1521 может быть выражен как 39/1 и -39/1. Оба числа могут быть представлены в виде рационального числа, т. е. в форме p/q. Таким образом, мы заключаем, что квадратный корень из 1521 является рациональным числом.
Является ли квадратный корень 1521 идеальным квадратом?1521 — правильный квадрат. Число является полным квадратом, если его квадратный корень является рациональным числом. Здесь квадратный корень из 1521 равен 39, а 39 — рациональное число. Таким образом, мы заключаем, что 1521 — совершенный квадрат. 92=1521\\
\\Rightarrow x=\sqrt{1521}\\
\Rightarrow x=\pm39\end{array}
\(\)
Если вы хотите получить высокие баллы на экзамене по математике тогда вы находитесь в правильном месте. Здесь вы будете учиться посредством еженедельной подготовки к тестам, живых занятий и серии экзаменов. Кроме того, загрузите приложение Testbook, чтобы подготовить умную и высокорейтинговую стратегию к экзамену.
В.1. Является ли квадратный корень из 1521 рациональным числом?
Ответ 1
Q.2 Чему равны 2 квадратных корня из 1521?
Ответ 2 39 и -39 — два квадратных корня из 1521.
Ответ 3 Квадратный корень из 1521 равен 39.
Q.4 Можно ли найти квадратный корень из 1521, используя метод повторного вычитания?
Ответ 4 Да, мы находим квадратный корень из 1521, используя метод повторного вычитания.
Q.5 Является ли число 1521 идеальным квадратом?
Ответ 5 Да, 1521 — полный квадрат.
Скачать публикацию в формате PDF| Кубический корень из 432: определение, методы и примеры решения |
| Тупой угол: определение, методы построения, характеристики и примеры решения |
| Список кубических корней от 1 до 30 Таблица для идеальных и несовершенных кубов |
| Кубический корень от 1 до 20: метод, идеальный куб и примеры решения Примеры |
1521 квадратный корень? | √1521
| Пожалуйста, введите реальный номер: |
| Результат квадратного корня: |
Вот ответ на вопросы типа: 1521 квадратный корень? | √1521 или чему равен квадратный корень из 1521?
Используйте приведенный ниже калькулятор квадратного корня, чтобы найти квадратный корень любого мнимого или действительного числа.
Вавилонский метод, также известный как метод Героя.
Что такое квадратный корень?
Определение квадратного корня
Квадратный корень из числа а — это число х, такое что х 2 = а, другими словами, число х, квадрат которого равен а. Например, 39 — это квадратный корень из 1521, потому что 39 2 = 39•39 = 1521, —39 — это квадратный корень из 1521, потому что (-39) 2 = (—39)•(—39) = 1521.
Таблица квадратных корней 1-100
Квадратные корни от 1 до 100, округленные до тысячных.
| нет | нет 2 | √ |
|---|---|---|
| 1 | 1.000 | |
| 2 | 4 | 1.414 |
| 3 | 9 | 1.732 |
| 4 | 16 | 2. 000 |
| 5 | 25 | 2.236 |
| 6 | 36 | 2.449 |
| 7 | 49 | 2.646 |
| 8 | 64 | 2.828 |
| 9 | 81 | 3.000 |
| 10 | 100 | 3.162 |
| 11 | 121 | 3.317 |
| 12 | 144 | 3.464 |
| 13 | 169 | 3.606 |
| 14 | 196 | 3.742 |
| 15 | 225 | 3.873 |
| 16 | 256 | 4.000 |
| 17 | 289 | 4.123 |
| 18 | 324 | 4.243 |
| 19 | 361 | 4.359 |
| 20 | 400 | 4.472 |
| 21 | 441 | 4. 583 |
| 22 | 484 | 4.690 |
| 23 | 529 | 4.796 |
| 24 | 576 | 4.899 |
| 25 | 625 | 5.000 |
| нет | нет 2 | √ |
|---|---|---|
| 26 | 676 | 5.099 |
| 27 | 729 | 5.196 |
| 28 | 784 | 5.292 |
| 29 | 841 | 5.385 |
| 30 | 900 | 5.477 |
| 31 | 961 | 5.568 |
| 32 | 1,024 | 5.657 |
| 33 | 1,089 | 5.745 |
| 34 | 1,156 | 5.831 |
| 35 | 1,225 | 5.916 |
| 36 | 1,296 | 6. 000 |
| 37 | 1,369 | 6.083 |
| 38 | 1,444 | 6.164 |
| 39 | 1,521 | 6.245 |
| 40 | 1,600 | 6.325 |
| 41 | 1,681 | 6.403 |
| 42 | 1,764 | 6.481 |
| 43 | 1,849 | 6.557 |
| 44 | 1,936 | 6.633 |
| 45 | 2,025 | 6.708 |
| 46 | 2,116 | 6.782 |
| 47 | 2,209 | 6.856 |
| 48 | 2,304 | 6.928 |
| 49 | 2,401 | 7.000 |
| 50 | 2500 | 7,071 |
| нет | нет 2 | √ |
|---|---|---|
| 51 | 2,601 | 7. 141 |
| 52 | 2,704 | 7.211 |
| 53 | 2,809 | 7.280 |
| 54 | 2,916 | 7.348 |
| 55 | 3,025 | 7.416 |
| 56 | 3,136 | 7.483 |
| 57 | 3,249 | 7.550 |
| 58 | 3,364 | 7.616 |
| 59 | 3,481 | 7.681 |
| 60 | 3,600 | 7.746 |
| 61 | 3,721 | 7.810 |
| 62 | 3,844 | 7.874 |
| 63 | 3,969 | 7.937 |
| 64 | 4,096 | 8.000 |
| 65 | 4,225 | 8.062 |
| 66 | 4,356 | 8.124 |
| 67 | 4,489 | 8. 185 |
| 68 | 4,624 | 8.246 |
| 69 | 4,761 | 8.307 |
| 70 | 4,900 | 8.367 |
| 71 | 5,041 | 8.426 |
| 72 | 5,184 | 8.485 |
| 73 | 5,329 | 8.544 |
| 74 | 5,476 | 8.602 |
| 75 | 5,625 | 8.660 |
| нет | нет 2 | √ |
|---|---|---|
| 76 | 5,776 | 8.718 |
| 77 | 5,929 | 8.775 |
| 78 | 6,084 | 8.832 |
| 79 | 6,241 | 8.888 |
| 80 | 6,400 | 8.944 |
| 81 | 6,561 | 9.000 |
| 82 | 6,724 | 9. 055 |
| 83 | 6,889 | 9.110 |
| 84 | 7,056 | 9.165 |
| 85 | 7,225 | 9.220 |
| 86 | 7,396 | 9.274 |
| 87 | 7,569 | 9.327 |
| 88 | 7,744 | 9.381 |
| 89 | 7,921 | 9.434 |
| 90 | 8,100 | 9.487 |
| 91 | 8,281 | 9.539 |
| 92 | 8,464 | 9.592 |
| 93 | 8,649 | 9.644 |
| 94 | 8,836 | 9.695 |
| 95 | 9,025 | 9.747 |
| 96 | 9,216 | 9.798 |
| 97 | 9,409 | 9.849 |
| 98 | 9,604 | 9. |