Корень 5 степени из 128 y 2: Mathway | Популярные задачи

2

Корень n ой степени » задачи

степени »

• 4в степени х-корень х в квадрате -5 дальше 12*2 в степени х-1-корень х в квадрате -5 дальше +8=0

  
  Решение: После (-5), видимо, надо написать » — «. Тогда все получается, если использовать способы решения показательных уравнений и иррациональных уравнений. И еще надо найти ОДЗ и проверить по ней полученные корни, или проверить их просто подстановкой в исходное уравнение

• Корень 4 степени из 5/8 * корень 4 степени из 128 и это все деленное на корень 4 степени из 125.

  
  Решение: $$ \frac{ \sqrt[4]{ \frac{5}{8} }* \sqrt[4]{128} }{ \sqrt[4]{125} }=\\= \frac{ \sqrt[4]{ \frac{5*128}{8} } }{ \sqrt[4]{125} }= \sqrt[4]{ \frac{5*16}{125} }= \sqrt[4]{ \frac{16}{25} }= \frac{2}{ \sqrt{5} }= \frac{2 \sqrt{5} }{5} $$

  $$ \frac{ \sqrt[4]{ \frac{5}{8} }* \sqrt[4]{128} }{ \sqrt[4]{125} } =\frac{ \sqrt[4]{ \frac{5}{8} * {128} } }{ \sqrt[4]{125} }=\\= \frac{ \sqrt[4]{5*16} }{ \sqrt[4]{125} } = \sqrt[4]{ \frac{5*16}{125} }= \sqrt[4]{ \frac{16}{25} } = \frac{2}{ \sqrt{5} } =\frac{2 \sqrt{5} }{ 5 } =0,4 \sqrt{5} \\ $$

• Корень 4 степени из x-1 плюс корень из x-1 равно 30

  
  Решение:

  Корень 4 степени из х-1+корень квадратный из х-1=30
  Делаем замену: Корень квадратный из х-1=t получаем: t^2+t=30 решаем уравнение t^2+t-30=0
  D=121. 5 \leq -331772}} \right.; (-\infty;- \sqrt[5]{-331772} ] $$
  Ответ: $$ (0;4]; $$ $$ (-\infty;- \sqrt[5]{-331772} ] $$

• Корень 4 степени из 54 * на корень 4 степени из 120 деленное в виде дроби на корень 4 степени из5

  
  Решение: Корень 4 степени из 54*120 корень 4 степени из 6480  6480
  ——————————————— =—————————————=корень 4 степени из———=
  корень 4 степени из 5 корень 4 степени из 5 5

  корень 4 степени 1296=6
  

• Вычислите: корень в 4 степени 256 минус 1/3корень в 3 степени 27деленное на 8

  
  Решение: $$ \sqrt[4]{256} — \frac{1}{3} \sqrt[3]{ \frac{27}{8}} = \sqrt{16} — \frac{1}{3} * \frac{3}{2} = 4 — \frac{1}{2} = 3.5 $$
  

• Корень квадратный из х + корень 4 степени из х = 12

  
  Решение:

  $$ \sqrt{x} + \sqrt[4]{x} =12 $$
  ОДЗ: $$ x \geq 0 $$
  введем замену: $$ \sqrt[4]{x} =t $$ $$ t \geq 0 $$

  $$ t^2+t-12=0 $$
  $$ D=1+48=49 $$
  $$ t_1=3 $$
  $$ t_2=-4 $$ — не подходит

  $$ \sqrt[4]{x} =3 \\ x=3^4 \\ x=81 $$
  Ответ: 81

• (корень 4степени из а+ корень 4 степени из 16а)(корень 4степени из 81а- корень 4 степени из625)

  
  Решение: $$ (\sqrt[4]{a}+2\sqrt[4]{a})(3\sqrt[4]{a}-5)=3\sqrt[4]{a}(3\sqrt[4]{a}-5)=9\sqrt[2]{a}-15\sqrt[4]{a} $$

  (корень 4степени из а+ корень 4 степени из 16а)(корень 4степени из 81а- корень 4 степени из 625)=(корень 4степени из а+2корень 4степени из а)(3корень 4степени из а-5)=

  =3корень 4степени из а((3корень 4степени из а-5)=9Va-15корень 4степени из а

• Решить через формулы дифференцирования.

  5;
    2y = — 1024;
    y = — 512

12 3 4 > >>

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Радикалы и рациональные показатели | Алгебра и тригонометрия

Цели обучения

В этом разделе студенты будут:

• Вычислять квадратные корни.
• Используйте правило произведения, чтобы упростить квадратный корень.
• Используйте правило отношения для упрощения квадратных корней.
• Сложение и вычитание квадратных корней.
• Рационализировать знаменатели.
• Используйте рациональные корни.

9{2}=16,[/latex]квадратный корень из[latex]\,16\,[/latex]равен[latex]\,4.\,[/latex]Функция квадратного корня обратна возведению в квадрат так же, как вычитание является обратным сложением. Чтобы отменить возведение в квадрат, мы извлекаем квадратный корень.

В общих чертах, если [латекс]\,а\,[/латекс] — положительное действительное число, то квадратный корень из [латекс]\,а\,[/латекс] — это число, которое при умножении на сам по себе дает[латекс]\,а.\,[/латекс]Квадратный корень может быть положительным или отрицательным, потому что умножение двух отрицательных чисел дает положительное число. Главный квадратный корень — это неотрицательное число, которое при умножении само на себя равно[latex]\,a. \,[/latex].Квадратный корень, полученный с помощью калькулятора, является главным квадратным корнем.

Главный квадратный корень из [латекс]\,а\,[/латекс] записывается как [латекс]\,\sqrt{а}.\,[/латекс] Символ называется радикалом, член под символ называется подкоренным, а все выражение называется подкоренным выражением.

Главный квадратный корень

Главный квадратный корень из [латекс]\,а\,[/латекс] — это неотрицательное число, которое при умножении на себя равно [латекс]\,а.\,[/латекс ] Оно записывается как подкоренное выражение , с символом, называемым радикалом, над термином, называемым подкоренным и:[латекс]\,\sqrt{a}.[/латекс] 9{2}\,[/latex] равно [latex]\,25,[/latex] подкоренной символ подразумевает только неотрицательный корень, главный квадратный корень. Главный квадратный корень из 25 равен [латекс]\,\sqrt{25}=5.[/латекс]

Вычисление квадратных корней

Вычислите каждое выражение.

1. [латекс]\sqrt{100}[/латекс]
2. [латекс]\sqrt{\sqrt{16}}[/латекс]
3. [латекс]\sqrt{25+144}[/латекс]
4. [латекс]\sqrt{49}-\sqrt{81}[/латекс]

Показать решение

Для [латекс]\,\sqrt{25+144},[/латекс] можем ли мы найти квадратные корни перед сложением?

№ [латекс]\,\sqrt{25}+\sqrt{144}=5+12=17.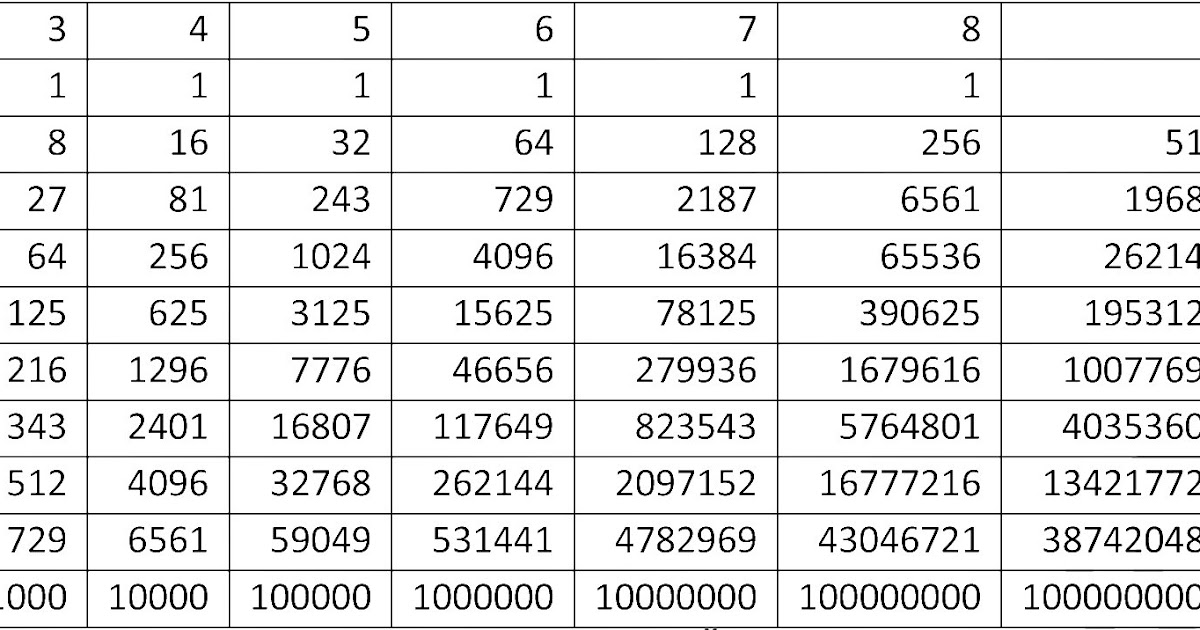 \,[/латекс] Это не эквивалентно [латекс]\,\sqrt {25+144}=13.\,[/latex] Порядок операций требует, чтобы мы складывали члены в подкоренном члене перед нахождением квадратного корня.

Попробуйте

Оцените каждое выражение.

1. [латекс]\sqrt{225}[/латекс]
2. [латекс]\sqrt{\sqrt{81}}[/латекс]
3. [латекс]\sqrt{25-9}[/латекс]
4. [латекс]\sqrt{36}+\sqrt{121}[/латекс]

Показать решение

Использование правила произведения для упрощения квадратных корней

Чтобы упростить квадратный корень, мы перепишем его так, чтобы в подкоренной части не было полных квадратов. Есть несколько свойств квадратных корней, которые позволяют нам упростить сложные подкоренные выражения. Первое правило, которое мы рассмотрим, — это правило произведения для упрощения квадратных корней, , которое позволяет нам разделить квадратный корень из произведения двух чисел на произведение двух отдельных рациональных выражений. Например, мы можем переписать [латекс]\,\sqrt{15}\,[/latex] как [латекс]\,\sqrt{3}\cdot \sqrt{5}.\,[/latex]Мы также можем используйте правило произведения, чтобы выразить произведение нескольких подкоренных выражений как одно подкоренное выражение.

Правило произведения для упрощения квадратных корней

Если [латекс]\,а\,[/латекс] и [латекс]\,b\,[/латекс] неотрицательны, квадратный корень произведения [латекс]\ ,ab\,[/latex]равно произведению квадратных корней из[латекс]\,а\,[/латекс]и[латекс]\,b.\,[/латекс]

[латекс]\ sqrt{ab}=\sqrt{a}\cdot \sqrt{b}[/latex]

How To

Имея радикальное выражение с квадратным корнем, используйте правило произведения, чтобы упростить его.

1. Выразите любые совершенные квадраты из подкоренного числа. 9{3}z}.[/latex]

   Показать решение

   How To

   Получив произведение нескольких подкоренных выражений, используйте правило произведения, чтобы объединить их в одно подкоренное выражение.
   

   1. Выразите произведение нескольких радикальных выражений как одно радикальное выражение.
   2. Упростить.

   Использование правила произведения для упрощения произведения кратных квадратных корней

   Упростите подкоренное выражение.

   Показать раствор

   Попробуйте

   Упростить[латекс]\,\sqrt{50x}\cdot \sqrt{2x}\,[/latex]при условии, что [латекс]\,x>0.[/latex]

   Показать решение

   Использование правила отношения для упрощения квадратных корней

   Точно так же, как мы можем переписать квадратный корень произведения как произведение квадратных корней, мы также можем переписать квадратный корень частного как частное квадратных корней, используя частное правило для упрощения квадратных корней. Может быть полезно разделить числитель и знаменатель дроби под корнем, чтобы мы могли отдельно извлекать их квадратные корни. Мы можем переписать [латекс]\,\sqrt{\frac{5}{2}}\,[/latex] как [латекс]\,\frac{\sqrt{5}}{\sqrt{2}}.[ /латекс]

   Частное правило для упрощения квадратных корней

   Квадратный корень из частного [латекс]\,\frac{a}{b}\,[/latex] равен частному квадратного корня из [латекс]\ ,a\,[/latex]и[латекс]\,b,[/latex],где[латекс]\,b\ne 0.[/latex]

   [латекс]\sqrt{\frac{a}{b }}=\frac{\sqrt{a}}{\sqrt{b}}[/latex]

   How To

   Если задано подкоренное выражение, используйте правило частного, чтобы упростить его.
   

   1. Запишите подкоренное выражение как частное двух подкоренных выражений. 9{5}}}.[/latex]

      Показать решение

      Сложение и вычитание квадратных корней

      Мы можем складывать или вычитать подкоренные выражения, только если они имеют одинаковые подкоренные числа и когда они имеют один и тот же подкоренный тип, например, квадратные корни. Например, сумма [латекс]\,\sqrt{2}\,[/латекс]и[латекс]\,3\sqrt{2}\,[/латекс]равна [латекс]\,4\sqrt{ 2}. \,[/latex]Однако часто можно упростить радикальные выражения, и это может изменить подкоренное выражение. Подкоренное выражение[латекс]\,\sqrt{18}\,[/латекс] может быть записано с [латекс]\,2\,[/латекс] в подкоренном члене, как [латекс]\,3\sqrt{ 2},[/latex]так[латекс]\,\sqrt{2}+\sqrt{18}=\sqrt{2}+3\sqrt{2}=4\sqrt{2}.[/latex]

      How To

      Учитывая подкоренное выражение, требующее сложения или вычитания квадратных корней, решить.

      1. Упростите каждое подкоренное выражение.
      2. Сложение или вычитание выражений с одинаковыми подкоренными числами.

      Добавление квадратных корней

      Добавить[latex]\,5\sqrt{12}+2\sqrt{3}.[/latex]

      Показать решение

      Попробуйте

      Добавить[латекс]\,\sqrt{5}+6\sqrt{20}.[/латекс]

      Показать решение

      Вычитание квадратных корней 9{4}c}.[/latex]

      Показать решение

      Попробуйте

      Вычтите[латекс]\,3\sqrt{80x}\,-4\sqrt{45x}.

      [/latex]

      Показать решение

      Рационализация знаменателей

      Если выражение, включающее радикалы квадратного корня, записано в простейшей форме, оно не будет содержать радикала в знаменателе. Мы можем удалить радикалы из знаменателей дробей, используя процесс, называемый , рационализирующий знаменатель .

      Мы знаем, что умножение на 1 не меняет значения выражения. Мы используем это свойство умножения, чтобы изменять выражения, содержащие радикалы в знаменателе. Чтобы удалить радикалы из знаменателей дробей, умножьте на форму 1, которая удалит радикал.

      Для знаменателя, содержащего один член, умножить на радикал в знаменателе над самим собой. Другими словами, если знаменатель равен [латекс]\,b\sqrt{c},[/latex], умножить на [латекс]\,\frac{\sqrt{c}}{\sqrt{c}}.[/ латекс]

      Для знаменателя, содержащего сумму или разность рационального и иррационального членов, умножьте числитель и знаменатель на сопряженное значение знаменателя, которое находится путем изменения знака радикальной части знаменателя.

      Если знаменатель равен [латекс]\,а+b\sqrt{c},[/латекс], то сопряженным является [латекс]\,а-b\sqrt{c}.[/латекс]

      How To

      Имея выражение с единственным квадратным корнем в знаменателе, рационализируйте знаменатель.

      1. Умножьте числитель и знаменатель на радикал в знаменателе.
      2. Упростить.

      Рационализация знаменателя, содержащего один член

      Напишите [latex]\,\frac{2\sqrt{3}}{3\sqrt{10}}\,[/latex]в простейшей форме.

      Показать раствор

      Попробуйте

      Напишите [латекс]\,\frac{12\sqrt{3}}{\sqrt{2}}\,[/latex]в простейшей форме.

      Показать решение

      How To

      Дано выражение с подкоренным членом и константой в знаменателе, рационализируйте знаменатель.

      1. Найдите сопряженное число знаменателя.
      2. Умножить числитель и знаменатель на сопряженное.
      3. Используйте свойство дистрибутива.
      4. Упростить.

      Рационализация знаменателя, содержащего два члена

      Напишите [latex]\,\frac{4}{1+\sqrt{5}}\,[/latex]в простейшей форме.

      Показать решение

      Попробуйте

      Напишите [латекс]\,\frac{7}{2+\sqrt{3}}\,[/latex]в простейшей форме.

      Показать раствор

      Использование рациональных корней

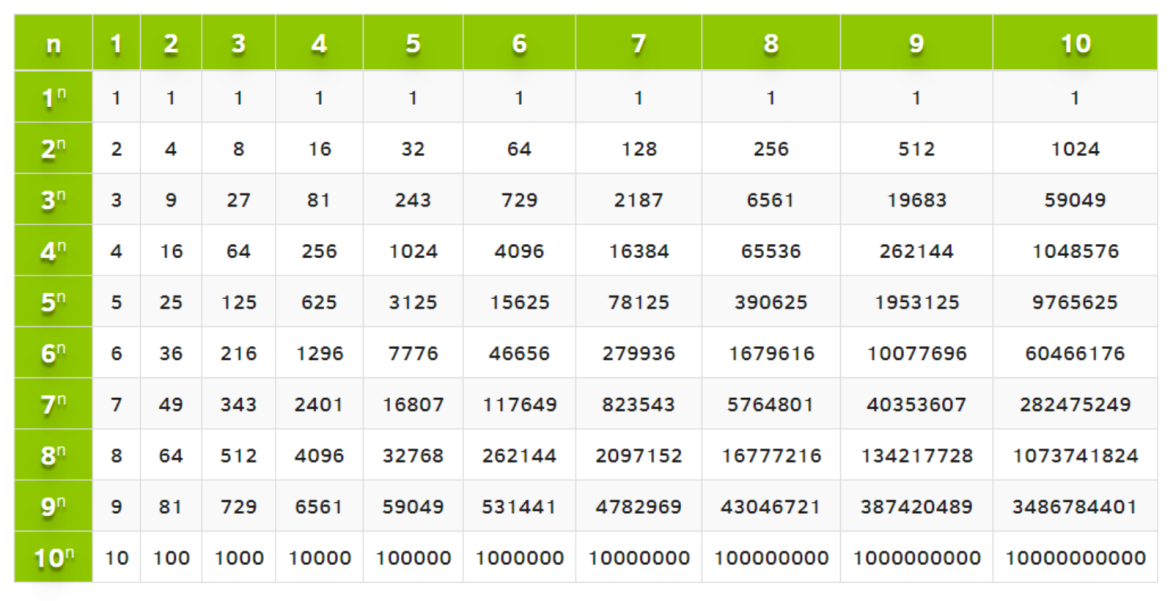
      Хотя квадратные корни являются наиболее распространенными рациональными корнями, мы также можем найти кубические корни, корни четвертой и пятой степени и т. д. Точно так же, как функция квадратного корня является обратной функцией возведения в квадрат, эти корни являются обратными их соответствующим степенным функциям. Эти функции могут быть полезны, когда нам нужно определить число, которое при возведении в определенную степень дает определенное число. 9{5}=-243.\,[/latex]Если[latex]\,a\,[/latex] является вещественным числом, имеющим хотя бы один корень n -го числа, то главный корень n -го числа[ латекс]\,а\,[/латекс] — это число с тем же знаком, что и [латекс]\,а\,[/латекс], которое при возведении в степень n равно [латекс]\,а . [/latex]

      Основной n -й корень [latex]\,a\,[/latex] записывается как [latex]\,\sqrt[n]{a},[/latex]где[ латекс]\,n\,[/латекс] — целое положительное число, большее или равное 2. В подкоренном выражении [латекс]\,n\,[/латекс] называется индексом подкореня.

      Основной

      n -й корень

      Если [latex]\,a\,[/latex] является вещественным числом, имеющим хотя бы один корень n -й, то главный n -й корень из [latex]\ ,a,[/latex]записывается как[latex]\,\sqrt[n]{a},[/latex] — это число с тем же знаком, что и [latex]\,a\,[/latex], что при возведенное в n -ю степень, равно[latex]\,a.\,[/latex]Индекс радикала равен[latex]\,n.[/latex]

      Упрощение

      n -й Корни

      Упростите каждое из следующего: 9{6}}{125}}[/латекс]

   2. [латекс]8\sqrt[4]{3}-\sqrt[4]{48}[/латекс]

   Показать решение

   Попробуйте

   Упростите.
   1. [латекс]\sqrt[3]{-216}[/латекс]
   2. [латекс]\frac{3\sqrt[4]{80}}{\sqrt[4]{5}}[/латекс]
   3. [латекс]6\sqrt[3]{9,000}+7\sqrt[3]{576}[/латекс]

   Показать решение

   Использование Rational Exponents

   Подкоренные выражения также можно записывать без использования подкоренного символа. {\frac{2}{3}}\,[/латекс]в виде радикала. Упрощать. 9{\frac{6}{5}}\right).[/latex]

   Показать решение

   Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с радикалами и рациональными представителями.

   • Радикалы
   • Рациональные показатели
   • Упростить радикалы
   • Рационализировать знаменатель

   Ключевые понятия

   • Главный квадратный корень числа[latex]\,a\,[/latex] — это неотрицательное число, которое при умножении само на себя равно[latex]\,a.\,[/latex]См. (Фигура).
   • Если [латекс]\,а\,[/латекс] и [латекс]\,b\,[/латекс] неотрицательны, квадратный корень произведения [латекс]\,аб\,[/латекс] равен к произведению квадратных корней из [латекс]\,а\,[/латекс]и[латекс]\,b\,[/латекс] См. (Рисунок) и (Рисунок).
   • Если [латекс]\,а\,[/латекс] и [латекс]\,b\,[/латекс] неотрицательны, квадратный корень из частного[латекс]\,\фракция{а}{b}\ ,[/latex]равно частному квадратному корню из [латекса]\,а\,[/латекс]и[латекс]\,b\,[/латекс]См. (Рисунок) и (Рисунок).
   • Мы можем складывать и вычитать подкоренные выражения, если они имеют одинаковые подкоренные числа и один и тот же индекс. См. (Рисунок) и (Рисунок).
   • Подкоренные выражения, записанные в простейшей форме, не содержат подкоренных в знаменателе. Чтобы исключить квадратный корень из знаменателя, умножьте и числитель, и знаменатель на сопряженную часть знаменателя. См. (Рисунок) и (Рисунок).
   • Главный n -й корень [latex]\,a\,[/latex] — это число с тем же знаком, что и [latex]\,a\,[/latex], которое при возведении в n -я степень равна[латекс]\,а.\,[/латекс]Эти корни обладают теми же свойствами, что и квадратные корни. См. (Рисунок).
   • Радикалы можно переписать как рациональные показатели, а рациональные показатели можно переписать как радикалы. См. (Рисунок) и (Рисунок).
   • Свойства показателей применяются к рациональным показателям. См. (Рисунок).

   Упражнения по разделам

   Вербальные

   Что означает отсутствие индекса у корня? Равно ли выражение подкоренному? Объяснять.

   Показать решение

   Куда придут радикалы в порядке операций? Объяснить, почему.

   Каждое число будет иметь два квадратных корня. Что такое главный квадратный корень?

   Показать раствор

   Может ли радикал с отрицательным корнем и иметь действительный квадратный корень? Почему или почему нет?

   Числовой

   В следующих упражнениях упростите каждое выражение.

   [латекс]\sqrt{256}[/латекс]

   Показать решение

   [латекс]\sqrt{\sqrt{256}}[/латекс]

   [латекс]\sqrt{4\left(9+16\right)}[/latex]

   Показать решение

   [латекс]\sqrt{289}-\sqrt{121}[/латекс]

   [латекс]\sqrt{196}[/латекс]

   Показать решение

   [латекс]\sqrt{1}[/латекс]

   [латекс]\sqrt{98}[/латекс]

   Показать решение

   [латекс]\sqrt{\frac{27}{64}}[/латекс]

   [латекс]\sqrt{\frac{81}{5}}[/латекс]

   Показать решение

   [латекс]\sqrt{800}[/латекс]

   [латекс]\sqrt{169}+\sqrt{144}[/латекс]

   Показать решение

   [латекс]\sqrt{\frac{8}{50}}[/latex]

   [латекс]\frac{18}{\sqrt{162}}[/latex]

   Показать решение

   [латекс]\sqrt{192}[/латекс]

   [латекс]14\sqrt{6}-6\sqrt{24}[/латекс]

   Показать решение

   [латекс]15\sqrt{5}+7\sqrt{45}[/латекс]

   [латекс]\sqrt{150}[/латекс]

   Показать решение

   [латекс]\sqrt{\frac{96}{100}}[/латекс]

   [латекс]\влево(\sqrt{42}\вправо)\влево(\sqrt{30}\вправо)[/ латекс]

   Показать решение

   [латекс]12\sqrt{3}-4\sqrt{75}[/латекс]

   [латекс]\sqrt{\frac{4}{225}}[/латекс]

   Показать решение

   [латекс]\sqrt{\frac{405}{324}}[/латекс]

   [латекс]\sqrt{\frac{360}{361}}[/латекс]

   Показать решение

   [латекс]\frac{5}{1+\sqrt{3}}[/latex]

   [латекс]\frac{8}{1-\sqrt{17}}[/latex]

   Показать решение

   [латекс]\sqrt[4]{16}[/латекс]

   [латекс]\sqrt[3]{128}+3\sqrt[3]{2}[/латекс] 9{10}}[/latex]

   Реальные приложения

   Растяжка подвесного моста проходит от земли по диагонали к вершине ближайшей опоры, образуя треугольник.

   No related posts.