Корень из 2 в 3 степени. Кубический корень (извлечение без калькулятора)
Если под рукой есть калькулятор, извлечь кубический корень из любого числа не составит никаких проблем. Но если калькулятора нет или вы просто хотите произвести впечатление на окружающих, извлеките кубический корень вручную. Большинству людей описываемый здесь процесс покажется довольно сложным, но с практикой извлекать кубические корни станет намного легче. Перед тем как приступить к чтению данной статьи, вспомните основные математические операции и вычисления с числами в кубе.
Шаги
Часть 1
Извлечение кубического корня на простом примереЗапишите задачу. Извлечение кубического корня вручную похоже на деление в столбик, но с некоторыми нюансами. Сначала запишите задачу в определенной форме.
- Запишите число, из которого нужно извлечь кубический корень. Число разбейте на группы по три цифры, причем отсчет начните с десятичной запятой.
Умножьте и вычтите. Умножьте последнюю цифру ответа (в нашем примере это 1) на найденный множитель (1261): 1*1261 = 1261. Запишите это число под 2000 и вычтите его из 2000. Вы получите 739 (это второй остаток).
Подумайте, является ли полученный ответ достаточно точным. Делайте это каждый раз, после того как завершите очередное вычитание. После первого вычитания ответ был равен 2, что не является точным результатом. После второго вычитания ответ равен 2,1.
- Чтобы проверить точность ответа, возведите его в куб: 2,1*2,1*2,1 = 9,261.
- Если вы считаете, что ответ достаточно точный, вычисления можно не продолжать; в противном случае проделайте еще одно вычитание.
Найдите второй множитель. Чтобы попрактиковаться в вычислениях и получить более точный результат, повторите действия, которые описаны выше.
Оцените второе число. Первое число вы нашли благодаря знанию кубов целых чисел. Теперь целое число превратите в десятичную дробь, приписав к нему (после десятичной запятой) некоторую цифру от 0 до 9. Необходимо найти десятичную дробь, куб которой будет близок, но меньше исходного числа.
- В нашем примере число 600 находится между числами 512 и 729. Например, к первому найденному числу (8) припишите цифру 5. Получится число 8,5.
- В нашем примере: 8 , 5 ∗ 8 , 5 ∗ 8 , 5 = 614 , 1. {\displaystyle 8,5*8,5*8,5=614,1.}
Сравните куб полученного числа с исходным числом. Если куб полученного числа больше исходного числа, попробуйте оценить меньшее число. Если же куб полученного числа намного меньше исходного числа, оценивайте большие числа до тех пор, пока куб одного из них не превысит исходное число.
Если нужно, оцените другое число. Сравните куб полученного числа с исходным числом. Если куб полученного числа больше исходного числа, попробуйте оценить меньшее число. Короче говоря, нужно найти такие два числа, кубы которых чуть больше и чуть меньше исходного числа.
- В нашем примере 8 , 44 ∗ 8 , 44 ∗ 8 , 44 = 601 , 2 {\displaystyle 8,44*8,44*8,44=601,2} . Это чуть больше исходного числа, поэтому оцените другое (меньшее) число, например, 8,43: 8 , 43 ∗ 8 , 43 ∗ 8 , 43 = 599 , 07 {\displaystyle 8,43*8,43*8,43=599,07} . Таким образом, значение кубического корня из 600 лежит между 8,43 и 8,44.
Выполняйте описанный процесс до тех пор, пока не получите ответ, точность которого вас устроит. Оцените следующее число, сравните его с исходным, затем, если нужно, оцените другое число и так далее.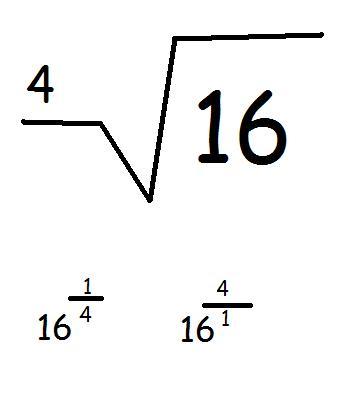
{3}=599,93}
, то есть результат меньше исходного числа менее чем на 0,1.
Корень n-ной степени из числа x — это такое неотрицательное число z, которое при возведении в n-ную степень превращается в x. Определение корня входит в список основных арифметических операций, с которыми мы знакомимся еще в детстве.
Математическое обозначение
«Корень» произошел от латинского слова radix и сегодня слово «радикал» используется как синоним данного математического термина. С 13-го века математики обозначали операцию извлечения корня буквой r с горизонтальной чертой над подкоренным выражением. В 16-веке было введено обозначение V, которое постепенно вытеснило знак r, однако горизонтальная черта сохранилась. Его легко набирать в типографии или писать от руки, но в электронных изданиях и программировании распространилось буквенное обозначение корня — sqrt. Именно так мы и будем обозначать квадратные корни в данной статье.
Квадратный корень
Квадратным радикалом числа x называется такое число z, которое при умножении на самого себя превращается в x.
Например, если мы умножим 2 на 2, то получим 4. Двойка в этом случае и есть квадратный корень из четырех. Умножим 5 на 5, получим 25 и вот мы уже знаем значение выражения sqrt(25). Мы можем умножить и – 12 на −12 и получить 144, а радикалом 144 будет как 12, так и −12. Очевидно, что квадратные корни могут быть как положительными, так и отрицательными числами.
Своеобразный дуализм таких корней важен для решения квадратных уравнений, поэтому при поиске ответов в таких задачах требуется указывать оба корня. При решении алгебраических выражений используются арифметические квадратные корни, то есть только их положительные значения.
Числа, квадратные корни которых являются целыми, называются идеальными квадратами. Существует целая последовательность таких чисел, начало которой выглядит как:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256…
Квадратные корни других чисел представляют собой иррациональные числа. К примеру, sqrt(3) = 1,73205080757… и так далее.
Это число бесконечно и не периодично, что вызывает некоторые затруднения при вычислении таких радикалов.
Школьный курс математики утверждает, что нельзя извлекать квадратные корни из отрицательных чисел. Как мы узнаем в вузовском курсе матанализа, делать это можно и нужно – для этого и нужны комплексные числа. Однако наша программа рассчитана для извлечения действительных значений корней, поэтому она не вычисляет радикалы четной степени из отрицательных чисел.
Кубический корень
Кубический радикал числа x — это такое число z, которое при умножении на себя три раза дает число x. Например, если мы умножим 2 × 2 × 2, то получим 8. Следовательно, двойка является кубическим корнем восьми. Умножим три раза на себя четверку и получим 4 × 4 × 4 = 64. Очевидно, что четверка является кубическим корнем для числа 64. Существует бесконечная последовательность чисел, кубические радикалы которых являются целыми. Ее начало выглядит как:
1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197, 2744…
Для остальных чисел кубические корни являются иррациональными числами.
В отличие от квадратных радикалов, кубические корни, как и любые нечетные корни, можно извлекать из отрицательных чисел. Все дело в произведении чисел меньше нуля. Минус на минус дает плюс – известное со школьной скамьи правило. А минус на плюс – дает минус. Если перемножать отрицательные числа нечетное количество раз, то результат будет также отрицательным, следовательно, извлечь нечетный радикал из отрицательного числа нам ничего не мешает.
Однако программа калькулятора работает иначе. По сути, извлечение корня – это возведение в обратную степень. Квадратный корень рассматривается как возведение в степень 1/2, а кубический – 1/3. Формулу возведения в степень 1/3 можно переиначить и выразить как 2/6. Результат один и тот же, но извлекать такой корень из отрицательного числа нельзя. Таким образом, наш калькулятор вычисляет арифметические корни только из положительных чисел.
Корень n-ной степени
Столь витиеватый способ вычисления радикалов позволяет определять корни любой степени из любого выражения.
Вы можете извлечь корень пятой степени из куба числа или радикал 19 степени из числа в 12 степени. Все это элегантно реализовано в виде возведения в степени 3/5 или 12/19 соответственно.
Рассмотрим пример
Диагональ квадрата
Иррациональность диагонали квадрата была известна еще древним греками. Они столкнулись с проблемой вычисления диагонали плоского квадрата, так как ее длина всегда пропорциональна корню из двух. Формула для определения длины диагонали выводится из и в конечном итоге принимает вид:
d = a × sqrt(2).
Давайте определим квадратный радикал из двух при помощи нашего калькулятора. Введем в ячейку «Число(x)» значение 2, а в «Степень(n)» также 2. В итоге получим выражение sqrt(2) = 1,4142. Таким образом, для грубой оценки диагонали квадрата достаточно умножить его сторону на 1,4142.
Заключение
Поиск радикала – стандартная арифметическая операция, без которой не обходятся научные или конструкторские вычисления. Конечно, нам нет нужды определять корни для решения бытовых задач, но наш онлайн-калькулятор определенно пригодится школьникам или студентам для проверки домашних заданий по алгебре или математическому анализу.
При решении некоторых технических задач бывает нужно посчитать корень третьей степени . Иногда это число еще называют кубическим корнем. Корнем третьей степени из данного числа называют такое число, куб (третья степень) которого равняется данному. То есть если y – корень третьей степени числа x, то должно выполняться условие: y?=x (икс равно игрек куб).
Вам понадобится
- калькулятор или компьютер
Инструкция
- Чтобы посчитать корень третьей степени , воспользуйтесь калькулятором. Желательно, чтобы это был не обычный калькулятор, а калькулятор, используемый для инженерных расчетов. Однако даже на таком калькуляторе вы не найдете специальную кнопку для извлечения корня третьей степени . Поэтому используйте функцию для возведения числа в степень. Извлечению корня третьей степени соответствует возведение в степень 1/3 (одна треть).
- Для возведения числа в степень 1/3 наберите на клавиатуре калькулятора само число. y.
- Если корень третьей степени приходится считать систематически, то воспользуйтесь программой MS Excel. Чтобы посчитать корень третьей степени в «Екселе», введите в любую клетку знак «=», а затем, выберите значок «fx» — вставка функции. В появившемся окошке в списке «Выберите функцию» выберите строку «СТЕПЕНЬ». Нажмите кнопку «Ок». Во вновь появившемся окошке введите в строку «Число» значение числа, из которого нужно извлечь корень. В строку «Степень» введите число «1/3» и нажмите «Ок». В клетке таблицы появится искомое значение кубического корня из исходного числа.
y.Сколько гневных слов произнесено в его адрес? Порой кажется, что кубический корень невероятно сильно отличается от квадратного. На самом деле разница не настолько велика. Особенно, если понять, что они только частные случаи общего корня n-ой степени.
Зато с его извлечением могут возникнуть проблемы. Но чаще всего они связаны с громоздкостью вычислений.
Что нужно знать о корне произвольной степени?
Во-первых, определение этого понятия.
Корнем n-ой степени из некоторого «а» называется такое число, которое при возведении в степень n дает исходное «а».
Причем бывают четные и нечетные степени у корней. Если n — четное, то подкоренное выражение может быть только нулем или положительным числом. В противном случае вещественного ответа не будет.
Когда же степень нечетная, то существует решение при любом значении «а». Оно вполне может быть и отрицательным.
Во-вторых, функцию корня всегда можно записать, как степень, показателем которой является дробь. Иногда это бывает очень удобным.
Например, «а» в степени 1/n как раз и будет корнем n-ой степени из «а». В этом случае основание степени всегда больше нуля.
Аналогично «а» в степени n/m будет представлено, как корень m-ой степени из «а n ».
В-третьих, для них справедливы все действия со степенями.
- Их можно перемножать. Тогда показатели степеней складываются.
- Корни можно разделить. Степени нужно будет вычесть.
- И возвести в степень.
В чем сходства и различия квадратного и кубического корней?
Они похожи, как родные братья, только степень у них разная. И принцип их вычисления одинаков, различие только в том, сколько раз должно число на себя умножиться, чтобы получить подкоренное выражение.
А о существенном отличии было сказано чуть выше. Но повториться не будет лишним. Квадратный извлекается только из неотрицательного числа. В то время, как вычислить кубический корень из отрицательной величины не составит труда.
Извлечение кубического корня на калькуляторе
Каждый человек хоть раз делал это для квадратного корня. А как быть если степень «3»?
На обычном калькуляторе имеется только кнопочка для квадратного, а кубического — нет. Здесь поможет простой перебор чисел, которые трижды умножаются на себя. Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.
А что в инженерном виде калькулятора в компьютере? Ура, здесь есть кубический корень. Эту кнопочку можно просто нажать, и программа выдаст ответ. Но это не все. Здесь можно вычислить корень не только 2 и 3 степени, но и любой произвольной. Потому что есть кнопка у которой в степени корня стоит «у». То есть после нажатия этой клавиши потребуется ввести еще одно число, которое будет равно степени корня, а уже потом «=».
Извлечение кубического корня вручную
Этот способ потребуется, когда калькулятора под рукой нет или воспользоваться им нельзя. Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.
Сначала посмотреть, а не получается ли полный куб от какого-нибудь целого значения. Может быть под корнем стоит 2, 3, 5 или 10 в третьей степени?
- Мысленно разделить подкоренное выражение на группы по три цифры от десятичной запятой. Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
- Определить число, куб которого меньше целой части подкоренного выражения. Его записать в промежуточный ответ над знаком корня. А под этой группой расположить его куб.
- Выполнить вычитание.
- К остатку приписать первую группу цифр после запятой.
- В черновике записать выражение: а 2 * 300 * х + а * 30 * х 2 + х 3 . Здесь «а» — это промежуточный ответ, «х» является числом, которое меньше получившегося остатка с приписанными к нему числами.
- Число «х» нужно записать после запятой промежуточного ответа. А значение всего этого выражения записать под сравниваемым остатком.
- Если точности достаточно, то расчеты прекратить. В противном случае нужно возвращаться к пункту под номером 3.
Его записать в промежуточный ответ над знаком корня. А под этой группой расположить его куб.Наглядный пример вычисления кубического корня
Он нужен потому, что описание может показаться сложным. На рисунке ниже показано, как извлечь кубический корень из 15 с точностью до сотых.
Единственной сложностью, которую имеет этот метод, заключается в том, что с каждым шагом числа увеличиваются многократно и считать в столбик становится все сложнее.
- 15> 2 3 , значит под целой частью записана 8, а над корнем 2.
- После вычитания из 15 восьми получается остаток 7. К нему нужно приписать три нуля.
- а = 2. Поэтому: 2 2 * 300 * х +2 * 30 * х 2 + х 3
- Методом подбора получается, что х = 4. 1200 * 4 + 60 * 16 + 64 = 5824.
- Вычитание дает 1176, а над корнем появилось число 4.
- Приписать к остатку три нуля.
- а = 24. Тогда 172800 х + 720 х 2 + х 3
- х = 6. Вычисление выражения дает результат 1062936. Остаток: 113064, над корнем 6.
- Снова приписать нули.
- а = 246. Неравенство получается таким: 18154800х + 7380х 2 + х 3
- х = 6. Расчеты дают число: 109194696, Остаток: 3869304. Над корнем 6.
Ответом получается число: 2, 466. Поскольку ответ должен быть дан до сотых, то его нужно округлить: 2,47.
Необычный способ извлечения кубического корня
Его можно использовать тогда, когда ответом является целое число. Тогда кубический корень извлекается разложением подкоренного выражения на нечетные слагаемые.
Причем таких слагаемых должно быть минимально возможное число.
К примеру, 8 представляется суммой 3 и 5. А 64 = 13 + 15 + 17 + 19.
Ответом будет число, которое равно количеству слагаемых. Так корень кубический из 8 будет равен двум, а из 64 — четырем.
Если под корнем стоит 1000, то его разложением на слагаемые будет 91 + 109 + 93 + 107 + 95 + 105 + 97 + 103 + 99 + 101. Всего 10 слагаемых. Это и есть ответ.
Из большого числа без калькулятора мы уже разобрали. В этой статье рассмотрим как извлечь кубический корень (корень третьей степени). Оговорюсь, что речь идёт о натуральных числах. Как вы думаете, сколько времени нужно, чтобы устно вычислить такие корни как:
Совсем немного, а если потренируетесь два-три раза минут по 20, то любой такой корень вы сможете извлечь за 5 секунд устно.
*Нужно отметить, что речь идёт о таких числах стоящих под корнем, которые являются результатом возведения в куб натуральных чисел от 0 до 100.
Мы знаем, что:
Так вот, число а, которое мы будем находить – это натуральное число от 0 до 100.
Посмотрите на таблицу кубов этих чисел (результаты возведения в третью степень):
Вы без труда сможете извлечь кубический корень из любого числа в этой таблице. Что нужно знать?
1. Это кубы чисел кратных десяти:
Я бы даже сказал, что это «красивые» числа, запоминаются они легко. Выучить несложно.
2. Это свойство чисел при произведении.
Его суть заключается в том, что при возведении в третью степень какого-либо определённого числа, результат будет иметь особенность. Какую?
Например, возведём в куб 1, 11, 21, 31, 41 и т.д. Можно посмотреть по таблице.
1 3 = 1, 11 3 = 1331, 21 3 = 9261, 31 3 = 26791, 41 3 = 68921 …
То есть, при возведении в куб числа с единицей на конце в результате у нас всегда получится число с единицей в конце.
При возведении в куб числа с двойкой на конце в результате всегда получится число с восьмёркой в конце.
Покажем соответствие в табличке для всех чисел:
Знания представленных двух моментов вполне достаточно.
Рассмотрим примеры:
Извлечь кубический корень из 21952.
Данное число находится в пределах от 8000 до 27000. Это означает, что результат корня лежит в пределах от 20 до 30. Число 29952 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 28.
Извлечь кубический корень из 54852.
Данное число находится в пределах от 27000 до 64000. Это значит, что результат корня лежит в пределах от 30 до 40. Число 54852 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 38.
Извлечь кубический корень из 571787.
Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 571787 заканчивается на 7. Такой вариант возможен только тогда, когда в куб возводится число с тройкой в конце. Таким образом, результат корня равен 83.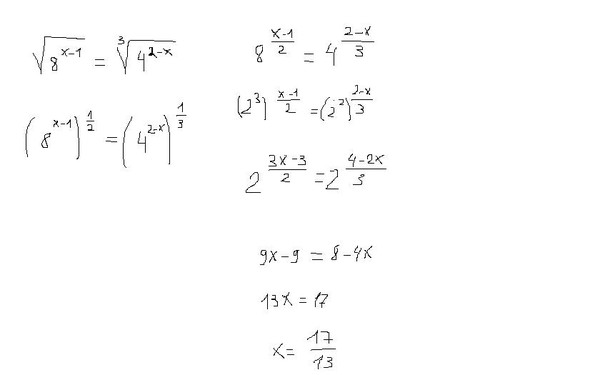
Извлечь кубический корень из 614125.
Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 614125 заканчивается на 5. Такой вариант возможен только тогда, когда в куб возводится число с пятёркой в конце. Таким образом, результат корня равен 85.
Думаю, что вы теперь без труда сможете извлечь кубический корень из числа 681472.
Конечно, чтобы извлекать такие корни устно, нужна небольшая практика. Но восстановив две указанные таблички на бумаге, вы без труда в течение минуты, в любом случае, такой корень извлечь сможете.
После того, как нашли результат обязательно сделайте проверку (возведите его с третью степень). *Умножение столбиком никто не отменял 😉
На самом ЕГЭ задач с такими «страшненькими» корнями нет. Например, в требуется извлечь кубический корень из 1728. Думаю, что это теперь для вас не проблема.
Если вы знаете какие-то интересные приёмы вычислений без калькулятора, присылайте, со временем опубликую.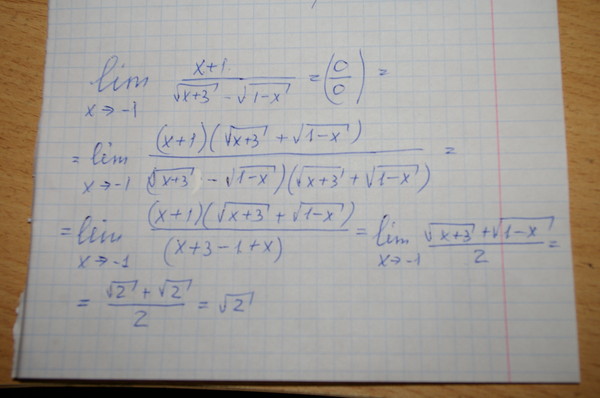
На этом всё. Успеха Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Сил Корней, Сила
246. Было показано, каким образом любая степень или корень может быть выражена посредством индекса. Индекс мощности — целое число. Корень — это дробь, числитель которой равен 1. Существует также другой класс величин, которые можно рассматривать либо как степени корней, либо как корни степеней.
Предположим, что 1/2 умножается само на себя, чтобы повториться три раза как множитель.
Продукт a 1/2+1/2+1/2 или 3/2 (ст. 243), очевидно, является кубом 1/2 , то есть кубом квадратного корня из а. Этот дробный индекс обозначает, таким образом, степень корня . Знаменатель выражает корень, а числитель степень. Знаменатель показывает, на сколько равных делителей или корней разлагается данная величина; а числитель показывает, сколько из этих корней нужно перемножить.
Таким образом, 4/3 — это четвертая степень кубического корня из a.
Знаменатель показывает, что а делится на три множителя или корня: 1/3 , 1/3 и 1/3 . И числитель показывает, что четыре из них должны быть умножены вместе; что даст четвертую степень числа 1/3 ; то есть,
a 1/3 .a 1/3 .a 1/3 .a 1/3 = a 4/3 .
247. Как 3/2 есть степень корня, так есть корень степени . Возведем в третью степень a 3 . Квадратный корень из этого равен 3/2 . Корень 3 есть количество, которое, умножив само на себя, даст 3 .
Но согласно ст. 243, а 3/2 = а 1/2 .а 1/2 .а 1/2 ; и это, умноженное само на себя (ст. 100), есть
a 1/2 .a 1/2 .a 1/2 .a 1/2 .a 1/2 .
a 1/2 = а 3 .
Следовательно, 3/2 — это квадратный корень из куба a.
Таким же образом можно показать, что m/n есть m-я степень n-го корня из a; или n-й корень m-й степени: то есть корень степени равен той же степени того же корня . Например, четвертая степень кубического корня из а равна кубическому корню из четвертой степени из а.
248. Корни и степени одной буквы можно умножить на 9.0015 добавляя свои показатели степени . (Статья 243.) Легко видеть, что тот же принцип может быть распространен на степени корней, когда показатели имеют общий знаменатель.
Таким образом, а 2/7 .а 3/7 = а 2/7+3/7 = а 5/7 .
Первый числитель показывает, как часто 1/7 берется в качестве множителя для получения 2/7 . (Статья 246.)
А второй числитель показывает, как часто 1/7 берется в качестве множителя для получения 3/7 .
Таким образом, сумма числителей показывает, как часто нужно извлекать корень для произведения . (Статья 100.)
Или, таким образом, 2/7 = 1/7 .a 1/7 .
А 3/7 = 1/7 .а 1/7 .а 1/7 .
Следовательно, a 2/7 .a 3/7 = a 1/7 .a 1/7 .a 1/7 .a 1/7 .a 1/7 = а 5/7 .
249. Значение количества не меняется от применения к нему дробного показателя, числитель и знаменатель которого равны.
Таким образом, а = 2/2 = а 3/3 = а н/н . Ибо знаменатель показывает, что а разлагается на определенное число множителей; и числитель показывает, что все эти факторы включены в n/n .
Таким образом, a 3/3 = a 1/3 .a 1/3 .a 1/3 , что равно a.
И н/н = а 1/н .
а 1/н ….. n раз.
С другой стороны, когда числитель дробного индекса становится равным знаменателю, выражение можно сделать более простым, отбросив индекс.
Вместо n/n мы можем написать a.
250. Индекс степени или корня может быть заменен на любой другой индекс того же значения.
Вместо 2/3 мы можем поставить 4/6 .
Ибо в последнем из этих выражений предполагается, что а разлагается на вдвое больше множителей, чем в первом; а числитель показывает, что умножить на — столько этих множителей нужно перемножить. Так что вся стоимость не изменена.
Таким образом, х 2/3 = х 4/6 = х 6/9 . то есть квадрат кубического корня такой же, как четвертая степень шестого корня, шестая степень девятого корня.
Таким образом, 2 = 4/2 = 6/3 = 2н/н . Ибо значение каждого из этих индексов равно 2.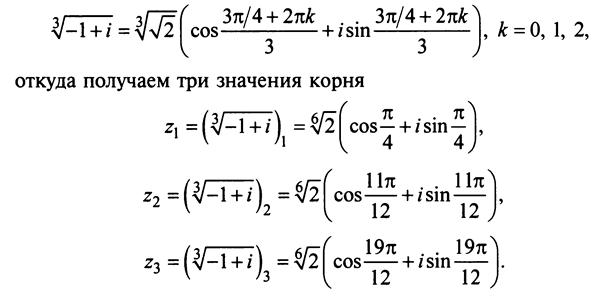
(Статья 132.)
251. Из предыдущей статьи легко увидеть, что дробный индекс может быть выражен в десятичных знаков .
1. Таким образом, 1/2 = 5/10 или 0,5 ; то есть квадратный корень равен 5-й степени десятого корня.
2. 1/4 = 25/100 или 0,25 ; то есть корень четвертой степени равен 25-й степени корня из 100-й степени.
3. а 2/5 = а 0,4 .
4. а 7/2 = а 3,5 .
5. 9/5 = 1,8
Однако во многих случаях десятичная дробь может быть только приближением к истинному индексу.
Таким образом, 1/3 = 0,3 почти. а 1/3 = а 0,333334 очень близко.
Таким образом, аппроксимация может быть доведена до любой требуемой степени точности.
Таким образом, 5/3 = 1,66666 .
NBSP; а 7 11 = а 1,87142 .
Эти десятичные индексы образуют очень важный класс чисел, называемый логарифмами .
Часто удобно варьировать обозначение степеней корней, используя винкулум или радикальный знак √. При этом мы должны помнить, что сила корня такая же, как и корень силы; (ст. 247,), а также, что 9Знаменатель 0015 дробной степени выражает корень , а числитель — степень . (Статья 246.)
Следовательно, вместо 2/3 мы можем написать (a 1/3 ) 2 или (a 2 ) 1/3 или 3 √a 900. 05 2 .
Первая из этих трех форм обозначает квадрат кубического корня из а; и каждый из двух последних, кубический корень из квадрата a.
Итак, m/n = (a 1/n ) m = (a m ) 1/n = n √a m .
А (бх) 3/4 = (б 3 х 3 ) 1/4 = 4 √б 3 х 3 9 0006 .
И (а + у) 3/5 = [(а + у) 3 ] 1/5 = 5 √(а + у) 3 .
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями. Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически конвертируются в дроби — т.е. 1.45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример |
|---|---|---|---|
| + | плюс | сложение | 1/2 + 1/3 |
| — | минус | вычитание | 90 368 1 1/2 — 2/3 |
| * | звездочка | умножение | 2/3 * 3/4 |
| × | знак умножения | умножение | 2/3 × 5/6 |
| : | знак деления | деление 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • сокращение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .  Наиболее распространенные мнемоники для запоминания этого порядка операций: PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание. BEDMAS — скобки, экспоненты, деление, умножение, сложение, вычитание BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание. GEMDAS — символы группировки — скобки (){}, показатели степени, умножение, деление, сложение, вычитание. MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS. Будь осторожен; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо.
|
Двести пятьдесят два ученика переходят на 1-й уровень. Напишите дробью, какая часть учеников идет в 1-й класс, а какая во 2-й. Сократите обе дроби до их основной формы.