Корень из 1 i: Извлечение корня из комплексного числа онлайн

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значение tan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Алгебра. Учебник для 6-8 классов

Алгебра. Учебник для 6-8 классов
  

Барсуков А. Н. Алгебра. Учебник для 6-8 классов. 11-е изд., стер. — М.: Просвещение, 1966. — 296 с.

Учебник для средних общеобразовательных школ СССР в 50-60-е годы.

Шестое издание „Алгебры» А.Н. Барсукова переработано и приведено в соответствие с новой программой. Переработка учебника и изложение вопросов, вновь включенных в программу восьмилетней школы, выполнены С.И. Новоселовым.

Главу „Счётная (логарифмическая) линейка* и о возвышении в квадрат и куб, извлечении квадратного и кубического корней при помощи счётной линейки написал учитель математики школы № 315 Москвы И. Б. Вейцман. Одиннадцатое издание печатается с десятого без изменений.



Оглавление

ГЛАВА ПЕРВАЯ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ.
§ 2. Алгебраические выражения.
§ 3. Допустимые значения букв.
§ 4. Порядок действий.
§ 5. Основные законы сложения и умножения.
§ 6. Краткие исторические сведения.
ГЛАВА ВТОРАЯ. РАЦИОНАЛЬНЫЕ ЧИСЛА.
§ 7. Положительные и отрицательные числа.
§ 8. Числовая ось.
§ 9. Противоположные числа.
§ 10. Абсолютная величина числа.
§ 11. Сравнение рациональных чисел.
§ 12. Сложение рациональных чисел.
§ 13. Сложение нескольких чисел.
§ 14. Законы сложения.
§ 15. Вычитание рациональных чисел.
§ 16. Алгебраическая сумма.
§ 17. Умножение.
§ 18. Умножение нескольких чисел.
§ 19. Законы умножения.
§ 20. Деление.
§ 21. Свойства деления.
§ 22. Возведение в степень.
§ 23. Порядок выполнения действий.
§ 24. Уравнения.
§ 25. Решение задач с помощью уравнений.
§ 26. Графики.
§ 27. Краткие исторические сведения. (Из истории отрицательных чисел.)
ГЛАВА ТРЕТЬЯ. ДЕЙСТВИЯ НАД ЦЕЛЫМИ АЛГЕБРАИЧЕСКИМИ ВЫРАЖЕНИЯМИ.
§ 28. Одночлен и многочлен.
§ 29. Тождества и тождественные преобразования.
§ 30. Коэффициент.
§ 31. Расположенные многочлены.
§ 32. Приведение подобных членов.
§ 33. Сложение одночленов и многочленов.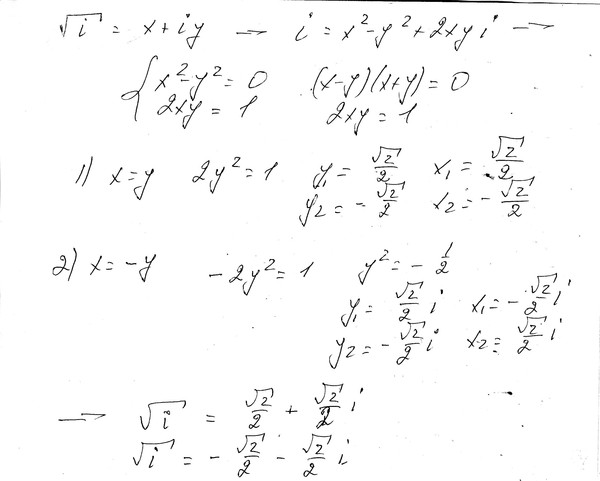
§ 34. Противоположные многочлены.
§ 35. Вычитание одночленов и многочленов
§ 36. Умножение одночленов.
§ 37. Умножение многочлена на одночлен.
§ 38. Умножение многочленов.
§ 39. Умножение расположенных многочленов.
§ 40. Возведение одночленов в степень.
§ 41. Формулы сокращённого умножения.
§ 42. Общие замечания о делении целых алгебраических выражений.
§ 43. Деление одночленов.
§ 44. Деление многочлена на одночлен
§ 45. Примеры решения уравнений.
ГЛАВА ЧЕТВЁРТАЯ. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ.
§ 47. Равносильные уравнения.
§ 48. Два основных свойства уравнений.
§ 49. Уравнения, содержащие неизвестное в обеих частях.
§ 50. Уравнение первой степени с одним неизвестным.
§ 51. Общие указания к решению уравнений.
§ 52. Решение задач с помощью уравнений.
§ 53. Краткие исторические сведения. (Из истории уравнений.)
ГЛАВА ПЯТАЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ.
§ 54. Понятие о разложении на множители.
§ 55. Вынесение за скобки общего множителя.
§ 56. Способ группировки.
§ 57. Применение формул сокращённого умножения.
§ 58. Применение нескольких способов.
§ 59. Деление многочленов при помощи разложения на множители.
ГЛАВА ШЕСТАЯ. АЛГЕБРАИЧЕСКИЕ ДРОБИ.
§ 60. Понятие об алгебраической дроби.
§ 61. Основное свойство дроби и сокращение дробей.
§ 62. Перемена знака у членов дроби.
§ 63. Целая отрицательная и нулевая степени числа.
§ 64. Приведение дробей к общему знаменателю.
§ 65. Сложение дробей.
§ 66. Вычитание дробей.
§ 67. Умножение дробей.
§ 68. Деление дробей.
§ 69. Возведение дроби в натуральную степень.
§ 70. Дробные уравнения.
§ 71. Примеры решения уравнений с буквенными коэффициентами.
ГЛАВА СЕДЬМАЯ. КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ.
§ 72. Координаты точки на плоскости.
§ 73. Прямо пропорциональная зависимость.
§ 74. График прямо пропорциональной зависимости.
§ 75. Линейная зависимость.
§ 76. (1/3)
§ 130. Примеры графического решения уравнений и систем уравнений.

комплексных чисел. Показать, что $\frac{-1+\sqrt{3}i}{2}$ является кубическим корнем из 1?

спросил

Изменено 5 лет, 8 месяцев назад

Просмотрено 3к раз

$\begingroup$

Я знаю, как напрямую доказать, что комплексное число является одним из кубических корней из 1. Но решение из учебника также дает другое решение, как показано ниже,

Однако я не понимаю, как можно сделать вывод, что $\frac{-1+\sqrt{3}i}{2}$ является корнем квадратного уравнения, следующего за двумя уравнениями вверху . Спасибо!

  • комплексные числа
  • квадратичные

$\endgroup$

6

$\begingroup$

Возможно, он использует теорему о комплексно-сопряженном корне и формулу Виета, чтобы сказать, что $\alpha+ \bar{\alpha}=-1$ и $\alpha \bar{\alpha}=1$. 3-1$. 92 = — (\ frac34) \\ (x- \ frac12) = \ pm \ frac {\ sqrt {- 3}} {2} \\ (x-\frac12)=\pm\frac {\sqrt{3}i}{2}\\ х = \ frac {1} {2} \ pm \ frac {\ sqrt {3} i} {2} $ $

$\endgroup$

Сколько кубических корней из 1 существует? | by Вир Вишал Дубей | Math Simplified

Кубический корень Unity? Это просто, верно? Это один! Вы были бы правы, но правы только на 1/3! Настало время глубже погрузиться в мир математики, исследовать числа за пределами нашего понимания и понять, что означает кубический корень из единицы и некоторые связанные с ним свойства. Но перед этим давайте рассмотрим некоторые основные понятия, связанные с комплексными числами и полиномами.

(если вы знакомы с основами алгебры и комплексными числами, вы можете сразу перейти к разделу, где я рассказываю о теореме Де Муавера)

Мы знаем, что любой многочлен с наибольшей степенью n имеет n корней, они могут равные или разные, или даже сложные по своей природе. Другими словами, многочленов степени n будут иметь n корней, действительных или комплексных, равных или различных.

Но что это за сложные корни, о которых я говорю? Комплексные корни — это комплексные числа или числа в форме z=(a+ib), где i — мнимая единица. (I обозначает йоту, и его числовое значение равно √-1, где a и b — рациональные числа.)

Одна из замечательных особенностей комплексных корней заключается в том, что они идут парами. Сопряженные пары, чтобы быть более точным. Это означает, что если мой многочлен имеет корень (x+iy), он также должен иметь (x-iy) в качестве корня. Они идут парами, в которых знак величины множителя с йотой изменен.

Когда мы смотрим на набор координат, все, что мы представляем, это набор точек, определяемых их расстояниями от осей x и y. Но у нас также есть удивительная система, использующая параметрические координаты окружности, чтобы узнать, что такое координаты точки с помощью углов. Мы называем эту систему «Полярная система координат». Основная идея заключается в том, что если у вас есть круг с центром в начале координат или (0,0) с радиусом ‘a’, любая координата может быть описана в виде (a cosθ, a sinθ) , просто из-за достоинства радиальной линии , соединяющей его и начало координат, и угла, который он образует с осью x. Это легко доказать с помощью простой тригонометрии. На самом деле, если вы укажете θ в качестве параметра, это даст вам геометрическое место окружности.

Используя desmos, я начертил единичный круг, используя параметрические координаты (a cosθ, a sinθ)

Точно так же вы можете найти точку, используя круг. Например, если мне нужно найти точку (0,5,0,855), я подставляю угол, соответствующий 0,5 по косинусу и 0,855 по греху (что равно пи/3 радиан или 60⁰), и получаю точку.

точка на единичной окружности может быть указана с использованием разных углов для разных значений cos и sin.

Точно так же вы можете построить график комплексных чисел, используя ось Y в качестве мнимой части и ось X в качестве действительной части. Точка (x,y) на этой плоскости (называемой плоскостью Гаусса) представляет (x+iy).

Чтобы теорема Муавра работала, вам нужно знать представление (a+bi) в полярной системе координат. Для этого делаем простые шаги.

Сначала возведите в квадрат действительную часть и действительный коэффициент i, сложите их и извлеките квадратный корень. Затем умножьте и разделите на этот коэффициент.

(a+bi)= √(a²+b²)(a+bi)/√(a²+b²)

Теперь разделите внутри скобки

(a+bi)= √(a²+b²) (а/√(а²+b²)+би/√(а²+b²))

Теперь найдите угол, значения которого в cos и sin дают a/√(a²+b²)&b/√(a²+b²) соответственно. Назовем этот угол θ.

(a+bi)= √(a²+b²)(cosθ+isinθ)

или

(a+bi)= √(a²+b²)(cisθ)

ci представляет (cisθ)

ci cosθ+isinθ). Здесь мы завершили преобразование в полярную форму. Теперь вернемся к теореме Муавра.

Важно отметить, что θ Должен быть углом в радианах,

9(p/q) = cos((2k π+ pθ/q)) + i sin((2k π+ pθ/q))

Расширение второго правила

Здесь количество решений = q
, и мы даем значения k, начиная с 0 и до q-1, то есть множество значений k может принимать:
k ∈ {0,1,2,3,4,……,q -1}

Теперь, когда мы поняли правила Де Муавра, давайте приступим к делу.

Пусть есть комплексное число z( в виде a+ib, помните, что действительные числа также являются комплексными числами, потому что если b=0, то нет мнимой части ), который представлен в виде (cosθ+isinθ) в полярной форме, так что z-1³=0

Теперь проделаем нехитрые алгебраические вычисления, чтобы получить:

Извлечем кубический корень с обеих сторон:

Теперь преобразуем z к полярной форме.

Теперь нам нужно найти такое θ, что cos θ=1, а sin θ=0. Какой это может быть угол? Правильно, это 0⁰!.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *