Сколько действительных корней четвертой степени имеет число 625? – Обзоры Вики
Идеальные 4-е корни:
| Четвертый корень X | 4√х |
|---|---|
| Четвертый корень из 81 | 3 |
| Четвертый корень из 256 | 4 |
| Четвертый корень из 625 | 5 |
| Четвертый корень из 1296 | 6 |
Точно так же, каковы настоящие 4-е корни числа 256? Четвертые корни
Корень четвертой степени 256 — это ± 4. Корень четвертой степени из 625 составляет ± 5. Корень четвертой степени из 1296 равен ± 6. Корень четвертой степени из 2401 составляет ± 7.
Сколько корней четвертой степени имеет число 4? Четвертый корень из 81 равен 3. По определению корень четвертой степени из 81 — это число y, такое что y4, или y × y × y × y, равно 81.
По определению корень четвертой степени из 81 — это число y, такое что y4, или y × y × y × y, равно 81.
Во-вторых, сколько действительных корней имеет число 625? Квадратный корень из 625 равен 25. Это положительное решение уравнения x 2 = 625. Число 625 представляет собой полный квадрат.
…
Корень квадратный из 625 в радикальной форме: √625.
| 1. | Что такое квадратный корень из 625? |
|---|---|
| 2. | Является ли квадратный корень из 625 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 625? |
Как найти квадратный корень из 625?
Квадратный корень из 625 равен 25. Это положительное решение уравнения x 2 = 625 . Число 625 представляет собой полный квадрат.
…
Корень квадратный из 625 в радикальной форме: √625.
| 1. | Что такое квадратный корень из 625? |
|---|---|
2. | Является ли квадратный корень из 625 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 625? |
| 4. | Часто задаваемые вопросы о квадратном корне из 625 |
тогда каковы настоящие 4-е корни 1296? Корень четвертой степени из 1296 равен ± 6. Корень четвертой степени из 2401 равен ±7.
Чему равны четыре корня четвертой степени из 1? Они соответствуют четырем числам 1, я, -1 и -я, как показано на рисунке ниже: Корни четвертой степени из 1 равномерно делят единичный круг на четыре части.
625 рационально или иррационально?
625 это рациональное число потому что это может быть выражено как частное двух целых чисел: 625 ÷ 1.
Какой куб равен 625? Простая факторизация числа 625 равна 5 × 5 × 5 × 5, следовательно, кубический корень из 625 в его низшей радикальной форме выражается как 5 ∛5 .
…
Кубический корень 625.
1. | Что такое кубический корень из 625? |
|---|---|
| 3. | Является ли кубический корень из 625 иррациональным? |
| 4. | Часто задаваемые вопросы о Cube Root of 625 |
Как найти корень четвертой степени на инженерном калькуляторе?
Как извлечь 4 квадратных корня на калькуляторе?
Сколько корней четвертой степени у меня?
Примеры Корни четвертой степени для чисел от 1 до 10:
Корень четвертой степени 1 — это ± 1. Корень четвертой степени из 16 составляет ± 2. Корень четвертой степени из 81 равен ± 3. Корень четвертой степени из 1296 составляет ± 6.
Корень четвертой степени из 16 составляет ± 2. Корень четвертой степени из 81 равен ± 3. Корень четвертой степени из 1296 составляет ± 6.
Как найти квадратный корень из 2025? Что такое квадратный корень из 2025? Квадратный корень из 2025 (или корень из 2025) — это число, которое при умножении само на себя дает произведение 2025. Следовательно, квадратный корень из 2025 = √2025 = 45.
Как найти квадратный корень из 841?
Таким образом, квадратный корень из 841 = 29. Поскольку 841 — это полный квадрат, мы также можем выразить его как 29. Число в пределах квадратного корня, которое повторяется, равно √(29 × 29) = 29. Следовательно, квадратный корень из 841 равен 29.
Как найти квадратный корень из 1089? Это положительное решение уравнения x 2 = 1089 . Число 1089 представляет собой полный квадрат.
…
Корень квадратный из 1089 в радикальной форме: √1089.
| 1. | Что такое квадратный корень из 1089? |
|---|---|
| 2. | Как найти квадратный корень из 1089? |
| 3. | Является ли квадратный корень из 1089 рациональным? |
| 4. | Часто задаваемые вопросы |
Сколько возможных действительных корней четвертой степени может иметь число?
На самом деле все числа (действительные, мнимые или комплексные), кроме нуля, имеют четыре четвертых корня. У нуля только один корень четвертой степени; сам. да. Если можно что-то возвести в квадрат в степени х, то возможно получить что-то, что является корнем х.
Каковы действительные корни четвертой степени из 256 действительных корней четвертой степени и? 4-й корень из 256 равен 4. Как известно, квадратный корень из числа — это значение, которое при умножении само на себя дает исходное число. Точно так же корень 4-й степени любого числа равен числу, которое при возведении в степень 4 дает исходное число.
Точно так же корень 4-й степени любого числа равен числу, которое при возведении в степень 4 дает исходное число.
Является ли я четвертым корнем из 1?
Комплексное число z такое, что z 4=1. Есть 4 четвертых корня из единицы, и они 1, я, −1 и-я.
Чему равен квадратный корень 4?
Квадратный корень из 4 обозначается √4, где символ «√» — это символ квадратного корня. Число 4 — идеальный квадрат. Таким образом, легко найти корень из 4 и других таких совершенных чисел.
…
Квадратный корень от 1 до 50.
| Число | Квадратный корень |
|---|---|
| 4 | 2 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
Площадь квадрата ABCD равна 1296 см2.
 2
2тогда сторона =корень из 1296=36
S=a²
a=√S
a=√1296
a=36 см
Ответ:сторона квадрата 36 см
Похожие вопросы
Читатель в 1-й день прочитал 5/12 части книги, во второй день — на 1/4 часть меньше,чем в 1-й день. Какую часть книги прочитал читатель за 2 дня? 2) Собственная скорость моторной лодки 28 целых 1/10 км/ч. Скорость течения реки 2 целых 3/10км/ч. Склько км. прорлывёт моторная лодка против течения реки за 1 час?…
Как ришать по матем. как ришать…
Сколько будет 12345-780…
(90+1)×100-64÷4 покажите действия пожалуйста…
Угол м.
Помогите
711 ))))))()))))))…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
ЭкономикаМузыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
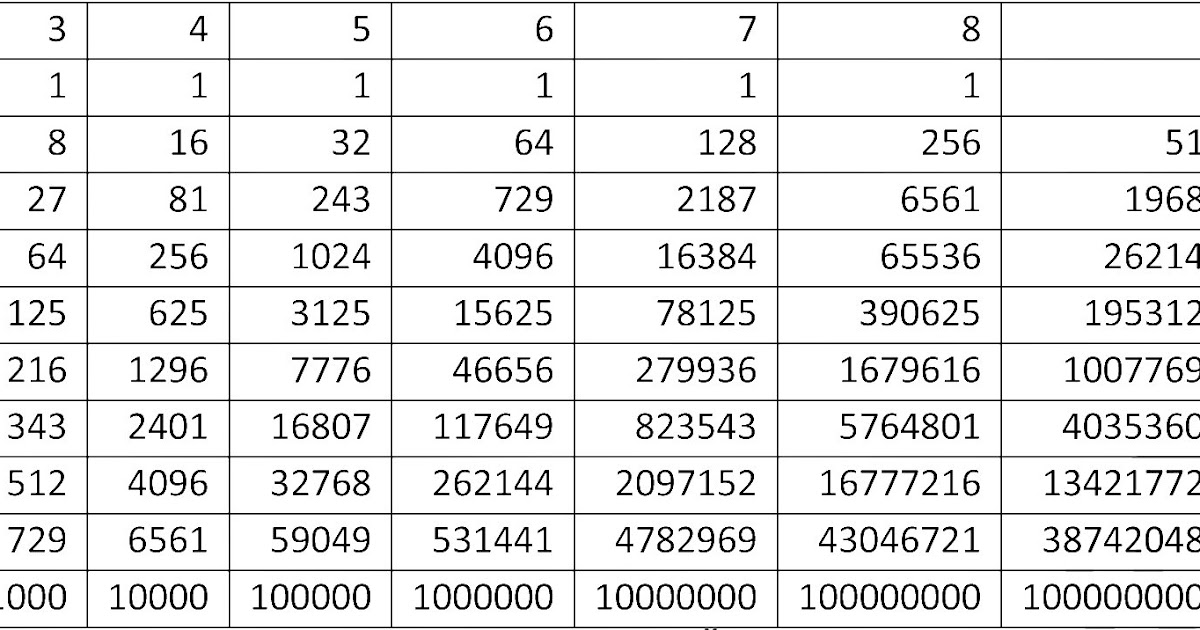
| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Математический справочник/ / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Степени — квадрат и куб, корни — квадратный и кубический и обратные величины чисел от 1 до 100. Таблица степеней.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ю Гуй Вань (You Gui Wan)
В этом разделе Вашему вниманию представлены классические рецепты китайской медицины с подробным описанием из различных авторитетных источников. Некоторые из рецептов впервые были упомянуты в старинных руководствах около двух тысяч лет назад. При описании рецептов обязательно указывается источник, где впервые был упомянут настоящий рецепт, его состав, действие отдельных компонентов в составе рецепта и варианты его применения с точки зрения китайской медицины и, по возможности, с точки зрения современной (конвенциональной) медицины. За несколько сот лет рецепты традиционной китайской медицины доказали свою эффективность и безопасность и активно используются врачами в настоящее время.
При описании рецептов обязательно указывается источник, где впервые был упомянут настоящий рецепт, его состав, действие отдельных компонентов в составе рецепта и варианты его применения с точки зрения китайской медицины и, по возможности, с точки зрения современной (конвенциональной) медицины. За несколько сот лет рецепты традиционной китайской медицины доказали свою эффективность и безопасность и активно используются врачами в настоящее время.
Dan Bensky and Randall Barolet, Formulas & Strategies, 2nd edition, 2009, p. 401
В Традиционной Китайской Медицине Правая Почка большинством авторов рассматривается как место Врат Жизни и связана с Ян Почек. Эта формула фокусируется на согревании и тонизации Ян Почек, таким образом восстанавливая функцию и способности Правой Почки.
Первоисточник: Collected Treatises of [Zhang] Jing-Yue (1624 г.)
Обработанный боковой корень аконита (Zhi Fu Zi) Aconiti Radix lateralis preparata 60-180 г
Кора коричника (Rou Gui) Cinnamomi Cortex 60-120 г
Желатин из рогов оленя (Lu Jiao Jiao) Cervi Cornus Colla 120 г
Обработанный корень ремании (Shu Di Huang) Rehmanniae Radix preparata 240 г
Плод кизила (Shan Zhu Yu) Corni Fructus 90 г
Корневище диоскореи, обжаренное (сухая обжарка) (Chao Shan Yao) dry-fried Dioscoreae Rhizoma 120 г
Плод дерезы, обжаренный (сухая обжарка) (Chao Gou Qi Zi) dry-fried Lycii Fructus 120 г
Семя повилики (Tu Si Zi) Cuscutae Semen 120 г
Кора эвкомии (Du Zhong) Eucommiae Cortex 120 г
Корень дудника китайского (Dang Gui) Angelicae sinensis Radix 90 г
Измельчите ингредиенты в порошок и сформируйте пилюлю с медом. Принимать по 9-15 г с горячей водой 2-3 раза в день. Можно также приготовить в форме отвара с пропорциональным уменьшением дозировки ингредиентов.
Принимать по 9-15 г с горячей водой 2-3 раза в день. Можно также приготовить в форме отвара с пропорциональным уменьшением дозировки ингредиентов.
Согревает и тонизирует Ян Почек, пополняет Эссенцию и тонизирует Кровь.
Истощение из-за длительной болезни, отвращения к холоду, прохладные конечности, импотенция, сперматорея, боль и слабость поясницы и коленей. Может также быть бесплодие, частый жидкий стул (иногда с непереваренными остатками пищи), недержание, отек нижних конечностей.
ОбъяснениеЭто признаки Пустоты Ян Почек с затуханием Огня во Вратах Жизни. В исходном тексте это состояние описывается как Пустота Изначального Ян и уменьшение пренатального дара, таким образом, что Огонь во Вратах Жизни затухает. Поскольку он неспособен произвести Землю, Селезенка и Желудок холодны и недостаточны. …в Нижнем обогревателе появляется Холод и возникает патогенная Вода, что приводит к блуждающему отеку.
Коренная причина этого состояния, Пустота Ян Почек, вызывает появление таких симптомов как отвращение к холоду, прохладные конечности, импотенция, сперматорея, боли и слабость в области поясницы и коленей, бесплодие, недержание и отек нижних конечностей. Вторичная причина, Холод и Пустота в Среднем Обогревателе, вызывает частый жидкий стул с остатками непереваренной пищи.
Главные ингредиенты, Обработанный боковой корень аконита (Zhi Fu Zi), Кора коричника (Rou Gui) и Желатин из рогов оленя (Lu Jiao Jiao), согревают и тонизируют Изначальный Ян. Желатин из рогов оленя (Lu Jiao Jiao) также имеет некоторое “блеск-и-кровь” (“flash-and-blood”) качество, пополняет Эссенцию и тонизирует Костный мозг.
Травы-помощники, Обработанный корень ремании (Shu Di Huang), Плод кизила (Shan Zhu Yu) Корневище диоскореи (Shan Yao), Плод дерезы (Gou Qi Zi), Семя повилики (Tu Si Zi) и Кора эвкомии (Du Zhong) питают Инь, приносят пользу Почкам, питают Печень и тонизируют Селезенку.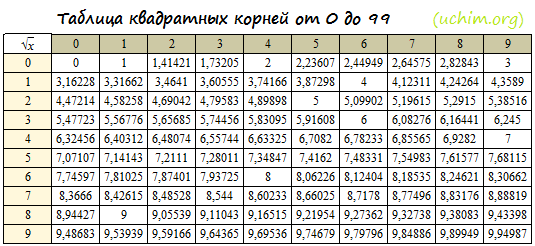 Сладкий и теплый Обработанный корень ремании (Shu Di Huang) питает Инь и тонизирует Почки, особенно Кровь; Плод кизила (Shan Zhu Yu) и Корневище диоскореи (Shan Yao) тонизируют Печень и приносят пользу Селезенке путем общей тонизации и пополнения Эссенции и Крови. Плод дерезы (Gou Qi Zi), Семя повилики (Tu Si Zi) и Кора эвкомии (Du Zhong) питают и тонизируют Печень и Почки; они особенно полезны в лечении боли и слабости поясницы. Корень дудника китайского (Dang Gui) добавляют для тонизации Крови и питания Печени.
Сладкий и теплый Обработанный корень ремании (Shu Di Huang) питает Инь и тонизирует Почки, особенно Кровь; Плод кизила (Shan Zhu Yu) и Корневище диоскореи (Shan Yao) тонизируют Печень и приносят пользу Селезенке путем общей тонизации и пополнения Эссенции и Крови. Плод дерезы (Gou Qi Zi), Семя повилики (Tu Si Zi) и Кора эвкомии (Du Zhong) питают и тонизируют Печень и Почки; они особенно полезны в лечении боли и слабости поясницы. Корень дудника китайского (Dang Gui) добавляют для тонизации Крови и питания Печени.
Поскольку эта формула тонизирует без дренирования, ее нельзя применять, когда Пустота Почек сопровождается Сыростью или Мутностью.
Эта формула может рассматриваться как разновидность Пилюли Ци Почек (Shen Qi Wan). Основные модификации заключаются в изменении дозировки согревающих трав, которые усиливают Ян, в удалении трех трав, которые по природе обладают преимущественно дренирующими свойствами: Пории кокосовидной (Fu Ling), Корневища частухи (Ze Xie) и Коры корня пиона мудань (Mu Dan Pi), и в добавлении компонентов, которые усиливают тонизирующее действие формулы и увеличивают Инь и Ян Почек – Желатина из рогов оленя (Lu Jiao Jiao), Семени повилики (Tu Si Zi) и Коры эвкомии (Du Zhong). Некоторые врачи предпочитают использовать Панты оленя (Lu Rong) вместо Желатина из рогов оленя (Lu Jiao Jiao) из-за их выдающейся способности пополнять Эссенцию.
Некоторые врачи предпочитают использовать Панты оленя (Lu Rong) вместо Желатина из рогов оленя (Lu Jiao Jiao) из-за их выдающейся способности пополнять Эссенцию.
Это одна из лучших формул для лечения Пустоты Ян Почек с Пустотой Эссенции и Крови. Ее обычно используют при затухании Огня во Вратах Жизни, что чаще всего отмечается у пожилых и страдающих хроническими болезнями пациентов. Хотя, согласно исходному тексту, это нарушение дает начало симптомам и в Среднем (Селезенка), и в Нижнем (Почки) Обогревателях, его причина всегда в Пустоте Изначального Ян. Эта формула предназначена для увеличения источника Огня укреплением Изначального Ян Правой [Почки].» То есть это тонизирование “Ян в Инь”, так как сами Почки связаны с Инь. Поэтому нужно объединить в формуле компоненты, которые питают Инь и пополняют Эссенцию с компонентами, которые укрепляют и тонизируют Ян Почек. Этот подход обычно используют для укрепления и тонизации Изначального Ян.
С Пилюлей Ци Почек (Shen Di Wan)
Обе формулы согревают и усиливают Изначальный Ян и тонизируют Почки. Однако Восстанавливающая Правую [Почку] Пилюля (You Gui Wan) направлена на тонизацию без дренирования. Содержащая Обработанный боковой корень аконита (Zhi Fu Zi) и Кору коричника (Rou Gui), которые сохраняют и тонизируют Огонь во Вратах Жизни (или Изначальный Янн), она, прежде всего, относится к тонизирующим Почки средствам. Эти травы не только согревают, но также сладкие по природе, дают тело эссенциям, которые могут питать недостаток. Поэтому эта формула показана для лечения хронических заболеваний, сопровождающихся слабостью и истощением в дополнение к Холоду.
Однако Восстанавливающая Правую [Почку] Пилюля (You Gui Wan) направлена на тонизацию без дренирования. Содержащая Обработанный боковой корень аконита (Zhi Fu Zi) и Кору коричника (Rou Gui), которые сохраняют и тонизируют Огонь во Вратах Жизни (или Изначальный Янн), она, прежде всего, относится к тонизирующим Почки средствам. Эти травы не только согревают, но также сладкие по природе, дают тело эссенциям, которые могут питать недостаток. Поэтому эта формула показана для лечения хронических заболеваний, сопровождающихся слабостью и истощением в дополнение к Холоду.
Пилюля Ци Почек (Shen Di Wan), с другой стороны, использует низкие дозировки Обработанного бокового корня аконита (Zhi Fu Zi) и Ветви коричника (Gui Zhi), чтобы «производить Ци [с помощью] небольшого Огня» (Shao Huo Sheng Qi), а также травы, которые активизируют водный метаболизм и двигают Инь. Ци, упомянутая в этой пословице, это Ци Почек и Мочевого пузыря, Ци, которая облегчает трансформацию Воды в Нижнем Обогревателе. Соответственно, Пилюля Ци Почек (Shen Di Wan), используют для лечения избытка Воды из-за Пустоты Ян Почек.
Соответственно, Пилюля Ци Почек (Shen Di Wan), используют для лечения избытка Воды из-за Пустоты Ян Почек.
При соответствующей симптоматике эта формула может использоваться для лечения различных нарушений, таких как нефротический синдром, остеопороз, бесплодие (особенно из-за малого количества спермы), различные формы анемии, лейкопения и астма.
— Для того, чтобы уменьшить Пустоту Ян и Ци, добавьте Корень женьшеня (Ren Shen) в количестве 60-90 г, или не более 150-180 г в зависимости от степени недостатка. Добавление этой травы ускоряет эффект прописи.
— При Пустоте Ян, которая проявляется в виде сперматореи, мутной лейкореи, и/или вязкого стула, добавьте пропитанный вином Плод псоралеи (Bui Gu Zhi).
— При непрекращающейся Почечной диарее добавьте Плод лимонника (Wu Wei Zi) и Семя мускатника (Rou Dou Cou).
— При снижении аппетита, нарушении пищеварения, тошноте и кислотном рефлюксе из-за Пустоты и Холода и Селезенки и Желудка добавьте Корневище имбиря (Gan Jiang).
— При непрекращающейся боли в животе добавьте Плод эводии (Wu Zhu Yu).
— При импотенции добавьте Корень моринды лекарственной (Ba Ji Tian) и Траву цистанхе (Rou Cong Rong).
Первоисточник: Collected Treatisesof [Zhang] Jing-Yue (1624)
СоставОбработанный корень ремании (Shu Di Huang) Rehmanniae Radix preparata 6-60 г
Корневище диоскореи, обжаренное (сухая обжарка) (Chao Shan Yao) dry-fried Dioscoreae Rhizoma 6 г
Плод кизила (Shan Zhu Yu) Corni Fructus 3 г
Плод дерезы (Gou Qi Zi) Lycii Fructus 6 г
Обработанный корень солодки (Zhi Gan Cao) Glycyrrhizae Radix preparata 3-6 г
Кора эвкоммии (Du Zhong) Eucommiae Cortex 6 г
Кора коричника (Rou Gui) Cinnamomi Cortex 3-6 г
Обработанный боковой корень аконита (Zhi Fu Zi) Aconiti Radix lateralis preparata 3 -9g
Согревает Почки и пополняет Эссенцию. При Пустоте Ян Почек со слабостью и истощением, болью в животе, болезненностью в пояснице, холодными конечностями и тонким пульсом. Также для паттернов истинного Холода и ложного Жара, в которых преобладание Инь вызывает разделение Ян, который плывет Наружу; то есть избыточная Инь заставляет оставшийся Ян двигаться к поверхностным уровням тела. Эта формула несколько слабее, чем основная.
При Пустоте Ян Почек со слабостью и истощением, болью в животе, болезненностью в пояснице, холодными конечностями и тонким пульсом. Также для паттернов истинного Холода и ложного Жара, в которых преобладание Инь вызывает разделение Ян, который плывет Наружу; то есть избыточная Инь заставляет оставшийся Ян двигаться к поверхностным уровням тела. Эта формула несколько слабее, чем основная.
Первоисточник: Formulary of the Pharmacy Service for Benefiting the People in the Taiping Era (1107)
СоставКора эвкоммии, обжаренная в соке имбиря (Jiang Zhu Chao Du Zhong) ginger-juice fried Eucommiae Cortex 40 г
Плод псоралеи, обжаренный в вине (Jiu Chao Bu Gu Zhi) wine-fried Psoraleae Fuctus 240 г
Семя грецкого ореха (He Tao Ren) Juglandis Semen 150 г
Измельчите ингредиенты в порошок и сформируйте пилюлю со 120 г пасты из раздавленных Луковиц чеснока (Da Suan). Для получения пилюли можно также использовать мед. Принимать по 3 г натощак с теплым вином.
Принимать по 3 г натощак с теплым вином.
Тонизирует Почки, укрепляет поясницу и облегчает боль в пояснице.
При сильной боли в пояснице из-за Пустоты Ян Почек с нарушениями из-за Ветра-Холода-Влажности или из-за травмы. Боль непрерывная, трудно встать из сидячего положения, трудно согнуться вперед или назад и невозможно делать круговые движения в пояснице. Боль сопровождается слабостью ног и крайним истощением. Может также быть головокружение, боль в ушах, мочеиспускание по каплям или выделения из влагалища. Все эти симптомы улучшаются при постельном режиме. Также характерны ощущение напряжения в нижней части живота, холодные конечности, бледное и блестящее лицо, бледный язык и глубокий, тонкий пульсе.
Корень по основанию. Извлечение корня квадратного. Извлечение корней из дробных чисел
Удивительно, но в русском языке есть всего одно слово, которое не содержит в своем морфемном составе корневую часть. Глагол «вынуть» состоит из приставки «вы», суффикса «ну» и инфинитивного суффикса «ть». В доказательство, что «ну» не является корнем, привожу другие подобные глаголы – «выдернуть», «перевернуть», «примкнуть».
В доказательство, что «ну» не является корнем, привожу другие подобные глаголы – «выдернуть», «перевернуть», «примкнуть».
Видовой парой «вынуть» является глагол «вынимать» с корнем «ним». По мнению некоторых филологов (в том числе Н.М.Шанского) в слове «вынуть» корнем является буква «н», просто корень в процессе лингвистических метаморфоз слился с суффиксом «ну». Глагол поддался процессам переразложения основ и аппликации морфем.
Секрет в этимологии
Дело в том, что глагол образован от праславянского *jьmǫ : jęti («яти», значение — «брать»). От этого же слова произошли древнерусские глаголы «имѣти», «възѩти». Первоначально глагол звучал как «выяти», позже добавилась вставка «н» – «вынять». Со временем лексема поддалась влиянию глаголов совершенного вида на -нуть. По типу «стукнуть», «кинуть» появился глагол «вынуть». Официально это единственное слово в русском языке без корня!
Библиографический список
- Шанский Н.М. Лингвистические детективы. — М., 2002.

- Энциклопедия. Русский язык. Под ред. Ю.Н.Караулова — М., 1997.
Ученики всегда спрашивают: «Почему нельзя пользоваться калькулятором на экзамене по математике? Как извлечь корень квадратный из числа без калькулятора?» Попробуем ответить на этот вопрос.
Как же извлечь корень квадратный из числа без помощи калькулятора?
Действие извлечения корня квадратного обратно действию возведения в квадрат.
√81= 9 9 2 =81
Если из положительного числа извлечь корень квадратный и результат возвести в квадрат, получим то же число.
Из небольших чисел, являющихся точными квадратами натуральных чисел, например 1, 4, 9, 16, 25, …,100 квадратные корни можно извлечь устно. Обычно в школе учат таблицу квадратов натуральных чисел до двадцати. Зная эту таблицу легко извлечь корни квадратные из чисел 121,144, 169, 196, 225, 256, 289, 324, 361, 400. Из чисел больших 400 можно извлекать методом подбора используя, некоторые подсказки. Давайте попробуем на примере рассмотреть этот метод.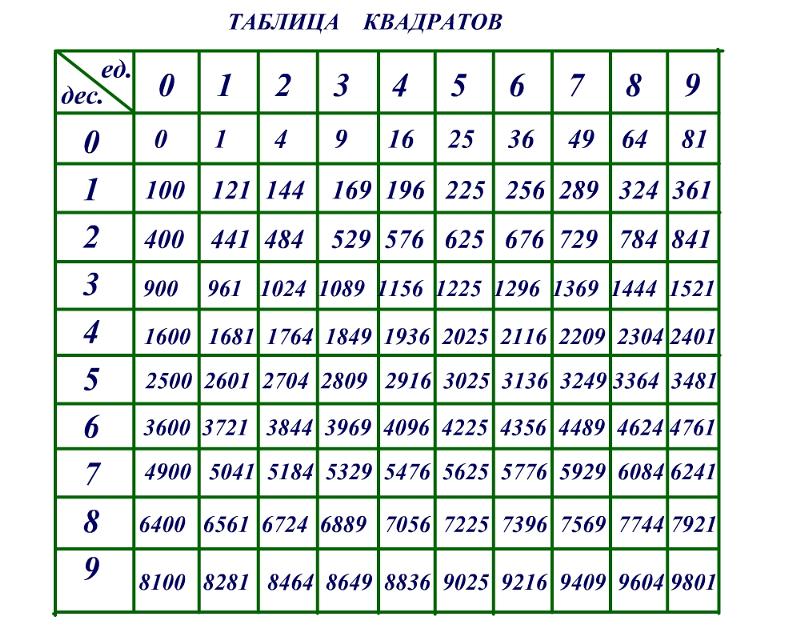
Пример: Извлечь корень из числа 676 .
Замечаем, что 20 2 = 400, а 30 2 = 900, значит 20
Точные квадраты натуральных чисел оканчиваются цифрами 0; 1; 4; 5; 6; 9.
Цифру 6 дают 4 2 и 6 2 .
Значит, если из 676 извлекается корень, то это либо 24, либо 26.
Осталось проверить: 24 2 = 576, 26 2 = 676.
Ответ: √676 = 26 .
Еще пример: √6889 .
Так как 80 2 = 6400, а 90 2 = 8100, то 80 Цифру 9 дают 3 2 и 7 2 , то √6889 равен либо 83, либо 87.
Проверяем: 83 2 = 6889.
Ответ: √6889 = 83 .
Если затрудняетесь решать методом подбора, то можно подкоренное выражение разложить на множители.
Например, найти √893025 .
Разложим число 893025 на множители, вспомните, вы делали это в шестом классе.
Получаем: √893025 = √3 6 ∙5 2 ∙7 2 = 3 3 ∙5 ∙7 = 945.
Еще пример: √20736 . Разложим число 20736 на множители:
Получаем √20736 = √2 8 ∙3 4 = 2 4 ∙3 2 = 144.
Конечно, разложение на множители требует знания признаков делимости и навыков разложения на множители.
И, наконец, есть же правило извлечение корней квадратных . Давайте познакомимся с этим правилом на примерах.
Вычислите √279841 .
Чтобы извлечь корень из многоцифрового целого числа, разбиваем его справа налево на грани, содержащие по 2 цифры (в левой крайней грани может оказаться и одна цифра). Записываем так 27’98’41
Чтобы получить первую цифру корня (5), извлекаем квадратный корень из наибольшего точного квадрата, содержащегося в первой слева грани (27).
Потом вычитают из первой грани квадрат первой цифры корня (25) и к разности приписывают (сносят) следующую грань (98).
Слева от полученного числа 298 пишут удвоенную цифру корня (10), делят на нее число всех десятков раннее полученного числа (29/2 ≈ 2), испытывают частное (102 ∙2 = 204 должно быть не больше 298) и записывают (2) после первой цифры корня.
Потом вычитают от 298 полученное частное 204 и к разности (94) приписывают (сносят) следующую грань (41).
Слева от полученного числа 9441 пишут удвоенное произведение цифр корня (52 ∙2 = 104), делят на это произведение число всех десятков числа 9441 (944/104 ≈ 9), испытывают частное (1049 ∙9 = 9441) должно быть 9441 и записывают его (9) после второй цифры корня.
Получили ответ √279841 = 529.
Аналогично извлекают корни из десятичных дробей . Только подкоренное число надо разбивать на грани так, чтобы запятая была между гранями.
Пример . Найдите значение √0,00956484.
Только надо помнить, что если десятичная дробь имеет нечетное число десятичных знаков, из нее точно квадратный корень не извлекается .
Итак, теперь вы познакомились с тремя способами извлечения корня. Выбирайте тот, который вам больше подходит и практикуйтесь. Чтобы научиться решать задачи, их надо решать. А если у Вас возникнут вопросы, записывайтесь на мои уроки .
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
До появления калькуляторов студенты и преподаватели вычисляли квадратные корни вручную. Существует несколько способов вычисления квадратного корня числа вручную. Некоторые из них предлагают только приблизительное решение, другие дают точный ответ.
Шаги
Разложение на простые множители
Разложите подкоренное число на множители, которые являются квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа – числа, из которых можно извлечь целый квадратный корень. Множители – числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как √25 = 5, √36 = 6, √49 = 7. Квадратные множители – это множители, которые являются квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
- Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 – это квадратное число. Разделив 400 на 25, вы получите 16. Число 16 также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.

- Записать это можно следующим образом: √400 = √(25 х 16).
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть √(а х b) = √a x √b. Воспользуйтесь этим правилом и извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
- В нашем примере извлеките корень из 25 и из 16.
- √(25 х 16)
- √25 х √16
- 5 х 4 = 20
Если подкоренное число не раскладывается на два квадратных множителя (а так происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
- Например, вычислите квадратный корень из числа 147.
 Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:- = √(49 х 3)
- = √49 х √3
- = 7√3
Если нужно, оцените значение корня. Теперь можно оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
- Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.

- Этот метод также работает с большими числами. Например, рассмотрим √35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (√25 = 5) и 36 (√36 = 6). Таким образом, значение √35 расположено между 5 и 6. Так как значение √35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что √35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.
Еще один способ – разложите подкоренное число на простые множители . Простые множители – числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
- Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, √45 = √(3 х 3 х 5). 3 можно вынести за знак корня: √45 = 3√5. Теперь можно оценить √5.
- Рассмотрим другой пример: √88.
- = √(2 х 44)
- = √ (2 х 4 х 11)
- = √ (2 х 2 х 2 х 11).
 Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня. - = 2√(2 х 11) = 2√2 х √11. Теперь можно оценить √2 и √11 и найти приблизительный ответ.
Вычисление квадратного корня вручную
При помощи деления в столбик
Этот метод включает процесс, аналогичный делению в столбик, и дает точный ответ. Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70».
- Для примера вычислим квадратный корень числа 780,14. Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде «7 80, 14». Это нормально, что первая слева цифра является непарной цифрой. Ответ (корень из данного числа) будете записывать справа сверху.

- Для примера вычислим квадратный корень числа 780,14. Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде «7 80, 14». Это нормально, что первая слева цифра является непарной цифрой. Ответ (корень из данного числа) будете записывать справа сверху.
Для первой слева пары чисел (или одного числа) найдите наибольшее целое число n, квадрат которого меньше или равен рассматриваемой паре чисел (или одного числа). Другими словами, найдите квадратное число, которое расположено ближе всего к первой слева паре чисел (или одному числу), но меньше ее, и извлеките квадратный корень из этого квадратного числа; вы получите число n. Напишите найденное n сверху справа, а квадрат n запишите снизу справа.
- В нашем случае, первым слева числом будет число 7. Далее, 4
Вычтите квадрат числа n, которое вы только что нашли, из первой слева пары чисел (или одного числа). Результат вычисления запишите под вычитаемым (квадратом числа n).
- В нашем примере вычтите 4 из 7 и получите 3.
Снесите вторую пару чисел и запишите ее около значения, полученного в предыдущем шаге. Затем удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».

- В нашем примере второй парой чисел является «80». Запишите «80» после 3. Затем, удвоенное число сверху справа дает 4. Запишите «4_×_=» снизу справа.
Заполните прочерки справа.
- В нашем случае, если вместо прочерков поставить число 8, то 48 х 8 = 384, что больше 380. Поэтому 8 — слишком большое число, а вот 7 подойдет. Напишите 7 вместо прочерков и получите: 47 х 7 = 329. Запишите 7 сверху справа — это вторая цифра в искомом квадратном корне числа 780,14.
Вычтите полученное число из текущего числа слева. Запишите результат из предыдущего шага под текущим числом слева, найдите разницу и запишите ее под вычитаемым.
- В нашем примере, вычтите 329 из 380, что равно 51.
Повторите шаг 4. Если сносимой парой чисел является дробная часть исходного числа, то поставьте разделитель (запятую) целой и дробной частей в искомом квадратном корне сверху справа. Слева снесите вниз следующую пару чисел.
 Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».- В нашем примере следующей сносимой парой чисел будет дробная часть числа 780.14, поэтому поставьте разделитель целой и дробной частей в искомом квадратном корне сверху справа. Снесите 14 и запишите снизу слева. Удвоенным числом сверху справа (27) будет 54, поэтому напишите «54_×_=» снизу справа.
Повторите шаги 5 и 6. Найдите такое наибольшее число на место прочерков справа (вместо прочерков нужно подставить одно и тоже число), чтобы результат умножения был меньше или равен текущему числу слева.
- В нашем примере 549 х 9 = 4941, что меньше текущего числа слева (5114). Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 — 4941 = 173.
Если для квадратного корня вам необходимо найти больше знаков после запятой, напишите пару нулей у текущего числа слева и повторяйте шаги 4, 5 и 6. Повторяйте шаги, до тех пор пока не получите нужную вам точность ответа (число знаков после запятой).

Понимание процесса
Рассмотрим первую пару цифр Sa числа S (Sa = 7 в нашем примере) и найдем ее квадратный корень.
 В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен S a (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa
В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен S a (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa- Допустим, что нужно разделить 88962 на 7; здесь первый шаг будет аналогичным: рассматриваем первую цифру делимого числа 88962 (8) и подбираем такое наибольшее число, которое при умножении на 7 дает значение меньшее или равное 8. То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8
Мысленно представьте квадрат, площадь которого вам нужно вычислить. Вы ищите L, то есть длину стороны квадрата, площадь которого равна S. A, B, C — цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.
- Пусть (10A+B)² = L² = S = 100A² + 2×10A×B + B² . Запомните, что 10A+B — это такое число, у которого цифра B означает единицы, а цифра A — десятки. Например, если A=1 и B=2, то 10A+B равно числу 12.
 (10A+B)² — это площадь всего квадрата, 100A² — площадь большого внутреннего квадрата, B² — площадь малого внутреннего квадрата, 10A×B — площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
(10A+B)² — это площадь всего квадрата, 100A² — площадь большого внутреннего квадрата, B² — площадь малого внутреннего квадрата, 10A×B — площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
- Пусть (10A+B)² = L² = S = 100A² + 2×10A×B + B² . Запомните, что 10A+B — это такое число, у которого цифра B означает единицы, а цифра A — десятки. Например, если A=1 и B=2, то 10A+B равно числу 12.
Для усвоения данного метода представьте число, квадратный корень которого необходимо найти, как площадь квадрата S. В этом случае вы будете искать длину стороны L такого квадрата. Вычисляем такое значение L, при котором L² = S.
Задайте букву для каждой цифры в ответе. Обозначим через A первую цифру в значении L (искомый квадратный корень). B будет второй цифрой, C — третьей и так далее.
Задайте букву для каждой пары первых цифр. Обозначим через S a первую пару цифр в значении S, через S b — вторую пару цифр и так далее.
Уясните связь данного метода с делением в столбик. Как и в операции деления, где каждый раз нас интересует только одна следующая цифра делимого числа, при вычислении квадратного корня мы последовательно работаем с парой цифр (для получения одной следующей цифры в значении квадратного корня).
Что такое квадратный корень?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Это понятие очень простое. Естественное, я бы сказал. Математики на каждое действие стараются найти противодействие. Есть сложение — есть и вычитание. Есть умножение — есть и деление. Есть возведение в квадрат… Значит есть и извлечение квадратного корня! Вот и всё. Это действие (извлечение квадратного корня ) в математике обозначается вот таким значком:
Сам значок называется красивым словом «радикал «.
Как извлечь корень? Это лучше рассмотреть на примерах .
Сколько будет квадратный корень из 9? А какое число в квадрате даст нам 9? 3 в квадрате даст нам 9! Т.е:
А вот сколько будет квадратный корень из нуля? Не вопрос! Какое число в квадрате ноль даёт? Да сам же ноль и даёт! Значит:
Уловили, что такое квадратный корень? Тогда считаем примеры :
Ответы (в беспорядке): 6; 1; 4; 9; 5.
Решили? Действительно, уж куда проще-то?!
Но… Что делает человек, когда видит какое-нибудь задание с корнями?
Тосковать начинает человек… Не верит он в простоту и лёгкость корней. Хотя, вроде, и знает, что такое квадратный корень …
Всё потому, что человек проигнорировал несколько важных пунктиков при изучении корней. Потом эти пунктики жестоко мстят на контрольных и экзаменах…
Пунктик первый. Корни надо узнавать в лицо!
Сколько будет корень квадратный из 49? Семь? Верно! А как вы узнали, что семь? Возвели семёрку в квадрат и получили 49? Правильно! Обратите внимание, чтобы извлечь корень из 49 нам пришлось проделать обратную операцию — возвести 7 в квадрат! И убедиться, что мы не промахнулись. А могли и промахнуться…
А могли и промахнуться…
В этом и есть сложность извлечения корней . Возвести в квадрат можно любое число без особых проблем. Умножить число само на себя столбиком — да и все дела. А вот для извлечения корня такой простой и безотказной технологии нет. Приходится подбирать ответ и проверять его на попадание возведением в квадрат.
Этот сложный творческий процесс — подбор ответа — сильно упрощается, если вы помните квадраты популярных чисел. Как таблицу умножения. Если, скажем, надо умножить 4 на 6 — вы же не складываете четверку 6 раз? Сразу выплывает ответ 24. Хотя, не у всех он выплывает, да…
Для свободной и успешной работы с корнями достаточно знать квадраты чисел от 1 до 20. Причём туда и обратно. Т.е. вы должны легко называть как, скажем, 11 в квадрате, так и корень квадратный из 121. Чтобы добиться такого запоминания, есть два пути. Первый — выучить таблицу квадратов. Это здорово поможет решать примеры. Второй — решать побольше примеров. Это здорово поможет запомнить таблицу квадратов.
Это здорово поможет запомнить таблицу квадратов.
И никаких калькуляторов! Только для проверки. Иначе на экзамене будете тормозить нещадно…
Итак, что такое квадратный корень и как извлекать корни — думаю, понятно. Теперь выясним ИЗ ЧЕГО можно их извлекать.
Пунктик второй. Корень, я тебя не знаю!
Из каких чисел можно извлекать квадратные корни? Да почти из любых. Проще понять, из чего нельзя их извлекать.
Попробуем вычислить вот такой корень:
Для этого нужно подобрать число, которое в квадрате даст нам -4. Подбираем.
Что, не подбирается? 2 2 даёт +4. (-2) 2 даёт опять +4! Вот-вот… Нет таких чисел, которые при возведении в квадрат дадут нам отрицательное число! Хотя я такие числа знаю. Но вам не скажу). Поступите в институт — сами узнаете.
Такая же история будет с любым отрицательным числом. Отсюда вывод:
Выражение, в котором под знаком квадратного корня стоит отрицательное число — не имеет смысла ! Это запретная операция. Такая же запретная, как и деление на ноль. Запомните этот факт железно! Или, другими словами:
Такая же запретная, как и деление на ноль. Запомните этот факт железно! Или, другими словами:
Квадратные корни из отрицательных чисел извлечь нельзя!
Зато из всех остальных — можно. Например, вполне можно вычислить
На первый взгляд это очень сложно. Подбирать дроби, да в квадрат возводить… Не волнуйтесь. Когда разберёмся со свойствами корней, такие примеры будут сводиться к всё той же таблице квадратов. Жизнь станет проще!
Ну ладно дроби. Но нам ведь ещё попадаются выражения типа:
Ничего страшного. Всё то же самое. Корень квадратный из двух — это число, которое при возведении в квадрат даст нам двойку. Только число это совсем неровное… Вот оно:
Что интересно, эта дробь не кончается никогда… Такие числа называются иррациональными. В квадратных корнях это — самое обычное дело. Кстати, именно поэтому выражения с корнями называют иррациональными . Понятно, что писать всё время такую бесконечную дробь неудобно. Поэтому вместо бесконечной дроби так и оставляют:
Поэтому вместо бесконечной дроби так и оставляют:
Если при решении примера у вас получилось что-то неизвлекаемое, типа:
то так и оставляем. Это и будет ответ.
Нужно чётко понимать, что под значками
Конечно, если корень из числа извлекается ровно , вы обязаны это сделать. Ответ задания в виде, например
вполне себе полноценный ответ.
И, конечно, надо знать на память приблизительные значения:
Это знание здорово помогает оценить ситуацию в сложных заданиях.
Пунктик третий. Самый хитрый.
Основную путаницу в работу с корнями вносит как раз этот пунктик. Именно он придаёт неуверенность в собственных силах… Разберёмся с этим пунктиком как следует!
Для начала опять извлечём квадратный корень их четырёх. Что, уже достал я вас с этим корнем?) Ничего, сейчас интересно будет!
Какое число даст в квадрате 4? Ну два, два — слышу недовольные ответы…
Верно. Два. Но ведь и минус два даст в квадрате 4… А между тем, ответ
правильный, а ответ
грубейшая ошибка. Вот так.
Вот так.
Так в чём же дело?
Действительно, (-2) 2 = 4. И под определение корня квадратного из четырёх минус два вполне подходит… Это тоже корень квадратный из четырёх.
Но! В школьном курсе математики принято считать за квадратные корни только неотрицательные числа! Т.е ноль и все положительные. Даже термин специальный придуман: из числа а — это неотрицательное число, квадрат которого равен а . Отрицательные результаты при извлечении арифметического квадратного корня попросту отбрасываются. В школе все квадратные корни — арифметические . Хотя особо об этом не упоминается.
Ну ладно, это понятно. Это даже и лучше — не возиться с отрицательными результатами… Это ещё не путаница.
Путаница начинается при решении квадратных уравнений. Например, надо решить вот такое уравнение.
Уравнение простое, пишем ответ (как учили):
Такой ответ (совершенно правильный, кстати) — это просто сокращённая запись двух ответов:
Стоп-стоп! Чуть выше я написал, что квадратный корень — число всегда неотрицательное! А здесь один из ответов — отрицательный ! Непорядок. Это первая (но не последняя) проблемка, которая вызывает недоверие к корням… Решим эту проблемку. Запишем ответы (чисто для понимания!) вот так:
Это первая (но не последняя) проблемка, которая вызывает недоверие к корням… Решим эту проблемку. Запишем ответы (чисто для понимания!) вот так:
Скобки сути ответа не меняют. Просто я отделил скобками знаки от корня . Теперь наглядно видно, что сам корень (в скобках) — число всё равно неотрицательное! А знаки — это результат решения уравнения . Ведь при решении любого уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат. В наше уравнение подходит корень из пяти (положительный!) как с плюсом, так и с минусом.
Вот так. Если вы просто извлекаете квадратный корень из чего-либо, вы всегда получаете один неотрицательный результат. Например:
Потому, что это — арифметический квадратный корень .
Но если вы решаете какое-нибудь квадратное уравнение, типа:
то всегда получается два ответа (с плюсом и минусом):
Потому, что это — решение уравнения.
Надеюсь, что такое квадратный корень со своими пунктиками вы уяснили. Теперь осталось узнать, что можно делать с корнями, каковы их свойства. И какие там пунктики и подводные кор… извините, камни!)
Всё это — в следующих уроках.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Квадратный корень из 1296 — Как найти квадратный корень из 1296?
LearnPracticeDownload
Квадратный корень из 1296 также сокращенно называется корнем 1296. Квадратный корень числа может быть рациональным/иррациональным числом, положительным/отрицательным числом, действительным/мнимым числом. 1296 — это особое число, квадратный корень которого представляет собой полный квадрат. Теперь мы увидим несколько интересных фактов о квадратном корне из 1296, а также несколько интересных задач.
- Квадратный корень из 1296: 36
- Квадрат 1296: 16,79,616
| 1. | Чему равен квадратный корень из 1296? |
| 2. | Является ли квадратный корень из 1296 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 1296? |
| 4. | Важные примечания по квадратному корню из 1296 |
| 5. | Часто задаваемые вопросы о квадратном корне из 1296 |
Что такое квадратный корень из 1296?
- Квадратный корень из 1296 можно представить как √1296 и (1296) 1/2
- Квадратом 1296 будет число (n), такое что n × n = 1296
36 × 36 = 1296 также -36 × -36 = 1296
Следовательно, +36 и -36 — это квадратные корни из 1296.
Является ли квадратный корень из 1296 рациональным или иррациональным?
Квадратные корни из 1296 равны +36 и -36. Оба числа являются целыми числами, и все целые числа являются рациональными числами. Следовательно, квадратный корень из 1296 — рациональное число.
Оба числа являются целыми числами, и все целые числа являются рациональными числами. Следовательно, квадратный корень из 1296 — рациональное число.
Как найти квадратный корень из 1296?
Теперь найдем квадратный корень из 1296, используя простые методы факторизации и деления в длинную сторону.
Извлечение квадратного корня из 1296 методом простой факторизации
- Простая факторизация числа 1296: 2 4 × 3 4
- Простые множители числа 1296 в парах: (2 × 2) × (2 × 2) × (3 × 3) × (3 × 3)
- Квадратный корень из 1296: √((2 × 2) 2 × (3 × 3) 2 ) = (2) 2 × (3) 2 = ±36
- Следовательно, √1296 = ±36
Квадратный корень из 1296 методом деления в длину
Теперь мы найдем квадратный корень из 1296 методом деления в длину:
- Начните группировать цифры с места единицы в пары по две, поместив черту сверху . У нас есть две пары в этом случае, 12 и 96.

- Найдите число (a) такое, что a × a ≤ 12. Таким образом, a будет равно 3, так как 3 × 3 = 9 ≤ 12.
- Получаем остаток и частное как 3. Также добавляем делитель a к самому себе (3 + 3). Мы получаем новый делитель как 6.
- Сократите следующую пару чисел, чтобы сформировать новое делимое. Итак, новое делимое равно 396, .
- Найдите число (n), такое что 6n × n ≤ 396. Получаем n = 6, поскольку 66 × 6 = 396.
Итак, мы получаем квадратный корень из √1296 = 36 методом деления в большую сторону.
Исследуйте квадратные корни с помощью иллюстраций и интерактивных примеров.
- Квадратный корень из 35
- Квадратный корень из 1225
- Квадратный корень из 192
- Квадратный корень из 98
- Квадратный корень из 289
Важные примечания:
- Число 1296 является полным квадратом.
- Квадратный корень из 1296 является рациональным числом.

- Квадратный корень из -1296 является мнимым числом.
Пример 1: Алекс хочет узнать значение √√1296. Можете ли вы помочь Алексу найти ответ?
Решение:
Квадратный корень из 1296 равен √1296 = 36
. Теперь простая факторизация числа 36 = 2 2 × 3 2
. Квадратный корень 36 равен (36) 1/2 = ((2) 2 × (3) 2 ) 1/2 = (2 × 3) = ±6.Пример 2: Харпер хочет найти среднее положительное значение √1296 и √576. Можете ли вы помочь Харпер найти значение?
Решение:
.
Квадратный корень из 1296 равен √1296 = 36
. Квадратный корень из 476 равен √576 = 24
. Среднее значение обоих чисел = (36 + 24)/2 = 60/2 = 30
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила.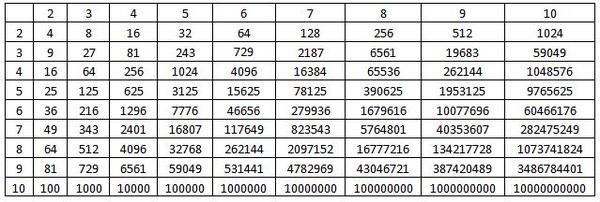 Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.
Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.
Забронировать бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о квадратном корне из 1296
Чему равен квадратный корень из -1296?
Квадратный корень из отрицательных чисел является мнимым, потому что квадраты положительных и отрицательных чисел дают положительные числа.
Квадратный корень из -1296 представлен как ±36i. (где i = √-1)
Чему равен квадрат числа 1296?
Квадрат числа 1296 равен (1296) 2 = 16,79,616
Чему равен квадратный корень из 1296 в простой форме факторизации?
Квадратный корень из 1296 равен √1296 = 36.
Теперь разложение числа 36 на простые множители = 2 × 2 × 3 × 3
. Можем ли мы найти квадратный корень из 1296, используя метод аппроксимации?
Нет, мы не можем найти квадратный корень из 1296 методом аппроксимации, потому что число 1296 является полным квадратом, и этот метод не может быть использован в случае, если данное число является полным квадратом.
Чему равен квадратный корень из 1293-8
Квадратный корень из 1296 пошаговое решение
| Введите реальное число: |
| Результат квадратного корня: |
Вот ответ на такие вопросы, как: Квадратный корень из 1296 пошаговое решение | √1296 или чему равен квадратный корень из 1296?
Используйте приведенный ниже калькулятор квадратного корня, чтобы найти квадратный корень любого мнимого или действительного числа.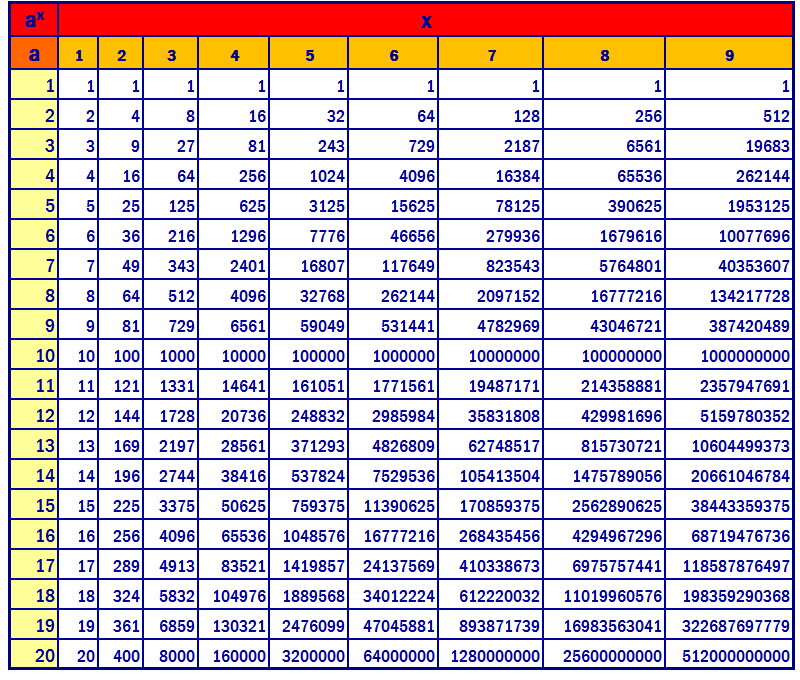 См. также на этой веб-странице таблицу квадратного корня от 1 до 100, а также вавилонский метод или метод Героя.
См. также на этой веб-странице таблицу квадратного корня от 1 до 100, а также вавилонский метод или метод Героя.
Вавилонский метод, также известный как метод Героя.
Что такое квадратный корень?
Определение квадратного корня
Квадратный корень из числа «а» — это число x, такое что x 2 = a, другими словами, число x, квадрат которого равен a. Например, 36 — это квадратный корень из 1296, потому что 36 2 = 36•36 = 129.6, -36 является квадратным корнем из 1296, потому что (-36) 2 = (-36)•(-36) = 1296.
Таблица квадратных корней 1-100
Квадратные корни от 1 до 100, округленные до тысячных.
| нет | нет 2 | √ |
|---|---|---|
| 1 | 1 | 1.000 |
| 2 | 4 | 1.414 |
| 3 | 9 | 1.732 |
| 4 | 16 | 2.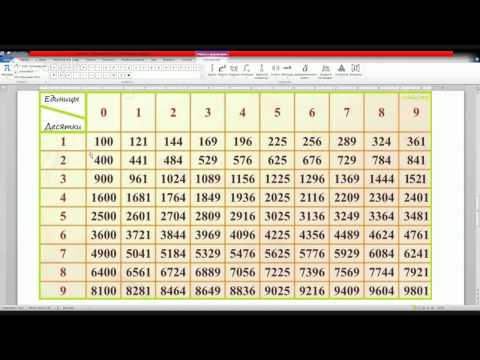 000 000 |
| 5 | 25 | 2.236 |
| 6 | 36 | 2.449 |
| 7 | 49 | 2.646 |
| 8 | 64 | 2.828 |
| 9 | 81 | 3.000 |
| 10 | 100 | 3.162 |
| 11 | 121 | 3.317 |
| 12 | 144 | 3.464 |
| 13 | 169 | 3.606 |
| 14 | 196 | 3.742 |
| 15 | 225 | 3.873 |
| 16 | 256 | 4.000 |
| 17 | 289 | 4.123 |
| 18 | 324 | 4.243 |
| 19 | 361 | 4.359 |
| 20 | 400 | 4.472 |
| 21 | 441 | 4. 583 583 |
| 22 | 484 | 4.690 |
| 23 | 529 | 4.796 |
| 24 | 576 | 4.899 |
| 25 | 625 | 5.000 |
9
| нет | нет 2 | √ |
|---|---|---|
| 26 | 676 | 5.099 |
| 27 | 729 | 5.196 |
| 28 | 784 | 5.292 |
| 29 | 841 | 5.385 |
| 30 | 900 | 5,477 |
| 31 | 961 | 5,568 |
| 32 | 1 024 | 5,657 |
| 339 | 5,657 | |
| 339 | 5,657 | |
| 339 | 5,657 | |
| 33 | 5,657 | |
| 33 | 5,657 | |
| 0020 | 1,089 | 5.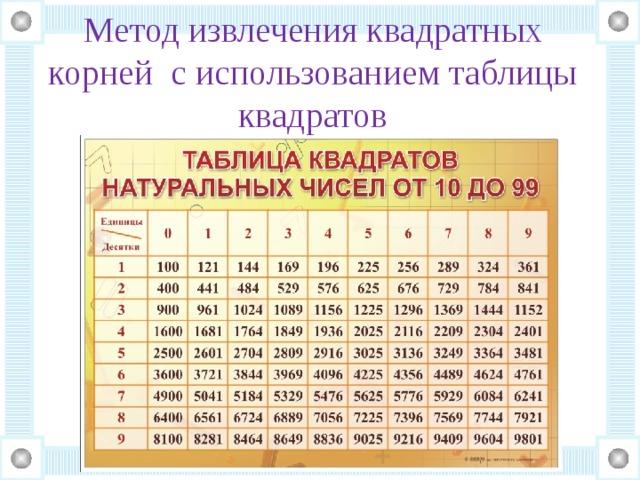 745 745 |
| 34 | 1,156 | 5.831 |
| 35 | 1,225 | 5.916 |
| 36 | 1,296 | 6.000 |
| 37 | 1,369 | 6.083 |
| 38 | 1,444 | 6.164 |
| 39 | 1,521 | 6.245 |
| 40 | 1,600 | 6.325 |
| 41 | 1,681 | 6.403 |
| 42 | 1,764 | 6.481 |
| 43 | 1,849 | 6.557 |
| 44 | 1,936 | 6.633 |
| 45 | 2,025 | 6.708 |
| 46 | 2,116 | 6.782 |
| 47 | 2,209 | 6.856 |
| 48 | 2,304 | 6.928 |
| 49 | 2,401 | 7. 000 000 |
| 50 | 2,500 | 7.071 |
| нет | нет 2 | √ |
|---|---|---|
| 51 | 2,601 | 7.141 |
| 52 | 2,704 | 7.211 |
| 53 | 2,809 | 7.280 |
| 54 | 2,916 | 7.348 |
| 55 | 3,025 | 7.416 |
| 56 | 3,136 | 7.483 |
| 57 | 3,249 | 7.550 |
| 58 | 3,364 | 7,616 |
| 59 | 3,481 | 7,681 |
| 60 | 3600 | 7,746 |
| 7746 | ||
| 7746 | ||
| 7746 | ||
| 7746 | ||
| 7746 | ||
7. 746.0019 3,721 746.0019 3,721 | 7.810 | |
| 62 | 3,844 | 7.874 |
| 63 | 3,969 | 7.937 |
| 64 | 4,096 | 8.000 |
| 65 | 4,225 | 8.062 |
| 66 | 4,356 | 8.124 |
| 67 | 4,489 | 8.185 |
| 68 | 4,624 | 8.246 |
| 69 | 4,761 | 8.307 |
| 70 | 4,900 | 8.367 |
| 71 | 5,041 | 8.426 |
| 72 | 5,184 | 8.485 |
| 73 | 5,329 | 8.544 |
| 74 | 5,476 | 8.602 |
| 75 | 5,625 | 8.660 |
| нет | нет 2 | √ |
|---|---|---|
| 76 | 5,776 | 8. 718 718 |
| 77 | 5,929 | 8.775 |
| 78 | 6,084 | 8.832 |
| 79 | 6,241 | 8.888 |
| 80 | 6,400 | 8,944 |
| 81 | 6,561 | 9,000 |
| 82 | 6,724 | 9.055 |
| 83 | 6,889 | 9.110 |
| 84 | 7,056 | 9.165 |
| 85 | 7,225 | 9.220 |
| 86 | 7,396 | 9.274 |
| 87 | 7,569 | 9.327 |
| 88 | 7,744 | 9.381 |
| 89 | 7,921 | 9.434 |
| 90 | 8,100 | 9.487 |
| 91 | 8,281 | 9.539 |
| 92 | 8,464 | 9. 592 592 |
| 93 | 8,649 | 9.644 |
| 94 | 8,836 | 9.695 |
| 95 | 9,025 | 9.747 |
| 96 | 9,216 | 9.798 |
| 97 | 9,409 | 9.849 |
| 98 | 9,604 | 9.899 |
| 99 | 9,801 | 9.950 |
| 100 | 10,000 | 10.000 |
Квадратный корень из 1296
Sqrt(1296). Найдите квадратный корень из 1296 или любого другого действительного числа, положительного или отрицательного. Вот ответы на такие вопросы, как: Квадратный корень из 1296 или что такое квадратный корень из 1296?
Что такое квадратный корень? Определение квадратного корня
Квадратный корень из числа ‘x’ – это число y такое, что y 2 = x, другими словами, число y, квадрат которого равен y. Например, 36 — это квадратный корень из 1296, потому что 36 2 = 36•36 = 1296, -36 — это квадратный корень из 1296, потому что (-36) 2 = (-36)•(-36) = 1296. При написании математических выражений люди часто используют sqrt(x) для обозначения квадратного корня из x. Подробнее о квадратном корне читайте здесь: Квадратный корень — Википедия и здесь: Квадратный корень — Wolfram
Например, 36 — это квадратный корень из 1296, потому что 36 2 = 36•36 = 1296, -36 — это квадратный корень из 1296, потому что (-36) 2 = (-36)•(-36) = 1296. При написании математических выражений люди часто используют sqrt(x) для обозначения квадратного корня из x. Подробнее о квадратном корне читайте здесь: Квадратный корень — Википедия и здесь: Квадратный корень — Wolfram
Квадратный символ?
Вот символ квадратного корня. Он обозначается √, известным как радикальный знак или основание.
Таблица квадратного корня 1-100
Квадратные корни от 1 до 100 округляются до тысячных.
| номер | квадрат | квадрат корень | |
|---|---|---|---|
| 1 | 1 | 1.000 | |
| 2 | 4 | 1.414 | 1 | 39018 |
| 1.732 | |||
| 4 | 16 | 2.000 | |
| 5 | 25 | 2. 236 236 | |
| 6 | 36 | 2.449 | |
| 7 | 49 | 2.646 | |
| 8 | 64 | 2.828 | |
| 9 | 81 | 3.000 | |
| 10 | 100 | 3.162 | |
| 11 | 121 | 3.317 | |
| 12 | 144 | 3.464 | |
| 13 | 169 | 3.606 | |
| 14 | 196 | 3.742 | |
| 15 | 225 | 3.873 | |
| 16 | 256 | 4.000 | |
| 17 | 289 | 4,123 | |
| 18 | 324 | 4.243434393 3 3 3439393 343 | .0023 |
| 19 | 361 | 4.359 | |
| 20 | 400 | 4.472 | |
| 21 | 441 | 4.583 | |
| 22 | 484 | 4. 690 690 | |
| 23 | 529 | 4.796 | |
| 24 | 576 | 4.899 | |
| 25 | 625 | 5.000 |
| номер | квадрат | квадрат корень | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 26 | 676 | 5.099 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27 | 729 | 5.196 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 | 784 | 5.292 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29 | 841 | 5.385 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | 900 | 5.477 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 | 961 | 5.568 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32 | 1,024 | 5.657 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33 | 1,089 | 5.745 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34 | 1,156 | 5.831 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35 | 1,225 | 5.916 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36 | 1,296 | 6.000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37 | 1,369 | 6. 083 083 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 | 1,444 | 6.164 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39 | 1,521 | 6.245 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | 1,600 | 6.325 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41 | 1,681 | 6.403 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42 | 1,764 | 6.481 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 | 1,849 | 6.557 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44 | 1,936 | 6.633 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45 | 2,025 | 6,708 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46 | 2116 | 6.782 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6.782 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6.782 | 2|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6.782 | 2333333339||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6.782 | 2333333339||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .47 | 2,209 | 6.856 |
| 48 | 2,304 | 6.928 |
| 49 | 2,401 | 7. 000 000 |
| 50 | 2,500 | 7.071 |
| number | квадрат | квадрат корень |
|---|---|---|
| 51 | 2 601 | 7,141 |
| 52 | 2 704 | 7,211 |
| 53 | 2,809 | 7.280 |
| 54 | 2,916 | 7.348 |
| 55 | 3,025 | 7.416 |
| 56 | 3,136 | 7.483 |
| 57 | 3,249 | 7.550 |
| 58 | 3,364 | 7.616 |
| 59 | 3,481 | 7.681 |
| 60 | 3,600 | 7.746 |
| 61 | 3,721 | 7.810 |
| 62 | 3,844 | 7.874 |
| 63 | 3,969 | 7.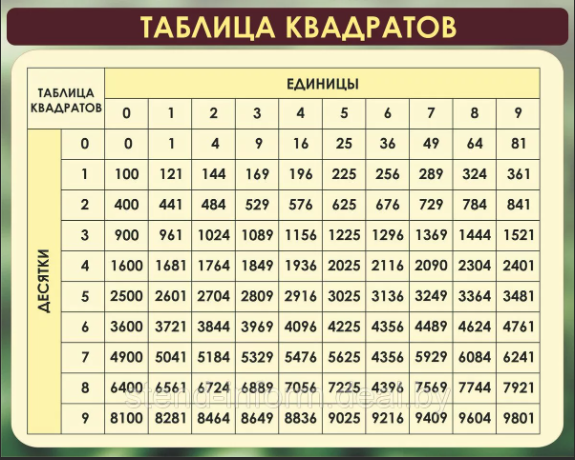 937 937 |
| 64 | 4,096 | 8.000 |
| 65 | 4,225 | 8.062 |
| 66 | 4,356 | 8.124 |
| 67 | 4,489 | 8.185 |
| 68 | 4,624 | 8.246 |
| 69 | 4,761 | 8.307 |
| 70 | 4,900 | 8.367 |
| 71 | 5,041 | 8.426 |
| 72 | 5,184 | 8.485 |
| 73 | 5,329 | 8.544 |
| 74 | 5,476 | 8.602 |
| 75 | 5625 | 8.660 |
| номер | квадрат | квадрат3 корень |
|---|---|---|
| 76 | 5,776 | 8.718 |
| 77 | 5,929 | 8.775 |
| 78 | 6,084 | 8.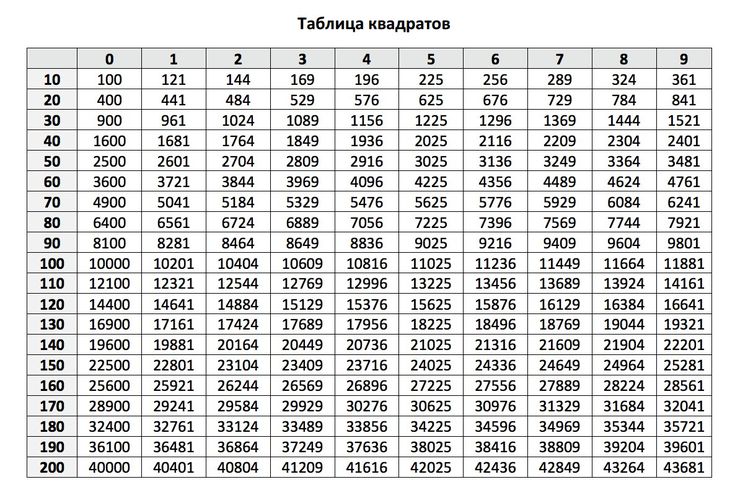 832 832 |
| 79 | 6,241 | 8.888 |
| 80 | 6,400 | 8,944 |
| 81 | 6,561 | 9.000 |
| 82 | 6,724 | 9.055 |
| 83 | 6,889 | 9.110 |
| 84 | 7,056 | 9.165 |
| 85 | 7,225 | 9.220 |
| 86 | 7,396 | 9.274 |
| 87 | 7,569 | 9.327 |
| 88 | 7,744 | 9.381 |
| 89 | 7,921 | 9.434 |
| 90 | 8,100 | 9.487 |
| 91 | 8,281 | 9.539 |
| 92 | 8,464 | 9.592 |
| 93 | 8,649 | 9.644 |
| 94 | 8,836 | 9.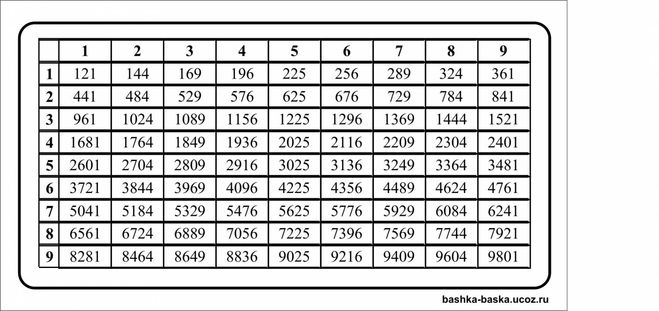 695 695 |
| 95 | 9,025 | 9.747 |
| 96 | 9,216 | 9.798 |
| 97 | 9,409 | 9.849 |
| 98 | 9,604 | 9.899 |
| 99 | 9,801 | 9.950 |
| 100 | 10 000 | 10.000 |
Квадратный корень из значений около 1296
| Номер | SQRT |
|---|---|
| SQRT | |
| SQRT | |
| 32.404 | |
| 1100 | 33.166 |
| 1150 | 33.912 |
| 1200 | 34.641 |
| 1250 | 35.355 |
| 1300 | 36.056 |
| 1350 | 36,742 |
| 1400 | 37,417 |
| 1450 | 38,079 |
| 1500 | 38.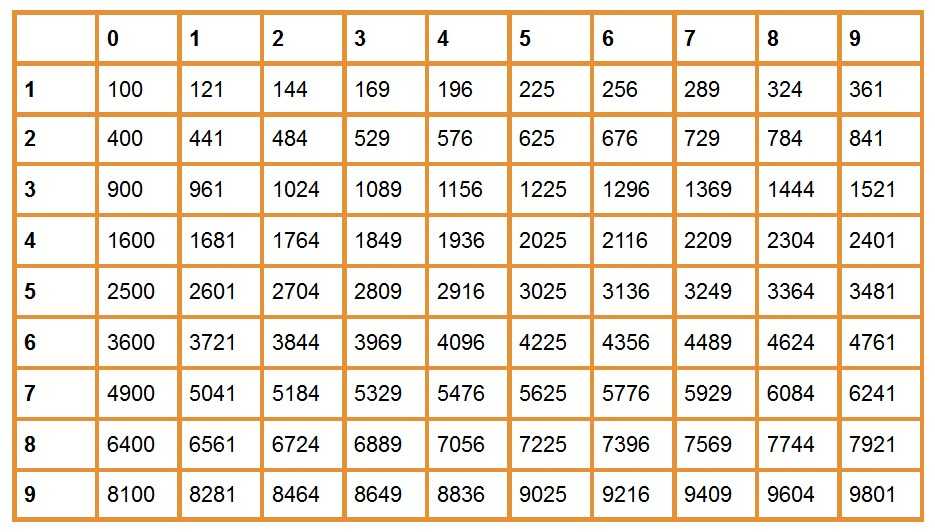 730 730 | 023
Квадратный корень из 1296 (√1296)
Здесь мы определим, проанализируем, упростим и вычислим квадратный корень из 1296. Мы начнем с определения, а затем ответим на некоторые общие вопросы. вопросы о квадратном корне из 1296. Затем мы покажем вам различные способы вычисления квадратного корня из 1296 с и без компьютер или калькулятор. У нас есть много информации, чтобы поделиться, так что давайте начнем!
Корень квадратный из 1296 определение
Квадратный корень из 1296 в математической форме записывается с таким знаком радикала √1296. Мы называем это квадратным корнем из 1296 в радикальной форме.
Квадратный корень из 1296 — это величина (q), которая при умножении сама на себя будет равна 1296.
√1296 = q × q = q 2
Является ли 1296 полным квадратом?
1296 является полным квадратом, если квадратный корень из 1296 равен целому числу.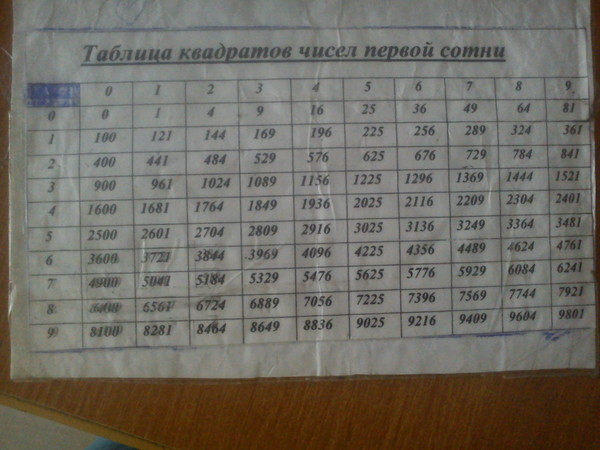 Как мы рассчитали дальше
внизу на этой странице квадратный корень из 1296 — целое число.
Как мы рассчитали дальше
внизу на этой странице квадратный корень из 1296 — целое число.
1296 — правильный квадрат.
Является ли квадратный корень из 1296 рациональным или иррациональным?
Квадратный корень из 1296 является рациональным числом, если 1296 является полным квадратом. Это иррациональное число, если оно не является полным квадратом.
Поскольку 1296 — совершенный квадрат, это рациональное число. Это означает, что ответ на вопрос «квадратный корень из 1296?» не будет иметь десятичных знаков.
√1296 является рациональным числом
Может ли квадратный корень из 1296 упростить?
Квадратный корень из полного квадрата можно упростить, потому что квадратный корень из полного квадрата будет равен целому числу:
√1296 = 36
Как вычислить квадратный корень из 1296 с помощью калькулятора
Самый простой и скучный способ вычислить квадратный корень из 1296 — воспользоваться калькулятором!
Просто введите 1296, а затем √x, чтобы получить ответ. Мы сделали это с помощью нашего калькулятора и получили следующий ответ:
Мы сделали это с помощью нашего калькулятора и получили следующий ответ:
√1296 = 36
Как вычислить квадратный корень из 1296 на компьютере
Если вы используете компьютер с Excel или Numbers, вы можете ввести SQRT(1296) в ячейку, чтобы получить квадратный корень из 1296 .
Ниже приведен результат, который мы получили:
SQRT(1296) = 36
Чему равен квадратный корень из 1296, записанный с показателем степени?
Все квадратные корни можно преобразовать в число (по основанию) с дробной степенью. Квадратный корень из 1296 не является исключением. Вот правило и ответ
в «квадратный корень из 1296 преобразовать в основание с показателем степени?»:
√b = b ½
√1296 = 1296 ½
Здесь мы будем 9016 9016 методом деления в длину. показать вам, как вычислить квадратный корень из 1296, используя метод деления в длинную сторону. искусство того, как они вычисляли квадратный корень из 1296 вручную до того, как были изобретены современные технологии.
искусство того, как они вычисляли квадратный корень из 1296 вручную до того, как были изобретены современные технологии.
Шаг 1)
Наберите 1296 парами по две цифры справа налево:
Шаг 2)
Начнем с первого набора: самый большой полный квадрат, меньше или равный 12, равен 9, а квадратный корень из 9 равен 3. Следовательно, поместите 3 сверху и 9 снизу, как this:
| 3 | ||||
| 12 | 96 | |||
| 9 | ||||
Step 3)
Calculate 12 minus 9 and put the difference ниже. Затем переместитесь вниз к следующему набору чисел.
| 3 | ||||
| 12 | 96 | |||
| 9 | ||||
| 3 | 96 | |||
Шаг 4)
Удвойте число, выделенное зеленым сверху: 3 × 2 = 6. Затем используйте 6 и нижнее число, чтобы решить эту задачу:
Затем используйте 6 и нижнее число, чтобы решить эту задачу:
6? × ? ≤ 396
Знаки вопроса «пробел» и такие же «пробел». Методом проб и ошибок мы нашли, что наибольшее число «пустых» может быть равно 6. Замените вопросительные знаки в задаче на 6, чтобы получить:
66 × 6 = 396.
Now, enter 6 on top, and 396 at the bottom:
| 3 | 6 | |||
| 12 | 96 | |||
| 9 | ||||
| 3 | 96 | |||
| 3 | 96 | |||
Разница между двумя нижними числами равна нулю, поэтому все готово! Ответ — зеленые цифры сверху.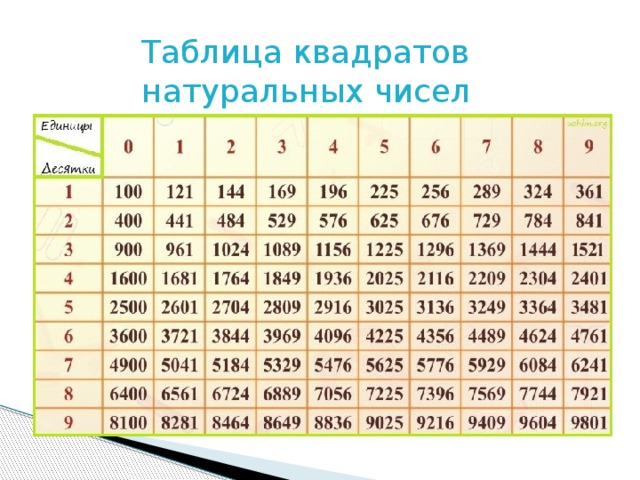 Еще раз, квадратный корень из
1296 равно 36.
Еще раз, квадратный корень из
1296 равно 36.
Квадратный корень из числа
Пожалуйста, введите другое число в поле ниже, чтобы получить квадратный корень из числа и другую подробную информацию, как вы получили для 1296 на этой странице.
Примечания
Помните, что отрицательное число, умноженное на отрицательное, равно положительному. Таким образом, квадратный корень из 1296 имеет не только положительный ответ
что мы объяснили выше, но и отрицательный аналог.
На этой странице мы часто ссылаемся на совершенные квадратные корни. Вы можете использовать список идеальных квадратов для справки.
Квадратный корень из 1297
Вот следующее число в нашем списке, о котором у нас есть такая же подробная информация о квадратном корне.
Авторское право | Политика конфиденциальности | Отказ от ответственности | Контакт
Квадратный корень из 1296 | Как найти квадратный корень из 1296
Реклама
Как найти квадратный корень из 1296Квадрат 36:
- В математике найти квадрат любого числа в основном легко, потому что, когда мы умножаем одно и то же число на себя, мы получаем квадрат этого числа.

Например:
- Предположим, нам нужно найти квадрат любого числа, скажем, X , затем мы умножаем X само на себя, т. Это можно записать как (X) 2 = X*X= Y
- Аналогичным образом находим квадрат числа 36 .
- Чтобы найти квадрат 36, умножаем 36 на само число, т.е. на 36, и записываем его следующим образом: (36) 2 = 36*36 = 1296
Квадратный корень из 1296:
- Теперь в обратном порядке, если нам нужно найти квадратный корень из Y . Квадратный корень из Y — это единственное значение, которое при умножении само на себя дает значение Y .
- Это означает, что √ Y = √(X*X) = X
Где √ — символ, названный радикалом.
Например:
- Квадратный корень из 1296 можно записать как
√1296= √ (36*36) = 36
Где √ – это символ, который называется подкоренным знаком.
- Короче говоря, мы помним квадрат из 36 и квадратный корень из 1296 как .
Примечание:
- Каждое положительное действительное число имеет два корня.
- Квадрат любого отрицательного числа всегда является положительным числом.
Например:
- 1296 — положительный совершенный квадрат, который также имеет два корня +36 и -36.
- Но в основном берется положительное значение квадратного корня, которое называется главным квадратным корнем или неотрицательным квадратным корнем.
- Следовательно, √1296 = √(-36)*(-36) = -36 и √1296 = √(36)*(36) = 36
Аналогично,
- (-36)*(-36) = (-36) 2 = +1296 и (+36)*(+36) = (+36) 2 = 1296
Существует множество методов нахождения квадратного корня из полного квадрата, из которых мы подробно рассмотрим следующий метод.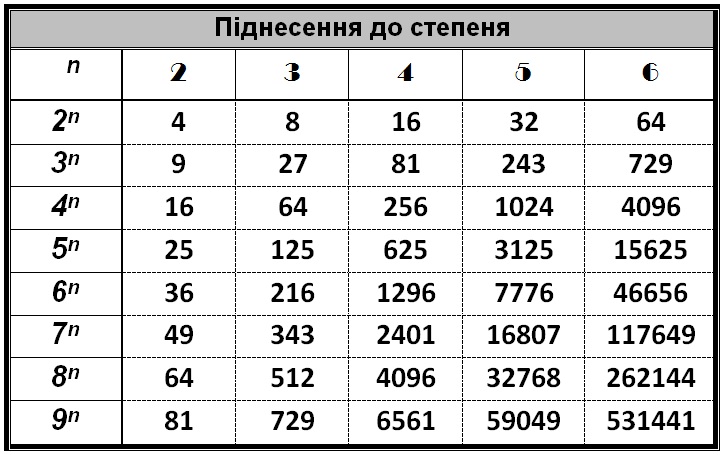
- Метод повторного вычитания
- Метод простой факторизации
- В методе многократного вычитания мы должны вычесть последовательные нечетные числа, начиная с 1, из совершенного квадратного числа, квадратный корень которого мы должны найти.
- эл. чтобы найти квадратный корень из 1296, сначала мы вычитаем из него 1.
1296 – 1 = 1295
- Тогда следующее нечетное число равно 3, поэтому мы должны вычесть его из 1295
1295– 3 = 1292
- Таким образом, мы вычитаем последовательные нечетные числа из соответствующих значений, полученных после непрерывного вычитания, пока не получим окончательное значение 0, .
- И значение количества нечетных чисел, необходимых для получения 0, является искомым квадратным корнем.
Например:
- Квадратный корень из 1296 находим методом многократного вычитания следующим образом:
1296-1 = 1295
1295-3 = 1292
1292 -5 = 1287
1287-7 = 1280
1280-9 = 1271
1271-11 = 1260
1260 -13 = 1247
1271-11.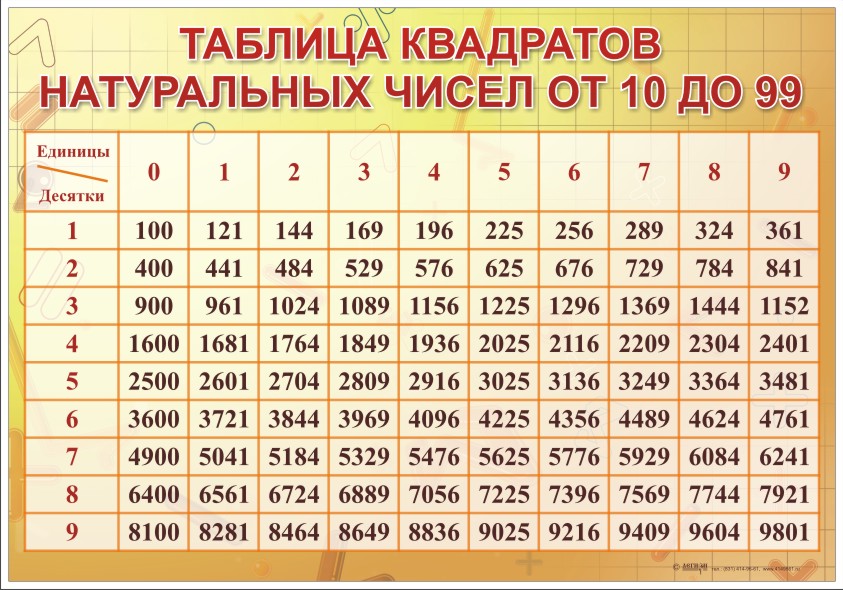
1247 -15 = 1232
1232-17 = 1215
1215-19 = 1196
1196-21 = 1175
1175-23 = 1152
1152-25 = 1127
975-23.0002 1127-27 = 11001100-29 = 1071
1071-31 = 1040
1040-33 = 1007
Я 896-41=855
855-43=812
812-45=767
767 -47=720
720-49=671
671-51=620
620-53=567
567 -55=512
512-57=455
455- 59 = 396
396- 61 = 335
335 – 63 = 272
272 – 7 650002 207 – 67=140
140-69=71
71-71= 0
- Таким образом, здесь используются нечетные числа 1, 3, 5, 7, 9, 12, 13, 15, 17, 19, 21, 23,25,27,29,31,33,35,37,39,41,43,45,47,49,51,53,55,57,59 61,63,65,67,69 and71, которые равны 36 числам.
- Следовательно, квадратный корень из 1296 методом многократного вычитания равен 36
- В методе простой факторизации мы должны разделить идеальное квадратное число, квадратный корень которого мы должны найти, на простое число, начиная с 2, 3, 5… и так далее, пока мы не получим остаток как 1.


 Таблица степеней.
Таблица степеней. ru:
ru:



 Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
 Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.

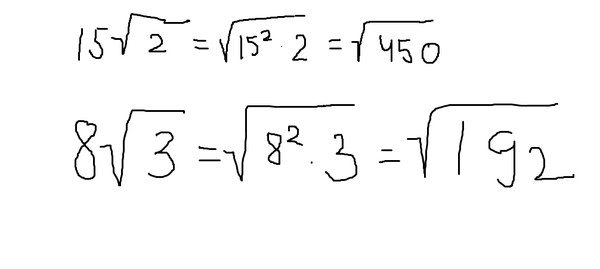 Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
 В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен S a (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa
В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен S a (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa (10A+B)² — это площадь всего квадрата, 100A² — площадь большого внутреннего квадрата, B² — площадь малого внутреннего квадрата, 10A×B — площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
(10A+B)² — это площадь всего квадрата, 100A² — площадь большого внутреннего квадрата, B² — площадь малого внутреннего квадрата, 10A×B — площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.