Как посчитать окружность зная диаметр формула. Как найти длину окружности: через диаметр и радиус
Окружностью называют кривую линию, которая ограничивает собой круг. В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению. Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.
У окружности есть несколько характеристик, на основе которых производят расчеты, связанные с этой геометрической фигурой. В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.
- Радиус окружности – это отрезок внутри окружности, соединённый с ее центром.
- Диаметр – это отрезок внутри окружности, соединяющий ее точки и проходящий через центр. По сути, диаметр – это два радиуса. Именно так выглядит формула для его вычисления: D=2r.

- Есть еще одна составляющая окружности – хорда. Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром.
Как узнать длину окружности? Сейчас выясним.
Длина окружности: формула
Для обозначения этой характеристики выбрана латинская буква p. Еще Архимед доказал, что отношение длины окружности к ее диаметру является одним и тем же числом для всех окружностей: это число π, которое приблизительно равно 3,14159. Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr.Рассмотрим применение формулы на примере простых задач:
Задача 1
У основания царь-колокола диаметр равен 6,6 метров. Какова длина окружности основания колокола?
- Итак, формула для вычисления окружности — p= πd
- Подставляем имеющееся значение в формулу: p=3,14*6,6= 20,724
Ответ: длина окружности основания колокола 20,7 метра.
Задача 2
Искусственный спутник Земли вращается на расстоянии 320 км от планеты. Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?
- 1.Вычислим радиус круговой орбиты спутника Земли: 6370+320=6690 (км)
- 2.Вычислим длину круговой орбиты спутника по формуле: P=2πr
- 3.P=2*3,14*6690=42013,2
Ответ: длина круговой орбиты спутника Земли 42013,2 км.
Способы измерения длины окружности
Вычисление длины окружности на практике используется не часто. Причиной тому приблизительное значение числа π. В быту для поиска длины круга используют специальный прибор – курвиметр. На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.
Как найти длину окружности? Нужно просто держать в голове незамысловатые формуля для вычислений.
Знаете ли вы, что человек за всю свою жизнь забывает около 40% информации, которую он воспринимал. Из этого следует, что все запомнить, и тем более все знать очень тяжело, а порой даже нереально. К примеру, после того, как ученик закончил школу, а потом институт, допустим, по гуманитарной специальности, а не по технической (строительный или инженерный факультет), можно с большой вероятностью утверждать, что он уже давно забыл элементарную математику.
К примеру, после того, как ученик закончил школу, а потом институт, допустим, по гуманитарной специальности, а не по технической (строительный или инженерный факультет), можно с большой вероятностью утверждать, что он уже давно забыл элементарную математику.
Вот вы помните, как найти высоту трапеции, как найти производную функции или же правильно построить график? Наверняка, нет. Редко кто сможет осилить такую задачу без дополнительной помощи. Возьмем, например, студента, который плохо изучал геометрию в школе, и просто забыл, как найти периметр круга. Эта статья пригодится тем, кто желает возобновить в памяти школьную программу математики. Зачастую такая необходимость возникает у родителей, к которым дети-школьники обращаются за помощью по домашнему заданию по геометрии, а также ученикам, которые сейчас изучают материал.
Необходимо:
— круг, периметр которого нужно найти;
— школьный циркуль и линейка;
— листок бумаги и карандаш;
— калькулятор.
Инструкция:
- Найти периметр круга – это аналогичное задание вычислению длины окружности.
 Для начала потребуется измерять его радиус . Для этого нужно воспользоваться циркулем. Одну его ножку ставим в центр круга, а вторую на любую точку окружности. Поскольку окружность представляет собой совокупность всех равно-отдаленных точек от центра, то куда именно станет вторая ножка циркуля — роли не играет, поскольку везде будет одинаковое расстояние.
Для начала потребуется измерять его радиус . Для этого нужно воспользоваться циркулем. Одну его ножку ставим в центр круга, а вторую на любую точку окружности. Поскольку окружность представляет собой совокупность всех равно-отдаленных точек от центра, то куда именно станет вторая ножка циркуля — роли не играет, поскольку везде будет одинаковое расстояние. - Если же под рукой нет циркуля, то можно узнать диаметр круга при помощи линейки. Для этого измеряем длину, положив линейку так, чтобы она проходила через центр круга. Расстояние, которое мы получим, будет диаметром . Он равен двум радиусам, поэтому формула, приведенная немного дальше, остается актуальной.
- Если центр круга не обозначен, то линейкой измеряем самое большое расстояние от одной точки окружности к другой. При таком способе расчета, полученный периметр круга будет числом неточным, так как диаметр мы могли определить не совсем точно. Полученное расстояние измеряем на линейке, приложив к ней циркуль.

- Чтобы узнать периметр круга, нужно воспользоваться формулой . Она очень проста: радиус нашей окружности умножается на два, после чего умножается на число Пи , которое является постоянным и равняется значению 3,14 . Рассчитали его еще древние математики, а последующие поколения успешно применяют в вычислениях уже не одну тысячу лет, поэтому в его правильности можно не сомневаться. После того, как мы проведем расчеты, получим число, которое и является искомым.
- Для окружностей больших размеров алгоритм и инструкция по измерению остается прежней, вот только линейка и циркуль заменяются строительной рулеткой, и специальными программами для расчетов.
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
- Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка. Это определение выводится из теоремы Пифагора.
Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).
Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски:
L = πD = 3,14 * 20 = 62,8 см.
Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии.
L = 2πR = 2 * 3,14 * 13 = 81,68 м.
Полезное видео: круг — радиус, диаметр, длина окружности
Итог
Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Инструкция
Вспомните, что впервые математически вычислил это соотношение Архимед. Он правильные 96-тиугольники внутри окружности и вокруг нее. Периметр вписанного многоугольника принял за минимально возможную длину окружности, периметр описанной фигуры – за максимальный размер. По Архимеду соотношение длины окружности и диаметра равно 3,1419. Значительно позже это число «удлинил» до восьми знаков китайский математик Цзу Чунчжи. Его вычисления 900 лет оставались наиболее точными. Только в XVIII веке было посчитано сто знаков после запятой. А с 1706 года эта бесконечная десятичная дробь благодаря Уильяму Джонсу приобрела имя. Он обозначил ее первой буквой греческих слов периметр (периферия). Сегодня компьютер легко вычисляет знаков числа Пи: 3,141592653589793238462643…
Только в XVIII веке было посчитано сто знаков после запятой. А с 1706 года эта бесконечная десятичная дробь благодаря Уильяму Джонсу приобрела имя. Он обозначил ее первой буквой греческих слов периметр (периферия). Сегодня компьютер легко вычисляет знаков числа Пи: 3,141592653589793238462643…
Для расчетов число Пи сократите до 3,14. Получится, что для любой окружности ее длина, деленная на диаметр равна этому числу: L:d=3,14.
Выразите из этого утверждения формулу для нахождения диаметра. Получится, чтобы найти диаметр окружности надо длину окружности поделить на число Пи. Это выглядит так: d = L:3,14. Это универсальный способ найти диаметр, когда у окружности известна ее длина.
Итак, известна длина окружности, допустим, 15,7 см, разделите эту цифру на 3,14. Диаметр будет равен 5 см. Запишите это так: d = 15,7: 3,14 = 5 см.
Найдите диаметр по длине окружности, используя специальные таблицы для вычисления длины окружности . Эти таблицы включают в разные справочники. Например, они есть в «Четырехзначные математические таблицы» В.М. Брадиса.
Например, они есть в «Четырехзначные математические таблицы» В.М. Брадиса.
Полезный совет
Запомните первые восемь цифр числа Пи с помощью стихотворения:
Нужно только постараться,
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Источники:
- Число «Пи» рассчитано с рекордной точностью
- диаметр и длина окружности
- Как найти длину окружности?
Круг — это плоская геометрическая фигура, все точки которой находятся на одинаковом и отличном от нуля удалении от выбранной точки, которую называют центром окружности. Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром . Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
Инструкция
Используйте для нахождения диаметра одно из основных свойств окружности, которое заключается в том, что соотношение длины ее периметра к диаметру одинаково для абсолютно всех окружностей. Конечно, постоянство не осталось не отмеченным математиками, и эта пропорция давно уже получила собственное — это число Пи (π — первая греческих слов «окружность » и «периметр»). Числовое этой определяется длиной окружности, у которой диаметр равен единице.
Конечно, постоянство не осталось не отмеченным математиками, и эта пропорция давно уже получила собственное — это число Пи (π — первая греческих слов «окружность » и «периметр»). Числовое этой определяется длиной окружности, у которой диаметр равен единице.
Делите известную длину окружности на число Пи, чтобы вычислить ее диаметр. Так как это число является « », то не имеет конечного значения — это дробь. Округляйте число Пи в соответствии с точностью результата, которую вам необходимо получить.
Видео по теме
Удивительное свойство окружности открыл нам древнегреческий ученый Архимед. Оно заключается в том, что отношение ее длины к длине диаметра одинаково для любой окружности . В своем труде «Об измерении круга» он вычислил его и обозначил числом «Пи». Оно иррационально, то есть его значение не может быть точно выражено. Для используется его величина, равная 3,14. Вы можете сами проверить утверждение Архимеда, сделав простые вычисления.
Вам понадобится
- — циркуль;
- — линейка;
- — карандаш;
- — нитка.
Инструкция
Начертите на бумаге циркулем окружность произвольного диаметра. Проведите с помощью линейки и карандаша через ее центр отрезок, соединяющий две , находящиеся на линии окружности . Линейкой измерьте длину получившегося отрезка. Допустим, окружности в данном случае 7 сантиметрам.
Возьмите нитку и расположите ее по длине окружности . Измерьте получившуюся длину нитки. Пусть она будет равна 22 сантиметрам. Найдите отношение длины окружности к длине ее диаметра — 22 см: 7 см = 3,1428…. Округлите полученное число (3,14). Получилось знакомое число «Пи».
Доказать это свойство окружности вы можете, используя чашку или стакан. Измерьте их диаметр линейкой. Обмотайте верх посуды ниткой, замерьте получившуюся длину. Поделив длину окружности чашки на длину ее диаметра, вы также получите число «Пи», убедившись в этом свойстве окружности , открытом Архимедом.
Используя это свойство, вы можете вычислить длину любой окружности по длине ее диаметра или по формулам:С = 2*п*R или С = D*п, где С — окружности , D — длина ее диаметра, R — длина ее радиуса.Для нахождения (плоскости, ограниченной линиями окружности ) используйте формулу S = π*R², если известен его радиус, либо формулу S = π*D²/4, если известен его диаметр.
Обратите внимание
А вы знаете, что четырнадцатого марта уже более двадцати лет отмечается День «Пи»? Это неофициальный праздник математиков, посвященный этому интересному числу, с которым в настоящее время связано множество формул, математических и физических аксиом. Придумал этот праздник американец Ларри Шоу, который обратил внимание, что в этот день (3.14 в системе записи дат в США) родился знаменитый ученый Эйнштейн.
Источники:
- Архимед
Иногда около выпуклого многоугольника можно начертить таким образом, чтобы вершины всех углов лежали на ней. Такую окружность по отношению к многоугольнику надо называть описанной. Ее центр не обязательно должен находиться внутри периметра вписанной фигуры, но пользуясь свойствами описанной окружности , найти эту точку, как правило, не очень трудно.
Ее центр не обязательно должен находиться внутри периметра вписанной фигуры, но пользуясь свойствами описанной окружности , найти эту точку, как правило, не очень трудно.
Вам понадобится
- Линейка, карандаш, транспортир или угольник, циркуль.
Инструкция
Если многоугольник, около которого нужно описать окружность, начерчен на бумаге, для нахождения центр а круга достаточно линейки, карандаша и транспортира либо угольника. Измерьте длину любой из сторон фигуры, определите ее середину и поставьте в этом месте чертежа вспомогательную точку. С помощью угольника или транспортира проведите внутри многоугольника перпендикулярный этой стороне отрезок до пересечения с противоположной стороной.
Проделайте эту же операцию с любой другой стороной многоугольника. Пересечение двух построенных отрезков и будет искомой точкой. Это вытекает из основного свойства описанной окружности — ее центр в выпуклом многоугольнике с любым сторон всегда лежит в точке пересечения серединных перпендикуляров, проведенных к этим .
Для правильных многоугольников центр а вписанной окружности может быть намного проще. Например, если это квадрат, то начертите две диагонали — их пересечение и будет центр ом вписанной окружности . В многоугольнике с любым четным числом сторон достаточно соединить вспомогательными две пары лежащих друг напротив друга углов — центр описанной окружности должен совпадать с точкой их пересечения. В прямоугольном треугольнике для решения задачи просто определите середину самой длинной стороны фигуры — гипотенузы.
Если из условий неизвестно, можно ли в принципе описанную окружность для данного многоугольника, после определения предполагаемой точки центр а любым из описанных способов вы можете это выяснить. Отложите на циркуле расстояние между найденной точкой и любой из , установите в предполагаемый центр окружности и начертите круг — каждая вершина должна лежать на этой окружности . Если это не так, значит, не выполняется одно из свойств и описать окружность около данного многоугольника .
Определение диаметра может пригодиться не только для решения геометрических задач, но и помочь на практике. Например, зная диаметр горлышка банки, вы точно не ошибетесь в выборе крышки для нее. То же утверждение справедливо и для более габаритных окружностей.
Инструкция
Итак, введите обозначения величин. Пусть d – диаметр колодца, L – длина окружности, п – число Пи, значение которого приблизительно равно 3,14, R – радиус окружности. Длина окружности (L) известна. Предположим, что она равна 628 сантиметрам.
Далее для нахождения диаметра (d) воспользуйтесь формулой длины окружности: L=2пR, где R – неизвестная величина, L=628 см, а п=3,14. Теперь воспользуйтесь правилом нахождения неизвестного множителя: «Чтобы найти множитель, нужно произведение разделить на известный множитель». Получается: R=L/2п. Подставьте значения к формуле: R=628/2×3,14. Получается: R=628/6,28, R=100 см.
После того как радиус окружности найден (R=100 см), воспользуйтесь следующей формулой: диаметр окружности (d) равен двум радиусам окружности (2R). Получается: d=2R.
Получается: d=2R.
Теперь, чтобы найти диаметр, подставьте в формулу d=2R значения и вычислите результат. Так как радиус (R) известен, получается: d=2×100, d=200 см.
Источники:
- как по длине окружности определить диаметр
Длина окружности и диаметр являются взаимосвязанными геометрическими величинами. Это означает, что первую из них можно перевести во вторую без каких-либо дополнительных данных. Математической константой, через которую они связаны между собой, является число π.
Инструкция
Если окружность представлена в виде изображения на бумаге, а ее диаметр требуется определить приблизительно, измерьте его непосредственно. Если ее центр показан на чертеже, проведите через него линию. Если же центр не показан, найдите его при помощи циркуля. Для этого используйте угольник с углами в 90 и . Приложите его 90-градусным углом к окружности таким образом, чтобы ее касались оба катета, и обведите. Приложив затем к получившемуся прямому углу 45-градусный угол угольника, начертите . Она пройдет через центр окружности. Затем аналогичным образом начертите в другом месте окружности второй прямой угол и его биссектрису. Они пересекутся в центре. Это позволит измерить диаметр.
Она пройдет через центр окружности. Затем аналогичным образом начертите в другом месте окружности второй прямой угол и его биссектрису. Они пересекутся в центре. Это позволит измерить диаметр.
Для измерения диаметра предпочтительно использовать линейку, изготовленную из как можно более тонкого листового материала, либо портновский метр. При наличии только толстой линейки измерьте диаметр окружности при помощи циркуля, а затем, не изменяя его раствора, перенесите его на миллиметровую бумагу.
Также при отсутствии в условиях задачи числовых данных и при наличии только чертежа можно измерить длину окружности при помощи курвиметра, а диаметр затем рассчитать. Чтобы воспользоваться курвиметром, вначале вращением его колесика установите стрелку точно на нулевое деление. Затем отметьте на окружности точку и прижмите курвиметр к листу таким образом, чтобы штрих над колесиком указывал на эту точку. Проведите колесиком по линии окружности, пока штрих снова не окажется над этой точкой. Прочитайте показания. Они будут в , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
Прочитайте показания. Они будут в , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
При увеличении числа сторон периметр вписанного многоугольника будет все больше приближаться к L. Р= b*n=2n*R*Sin (π/n)=n*D*Sin (π/n). Зависимость между длиной окружности L и ее диаметром D постоянна. Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для вычисления диаметра
Измерение окружности
О том, что наша планета имеет форму шара, ученым, занимающимся исследованиями в области геологии, было известно достаточно давно. Именно поэтому первые измерения величины окружности земной поверхности касались самой длинной параллели Земли — экватора. Эту величину, полагали ученые, можно считать правильной для любого другого способа измерения. Например, считалось, что если измерить окружность планеты по самому длинному
Именно поэтому первые измерения величины окружности земной поверхности касались самой длинной параллели Земли — экватора. Эту величину, полагали ученые, можно считать правильной для любого другого способа измерения. Например, считалось, что если измерить окружность планеты по самому длинному
Такое мнение существовало вплоть до XVIII века. Однако ученые ведущего научного учреждения того времени — Французской академии — придерживались мнения о том, что эта гипотеза неверна, и форма, которую имеет планета, не совсем правильна. Поэтому, по их мнению, длины окружности по самому длинному меридиану и по самой длинной параллели будут различаться.
В доказательство в 1735 и 1736 годах были предприняты две научные экспедиции, которые доказали истинность этого предположения. Впоследствии была установлена и величина различия между этими двумя — она составила 21,4 километра.
Длина окружности
В настоящее время длина окружности планеты Земля неоднократно измерена уже не посредством экстраполяции длины того или иного отрезка земной поверхности на ее полную величину, как это делалось раньше, а с применением современных высокоточных технологий. Благодаря этому удалось установить точную длину окружности по самому длинному меридиану и самой длинной параллели, а также уточнить величину различия между этими параметрами.
Благодаря этому удалось установить точную длину окружности по самому длинному меридиану и самой длинной параллели, а также уточнить величину различия между этими параметрами.Так, на сегодняшний день в научном сообществе в качестве официальной величины окружности планеты Земля по экватору, то есть наиболее длинной параллели, принято приводить цифру, составляющую 40075,70 километра. При этом аналогичный параметр, измеренный по самому длинному меридиану, то есть длина окружности, проходящей через земные полюсы, составляет 40008,55 километра.
Таким образом, разница между длинами окружностей составляет 67,15 километра, и экватор является самой длинной окружностью нашей планеты. Кроме того, различие означает, что один градус географического меридиана несколько короче, чем один градус географической параллели.
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Определение длины окружности
Произвести расчёт окружности можно по следующей формуле:
L = π D = 2 π r
r — радиус окружности
D — диаметр окружности
L — длина окружности
π — 3.14
Задача:
Вычислить длину окружности , имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
L = π D = 2 π r
где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 62,8 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Площадь круга расчет по формулам и онлайн
Определим площадь круга, если нам известны радиус круга, диаметр, длина окружности круга. Для того, чтобы мы могли рассчитать площадь круга, давайте вспомним формулы, по которым площадь рассчитывается.
Формула площади круга
Площадь круга равна произведению числа пи на квадрат радиуса круга:
Важно!
Площадь круга — это размер области плоскости, ограниченной окружностью, в квадратных единицах измерения.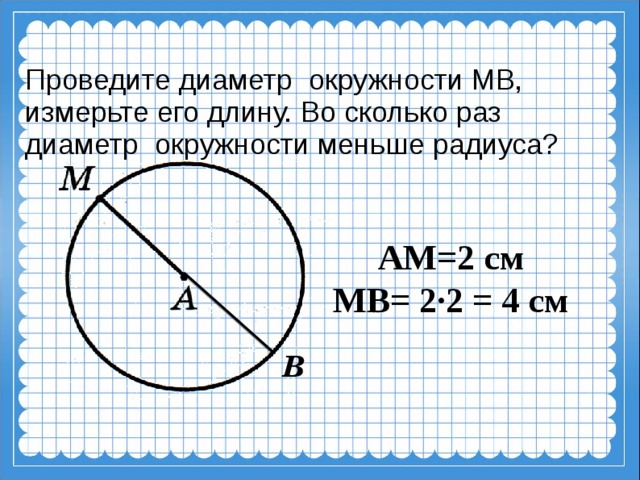
Для начала уточним несколько понятий:
- Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круга) на расстояние, которое не превышает радиус круга.
- Окружность круга — его граница. Множество точек на плоскости равноудаленных от заданной точки, которую называют центром круга. Простыми словами можно описать окружность замкнутой линией, описывающей круг, наподобие бублика или шины от машины.
- Площадь любого круга — размер плоскости, ограниченной окружностью круга.
- Единицей измерения площади круга является квадратная единица его длины (м2, см2, км2, ед2).
- Диаметр круга — отрезок, соединяющий две точки на окружности и проходящий через центр круга.
- Радиус круга — это отрезок, соединяющий центр круга и любую точку на его окружности.
Содержание
Окружность и круг
Многие школьники путают окружность и круг. Окружность — это линия! А круг — это плоскость.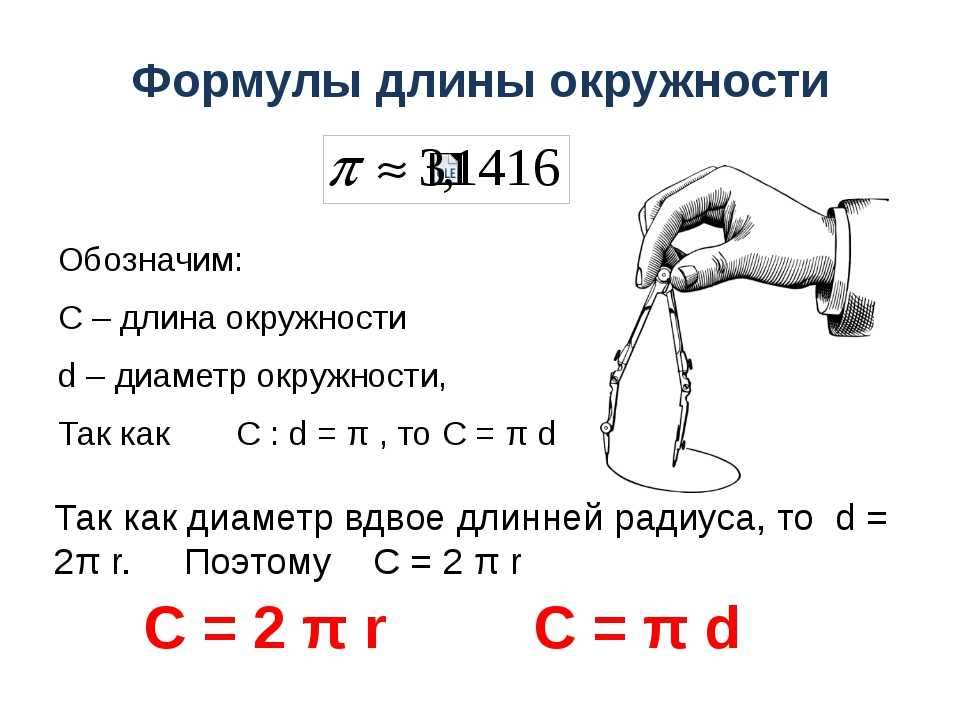 Сравнить окружность можно с обручем, с бубликом, с оправой от очков. А круг — это, например, круглый оладушек или блинчик, блюдце, крышки от банки. Длина окружности измеряется в единицах длины, а площадь любого блинчика, оладушка и вообще круга — в квадратных единицах длины. Ниже мы это с вами рассмотрим подробнее.
Сравнить окружность можно с обручем, с бубликом, с оправой от очков. А круг — это, например, круглый оладушек или блинчик, блюдце, крышки от банки. Длина окружности измеряется в единицах длины, а площадь любого блинчика, оладушка и вообще круга — в квадратных единицах длины. Ниже мы это с вами рассмотрим подробнее.
Вот известные части круга:
Части круга: радиус, диаметр, окружность, сектор, сегмент, хорда, касательная. В этой статье мы не будем рассматривать такие части круга, как хорда, сектор или сегмент. Но общее представление дадим. Важно, когда вы определяете что перед вами — круг или окружность, вы можете посмотреть на нашу инфографику. Как видно — окружность определяется замкнутой линией, описывающей круг. В детстве мы так начинали рисовать солнце — сначала рисовали эту линию. Получали окружность. Затем закрашивали область внутри линии — получали круг.
А теперь рассмотрим формулы для того, чтобы найти площадь круга.
Площадь круга по известному радиусу
Издавна человек наблюдал круглые объекты природы: солнце, луна, капли росы. Человек восхищался этими творениями природы. Он подражал им, воплощая в архитектуре и в живописи. Однажды пришла пора выяснить геометрические свойства круга. Сегодня мы с вами изучим формулы, по которым определяется его площадь. Выше мы уже выяснили разницу между понятиями круга и его окружностью. Между радиусом и диаметром.
Человек восхищался этими творениями природы. Он подражал им, воплощая в архитектуре и в живописи. Однажды пришла пора выяснить геометрические свойства круга. Сегодня мы с вами изучим формулы, по которым определяется его площадь. Выше мы уже выяснили разницу между понятиями круга и его окружностью. Между радиусом и диаметром.
Итак, площадь любого круга через радиус определяется по формуле: , где — радиус круга. Словами можно сказать так «площадь круга равна произведению числа пи на квадрат радиуса круга». Воспользуйтесь онлайн калькулятором, чтобы проверить правильность вычислений. Обратите внимание, если вы вводите радиус круга в см, то площадь круга получите в см2. Аналогично если в ед. или в м, то площадь будет в ед2 и в м2 соответственно. Десятичные значения радиуса вводите с точкой, вот так 5.5, 3.25.
Число пи — постоянная величина, равная приблизительно 3,14.
Найти площадь круга, зная его радиус. Онлайн калькулятор.
Введите радиус круга:
Площадь заданного круга:
Площадь данного круга в π:
Единицы измерения площади круга
Мы с вами уже научились определять площадь, зная радиус круга. Познакомимся теперь с популярными единицами измерения площади круга.
Познакомимся теперь с популярными единицами измерения площади круга.
- квадратные миллиметры — мм2,
- квадратные сантиметры — см2,
- квадратные метры — м2,
- квадратные километры — км2,
- квадратные единицы длины — ед2.
Площадь круга через его диаметр
Определить площадь любого заданного круга через его диаметр можно по формуле:
Эта формула звучит так: «Площадь круга через его диаметр равна произведению числа пи на диаметр круга в квадрате, деленному на 4». Эта формула получается из формулы после замены радиуса на диаметр (радиус круга — это половина его диаметра). Получаем . Если вы знаете диаметр круга, то вы можете вычислить площадь этого круга с помощью нашего калькулятора, в котором тоже используется эта же формула.
Площадь любого круга через диаметр
Введите диаметр круга:
Площадь определяемого круга:
Площадь полученного круга в π:
Кстати, сравните — определение площади любого круга через его радиус и через его диаметр должны совпадать. Потому что независимо от того, через что именно (радиус или диаметр) вы определяете площадь, это все тот же круг и все та же площадь.
Потому что независимо от того, через что именно (радиус или диаметр) вы определяете площадь, это все тот же круг и все та же площадь.
Площадь любого круга можно еще определить, если известна длина окружности — границы круга.
Определение площади круга через его длину окружности
Так как длина окружности , то определяя радиус и подставляя в начальную формулу площади круга , получим: . Формула читается так: «площадь равна отношению квадрата длины окружности круга к произведению 4 и пи».
Формула площади круга через длину окружности
Площадь круга равна отношению квадрата длины окружности к четырем пи:
Вы можете определить площадь круга через длину его окружности с помощью нашего онлайн-калькулятора. Нужно лишь ввести длину окружности круга.
Найти площадь круга через длину окружности
Введите длину окружности круга:
Площадь данного круга:
Площадь данного круга в π:
Онлайн калькуляторы площади круга дают результат с точностью до 15-го знака после запятой. При этом число берется равным 3,14.
При этом число берется равным 3,14.
Вы получается значение площади в абсолютных единицах. Если вы ввели радиус (диаметр, длину окружности) в метрах (сантиметрах, дециметрах, единицах), то площадь вы получите в таких же квадратных единицах. Конвертации единиц измерения калькулятор не делает, поэтому внимательно смотрите, в каких единицах вам нужно получить результат, и вводите исходные данные в этих же единицах.
Например, нужно определить площадь круга в квадратных метрах, а радиус дан в сантиметрах. Тогда вам нужно сначала перевести сантиметры в метры — умножив число в сантиметрах на 0,01 (или разделив на 100, так как в метре 100 см).
Пусть дан радиус круга 40 см, площадь круга вы хотите получить в м2. Тогда радиус надо перевести в метры: . Именно это число надо ввести в калькулятор для определения площади круга по его радиусу.
Как определяли площадь круга в древности
Уже издавна люди, разделяя шар сечениями на части, обнаружили, что круг — это сечение шара. Сечение, которые проходит через центр шара. Граница круга — множество точек, равноудаленных от одной точки. Известно, что площадь круга была известна еще Архимеду. В его трудах было найдено определение площади круга через предел.
Сечение, которые проходит через центр шара. Граница круга — множество точек, равноудаленных от одной точки. Известно, что площадь круга была известна еще Архимеду. В его трудах было найдено определение площади круга через предел.
Среди работ Архимеда три посвящены геометрии на плоскости. В работе «Измерение окружности» Архимед эффективно использовал концепцию приближения, предложенную Евклидом. Он предложил вписать в круг многоугольник. Чем больше многоугольник можно вписать в круг, тем точнее будет значение площадь круга. Сначала Архимед использовал шестиугольники, а затем последовательно удваивал количество сторон.
Когда Архимед получил девяностошестиугольник, он получил оценочное значение числа пи между 3,14163 и 3,14286.
Пи – это отношение длины окружности к ее диаметру.
Кроме того, он подсчитал, что площадь поверхности шара в четыре раза больше площади наибольшего вписанного в него круга. Он изобрел метод нахождения площади круга, метод нахождения площади шара и метод нахождения объема шара
Сейчас мы находим площадь разного рода кругов используя ту самую формулу, которую открыл Архимед.
Изучение темы «Площадь круга» проходят в школьном курсе геометрии. Формула определения площади через радиус круга является важной в геометрии. Она также часто используется и в химии, и в физике.
В дальнейшем помимо площади круга, можно определять площадь сегмента круга, площадь сектора круга.
Как рассчитать длину окружности по формулам через диаметр, равный двум радиусам
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты, устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
…
Оглавление:
- Характеристики фигуры
- Основные термины окружности
- Основные формулы для вычислений
- Диаметр в формулах вычисления
- Расчёты по радиусу
- Подручные способы вычисления
- Круглые предметы в истории человеческой жизни
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
Это интересно: как переводить градусы в радианы?
В пределах окружности имеются точки Х такие, что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда. Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками, проходящее через центр фигуры.
Диаметр — расстояние между точками, проходящее через центр фигуры.
Это интересно: какой четырёхугольник называется квадратом?
Основные формулы для вычислений
Параметры используются в формулах вычислений величин окружности:
- длину фигуры вычисляют умножением диаметра на число π и записывают таким образом: C = π*D.
- Величина диаметра в два раза превышает длину радиуса. Иной способ вычисления радиуса — необходимо разделить длину круга на удвоенное π: R = C/(2* π) = D/2.
- Диаметр рассчитывается с помощью радиуса или делением длины окружности на число π. Формула нахождения диаметра: D = C/π = 2*R.
- Площадь круга, ограниченного окружностью, можно найти двумя способами: через радиус или диаметр. По формуле площадь равна четвёртой части произведения числа π и диаметра в квадрате или радиусу в квадрате, умноженному на π: S = π*R2 = π*D2/4.
Это интересно: что такое горизонтально, что означает слово горизонталь?
Диаметр в формулах вычисления
В экономике и математике нередко появляется необходимость поиска длины окружности.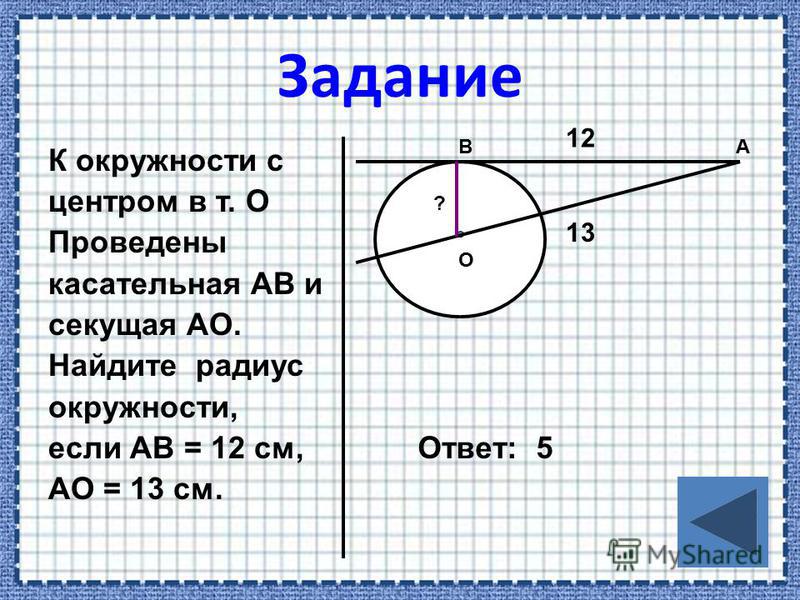 Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Расчёты по радиусу
Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?
А как вырезать бумажный круг подходящего размера?
Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Это интересно: формулировка и доказательство признаков параллелограмма.
Подручные способы вычисления
Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:
- При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
- Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
- Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.

Круглые предметы в истории человеческой жизни
Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Форму колеса имеет гончарный круг, большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
Радиус — что это такое и как найти радиус окружности
Обновлено 22 июля 2021 Просмотров: 125 583 Автор: Дмитрий ПетровЗдравствуйте, уважаемые читатели блога KtoNaNovenkogo. ru.
ru.
Сегодня мы продолжим знакомить вас с различными математическими терминами. И расскажем, что такое РАДИУС.
На самом деле эту тему проходят еще в начальных классах обычной школы. И все, кто хорошо учился, сразу смогут сказать, о чем идет речь. Ну, или хотя бы точно понять, что РАДИУС как-то связан с окружностью.
Что такое радиус
И действительно:
Радиус – это отрезок, который начинается в центре окружности и заканчивается в любой точке ее поверхности. В то же время так называется и длина этого отрезка.
Вот так это выглядит графически.
Само слово РАДИУС имеет латинские корни. Оно произошло от «radius», что можно перевести как «луч» или «спица колеса». Впервые этот математический термин ввел французский ученый П.Ромус. Было это в 1569 году.
Но потребовалось чуть более ста лет, чтобы слово РАДИУС прижилось и стало общепринятым.
Кстати, есть еще несколько значений слова РАДИУС:
- Размер охвата чего-нибудь или сфера распространения.
 Например, говорят «Огонь уничтожил все в радиусе 10 километров» или «ОН показал на карте радиус действия артиллерии»;
Например, говорят «Огонь уничтожил все в радиусе 10 километров» или «ОН показал на карте радиус действия артиллерии»; - В анатомии этим словом обозначают Лучевую кость предплечья.
Но, конечно, нас интересует РАДИУС как математический термин. А потому и продолжим говорить именно о нем.
Радиус и диаметр
Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.
А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:
Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.
Обозначается диаметр также первой буквой своего слова – D или d.
Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.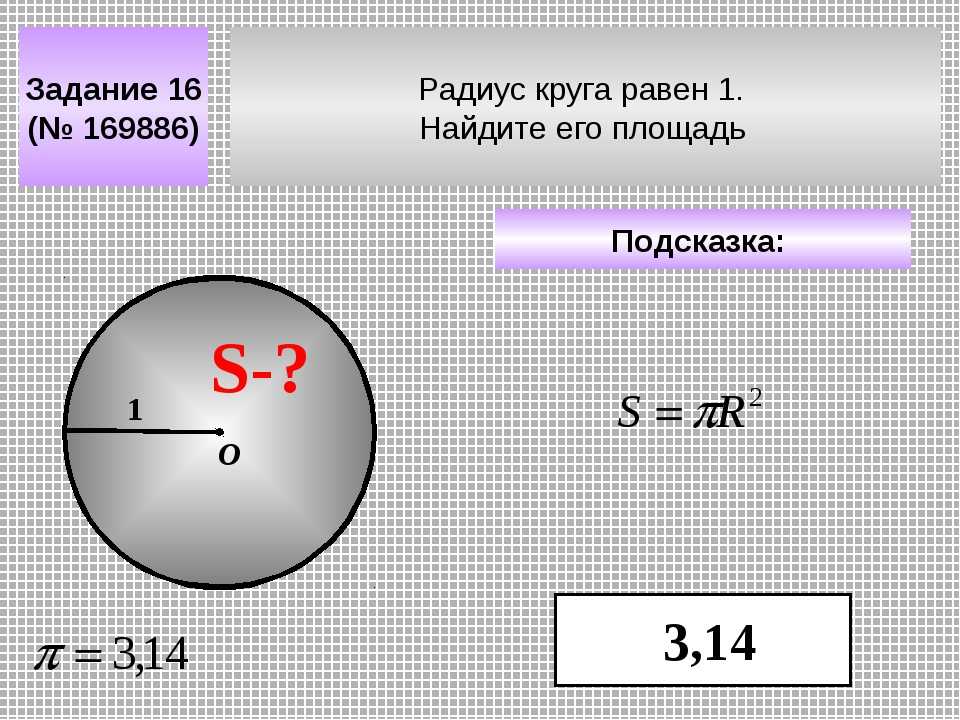
А именно:
Длина диаметра равна удвоенной длине радиуса.
Свойства радиуса
В отношении радиуса действуют несколько важных правил:
- Радиус составляет половину диаметра. Это мы продемонстрировали только что.
- У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.
- Если в точке пересечения радиуса с поверхностью окружности провести касательную, то эти две линии будут пересекаться под прямым углом. Доказательство этой теоремы наглядно приводится на следующем рисунке.
Радиус, который перпендикулярен хорде, делит ее на две равные части.
Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.

Длина и площадь окружности через радиус
Об этих математических величинах мы решили рассказать не случайно. Дело в том, что при их вычислении просто необходимо знать значение радиуса. И наоборот, зная длину окружности или ее площадь, можно найти радиус.
Длина окружности
Длина окружности – это кривая, которая состоит из точек, равноудаленных от центра окружности. Проще говоря, это длина поверхности окружности.
Длина окружности одновременно является и ее периметром, а потому в геометрии она обозначается латинской буквой «Р» (иногда встречаются и «L», и «C»). А формула для ее вычисления выглядит следующим образом:
Иногда ее пишут и как P=πD, так как 2R – это удвоенный радиус, что, как мы уже сказали выше, является диаметром. Но классическая формула во всех учебниках дается все-таки через радиус.
Гораздо интереснее здесь рассмотреть величину, обозначаемую буквой π. Это как многим известно, математическая постоянная. Она произносится как «Пи» и равна 3,14.
Хотя на самом деле количество знаков после запятой у «пи» не ограничено. Но для простоты вычислений решено брать именно так.
Площадь окружности
Площадь окружности – это пространство, которое находится внутри ее периметра. Она обозначается латинской буквой «S». А формула для ее вычисления выглядит так:
Опять же, здесь R- это радиус, а π – математическая постоянная, равная 3,14.
Вместо заключения
Чтобы еще больше понять, насколько важно понятие РАДИУС, вспомните инструмент, с помощью которого можно начертить окружность. Это циркуль и выглядит он вот так.
Пользоваться им просто. Ножка с острым концом ставится в центр будущей окружности.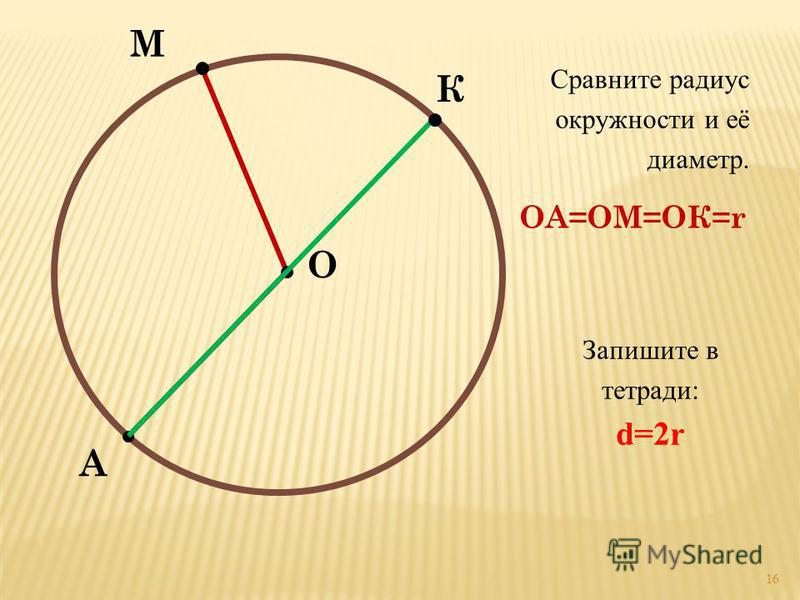 А ножка с грифелем прочерчивает линию. А расстояние, на котором они будут друг от друга, и есть РАДИУС.
А ножка с грифелем прочерчивает линию. А расстояние, на котором они будут друг от друга, и есть РАДИУС.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
- Математика
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva. Поделиться:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Поиск в инженерном справочнике DPVA. Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
 Free xml sitemap generator
Free xml sitemap generatorУзнать диаметр по длине окружности
Главная » Разное » Узнать диаметр по длине окружности
Диаметр окружности круга • как найти ⬅️ формула
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.
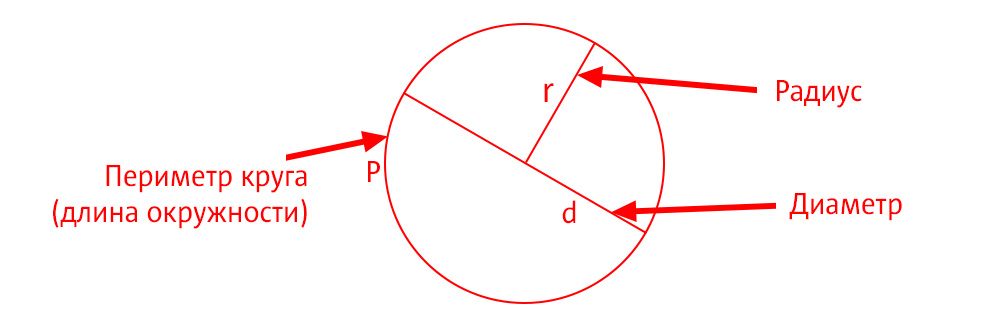
Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Как узнать диаметр.
 Формулы
ФормулыВ данной теме нам предстоит узнать три формулы:
1. Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
2. Если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
3. Если есть чертеж окружности
Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
Отметить точки пересечения прямой и окружности.
Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.
Провести прямую через две точки, в которых произошло пересечение.
 Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.Теперь осталось измерить диаметр круга при помощи линейки. Получилось!
Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.
Как рассчитать диаметр зная длину окружности. Площадь круга
Возьмем циркуль. Установим ножку циркуля с иглой в точку «O », а ножку циркуля с карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую линию. Такую замкнутую линию называют — окружность .
Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π (читается как «Пи»), которое так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Запомните!
Отношение длины окружности к её диаметру является одинаковым для всех окружностей и обозначается греческой буквой π («Пи»).
π ≈ 3,14…
Число «Пи» относится к числам, точное значение которых записать невозможно ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам для наших вычислений достаточно использовать значение π ,
округленное до разряда сотых π ≈ 3,14…
Теперь, зная, что такое число π , мы можем записать формулу длины окружности.
Запомните!
Длина окружности — это произведение числа π и диаметра окружности. Длина окружности обозначается буквой «С » (читается как «Це»).
C = π D
C = 2π R , так как D = 2R
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Виленкин 6 класс. Номер 831
Условие задачи:
Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2π R ≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.
Виленкин 6 класс. Номер 835
Условие задачи:
Определите диаметр окружности, если её длина равна 56,52 дм. (π ≈ 3,14 ).
Выразим из формулы длины окружности диаметр.
C = π D
D = С / π
D = 56,52 / 3,14 = 18 дм
Хорда и дуга окружности
На рисунке ниже отметим на окружности две точки «A » и «B ». Эти точки делят окружность на две части, каждую из которых называют дугой . Это синяя дуга «AB » и черная дуга «AB ». Точки «A » и «B » называют концами дуг .
И круг — геометрические фигуры, взаимосвязанные между собой. есть граничная ломаная линия (кривая) круга ,
Определение. Окружность — замкнутая кривая, каждая точка которой равноудалена от точки, называемой центром окружности.
Для построения окружности выбирается произвольная точка О, принятая за центр окружности, и с помощью циркуля проводится замкнутая линия.
Если точку О центра окружности соединить с произвольными точками на окружности, то все полученные отрезки будут между собой равны, и называются такие отрезки радиусами, сокращенно обозначаются латинской маленькой или большой буквой «эр» (r или R ). Радиусов в окружности можно провести столько же, сколько точек имеет длина окружности.
Радиусов в окружности можно провести столько же, сколько точек имеет длина окружности.
Отрезок, соединяющий две точки окружности и проходящий через ее центр, называется диаметром. Диаметр состоит из двух радиусов , лежащих на одной прямой. Диаметр обозначается латинской маленькой или большой буквой «дэ» ( d или D ).
Правило. Диаметр окружности равен двум ее радиусам .
d = 2r
D = 2R
Длина окружности вычисляется по формуле и зависит от радиуса (диаметра) окружности. В формуле присутствует число ¶, которое показывает во сколько раз длина окружности больше, чем ее диаметр. Число ¶ имеет бесконечное число знаков после запятой. Для вычислений принято ¶ = 3,14.
Длина окружности обозначается латинской большой буквой «цэ» (C ). Длина окружности пропорциональна ее диаметру. Формулы для расчета длины окружности по ее радиусу и диаметру:
C = ¶d
C = 2¶r
- Примеры
- Дано: d = 100 см.
- Длина окружности: C = 3,14 * 100 см = 314 см
- Дано: d = 25 мм.

- Длина окружности: С = 2 * 3,14 * 25 = 157 мм
Секущая окружности и дуга окружности
Всякая секущая (прямая линия) пересекает окружность в двух точках и делит ее на две дуги. Величина дуги окружности зависит от расстояния между центром и секущей и измеряется по замкнутой кривой от первой точки пересечения секущей с окружностью до второй.
Дуги окружности делятся секущей на большую и малую, если секущая не совпадает с диаметром, и на две равные дуги, если секущая проходит по диаметру окружности.
Если секущая проходит через центр окружности, то ее отрезок, расположенный между точками пересечения с окружностью, есть диаметр окружности, или самая большая хорда окружности.
Чем дальше секущая расположена от центра окружности, тем меньше градусная мера меньшей дуги окружности и больше — большей дуги окружности, а отрезок секущей, называемый хордой , уменьшается по мере удаления секущей от центра окружности.
Определение. Кругом называется часть плоскости, лежащая внутри окружности.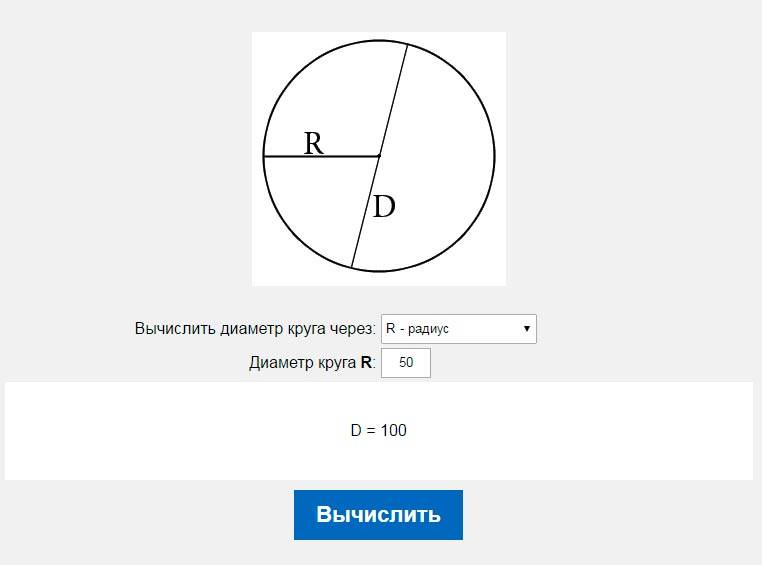
Центр, радиус, диаметр окружности являются одновременно центром, радиусом и диаметром соответствующего круга.
Так как круг — это часть плоскости, то одним из его параметров является площадь.
Правило. Площадь круга (S ) равна произведению квадрата радиуса (r 2 ) на число ¶.
- Примеры
- Дано: r = 100 см
- Площадь круга:
- S = 3,14 * 100 см * 100 см = 31 400 см 2 ≈ 3м 2
- Дано: d = 50 мм
- Площадь круга:
- S = ¼ * 3,14 * 50 мм * 50 мм = 1 963 мм 2 ≈ 20 см 2
Если в круге провести два радиуса к разным точкам окружности, то образуется две части круга, которые называется секторами . Если в круге провести хорду, то часть плоскости между дугой и хордой называется сегментом окружности .
§ 117. Длина окружности и площадь круга.
1. Длина окружности. Окружностью называется замкнутая плоская кривая линия, все точки которой находятся на равном расстоянии от одной точки (О), называемой центром окружности (рис. 27).
27).
Окружность вычерчивается с помощью циркуля. Для этого острую ножку циркуля ставят в центр, а другую (с карандашом) вращают вокруг первой до тех пор, пока конец карандаша не вычертит полной окружности. Расстояние от центра до любой точки окружности называется её радиусом. Из определения следует, что все радиусы одной окружности равны между собой.
Отрезок прямой линии (АВ), соединяющий две любые точки окружности и проходящий через её центр, называется диаметром . Все диаметры одной окружности равны между собой; диаметр равен двум радиусам.
Как найти длину окружности? Практически в некоторых случаях длину окружности можно найти путём непосредственного измерения. Это можно сделать, например, при измерении окружности сравнительно небольших предметов (ведро, стакан и т. п.). Для этого можно воспользоваться рулеткой, тесьмой или шнуром.
В математике применяется приём косвенного определения длины окружности. Он состоит в вычислении по готовой формуле, которую мы сейчас выведем.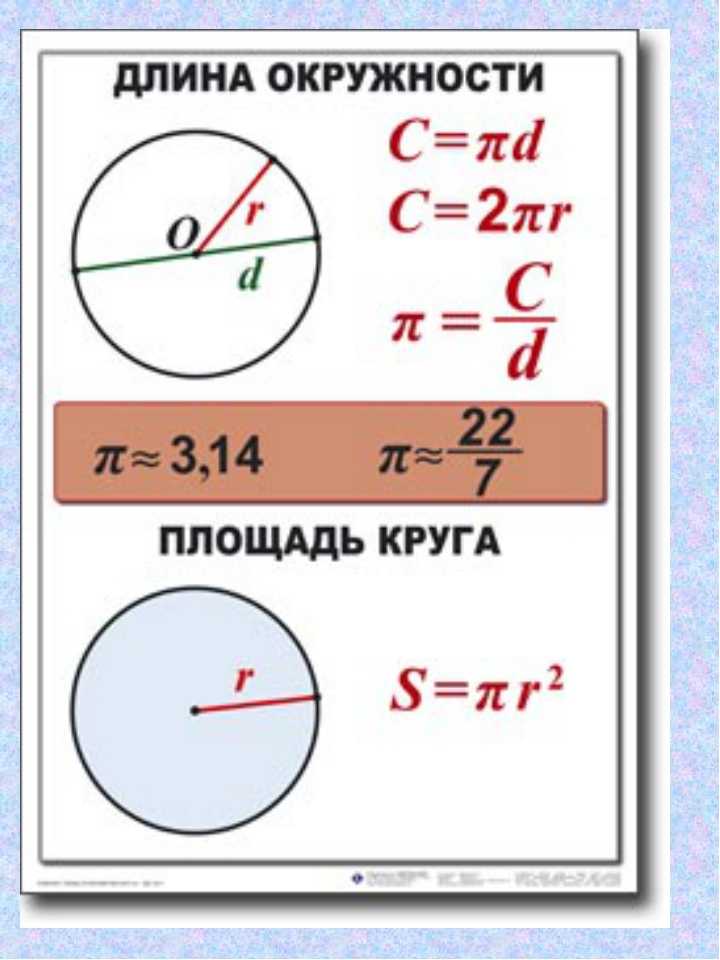
Если мы возьмём несколько больших и малых круглых предметов (монета, стакан, ведро, бочка и т. д.) и измерим у каждого из них длину окружности и длину диаметра, то получим для каждого предмета два числа (одно, измеряющее длину окружности, и другое — длину диаметра). Естественно, что для малых предметов эти числа будут небольшими, а для крупных — большими.
Однако если мы в каждом из этих случаев возьмём отношение полученных двух чисел (длины окружности и диаметра), то при тщательном выполнении измерения найдём почти одно и то же число. Обозначим длину окружности буквой С , длину диаметра буквой D , тогда отношение их будет иметь вид С: D . Фактические измерения всегда сопровождаются неизбежными неточностями. Но, выполнив указанный опыт и произведя необходимые вычисления, мы получим для отношения С: D примерно следующие числа: 3,13; 3,14; 3,15. Эти числа очень мало отличаются одно от другого.
В математике путём теоретических соображений установлено, что искомое отношение С: D никогда не меняется и оно равно бесконечной непериодической дроби, приближённое значение которой с точностью до десятитысячных долей равно 3,1416 . Это значит, что всякая окружность длиннее своего диаметра в одно и то же число раз. Это число принято обозначать греческой буквой π (пи). Тогда отношение длины окружности к диаметру запишется так: С: D = π . Мы будем ограничивать это число только сотыми долями, т. е. брать π = 3,14.
Это значит, что всякая окружность длиннее своего диаметра в одно и то же число раз. Это число принято обозначать греческой буквой π (пи). Тогда отношение длины окружности к диаметру запишется так: С: D = π . Мы будем ограничивать это число только сотыми долями, т. е. брать π = 3,14.
Напишем формулу для определения длины окружности.
Так как С: D = π , то
C = πD
т. е. длина окружности равна произведению числа π на диаметр.
Задача 1. Найти длину окружности (С ) круглой комнаты, если диаметр её D = 5,5 м.
Принимая во внимание изложенное выше, мы должны для решения этой задачи увеличить диаметр в 3,14 раза:
5,5 3,14 = 17,27 {м).
Задача 2. Найти радиус колеса, у которого длина окружности 125,6 см.
Эта задача обратна предыдущей. Найдём диаметр колеса:
125,6: 3,14 = 40 (см).
Найдём теперь радиус колеса:
40: 2 = 20 (см).
2. Площадь круга. Чтобы определить площадь круга, можно было бы начертить на бумаге круг данного радиуса, покрыть его прозрачной клетчатой бумагой и потом сосчитать клетки, находящиеся внутри окружности (рис. 28).
Но такой способ неудобен по многим причинам. Во-первых, вблизи контура круга получается ряд неполных клеток, о величине которых судить трудно. Во-вторых, нельзя покрыть листом бумаги большой предмет (круглую клумбу, бассейн, фонтан и др.). В-третьих, подсчитав клетки, мы всё-таки не получаем никакого правила, позволяющего нам решать другую подобную задачу. В силу этого поступим иначе. Сравним круг с какой-нибудь знакомой нам фигурой и сделаем это следующим образом: вырежем круг из бумаги, разрежем его сначала по диаметру пополам, затем каждую половину разрежем ещё пополам, каждую четверть — ещё пополам и т. д., пока не разрежем круг, например, на 32 части, имеющие форму зубцов (рис. 29).
Затем сложим их так, как показано на рисунке 30, т. е. сначала расположим 16 зубцов в виде пилы, а затем в образовавшиеся отверстия вложим 15 зубцов и, наконец, последний оставшийся зубец разрежем по радиусу пополам и приложим одну часть слева, другую — справа. Тогда получится фигура, напоминающая прямоугольник.
е. сначала расположим 16 зубцов в виде пилы, а затем в образовавшиеся отверстия вложим 15 зубцов и, наконец, последний оставшийся зубец разрежем по радиусу пополам и приложим одну часть слева, другую — справа. Тогда получится фигура, напоминающая прямоугольник.
Длина этой фигуры (основание) равна приблизительно длине полуокружности, а высота — приблизительно радиусу. Тогда площадь такой фигуры можно найти путём умножения чисел, выражающих длину полуокружности и длину радиуса. Если обозначим площадь круга буквой S , длину окружности буквой С , радиус буквой r , то можем записать формулу для определения площади круга:
которая читается так: площадь круга равна длине полуокружности, умноженной на радиус.
Задача. Найти площадь круга, радиус которого равен 4 см. Найдём сначала длину окружности, потом длину полуокружности, а затем умножим её на радиус.
1) Длина окружности С = π D = 3,14 8 = 25,12 (см).
2) Длина половины окружности C / 2 = 25,12: 2= 12,56 (см).
3) Площадь круга S = C / 2 r = 12,56 4 = 50,24 (кв. см).
§ 118. Поверхность и объём цилиндра.
Задача 1. Найти полную поверхность цилиндра, у которого диаметр основания 20,6 см и высота 30,5 см.
Форму цилиндра (рис. 31) имеют: ведро, стакан (не гранёный), кастрюля и множество других предметов.
Полная поверхность цилиндра (как и полная поверхность прямоугольного параллелепипеда) состоит из боковой поверхности и площадей двух оснований (рис. 32).
Чтобы наглядно представить себе, о чём идёт речь, необходимо аккуратно сделать модель цилиндра из бумаги. Если мы от этой модели отнимем два основания, т. е. два круга, а боковую поверхность разрежем вдоль и развернём, то будет совершенно ясно, как нужно вычислять полную поверхность цилиндра. Боковая поверхность развернётся в прямоугольник, основание которого равно длине окружности. Поэтому решение задачи будет иметь вид:
1) Длина окружности: 20,6 3,14 = 64,684 (см).
2) Площадь боковой поверхности: 64,684 30,5= 1972,862(кв.см).
3) Площадь одного основания: 32,342 10,3 = 333,1226 (кв.см).
4) Полная поверхность цилиндра:
1972,862 + 333,1226 + 333,1226 = 2639,1072 (кв. см) ≈ 2639 (кв. см).
Задача 2. Найти объём железной бочки, имеющей форму цилиндра с размерами: диаметр основания 60 см и высота 110 см.
Чтобы вычислить объём цилиндра, нужно припомнить, как мы вычисляли объём прямоугольного параллелепипеда (полезно прочитать § 61).
Единицей измерения объёма у нас будет кубический сантиметр. Сначала надо узнать, сколько кубических сантиметров можно расположить на площади основания, а затем найденное число умножить на высоту.
Чтобы узнать, сколько кубических сантиметров можно уложить на площади основания, надо вычислить площадь основания цилиндра. Так как основанием служит круг, то нужно найти площадь круга. Затем для определения объёма умножить её на высоту. Решение задачи имеет вид:
1) Длина окружности: 60 3,14 = 188,4 (см).
2) Площадь круга: 94,2 30 = 2826 (кв. см).
3) Объём цилиндра: 2826 110 = 310 860 (куб. см).
Ответ. Объём бочки 310,86 куб. дм.
Если обозначим объём цилиндра буквой V , площадь основания S , высоту цилиндра H , то можно написать формулу для определения объёма цилиндра:
V = S H
которая читается так: объём цилиндра равен площади основания, умноженной на высоту.
§ 119. Таблицы для вычисления длины окружности по диаметру.
При решении различных производственных задач часто приходится вычислять длину окружности. Представим себе рабочего, который изготовляет круглые детали по указанным ему диаметрам. Он должен всякий раз, зная диаметр, вычислить длину окружности. Чтобы сэкономить время и застраховать себя от ошибок, он обращается к готовым таблицам, в которых указаны диаметры и соответствующие им длины окружностей.
Приведём небольшую часть таких таблиц и расскажем, как ими пользоваться.
Пусть известно, что диаметр окружности равен 5 м. Ищем в таблице в вертикальном столбце под буквой D число 5. Это длина диаметра. Рядом с этим числом (вправо, в столбце под названием «Длина окружности») увидим число 15,708 (м). Совершенно так же найдём, что если D = 10 см, то длина окружности равна 31,416 см.
Ищем в таблице в вертикальном столбце под буквой D число 5. Это длина диаметра. Рядом с этим числом (вправо, в столбце под названием «Длина окружности») увидим число 15,708 (м). Совершенно так же найдём, что если D = 10 см, то длина окружности равна 31,416 см.
По этим же таблицам можно производить и обратные вычисления. Если известна длина окружности, то можно найти в таблице соответствующий ей диаметр. Пусть длина окружности равна приблизительно 34,56 см. Найдём в таблице число, наиболее близкое к данному. Таковым будет 34,558 (разница 0,002). Соответствующий такой длине окружности диаметр равен приблизительно 11 см.
Таблицы, о которых здесь сказано, имеются в различных справочниках. В частности, их можно найти в книжке «Четырёхзначные математические таблицы» В. М. Брадиса. и в задачнике по арифметике С. А. Пономарёва и Н. И. Сырнева.
Окружность — замкнутая кривая, все точки которой находятся на одинаковом расстоянии от центра. Эта фигура является плоской. Поэтому решение задачи, вопрос которой состоит в том, как найти длину окружности, является достаточно простым. Все имеющиеся способы, мы рассмотрим в сегодняшней статье.
Поэтому решение задачи, вопрос которой состоит в том, как найти длину окружности, является достаточно простым. Все имеющиеся способы, мы рассмотрим в сегодняшней статье.
Описания фигуры
Кроме достаточно простого описательного определения существуют еще три математических характеристики окружности, которые уже сами по себе содержат ответ на вопрос, как найти длину окружности:
- Состоит из точек A и B и всех других, из которых AB можно увидеть под прямым углом. Диаметр данной фигуры равен длине рассматриваемого отрезка.
- Включает исключительно такие точки X, что отношение AX/BX неизменно и не равно единице. Если это условие не соблюдается, то это не окружность.
- Состоит из точек, для каждой из которых выполняется следующее равенство: сумма квадратов расстояний до двух других — это заданная величина, которая всегда больше половине длины отрезка между ними.
Терминология
Не у всех в школе был хороший учитель математики. Поэтому ответ на вопрос, как найти длину окружности, осложняется еще и тем, что не все знают основные геометрические понятия.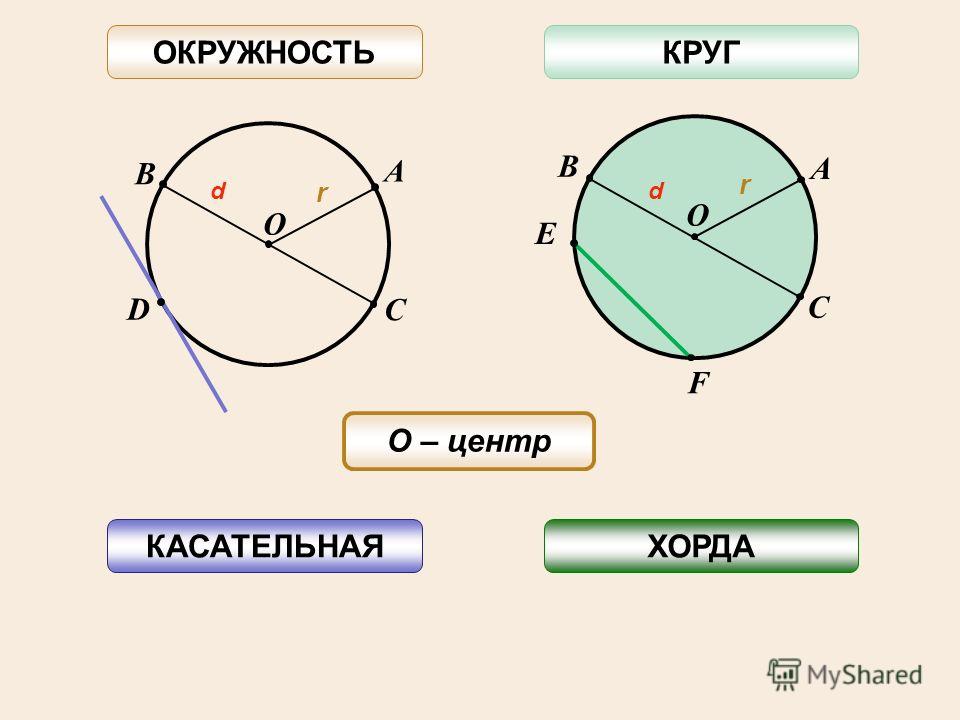 Радиус — отрезок, который соединяет центр фигуры с точкой на кривой. Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Радиус — отрезок, который соединяет центр фигуры с точкой на кривой. Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Основные формулы
Из определений непосредственно следуют геометрические формулы, которые позволяют рассчитать основные характеристики окружности:
- Длина равна произведению числа π и диаметра. Формулу обычно записывают следующим образом: C = π*D.
- Радиус равен половине диаметра. Его также можно рассчитать, вычислив частное от деления длины окружности на удвоенное число π. Формула выглядит так: R = C/(2* π) = D/2.
- Диаметр равен частному от деления длины окружности на π или удвоенному радиусу. Формула является достаточно простой и выглядит так: D = C/π = 2*R.
- Площадь круга равна произведению числа π и квадрата радиуса.
 Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Как найти длину окружности по диаметру
Для простоты объяснения обозначим буквами необходимые для расчета характеристики фигуры. Пусть C — это искомая длина, D — ее диаметр, а число π приблизительно равно 3,14. Если у нас есть всего одна известная величина, то задачу можно считать решенной. Зачем это нужно в жизни? Предположим мы решили обнести круглый бассейн забором. Как вычислить необходимое количество столбиков? И тут на помощь приходит умение, как вычислить длину окружности. Формула выглядит следующим образом: C = π D. В нашем примере диаметр определяется на основе радиуса бассейна и необходимого расстояния до забора. Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него.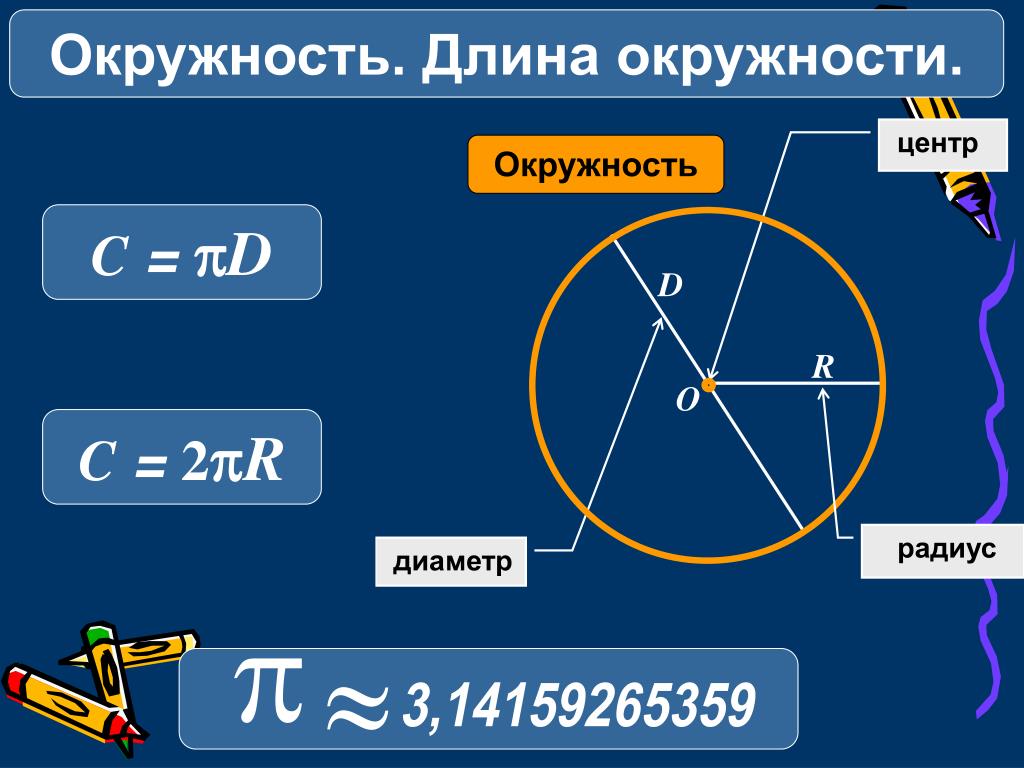 Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Длина через радиус
Как всегда, начнем с присвоения характеристикам окружности букв. На самом деле они являются универсальными, поэтому математикам из разных стран вовсе не обязательно знать язык друг друга. Предположим, что C — это длина окружности, r — ее радиус, а π приблизительно равно 3,14. Формула выглядит в этом случае следующим образом: C = 2*π*r. Очевидно, что это абсолютно правильное равенство. Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка. Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Примеры задач
Мы уже рассмотрели несколько практических случаев полученных знаний о том, как узнать длину окружности. Но зачастую нас заботят не они, а реальные математические задачи, которые содержатся в учебнике. Ведь за них учитель выставляет баллы! Поэтому давайте рассмотрим задачу повышенной сложности. Предположим, что длина окружности составляет 26 см. Как найти радиус такой фигуры?
Решение примера
Для начала запишем, что нам дано: C = 26 см, π = 3,14. Также вспомним формулу: C = 2* π*R. Из нее можно извлечь радиус окружности. Таким образом, R= C/2/π. Теперь приступим к непосредственному расчету. Сначала делим длину на два. Получаем 13. Теперь нужно разделить на значение числа π: 13/3,14 = 4,14 см. Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
И как бы досадно ни было, придется мириться с таким положением вещей.
Не так страшен зверь, как его малюют
Вот мы и разобрались с такой непростой на первый взгляд задачей. Как оказалось, нужно просто понимать значение терминов и запомнить несколько легких формул. Математика — это не так страшно, нужно только приложить немного усилий. Так что геометрия ждет вас!
В процессе выполнения строительных работ в быту или на производстве может появиться необходимость в измерении диаметра трубы, которая уже вмонтирована в систему водоснабжения или канализации. Также знать данный параметр необходимо на стадии проектирования прокладки инженерных коммуникаций.
Отсюда возникает необходимость разобраться с тем, как определить диаметр трубы. Выбор конкретного способа выполнения измерений зависит от размеров объекта и от того, доступно ли расположение трубопровода.
Определение диаметра в бытовых условиях
До того, как замерить диаметр трубы, нужно приготовить следующие инструменты и устройства:
- рулетка или стандартная линейка;
- штангенциркуль;
- фотоаппарат — его задействуют при необходимости.

Если трубопровод доступен для проведения замеров, а торцы труб можно без проблем измерить, тогда достаточно иметь в распоряжении обычную линейку или рулетку. При этом следует учитывать, что используют такой метод, когда к точности предъявляются минимальные требования.
В этом случае выполняют измерение диаметра труб в такой последовательности:
- Подготовленные инструменты прикладывают к месту, где находится самая широкая часть торца изделия.
- Потом отсчитывают количество делений, соответствующих размеру диаметра.
Данный способ позволяет узнавать параметры трубопровода с точностью, составляющую несколько миллиметров.
Для измерения внешнего диаметра труб с небольшим сечением можно задействовать такой инструмент как штангенциркуль:
- Раздвигают его ножки и прикладывают к торцу изделия.
- Затем их нужно сдвинуть так, чтобы они оказались плотно прижатыми к наружной стороне стенок трубы.

- Ориентируясь на шкалу значений приспособления, узнают требуемый параметр.
Этот метод определения диаметра трубы дает довольно точные результаты, до десятых миллиметра.
Когда трубопровод недоступен для обмера и является частью уже функционирующей конструкции водоснабжения или газовой магистрали, поступают следующим образом: штангенциркуль прикладывают к трубе, к ее боковой поверхности. Таким способом обмеряют изделие в тех случаях, если у измерительного приспособления длина ножек превышает половину диаметра трубной продукции.
Нередко в бытовых условиях возникает необходимость узнать, как измерять диаметр трубы, имеющей большое сечение. Существует простой вариант, как это сделать: достаточно знать длину окружности изделия и константу π, равную 3,14.
Сначала при помощи рулетки или куска шнура обмеряют трубу в обхвате. Потом подставляют известные величины в формулу d=l:π, где:
d – определяемый диаметр;
l – длина измеренной окружности.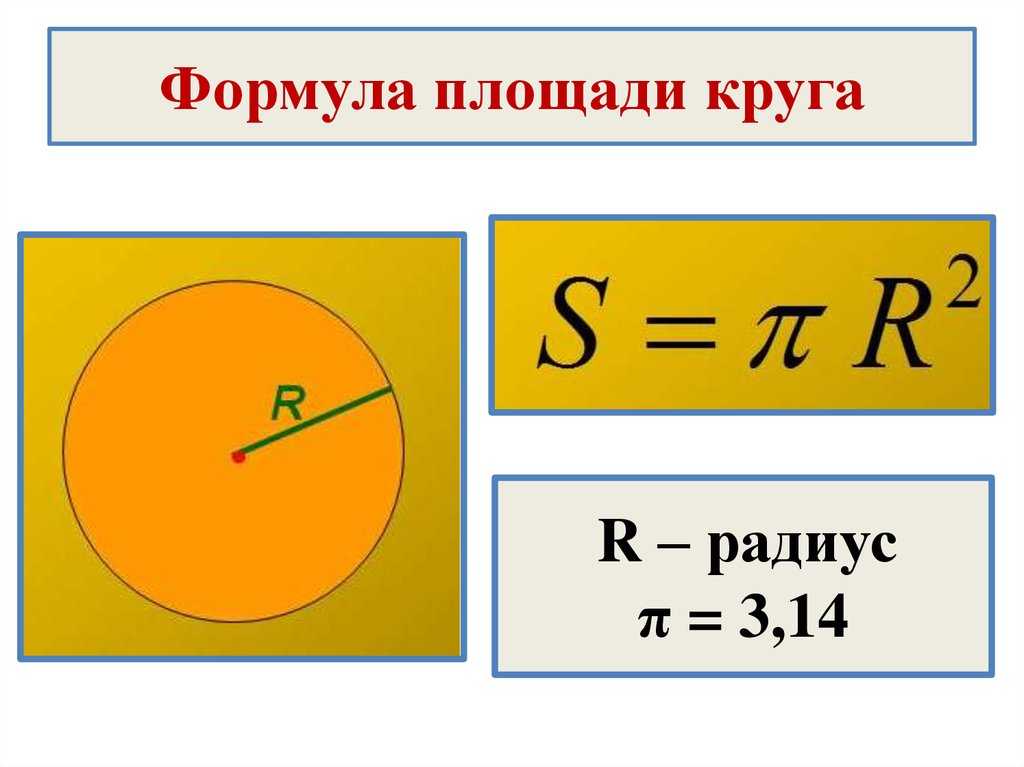
К примеру, обхват трубы составляет 62,8 сантиметра, тогда d = 62,8:3,14 =20 сантиметров или 200 миллиметров.
Бывают ситуации, когда проложенный трубопровод полностью недоступен. Тогда можно применить метод копирования. Суть его заключается в том, что к трубе прикладывают измерительный инструмент или небольшой по размеру предмет, у которого известны параметры.
К примеру, это может быть коробок спичек, длина которого равна 5 сантиметрам. Потом этот участок трубопровода фотографируют. Последующие вычисления выполняют по фотографии. На снимке измеряют видимую толщину изделия в миллиметрах. Потом нужно перевести все полученные величины в реальные параметры трубы с учетом масштаба произведенной фотосъемки.
Измерение диаметров в производственных условиях
На больших строящихся объектах трубы до начала проведения монтажа в обязательном порядке подвергают входному контролю. Прежде всего, проверяют сертификаты и маркировку, нанесенную на трубную продукцию.
Документация должна содержать определенную информацию, касающуюся труб:
- номинальные размеры;
- номер и дата ТУ;
- марка металла или вид пластика;
- номер товарной партии;
- итоги проведенных испытаний;
- хим. анализ выплавки;
- тип термической обработки;
- результаты рентгеновской дефектоскопии.
Кроме этого, на поверхности всех изделий на расстоянии примерно 50 сантиметров от одного из торцов всегда наносят маркировку, содержащую:
- наименование производителя;
- номер плавки;
- номер изделия и его номинальные параметры;
- дату изготовления;
- эквивалент углерода.
Длины труб в производственных условиях определяют мерной проволокой. Также не возникает сложностей с тем, как измерить диаметр трубы рулеткой.
Для изделий первого класса допустимой величиной отклонения в одну или другую сторону от заявленной длины являются 15 миллиметров. Для второго класса –100 миллиметров.
Для второго класса –100 миллиметров.
У труб наружный диаметр сверяют, пользуясь формулой d = l:π-2Δр-0,2 мм, где кроме вышеописанных значений:
Δр – толщина материала рулетки;
0,2 миллиметра– припуск на прилегание инструмента к поверхности.
Допускается отклонение величины внешнего диаметра от заявленной производителем:
- для продукции с сечением не более 200 миллиметров–1,5 миллиметра;
- для больших труб – 0,7%.
В последнем случае для проверки трубной продукции пользуются ультразвуковыми измерительными приборами. Для определения толщины стенок задействуют штангенциркули, у которых деление на шкале соответствует 0,01 миллиметра. Минусовой допуск не должен превышать 5% номинальной толщины. При этом кривизна не может быть более 1,5 миллиметра на 1 погонный метр.
Из вышеописанной информации ясно, что несложно разобраться с тем, как определить диаметр трубы по длине окружности или при помощи несложных измерительных инструментов.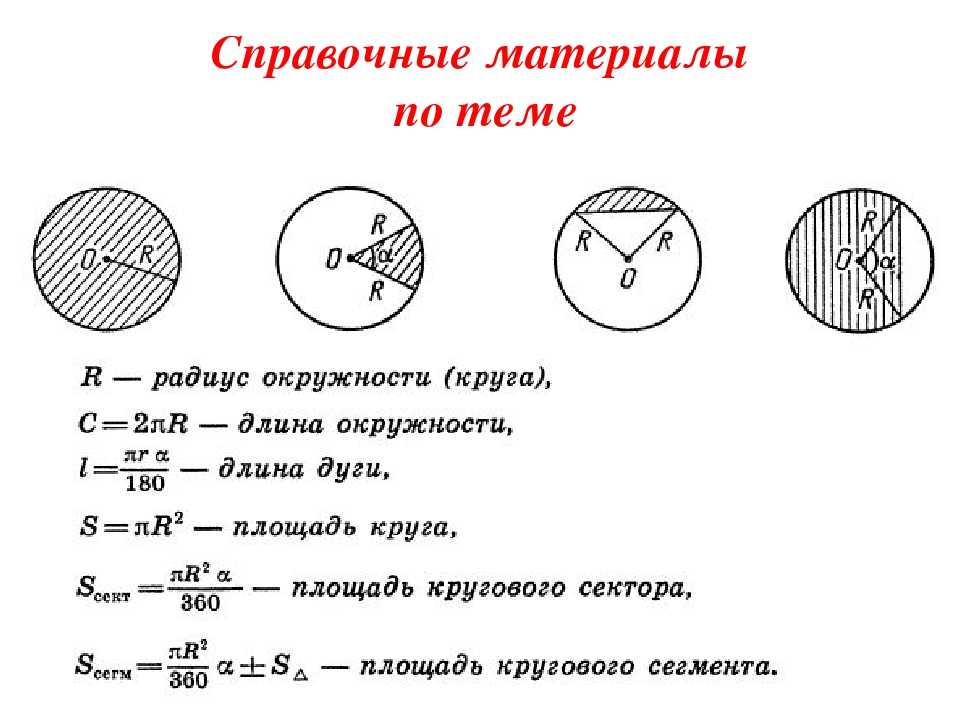
Таблица длины окружности. Как вычислить диаметр окружности: формула и пояснения
И в чем ее отличие от круга. Возьмите ручку или цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, — это окружность. А вот синее содержимое внутри нее — и есть круг.
Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.
Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.
Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.
Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:
К примеру, радиус — 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.
Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить Формула L = 2 Пи * R, где 2 — это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом
Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:
Ответ: диаметр равен 21,98 метрам.
Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:
D = 2 * (S / Пи) * (1 / 2)
S — в данном случае Допустим, в задаче она равна 30 кв. м. Получаем:
м. Получаем:
D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414
При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.
Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:
R = S / p (S — площадь заданного треугольника, а p — периметр, разделенный на 2).
Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.
Нередко находить диаметр окружности приходится и в быту. К примеру, при определении что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
Одной линейкой здесь не обойтись, необходимо знать специальные формулы. Единственное, что от нас потребуется — это определить диаметр или радиус круга. В некоторых задачах эти величины обозначены. Но что делать, если у нас нет ничего, кроме рисунка? Не беда. Диаметр и радиус можно вычислить с помощью обычной линейки. Теперь приступим к самому основному.
Формулы, которые должен знать каждый
Еще в почти 4 000 лет назад, учёные выявили удивительное соотношение: если длину окружности разделить на ее диаметр, то получается одно и то же число, которое равно примерно 3,14. Это значение назвали именно с этой буквы в древнегреческом языке начиналось слово «периметр» и «окружность». На основании того открытия, которое совершили древние ученые, можно рассчитать длину любой окружности:
Где P означает длину (периметр) окружности,
D — диаметр, П — число «Пи».
Длина окружности круга может также быть посчитана через ее радиус (r), который равен половине длины диаметра. Вот и вторая формула, которую нужно запомнить:
Как узнать диаметр окружности?
Представляет собой хорду, которая проходит через центр фигуры. При этом она соединяет две наиболее удалённые точки в круге. Исходя из этого, можно самостоятельно прочертить диаметр (радиус) и измерить его длину с помощью линейки.
Способ 1: вписываем прямоугольный треугольник в круг
Рассчитать длину окружности будет несложно, если мы найдем ее диаметр. Необходимо начертить в круге где гипотенуза будет равна диаметру окружности. Для этого необходимо иметь под рукой линейку и угольник, иначе ничего не получится.
Способ 2: вписываем любой треугольник
На стороне круга отмечаем три любые точки, соединяем их — получаем треугольник. Важно, чтобы центр окружности лежал в области треугольника, это можно сделать на глаз. Проводим к каждой стороне треугольника медианы, точка их пересечения совпадёт с центром окружности.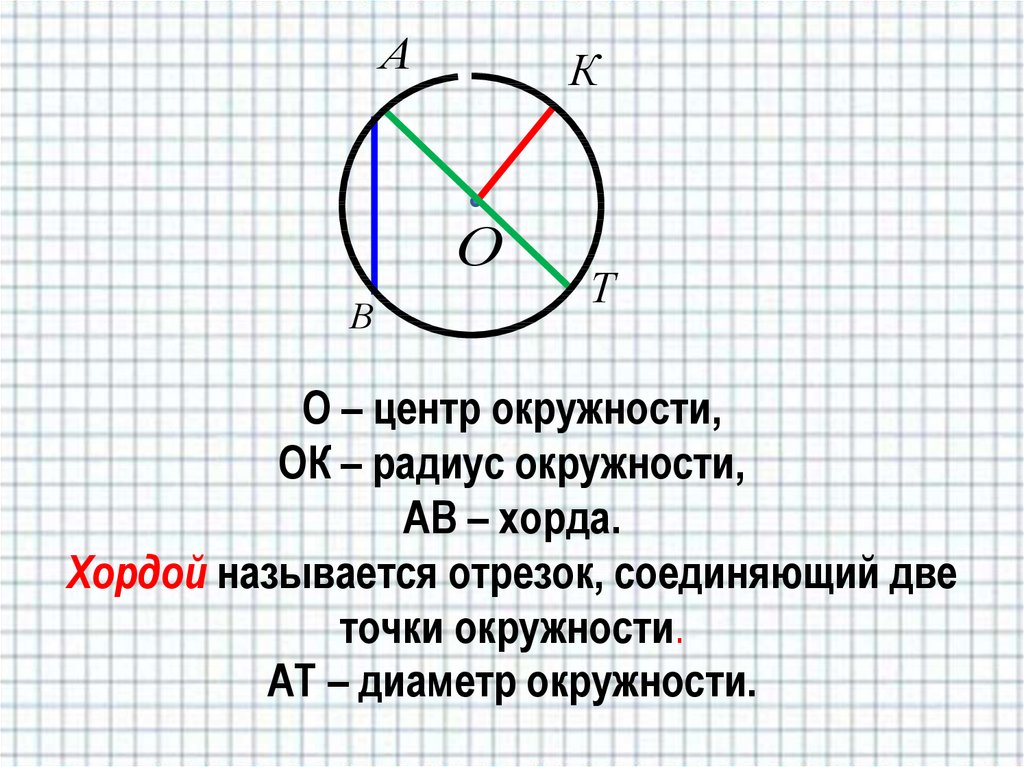 А когда нам известен центр, можно с помощью линейки легко провести диаметр.
А когда нам известен центр, можно с помощью линейки легко провести диаметр.
Данный способ очень похож на первый, но может применяться при отсутствии угольника или в тех случаях, когда нет возможности чертить на фигуре, например на тарелке. Необходимо взять лист бумаги с прямыми углами. Прикладываем лист к кругу так, чтобы одна вершина его угла соприкасалась с краем круга. Далее отмечаем точками места, где стороны бумаги пересекаются с линией окружности. Соединяем эти точки с помощью карандаша и линейки. Если под рукой ничего нет, просто согните бумагу. Эта линия и будет равна длине диаметра.
Пример задачи
- Ищем диаметр с помощью угольника, линейки и карандаша по способу № 1. Предположим, получилось 5 см.
- Зная диаметр, мы легко можем его вставить в нашу формулу: P = d П = 5*3,14 = 15,7В нашем случае получилось около 15,7. Теперь вы без особых проблем сможете объяснить, как рассчитать длину окружности.
Окружность встречается в повседневной жизни не реже, чем прямоугольник. А у многих людей задача о том, как рассчитать длину окружности, вызывает затруднение. И все потому, что у нее нет углов. При их наличии все стало бы намного проще.
А у многих людей задача о том, как рассчитать длину окружности, вызывает затруднение. И все потому, что у нее нет углов. При их наличии все стало бы намного проще.
Что такое окружность и где она встречается?
Эта плоская фигура представляет собой некоторое количество точек, которые расположены на одинаковом удалении от еще одной, которая является центром. Это расстояние называется радиусом.
В повседневной жизни нечасто приходится вычислять длину окружности, кроме людей, которые являются инженерами и конструкторами. Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.
В каждом из этих и других случаях требуется своя точность. Причем высчитать длину окружности совершенно точно оказывается невозможно. Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.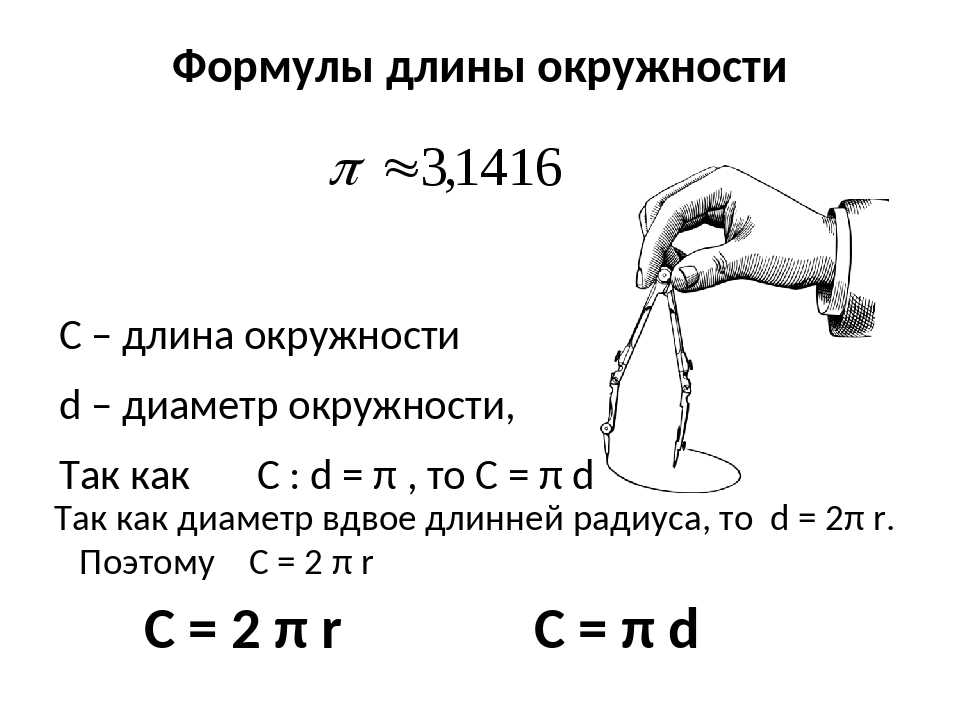
Обозначения величин и формулы
Теперь легко ответить на вопрос о том, как рассчитать длину окружности по радиусу, для этого потребуется такая формула:
Поскольку радиус и диаметр связаны друг с другом, то есть и другая формула для расчетов. Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:
l = π * d.
Как быть, если нужно вычислить периметр круга?
Просто вспомнить, что круг включает в себя все точки внутри окружности. А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.
Кстати, и обозначения у них такие же. Это касается радиуса и диаметра, а периметром является латинская буква P.
Примеры заданий
Задача первая
Условие. Узнать длину окружности, радиус которой равен 5 см.
Решение. Здесь несложно понять, как рассчитать длину окружности. Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение π. 3,14 * 10 = 31,4 (см).
Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение π. 3,14 * 10 = 31,4 (см).
Ответ: l = 31,4 см.
Задача вторая
Условие. Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.
Решение. В этом задании потребуется воспользоваться той же формулой. Но только известную длину нужно будет разделить на произведение 2 и π. Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.
Ответ: r = 200 мм.
Задача третья
Условие. Вычислить диаметр, если известна длина окружности, которая равна 56,52 см.
Решение. Аналогично предыдущей задаче потребуется разделить известную длину на значение π, округленное до сотых. В результате такого действия получается число 18. Результат получен.
Результат получен.
Ответ: d = 18 см.
Задача четвертая
Условие. Стрелки часов имеют длину 3 и 5 см. Нужно вычислить длины окружностей, которые описывают их концы.
Решение. Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.
Для первой длины произведение будет состоять из множителей: 2; 3,14 и 3. Итогом будет число 18,84 см.
Для второго ответа нужно перемножить 2, π и 5. Произведение даст число: 31,4 см.
Ответ: l 1 = 18,84 см, l 2 = 31,4 см.
Задача пятая
Условие. Белка бегает в колесе диаметром 2 м. Какое расстояние она пробегает за один полный оборот колеса?
Решение. Это расстояние равно длине окружности. Поэтому нужно воспользоваться подходящей формулой. А именно перемножить значение π и 2 м. Подсчеты дают результат: 6,28 м.
Ответ: Белка пробегает 6,28 м.
Инструкция
Вспомните, что впервые математически вычислил это соотношение Архимед. Он правильные 96-тиугольники внутри окружности и вокруг нее. Периметр вписанного многоугольника принял за минимально возможную длину окружности, периметр описанной фигуры – за максимальный размер. По Архимеду соотношение длины окружности и диаметра равно 3,1419. Значительно позже это число «удлинил» до восьми знаков китайский математик Цзу Чунчжи. Его вычисления 900 лет оставались наиболее точными. Только в XVIII веке было посчитано сто знаков после запятой. А с 1706 года эта бесконечная десятичная дробь благодаря Уильяму Джонсу приобрела имя. Он обозначил ее первой буквой греческих слов периметр (периферия). Сегодня компьютер легко вычисляет знаков числа Пи: 3,141592653589793238462643…
Он правильные 96-тиугольники внутри окружности и вокруг нее. Периметр вписанного многоугольника принял за минимально возможную длину окружности, периметр описанной фигуры – за максимальный размер. По Архимеду соотношение длины окружности и диаметра равно 3,1419. Значительно позже это число «удлинил» до восьми знаков китайский математик Цзу Чунчжи. Его вычисления 900 лет оставались наиболее точными. Только в XVIII веке было посчитано сто знаков после запятой. А с 1706 года эта бесконечная десятичная дробь благодаря Уильяму Джонсу приобрела имя. Он обозначил ее первой буквой греческих слов периметр (периферия). Сегодня компьютер легко вычисляет знаков числа Пи: 3,141592653589793238462643…
Для расчетов число Пи сократите до 3,14. Получится, что для любой окружности ее длина, деленная на диаметр равна этому числу: L:d=3,14.
Выразите из этого утверждения формулу для нахождения диаметра. Получится, чтобы найти диаметр окружности надо длину окружности поделить на число Пи. Это выглядит так: d = L:3,14. Это универсальный способ найти диаметр, когда у окружности известна ее длина.
Это универсальный способ найти диаметр, когда у окружности известна ее длина.
Итак, известна длина окружности, допустим, 15,7 см, разделите эту цифру на 3,14. Диаметр будет равен 5 см. Запишите это так: d = 15,7: 3,14 = 5 см.
Найдите диаметр по длине окружности, используя специальные таблицы для вычисления длины окружности . Эти таблицы включают в разные справочники. Например, они есть в «Четырехзначные математические таблицы» В.М. Брадиса.
Полезный совет
Запомните первые восемь цифр числа Пи с помощью стихотворения:
Нужно только постараться,
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Источники:
- Число «Пи» рассчитано с рекордной точностью
- диаметр и длина окружности
- Как найти длину окружности?
Круг — это плоская геометрическая фигура, все точки которой находятся на одинаковом и отличном от нуля удалении от выбранной точки, которую называют центром окружности. Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром . Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром . Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
Инструкция
Используйте для нахождения диаметра одно из основных свойств окружности, которое заключается в том, что соотношение длины ее периметра к диаметру одинаково для абсолютно всех окружностей. Конечно, постоянство не осталось не отмеченным математиками, и эта пропорция давно уже получила собственное — это число Пи (π — первая греческих слов «окружность » и «периметр»). Числовое этой определяется длиной окружности, у которой диаметр равен единице.
Делите известную длину окружности на число Пи, чтобы вычислить ее диаметр. Так как это число является « », то не имеет конечного значения — это дробь. Округляйте число Пи в соответствии с точностью результата, которую вам необходимо получить.
Видео по теме
Удивительное свойство окружности открыл нам древнегреческий ученый Архимед. Оно заключается в том, что отношение ее длины к длине диаметра одинаково для любой окружности . В своем труде «Об измерении круга» он вычислил его и обозначил числом «Пи». Оно иррационально, то есть его значение не может быть точно выражено. Для используется его величина, равная 3,14. Вы можете сами проверить утверждение Архимеда, сделав простые вычисления.
Вам понадобится
- — циркуль;
- — линейка;
- — карандаш;
- — нитка.
Инструкция
Начертите на бумаге циркулем окружность произвольного диаметра. Проведите с помощью линейки и карандаша через ее центр отрезок, соединяющий две , находящиеся на линии окружности . Линейкой измерьте длину получившегося отрезка. Допустим, окружности в данном случае 7 сантиметрам.
Возьмите нитку и расположите ее по длине окружности . Измерьте получившуюся длину нитки.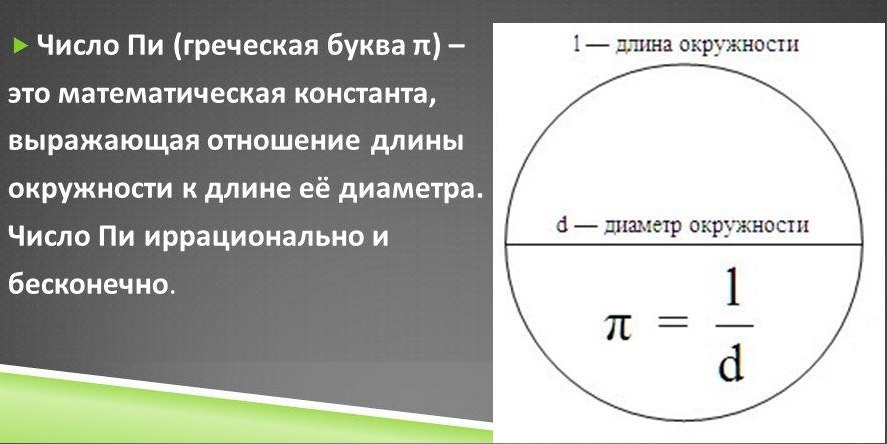 Пусть она будет равна 22 сантиметрам. Найдите отношение длины окружности к длине ее диаметра — 22 см: 7 см = 3,1428…. Округлите полученное число (3,14). Получилось знакомое число «Пи».
Пусть она будет равна 22 сантиметрам. Найдите отношение длины окружности к длине ее диаметра — 22 см: 7 см = 3,1428…. Округлите полученное число (3,14). Получилось знакомое число «Пи».
Доказать это свойство окружности вы можете, используя чашку или стакан. Измерьте их диаметр линейкой. Обмотайте верх посуды ниткой, замерьте получившуюся длину. Поделив длину окружности чашки на длину ее диаметра, вы также получите число «Пи», убедившись в этом свойстве окружности , открытом Архимедом.
Используя это свойство, вы можете вычислить длину любой окружности по длине ее диаметра или по формулам:С = 2*п*R или С = D*п, где С — окружности , D — длина ее диаметра, R — длина ее радиуса.Для нахождения (плоскости, ограниченной линиями окружности ) используйте формулу S = π*R², если известен его радиус, либо формулу S = π*D²/4, если известен его диаметр.
Обратите внимание
А вы знаете, что четырнадцатого марта уже более двадцати лет отмечается День «Пи»? Это неофициальный праздник математиков, посвященный этому интересному числу, с которым в настоящее время связано множество формул, математических и физических аксиом.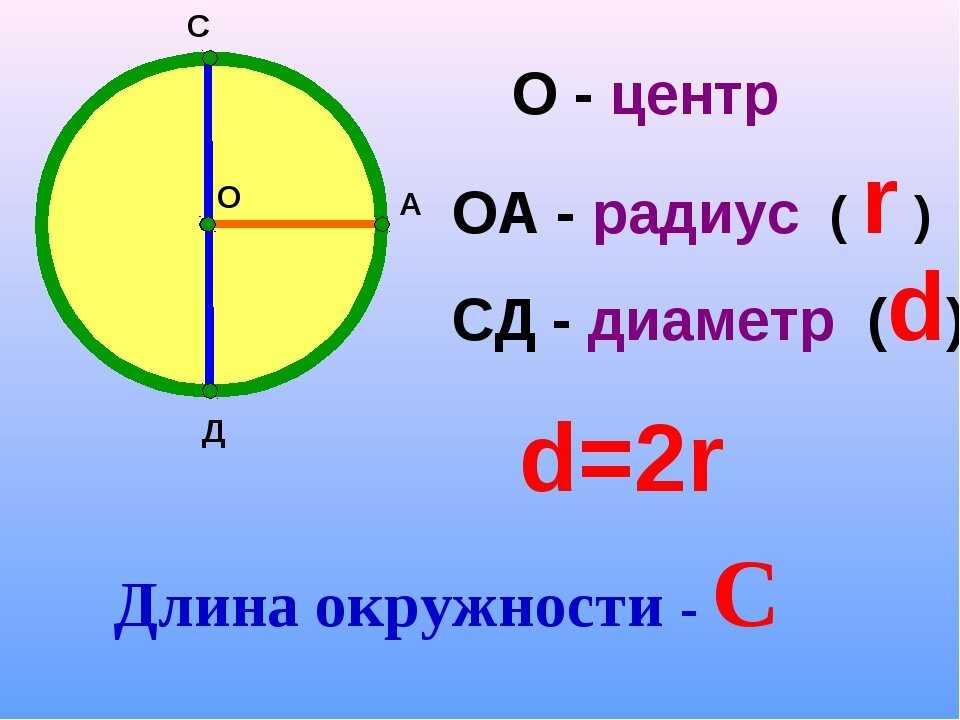 Придумал этот праздник американец Ларри Шоу, который обратил внимание, что в этот день (3.14 в системе записи дат в США) родился знаменитый ученый Эйнштейн.
Придумал этот праздник американец Ларри Шоу, который обратил внимание, что в этот день (3.14 в системе записи дат в США) родился знаменитый ученый Эйнштейн.
Источники:
Иногда около выпуклого многоугольника можно начертить таким образом, чтобы вершины всех углов лежали на ней. Такую окружность по отношению к многоугольнику надо называть описанной. Ее центр не обязательно должен находиться внутри периметра вписанной фигуры, но пользуясь свойствами описанной окружности , найти эту точку, как правило, не очень трудно.
Вам понадобится
- Линейка, карандаш, транспортир или угольник, циркуль.
Инструкция
Если многоугольник, около которого нужно описать окружность, начерчен на бумаге, для нахождения центр а круга достаточно линейки, карандаша и транспортира либо угольника. Измерьте длину любой из сторон фигуры, определите ее середину и поставьте в этом месте чертежа вспомогательную точку. С помощью угольника или транспортира проведите внутри многоугольника перпендикулярный этой стороне отрезок до пересечения с противоположной стороной.
Проделайте эту же операцию с любой другой стороной многоугольника. Пересечение двух построенных отрезков и будет искомой точкой. Это вытекает из основного свойства описанной окружности — ее центр в выпуклом многоугольнике с любым сторон всегда лежит в точке пересечения серединных перпендикуляров, проведенных к этим .
Для правильных многоугольников центр а вписанной окружности может быть намного проще. Например, если это квадрат, то начертите две диагонали — их пересечение и будет центр ом вписанной окружности . В многоугольнике с любым четным числом сторон достаточно соединить вспомогательными две пары лежащих друг напротив друга углов — центр описанной окружности должен совпадать с точкой их пересечения. В прямоугольном треугольнике для решения задачи просто определите середину самой длинной стороны фигуры — гипотенузы.
Если из условий неизвестно, можно ли в принципе описанную окружность для данного многоугольника, после определения предполагаемой точки центр а любым из описанных способов вы можете это выяснить.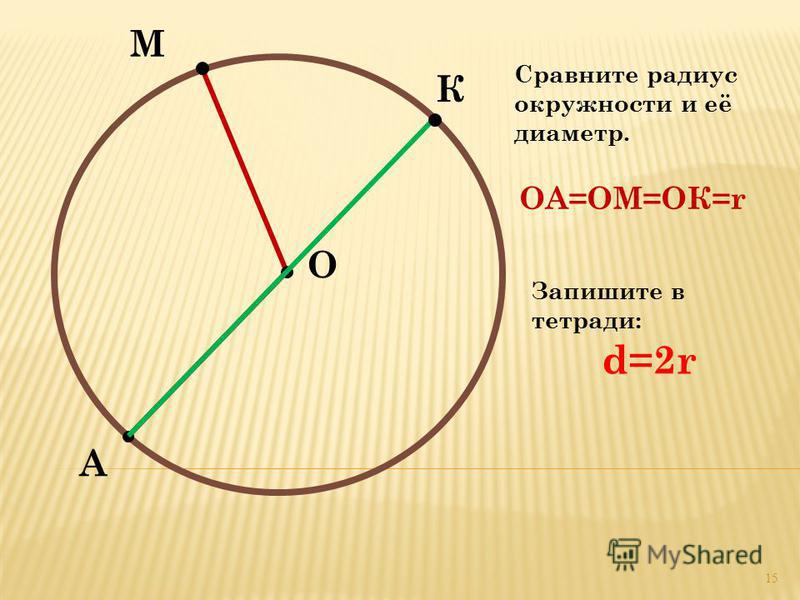 Отложите на циркуле расстояние между найденной точкой и любой из , установите в предполагаемый центр окружности и начертите круг — каждая вершина должна лежать на этой окружности . Если это не так, значит, не выполняется одно из свойств и описать окружность около данного многоугольника .
Отложите на циркуле расстояние между найденной точкой и любой из , установите в предполагаемый центр окружности и начертите круг — каждая вершина должна лежать на этой окружности . Если это не так, значит, не выполняется одно из свойств и описать окружность около данного многоугольника .
Определение диаметра может пригодиться не только для решения геометрических задач, но и помочь на практике. Например, зная диаметр горлышка банки, вы точно не ошибетесь в выборе крышки для нее. То же утверждение справедливо и для более габаритных окружностей.
Инструкция
Итак, введите обозначения величин. Пусть d – диаметр колодца, L – длина окружности, п – число Пи, значение которого приблизительно равно 3,14, R – радиус окружности. Длина окружности (L) известна. Предположим, что она равна 628 сантиметрам.
Далее для нахождения диаметра (d) воспользуйтесь формулой длины окружности: L=2пR, где R – неизвестная величина, L=628 см, а п=3,14. Теперь воспользуйтесь правилом нахождения неизвестного множителя: «Чтобы найти множитель, нужно произведение разделить на известный множитель». Получается: R=L/2п. Подставьте значения к формуле: R=628/2×3,14. Получается: R=628/6,28, R=100 см.
Получается: R=L/2п. Подставьте значения к формуле: R=628/2×3,14. Получается: R=628/6,28, R=100 см.
После того как радиус окружности найден (R=100 см), воспользуйтесь следующей формулой: диаметр окружности (d) равен двум радиусам окружности (2R). Получается: d=2R.
Теперь, чтобы найти диаметр, подставьте в формулу d=2R значения и вычислите результат. Так как радиус (R) известен, получается: d=2×100, d=200 см.
Источники:
- как по длине окружности определить диаметр
Длина окружности и диаметр являются взаимосвязанными геометрическими величинами. Это означает, что первую из них можно перевести во вторую без каких-либо дополнительных данных. Математической константой, через которую они связаны между собой, является число π.
Инструкция
Если окружность представлена в виде изображения на бумаге, а ее диаметр требуется определить приблизительно, измерьте его непосредственно. Если ее центр показан на чертеже, проведите через него линию. Если же центр не показан, найдите его при помощи циркуля. Для этого используйте угольник с углами в 90 и . Приложите его 90-градусным углом к окружности таким образом, чтобы ее касались оба катета, и обведите. Приложив затем к получившемуся прямому углу 45-градусный угол угольника, начертите . Она пройдет через центр окружности. Затем аналогичным образом начертите в другом месте окружности второй прямой угол и его биссектрису. Они пересекутся в центре. Это позволит измерить диаметр.
Для этого используйте угольник с углами в 90 и . Приложите его 90-градусным углом к окружности таким образом, чтобы ее касались оба катета, и обведите. Приложив затем к получившемуся прямому углу 45-градусный угол угольника, начертите . Она пройдет через центр окружности. Затем аналогичным образом начертите в другом месте окружности второй прямой угол и его биссектрису. Они пересекутся в центре. Это позволит измерить диаметр.
Для измерения диаметра предпочтительно использовать линейку, изготовленную из как можно более тонкого листового материала, либо портновский метр. При наличии только толстой линейки измерьте диаметр окружности при помощи циркуля, а затем, не изменяя его раствора, перенесите его на миллиметровую бумагу.
Также при отсутствии в условиях задачи числовых данных и при наличии только чертежа можно измерить длину окружности при помощи курвиметра, а диаметр затем рассчитать. Чтобы воспользоваться курвиметром, вначале вращением его колесика установите стрелку точно на нулевое деление. Затем отметьте на окружности точку и прижмите курвиметр к листу таким образом, чтобы штрих над колесиком указывал на эту точку. Проведите колесиком по линии окружности, пока штрих снова не окажется над этой точкой. Прочитайте показания. Они будут в , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
Затем отметьте на окружности точку и прижмите курвиметр к листу таким образом, чтобы штрих над колесиком указывал на эту точку. Проведите колесиком по линии окружности, пока штрих снова не окажется над этой точкой. Прочитайте показания. Они будут в , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
При увеличении числа сторон периметр вписанного многоугольника будет все больше приближаться к L. Р= b*n=2n*R*Sin (π/n)=n*D*Sin (π/n). Зависимость между длиной окружности L и ее диаметром D постоянна. Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14.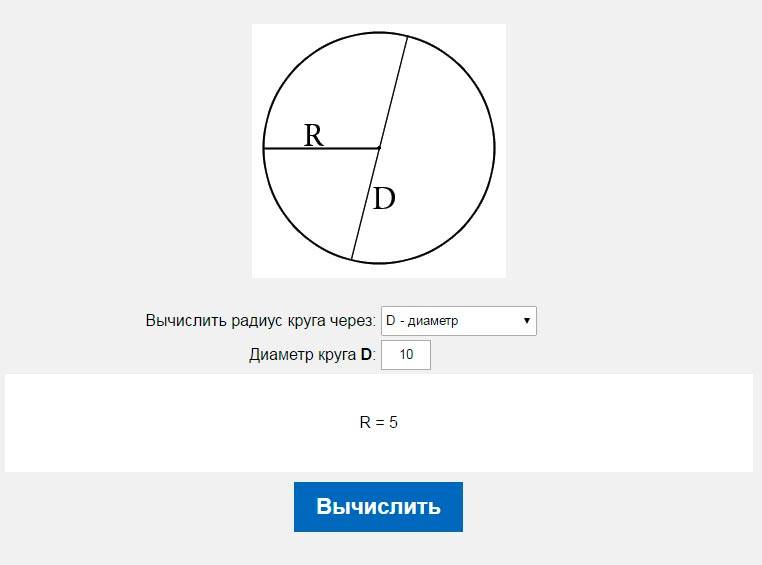 Длина окружности и ее диаметр связаны формулой: L= πD. Для вычисления диаметра
Длина окружности и ее диаметр связаны формулой: L= πD. Для вычисления диаметра
Измерение окружности
О том, что наша планета имеет форму шара, ученым, занимающимся исследованиями в области геологии, было известно достаточно давно. Именно поэтому первые измерения величины окружности земной поверхности касались самой длинной параллели Земли — экватора. Эту величину, полагали ученые, можно считать правильной для любого другого способа измерения. Например, считалось, что если измерить окружность планеты по самому длинному меридиану , полученная цифра будет точно такой же.
Такое мнение существовало вплоть до XVIII века. Однако ученые ведущего научного учреждения того времени — Французской академии — придерживались мнения о том, что эта гипотеза неверна, и форма, которую имеет планета, не совсем правильна. Поэтому, по их мнению, длины окружности по самому длинному меридиану и по самой длинной параллели будут различаться.
В доказательство в 1735 и 1736 годах были предприняты две научные экспедиции, которые доказали истинность этого предположения. Впоследствии была установлена и величина различия между этими двумя — она составила 21,4 километра.
Впоследствии была установлена и величина различия между этими двумя — она составила 21,4 километра.
Длина окружности
В настоящее время длина окружности планеты Земля неоднократно измерена уже не посредством экстраполяции длины того или иного отрезка земной поверхности на ее полную величину, как это делалось раньше, а с применением современных высокоточных технологий. Благодаря этому удалось установить точную длину окружности по самому длинному меридиану и самой длинной параллели, а также уточнить величину различия между этими параметрами.
Так, на сегодняшний день в научном сообществе в качестве официальной величины окружности планеты Земля по экватору, то есть наиболее длинной параллели, принято приводить цифру, составляющую 40075,70 километра. При этом аналогичный параметр, измеренный по самому длинному меридиану, то есть длина окружности, проходящей через земные полюсы, составляет 40008,55 километра.
Таким образом, разница между длинами окружностей составляет 67,15 километра, и экватор является самой длинной окружностью нашей планеты. Кроме того, различие означает, что один градус географического меридиана несколько короче, чем один градус географической параллели.
Кроме того, различие означает, что один градус географического меридиана несколько короче, чем один градус географической параллели.
Чтобы написать, как найти диаметр круга, необходимо сначала определить, что это такое. Итак, диаметр круга — это прямая, которая проходит через центр круга и соединяет точки на окружности.
Ниже мы рассмотрим способы нахождения диаметра окружности через её длину, площадь вписанного круга, и через радиус.
Определение диаметра
Принято считать, что какой бы величины ни была окружность, отношение ее длины к диаметру — это постоянное число «Пи», которое примерно равно 3,14. Чтобы понять, как найти диаметр круга, следует привести формулы и на примере показать вычисления данной величины.
Радиус
Если известен радиус круга, то диаметр вычислить очень просто:
D = 2R, где D — это диаметр, а R — радиус. Получается, диаметр равен двум радиусам. Например, известно, что радиус равен 10 см, тогда диаметр вычисляем так: D=2*10, получается, что диаметр равен 20 см.
Длина окружности
В случае, если известна длина окружности, для вычисления может быть полезным число . Вот какой формулой можно воспользоваться: D = l/, где l — это длина круга. Получается, если длина окружности равна 18 см, то диаметр вычисляем так: D = 18 / 3,14 ≈ 5,73 см.
Площадь круга
Если известна только площадь круга, то это значение также можно применить. При этом площадь обозначается буквой S. Исходя из формулы S=R 2 , можно найти радиус, а значит, и диаметр. Итак, радиус R = √ (S / ). Для нахождения радиуса делим площадь на число Пи и извлекаем из этого значения квадратный корень. Таким образом, если площадь равна 25 см, то радиус вычисляется так: R = √ (25 / 3,14) ≈ √8 ≈ 2,8 см. Затем можно вычислить диаметр: D = 2R, D = 2,8*2= 5,6 см.
Диаметр с помощью длины окружности. Как найти длину окружности: через диаметр и радиус
Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам.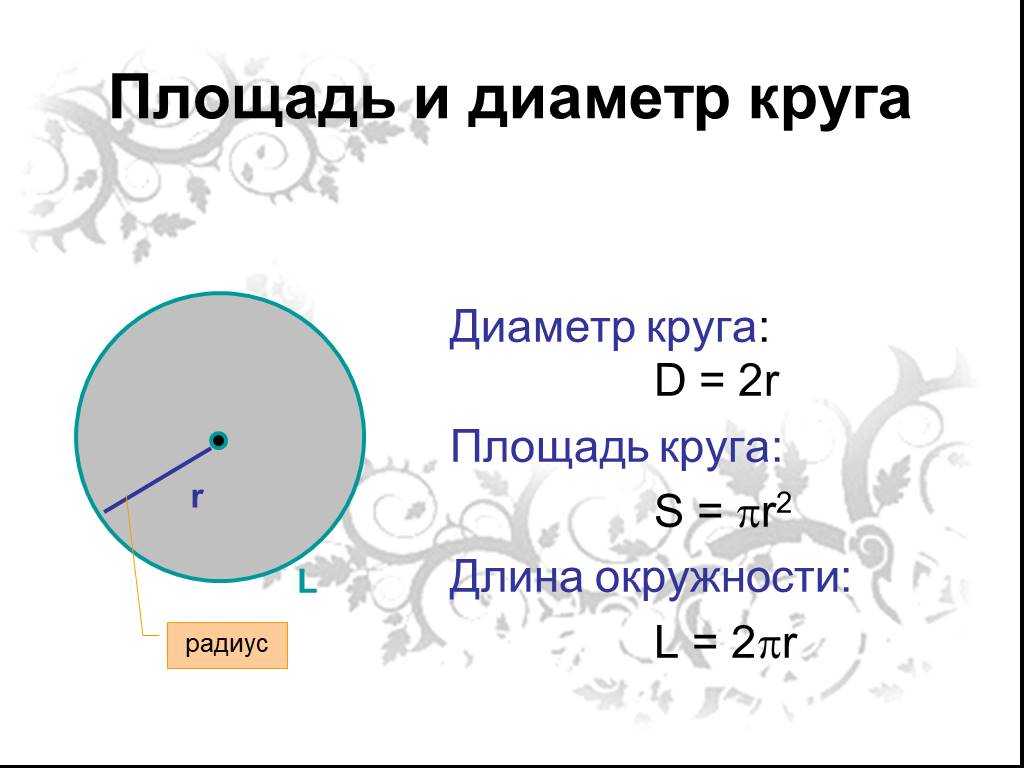 Следовательно, формула длины окружности будет выглядеть так:
Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR
где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.
Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м)
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м)
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга :
Формула нахождения площади круга :
S = πr 2
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2:
7: 2 = 3,5 (см)
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 | 7 2 | = 3,14 | 49 | = | 153,86 | = 38,465 (см 2) |
| 4 | 4 | 4 | 4 |
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Найти радиус круга, если его площадь равна 12,56 м 2 .
Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:
r = √S : π
следовательно радиус будет равен:
r ≈ √12,56: 3,14 = √4 = 2 (м)
Число
πДлину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π .
Это отношение и обозначается буквой π .
Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π . В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.
Окружностью называют кривую линию, которая ограничивает собой круг. В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению. Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.
У окружности есть несколько характеристик, на основе которых производят расчеты, связанные с этой геометрической фигурой. В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.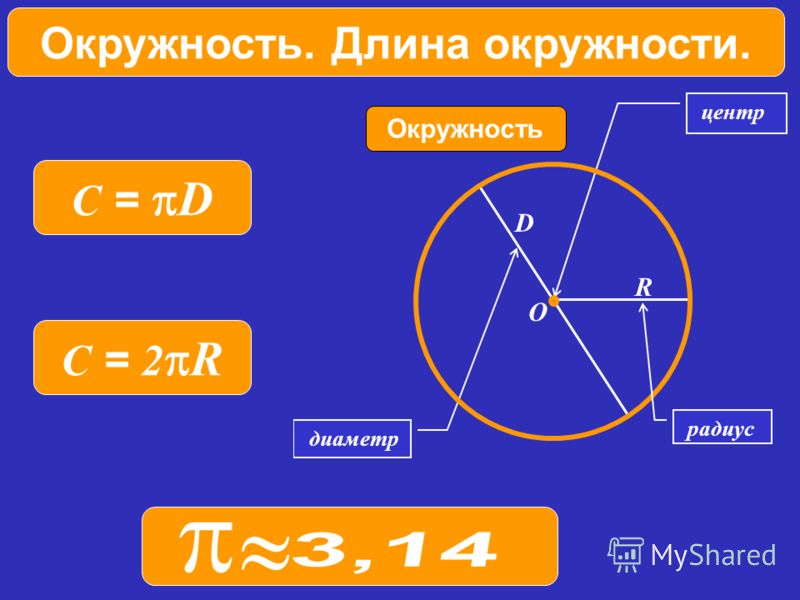
- Радиус окружности – это отрезок внутри окружности, соединённый с ее центром.
- Диаметр – это отрезок внутри окружности, соединяющий ее точки и проходящий через центр. По сути, диаметр – это два радиуса. Именно так выглядит формула для его вычисления: D=2r.
- Есть еще одна составляющая окружности – хорда. Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром.
Как узнать длину окружности? Сейчас выясним.
Длина окружности: формула
Для обозначения этой характеристики выбрана латинская буква p. Еще Архимед доказал, что отношение длины окружности к ее диаметру является одним и тем же числом для всех окружностей: это число π, которое приблизительно равно 3,14159. Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr. Рассмотрим применение формулы на примере простых задач:
Рассмотрим применение формулы на примере простых задач:
Задача 1
У основания царь-колокола диаметр равен 6,6 метров. Какова длина окружности основания колокола?
- Итак, формула для вычисления окружности — p= πd
- Подставляем имеющееся значение в формулу: p=3,14*6,6= 20,724
Ответ: длина окружности основания колокола 20,7 метра.
Задача 2
Искусственный спутник Земли вращается на расстоянии 320 км от планеты. Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?
- 1.Вычислим радиус круговой орбиты спутника Земли: 6370+320=6690 (км)
- 2.Вычислим длину круговой орбиты спутника по формуле: P=2πr
- 3.P=2*3,14*6690=42013,2
Ответ: длина круговой орбиты спутника Земли 42013,2 км.
Способы измерения длины окружности
Вычисление длины окружности на практике используется не часто. Причиной тому приблизительное значение числа π. В быту для поиска длины круга используют специальный прибор – курвиметр.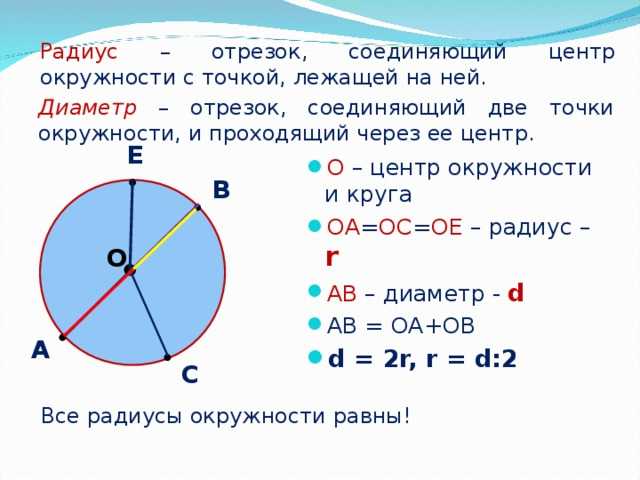 На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.
На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.
Как найти длину окружности? Нужно просто держать в голове незамысловатые формуля для вычислений.
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Определение длины окружности
Произвести расчёт окружности можно по следующей формуле:
L = π D = 2 π r
r — радиус окружности
D — диаметр окружности
L — длина окружности
π — 3.14
Задача:
Вычислить длину окружности , имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
L = π D = 2 π r
где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 5 = 31,4 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах.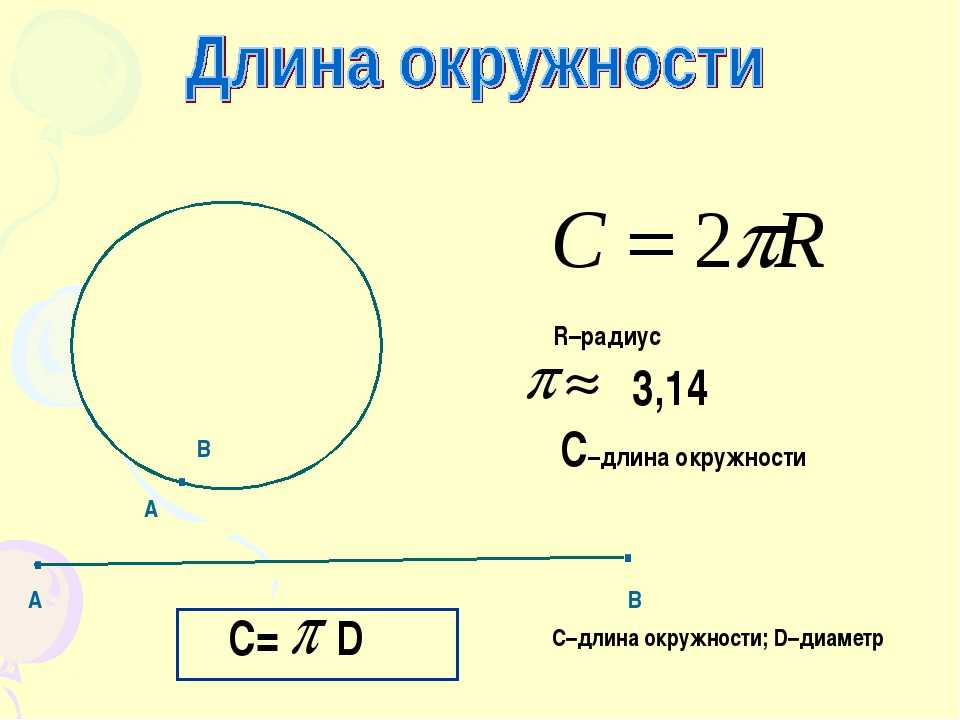 Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
1. Сложнее найти длину окружности через диаметр , по этому сначала разберём этот вариант.
Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.
2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см
Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см — это найденная длина окружности для радиуса 5 см!
Онлайн калькулятор длины окружности
Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.
Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы , понятия и определения требуются для этого.
Вконтакте
Основные понятия и определения
- Радиус — это линия, соединяющая центр окружности и её произвольную точку . Он обозначается латинской буквой r.
- Хордой называется линия, соединяющая две произвольные точки лежащие на окружности .

- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр . Он обозначается латинской буквой d.
- — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром. Её длину будем обозначать латинской буквой l.
Площадь круга — это вся территория, заключённая внутри окружности . Она измеряется в квадратных единицах и обозначается латинской буквой s.
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях!
Диаметр окружности.
Нахождение длины окружности и её площади
Если нам дан радиус окружности, то диаметр окружности описывает формула d = 2*r . Таким образом, для ответа на вопрос, как найти диаметр круга, зная его радиус, достаточно последний умножить на два . 2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга. Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см . Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
- Пусть нам требуется определить площадь данной окружности по формуле через её известный диаметр. Пусть d = 815 метров.
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
Длина окружности
Расчет длины окружности по диаметру онлайн. Как рассчитать длину окружности, если не указан диаметр и радиус круга
Одной линейкой здесь не обойтись, необходимо знать специальные формулы. Единственное, что от нас потребуется — это определить диаметр или радиус круга. В некоторых задачах эти величины обозначены. Но что делать, если у нас нет ничего, кроме рисунка? Не беда. Диаметр и радиус можно вычислить с помощью обычной линейки. Теперь приступим к самому основному.
Формулы, которые должен знать каждый
Еще в почти 4 000 лет назад, учёные выявили удивительное соотношение: если длину окружности разделить на ее диаметр, то получается одно и то же число, которое равно примерно 3,14. Это значение назвали именно с этой буквы в древнегреческом языке начиналось слово «периметр» и «окружность». На основании того открытия, которое совершили древние ученые, можно рассчитать длину любой окружности:
Где P означает длину (периметр) окружности,
D — диаметр, П — число «Пи».
Длина окружности круга может также быть посчитана через ее радиус (r), который равен половине длины диаметра. Вот и вторая формула, которую нужно запомнить:
Как узнать диаметр окружности?
Представляет собой хорду, которая проходит через центр фигуры. При этом она соединяет две наиболее удалённые точки в круге. Исходя из этого, можно самостоятельно прочертить диаметр (радиус) и измерить его длину с помощью линейки.
Способ 1: вписываем прямоугольный треугольник в круг
Рассчитать длину окружности будет несложно, если мы найдем ее диаметр. Необходимо начертить в круге где гипотенуза будет равна диаметру окружности. Для этого необходимо иметь под рукой линейку и угольник, иначе ничего не получится.
Способ 2: вписываем любой треугольник
На стороне круга отмечаем три любые точки, соединяем их — получаем треугольник. Важно, чтобы центр окружности лежал в области треугольника, это можно сделать на глаз. Проводим к каждой стороне треугольника медианы, точка их пересечения совпадёт с центром окружности. А когда нам известен центр, можно с помощью линейки легко провести диаметр.
А когда нам известен центр, можно с помощью линейки легко провести диаметр.
Данный способ очень похож на первый, но может применяться при отсутствии угольника или в тех случаях, когда нет возможности чертить на фигуре, например на тарелке. Необходимо взять лист бумаги с прямыми углами. Прикладываем лист к кругу так, чтобы одна вершина его угла соприкасалась с краем круга. Далее отмечаем точками места, где стороны бумаги пересекаются с линией окружности. Соединяем эти точки с помощью карандаша и линейки. Если под рукой ничего нет, просто согните бумагу. Эта линия и будет равна длине диаметра.
Пример задачи
- Ищем диаметр с помощью угольника, линейки и карандаша по способу № 1. Предположим, получилось 5 см.
- Зная диаметр, мы легко можем его вставить в нашу формулу: P = d П = 5*3,14 = 15,7В нашем случае получилось около 15,7. Теперь вы без особых проблем сможете объяснить, как рассчитать длину окружности.
Инструкция
Сначала надо исходные данные к задаче. Дело в том, что ее условии не может быть явно сказано, какова радиуса окружности . Вместо этого в задаче может быть дана длина диаметра окружности . Диаметр окружности — отрезок, который объединяет между собой две противоположные точки окружности , проходя через ее центр. Проанализировав определения окружности , можно сказать, что длина диаметра удвоенной длине радиуса.
Дело в том, что ее условии не может быть явно сказано, какова радиуса окружности . Вместо этого в задаче может быть дана длина диаметра окружности . Диаметр окружности — отрезок, который объединяет между собой две противоположные точки окружности , проходя через ее центр. Проанализировав определения окружности , можно сказать, что длина диаметра удвоенной длине радиуса.
Теперь можно принять радиус окружности равным R. Тогда для длины окружности необходимо воспользоваться формулой:
L = 2πR = πD, где L — длина окружности , D — диаметр окружности , который всегда в 2 раза радиуса.
Обратите внимание
Окружность можно вписать в многоугольник, либо описать вокруг него. При этом, если окружность вписана, то она в точках касания со сторонами многоугольника будет делить их пополам. Чтобы узнать радиус вписанной окружности, нужно поделить площадь многоугольника на половину его периметра:
R = S/p.
Если окружность описана вокруг треугольника, то ее радиус находится по следующей формуле:
R = a*b*c/4S, где a, b, c — это стороны данного треугольника, S — площадь треугольника, вокруг которого описана окружность.
Если требуется описать окружность вокруг четырехугольника, то это можно будет сделать при соблюдении двух условий:
Четырехугольник должен быть выпуклым.
В сумме противоположные углы четырехугольника должны составлять 180°
Полезный совет
Помимо традиционного штангенциркуля, для начертания окружности можно применять и трафареты. В современных трафаретах включены окружность разных диаметров. Данные трафареты можно приобрести в любом магазине канцтоваров.
Источники:
- Как найти длину окружности?
Окружность — замкнутая кривая линия, все точки которой находятся на равном расстоянии от одной точки. Эта точка — центр окружности, а отрезок между точкой на кривой и ее центром называется радиусом окружности.
Инструкция
Если через центр окружности провести прямую линию, то ее отрезок между двумя точками пересечения этой прямой с окружностью называется диаметром данной окружности. Половина диаметра, от центра до точки пересечения диаметра с окружность — это радиус
окружности.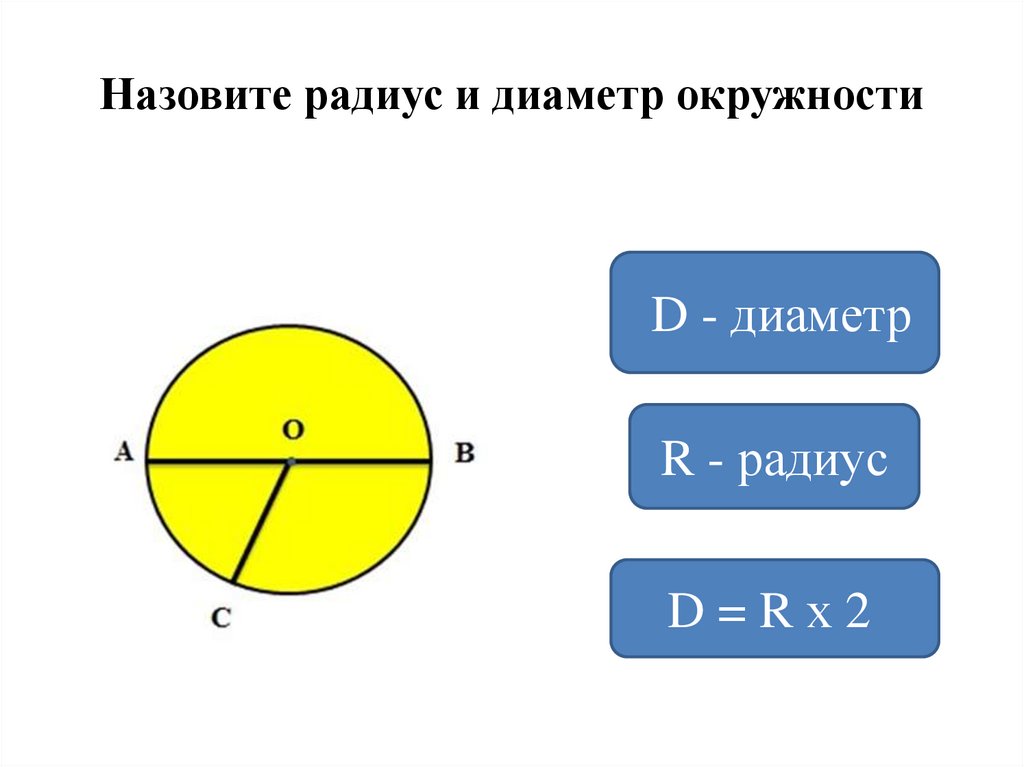 Если окружность разрезать в произвольной точке, выпрямить и измерить, то полученная величина является длиной данной окружности.
Если окружность разрезать в произвольной точке, выпрямить и измерить, то полученная величина является длиной данной окружности.
Начертите несколько окружностей разным раствором циркуля. Визуальное сравнение позволяет сделать вывод, что больший диаметр очерчивает больший круг, ограниченный окружностью с большей длиной. Следовательно, между диаметром окружности и ее длиной существует прямо пропорциональная зависимость.
По физическому смыслу параметр «длина окружности» соответствует , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
При увеличении числа сторон периметр вписанного многоугольника будет все больше приближаться к L. Р= b*n=2n*R*Sin (π/n)=n*D*Sin (π/n). Зависимость между длиной окружности L и ее диаметром D постоянна. Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для окружности разделите ее длину на число π=3,14.
Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для окружности разделите ее длину на число π=3,14.
Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика.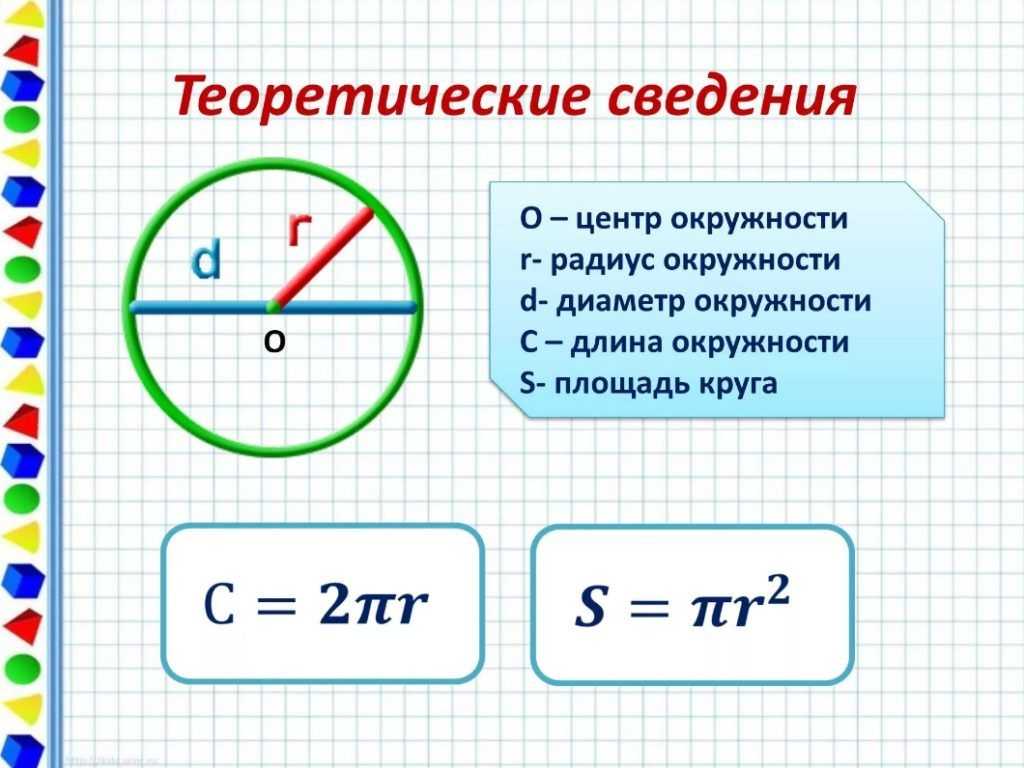 Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
- если известен диаметр окружности, то формула выглядит так L = ПD
- если известен радиус окружности, то формула имеет следующий вид L = 2Пr.
Формула длины окружности
Если воспользоваться Яндексом, то длину окружности можно посчитать в самом поисковом интерфейсе.
 Введите в Яндексе формула длины окружности , он вам выдаст формулу расчета и окошко для ввода значения. Дальше нужно будет нажать кнопку quot;Посчитатьquot;.
Введите в Яндексе формула длины окружности , он вам выдаст формулу расчета и окошко для ввода значения. Дальше нужно будет нажать кнопку quot;Посчитатьquot;.Окружность это такая геометрическая фигура, которая является совокупностью всех своих точек на плоскости, равноудаленных от ее центра, на расстояние, называемое радиусом.
Для того, чтобы вычислить длину окружности, обозначаемую обычно как L, надо радиус, обозначаемый как R, умножить на 2 и на число Пи. L=2ПиR. Пи — величина постоянная и равна 3,14.
Или можно взять удвоенный радиус, то есть диаметр (D) и тогда формула будет выглядеть так: L=ПиD.
Можно найти длину окружности не зная радиуса. Для этого нужно знать площадь круга.
Формула для расчета длины окружности по известной площади круга выглядит так:
L=2*корень квадратный пи*S
где S площадь круга.
Длина окружности
Можете скопировать себе на компьютер нижеприведенную табличку с основными формулами окружности и круга.
 Она вас, при решении геометрических задач, еще не раз выручит.
Она вас, при решении геометрических задач, еще не раз выручит.Здесь же присутствует формула длины окружности. Она имеет вид: L=2ПR
На сайте quot;Сборник формулquot;, можно посчитать длину окружности, введя имеющиеся у вас данные. Там же,
Решение уравнений:
Геометрическая прогрессия:
Комбинаторика:
Решить химическое уравнение
Известно, что независимо от длины окружности, ее отношение к диаметру является постоянным числом. Если известен диаметр окружности, то нужно эту величину умножить на число Пи (3,14).
Если известен диаметр окружности, то нужно эту величину умножить на число Пи (3,14).
Формула выглядит так:
Если известен радиус, то чтобы найти диаметр, умножаем его на два, а для нахождения длины окружности опять же на число Пи.
Окружностью в геометрии называют фигуру на плоскости, все точки, лежащие на окружности круга, удалены на равном расстоянии от центра окружности
Радиусом окружности называют в геометрии величину расстояния, отрезок от центра окружности до ее любой точки на окружности.
Длину окружности с радиусом вычисляют по формуле
Длина окружности L равно 2pi умножить на R.
Или выглядит формула так. Чтобы не путаться, запомните, что длина окружности это есть периметр круга.
r — это радиус
D — диаметр
Приблизительно 3,14
Но окружность — это не круг
Смотрите картинку, на которой видна разница между кругом и окружностью
Окружность это кривая, ограничивающая круг. Все ее точки находятся на равном от центра расстоянии. В формуле вычисления длины окружности используются значения радиуса или двойная величина радиуса — диаметр и число, всегда имеющее значение 3,14.
В формуле вычисления длины окружности используются значения радиуса или двойная величина радиуса — диаметр и число, всегда имеющее значение 3,14.
Формула, таким образом, выглядит так: L=d или L=2R , где L — значение длины окружности, получаемое умножением числа (3,14) на величину радиуса окружности или двойного диаметра.
Еще из средней школьной программы отчетливо помню формулу измерения длины окружности. Эта формула выглядит так- 2Пr, где r- это радиус окружности, которая равна половине диаметра, а число П неизменна и равна 3.14.
Формула длины окружности равна Пи умноженное на Диаметр или Пи умноженное на Радиус умноженный на 2.
Длину окружности можно найти одним из представленных способов:
В какой бы сфере экономики человек ни трудился, вольно или невольно он пользуется математическими знаниями, накопленными за многие столетия. С устройствами и механизмами, содержащими окружности, мы сталкиваемся ежедневно. Круглую форму имеет колесо, пицца, многие овощи и фрукты в разрезе образуют круг, а также тарелки, чашки, да и многое другое. Однако, правильно рассчитывать длину окружности умеет не каждый.
Чтобы вычислить длину окружности, необходимо вначале вспомнить, что такое окружность. Это множество всех точек плоскости, равноудаленных от данной. А круг – это геометрическое место точек плоскости, находящееся внутри окружности. Из вышесказанного следует, что периметр круга и длина окружности – это одно и то же.
Из вышесказанного следует, что периметр круга и длина окружности – это одно и то же.
Способы нахождения длины окружности
Помимо математического способа нахождения периметра круга, есть и практические.
- Взять веревку или шнур и обернуть один раз вокруг.
- Затем веревку измерить, полученное число и будет длиной окружности.
- Прокатить круглый предмет один раз и посчитать длину пути. Если предмет очень небольшой, можно несколько раз обмотать его бечевкой, затем размотать нить, измерить и поделить на число витков.
- Найти требуемую величину по формуле:
L = 2πr = πD ,
где L – искомая длина;
π – константа, приблизительно равна 3,14 r – радиус окружности, расстояние от ее центра до любой точки;
D – диаметр, он равен двум радиусам.
Применение формулы, чтобы найти длину окружности
- Пример 1. Беговая дорожка проходит вокруг окружности радиусом 47,8 метров. Найти длину данной беговой дорожки, приняв π = 3,14.

L = 2πr =2*3,14*47,8 ≈ 300(м)
Ответ: 300 метров
- Пример 2. Колесо велосипеда, обернувшись 10 раз, проехало 18,85 метра. Найти радиус колеса.
18,85: 10 =1,885 (м) – это периметр колеса.
1,885: π = 1,885: 3,1416 ≈ 0,6(м) – искомый диаметр
Ответ: диаметр колеса 0,6 метра
Удивительное число π
Несмотря на кажущуюся простоту формулы, почему-то многим трудно ее запомнить. Видимо, это происходит из-за того, что в формуле есть иррациональное число π, которое не присутствует в формулах площади других фигур, например, квадрата, треугольника или ромба. Нужно просто запомнить, что это константа, то есть постоянная, означающая отношение длины окружности к диаметру. Около 4 тысяч лет назад люди заметили, что отношение периметра круга к его радиусу (или диаметру) одинаково для любых окружностей.
Древние греки приближали число π дробью 22/7. Долгое время π высчитывали как среднее между длинами вписанных и описанных многоугольников в окружность. В третьем столетии нашей эры китайский математик провёл вычисление для 3072-угольника и получил приближённое значение π = 3,1416. Необходимо помнить, что π всегда постоянно для любой окружности. Его обозначение греческой буквой π появилось в 18 веке. Это первая буква греческих слов περιφέρεια — окружность и περίμετρος — периметр. В восемнадцатом веке было доказано, что эта величина иррациональна, то есть ее нельзя представить в виде m/n, где m – целое, а n – натуральное число.
В третьем столетии нашей эры китайский математик провёл вычисление для 3072-угольника и получил приближённое значение π = 3,1416. Необходимо помнить, что π всегда постоянно для любой окружности. Его обозначение греческой буквой π появилось в 18 веке. Это первая буква греческих слов περιφέρεια — окружность и περίμετρος — периметр. В восемнадцатом веке было доказано, что эта величина иррациональна, то есть ее нельзя представить в виде m/n, где m – целое, а n – натуральное число.
Калькулятор круга и шара. Рассчитать радиус, диаметр, длину окружности, площадь круга и шара, объем шара онлайн.
Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR2. Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR2. Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr2. Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr3). Она была использована при создании нашего онлайн сервиса. Сайт tellaboutall.ru дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Она была использована при создании нашего онлайн сервиса. Сайт tellaboutall.ru дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
как найти длину окружности зная диаметр
Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы , понятия и определения требуются для этого.
Вконтакте
Основные понятия и определения
- Радиус — это линия, соединяющая центр окружности и её произвольную точку .
 Он обозначается латинской буквой r.
Он обозначается латинской буквой r. - Хордой называется линия, соединяющая две произвольные точки лежащие на окружности .
- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр . Он обозначается латинской буквой d.
- — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром. Её длину будем обозначать латинской буквой l.
Площадь круга — это вся территория, заключённая внутри окружности . Она измеряется в квадратных единицах и обозначается латинской буквой s.
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях!
Диаметр окружности.
Нахождение длины окружности и её площади
Если нам дан радиус окружности, то диаметр окружности описывает формула d = 2*r . 2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга. Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см . Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
- Пусть нам требуется определить площадь данной окружности по формуле через её известный диаметр.
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
Длина окружности
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Определение длины окружности
Произвести расчёт окружности можно по следующей формуле:
L = π D = 2 π r
r — радиус окружности
D — диаметр окружности
L — длина окружности
π — 3.14
Задача:
Вычислить длину окружности , имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
L = π D = 2 π r
где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 62,8 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Инструкция
Вспомните, что впервые математически вычислил это соотношение Архимед. Он правильные 96-тиугольники внутри окружности и вокруг нее. Периметр вписанного многоугольника принял за минимально возможную длину окружности, периметр описанной фигуры – за максимальный размер. По Архимеду соотношение длины окружности и диаметра равно 3,1419. Значительно позже это число «удлинил» до восьми знаков китайский математик Цзу Чунчжи. Его вычисления 900 лет оставались наиболее точными. Только в XVIII веке было посчитано сто знаков после запятой. А с 1706 года эта бесконечная десятичная дробь благодаря Уильяму Джонсу приобрела имя. Он обозначил ее первой буквой греческих слов периметр (периферия). Сегодня компьютер легко вычисляет знаков числа Пи: 3,141592653589793238462643…
Периметр вписанного многоугольника принял за минимально возможную длину окружности, периметр описанной фигуры – за максимальный размер. По Архимеду соотношение длины окружности и диаметра равно 3,1419. Значительно позже это число «удлинил» до восьми знаков китайский математик Цзу Чунчжи. Его вычисления 900 лет оставались наиболее точными. Только в XVIII веке было посчитано сто знаков после запятой. А с 1706 года эта бесконечная десятичная дробь благодаря Уильяму Джонсу приобрела имя. Он обозначил ее первой буквой греческих слов периметр (периферия). Сегодня компьютер легко вычисляет знаков числа Пи: 3,141592653589793238462643…
Для расчетов число Пи сократите до 3,14. Получится, что для любой окружности ее длина, деленная на диаметр равна этому числу: L:d=3,14.
Выразите из этого утверждения формулу для нахождения диаметра. Получится, чтобы найти диаметр окружности надо длину окружности поделить на число Пи. Это выглядит так: d = L:3,14. Это универсальный способ найти диаметр, когда у окружности известна ее длина.
Итак, известна длина окружности, допустим, 15,7 см, разделите эту цифру на 3,14. Диаметр будет равен 5 см. Запишите это так: d = 15,7: 3,14 = 5 см.
Найдите диаметр по длине окружности, используя специальные таблицы для вычисления длины окружности . Эти таблицы включают в разные справочники. Например, они есть в «Четырехзначные математические таблицы» В.М. Брадиса.
Полезный совет
Запомните первые восемь цифр числа Пи с помощью стихотворения:
Нужно только постараться,
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Источники:
- Число «Пи» рассчитано с рекордной точностью
- диаметр и длина окружности
- Как найти длину окружности?
Круг — это плоская геометрическая фигура, все точки которой находятся на одинаковом и отличном от нуля удалении от выбранной точки, которую называют центром окружности. Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром . Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
Инструкция
Используйте для нахождения диаметра одно из основных свойств окружности, которое заключается в том, что соотношение длины ее периметра к диаметру одинаково для абсолютно всех окружностей. Конечно, постоянство не осталось не отмеченным математиками, и эта пропорция давно уже получила собственное — это число Пи (π — первая греческих слов «окружность » и «периметр»). Числовое этой определяется длиной окружности, у которой диаметр равен единице.
Делите известную длину окружности на число Пи, чтобы вычислить ее диаметр. Так как это число является « », то не имеет конечного значения — это дробь. Округляйте число Пи в соответствии с точностью результата, которую вам необходимо получить.
Видео по теме
Удивительное свойство окружности открыл нам древнегреческий ученый Архимед. Оно заключается в том, что отношение ее длины к длине диаметра одинаково для любой окружности . В своем труде «Об измерении круга» он вычислил его и обозначил числом «Пи». Оно иррационально, то есть его значение не может быть точно выражено. Для используется его величина, равная 3,14. Вы можете сами проверить утверждение Архимеда, сделав простые вычисления.
Оно заключается в том, что отношение ее длины к длине диаметра одинаково для любой окружности . В своем труде «Об измерении круга» он вычислил его и обозначил числом «Пи». Оно иррационально, то есть его значение не может быть точно выражено. Для используется его величина, равная 3,14. Вы можете сами проверить утверждение Архимеда, сделав простые вычисления.
Вам понадобится
- — циркуль;
- — линейка;
- — карандаш;
- — нитка.
Инструкция
Начертите на бумаге циркулем окружность произвольного диаметра. Проведите с помощью линейки и карандаша через ее центр отрезок, соединяющий две , находящиеся на линии окружности . Линейкой измерьте длину получившегося отрезка. Допустим, окружности в данном случае 7 сантиметрам.
Возьмите нитку и расположите ее по длине окружности . Измерьте получившуюся длину нитки. Пусть она будет равна 22 сантиметрам. Найдите отношение длины окружности к длине ее диаметра — 22 см: 7 см = 3,1428. … Округлите полученное число (3,14). Получилось знакомое число «Пи».
… Округлите полученное число (3,14). Получилось знакомое число «Пи».
Доказать это свойство окружности вы можете, используя чашку или стакан. Измерьте их диаметр линейкой. Обмотайте верх посуды ниткой, замерьте получившуюся длину. Поделив длину окружности чашки на длину ее диаметра, вы также получите число «Пи», убедившись в этом свойстве окружности , открытом Архимедом.
Используя это свойство, вы можете вычислить длину любой окружности по длине ее диаметра или по формулам:С = 2*п*R или С = D*п, где С — окружности , D — длина ее диаметра, R — длина ее радиуса.Для нахождения (плоскости, ограниченной линиями окружности ) используйте формулу S = π*R², если известен его радиус, либо формулу S = π*D²/4, если известен его диаметр.
Обратите внимание
А вы знаете, что четырнадцатого марта уже более двадцати лет отмечается День «Пи»? Это неофициальный праздник математиков, посвященный этому интересному числу, с которым в настоящее время связано множество формул, математических и физических аксиом. Придумал этот праздник американец Ларри Шоу, который обратил внимание, что в этот день (3.14 в системе записи дат в США) родился знаменитый ученый Эйнштейн.
Придумал этот праздник американец Ларри Шоу, который обратил внимание, что в этот день (3.14 в системе записи дат в США) родился знаменитый ученый Эйнштейн.
Источники:
Иногда около выпуклого многоугольника можно начертить таким образом, чтобы вершины всех углов лежали на ней. Такую окружность по отношению к многоугольнику надо называть описанной. Ее центр не обязательно должен находиться внутри периметра вписанной фигуры, но пользуясь свойствами описанной окружности , найти эту точку, как правило, не очень трудно.
Вам понадобится
- Линейка, карандаш, транспортир или угольник, циркуль.
Инструкция
Если многоугольник, около которого нужно описать окружность, начерчен на бумаге, для нахождения центр а круга достаточно линейки, карандаша и транспортира либо угольника. Измерьте длину любой из сторон фигуры, определите ее середину и поставьте в этом месте чертежа вспомогательную точку. С помощью угольника или транспортира проведите внутри многоугольника перпендикулярный этой стороне отрезок до пересечения с противоположной стороной.
Проделайте эту же операцию с любой другой стороной многоугольника. Пересечение двух построенных отрезков и будет искомой точкой. Это вытекает из основного свойства описанной окружности — ее центр в выпуклом многоугольнике с любым сторон всегда лежит в точке пересечения серединных перпендикуляров, проведенных к этим .
Для правильных многоугольников центр а вписанной окружности может быть намного проще. Например, если это квадрат, то начертите две диагонали — их пересечение и будет центр ом вписанной окружности . В многоугольнике с любым четным числом сторон достаточно соединить вспомогательными две пары лежащих друг напротив друга углов — центр описанной окружности должен совпадать с точкой их пересечения. В прямоугольном треугольнике для решения задачи просто определите середину самой длинной стороны фигуры — гипотенузы.
Если из условий неизвестно, можно ли в принципе описанную окружность для данного многоугольника, после определения предполагаемой точки центр а любым из описанных способов вы можете это выяснить. Отложите на циркуле расстояние между найденной точкой и любой из , установите в предполагаемый центр окружности и начертите круг — каждая вершина должна лежать на этой окружности . Если это не так, значит, не выполняется одно из свойств и описать окружность около данного многоугольника .
Отложите на циркуле расстояние между найденной точкой и любой из , установите в предполагаемый центр окружности и начертите круг — каждая вершина должна лежать на этой окружности . Если это не так, значит, не выполняется одно из свойств и описать окружность около данного многоугольника .
Определение диаметра может пригодиться не только для решения геометрических задач, но и помочь на практике. Например, зная диаметр горлышка банки, вы точно не ошибетесь в выборе крышки для нее. То же утверждение справедливо и для более габаритных окружностей.
Инструкция
Итак, введите обозначения величин. Пусть d – диаметр колодца, L – длина окружности, п – число Пи, значение которого приблизительно равно 3,14, R – радиус окружности. Длина окружности (L) известна. Предположим, что она равна 628 сантиметрам.
Далее для нахождения диаметра (d) воспользуйтесь формулой длины окружности: L=2пR, где R – неизвестная величина, L=628 см, а п=3,14. Теперь воспользуйтесь правилом нахождения неизвестного множителя: «Чтобы найти множитель, нужно произведение разделить на известный множитель». Получается: R=L/2п. Подставьте значения к формуле: R=628/2×3,14. Получается: R=628/6,28, R=100 см.
Получается: R=L/2п. Подставьте значения к формуле: R=628/2×3,14. Получается: R=628/6,28, R=100 см.
После того как радиус окружности найден (R=100 см), воспользуйтесь следующей формулой: диаметр окружности (d) равен двум радиусам окружности (2R). Получается: d=2R.
Теперь, чтобы найти диаметр, подставьте в формулу d=2R значения и вычислите результат. Так как радиус (R) известен, получается: d=2×100, d=200 см.
Источники:
- как по длине окружности определить диаметр
Длина окружности и диаметр являются взаимосвязанными геометрическими величинами. Это означает, что первую из них можно перевести во вторую без каких-либо дополнительных данных. Математической константой, через которую они связаны между собой, является число π.
Инструкция
Если окружность представлена в виде изображения на бумаге, а ее диаметр требуется определить приблизительно, измерьте его непосредственно. Если ее центр показан на чертеже, проведите через него линию. Если же центр не показан, найдите его при помощи циркуля. Для этого используйте угольник с углами в 90 и . Приложите его 90-градусным углом к окружности таким образом, чтобы ее касались оба катета, и обведите. Приложив затем к получившемуся прямому углу 45-градусный угол угольника, начертите . Она пройдет через центр окружности. Затем аналогичным образом начертите в другом месте окружности второй прямой угол и его биссектрису. Они пересекутся в центре. Это позволит измерить диаметр.
Для этого используйте угольник с углами в 90 и . Приложите его 90-градусным углом к окружности таким образом, чтобы ее касались оба катета, и обведите. Приложив затем к получившемуся прямому углу 45-градусный угол угольника, начертите . Она пройдет через центр окружности. Затем аналогичным образом начертите в другом месте окружности второй прямой угол и его биссектрису. Они пересекутся в центре. Это позволит измерить диаметр.
Для измерения диаметра предпочтительно использовать линейку, изготовленную из как можно более тонкого листового материала, либо портновский метр. При наличии только толстой линейки измерьте диаметр окружности при помощи циркуля, а затем, не изменяя его раствора, перенесите его на миллиметровую бумагу.
Также при отсутствии в условиях задачи числовых данных и при наличии только чертежа можно измерить длину окружности при помощи курвиметра, а диаметр затем рассчитать. Чтобы воспользоваться курвиметром, вначале вращением его колесика установите стрелку точно на нулевое деление. Затем отметьте на окружности точку и прижмите курвиметр к листу таким образом, чтобы штрих над колесиком указывал на эту точку. Проведите колесиком по линии окружности, пока штрих снова не окажется над этой точкой. Прочитайте показания. Они будут в , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
Затем отметьте на окружности точку и прижмите курвиметр к листу таким образом, чтобы штрих над колесиком указывал на эту точку. Проведите колесиком по линии окружности, пока штрих снова не окажется над этой точкой. Прочитайте показания. Они будут в , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
При увеличении числа сторон периметр вписанного многоугольника будет все больше приближаться к L. Р= b*n=2n*R*Sin (π/n)=n*D*Sin (π/n). Зависимость между длиной окружности L и ее диаметром D постоянна. Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для вычисления диаметра
Длина окружности и ее диаметр связаны формулой: L= πD. Для вычисления диаметра
Измерение окружности
О том, что наша планета имеет форму шара, ученым, занимающимся исследованиями в области геологии, было известно достаточно давно. Именно поэтому первые измерения величины окружности земной поверхности касались самой длинной параллели Земли — экватора. Эту величину, полагали ученые, можно считать правильной для любого другого способа измерения. Например, считалось, что если измерить окружность планеты по самому длинному меридиану , полученная цифра будет точно такой же.
Такое мнение существовало вплоть до XVIII века. Однако ученые ведущего научного учреждения того времени — Французской академии — придерживались мнения о том, что эта гипотеза неверна, и форма, которую имеет планета, не совсем правильна. Поэтому, по их мнению, длины окружности по самому длинному меридиану и по самой длинной параллели будут различаться.
В доказательство в 1735 и 1736 годах были предприняты две научные экспедиции, которые доказали истинность этого предположения. Впоследствии была установлена и величина различия между этими двумя — она составила 21,4 километра.
Впоследствии была установлена и величина различия между этими двумя — она составила 21,4 километра.
Длина окружности
В настоящее время длина окружности планеты Земля неоднократно измерена уже не посредством экстраполяции длины того или иного отрезка земной поверхности на ее полную величину, как это делалось раньше, а с применением современных высокоточных технологий. Благодаря этому удалось установить точную длину окружности по самому длинному меридиану и самой длинной параллели, а также уточнить величину различия между этими параметрами.
Так, на сегодняшний день в научном сообществе в качестве официальной величины окружности планеты Земля по экватору, то есть наиболее длинной параллели, принято приводить цифру, составляющую 40075,70 километра. При этом аналогичный параметр, измеренный по самому длинному меридиану, то есть длина окружности, проходящей через земные полюсы, составляет 40008,55 километра.
Таким образом, разница между длинами окружностей составляет 67,15 километра, и экватор является самой длинной окружностью нашей планеты. Кроме того, различие означает, что один градус географического меридиана несколько короче, чем один градус географической параллели.
Кроме того, различие означает, что один градус географического меридиана несколько короче, чем один градус географической параллели.
- если известен диаметр окружности, то формула выглядит так L = ПD
- если известен радиус окружности, то формула имеет следующий вид L = 2Пr.
Формула длины окружности
Если воспользоваться Яндексом, то длину окружности можно посчитать в самом поисковом интерфейсе.
 Введите в Яндексе формула длины окружности , он вам выдаст формулу расчета и окошко для ввода значения. Дальше нужно будет нажать кнопку quot;Посчитатьquot;.
Введите в Яндексе формула длины окружности , он вам выдаст формулу расчета и окошко для ввода значения. Дальше нужно будет нажать кнопку quot;Посчитатьquot;.Окружность это такая геометрическая фигура, которая является совокупностью всех своих точек на плоскости, равноудаленных от ее центра, на расстояние, называемое радиусом.
Для того, чтобы вычислить длину окружности, обозначаемую обычно как L, надо радиус, обозначаемый как R, умножить на 2 и на число Пи. L=2ПиR. Пи — величина постоянная и равна 3,14.
Или можно взять удвоенный радиус, то есть диаметр (D) и тогда формула будет выглядеть так: L=ПиD.
Можно найти длину окружности не зная радиуса. Для этого нужно знать площадь круга.
Формула для расчета длины окружности по известной площади круга выглядит так:
L=2*корень квадратный пи*S
где S площадь круга.
Длина окружности
Можете скопировать себе на компьютер нижеприведенную табличку с основными формулами окружности и круга.
 Она вас, при решении геометрических задач, еще не раз выручит.
Она вас, при решении геометрических задач, еще не раз выручит.Здесь же присутствует формула длины окружности. Она имеет вид: L=2ПR
На сайте quot;Сборник формулquot;, можно посчитать длину окружности, введя имеющиеся у вас данные. Там же,
Решение уравнений:
Геометрическая прогрессия:
Комбинаторика:
Решить химическое уравнение
Известно, что независимо от длины окружности, ее отношение к диаметру является постоянным числом. Если известен диаметр окружности, то нужно эту величину умножить на число Пи (3,14).
Формула выглядит так:
Если известен радиус, то чтобы найти диаметр, умножаем его на два, а для нахождения длины окружности опять же на число Пи.
Окружностью в геометрии называют фигуру на плоскости, все точки, лежащие на окружности круга, удалены на равном расстоянии от центра окружности
Радиусом окружности называют в геометрии величину расстояния, отрезок от центра окружности до ее любой точки на окружности.
Длину окружности с радиусом вычисляют по формуле
Длина окружности L равно 2pi умножить на R.
Или выглядит формула так. Чтобы не путаться, запомните, что длина окружности это есть периметр круга.
r — это радиус
D — диаметр
Приблизительно 3,14
Но окружность — это не круг
Смотрите картинку, на которой видна разница между кругом и окружностью
Окружность это кривая, ограничивающая круг. Все ее точки находятся на равном от центра расстоянии. В формуле вычисления длины окружности используются значения радиуса или двойная величина радиуса — диаметр и число, всегда имеющее значение 3,14.
Все ее точки находятся на равном от центра расстоянии. В формуле вычисления длины окружности используются значения радиуса или двойная величина радиуса — диаметр и число, всегда имеющее значение 3,14.
Формула, таким образом, выглядит так: L=d или L=2R , где L — значение длины окружности, получаемое умножением числа (3,14) на величину радиуса окружности или двойного диаметра.
Еще из средней школьной программы отчетливо помню формулу измерения длины окружности. Эта формула выглядит так- 2Пr, где r- это радиус окружности, которая равна половине диаметра, а число П неизменна и равна 3.14.
Формула длины окружности равна Пи умноженное на Диаметр или Пи умноженное на Радиус умноженный на 2.
Длину окружности можно найти одним из представленных способов:
Окружностью называют кривую линию, которая ограничивает собой круг. В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению. Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.
У окружности есть несколько характеристик, на основе которых производят расчеты, связанные с этой геометрической фигурой. В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.
- Радиус окружности – это отрезок внутри окружности, соединённый с ее центром.
- Диаметр – это отрезок внутри окружности, соединяющий ее точки и проходящий через центр. По сути, диаметр – это два радиуса. Именно так выглядит формула для его вычисления: D=2r.
- Есть еще одна составляющая окружности – хорда. Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром.
Как узнать длину окружности? Сейчас выясним.
Длина окружности: формула
Для обозначения этой характеристики выбрана латинская буква p. Еще Архимед доказал, что отношение длины окружности к ее диаметру является одним и тем же числом для всех окружностей: это число π, которое приблизительно равно 3,14159. Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr. Рассмотрим применение формулы на примере простых задач:
Рассмотрим применение формулы на примере простых задач:
Задача 1
У основания царь-колокола диаметр равен 6,6 метров. Какова длина окружности основания колокола?
- Итак, формула для вычисления окружности — p= πd
- Подставляем имеющееся значение в формулу: p=3,14*6,6= 20,724
Ответ: длина окружности основания колокола 20,7 метра.
Задача 2
Искусственный спутник Земли вращается на расстоянии 320 км от планеты. Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?
- 1.Вычислим радиус круговой орбиты спутника Земли: 6370+320=6690 (км)
- 2.Вычислим длину круговой орбиты спутника по формуле: P=2πr
- 3.P=2*3,14*6690=42013,2
Ответ: длина круговой орбиты спутника Земли 42013,2 км.
Способы измерения длины окружности
Вычисление длины окружности на практике используется не часто. Причиной тому приблизительное значение числа π. В быту для поиска длины круга используют специальный прибор – курвиметр. На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.
На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.
Как найти длину окружности? Нужно просто держать в голове незамысловатые формуля для вычислений.
Площадь круга и длина круга
Теорема
Площадь круга радиусом r равна:
Пример 1
Вычислим площадь круга диаметром 8 см .
Окружность диаметром 8 см имеет радиус длины r = 4 см (половина диаметра). Следовательно, площадь круга равна:
Пример 2
Найдите примерную площадь круга диаметром 2.
Если диаметр имеет длину 2, радиус окружности имеет длину 1. Используем формулу площади круга P = πr 2 = π · 1 2 = π≈ 3.14.
Площадь круга — калькулятор
Введите радиус круга и наш калькулятор рассчитает площадь круга.
Введите данные:
Радиус окружности: Вычислить площадь круга
Пояснения:
- Если результат «бесконечность», он выходит за пределы диапазона, доступного для этого калькулятора.

- Запись результата 1.2e + 12 означает число 1.2, умноженное на 10 12 .
- Когда одно из полученных чисел больше, чем его 64-битное представление, калькулятор использует аппроксимацию результата.
- Если указать действительное число, в расчете будет использоваться только целая часть.
Формула площади круга диаметром
Если мы дали диаметр круга d , то площадь круга вычисляется по следующей формуле:
P = πd 2
Длина круга
Длина окружности равна длине окружности.Приводим формулу длины окружности:
Теорема
Длина окружности с радиусом r равна:
Пример
Вычислим длину круга диаметром 1 м .
Круг диаметром 1 м имеет радиус r = 0,5 м (половина диаметра). Таким образом, длина окружности равна:
вопросов
Как вычислить площадь круга?
Если мы знаем длину радиуса, возводим ее в квадрат и умножаем на число π≈3,14.
Какова площадь круга?
Круг имеет нулевую площадь.
Задачи с решениями
Задачи по теме:
Площадь круга и длина круга
Задача — вычисление площади круга
Вычислить площадь круг диаметром
Показать решение задачи
Задача — длина окружности, вычисление длины окружности
Вычислить длину окружности диаметром d = 7
Показать решение задачи
Задача — площадь и радиус круга
Чему равен радиус круга с площадью 1?
Покажите решение задачи
Задача — Длина окружности
Сколько нужно нити, чтобы сделать из нее окружность диаметром 2 м?
Показать решение задачи
Задача — площадь круга
Площадь круга равна π.Чему равен радиус круга, площадь которого в два раза меньше? Вычислите отношение радиусов этих окружностей.
Показать решение задачи
Задача — площадь круга, практическое задание с содержанием
Из квадратной пластины со стороной 1 м вырезали круги радиусом r = 10 см так, что центры этих окружностей лежат на параллельных и перпендикулярных прямых. Какова площадь поверхности обрезков? Какой процент поверхности листа составляют обрезки?
Какова площадь поверхности обрезков? Какой процент поверхности листа составляют обрезки?
Показать решение задачи
Задача — площадь круга, площадь квадрата, квадрат вписанный в круг
В круг радиусом r вписан квадрат.Вычислите площадь фигуры, которая является разницей между этим кругом и квадратом?
Показать решение задачи
Задача — треугольник, вписанный в окружность
Равносторонний треугольник со стороной а = 1 описывает окружность. Найдите длину окружности этого круга и площадь круга, определяемого этим кругом.
Показать решение задачи
Задача — Окружность, вписанная в равносторонний треугольник
Введен равносторонний треугольник с длиной стороны а = 1 окружности. Вычислите его площадь и длину окружности.
Показать решение задачи
Задача — окружность, описанная треугольником
Прямоугольный треугольник с катетами 3 и 4 описывает окружность. Вычислите площадь и длину окружности этого круга.
Вычислите площадь и длину окружности этого круга.
Показать решение задачи
Задача — длина окружности
Вычислить длину окружности, заданной уравнением
Показать решение задачи
Другие вопросы из этого урока окружность
Окружность с центром S и радиусом r — это набор точек на плоскости, расстояние от которых до точки S равно положительному числу r.
Взаимное положение окружностей
Описание случаев взаимного расположения окружностей.
связанные викторины
Круг и круг Начальная школа
Начальная школа
класс 6
Количество вопросов: 10
Круг и круг
CARD086.PDF
Начальная школа
класс 6
© Medianauka.pl, 2010 -12-10, АРТ-1046
.
Формула длины окружности круга. Как рассчитать диаметр круга: формула
и пояснения
Одной строчки здесь нет, нужно знать специальные формулы. Единственное, что нас уводит, это определение диаметра или радиуса окружности. В некоторых заданиях эти значения указаны. Но что делать, если у нас нет ничего, кроме чертежа? Без проблем. Диаметр и радиус можно рассчитать с помощью обычной линейки. Теперь переходим к самому основному.
Единственное, что нас уводит, это определение диаметра или радиуса окружности. В некоторых заданиях эти значения указаны. Но что делать, если у нас нет ничего, кроме чертежа? Без проблем. Диаметр и радиус можно рассчитать с помощью обычной линейки. Теперь переходим к самому основному.
Формулы, которые должен знать каждый
Еще 4000 лет назад ученые раскрыли удивительную историю: если длину окружности разделить на ее диаметр, то получается такое же число, которое примерно равно 3.14. Это значение было названо именно от этой буквы в древнегреческом, слово начиналось с «окружность» и «окружность». На основе открытий, сделанных древними учеными, можно вычислить длину любой окружности:
Где p — длина (длина окружности) окружности,
D — диаметр, n — число «пи».
Длина окружности также может быть рассчитана по ее радиусу (R), который равен половине длины ее диаметра. Вот вторая формула, которую нужно запомнить:
Как найти диаметр круга?
Это хорда, проходящая через центр фигуры. При этом он соединяет две самые удаленные точки по окружности. Исходя из этого, вы можете сами прочитать диаметр (радиус) и измерить линейкой его длину.
При этом он соединяет две самые удаленные точки по окружности. Исходя из этого, вы можете сами прочитать диаметр (радиус) и измерить линейкой его длину.
Способ 1: Вписать прямоугольный треугольник в окружность
Вычислить длину окружности легко, если найдем ее диаметр. Необходимо чертить в круге, где закладная будет равна диаметру круга. Для этого обязательно иметь под рукой линейку и уголь, иначе ничего не получится.
Способ 2: Вводим любой треугольник
На стороне круга отмечаем любые три точки, соединяем их — получаем треугольник. Важно, чтобы центр круга лежал в районе треугольника, это можно сделать на глаз. Делаем каждую сторону средними, точка их пересечения совпадает с центром окружности. А когда мы знаем центр, можно легко нарисовать диаметр с помощью линий.
Этот способ очень похож на первый, но его можно использовать, когда нет квадрата или где невозможно рисовать на чертеже, например на тарелке.Необходимо сделать лист бумаги с прямыми углами. Прикладываем лист к окружности так, чтобы одна вершина его угла соприкасалась с краем окружности. Затем отмечаем точки пересечения сторон бумаги с линией окружности. Соедините эти точки карандашом и линейкой. Если на руках ничего нет, подождите бумагу. Эта линия будет равна длине диаметра.
Прикладываем лист к окружности так, чтобы одна вершина его угла соприкасалась с краем окружности. Затем отмечаем точки пересечения сторон бумаги с линией окружности. Соедините эти точки карандашом и линейкой. Если на руках ничего нет, подождите бумагу. Эта линия будет равна длине диаметра.
Пример задачи
- Ищем диаметр с помощью начертания, линии и карандаша по методике №1.5 см.
- Зная диаметр, мы легко подставим его в нашу формулу: p = D n = 5 * 3,14 = 15,7 в нашем случае получилось около 15,7. Теперь вы сможете объяснить, как рассчитать длину окружности.
Если в задаче известны такие значения, как длина круга, его радиус или площадь круга, ограниченного этим кругом, то вычисление диаметра будет простым. Существует несколько способов расчета диаметра позвонков. Они довольно просты и совершенно не вызывают никаких затруднений, как на первый взгляд.
Как найти диаметр окружности — 1 способ
После указания радиуса круга проблема наполовину решена, потому что радиус — это расстояние от точки, где он находится в любом месте круга, до центра окружности. Все, что вам нужно сделать, чтобы найти диаметр в этом случае, это умножить эту величину радиуса на 2. Этот метод расчета объясняется тем, что радиус равен половине диаметра. Следовательно, если известно, что радиус равен, то уже найдено значение, равное половине искомого размера диаметра.
Все, что вам нужно сделать, чтобы найти диаметр в этом случае, это умножить эту величину радиуса на 2. Этот метод расчета объясняется тем, что радиус равен половине диаметра. Следовательно, если известно, что радиус равен, то уже найдено значение, равное половине искомого размера диаметра.
Как найти диаметр окружности — 2 способа
Если в задаче задана только длина окружности, то для нахождения размера диаметра необходимо просто разделить его на число, известное как π, приблизительное значение которого равно 3,14. То есть если значение длины 31,4, то разделив его на 3,14, получим значение диаметра 10.
Как найти диаметр окружности — 3 способа
Если исходные данные получают значение площади круга, диаметр также является прямым.Все, что вам нужно сделать, это извлечь квадратный корень из этого значения и разделить полученный результат на число π. Это означает, что если значение площади равно 64, то при удалении корня остается число 8. Если мы разделим результат 8 на 3,14, мы получим значение диаметра около 2,5.
Как найти диаметр колеса — 4-ходовой
Внутри круга необходимо провести прямую линию или горизонтальную линию веревки от одной точки к другой. Пересеките эту прямую линию с линией круга, чтобы выбрать такие буквы, как A и V.Неважно, какие части круга находятся прямо.
Затем нужно нарисовать еще два круга. Но так, что точки в стальных центрах. Фигуры новой формы пересекаются в двух точках. Через них нужно провести еще одну прямую. Затем линейкой измеряем его длину. Измеренное значение i будет равно длине диаметра, так как в последней строке указан только диаметр.
Интересно, что еще очень далеко в прошлом, когда плетение корзин из определенного количества веточек занимало примерно в 3 раза больше времени.Ученые объяснили и экспериментально доказали, что если длину любой окружности разделить на диаметр, то в результате получится почти одно и то же число.
Нас окружает множество объектов. И многие из них имеют круглую форму. Его просят для удобного использования. Возьмем, к примеру, колесо. Если бы его сделали в виде квадрата, как бы он катился по дороге?
Возьмем, к примеру, колесо. Если бы его сделали в виде квадрата, как бы он катился по дороге?
Чтобы сделать круг, нужно знать, как выглядит формула длины окружности через диаметр. Для этого сначала определим, что такое понятие.
Окружность и окружность
Окружность – это множество точек, равноудаленных от главной точки – центра. Это расстояние называется радиусом.
Расстояние между двумя точками на этой прямой называется хордой. Также, если хорда проходит через главную точку (центр), она называется диаметром.
Теперь рассмотрим, что такое колесо. Совокупность всех точек, находящихся внутри контуров, называется окружностью.
Какова длина цепи?
Рассмотрев все определения, мы можем вычислить диаметр окружности.Формула будет рассмотрена чуть позже.
Начнем с того, что мы попробуем измерить длину стеклянной формы. Для этого обматываем его ниткой, то есть измеряемой линейкой, и узнаем примерную длину воображаемой линии вокруг стакана. Поскольку размер зависит от правильного измерения предмета, этот метод не является надежным. Но все же точные измерения вполне возможны.
Поскольку размер зависит от правильного измерения предмета, этот метод не является надежным. Но все же точные измерения вполне возможны.
Чтобы сделать это снова, вспомните колеса. Мы много раз видели, что если увеличить иглу в окружностях (радиусах), то увеличится и длина обода окружности (окружности).А также, с уменьшением радиуса колеса, обод становится меньше.
Если загрузить именно эти изменения, мы увидим, что длина воображаемой круглой линии пропорциональна ее радиусу. И этот номер постоянный. Затем рассмотрим, как определяется диаметр окружности: формула для этого есть для в примере ниже. И рассмотрим поэтапно.
Формула окружности по диаметру
Поскольку длина контура пропорциональна радиусу, она пропорциональна диаметру соответственно.Следовательно, его длина освободила буквы С, диаметр — д. Так как отношение длины контура и диаметра является постоянным числом, его можно определить.
Завершив все вычисления, определяем число, которое примерно равно 3 1415. .. т.к. конкретно в счете не получилось, обозначим нашей буквой π . Этот значок нам пригодится тем, что формула длины окружности выводится через диаметр.
.. т.к. конкретно в счете не получилось, обозначим нашей буквой π . Этот значок нам пригодится тем, что формула длины окружности выводится через диаметр.
Мы проведем воображаемую линию через центральную точку и измерим расстояние между двумя крайними точками.Это будет диаметр. Если нам известен диаметр окружности, то формула определения ее длины будет такой: С = d * π .
Если определить длину разных контуров, если известен их диаметр, то формула будет использоваться одна и та же. От марки π — Это приблизительный расчет, было принято решение умножить диаметр на 3,14 (число округлить до сотых).
Как рассчитать диаметр: Формула
На этот раз мы пытаемся использовать эту формулу для расчета других значений помимо длины контура.Для расчета диаметра по длине окружности используется та же формула. Только для этого он будет делить пи . Это будет выглядеть как d = c/π .
Подумайте, насколько важна эта формула на практике. Например, нам известна длина контура колодца, необходимо рассчитать его диаметр. Его нельзя измерить, потому что из-за погодных условий к нему нет доступа. И у нас есть задача сделать обложку. Что мы будем делать в этом случае?
Например, нам известна длина контура колодца, необходимо рассчитать его диаметр. Его нельзя измерить, потому что из-за погодных условий к нему нет доступа. И у нас есть задача сделать обложку. Что мы будем делать в этом случае?
Вы должны использовать формулу.Возьмем длину контура колодца — например, 600 см. Подставляем в формулу определенное число, а именно С = 600/3,14. В итоге получаем примерно 191 см. Округленный результат до 200 см. Затем с помощью циркуляции проводим круговую линию радиусом 100 см.
Так как контур большого диаметра приходится рисовать подходящей схемой, такой инструмент можно сделать самому. Для этого возьмите железную дорогу нужной длины и вбейте на каждом конце гвозди. Вставляем в заготовку один гвоздь и слегка вбиваем, чтобы он не сдвинулся с описанного места.И используя вторую черную линию. Устройство очень простое и удобное.
Современные технологии позволяют рассчитать длину контура для использования онлайн-калькулятора. Для этого просто введите диаметр круга. Формула будет применена автоматически. Вы также можете рассчитать длину окружности, используя радиус. Также, если известна длина окружности, онлайн-калькулятор вычисляет радиус и диаметр по этой формуле.
Формула будет применена автоматически. Вы также можете рассчитать длину окружности, используя радиус. Также, если известна длина окружности, онлайн-калькулятор вычисляет радиус и диаметр по этой формуле.
.
Окружность и окружность
Окружность — это множество всех точек на плоскости, расстояние которых от фиксированной точки (называемой центром окружности) меньше или равно заданному расстоянию (называемому радиусом окружности).
Окружность
Окружность — это множество всех точек на плоскости, расстояние которых от фиксированной точки (называемой центром окружности) равно заданному расстоянию (называемому радиусом окружности).
Проще говоря, круг — это край круга.
Окружность
С окружностью связаны следующие термины:
- хорда — отрезок, соединяющий две точки, лежащие на окружности,
- диаметр — хорда, проходящая через центр окружности,
- касательная — это прямая с окружностью ровно одной общей точки.
 2\] где \(r\) — радиус окружности.2 = 25\pi\]
2\] где \(r\) — радиус окружности.2 = 25\pi\]В окружности можно выделить два очень важных угла:
- центральный угол — это угол, вершина которого лежит в центре окружности, а стороны являются радиусами,
- угол вписанный угол — это угол, вершина которого лежит на окружности, а стороны — хорды.
Примеры центральных углов
Примеры вписанных углов
Дуги, на которых основаны вышеуказанные центральные и вписанные углы, отмечены синим цветом.
Если центральный угол и угол надписей основаны на одной и той же дуге, мера центрального угла в два раза больше.2 \sin\alpha}{2}\] где \(r\) — радиус окружности
Сегмент окружности определяется углом \(\alpha\)
.
с диаметром и радиусом
Таким образом, периметр ( C ) можно рассчитать, умножив константу пи на диаметр ( D ) или путем умножения pi на удвоенный радиус, так как диаметр равен двум радиусам.
 Следовательно, шаблон для периметра будет
Следовательно, шаблон для периметра будет.
С = πD = 2πR
где C — схема, pi — фиксированный, D — диаметр окружности, r — радиус окружности.
Поскольку окружность является границей окружности, длину окружности также можно назвать длиной окружности или окружностью окружности.
Проблемы со схемой
Задача 1. Найдите длину окружности, если ее диаметр равен 5 см.
Потому что периметр равен π умножить на диаметр, длина окружности диаметром 5см будет:
С ≈ 3,14 5 = 15,7 (см)
Упражнение 2. Найдите длину окружности радиусом 3,5 м.
Сначала найдите диаметр окружности, умножив длину радиуса на 2:
D = 3,5 2 = 7 (м)
Теперь найдите длину окружности, умножив пи для диаметра:
С ≈ 3,14 7 = 21,98 (м)
Упражнение 3. Найдите радиус окружности длиной 7,85 м.

Чтобы вычислить радиус окружности по длине окружности, разделите длину окружности на 2. π
Поверхность колеса
Площадь круга равна произведению π квадратных радиуса. Формула нахождения площади круга :
S = пр 2
где S площадь круга и r радиус круга.
Поскольку диаметр круга в два раза больше радиуса, радиус равен диаметру, деленному на 2:
Задачи на площадь круга
Задание 1. Найдите площадь круга, если его радиус равен 2 см.
Потому что площадь круга пи умножить на квадрат радиуса, площадь круга радиусом 2см будет:
S ≈ 3,14 2 2 = 3,14 4 = 12,56 (см 2)
Задача 2. Найдите площадь круга, если его диаметр равен 7 см.
Сначала найдите радиус круга, разделив его диаметр на 2:
7:2 = 3,5 (см)
Теперь посчитаем площадь круга по формуле:
S = пр 2 ≈ 3,14 3,5 2 = 3,14 12,25 \ u003d 38,465 (см 2)
Существуют и другие способы решения этой проблемы.
 Вместо того, чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
Вместо того, чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:90 130 S = пи 90 135 90 136 Д 2 90 135 90 130 ≈ 3,14 90 135 90 136 7 2 90 135 90 130 = 3,14 90 135 90 136 49 90 135 90 130 = 90 135 90 136 153,86 90 135 90 130 = 38,465 (см 2) 90 135 90 154 4 90 135 90 136 4 90 135 90 136 4 90 135 90 136 4 Задача 3. Найдите радиус круга, если его площадь равна 12,56 м2.
Чтобы найти радиус круга по его площади, разделите площадь круга на π , затем извлеките из результата квадратный корень:
.
r = √ S : пи
, поэтому радиус будет:
r ≈ √12,56: 3,14 = √4 = 2 (м)
Число
πОкружность окружающих нас предметов можно измерить сантиметровой лентой или веревкой (ниткой), длину которой затем можно измерить отдельно.Но в некоторых случаях трудно или почти невозможно измерить окружность, например, внутреннюю окружность бутылки или просто окружность, нарисованную на бумаге.
 В таких случаях можно вычислить длину окружности, если известна длина ее диаметра или радиуса.
В таких случаях можно вычислить длину окружности, если известна длина ее диаметра или радиуса.Чтобы понять, как это можно сделать, возьмем несколько круглых предметов, у которых можно измерить и длину окружности, и диаметр. Вычисляем отношение длины к диаметру, в результате чего получаем следующую последовательность цифр:
Отсюда можно сделать вывод, что отношение длины окружности к ее диаметру есть величина постоянная для каждой окружности и для всех окружностей в целом.Это отношение обозначено буквой π .
Используя эти знания, вы можете использовать радиус или диаметр круга, чтобы найти его длину. Например, чтобы вычислить длину окружности радиусом 3 см, нужно радиус умножить на 2 (так мы получаем диаметр) и полученный диаметр умножить на π . Наконец с числом π мы выяснили, что длина окружности радиусом 3 см равна 18,84 см.
Окружность — это изогнутая линия, окружающая окружность. В геометрии фигуры плоские, поэтому определение относится к двумерному изображению.
 Предполагается, что все точки этой кривой равноудалены от центра окружности.
Предполагается, что все точки этой кривой равноудалены от центра окружности.Колесо имеет несколько характеристик, на основании которых производятся расчеты, связанные с этой геометрической фигурой. К ним относятся: диаметр, радиус, площадь и периметр. Эти характеристики взаимосвязаны, а значит, для их расчета достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле, можно найти ее периметр, диаметр и площадь.
- Радиус окружности — это отрезок внутри окружности, соединенный с ее центром.
- Диаметр — это отрезок внутри окружности, соединяющий ее точки и проходящий через центр. На самом деле диаметр равен двум радиусам. Именно так выглядит формула его расчета: D = 2r.
- Есть еще одна составляющая окружности — хорда. Это прямая линия, соединяющая две точки на окружности, но не всегда проходящая через центр. Таким образом, хорда, проходящая через него, также называется диаметром.
Как найти окружность колеса? Теперь давайте узнаем.

Окружность: шаблон
Для обозначения этого признака была выбрана латинская буква р. Архимед также доказал, что отношение длины окружности к ее диаметру одинаково для всех окружностей: это число π, приблизительно равное 3,14159. Формула расчета π выглядит так: π = p/d. Согласно этой формуле значение p равно πd, то есть периметру: p = πd. Поскольку d (диаметр) равен двум радиусам, ту же формулу длины окружности можно записать как p = 2πr.Рассмотрим применение формулы на примере простых задач:
Задача 1
У основания Царского колокола диаметр 6,6 метра. Чему равна окружность основания колокола?
- Итак, формула для вычисления окружности: p = πd
- Подставляем имеющееся значение в формулу: p = 3,14 * 6,6 = 20,724 Ответ: Периметр основания колокола равен 20,7 метра.
- 1. Рассчитайте радиус круговой орбиты спутника Земли: 6370 + 320 = 6690 (км)
- 2.
 Рассчитайте длину круговой орбиты спутника по формуле: P = 2πr
Рассчитайте длину круговой орбиты спутника по формуле: P = 2πr - 3.Р = 2 * 3,14 * 6690 = 42013,2
- Радиус – это линия, соединяющая центр окружности и любую ее точку . Обозначается латинской буквой r
- Хорда — это линия, соединяющая любые две точек на окружности .
- Диаметром является линия, соединяющая две точки окружности и проходящая через ее центр .
 Обозначается латинской буквой d.
Обозначается латинской буквой d. - – это линия, состоящая из всех точек, находящихся на равном расстоянии от одной выбранной точки, называемой ее центром.Его длина будет обозначена латинской буквой l.
- Научитесь находить диаметр по длине окружности. Пусть оно будет равно 778,72 км. Вы должны найти ре. d = 778,72 / 3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого делим определенное выше значение d пополам.
 Получилось 90 011 р = 248/2 = 124 90 012 километров.
Получилось 90 011 р = 248/2 = 124 90 012 километров. - Рассмотрим, как найти длину данного круга, зная его радиус. Пусть r будет 8 дм 7 см. Переведем все в сантиметры, тогда r будет 87 сантиметров. Воспользуемся формулой, чтобы найти неизвестную длину окружности. Тогда наше искомое будет равно л = 2 * 3,14 * 87 = 546,36 см . Переведем наше полученное значение в целые числа метрических значений l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
- Предположим, нам нужно найти площадь данного круга по формуле его известного диаметра.2/(4П) = 2209/12,56 = 175,87 тыс. м.
- Как пользоваться вантузом в раковине
- Вытяжка для туалета с вентилятором
- Сруб бани построить
- 1 sqft в м2
- Чем лучше утеплить дом из керамзитобетонных блоков снаружи
- Как подключить двойной выключатель света на два провода
- Сварка по контуру
- Как измеряется влажность воздуха
- Расстояние от унитаза до гигиенического душа
- Чем вымыть зеркало без разводов в домашних условиях
- Как строить забор из профлиста своими руками
Задача 2
Искусственный спутник Земли вращается на расстоянии 320 км от планеты.Радиус Земли 6370 км. Какова длина круговой орбиты спутника?
Ответ: Длина круговой орбиты Земли составляет 42 013,2 км.
Методы измерения цепи
Вычисление длины окружности на практике используется нечасто. Причиной этого является приблизительное значение числа π.В быту для нахождения длины окружности используют специальный прибор — кривизну. Любая точка отсчета отмечается на окружности, и прибор направляется от нее строго по линии до этой точки.
Как найти длину окружности колеса? Нужно только помнить о простых формулах для расчетов.
Окружность представляет собой ряд точек, равноудаленных от одной точки, которая, в свою очередь, является центром окружности. Окружность также имеет свой радиус, равный расстоянию этих точек от центра.
Отношение длины круга к его диаметру одинаково для всех кругов. Это отношение представляет собой число, представляющее собой математическую константу, которая обозначается греческой буквой π.
 .
.Определение окружности колеса
Окружность можно рассчитать по следующей формуле:
Д = Пи D = 2 пи р
r — радиус окружности
D — диаметр колеса
Л — цепь
пи — 3.14
Задача:
Вычислите длину окружности с радиусом 10 сантиметров.
Решение:Формула для расчета колеса dyna выглядит так:
Д = Пи D = 2 пи р
, где L — длина окружности, π — 3,14, r — радиус окружности, D — диаметр окружности.
Таким образом, длина окружности радиусом 10 сантиметров равна:
Д = 2 × 3,14 × 5 = 31,4 см
Окружность — геометрическая фигура, представляющая собой множество всех точек плоскости, удаленных от данной точки, называемой ее центром, на некотором расстоянии, не равном нулю, и называемом радиусом.Уже в древности ученые умели определять его длину с разной степенью точности: историки науки считают, что первая формула для вычисления длины окружности была разработана около 1900 г.
 до н.э. в древнем Вавилоне.
до н.э. в древнем Вавилоне.С геометрическими фигурами, такими как круги, с которыми мы сталкиваемся каждый день и везде. Именно его форму имеет внешняя поверхность колес, которыми оснащены различные транспортные средства. Эта деталь, несмотря на кажущуюся простоту и незатейливость, считается одним из величайших изобретений человечества, и интересно, что аборигены Австралии и американские индейцы до прихода европейцев совершенно не представляли, что это такое.
Скорее всего, первые колеса представляли собой куски бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, его конструкция становилась все более сложной, и для их изготовления приходилось использовать множество различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем для уменьшения износа их наружной поверхности стали обить металлическими полосками. Для того, чтобы определить длину этих элементов, следует использовать формулу для расчета длины окружности (хотя на практике, скорее всего, мастера делали это «на глаз» или просто обвязывали колесо ремнем и отрезали от него необходимую часть) .

Следует отметить, что колесо используется далеко не только на транспортных средствах. Например, гончарный круг имеет свою форму, как и элементы зубчатых колес, широко используемых в технике. С древних времен строили водяные мельницы с колесами (древнейшие известные ученым конструкции такого типа были построены в Месопотамии), а также барабанами, из которых изготавливали нити из шерсти животных и растительных волокон.
Катушки часто встречаются в строительстве.Их форма — вполне обычные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций является очень сложной задачей и требует высокой квалификации, а также наличия специального инструмента. Одним из видов круглых окон являются иллюминаторы, устанавливаемые на кораблях и самолетах.
Поэтому часто приходится решать задачу определения длины окружности колеса инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и конструкторам.
 От пи Необходимое для этого бесконечно, определить этот параметр с абсолютной точностью не представляется возможным, поэтому в расчетах учитывается та степень, которая необходима и достаточна в конкретном случае.
От пи Необходимое для этого бесконечно, определить этот параметр с абсолютной точностью не представляется возможным, поэтому в расчетах учитывается та степень, которая необходима и достаточна в конкретном случае.1. Сложнее найти окружность по диаметру Итак, сначала рассмотрим этот вариант.
Пример: Найдите длину окружности диаметром 6 см . Воспользуемся приведенной выше формулой для длины окружности, но сначала нам нужно найти радиус.Для этого делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
Дальше все предельно просто: умножаем Пи на 2 и на полученный радиус 3см.
2 * 3,14 * 3 см = 6,28 * 3 см = 18,84 см.2. Теперь давайте снова рассмотрим простой вариант найти длину окружности радиусом 5 см
Решение: Радиус 5 см надо умножить на 2 и умножить на 3,14. Не беспокойтесь, перестановка факторов не влияет на результат, а паттерн на периметр можно накладывать в любом порядке.
5см * 2 * 3,14 = 10 см * 3,14 = 31,4 см — это длина окружности, найденная для радиуса 5 см!
Онлайн-калькулятор цепи
Наш схемотехнический калькулятор сразу сделает все эти несложные расчеты и напишет решение в соответствии с комментариями.
 Вычисляем окружность для радиуса 3, 5, 6, 8 или 1 см, или диаметр 4, 10, 15, 20 дм, нашему калькулятору все равно какое значение радиуса находит окружность.
Вычисляем окружность для радиуса 3, 5, 6, 8 или 1 см, или диаметр 4, 10, 15, 20 дм, нашему калькулятору все равно какое значение радиуса находит окружность.Все расчеты будут точными, проверенными математиками.Полученные результаты можно использовать при решении школьных задач по геометрии или математике, а также при рабочих расчетах в строительстве или при ремонте и отделке помещений, когда требуются точные расчеты по этой формуле.
Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле сложности в решении этой задачи нет, нужно только четко понимать, какие формулы требуются для этого понятия и определения.
В контакте с
Основные термины и определения
Площадь круга – это вся площадь , заключенная в круг . это измеряется в квадратных единицах и обозначается латинской буквой s.
Используя наши определения, мы заключаем, что диаметр окружности равен ее наибольшей хорде.
Внимание! По определению радиуса окружности можно узнать диаметр окружности. Это два луча, направленные в противоположные стороны!
Диаметр колеса.
Нахождение длины окружности и ее площади
Если получить радиус окружности, то диаметр окружности описывается формулой d = 2 * r . Итак, чтобы ответить на вопрос, как найти диаметр окружности, зная ее радиус, достаточно последнего, умножить на два .
Формула длины окружности, выраженная через радиус, равна l = 2 * P * r .

Внимание! Латинская буква P (Pi) обозначает отношение длины окружности к ее диаметру и является непериодической десятичной дробью.2/(4П) . Длина окружности определяется точно так же, как и площадь окружности.
Определение длины и диаметра радиуса
Важно! Первым делом учимся измерять диаметр. Очень просто — рисуем любой радиус, продлеваем его в обратную сторону до пересечения с дугой. Измеряем полученное расстояние компасом и с помощью любого метрического инструмента выясняем, что ищем!
Ответим на вопрос, как найти диаметр круга, зная его длину.2 = 4*с/р . Для определения самого диаметра нужно извлечь квадратный корень из правой части . Получается д=2*кврт(с/п).
Решение типовых задач
Цепь
.Rasmus.is — Руководство по математике — Расчет площади
2000 — 2009 Расмус эф
Расчет площади
Демонстрационный номер 4
Площадь и длина окружности
O = длина черного цвета линия, образующая окружность, называется окружностью.
 Его длину обозначим O.
Его длину обозначим O.d = диаметр — это хорда, через центр окружности и отмечен на рисунке в синем.
r = Радиус представляет собой сегмент соединяющий центр круга с его краем. есть на чертеже отмечены красным.
Если вы измеряете окружность и диаметр и разделите их на себя, вы получите число Пи, то есть 3,14.
число Пи является общим пишется греческой буквой .
Древние греки использовали это отметка для определения пропорции между окружностью и Диаметр круга. Если у вас нет знака на на калькуляторе можно использовать общепринятый приближения, т. е. число 3,14. Это достаточно точно для большинства расчетов.
Некоторые шаблоны, которые хорошо работают знать и понимать еще лучше.
№ по каталогу
Имя
Модель
Пи
= О / г
д
Диаметр
d = 2 ∙ r и d = О /
О
Цепь
д∙ знак равно О
р
Радиус
г = д / 2
С
Площадь поверхности
S = г 2 ∙
Некоторые примеры в
Пример № 1
Найдем диаметр.
 д = 2 ∙ 3см = 6см
д = 2 ∙ 3см = 6смПример № 2
Рассчитаем периметр. О = д ∙ = 6 см ∙ знак равно 18,8 см
Пример № 3
Найдем диаметр. д = О / = 18,8 см / = 6 см
Пример № 4
Площадь поверхности: S = r 2 ∙
S = 5м∙ 5м ∙ 78,5 м 2
(Примечание! Отметка означает приблизительное значение.)
Вы знаете вид квадрата прямоугольника. Маленький желтый прямоугольник — это четверть большой.
Маленький прямоугольник имеет площадь S. = 5м ∙ 5м = 25м 2 , значит весь большой прямоугольник имеет площадь S = 4 ∙ 25 м 2 = 100 м 2 .
Мы видим, что колесо имеет площадь меньше, чем у большого прямоугольника, потому что он находится в вошел в него. Зная площадь маленького квадрата, мы можем Умножаем на Пи и получаем площадь поверхности. колеса, то есть S = ∙ 25 м 2 = 78,5 м 2 .
Практикуйте вышеперечисленное примеры, затем выполните тест № 4.

PS Не забудьте регулярно заполнять табло.
.Вычисление длины окружности — план урока
Вычисление длины окружностиЗанятие во IIа классе — 15.11.2010.
Цели урока:
Учащийся умеет:
— вычислять длину круга, зная его диаметр или радиус,
— вычислять длину радиуса или диаметра круга, зная его длину,
— решать текстовые задачи, связанные на вычисление длины окружности,
— решать текстовые задачи, связанные со сравнением фигурных цепей,
Методы работы:
— демонстрация,
— собеседование,
— упражнения.
Формы работы:
— индивидуальная работа,
— групповая работа.
Учебные пособия и материалы:
— рабочие листы,
— 3 круга диаметром 6 см, 8 см, 10 см (каждому ученику),
— калькулятор,
— линейка,
— веревка около 50 см.Ход урока:
I Подготовительный этап
1. Проверка домашнего задания.
2. Введение в тему, уточнение цели занятия.
На сегодняшние занятия вы должны были принести три колеса диаметром 6см, 8см, 10см
и веревку ок. 50 см, линейка и калькулятор. Как вы думаете, для чего сегодня понадобятся эти предметы?
50 см, линейка и калькулятор. Как вы думаете, для чего сегодня понадобятся эти предметы?
А Мы рассчитаем окружности кругов с помощью веревки и линейки.3. Уточнение темы.
II Этап реализацииДа, сегодня мы посчитаем длину окружности колеса струной, но будем делать это не всегда, а именно сегодня. Как вы, наверное, помните, периметры любых многоугольников связаны в
раз с длинами соответствующих сторон. Периметр квадрата – это длина четырех сторон одинаковой длины, периметр прямоугольника – это две длины и две ширины, периметр прямоугольного треугольника – это длина трех его сторон, и какое соотношение можно найти, когда дело доходит до круга или круга?
Азрачки: длина окружности зависит от ее радиуса.
Да, сегодня мы будем изучать зависимость между длиной окружности колеса и длиной диаметра данного колеса
и длиной радиуса колеса.Упражнение 1
Измерьте длину диаметра объекта. Измерьте его окружность, т.е. длину окружности, используя нитку, бечевку или рулетку.
Разделите длину окружности на длину диаметра.
Повторите эти измерения и счета за принесенные предметы. Внесите результаты в таблицу.
Сравните полученные результаты.Длина окружности предмета Диаметр Отношение длины окружности к длине диаметра
Задание 2
На основании произведенных измерений вычислить, во сколько раз длина окружности равна
в окружности окружности — L/d. Проведите расчеты с помощью калькуляторов, результаты округлите до 0,01.Напишите на доске несколько образцов измерений. Учащиеся замечают, что количество
диаметров в окружности окружности чуть больше 3.Назовем найденное число пи и запишем его символом.
Уже много лет ученые пытаются определить точную величину числа пи, к сожалению, это число иррациональное и вычислить его полностью невозможно. В наших расчетах мы будем чаще всего использовать обозначение или приближение числа.Упражнение 3
Определение формулы длины окружности.
На основании сделанных измерений мы знаем, что:.
Умножив обе части этого уравнения на d, получим.Вместо длины диаметра мы можем подставить длину двух радиусов и получим формулу длины окружности:.
Разделите класс на 4 группы и решите задачи. Каждая группа задач 1, 2 и 6 получает
1 примера для решения.Задача 1.
Вычислите длину окружности с радиусом:
1см
2м
13дм
0,7км
Ответ:
L = 2 см Задача 2.
Вычислите длину окружности диаметром:
25см
123дм
345м
12ммОтвет:
L = 25 см
L = 123 дм
L = 345 м3 L = 0 .
Найдите приблизительную длину круга с радиусом 24см.Решение:
L = 2 r
L = 2 • 24 см
L 2 • 3,14 • 24 см
L 150,72 смУпражнение 4.
Вычислите примерную длину окружности диаметром 18 дм.Решение:
L = d
L = • 18 дм
L 3,14 • 18 дм
L 56,52 дмЗадача 5.
На сколько длина окружности с радиусом 10см больше длины окружности с диаметром 10см ?Решение:
Вычислим длины окружностей отдельных кругов:
L1 = 2 rr = 10 см
L1 = 2 • 10 см
L1 = 20 смL2 = dd = 10 см
20 см- 10 см = 10 см.

Ответ:
Окружность радиусом 10 см имеет длину окружности на 10 см больше, чем длина окружности диаметром 10 см.Задача 6.
Вычислить радиус окружности с длиной окружности:
12 см
6,2 м
34,8 дм
16,6 кмРешение:
Из формулы длины окружности вычисляем значение r:Отсюда соответствующие результаты:
6см
3.1м
17.4дм
8.3км
III Итоговый этапВо время занятий учитель записывает баллы, набранные отдельными группами, в таблицу. В конце урока он подсчитывает набранные баллы. Сумма очков в группе определяет место в группе.
Собирать и систематизировать сообщения. Повторение основных сведений о круге и круге: отличие круга от круга, радиус, диаметр. Как мы определяем число пи, по какой формуле мы можем вычислить длину окружности, зная длину радиуса или длину диаметра.IV Домашнее задание — учебник п.72 задание. 3 — 8.
Приложение:
Рабочий лист
Задание 1.
Вычислите длину окружности с радиусом:
1см
2м
13дм
0. 7км
7кмЗадание 2.
Вычислите длину круга с диаметром:
25см
123дм
345м
12ммЗадача 3.
Вычислите примерную длину круга с радиусом 24см.Упражнение 4.
Найдите примерную длину окружности диаметром 18 дм.Упражнение 5.
На сколько длина окружности с радиусом 10см больше длины окружности с диаметром 10см?Задание 6.
.
Вычислите радиус окружности с окружностью:
12 см
6,2 м
34,8 дм
16,6 кмМодуль шестерни — таблица, что это такое, как рассчитать, формула
Что такое модуль шестерни?
Рис. 1 Основные параметры зубчатого колеса, источник [1]
Модуль зубчатого колеса является параметром, необходимым для выбора взаимодействующих звездочек, т.к. быть одинаковым. Модуль – характерный размер шестерни. Это сегмент диаметра делительной окружности, приходящийся на один зуб колеса.
Каждая шестерня имеет несколько параметров. Шаг или количество зубьев — это еще не все.
 К параметрам относятся наружный диаметр рейки, ширина зуба, диаметр отверстия и модуль. Хотя эти первые термины не нужно никому объяснять, понятие модуля может быть трудным.
К параметрам относятся наружный диаметр рейки, ширина зуба, диаметр отверстия и модуль. Хотя эти первые термины не нужно никому объяснять, понятие модуля может быть трудным.Модуль — характерный размер шестерни. Это размер, необходимый для определения размеров зубьев и шестерен, вытекающих из условий его прочности.Конструкция такой модели должна ограничивать размер используемых шестерен, особенно прямозубых. Другими словами, слишком большая звездочка может просто не подойти. При выборе атакующей стойки и приемной стойки (и наоборот) модуль обеих стоек должен быть идентичен. В противном случае они не приживутся должным образом и не будут сидеть идеально, что приведет к быстрому износу зубов.
Модуль формулы зубчатого колеса
Рассчитаем модуль видимого зубчатого колеса, можем воспользоваться следующей формулой:
зубьев 15, его модуль равен 2, потому что 34/(15+2) равно 2.
Выбор шестерен с разными модулями имеет определенные последствия, например, то, что они не будут идеально зацепляться, что приведет к быстрому износу зубьев.
 Надеемся, что благодаря этой информации выбор подходящей передачи больше не будет проблемой.
Надеемся, что благодаря этой информации выбор подходящей передачи больше не будет проблемой.Таблица модулей зубчатых колес
Модули зубчатых колес стандартизированы, наряду с параметрами шага, высотой головки зуба, высотой основания, общей высотой зуба. Эти значения перечислены в таблице ниже.
Таблица 1. Значения модулей, шагов, высоты зуба, высоты стопы
и суммарной нормальной высоты зуба, источник [2]Модуль определяет не только диаметр делительной окружности, но и высота зуба. Для нормальных зубьев высота головки зуба ha равна модулю м.
В странах, использующих дюймовую систему, характерным размером зубчатого колеса является не модуль, а Диаметральный шаг, DP , это количество зубьев шестерни на один английский дюйм диаметра делительной окружности.
Зубчатые колеса могут быть изготовлены самостоятельно на горизонтально-фрезерных и универсально-фрезерных станках. Широкий выбор готовых шестерен по цене от 5,25 злотых за штуку можно найти на сайте Магазина EBMiA .

Библиография:
1. Добжански Т., Технический чертеж, Научное издательство PWN, Варшава, 2020.
2. Гурски Э., Порадник Фрезера, Научное издательство PWN, Варшава, 2016.В следующих статьях мы опишем:
Механические шестерни
.Смотрите также
Окружности — Окружности и площади
Окружности и площади окружностей с диаметром в дюймах.

Sponsored Links
Download and print Circumference and Area vs. Circle Diameter chart
Circumference and area vs circle diameter:
Diameter
(in)Circumference
(in)Площадь
(в 2 )1/64 0.049 0.00019 1/32 0.098 0.00077 3/64 0.147 0.0017 1/16 0.196 0.0031 3/32 0.295 0.0069 1/8 0.393 0.012 5/32 0.491 0.019 3/16 0.589 0.028 7/32 0.687 0.038 1/4 0.  785
7850.049 9/32 0.884 0.062 5/16 0.982 0.077 11/32 1.08 0.093 3/8 1.18 0.11 13/32 1.28 0.13 7/16 1.37 0.15 15/32 1.47 0.17 1/2 1.57 0.20 17/32 1.67 0.22 9/16 1.77 0.25 19/32 1.87 0.28 5/8 1.96 0.31 21/32 2.06 0.34 11/16 2.16 0.37 23/32 2.  26
260.41 3/4 2.36 0.44 25/32 2.45 0.48 13/16 2.55 0.52 27/32 2.65 0.56 7/8 2.75 0.60 29/32 2.85 0.65 15/16 2.95 0.69 31/32 3.04 0.74 1 1/16 3.34 0.89 1 1/8 3.53 0.99 1 3/16 3.73 1.11 1 1/4 3.93 1.23 1 5/16 4.12 1.35 1 3 /8 4.32 1.48 1 7/16 4.  52
521.62 1 1/2 4.71 1.77 1 9/16 4.91 1.92 1 5/8 5.11 2.07 1 11/16 5.30 2.24 1 3/4 5.50 2.41 1 13 /16 5.69 2.58 1 7/8 5.89 2.76 1 15/16 6.09 2.95 2 1/16 6.48 3.34 2 1/8 6.68 3.55 2 3/16 6.87 3.76 2 1/4 7.07 3.98 2 5/16 7.26 4.20 2 3/8 7.46 4.43 2 7/16 7.  66
664.67 2 1/2 7.85 4.91 2 9/16 8.05 5.16 2 5/8 8.25 5.41 2 11/16 8.44 5.67 2 3/4 8.64 5.94 2 13/16 8.84 6.21 2 7/8 9.03 6.49 2 15/16 9.23 6.78 3 1/16 9.62 7.37 3 1/8 9.82 7.67 3 3/16 10.01 7.98 3 1/4 10.21 8.30 3 5/16 10.41 8.62 3 3/8 10.60 8.95 3 7/16 10.  80
809.28 3 1/2 11.00 9.62 3 9/16 11.19 9.97 3 5/8 11.39 10.32 3 11/16 11.58 10.68 3 3/4 11.78 11.04 3 13/16 11.98 11.42 3 7/8 12.17 11.79 3 15/16 12.37 12.18 4 1/8 12.96 13.36 4 3/16 13.16 13.77 4 1/4 13.35 14.19 4 5/16 13.55 14.61 4 3/8 13.74 15.03 4 7/16 13.94 15.  47
474 1/2 14.14 15.90 4 9/16 14.33 16.35 4 5/8 14.53 16.80 4 11/16 14.73 17.26 4 3/4 14.92 17.72 4 13/16 15.12 18.19 4 7/8 15.32 18.67 4 15/16 15.51 19.15 5 1/8 16.10 20.63 5 3 /16 16.30 21.14 5 1/4 16.49 21.65 5 5/16 16.69 22.17 5 3/8 16.89 22.69 5 7/16 17.08 23.22 5 1/2 17.  28
2823.76 5 9/16 17.48 24.30 5 5/8 17.67 24.85 5 11/16 17.87 25.41 5 3/4 18.06 25.97 5 13/16 18.26 26.53 5 7/8 18.46 27.11 5 15/16 18.65 27.69 6 1/8 19.24 29.46 6 1/4 19.63 30.68 6 3/8 20.03 31.92 6 1/2 20.42 33.18 6 5/8 20.81 34.47 6 3/4 21.21 35.78 6 7/8 21.60 37.  12
127 1/8 22.38 39.87 7 1/4 22.78 41.28 7 3/8 23.17 42.72 7 1/2 23.56 44.18 7 5/8 23.95 45.66 7 3/4 24.35 47.17 7 7/8 24.74 48.71 8 1 /8 25.53 51.85 8 1/4 25.92 53.46 8 3/8 26.31 55.09 8 1/2 26.70 56.75 8 5/8 27.10 58.43 8 3/4 27.49 60.13 8 7/8 27.88 61.86 9 1/8 28.  67
6765.40 9 1/4 29.06 67.20 9 3/8 29.45 69.03 9 1/2 29.85 70.88 9 5/8 30.24 72.76 9 3/4 30.63 74.66 9 7/8 31.02 76.59 10 1/8 31.81 80.52 10 1/4 32.20 82.52 10 3/8 32.59 84.54 10 1/2 32.99 86.59 10 5/8 33.38 88.66 10 3/4 33.77 90.76 10 7/8 34.16 92.89 - 1 in (inch) = 25.
 4 mm
4 mm - 1 in 2 = 645.2 mm 2 = 6.452 cm 2 = 6.452×10 -4 m 2
Рекламные ссылки
Связанные темы
Связанные документы
Engineering ToolBox — Расширение SketchUp — 3D-моделирование в режиме онлайн!
Добавляйте стандартные и настраиваемые параметрические компоненты, такие как балки с полками, пиломатериалы, трубопроводы, лестницы и т. д., в свою модель Sketchup с помощью Engineering ToolBox — расширение SketchUp, которое можно использовать с потрясающими, интересными и бесплатными программами SketchUp Make и SketchUp Pro. .Добавьте расширение Engineering ToolBox в свой SketchUp из хранилища расширений SketchUp Pro Sketchup!
Перевести
О Engineering ToolBox!
Мы не собираем информацию от наших пользователей. В нашем архиве сохраняются только электронные письма и ответы. Файлы cookie используются только в браузере для улучшения взаимодействия с пользователем.

Некоторые из наших калькуляторов и приложений позволяют сохранять данные приложения на локальном компьютере. Эти приложения будут — из-за ограничений браузера — отправлять данные между вашим браузером и нашим сервером. Мы не сохраняем эти данные.
Google использует файлы cookie для показа нашей рекламы и обработки статистики посетителей. Пожалуйста, прочитайте Конфиденциальность и условия Google для получения дополнительной информации о том, как вы можете контролировать показ рекламы и собираемую информацию.
AddThis использует файлы cookie для обработки ссылок на социальные сети. Пожалуйста, прочитайте AddThis Privacy для получения дополнительной информации.
Реклама в ToolBox
Если вы хотите продвигать свои товары или услуги в Engineering ToolBox — используйте Google Adwords. Вы можете настроить таргетинг на Engineering ToolBox с помощью управляемых мест размещения AdWords.
Citation
Эту страницу можно цитировать как
- Engineering ToolBox, (2008).
 Круги — Окружности и площади . [онлайн] Доступно по адресу: https://www.engineeringtoolbox.com/circles-circumferences-areas-d_1346.html [День доступа, мес. год].
Круги — Окружности и площади . [онлайн] Доступно по адресу: https://www.engineeringtoolbox.com/circles-circumferences-areas-d_1346.html [День доступа, мес. год].
Изменить дату доступа.
. .
закрыть
Изменить размер RADIUS на DIAMETER
Добро пожаловать в MCAD Central
Присоединяйтесь к нашим форумам сообщества MCAD Central, крупнейшему ресурсу для профессионалов MCAD (механического автоматизированного проектирования), включая файлы, форумы, вакансии, статьи, календарь и многое другое.
Регистрация Авторизоваться
JavaScript отключен. Для лучшего опыта, пожалуйста, включите JavaScript в вашем браузере, прежде чем продолжить.
- Автор темы jzamarr2
- Дата начала
джзамарр2
Новый участник
Привет всем,
Мне нужна помощь с уточнением DIMENSION.
Я не могу найти способ изменить размер RADIUS
на размер DIAMETER.Прикрепите снимок экрана.
Спасибо за помощь, Тони
Посмотреть вложение 4986
джсантанжело
Новый участник
Если вы используете на чертеже размеры «Показать/скрыть» (что вы и должны делать), то вам нужно отредактировать элемент в детали с таким диаметром/радиусом и изменить его размеры. При указании размера нужного элемента выберите его дважды, и он будет указан как диаметр. Если вы просто выберете его один раз, он будет измерять его как радиус. Вернитесь к чертежу, снова покажите размеры и выберите новый диаметр.
джзамарр2
Новый участник
Спасибо!
дбреда
Новый участник
Я просто хотел сообщить вам, что мы упростили эту задачу в Wildfire 5.
 0 (теперь Creo Elements Pro 5.0). Теперь вы можете преобразовать размер радиуса в диаметр и наоборот в Sketcher, выбрав размер RMB и соответствующую опцию.
0 (теперь Creo Elements Pro 5.0). Теперь вы можете преобразовать размер радиуса в диаметр и наоборот в Sketcher, выбрав размер RMB и соответствующую опцию.Дон
контраст
Новый участник
Если это размер, размещенный на чертеже, просто дважды щелкните круг, и он должен отображаться как диаметр.
смб
Новый участник
Я выполнил преобразование, дважды щелкнув соответствующую кривую. Работает все время.
Фрикат
Член
Как насчет того, чтобы по-настоящему произвести на нас, креосцев, PTC впечатление… Для показанных размеров, как насчет того, чтобы не заставлять нас заходить в скетчер, чтобы сделать это простое изменение?
Логика — вы можете настроить размеры показанных размеров на чертеже, почему не диаметр/радиус?
Подготовил: Richhdr_gallup
Модератор
Раньше мы могли напрямую переходить к тому, что называлось переопределением схемы из чертежа.
 Я думаю, что это было в меню ПКМ из любого показанного размера эскиза. Он позволяет полностью переопределить схему размеров сечения, а не просто изменить радиус на диаметр. Вам не нужно было переходить от чертежа к детали, находить элемент, переопределять сечение и возвращаться к чертежу, как мы должны сделать сегодня. Я думаю, что этот радикальный инструмент повышения производительности ушел где-то после R20.
Я думаю, что это было в меню ПКМ из любого показанного размера эскиза. Он позволяет полностью переопределить схему размеров сечения, а не просто изменить радиус на диаметр. Вам не нужно было переходить от чертежа к детали, находить элемент, переопределять сечение и возвращаться к чертежу, как мы должны сделать сегодня. Я думаю, что этот радикальный инструмент повышения производительности ушел где-то после R20.Фрикат
Член
dr_gallup сказал:
Раньше мы могли напрямую переходить к тому, что называлось переопределением схемы из чертежа. Я думаю, что это было в меню ПКМ из любого показанного размера эскиза. Он позволяет полностью переопределить схему размеров сечения, а не просто изменить радиус на диаметр. Вам не нужно было переходить от чертежа к детали, находить элемент, переопределять сечение и возвращаться к чертежу, как мы должны сделать сегодня.
 Я думаю, что этот радикальный инструмент повышения производительности ушел где-то после R20.
Я думаю, что этот радикальный инструмент повышения производительности ушел где-то после R20.Нажмите, чтобы развернуть…
sketcher_allow_redefine_scheme да
Под редакцией: Richh
dr_gallup
Модератор
Рич сказал:
dr_gallup сказал:
Раньше мы могли напрямую переходить к тому, что называлось переопределением схемы из чертежа. Я думаю, что это было в меню ПКМ из любого показанного размера эскиза. Он позволяет полностью переопределить схему размеров сечения, а не просто изменить радиус на диаметр. Вам не нужно было переходить от чертежа к детали, находить элемент, переопределять сечение и возвращаться к чертежу, как мы должны сделать сегодня. Я думаю, что этот радикальный инструмент повышения производительности ушел где-то после R20.

Нажмите, чтобы развернуть…
sketcher_allow_redefine_scheme да
Нажмите, чтобы развернуть…
Какой релиз? Этого нет ни в WF2, ни в WF4.
джсантанжело
Новый участник
Рич сказал:
sketcher_allow_redefine_scheme да
Нажмите, чтобы развернуть…
dr_gallup сказал:
Какой выпуск? Этого нет ни в WF2, ни в WF4.
Нажмите, чтобы развернуть…
У меня тоже не работает в WF4.
Вы должны войти или зарегистрироваться, чтобы ответить здесь.
Делиться:
Фейсбук Твиттер Реддит Пинтерест Тамблер WhatsApp Эл.
 адрес Делиться Ссылка на сайт
адрес Делиться Ссылка на сайтВерх
Площадь поперечного сечения в диаметр преобразование окружности сечение поперечное сечение диаметр электрического кабеля формула проводника диаметр провода и проводка и расчетное сечение AGW American Wire Gauge толщина сплошного провода формула проводимость удельное сопротивление многожильный провод литц длина ток
Площадь поперечного сечения в диаметр преобразование окружности поперечное сечение диаметра электрического кабеля формула проводника диаметр провода и проводка и расчет поперечного сечения AGW American Wire Gauge толщина сплошного провода формула проводимость удельное сопротивление многожильный провод литц длина ток — sengpielaudio Sengpiel BerlinНемецкая версия Преобразование и calculation − cross section < > diameter
● Cable diameter to circle cross-sectional area and vice versa ●
Round electric cable , проводник , провод , шнур , строка , проводка и трос
Поперечное сечение — это просто двумерное изображение среза объекта. 
Часто задаваемый вопрос: Как можно преобразовать диаметр круглого провода d = 2 × r в поверхность поперечного сечения круга
или площадь поперечного сечения A (плоскость сечения) в кабель диаметр d ?
Почему значение диаметра больше значения площади? Потому что это не то же самое.
Сопротивление обратно пропорционально площади поперечного сечения провода.
Требуемое сечение электрической линии зависит от следующих факторов:
1) Номинальное напряжение. Чистая форма. (трехфазный (DS) / переменный ток (WS))
2) Предохранитель — входной резерв = Максимально допустимый ток (А)
3) По графику передаваемая мощность (кВА)
4) Длина кабеля в метрах (м)
5) Допустимое падение напряжения (% от номинального напряжения)
6) Материал линии. Медь (Cu) или алюминий (Al)Используемый браузер не поддерживает JavaScript.
Вы увидите программу, но функция не будет работать.
«Единицей измерения» обычно являются миллиметры, но также могут быть дюймы, футы, ярды, метры (метры),
или сантиметры, если взять за площадь квадрат этой меры.
Многожильный провод (многожильный провод), состоящий из множества тонких проводов, требует на 14 % большего диаметра по сравнению со сплошным проводом.
Площадь поперечного сечения не является диаметром.
Сечение – это площадь.
Диаметр является линейной мерой.
Этого не может быть.
Диаметр кабеля в миллиметрах
не является поперечным сечением кабеля в
квадратных миллиметрах.
Поперечное сечение или площадь поперечного сечения представляет собой площадь такого разреза. 0 9
Это не обязательно должен быть круг.
Размер имеющегося в продаже провода (кабеля) по площади поперечного сечения:
0,75 мм 2 , 1,5 мм 2 , 2,5 мм 2 , 4 мм 2 , 6 мм 2 , 10 мм 3 0 2Расчет поперечного сечения A , входя в диаметр D = 2 R :
R = Radius проволоки OR CABLE
R = Radius проволоки или кабеля
R = Radius проволоки OR CABLE
R = RADIUS OR CABLE
R = радио провод или кабельРасчет диаметра d = 2 r , входящий в сечение А : Проводник (кабель электрический) На сопротивление проводника влияют четыре фактора:
1) площадь поперечного сечения проводника A , рассчитанная по диаметру d
2) длина проводника
3) длина проводника температура в проводнике
4) материал, из которого изготовлен проводникНе существует точной формулы для определения минимального размера провода из максимальной силы тока . 
Это зависит от многих обстоятельств, например, если расчет ведется для постоянного тока, переменного тока или
даже для трехфазного тока, свободно ли освобождается кабель, или он находится под заземлением
. Кроме того, это зависит от температуры окружающей среды, допустимой плотности тока и допустимого падения напряжения
, а также от наличия сплошного или многожильного провода. И всегда есть
хороший, но неудовлетворительный совет использовать из соображений безопасности более толстый и, следовательно,
более дорогой кабель. Часто возникают вопросы о падении напряжения на проводах.Падение напряжения Δ В
The voltage drop formula with the specific resistance (resistivity) ρ (rho) is:
Δ V = I × R = I × (2 × л × ρ / A )
I = ток в амперах
l = длина провода (кабеля) в метрах (умножить на 2, потому что всегда есть обратный провод)
ρ = rho, удельное электрическое сопротивление (также известное как удельное электрическое сопротивление или объем
удельное сопротивление) меди = 0,01724 Ом×мм 2 /м (также Ом×м)
(Ом для l = 1 м длины и A = 1 мм 2 площадь поперечного сечения провода) ρ = 1 / σ
A = площадь поперечного сечения в мм · м/мм 2Количество сопротивлений R = сопротивление Ом ρ = удельное сопротивление Ом×м l = двойная длина кабеля м A = поперечное сечение мм 2 Производная единица удельного электрического сопротивления в системе СИ ρ равна Ом × м, сокращенно чистый Ом × мм/м.

Обратной величиной удельного электрического сопротивления является электропроводность.Electrical conductivity and electrical resistivity κ or σ = 1/ ρ
Electrical conductance and electrical resistance ρ = 1/ κ = 1/ σРазница между удельным электрическим сопротивлением и электропроводностью
Проводимость в сименсах пропорциональна сопротивлению в омах. Чтобы использовать калькулятор, просто введите значение.
Калькулятор работает в обе стороны знака ↔ .Величина электропроводности (проводимости) и удельного электрического сопротивления
(удельное сопротивление) представляет собой константу материала, зависящую от температуры. В основном это дается при 20 или 25°C.
В основном это дается при 20 или 25°C.Сопротивление = удельное сопротивление x длина / площадь
2 0 293,15 К = 20°С, при котором известно удельное электрическое сопротивление ρ ( Тл 0 ).Удельное сопротивление проводников зависит от температуры.
В ограниченном диапазоне температур приблизительно линейна:
где α температурный коэффициент, T температура и T 0 любая температура,
например TПреобразование сопротивления в электрическую проводимость
Преобразование обратной величины сименса в омы
1 ом [Ом] = 1 / сименс [1/См]
1 сименс [См] = 1 / ом [1/Ом] 7Чтобы использовать калькулятор, просто введите значение. 
Калькулятор работает в обе стороны знака ↔ .1 миллисименс = 0,001 МОм = 1000 Ом
Математически проводимость обратно пропорциональна сопротивлению: Символом проводимости является заглавная буква «G», а единицей измерения является
мОм, что означает «Ом», написанный наоборот. Позже единицу mho
заменили единицей Siemens, сокращенно буквой «S».Калькулятор: закон Ома
Таблица типовых кабелей громкоговорителей
Диаметр кабеля d 0,798 мм 0,977 мм 1,128 мм 1,382 мм 1,784 мм 2,257 мм 2,764 мм 3,568 мм Номинальное сечение кабеля A 0,5 мм 2 0,75 мм 2 1,0 мм 2 1,5 мм 2 2,5 мм 2 4,0 мм 2 6,0 мм 2 10,0 мм 2 Максимальный электрический ток 3 А 7,6 А 10,4 А 13,5 А 18,3 А 25 А 32 А — Всегда учитывайте, что сечение должно быть больше при большей мощности и длине
кабеля, но также и при меньшем импедансе. Вот таблица, показывающая возможные потери мощности.
Вот таблица, показывающая возможные потери мощности.Длина кабеля
в мСечение
в мм 2Сопротивление
в ОмПотеря питания на Коэффициент демпфирования при Полное сопротивление
8 ОмПолное сопротивление
4 ОмПолное сопротивление
8 ОмПолное сопротивление
4 Ом1 0,75 0,042 0,53% 1,05% 98 49 1,50 0,021 0,31% 0,63% 123 62 2,50 0,013 0,16% 0,33% 151 75 4,00 0,008 0,10% 0,20% 167 83 2 0,75 0,084 1,06% 2,10% 65 33 1,50 0,042 0,62% 1,26% 85 43 2,50 0,026 0,32% 0,66% 113 56 4,00 0,016 0,20% 0,40% 133 66 5 0,75 0,210 2,63% 5,25% 32 16 1,50 0,125 1,56% 3,13% 48 24 2,50 0,065 0,81% 1,63% 76 38 4,00 0,040 0,50% 1,00% 100 50 10 0,75 0,420 5,25% 10,50% 17 9 1,50 0,250 3,13% 6,25% 28 14 2,50 0,130 1,63% 3,25% 47 24 4,00 0,080 1,00% 2,00% 67 33 20 0,75 0,840 10,50% 21,00% 9 5 1,50 0,500 6,25% 12,50% 15 7 2,50 0,260 3,25% 6,50% 27 13 4,00 0,160 2,00% 4,00% 40 20 Значения коэффициента демпфирования показывают, что остается от принятого коэффициента демпфирования 200
в зависимости от длины кабеля, поперечного сечения и импеданса громкоговорителя.
Преобразование и расчет диаметра кабеля в AWG
и AWG в диаметр кабеля в мм — American Wire GaugeЧаще всего мы используем четные числа, такие как 18, 16, 14 и т. д.
Если вы получили нечетный ответ, например 17, 19 и т. д., используйте ближайшее меньшее четное число.
AWG расшифровывается как American Wire Gauge и относится к прочности проводов.
Эти номера AWG показывают диаметр и, соответственно, поперечное сечение в виде кода.
Они используются только в США. Иногда вы найдете номера AWG также в каталогах
и технических данных в Европе.Американский калибр проводов — таблица AWG
AWG
номер46 45 44 43 42 41 40 39 38 37 36 35 34 Диаметр
в дюймах0,0016 0,0018 0,0020 0,0022 0,0024 0,0027 0,0031 0,0035 0,0040 0,0045 0,0050 0,0056 0,0063 Диаметр (Ø)
в мм0,04 0,05 0,05 0,06 0,06 0,07 0,08 0,09 0,10 0,11 0,13 0,14 0,16 Сечение
в мм 20,0013 0,0016 0,0020 0,0025 0,0029 0,0037 0,0049 0,0062 0,0081 0,010 0,013 0,016 0,020 AWG
номер33 32 31 30 29 28 27 26 25 24 23 22 21 Диаметр
в дюймах0,0071 0,0079 0,0089 0,0100 0,0113 0,0126 0,0142 0,0159 0,0179 0,0201 0,0226 0,0253 0,0285 Диаметр (Ø)
в мм0,18 0,20 0,23 0,25 0,29 0,32 0,36 0,40 0,45 0,51 0,57 0,64 0,72 Сечение
в мм 20,026 0,032 0,040 0,051 0,065 0,080 0,10 0,13 0,16 0,20 0,26 0,32 0,41 AWG
номер20 19 18 17 16 15 14 13 12 11 10 9 8 Диаметр
в дюймах0,0319 0,0359 0,0403 0,0453 0,0508 0,0571 0,0641 0,0719 0,0808 0,0907 0,1019 0,1144 0,1285 Диаметр (Ø)
в мм0,81 0,91 1,02 1,15 1,29 1,45 1,63 1,83 2,05 2,30 2,59 2,91 3,26 Поперечное сечение
в мм 20,52 0,65 0,82 1,0 1,3 1,7 2.  1
12,6 3,3 4,2 5,3 6,6 8,4 AWG
номер7 6 5 4 3 2 1 0
(1/0)
(0)00
(2/0)
(-1)000
(3/0)
(-2)0000
(4/0)
(-3)00000
(5/0)
(-4)000000
(6/0)
(-5)Диаметр
в дюймах0,1443 0,1620 0,1819 0,2043 0,2294 0,2576 0,2893 0,3249 0,3648 0,4096 0,4600 0,5165 0,5800 Диаметр (Ø)
в мм3,67 4.11 4,62 5,19 5,83 6,54 7,35 8,25 9,27 10,40 11,68 13. 

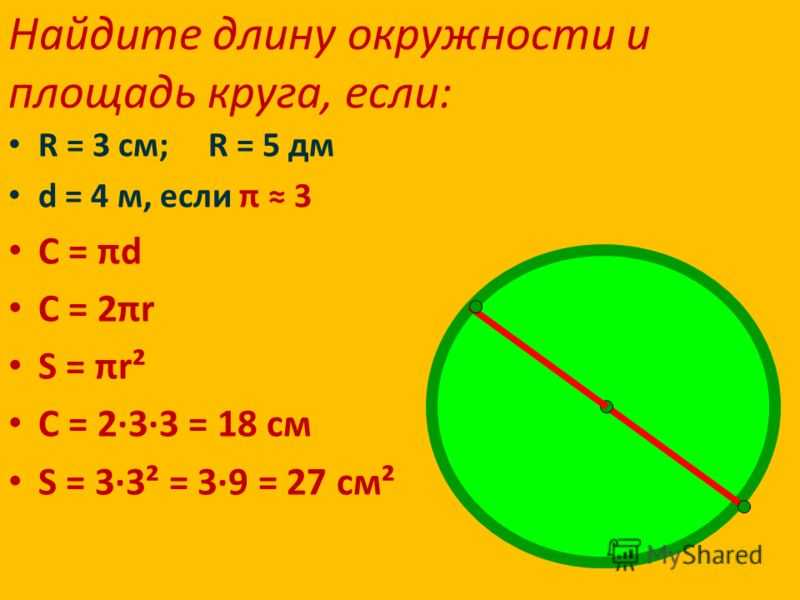 Для начала потребуется измерять его радиус . Для этого нужно воспользоваться циркулем. Одну его ножку ставим в центр круга, а вторую на любую точку окружности. Поскольку окружность представляет собой совокупность всех равно-отдаленных точек от центра, то куда именно станет вторая ножка циркуля — роли не играет, поскольку везде будет одинаковое расстояние.
Для начала потребуется измерять его радиус . Для этого нужно воспользоваться циркулем. Одну его ножку ставим в центр круга, а вторую на любую точку окружности. Поскольку окружность представляет собой совокупность всех равно-отдаленных точек от центра, то куда именно станет вторая ножка циркуля — роли не играет, поскольку везде будет одинаковое расстояние.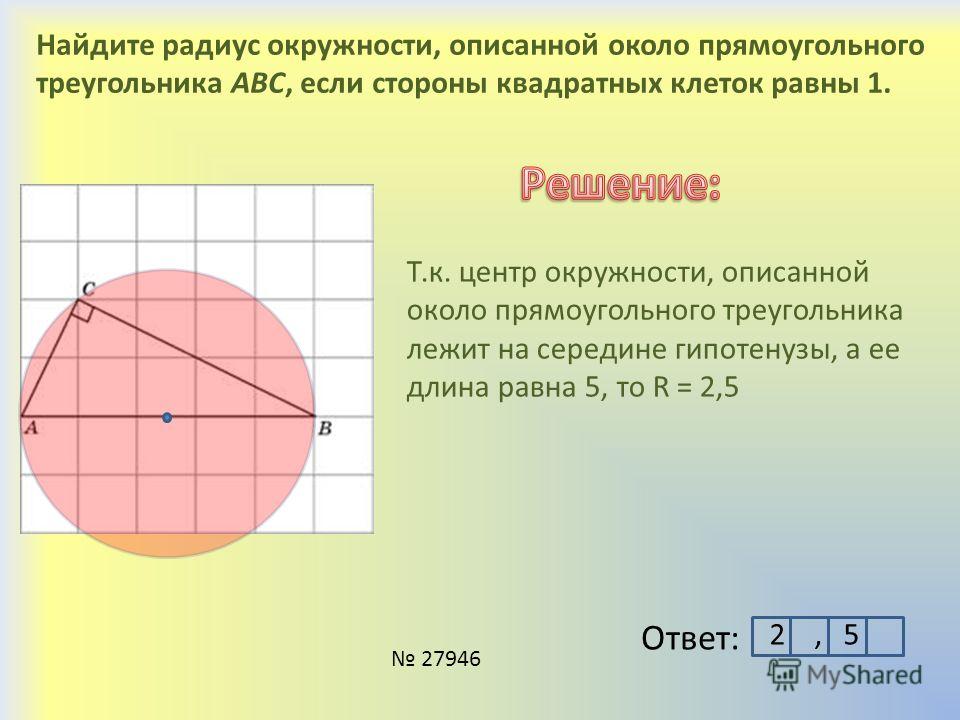

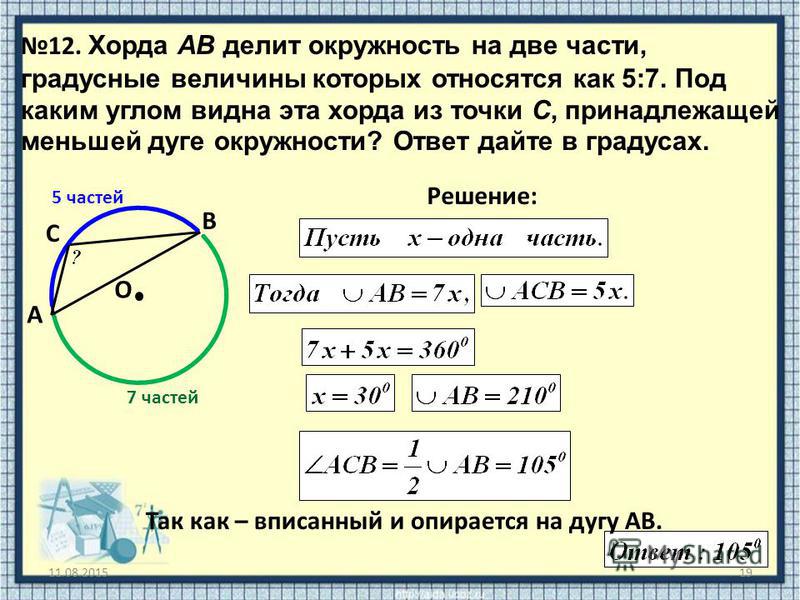
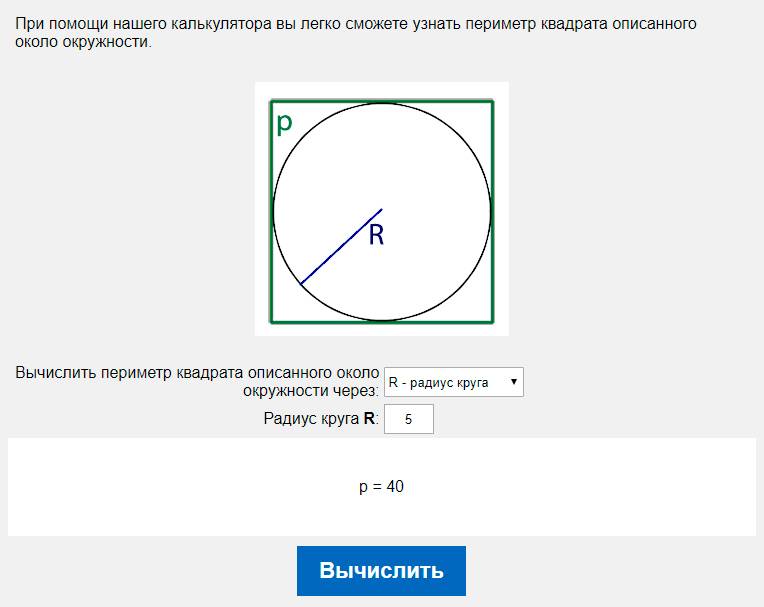 Например, говорят «Огонь уничтожил все в радиусе 10 километров» или «ОН показал на карте радиус действия артиллерии»;
Например, говорят «Огонь уничтожил все в радиусе 10 километров» или «ОН показал на карте радиус действия артиллерии»;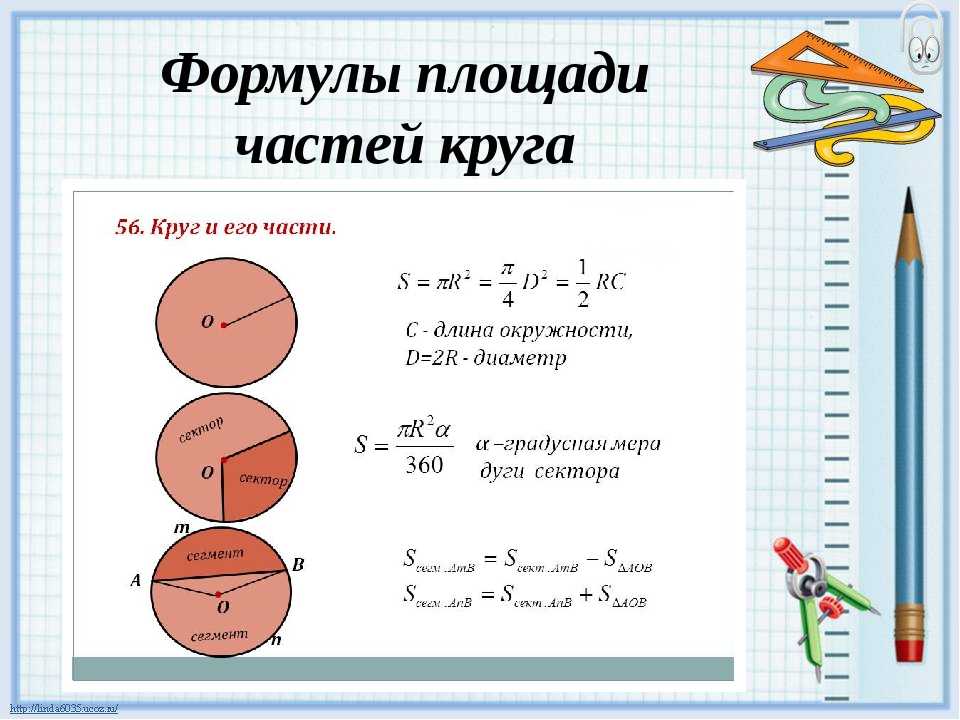
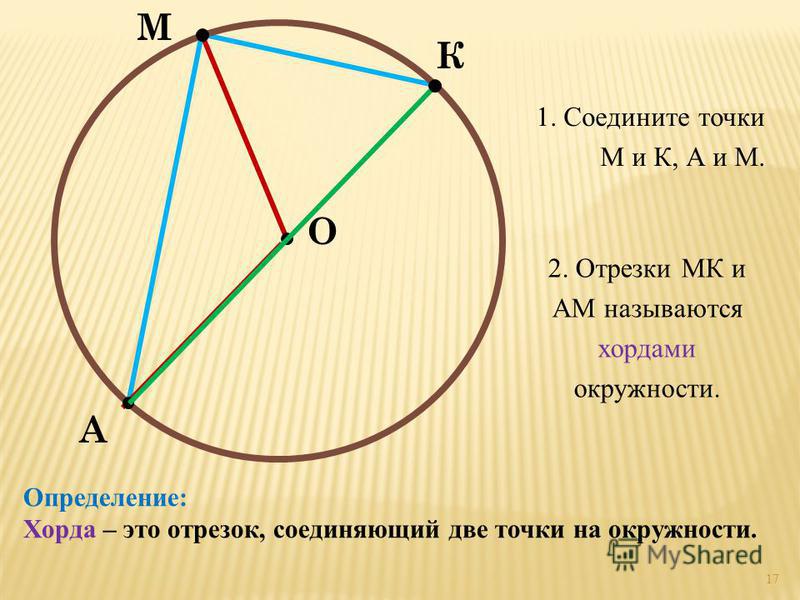 ru: главная страница / / Техническая информация/ / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица. Длина окружности диаметра D. Длина окружности через радиус (радиус=полдиаметра). Диаметр через длину окружности. Диаметр (радиус) через охват. Окружность трубы. Окружность столба.
ru: главная страница / / Техническая информация/ / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица. Длина окружности диаметра D. Длина окружности через радиус (радиус=полдиаметра). Диаметр через длину окружности. Диаметр (радиус) через охват. Окружность трубы. Окружность столба.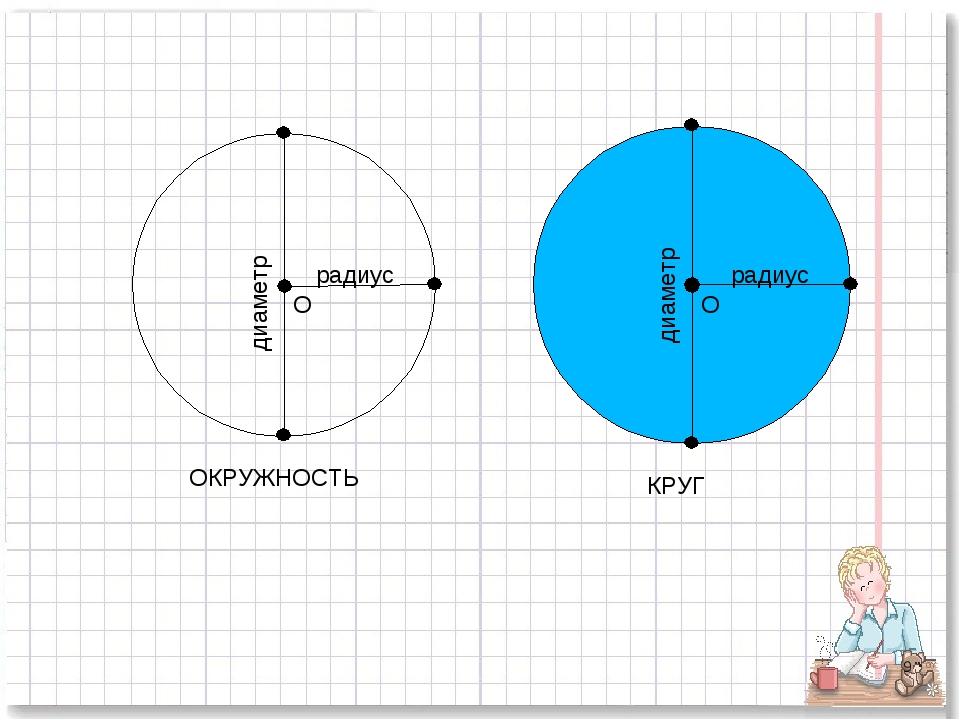 Введите свой запрос:
Введите свой запрос: Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.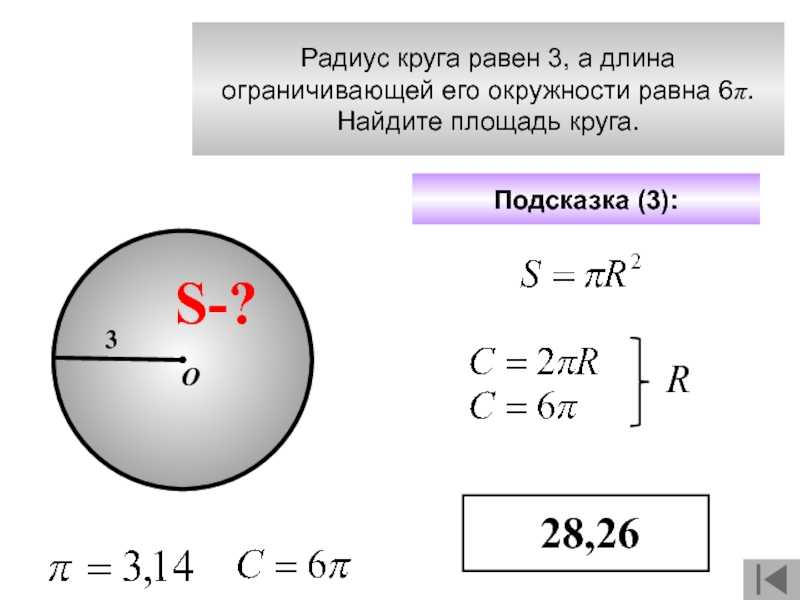
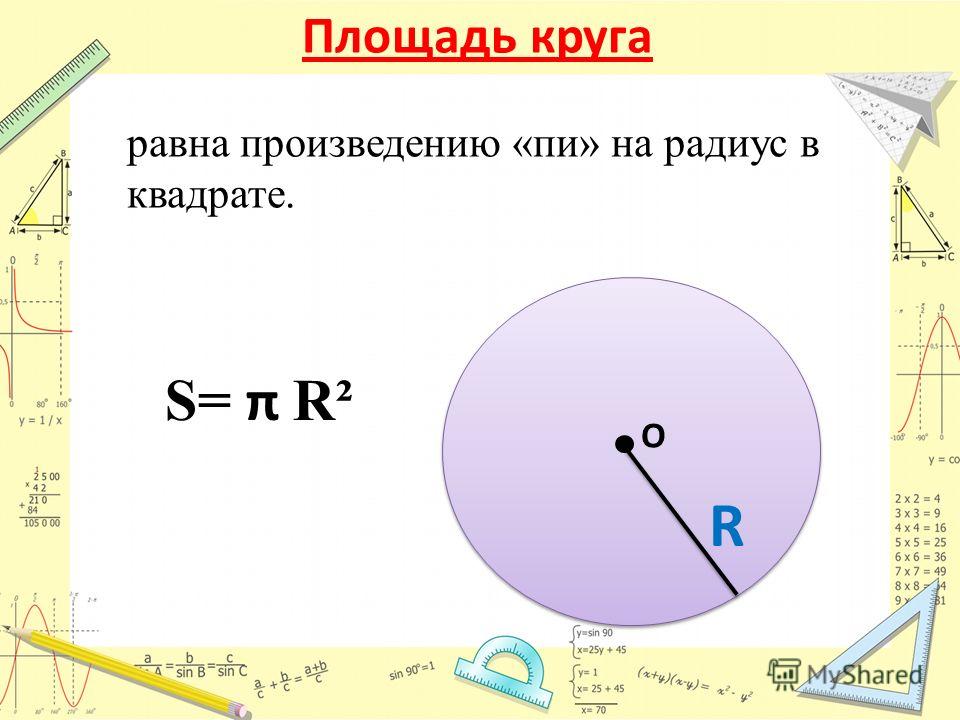 Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.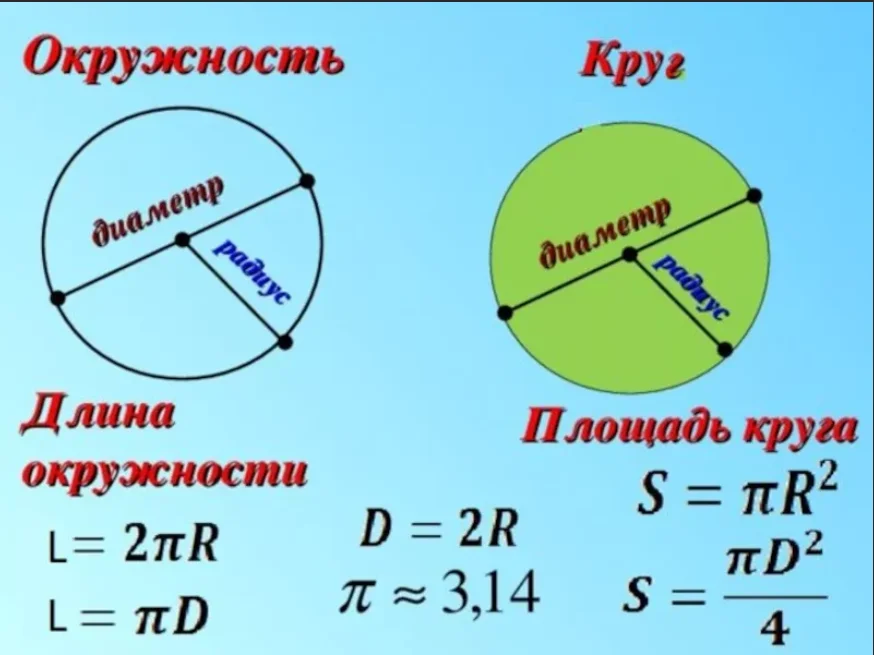
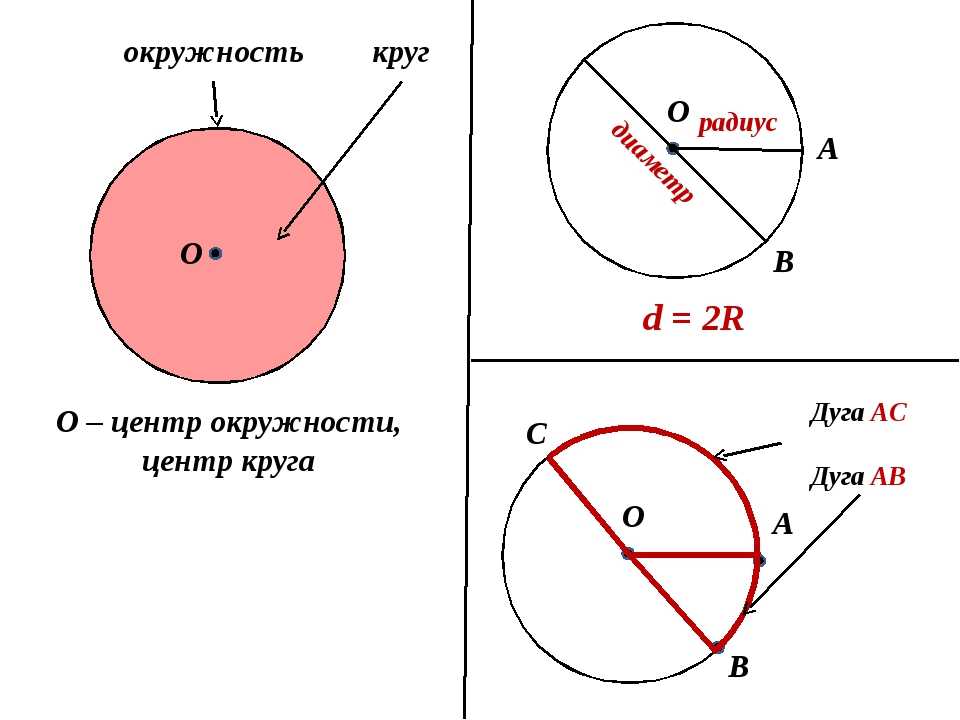

 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м. Введите в Яндексе формула длины окружности , он вам выдаст формулу расчета и окошко для ввода значения. Дальше нужно будет нажать кнопку quot;Посчитатьquot;.
Введите в Яндексе формула длины окружности , он вам выдаст формулу расчета и окошко для ввода значения. Дальше нужно будет нажать кнопку quot;Посчитатьquot;.